Adaptive Channel Estimation Based on Multidirectional Structure in Delay-Doppler Domain for Underwater Acoustic OTFS System
Abstract
1. Introduction
2. System Model
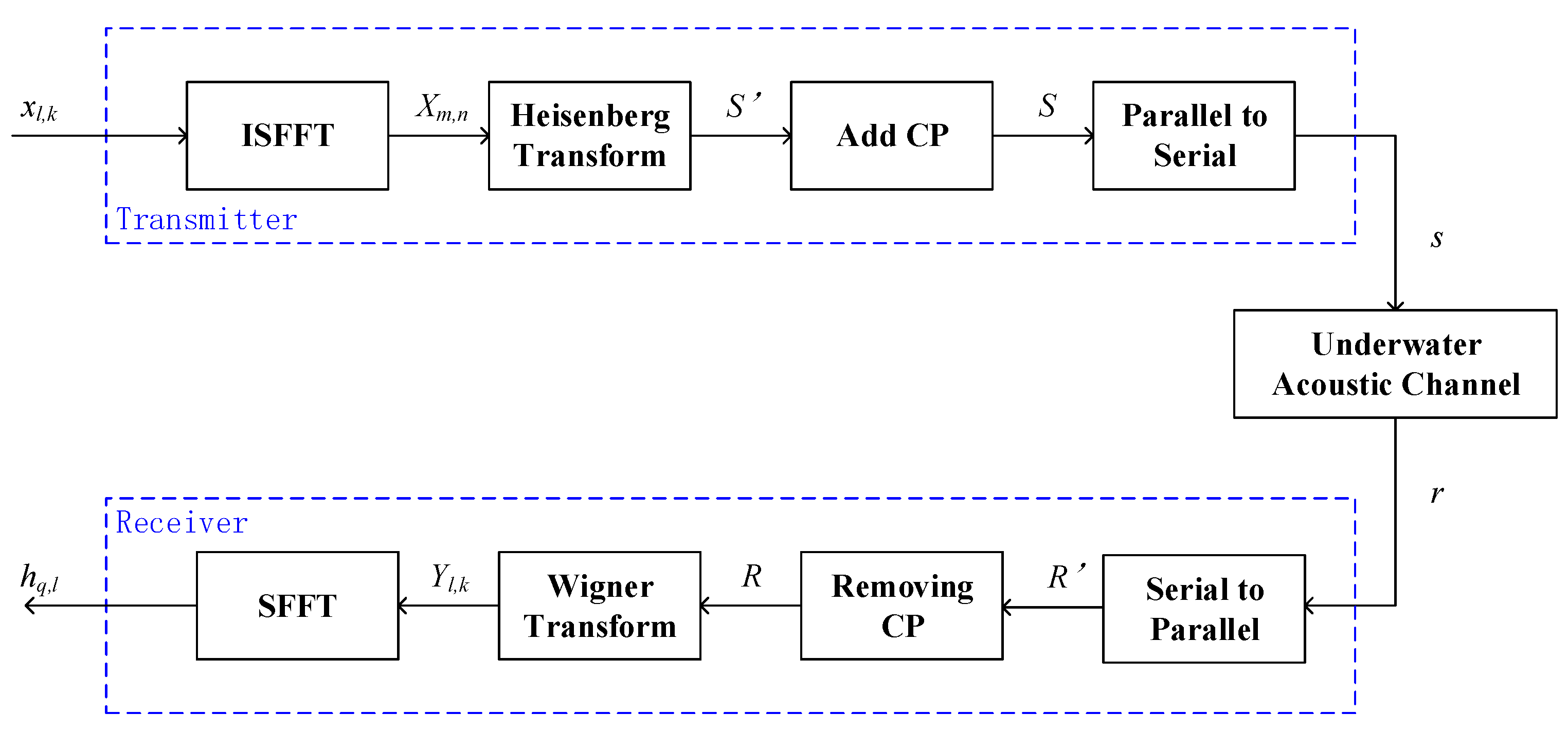
2.1. OTFS Modulation
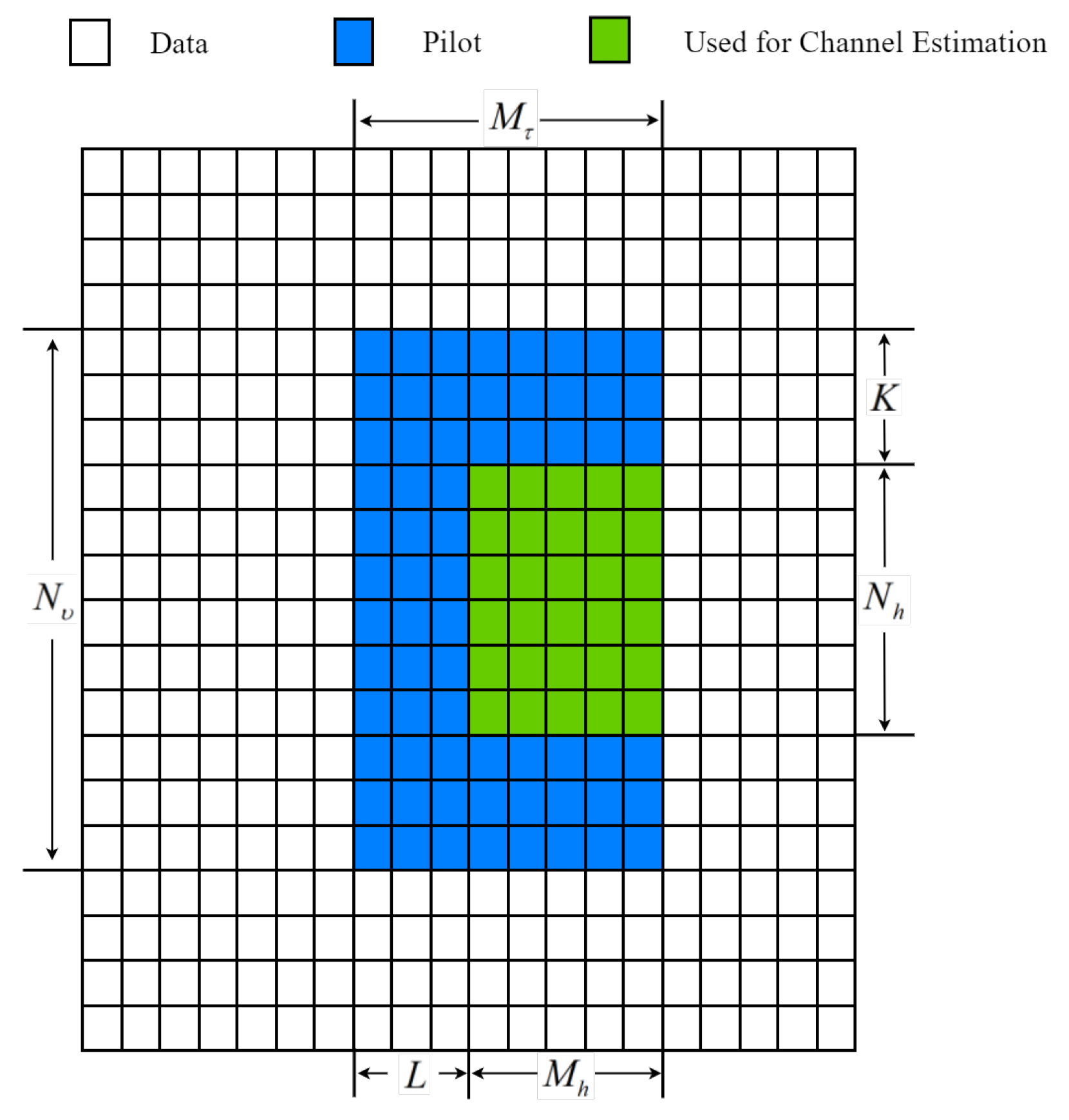
2.2. Adaptive Channel Estimation
| Algorithm 1: Pseudo codes of Adaptive channel estimation based on IPNLMS |
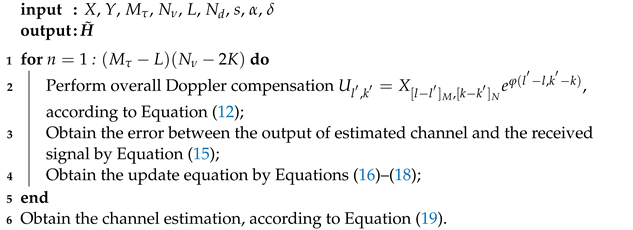 |
3. The Proposed Channel Estimation Methods
3.1. Denoising Method 1
3.2. Denoising Method 2
3.3. Denoising Method 3
| Algorithm 2: Pseudocodes of IPNLMS-MA-MuD |
 |
3.4. Computation Complexity Analysis
4. Simulation and Lake Experiment Results
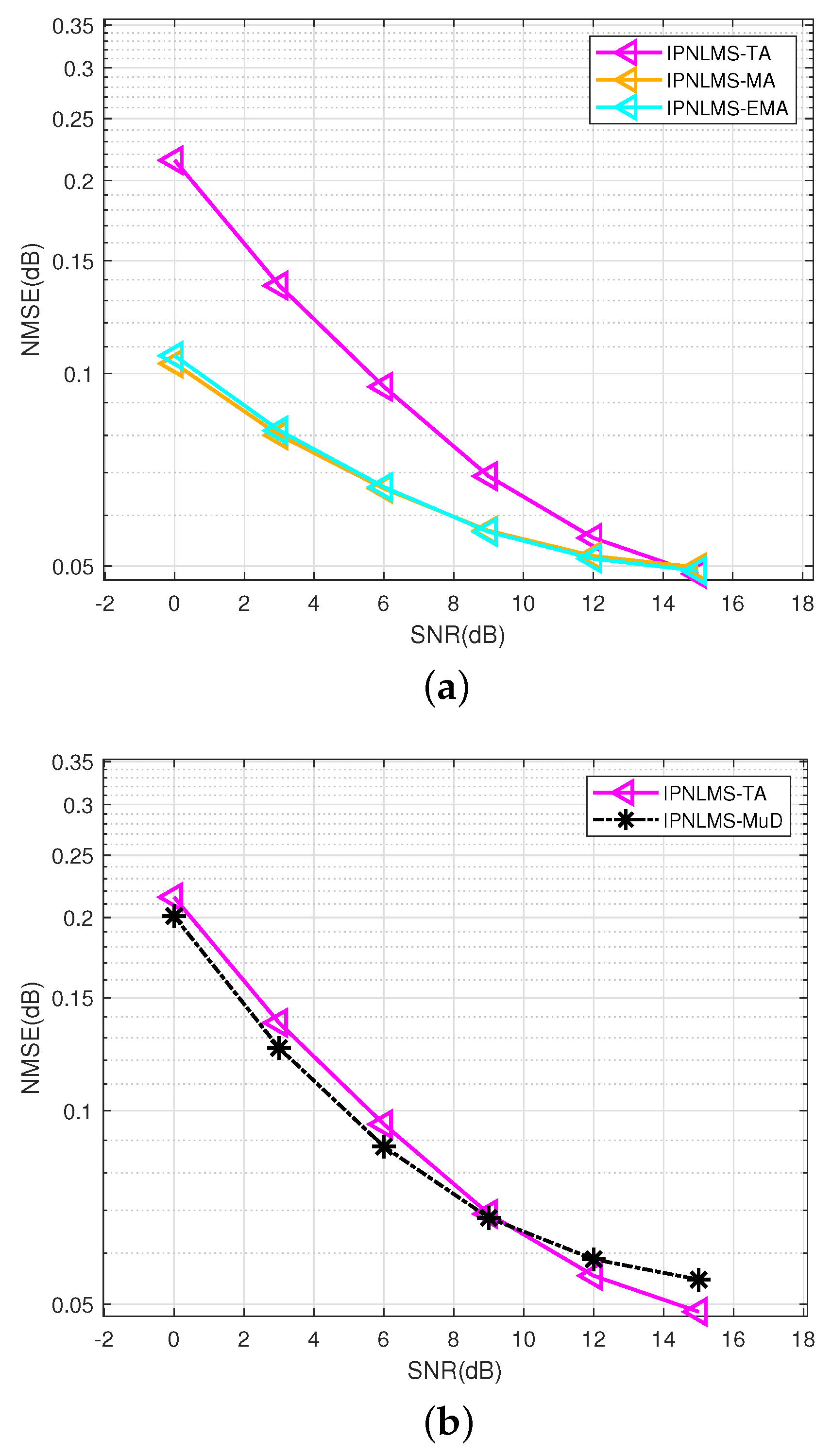
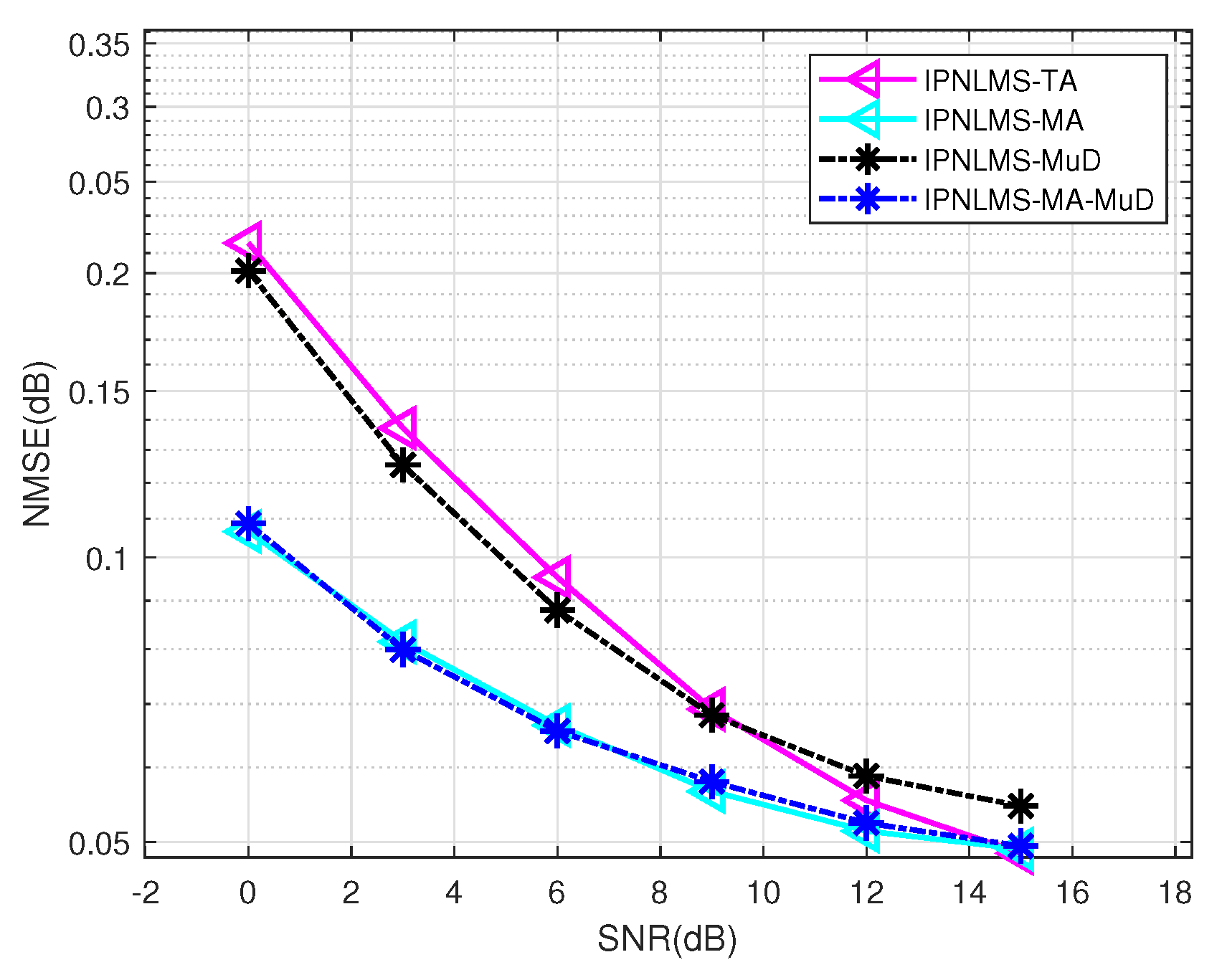
4.1. Results of Simulations
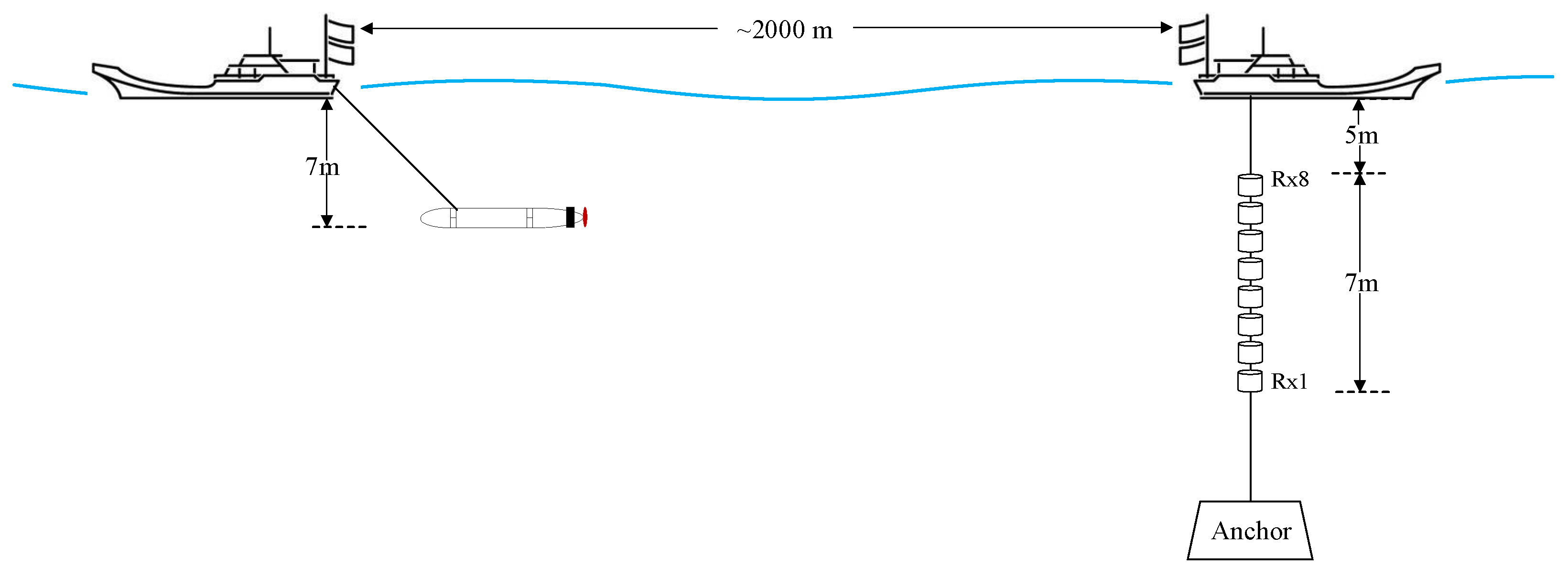
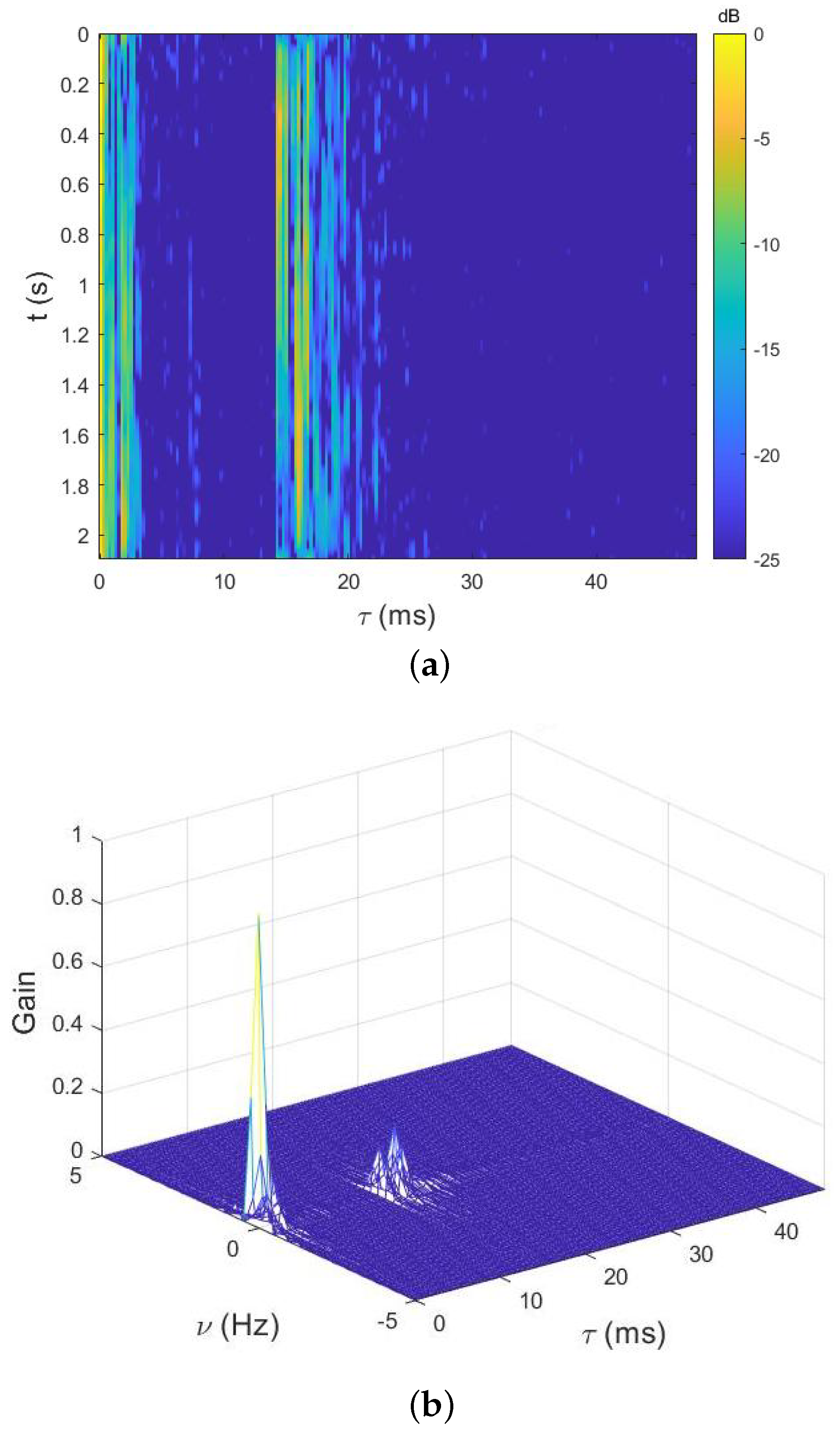
4.2. Results of Lake Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UWA | time-varying underwater acoustic |
| UAC | underwater acoustic communication |
| DD | delay-Doppler |
| OTFS | orthogonal time frequency space |
| IPNLMS | improving proportionate normalized least mean squares |
| OFDM | orthogonal frequency division multiplexing |
| IDI | inter-Doppler interference |
| OMP | orthogonal matching pursuit |
| BER | bit error rate |
| MSP | modified subspace pursuit |
| TCHTP | two-choice hard thresholding pursuit |
| MU | Multi-User |
| TF | time–frequency |
| CS | compressed sensing |
| ISFFT | inverse symplectic finite Fourier transform |
| FFT | fast Fourier transform |
| IFFT | inverse finite Fourier transform |
| CP | cyclic prefix |
| NLMS | normalized least mean square |
| PNLMS | proportionate normalized least mean square |
| MA | moving average |
| EMA | exponential moving average |
| DFE | decision feedback equalization |
| SNR | signal noise ratios |
| NMSE | normalized mean square error |
| SISO | single-input single-output |
| UWA CIRs | underwater acoustic channel impulse responses |
References
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Jing, L.; Zheng, T.; He, C.; Long, C.; Liu, X.; Yin, H. Frequency domain direct adaptive turbo equalization based on block least mean square for underwater acoustic communications. Appl. Acoust. 2022, 190, 108631. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J.; Zheng, Y.R. Frequency-domain turbo equalization with iterative channel estimation for mimo underwater acoustic communications. IEEE J. Ocean. Eng. 2017, 42, 711–721. [Google Scholar] [CrossRef]
- Qu, F.; Nie, X.; Xu, W. A two-stage approach for the estimation of doubly spread acoustic channels. IEEE J. Ocean. Eng. 2015, 40, 131–143. [Google Scholar] [CrossRef]
- Li, B.; Huang, J.; Zhou, S.; Ball, K.; Stojanovic, M.; Freitag, L.; Willett, P. MIMO-OFDM for High-Rate Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2009, 34, 634–644. [Google Scholar]
- Zhang, Y.; Li, J.; Zakharov, Y.; Li, X.; Li, J. Deep learning based underwater acoustic OFDM communications. Appl. Acoust. 2019, 154, 53–58. [Google Scholar] [CrossRef]
- Qiao, G.; Song, Q.; Ma, L.; Wan, L. A low-complexity orthogonal matching pursuit based channel estimation method for time-varying underwater acoustic OFDM systems. Appl. Acoust. 2019, 148, 246–250. [Google Scholar] [CrossRef]
- Ma, L.; Li, T.; Liu, S.; Qiao, G.; Jia, H. Efficient interpolation based omp for sparse channel estimation in underwater acoustic OFDM. Appl. Acoust. 2021, 172, 107606. [Google Scholar] [CrossRef]
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.J.; Molisch, A.F.; Calderbank, R. Orthogonal time frequency space modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference, San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Farhang, A.; RezazadehReyhani, A.; Doyle, L.E.; Farhang-Boroujeny, B. Low complexity modem structure for OFDM-based orthogonal time frequency space modulation. IEEE Wirel. Commun. Lett. 2018, 7, 344–347. [Google Scholar] [CrossRef]
- Raviteja, R.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference cancellation and iterative detection for orthogonal time frequency space modulation. IEEE Trans. Wirel. Commun. 2018, 17, 5605–5615. [Google Scholar] [CrossRef]
- Murali, K.R.; Chockalingam, A. On OTFS modulation for high-doppler fading channels. In Proceedings of the 2018 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 11–16 February 2018; pp. 1–10. [Google Scholar]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Ng, D.W.K. Transmitter and receiver window designs for orthogonal time frequency space modulation. IEEE Trans. Commun. 2021, 69, 2207–2223. [Google Scholar] [CrossRef]
- Jing, L.; Wang, H.; He, C.; Zhang, Y.; Yin, H. Two dimensional adaptive multichannel decision feedback equalization for OTFS system. IEEE Commun. Lett. 2021, 25, 840–844. [Google Scholar] [CrossRef]
- Tiwari, S.; Das, S.S.; Rangamgari, V. Low complexity LMMSE Receiver for OTFS. IEEE Commun. Lett. 2019, 23, 2205–2209. [Google Scholar] [CrossRef]
- Long, F.; Niu, K.; Dong, C.; Lin, J. Low Complexity Iterative LMMSE-PIC Equalizer for OTFS. In Proceedings of the 2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Kollengode Ramachandran, M.; Chockalingam, A. Mimo-otfs in high-doppler fading channels: Signal detection and channel estimation. In Proceedings of the 2018 IEEE Global Communications Conference, Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 206–212. [Google Scholar]
- Raviteja, R.; Phan, K.T.; Hong, Y. Embedded pilot-aided channel estimation for OTFS in delay-doppler channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Shi, D.; Wang, W.; You, L.; Song, X.; Hong, Y.; Gao, X.; Fettweis, G. Deterministic Pilot Design and Channel Estimation for Downlink Massive MIMO-OTFS Systems in Presence of the Fractional Doppler. IEEE Trans. Wirel. Commun. 2021, 20, 7151–7165. [Google Scholar] [CrossRef]
- Long, F.; Niu, K.; Lin, J. Joint Channel Estimation and Equalization for OTFS Based on EP. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Shen, W.; Dai, L.; An, J.; Fan, P.; Heath, R.W. Channel estimation for orthogonal time frequency space (OTFS) massive MIMO. IEEE Trans. Signal Process. 2019, 67, 2402–2417. [Google Scholar] [CrossRef]
- Rasheed, O.K.; Surabhi, G.; Chockalingam, A. Sparse delay-Doppler channel estimation in rapidly time-varying channels for mul-tiuser OTFS on the uplink. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Kumari, S.; Dikkala, M.K.; Mukhopadhyay, S.; Mishra, H.B. Two Choice Hard Thresholding Pursuit (TCHTP) for Delay-Doppler Channel Estimation in OTFS. IEEE Wirel. Commun. Lett. 2023, 12, 1032–1036. [Google Scholar] [CrossRef]
- Kumari, S.; Mishra, H.B.; Mukhopadhyay, S. Greedy Sparse Channel Estimation Framework for Multi-User OTFS Systems. In Proceedings of the 2024 National Conference on Communications (NCC), Chennai, India, 28 February–2 March 2024; pp. 1–6. [Google Scholar]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Ng, D.W.K. Performance Analysis and Window Design for Channel Estimation of OTFS Modulation. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–18 June 2021; pp. 1–7. [Google Scholar]
- Zhao, L.; Gao, W.; Guo, W. Sparse bayesian learning of delay-doppler channel for OTFS system. IEEE Commun. Lett. 2020, 24, 2766–2769. [Google Scholar] [CrossRef]
- Hang, S.; Li, W. OTFS for Underwater Acoustic Communications: Practical System Design and Channel Estimation. In Proceedings of the OCEANS 2022, Hampton Roads, VA, USA, 17–20 October 2022; pp. 1–7. [Google Scholar]
- Hebron, Y.; Rakib, S.S.; Hadani, R.; Tsatsanis, M. Channel Acquisition Using Orthogonal Time Frequency Space Modulated Pilot Signal. U.S. Patent 10 749 651 B2, 18 August 2020. [Google Scholar]
- Das, S.S.; Rangamgari, V.; Tiwari, S.; Mondal, S.C. Time Domain Channel Estimation and Equalization of CP-OTFS Under Multiple Fractional Dopplers and Residual Synchronization Errors. IEEE Access 2021, 9, 10561–10576. [Google Scholar] [CrossRef]
- Qin, F.; Ji, Y.; Sun, X.; Wei, Z. Research on Frequency Domain Channel Estimation Method Based on OTFS System. In Proceedings of the 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 4–6 March 2022; pp. 973–978. [Google Scholar]
- Pfadler, A.; Szollmann, T.; Jung, P.; Stanczak, S. Leakage Suppression in Pulse-Shaped OTFS Delay-Doppler-Pilot Channel Estimation. IEEE Wirel. Commun. Lett. 2022, 11, 1181–1185. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Gómez-Cuba, F. Compressed Sensing Channel Estimation for OTFS Modulation in Non-Integer Delay-Doppler Domain. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Luo, K.; Deng, Z.; Guo, X. Compressed Sensing-Based Channel Estimation for OTFS in Continuous Delay-Doppler Domain. In Proceedings of the 2023 IEEE 11th International Conference on Computer Science and Network Technology (ICCSNT), Dalian, China, 21–22 October 2023; pp. 43–47. [Google Scholar]
- Yang, C.; Wang, J.; Pan, Z.; Shimamoto, S. Delay-Doppler Frequency Domain-Aided Superimposing Pilot OTFS Channel Estimation Based on Deep Learning. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022; pp. 1–6. [Google Scholar]
- Zhang, X.; Yuan, W.; Liu, C.; Liu, F.; Wen, M. Deep Learning with a Self-Adaptive Threshold for OTFS Channel Estimation. In Proceedings of the 2022 International Symposium on Wireless Communication Systems (ISWCS), Hangzhou, China, 19–22 October 2022; pp. 1–5. [Google Scholar]
- Li, Q.; Gong, Y.; Meng, F.; Han, L.; Xu, Z. A novel Channel Estimation Method based on Deep Neural Network for OTFS system. In Proceedings of the 2022 15th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Beijing, China, 5–7 November 2022; pp. 1–6. [Google Scholar]
- Suárez, L.M.-M.; Chen-Hu, K.; García, M.J.F.-G.; Armada, A.G. Deep Learning-aided Robust Integrated Sensing and Communications with OTFS and Superimposed Training. In Proceedings of the 2023 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Dubrovnik, Croatia, 4–7 September 2023; pp. 1–6. [Google Scholar]
- Zhang, X.; Huang, H.; Tan, L.; Yuan, W.; Liu, C. Enhanced Channel Estimation for OTFS-Assisted ISAC in Vehicular Networks: A Deep Learning Approach. In Proceedings of the 2023 21st International Symposium on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks (WiOpt), Singapore, 24–27 August 2023; pp. 703–707. [Google Scholar]
- Hu, J.; Bai, Z.; Yang, J.; Cai, Y.; Zhou, D.; Wang, Y.; Kwak, K. DNN and LS Based Channel Estimation in OTFS System. In Proceedings of the 2023 IEEE 23rd International Conference on Communication Technology (ICCT), Wuxi, China, 20–22 October 2023; pp. 106–110. [Google Scholar]
- Benesty, J.; Gay, S.L. An improved PNLMS algorithm. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; pp. II-1881–II-1884. [Google Scholar]
- Pelekanakis, K.; Chitre, M. New Sparse Adaptive Algorithms Based on the Natural Gradient and the L0-Norm. IEEE J. Ocean. Eng. 2012, 38, 323–332. [Google Scholar] [CrossRef]
- Qarabaqi, P.; Stojanovic, M. Statistical characterization and computationally efficient modeling of a class of underwater acoustic communication channels. IEEE J. Ocean. Eng. 2013, 38, 701–717. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Water Depth | 500 (m) |
| Height of Transmitter | 200 (m) |
| Height of Receiver | 200 (m) |
| Distance between Transmitter to Receiver | 1000 (m) |
| Underwater Sound Velocity | 1500 (m/s) |
| Center Frequency | 14.5 (kHz) |
| Bandwidth B | 5 (kHz) |
| Vessel Speed | 0 (m/s) |
| Spreading Factor | 1.7 |
| Parameter | Value |
|---|---|
| M | 64 |
| N | 32 |
| Bandwidth B | 5 (kHz) |
| Subcarrier Interval | 78.1 (Hz) |
| Symbol Interval | 0.2 (ms) |
| Modulation Type | QPSK |
| 32 | |
| 32 |
| Parameter | Value |
|---|---|
| 0.5 | |
| 0.9 | |
| 0.1 | |
| 0.01 | |
| 0.01 | |
| 500 |
| Number of Frame | IPNLMS-TA | IPNLMS-MA-MuD 1 |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 0 | 0 |
| 7 | 0 | 0 |
| 8 | 6.73% | 0 |
| 9 | 0 | 0 |
| 10 | 0 | 0 |
| 11 | 0 | 0 |
| 12 | 0 | 0 |
| 13 | 1.83% | 0 |
| 14 | 2.51% | 0 |
| 15 | 10.44% | 7.29% |
| 16 | 0 | 0 |
| Average | 1.34% | 0.46% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Jin, M.; Jing, L.; Tu, N.; He, C. Adaptive Channel Estimation Based on Multidirectional Structure in Delay-Doppler Domain for Underwater Acoustic OTFS System. Remote Sens. 2024, 16, 3157. https://doi.org/10.3390/rs16173157
Shi W, Jin M, Jing L, Tu N, He C. Adaptive Channel Estimation Based on Multidirectional Structure in Delay-Doppler Domain for Underwater Acoustic OTFS System. Remote Sensing. 2024; 16(17):3157. https://doi.org/10.3390/rs16173157
Chicago/Turabian StyleShi, Wentao, Mingqi Jin, Lianyou Jing, Nan Tu, and Chengbing He. 2024. "Adaptive Channel Estimation Based on Multidirectional Structure in Delay-Doppler Domain for Underwater Acoustic OTFS System" Remote Sensing 16, no. 17: 3157. https://doi.org/10.3390/rs16173157
APA StyleShi, W., Jin, M., Jing, L., Tu, N., & He, C. (2024). Adaptive Channel Estimation Based on Multidirectional Structure in Delay-Doppler Domain for Underwater Acoustic OTFS System. Remote Sensing, 16(17), 3157. https://doi.org/10.3390/rs16173157








