Efficient Jamming Policy Generation Method Based on Multi-Timescale Ensemble Q-Learning
Abstract
1. Introduction
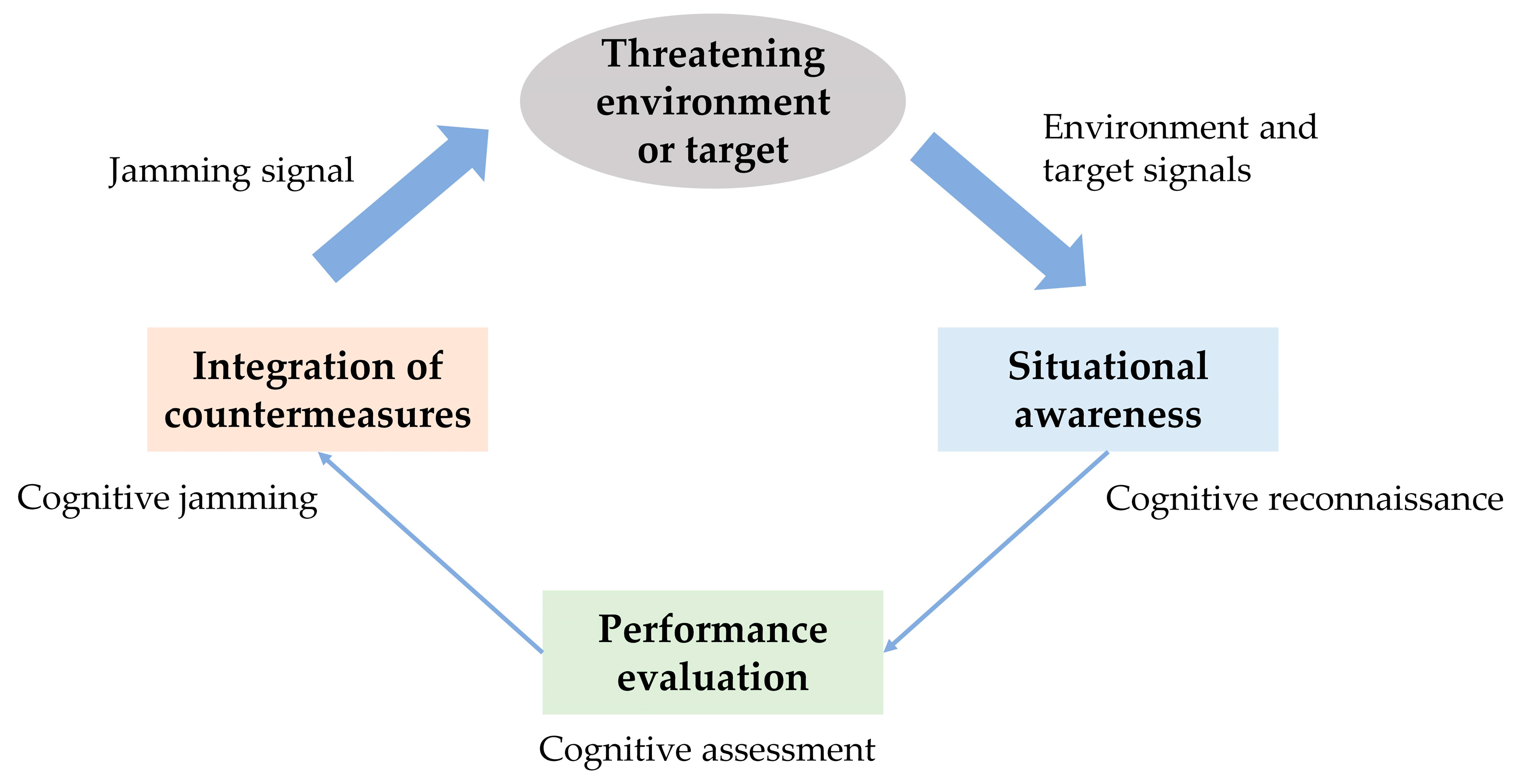
1.1. Cognitive Radar Countermeasure Process
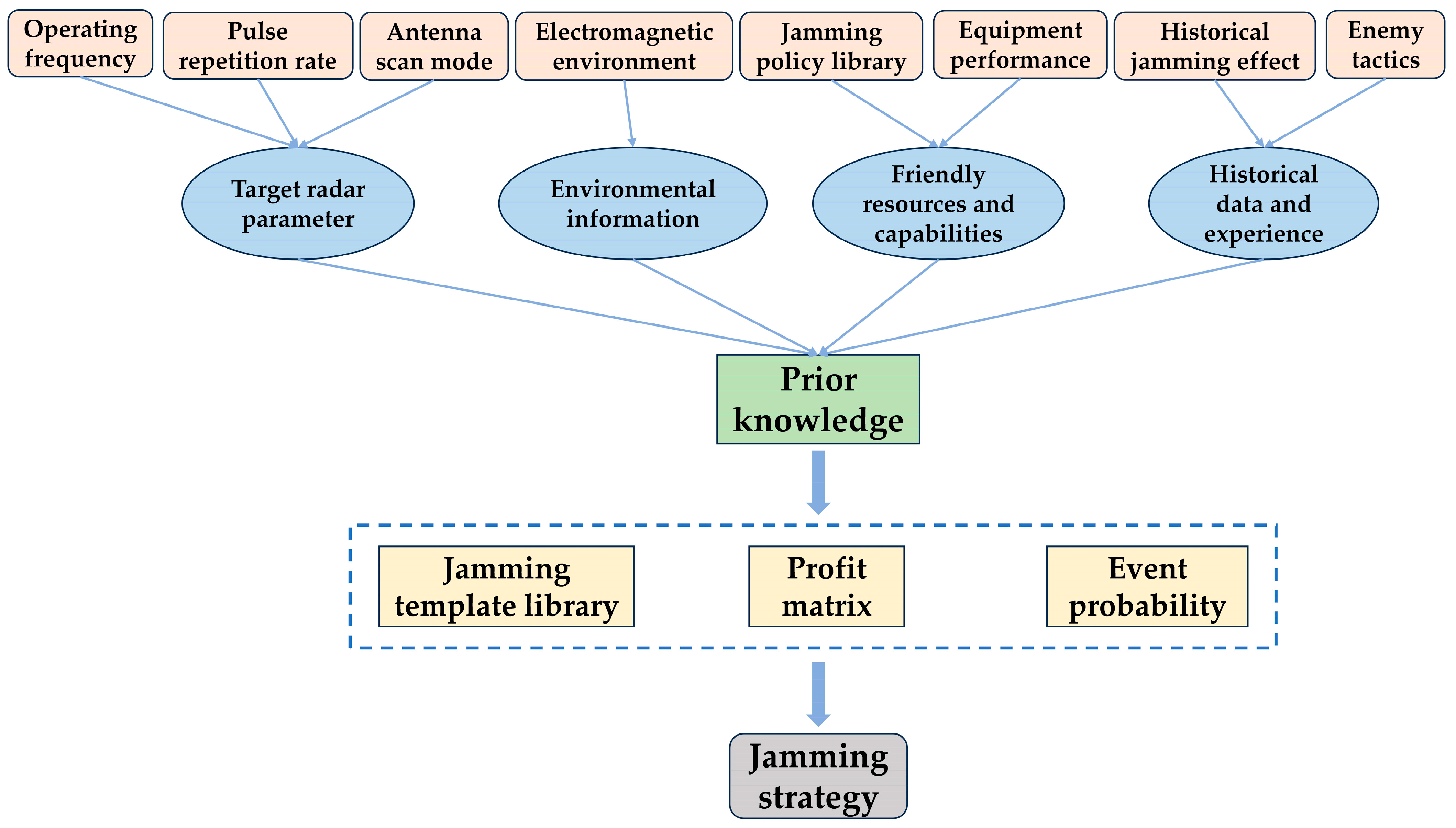
1.2. Traditional Jamming Strategy Generation Methods
1.3. Jamming Strategy Generation Methods Based on Reinforcement Learning
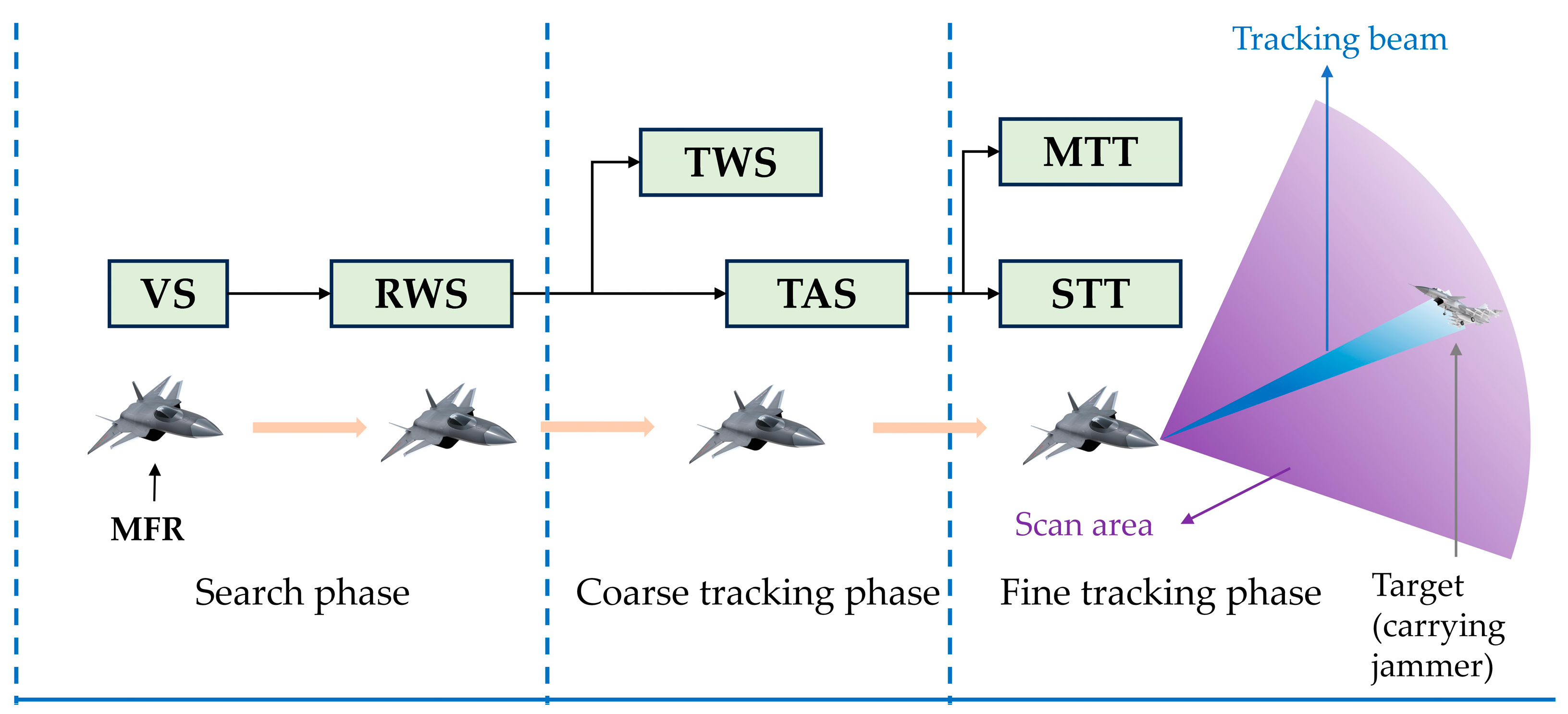
- A realistic radar countermeasure scenario was established, in which an aircraft carries a jammer for self-protection to avoid being locked by radar during mission execution. The transition modes of the MFR operating modes were analyzed, and mode-switching rules were designed for scenarios both with and without jamming.
- The problem of generating jamming strategies was modeled as a MDP, with the goal of identifying the optimal jamming strategy in the dynamic interaction between the MFR and the jammer.
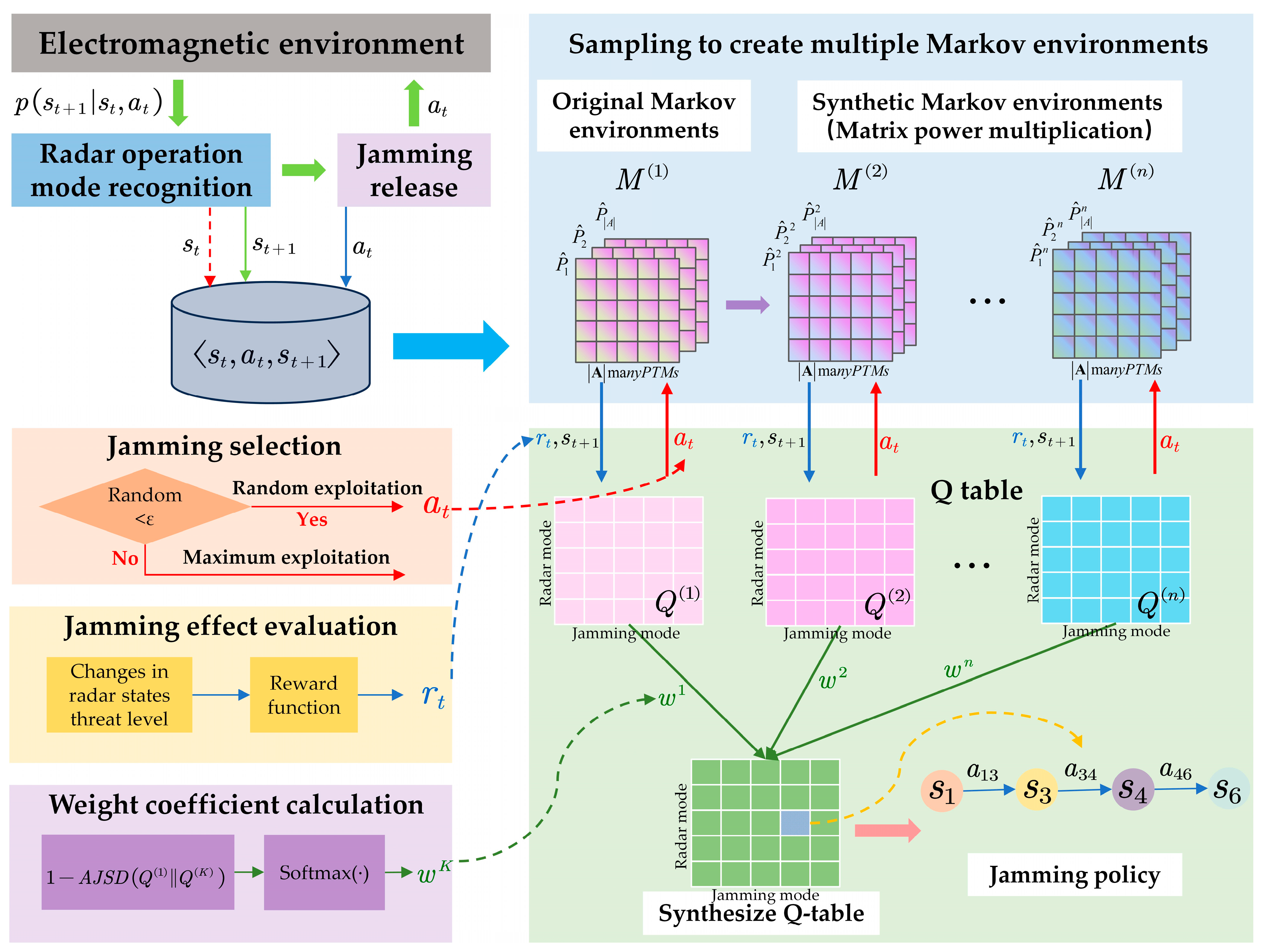
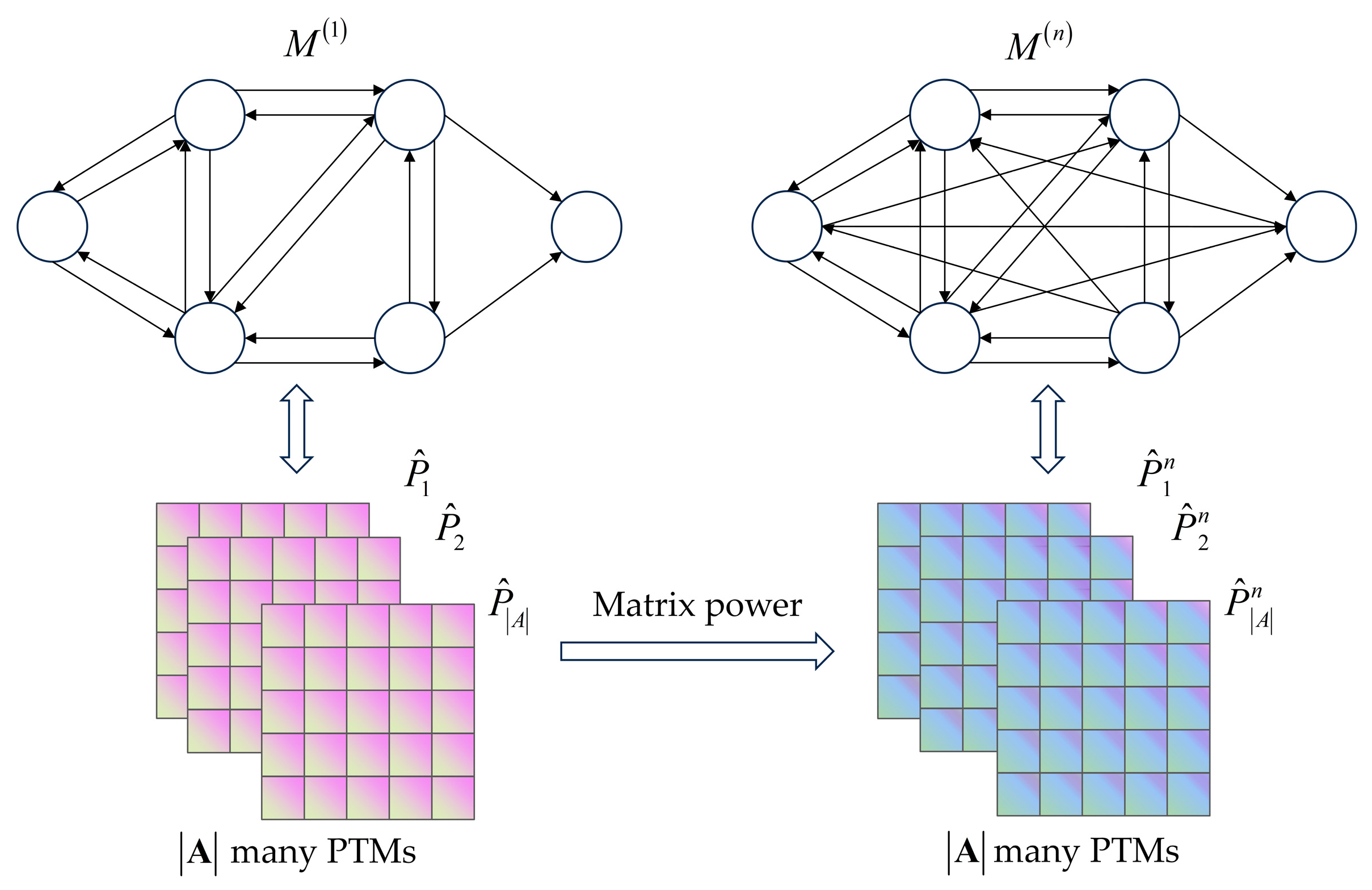
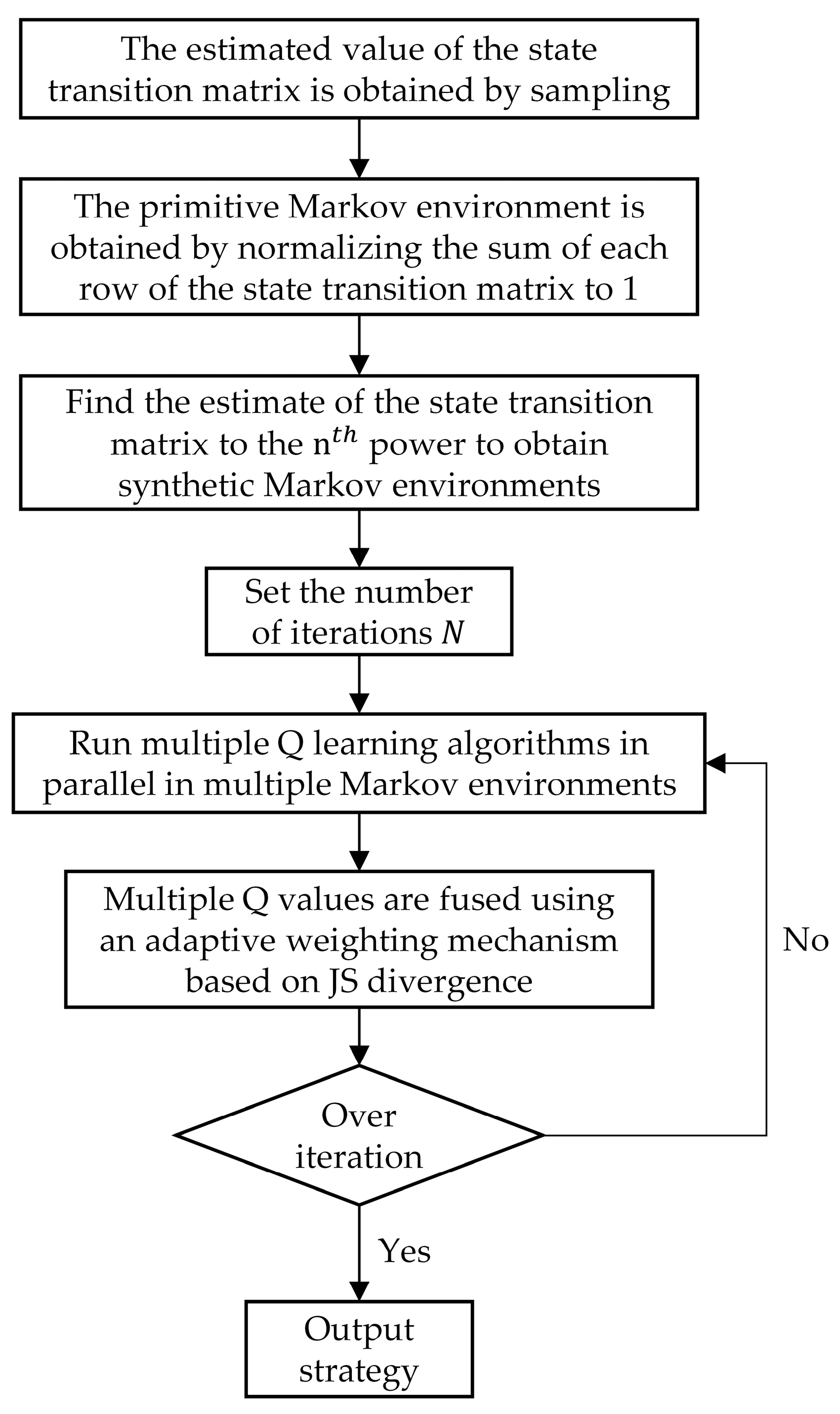
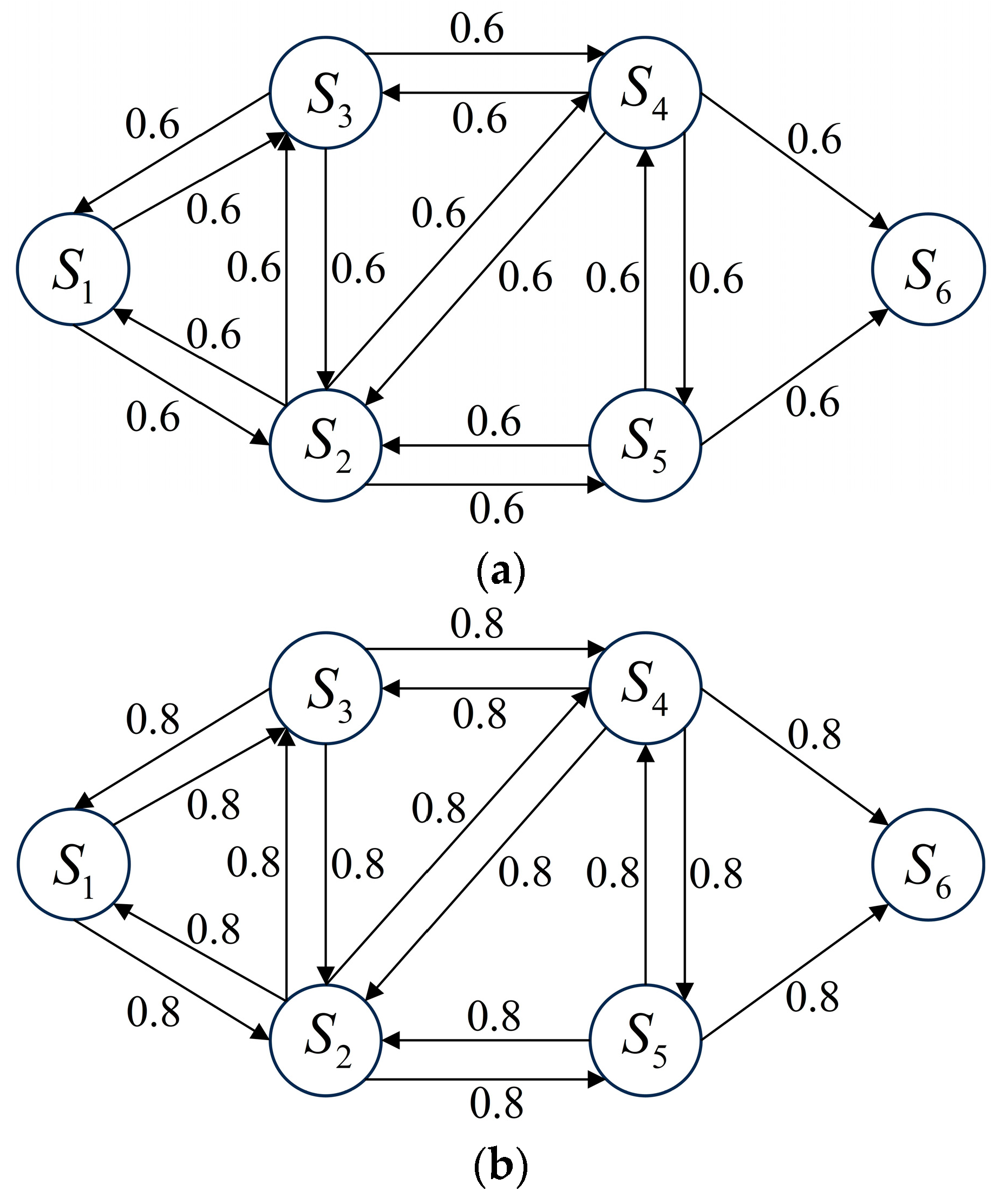
- An efficient jamming strategy generation method based on MTEQL was proposed. First, the adversarial process between the radar and the jammer was sampled to construct multiple structurally related Markov environments. The Q-learning algorithm was then run in parallel across these environments. A JSD-based adaptive weighting mechanism was employed to combine the multiple output Q-values, ultimately obtaining the optimal jamming strategy.
- Numerical simulations and experimental investigations were carried out to demonstrate the effectiveness of the proposed method. Results highlighted that the proposed method achieved faster jamming strategy generation and higher decision accuracy.
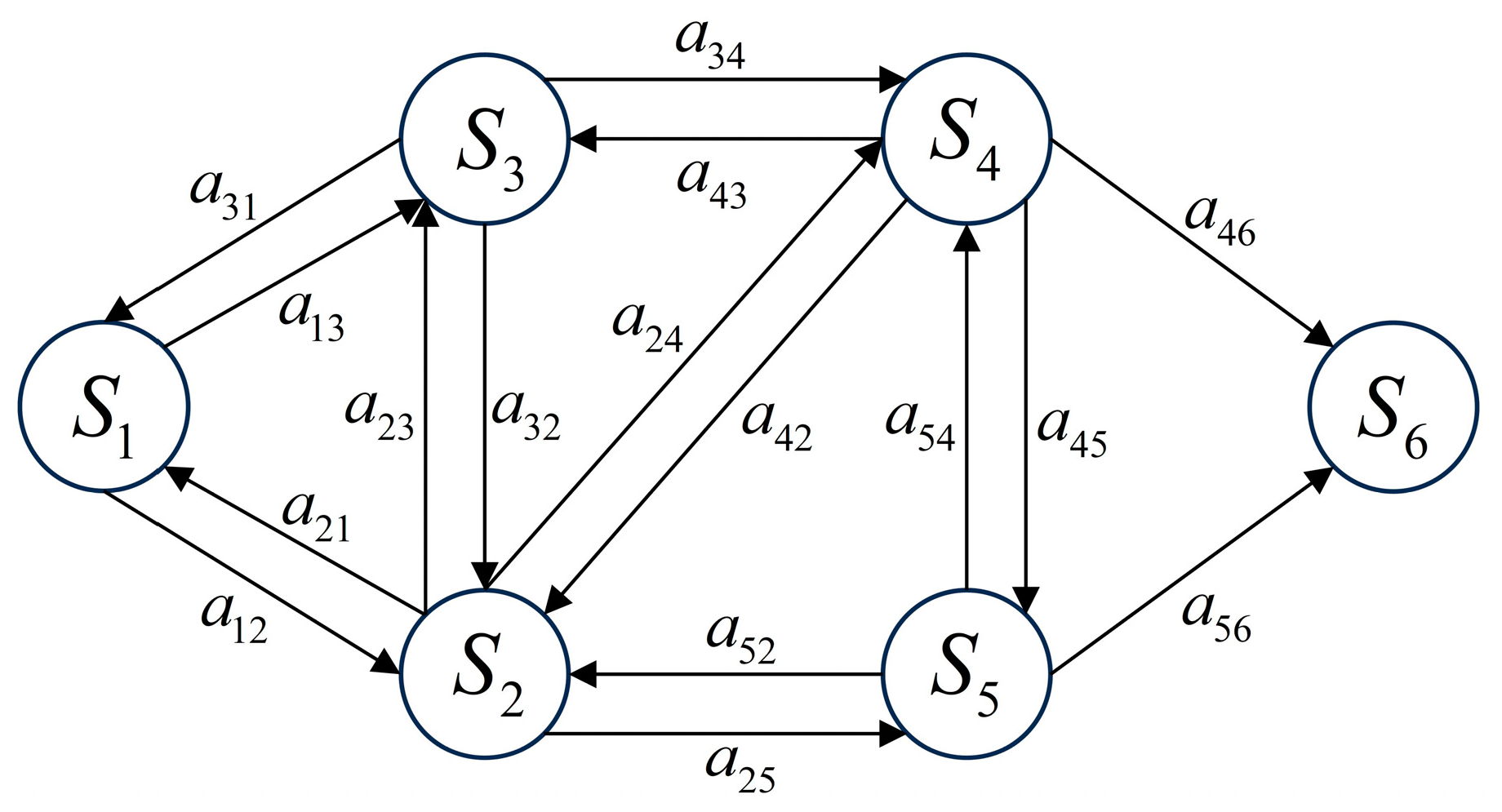
2. Radar Countermeasure Scenario Design and Problem Modeling
2.1. Radar Countermeasure Scenario Design
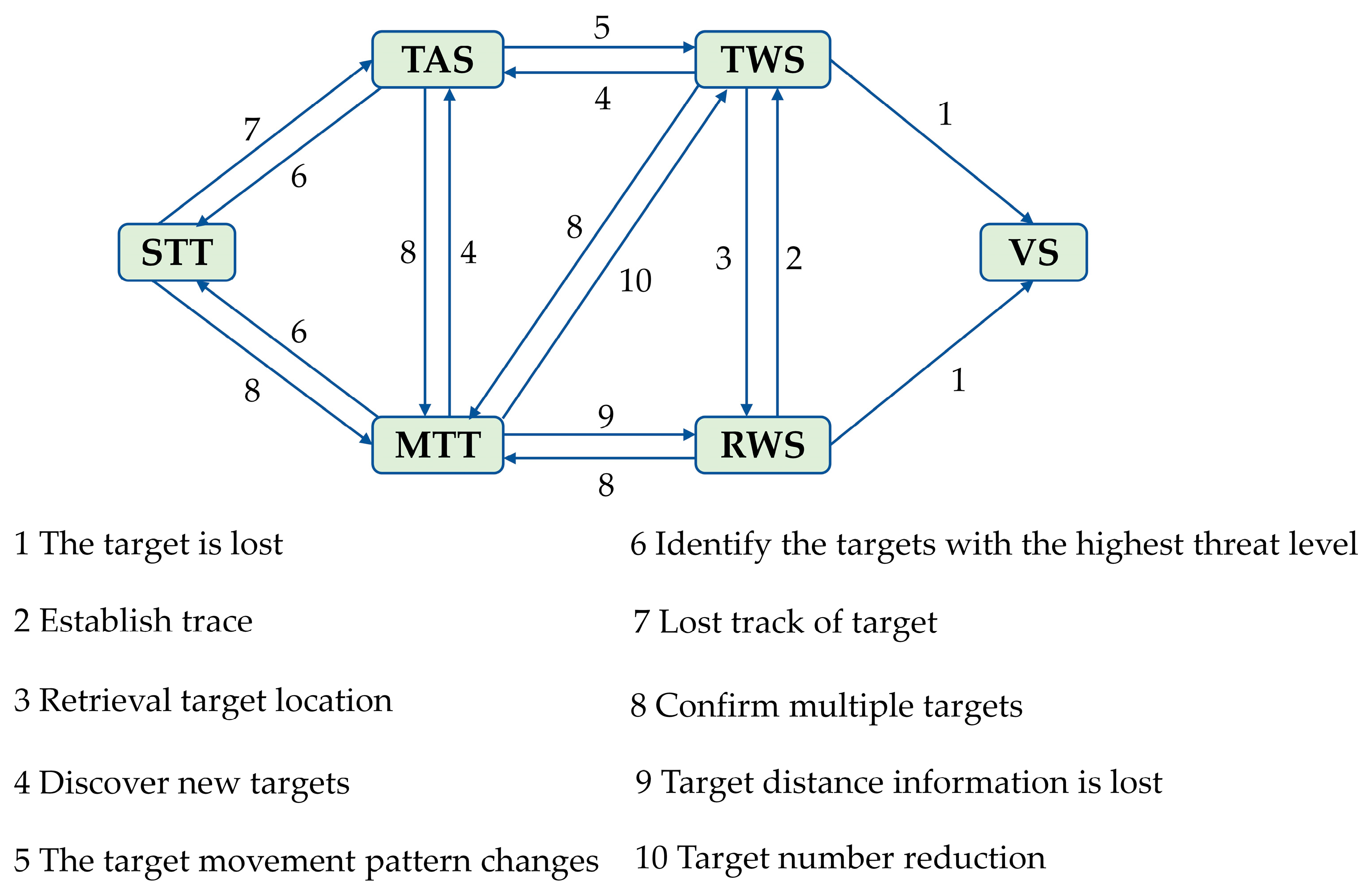
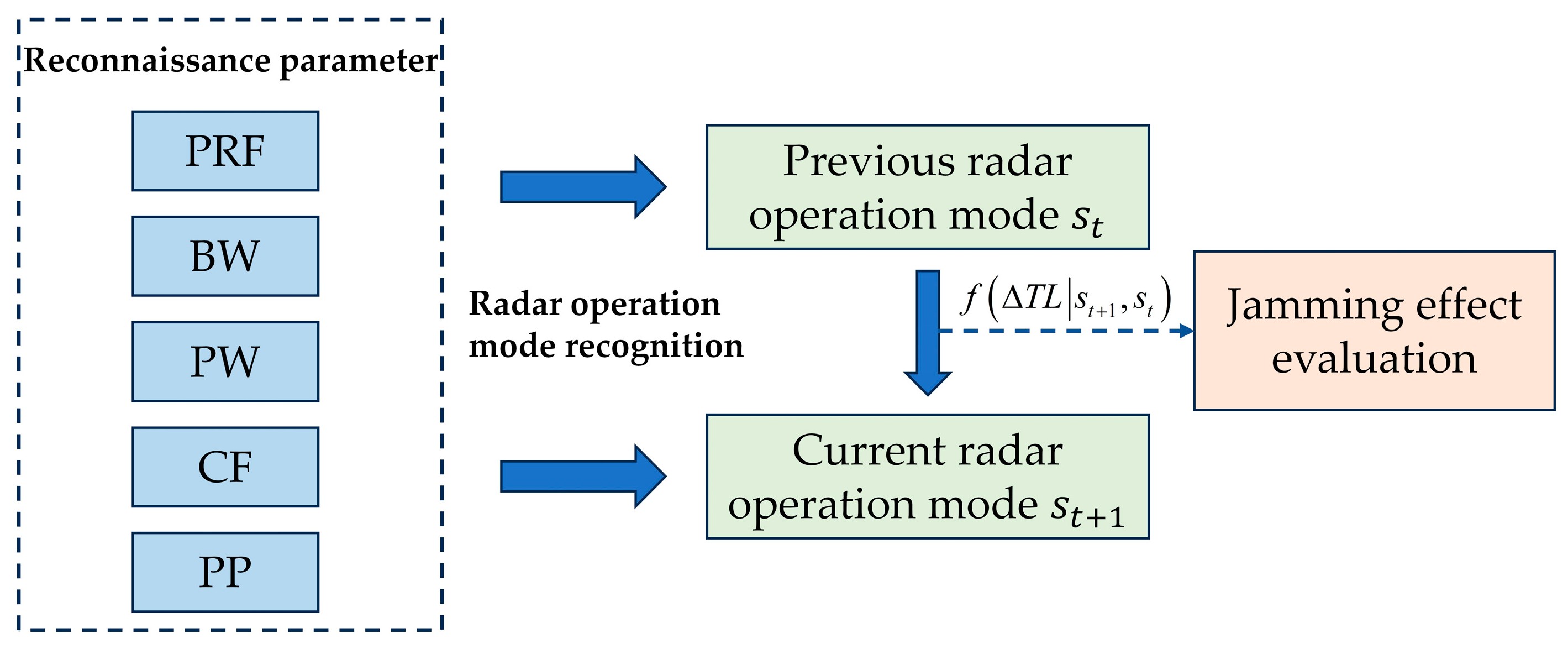
2.2. Radar Operation Mode Modeling
2.3. Problem Modeling
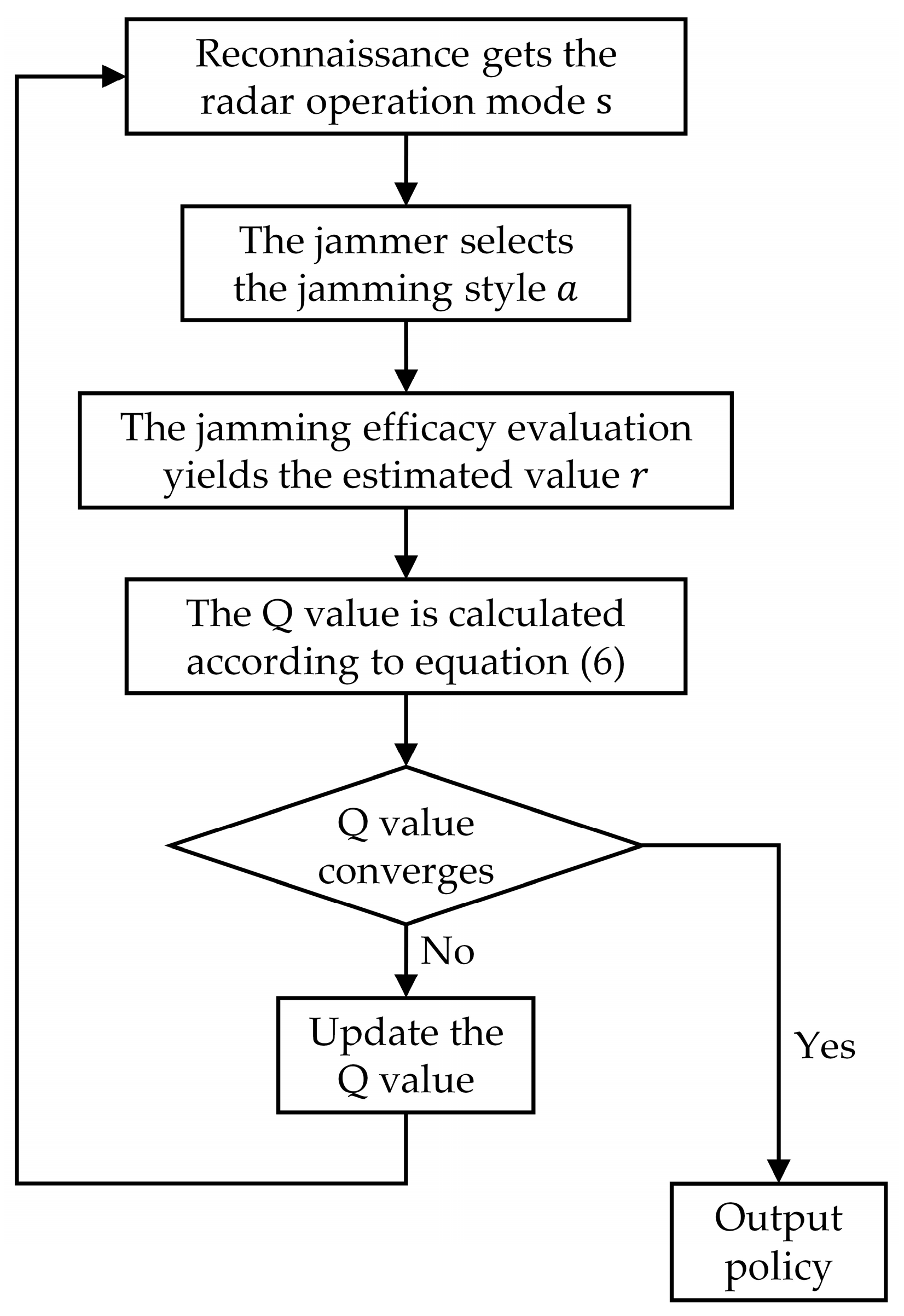
3. Jamming Policy Generation Method Based on MTEQL
| Algorithm 1 The pseudocode for the jamming policy generation method based on MTEQL |
| Input: Sampling path length, , the total number of Markov environments, , minimum number of times for each state transition pair, , training episodes, , learning rate, , discount factor, , replacement rate, ut, and Q-tables for K different environments, , . |
| Output: The resultant Q-table, , and jamming policy, . |
| 01. Initialize each element of to |
| 02. while the number of samples for does not exceed times do |
| 03. Randomly select an initial radar operation mode |
| 04. repeat times |
| 05. The jammer obtains after randomly applying jamming |
| 06. |
| 07. end |
| 08. end while |
| 09. Normalize the sum of each row in to 1, and obtain through sampling |
| 10. for n = 2,3,,K do |
| 11. Compute the power of the matrix to obtain |
| 12. Use to represent the synthesized Markov environment corresponding to |
| 13. end for |
| 14. Randomly initialize the weights , , |
| 15. for episode = 1,2,, do |
| 16. for n = 1,2,,K do |
| 17. Reconnaissance obtains the initial radar operation mode |
| 18. while do |
| 19. Select the jamming pattern according to the -greedy policy |
| 20. Obtain the next radar operation mode from |
| 21. Obtain the reward based on the radar state transition |
| 22. Update using (5) |
| 23. end while |
| 24. Use SoftMax to convert to state probabilities |
| 25. |
| 26. end for |
| 27. |
| 28. |
| 29. |
| 30. end for |
| 31. |
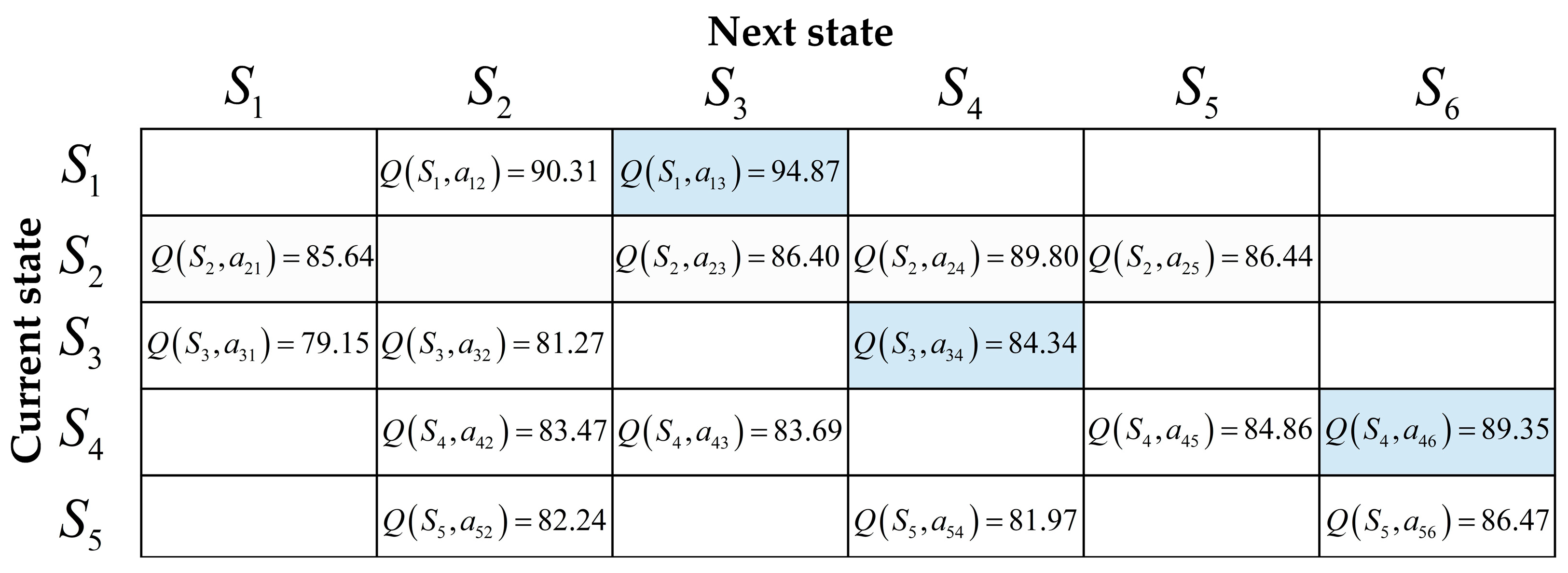
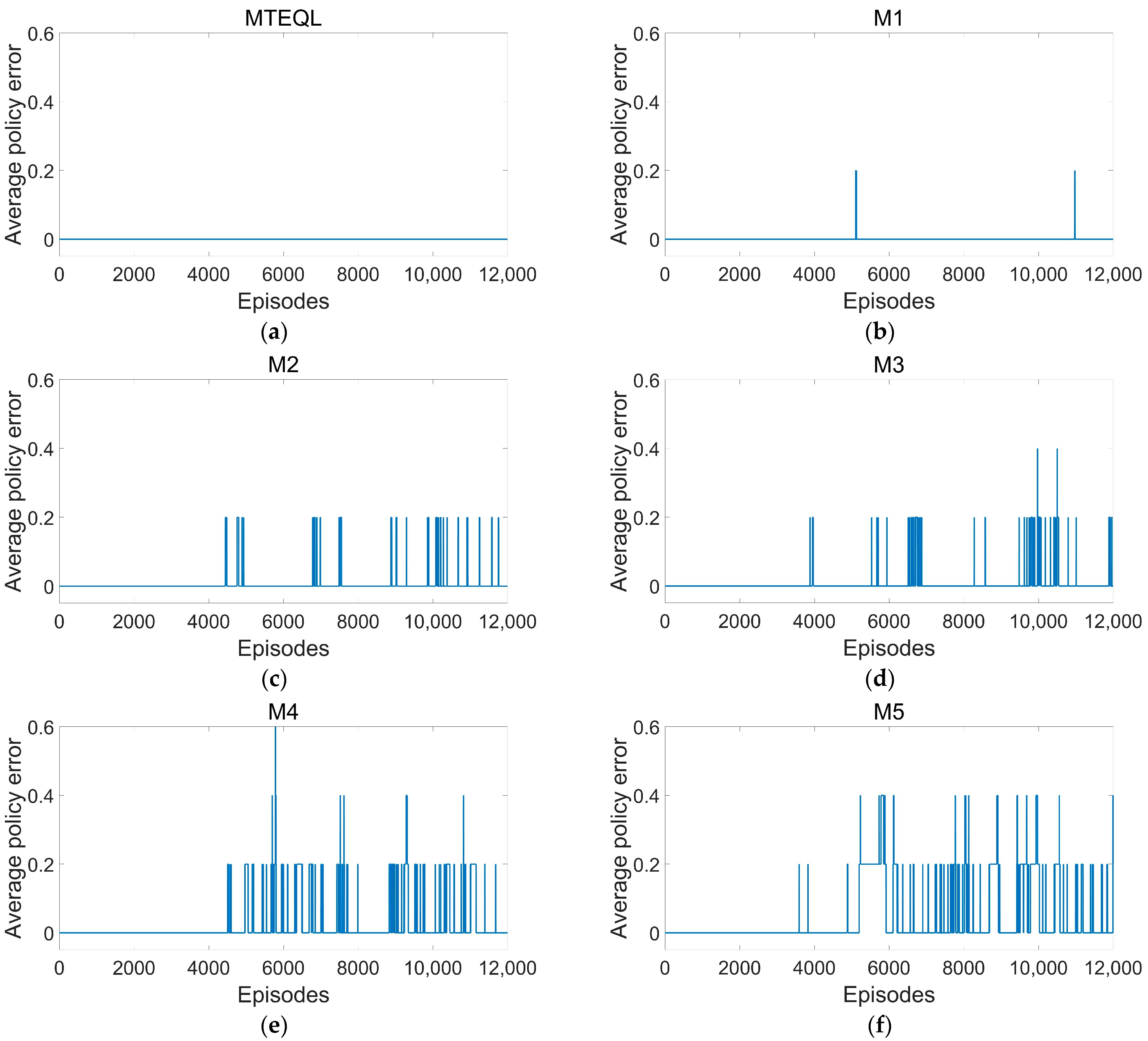
4. Simulation Experiments and Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.; An, W.; Guo, F.; Liu, Z.; Jiang, W. Principles and Technologies of Electronic Warfare System; Publishing House of Electronics Industry: Beijing, China, 2014. [Google Scholar]
- Huang, Z.; Wang, X.; Zhao, Y. Overview of cognitive electronic warfare. J. Natl. Univ. Def. Technol. 2023, 45, 1–11. [Google Scholar]
- Charlish, A. Autonomous Agents for Multi-Function Radar Resource Management. Ph.D. Thesis, University College London, London, UK, 2011. [Google Scholar]
- Apfeld, S.; Charlish, A.; Ascheid, G. Modelling, learning and prediction of complex radar emitter behaviour. In Proceedings of the 2019 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 305–310. [Google Scholar]
- Liu, D.; Zhao, Y.; Cai, X.; Xu, B.; Qiu, T. Adaptive scheduling algorithm based on cpi and impact of tasks for multifunction radar. IEEE Sens. J. 2019, 19, 11205–11212. [Google Scholar] [CrossRef]
- Han, C.; Kai, L.; Zhou, Z.; Zhao, Y.; Yan, H.; Tian, K.; Tang, B. Syntactic modeling and neural based parsing for multifunction radar signal interpretation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 5060–5072. [Google Scholar]
- Wang, S.; Zhu, M.; Li, Y.; Yang, J.; Li, Y. Recognition, inference, and prediction of advanced Multi-Function radar systems behaviors: Overview and prospects. J. Signal Process. 2024, 40, 17–55. [Google Scholar]
- Johnston, S.L. Radar Electronic Counter-Countermeasures. IEEE Trans. Aerosp. Electron. Syst. 1978, AES14, 109–117. [Google Scholar] [CrossRef]
- Wang, S.; Bao, Y.; Li, Y. The architecture and technology of cognitive electronic warfare. Sci. Sin. Inform. 2018, 48, 1603–1613. [Google Scholar] [CrossRef]
- Dahle, R. EW 104: Electronic Warfare Against a New Generation of Threats. Microw. J. 2024, 67, 118. [Google Scholar]
- Haykin, S. Cognitive radar: A way of the future. IEEE Signal Process. Mag. 2006, 23, 30–40. [Google Scholar] [CrossRef]
- Sudha, Y.; Sarasvathi, V. A Model-Free Cognitive Anti-Jamming Strategy Using Adversarial Learning Algorithm. Cybern. Inf. Technol. 2022, 22, 56–72. [Google Scholar] [CrossRef]
- Darpa, A. Behavioral Learning for Adaptive Electronic Warfare. In Darpa-BAA-10-79; Defense Advanced Research Projects Agency: Arlington, TX, USA, 2010. [Google Scholar]
- Knowles, J. Regaining the advantage—Cognitive electronic warfare. J. Electron. Def. 2016, 39, 56–62. [Google Scholar]
- Zhou, H. An introduction of cognitive electronic warfare system. In Proceedings of the International Conferences on Communications, Signal Processing, and Systems, Dalian, China, 14–16 July 2018. [Google Scholar]
- So, R.P.; Ilku, N.; Sanguk, N. Modeling and simulation for the investigation of radar responses to electronic attacks in electronic warfare environments. Secur. Commun. Netw. 2018, 2018, 3580536. [Google Scholar]
- Purabi, S.; Kandarpa, K.S.; Nikos, E.M. Artificial Intelligence Aided Electronic Warfare Systems- Recent Trends and Evolving Applications. IEEE Access 2020, 8, 224761–224780. [Google Scholar]
- Nepryaev, A.A. Cognitive radar control system using machine learning. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1047, p. 012119. [Google Scholar]
- BIS Research. Cognitive electronic warfare: An artificial intelligence approach. Microw. J. 2021, 64, 110. [Google Scholar]
- du Plessis, W.P.; Osner, N.R. Cognitive electronic warfare (EW) systems as a training aid. In Proceedings of the Electronic Warfare International Conference (EWCI), Bangalore, India, 13–16 February 2018; pp. 1–7. [Google Scholar]
- Xiao, L.; Liu, D. Modeling method of combat mission based on OODA loop. MATEC Web Conf. 2022, 355, 02015. [Google Scholar]
- Zhang, B.; Zhu, W. Overview of jamming decision-making method for Multi-Function phased array radar. J. Ordnance Equip. Eng. 2019, 40, 178–183. [Google Scholar]
- Zhang, C.; Wang, L.; Jiang, R.; Hu, J.; Xu, S. Radar jamming decision-making in cognitive electronic warfare: A review. IEEE Sens. J. 2023, 23, 11383–11403. [Google Scholar] [CrossRef]
- Liangliang, G.; Shilong, W.; Tao, L. A radar emitter identification method based on pulse match template sequence. In Proceedings of the 2010 2nd International Conference on Signal Processing Systems, Dalian, China, 5–7 July 2010. [Google Scholar]
- Li, K.; Jiu, B.; Liu, H. Game theoretic strategies design for monostatic radar and jammer based on mutual information. IEEE Access 2019, 7, 72257–72266. [Google Scholar] [CrossRef]
- Bachmann, D.J.; Evans, R.J.; Moran, B. Game theoretic analysis of adaptive radar jamming. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1081–1100. [Google Scholar] [CrossRef]
- Sun, H.; Tong, N.; Sun, F. Jamming design selection based on D-S Theory. J. Proj. Rocket. Missiles Guid. 2003, 202, 218–220. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction. Neural Netw. IEEE Trans. 1998, 19, 1054. [Google Scholar] [CrossRef]
- Rummery, G.A.; Niranjan, M. On-line q-learning using connectionist systems. Tech. Rep. 1994, 37, 335–360. [Google Scholar]
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Watkins, C.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Ribeiro, R.; Koerich, A.L.; Enembreck, F. Noise tolerance in reinforcement learning algorithms. In Proceedings of the 2007 IEEE/WIC/ACM International Conference on Intelligent Agent Technology (IAT’07), Fremont, CA, USA, 2–5 November 2007. [Google Scholar]
- Llorente, F.; Martino, L.; Read, J.; Delgado-Gómez, D. A survey of Monte Carlo methods for noisy and costly densities with application to reinforcement learning and ABC. Int. Stat. Rev. 2024, 1. [Google Scholar] [CrossRef]
- Liu, W.; Xiang, S.; Zhang, T.; Han, Y.; Guo, X.; Zhang, Y.; Hao, Y. Judgmentally adjusted Q-values based on Q-ensemble for offline reinforcement learning. Neural Comput. Appl. 2024, 36, 15255–15277. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Y.; Gao, M. Design of cognitive radar jamming based on Q-Learning Algorithm. Trans. Beijing Inst. Technol. 2015, 35, 1194–1199. [Google Scholar]
- Zhang, B.; Zhu, W. Construction and key technologies of cognitive jamming decision-making system against MFR. Syst. Eng. Electron. 2020, 42, 1969–1975. [Google Scholar]
- Zhu, B.; Zhu, W.; Li, W.; Yang, Y.; Gao, T. Research on decision-making modeling of cognitive jamming for multi-functional radar based on Markov. Syst. Eng. Electron. 2022, 44, 2488–2497. [Google Scholar]
- Zhu, B.; Zhu, W.; Li, W.; Li, J.; Yang, Y. Multi-function radar jamming decision method based on planning steps adaptive Dyna-Q. Ordnance Ind. Autom. 2022, 41, 52–58. [Google Scholar]
- Li, H.; Li, Y.; He, C.; Zhan, J.; Zhang, H. Cognitive electronic jamming decision-making method based on improved Q-learning algorithm. Int. J. Aerosp. Eng. 2021, 2021, 8647386. [Google Scholar] [CrossRef]
- Zhang, C.; Song, Y.; Jiang, R.; Hu, J.; Xu, S. A cognitive electronic jamming decision-making method based on q-learning and ant colony fusion algorithm. Remote Sens. 2023, 15, 3108. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, C.; Hu, J.; Xu, S. Radar-jamming decision-making based on improved q-learning and fpga hardware implementation. Remote Sens. 2024, 16, 1190. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, W. DQN based decision-making method of cognitive jamming against multifunctional radar. Syst. Eng. Electron. 2020, 42, 819–825. [Google Scholar]
- Zou, W.; Niu, C.; Liu, W.; Gao, O.; Zhang, H. Cognitive jamming decision-making method against multifunctional radar based on A3C. Syst. Eng. Electron. 2023, 45, 86–92. [Google Scholar]
- Feng, L.W.; Liu, S.T.; Xu, H.Z. Multifunctional radar cognitive jamming decision based on dueling double deep q-network. IEEE Access 2022, 99, 112150–112157. [Google Scholar] [CrossRef]
- Zhang, Y.; Huo, W.; Huang, Y.; Zhang, C.; Pei, J.; Zhang, Y.; Yang, J. Jamming policy generation via heuristic programming reinforcement learning. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8782–8799. [Google Scholar] [CrossRef]
- Mao, S. Research on Intelligent Jamming Decision-Making Methods Based on Reinforcement Learning. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Zhang, P.; Ding, H.; Zhang, Y.; Li, B.; Huang, F.; Jin, Z. Multi-agent autonomous electronic jamming system based on information sharing. J. Zhejiang Univ. Eng. Sci. 2022, 56, 75–83. [Google Scholar]
- Pan, Z.; Li, Y.; Wang, S.; Li, Y. Joint optimization of jamming type selection and power control for countering multi-function radar based on deep reinforcement learning. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 108965. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, T.; Zhao, Z.; Ma, D.; Liu, F. Performance analysis of deep reinforcement learning-based intelligent cooperative jamming method confronting multi-functional networked radar. Signal Process. 2023, 207, 108965. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Bozkus, T.; Mitra, U. Multi-timescale ensemble Q-learning for markov decision process policy optimization. IEEE Trans. Signal Process. 2024, 72, 1427–1442. [Google Scholar] [CrossRef]




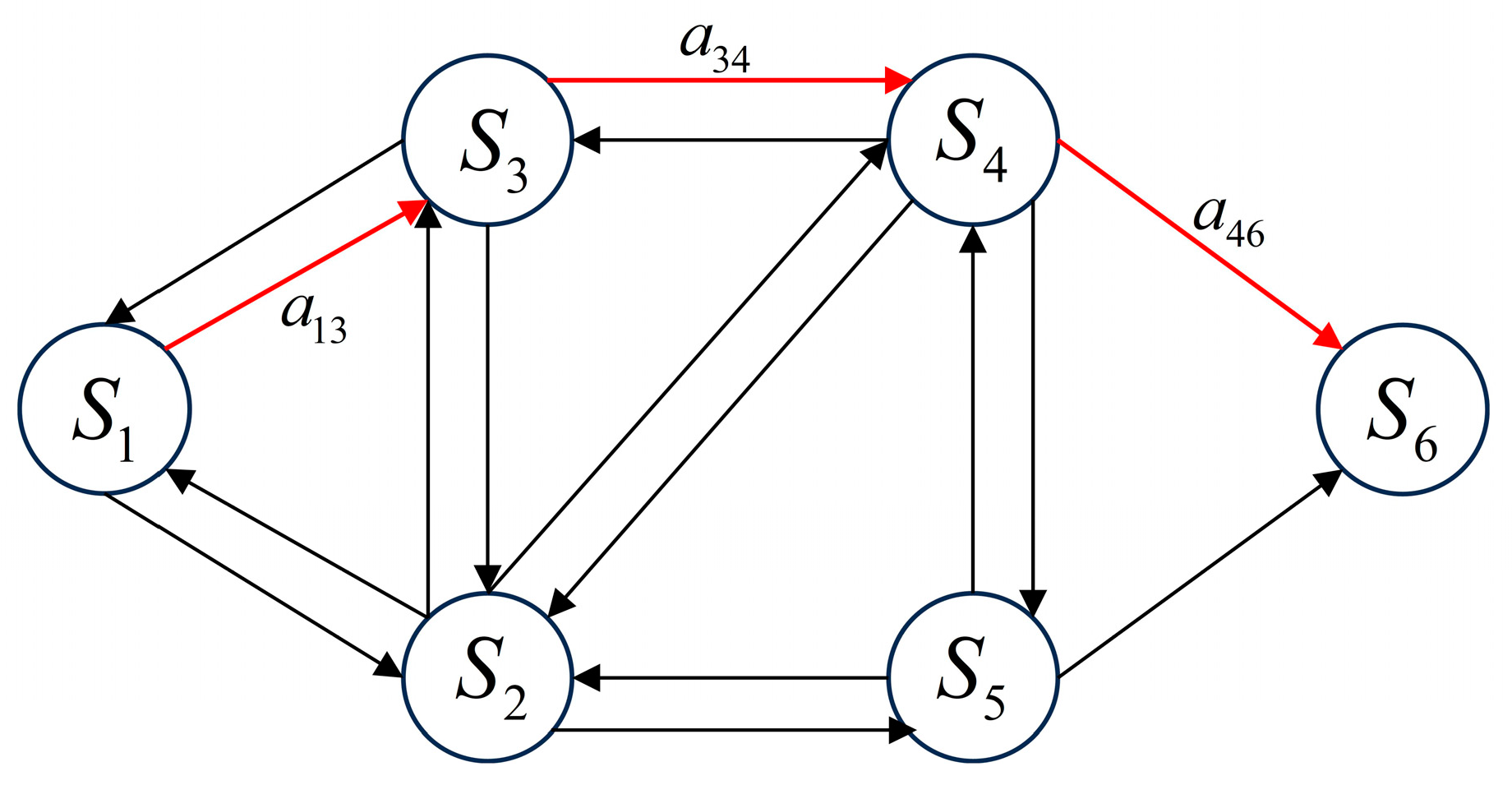

| Parameters | Value |
|---|---|
| Sampling path length, | 200 |
| Minimum number of times for each state transition pair, | 40 |
| Training episodes, | 12,000 |
| The total number of Markov environments, | 5 |
| Learning rate, | 0.1 |
| Discount factor, | 0.9 |
| Replacement rate, | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, J.; Zhou, Q.; Li, Z.; Yang, Z.; Shi, S.; Xu, Z.; Xu, Q. Efficient Jamming Policy Generation Method Based on Multi-Timescale Ensemble Q-Learning. Remote Sens. 2024, 16, 3158. https://doi.org/10.3390/rs16173158
Qian J, Zhou Q, Li Z, Yang Z, Shi S, Xu Z, Xu Q. Efficient Jamming Policy Generation Method Based on Multi-Timescale Ensemble Q-Learning. Remote Sensing. 2024; 16(17):3158. https://doi.org/10.3390/rs16173158
Chicago/Turabian StyleQian, Jialong, Qingsong Zhou, Zhihui Li, Zhongping Yang, Shasha Shi, Zhenjia Xu, and Qiyun Xu. 2024. "Efficient Jamming Policy Generation Method Based on Multi-Timescale Ensemble Q-Learning" Remote Sensing 16, no. 17: 3158. https://doi.org/10.3390/rs16173158
APA StyleQian, J., Zhou, Q., Li, Z., Yang, Z., Shi, S., Xu, Z., & Xu, Q. (2024). Efficient Jamming Policy Generation Method Based on Multi-Timescale Ensemble Q-Learning. Remote Sensing, 16(17), 3158. https://doi.org/10.3390/rs16173158





