Improvement of the Estimation of the Vertical Crustal Motion Rate at GNSS Campaign Stations Based on the Information of GNSS Reference Stations
Abstract
1. Introduction
2. Data and Methods
2.1. Observation Data
2.2. Experimental Methods
2.2.1. GNSS Coordinate Time Series Fitting
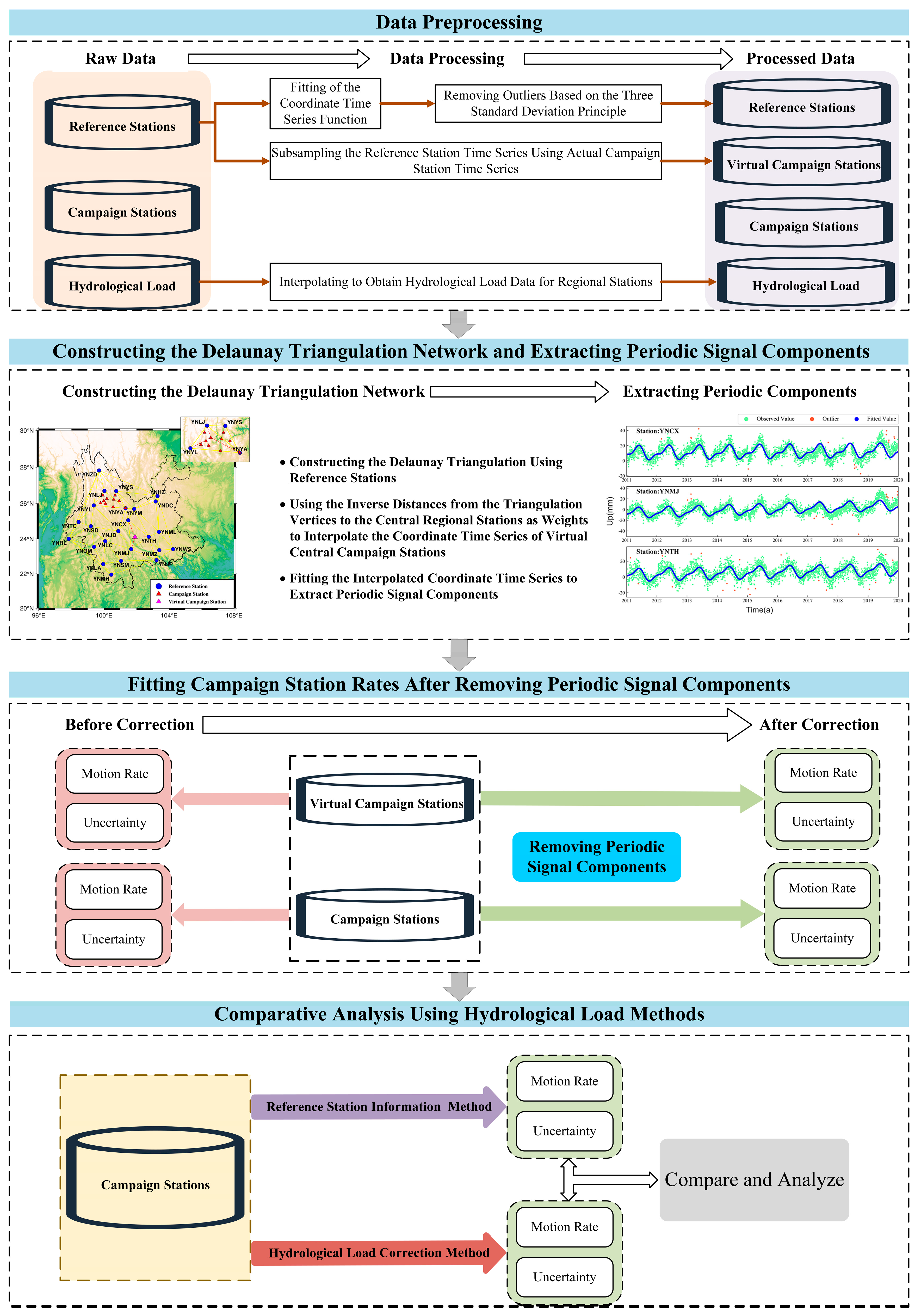
2.2.2. Preprocessing of GNSS Coordinate Time Series
- (1)
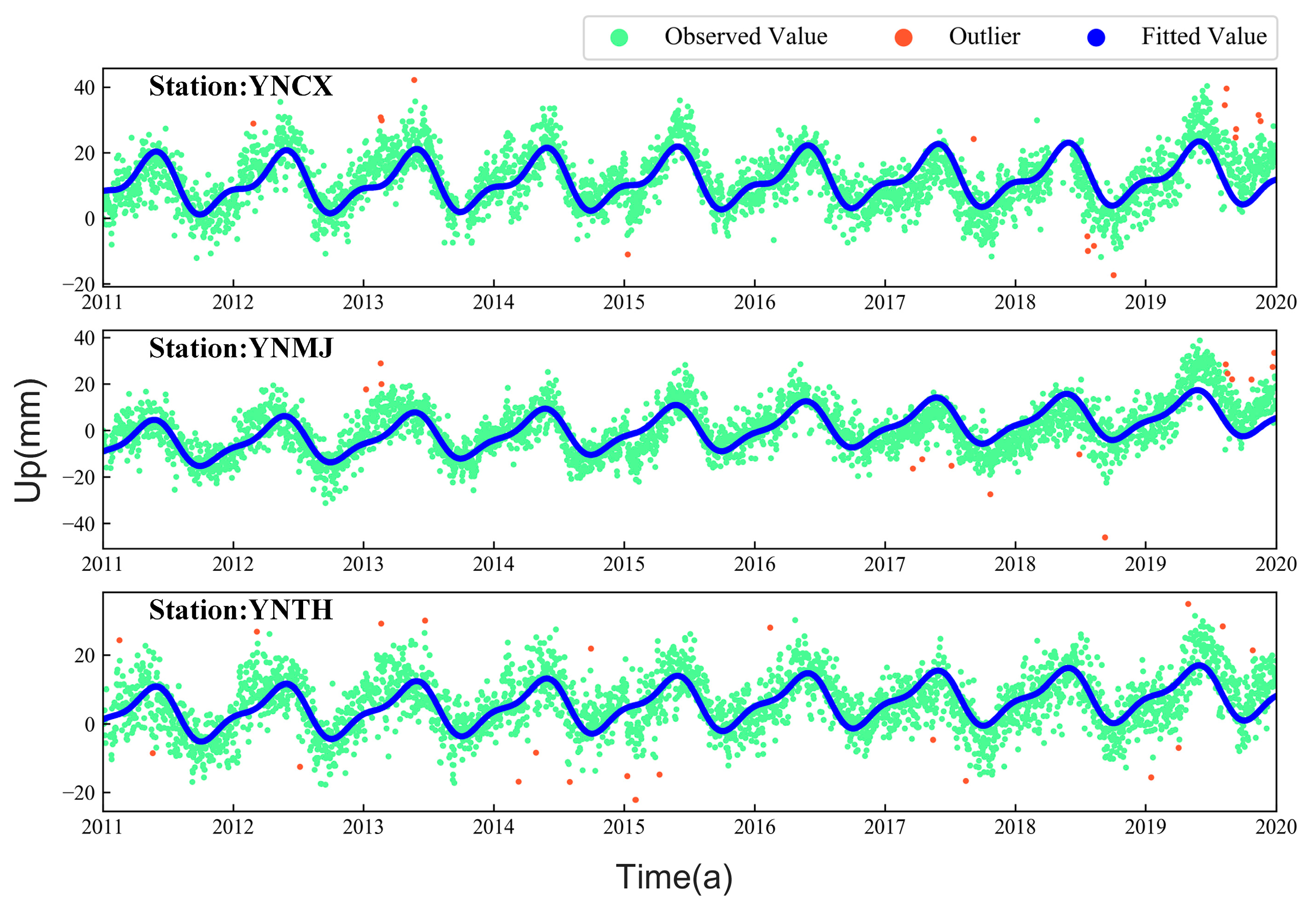
- Use the least squares method to process the original coordinate time series, obtain the residual sequence matrix , and calculate its standard deviation [20]. The standard deviation is calculated as shown in Equation (7), where and are the observed and simulated values of the coordinate time series components, respectively, and n is the number of epochs of observations.
- (2)
- According to the criterion, if the residual value between the observed and simulated values at a certain time exceeds , the observation at that time is considered a gross error and should be eliminated [21].
- (3)
- Repeat steps 1 and 2 until all values in the residual time series are within . After completing the gross error detection and elimination, use the Regularized Expectation-Maximum (RegEM) algorithm to fill in the missing data in the original coordinate time series of the reference station [22].
2.2.3. Estimation of Non-Tectonic Motion Signals at Campaign Stations
3. Results and Analysis
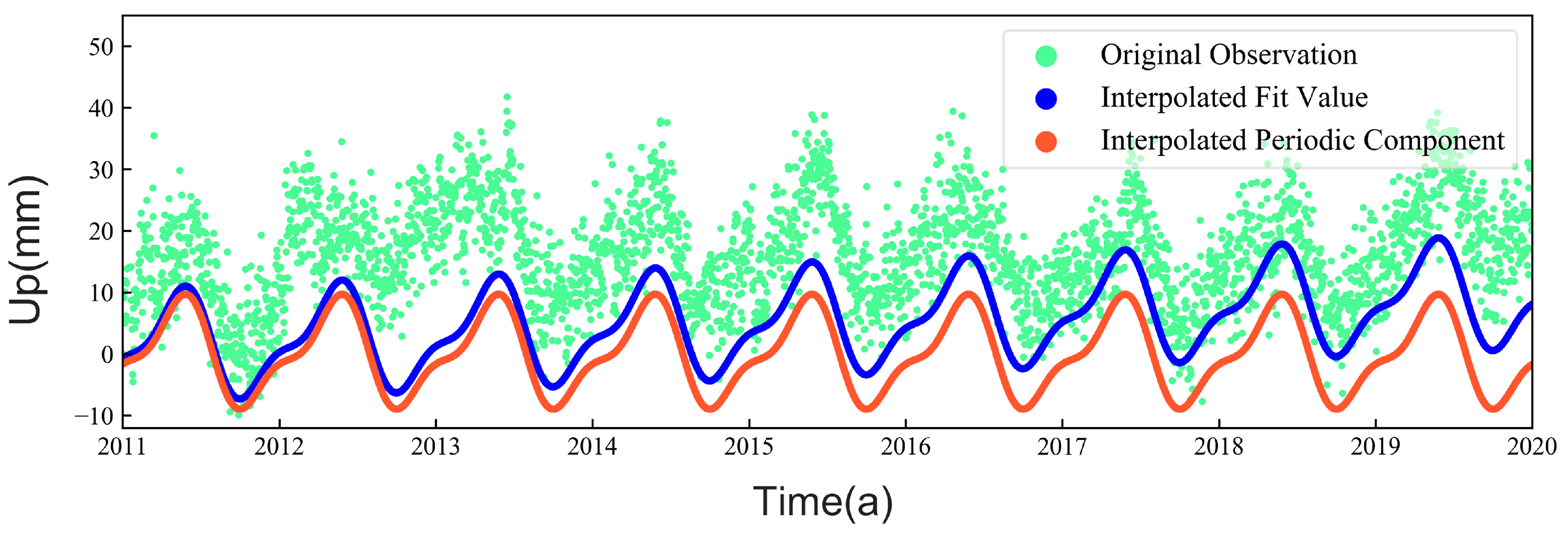
3.1. Analysis of Reference Station Coordinate Time Series
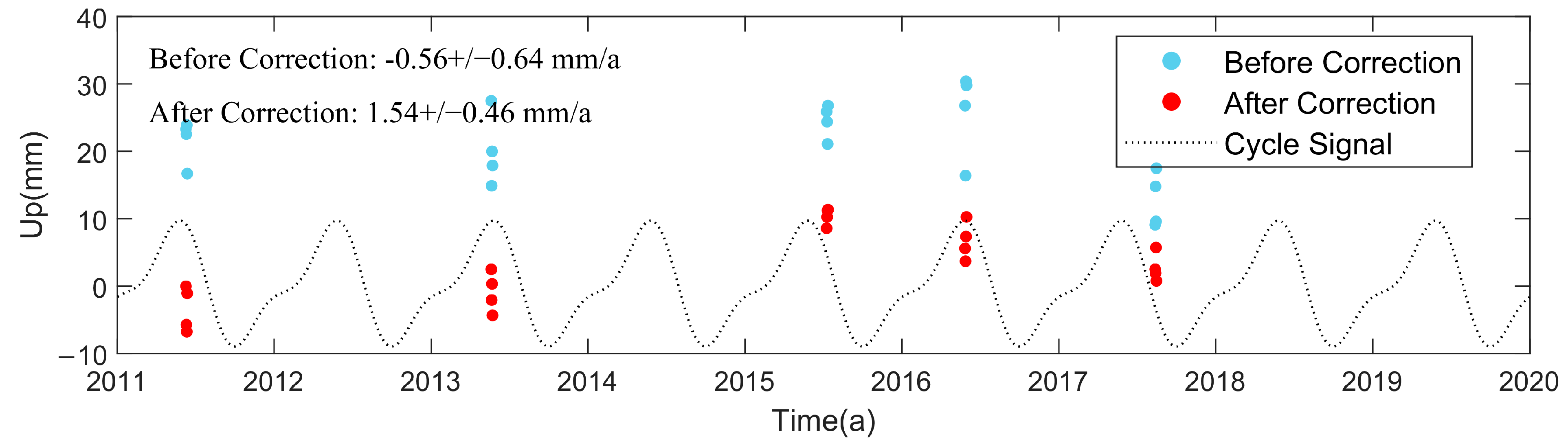
3.2. Analysis of Virtual Campaign Station Results
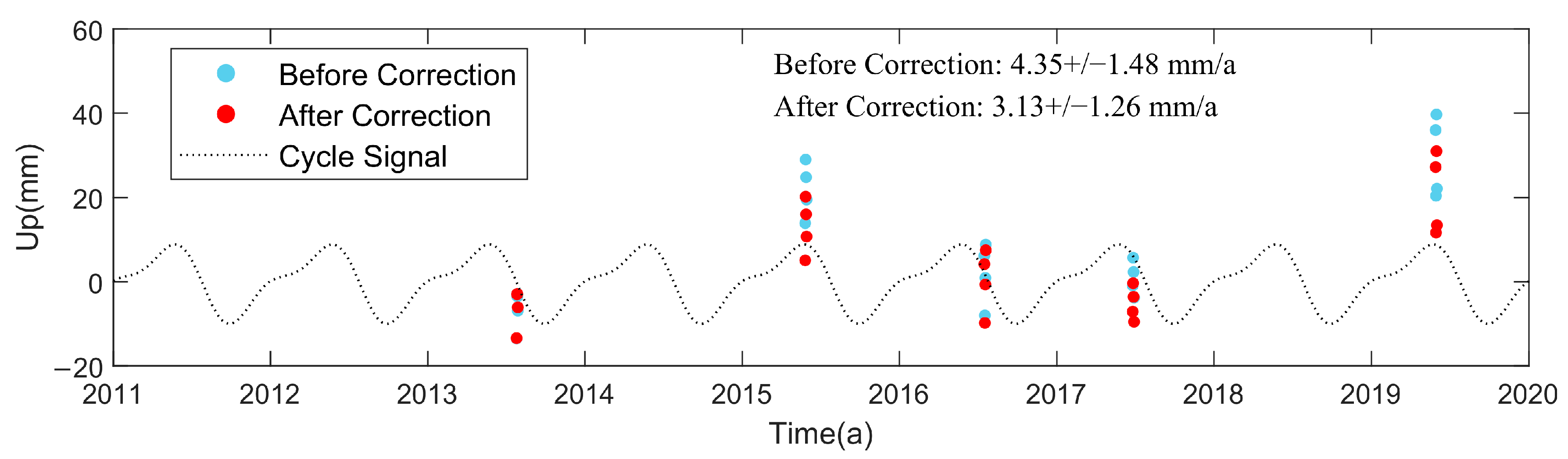
3.3. Analysis of Real Campaign Station Results
4. Discussion
5. Conclusions
- (1)
- Virtual campaign stations: After correcting the coordinate time series of virtual campaign stations, the precision of velocity estimation improved for all virtual campaign stations. The range of improvement percentages was 10–36%, with an average improvement of 24.4%, indicating a significant correction effect.
- (2)
- Real campaign stations: After correcting the coordinate time series of the real campaign stations, 9 out of 10 campaign stations showed improved precision in vertical motion velocity estimation. One station’s precision decreased by 0.49%, with an overall average precision improvement of approximately 9.6%. In contrast, the correction results using the environmental load method were unstable, with only six stations showing improved precision and an overall average improvement of about 8.2%.
- (3)
- Comparison between virtual and real stations: The improvement effect for virtual campaign stations was better than for real campaign stations. This is because the virtual campaign stations’ time series were obtained by downsampling the reference station coordinate time series, resulting in higher estimation precision compared to the campaign stations. Therefore, the daily solution precision of the campaign stations also affects the effectiveness of this method.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, S.M.; Pan, P.F.; Zhou, X.H. Research on Common Mode Error Extraction Method for Large Spatial Scale GPS Networks. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 1168–1173. [Google Scholar] [CrossRef]
- Jia, L.L.; Wang, Y.B.; Lian, W.P.; Xiang, L.W. Comparative Analysis of Vertical Deformation of the Chinese Mainland Surface Using “China’s Crustal Movement Observation Network” GPS and GRACE Data. Acta Geod. Cartogr. Sin. 2018, 47, 899–906. [Google Scholar]
- Liang, S.; Gan, W.; Shen, C.; Xiao, G.; Liu, J.; Chen, W.; Ding, X.; Zhou, D. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. Solid Earth 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
- Zhan, W.; Li, F.; Hao, W.; Yan, J. Regional characteristics and influencing factors of seasonal vertical crustal motions in Yunnan, China. Geophys. J. Int. 2017, 210, 1295–1304. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, P.; Chen, H.; Cai, J.; Li, Z.; Chao, N.; Sneeuw, N. Annual variations of monsoon and drought detected by GPS: A case study in Yunnan, China. Sci. Rep. 2017, 7, 5874. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Ding, K.; Liu, P.; Lan, G.; Ming, Z. Spatiotemporal filtering for continuous GPS coordinate time series in mainland China by using independent component analysis. Remote Sens. 2022, 14, 2904. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.K.; Dong, D.N. The Impact and Correction of Non-Tectonic Deformation on GPS Continuous Station Position Time Series. Chin. J. Geophys. 2005, 48, 1045–1052. [Google Scholar] [CrossRef]
- Li, Q.; You, X.Z.; Yang, S.M.; Du, R.L.; Qiao, X.J.; Zou, R.; Wang, Q. High-Precision and High-Density GPS Monitoring of Tectonic Deformation in the Chinese Mainland: Present-Day Velocity Field. Sci. Sin. (Terrae) 2012, 42, 629–632. [Google Scholar]
- Wang, D.Z.; Zhao, B.; Yu, J.S.; Tan, K. Can Mobile GPS Observation Data Be Used for Crustal Vertical Deformation Monitoring? A Case Study of the Chinese Mainland. J. Geod. Geodyn. 2021, 41, 290–295. [Google Scholar]
- Zhan, W.; Li, F.; Zhu, S.; Zhang, J. Analysis and Experiment on Correcting Vertical Velocity of Mobile Observations Using Continuous GPS Observations. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 963–968. [Google Scholar]
- Liang, H.B.; Yang, G.H. Characteristics of Vertical Deformation in the Northern Section of the North-South Seismic Belt Before and After the Wenchuan M_S8.0 Earthquake. J. Seismol. Res. 2021, 44, 613–621. [Google Scholar]
- Li, J.W.; Zhan, W.; Liang, H.B.; Wang, Y.; Guo, N.N. Accurate Acquisition and Method Evaluation of GPS Vertical Annual Periodic Motion. J. Seismol. Res. 2020, 43, 95–100. [Google Scholar]
- Bos, M.; Bastos, L.; Fernandes, R. The influence of seasonal signals on the estimation of the tectonic motion in short continuous GPS time-series. J. Geodyn. 2010, 49, 205–209. [Google Scholar] [CrossRef]
- Liu, B.; Dai, W.; Peng, W.; Meng, X. Spatiotemporal analysis of GPS time series in vertical direction using independent component analysis. Earth Planets Space 2015, 67, 1–10. [Google Scholar] [CrossRef]
- Ding, Y.H.; Huang, D.F.; Shi, Y.L.; Jiang, Z.S.; Chen, T. Analysis of Vertical Surface Displacement Changes in Sichuan Using GPS and GRACE. Chin. J. Geophys. 2018, 61, 4777–4788. [Google Scholar]
- Qiao, X.J.; Wang, Q.; Du, R.L. Present-Day Crustal Deformation Characteristics of Active Blocks in the Sichuan-Yunnan Region. Chin. J. Geophys. 2004, 47, 805–811. [Google Scholar]
- Sheng, C.Z.; Gan, W.J.; Liang, S.M.; Chen, W.T.; Xiao, G.R. Identification and Removal of Terrestrial Water Load Deformation Interference in GPS Time Series in Western Yunnan Using GRACE. Chin. J. Geophys. 2014, 57, 42–52. [Google Scholar]
- Gülal, E.; Erdoğan, H.; Tiryakioğlu, İ. Research on the stability analysis of GNSS reference stations network by time series analysis. Digit. Signal Process. 2013, 23, 1945–1957. [Google Scholar] [CrossRef]
- Jiang, W.P.; Li, Z.H.; Liu, H.F.; Zhao, Q. Analysis of the Causes of Nonlinear Changes in the Coordinate Time Series of IGS Reference Stations in China. Chin. J. Geophys. 2013, 56, 2228–2237. [Google Scholar]
- Wu, H.; Lu, N.; Zou, J.G.; Guo, S.T. Improved 3σ Outlier Detection Method for GNSS Deformation Monitoring Time Series. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 1282–1288. [Google Scholar] [CrossRef]
- Xu, H.Q.; Lu, T.D.; He, X.X.; Zhou, S.J.; Tao, R. Outlier Detection in GNSS Coordinate Time Series Based on the SSA-S_n Method. J. Geod. Geodyn. 2022, 42, 258–263+285. [Google Scholar] [CrossRef]
- Hu, S.Q.; Wang, T.; Guan, Y.H.; Yang, Z.Y. Study on Vertical Seasonal Fluctuation Changes and Tectonic Deformation in Yunnan Using GPS and Hydrological Load Models. Chin. J. Geophys. 2021, 64, 2613–2630. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Li, X.W.; Cao, C.X.; Chang, C.Y. The First Law of Geography and the Proposal of Spatio-temporal Proximity. Chin. J. Nat. 2007, 29, 69–71. [Google Scholar]
- Ren, Y.Y.; Wang, J.X.; Wang, H.; Lian, L.Z.; Hou, Y.F.; Wang, Y.Z. Construction of the Velocity Field of the Chinese Mainland Based on the Local Seamless Delaunay Triangulation Inverse Distance Weighting Method. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1071–1080. [Google Scholar]
- Dhevi, A.S. Imputing missing values using Inverse Distance Weighted Interpolation for time series data. In Proceedings of the 2014 Sixth International Conference on Advanced Computing (ICoAC), Chennai, India, 17–19 December 2014; pp. 255–259. [Google Scholar]
- Yan, X.R.; Wang, X.C.; Liang, W.; Mu, Y.X.; Song, Y.L.; Ding, N.; Zhang, W.Y. Optimized IDW Interpolation Method Considering GNSS Water Vapor Distribution Characteristics and Inter-Station Distance. J. Nanjing Univ. Inf. Sci. Technol. (Nat. Sci. Ed.) 2022, 14, 287–293. [Google Scholar] [CrossRef]
- He, Y.F.; Nie, G.G.; Wu, S.G.; Li, H.Y.; Liao, M.; Guo, Y. Analysis of the Relationship Between CMONOC Coordinate Time Series Considering Rainfall and Hydrological Load in the ITRF2014 Framework. Geomat. Inf. Sci. Wuhan Univ. 2024, 49, 960–969. [Google Scholar] [CrossRef]
- Feng, T.F.; Shen, Y.Z.; Wang, F.W.; Chen, Q.J. Extraction and Physical Mechanism Analysis of Seasonal Vertical Displacement Signals in North China. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 866–874. [Google Scholar] [CrossRef]
- Ming, F.; Yang, Y.; Zeng, A.; Zhao, B. Spatiotemporal filtering for regional GPS network in China using independent component analysis. J. Geod. 2017, 91, 419–440. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools version 6. Geochem. Geophys. Geosystems 2019, 20, 5556–5564. [Google Scholar] [CrossRef]


| Station | Longitude (°) | Latitude (°) | Distance (km) | Weight |
|---|---|---|---|---|
| YNCX | 101.493 | 25.050 | 113.0 | 0.268 |
| YNMJ | 101.675 | 23.416 | 79.5 | 0.380 |
| YNTH | 102.751 | 24.118 | 85.9 | 0.352 |
| Station | Velocity before Correction (mm/a) | Velocity after Correction (mm/a) | Improvement Percentage in Precision (%) |
|---|---|---|---|
| YNXP | 28% | ||
| YNMZ | 25% | ||
| YNDC | 18% | ||
| YNLJ | 33% | ||
| YNMJ | 20% | ||
| YNLC | 36% | ||
| YNSD | 30% | ||
| YNML | 29% | ||
| YNSM | 33% | ||
| YNTH | 10% | ||
| YNCX | 29% | ||
| YNGM | 20% | ||
| YNLA | 16% | ||
| YNYL | 27% | ||
| YNYM | 24% | ||
| YNYS | 13% |
| Station | Velocity before Correction (mm/a) | Reference Station Information | Hydrological Load | ||
|---|---|---|---|---|---|
| Velocity after Correction (mm/a) | Improvement Percentage in Precision (%) | Velocity after Correction (mm/a) | Improvement Percentage in Precision (%) | ||
| H198 | 4% | −13% | |||
| H328 | 15% | 26% | |||
| H201 | 8% | 19% | |||
| H323 | 0.36% | −2% | |||
| H124 | 16% | 14% | |||
| H123 | 10% | 16% | |||
| H131 | 7% | 10% | |||
| H334 | −0.49% | −7% | |||
| H340 | 8% | 0% | |||
| H130 | 27% | 19% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Ding, K.; Lan, G. Improvement of the Estimation of the Vertical Crustal Motion Rate at GNSS Campaign Stations Based on the Information of GNSS Reference Stations. Remote Sens. 2024, 16, 3144. https://doi.org/10.3390/rs16173144
Jiang J, Ding K, Lan G. Improvement of the Estimation of the Vertical Crustal Motion Rate at GNSS Campaign Stations Based on the Information of GNSS Reference Stations. Remote Sensing. 2024; 16(17):3144. https://doi.org/10.3390/rs16173144
Chicago/Turabian StyleJiang, Jiazheng, Kaihua Ding, and Guanghong Lan. 2024. "Improvement of the Estimation of the Vertical Crustal Motion Rate at GNSS Campaign Stations Based on the Information of GNSS Reference Stations" Remote Sensing 16, no. 17: 3144. https://doi.org/10.3390/rs16173144
APA StyleJiang, J., Ding, K., & Lan, G. (2024). Improvement of the Estimation of the Vertical Crustal Motion Rate at GNSS Campaign Stations Based on the Information of GNSS Reference Stations. Remote Sensing, 16(17), 3144. https://doi.org/10.3390/rs16173144







