MLF-PointNet++: A Multifeature-Assisted and Multilayer Fused Neural Network for LiDAR-UAS Point Cloud Classification in Estuarine Areas
Abstract
1. Introduction
- (1)
- The feature learning ability of the MLF-PointNet++ model is improved by fusing feature vectors from different layers.
- (2)
- The input of auxiliary features such as 3D shape features and vegetation indices is expanded to the MLF-PointNet++ model to increase the learning range of terrain target features in estuarine areas.
- (3)
- The focal loss function is introduced to address the issue of imbalanced point cloud data among various object categories, improving the accuracy of object classification.
2. Materials and Methods
2.1. Study Area and Dataset
2.2. Methods
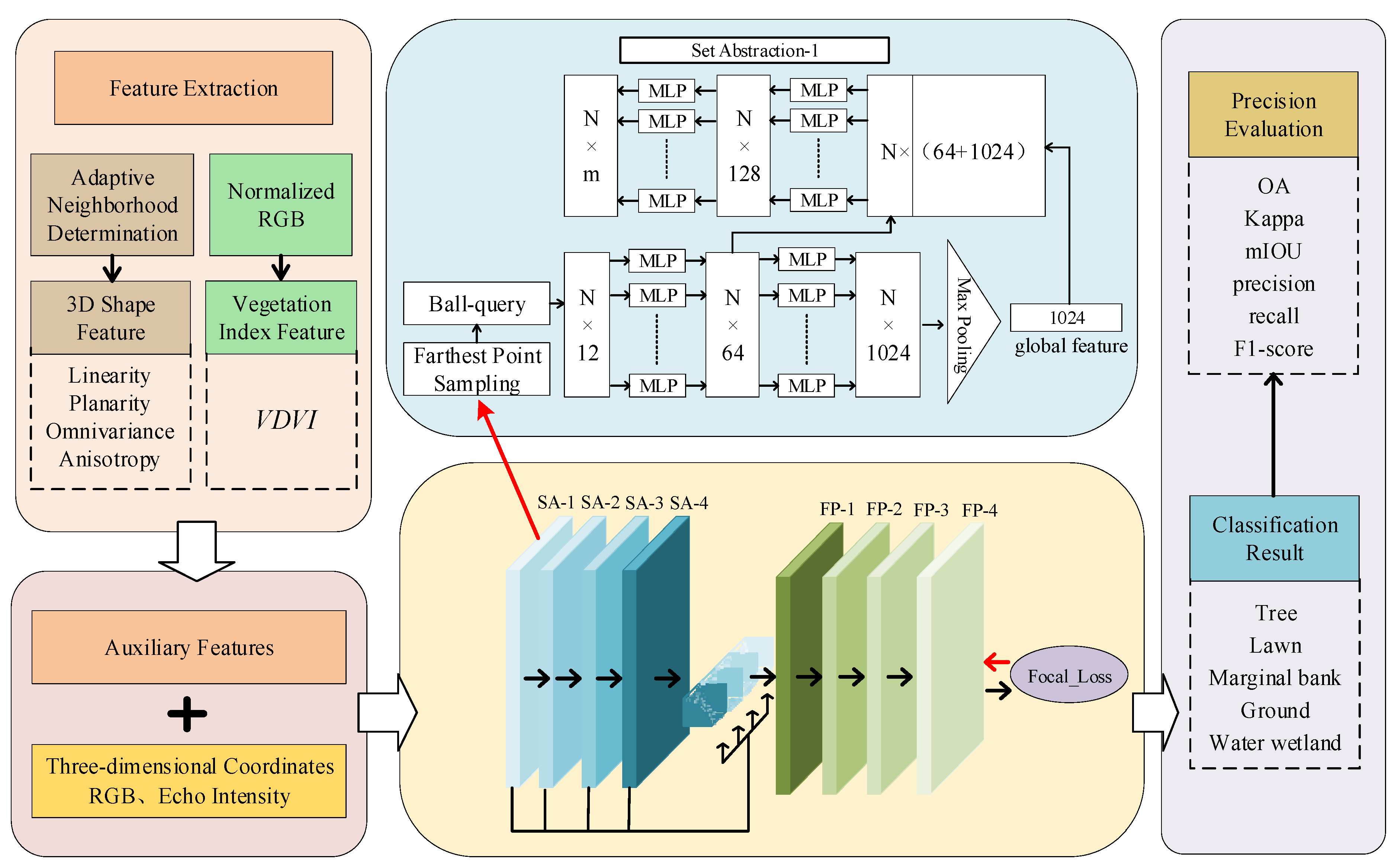
2.2.1. Feature Extraction
- (1)
- Extraction of 3D shape features. Owing to the different scanning distances, scanning angles, and scanning target characteristics (discrete distributions of tree point clouds and uniform distributions of ground point clouds), the acquired point cloud data are nonuniform. To reduce the feature calculation errors caused by uneven point cloud density, a neighborhood adaptive method is adopted to calculate 3D shape features. To calculate the optimal neighborhood radius of a point, the principal component analysis method is first used to calculate the eigenvalues of the feature matrix composed of neighborhood point coordinates. The optimal neighborhood radius is determined by changing the radius parameter and selecting the value that produces the minimum feature entropy. The 3D shape features are subsequently calculated via the eigenvalues , , and () of the feature matrix composed of the point cloud coordinates in the optimal neighborhood. 3D shape features include linearity, planarity, scattering, omnivariance, anisotropy, eigenentropy, traces, and changes in curvature. Adding all the features increases the complexity of the model calculations. To improve the calculation efficiency of the algorithm, we use the random forest algorithm to analyze the importance of these 3D shape features. The first four 3D shape features with significant influence—linearity, planarity, omnivariance, and anisotropy—were selected as auxiliary features. The specific calculation formula can be found in reference [40].
- (2)
- Extraction of the VDVI. The dense vegetation (lawns and trees) on the slopes in the estuarine area has elevation and fitting residual information similar to the ground on the tops of the slopes. The vegetation on the slopes and the ground at the tops of the slopes may be mixed into one category during point cloud classification [41]. The vegetation index can effectively reflect the distribution of vegetation and help distinguish ground from vegetation. Because the same object often has similar or continuous RGB color information and because the color changes between different objects are significant, this article transforms the target RGB color information into the VDVI to highlight the differences between the vegetation and ground [41]. The calculation formula for the VDVI is as follows:where R, G, and B denote the red, green, and blue color values of the target, respectively.
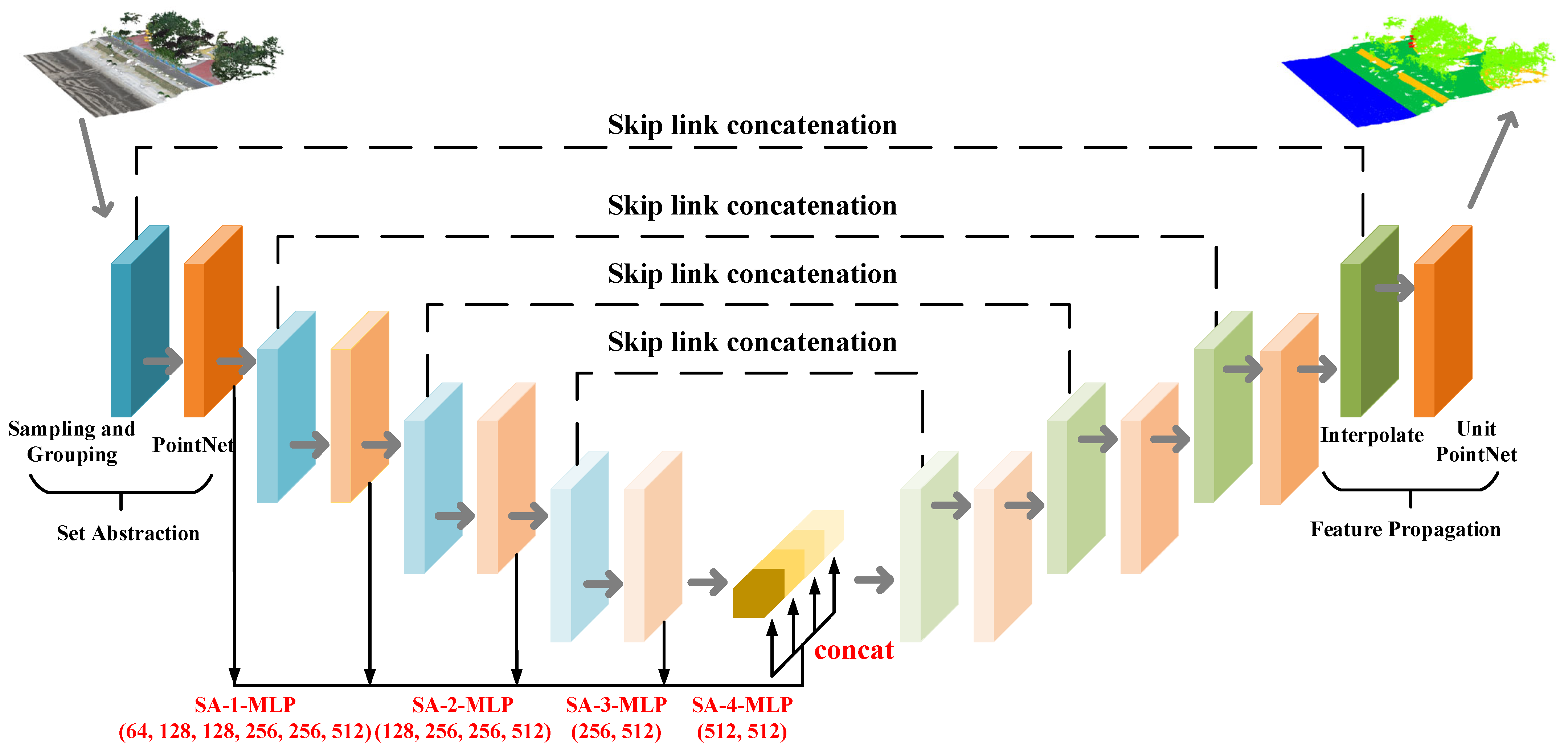
2.2.2. MLF-PointNet++ Model Construction
2.2.3. Focus Loss Function
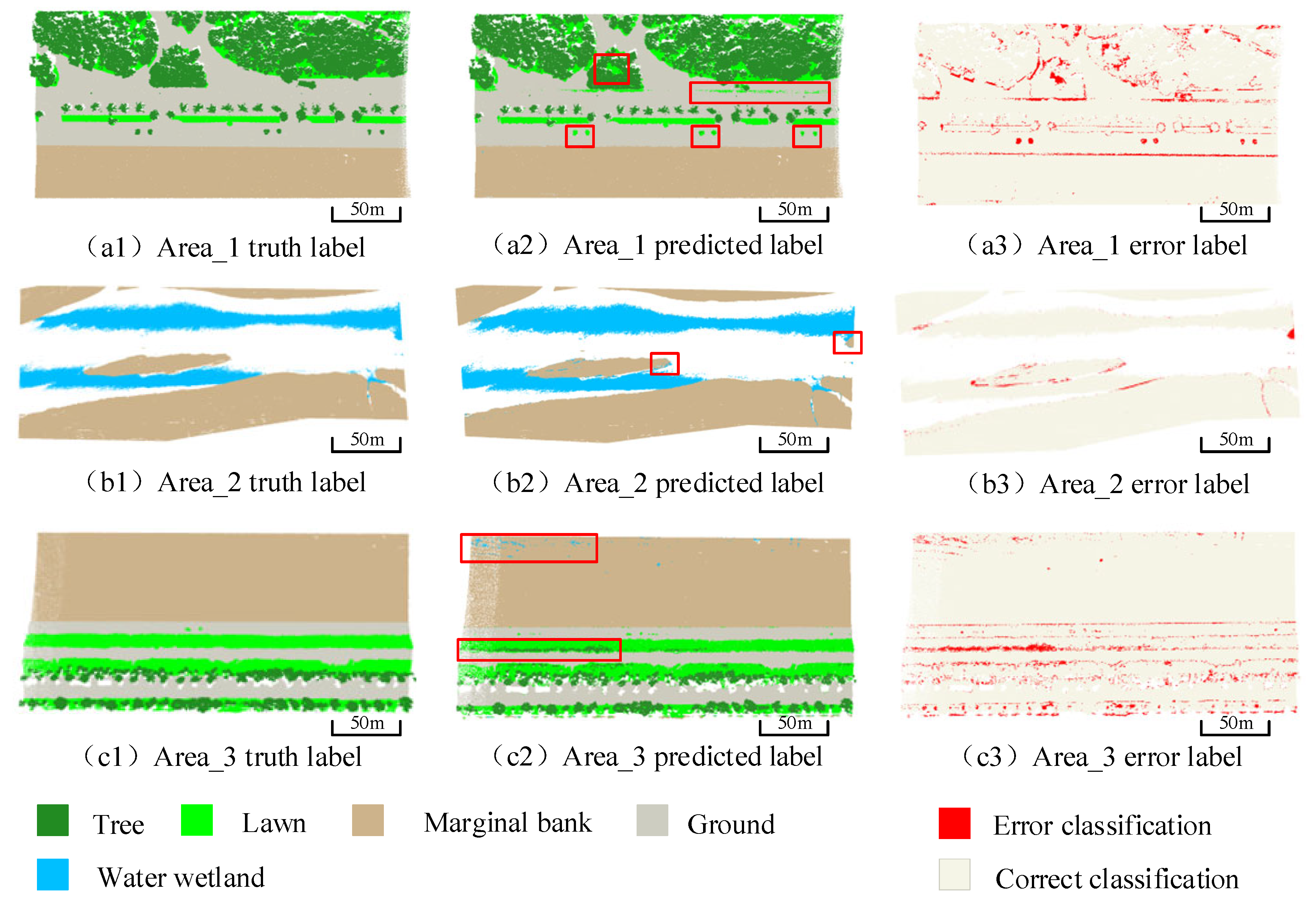
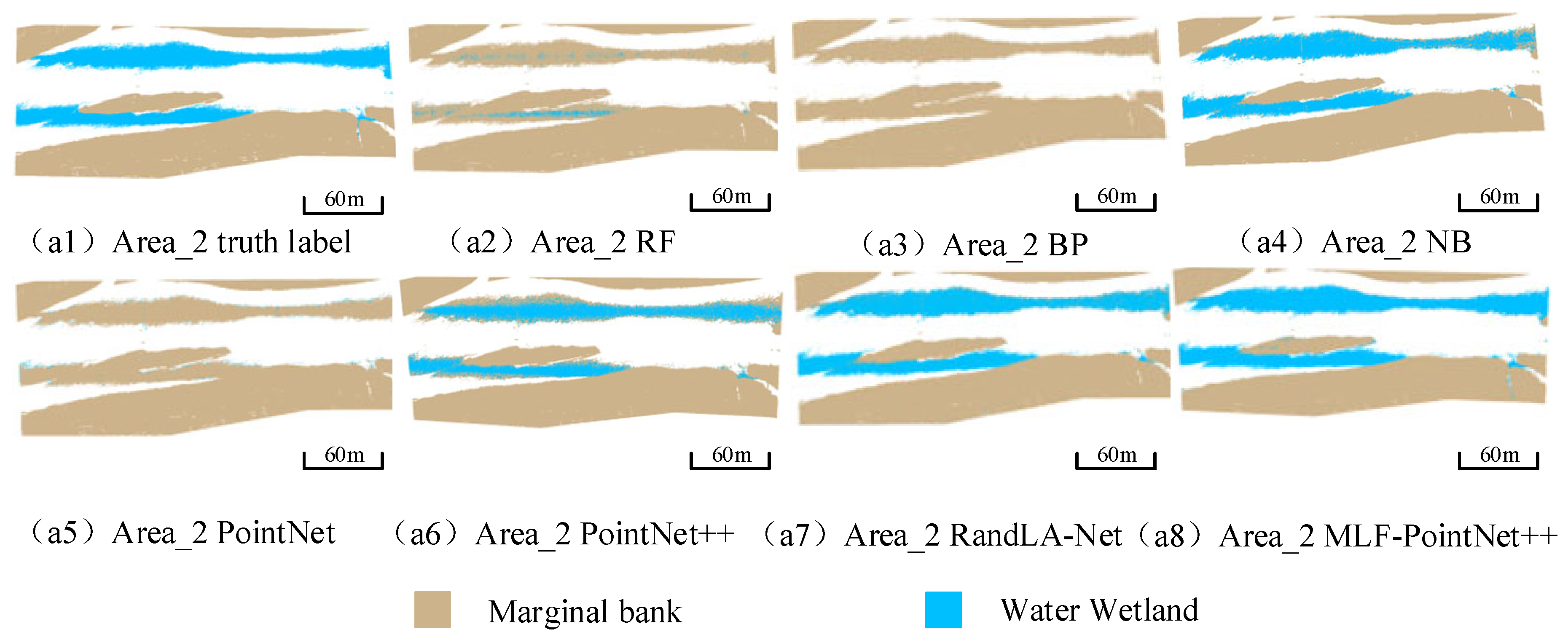
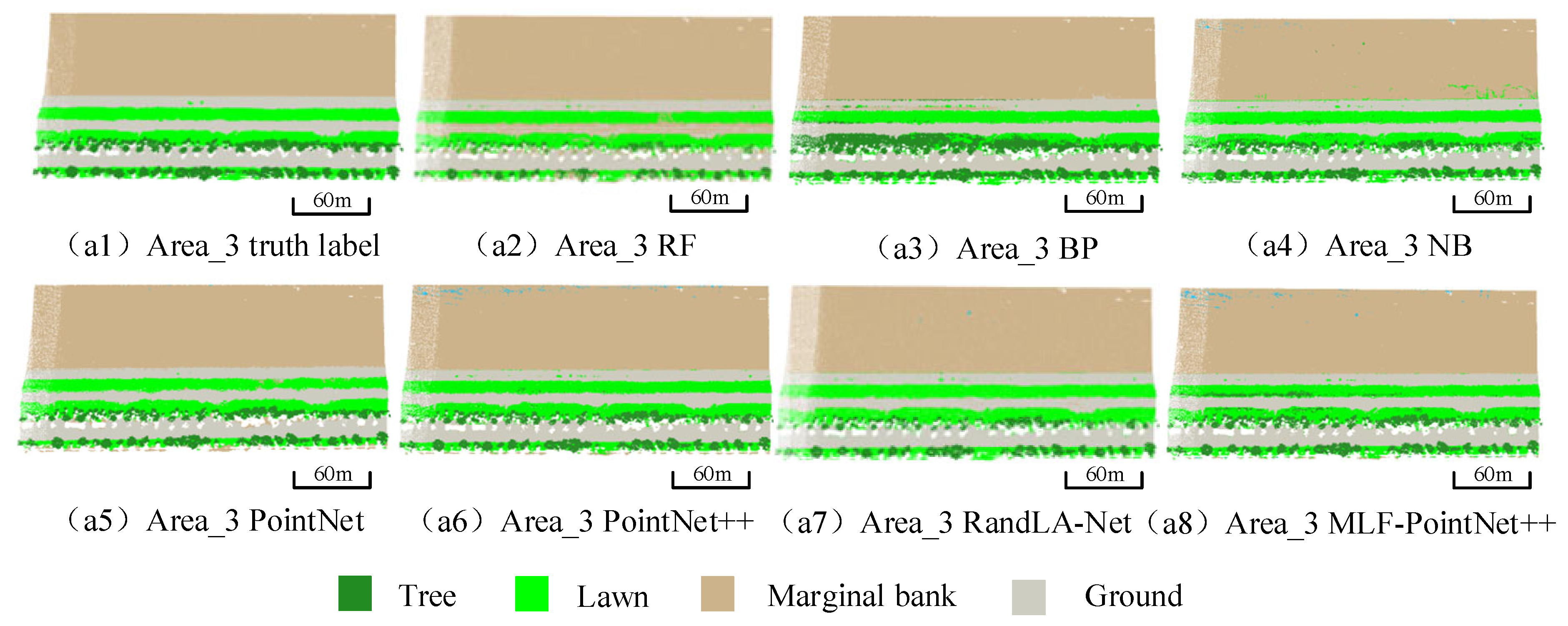
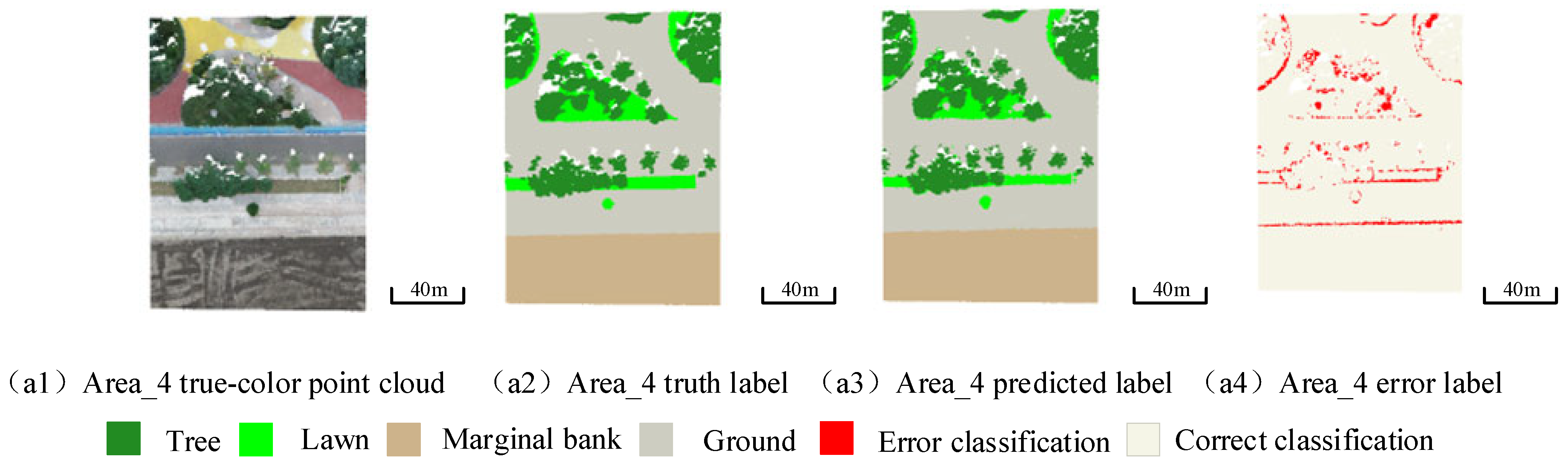
3. Results
3.1. Experimental Parameter Settings
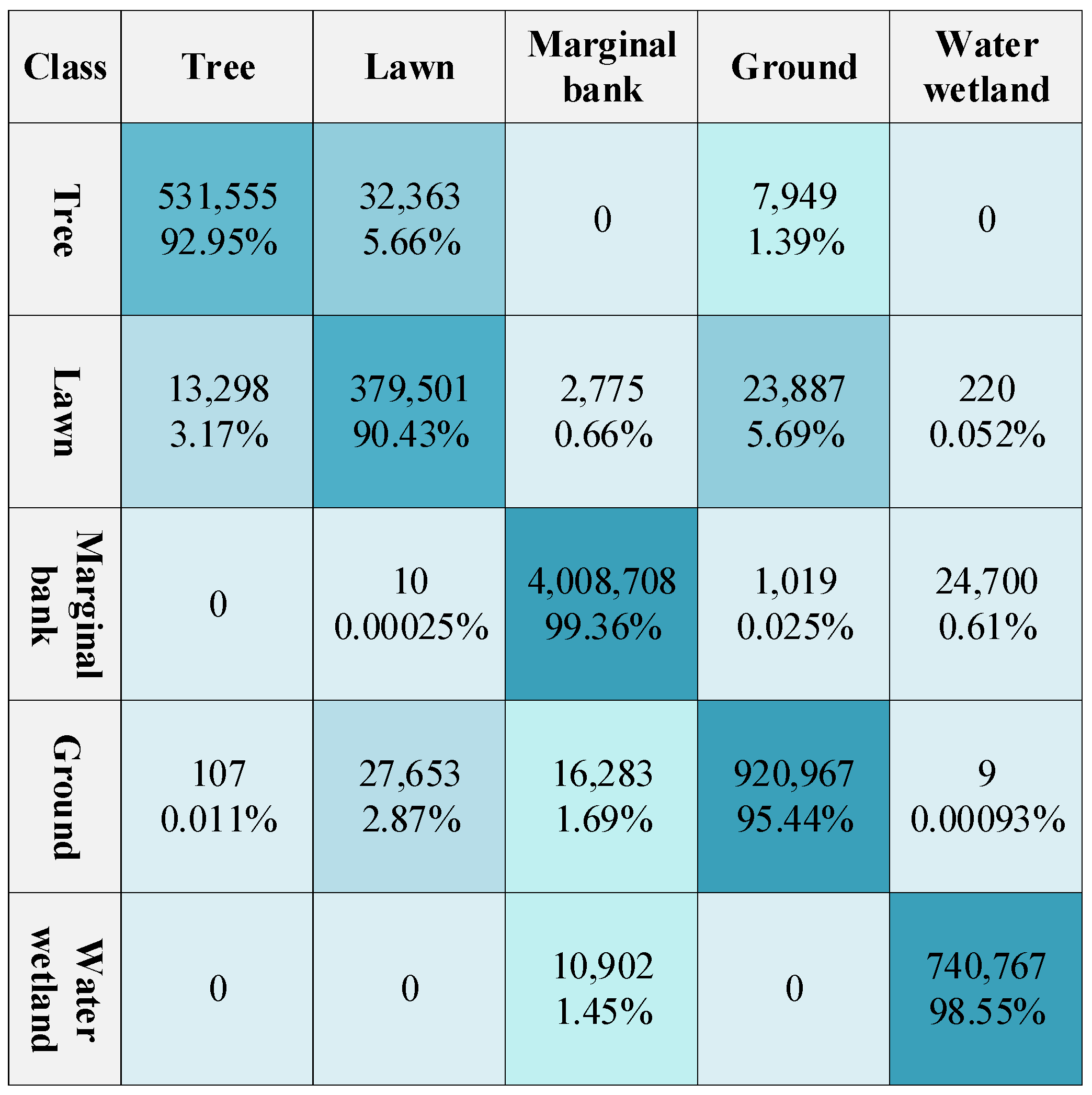
3.2. Experimental Results
4. Discussion
4.1. Auxiliary Feature Ablation Experiment
4.2. Loss Function Ablation Experiment
4.3. Epoch Discussion Experiment
4.4. Model Characterization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elliott, M.; Whitfield, A. Challenging paradigms in estuarine ecology and management estuarine. Coast. Shelf Sci. 2011, 94, 306–314. [Google Scholar] [CrossRef]
- Al-Mahfadi, A.; Dakki, M.; Alaoui, A.; Hichou, B. Classification of estuarine wetlands in Yemen using local and catchment descriptors. Estuaries Coasts 2021, 44, 1946–1974. [Google Scholar] [CrossRef]
- Pricope, N.; Halls, J.; Dalton, E.; Minei, A.; Chen, C.; Wang, Y. Precision Mapping of Coastal Wetlands: An Integrated Remote Sensing Approach Using Unoccupied Aerial Systems Light Detection and Ranging and Multispectral Data. J. Remote Sens. 2024, 4, 0169. [Google Scholar] [CrossRef]
- Chen, Y.; Wan, J.; Xi, Y.; Jiang, W.; Wang, M.; Kang, M. Extraction and classification of the supervised coastal objects based on HSRIs and a novel lightweight fully connected spatial dropout network. Wirel. Commun. Mob. Comput. 2022, 1, 2054877. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Feng, S.; Peng, B.; Huang, L.; Fatholahi, S.; Tang, L.; Li, J. An overview of shoreline mapping by using airborne LiDAR. Remote Sens. 2023, 15, 253. [Google Scholar] [CrossRef]
- Guo, F.; Meng, Q.; Li, Z.; Ren, G.; Wang, L.; Zhang, J. Multisource feature embedding and interaction fusion network for coastal wetland classification with hyperspectral and LiDAR data. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Benedetto, A.; Fiani, M. Integration of LiDAR data into a regional topographic database for the generation of a 3D city model. In Italian Conference on Geomatics and Geospatial Technologies; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Yip, K.; Liu, R.; Wu, J.; Hau, B.; Lin, Y.; Zhang, H. Community-based plant diversity monitoring of a dense-canopy and species-rich tropical forest using airborne LiDAR data. Ecol. Indic. 2024, 158, 111346. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Automatic structure detection in a point-cloud of an urban landscape. In Proceedings of the 2003 2nd GRSS/ISPRS Joint Workshop on Remote Sensing and Data Fusion over Urban Areas, Berlin, Germany, 22–23 May 2003; pp. 67–71. [Google Scholar]
- Vosselman, G.; Gorte, B.; Sithole, G. Change detection for updating medium scale maps using laser altimetry. International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2004, 34, 207–212. [Google Scholar]
- Pu, S.; Vosselman, G. Automatic extraction of building features from terrestrial laser scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 25–27. [Google Scholar]
- Vosselman, G.; Coenen, M.; Rottensteiner, F. Contextual segment-based classification of airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 2017, 128, 354–371. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, H.; Zhao, J.; Liu, H. Fast-spherical-projection-based point cloud clustering algorithm. Transp. Res. Rec. 2022, 2676, 315–329. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, X.; Ning, X. SVM-based classification of segmented airborne LiDAR point clouds in urban areas. Remote Sens. 2013, 5, 3749–3775. [Google Scholar] [CrossRef]
- Jiang, S.; Guo, W.; Fan, Y.; Fu, H. Fast semantic segmentation of 3D LiDAR point cloud based on random forest method. In China Satellite Navigation Conference; Springer Nature Singapore: Singapore, 2022; pp. 415–424. [Google Scholar]
- Hansen, S.; Ernstsen, V.; Andersen, M.; AI-Hamdani, Z.; Baran, R.; Niederwieser, M.; Steinbacher, F.; Kroon, A. Classification of boulders in coastal environments using random forest machine learning on topo-bathymetric LiDAR data. Remote Sens. 2021, 13, 4101. [Google Scholar] [CrossRef]
- Salti, S.; Tombari, F.; Di Stefano, L. SHOT: Unique signatures of histograms for surface and texture description. Comput. Vis. Image Underst. 2014, 125, 251–264. [Google Scholar] [CrossRef]
- Drost, B.; Ulrich, M.; Navab, N.; Ilic, S. Model globally, match locally: Efficient and robust 3D object recognition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.; Khan, F.; Shah, M. Transformers in vision: A survey. ACM Comput. Surv. (CSUR) 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Cheng, B.; Misra, I.; Schwing, A.; Kirillov, A.; Girdhar, R. Masked-attention mask transformer for universal image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1290–1299. [Google Scholar]
- Wang, C.; Bochkovskiy, A.; Liao, H. YOLOv7, Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view convolutional neural networks for 3D shape recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Feng, Y.; Zhang, Z.; Zhao, X.; Ji, R.; Gao, Y. GVCNN: Group-view convolutional neural networks for 3D shape recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 264–272. [Google Scholar]
- Wang, W.; Cai, Y.; Wang, T. Multi-view dual attention network for 3D object recognition. Neural Comput. Appl. 2022, 34, 3201–3212. [Google Scholar] [CrossRef]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Maturana, D.; Scherer, S. VoxNet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Riegler, G.; Osman Ulusoy, A.; Geiger, A. OctNet: Learning deep 3D representations at high resolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3577–3586. [Google Scholar]
- Bello, S.; Yu, S.; Wang, C.; Adam, J.; Li, J. Review: Deep learning on 3D point clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Qi, C.; Su, H.; Mo, K.; Guibas, L. Pointnet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.; Yi, L.; Su, H.; Guibas, L. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar]
- Nong, X.; Bai, W.; Liu, G. Airborne LiDAR point cloud classification using PointNet++ network with full neighborhood features. PLoS ONE 2023, 18, e0280346. [Google Scholar] [CrossRef] [PubMed]
- Jing, Z.; Guan, H.; Zhao, P.; Li, D.; Yu, Y.; Zang, Y.; Wang, H.; Li, J. Multispectral LiDAR point cloud classification using SE-PointNet++. Remote Sens. 2021, 13, 2516. [Google Scholar] [CrossRef]
- Wang, G.; Wang, L.; Wu, S.; Zu, S.; Song, B. Semantic segmentation of transmission corridor 3D point clouds based on CA-PointNet++. Electronics 2023, 12, 2829. [Google Scholar] [CrossRef]
- Lin, Y.; Knudby, A. Global automated extraction of bathymetric photons from ICESat-2 data based on a PointNet++ model. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103512. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, G.; Ao, J.; Wang, C.; Kang, R.; Wu, Y. Multi-information PointNet++ fusion method for DEM construction from airborne LiDAR data. Geocarto Int. 2023, 38, 2153929. [Google Scholar] [CrossRef]
- Fan, Z.; Wei, J.; Zhang, R.; Zhang, W. Tree species classification based on PointNet++ and airborne laser survey point cloud data enhancement. Forests 2023, 14, 1246. [Google Scholar] [CrossRef]
- Dai, W.; Jiang, Y.; Zeng, W.; Chen, R.; Xu, Y.; Zhu, N.; Xiao, W.; Dong, Z.; Guan, Q. MDC-Net: A multi-directional constrained and prior assisted neural network for wood and leaf separation from terrestrial laser scanning. Int. J. Digit. Earth 2023, 16, 1224–1245. [Google Scholar] [CrossRef]
- dji, “Technical Parameters”. Available online: https://enterprise.dji.com/cn/zenmuse-l1/specs (accessed on 21 March 2024).
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, S.; Xu, B.; Zhang, J. An improved progressive morphological filter for UAV-based photogrammetric point clouds in river bank monitoring. ISPRS J. Photogramm. Remote Sens. 2018, 146, 421–429. [Google Scholar] [CrossRef]
- Zhang, P.; He, H.; Wang, Y.; Liu, Y.; Lin, H.; Guo, L.; Yang, W. 3D urban buildings extraction based on airborne lidar and photogrammetric point cloud fusion according to U-Net deep learning model segmentation. IEEE Access 2022, 10, 20889–20897. [Google Scholar] [CrossRef]
- Lin, T.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]


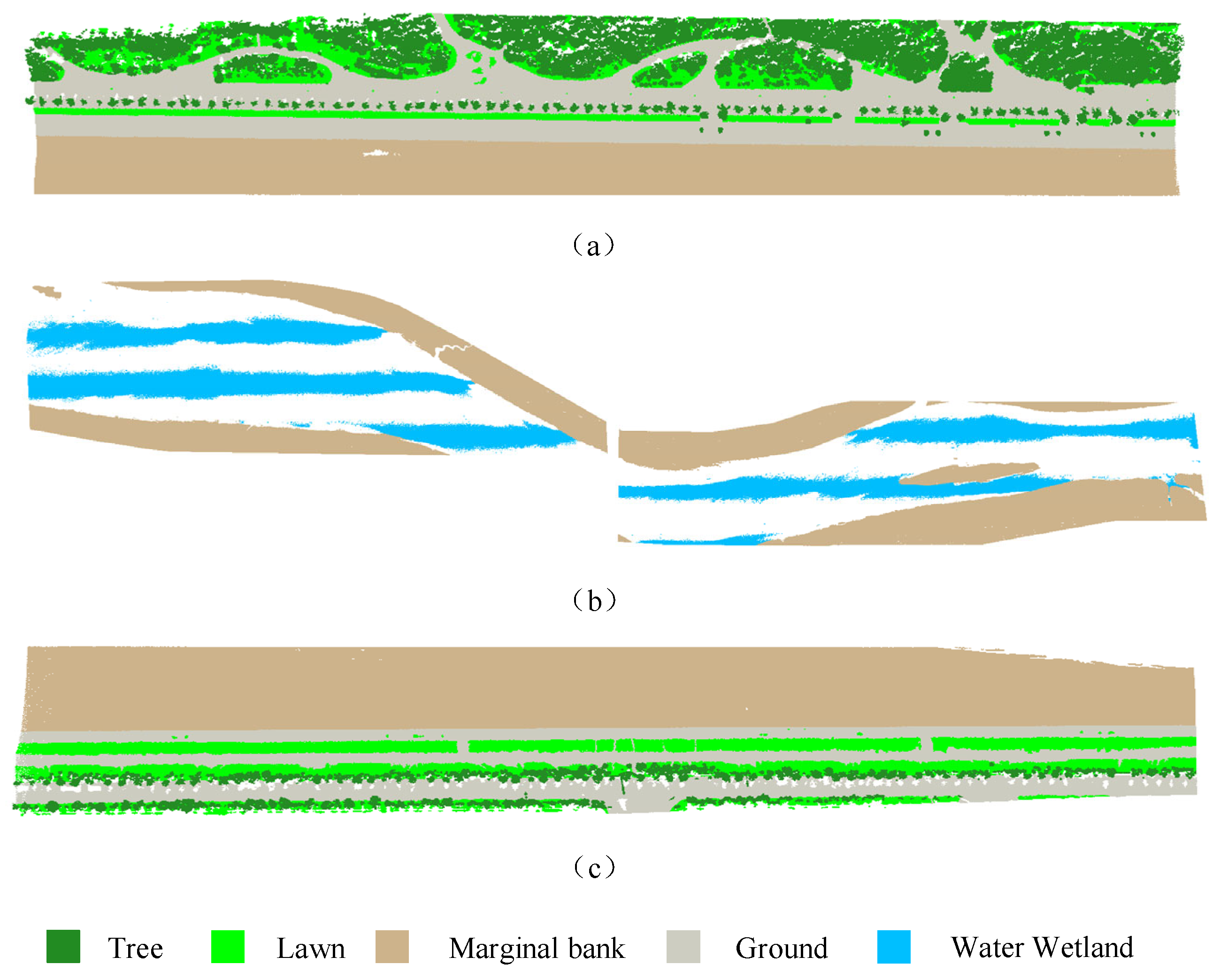








| Area | Tree | Lawn | Marginal Bank | Ground | Water Wetland |
|---|---|---|---|---|---|
| Area_1 | 1,508,987 | 765,610 | 16,206,559 | 1,901,110 | 0 |
| Area_2 | 638,955 | 1,419,880 | 3,362,761 | 2,149,429 | 0 |
| Area_3 | 0 | 0 | 13,455,119 | 0 | 3,440,744 |
| All points 44,849,154 | 2,147,942 | 2,185,490 | 33,024,439 | 4,050,539 | 3,440,744 |
| (4.8%) | (4.9%) | (73.6%) | (9.0%) | (7.7%) |
| Model | OA | mIOU | Kappa | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| RF | 0.843 | 0.641 | 0.706 | 0.711 | 0.909 | 0.755 |
| BP | 0.857 | 0.642 | 0.737 | 0.722 | 0.703 | 0.710 |
| NB | 0.949 | 0.837 | 0.917 | 0.912 | 0.904 | 0.907 |
| PointNet | 0.863 | 0.675 | 0.747 | 0.744 | 0.905 | 0.733 |
| PointNet++ | 0.956 | 0.870 | 0.924 | 0.919 | 0.944 | 0.929 |
| RandLA-Net | 0.969 | 0.900 | 0.948 | 0.942 | 0.952 | 0.946 |
| MLF-PointNet++ | 0.976 | 0.912 | 0.960 | 0.953 | 0.953 | 0.953 |
| Model | RF | BP | NB | PointNet | PointNet++ | RandLA-Net | MLF-PointNet++ |
|---|---|---|---|---|---|---|---|
| Tree | 0.799 | 0.945 | 0.944 | 0.895 | 0.927 | 0.903 | 0.930 |
| Lawn | 0.819 | 0.729 | 0.752 | 0.886 | 0.935 | 0.939 | 0.904 |
| Marginal bank | 0.998 | 0.999 | 0.972 | 0.999 | 0.995 | 0.996 | 0.994 |
| Ground | 0.722 | 0.935 | 0.954 | 0.932 | 0.935 | 0.922 | 0.954 |
| Water wetland | 0.220 | 0.000 | 0.939 | 0.008 | 0.806 | 0.952 | 0.986 |
| Test | OA | mIOU | Kappa | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| M1 | 0.948 | 0.845 | 0.910 | 0.901 | 0.932 | 0.913 |
| M2 | 0.958 | 0.866 | 0.929 | 0.918 | 0.937 | 0.926 |
| M3 | 0.965 | 0.887 | 0.941 | 0.932 | 0.947 | 0.939 |
| M4 | 0.976 | 0.912 | 0.960 | 0.953 | 0.953 | 0.953 |
| Test | OA | mIOU | Kappa | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| M5 | 0.972 | 0.898 | 0.953 | 0.940 | 0.951 | 0.944 |
| M6 | 0.963 | 0.878 | 0.937 | 0.931 | 0.937 | 0.933 |
| M7 | 0.976 | 0.913 | 0.960 | 0.953 | 0.953 | 0.953 |
| M8 | 0.970 | 0.904 | 0.950 | 0.951 | 0.950 | 0.948 |
| M9 | 0.971 | 0.897 | 0.951 | 0.941 | 0.949 | 0.944 |
| Epoch | OA | mIOU | Kappa | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| M10(16) | 0.9727 | 0.8910 | 0.9543 | 0.9384 | 0.9416 | 0.9393 |
| M11(32) | 0.9761 | 0.9125 | 0.9600 | 0.9534 | 0.9529 | 0.9529 |
| M12(64) | 0.9764 | 0.9136 | 0.9606 | 0.9543 | 0.9533 | 0.9536 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Xu, W.; Guo, Y.; Liu, Y.; Tian, Z.; Lv, J.; Guo, Z.; Guo, K. MLF-PointNet++: A Multifeature-Assisted and Multilayer Fused Neural Network for LiDAR-UAS Point Cloud Classification in Estuarine Areas. Remote Sens. 2024, 16, 3131. https://doi.org/10.3390/rs16173131
Ren Y, Xu W, Guo Y, Liu Y, Tian Z, Lv J, Guo Z, Guo K. MLF-PointNet++: A Multifeature-Assisted and Multilayer Fused Neural Network for LiDAR-UAS Point Cloud Classification in Estuarine Areas. Remote Sensing. 2024; 16(17):3131. https://doi.org/10.3390/rs16173131
Chicago/Turabian StyleRen, Yingjie, Wenxue Xu, Yadong Guo, Yanxiong Liu, Ziwen Tian, Jing Lv, Zhen Guo, and Kai Guo. 2024. "MLF-PointNet++: A Multifeature-Assisted and Multilayer Fused Neural Network for LiDAR-UAS Point Cloud Classification in Estuarine Areas" Remote Sensing 16, no. 17: 3131. https://doi.org/10.3390/rs16173131
APA StyleRen, Y., Xu, W., Guo, Y., Liu, Y., Tian, Z., Lv, J., Guo, Z., & Guo, K. (2024). MLF-PointNet++: A Multifeature-Assisted and Multilayer Fused Neural Network for LiDAR-UAS Point Cloud Classification in Estuarine Areas. Remote Sensing, 16(17), 3131. https://doi.org/10.3390/rs16173131






