CO2 Emissions Associated with Groundwater Storage Depletion in South Korea: Estimation and Vulnerability Assessment Using Satellite Data and Data-Driven Models
Abstract
1. Introduction
2. Study Area and Data
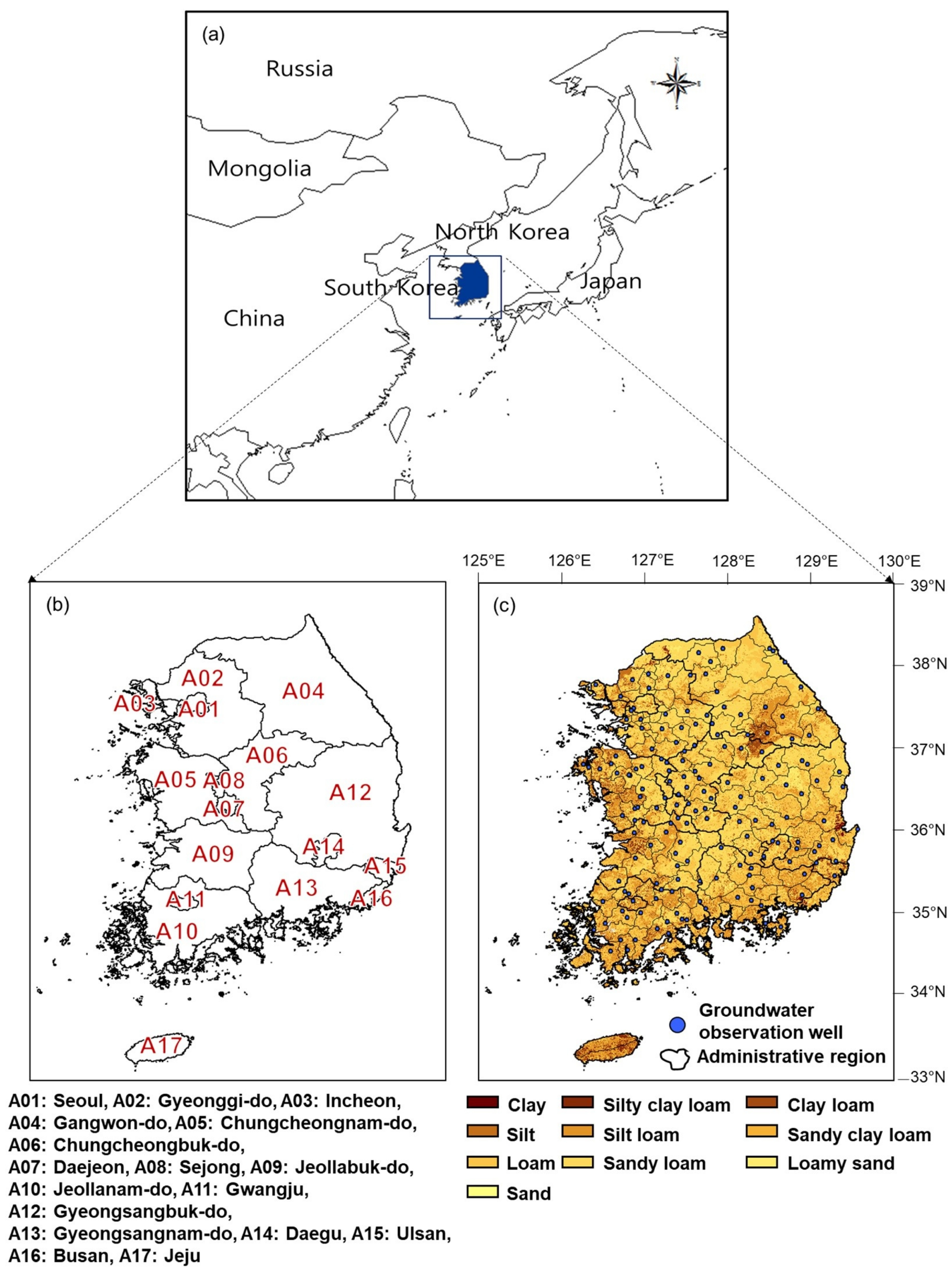
2.1. Study Area
2.2. Data
3. Methods
3.1. Prediction of GWSA
3.1.1. Machine and Deep Learning Models
3.1.2. Hyperparameter Tuning
3.2. Quantification of CO2 Emission Due to Groundwater Storage Depletion
3.2.1. Trend Analysis of Model-Predicted GWSA
3.2.2. CO2 Emission from Groundwater Storage Depletion
3.3. Determining Groundwater Storage Depletion and CO2 Emission Vulnerability Using Entropy Weight and TOPSIS Method
3.3.1. Selection of Indicators
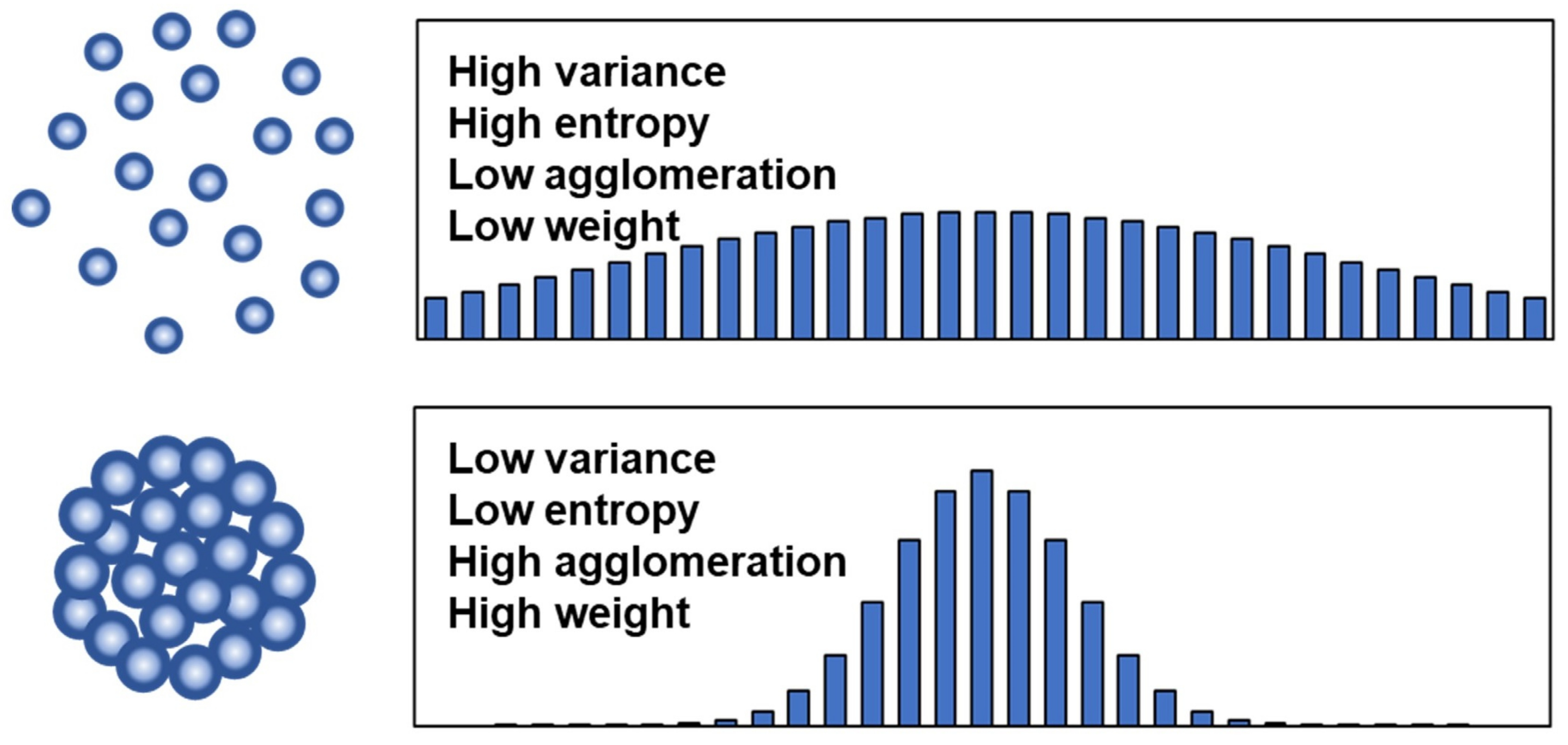
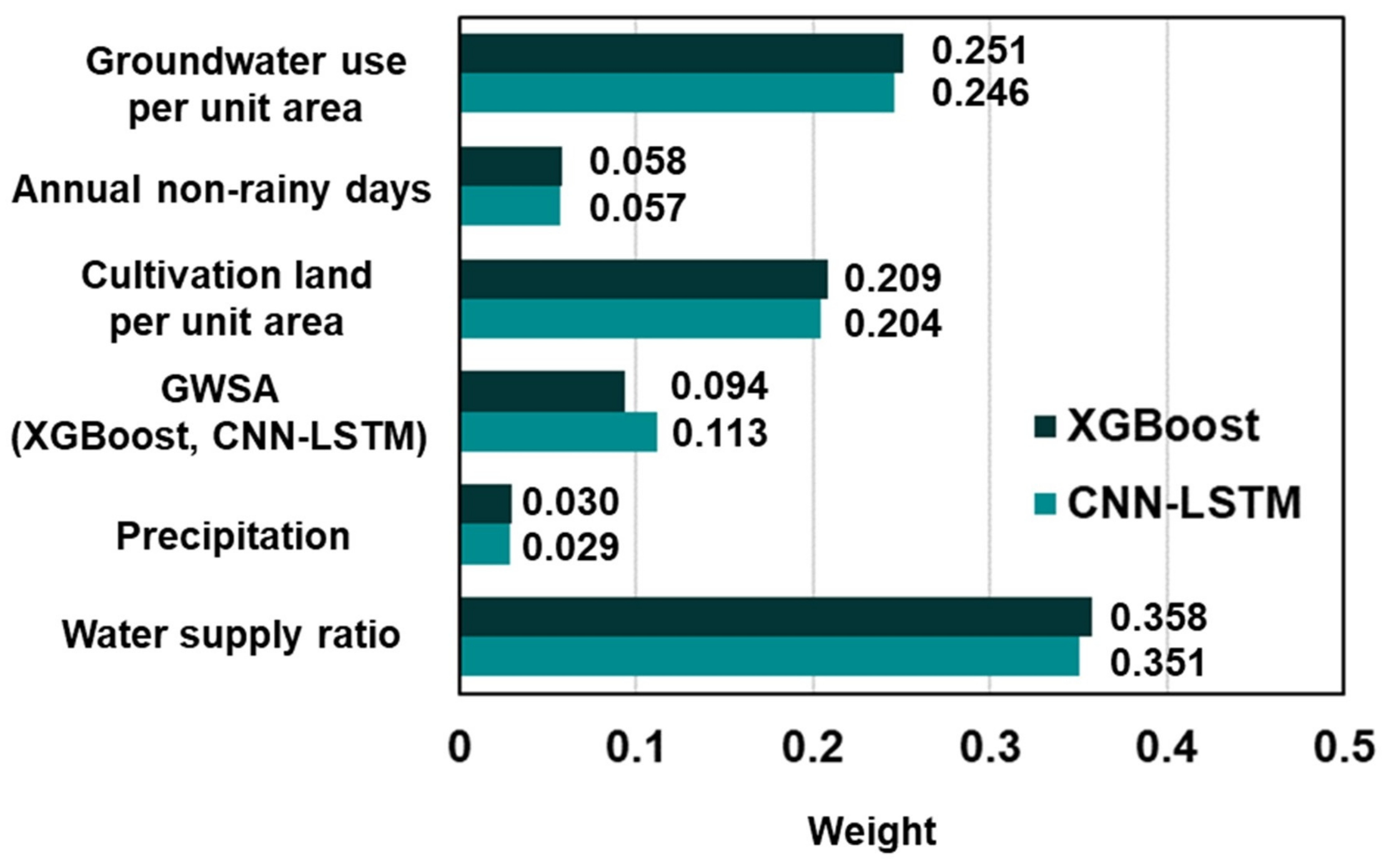
3.3.2. Determining Weights Using Entropy Weight Method
3.3.3. TOPSIS
4. Results
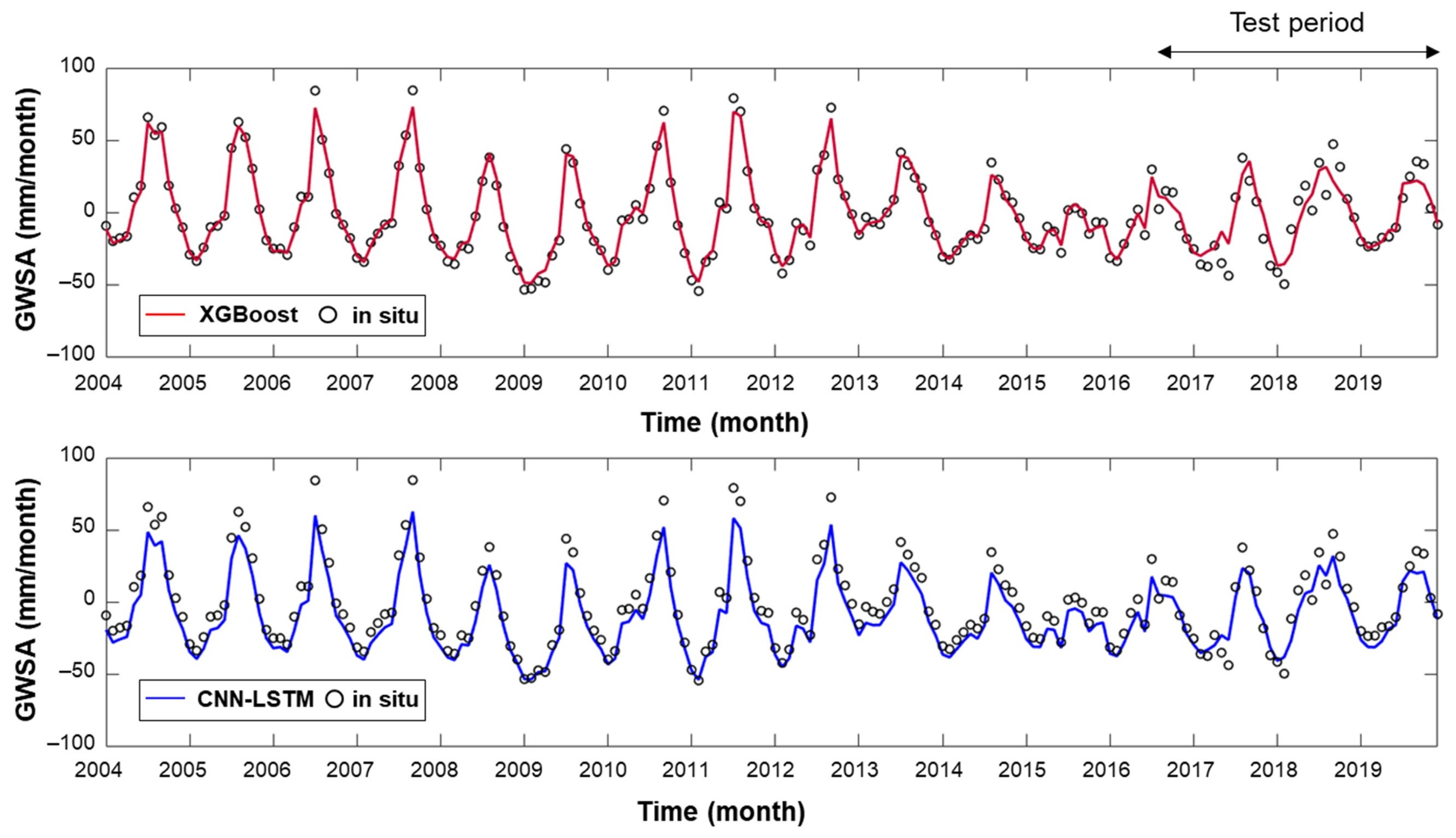
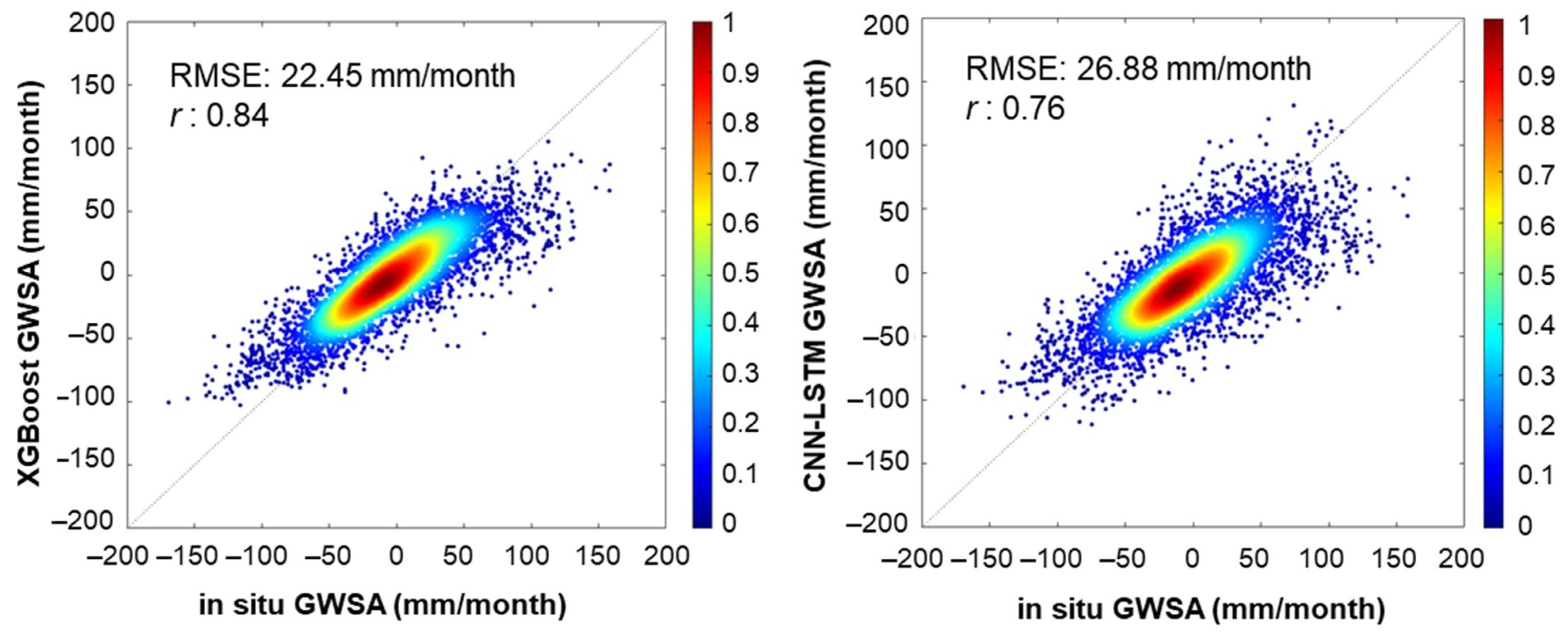
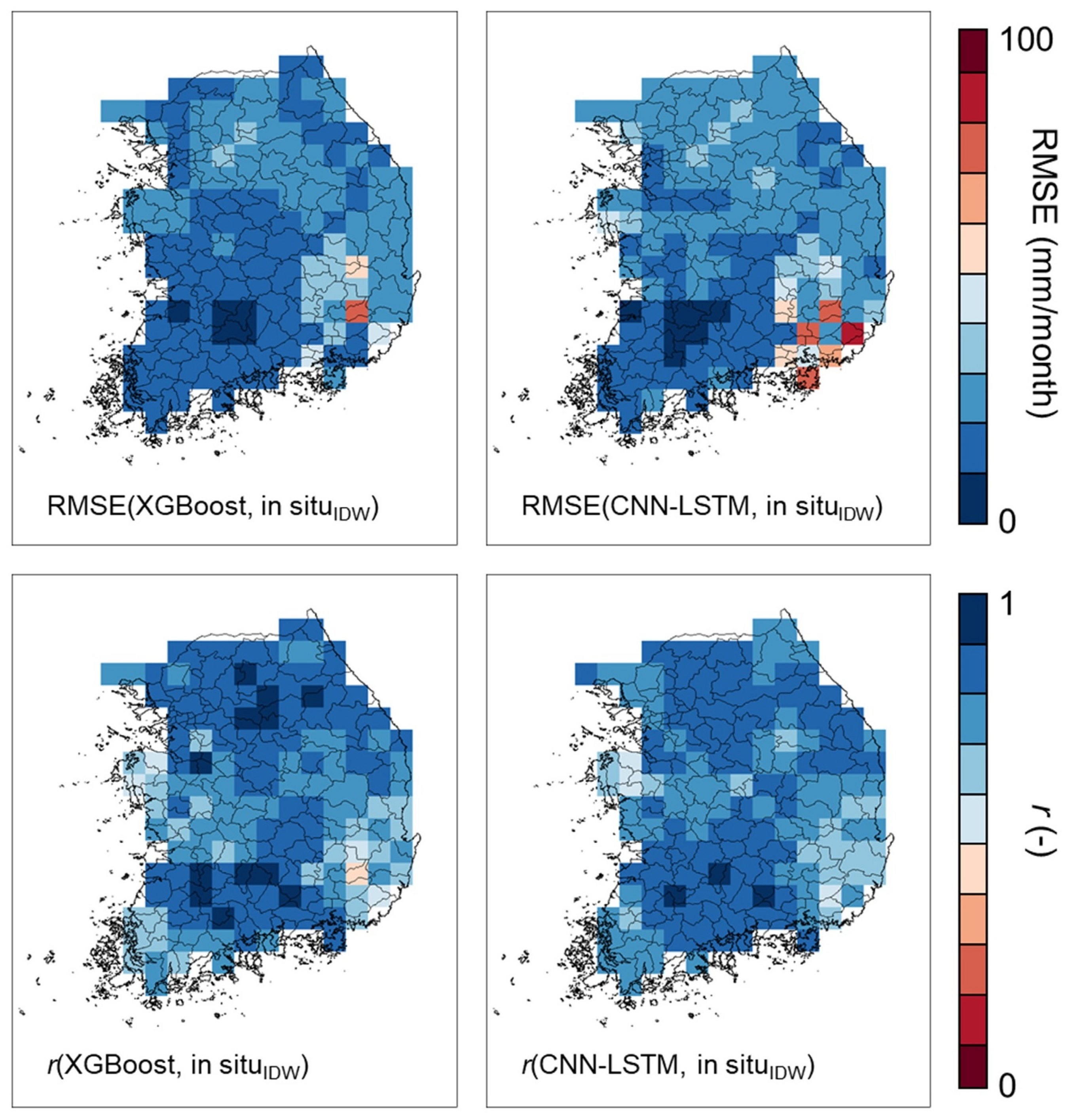
4.1. Model Performance in GWSA Prediction
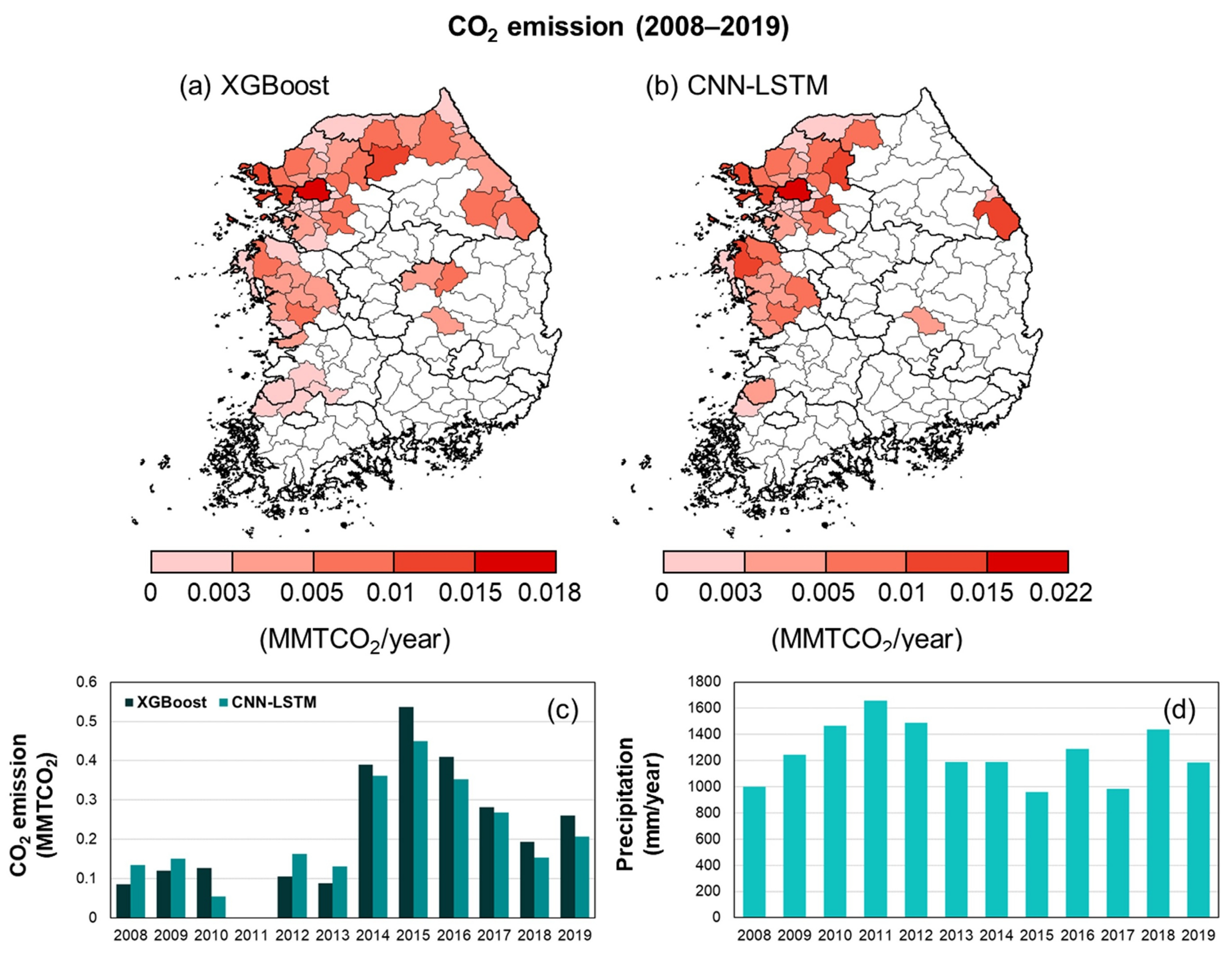
4.2. Estimation of CO2 Emission Due to Groundwater Storage Depletion
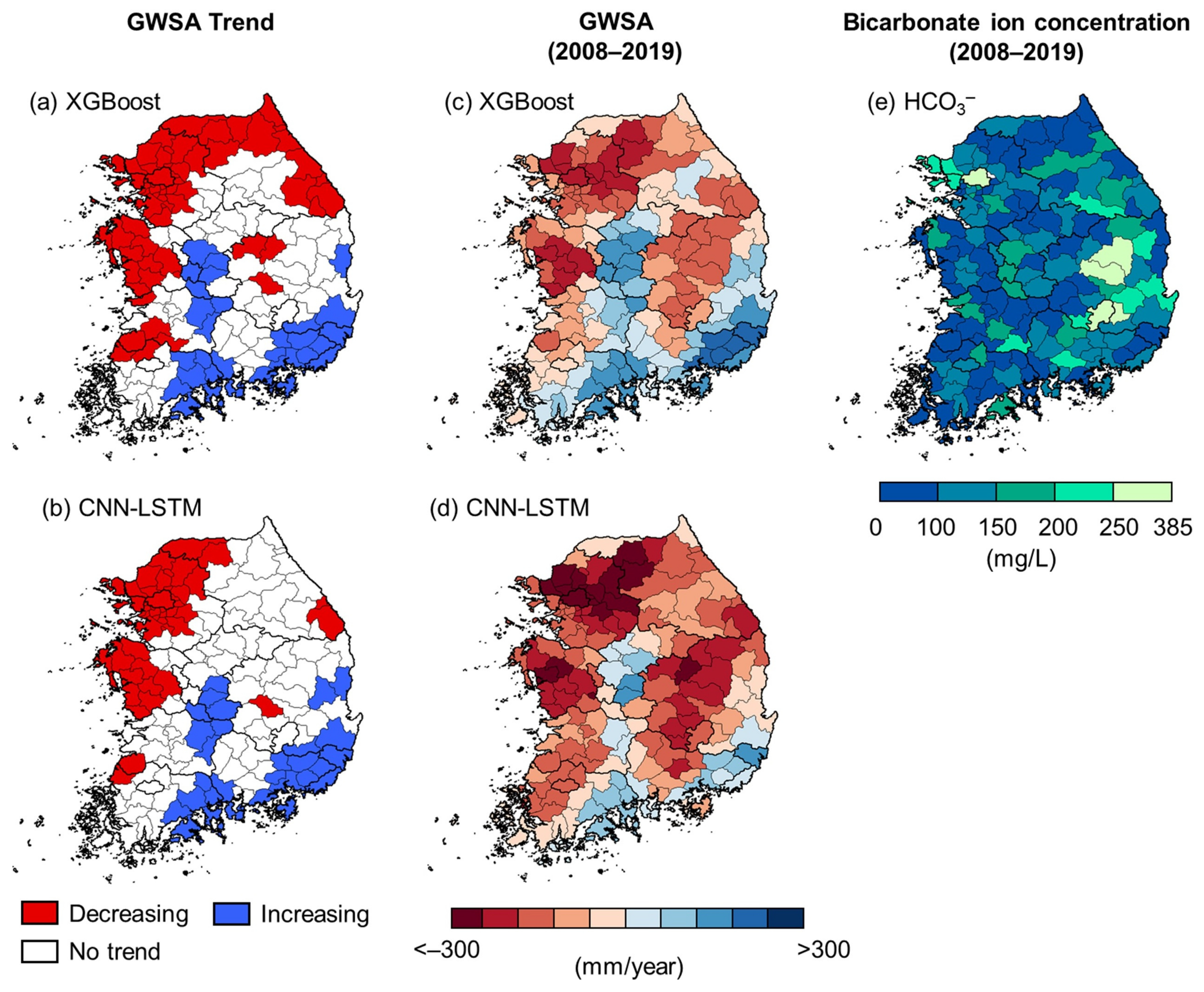
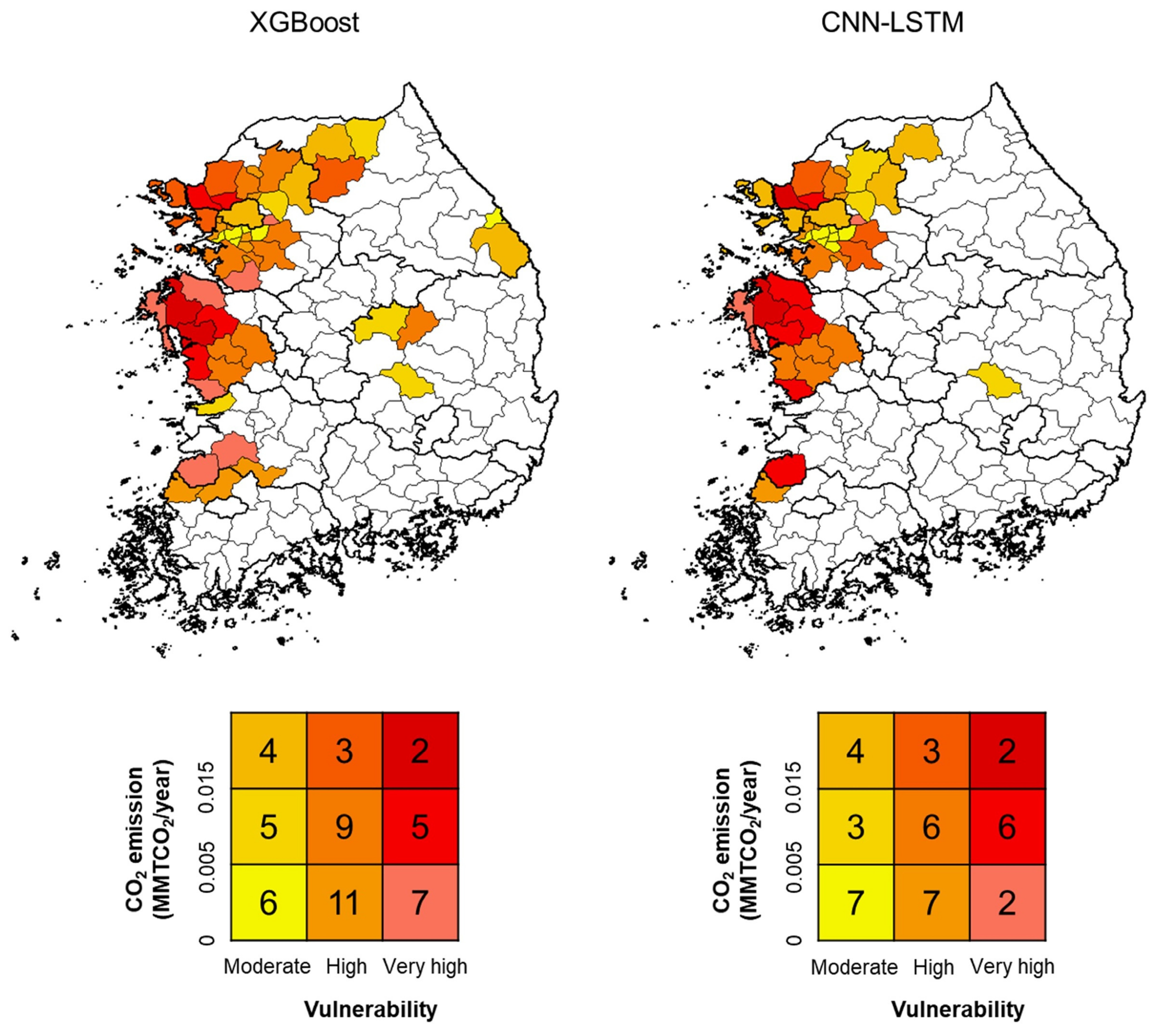
4.3. Evaluation of Groundwater Storage Depletion and CO2 Emission Vulnerability
5. Discussion
5.1. Groundwater Storage Depletion Using Data-Driven Models Based on Multi-Satellite and Reanalysis Data
5.2. Relationships between Groundwater Storage Depletion-Associated CO2 Emissions and Vulnerability
5.3. Significance and Limitations
6. Conclusions
- Data-driven models based on multi-satellite and reanalysis data can predict spatiotemporal GWSA with relatively high accuracy.
- CO2 emissions from groundwater storage depletion in South Korea were estimated to be 0.216 and 0.202 MMTCO2/year using XGBoost and CNN-LSTM models, respectively.
- Western regions of South Korea are highly or very highly vulnerable to groundwater storage depletion and prone to CO2 emissions.
- A correlation relationship was identified between the co-occurrence of CO2 emissions from groundwater storage depletion and vulnerability to groundwater storage depletion.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Fawzy, S.; Osman, A.I.; Doran, J.; Rooney, D.W. Strategies for Mitigation of Climate Change: A Review. Environ. Chem. Lett. 2020, 18, 2069–2094. [Google Scholar] [CrossRef]
- Armour, K.C. Energy Budget Constraints on Climate Sensitivity in Light of Inconstant Climate Feedbacks. Nat. Clim. Chang. 2017, 7, 331–335. [Google Scholar] [CrossRef]
- Ahlström, A.; Raupach, M.R.; Schurgers, G.; Smith, B.; Arneth, A.; Jung, M.; Reichstein, M.; Canadell, J.G.; Friedlingstein, P.; Jain, A.K.; et al. The Dominant Role of Semi-Arid Ecosystems in the Trend and Variability of the Land CO2 Sink. Science 2015, 348, 895–899. [Google Scholar] [CrossRef] [PubMed]
- Raymond, P.A.; Hartmann, J.; Lauerwald, R.; Sobek, S.; McDonald, C.; Hoover, M.; Butman, D.; Striegl, R.; Mayorga, E.; Humborg, C.; et al. Global Carbon Dioxide Emissions from Inland Waters. Nature 2013, 503, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Jasechko, S.; Seybold, H.; Perrone, D.; Fan, Y.; Shamsudduha, M.; Taylor, R.G.; Fallatah, O.; Kirchner, J.W. Rapid Groundwater Decline and Some Cases of Recovery in Aquifers Globally. Nature 2024, 625, 715–721. [Google Scholar] [CrossRef]
- Castellazzi, P.; Garfias, J.; Martel, R. Assessing the Efficiency of Mitigation Measures to Reduce Groundwater Depletion and Related Land Subsidence in Querétaro (Central Mexico) from Decadal InSAR Observations. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102632. [Google Scholar] [CrossRef]
- Ramjeawon, M.; Demlie, M.; Toucher, M. Analyses of Groundwater Storage Change Using GRACE Satellite Data in the Usutu-Mhlatuze Drainage Region, North-Eastern South Africa. J. Hydrol. Reg. Stud. 2022, 42, 101118. [Google Scholar] [CrossRef]
- Mohamed, A.; Alarifi, S.S.; Mohammed, M.A.A. Geophysical Monitoring of the Groundwater Resources in the Southern Arabian Peninsula Using Satellite Gravity Data. Alex. Eng. J. 2024, 86, 311–326. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, L.; Liu, Z.; Kittel, C.M.M.; Yao, Z.; Druce, D.; Wang, R.; Tøttrup, C.; Liu, J.; Jiang, H.; et al. Flow Regime Changes in the Lancang River, Revealed by Integrated Modeling with Multiple Earth observation Datasets. Sci. Total Environ. 2023, 862, 160656. [Google Scholar] [CrossRef]
- Rodell, M.; Velicongna, I.; Famiglietti, J.S. Satellite-Based Estimates of Groundwater Depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef]
- Wood, W.W.; Hyndman, D.W. Groundwater Depletion: A Significant Unreported Source of Atmospheric Carbon Dioxide. Earths Future 2017, 5, 1133–1135. [Google Scholar] [CrossRef]
- Macpherson, G.L. CO2 Distribution in Groundwater and the Impact of Groundwater Extraction on the Global C Cycle. Chem. Geol. 2009, 264, 328–336. [Google Scholar] [CrossRef]
- Rajan, A.; Ghosh, K.; Shah, A. Carbon Footprint of India’s Groundwater Irrigation. Caron Manag. 2020, 11, 265–280. [Google Scholar] [CrossRef]
- US EPA, Inventory of U.S. Greenhouse Gas Emissions and Sinks: 1990–2014; U.S. Environmental Protection Agency: Washington, DC, USA, 2016.
- Mishra, V.; Asoka, A.; Vatta, K.; Lall, U. Groundwater Depletion Associated CO2 Emissions in India. Earths Future 2018, 6, 1672–1681. [Google Scholar] [CrossRef]
- Rohde, M.M.; Biswas, T.; Housman, I.W.; Campbell, L.S.; Klausmeyer, K.R.; Howard, J.K. A Machine Learning Approach to Predict Groundwater Levels in California Reveals Ecosystems at Risk. Front. Earth Sci. 2021, 9, 784499. [Google Scholar] [CrossRef]
- Seo, J.Y.; Lee, S.-I. Predicting Changes in Spatiotemporal Groundwater Storage through the Integration of Multi-Satellite Data and Deep Learning Models. IEEE Access 2021, 9, 15757–157583. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Deep Learning shows Declining Groundwater Levels in Germany until 2100 due to Climate Change. Nat. Commun. 2022, 13, 1221. [Google Scholar] [CrossRef] [PubMed]
- Jaafarzadeh, M.S.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Rouhani, H. Groundwater Recharge Potential Zonation using an Ensemble of Machine Learning and Bivariate Statistical Models. Sci. Rep. 2021, 11, 5587. [Google Scholar] [CrossRef]
- Arabameri, A.; Pal, S.C.; Rezaie, F.; Nalivan, O.A.; Chowdhuri, I.; Saha, A.; Lee, S.; Moayedi, H. Modeling Groundwater Potential Using Novel GIS-Based Machine-Learning Ensemble Techniques. J. Hydrol. Reg. Stud. 2021, 36, 100848. [Google Scholar] [CrossRef]
- Madani, A.; Niyazi, B. Groundwater Potential Mapping Using Remote Sensing and Random Forest Machine Learning Model: A Case Study from Lower Part of Wadi Yalamlam, Western Saudi Arabia. Sustainability 2023, 15, 2772. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.J.M.; Pal, S.C.; Arshad, A.; Pham, Q.B.; Zhang, L. Constructing High-Resolution Groundwater Drought at Spatio-Temporal Scale Using GRACE Satellite Data based on Machine Learning in the Indus Basin. J. Hydrol. 2022, 612, 128295. [Google Scholar] [CrossRef]
- Seo, J.Y.; Lee, S.-I. Probabilistic Evaluation of Drought Propagation Using Satellite Data and Deep Learning Model: From Precipitation to Soil Moisture and Groundwater. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 6048–6061. [Google Scholar] [CrossRef]
- Zhu, R.; Zheng, H.; Jakeman, A.J.; Chiew, F.H.S. Multi-Timescale Performance of Groundwater Drought in Connection with Climate. Water Resour. Manag. 2023, 37, 3599–3614. [Google Scholar] [CrossRef]
- Sabzehee, F.; Amiri-Simkooei, A.R.; Iran-Pour, S.; Vishwakarma, B.D.; Kerachian, R. Enhancing Spatial Resolution of GRACE-Derived Groundwater Storage Anomalies in Urmia Catchment Using Machine Learning Downscaling Methods. J. Environ. Manag. 2023, 330, 117180. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, V.; Akyilmaz, O.; Shum, C.K.; Feng, W.; Yang, T.-Y.; Forootan, E.; Syed, T.H.; Haritashya, U.K.; Uz, M. Machine Learning based Downscaling of GRACE-Estimated Groundwater in Central Valley, California. Sci. Total Environ. 2023, 865, 161138. [Google Scholar] [CrossRef]
- Wang, J.; Xu, D.; Li, H. Constructing GRACE-Based 1 km Resolution Groundwater Storage Anomalies in Arid Regions Using an Improved Machine Learning Downscaling Method: A Case Study in Alxa League, China. Remote Sens. 2023, 15, 2913. [Google Scholar] [CrossRef]
- Yang, W.; Xu, K.; Lian, J.; Ma, C.; Bin, L. Integrated Flood Vulnerability Assessment Approach based on TOPSIS and Shannon Entropy Methods. Ecol. Indic. 2018, 89, 269–280. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2001: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- Adger, W.N. Vulnerability. Glob. Environ. Change 2006, 16, 268–281. [Google Scholar] [CrossRef]
- Koo, M.-S.; Hong, S.-Y.; Kim, J. An Evaluation of the Tropical Rainfall Measuring Mission (TRMM) Multi-Satellite Precipitation Analysis (TMPA) Data over South Korea. Asia Pac. J. Atmos. Sci. 2009, 45, 265–282. [Google Scholar]
- Seo, J.Y.; Lee, S.-I. Total Discharge Estimation in the Korean Peninsula Using Multi-Satellite Products. Water. 2017, 9, 532. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Cooley, T.; Anderson, G.P.; Felde, G.W.; Hoke, M.L.; Ratkowski, A.J.; Chetwynd, J.H.; Gardner, J.A.; Adler-Golden, S.M.; Matthew, M.W.; Berk, A.; et al. FLAASH, a MODTRAN4-Based Atmospheric Correction Algorithm, Its Application and Validation. In Proceedings of the IEEE International Symposium on Geoscience Remote Sensing, Toronto, ON, Canada, 24–28 June 2002. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The Gravity Recovery and Climate Experiment: Mission Overview and Early Result. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High Resolution CSR GRACE RL05 Mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Save, H. CSR GRACE and GRACE-FO RL06 Mascon Solutions v02. Available online: https://www2.csr.utexas.edu/grace/RL06_mascons.html (accessed on 20 November 2023).
- Wang, S.; Cui, G.; Li, X.; Liu, Y.; Li, X.; Tong, S.; Zhang, M. GRACE Satellite-Based Analysis of Spatiotemporal Evolution and Driving Factors of Groundwater Storage in the Black Soil Region of Northeast China. Remote Sens. 2023, 15, 704. [Google Scholar] [CrossRef]
- Cho, Y. Analysis of Terrestrial Water Storage Variations in South Korea Using GRACE Satellite and GLDAS Data in Google Earth Engine. Hydrol. Sci. J. 2024, 69, 1032–1045. [Google Scholar] [CrossRef]
- Guo, J.; Li, W.; Chnag, X.; Zhu, G.; Liu, X.; Guo, B. Terrestrial Water Storage Changes over Xinjiang Extracted by Combining Gaussian Filter and Multichannel Singular Spectrum Analysis from GRACE. Geophys. J. Int. 2018, 213, 397–407. [Google Scholar] [CrossRef]
- Nigatu, Z.M.; Fan, D.; You, W.; Melesse, A.M. Hydroclimatic Extremes Evaluation Using GRACE/GRACE-FO and Multidecadal Climatic Variables over the Nile River Basin. Remote Sens. 2021, 13, 651. [Google Scholar] [CrossRef]
- Qu, W.; Jin, Z.; Zhang, Q.; Gao, Y.; Zhang, P.; Chen, P. Estimation of Evapotranspiration in the Yellow River Basin from 2002 to 2020 based on GRACE and GRACE Follow-On Observations. Remote Sens. 2022, 14, 730. [Google Scholar] [CrossRef]
- Shi, Z.; Zheng, W.; Yin, W. Improving the Reliability of the Prediction of Terrestrial Water Storage in Yunnan Using the Artificial Neural Network Selective Joint Prediction Model. IEEE Access 2021, 9, 31865–31879. [Google Scholar] [CrossRef]
- Johnson, A.I. Specific Yield: Compilation of Specific Yields for Various Materials; Water Supply Paper, 1662-D; U.S. Government Printing Office: Washington, DC, USA, 1967; pp. D1–D70. [Google Scholar]
- Loheide, S.P., II; Butler, J.J., Jr.; Gorelick, S.M. Estimation of Groundwater Consumption by Phreatophytes Using Diurnal Water Table Fluctuations: A Saturated-Unsaturated Flow Assessment. Water Resour. Res. 2005, 41, W07030. [Google Scholar] [CrossRef]
- Niazkar, M.; Menapace, A.; Brentan, B.; Piraei, R.; Jimenez, D.; Dhawan, P.; Righetti, M. Applications of XGBoost in Water Resources Engineering: A Systematic Literature Review (Dec 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
- Yang, R.; Singh, S.K.; Tavakkoli, M.; Amiri, N.; Yang, Y.; Karami, M.A.; Rai, R. CNN-LSTM Deep Learning Architecture for Computer Vision-Based Modal Frequency Detection. Mech. Syst. Signal Process. 2020, 144, 106885. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter Optimization for Machine Learning Models based on Bayesian Optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; Van Nostrand Reinhold: New York, NY, USA, 1987. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of Prewhitening to Eliminate the Influence of Serial Correlation on the Mann-Kendall Test. Water Resour. Res. 2002, 38, 4-1–4-7. [Google Scholar] [CrossRef]
- Collaud Coen, M.; Andrews, E.; Bigi, A.; Martucci, G.; Romanens, G.; Vogt, F.P.A.; Vuilleumier, L. Effects of the Prewhitening Method, the Time Granularity, and the Time Segmentation on the Mann–Kendall Trend Detection and the Associated Sen’s slope. Atmos. Meas. Tech. 2020, 13, 6945–6964. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making: Methods and Applications; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Sahana, V.; Mondal, A.; Sreekumar, P. Drought Vulnerability and Risk Assessment in India: Sensitivity Analysis and Comparison of Aggregation Techniques. J. Environ. Manag. 2021, 299, 113689. [Google Scholar] [CrossRef]
- Shin, H.; Lee, G.; Lee, J.; Lee, J.; Park, M.; Park, C. An Approach to Drought Vulnerability Assessment Focused on Groundwater Wells in Upland Cultivation Areas of South Korea. Agronomy 2021, 11, 1783. [Google Scholar] [CrossRef]
- Meshram, S.G.; Alvandi, E.; Meshram, C.; Kahya, E.; AI-Quraishi, A.M.F. Application of SAW and TOPSIS in Prioritizing Watersheds. Water Resour. Manag. 2020, 34, 715–732. [Google Scholar] [CrossRef]
- Pathan, A.I.; Agnihotri, P.G.; Said, S.; Patel, D. AHP and TOPSIS based Flood Risk Assessment-A Case Study of the Navsari City, Gujarat, India. Environ. Monit. Assess. 2022, 194, 509. [Google Scholar] [CrossRef]
- Shafiei Shiva, J.; Chandler, D.G.; Kunkel, K.E. Mapping Heat Wave Hazard in Urban Areas: A Novel Multi-Criteria Decision Making Approach. Atmosphere 2022, 13, 1037. [Google Scholar] [CrossRef]
- Zong, J.; Wang, L.; Lu, C.; Du, Y.; Wang, Q. Mapping Health Vulnerability to Short-Term Summer Heat Exposure based on a Directional Interaction Network: Hotspots and Coping Strategies. Sci. Total Environ. 2023, 881, 163401. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Méndez, M.; Galván, B.; Salazar, D.; Greiner, D. Multiple-Objective Genetic Algorithm Using the Multiple Criteria Decision Making Method TOPSIS. In Lecture Notes in Economics and Mathematical Systems; Barichard, V., Ehrgott, M., Gandibleux, X., T’Kindt, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 145–154. [Google Scholar]
- Gautam, P.K.; Chandra, S.; Henry, P.K. Monitoring of the Groundwater Level Using GRACE with GLDAS Satellite Data in Ganga Plain, India to Understand the Challenges of Groundwater, Depletion, Problems, and Strategies for Mitigation. Environ. Chall. 2024, 15, 100874. [Google Scholar] [CrossRef]
- Panday, D.P.; Kumar, M. Application of Remote Sensing Techniques to Deal with Scale Aspects of GRACE Data to Quantify Groundwater Levels. MethodsX 2023, 10, 102108. [Google Scholar] [CrossRef] [PubMed]
- Kazakis, N.; Karakatsanis, D.; Ntona, M.M.; Polydoropoulos, K.; Zavridou, E.; Voudouri, K.A.; Busico, G.; Kalaitzidou, K.; Patsialis, T.; Perdikaki, M.; et al. Groundwater Depletion. Are Environmentally Friendly Energy Recharge Dams a Solution? Water 2024, 16, 1541. [Google Scholar] [CrossRef]



| Variables | Data | Properties | Reference |
|---|---|---|---|
| P | TMPA3B43V7 | 0.25° resolution, January 2003–December 2019 | https://disc.gsfc.nasa.gov/datasets/TRMM_3B43_7/summary, accessed on 20 November 2023 |
| T and SM | GLDAS NOAH025_M | 0.25° resolution, January 2003–December 2019 | https://ldas.gsfc.nasa.gov/gldas, accessed on 20 November 2023 |
| NDVI and MNDWI | Landsat 5 and 8 | 30m resolution, January 2003–February 2013 (Landsat 5) March 2013–December 2019 (Landsat 8) | https://earthexplorer.usgs.gov, accessed on 20 November 2023 |
| TWSA | CSR RL06M | 0.25° resolution, January 2003–April 2017 (GRACE) June 2018–December 2019 (GRACE-FO) | https://grace.jpl.nasa.gov, accessed on 20 November 2023 |
| Model | Hyperparameter | Setting Value Range |
|---|---|---|
| XGBoost | Number of estimators | {1, …, 1000} |
| Maximum depth | {3, 5, …, 15} | |
| Minimum child weight | {1, 2, …, 9} | |
| Subsample | {0.5, 0.6, …, 0.9} | |
| Colsample_bytree | {0.5, 0.6, …, 0.9} | |
| Gamma | {0, 0.1, …, 0.7} | |
| Lambda | {0, …, 100} | |
| Alpha | {0, …, 100} | |
| Learning rate | {0.001, …, 0.01} | |
| Time lags (month) | {1, 2, …, 12} | |
| CNN-LSTM | Number of filters | {16, …, 128} |
| Number of hidden layers | {1, 2, 3} | |
| Hidden unit | {0, …, 100} | |
| Dropout | {0.1, 0.2, …, 0.5} | |
| Learning rate | {0.001, …, 0.01} | |
| Epochs | {1, 2, …, 100} | |
| Iteration | {1, 2, …, 100} | |
| Time lags (month) | {1, 2, …, 12} |
| Effect | Indicators | Source | Period |
|---|---|---|---|
| Positive | Groundwater use per unit area (m3/year/km2) | Korea Groundwater Annual Report | 2004–2019 |
| Annual non-rainy days (day) | Korea Annual Hydrological Report | ||
| Cultivation land per unit area (%) | Korean Statistical Information Service | ||
| Negative | Annual GWSA (mm/year) | XGBoost and CNN-LSTM models | |
| Annual precipitation (mm/year) | Korea Annual Hydrological Report | ||
| Water supply ratio (%) | Waterworks Statistics |
| Model | Hyperparameter | Optimal Value |
|---|---|---|
| XGBoost | Number of estimators | 88 |
| Maximum depth | 5 | |
| Minimum child weight | 5 | |
| Subsample | 0.7 | |
| Colsample_bytree | 0.8 | |
| Gamma | 0.0 | |
| Lambda | 1.0 | |
| Alpha | 0.0 | |
| Learning rate | 0.1 | |
| Time lags (month) | 8 | |
| CNN-LSTM | Number of filters | 72 |
| Number of hidden layers | 2 | |
| Hidden unit | 70 (layer 1), 60 (layer 2) | |
| Dropout | 0.01 | |
| Learning rate | 0.01 | |
| Epochs | 60 | |
| Iteration | 50 | |
| Time lags (month) | 7 |
| Sector | CO2 Emission (MMTCO2/Year) | Percentage (%) | |
|---|---|---|---|
| Energy | 585.408 | 86.064 | |
| Industry | 53.690 | 7.893 | |
| Agriculture | Rice paddies | 7.070 | 1.039 |
| Farmland soil | 5.199 | 0.764 | |
| Livestock manure treatment | 4.662 | 0.685 | |
| Livestock enteric fermentation | 4.305 | 0.633 | |
| Crop residue burning | 0.017 | 0.002 | |
| Land use Land use change | Farmland | 2.944 | 0.433 |
| Wetland | 0.312 | 0.046 | |
| Waste | Landfill | 7.641 | 1.123 |
| Burning | 6.499 | 0.956 | |
| Wastewater treatment | 1.716 | 0.252 | |
| Etc. | 0.516 | 0.076 | |
| Groundwater storage depletion | 0.202–0.216 | 0.030–0.032 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, J.Y.; Lee, S.-I. CO2 Emissions Associated with Groundwater Storage Depletion in South Korea: Estimation and Vulnerability Assessment Using Satellite Data and Data-Driven Models. Remote Sens. 2024, 16, 3122. https://doi.org/10.3390/rs16173122
Seo JY, Lee S-I. CO2 Emissions Associated with Groundwater Storage Depletion in South Korea: Estimation and Vulnerability Assessment Using Satellite Data and Data-Driven Models. Remote Sensing. 2024; 16(17):3122. https://doi.org/10.3390/rs16173122
Chicago/Turabian StyleSeo, Jae Young, and Sang-Il Lee. 2024. "CO2 Emissions Associated with Groundwater Storage Depletion in South Korea: Estimation and Vulnerability Assessment Using Satellite Data and Data-Driven Models" Remote Sensing 16, no. 17: 3122. https://doi.org/10.3390/rs16173122
APA StyleSeo, J. Y., & Lee, S.-I. (2024). CO2 Emissions Associated with Groundwater Storage Depletion in South Korea: Estimation and Vulnerability Assessment Using Satellite Data and Data-Driven Models. Remote Sensing, 16(17), 3122. https://doi.org/10.3390/rs16173122







