Noise-Disruption-Inspired Neural Architecture Search with Spatial–Spectral Attention for Hyperspectral Image Classification
Abstract
1. Introduction
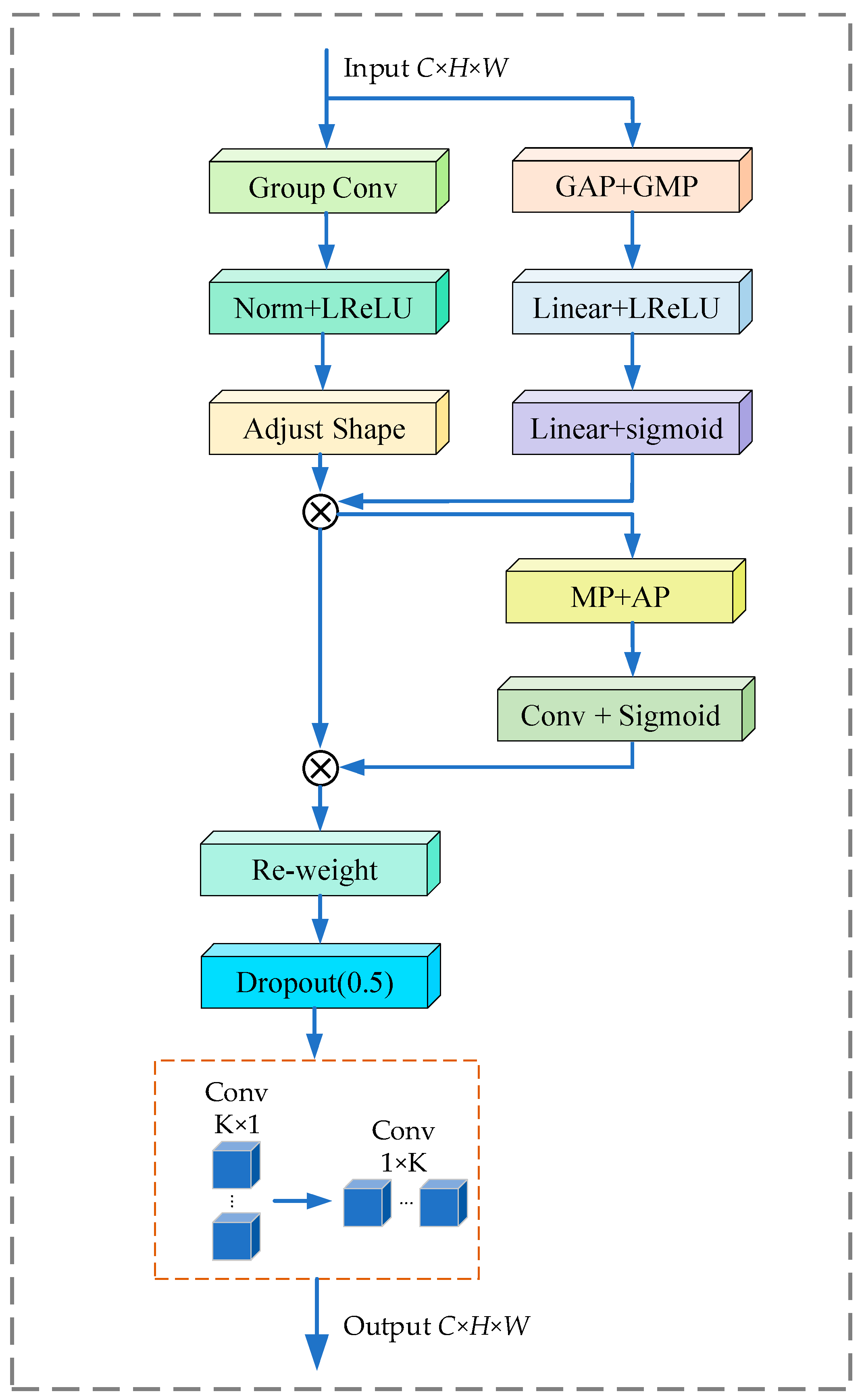
- By investigating the characteristics of HSI, a new and efficient search space is proposed, which consists of receptive field spatial–spectral attention separable convolution operators. The convolution operators focus on receptive field features, separately weighting spatial and spectral attention to ensure different attention weights for each spectral and spatial dimension. Accordingly, the operators can effectively extract discriminatory features from HSI data.
- The proposed RFSS-NAS successfully solves the unfair competition problem in the search process through the Noisy-DARTS strategy, and efficiently realizes the automatic DL network architecture design for the HSIC task. Therefore, the efficient neural architecture search strategy proposed in the paper automatically builds task-driven deep-learning optimal models for HSI with different characteristics.
- HSIs have an uneven distribution of sample sizes for certain classes, creating a long-tailed distribution phenomenon. Therefore, we proposed a novel fusion loss function by combining the label smoothing (SM) loss function with the polynomial expansion perspective (PL) loss function to cope with the phenomenon of long-tailed distributions in unbalanced HSI datasets.
- By analyzing the effectiveness of architectures, we determined that RFSS-NAS improves classification accuracy by searching for effective architectures rather than simply integrating operations. The searched architectures possess topological and local optimality.
2. Materials and Methods
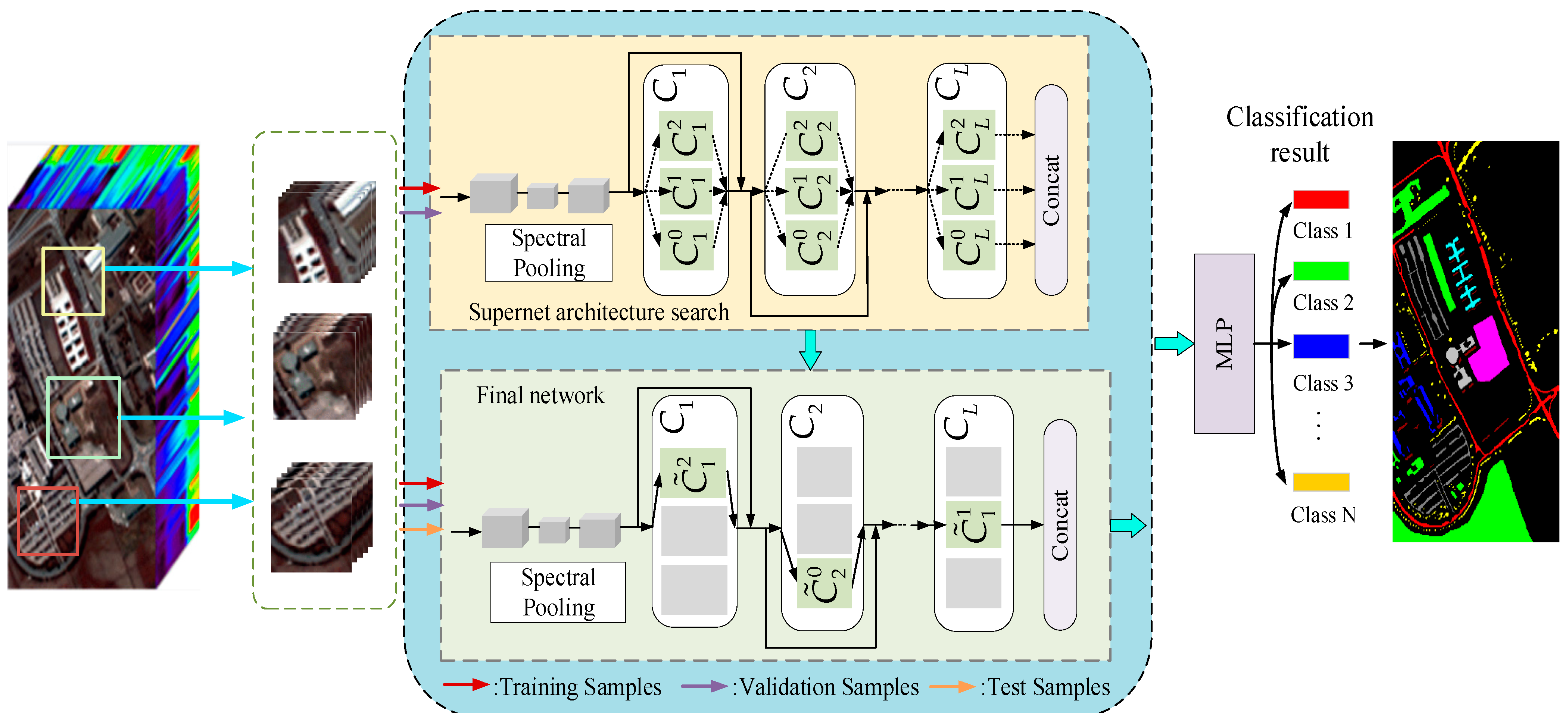
2.1. Overall Framework
2.2. Neural Architecture Search
2.2.1. Modular Search Space
2.2.2. Search Strategy
2.2.3. Performance Evaluation Strategy
| Algorithm 1 |
| Input: Training set |
| Initialization: Defining the search space (including candidate operation set ), construct supernet (network weights ), noise standard variance , batch size = 32, epochs = 100. |
| Search Stage: While reach epochs do 1. Inject Gaussian noise into the output of skip-connections 2. 3. Update the weight 4. 5. Fix and update the architecture parameters End while |
| Deducing the Final Network: Derive sub-network consisting of the operations with the highest weights at each layer is selected as the final network according to learned . |
| Final Network: Input training set and validation set to train the final network and optimizes weighs . |
| Classification Stage: for sample in : Output the predicted results. Obtain classification results. |
3. Results
3.1. Datasets Description
- The KSC dataset was taken by the AVIRIS sensor at the Kennedy Space Center in Florida in 1996. There are 224 bands in the raw data, and, after removing the water vapor noise and low signal-to-noise bands, 176 bands remained for the experiments. The spectral range is 0.4–2.5 µm and the spatial resolution is 18 m with 13 categories. The KSC dataset labeled sample information is described in Table 2.
- 2.
- The PU dataset was gathered on the campus map of the Pavia University in northern Italy in 2003. The spatial resolution is 1.3 m size of 610 × 340 pixels. It covers nine different urban categories, totaling 42,776 samples and retaining 103 spectral bands, with a spectral region of 0.43–0.86 µm. The PU dataset labeled sample information is described in Table 3.
- 3.
- The HU dataset was acquired in 2013 by the ITRES CASI-1500 sensor, which covered the University of Houston campus and surrounding urban land area. The spatial dimension is 329 × 1905 pixels with spatial resolution of 2.5 m. It contains a total of 54,129 samples, covering 15 land cover categories and retaining 144 spectral bands for research with a spectral region of 0.36–1.05 µm. The HU dataset labeled sample information is described in Table 4.
3.2. Implementation Details
3.3. Comparison of the Proposed RFSS-NAS with the State-of-the-Art Methods
3.3.1. Quantitative Analysis
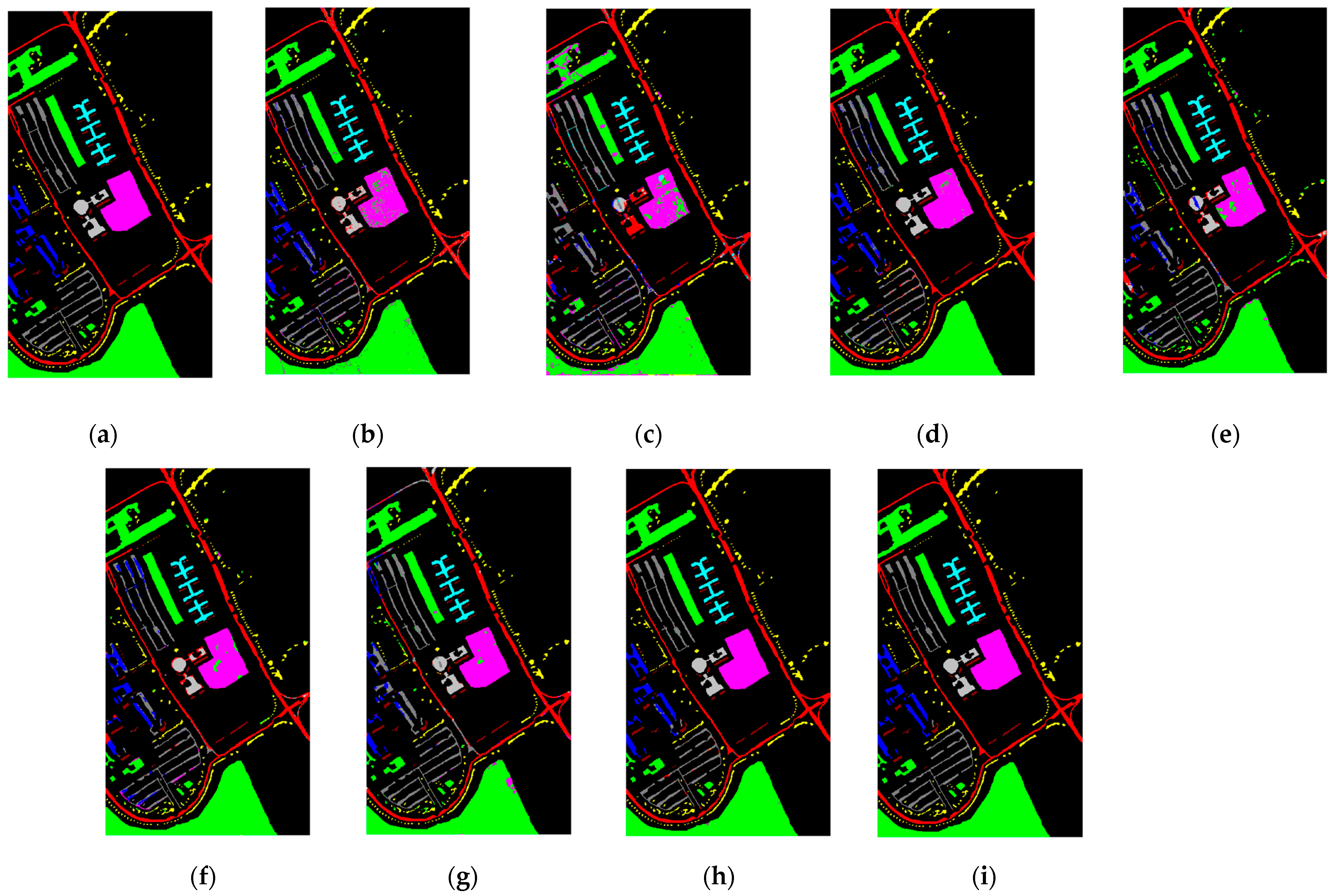
3.3.2. Qualitative Analysis
4. Discussion
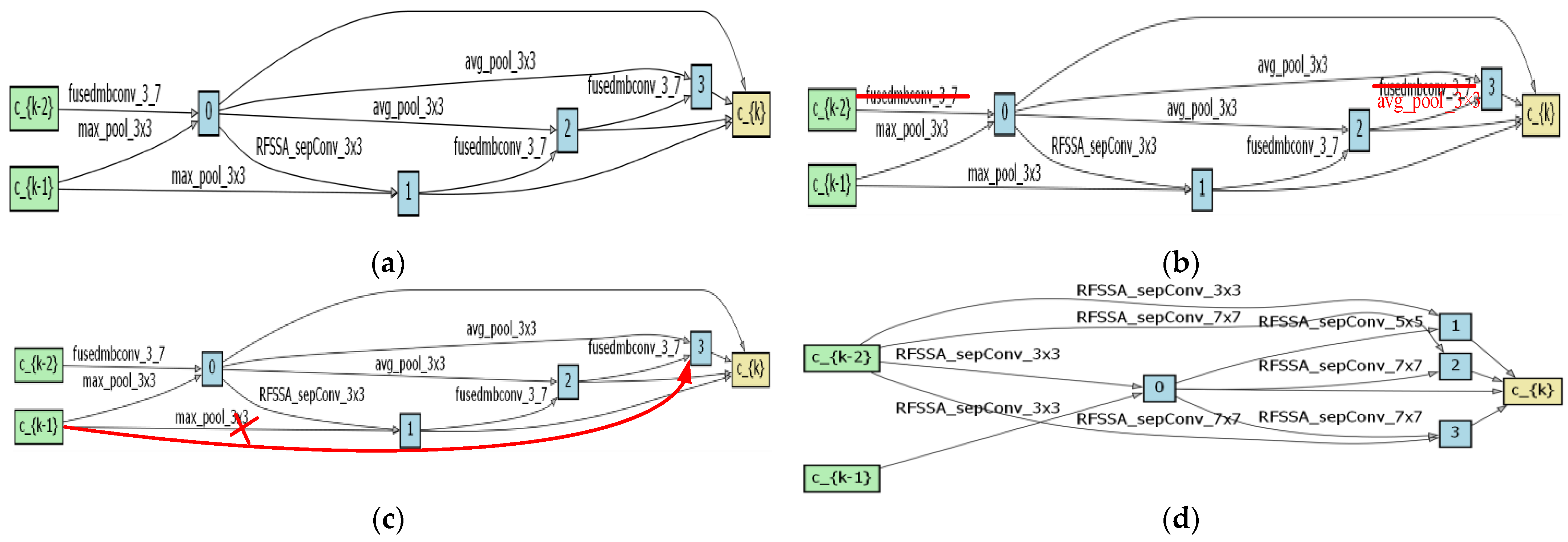
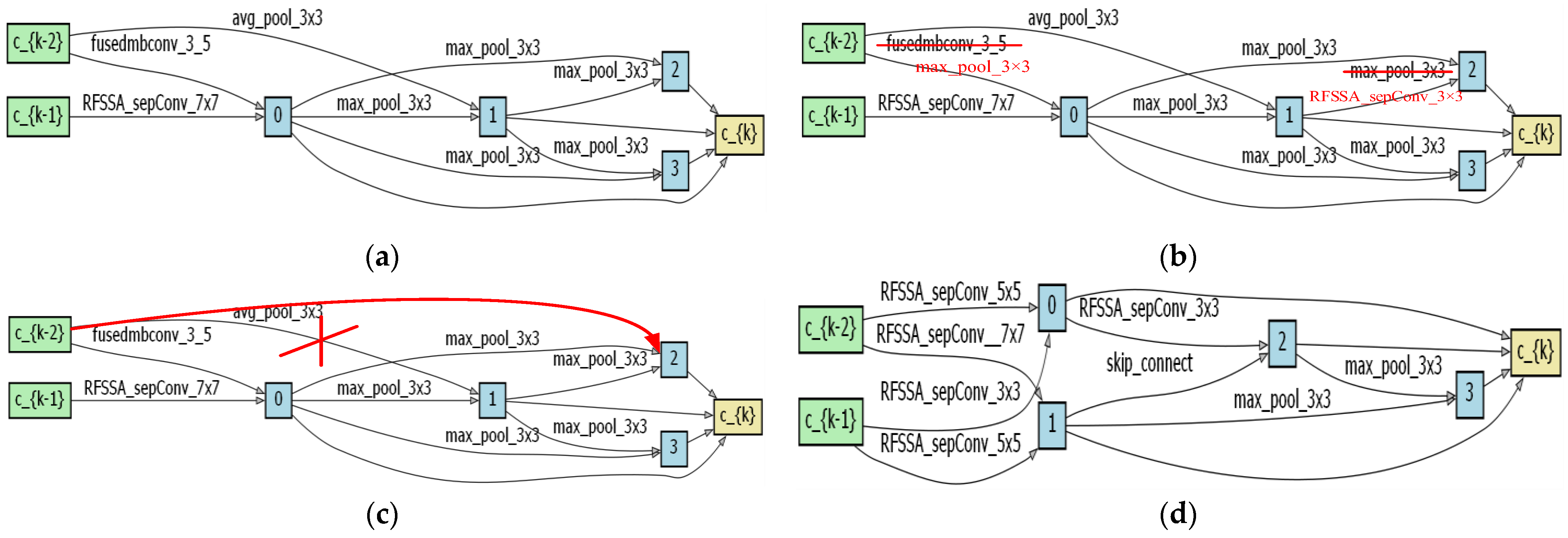
4.1. Optimal Architecture Analysis
4.2. Search Space Validity Analysis
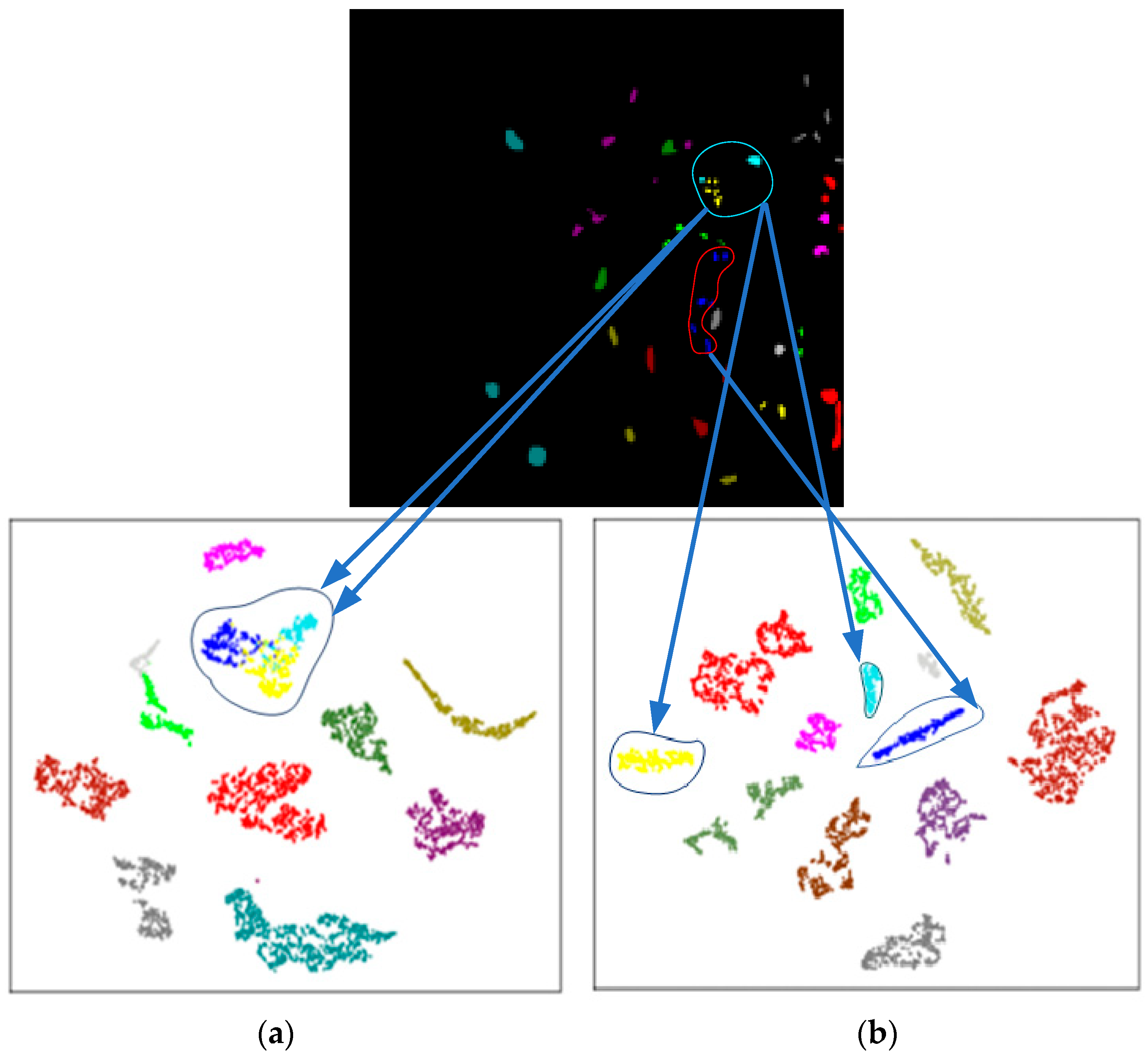
4.3. The T-Distributed Stochastic Neighbor Embedding Analysis
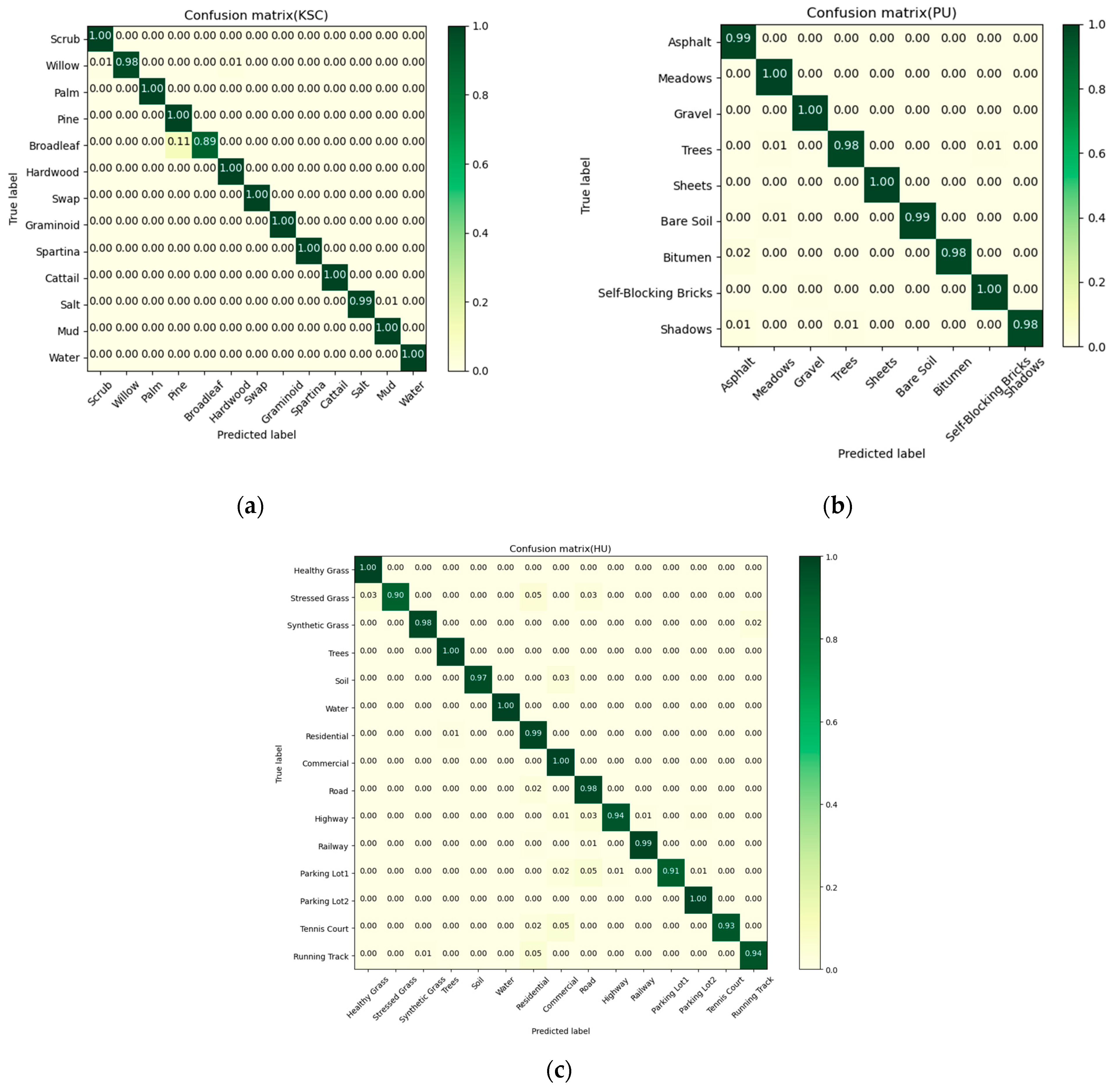
4.4. Confusion Matrix
4.5. Ablation Experiments and Dada Imbalance Analysis
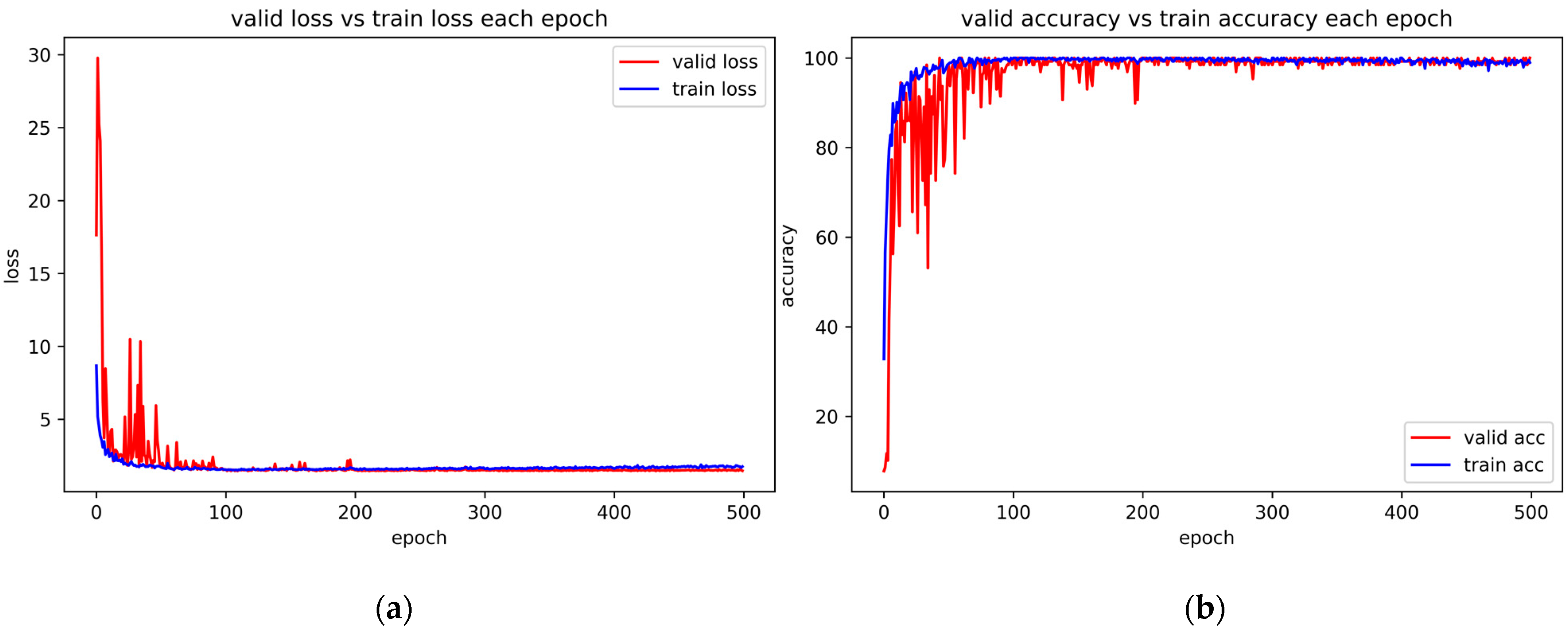
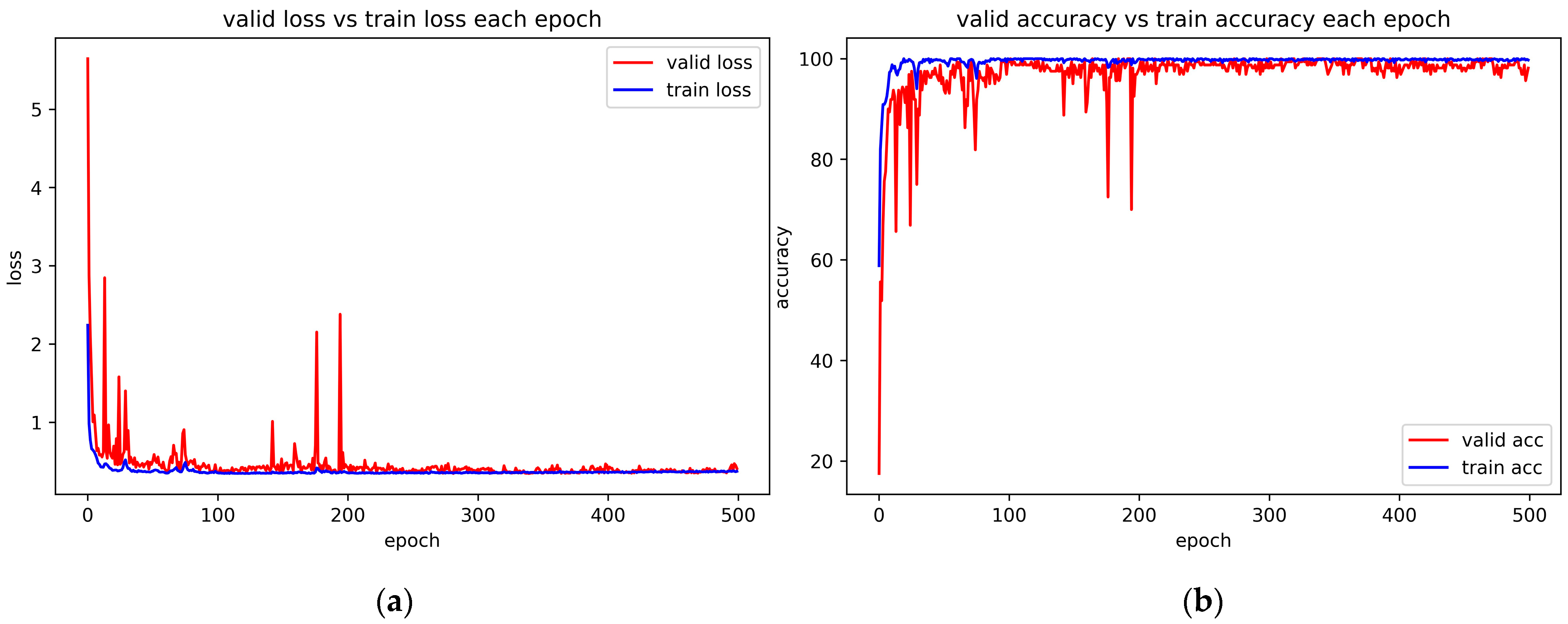
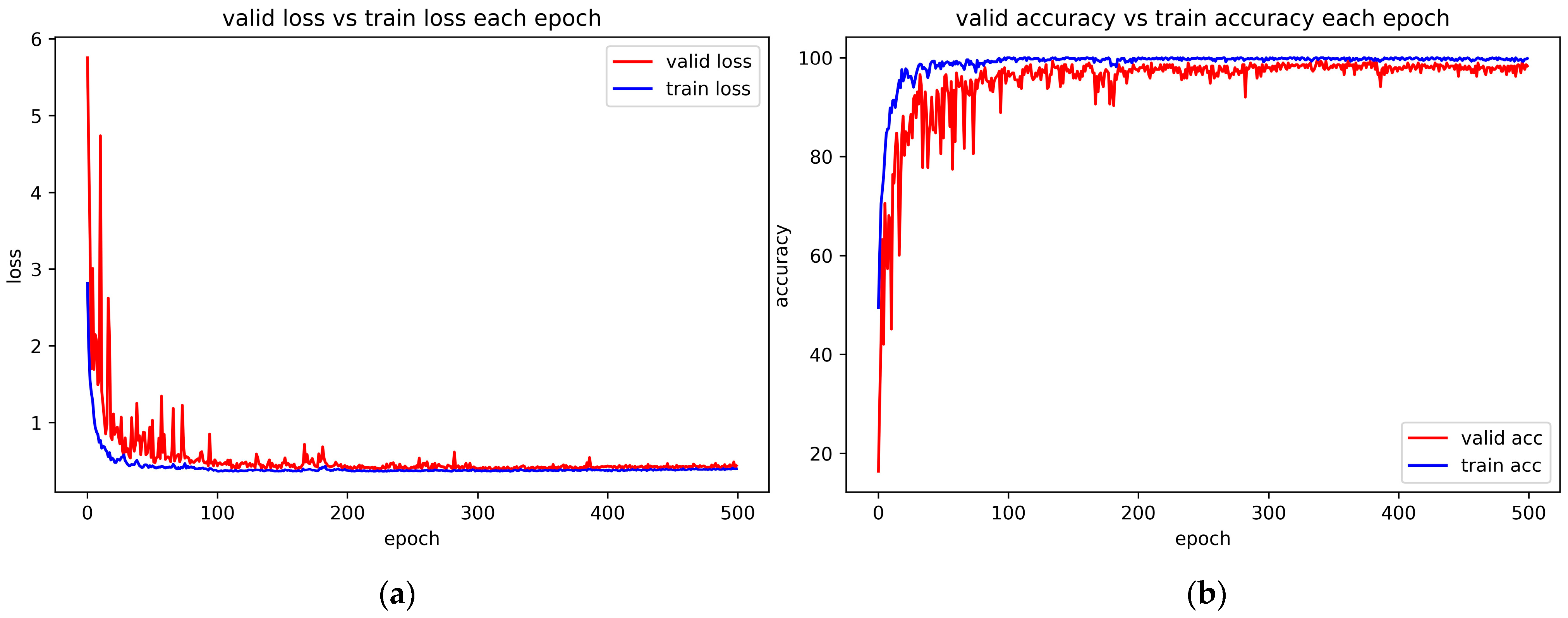
4.6. Convergence Experiment and Correlative Parameter Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghamisi, P.; Maggiori, E.; Li, S.; Souza, R.; Tarablaka, Y.; Moser, G.; Giorgi, A.D.; Fang, L.; Chen, Y.; Chi, M.; et al. New frontiers in spectral-spatial hyperspectral image classification: The latest advances based on mathematical morphology, Markov random fields, segmentation, sparse representation, and deep learning. IEEE Geosci. Remote Sens. Mag. 2018, 6, 10–43. [Google Scholar] [CrossRef]
- Della, C.; Bekit, A.; Lampe, B.; Chang, C.-I. Hyperspectral image classification via compressive sensing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8290–8303. [Google Scholar] [CrossRef]
- Hestir, E.; Brando, V.; Bresciani, M.; Giardino, C.; Matta, E.; Villa, P.; Dekker, A. Measuring freshwater aquatic ecosystems: The need for a hyperspectral global mapping satellite mission. Remote Sens. Environ. 2015, 167, 181–195. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef] [PubMed]
- Murphy, R.; Schneider, S.; Monteiro, S. Consistency of measurements of wavelength position from hyperspectral imagery: Use of the ferric iron crystal field absorption at ~900 nm as an indicator of mineralogy. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2843–2857. [Google Scholar] [CrossRef]
- Samadzadegan, F.; Hasani, H.; Schenk, T. Simultaneous feature selection and SVM parameter determination in classification of hyperspectral imagery using Ant Colony Optimization. Can. J. Remote Sens. 2012, 38, 139–156. [Google Scholar] [CrossRef]
- Friedl, M.; Brodley, C. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, B.; He, X.; Qiu, Q.; Liu, F. Class-specific random forest with cross-correlation constraints for spectral–spatial hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 257–261. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, Y.; Zhao, X.; Wang, G. Spectral-spatial classification of hyperspectral image using autoencoders. In Proceedings of the 2013 9th International Conference on Information, Communications & Signal Processing, Tainan, Taiwan, 10–13 December 2013; pp. 1–5. [Google Scholar]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.-B. Learning to diversify deep belief networks for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Zhu, K.; Chen, Y.; Ghamisi, P.; Jia, X.; Benediktsson, J.A. Deep convolutional capsule network for hyperspectral image spectral and spectral-spatial classification. Remote Sens. 2019, 11, 223. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Xue, X.; Zhang, H.; Fang, B.; Bai, Z.; Li, Y. Grafting transformer on automatically designed convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Chen, H.; Shen, C. Memory-efficient hierarchical neural architecture search for image denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 3654–3663. [Google Scholar]
- Zoph, B.; Le, Q.V. Neural architecture search with reinforcement earning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017; pp. 1–16. [Google Scholar]
- Tan, M.; Chen, B.; Pang, R.; Vasudevan, V.; Sandler, M.; Howard, A.; Le, Q.V. MnasNet: Platform-aware neural architecture search for mobile. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2820–2828. [Google Scholar]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized evolution for image classifier architecture search. In Proceedings of the Association for the Advancement of Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 4780–4789. [Google Scholar]
- Ye, P.; Li, B.; Li, Y.; Chen, T.; Fan, J.; Ouyan, W. β-DARTS: Beta-Decay regularization for differentiable architecture search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 10864–10873. [Google Scholar]
- Liu, H.; Simonyan, K.; Vinyals, O.; Fernando, C.; Kavukcuoglu, K. Hierarchical representations for efficient architecture search. arXiv 2017, arXiv:1711.00436. [Google Scholar] [CrossRef]
- Liu, H.; Simonyan, K.; Yang, Y. DARTS: Differentiable architecture search. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 30 April–30 May 2019; pp. 1–13. [Google Scholar]
- Chen, Y.; Zhu, K.; Zhu, L.; He, X.; Ghamisi, P.; Benediktsson, J.A. Automatic design of convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7048–7066. [Google Scholar] [CrossRef]
- Zhang, H.; Gong, C.; Bai, Y.; Bai, Z.; Li, Y. 3-D-ANAS: 3-D asymmetric neural architecture search for fast hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Cao, C.; Xiang, H.; Song, W.; Yi, H.; Xiao, F.; Gao, X. Lightweight multiscale neural architecture search with spectral–spatial attention for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Liu, Y.; Hua, Z.; Hao, S.; Yao, Y. EL-NAS: Efficient Lightweight Attention Cross-Domain Architecture Search for Hyperspectral Image Classification. Remote Sens. 2023, 15, 4688. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Zhang, X.; Liu, C.; Yang, D.G.; Song, T.T.; Ye, Y.C.; Li, K.; Song, Y.Z. RFAConv: Innovating Spatial Attention and Standard Convolutional Operation. arXiv 2023, arXiv:2304.03198v5. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Marseille, France, 12–18 October 2018; pp. 3–19. [Google Scholar]
- Tan, M.; Le, Q. Efficientnetv2: Smaller models and faster training. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021; pp. 10096–10106. [Google Scholar]
- Chu, X.; Zhang, B. Noisy differentiable architecture search. arXiv 2020, arXiv:2005.03566v3. [Google Scholar] [CrossRef]
- Leng, Z.; Tan, M.; Liu, C. PolyLoss: A polynomial expansion perspective of classification loss functions. arXiv 2022, arXiv:2204.12511. [Google Scholar] [CrossRef]
- Li, P.; Hu, H.; Cheng, T.; Xiao, X. High-resolution Multispectral Image Classification over Urban Areas by Image Segmentation and Extended Morphological Profile. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 3252–3254. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, L.; Ghamisi, P.; Jia, X.; Li, G.; Tang, L. Hyperspectral Images Classification with Gabor Filtering and Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2355–2359. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R. Deep pyramidal residual networks for spectral-spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 740–754. [Google Scholar] [CrossRef]
- Wang, A.L.; Song, Y.; WU, H. A hybrid neural architecture search for hyperspectral image classification. Front. Phys. 2023, 11, 1159266. [Google Scholar] [CrossRef]








| Number | Name | Operation |
|---|---|---|
| Skip_connection | ||
| Avg_pool_3 × 3 | Avgpoling (3 × 3) | |
| Max_pool_3 × 3 | Maxpooling (3 × 3) | |
| RFSSA_SepConv_3 × 3 | RFA-CBMA-Conv2d (3 × 1)-Conv2d (1 × 3) | |
| RFSSA_SepConv_5 × 5 | RFA-CBMA-Conv2d (5 × 1)-Conv2d (1 × 5) | |
| RFSSA_SepConv_7 × 7 | RFA-CBMA-Conv2d (7 × 1)-Conv2d (1 × 7) | |
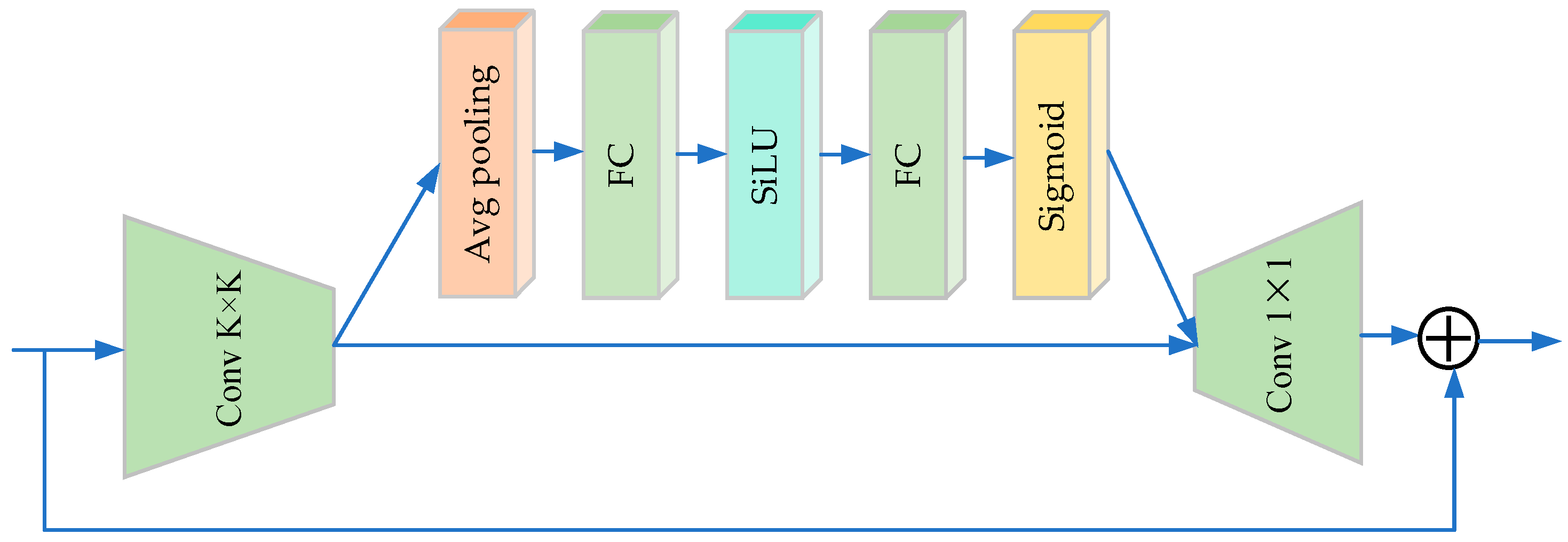
| Fused_MBConv_3_3 | Conv2d (3 × 3)-SE-Conv (1 × 1) | |
| Fused_MBConv_3_5 | Conv2d (3 × 5)-SE-Conv (1 × 1) | |
| Fused_MBConv_3_7 | Conv2d (3 × 7)-SE-Conv (1 × 1) | |
| None |
| No. | Class Name | Color | Sample | False-Color Map | Ground-Truth Map |
|---|---|---|---|---|---|
| 1 | Scrub |  | 761 |  |  |
| 2 | Willow |  | 243 | ||
| 3 | Palm |  | 256 | ||
| 4 | Pine |  | 252 | ||
| 5 | Broadleaf |  | 161 | ||
| 6 | Hardwood |  | 229 | ||
| 7 | Swap |  | 105 | ||
| 8 | Graminoid |  | 431 | ||
| 9 | Spartina |  | 520 | ||
| 10 | Cattail |  | 404 | ||
| 11 | Salt |  | 419 | ||
| 12 | Mud |  | 503 | ||
| 13 | Water |  | 927 | ||
| Total | 5211 | ||||
| Sensor: VIRIS; Spectral Bands: 176; Spectral Region: 0.4–2.5 µm; Categories: 13 | |||||
| No. | Class | Color | Sample Numbers | False-Color Map | Ground-Truth Map |
|---|---|---|---|---|---|
| 1 | Asphalt |  | 6631 |  |  |
| 2 | Meadows |  | 18,649 | ||
| 3 | Gravel |  | 2099 | ||
| 4 | Trees |  | 3064 | ||
| 5 | Sheets |  | 1345 | ||
| 6 | Bare Soil |  | 5029 | ||
| 7 | Bitumen |  | 1330 | ||
| 8 | Self-Blocking Bricks |  | 3682 | ||
| 9 | Shadows |  | 947 | ||
| Total | 42,776 | ||||
| Sensor: ROSIS; Spectral Bands: 103; Spectral Region: 0.43–0.86 µm; Categories: 9 | |||||
| No. | Class | Color | Sample Numbers | False-Color Map | Ground-Truth Map |
|---|---|---|---|---|---|
| 1 | Healthy Grass |  | 1251 |  |  |
| 2 | Stressed Grass |  | 1254 | ||
| 3 | Synthetic Grass |  | 697 | ||
| 4 | Trees |  | 1244 | ||
| 5 | Soil |  | 1242 | ||
| 6 | Water |  | 325 | ||
| 7 | Residential |  | 1268 | ||
| 8 | Commercial |  | 1244 | ||
| 9 | Road |  | 1252 | ||
| 10 | Highway |  | 1227 | ||
| 11 | Railway |  | 1235 | ||
| 12 | Parking Lot1 |  | 1233 | ||
| 13 | Parking Lot2 |  | 469 | ||
| 14 | Tennis Court |  | 428 | ||
| 15 | Running Track |  | 660 | ||
| Total | 15,029 | ||||
| Sensor: ITRES CASI-1500; Spectral Bands: 144; Spectral Region: 0.36–1.05 µm; Categories: 15 | |||||
| Dataset | Categories | Training Samples | Validation Samples | Test Samples | Training Sample Rate |
|---|---|---|---|---|---|
| KSC | 13 | 30 pixel/category | 10 pixel/category | 4691 | 7.4% |
| PU | 9 | 42,416 | 0.63% | ||
| HU | 15 | 14,429 | 2.99% |
| Method | RBF-SVM | CNN | PyResNet | SSRN | 3-D AT-CNN | HNAS | LMSS-NAS | RFSS-NAS | |
|---|---|---|---|---|---|---|---|---|---|
| Class | |||||||||
| 1 | 92.81 ± 0.79 | 95.94 ± 2.92 | 92.80 ± 9.48 | 98.38 ± 1.14 | 93.57 ± 2.10 | 99.01 ± 0.25 | 99.92 ± 0.18 | 100.00 ± 0.00 | |
| 2 | 86.61 ± 5.10 | 79.58 ± 6.22 | 85.58 ± 8.17 | 94.94 ± 6.35 | 96.83 ± 4.61 | 98.81 ± 0.77 | 99.51 ± 0.76 | 99.51 ± 0.24 | |
| 3 | 73.32±8.34 | 65.81±17.01 | 85.94±7.50 | 96.81 ± 2.35 | 94.12 ± 0.57 | 99.50 ± 0.12 | 99.69 ± 0.64 | 100.00 ± 0.00 | |
| 4 | 54.48 ± 8.64 | 52.27 ± 13.05 | 69.89 ± 10.31 | 85.55 ± 7.02 | 96.50 ± 5.10 | 98.78 ± 0.13 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| 5 | 60.22 ± 12.13 | 38.73 ± 22.02 | 68.35 ± 14.30 | 77.22 ± 9.12 | 97.46 ± 2.41 | 96.46 ± 0.31 | 97.40 ± 4.20 | 97.90 ± 8.70 | |
| 6 | 65.46 ± 8.34 | 73.97 ± 7.22 | 92.05 ± 12.32 | 92.93 ± 5.15 | 99.04 ± 0.53 | 96.26 ± 0.43 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| 7 | 76.21 ± 3.82 | 58.28 ± 19.24 | 97.22 ± 2.07 | 94.54 ± 4.59 | 95.31 ± 2.17 | 94.99 ± 0.82 | 99.35 ± 1.93 | 100.00 ± 0.00 | |
| 8 | 86.60 ± 5.03 | 85.67 ± 9.54 | 96.38 ± 2.46 | 97.54 ± 0.90 | 93.19 ± 1.24 | 96.72 ± 0.44 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| 9 | 88.44 ± 2.66 | 87.21 ± 6.24 | 91.32 ± 12.37 | 98.79 ± 1.25 | 85.37 ± 4.86 | 96.99 ± 0.35 | 99.79 ± 0.37 | 99.72 ± 0.01 | |
| 10 | 96.30 ± 4.93 | 94.12 ± 1.51 | 99.45 ± 0.97 | 99.65 ± 0.60 | 98.98 ± 1.50 | 95.25 ± 1.02 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| 11 | 96.15 ± 1.52 | 98.32 ± 1.42 | 96.34 ± 8.61 | 98.65 ± 1.46 | 100.00 ± 0.00 | 93.35 ± 0.85 | 98.80 ± 1.67 | 98.89 ± 3.67 | |
| 12 | 93.60 ± 2.66 | 94.37 ± 2.01 | 96.10 ± 2.19 | 97.15 ± 1.21 | 98.08 ± 4.86 | 99.88 ± 0.20 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| 13 | 99.67 ± 0.68 | 99.79 ± 0.24 | 99.12 ± 1.25 | 94.55 ± 2.53 | 99.30 ± 1.84 | 99.32 ± 0.38 | 100.00 ± 0.00 | 100.00 ± 0.00 | |
| OA (%) | 87.94 ± 1.57 | 86.31 ± 1.48 | 92.08 ± 1.72 | 96.02 ± 4.82 | 97.97 ± 0.58 | 97.57 ± 0.13 | 98.51 ± 0.26 | 99.83 ± 0.02 | |
| AA (%) | 82.30 ± 2.49 | 78.77 ± 3.01 | 90.13 ± 5.38 | 94.89 ± 3.47 | 86.72 ± 7.45 | 97.72 ± 0.11 | 97.05 ± 1.35 | 99.70 ± 0.03 | |
| K × 100 | 86.57 ± 1.74 | 84.77 ± 1.65 | 90.96 ± 1.97 | 96.47 ± 5.37 | 97.69 ± 0.67 | 97.37 ± 0.14 | 98.58 ± 0.30 | 99.78 ± 0.02 | |
| Method | RBF-SVM | CNN | PyResNet | SSRN | 3-D AT-CNN | HNAS | LMSS-NAS | RFSS-NAS | |
|---|---|---|---|---|---|---|---|---|---|
| Class | |||||||||
| 1 | 81.26 ± 5.08 | 84.16 ± 7.76 | 92.35 ± 9.26 | 98.09 ± 1.77 | 92.11 ± 5.22 | 92.63 ± 3.54 | 98.57 ± 0.26 | 97.05 ± 1.89 | |
| 2 | 84.53 ± 3.81 | 90.26 ± 3.94 | 97.02 ± 6.60 | 97.88 ± 0.77 | 98.61 ± 0.78 | 98.92 ± 0.66 | 98.75 ± 0.24 | 99.70 ± 0.12 | |
| 3 | 56.56 ± 16.17 | 38.89 ± 2.29 | 95.08 ± 4.01 | 82.55 ± 12.50 | 92.73 ± 3.59 | 94.14 ± 2.83 | 93.09 ± 1.23 | 99.33 ± 0.17 | |
| 4 | 94.34 ± 3.50 | 92.80 ± 6.21 | 91.13 ± 3.80 | 95.07 ± 6.95 | 95.12 ± 3.59 | 91.68 ± 3.88 | 87.03 ± 7.70 | 98.50 ± 1.74 | |
| 5 | 95.38 ± 3.40 | 94.01 ± 5.92 | 99.83 ± 0.21 | 99.77 ± 0.22 | 92.53 ± 6.59 | 91.65 ± 5.98 | 99.19 ± 0.12 | 100.00 ± 0.00 | |
| 6 | 80.66 ± 7.54 | 76.20 ± 8.71 | 97.68 ± 3.41 | 94.25 ± 1.71 | 98.84 ± 1.02 | 98.99 ± 0.75 | 94.13 ± 1.49 | 99.94 ± 0.07 | |
| 7 | 69.13 ± 11.04 | 46.25 ± 27.85 | 95.05 ± 7.15 | 82.64 ± 14.7 | 91.38 ± 4.63 | 90.81 ± 4.60 | 86.78 ± 8.26 | 99.68 ± 0.33 | |
| 8 | 71.16 ± 6.24 | 64.98 ± 3.96 | 83.29 ± 14.23 | 81.60 ± 8.63 | 87.11 ± 3.65 | 91.23 ± 4.17 | 87.93 ± 0.35 | 95.50 ± 3.69 | |
| 9 | 99.94 ± 0.07 | 88.72 ± 9.15 | 98.21 ± 1.43 | 98.89 ± 1.55 | 87.52 ± 6.92 | 86.03 ± 4.17 | 89.10 ± 8.84 | 99.09 ± 1.27 | |
| OA (%) | 82.06 ± 2.78 | 83.35 ± 3.64 | 92.14 ± 10.87 | 94.12 ± 0.75 | 94.82 ± 0.94 | 95.31 ± 0.70 | 96.34 ± 0.28 | 98.79 ± 0.07 | |
| AA (%) | 79.22 ± 5.87 | 75.14 ± 9.16 | 94.40 ± 5.34 | 92.30 ± 1.65 | 92.82 ± 0.98 | 92.86 ± 0.73 | 96.73 ± 1.10 | 98.76 ± 0.15 | |
| K × 100 | 75.44 ± 4.26 | 77.63 ± 5.13 | 90.21 ± 12.97 | 92.22 ± 1.01 | 93.41 ± 1.21 | 94.06 ± 0.90 | 96.33 ± 0.48 | 98.65 ± 0.20 | |
| Method | RBF-SVM | CNN | PyResNet | SSRN | 3-D AT-CNN | HNAS | LMSS-NAS | RFSS-NAS | |
|---|---|---|---|---|---|---|---|---|---|
| Class | |||||||||
| 1 | 86.22 ± 5.47 | 94.30 ± 2.22 | 91.48 ± 3.21 | 98.85 ± 0.84 | 90.26 ± 4.70 | 91.02 ± 3.12 | 81.29 ± 1.97 | 99.76 ± 0.06 | |
| 2 | 94.70 ± 0.83 | 91.09 ± 1.88 | 93.41 ± 5.47 | 98.48 ± 1.40 | 88.73 ± 4.33 | 86.90 ± 5.10 | 96.01 ± 3.10 | 91.39 ± 1.35 | |
| 3 | 91.98 ± 7.89 | 99.20 ± 0.39 | 98.63 ± 0.16 | 96.90 ± 0.67 | 86.80 ± 7.29 | 94.29 ± 5.82 | 98.86 ± 4.15 | 97.25 ± 4.32 | |
| 4 | 99.10 ± 0.55 | 98.61 ± 1.17 | 97.35 ± 1.23 | 93.88 ± 7.76 | 90.36 ± 3.22 | 89.40 ± 0.91 | 96.23 ± 2.56 | 99.33 ± 0.45 | |
| 5 | 91.92 ± 2.94 | 93.59 ± 0.37 | 98.40 ± 0.05 | 98.79 ± 0.55 | 97.61 ± 2.34 | 96.50 ± 3.98 | 92.46 ± 2.63 | 96.97 ± 0.06 | |
| 6 | 90.15 ± 0.85 | 98.21 ± 0.02 | 95.65 ± 4.20 | 96.85 ± 0.86 | 86.54 ± 6.03 | 88.19 ± 8.68 | 87.21 ± 9.38 | 97.95 ± 3.97 | |
| 7 | 60.10 ± 6.20 | 92.73 ± 2.42 | 90.37 ± 1.89 | 87.86 ± 6.48 | 80.83 ± 5.06 | 79.33 ± 6.19 | 88.95 ± 5.26 | 98.30 ± 0.75 | |
| 8 | 69.58 ± 6.05 | 97.18 ± 1.19 | 88.49 ± 5.18 | 89.14 ± 11.06 | 90.51 ± 6.26 | 88.66 ± 6.26 | 98.07 ± 0.74 | 98.48 ± 1.94 | |
| 9 | 65.07 ± 7.77 | 94.92 ± 5.48 | 90.72 ± 4.70 | 95.41 ± 2.28 | 85.82 ± 4.19 | 79.77 ± 3.82 | 91.77 ± 4.88 | 97.68 ± 0.79 | |
| 10 | 59.29 ± 7.60 | 85.33 ± 6.11 | 73.72 ± 8.03 | 91.72 ± 4.95 | 90.53 ± 4.29 | 86.24 ± 6.78 | 95.68 ± 7.37 | 95.39 ± 1.47 | |
| 11 | 57.10 ± 10.78 | 92.43 ± 6.54 | 92.09 ± 4.36 | 95.55 ± 4.03 | 97.81 ± 2.96 | 97.13 ± 2.45 | 97.07 ± 5.49 | 99.28 ± 0.34 | |
| 12 | 61.25 ± 6.52 | 93.27 ± 3.11 | 90.44 ± 3.77 | 92.58 ± 1.83 | 89.91 ± 4.23 | 87.71 ± 4.06 | 93.72 ± 8.91 | 95.81 ± 1.55 | |
| 13 | 60.41 ± 27.33 | 97.36 ± 2.31 | 95.70 ± 2.17 | 96.89 ± 2.63 | 96.85 ± 2.47 | 88.34 ± 10.21 | 88.69 ± 8.96 | 99.49 ± 0.51 | |
| 14 | 82.35 ± 10.02 | 98.35 ± 0.50 | 98.55 ± 2.34 | 99.03 ± 0.11 | 87.24 ± 4.64 | 92.98 ± 6.66 | 99.21 ± 3.15 | 91.49 ± 5.42 | |
| 15 | 99.48 ± 0.06 | 99.25 ± 0.86 | 99.20 ± 1.08 | 98.05 ± 0.89 | 90.91 ± 6.80 | 92.74 ± 5.16 | 97.05 ± 1.40 | 94.20 ± 2.90 | |
| OA (%) | 76.15 ± 2.74 | 93.55 ± 1.64 | 91.29 ± 1.65 | 94.69 ± 1.93 | 89.59 ± 0.91 | 88.40 ± 1.62 | 93.07 ± 0.41 | 96.91 ± 0.20 | |
| AA (%) | 78.97 ± 0.62 | 94.57 ± 1.43 | 93.11 ± 0.08 | 95.87 ± 1.35 | 90.04 ± 0.70 | 89.28 ± 1.78 | 93.48 ± 0.57 | 96.86 ± 0.05 | |
| K × 100 | 74.17 ± 2.98 | 94.10 ± 1.77 | 90.59 ± 1.79 | 94.26 ± 2.09 | 88.76 ± 0.98 | 87.42 ± 1.65 | 92.50 ± 0.48 | 96.65 ± 0.22 | |
| Models | RFSS-NAS | RFSS-NAS-Rop | RFSS-NAS-Rtopo | RFSS-NAS-Rbop |
|---|---|---|---|---|
| OA (%) | 99.85 | 99.38 | 99.08 | 99.50 |
| AA (%) | 99.90 | 98.98 | 98.63 | 99.51 |
| K × 100 | 99.83 | 99.17 | 98.78 | 99.45 |
| Fused_MBConv | RFSSA | Noisy-DARTS | OA (%) | AA (%) | K × 100 |
|---|---|---|---|---|---|
| √ | √ | 97.69 ± 1.30 | 97.15 ± 2.11 | 97.30 ± 2.18 | |
| √ | √ | 96.36 ± 1.53 | 96.68 ± 0.72 | 96.06 ± 0.57 | |
| √ | √ | 98.20 ± 0.29 | 98.29 ± 0.83 | 98.37 ± 1.13 | |
| √ | √ | √ | 98.79 ± 0.07 | 98.76 ± 0.15 | 98.65 ± 0.20 |
| Dataset | Loss | OA (%) | AA (%) | K × 100 | Test Time (s) | Params (M) |
|---|---|---|---|---|---|---|
| KSC | SM Loss | 98.55 ± 0.42 | 98.57 ± 0.41 | 98.27 ± 0.23 | 10.01 | 1.39 |
| PL Loss | 99.01 ± 0.22 | 98.62 ± 0.57 | 98.94 ± 0.61 | 10.30 | 1.42 | |
| SM Loss + PL Loss | 99.83 ± 0.02 | 99.70 ± 0.03 | 99.78 ± 0.02 | 10.37 | 1.46 | |
| PU | SM Loss | 98.32 ± 0.12 | 97.98 ± 0.44 | 98.03 ± 0.17 | 10.85 | 1.49 |
| PL Loss | 98.25 ± 0.03 | 97.50 ± 0.18 | 97.88 ± 0.22 | 11.21 | 1.54 | |
| SM Loss + PL Loss | 98.79 ± 0.07 | 98.76 ± 0.15 | 98.65 ± 0.20 | 12.99 | 1.61 | |
| HU | SM Loss | 95.41 ± 0.16 | 95.95 ± 0.07 | 95.19 ± 0.12 | 7.28 | 1.25 |
| PL Loss | 96.21 ± 0.11 | 95.97 ± 0.13 | 96.10 ± 0.06 | 8.56 | 1.31 | |
| SM Loss + PL Loss | 96.91 ± 0.20 | 96.86 ± 0.05 | 96.65 ± 0.22 | 9.82 | 1.37 |
| Methods | KSC | PU | HU | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Params (M) | Train (m) | Test (s) | Params (M) | Train (m) | Test (s) | Params (M) | Train (m) | Test (s) | |
| 3D-CNN | 0.14 | 6.18 | 5.57 | 0.09 | 9.94 | 6.21 | 0.15 | 8.79 | 5.93 |
| PyResNet | 85.10 | 22.38 | 7.16 | 84.21 | 175.41 | 52.67 | 84.73 | 65.88 | 21.62 |
| SSRN | 1.25 | 8.21 | 2.47 | 0.83 | 63.10 | 16.19 | 1.06 | 47.77 | 15.93 |
| 3-D AT-CNN | 0.12 | 19.41 | 7.72 | 0.19 | 11.22 | 5.79 | 0.09 | 13.02 | 6.11 |
| HNAS | 2.70 | 31.63 | 8.94 | 2.73 | 15.35 | 8.89 | 2.64 | 30.81 | 9.42 |
| LMSS-NAS | 0.08 | 9.39 | 8.23 | 0.16 | 10.59 | 9.29 | 0.05 | 7.82 | 9.01 |
| RFSS-NAS | 1.46 | 12.14 | 10.37 | 1.61 | 12.92 | 12.99 | 1.37 | 10.88 | 9.82 |
| Dataset | Noise Type | OA (%) | AA (%) | K × 100 |
|---|---|---|---|---|
| KSC | w/o Noise | 99.57 ± 0.26 | 99.01 ± 0.12 | 99.52 ± 0.11 |
| Gaussian | 99.63 ± 0.14 | 99.66 ± 0.07 | 99.59 ± 0.17 | |
| Uniform | 99.83 ± 0.02 | 99.70 ± 0.03 | 99.78 ± 0.02 |
| Training Sample Sizes | OA (%) | AA (%) | K × 100 |
|---|---|---|---|
| 0.10% | 66.82 ± 0.27 | 70.63 ± 0.34 | 59.90 ± 0.26 |
| 0.21% | 79.06 ± 0.32 | 77.34 ± 0.26 | 73.62 ± 0.31 |
| 0.31% | 82.74 ± 0.12 | 86.15 ± 0.27 | 78.27 ± 0.14 |
| 0.42% | 90.40 ± 0.09 | 90.34 ± 0.11 | 87.66 ± 0.06 |
| 0.53% | 94.70 ± 0.13 | 93.81 ± 0.07 | 93.04 ± 0.11 |
| 0.63% | 98.79 ± 0.07 | 98.76 ± 0.15 | 98.65 ± 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Zhang, K.; Wu, H.; Dai, S.; Iwahori, Y.; Yu, X. Noise-Disruption-Inspired Neural Architecture Search with Spatial–Spectral Attention for Hyperspectral Image Classification. Remote Sens. 2024, 16, 3123. https://doi.org/10.3390/rs16173123
Wang A, Zhang K, Wu H, Dai S, Iwahori Y, Yu X. Noise-Disruption-Inspired Neural Architecture Search with Spatial–Spectral Attention for Hyperspectral Image Classification. Remote Sensing. 2024; 16(17):3123. https://doi.org/10.3390/rs16173123
Chicago/Turabian StyleWang, Aili, Kang Zhang, Haibin Wu, Shiyu Dai, Yuji Iwahori, and Xiaoyu Yu. 2024. "Noise-Disruption-Inspired Neural Architecture Search with Spatial–Spectral Attention for Hyperspectral Image Classification" Remote Sensing 16, no. 17: 3123. https://doi.org/10.3390/rs16173123
APA StyleWang, A., Zhang, K., Wu, H., Dai, S., Iwahori, Y., & Yu, X. (2024). Noise-Disruption-Inspired Neural Architecture Search with Spatial–Spectral Attention for Hyperspectral Image Classification. Remote Sensing, 16(17), 3123. https://doi.org/10.3390/rs16173123










