Assessment of Satellite Differential Code Biases and Regional Ionospheric Modeling Using Carrier-Smoothed Code of BDS GEO and IGSO Satellites
Abstract
1. Introduction
2. Methods
2.1. Extraction of DCB and Vertical TEC
2.2. Estimation of Vertical TECs and DCBs
2.2.1. Polynomial Model (POLY)
2.2.2. Spherical Harmonic Function Model (SHF)
2.2.3. Least Squares Adjustment
2.2.4. Enhanced Weight Matrix Formulation
3. Results
3.1. Experimental Datasets
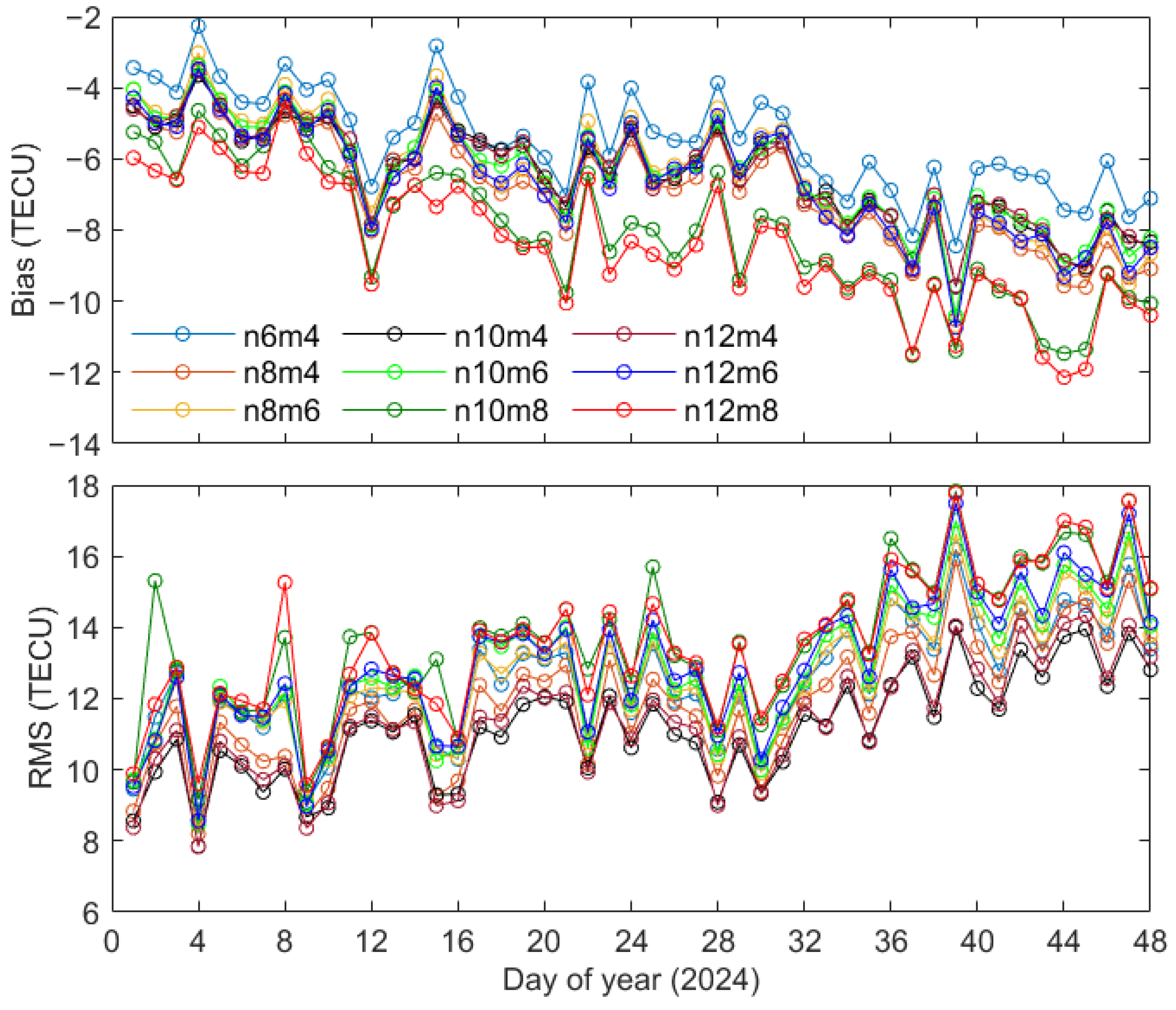
3.2. Select an Appropriate Method for Estimating BDS High-Orbit Satellite DCB
3.3. Performance of Estimated RIMs Using Dual-Frequency Signals from BDS High-Orbit Satellites
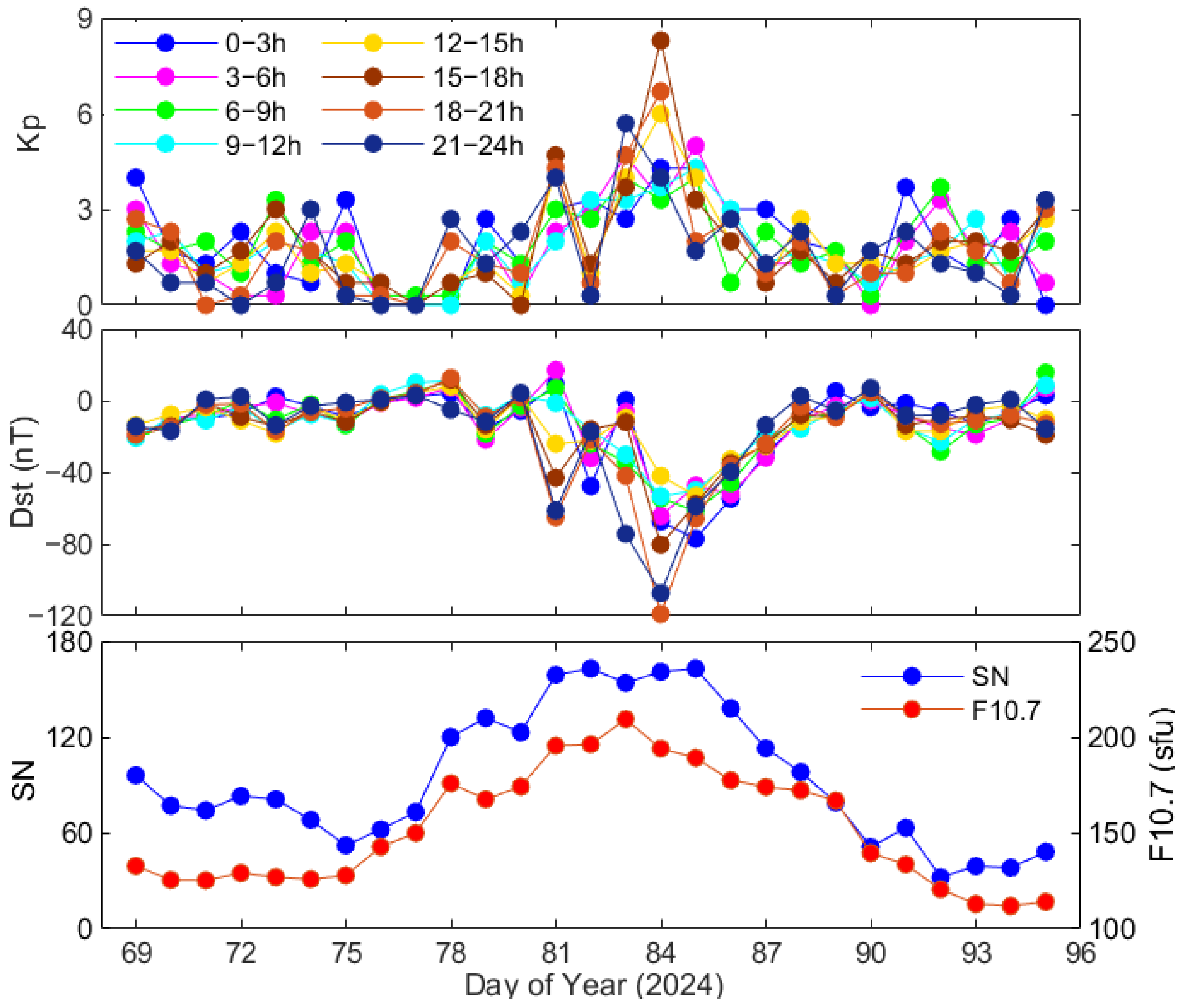
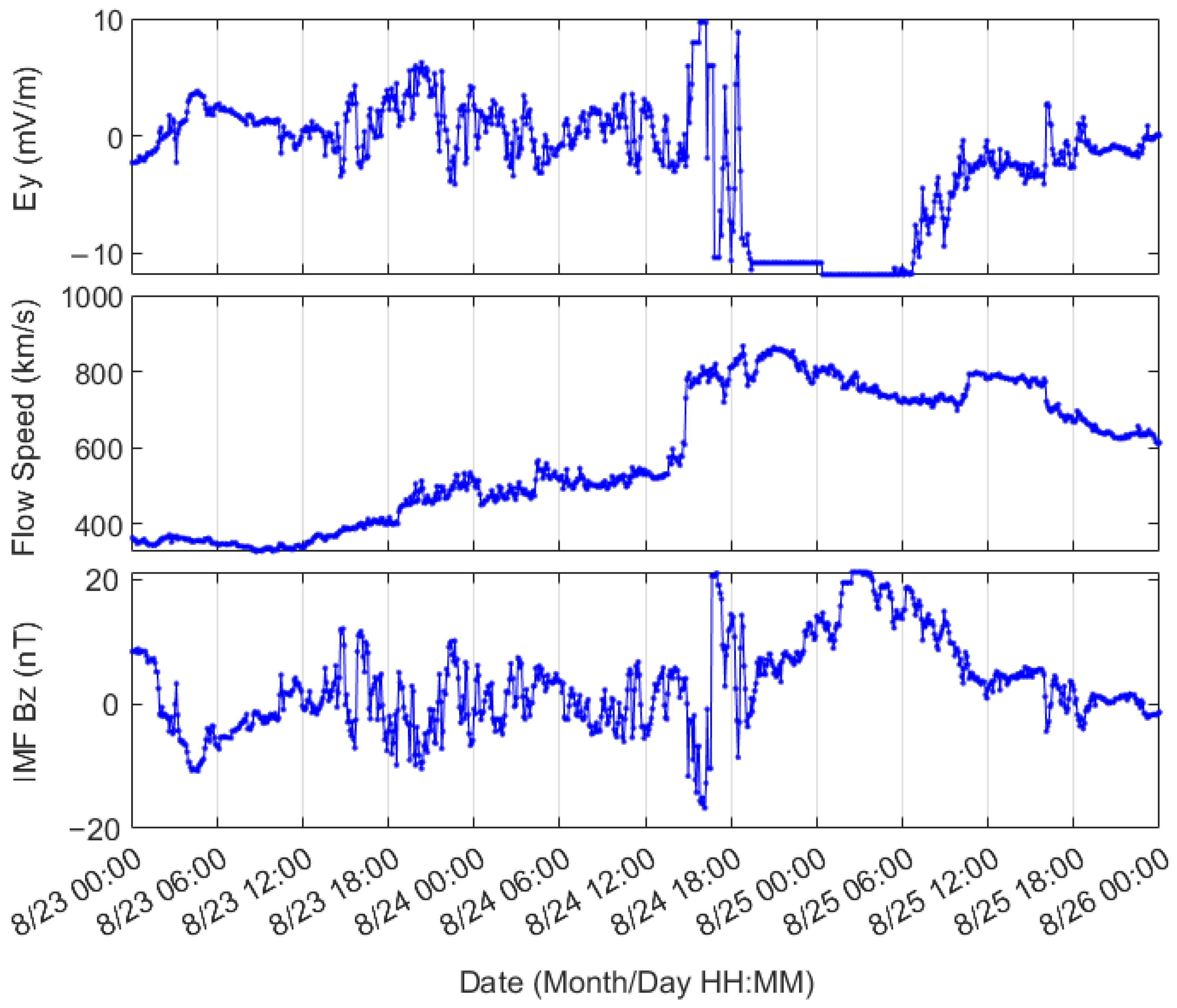
3.4. Analysis of the Ionospheric Disturbance Responses to Severe Geomagnetic Storm
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davies, K. Ionospheric Radio, 1st ed.; Peter Peregrinus Ltd.: London, UK, 1990; pp. 1–5. [Google Scholar]
- Kintner, P.M.; Ledvina, B.M. The ionosphere, radio navigation, and global navigation satellite systems. Adv. Space Res. 2005, 35, 788–811. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 177–183. [Google Scholar]
- Milan, S.E.; Clausen, L.B.; Coxon, J.C.; Carter, J.A.; Walach, M.T.; Laundal, K.; Østgaard, N.; Tenfjord, P.; Reistad, J.; Snekvik, K.; et al. Overview of solar wind–magnetosphere–ionosphere–atmosphere coupling and the generation of magnetospheric currents. Space Sci. Rev. 2017, 206, 547–573. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.J.; Codrescu, M.V.; Moffett, R.J.; Quegan, S. Response of the thermosphere and ionosphere to geomagnetic storms. J. Geophys. Res. Space Phys. 1994, 99, 3893–3914. [Google Scholar] [CrossRef]
- Di Giovanni, G.; Radicella, S.M. An analytical model of the electron density profile in the ionosphere. Adv. Space Res. 1990, 10, 27–30. [Google Scholar] [CrossRef]
- Nava, B.; Coisson, P.; Radicella, S.M. A new version of the NeQuick ionosphere electron density model. J. Atmos. Solar-Terr. Phys. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Mendillo, M. Storms in the ionosphere: Patterns and processes for total electron content. Rev. Geophys. 2006, 44, RG4001. [Google Scholar] [CrossRef]
- Landa, V.; Reuveni, Y. Assessment of dynamic mode decomposition (DMD) model for ionospheric TEC map predictions. Remote Sens. 2023, 15, 365. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Aragón-Ángel, À.; Defraigne, P.; Bergeot, N.; Prieto-Cerdeira, R.; García-Rigo, A. Distribution and mitigation of higher-order ionospheric effects on precise GNSS processing. J. Geophys. Res. Solid Earth 2014, 119, 3823–3837. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X.; Zhang, X. Ionospheric total electron content estimation using GNSS carrier phase observations based on zero-difference integer ambiguity: Methodology and assessment. IEEE Trans. Geosci. Remote Sens. 2020, 59, 817–830. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Y.; Skone, S. A study of smoothed TEC precision inferred from GPS measurements. Earth Planets Space 2005, 57, 999–1007. [Google Scholar] [CrossRef][Green Version]
- Skone, S. Variations in point positioning accuracies for single frequency GPS users during solar maximum. Geomatica 2002, 56, 131–140. [Google Scholar]
- Hernández-Pajares, M.; Juan, J.; Sanz, J. High resolution TEC monitoring method using permanent ground GPS receivers. Geophys. Res. Lett. 1997, 24, 1643–1646. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.; Wang, J.; Choi, B.; Park, P. Electron density profiles derived from ground-based GPS observations. J. Navig. 2006, 59, 395–401. [Google Scholar] [CrossRef]
- Hatch, R. Dynamic differential GPS at the centimeter level. In Proceedings of the 4th International Geodetic Symposium on Satellite Positioning, Austin, TX, USA, 28 April–2 May 1986. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps. Navigation 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Crowley, G.; Hackert, C.L.; Meier, R.R.; Strickland, D.J.; Paxton, L.J.; Pi, X.; Mannucci, A.; Christensen, A.B.; Morrison, D.; Bust, G.S.; et al. Global thermosphere-ionosphere response to onset of 20 November 2003 magnetic storm. J. Geophys. Res. 2006, 111, A10S18. [Google Scholar] [CrossRef]
- Rama Rao, P.V.; Gopi Krishna, S.; Vara Prasad, J.; Prasad, S.N.; Prasad, D.S.; Niranjan, K. Geomagnetic storm effects on GPS based navigation. Ann. Geophys. 2009, 27, 2101–2110. [Google Scholar] [CrossRef]
- Wen, D.; Mei, D. Ionospheric TEC disturbances over China during the strong geomagnetic storm in September 2017. Adv. Space Res. 2020, 65, 2529–2539. [Google Scholar] [CrossRef]
- Nayak, K.; López-Urías, C.; Romero-Andrade, R.; Sharma, G.; Guzmán-Acevedo, G.M.; Trejo-Soto, M.E. Ionospheric Total Electron Content (TEC) anomalies as earthquake precursors: Unveiling the geophysical connection leading to the 2023 Moroccan 6.8 Mw earthquake. Geosciences 2023, 13, 319. [Google Scholar] [CrossRef]
- Sharma, G.; Nayak, K.; Romero-Andrade, R.; Aslam, M.M.; Sarma, K.K.; Aggarwal, S.P. Low ionosphere density above the earthquake epicentre region of M 7.2, El Mayor–Cucapah earthquake evident from dense CORS data. J. Indian Soc. Remote Sens. 2024, 52, 543–555. [Google Scholar] [CrossRef]
- Brunini, C.; Azpilicueta, F. GPS slant total electron content accuracy using the single layer model under different geomagnetic regions and ionospheric conditions. J. Geod. 2010, 84, 293–304. [Google Scholar] [CrossRef]
- Zhao, X.; Jin, S.; Mekik, C.; Feng, J. Evaluation of regional ionospheric grid model over China from dense GPS observations. Geod. Geodyn. 2016, 7, 361–368. [Google Scholar] [CrossRef]
- Chen, M.; Liu, L.; Xu, C.; Wang, Y. Improved IRI-2016 model based on BeiDou GEO TEC ingestion across China. GPS Solut. 2020, 24, 1–11. [Google Scholar] [CrossRef]
- Yang, H.; Xuhai, Y.; Zhe, Z.; Zhao, K. High-precision ionosphere monitoring using continuous measurements from BDS GEO satellites. Sensors 2018, 18, 714. [Google Scholar] [CrossRef]
- Huang, F.; Lei, J.; Dou, X.; Luan, X.; Zhong, J. Nighttime medium-scale traveling ionospheric disturbances from airglow imager and Global Navigation Satellite Systems observations. Geophys. Res. Lett. 2018, 45, 31–38. [Google Scholar] [CrossRef]
- Jin, S.; Jin, R.; Kutoglu, H. Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. J. Geod. 2017, 91, 613–626. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, L.; Wang, J.; Zhang, C. Studying ionosphere responses to a geomagnetic storm in June 2015 with multi-constellation observations. Remote Sens. 2018, 10, 666. [Google Scholar] [CrossRef]
- Tang, J.; Gao, X.; Yang, D.; Zhong, Z.; Huo, X.; Wu, X. Local persistent ionospheric positive responses to the geomagnetic storm in August 2018 using BDS-GEO satellites over low-latitude regions in Eastern Hemisphere. Remote Sens. 2022, 14, 2272. [Google Scholar] [CrossRef]
- Jia, X.; Liu, J.; Zhang, X. The Analysis of Ionospheric TEC Anomalies Prior to the Jiuzhaigou Ms7. 0 Earthquake Based on BeiDou GEO Satellite Data. Remote Sens. 2024, 16, 660. [Google Scholar] [CrossRef]
- Sardón, E.; Rius, A.; Zarraoa, N. Estimation of the transmitter and receiver differential biases and the ionospheric total electron content from Global Positioning System observations. Radio Sci. 1994, 29, 577–586. [Google Scholar] [CrossRef]
- Jin, R.; Jin, S.; Feng, G. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solut. 2012, 16, 541–548. [Google Scholar] [CrossRef]
- Wilson, B.; Mannucci, A. Instrumental Biases in Ionospheric Measurements derived from GPS data. In Proceedings of the ION GPS-93, Salt Lake City, UT, USA, 22–24 September 1993. [Google Scholar]
- Wang, Q.; Zhu, J.; Hu, F. Ionosphere total electron content modeling and multi-type differential code bias estimation using multi-mode and multi-frequency global navigation satellite system observations. Remote Sens. 2023, 15, 4607. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, Z.; Gong, X.; Zheng, F.; Gu, S.; Shi, C. Estimating GPS satellite and receiver differential code bias based on signal distortion bias calibration. GPS Solut. 2023, 27, 48. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Dissertation, University of Berne, Berne, Switzerland, 1999. [Google Scholar]
- Sophan, S.; Myint, L.M.; Saito, S.; Supnithi, P. Performance improvement of the GAGAN satellite-based augmentation system based on local ionospheric delay estimation in Thailand. GPS Solut. 2022, 26, 130. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Li, H.; Ou, J.; Huo, X. Two-step method for the determination of the Differential Code Biases of COMPASS satellites. J. Geod. 2012, 86, 1059–1076. [Google Scholar] [CrossRef]
- Li, W.; Wang, K.; Yuan, K. Performance and consistency of final global ionospheric maps from different IGS analysis centers. Remote Sens. 2023, 15, 1010. [Google Scholar] [CrossRef]
- Li, X.; Xie, W.; Huang, J.; Ma, T.; Zhang, X.; Yuan, Y. Estimation and analysis of differential code biases for BDS3/BDS2 using iGMAS and MGEX observations. J. Geod. 2019, 93, 419–435. [Google Scholar] [CrossRef]
- Li, M.; Yuan, Y. Estimation and analysis of BDS2 and BDS3 differential code biases and global ionospheric maps using BDS observations. Remote Sens. 2021, 13, 370. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Li, Z.; Zhong, J.; Hao, Y.; Zhang, M.; Niu, J.; Wan, X.; Huang, F.; Han, H.; Song, X.; Chen, J. Assessment of the orbital variations of GNSS GEO and IGSO satellites for monitoring ionospheric TEC. GPS Solut. 2023, 27, 62. [Google Scholar] [CrossRef]
- Chen, C.; Chang, G.; Luo, F.; Zhang, S. Dual-frequency carrier smoothed code filtering with dynamical ionospheric delay modeling. Adv. Space Res. 2019, 63, 857–870. [Google Scholar] [CrossRef]
- Hwang, P.Y.; McGraw, G.A.; Bader, J.R. Enhanced differential GPS carrier-smoothed code processing using dual-frequency measurements. Navigation 1999, 46, 127–138. [Google Scholar] [CrossRef]
- Kim, E.; Walter, T.; Powell, J.D. Adaptive carrier smoothing using code and carrier divergence. In Proceedings of the 2007 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 22–24 January 2007. [Google Scholar]
- Park, B.; Sohn, K.; Kee, C. Optimal Hatch filter with an adaptive smoothing window width. J. Navig. 2008, 61, 435–454. [Google Scholar] [CrossRef]
- Gunther, C.; Henkel, P. Reduced-noise ionosphere-free carrier smoothed code. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 323–334. [Google Scholar] [CrossRef]
- Zhou, H.; Li, Z.; Liu, C.; Xu, J.; Li, S.; Zhou, K. Assessment of the performance of carrier-phase and Doppler smoothing code for low-cost GNSS receiver positioning. Results Phys. 2020, 19, 103574. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Kiselev, A.V.; Zhivetiev, I.V.; Edemskiy, I.K.; Syrovatskii, S.V.; Maletckii, B.M.; Vesnin, A.M. SIMuRG: System for ionosphere monitoring and research from GNSS. GPS Solut. 2020, 24, 1–12. [Google Scholar] [CrossRef]
- Chen, J.; Ren, X.; Xiong, S.; Zhang, X. Modeling and analysis of an ionospheric mapping function considering azimuth angle: A preliminary result. Adv. Space Res. 2022, 70, 2867–2877. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, C. On the optimal height of ionospheric shell for single-site TEC estimation. GPS Solut. 2018, 22, 1–11. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Wang, N.; Hernandez-Pajares, M.; Huo, X. SHPTS: Towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J. Geod. 2015, 89, 331–345. [Google Scholar] [CrossRef]
- Li, B.; Wang, M.; Wang, Y.; Guo, H. Model assessment of GNSS-based regional TEC modeling: Polynomial, trigonometric series, spherical harmonic and multi-surface function. Acta Geod. Geophys. 2019, 54, 333–357. [Google Scholar] [CrossRef]
- Komjathy, A.; Sparks, L.; Wilson, B.; Mannucci, A. Automated daily processing of more than 1000 ground-based GPS receivers for studying intense ionospheric storms. Radio Sci. 2005, 40, 1–11. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Olivares-Pulido, G.; Hoque, M.M.; Prol, F.S.; Yuan, L.; Notarpietro, R.; Graffigna, V. Topside ionospheric tomography exclusively based on LEO POD GPS carrier phases: Application to autonomous LEO DCB estimation. Remote Sens. 2023, 15, 390. [Google Scholar] [CrossRef]
- Paige, C.; Saunders, M. LSQR: An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. (TOMS) 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Jin, S.; Wang, J.; Park, P. An improvement of GPS height estimations: Stochastic modeling. Earth Planets Space 2005, 57, 253–259. [Google Scholar] [CrossRef]
- Astafyeva, E.; Heki, K. Vertical TEC over seismically active region during low solar activity. J. Atmos. Sol.-Terr. Phys. 2011, 73, 1643–1652. [Google Scholar] [CrossRef]
- Zhang, F.; Tang, L.; Li, J.; Du, X. A simple approach to determine single-receiver differential code bias using precise point positioning. Sensors 2023, 23, 8230. [Google Scholar] [CrossRef] [PubMed]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Clette, F.; Lefèvre, L. The New Sunspot Number: Assembling All Corrections. Sol. Phys. 2016, 291, 2629–2651. [Google Scholar] [CrossRef]
- Saiz, E.; Cerrato, Y.; Cid, C.; Dobrica, V.; Hejda, P.; Nenovski, P.; Stauning, P.; Bochnicek, J.; Danov, D.; Demetrescu, C.; et al. Geomagnetic response to solar and interplanetary disturbances. J. Space Weather Spac. 2013, 3, A26. [Google Scholar] [CrossRef]
- Lockwood, M.; Stamper, R.; Wild, M. A doubling of the Sun’s coronal magnetic field during the past 100 years. Nature 1999, 399, 437–439. [Google Scholar] [CrossRef]
- Lissa, D.; Srinivasu, V.K.D.; Prasad, D.S.V.V.D.; Niranjan, K. Ionospheric response to the 26 August 2018 geomagnetic storm using GPS-TEC observations along 80 E and 120 E longitudes in the Asian sector. Adv. Space Res. 2020, 66, 1427–1440. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Hajra, R. Energetics of shock-triggered supersubstorms (SML < −2500 nT). Astrophys. J. 2023, 946, 17. [Google Scholar]
- Lee, W.; Kil, H.; Paxton, L.; Zhang, Y.; Shim, J. The effect of geomagnetic-storm-induced enhancements to ionospheric emissions on the interpretation of the TIMED/GUVI O/N2 ratio. J. Geophys. Res. Space 2013, 118, 7834–7840. [Google Scholar] [CrossRef]


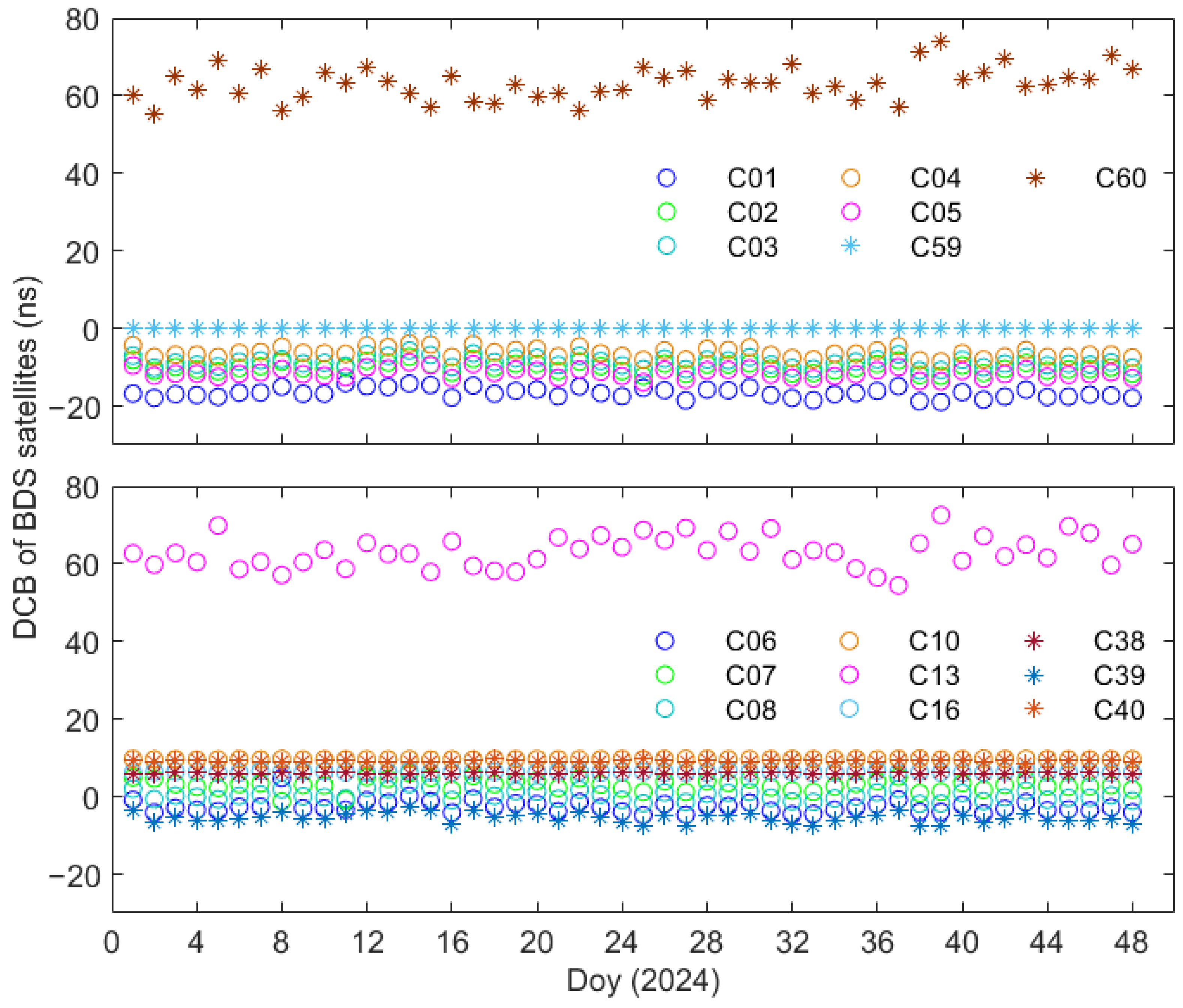
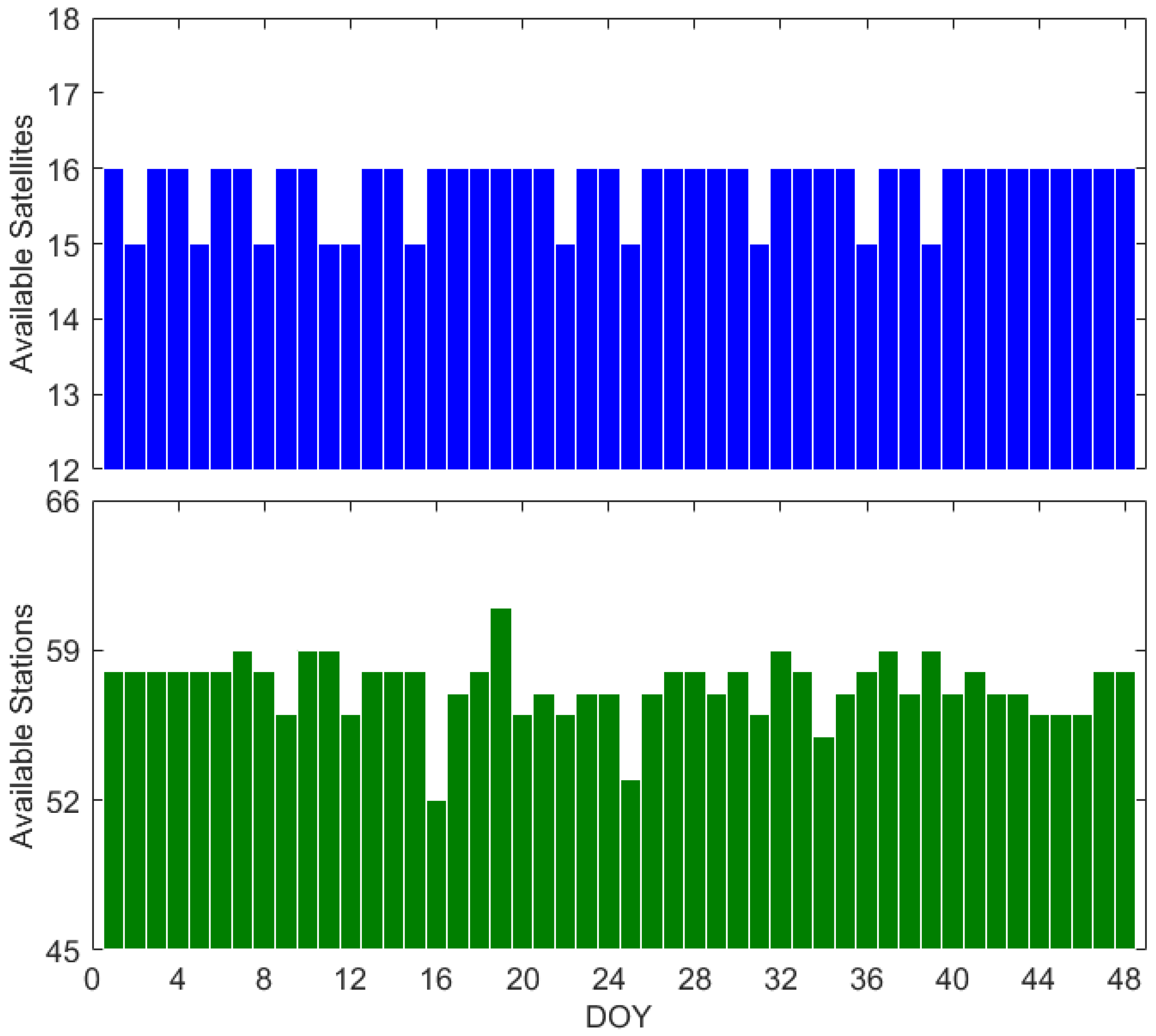
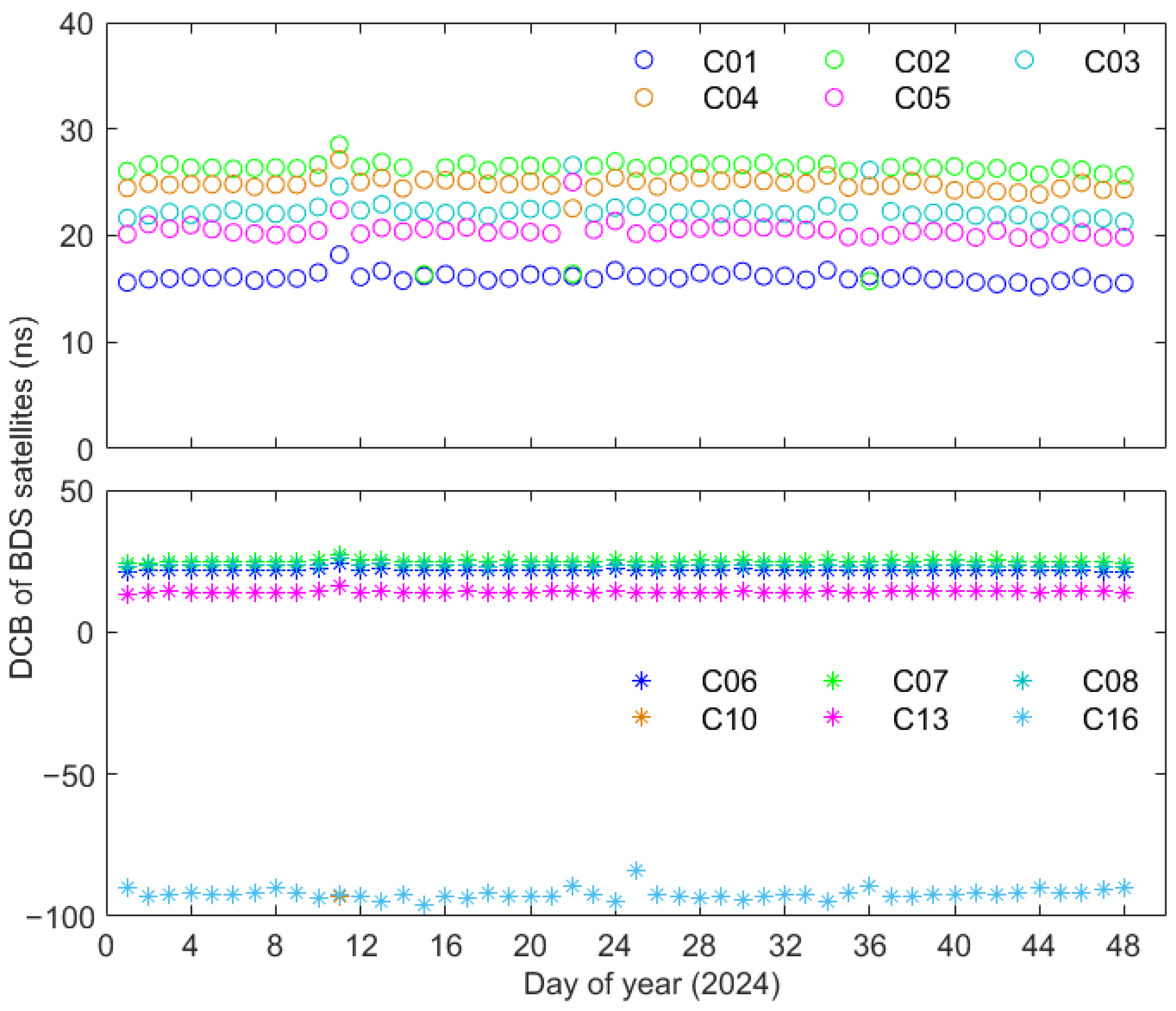


| System | PRN | SVN | NORADID | ClockType | Launch | Inclination (rad) |
|---|---|---|---|---|---|---|
| BDS-2 | C01 | GEO-8 | 44231 | Rubidium | 2019/05/17 | 0.095815041 |
| C02 | GEO-6 | 38953 | 2012/10/25 | 0.061223427 | ||
| C03 | GEO-7 | 41586 | 2016/06/12 | 0.061247412 | ||
| C04 | GEO-4 | 37210 | 2010/11/01 | 0.078722163 | ||
| C05 | GEO-5 | 38091 | 2012/02/25 | 0.060379663 | ||
| BDS-3 | C59 | GEO-1 | 43683 | Hydrogen | 2018/11/01 | 0.107197479 |
| C60 | GEO-2 | 45344 | 2020/03/09 | 0.121404913 |
| System | PRN | SVN | NORADID | ClockType | Launch | Inclination (rad) |
|---|---|---|---|---|---|---|
| BDS-2 | C06 | IGSO-1 | 36828 | Rubidium | 2010/08/01 | 0.944323177 |
| C07 | IGSO-2 | 37256 | 2010/12/18 | 0.893534803 | ||
| C08 | IGSO-3 | 37384 | 2011/04/10 | 1.039540317 | ||
| C09 | IGSO-4 | 37763 | 2011/07/27 | 0.949210898 | ||
| C10 | IGSO-5 | 37948 | 2011/12/02 | 0.895253611 | ||
| C13 | IGSO-6 | 41434 | 2016/03/30 | 1.000638794 | ||
| C16 | IGSO-7 | 43539 | 2018/07/10 | 0.959717824 | ||
| BDS-3 | C38 | IGSO-1 | 44204 | Hydrogen | 2019/04/20 | 0.973775532 |
| C39 | IGSO-2 | 44337 | 2019/06/25 | 0.960276832 | ||
| C40 | IGSO-3 | 44709 | 2019/11/05 | 1.014828481 |
| Signals | Frequency (MHz) | Observation Type | Number of Stations |
|---|---|---|---|
| B1I | 1561.098 | C2I | 71 (100.0%) |
| B1C | 1575.420 | C1P | 36 (50.7%) |
| C1X | 21 (29.6%) | ||
| C1A | 4 (5.6%) | ||
| C1B | 3 (4.2%) | ||
| B2a | 1176.450 | C5I | 6 (8.4%) |
| C5Q | 1 (1.4%) | ||
| C5P | 36 (50.7%) | ||
| C5X | 21 (29.6%) | ||
| B2b | 1207.140 | C7A | 4 (5.6%) |
| C7Z | 6 (8.4%) | ||
| C7D | 45 (63.4%) | ||
| B2 (B2a + B2b) | 1191.795 | C8X | 6 (8.4%) |
| B2I | 1207.140 | C7I | 65 (91.5%) |
| B3I | 1268.520 | C6I | 71 (100.0%) |
| System | Type | PRN | SHF Model | POLY Model | ||
|---|---|---|---|---|---|---|
| Max-Min | RMS | Max-Min | RMS | |||
| BDS2 | GEO | C01 | 4.8246 | 1.2649 | 6.6541 | 1.1965 |
| C02 | 4.9965 | 1.2159 | 8.3969 | 1.3651 | ||
| C03 | 5.1077 | 1.2750 | 4.9093 | 1.0269 | ||
| C04 | 4.6221 | 1.2400 | 7.4510 | 1.4082 | ||
| C05 | 5.1241 | 1.2115 | 7.4002 | 1.4676 | ||
| IGSO | C06 | 9.6017 | 1.6393 | 7.5681 | 1.5817 | |
| C07 | 7.3000 | 1.5195 | 7.2643 | 1.3439 | ||
| C08 | 5.1083 | 1.2832 | 9.8651 | 1.8937 | ||
| C10 | 4.3504 | 1.0744 | 4.9504 | 1.1315 | ||
| C13 | 18.1176 | 4.0828 | 8.8104 | 1.9778 | ||
| C16 | 4.8246 | 1.2649 | 1.2168 | 1.1887 | ||
| BDS3 | GEO | C60 | 18.5698 | 4.2157 | 8.8075 | 1.9859 |
| IGSO | C38 | 4.6810 | 1.1508 | 4.5810 | 1.1545 | |
| C39 | 5.1334 | 1.2644 | 7.4864 | 1.2103 | ||
| C40 | 4.9550 | 1.2441 | 4.9550 | 1.2450 | ||
| Doy | 001 | 002 | 003 | 004 | 005 | 006 | 007 | 008 |
|---|---|---|---|---|---|---|---|---|
| Classical | 8.838 | 10.746 | 11.782 | 8.210 | 11.339 | 10.706 | 10.237 | 10.384 |
| Ours | 8.570 | 9.937 | 10.855 | 7.853 | 10.543 | 10.107 | 9.373 | 10.022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Ma, Z.; Shu, L.; Pan, L.; Zhang, H.; Yang, S. Assessment of Satellite Differential Code Biases and Regional Ionospheric Modeling Using Carrier-Smoothed Code of BDS GEO and IGSO Satellites. Remote Sens. 2024, 16, 3118. https://doi.org/10.3390/rs16173118
Gao X, Ma Z, Shu L, Pan L, Zhang H, Yang S. Assessment of Satellite Differential Code Biases and Regional Ionospheric Modeling Using Carrier-Smoothed Code of BDS GEO and IGSO Satellites. Remote Sensing. 2024; 16(17):3118. https://doi.org/10.3390/rs16173118
Chicago/Turabian StyleGao, Xiao, Zongfang Ma, Lina Shu, Lin Pan, Hailong Zhang, and Shuai Yang. 2024. "Assessment of Satellite Differential Code Biases and Regional Ionospheric Modeling Using Carrier-Smoothed Code of BDS GEO and IGSO Satellites" Remote Sensing 16, no. 17: 3118. https://doi.org/10.3390/rs16173118
APA StyleGao, X., Ma, Z., Shu, L., Pan, L., Zhang, H., & Yang, S. (2024). Assessment of Satellite Differential Code Biases and Regional Ionospheric Modeling Using Carrier-Smoothed Code of BDS GEO and IGSO Satellites. Remote Sensing, 16(17), 3118. https://doi.org/10.3390/rs16173118








