Next Article in Journal
Underwater Acoustic Scattering from Multiple Ice Balls at the Ice–Water Interface
Previous Article in Journal
Causes of Increased Compound Temperature and Precipitation Extreme Events in the Arid Region of Northwest China from 1961 to 2100
Previous Article in Special Issue
A Multi-Satellite Space Environment Risk Prediction and Real-Time Warning System for Satellite Safety Management
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 16
Issue 17
10.3390/rs16173112
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Ionospheric and Meteorological Anomalies Associated with the Earthquake in Central Asia on 22 January 2024

by
Renata Lukianova
1,2,*,
Gulbanu Daurbayeva
1 and
Akgenzhe Siylkanova
1
1
National Scientific Center for Seismological Observations and Research, Almaty 050060, Kazakhstan
2
Space Research Institute, 117997 Moscow, Russia
*
Author to whom correspondence should be addressed.
Remote Sens. 2024, 16(17), 3112; https://doi.org/10.3390/rs16173112
Submission received: 28 June 2024 / Revised: 6 August 2024 / Accepted: 10 August 2024 / Published: 23 August 2024
(This article belongs to the Special Issue Using Remote Sensing Satellites to Explore the Electromagnetic Environment and Natural Hazard Disturbances in Space)
Browse Figures
Versions Notes

Abstract

:
On 22 January 2024, at 18 UT, a strong earthquake (EQ), Mw = 7, occurred with the epicenter at 41°N, 79°E. This seismic event generated a complex response, the elements of which correspond to the concept of lithosphere–atmosphere–ionosphere coupling through electromagnetic processes. While flying over the EQ area on the night-ide of the Earth, the tandem of low-orbiting Swarm satellites observed small-scale irregularities in the plasma density with an amplitude of ~1.5 × 104 el/cm3, which are likely associated with the penetration of the coseismic electric field into the ionosphere. The local anomaly was detected against the background of a global increase in total electron content, TEC (although geomagnetic indices remained quiet), since the moment of EQ coincided with the ionospheric response to a solar flare. In the troposphere, specific humidity decreased while latent heat flux and aerosol optical depth increased, all exhibiting the co-located disturbances that can be attributed to the effect of increased air ionization rates, resulting in greater electrical conductivity in the near-Earth boundary layer. Anomalies started developing over the epicenter the day before and maximized on the day of the main shock and aftershocks.

1. Introduction

Detecting anomalous changes in the atmosphere and ionosphere before and during strong earthquakes (EQ) is a subject of intensive research due to the importance of developing prediction and early warning methods. Over the past decade, numerous ground-based and satellite observations have been carried out from the Earth’s surface to the ionosphere to detect possible effects associated with seismic activity and its precursors (e.g., [1,2,3,4,5,6,7,8,9]). The working hypothesis of the “electromagnetic signal” is that in the ionosphere, an electric field, somehow generated over a fault due to seismic activity, causes plasma to drift in crossed electric (E) and geomagnetic (B) fields. In particular, the eastward component of E moves the ionospheric plasma upwards and thereby leads to an increase in the electron concentration at a certain altitude above the maximum of the F2-layer. An average magnitude of the E-field in the ionosphere is estimated to be 10 mV/m and horizontal scales of 100–1000 km. Such fields were frequently detected by the high-latitude radars [10]. At low and middle latitudes, the radars observed the plasma motion corresponding to the E-fields of units mV/m or less [11]. Model simulations confirmed that the E-field generated in the polar regions covers a wide range of latitudes in both hemispheres [12]. Observations from the Demeter and CSES satellites showed disturbances in the ionospheric electric field possibly associated with VLF/ULF electromagnetic waves detected over seismic regions [13,14,15]. Observations also indicated that the total electron content (TEC) may anomalously decrease or increase up to 5–20% before the occurrence of strong earthquakes [16,17]. The investigation of magnetic data from the Swarm satellite a month before and after the Nepal earthquake identified a common pattern in magnetic anomalies and seismicity [18]. The timeframe during which these anomalies typically occur is variable, manifesting anywhere from a few minutes to 30 days before a significant EQ. In particular, in [19], anomalies in ionospheric TEC observed approximately 40 min before the earthquake in North–East Japan were reported; Ref. [20] documented anomalies two days prior to the Cucapah event; Ref. [21] identified anomalies six to seven days before the Morocco EQ in September 2023; Ref. [22] statistically determined that more than 90% of earthquake-related TEC anomalies occur approximately seven days before the event; and Ref. [23] specified a 25–80 min anomaly window prior to EQs, depending on their magnitude. Statistically, ionospheric anomalies were found before some strong earthquakes, but no anomalies occurred before the others [24]. It still remains unclear why the precursor may disappear long before the event.
The statistical analysis of the measurements of the European Space Agency’s (ESA’s) Swarm satellite constellation demonstrated that the ionosphere is indeed affected by EQs, and the rapid disturbance in electron density (Ne) is a form of seismic ionospheric response [6,25,26]. At the same time, it was noted that these disturbances are weak and often hidden among the background of general disturbances of the magnetospheric or thermospheric origin, such as atmospheric gravity waves and associated traveling ionospheric disturbances (TIDs) [27], plasma bubbles [28], sporadic E-layers [29], ionospheric perturbations due to prompt penetration electric field at the middle latitudes [30], or large-scale irregularities originated in the high latitudes [31] and dependent on the solar wind–magnetosphere interaction. The severity of ionospheric variability, including the horizontal and vertical displacements of the plasma, increases with growing geomagnetic activity.
The modeling results showed that to ensure the penetration of a sufficient part of the E-field to ionospheric heights, increased air conductivity is required [32,33,34]. With the appearance of free charges, a vertical electric current arises in the atmosphere. This is a general approach within the Global Electric Circuit (GEC) theory that can be applied to the coseismic E-field and its ionospheric and atmospheric effects [35]. Pre- and coseismic ionospheric effects are considered to be a result of the intensification of natural radioactivity near the Earth surface [36,37]. Radioactive gases such as radon emanating from the crust provide additional charges accumulating on aerosols in the low troposphere. In the presence of large, heavy molecules, such as soil gases, dust, ash, metal particles, and other aerosols, free electrons quickly attach to them. Due to the slow recombination rate of the newly formed large charged particles, an increase in charge concentrations occurs. Charged aerosols lead to increased ionization of the air boundary layer, changes in the air’s electrical conductivity, the generation of electric field perturbations, and their effective penetration into the ionosphere.
The half-life time of Rn-222 is 3.8 days. Registration of radon is quite complex since it is indirect, based mainly on the α and γ components of radon decay, and has a large degree of uncertainty. Regular radon monitoring data are available only in a very few places. There are no such measurements in the area of the EQ epicenter of the event under consideration. However, it is possible to measure the atmospheric response to air ionization caused by radon. Increased radon concentration and charged particles (ions, clusters, and aerosols) at which the water vapor condensates produce a decrease in the air relative humidity and, as a consequence, an increase in the latent heat [4].
This paper presents a comprehensive analysis of ionospheric and meteorological observations during the strong (M = 7) earthquake that occurred on 22 January 2024 in Central Asia (epicenter near Xinjiang). The spatial extent of the shaking was relatively large, affecting the southern part of Kazakhstan. Observations from Swarm satellites, which provide in situ measurements of the electron density, and spatiotemporal distributions of meteorological parameters are analyzed in order to identify possible earthquake-related anomalies and distinguish them from background variability.

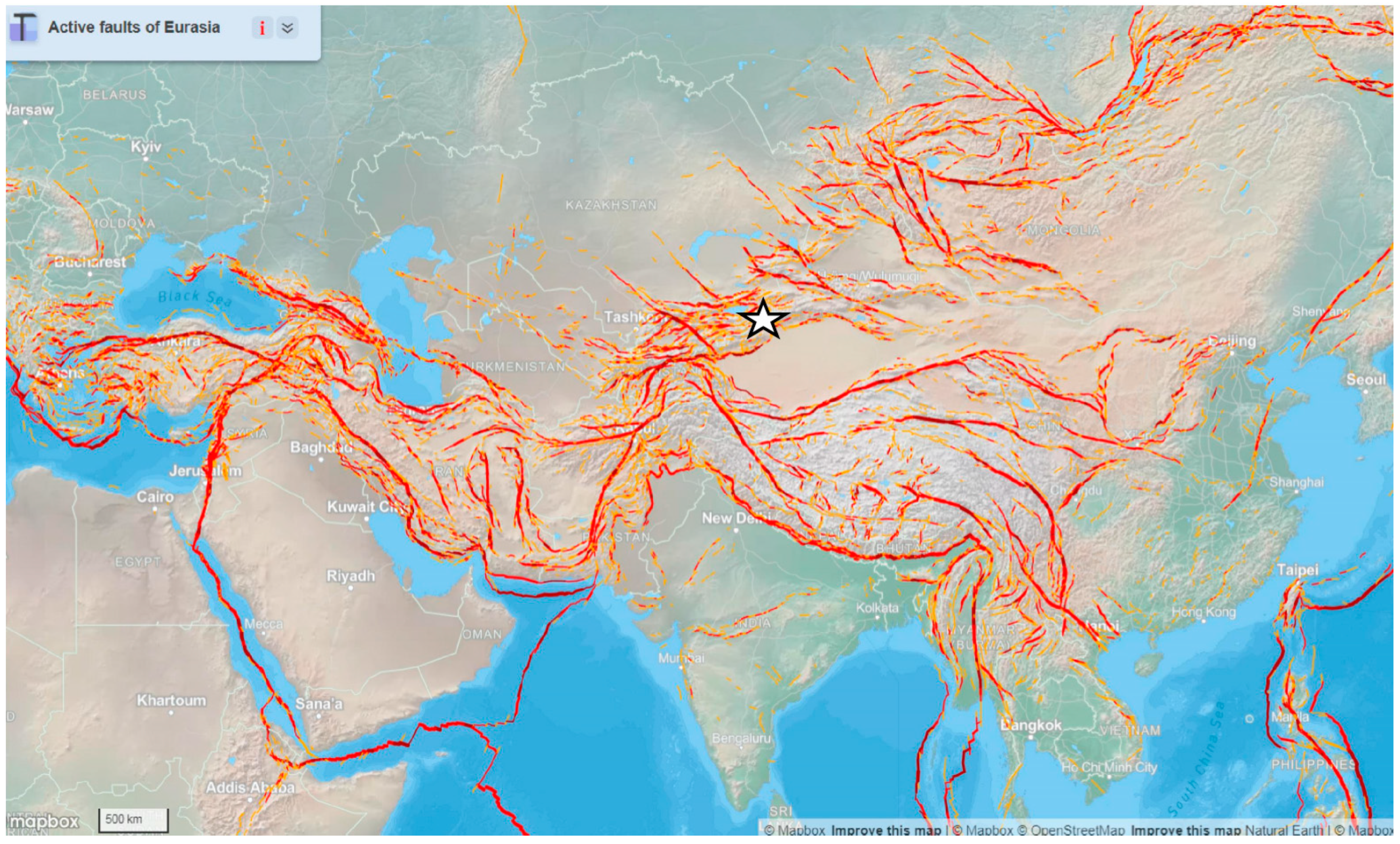
2. The M7 Earthquake on 22 January 2024

On 22 January 2024, at 18:09 UT, a large EQ occurred within the Tien Shan mountain range at the border between China (Southern Xinjiang) and the Kyrgyz Republic, with the epicenter at 41.2°N, 78.6°E in the Kok-Shaal-Tau ridge. The depth of the source was 13 km, and the magnitude was M ≥ 7 (Richter scale). The Tien Shan mountain range is the intraplate fold-and-thrust belt, tectonically controlled by the collision of India with Asia. According to the tectonic summary provided by the US Geological Survey (USGS), the EQ on 22 January 2024 was the result of an oblique reverse fault and a strike-slip fault at shallow depth [38]. Immediately after the main shock at 18:09 UT, a series of aftershocks from the same source occurred. By the local morning (~05 UT) of 23 January, 22 repeated EQs with a magnitude of about 4.0 and more than 100 weaker aftershocks were registered. Figure 1 shows the location of the EQ epicenter on the map of active faults in Eurasia provided by the Geological Institute of the Russian Academy of Science according to the corresponding database [39,40].
It is a seismically active region, although major EQs have occurred quite rarely. Over the previous 100 years, three events M > 6.5 occurred within a 250 km radius from the epicenter of the 22 January event. These were the M8.0 Kemin EQ in January 1911, near the modern border of Kyrgyzstan and Kazakhstan, and the M7.1 EQ in March 1978 in Tyup, Kyrgyzstan. The Tyup event provoked a shaking with the intensity quite close to that on 22 January 2024, while the Kemin M8.0 event completely destroyed the city of Verny (now Almaty). It is possible that a new long-term period of increased seismicity may now begin in the Tien Shan region. In addition to the scientific objectives mentioned in the Introduction, this fact further motivated us to conduct a detailed study of the Xinjiang M7.0 EQ, taking advantage of different datasets from the Earth Observing System.

3. Geomagnetic Activity and Ionospheric Weather

Various global ionospheric disturbances are associated with solar flares and coronal mass ejections (e.g., [42,43]). The released seismic energy associated with large earthquakes causes local and more short-term ionospheric anomalies that are superimposed on the current state of the ionosphere, i.e., the ionospheric weather. The challenge is to separate the individual sources of Ne disturbances, especially if the Sun is not quiet.

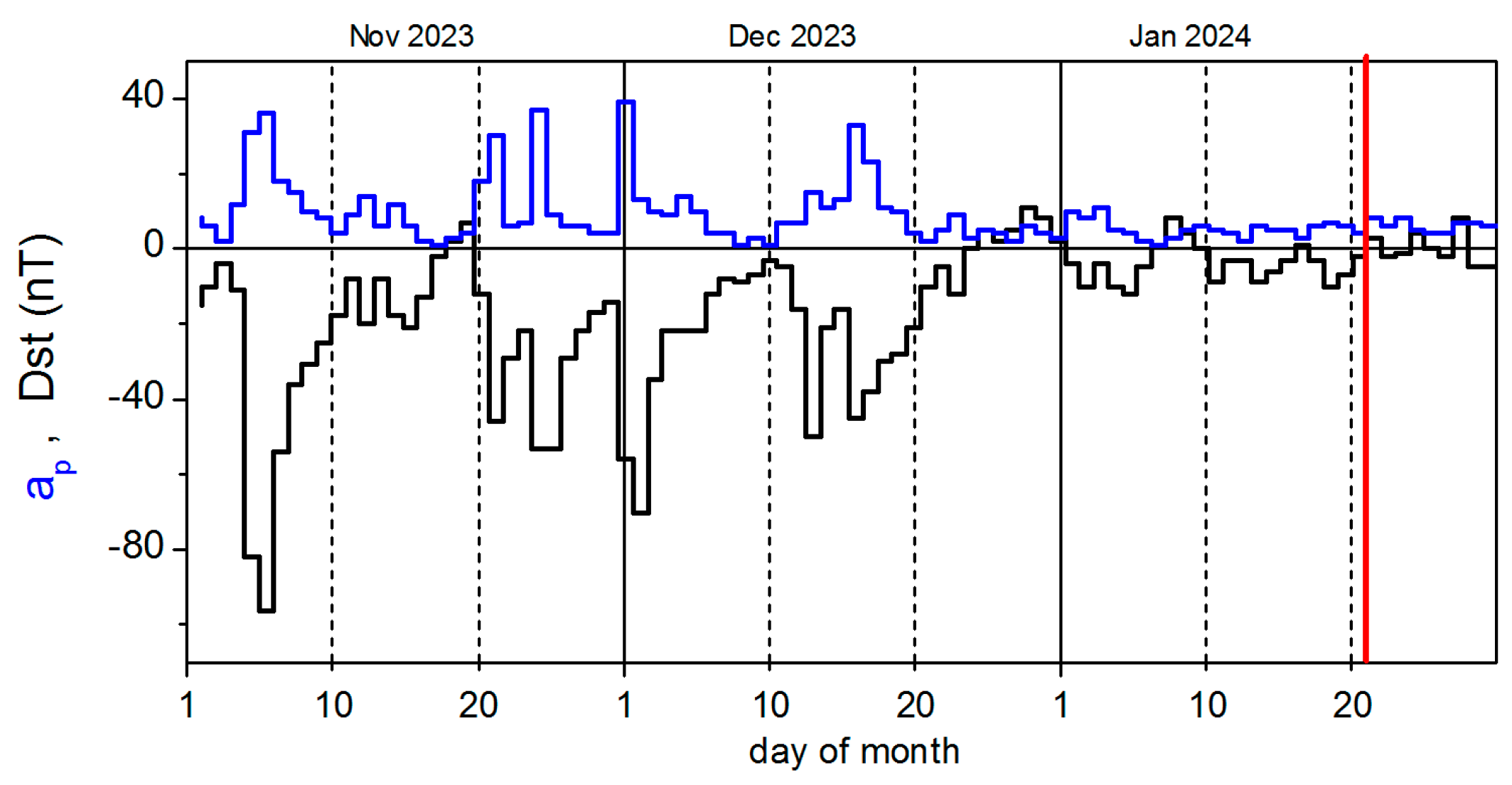
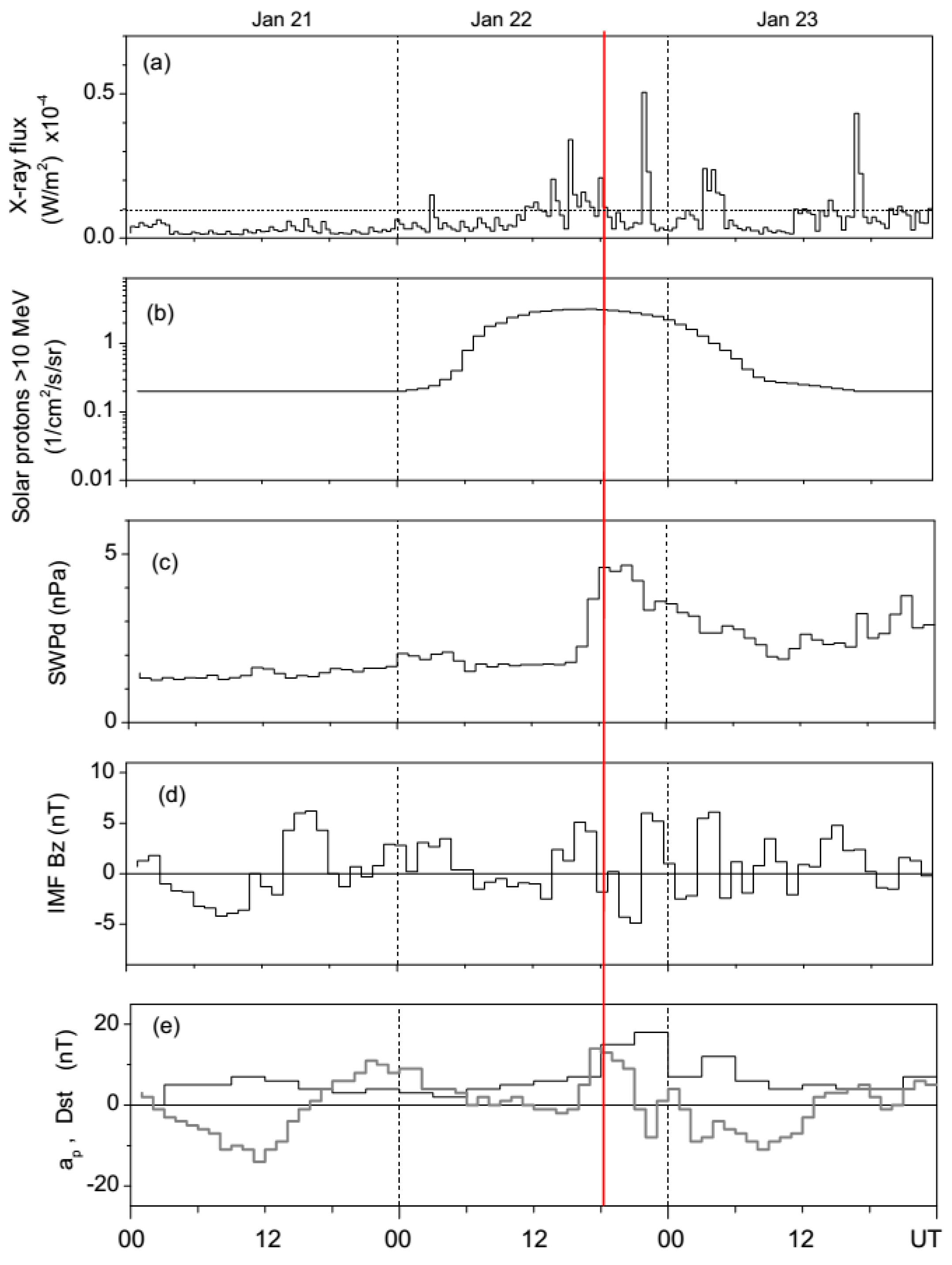
3.1. Geomagnetic Indices and Solar Activity

Any possible coseismic signal in the ionospheric plasma density is expected to manifest itself as a deviation from the background level typical for a particular location and time. Among the two geographic coordinates, the most important is the latitude. It is believed that the globally quiet geomagnetic conditions, as monitored by the planetary geomagnetic indices, are a primary criterion for excluding the possible external effect (i.e., associated with space weather) on the ionospheric variability. The EQ under consideration occurred during a prolonged period of geomagnetic quietness. Figure 2 depicts the storm-time ring current Dst and the midlatitude ap indices for the 3-month period from November 2023 to January 2024 obtained from the NASA OMNI data portal [44]. The background level of Dst and ap is zero. It is commonly accepted that, when Dst > −50 nT, there is no magnetic storm. The ap index can be graded according to the US National Oceanic and Atmospheric Administration (NOAA) criteria for the planetary Kp index, namely Kp < 2 (ap < 20 nT), which is the geomagnetic quietness. Only in early November did a weak magnetic storm occur, during which the ring current Dst index dropped below −80 nT. Magnetic activity continued to remain somewhat elevated until the end of December, and after that, the Dst index did not fall below −20 nT, indicating the absence of geomagnetic storms. The planetary index ap increased in accordance with the evolution of Dst. During the first half of the period, ap sometimes reached 40 nT, while in January it did not exceed 10 nT.
In Figure 3, the solar and space weather parameters are described for a shorter period centered on the day of EQ. It appears that, despite the geomagnetic quietness, the Sun was not quiet. Solar emissions could affect mainly the density of the ionospheric plasma, while the electrical currents flowing in the magnetosphere–ionosphere circuit (these currents are responsible for the ground magnetic variations) remained relatively undisturbed. The first panel (Figure 3a) depicts solar flare activity. This is the GOES-R X-Ray Sensor (XRS) Level 2 data, which are based on soft X-ray irradiance measurements covering 0.1–0.8 nm integrated passbands [45]. According to the NOAA classification in terms of peak emission, the X-ray flux level of ≥10−8, 10−7, 10−6, 10−5, and 10−4 W/m2 corresponds to A, B, C, M, and X flare, respectively. Figure 3a shows that on 21 January the flare activity was relatively weak (taking into account the solar maximum phase). On 22 January, the X-ray flux reached 3 × 10−5 (15 UT) and 5 × 10−5 W/m2 (23 UT), implying that the M-class flares occurred. The next day, a pair of peaks of similar amplitude was observed. Typically, the increase in X-rays is accompanied by more intense EUV emissions. The increased level of X-ray and EUV radiation results in ionization in the lower layers of the ionosphere, especially on the dayside, which leads to an increase in TEC.
The second panel (Figure 3b) shows the solar flux of a proton with energy ≥10 MeV. Data were taken from the SpaceWeatherLive.com portal [46], then digitized, and finally averaged over an hour. Protons started to increase on 22 January. The particle fluxes reduce the ionization altitude and increase the ionization intensity and electron density in the ionosphere. Peak altitudes of the ionization rates for solar protons, depending on their energy, are about 40 km but also affect the ionospheric layers [47]. However, compared with high-intensity solar flares, the 22 January event was rather minor. This period was not included in the NOAA Space Weather Prediction Center list of solar proton events affecting the Earth environment [48]. Nevertheless, any additional ionization contributes to increased electrical conductivity at certain altitudes.
In the last three panels (Figure 3c–e), the hourly values of the solar wind (SW) dynamic pressure Pd (Pd = n ∙ V2, where V and n is the SW speed and density, respectively), the interplanetary magnetic field (IMF) Bz component, and the Dst and ap indices are presented. The data were obtained from the NASA OMNI database, which provides interplanetary parameters referred to as the Earth’s orbit (1 AU). At 18 UT, 22 January, an abrupt increase in Pd from 1 hPa up to 4.5 nPa was observed. A steep front and a gradual trailing edge are typical features of an interplanetary magnetic cloud. At the same time, the IMF Bz turned south for several hours but reached only −5 nT. The compression of the magnetopause resulted in a positive excursion of Dst up to 15 nT. The geomagnetic response to the arrival of the SWPd pulse is global and covers a wide range of latitudes [49]. This effect is manifested in the growth of the ap index up to 18 nT at the end of 22 January, when it approached the upper limit of the quiet activity level. The SW driver was too weak to trigger even a minor magnetic storm (according to NOAA criteria, a G1 minor storm occurs when ap > 48 nT). At the same time, increased fluxes of X-rays and EUV, as well as solar protons, do produce additional ionization throughout the ionosphere and even the middle atmosphere. The flare at 23 UT on 22 January seemed to be the most geoeffective because it was accompanied by (while minor) a magnetic cloud and solar proton flux enhancement. Even under geomagnetic conditions that are formally considered quiet, the ionosphere may become irregular or disturbed, making it difficult to distinguish between the growth of Ne due to seismicity and the natural variability caused by space weather effects. Examination of TEC is important in establishing the background ionospheric plasma density over the area of occurrence of a possible ionospheric anomaly associated with the coseismic effect.

3.2. Variation of TEC Measurements

TEC (due to its definition) accounts for the entire ionospheric slab up to the plasmasphere. TEC primarily depends on solar EUV radiation, which forms its regular diurnal cycle. As geomagnetic activity increases, the picture becomes more complex due to increased electric fields, plasma drift, outgoing ion flows, ionospheric currents, and auroral precipitation that vary over different spatial and temporal scales. To account for natural ionospheric variations, we used the Global Ionospheric Maps (GIM) of TEC. The GIM-TEC maps with a spatial resolution of 2.5° × 5° for each hour are continually produced by the Jet Propulsion Laboratory [50,51].
In Figure 4, the Northern Hemisphere (0°–70°N) GIM-TEC maps for 18 and 23 UT on 21–23 January are presented. The epicenter of EQ is shown as a white dot in panels (b) and (e). The choice of these particular UTs is due to the fact that at 18 UT the main shock of EQ occurred, while at 23 UT the EQ area was crossed by the descending orbits of the Swarm satellites (as will be discussed below). The TEC distribution is dominated by diurnal variations, and they gradually decrease with increasing latitudes. At 18 UT, the EQ area is almost on the Earth’s night side. Visually, the difference between the TEC distributions at 18 UT for the three consecutive days presented in Figure 4a–c is quite minor. At 23 UT (Figure 4d–f), the EQ meridian moved toward the sunrise terminator, resulting in a naturally larger TEC over the epicentre. The TEC map for 22 January, 23 UT (Figure 4e) differs significantly from the maps for adjacent days. Assuming the TEC distribution on 21 January, 23 UT, was undisturbed by a solar flare, on 22 January, 23 UT, a relative increase in TEC throughout the hemisphere was observed. The elevated ionospheric TEC plume tends to expand from the daytime to the nighttime and from the equator to higher latitudes. The global increase in plasma density can most likely be explained by a response of the ionosphere to the increased ionization rate associated with the solar flare effect. The arrival of the SW Pd front, although its magnitude is minor, may also somewhat contribute to TEC [52].
Any possible anomalous signatures in ionospheric Ne, as they may contain the effects of induced coseismic signals, should be considered against the background of natural intra-ionospheric disturbances caused by space weather. At 23 UT, 22 January, due to the solar flare, TEC increased globally, including the ionosphere over the EQ area. A rough reference point, in particular, for subsequent analysis of the Swarm observations, appeared to be much higher than could be expected based on geomagnetic indices alone.
To quantify the evolution of TEC on a global scale and near the EQ epicentre, a 3-day time series of hourly values was constructed. Figure 5 shows TEC values averaged over the Northern Hemisphere (0°–70°N) and collected at a grid point of 40°N, 80°E for the period of 21–23 January. The times of the Swarm A/C satellite passages near the epicentre in ascending and descending orbits are indicated by vertical lines. Usually, the hemispheric TEC (Figure 5a) exhibits a regular diurnal variation with slightly greater values around 00 UT. At the end of 22 January, the hemispheric TEC began to increase rapidly, and at 23 UT, it reached a peak of ~40 TECU, which is at least twice as high as on the previous or subsequent day. At the particular geographic location, the UT variation is quite large (~30 TECU). The nighttime TEC is about 10 TECU. At 23 UT, 22 January, a notable excursion to the higher values is seen (Figure 5b). This peak is small compared with the amplitude of daily UT variation; however, for the night-side ionosphere, it is more than 10% of TEC. It is also noteworthy that in Figure 5b, a decrease in TEC at ~16 UT on 22 January can be identified. Probably this negative excursion can be considered a signature of the ionospheric precursor of EQ, but the exact origin of this reduction is difficult to locate.
Even though in the following analysis we avoid subtracting the level of reference (instead we consider the difference between Ne from the two satellites flying side by side, thus the ionospheric background is removed automatically), careful examination of the ionospheric weather before searching for coseismic anomalies is important. Otherwise, the short-term response of the ionosphere, even to a relatively minor change in the solar radiation flux, can be unreasonably interpreted as a coseismic anomaly.

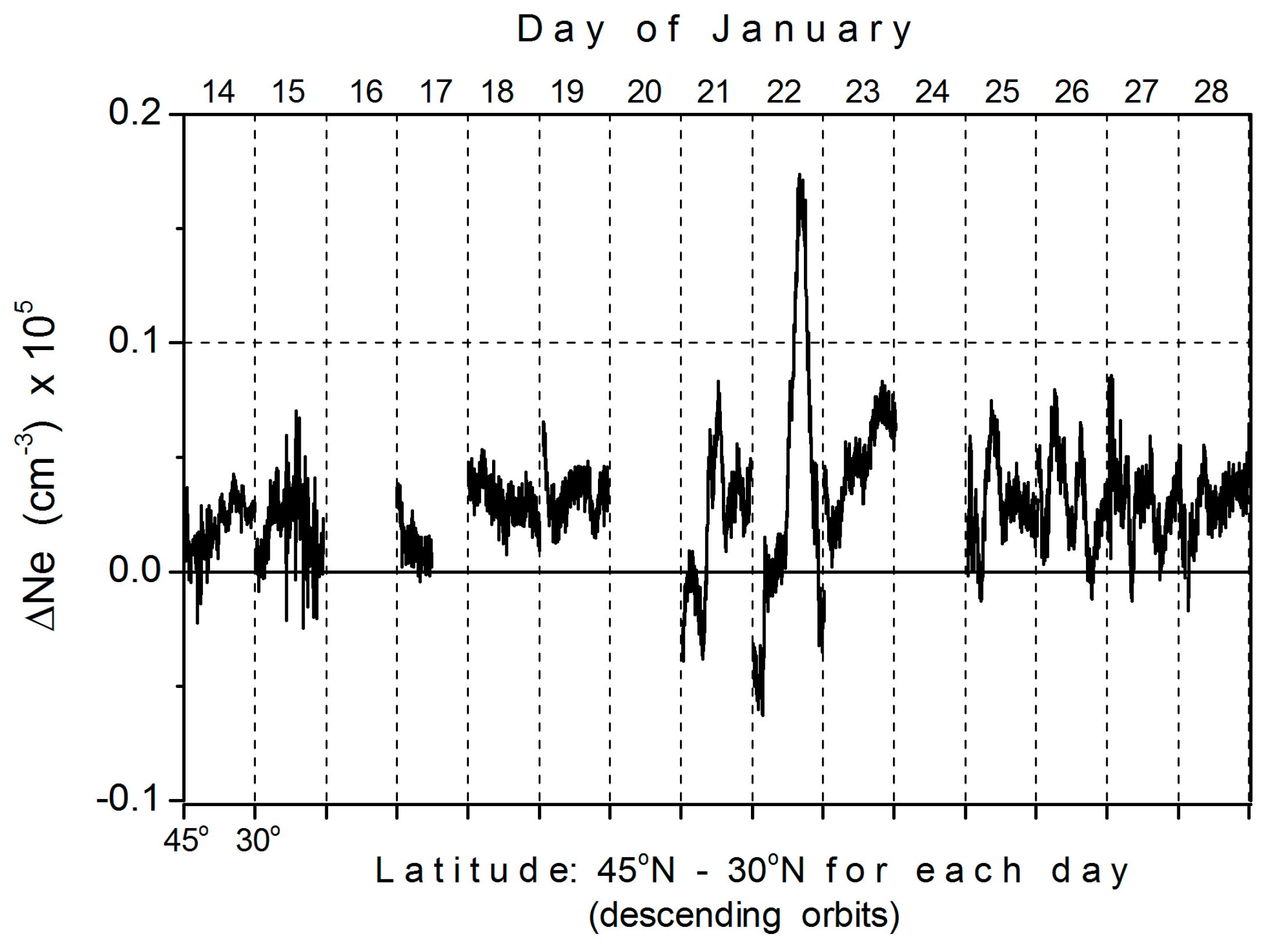
4. Local Variations of Ne in the Topside Ionosphere during Seismic Activity

To reveal the local ionospheric features during the period of interest, we used the Swarm data. These measurements allow in situ detection of ionospheric perturbations at a fixed altitude above the peak height of the F2 layer and investigate how the effect of the EQ on 22 January manifests itself on actual variations in Ne.

4.1. Swarm Satellites and Data

The three identical satellites of the ESA’s Swarm mission [53] are in specific low-quasi-polar orbits. They are not sun-synchronous, and as such, they allow the satellites to move rapidly through local time (LT). Two satellites (SwA and SwC) fly in tandem at an altitude of ~460 km (in the upper F-layer) close to each other at a distance of about 150 km, with a differential delay in orbit of several seconds. The third satellite (SwB) flies in another meridional plane at an altitude of ~530 km. Satellites orbit the Earth 14–15 times a day, flying in certain LT sectors. Gradually drifting in longitude, the orbits cover all LTs in a few months. Each satellite is equipped with scalar and vector magnetometers, sampling at 1 Hz (scalar) and 50 Hz (vectorial). A Langmuir probe (LP) monitors the ionospheric plasma density with a sampling rate of 2 Hz. The Level 2 data products are freely available on the ESA server (swarm-diss.eo.esa.int) (last access: 20 January 2023). The details are available in the Swarm Level 2 Processing handbook: (https://earth.esa.int/eogateway/missions/swarm/product-data-handbook/level-2-product-definitions; accessed on 2 March 2024).
Figure 6 illustrates the global distribution of Ne as measured by an individual Swarm satellite. In late January 2024, SwA and SwC orbits were centered at about 17 LT (the ascending branch corresponding to the day-side half-orbit) and 05 LT (the descending branch corresponding to the night-side half-orbit).
Figure 6 depicts the latitudinal profiles of Ne along the SwC passages for a full day on 22 January. At 17 LT, Ne reaches 2 × 106 el/cm3, while at 05 LT, almost on the night-side of the Earth, Ne is by an order of magnitude smaller. The transition to the mid-latitude ionosphere (20–30°) is characterized by a rapid change in plasma density. In both hemispheres, as the satellite moves from the middle latitudes to the auroral zone, Ne increases and becomes more variable. At mid/high latitudes, seasonal interhemispheric asymmetry is manifested in the predominance of the southern hemisphere. In Figure 6, the first and last passages of the day are shown by colored lines. The first orbit passed along the meridians at approximately 120°E and 50°W. The last orbit passed along 90°E (ascending) and 80°W (descending), i.e., the last descending passage was almost along the meridian of the EQ epicenter. At the end of 22 January, the Ne measured along both branches of the orbit was considerably larger than during the previous hours. This is consistent with the increase in TEC observed at 23 UT on 22 January (cf. Figure 4 and Figure 5).

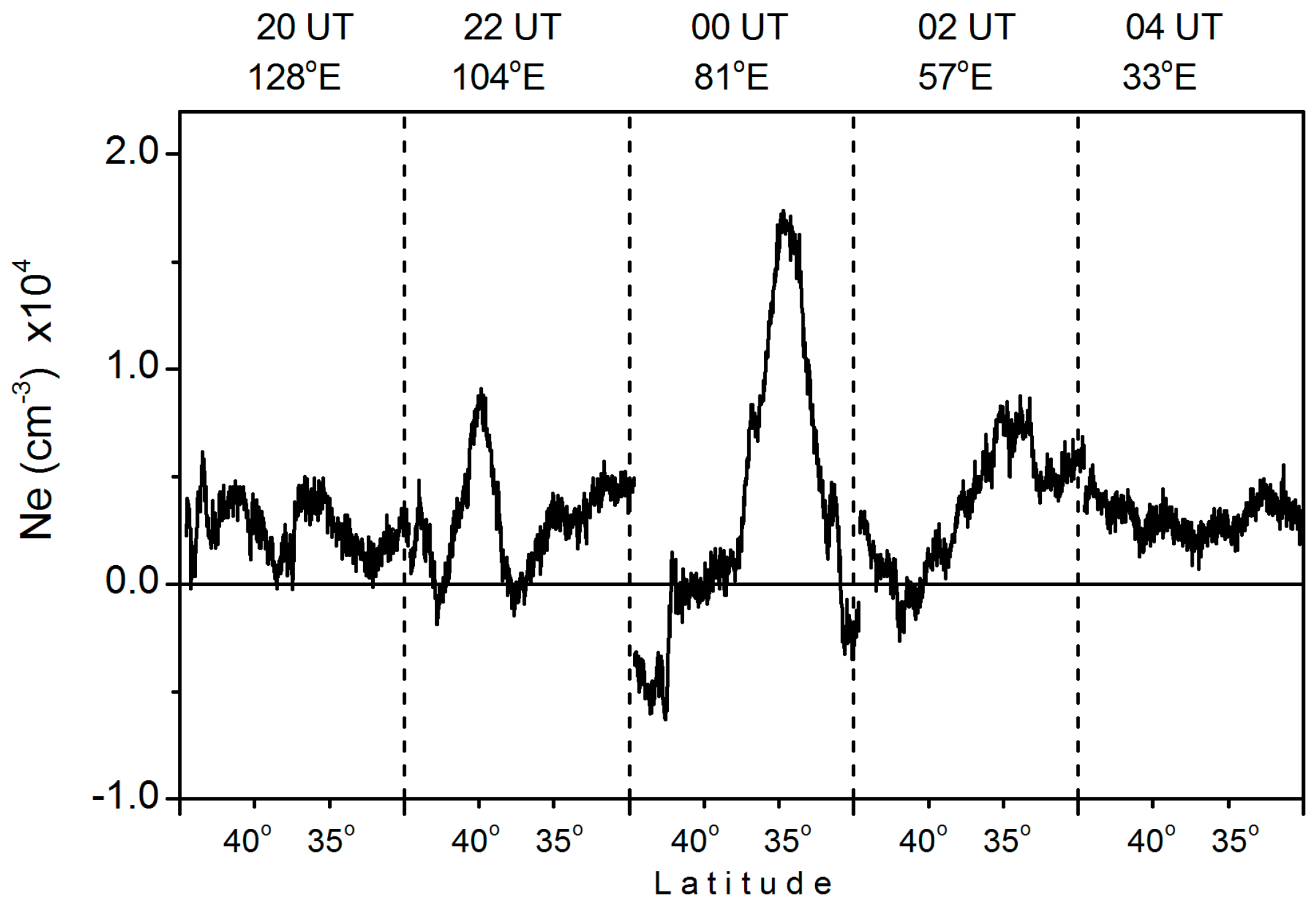
4.2. Ionospheric Disturbances over the EQ Area

Along-track satellite observations provide a brief overview of the surrounding EQ regions. To detect local Ne anomalies over the area surrounding the EQ epicenter, the Swarm passages in the region 30°–45°N, 64°–94°E were selected. The spatial scale of this area roughly corresponds to the Dobrovolsky radius of influence, R (km) = 100.43M [54]. For the event under study, R ≈ 1000 km. A rectangle is centered on the meridian of the EQ epicenter with a side of 15°. The latitudinal extent was chosen to be half as long as the longitudinal one. The geometry and size of the rectangle were chosen for two reasons. Firstly, active faults are elongated in latitude. Secondly, it is desirable to catch more satellite passages over the selected area (the rotation of the Earth during the time between consecutive passages is about 25°). At the orbital altitude, a spatial window is taken larger than that controlled by the ground-based parameter R. Within this window, the along-track measurements show the exact coordinates of the Ne anomaly. Relative to the epicentre, the latitudinal boundaries are slightly shifted to the south. This is because the seismo-electromagnetic signal in the ionosphere is supposed to be propagating along geomagnetic field lines [55], which in the northern hemisphere tilt south. According to the IGRF model [56], the ground-level latitude of 40°N is mapped to about 35°N at the orbital height. It was previously noted that the affected area extends approximately 600 km in the equatorial direction from the epicenter located at 40°N [1].
Figure 7 illustrates the Swarm satellites passing in the proximity of the epicenter of the 22 January EQ (thick lines) along with the other nearby tracks on this day (thin lines). Passages of the tandem of SwA/SwC satellites were at ~12 and ~23 UT; the Swarm_B passages occurred at ~08 and 14 UT. The time characteristics of satellite passages through the EQ area are presented in Table 1. Typically, the SwA/SwC trajectories cross this area twice a day: once along the ascending branch and once along the descending one. Since the orbit drifts in longitude, the distance between successive passages is about 25°, giving rise to gaps in the satellite coverage of the seismically investigated region.
To investigate the temporal evolution of Ne before, during, and after the earthquake, for the 15-day period centered on the day of the main shock, the data from SwA and SwC flying in pairs were selected. For each day from 14 January to 28 January, the Ne data were extracted, respectively, between 30°–45°N and 64°–94°E, for the descending (night-side half-orbits) and ascending (day-side half-orbits) nodes. Then the time series of the successive passages was formed. Figure 8 presents a stacked panel of the Ne variations from SwA and SwC vs. latitude in the range 30°–45°N as actually observed along successive descending (Figure 8a) and ascending (Figure 8b) orbits on 14–28 January. The Ne for the EQ date, 22 January, is shown on a larger scale in a separate panel (c). As Figure 8a shows, in the early morning, the Ne ionospheric values are close to 0.7 × 105 el/cm3. On 18 and 19 January, Ne dropped below 0.5 × 105 el/cm3 (on January 20, there were no appropriated passages over the selected area). On 22 January, the day of the main shock occurrence at 18 UT, Ne jumped up to 1.5 × 105 el/cm3. Such an abrupt Ne three-fold enhancement may be expected because this feature is likely a part of a large-scale expansion of TEC on the day-side (cf. Figure 4b). In the context of a possible coseismic effect, we pay attention to a smaller-scale anomaly in Ne, which appears when comparing data from two satellites flying nearby. During all days except 22 January, the Ne variations from SwA and SwC look quite similar. SwC observes a localized drop in Ne at ~35°N, while Ne from SwA peaks. Below, this feature will be discussed in more detail.
Passages through the more sunlit (17 LT) ionosphere revealed much larger Ne values (Figure 8b). The satellites observed a gradual decrease in Ne with increasing latitude. Intense ionization by solar UV radiation effectively smoothed out any small-scale irregularities in plasma density. It is only noteworthy that, among the days under consideration, 22 January is characterized by the lowest Ne values. The reason for this feature is not clear but may be related to the local redistribution of ionospheric plasma.
From Figure 8, it is clear that the Ne variations measured along the descending orbits of SwA/SwC, when the winter ionosphere is in darkness, are more informative in the sense of a possible coseismic signal than the sunlit ionosphere. They deserve further analysis. To detect the anomalies possibly associated with a strong EQ, we calculated the difference (∆Ne) between the SwA and SwC Ne values. With this approach, the background field is automatically eliminated. SwC flew 7 s ahead of SwA, and the distance between satellites was 1.4° in longitude, giving a total distance of about 150 km. We subtract the samples at the same acquisition time (thus at different geographical latitudes). To reveal the specific changes in the plasma density on 22 January compared with other days, Figure 9 shows a stacked plot of ∆Ne for 14–28 January. From Figure 9, it can be seen that ∆Ne is usually slightly positive (i.e., the SwA Ne exceeds the SwC Ne, which is likely due to the calibration of LPs), with irregular fluctuations in the range of <104 el/cm3. On 22 January, the shape of the ∆Ne variation was quite different. It looks like a peak that is almost twice as high and exceeds 0.15 × 105 el/cm3, with a maximum at ~35°N. At the edges of the latitudinal segment, ∆Ne is negative. The amplitude of the ∆Ne peak is about 10% of the background level compared with the enhanced Ne on 22 January and ~20% compared with other days.
This signature implies the presence of horizontal ionospheric irregularities and steep gradients in Ne. Another possibility is a lifting or lowering of the ionospheric layer with respect to the satellite altitude. Rapid changes in the plasma density via the production/recombination processes are unlikely at midlatitudes [57]. The change in Ne may only be due to transportation processes. Although there is no possibility to distinguish whether the transport is vertical, horizontal, or a combination of both, the most likely candidate for the driving force behind any plasma motion is an E-field generated somehow in the ionosphere above the EQ epicenter. If the E-field varies in the horizontal plane, the plasma moves vertically. Its vertical profile is modified so that Ne changes at a given height. In addition, TIDs may play a role in the plasma motion in the topside ionosphere, but this phenomenon is manifested in regular variations of smaller amplitude detected by both satellites [27,58].
The observed irregularities are localized in the vicinity of the meridian 81°E (the EQ epicenter is at 79°E) and do not extend to adjacent longitudes. Additional validation is supplied through observations from different longitudes. Figure 10 shows a stacked plot of ∆Ne along the segments of two consecutive orbits (descending, 05 LT) adjoining the 81°E orbit from the west and east. These trajectories are separated from each other by approximately 25° in longitude and 1.5 h in time. The approximate meridians and corresponding UTs are as follows: 128°E (20:30 UT, 22 January), 104°E (22:10 UT, 22 January), 81°E (23:50 UT, 22 January), 57°E (01:30 UT, 23 January), and 33°E (03:10 UT, 23 January). Since Figure 10 is not a snapshot and the trajectories are separated in time, the comparison is not entirely correct. However, it is possible to give some qualitative assessment. The largest anomaly in ∆Ne is observed along the 81°E meridian and fades with distance from it. Although it is not possible to separate the temporal and spatial variations well, this picture is in favor of the formation of a localized ionospheric irregularity just near 36°N, 81°E. Among the satellites flying side by side at a distance of ~200 km, the first one observed a density about 20% larger than the second one.

5. Co-Located Atmospheric Disturbances

In this section, we examine the evolution of the meteorological parameters, namely the humidity, latent heat flux, and aerosol load, over the same area surrounding the epicenter as sampled for the Swarm satellite passages. We extracted climatological data for January 2024 from the MERRA-2 reanalysis [59]. The 3-h and daily values of the selected parameters are available via a web-based system, NASA Geospatial Interactive Online Visualization and Analysis Infrastructure (GIOVANNI), developed by the Goddard Earth Sciences Data and Information Services Center (GES DISC), with a spatial resolution of 0.5° × 0.625°.
For the local tropospheric parameters, the situation with the reference point is not as clear as that for the ionospheric Ne (for which the background is removed due to subtraction of the data collected by the paired satellites). While the approach is not strict, we define the meteorological anomaly as a deviation from the level established 10 days before and 10 days after the EQ under consideration. Another possibility is to construct the long-term composite for a particular day. According to climatological practice, the 30-year period should be used. However, the natural interannual variability of the meteorological parameters does not allow for the construction of a reliable long-term composite with a small enough standard deviation. Thus, the use of the 20-day window centered on the EQ day was considered a preferable method to establish the reference point.

5.1. Specific Humidity

Specific humidity (SH) is a ratio of the weight of water vapor in a specified volume to the weight of dry air in the same volume. In the selected area, the rate of the seasonal cycle with a minimum in the winter months is about 10−4 SH units per one degree in temperature according to MERRA-2. In the context of the link between earthquakes and atmospheric perturbations, one may expect that due to moisture condensation on ion clusters, the number of free water vapor molecules in the air decreases, which is recorded as a decrease in humidity.
Figure 11a depicts the near-surface SH variations over ten days prior to and after EQ. The curve is composed of the 3-h data averaged over the area 36°–45°N, 65°–95°E. From this figure, one can see the temporal dynamics of the regional SH with a gradual decrease starting approximately 7 days prior to the EQ, a deep minimum on 21–22 January, when the SH dropped to ~0.0008 from ~0.0016, and a gradual recovery within 5 days after the EQ. It should be noted that SH is directly linked to the air temperature. The air temperature actually measured in Almaty City (https://www.accuweather.com/; accessed on 30 March 2024) is presented in Figure 11b. The temperature was mostly negative. After 15 January, it tended to become cooler, while no pronounced reduction similar to that in SH was observed. Thus, the thermal changes in the near-surface air layer and the behavior of SH were rather consistent with atmospheric thermodynamics. Some studies have reported the occurrence of positive thermal anomalies associated with earthquakes [8,60]. However, for this event, no clear indication of the increased air temperature at the time period around EQ is found. This could be due to the investigated period, as previous studies reported thermal anomalies with more weeks in advance [61].
To identify the geographical location of the minimum, in Figure 12, we show a diagram of the spatiotemporal variability of the SH, which allows one to visualize the evolution of the parameter from its static images. The diagram is plotted along the time–latitude axes (the x-axis is days of January, and the y-axis is latitude between 29.5°N and 44.5°N). Each column of pixels represents the SH averaged over the longitudes 65°–95°E. The spatial distribution of anomalies shown in Figure 12 suggests that the SH drops just above the epicenter and a day before the main shock. The diagram also reveals a quasi-systematic latitudinal variation in SH, which persists throughout the entire time period. Positive ridges are identified near 42° and 30°N, while a decrease is observed at ~35°N. This resembles the signature of the planetary wave, which is often observed in the atmospheric parameters (e.g., [62]). However, the drop in humidity that occurred on 22 January at 40°–42°N does not seem to be related to a wave train. Rather, this is a “stay-alone” signature of enhanced condensation of water vapor and latent heat release, which can be associated with EQ since the strengthening of the fault is accompanied by additional ionization of air due to radon emanation.

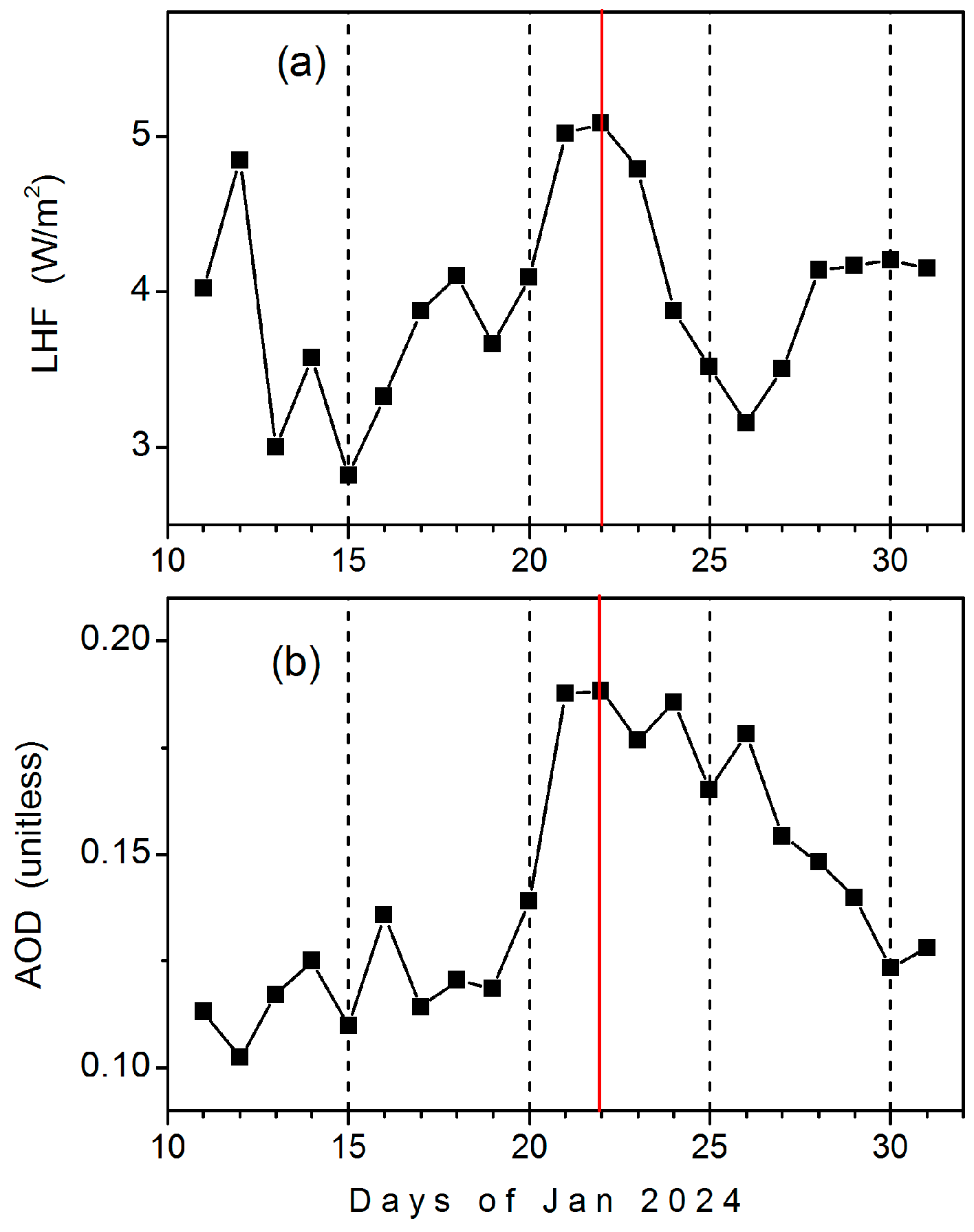
5.2. Latent Heat Flux and Aerosol Optical Depth

Further evidence of the meteorological perturbations can be obtained from Figure 13. Figure 13a shows daily latent heat flux (LHF) values from 11January to 1 February. This figure is focused on the LHF behavior in the more narrow latitudinal range of 40°–42°N, where the anomalous SH was observed. One can see that between 21 and 23 January, a pronounced enhancement is observed, with a maximum of 5 W/m2 on 22 January. LHF also tends to increase at the beginning and end of the 20-day period centered on the day of EQ. This implies the release of additional amounts of energy into the atmosphere due to the condensation of water vapor on ions. It should be noted that LHF exhibits a large and asymmetric diurnal variation of about 15 W/m2, which maximizes around 6–7 UT and drops between 11 and 03 UT). This implies that daily averaging is dominated by local midday hours. Keeping this source of uncertainty in mind, from Figure 13a, it can be concluded that the LHF magnitude appears to be considerably larger over a 3-day period centered on the day of EQ.
Finally, Figure 13b depicts the evolution of the aerosol load over the area around the epicenter. The aerosol optical depth (AOD) is the degree to which aerosols prevent the transmission of light by absorption or scattering of light. In Figure 13b, the 500 nm AODs as measured by the MODIS-Terra satellite and collected in MERRA-2 as daily values are presented. It can be seen that AOD increased from 0.12 on 19 January up to 0.19 on 21 January. This enhancement then gradually decays over several days. The behavior of AOD confirms an increase in the number of aerosol particles, which occurred simultaneously with intense condensation of water vapor and an increase in latent heat flux.

6. Discussion

According to the lithosphere–atmosphere–ionosphere coupling (LAIC) model [3], the earthquake precursor anomalies are caused by enhanced radon emission, ionization, ion hydration, charged clusters, aerosol formation and relaxation, and air turbulence, which transfers aerosols upward. Injection of charged aerosols into the atmosphere provides carriers for an external electric current and the generation of the vertical electric field near the Earth’s surface. Penetrating to the ionospheric altitudes, where the conductivity is relatively high, this E-field becomes horizontal. In the presence of a geomagnetic field that has a vertical component, the E-field transports the plasma up or downward. As such, a spacecraft flying at a certain altitude can detect changes in plasma density. Various case studies and statistical analyses have been conducted in an attempt to prove the phenomenological chain of LAIC. It is always difficult to isolate a coseismic signal against the background of natural environmental variability. The limited ability to measure the required parameters is also a problem. Finally, the relationship between the magnitudes of surface and ionospheric E-fields is ambiguous and depends on the approach to calculating the electrical conductivity of the atmospheric air column [63,64].

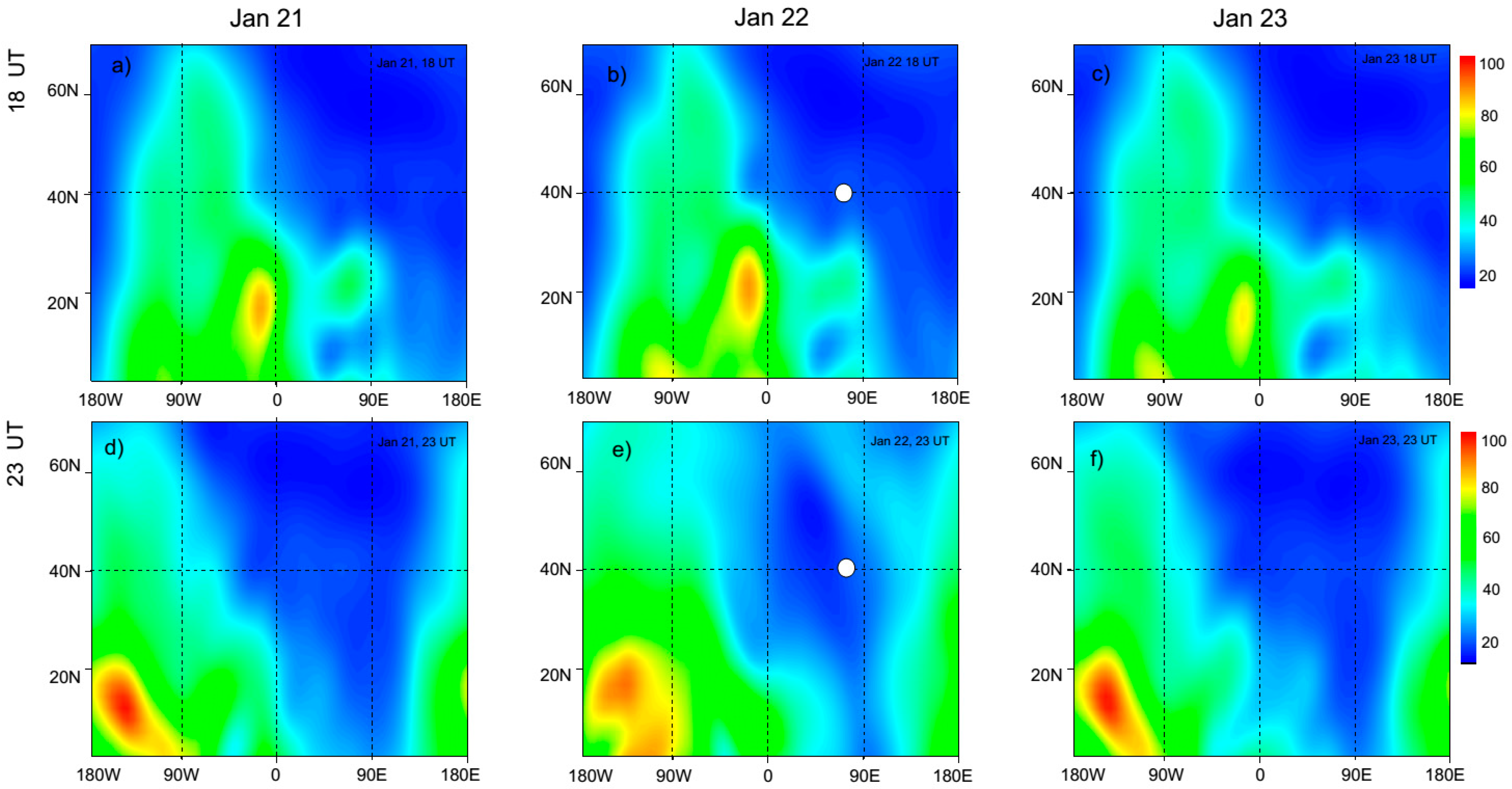
6.1. Assessment of the E-Field Causing Ionospheric Irregularities over the EQ Area

On the Earth’s night-side, the ionospheric plasma density is more sensitive to a possible signal of non-solar origin. A comparison of two time series of plasma densities measured by the LP instruments on board the Swarm satellites flying side by side at a distance of ~150 km over the region of the strong EQ in Central Asia at 23 UT revealed a considerable difference in Ne. SwC, flying first, detected higher along-track Ne values, while the second satellite (SwA) detected a drop of about 1.5 × 104 el/cm3. Comparison with other passages showed that the difference in plasma density was maximized on the day of the main shocks and aftershocks. This spatially localized ionospheric anomaly is attributed to the coseismic effect. Another notable feature is that this regional anomaly arose against the background of a global increase in Ne. A series of GIM-TEC maps suggests that this enhancement is caused by a plasma plume propagating from the dayside lower latitudes. TEC increased globally in response to the solar flares.
There are two main possibilities for the formation of small or medium-scale ionospheric irregularities similar to those observed. The first possibility is an uplift or downlift of the F layer, while the second is a drift of the plasma irregularities in the horizontal plane. Any transport of plasma implies the presence of an enhanced E-field in the ionosphere. In particular, eastward (westward) electric fields will convect the mid-latitude ionosphere upward (downward). Rapid changes in the ionosphere can also be associated with TIDs, which are manifestations of atmospheric gravity waves (AGWs) originated, among other sources, from earthquakes [7]. However, since the Swarm orbital height is above the peak of the F2 layer, the coseismic TID signatures may hardly be observed directly.
In the frame of the LAIC concept [3,65], drastic changes in Ne in the ionospheric heights can be produced by intense disturbance E-fields originating from the ground. For the plasma density change of 1.5 × 104 el/cm3 (the value observed by Swarm during the event under consideration), estimating the vertical displacement of the plasma using the International Reference Ionosphere (IRI) model [66] gives a height difference of ∆h~30 km (online calculation [67]). The authors of [68] studied zonal and vertical disturbance dynamo drifts in low/middle latitudes associated with storm-time prompt penetration electric fields, which originate at high latitudes. Their observations have shown that temporal variations in the height of the nighttime F layer can reach tens of kilometers under the influence of E-fields of about 0.5–1 mV/m. These estimates can be compared with values obtained from Swarm observations on 22 January. The chain is as follows: ∆Ne~1.5 × 104 el/cm3, ∆h~30 km, E~0.5 mV/m. At 45° latitude, the vertical drift E×B velocity is in the order of 10 m/s, so it takes about an hour for plasma to uplift 30 km.
Modeling revealed that a 10 kV/m vertical E-field above ground would produce a few mV/m horizontal E-field in the ionosphere [69,70,71]. Since the actual observed near-ground atmospheric E-field is less than 100 V/m [72,73], the E-field of lithospheric origin is too weak for measurable perturbations at ionospheric heights. An estimate based on approaches from other models [32,74] allows an E-field of about 1 mV/m in the ionosphere if a 100 V/m vertical E-field appears near ground. The discrepancies between the modeling results are due to different approaches to boundary conditions in the upper atmosphere and different approximations of the vertical profile of air conductivity. Both parameters are poorly defined. Note that on 22 January, the air conductivity was likely increased due to the flux of solar protons. More case studies are critical to revealing typical and specific characteristics of the ionospheric response to large earthquakes and quantitatively testing the models.
The peak-like pattern of the Ne disturbance observed by the Swarm tandem on 22 January is in qualitative agreement with the model predictions. According to the model proposed in [1], the horizontal distribution of the perturbed plasma density in the F-region is divided into regions of increased and reduced concentration. Both regions move towards the equator with increasing altitude. The ionosphere simulation code SAMI3 [75] used to study TEC variations caused by the E-field from the surface charges of the earthquake fault zone also demonstrated splitting [17]. These authors found that plasma density enhancement (reduction) was on the west (east) side of the epicenter. The models and observations suggest that the E-field penetration efficiency at night is higher than during the day, which strongly depends on the size of the ground-level vertical E-field localization.
The Ne anomalies observed by the Swarm satellite occurred exactly on the day of the main shock and a series of aftershocks. The statistical and case studies convincingly demonstrated that the pre-seismic signals may be detected in the ionosphere above the earthquake preparation zone for several days or even months (e.g., [25,76,77,78]). This approach was considered promising for searching for earthquake precursors. However, in our particular event, no relevant anomalies during the preceding period of reasonable duration were found. On a relatively long-term time scale, it seems quite difficult to distinguish coseismic ionospheric anomalies from ionospheric variability due to variable space weather conditions. Also, the question remains open as to why the pre-seismic signal disappears for some time and does not continuously evolve into a coseismic signal.
We believe that the large global increase in Ne, from ~0.5 × 105 (the typical level for nearby days) up to about 1.5 × 105 el/cm3 observed by both satellites on 22 January (Figure 8), cannot be considered a seismo-induced signature. By coincidence, a series of moderate solar flares accompanied by X-ray and solar proton fluxes occurred immediately before and after the main seismic shock. The solar irradiance increased the ionization rates and the amount of plasma in the ionosphere. At the same time, the geomagnetic indices (the parameters that are commonly used to identify periods of geomagnetic quietness suitable for searching for pre- or coseismic anomalies in the ionosphere) remained almost undisturbed. It is because the SW disturbance (a magnetic cloud but not the irradiance or solar energetic particles) was weak, and thus the ionospheric auroral electrojets and ring current (the electric currents that are responsible for ground geomagnetic disturbances) were not affected.
In this regard, we note that the idea exists that space weather disturbances may play a role in the occurrence of earthquakes. Some evidence of such a link, albeit with a prolonged time delay between a geomagnetic storm and a seismic event, is presented in [79]. Another idea, supported by numerical simulations, is that solar flares can cause changes in the density of telluric currents in faults in the Earth’s crust, capable of triggering earthquakes [80].

6.2. On the Mechanismof Coseismic Effects in the Lower Atmosphere

In addition to anomalies observed in the ionosphere plasma density above the seismic preparation area, seismicity can manifest itself in co-located disturbances of meteorological parameters. The main factor leading to the generation of electromagnetic anomalies in the ionosphere is associated with changes in the conductivity of the air column, especially at the boundary layers between the atmosphere and the ionosphere. During the motion of tectonic plates in the pre-earthquake period, a significant amount of radon and its progeny substances are released. The decay, accompanied by the emission of energetic α-particles, may result in the ionization of the air and the formation of ion clusters in the lower troposphere. With turbulent diffusion, radon can reach a height of 1 km. Due to chemical reactions and the adhesion of molecules to ion clusters, large charged particles are formed, on which water vapor condenses. Compared with normal conditions, the consequences of increased radon emissions lead to a decrease in relative humidity. When water vapor condenses, the latent heat of evaporation is released. Also, the radon-related ionization of air molecules consequently influences the aerosol number and the particle size distribution. The air ionization mechanism is probably at the origin of the tropospheric anomalies observed in the case of the investigated EQ. The meteorological parameters extracted from the MERRA-2 reanalysis indicate a pronounced tropospheric response. In particular, the specific humidity drops by ~30%, while the latent heat and AOD increase by ~25% and 80%, respectively. Ionospheric anomalies and meteorological anomalies appeared in the area of EQ almost simultaneously, although the anomalies in meteo parameters began growing 1–2 days prior to the main seismic shock and peaked on the day of the shock (not in the several days before the EQ though). The tropospheric response can be associated with the increased pre-EQ radon emanation during the relatively short period preceding the shock. The decay time of the meteo parameters is also about 1–2 days, likely due to atmospheric inertia and a relatively slow relaxation. The ionospheric anomaly seemed to be shorter-lived than the tropospheric anomaly. This is likely because the ionospheric anomaly is associated with the electromagnetic signal, while the meteo anomalies involve chemical and dynamic processes.
Looking from the perspective of the LAIC model, radon variations are the primary source of the atmospheric electricity changes a few days before the strong EQs. Sometimes it was reported that meteorological precursors appeared prior to EQs. However, on such time scales, possible coseismic anomalies may be hidden by atmospheric wave signatures. In addition, the possibility of detecting specific atmospheric anomalies due to enhanced ionization depends on the general meteorological conditions in the seismic area. During rain, snow, fog, strong wind, or clouds, the corresponding disturbances are many times greater than a possible coseismic signal. However, this is not the case for the EQ studied here. According to the World Weather Service, in late January 2024, in the area of the EQ epicenter in Central Asia, the weather was fine for a fairly long period, and no extreme conditions were observed.

7. Summary and Conclusions

Analysis of plasma density perturbations along the trajectories of Swarm satellites over the area of the strong Xinjiang earthquake (~40°N, 80°E; Mw = 7) on 22 January 2024, revealed several complementary features that are likely associated with the generation and penetration of the coseismic electric field into the ionosphere. The EQ occurred during a prolonged period of geomagnetic quietness. Several hours after the main shock, the tandem of SwC and SwA satellites crossed the EQ area for the night-side orbits and observed a small-scale anomaly in the plasma density.
In the approach used in this work, we propose analyzing the difference between the observations of the two satellites rather than the absolute values of the plasma density. In this way, explicit subtraction of the reference field can be avoided. The satellite flying first measured lower values of Ne, while the second satellite, flying 12 s later and ~150 km to the east, detected an increase of about 1.5 × 104 el/cm3. The anomaly started developing over the epicenter a day before the EQ and maximized on the day of the main shock and aftershocks. We suppose that the observed irregularity is a signature of a coseismic electric field penetrating the ionosphere due to additional ionization of the air over the epicentre and increased conductivity of the air column. The observed chain of the ionospheric and tropospheric anomalies is consistent with the LAIC concept. The magnitude and shape of the observed ionospheric irregularity appear to be consistent with the predictions of the “optimistic” models representing the concept of lithosphere–atmosphere–ionosphere coupling in terms of electrodynamic, chemical, and thermal processes.
On 22 January, the local coseismic anomaly was detected against the background of a global increase in plasma density due to solar flares and associated enhancement of the X-ray and proton fluxes, which affected the ionization rate, TEC distribution, and air conductivity. It is important to distinguish specific, relatively low-amplitude anomalies of coseismic origin from intra-ionospheric variability, even if the geomagnetic conditions are quiet.
The ionospheric anomaly is in agreement with simultaneously observed disturbances of meteorological parameters in the EQ region. The MERRA-2 specific humidity, latent heat flux, and aerosol optical depth all exhibit co-located disturbances that can be attributed to the effect of increased ionization rates of tropospheric air, resulting in greater electrical conductivity in the near-Earth boundary layer. Around the day of the EQ, the emanation of radon and its subsequent decay associated with the preparation of the seismic event caused a local drop in humidity and a pronounced enhancement in latent heat flow and AOD.
Thus, the large EQ that occurred on 22 January 2024 provides a comprehensive example of the complex geospheric response to seismic activity. Observations confirm the chain of elements included in the LAIC through electromagnetic processes, which, in turn, is a part of the GEC theory. The most pronounced disturbances of seismic origin occurred on the day of EQ, and some indications can be noticed a day before.

Author Contributions

Conceptualization, R.L.; methodology, R.L.; software, G.D.; validation, G.D. and A.S.; formal analysis, D.G and A.S.; investigation, R.L., G.D. and A.S.; writing—original draft preparation, R.L.; writing—review and editing, R.L.; visualization, G.D. and A.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan under the grant IRN-AP19677977.

Data Availability Statement

The Swarm satellite data are available at Swarm mission’s website (https://swarm-iss.eo.esa.int). The seismic catalogues containing the earthquake source parameters can be extracted from the USGS database (https://earthquake.usgs.gov/earthquakes/search/). The geomagnetic activity indices and the solar wind data are from the OMNI database (https://omniweb.gsfc.nasa.gov/). GIM-TEC maps are provided by JPL at https://sideshow.jpl.nasa.gov/pub/iono_daily/. NASA MERRA-2 data are available from NASA’s GES DISC web-based system, Giovanni (https://giovanni.gsfc.nasa.gov/giovanni/). GOES-R data on the solar flare are provided by NOAA (https://www.ngdc.noaa.gov/stp/satellite/goes-r.html). The last access to all data sets is on 30 June 2024.

Acknowledgments

R.L. acknowledges discussions on the GEC concept within the International Space Science Institute (ISSI) Workshop “Physical Links Between Weather and Climate in Space and the Lower Atmosphere”.

Conflicts of Interest

The authors declare no conflict of interest. The funder had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Pulinets, S.A.; Boyarchuk, K.A. Ionospheric Precursors of Earthquakes; Springer: Berlin, Germany, 2004; 288p. [Google Scholar]
  2. Balasis, G.; Mandea, M. Can electromagnetic disturbances related to the recent great earthquakes be detected by satellite magnetometers? Tectonophysics 2007, 431, 173–195. [Google Scholar] [CrossRef]
  3. Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
  4. Ouzounov, D.; Pulinets, S.; Hattori, K.; Taylor, P. (Eds.) Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies; Wiley: New York, NY, USA, 2018; Volume 234, 384p. [Google Scholar]
  5. De Santis, A.; Marchetti, D.; Spogli, L.; Cianchini, G.; Pav’on-Carrasco, F.J.; De Franceschi, G.; Di Giovambattista, R.; Perrone, L.; Qamili, E.; Cesaroni, C.; et al. Magnetic field and electron density data analysis from Swarm satellites searching for ionospheric effects by great earthquakes: 12 case studies from 2014 to 2016. Atmosphere 2019, 10, 371. [Google Scholar] [CrossRef]
  6. Marchetti, D.; Pavón-Carrasco, F.J.; Cianchini, G.; Perrone, L.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; Cesaroni, C.; et al. Precursory worldwide signatures of earthquake occurrences on Swarm satellite data. Sci. Rep. 2019, 9, 20287. [Google Scholar] [CrossRef]
  7. Astafyeva, E. Ionospheric detection of natural hazards. Rev. Geophys. 2019, 57, 1265–1288. [Google Scholar] [CrossRef]
  8. Marchetti, D.; De Santis, A.; Shen, X.; Campuzano, S.A.; Perrone, L.; Piscini, A.; Di Giovambattista, R.; Jin, S.; Ippolito, A.; Cianchini, G.; et al. Possible Lithosphere-Atmosphere-Ionosphere Coupling effects prior to the 2018 Mw=7.5 Indonesia earthquake from seismic, atmospheric and ionospheric data. J. Asian Earth Sci. 2020, 188, 104097. [Google Scholar] [CrossRef]
  9. Parrot, M.; Tramutoli, V.; Liu, T.J.Y.; Pulinets, S.; Ouzounov, D.; Genzano, N.; Lisi, M.; Hattori, K.; Namgaladze, A. Atmospheric and ionospheric coupling phenomena related to large earthquakes. Nat. Hazard. Earth Syst. Sci. 2021, 230, 197–225. [Google Scholar] [CrossRef]
  10. Chisham, G.; Lester, M.; Milan, S.E.; Freeman, M.P.; Bristow, W.A.; Grocott, A.; McWilliams, K.A.; Ruohoniemi, J.M.; Yeoman, T.K.; Dyson, P.L.; et al. A decade of the Super Dual Auroral Radar Network (SuperDARN): Scientific achievements, new techniques and future directions. Surv. Geophys. 2007, 28, 33–109. [Google Scholar] [CrossRef]
  11. Fejer, B.G. Low Latitude Ionospheric Electrodynamics. Space Sci. Rev. 2011, 158, 145–166. [Google Scholar] [CrossRef]
  12. Lukianova, R.; Christiansen, F. Modeling of the global distribution of ionospheric electric fields based on realistic maps of field-aligned currents. J. Geophys. Res. 2006, 111, A03213. [Google Scholar] [CrossRef]
  13. Sarkar, S.; Choudhary, S.; Sonakia, A.; Vishwakarma, A.; Gwal, A.K. Ionospheric anomalies associated with the Haiti earthquake of 12 January 2010 observed by DEMETER satellite. Nat. Hazards Earth Syst. Sci. 2012, 12, 671–678. [Google Scholar] [CrossRef]
  14. Fan, Y.; Du, X.; An, Z.; Liu, J.; Tan, D.; Chen, J. Earthquake-related Electric Field Changes Observed in the Ionosphere and Ground. Acta Geophys. 2015, 63, 679–697. [Google Scholar] [CrossRef]
  15. Li, M.; Shen, X.; Parrot, M.; Zhang, X.; Zhang, Y.; Yu, C.; Yan, R.; Liu, D.; Lu, H.; Guo, F.; et al. Primary Joint Statistical Seismic Influence on Ionospheric Parameters Recorded by the CSES and DEMETER Satellites. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028116. [Google Scholar] [CrossRef]
  16. Liu, J.Y.; Chen, Y.I.; Chen, C.H.; Liu, C.Y.; Chen, C.Y.; Nishihashi, M.; Li, J.Z.; Xia, Y.Q.; Oyama, K.I.; Hattori, K.; et al. Seismo-ionospheric GPS total electron content anomalies observed before the 12 May 2008 Mw 7.9 Wenchuan earthquake. J. Geophys. Res. 2009, 114, A04320. [Google Scholar] [CrossRef]
  17. Kuo, C.L.; Huba, J.D.; Joyce, G.; Lee, L.C. Ionosphere plasma bubbles and density variations induced by pre-earthquake rock currents and associated surface charges. J. Geophys. Res. 2011, 116, A10317. [Google Scholar] [CrossRef]
  18. De Santis, A.; Balasis, G.; Pavon-Carrasco, F.J.; Cianchini, G.; Mandea, M. Potential earthquake precursory pattern from space: The 2015 Nepal event as seen by magnetic Swarm satellites. Earth Planet. Sci. Lett. 2017, 461, 119–126. [Google Scholar] [CrossRef]
  19. Heki, K. Ionospheric electron enhancement preceding the 2011 Tohoku-Oki Earthquake. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
  20. Sharma, G.; Nayak, K.; Romero-Andrade, R.; Aslam, M.A.M.; Sarma, K.K.; Aggarwal, S.P. Low Ionosphere Density Above the Earthquake Epicentre Region of Mw7.2, El Mayor–Cucapah Earthquake Evident from Dense CORS Data. J. Indian. Soc. Remote Sens. 2024, 52, 543–555. [Google Scholar] [CrossRef]
  21. Nayak, K.; López-Urías, C.; Romero-Andrade, R.; Sharma, G.; Guzmán-Acevedo, G.M.; Trejo-Soto, M.E. Ionospheric Total Electron Content (TEC) Anomalies as Earthquake Precursors: Unveiling the Geophysical Connection Leading to the 2023 Moroccan 6.8 Mw Earthquake. Geosciences 2023, 13, 319. [Google Scholar] [CrossRef]
  22. Zhu, F.; Wu, Y.; Zhou, Y.; Lin, J. A statistical investigation of pre-earthquake ionospheric TEC anomalies. Geodesy Geodyn. 2011, 2, 61–65. [Google Scholar] [CrossRef]
  23. Heki, K.; Enomoto, Y. Mw ependence of the preseismic ionospheric electron enhancements. J. Geophys. Res. Space Phys. 2015, 120, 7006–7020. [Google Scholar] [CrossRef]
  24. Li, W.; Yue, J.; Guo, J.; Yang, Y.; Zou, B.; Shen, Y.; Zhang, K. Statistical seismo-ionospheric precursors of M7.0+ earthquakes in Circum-Pacific seismic belt by GPS TEC measurements. Adv. Space Res. 2018, 61, 1206–1219. [Google Scholar] [CrossRef]
  25. De Santis, A.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; Cesaroni, C.; Cianchini, G.; De Franceschi, G.; De Santis, A.; et al. Geosystemics View of Earthquakes. Entropy 2019, 21, 412. [Google Scholar] [CrossRef] [PubMed]
  26. He, Y.; Zhao, X.; Yang, D.; Wu, Y.; Li, Q. A study to investigate the relationship between ionospheric disturbance and seismic activity based on Swarm satellite data. Phys. Earth Planet. Inter. 2022, 323, 106826. [Google Scholar] [CrossRef]
  27. Haralambous, H.; Paul, K.S. Travelling Ionospheric Disturbance Direction of Propagation Detection Using SwarmA-C In-Situ Electron Density. Remote Sens. 2023, 15, 897. [Google Scholar] [CrossRef]
  28. Bhattacharyya, A. Equatorial Plasma Bubbles: A Review. Atmosphere 2022, 13, 1637. [Google Scholar] [CrossRef]
  29. Arras, C.; Wickert, J.; Beyerle, G.; Heise, S.; Schmidt, T.; Jacobi, C. A global climatology of ionosphericir regularities derived from GPS radio occultation. Geophys. Res. Lett. 2008, 35, L14809. [Google Scholar] [CrossRef]
  30. Kikuchi, T. Penetration of the Magnetospheric Electric Fields to the Low Latitude Ionosphere. In Ionosphere Dynamics and Applications; Huang, C., Lu, G., Zhang, Y., Paxton, L.J., Eds.; American Geophysical Union: Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
  31. Lukianova, R.; Uvarov, V.M.; Coisson, P. High-latitude F region large-scale ionospheric irregularities under different solar wind and zenith angle conditions. Adv. Space Res. 2017, 59, 557–570. [Google Scholar] [CrossRef]
  32. Namgaladze, A.; Karpov, M.; Knyazeva, M. Aerosols and seismo-ionosphere coupling: A review. J. Atmos. Sol.-Terr. Phys. 2018, 171, 83–93. [Google Scholar] [CrossRef]
  33. Denisenko, V.V.; Boudjada, M.Y.; Lammer, H. Propagation of seismogenic electric currents. J. Geophys. Res. Space Phys. 2018, 123, 4290–4297. [Google Scholar] [CrossRef]
  34. Denisenko, V.V.; Rycroft, M.J.; Harrison, R.G. Mathematical Simulation of the Ionospheric Electric Field as a part of the Global Electric Circuit. Surv. Geophys. 2019, 40, 1–35. [Google Scholar] [CrossRef]
  35. Pulinets, S.; Khachikyan, G. The Global Electric Circuit and Global Seismicity. Geosciences 2021, 11, 491. [Google Scholar] [CrossRef]
  36. Akhoondzadeh, M. Ant Colony Optimization detects anomalous aerosol variations associated with the Chile earthquake of 27 February 010. Adv. Space Res. 2015, 55, 1754–1763. [Google Scholar] [CrossRef]
  37. Pulinets, S.A.; Ouzounov, D. The Possibility of Earthquake Forecasting: Learning from Nature; IOP Publishing: Bristol, UK, 2018; Volume 167. [Google Scholar] [CrossRef]
  38. USGS. Earthquakes. Available online: https://www.usgs.gov/programs/earthquake-hazards/earthquakes (accessed on 20 March 2024).
  39. Zelenin, E.A.; Bachmanov, D.M.; Garipova, S.T.; Trifonov, V.G.; Kozhurin, A.I. The Active Faults of Eurasia Database (AFEAD): Theontology and design behind the continental-scale dataset. Earth Syst. Sci. Data 2022, 14, 4489–4503. [Google Scholar] [CrossRef]
  40. Active Faults of Eurasia Database (AFEAD). Available online: http://neotec.ginras.ru/index/english/database_eng.html (accessed on 2 June 2024).
  41. Active Faults of Eurasia Database (AFEAD). ViewonMapBox. Available online: http://neotec.ginras.ru/index/mapbox/database_map.html (accessed on 2 June 2024).
  42. Gopalswamy, N. History and development of coronal mass ejections as a key player in solar terrestrial relationship. Geosci. Lett. 2016, 3, 8. [Google Scholar] [CrossRef]
  43. Rozhnoi, A.; Solovieva, M.; Fedun, V.; Gallagher, P.; McCauley, J.; Boudjada, M.J.; Shelyag, S.; Eichelberger, H.U. Strong influence of solar X-ray flares on low-frequency electromagnetic signals in middle latitudes. Ann. Geophys. 2019, 37, 843–850. [Google Scholar] [CrossRef]
  44. OMNI WebPlus Data and Service. Available online: https://omniweb.gsfc.nasa.gov/ (accessed on 2 June 2024).
  45. GOES-R Space Weather. Available online: https://www.ngdc.noaa.gov/stp/satellite/goes-r.html (accessed on 2 June 2024).
  46. Space Weather Live Viewing Archive, >10 MeV Solar Protons. Available online: https://www.spaceweatherlive.com/en/archive/2024/01/22/proton.html (accessed on 15 June 2024).
  47. NOAA Space Weather Prediction Center. Solar Proton Events Affecting the Earth Environment. Available online: https://www.ngdc.noaa.gov/stp/space-weather/interplanetary-data/solar-proton-events/SEP%20page%20code.html (accessed on 15 June 2024).
  48. Mironova, I.A.; Aplin, K.L.; Arnold, F.; Bazilevskaya, G.A.; Harrison, R.G.; Krivolutsky, A.A.; Nicoll, K.A.; Rozanov, E.V.; Turunen, E.; Usoskin, I.G. Energetic particle influence on the Earth’s atmosphere. Space Sci. Rev. 2015, 194, 1–96. [Google Scholar] [CrossRef]
  49. Lukianova, R. Magnetospheric response to sudden changes in solar wind dynamic pressure inferred from polar ap index. J. Geophys. Res. 2003, 108, 1428. [Google Scholar] [CrossRef]
  50. Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.M.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
  51. 51 Jet Propulsion Laboratory. Global GNSS Data Service. Available online: https://sideshow.jpl.nasa.gov/pub/iono_daily/ (accessed on 2 May 2024).
  52. Sori, T.; Shinbori, A.; Otsuka, Y.; Nishioka, M.; Perwitasari, S. Dependence of ionospheric responses on solar wind dynamic pressure during geomagnetic storms using global long-term GNSS-TEC data. J. Geophys. Res. Space Phys. 2023, 128, e2022JA030913. [Google Scholar] [CrossRef]
  53. Friis-Christensen, E.; Luhr, H.; Knudsen, D.; Haagmans, R. Swarm—An earth observation mission investigating geospace. Adv. Space Res. 2008, 41, 210–216. [Google Scholar] [CrossRef]
  54. Dobrovolsky, I.; Zubkov, S.; Miachki, V. Estimation of the size of earthquake preparation zone. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
  55. Kuo, C.L.; Lee, L.C.; Huba, J.D. An Improved Coupling Model for the Lithosphere-Atmosphere-Ionosphere System. J. Geophys. Res. Space Phys. 2014, 119, 3189–3205. [Google Scholar] [CrossRef]
  56. Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The Thirteenth Generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
  57. Kelley, M.C. The Earth’s Ionosphere: Plasma Physics and Electrodynamics, 2nd ed.; Academic Press: Burlington, MA, USA, 2009; Volume 96, pp. 267–342. [Google Scholar]
  58. Spogli, L.; Jin, Y.; Urbář, J.; Wood, A.G.; Donegan-Lawley, E.; Clausen, L.; Shahtahmassebi, G.; Alfonsi, L.; Rawlings, J.T.; Cicone, A.; et al. Statistical models of the variability of plasma in the topside ionosphere: 2. Performance assessment. J. Space Weather. Space Clim. 2024, 14, 4. [Google Scholar] [CrossRef]
  59. Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version-2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
  60. Wu, L.; Zheng, S.; De Santis, A.; Qin, K.; Di Mauro, R.; Liu, S.; Rainone, M.L. Geosphere coupling and hydrothermal anomalies before the 2009 Mw6.3 L’Aquila earthquake in Italy. Nat. Hazards Earth Syst. Sci. 2016, 16, 1859–1880. [Google Scholar] [CrossRef]
  61. Liu, S.; Cui, Y.; Wei, L.; Liu, W.; Ji, M. Pre-earthquake MBT anomalies in the Central and Eastern Qinghai-Tibet Plateau and their association to earthquakes. Remote Sens. Environ. 2023, 298, 113815. [Google Scholar] [CrossRef]
  62. Pal, S.; Chakraborty, S.; Chakrabarti, S.K. On the use of Very Low Frequency transmitter data for remote sensing of atmospheric gravity and planetary waves. Adv. Space Res. 2015, 55, 1190–1198. [Google Scholar] [CrossRef]
  63. Denisenko, V.V.; Boudjada, M.Y.; Horn, M.; Pomozov, E.V.; Biernat, H.K.; Schwingenschuh, K.; Lammer, H.; Prattes, G.; Cristea, E. Ionospheric conductivity effects on electrostatic field penetration into the ionosphere. Nat. Hazards Earth Syst. Sci. 2008, 8, 1009–1017. [Google Scholar] [CrossRef]
  64. Ampferer, M.; Denisenko, V.V.; Hausleitner, W.; Krauss, S.; Stangl, G.; Boudjada, M.Y.; Biernat, H.K. Decrease of the electric field penetration into the ionosphere due to low conductivity at the near ground atmospheric layer. Ann. Geophys. 2010, 28, 779–787. [Google Scholar] [CrossRef]
  65. Hayakawa, M.; Molchanov, O. Seismo-Electromagnetics (Lithosphere–Atmosphere–IonosphereCoupling); Terrapub: Tokyo, Japan, 2002; 477p. [Google Scholar]
  66. Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere model: A review and description of an ionospheric benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar] [CrossRef]
  67. CCMC Instant Run System. Available online: https://kauai.ccmc.gsfc.nasa.gov/instantrun/iri/ (accessed on 2 May 2024).
  68. Fejer, B.G.; Emmert, J.T. Low-latitude ionospheric disturbance electric field effects during the recovery phase of the 19–21 October 1998 magnetic storm. J. Geophys. Res. 2003, 108, 1454. [Google Scholar] [CrossRef]
  69. Pulinets, S.A.; Ouzounov, D.P.; Karelin, A.V.; Davidenko, D.V. Physical bases of the generation of short-term earthquake precursors: A complex model of ionization-induced geophysical processes in the lithosphere-atmosphere-ionosphere-magnetosphere system. Geomagn. Aeron. 2015, 55, 521–538. [Google Scholar] [CrossRef]
  70. Klimenko, M.V.; Klimenko, V.V.; Zakharenkova, I.E.; Pulinets, S.A.; Zhao, B.; Tzidilina, M.N. Formation mechanism of great positive TEC disturbances prior to Wenchuan earthquake on May 12, 2008. Adv. Space Res. 2011, 48, 488–499. [Google Scholar] [CrossRef]
  71. Rycroft, M.J.; Harrison, G.R.; Nicoll, K.A.; Mareev, E.A. An overview of Earth’s global electric circuit and atmospheric conductivity. Space Sci. Rev. 2008, 137, 83–105. [Google Scholar] [CrossRef]
  72. Burns, G.; Frank-Kamenetsky, A.; Tinsley, B.; French, W.; Grigioni, P.; Camporeale, G.; Bering, E. Atmospheric Global Circuit Variations from Vostok and Concordia Electric Field Measurements. J. Atmos. Sci. 2017, 74, 783–800. [Google Scholar] [CrossRef]
  73. Nicoll, K.; Harrison, R.; Barta, V.; Bor, J.; Brugge, R.; Chillingarian, A.; Chum, J.; Georgoulias, A.; Guha, A.; Kourtidis, K.; et al. A global atmospheric electricity monitoring network for climate and geophysical research. J. Atmos. Sol.-Terr. Phys. 2019, 184, 18–29. [Google Scholar] [CrossRef]
  74. Sorokin, V.; Hayakawa, M. Generation of seismic-related DC electric fields and lithosphere atmosphere-ionosphere coupling. Modern Appl. Sci. 2013, 7, 1–25. [Google Scholar] [CrossRef]
  75. Huba, J.D.; Joyce, G.; Krall, J. Three-dimensional equatorial spread F modeling. Geophys. Res. Lett. 2008, 35, L10102. [Google Scholar] [CrossRef]
  76. Li, M.; Parrot, M. Statistical analysis of an ionospheric parameter as a base for earthquake prediction. J. Geophys. Res. Space Phys. 2013, 118, 3731–3739. [Google Scholar] [CrossRef]
  77. Xiong, P.; Marchetti, D.; De Santis, A.; Zhang, X.; Shen, X. SafeNet: SwArm for Earthquake Perturbations Identification Using Deep Learning Networks. Remote Sens. 2021, 13, 5033. [Google Scholar] [CrossRef]
  78. Marchetti, D.; De Santis, A.; Campuzano, S.A.; Zhu, K.; Soldani, M.; D’Arcangelo, S.; Orlando, M.; Wang, T.; Cianchini, G.; Di Mauro, D.; et al. Worldwide Statistical Correlation of Eight Years of Swarm Satellite Data with M5.5+ Earthquakes: New Hints about the Preseismic Phenomena from Space. Remote Sens. 2022, 14, 2649. [Google Scholar] [CrossRef]
  79. Ouzounov, D.; Khachikyan, G. Studying the Impact of the Geospace Environment on Solar Lithosphere Coupling and Earthquake Activity. Remote Sens. 2024, 16, 24. [Google Scholar] [CrossRef]
  80. Sorokin, V.; Yaschenko, A.; Mushkarev, G.; Novikov, V. Telluric Currents Generated by Solar Flare Radiation: Physical Model and Numerical Estimations. Atmosphere 2023, 14, 458. [Google Scholar] [CrossRef]
Remotesensing 16 03112 g001
Figure 1. Location of the EQ epicenter (white star) on the map of active faults in Eurasia. Adapted from [41]. The fault intensity is indicated by the yellow-to-dark red color.
Figure 1. Location of the EQ epicenter (white star) on the map of active faults in Eurasia. Adapted from [41]. The fault intensity is indicated by the yellow-to-dark red color.
Remotesensing 16 03112 g001
Remotesensing 16 03112 g002
Figure 2. Dst and ap indices for the 3-month period from November 2023 to January 2024. The EQ day on 22 January is marked by vertical red line.
Figure 2. Dst and ap indices for the 3-month period from November 2023 to January 2024. The EQ day on 22 January is marked by vertical red line.
Remotesensing 16 03112 g002
Remotesensing 16 03112 g003
Figure 3. (a) the X-ray flux (the horizontal line shows the M-flare level), (b) the solar proton >10 MeV flux, (c) the SW Pd, (d) the IMF Bz component, (e) the Dst and ap indices on 21–23 January 2024. The EQ time is marked by vertical red line.
Figure 3. (a) the X-ray flux (the horizontal line shows the M-flare level), (b) the solar proton >10 MeV flux, (c) the SW Pd, (d) the IMF Bz component, (e) the Dst and ap indices on 21–23 January 2024. The EQ time is marked by vertical red line.
Remotesensing 16 03112 g003
Remotesensing 16 03112 g004
Figure 4. GIM-TEC distribution in the latitudinal range 0°–70°N at 18 UT (first row) and 23 UT (second row) for (a,d) January 21, (b,e) January 22, (c,f) January 23. The epicenter of EQ is shown as a white dot in panels (b,e). The color bar shows TEC is in TECU.
Figure 4. GIM-TEC distribution in the latitudinal range 0°–70°N at 18 UT (first row) and 23 UT (second row) for (a,d) January 21, (b,e) January 22, (c,f) January 23. The epicenter of EQ is shown as a white dot in panels (b,e). The color bar shows TEC is in TECU.
Remotesensing 16 03112 g004
Remotesensing 16 03112 g005
Figure 5. TEC values (a) averaged over the Northern Hemisphere (0°–70°N) and (b) at a grid point 40°N, 80°E for the period of 21–23 January. The EQ time is indicated by the black triangle on the x-axes. Note the logarithmic scale in panel (b). Red (blue) vertical lines mark the time of the descending (ascending) orbit of the satellite when it passed near the epicenter.
Figure 5. TEC values (a) averaged over the Northern Hemisphere (0°–70°N) and (b) at a grid point 40°N, 80°E for the period of 21–23 January. The EQ time is indicated by the black triangle on the x-axes. Note the logarithmic scale in panel (b). Red (blue) vertical lines mark the time of the descending (ascending) orbit of the satellite when it passed near the epicenter.
Remotesensing 16 03112 g005
Remotesensing 16 03112 g006
Figure 6. Latitudinal profiles of the SwC Ne (in 106 cm−3) measured along (a) the ascending (17 LT) and (b) the descending (05 LT) trajectories on 22 January. The first (last) passage during the day is shown in blue (red).
Figure 6. Latitudinal profiles of the SwC Ne (in 106 cm−3) measured along (a) the ascending (17 LT) and (b) the descending (05 LT) trajectories on 22 January. The first (last) passage during the day is shown in blue (red).
Remotesensing 16 03112 g006
Remotesensing 16 03112 g007
Figure 7. Swarm orbit projections for 22 January. The trajectory of SwA, SwB, and SwC is shown as a thin line in blue, red, and green, respectively. Trajectory segments that fall into a rectangular area around the epicenter (white star) are highlighted with thick lines: orange (purple) for SwA/SwC (SwB).
Figure 7. Swarm orbit projections for 22 January. The trajectory of SwA, SwB, and SwC is shown as a thin line in blue, red, and green, respectively. Trajectory segments that fall into a rectangular area around the epicenter (white star) are highlighted with thick lines: orange (purple) for SwA/SwC (SwB).
Remotesensing 16 03112 g007
Remotesensing 16 03112 g008
Figure 8. Stacked plot of the Ne variations (in 105 cm−3) along the SwA (blue) and SwC (red) trajectory between 30°N and 45°N on 14–28 January: (a) descending orbits, 05 LT; (b) ascending orbits, 17 LT; (c) descending orbit on 22 January. In panels (a,b), each individual day is separated by a vertical dotted line.
Figure 8. Stacked plot of the Ne variations (in 105 cm−3) along the SwA (blue) and SwC (red) trajectory between 30°N and 45°N on 14–28 January: (a) descending orbits, 05 LT; (b) ascending orbits, 17 LT; (c) descending orbit on 22 January. In panels (a,b), each individual day is separated by a vertical dotted line.
Remotesensing 16 03112 g008
Remotesensing 16 03112 g009
Figure 9. Stack plot of the differences (∆Ne in 105 cm−3) between the Ne values from SwA and SwC along the descending orbits on 14–28 January.
Figure 9. Stack plot of the differences (∆Ne in 105 cm−3) between the Ne values from SwA and SwC along the descending orbits on 14–28 January.
Remotesensing 16 03112 g009
Remotesensing 16 03112 g010
Figure 10. Stack plot of ∆Ne (in 104 cm−3) for four consecutive passages (descending orbit) closest to the passage along the 81°E meridian (00 UT, 22 January) from the west and east sides.
Figure 10. Stack plot of ∆Ne (in 104 cm−3) for four consecutive passages (descending orbit) closest to the passage along the 81°E meridian (00 UT, 22 January) from the west and east sides.
Remotesensing 16 03112 g010
Remotesensing 16 03112 g011
Figure 11. Time series of (a) daily values of specific humidity from 10 January to 1 February; each point represents the SH value averaged over the area of 35°–45°N, 65°–95°E, and (b) temperature in Almaty City; the mean of the highest and lowest daily values. The EQ time is indicated by red line.
Figure 11. Time series of (a) daily values of specific humidity from 10 January to 1 February; each point represents the SH value averaged over the area of 35°–45°N, 65°–95°E, and (b) temperature in Almaty City; the mean of the highest and lowest daily values. The EQ time is indicated by red line.
Remotesensing 16 03112 g011
Remotesensing 16 03112 g012
Figure 12. The “time–latitude” diagram for the hourly means of SH averaged over the longitudes 65°–95°E. The EQ time (EQ latitude) is indicated by vertical (horizontal) line.
Figure 12. The “time–latitude” diagram for the hourly means of SH averaged over the longitudes 65°–95°E. The EQ time (EQ latitude) is indicated by vertical (horizontal) line.
Remotesensing 16 03112 g012
Remotesensing 16 03112 g013
Figure 13. Time series of daily values of (a) latent heat flux and (b) AOD from 11 January to 1 February. Both parameters are averaged over 35°–45°N, 65°–95°E. The day of EQ occurrence is indicated by red line.
Figure 13. Time series of daily values of (a) latent heat flux and (b) AOD from 11 January to 1 February. Both parameters are averaged over 35°–45°N, 65°–95°E. The day of EQ occurrence is indicated by red line.
Remotesensing 16 03112 g013
Table 1. Characteristics of satellite passages through the selected area 30°–45°N, 65°–95°E on 22 January.
Table 1. Characteristics of satellite passages through the selected area 30°–45°N, 65°–95°E on 22 January.
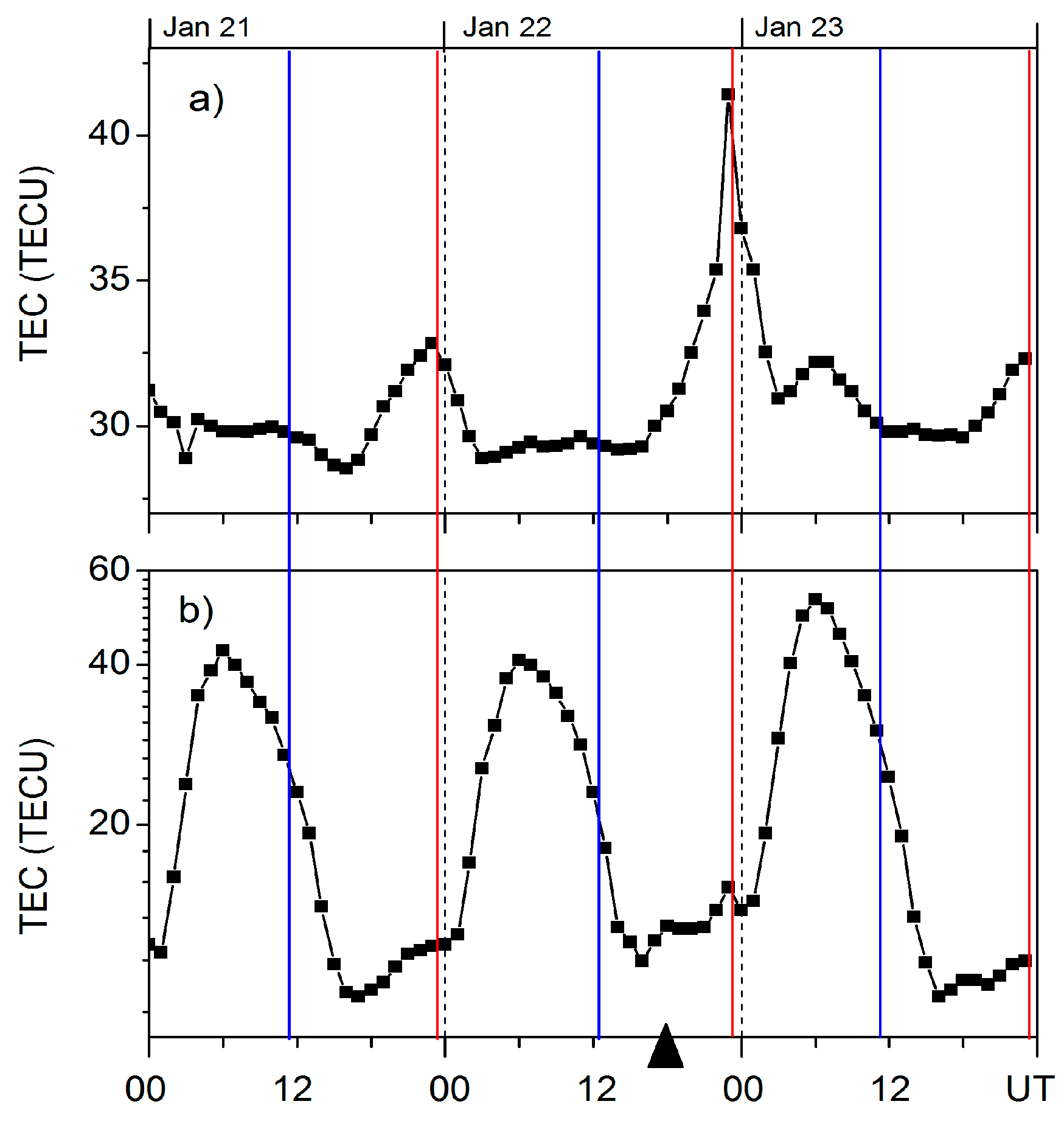
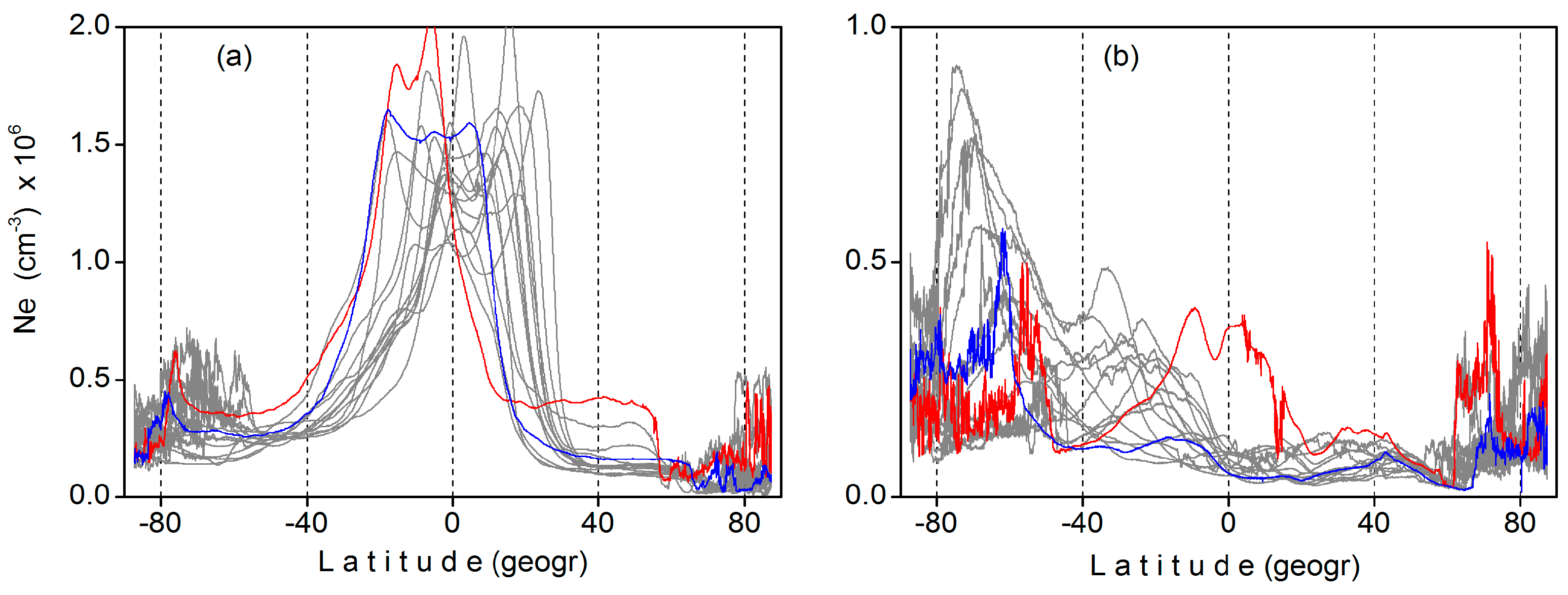
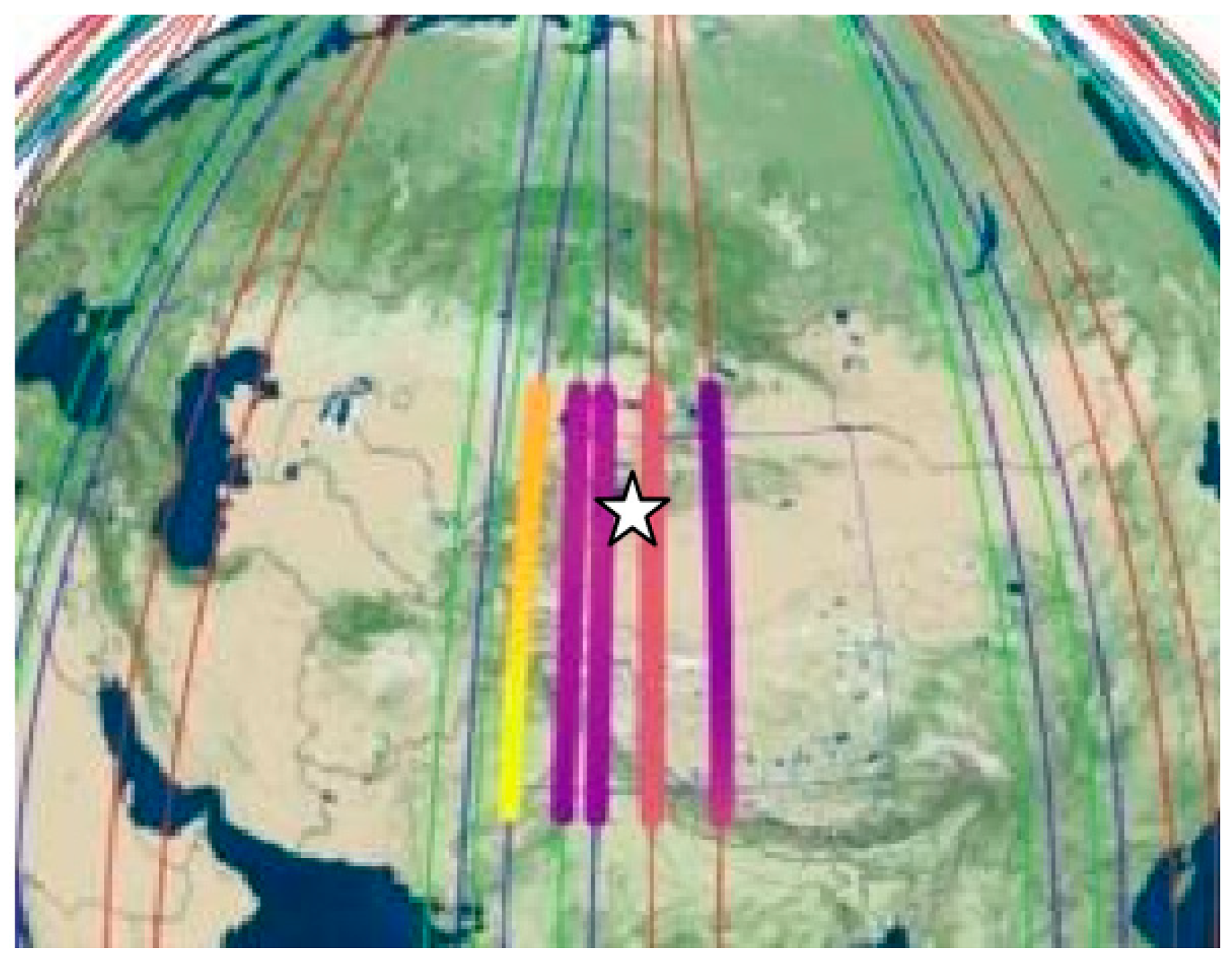
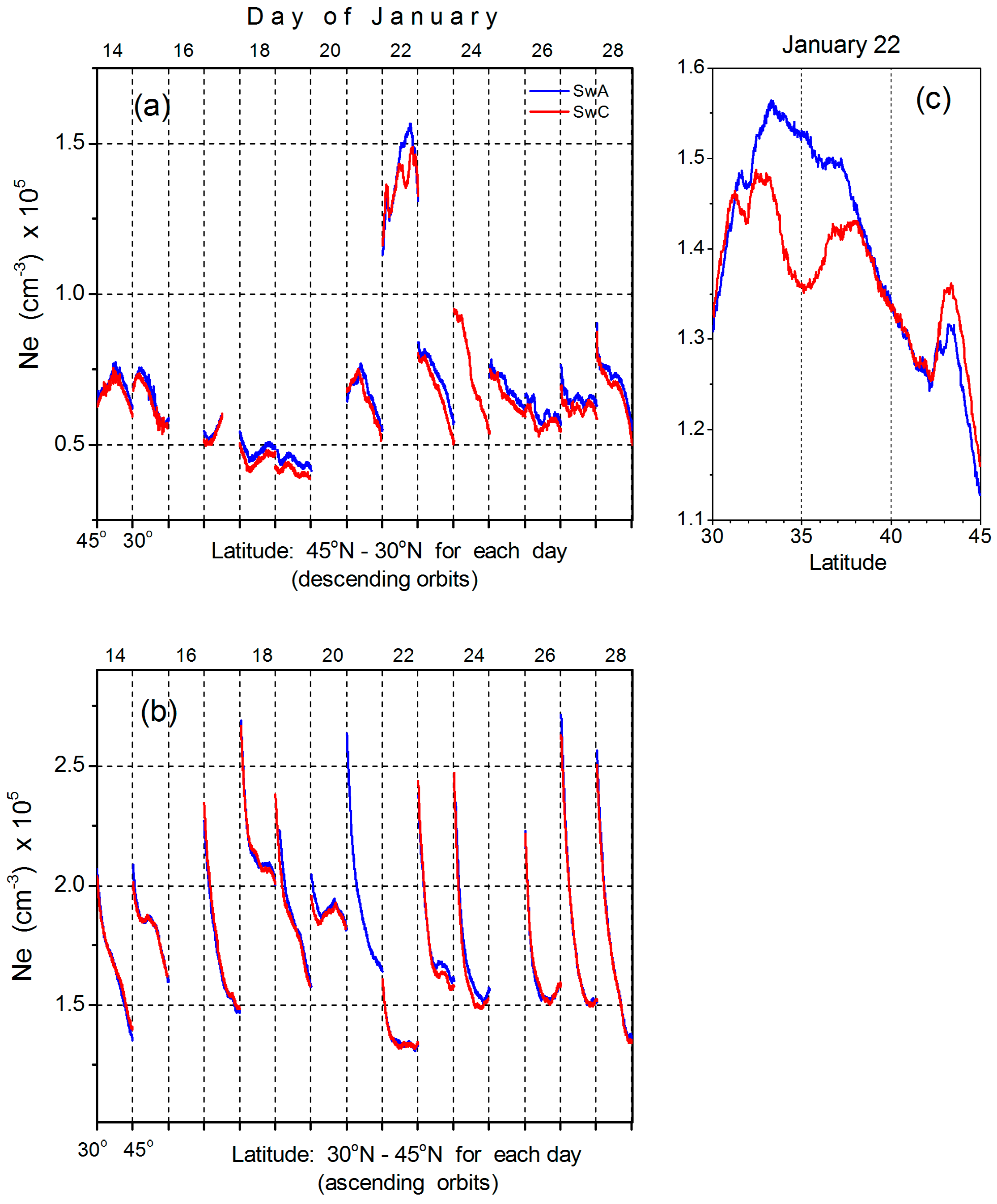
SatOrbitAppr. UTAppr. LT
Swarm_A, Swarm_Cascending1217
descending2305
Swarm_Bascending0208
descending1420
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Lukianova, R.; Daurbayeva, G.; Siylkanova, A. Ionospheric and Meteorological Anomalies Associated with the Earthquake in Central Asia on 22 January 2024. Remote Sens. 2024, 16, 3112. https://doi.org/10.3390/rs16173112

AMA Style

Lukianova R, Daurbayeva G, Siylkanova A. Ionospheric and Meteorological Anomalies Associated with the Earthquake in Central Asia on 22 January 2024. Remote Sensing. 2024; 16(17):3112. https://doi.org/10.3390/rs16173112

Chicago/Turabian Style

Lukianova, Renata, Gulbanu Daurbayeva, and Akgenzhe Siylkanova. 2024. "Ionospheric and Meteorological Anomalies Associated with the Earthquake in Central Asia on 22 January 2024" Remote Sensing 16, no. 17: 3112. https://doi.org/10.3390/rs16173112

APA Style

Lukianova, R., Daurbayeva, G., & Siylkanova, A. (2024). Ionospheric and Meteorological Anomalies Associated with the Earthquake in Central Asia on 22 January 2024. Remote Sensing, 16(17), 3112. https://doi.org/10.3390/rs16173112

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop