Effect of Albedo Footprint Size on Relationships between Measured Albedo and Forest Attributes for Small Forest Plots
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area

2.2. Field Data
2.2.1. Tree Measurements
2.2.2. Estimation of Biomass and Volume
2.2.3. Estimation of Site Productivity
2.2.4. Estimation of Complexity Indices
2.3. ALS Data
2.4. UAV Albedo
2.4.1. UAV Platform
2.4.2. Flight Description
2.4.3. Flight Campaign
2.4.4. Processing of UAV Data
2.5. Statistical Analysis
3. Results
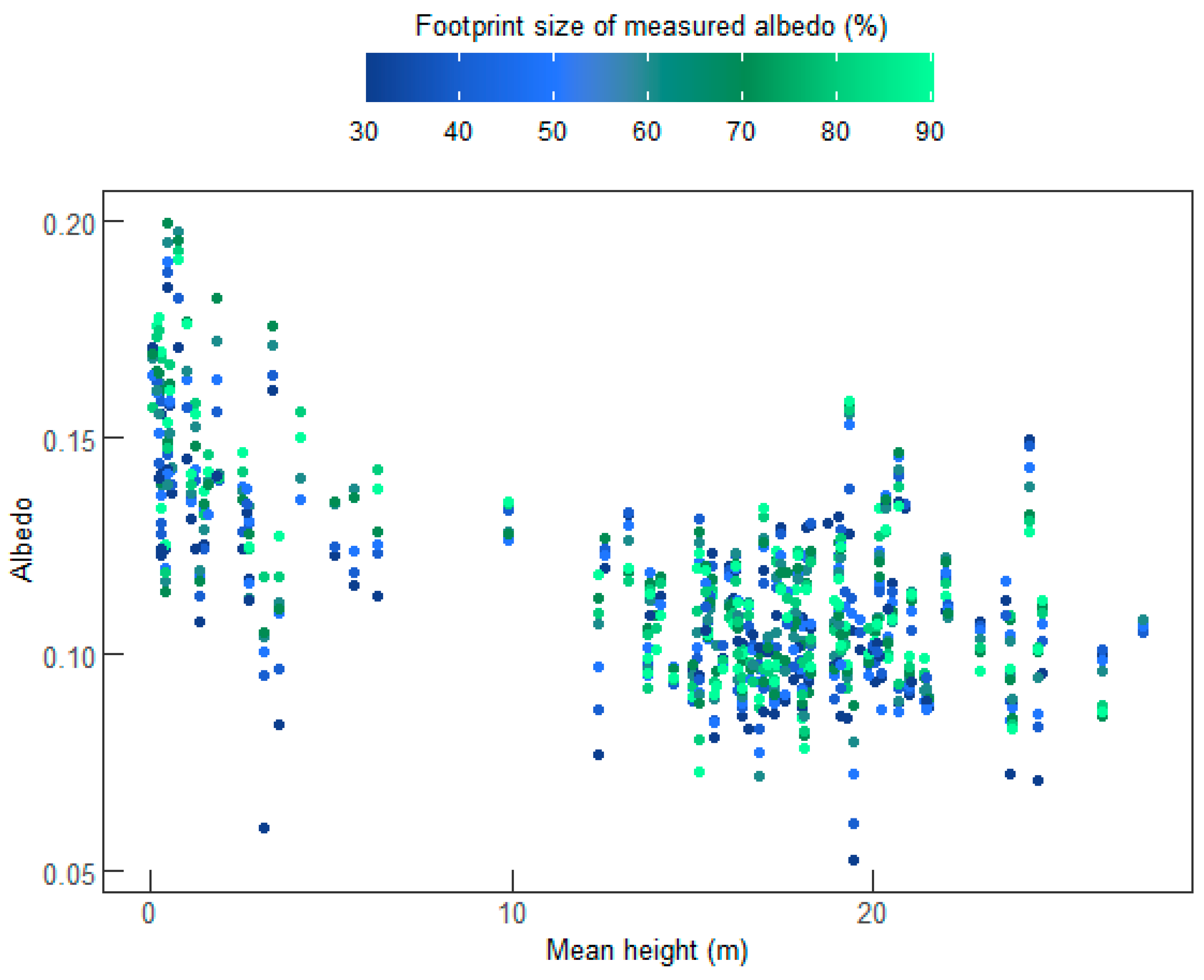
3.1. Impact of Footprint Size of Measured Albedo on Correlation with Field Measured Forest Attributes
3.2. Impact of Footprint Size of Measured Albedo on Correlation with Als-Derived Metrics
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Trishchenko, A.P.; Sun, X. Simulation of canopy radiation transfer and surface albedo in the EALCO model. Clim. Dyn. 2007, 29, 615–632. [Google Scholar] [CrossRef]
- Wang, S.; Grant, R.F.; Verseghy, D.L.; Black, T.A. Modelling carbon-coupled energy water dynamics of boreal forest in a general circulation model land surface scheme. Int. J. Climatol. 2002, 20, 1249–1265. [Google Scholar] [CrossRef]
- Shen, X.; Liu, Y.; Liu, B.; Zhang, J.; Wang, L.; Lu, X.; Jiang, M. Effect of shrub encroachment on land surface temperature in semi-arid areas of temperate regions of the Northern Hemisphere. Agric. For. Meteorol. 2022, 320, 108943. [Google Scholar] [CrossRef]
- Kuusinen, N.; Stenberg, P.; Korhonen, L.; Rautiainen, M.; Tomppo, E. Structural factors driving boreal forest albedo in Finland. Remote Sens. Environ. 2016, 175, 43–51. [Google Scholar] [CrossRef]
- Ramtvedt, E.N.; Bollandsås, O.M.; Næsset, E.; Gobakken, T. Relationships between single-tree mountain birch summertime albedo and vegetation properties. Agric. For. Meteorol. 2021, 307, 108470. [Google Scholar] [CrossRef]
- Lukeš, P.; Stenberg, P.; Rautiainen, M. Relationship between forest density and albedo in the boreal zone. Ecol. Modell. 2013, 261–262, 74–79. [Google Scholar] [CrossRef]
- Lukeš, P.; Rautiainen, M.; Manninen, T.; Stenberg, P.; Mõttus, M. Geographical gradients in boreal forest albedo and structure in Finland. Remote Sens. Environ. 2014, 152, 526–535. [Google Scholar] [CrossRef]
- Hovi, A.; Lindberg, E.; Lang, M.; Arumäe, T.; Peuhkurinen, J.; Sirparanta, S.; Pyankov, S.; Rautiainen, M. Seasonal dynamics of albedo across European boreal forests: Analysis of MODIS albedo and structural metrics from airborne LiDAR. Remote Sens. Environ. 2019, 224, 365–381. [Google Scholar] [CrossRef]
- Kuusinen, N.; Tomppo, E.; Shuai, Y.; Berninger, F. Effects of forest age on albedo in boreal forests estimated from MODIS and Landsat albedo retrievals. Remote Sens. Environ. 2014, 145, 145–153. [Google Scholar] [CrossRef]
- Kuusinen, N.; Lukeš, P.; Stenberg, P.; Levula, J.; Nikinmaa, E.; Berninger, F. Measured and modelled albedos in Finnish boreal forest stands of different species, structure and understory. Ecol. Modell. 2014, 284, 10–18. [Google Scholar] [CrossRef]
- Qu, Y.; Liang, S.; Liu, Q.; He, T.; Liu, S.; Li, X. Mapping surface broadband albedo from satellite observations: A review of literatures on algorithms and products. Remote Sens. 2015, 7, 990–1020. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Sun, Q.; Shuai, Y.; Román, M.O. Capturing rapid land surface dynamics with Collection V006 MODIS BRDF/NBAR/Albedo (MCD43) products. Remote Sens. Environ. 2018, 207, 50–64. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B.; Santhana Vannan, S.K.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G.; et al. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef]
- Li, Z.; Erb, A.; Sun, Q.; Liu, Y.; Shuai, Y.; Wang, Z.; Boucher, P.; Schaaf, C. Preliminary assessment of 20-m surface albedo retrievals from sentinel-2A surface reflectance and MODIS/VIIRS surface anisotropy measures. Remote Sens. Environ. 2018, 217, 352–365. [Google Scholar] [CrossRef]
- Lin, X.; Wu, S.; Chen, B.; Lin, Z.; Yan, Z.; Chen, X.; Yin, G.; You, D.; Wen, J.; Liu, Q.; et al. Estimating 10-m land surface albedo from Sentinel-2 satellite observations using a direct estimation approach with Google Earth Engine. ISPRS J. Photo. Remote Sens. 2022, 194, 1–20. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Canisius, F.; Wang, S.; Croft, H.; Leblanc, S.G.; Russell, H.A.; Chen, J.; Wang, R. A UAV-based sensor system for measuring land surface albedo: Tested over a boreal peatland ecosystem. Drones 2019, 3, 27. [Google Scholar] [CrossRef]
- Levy, C.; Burakowski, E.; Richardson, A. Novel Measurements of Fine-Scale Albedo: Using a Commercial Quadcopter to Measure Radiation Fluxes. Remote Sens. 2018, 10, 1303. [Google Scholar] [CrossRef]
- Ramtvedt, E.N.; Gobakken, T.; Næsset, E. Fine-Spatial Boreal–Alpine Single-Tree Albedo Measured by UAV: Experiences and Challenges. Remote Sens. 2022, 14, 1482. [Google Scholar] [CrossRef]
- Webster Cm Jonas, T. Influence of canopy shading and snow coverage on effective albedo in a snow-dominated evergreen needleleaf forest. Remote Sens. Environ. 2018, 214, 48–58. [Google Scholar] [CrossRef]
- Lellouch, G.; Carrer, D.; Vincent, C.; Pardé, M.C.; Frietas, S.; Trigo, I.F. Evaluation of two global land surface albedo datasets distributed by the copernicus climate change service and the EUMETSAT LSA-SAF. Remote Sens. 2020, 12, 1888. [Google Scholar] [CrossRef]
- Liang, S.; Fang, H.; Chen, M.; Shuey, C.J.; Walthall, C.; Daughtry, C.; Morisette, J.; Schaaf, C.; Strahler, A. Validating MODIS land surface reflectance and albedo products: Methods and preliminary results. Remote Sens. Environ. 2002, 83, 149–162. [Google Scholar] [CrossRef]
- Næsset, E. Accuracy of forest inventory using airborne laser-scanning: Evaluating the first Nordic full-scale operational project. Scand. J. For. Res. 2004, 19, 554–557. [Google Scholar] [CrossRef]
- Kangas, A.; Astrup, R.; Breidenbach, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-Larsen, T.; Næsset, E.; et al. Remote sensing forest inventories in Nordic countries–roadmap for the future Scand. J. For. Res. 2018, 33, 397–412. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E.; Bjerknes, K.-O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner data. Remote Sens. Environ. 2001, 78, 328–340. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Gregoire, T.G.; Ståhl, G. Model-assisted estimation of change in forest biomass over an 11year period in a sample survey supported by airborne LiDAR: A case study with post-stratification to provide “activity data”. Remote Sens. Environ. 2013, 128, 299–314. [Google Scholar] [CrossRef]
- Fitje, A.; Vestjordet, E. Stand height curves and new tariff tables for Norway spruce. Meddelelser Nor. Inst. Skogforsk. 1977, 34, 23–68. [Google Scholar]
- Vestjordet, E. Functions and tables for volume of standing trees. Norway spruce. Meddelelser Nor. Skogforsøksvesen 1967, 22, 539–574. [Google Scholar]
- Brantseg, A. Volume functions and tables for Scots pine: South Norway. Meddelelser Nor. Skogforsøksvesen 1967, 22, 689–739. [Google Scholar]
- Braastad, H. Volume tables for birch. Meddelelser Nor. Skogforsøksvesen 1966, 21, 23–78. [Google Scholar]
- Marklund, L.G. Biomass functions for pine, spruce and birch in Sweden. Rapport. Swed. Univeristy Agric. Sci. 1988, 45, 1–73. [Google Scholar]
- Kolstad, A.L.; Austrheim, G.; Solberg, E.J.; Venete, A.M.; Woodin, S.J.; Speed, J.D. Cervid exclusion alters boreal forest properties with little cascading impacts on soils. Ecosystems 2018, 21, 1027–1041. [Google Scholar] [CrossRef]
- Nieppola, J.; Carleton, T. Relations between understorey vegetation, site productivity, and environmental factors in Pinus sylvestris L. stands in southern Finland. stands in southern Finland. Vegetatio 1991, 93, 57–72. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A.; Eid, T.; Øyen, B.-H. Modelling dominant height growth from national forest inventory individual tree data with short time series and large age errors. For. Ecol. Manag. 2011, 262, 2162–2175. [Google Scholar] [CrossRef]
- Ceriani, L.; Verme, P. The origins of the Gini index: Extracts from Variabilità e Mutabilità (1912) by Corrado Gini. J. Econ. Inequal. 2012, 10, 421–443. [Google Scholar] [CrossRef]
- Lexerød, N.L.; Eid, T. An evaluation of different diameter diversity indices based on criteria related to forest management planning. For. Ecol. Manag. 2006, 222, 17–28. [Google Scholar] [CrossRef]
- Shannon, C.E. The mathematical theory of communication. In The Mathematical Theory of Communication; Shannon, C.E., Weaver, W., Eds.; University of Illinois Press: Urbana, IL, USA, 1948; pp. 29–125. [Google Scholar]
- Clark, P.J.; Evans, F.C. Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology 1954, 35, 445–453. [Google Scholar] [CrossRef]
- Vorčák, J.; Merganič, J.; Saniga, M. Structural diversity change and regeneration processes of the Norway spruce natural forest in Babia hora NNR in relation to altitude. J. For. Sci. 2006, 52, 399–409. [Google Scholar] [CrossRef]
- Næsset, E. Estimating above-ground biomass in young forests with airborne laser scanning. Int. J. Remote Sens. 2011, 32, 473–501. [Google Scholar] [CrossRef]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ. 2011, 115, 1065–1080. [Google Scholar] [CrossRef]
- Ramtvedt, E.N.; Næsset, E. A simple slope correction of horizontally measured albedo in sloping terrain. Agric. For. Meteorol. 2023, 339, 109547. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistcal Computing. 2023. Available online: https://www.r-project.org/ (accessed on 7 July 2023).
- Cramer, J.S. Mean variance of R2 in small moderate samples. J. Econom. 1987, 35, 253–266. [Google Scholar] [CrossRef]
- Patterson, H.D.; Thompson, R. Recovery of inter-block information when block sizes are unequal. Biometrika 1971, 58, 545–554. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Satterthwaite, F.E. Synthesis of variance. Psychometrika 1941, 6, 309–316. [Google Scholar] [CrossRef]
- Luke, S.G. Evaluating significance in linear mixed-effects models in R. Behav. Res. Methods 2017, 49, 1494–1502. [Google Scholar] [CrossRef] [PubMed]
- Kuusinen, N.; Tomppo, E.; Berninger, F. Linear unmixing of MODIS albedo composites to infer subpixel land cover type albedos. Int. J. Appl. Earth Obs. Geo. 2013, 23, 324–333. [Google Scholar] [CrossRef]
- Hovi, A.; Raitio, P.; Rautiainen, M. A spectral analysis of 25 boreal tree species. Silva Fenn. 2017, 51, 7753. [Google Scholar] [CrossRef]
- Hovi, A.; Rautiainen, M. Spectral composition of shortwave radiation transmitted by forest canopies. Trees 2020, 34, 1499–1506. [Google Scholar] [CrossRef]
- Rautiainen, M.; Stenberg, P. Application of photon recollision probability in coniferous canopy reflectance simulations. Remote Sens. Environ. 2005, 96, 98–107. [Google Scholar] [CrossRef]





| Field-Measured Forest Attributes | Mean | Range | Std |
|---|---|---|---|
| Biomass (Mg ha−1) | 117.5 | 0.0–380.4 | 92.0 |
| Pine | 39.6 | 0.0–173.7 | 47.1 |
| Spruce | 63.4 | 0.0–365.8 | 76.9 |
| Deciduous | 14.4 | 0.0–203.1 | 27.4 |
| Number of stems (ha−1) | 4428 | 275–57631 | 8543 |
| Mean height (m) | 14.2 | 0.0–27.5 | 7.7 |
| Basal area (m2 ha−1) 1 | 32.3 | 5.0–52.9 | 8.7 |
| Volume (m3 ha−1) 1 | 290.3 | 40.6–695.3 | 115.2 |
| Site productivity 1 | 15.8 | 6.7–24.2 | 5.1 |
| Gini index 1 | 0.47 | 0.23–0.72 | 0.09 |
| Shannon diversity index 1 | 1.18 | 0.00–2.15 | 0.38 |
| Clark–Evans aggregation index 1 | 1.05 | 0.71–1.42 | 0.16 |
| Flight Height Above Forest Canopy (m) | Proportion a Fixed-Area Forest Plot Constitutes of Measured Albedo (%) | Radius of UAV Albedo Footprint (m) | Area of UAV Albedo Footprint (ha) |
|---|---|---|---|
| 6.4 | 90 | 23.9 | 0.18 |
| 9.3 | 80 | 34.7 | 0.38 |
| 12.3 | 70 | 45.9 | 0.66 |
| 15.9 | 60 | 59.3 | 1.11 |
| 20.5 | 50 | 76.5 | 1.84 |
| 26.9 | 40 | 100.4 | 3.17 |
| 37.3 | 30 | 139.2 | 6.09 |
| Footprint Size of Measured Albedo (%) 1 | n | All Species | Species-Specific | Site Productivity- and Species-Specific | |||
|---|---|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | |||||
| 90 | 66 | 0.02 | 0.015 | 0.35 | 0.012 | 0.39 | 0.011 |
| 80 | 73 | 0.02 | 0.013 | 0.27 | 0.012 | 0.34 | 0.011 |
| 70 | 78 | 0.00 | 0.014 | 0.20 | 0.013 | 0.27 | 0.012 |
| 60 | 79 | 0.00 | 0.014 | 0.24 | 0.012 | 0.31 | 0.011 |
| 50 | 81 | 0.00 | 0.015 | 0.18 | 0.014 | 0.22 | 0.013 |
| 40 | 82 | 0.00 | 0.015 | 0.13 | 0.014 | 0.17 | 0.014 |
| 30 | 82 | 0.00 | 0.017 | 0.11 | 0.016 | 0.13 | 0.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramtvedt, E.N.; Ørka, H.O.; Bollandsås, O.M.; Næsset, E.; Gobakken, T. Effect of Albedo Footprint Size on Relationships between Measured Albedo and Forest Attributes for Small Forest Plots. Remote Sens. 2024, 16, 3085. https://doi.org/10.3390/rs16163085
Ramtvedt EN, Ørka HO, Bollandsås OM, Næsset E, Gobakken T. Effect of Albedo Footprint Size on Relationships between Measured Albedo and Forest Attributes for Small Forest Plots. Remote Sensing. 2024; 16(16):3085. https://doi.org/10.3390/rs16163085
Chicago/Turabian StyleRamtvedt, Eirik Næsset, Hans Ole Ørka, Ole Martin Bollandsås, Erik Næsset, and Terje Gobakken. 2024. "Effect of Albedo Footprint Size on Relationships between Measured Albedo and Forest Attributes for Small Forest Plots" Remote Sensing 16, no. 16: 3085. https://doi.org/10.3390/rs16163085
APA StyleRamtvedt, E. N., Ørka, H. O., Bollandsås, O. M., Næsset, E., & Gobakken, T. (2024). Effect of Albedo Footprint Size on Relationships between Measured Albedo and Forest Attributes for Small Forest Plots. Remote Sensing, 16(16), 3085. https://doi.org/10.3390/rs16163085






