Geoclimatic Distribution of Satellite-Observed Salinity Bias Classified by Machine Learning Approach
Abstract
1. Introduction
2. Data and Methods
2.1. Data
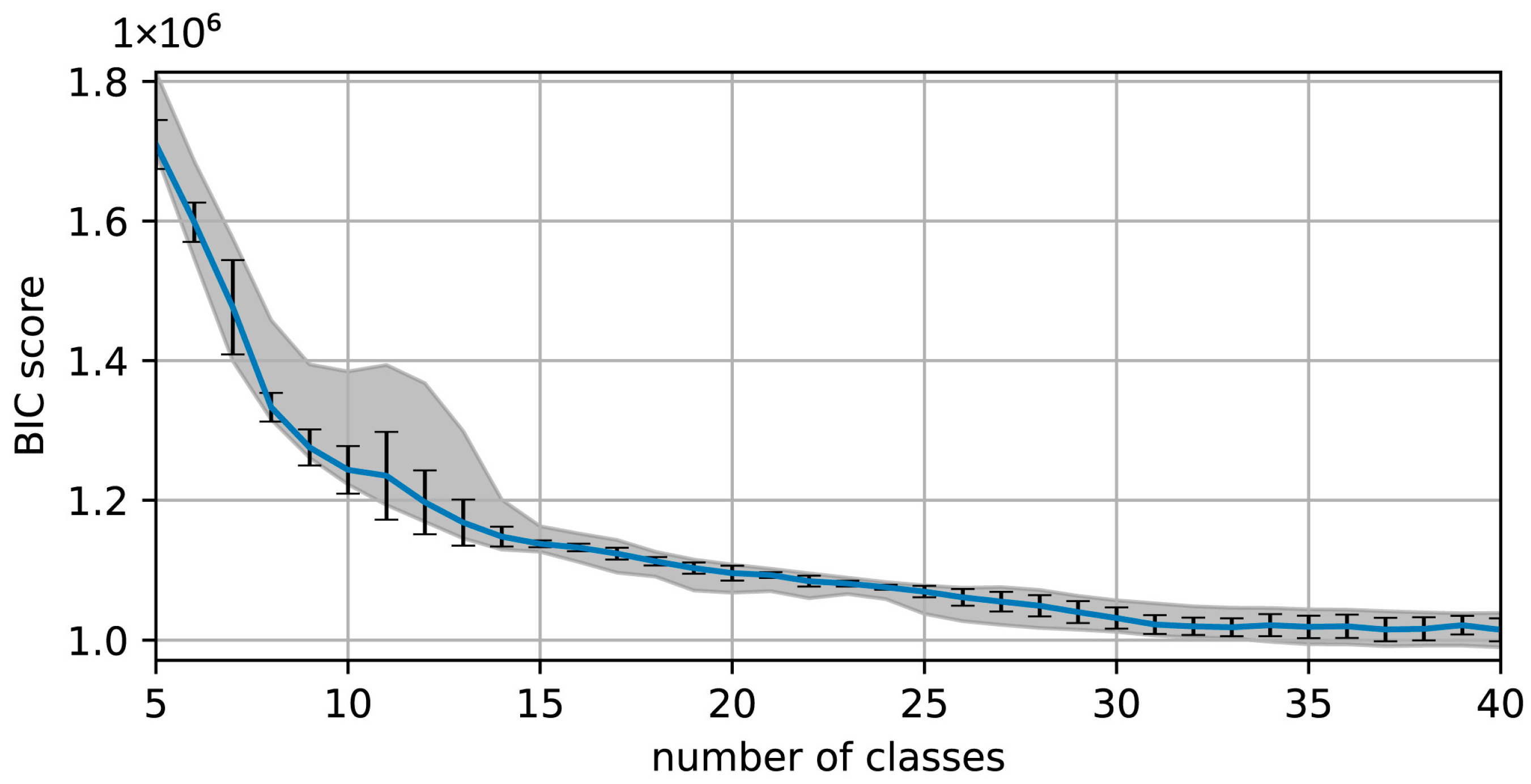
2.2. Unsupervised Machine Learning Classification
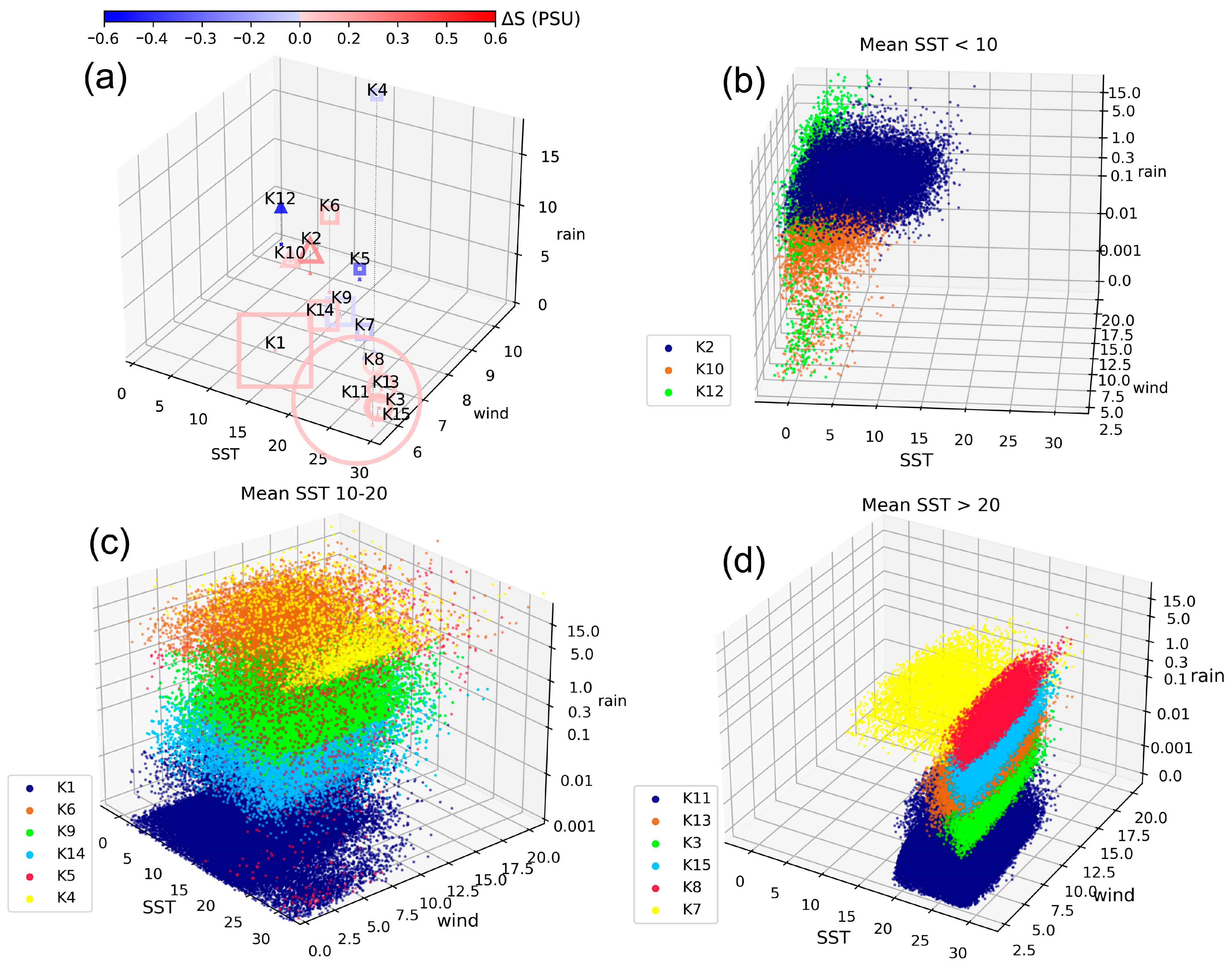
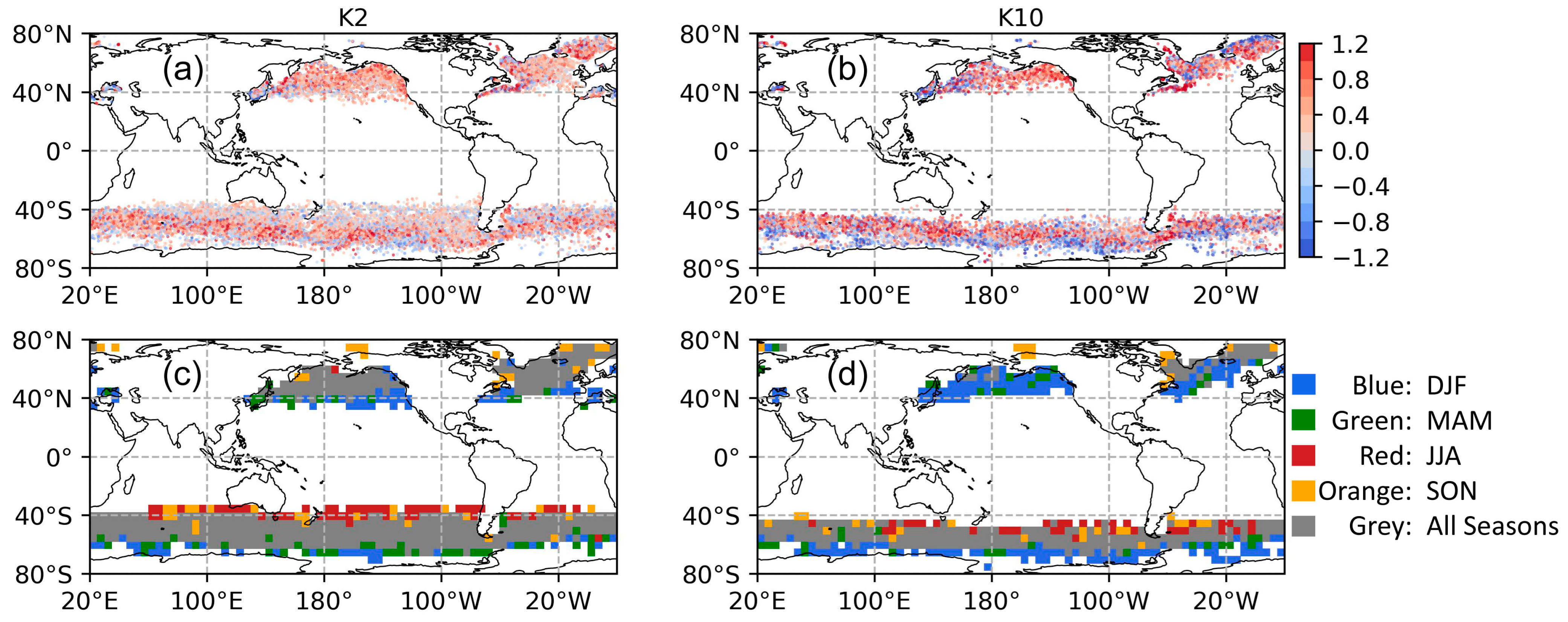
3. Geoclimatic Distribution of the Classes
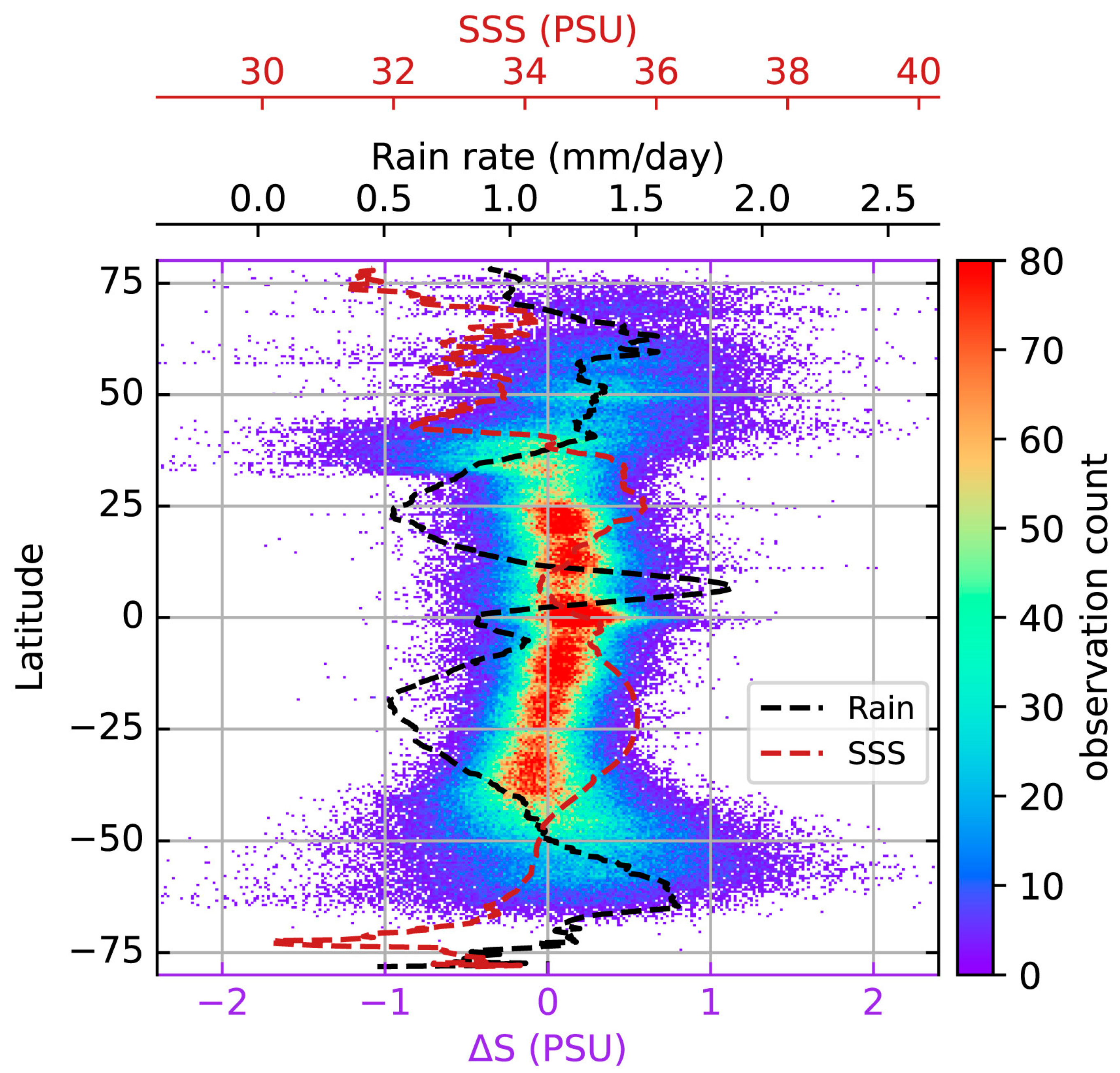
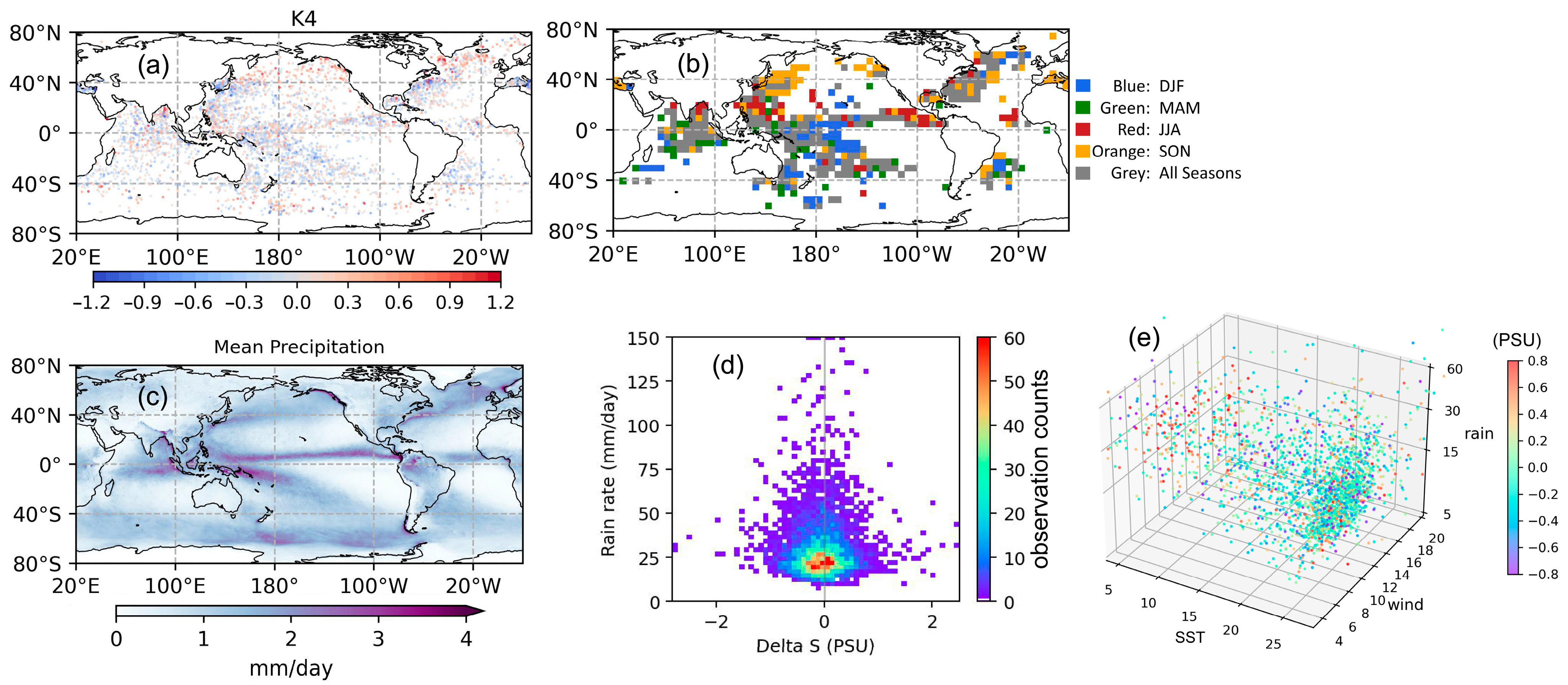
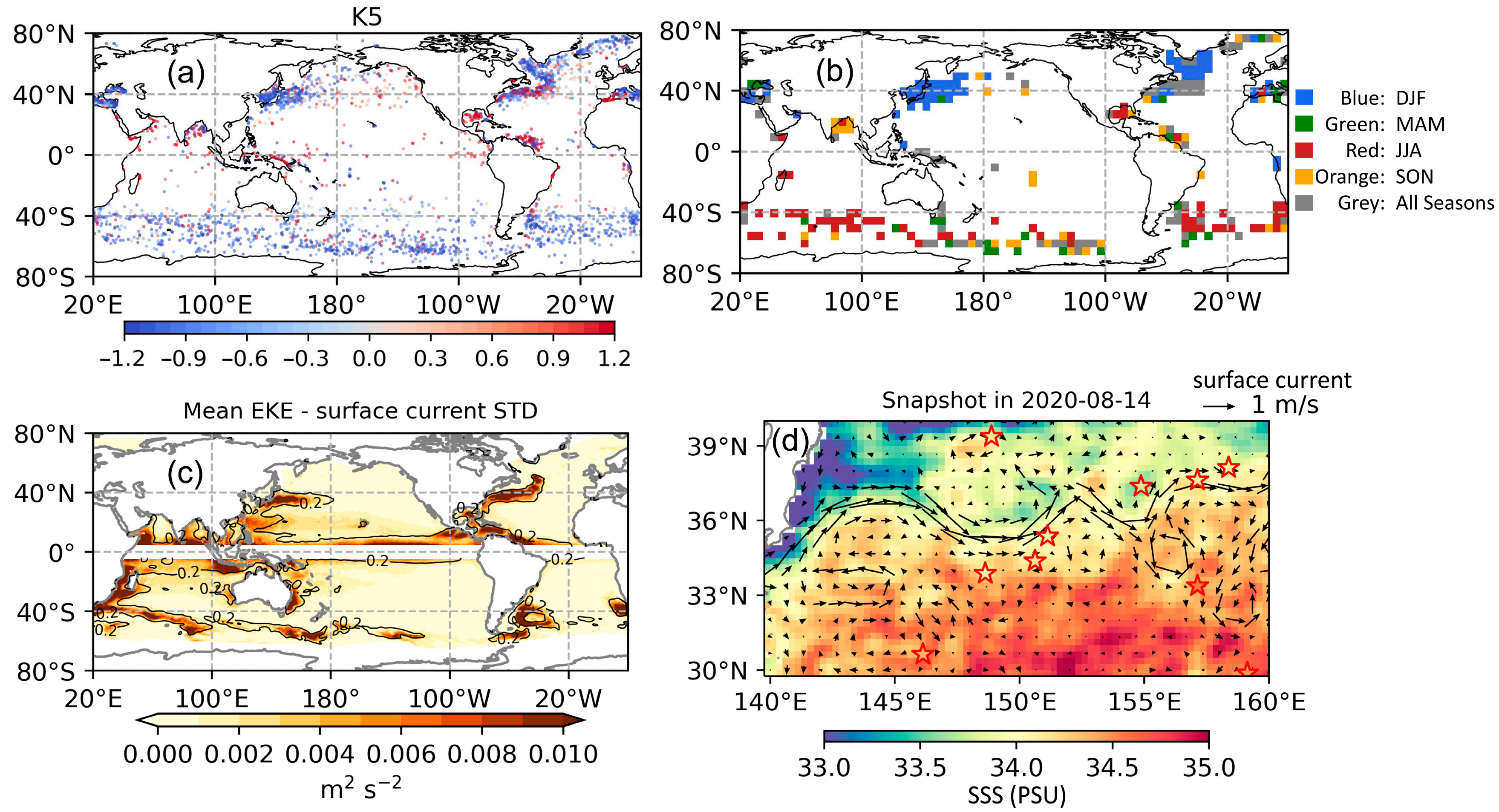
3.1. Environmental Signatures of the Classification Result
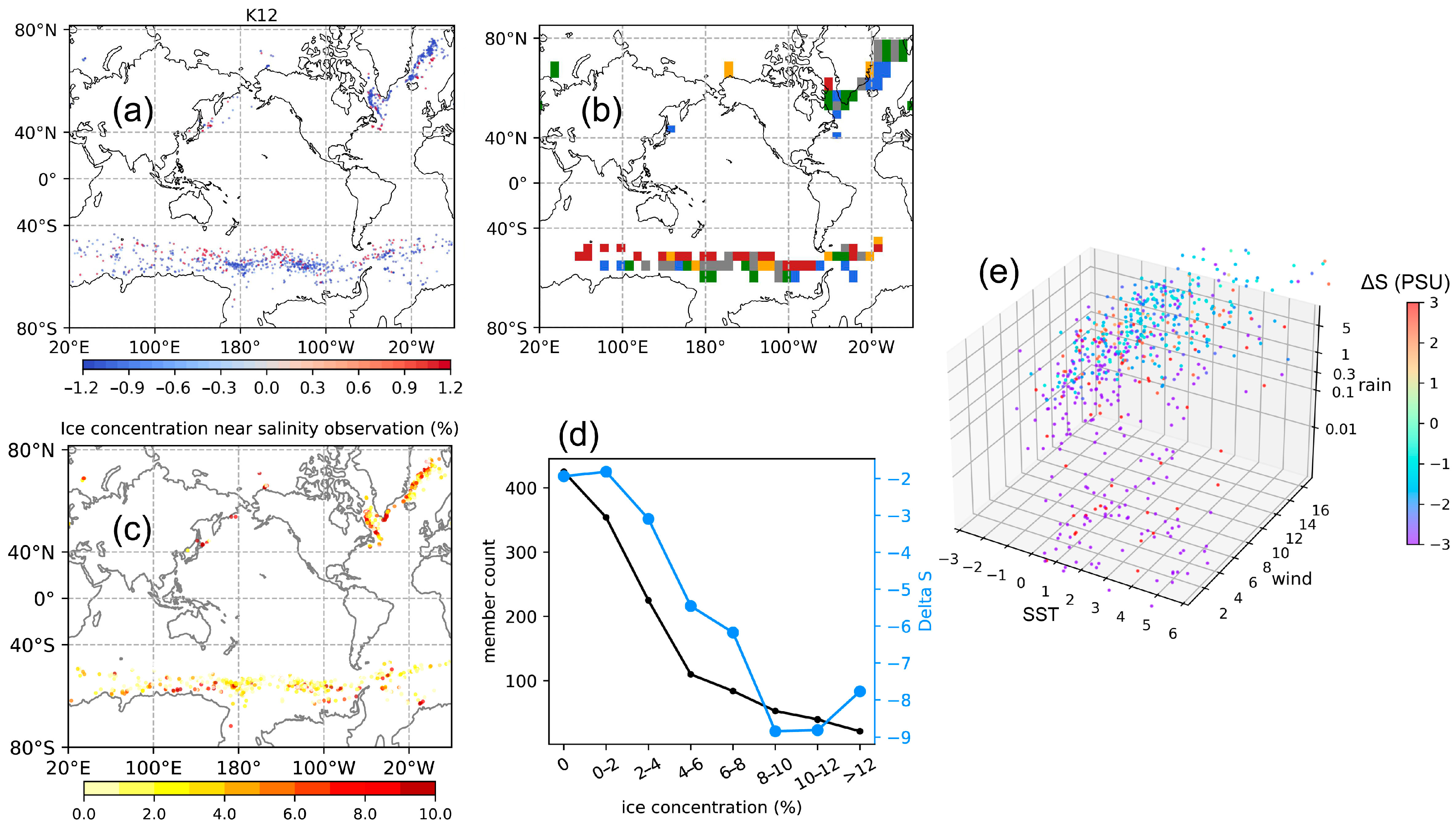
3.2. Similar Classes in the Different SST Range
3.3. Classifying the Outliers
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Lagerloef, G.; Colomb, F.R.; Le Vine, D.; Wentz, F.; Yueh, S.; Ruf, C.; Lilly, J.; Gunn, J.; Chao, Y.; deCharon, A.; et al. The Aquarius/SAC-D Mission: Designed to Meet the Salinity Remote-Sensing Challenge. Oceanography 2008, 21, 68–81. [Google Scholar] [CrossRef]
- Sirounian, V. Effect of temperature, angle of observation, salinity, and thin ice on the microwave emission of water. J. Geophys. Res. 1968, 73, 4481–4486. [Google Scholar] [CrossRef]
- Reul, N.; Grodsky, S.A.; Arias, M.; Boutin, J.; Catany, R.; Chapron, B.; D’Amico, F.; Dinnat, E.; Donlon, C.; Fore, A.; et al. Sea surface salinity estimates from spaceborne L-band radiometers: An overview of the first decade of observation (2010–2019). Remote Sens. Environ. 2020, 242, 111769. [Google Scholar] [CrossRef]
- Boutin, J.; Vergely, J.L.; Marchand, S.; D’Amico, F.; Hasson, A.; Kolodziejczyk, N.; Reul, N.; Reverdin, G.; Vialard, J. New SMOS Sea Surface Salinity with reduced systematic errors and improved variability. Remote Sens. Environ. 2018, 214, 115–134. [Google Scholar] [CrossRef]
- Vinogradova, N.; Lee, T.; Boutin, J.; Drushka, K.; Fournier, S.; Sabia, R.; Stammer, D.; Bayler, E.; Reul, N.; Gordon, A.; et al. Satellite Salinity Observing System: Recent Discoveries and the Way Forward. Front. Mar. Sci. 2019, 6, 243. [Google Scholar] [CrossRef]
- Yin, X.B.; Wang, Z.Z.; Liu, Y.G.; Cheng, Y.C. A new algorithm for microwave radiometer remote sensing of sea surface salinity without influence of wind. Int. J. Remote Sens. 2008, 29, 6789–6800. [Google Scholar] [CrossRef]
- Yin, X.B.; Boutin, J.; Dinnat, E.; Song, Q.T.; Martin, A. Roughness and foam signature on SMOS-MIRAS brightness temperatures: A semi-theoretical approach. Remote Sens. Environ. 2016, 180, 221–233. [Google Scholar] [CrossRef]
- Bao, S.; Wang, H.; Zhang, R.; Yan, H.; Chen, J. Comparison of Satellite-Derived Sea Surface Salinity Products from SMOS, Aquarius, and SMAP. J. Geophys. Res. Ocean. 2019, 124, 1932–1944. [Google Scholar] [CrossRef]
- Ouyang, Y.; Zhang, Y.; Chi, J.; Sun, Q.; Du, Y. Deviations of satellite-measured sea surface salinity caused by environmental factors and their regional dependence. Remote Sens. Environ. 2023, 285, 113411. [Google Scholar] [CrossRef]
- Lang, R.; Zhou, Y.; Utku, C.; Le Vine, D. Accurate measurements of the dielectric constant of seawater at L band. Radio Sci. 2016, 51, 2–24. [Google Scholar] [CrossRef]
- Tang, W.; Yueh, S.; Yang, D.; Fore, A.; Hayashi, A.; Lee, T.; Fournier, S.; Holt, B. The Potential and Challenges of Using Soil Moisture Active Passive (SMAP) Sea Surface Salinity to Monitor Arctic Ocean Freshwater Changes. Remote Sens. 2018, 10, 869. [Google Scholar] [CrossRef]
- Yu, L.; Josey, S.A.; Bingham, F.M.; Lee, T. Intensification of the global water cycle and evidence from ocean salinity: A synthesis review. Ann. N. Y. Acad. Sci. 2020, 1472, 76–94. [Google Scholar] [CrossRef]
- Yueh, S.H.; West, R.; Wilson, W.J.; Li, F.K.; Njoku, E.G.; Rahmat-Samii, Y. Error sources and feasibility for microwave remote sensing of ocean surface salinity. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1049–1060. [Google Scholar] [CrossRef]
- Boutin, J.; Chao, Y.; Asher, W.E.; Delcroix, T.; Drucker, R.; Drushka, K.; Kolodziejczyk, N.; Lee, T.; Reul, N.; Reverdin, G.; et al. Satellite and In Situ Salinity: Understanding Near-Surface Stratification and Subfootprint Variability. Bull. Am. Meteorol. Soc. 2016, 97, 1391–1407. [Google Scholar] [CrossRef]
- Birchfield, G.E. A coupled ocean-atmosphere climate model: Temperature versus salinity effects on the thermohaline circulation. Clim. Dyn. 1989, 4, 57–71. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Shi, J. Relationship between sea surface salinity and ocean circulation and climate change. Sci. China Earth Sci. 2019, 62, 771–782. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Pacanowski, R.C.; Philander, S.G.; Boccaletti, G. The Effect of Salinity on the Wind-Driven Circulation and the Thermal Structure of the Upper Ocean. J. Phys. Oceanogr. 2004, 34, 1949–1966. [Google Scholar] [CrossRef]
- Wong, A.P.S.; Wijffels, S.E.; Riser, S.C.; Pouliquen, S.; Hosoda, S.; Roemmich, D.; Gilson, J.; Johnson, G.C.; Martini, K.; Murphy, D.J.; et al. Argo Data 1999–2019: Two Million Temperature-Salinity Profiles and Subsurface Velocity Observations from a Global Array of Profiling Floats. Front. Mar. Sci. 2020, 7, 700. [Google Scholar] [CrossRef]
- Delcroix, T.; Hénin, C. Seasonal and interannual variations of sea surface salinity in the tropical Pacific Ocean. J. Geophys. Res. 1991, 96, 22135–122150. [Google Scholar] [CrossRef]
- Delcroix, T.; Henin, C.; Porte, V.; Arkin, P. Precipitation and sea-surface salinity in the tropical Pacific Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 1996, 43, 1123–1141. [Google Scholar] [CrossRef]
- Cronin, M.F.; McPhaden, M.J. Upper ocean salinity balance in the western equatorial Pacific. J. Geophys. Res. Ocean. 1998, 103, 27567–27587. [Google Scholar] [CrossRef]
- Medina-Lopez, E.; Ureña-Fuentes, L. High-Resolution Sea Surface Temperature and Salinity in the Global Ocean from Raw Satellite Data. Remote Sens. 2019, 11, 2191. [Google Scholar] [CrossRef]
- Akhil, V.P.; Vialard, J.; Lengaigne, M.; Keerthi, M.G.; Boutin, J.; Vergely, J.L.; Papa, F. Bay of Bengal Sea surface salinity variability using a decade of improved SMOS re-processing. Remote Sens. Environ. 2020, 248, 111964. [Google Scholar] [CrossRef]
- Jang, E.; Kim, Y.J.; Im, J.; Park, Y.-G.; Sung, T. Global sea surface salinity via the synergistic use of SMAP satellite and HYCOM data based on machine learning. Remote Sens. Environ. 2022, 273, 112980. [Google Scholar] [CrossRef]
- Jones, D.C.; Holt, H.J.; Meijers, A.J.S.; Shuckburgh, E. Unsupervised Clustering of Southern Ocean Argo Float Temperature Profiles. J. Geophys. Res. Ocean. 2019, 124, 390–402. [Google Scholar] [CrossRef]
- Maze, G.; Mercier, H.; Fablet, R.; Tandeo, P.; Lopez Radcenco, M.; Lenca, P.; Feucher, C.; Le Goff, C. Coherent heat patterns revealed by unsupervised classification of Argo temperature profiles in the North Atlantic Ocean. Prog. Oceanogr. 2017, 151, 275–292. [Google Scholar] [CrossRef]
- Xia, X.; Hong, Y.; Du, Y.; Xiu, P. Three Types of Antarctic Intermediate Water Revealed by a Machine Learning Approach. Geophys. Res. Lett. 2022, 49, e2022GL099445. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.J.T.J.O.M.L.R. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Cummings, J.A.; Smedstad, O.M. Ocean Data Impacts in Global HYCOM*. J. Atmos. Ocean. Technol. 2014, 31, 1771–1791. [Google Scholar] [CrossRef]
- Fore, A.G.; Yueh, S.H.; Tang, W.; Stiles, B.W.; Hayashi, A.K. Combined Active/Passive Retrievals of Ocean Vector Wind and Sea Surface Salinity With SMAP. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7396–7404. [Google Scholar] [CrossRef]
- Boutin, J.; Martin, N.; Reverdin, G.; Yin, X.; Gaillard, F. Sea surface freshening inferred from SMOS and ARGO salinity: Impact of rain. Ocean. Sci. 2013, 9, 183–192. [Google Scholar] [CrossRef]
- Xie, S.-P. The shape of continents, air-sea interaction, and the rising branch of the Hadley circulation. In The Hadley Circulation: Present, Past and Future; Springer: Cham, Switzerland, 2004; pp. 121–152. [Google Scholar]
- Asher, W.E.; Jessup, A.T.; Branch, R.; Clark, D. Observations of rain-induced near-surface salinity anomalies. J. Geophys. Res. Ocean. 2014, 119, 5483–5500. [Google Scholar] [CrossRef]
- Tang, W.; Yueh, S.H.; Hayashi, A.; Fore, A.G.; Jones, W.L.; Santos-Garcia, A.; Jacob, M.M. Rain-Induced Near Surface Salinity Stratification and Rain Roughness Correction for Aquarius SSS Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5474–5484. [Google Scholar] [CrossRef]
- ten Doeschate, A.; Sutherland, G.; Bellenger, H.; Landwehr, S.; Esters, L.; Ward, B. Upper Ocean Response to Rain Observed From a Vertical Profiler. J. Geophys. Res. Ocean. 2019, 124, 3664–3681. [Google Scholar] [CrossRef]
- Reverdin, G.; Supply, A.; Drushka, K.; Thompson, E.J.; Asher, W.E.; Lourenço, A. Intense and Small Freshwater Pools from Rainfall Investigated During Spurs-2 on 9 November 2017 in the Eastern Tropical Pacific. J. Geophys. Res. Ocean. 2020, 125, e2019JC015558. [Google Scholar] [CrossRef]
- Reul, N.; Chapron, B.; Grodsky, S.A.; Guimbard, S.; Kudryavtsev, V.; Foltz, G.R.; Balaguru, K. Satellite Observations of the Sea Surface Salinity Response to Tropical Cyclones. Geophys. Res. Lett. 2021, 48, e2020GL091478. [Google Scholar] [CrossRef]
- Chen, G.; Wang, D.; Hou, Y. The features and interannual variability mechanism of mesoscale eddies in the Bay of Bengal. Cont. Shelf Res. 2012, 47, 178–185. [Google Scholar] [CrossRef]
- Pujol, M.I.; Larnicol, G. Mediterranean sea eddy kinetic energy variability from 11 years of altimetric data. J. Mar. Syst. 2005, 58, 121–142. [Google Scholar] [CrossRef]


| Number of Class | ΔS (PSU) | SST (°C) | RAIN (mm/Day) | WIND (m/s) | ΔS SD (PSU) | Percentage of Total Data Volume |
|---|---|---|---|---|---|---|
| 1 | 0.09 | 12.58 | 0.00 | 6.96 | 0.56 | 19.17% |
| 2 | 0.24 | 7.53 | 2.43 | 9.82 | 0.55 | 4.63% |
| 3 | 0.10 | 28.13 | 0.04 | 6.23 | 0.23 | 4.97% |
| 4 | −0.04 | 22.19 | 24.82 | 7.88 | 0.42 | 0.84% |
| 5 | −0.37 | 13.19 | 1.11 | 10.12 | 1.50 | 0.67% |
| 6 | 0.09 | 11.61 | 7.99 | 9.38 | 0.58 | 2.71% |
| 7 | −0.07 | 21.93 | 2.71 | 7.57 | 0.24 | 2.36% |
| 8 | 0.02 | 29.10 | 5.96 | 5.66 | 0.30 | 3.20% |
| 9 | 0.00 | 15.38 | 0.58 | 8.66 | 0.33 | 5.85% |
| 10 | 0.05 | 4.05 | 0.31 | 10.05 | 1.03 | 2.74% |
| 11 | 0.07 | 25.26 | 0.00 | 6.25 | 0.22 | 35.04% |
| 12 | −2.43 | 1.14 | 3.92 | 10.54 | 5.64 | 0.23% |
| 13 | 0.07 | 26.58 | 0.16 | 6.80 | 0.19 | 5.81% |
| 14 | 0.05 | 13.61 | 0.07 | 8.53 | 0.43 | 6.43% |
| 15 | 0.06 | 28.66 | 0.84 | 5.99 | 0.25 | 5.35% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, Y.; Zhang, Y.; Feng, M.; Boschetti, F.; Du, Y. Geoclimatic Distribution of Satellite-Observed Salinity Bias Classified by Machine Learning Approach. Remote Sens. 2024, 16, 3084. https://doi.org/10.3390/rs16163084
Ouyang Y, Zhang Y, Feng M, Boschetti F, Du Y. Geoclimatic Distribution of Satellite-Observed Salinity Bias Classified by Machine Learning Approach. Remote Sensing. 2024; 16(16):3084. https://doi.org/10.3390/rs16163084
Chicago/Turabian StyleOuyang, Yating, Yuhong Zhang, Ming Feng, Fabio Boschetti, and Yan Du. 2024. "Geoclimatic Distribution of Satellite-Observed Salinity Bias Classified by Machine Learning Approach" Remote Sensing 16, no. 16: 3084. https://doi.org/10.3390/rs16163084
APA StyleOuyang, Y., Zhang, Y., Feng, M., Boschetti, F., & Du, Y. (2024). Geoclimatic Distribution of Satellite-Observed Salinity Bias Classified by Machine Learning Approach. Remote Sensing, 16(16), 3084. https://doi.org/10.3390/rs16163084








