DCFF-Net: Deep Context Feature Fusion Network for High-Precision Classification of Hyperspectral Image
Abstract
1. Introduction
- (1)
- The eigenvalues of each band of the hyperspectral image are transformed into polarization feature maps utilizing the polar co-ordinate conversion method. This process converts each pixel’s spectral value into a polygon, capturing all original pixel information. These transformed feature maps then serve as a novel input form, facilitating direct training and classification within a classic 2D-CNN deep learning network model, such as VGG or ResNet;
- (2)
- Based on the feature maps generated in the previous step, a novel deep learning residual network model called DCFF-Net is introduced for training and classifying the converted spectral feature maps. This study includes comprehensive testing and validation across three hyperspectral datasets: Indian Pines, Pavia University, and Salinas. The proposed model consistently exhibits superior classification performance across these datasets through comparative analysis with other advanced pixel-based classification methods;
- (3)
- The response mechanism of DCFF-Net’s classification accuracy to polar co-ordinate maps under different filling methods is analyzed. The DCFF-Net model, evaluated using the pixel-patch input mode, is compared to other advanced models for classification performance, consistently demonstrating outstanding results.
2. Method
2.1. Converting Hyperspectral Pixels into Feature Maps
2.2. Network Architectures
2.2.1. Spectral Information Embedding
2.2.2. Deep Spectral Feature Extract
2.2.3. Cross-Entropy Loss Function and Activation Function
3. Results and Analysis
3.1. Experimental Datasets and Implementation
3.2. Evaluation Criterion
3.3. Results Analysis Based on Feature Map
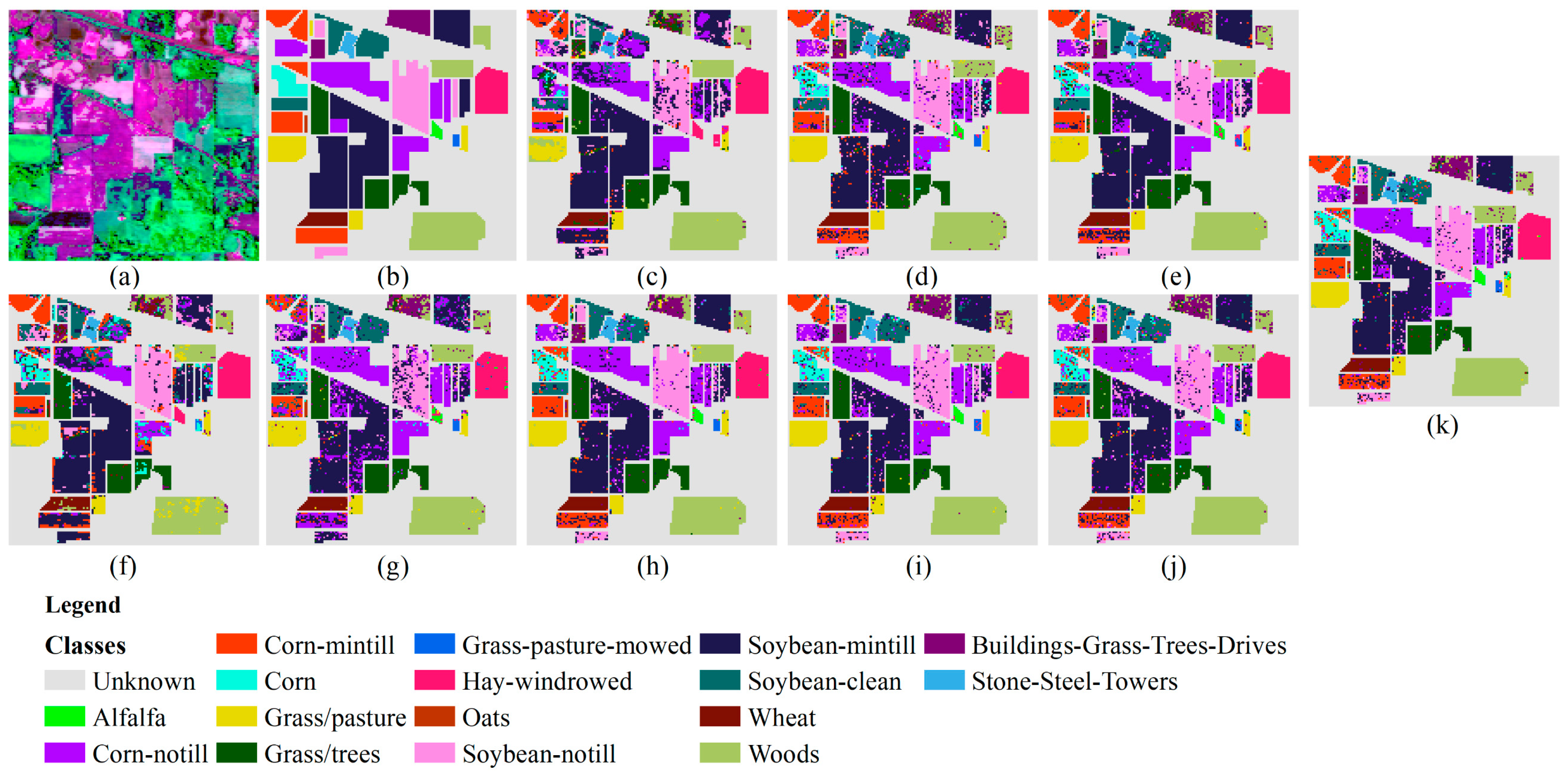
3.3.1. Results of Indian Pines
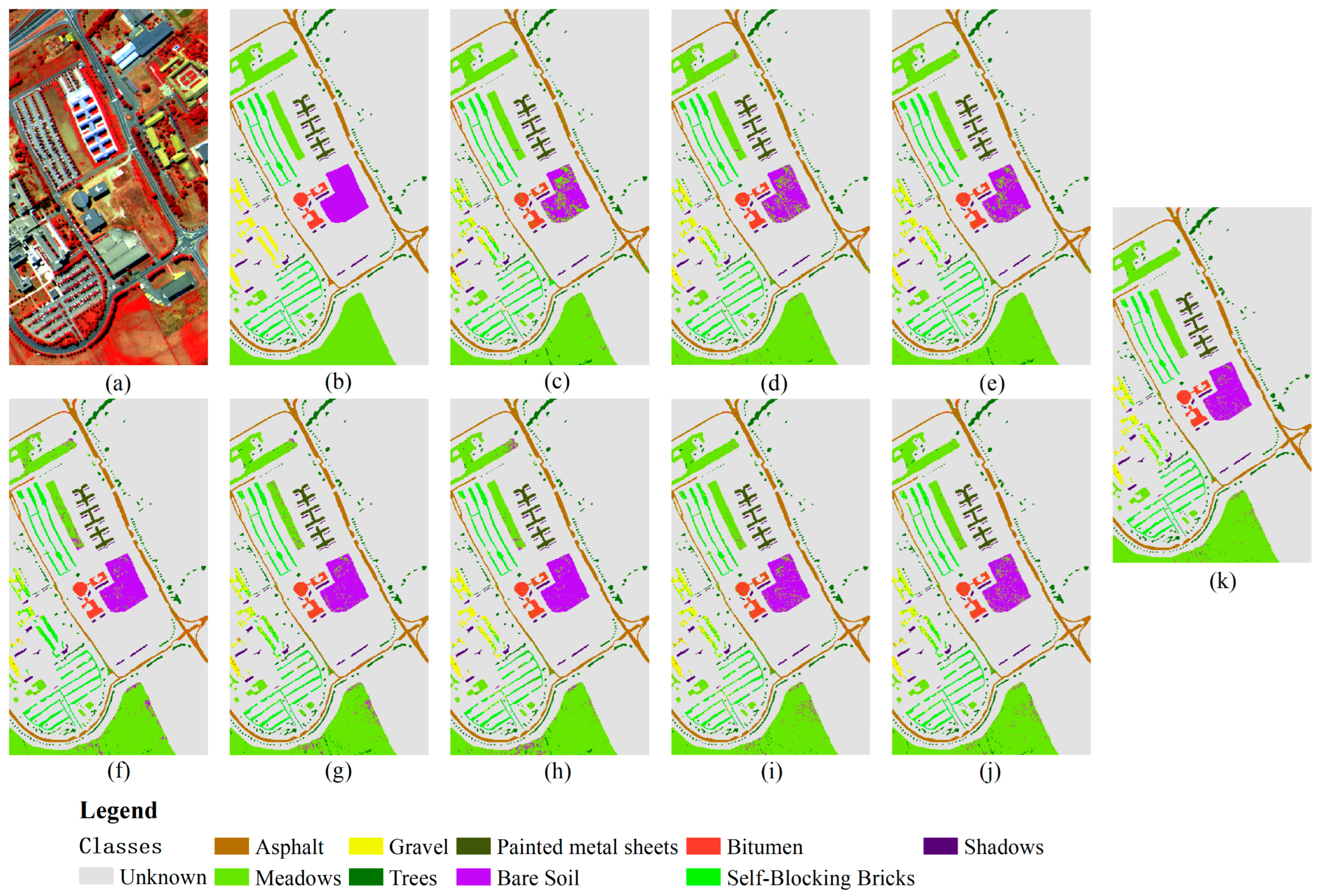
3.3.2. Results of Pavia University
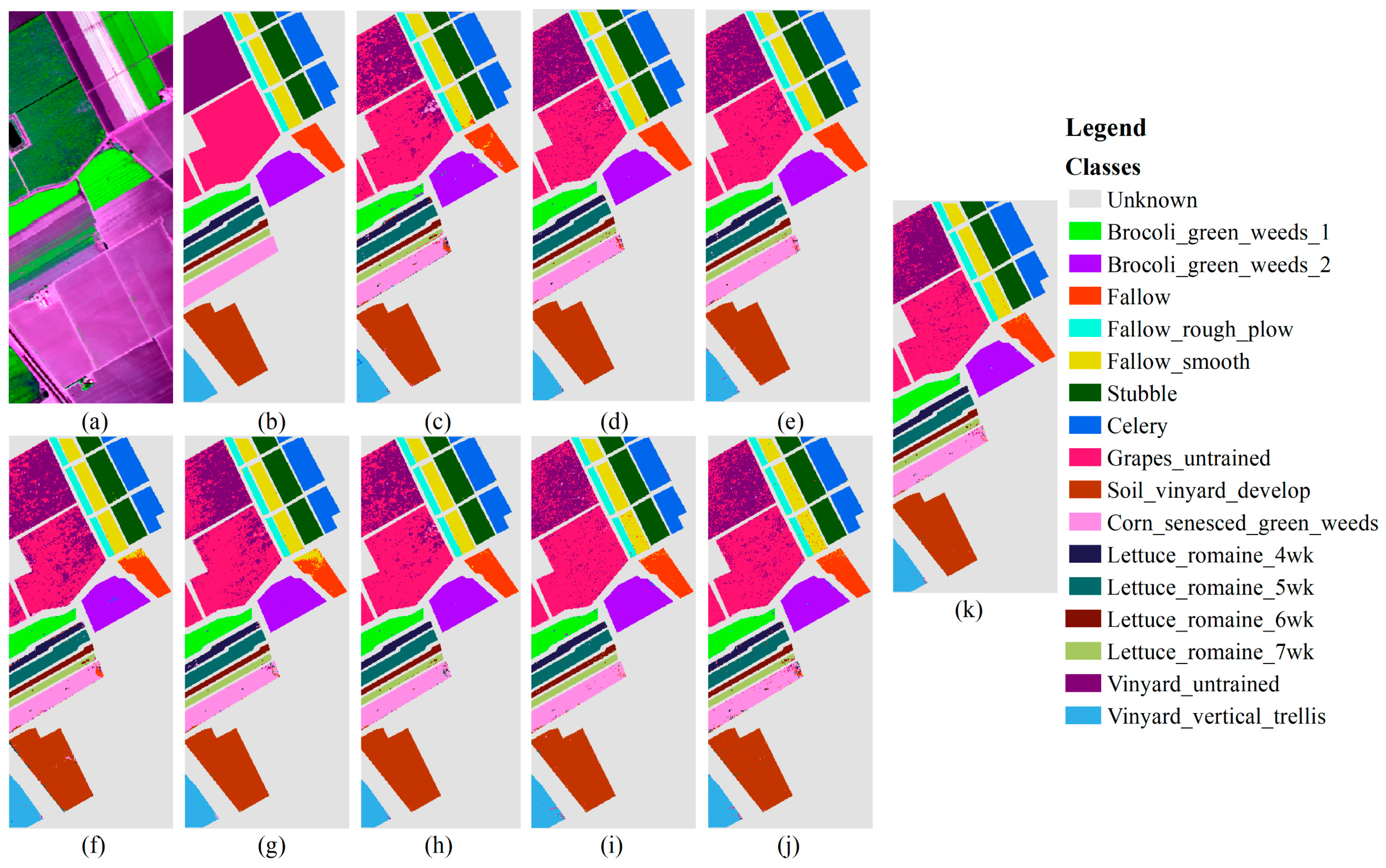
3.3.3. Results of Salinas
3.4. Results Analysis Based on Pixel-Patched
4. Discussion
4.1. Effect of Different Filling Methods
4.2. Effect of the Different Percentages of Training Samples for DCFF-NET
4.3. Ablation Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Benediktsson, J.A. Deep learning-based classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2383–2395. [Google Scholar]
- Liu, B.; Zhang, L.; Zhang, L.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Belhumeur, P.N.; Hespanha, J.P.; Kriegman, D.J. Eigenfaces vs. fisherfaces: Recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 711–720. [Google Scholar] [CrossRef]
- Tan, S.; Chen, X.; Zhang, D. Kernel discriminant analysis for face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2106–2112. [Google Scholar]
- Li, Y.; Chen, Y.; Jiang, J. A Novel KNN Classifier Based on Multi-Feature Fusion for Hyperspectral Image Classification. Remote Sens. 2020, 12, 745. [Google Scholar]
- Li, X.; Liang, Y. An Improved KNN Algorithm for Intrusion Detection Based on Feature Selection and Data Augmentation. IEEE Access. 2021, 9, 17132–17144. [Google Scholar]
- Domingos, P.; Pazzani, M. On the optimality of the simple Bayesian classifier under zero-one loss. Mach. Learn. 1997, 29, 103–130. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X. A survey on naive Bayes classifiers. Neurocomputing 2020, 399, 14–23. [Google Scholar]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–spatial hyperspectral image segmentation using subspace multinomial logistic regression and Markov random fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Mo, Y.; Li, M.; Liu, Y. Multinomial logistic regression with pairwise constraints for multi-label classification. IEEE Access 2020, 8, 74005–74016. [Google Scholar]
- Zhang, C.; Li, J. Multinomial logistic regression with manifold regularization for image classification. Pattern Recognit. Lett. 2021, 139, 55–63. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 40, 1778–1790. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodriguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, J. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H2) benchmark datasets classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, B.; Chen, Y.; Liang, F.; Dong, Z. JoKDNet: A joint keypoint detection and description network for large-scale outdoor TLS point clouds registration. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102534. [Google Scholar] [CrossRef]
- Jia, K.; Li, Q.Z.; Tian, Y.C.; Wu, B.F. A review of classification methods of remote sensing imagery. Spectrosc. Spectr. Anal. 2011, 31, 2618–2623. [Google Scholar]
- Liu, S.; Li, T.; Sun, Z. Discrimination of tea varieties using hyperspectral data based on wavelet transform and partial least squares-discriminant analysis. Food Chem. 2020, 325, 126914. [Google Scholar]
- He, L.; Huang, W.; Zhang, X. Hyperspectral image classification with principal component analysis and support vector machine. Neurocomputing 2015, 149, 962–971. [Google Scholar]
- Beirami, B.A.; Pirbasti, M.A.; Akbari, V. Fractal-Based Ensemble Classification System for Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Y.; Yang, Z. Spectral feature extraction based on key point detection and clustering algorithm. IEEE Access 2019, 7, 43100–43107. [Google Scholar]
- Huang, H.; Chen, X.; Guo, L. A novel method for spectral angle classification based on the support vector machine. PLoS ONE 2020, 15, e0237772. [Google Scholar]
- Wu, D.; Zhang, L.; Shen, X. A spectral curve matching algorithm based on dynamic programming and frequency-domain filtering. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4293–4307. [Google Scholar]
- Wang, Y.; Wang, C. Spectral curve shape index: A new spectral feature for hyperspectral image classification. J. Appl. Remote Sens. 2021, 15, 016524. [Google Scholar]
- Huang, J.; Zhang, J.; Li, Y. Discrimination of tea varieties using near infrared spectroscopy and chemometrics. J. Food Eng. 2015, 144, 75–80. [Google Scholar]
- Huang, M.; Gong, D.; Zhang, L.; Lin, H.; Chen, Y.; Zhu, D.; Xiao, C.; Altan, O. Spatiotemporal Dynamics and Forecasting of Ecological Security Pattern under the Consideration of Protecting Habitat: A Case Study of the Poyang Lake Ecoregion. Int. J. Digit. Earth 2024, 17, 2376277. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, F.; Pan, M. Rapid identification of intact paddy rice varieties using near-infrared spectroscopy and chemometric analysis. J. Cereal Sci. 2015, 62, 59–64. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Hinton, G.E. Learning multiple layers of representation. Trends Cogn. Sci. 2007, 11, 428–434. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.R.; Hinton, G.E. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process. Syst. 2013, 26, 3111–3119. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. Int. J. Comput. Vis. 2015, 113, 136–158. [Google Scholar]
- Chatfield, K.; Simonyan, K.; Vedaldi, A.; Zisserman, A. Return of the devil in the details: Delving deep into convolutional nets. In Proceedings of the British Machine Vision Conference (BMVC), Nottingham, UK, 1–5 September 2014; pp. 1–12. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 630–645. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Zhang, H.; Wu, C.; Zhang, J.; Zhu, Y.; Zhang, Z.; Lin, H.; Sun, Y. ResNeSt: Split-Attention Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 163–172. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Mao, J.; Xu, W.; Yang, Y.; Wang, J.; Huang, Z.; Yuille, A. Deep Captioning with Multimodal Recurrent Neural Networks (m-RNN). arXiv 2014, arXiv:1412.6632. [Google Scholar]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. Hybridsn: Exploring 3-d–2-d cnn feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-d deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectralspatial residual network for hyperspectral image classification: A 3-d deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Qing, Y.; Huang, Q.; Feng, L.; Qi, Y.; Liu, W. Multiscale Feature Fusion Network Incorporating 3D Self-Attention for Hyperspectral Image Classification. Remote Sens. 2022, 14, 742. [Google Scholar] [CrossRef]
- Qing, Y.; Liu, W. Hyperspectral image classification based on multi-scale residual network with attention mechanism. Remote Sens. 2021, 13, 335. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Chen, Y.; Li, W. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5518615. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Shah, C.; Jiang, L.; Li, W. Spectral–spatial morphological attention transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5503615. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Sun, W.; Wang, Y.; Liu, H. Single-source domain expansion network for cross-scene hyperspectral image classification. IEEE Trans. Image Process. 2023, 32, 1498–1512. [Google Scholar] [CrossRef]
- Liu, H.; Li, W.; Xia, X.G.; Chen, Y.; Zhang, Y. Multi-Area Target Attention for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5524916, Advance online publication. [Google Scholar]
- Liu, Y.; Li, X.; Zhang, Z.; Ma, Y. ESSAformer: Efficient transformer for hyperspectral image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Paris, France, 1–6 October 2023; pp. 17642–17651. [Google Scholar]
- Zhang, C.; Zhang, M.; Li, Y.; Gao, X.; Shi, Q. Difference curvature multidimensional network for hyperspectral image super-resolution. Remote Sens. 2021, 13, 3455. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, J.; Zhang, J.; Zhao, H.; Shang, W.; Gao, X. SPH-Net: Hyperspectral Image Super-Resolution via Smoothed Particle Hydrodynamics Modeling. IEEE Trans. Cybern. 2024, 54, 4150–4163. [Google Scholar] [CrossRef] [PubMed]
- Xia, Z.; Liu, Y.; Li, X.; Zhu, X.; Ma, Y.; Li, Y.; Hou, Y.; Qiao, Y. SCPNet: Semantic Scene Completion on Point Cloud. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 17642–17651. [Google Scholar]
- Wu, J.; Sun, X.; Qu, L.; Tian, X.; Yang, G. Learning Spatial–Spectral-Dimensional-Transformation-Based Features for Hyperspectral Image Classification. Appl. Sci. 2023, 13, 8451. [Google Scholar] [CrossRef]
- Wei, Y.; Feng, J.; Liang, X.; Cheng, M.-M.; Zhao, Y.; Yan, S. Object Region Mining with Adversarial Erasing: A Simple Classification to Semantic Segmentation Approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Bhattacharyya, C.; Kim, S. Black Ice Classification with Hyperspectral Imaging and Deep Learning. Appl. Sci. 2023, 13, 11977. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Tu, L. WHU-OHS: A benchmark dataset for large-scale hersepctral image classification. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 103022. [Google Scholar] [CrossRef]


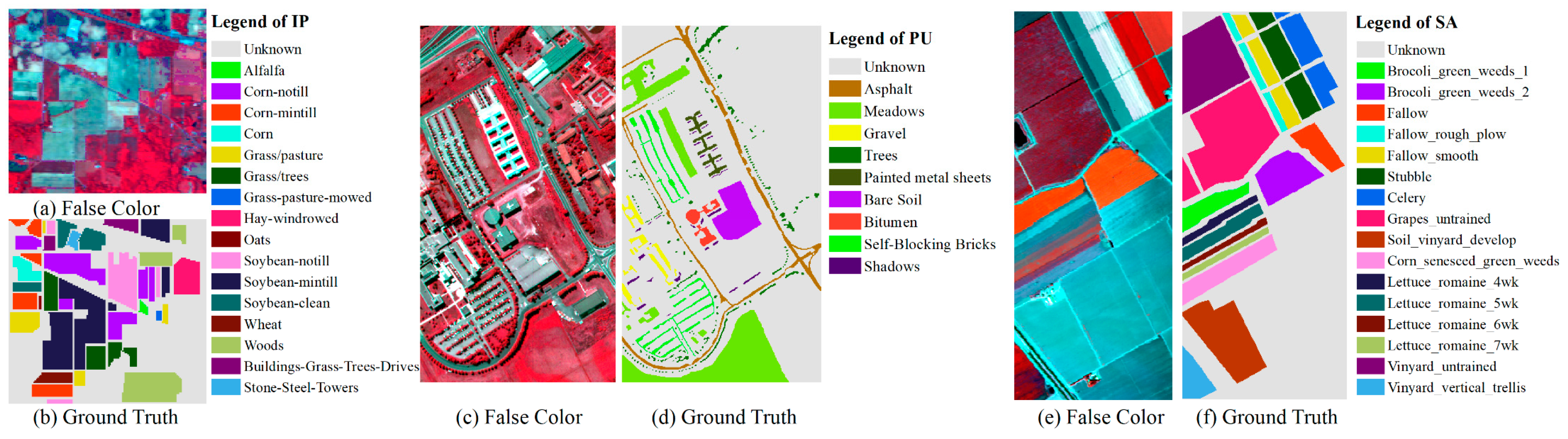


| Classes | Indian Pines | Salinas | Pavia University | |||
|---|---|---|---|---|---|---|
| Names | Samples | Names | Samples | Names | Samples | |
| 1 | Alfalfa | 46 | Brocoli_green_weeds_1 | 2009 | Asphalt | 6631 |
| 2 | Corn-no till | 1428 | Brocoli_green_weeds_2 | 3726 | Meadows | 18,649 |
| 3 | Corn-min till | 830 | Fallow | 1976 | Gravel | 2099 |
| 4 | Corn | 237 | Fallow_rough_plow | 1394 | Trees | 3064 |
| 5 | Grass-pasture | 483 | Fallow_smooth | 2678 | Painted metal sheets | 1345 |
| 6 | Grass-trees | 730 | Stubble | 3959 | Bare Soil | 5029 |
| 7 | Grass-pasture-mowed | 28 | Celery | 3579 | Bitumen | 1330 |
| 8 | Hay-windrowed | 478 | Grapes_untrained | 11,271 | Self-Blocking Bricks | 3682 |
| 9 | Oats | 20 | Soil_vinyard_develop | 6203 | Shadows | 947 |
| 10 | Soybean-no till | 972 | Corn_senesced_green_weeds | 3278 | - | - |
| 11 | Soybean-min till | 2455 | Lettuce_romaine_4wk | 1068 | - | - |
| 12 | Soybean-clean | 593 | Lettuce_romaine_5wk | 1927 | - | - |
| 13 | Wheat | 205 | Lettuce_romaine_6wk | 916 | - | - |
| 14 | Woods | 1265 | Lettuce_romaine_7wk | 1070 | - | - |
| 15 | Buildings-Grass-Trees-Drives | 386 | Vinyard_untrained | 7268 | - | - |
| 16 | Stone-Steel-Towers | 93 | Vinyard_vertical_trellis | 1807 | - | - |
| Total Samples | 10,249 | 54,129 | 42,956 | |||
| Methods | Train /Test | IP | PU | SA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| OA | KA | AA | OA | KA | AA | OA | KA | AA | ||
| NB | 30%/70% | 71.58 | 66.96 | 53.85 | 90.91 | 87.79 | 87.39 | 91.13 | 90.10 | 94.22 |
| KNN | 79.98 | 77.12 | 79.09 | 90.28 | 86.94 | 88.29 | 92.24 | 91.36 | 96.10 | |
| RF | 83.17 | 80.66 | 73.67 | 91.91 | 89.17 | 89.39 | 93.39 | 92.63 | 96.39 | |
| MLP | 77.65 | 74.52 | 77.12 | 93.88 | 91.86 | 90.31 | 92.31 | 91.43 | 95.67 | |
| 1DCNN | 79.90 | 76.94 | 76.65 | 93.97 | 92.00 | 92.42 | 93.34 | 92.58 | 96.91 | |
| SF-Pixel | 85.49 | 83.39 | 82.80 | 93.95 | 92.02 | 92.56 | 92.71 | 91.87 | 96.33 | |
| VGG16 | 85.18 | 83.16 | 83.21 | 92.19 | 89.64 | 89.56 | 94.25 | 93.59 | 96.66 | |
| Resnet50 | 82.13 | 79.60 | 77.71 | 93.44 | 91.28 | 90.49 | 94.62 | 94.01 | 97.23 | |
| DCFF-NET | 86.68 | 85.04 | 85.08 | 94.73 | 92.99 | 92.60 | 95.14 | 94.59 | 97.48 | |
| NB | 20%/80% | 66.14 | 60.52 | 48.63 | 89.36 | 85.61 | 85.24 | 90.21 | 89.09 | 93.37 |
| KNN | 78.12 | 75.00 | 76.38 | 89.34 | 85.61 | 87.25 | 91.38 | 90.40 | 95.54 | |
| RF | 80.75 | 77.85 | 66.60 | 91.04 | 87.95 | 88.05 | 92.60 | 91.75 | 95.90 | |
| MLP | 75.20 | 71.53 | 71.95 | 92.37 | 89.95 | 90.56 | 91.34 | 90.34 | 94.60 | |
| 1DCNN | 73.88 | 69.59 | 68.63 | 93.07 | 90.82 | 89.79 | 92.33 | 91.43 | 96.29 | |
| SF-Pixel | 82.91 | 80.38 | 76.87 | 92.77 | 90.50 | 91.41 | 91.62 | 90.68 | 95.80 | |
| VGG16 | 83.44 | 81.12 | 83.25 | 92.83 | 90.48 | 89.64 | 92.55 | 91.68 | 95.73 | |
| Resnet50 | 75.84 | 72.44 | 73.64 | 93.23 | 91.00 | 90.89 | 93.80 | 93.10 | 96.48 | |
| DCFF-NET | 84.05 | 81.77 | 79.90 | 94.11 | 92.18 | 91.86 | 94.24 | 93.58 | 96.81 | |
| NB | 10%/90% | 58.05 | 50.08 | 40.93 | 85.85 | 80.67 | 79.52 | 88.22 | 86.86 | 91.49 |
| KNN | 74.76 | 71.20 | 70.97 | 87.53 | 83.12 | 85.01 | 90.03 | 88.90 | 94.42 | |
| RF | 75.87 | 72.27 | 60.42 | 89.52 | 85.86 | 85.79 | 91.31 | 90.31 | 94.93 | |
| MLP | 69.20 | 64.93 | 60.60 | 92.02 | 89.40 | 89.34 | 90.41 | 89.35 | 94.91 | |
| 1DCNN | 69.36 | 64.98 | 64.48 | 92.71 | 90.39 | 90.85 | 91.55 | 90.58 | 94.98 | |
| SF-Pixel | 75.27 | 71.47 | 64.44 | 90.71 | 87.72 | 89.58 | 90.00 | 88.87 | 94.89 | |
| VGG16 | 77.88 | 74.73 | 72.80 | 91.59 | 88.84 | 88.61 | 92.12 | 91.23 | 95.50 | |
| Resnet50 | 70.90 | 66.54 | 64.14 | 91.51 | 88.73 | 89.18 | 92.35 | 91.47 | 94.86 | |
| DCFF-NET | 78.21 | 75.07 | 84.36 | 92.56 | 90.40 | 90.39 | 93.00 | 92.20 | 95.66 | |
| Classes Name | Train/Test | NB | KNN | RF | MLP | 1DCNN | SF-Pixel | VGG16 | Resnet50 | DCFF-NET |
|---|---|---|---|---|---|---|---|---|---|---|
| Alfalfa | 13/33 | 0.00 | 69.70 | 66.67 | 82.61 | 15.62 | 78.79 | 90.32 | 92.00 | 92.00 |
| Corn-no till | 428/1000 | 60.60 | 70.00 | 76.90 | 47.62 | 73.30 | 80.20 | 77.27 | 71.49 | 83.48 |
| Corn-min till | 249/581 | 39.07 | 65.58 | 60.24 | 70.24 | 72.98 | 78.01 | 86.70 | 82.30 | 84.42 |
| Corn | 71/166 | 13.25 | 59.04 | 56.02 | 70.04 | 64.46 | 63.25 | 80.29 | 73.03 | 86.40 |
| Grass-pasture | 144/339 | 70.80 | 93.51 | 89.09 | 83.64 | 84.62 | 92.55 | 96.99 | 92.57 | 98.65 |
| Grass-trees | 219/511 | 97.06 | 96.09 | 96.67 | 89.86 | 95.50 | 96.88 | 93.43 | 95.59 | 95.71 |
| Grass-pasture-mowed | 8/20 | 0.00 | 85.00 | 40.00 | 85.71 | 95.00 | 87.50 | 76.49 | 66.67 | 72.03 |
| Hay-windrowed | 143/335 | 99.40 | 98.51 | 98.81 | 96.44 | 94.03 | 97.57 | 92.31 | 91.43 | 92.86 |
| Oats | 6/14 | 0.00 | 71.43 | 21.43 | 25.00 | 78.57 | 58.33 | 80.91 | 80.30 | 83.78 |
| Soybean-no till | 291/681 | 66.81 | 79.15 | 82.09 | 73.97 | 60.15 | 81.65 | 72.41 | 67.08 | 77.41 |
| Soybean-min till | 736/1719 | 87.32 | 82.32 | 90.87 | 82.00 | 84.47 | 87.62 | 66.46 | 61.63 | 75.00 |
| Soybean-clean | 177/416 | 38.22 | 62.50 | 69.71 | 77.07 | 72.53 | 76.34 | 92.26 | 92.66 | 92.66 |
| Wheat | 61/144 | 93.75 | 100.00 | 95.83 | 99.51 | 98.60 | 98.55 | 97.60 | 94.48 | 96.84 |
| Woods | 379/886 | 97.97 | 91.99 | 95.03 | 97.08 | 94.13 | 96.94 | 72.22 | 63.64 | 81.82 |
| Buildings-Grass-Trees-Drives | 115/271 | 16.97 | 54.24 | 57.56 | 60.62 | 56.30 | 55.27 | 98.58 | 99.70 | 100.00 |
| Stone-Steel-Towers | 27/66 | 80.30 | 86.36 | 81.82 | 92.47 | 86.15 | 95.38 | 57.14 | 18.75 | 56.25 |
| OA | 3067/7182 | 71.58 | 79.98 | 83.17 | 77.65 | 79.90 | 85.39 | 85.18 | 82.13 | 86.68 |
| KA | 66.96 | 77.12 | 80.66 | 74.52 | 76.94 | 83.39 | 83.16 | 79.60 | 85.04 | |
| AA | 53.85 | 79.09 | 73.67 | 77.12 | 76.65 | 82.80 | 83.21 | 77.71 | 85.08 |
| Class Name | Train/Test | NB | KNN | RF | MLP | 1DCNN | SF-Pixel | VGG16 | Resnet50 | DCFF-NET |
|---|---|---|---|---|---|---|---|---|---|---|
| Asphalt | 1989/4642 | 90.69 | 89.19 | 92.20 | 92.45 | 94.64 | 96.41 | 93.08 | 94.46 | 93.84 |
| Meadows | 5594/13,055 | 98.47 | 97.88 | 97.94 | 97.82 | 97.65 | 95.02 | 96.51 | 97.36 | 97.54 |
| Gravel | 629/1470 | 66.87 | 74.56 | 74.15 | 65.66 | 88.16 | 88.21 | 71.34 | 73.13 | 77.70 |
| Trees | 919/2145 | 90.26 | 88.21 | 91.93 | 95.22 | 94.03 | 95.14 | 91.01 | 95.44 | 96.00 |
| Painted metal sheets | 403/942 | 99.15 | 99.47 | 99.15 | 99.26 | 100.00 | 99.57 | 99.37 | 99.38 | 99.17 |
| Bare Soil | 1508/3521 | 74.07 | 69.33 | 77.08 | 90.62 | 92.53 | 96.13 | 89.75 | 90.58 | 92.02 |
| Bitumen | 399/931 | 77.23 | 87.76 | 81.95 | 75.68 | 86.47 | 77.88 | 80.53 | 77.63 | 88.05 |
| Self-Blocking Bricks | 1104/2578 | 89.91 | 88.17 | 90.11 | 93.15 | 78.27 | 85.47 | 84.75 | 87.01 | 88.35 |
| Shadows | 284/663 | 99.85 | 100.00 | 100.00 | 99.25 | 100.00 | 100.00 | 99.70 | 99.39 | 99.70 |
| OA | 12,829/29,947 | 90.91 | 90.28 | 91.91 | 92.70 | 93.97 | 93.95 | 92.19 | 93.44 | 94.73 |
| KA | 87.79 | 86.94 | 89.17 | 90.22 | 92.00 | 92.02 | 89.64 | 91.28 | 92.99 | |
| AA | 87.39 | 88.29 | 89.39 | 89.90 | 92.42 | 92.56 | 89.56 | 90.49 | 92.60 |
| Classes Name | Train/Test | NB | KNN | RF | MLP | 1DCNN | SF-Pixel | VGG16 | Resnet50 | DCFF-NET |
|---|---|---|---|---|---|---|---|---|---|---|
| Brocoli_green_weeds_1 | 602/1407 | 97.51 | 99.29 | 99.93 | 99.36 | 100.00 | 99.58 | 99.86 | 99.79 | 99.59 |
| Brocoli_green_weeds_2 | 1117/2609 | 99.16 | 99.92 | 99.96 | 99.43 | 99.96 | 99.96 | 96.18 | 95.25 | 96.82 |
| Fallow | 592/1384 | 96.46 | 99.93 | 99.42 | 91.04 | 99.42 | 99.36 | 98.43 | 99.08 | 98.69 |
| Fallow_rough_plow | 418/976 | 99.08 | 99.39 | 99.39 | 99.08 | 99.18 | 99.47 | 98.12 | 99.41 | 99.48 |
| Fallow_smooth | 803/1875 | 96.48 | 98.51 | 98.77 | 98.72 | 99.20 | 99.37 | 94.71 | 99.06 | 99.22 |
| Stubble | 1187/2772 | 99.42 | 99.64 | 99.75 | 99.89 | 99.96 | 99.67 | 98.67 | 98.96 | 98.45 |
| Celery | 1073/2506 | 99.20 | 99.60 | 99.68 | 99.80 | 99.88 | 99.76 | 80.96 | 81.36 | 80.64 |
| Grapes_untrained | 3381/7890 | 87.93 | 85.02 | 89.91 | 79.62 | 86.43 | 90.43 | 97.17 | 98.65 | 98.96 |
| Soil_vinyard_develop | 1860/4343 | 99.06 | 99.52 | 99.36 | 98.83 | 99.93 | 99.91 | 98.66 | 99.77 | 99.92 |
| Corn_senesced_green_weeds | 983/2295 | 91.42 | 94.12 | 94.51 | 92.81 | 98.30 | 95.77 | 97.33 | 97.59 | 98.76 |
| Lettuce_romaine_4wk | 320/748 | 89.44 | 97.86 | 95.99 | 98.40 | 98.93 | 100.00 | 99.39 | 99.28 | 99.17 |
| Lettuce_romaine_5wk | 578/1349 | 99.56 | 99.85 | 99.41 | 85.17 | 99.48 | 100.00 | 98.97 | 99.05 | 99.31 |
| Lettuce_romaine_6wk | 274/642 | 97.82 | 98.75 | 98.44 | 97.66 | 99.38 | 99.84 | 99.78 | 99.74 | 99.93 |
| Lettuce_romaine_7wk | 321/749 | 92.79 | 96.66 | 97.06 | 97.46 | 97.33 | 94.71 | 99.88 | 99.68 | 99.52 |
| Vinyard_untrained | 2180/5088 | 65.33 | 71.29 | 72.27 | 78.83 | 73.92 | 64.34 | 88.61 | 89.51 | 91.71 |
| Vinyard_vertical_trellis | 542/1265 | 96.92 | 98.26 | 98.42 | 98.10 | 99.21 | 99.04 | 99.82 | 99.45 | 99.58 |
| OA | 16,231/37,898 | 91.13 | 92.24 | 93.39 | 91.13 | 93.34 | 92.71 | 94.25 | 94.62 | 95.14 |
| KA | 90.10 | 91.36 | 92.63 | 90.14 | 92.58 | 91.87 | 93.59 | 94.01 | 94.59 | |
| AA | 94.22 | 96.10 | 96.39 | 94.64 | 96.91 | 96.33 | 96.66 | 97.23 | 97.48 |
| Classes Name | Train/Test | VGG16 | Resnet50 | 3-DCNN | HybridSN | A2S2K | SF-Patch | DCFF-NET |
|---|---|---|---|---|---|---|---|---|
| Alfalfa | 4/42 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 93.50 ± 7.04 | 74.36 + 16.04 | 98.60 ± 1.15 |
| Corn-no till | 142/1286 | 96.68 ± 0.19 | 97.72 ± 0.10 | 90.86 ± 0.20 | 94.51 ± 0.20 | 97.45 ± 2.69 | 82.22 + 3.41 | 98.03 ± 0.14 |
| Corn-min till | 83/747 | 89.95 ± 0.26 | 96.48 ± 0.20 | 78.99 ± 0.29 | 93.47 ± 0.29 | 97.54 ± 1.63 | 87.75 + 4.63 | 99.62 ± 0.08 |
| Corn | 23/214 | 89.69 ± 0.63 | 84.84 ± 0.61 | 89.65 ± 1.16 | 69.14 ± 1.16 | 98.09 ± 1.30 | 89.95 + 9.67 | 95.54 ± 0.48 |
| Grass-pasture | 48/435 | 83.01 ± 0.84 | 89.3 ± 0.39 | 92.94 ± 0.24 | 94.3 ± 0.24 | 99.66 ± 0.31 | 88.01 + 2.47 | 87.01 ± 0.40 |
| Grass-trees | 73/657 | 99.08 ± 0.10 | 97.56 ± 0.18 | 100.00 ± 0.00 | 99.02 ± 0.10 | 99.28 ± 0.91 | 96.73 + 3.27 | 100.00 ± 0.00 |
| Grass-pasture-mowed | 2/26 | 100.00 ± 0.00 | 100.00 ± 0.00 | 88.54 ± 0.00 | 100.00 ± 0.00 | 90.63 ± 13.26 | 68.00 + 33.5 | 100.00 ± 0.00 |
| Hay-windrowed | 47/431 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.57 ± 0.60 | 94.68 + 2.29 | 99.77 ± 0.00 |
| Oats | 2/18 | 100.00 ± 0.00 | 100.00 ± 0.00 | 95.54 ± 0.00 | 100.00 ± 0.00 | 72.22 ± 20.79 | 66.67 + 27.4 | 100.00 ± 0.00 |
| Soybean-no till | 97/875 | 95.85 ± 0.08 | 98.29 ± 0.12 | 100.00 ± 0.20 | 95.94 ± 0.20 | 97.59 ± 0.97 | 84.25 + 3.09 | 96.90 ± 0.14 |
| Soybean-min till | 245/2210 | 98.63 ± 0.08 | 99.57 ± 0.05 | 88.44 ± 0.08 | 96.5 ± 0.08 | 99.11 ± 0.51 | 92.72 + 1.66 | 99.25 ± 0.07 |
| Soybean-clean | 59/534 | 91.56 ± 0.32 | 95.24 ± 0.23 | 93.28 ± 0.40 | 89.1 ± 0.40 | 98.52 ± 1.32 | 71.40 + 3.85 | 95.47 ± 0.22 |
| Wheat | 20/185 | 99.61 ± 0.25 | 98.97 ± 0.17 | 100.00 ± 0.00 | 100.00 ± 0.00 | 97.47 ± 1.46 | 94.51 + 5.45 | 100.00 ± 0.00 |
| Woods | 126/1139 | 96.14 ± 0.20 | 99.82 ± 0.00 | 99.91 ± 0.12 | 98.9 ± 0.12 | 99.55 ± 0.51 | 96.74 + 1.24 | 99.84 ± 0.03 |
| Buildings-Grass-Trees-Drives | 38/348 | 99.45 ± 0.09 | 99.02 ± 0.18 | 100.00 ± 0.00 | 97.91 ± 0.17 | 95.04 ± 3.20 | 77.84 + 7.96 | 100.00 ± 0.00 |
| Stone-Steel-Towers | 9/84 | 91.22 ± 0.80 | 83.69 ± 1.15 | 94.16 ± 1.24 | 85.64 ± 1.24 | 94.36 ± 6.10 | 75.00 + 16.17 | 93.67 ± 0.80 |
| OA | 1018/9231 | 95.82 ± 0.075 | 97.6 ± 0.039 | 93.18 ± 0.069 | 95.46 ± 0.063 | 98.29 ± 0.345 | 88.50 + 0.802 | 98.15 ± 0.036 |
| KA | 95.24 ± 0.084 | 97.26 ± 0.045 | 92.26 ± 0.079 | 94.81 ± 0.072 | 98.05 ± 0.394 | 86.86 + 0.907 | 97.89 ± 0.041 | |
| AA | 95.68 ± 0.094 | 96.28 ± 0.105 | 94.52 ± 0.168 | 94.65 ± 0.123 | 95.60 ± 0.649 | 83.80 + 3.993 | 97.73 ± 0.092 |
| Classes Name | Train/Test | VGG16 | Resnet50 | 3-DCNN | HybridSN | A2S2K | SF-Patch | DCFF-NET |
|---|---|---|---|---|---|---|---|---|
| Asphalt | 663/5968 | 99.49 ± 0.03 | 99.45 ± 0.03 | 99.76 ± 0.01 | 99.24 ± 0.03 | 99.91 ± 0.08 | 98.67 ± 0.58 | 99.89 ± 0.01 |
| Meadows | 1864/16,785 | 99.97 ± 0.01 | 99.98 ± 0.00 | 99.95 ± 0.01 | 99.98 ± 0.00 | 99.97 ± 0.02 | 99.86 ± 0.08 | 99.92 ± 0.01 |
| Gravel | 209/1890 | 99.77 ± 0.03 | 99.66 ± 0.03 | 99.85 ± 0.02 | 97.49 ± 0.09 | 99.80 ± 0.28 | 95.84 ± 1.23 | 100.00 ± 0.00 |
| Trees | 306/2758 | 98.10 ± 0.06 | 98.43 ± 0.04 | 99.32 ± 0.05 | 99.62 ± 0.03 | 99.96 ± 0.06 | 97.21 ± 0.67 | 99.17 ± 0.04 |
| Painted metal sheets | 134/1211 | 99.93 ± 0.03 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.97 ± 0.04 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| Bare Soil | 502/4527 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.83 ± 0.01 | 99.93 ± 0.06 | 99.74 ± 0.06 | 100.00 ± 0.00 |
| Bitumen | 133/1197 | 98.71 ± 0.11 | 98.63 ± 0.10 | 99.35 ± 0.10 | 96.98 ± 0.14 | 99.97 ± 0.04 | 95.41 ± 1.45 | 99.20 ± 0.06 |
| Self-Blocking Bricks | 368/3314 | 99.75 ± 0.02 | 99.96 ± 0.02 | 99.89 ± 0.01 | 99.76 ± 0.03 | 98.44 ± 1.13 | 97.34 ± 0.34 | 100.00 ± 0.00 |
| Shadows | 94/853 | 99.26 ± 0.08 | 99.14 ± 0.09 | 99.88 ± 0.00 | 99.89 ± 0.04 | 99.74 ± 0.21 | 98.59 ± 0.26 | 99.91 ± 0.05 |
| OA | 4273/38,503 | 99.68 ± 0.007 | 99.71 ± 0.007 | 99.85 ± 0.007 | 99.58 ± 0.004 | 99.81 ± 0.093 | 98.89 ± 0.164 | 99.86 ± 0.004 |
| KA | 99.58 ± 0.009 | 99.62 ± 0.009 | 99.80 ± 0.009 | 99.45 ± 0.005 | 99.75 ± 0.123 | 98.07 ± 0.235 | 99.82 ± 0.006 | |
| AA | 99.44 ± 0.013 | 99.47 ± 0.016 | 99.78 ± 0.014 | 99.20 ± 0.017 | 99.74 ± 0.103 | 98.53 ± 0.213 | 99.79 ± 0.011 |
| Classes Name | Train/Test | VGG16 | Resnet50 | 3-DCNN | HybridSN | A2S2K | SF-Patch | DCFF-NET |
|---|---|---|---|---|---|---|---|---|
| Brocoli_green_weeds_1 | 200/1809 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 98.78 ± 0.84 | 100.00 ± 0.00 |
| Brocoli_green_weeds_2 | 372/3354 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.91 ± 0.04 | 100.00 ± 0.00 |
| Fallow | 197/1779 | 100.00 ± 0.00 | 99.89 ± 0.02 | 99.96 ± 0.02 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.72 ± 0.13 | 100.00 ± 0.00 |
| Fallow_rough_plow | 139/1255 | 99.86 ± 0.03 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.92 ± 0.00 | 99.82 ± 0.15 | 99.84 ± 0.09 | 99.94 ± 0.03 |
| Fallow_smooth | 267/2411 | 99.88 ± 0.01 | 99.70 ± 0.03 | 99.88 ± 0.02 | 99.81 ± 0.02 | 99.95 ± 0.04 | 100.00 ± 0.00 | 99.96 ± 0.01 |
| Stubble | 395/3564 | 99.96 ± 0.02 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| Celery | 357/3222 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.63 ± 0.26 | 99.97 ± 0.00 |
| Grapes_untrained | 1127/10,144 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.98 ± 0.01 | 99.96 ± 0.01 | 99.95 ± 0.03 | 99.17 ± 0.54 | 99.99 ± 0.00 |
| Soil_vinyard_develop | 620/5583 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.97 ± 0.03 | 99.80 ± 0.03 | 100.00 ± 0.00 |
| Corn_senesced_green_weeds | 327/2951 | 99.60 ± 0.03 | 100.00 ± 0.00 | 99.81 ± 0.02 | 99.83 ± 0.04 | 99.94 ± 0.09 | 99.93 ± 0.05 | 100.00 ± 0.00 |
| Lettuce_romaine_4wk | 106/962 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.51 ± 0.05 | 100.00 ± 0.00 | 100.00 ± 0.00 | 98.96 ± 0.75 | 99.24 ± 0.08 |
| Lettuce_romaine_5wk | 192/1735 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.91 ± 0.03 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| Lettuce_romaine_6wk | 91/825 | 100.00 ± 0.00 | 99.88 ± 0.00 | 99.89 ± 0.04 | 99.90 ± 0.05 | 99.96 ± 0.06 | 99.88 ± 0.13 | 100.00 ± 0.00 |
| Lettuce_romaine_7wk | 107/963 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.61 ± 0.04 | 99.61 ± 0.55 | 99.79 ± 0.21 | 100.00 ± 0.00 |
| Vinyard_untrained | 726/6542 | 99.99 ± 0.00 | 99.82 ± 0.02 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.85 ± 0.18 | 98.67 ± 0.73 | 100.00 ± 0.00 |
| Vinyard_vertical_trellis | 180/1627 | 99.82 ± 0.02 | 100.00 ± 0.00 | 99.71 ± 0.03 | 99.77 ± 0.03 | 100.00 ± 0.00 | 99.38 ± 0.63 | 100.00 ± 0.00 |
| OA | 5403/48,726 | 99.95 ± 0.003 | 99.96 ± 0.003 | 99.95 ± 0.002 | 99.95 ± 0.003 | 99.95 ± 0.032 | 99.48 ± 0.085 | 99.98 ± 0.002 |
| KA | 99.95 ± 0.003 | 99.95 ± 0.003 | 99.95 ± 0.002 | 99.95 ± 0.003 | 99.94 ± 0.036 | 99.43 ± 0.097 | 99.98 ± 0.003 | |
| AA | 99.94 ± 0.003 | 99.96 ± 0.002 | 99.92 ± 0.004 | 99.92 ± 0.004 | 99.94 ± 0.039 | 99.59 ± 0.105 | 99.94 ± 0.006 |
| Datasets | IP | PU | SA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Filling Method | 10% | 20% | 30% | 10% | 20% | 30% | 10% | 20% | 30% |
| NotFill | 73.74 | 80.73 | 84.62 | 92.38 | 93.62 | 94.55 | 92.34 | 93.72 | 94.07 |
| InnerFill | 76.18 | 81.89 | 84.37 | 91.90 | 93.81 | 94.44 | 92.09 | 94.17 | 94.73 |
| BothFill | 78.21 | 84.05 | 86.68 | 92.56 | 94.11 | 94.73 | 93.00 | 94.24 | 95.14 |
| Dataset | Train Percentage | NB | KNN | RF | MLP | 1DCNN | SF-Pixel | VGG16 | Resnet50 | DCFF-NET |
|---|---|---|---|---|---|---|---|---|---|---|
| Indian pines | 5 | 50.81 | 68.96 | 69.63 | 64.19 | 63.26 | 55.21 | 73.03 | 62.11 | 69.84 |
| 7 | 53.75 | 72.04 | 71.74 | 67.32 | 65.37 | 74.84 | 73.43 | 65.03 | 73.51 | |
| 10 | 58.05 | 74.76 | 75.87 | 69.20 | 68.44 | 75.27 | 77.88 | 70.90 | 78.21 | |
| 15 | 61.83 | 76.86 | 78.82 | 73.47 | 69.21 | 81.80 | 79.45 | 75.12 | 79.88 | |
| 20 | 66.14 | 78.12 | 80.75 | 74.18 | 74.22 | 82.91 | 83.44 | 75.84 | 84.05 | |
| 25 | 69.55 | 79.23 | 82.11 | 75.25 | 75.27 | 83.94 | 84.39 | 81.62 | 84.41 | |
| 30 | 71.58 | 79.98 | 83.17 | 76.47 | 75.43 | 85.49 | 85.18 | 82.13 | 86.68 | |
| Pavia University | 0.5 | 72.31 | 77.33 | 78.03 | 79.12 | 82.46 | 75.90 | 78.09 | 75.06 | 78.40 |
| 1 | 76.12 | 79.54 | 81.38 | 81.21 | 84.40 | 78.16 | 81.95 | 80.69 | 83.67 | |
| 3 | 80.42 | 83.66 | 85.54 | 87.58 | 89.14 | 81.09 | 88.53 | 87.75 | 89.64 | |
| 5 | 82.33 | 85.32 | 87.23 | 89.18 | 90.36 | 84.82 | 89.70 | 89.08 | 90.97 | |
| 7 | 84.31 | 86.04 | 88.20 | 91.08 | 90.75 | 86.24 | 90.95 | 90.54 | 91.53 | |
| 10 | 85.85 | 87.53 | 89.52 | 92.02 | 91.43 | 90.71 | 91.59 | 91.51 | 92.56 | |
| 20 | 89.36 | 89.34 | 91.04 | 92.37 | 93.07 | 92.77 | 92.19 | 93.23 | 94.11 | |
| 30 | 90.91 | 90.28 | 91.91 | 92.70 | 93.97 | 93.95 | 92.83 | 93.44 | 94.73 | |
| Salinas | 0.5 | 67.87 | 81.42 | 82.16 | 81.53 | 84.61 | 82.06 | 82.87 | 81.17 | 85.01 |
| 1 | 77.42 | 84.14 | 85.50 | 83.72 | 87.25 | 82.06 | 87.33 | 84.98 | 87.13 | |
| 3 | 84.69 | 87.61 | 89.39 | 88.90 | 89.51 | 87.13 | 89.85 | 88.03 | 90.03 | |
| 5 | 86.19 | 88.91 | 90.13 | 89.20 | 90.17 | 87.94 | 90.17 | 90.88 | 91.42 | |
| 7 | 87.18 | 88.97 | 90.74 | 89.91 | 90.27 | 88.40 | 91.79 | 91.07 | 92.19 | |
| 10 | 88.22 | 90.03 | 91.31 | 90.41 | 91.50 | 90.00 | 92.12 | 92.35 | 93.00 | |
| 20 | 90.21 | 91.38 | 92.60 | 91.34 | 92.07 | 91.62 | 92.55 | 93.80 | 94.24 | |
| 30 | 91.13 | 92.24 | 93.39 | 92.31 | 92.58 | 92.71 | 94.25 | 94.62 | 95.14 |
| Dataset | Modules | Exp 1 | Exp 2 | Exp 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SIE | DSFE | OA | KA | AA | OA | KA | AA | OA | KA | AA | |
| Indian Pines | √ | -- | 84.72 ± 0.77 | 82.56 ± 0.89 | 81.13 ± 1.58 | 81.94 ± 1.28 | 79.38 ± 1.47 | 77.49 ± 2.66 | 75.00 ± 1.90 | 71.46 ± 2.19 | 66.66 ± 4.21 |
| -- | √ | 84.92 ± 0.63 | 82.82 ± 0.71 | 83.05 ± 1.98 | 81.77 ± 0.89 | 79.22 ± 1.02 | 77.10 ± 2.64 | 74.04 ± 1.92 | 70.34 ± 2.19 | 66.44 ± 2.10 | |
| √ | √ | 86.06 ± 0.37 | 84.12 ± 0.41 | 84.41 ± 1.07 | 83.46 ± 0.62 | 81.01 ± 0.71 | 79.11 ± 2.87 | 77.56 ± 0.95 | 74.22 ± 1.09 | 69.9 ± 2.87 | |
| Pavia University | √ | -- | 94.18 ± 0.12 | 92.26 ± 0.16 | 91.88 ± 0.25 | 93.36 ± 0.28 | 91.17 ± 0.37 | 90.89 ± 0.38 | 92.28 ± 0.13 | 89.73 ± 0.18 | 89.53 ± 0.37 |
| -- | √ | 94.44 ± 0.15 | 92.63 ± 0.20 | 92.71 ± 0.22 | 93.71 ± 0.22 | 91.66 ± 0.29 | 91.70 ± 0.27 | 91.61 ± 2.94 | 88.92 ± 3.73 | 89.60 ± 1.63 | |
| √ | √ | 94.58 ± 0.10 | 92.67 ± 0.14 | 92.35 ± 0.17 | 93.85 ± 0.18 | 91.83 ± 0.24 | 91.51 ± 0.31 | 92.65 ± 0.29 | 90.23 ± 0.39 | 89.91 ± 0.39 | |
| Salinas | √ | -- | 95.07 ± 0.13 | 94.51 ± 0.14 | 97.32 ± 0.07 | 94.25 ± 0.10 | 93.59 ± 0.11 | 96.77 ± 0.10 | 92.89 ± 0.18 | 92.08 ± 0.20 | 95.76 ± 0.17 |
| -- | √ | 94.92 ± 0.22 | 94.34 ± 0.25 | 97.37 ± 0.15 | 94.06 ± 0.12 | 93.39 ± 0.13 | 96.82 ± 0.13 | 92.71 ± 0.19 | 91.88 ± 0.21 | 95.93 ± 0.28 | |
| √ | √ | 95.19 ± 0.15 | 94.64 ± 0.17 | 97.51 ± 0.09 | 94.44 ± 0.17 | 93.81 ± 0.19 | 97.02 ± 0.16 | 92.94 ± 0.29 | 92.13 ± 0.32 | 95.98 ± 0.18 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Chen, Y.; Wang, Y.; Wang, X.; Wang, X.; Xiang, Z. DCFF-Net: Deep Context Feature Fusion Network for High-Precision Classification of Hyperspectral Image. Remote Sens. 2024, 16, 3002. https://doi.org/10.3390/rs16163002
Chen Z, Chen Y, Wang Y, Wang X, Wang X, Xiang Z. DCFF-Net: Deep Context Feature Fusion Network for High-Precision Classification of Hyperspectral Image. Remote Sensing. 2024; 16(16):3002. https://doi.org/10.3390/rs16163002
Chicago/Turabian StyleChen, Zhijie, Yu Chen, Yuan Wang, Xiaoyan Wang, Xinsheng Wang, and Zhouru Xiang. 2024. "DCFF-Net: Deep Context Feature Fusion Network for High-Precision Classification of Hyperspectral Image" Remote Sensing 16, no. 16: 3002. https://doi.org/10.3390/rs16163002
APA StyleChen, Z., Chen, Y., Wang, Y., Wang, X., Wang, X., & Xiang, Z. (2024). DCFF-Net: Deep Context Feature Fusion Network for High-Precision Classification of Hyperspectral Image. Remote Sensing, 16(16), 3002. https://doi.org/10.3390/rs16163002






