Abstract
Synthetic Aperture Radar (SAR) imagery presents significant advantages for observing ocean surface winds owing to its high spatial resolution and low sensitivity to extreme weather conditions. Nevertheless, signal noise poses a challenge, hindering precise wind retrieval from SAR imagery. Moreover, traditional geophysical model functions (GMFs) often falter, particularly in accurately estimating high wind speeds, notably during extreme weather phenomena like tropical cyclones (TCs). To address these limitations, this study proposes a novel hybrid model, CMOD-Diffusion, which integrates the strengths of GMFs with data-driven deep learning methods, thereby achieving enhanced accuracy and robustness in wind retrieval. Based on the coarse estimation of wind speed by the traditional GMF CMOD5.N, we introduce the recently developed data-driven method Denoising Diffusion Probabilistic Model (DDPM). It transforms an image from one domain to another domain by gradually adding Gaussian noise, thus achieving denoising and image synthesis. By introducing the DDPM, the noise from the observed normalized radar cross-section (NRCS) and the residual of the GMF methods can be largely compensated. Specifically, for wind speeds within the low-to-medium range, a DDPM is employed before proceeding to another CMOD iteration to recalibrate the observed NRCS. Conversely, a posterior-placed DDPM is applied after CMOD to reconstruct high-wind-speed regions or TC-affected areas, with the prior information from regions characterized by low wind speeds and recalibrated NRCS values. The efficacy of the proposed model is evaluated by using Sentinel-1 SAR imagery in vertical–vertical (VV) polarization, collocated with data from the European Centre for Medium-Range Weather Forecasts (ECMWF). Experimental results based on validation sets demonstrate significant improvements over CMOD5.N, particularly in low-to-medium wind speed regions, with the Structural Similarity Index (SSIM) increasing from 0.76 to 0.98 and the Root Mean Square Error (RMSE) decreasing from 1.98 to 0.63. Across the entire wind field, including regions with high wind speeds, the validation data obtained through the proposed method exhibit an RMSE of 2.39 m/s, with a correlation coefficient of 0.979.
1. Introduction
Tropical cyclones (TCs), regarded as being among the most devastating natural disasters, bring formidable wind speeds and heavy precipitation, thus inflicting significant economic losses on coastal regions. Synthetic Aperture Radar (SAR) is extensively employed for monitoring maritime conditions, such as wind fields [1,2], surface waves [3,4,5], oil spills [6], and vessel detection [7], by receiving radar echoes. Additionally, spaceborne SAR has the capability to observe TCs free from danger and extreme sea states with high resolution. Consequently, it has the potential to replace conventional on-scene observations for retrieving the wind information of TCs with the aim of timely preparation and reducing the impact of these disasters.
Wind field acquisition for TCs is a special case of traditional SAR wind retrieval. Referring to the principle of the wind retrieval methods, they can be categorized into two types, geophysical model functions (GMFs) and data-driven retrieval methods. The main idea of GMFs is to relate the normalized radar cross section (NRCS) to the wind field, incidence angle, and azimuth angle. GMFs mainly indicate the CMOD family in C-band SAR. To date, many empirical functions have been proposed. For co-polarized SAR (VV and HH) images, CMOD4 [8], CMOD5.N [9], and CMOD7 [10] have been proposed in turn. The above methods have been proven to be successful in retrieving low-to-moderate wind speeds (<25 m/s) in ordinary weather. However, the accuracy of CMOD series methods is highly related to the quality of the received NRCS. And the measured NRCS is affected by many noise sources, which can reduce the accuracy of wind retrieval. Moreover, when the wind speed is high, especially in extreme weather, the CMOD methods have residuals; hence, accuracy is not guaranteed (error of about 5 m/s). As cross-polarization (VH and HV polarization) has low sensitivity to noise with increasing wind speed [11,12], multiple cross-polarized GMF-based wind retrieval methods have been presented, like C-P2O [12], C-2POD [13], C-3PO [14], and MS1A [15]. On the other hand, cross-polarized GMFs suffer from weak sea-surface backscattering roughness. This is caused by different noise-equivalent sigma zero (NESZ) in different sub-swaths in interferometric-wide (IW) and extra-wide (EW) modes.
Deep learning (DL) models, due to their great generalization ability, are widely used in retrieval tasks in a data-driven way. In recent years, many studies have focused on using deep-learning algorithms for wind retrieval and storm analysis. Boussioux et al. [16] pioneered the integration of a multi-modal DL framework, amalgamating diverse data sources to enhance hurricane forecasting accuracy. Another endeavor is leveraging high-resolution Sentinel-1 data by the DL approach to enhance the precision of TC intensity detection [17]. Subsequent advancements have delved into SAR wind speed retrieval [18,19], encompassing the utilization of neural networks for sea surface wind speed inversion from SAR data. With the development of Convolutional Neural Networks (CNNs), they are tailored for SAR feature extraction to estimate TCs [20,21]. To generate the texture of TCs with high quality, Han et al. [22] proposed a dual-level TC wind retrieval method using generative adversarial networks (GANs). These methods demonstrate the great potential of DL in SAR wind field retrieval. However, data-driven DL methods in most cases can be regarded as black-box models that lack explainability. Moreover, in the context of wind retrieval, the complex nonlinear nature of the problem poses a significant challenge, compounded by the limitation of the model to encompass the entire domain due to inherent biases in the dataset. In addition to wind retrieval tasks, deep learning methods are also employed for SAR image denoising. Speckle noise, an artifact characteristic of SAR images due to the coherent nature of radar waves, adversely affects image quality and compromises the accuracy of wind retrieval. Several studies have explored the application of neural networks to address this signal noise issue. For instance, SAR-CNN [23] utilizes convolutional neural networks (CNNs) to predict and reduce additive noise in SAR images. Building on this, M.V. Perera et al. [24] developed an over-complete CNN architecture specifically tailored for SAR image denoising tasks, restricting the receptive field to enhance effectiveness. Recently, Denoising Diffusion Probabilistic Models (DDPMs) have emerged and reached the state of art in generative tasks, outperforming the GAN-based generative models [25,26]. Parameterized by a Markov chain, DDPM gradually adds noise to a clean image until the image is totally destroyed. During the training stage, the neural network in DDPM can learn the distribution of noise. Consequently, a randomly sampled Gaussian noise can transferred to a sample. Based on the principle, DDPM can be used in both denoising tasks and generative tasks. In the SAR despeckling task, Malsha et al. [27] pioneered the use of DDPMs to recover clean SAR images.
Figure 1 illustrates an instance of tropical cyclone (TC) retrieval outcomes generated by the CMOD5.N model. Upon assessing the performance of the conventional CMOD approach, it is observed that below speeds of 15 m/s, CMOD5.N demonstrates relatively high retrieval precision, albeit with a minor presence of outliers, evident in Figure 1a. However, as wind speeds escalate beyond 15 m/s, the precision steadily diminishes, culminating in the model becoming entirely ineffective at 20 m/s. The CMOD functions are fitted under moderate to low wind speeds under 20 m/s, although there are a few TC conditions [28]. Additionally, surface roughness change and rain cells caused by TCs severely affect the quality of the SAR signal received [29]. Therefore, the accuracy of wind field inversion, encompassing tropical cyclones, is constrained by both data quality and inherent model limitations. Specifically, the CMOD series model exhibits primarily data noise below 15 m/s, while encountering outright model failure beyond this threshold. The conclusion is consistent with the findings from [9].
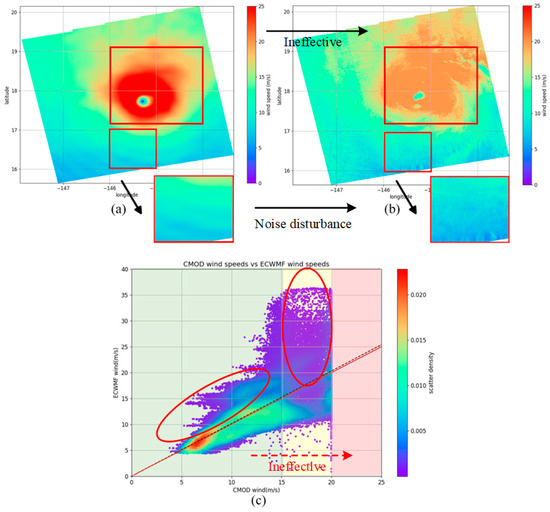
Figure 1.
An example of TC wind retrieval by a CMOD series method (CMOD5.N). (a,b) ECMWF wind speed and CMOD5.N-predicted wind speed; (c) scatterplots of CMOD5.N prediction vs. ERA5 for wind speed (green: high precision; yellow: precision drop; red: ineffective).
Based on the preceding research and addressing the identified issues, we introduce a novel approach combining the traditional CMOD method with a data-driven strategy to leverage their strengths and mitigate error sources. By integrating prior knowledge into CMOD series methods, we incorporate a data-driven DDPM to handle residual unmodeled elements. Specifically, we utilize a front-placed DDPM to denoise SAR data, thereby enhancing the accuracy of the data sources for wind retrieval. The CMOD method is then applied for primary wind retrieval, while a posterior-placed DDPM is employed to reconstruct detailed information for initially invalidated sections. Below, we demonstrate the effectiveness of the proposed method:
- The hybrid way of CMOD model and DDPM for wind retrieval has better explainability and robustness and is effective in large-wind-speed ranges, even TCs.
- The utilization of DDPMs before and after the CMOD series method can reduce the residuals of wind retrieval from both noises and the GMF itself. Validated and trained on the ECMWF data, the precision improvement is verified in an experiment.
- Compared with traditional data-driven methods, the proposed CMOD-Diffusion can strike a balance among model efficiency, accuracy, and the conversion of training samples.
The remaining part of the paper is organized as follows: Section 2 gives the basic illustration of the dataset used in this paper, including the observed Sentinel-1 images, collocated wind information, and so on. The methodology and principle of the proposed CMOD-Diffusion model are discussed in Section 3. We introduce and discuss the experimental configuration, evaluation metric, and results in Section 4 and Section 5 to validate the superiority of our method. Eventually, the conclusions are given as a summary in Section 6.
2. Dataset Description
2.1. Sentinel-1 SAR Image
Sentinel-1, launched by the European Space Agency (ESA) is a satellite carrying a C-band sensor. There are four types of operation modes for Sentinel-1: the Stripmap (SM) mode, the Wide Swath (IW) mode, the Extra Wide Swath (EW) mode, and the Wave mode (WV) mode. The TC SAR images are mostly captured with IW and EW modes, because of their large swaths. The SAR images in VV polarization in our dataset used for training and testing were collected from Sentinel-1A/B. Specifically, we extracted 300 SAR images with image dimensions of 256 × 256 cropped from the original large-scale images under tropical cyclone (TC) conditions from 2021 to 2023. These images are archived on the Copernicus Open Access Hub website (scihub.copernicus.eu, accessed on 20 July 2024) and the CyclObs website (cyclobs.ifremer.fr, accessed on 20 July 2024). Additionally, we gathered another 150 SAR images captured under normal weather conditions. This augmentation enriches our dataset and subsequently enhances the robustness of our training model. Figure 2 displays the geographical distribution of the SAR image data used in part.
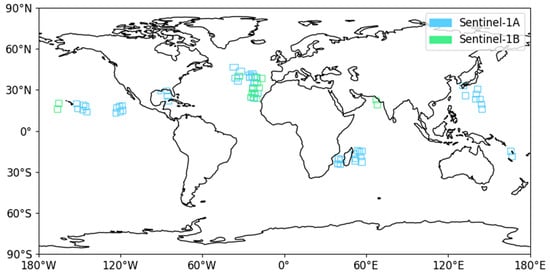
Figure 2.
Geographical locations of 45 (1/10 of all for better visualization) Sentinel-1A/B images including TC situations. The blue and green boxes represent the SAR images from Sentinel-1A and Sentinel-1B, respectively.
2.2. ECMWF Data
The ECMWF (European Centre for Medium-Range Weather Forecasts) offers a range of real-time meteorological and oceanographic products, covering the period from 1950 up to now. The fifth generation of the ECMWF product, ERA5, offers a dataset with a resolution of and an hourly temporal resolution. In the study, wind information from ERA5 was selected at the closest time to the SAR data acquisition, and SAR data were sampled to the same resolution as ERA5. ECMWF wind vectors have been widely applied in wind retrieval research as references due to their great conformity with the actual wind field [22,30]. In this study, the ERA5 dataset is utilized to train and validate the model. Additionally, to serve the process of training, according to the wind speed above 15 m/s or not, we generated the mask for the implementation of different retrieval strategies. Figure 3 below shows the wind speed distribution of the ERA-5 dataset.
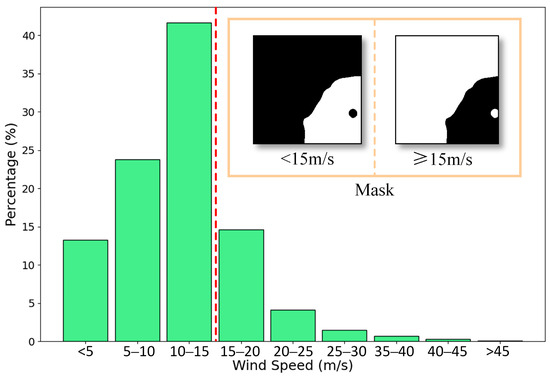
Figure 3.
The distribution of wind speeds in the dataset.
3. Methodology
The proposed method can be regarded as a hybrid of the conventional GMF and the data-driven algorithm DDPM. In this section, the principles of the GMF and DDPM will be discussed in turn. Then, how GMFs and DDPMs are combined to achieve more robust and precise wind retrieval will be briefly introduced.
3.1. GMFs
The fundamental principle underlying the Geophysical Model Function (GMF) is that alterations in wind speed lead to corresponding variations in the received backscatter, which can exhibit either Bragg or non-Bragg scattering. The CMOD series methods, as the representatives of GMFs, are developed gradually for wind retrieval in the C-band frequency range. Among the series of CMOD functions developed, notable ones include CMOD4, CMOD-IFR2, CMOD5, and CMOD5.N, and more recently, a newer function, CMOD7, has been proposed as a potential successor to CMOD5.N. However, CMOD7 has primarily been utilized in conjunction with scatterometer data, and its suitability for SAR data in the C-band remains to be fully validated.
The general form of the CMOD formula offers an empirical functional relationship that describes the dependence of Normalized Radar Cross Section (NRCS) on wind speed , wind direction, and incidence angle , which is provided as follows:
where is the angle between wind direction and the scatterometer azimuth look angle, the coefficient shapes the terms , and p is a constant parameter. B0 is the dominant term to set the speed scale. and are the two harmonics related to wind direction. Among them, determines the asymmetry level of upwind–crosswind, and helps resolve 180 ambiguity in wind direction. The above formula (1) represents the CMOD forward equation, which allows us to acquire based on known wind information. Additionally, we introduce a reverse function denoted by , enabling us to obtain wind speed with a given .
In previous studies, such as those conducted by Zhang et al, wind speed retrieval results were compared by using the above-mentioned CMOD functions along the U.S. coastlines. The findings of these studies indicated that CMOD5.N demonstrated the most optimal performance. Therefore, we chose CMOD5.N for the primary wind speed retrieval in our method. The specific value of the parameters can be found in [31].
3.2. DDPMs
The Denoising Diffusion Probabilistic Models (DDPM) is an image synthesis method whose main idea is to add a random noise vector in T diffusion steps, and during the reverse diffusion process, the noise vector is denoised by a noise predictor until it becomes the desired image . The role of the reverse diffusion process varies based on the specific application. In this study, when the task pertains to calibration, the backpropagation process serves as a mechanism for denoising the initial image. Conversely, when the task involves image generation, the reverse process facilitates the process of synthesizing texture in the high-speed region.
For the real data distribution , each step of diffusion, which comprises a total of T steps, adds Gaussian noise to the data obtained from the previous step as follows:
where is the variance schedule between 0 and 1. Under the variance schedule, every step of diffusion generates a denoised sample . The whole process is a Markov Chain [25]:
Based on the Markov Chain, at any arbitrary time step t can be sampled from , by setting and :
The reverse diffusion process is to train a neural network to predict the parameter and . The learning objective given by Ho et al. [25] is derived by considering the variational lower bound as
is to compute the KL divergence between distributions of and to train the neural network. With known ,
The loss of the DDPM can be simplified as the below equation, and the detailed derivation process can also be found in [32].
3.3. CMOD-DDPM
The proposed CMOD-DDPM method consists of two parts referring to the applied positions of DDPMs and their tasks. The DDPM preprocessing part is responsible for calibrating the CMOD5.N model’s input at low and medium wind speeds. The DDPM postprocessing part’s task is to retrieve the high speed in the high-speed range. How CMOD-DDPM assigns DDPM tasks and the way the CMOD series of methods and DDPM are hybridized are illustrated in below Figure 4.
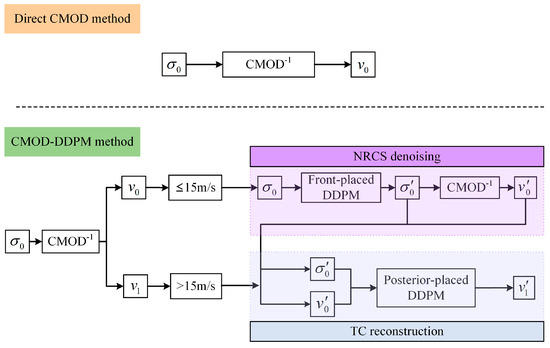
Figure 4.
The workflow of the proposed CMOD-DDPM compared with the direct CMOD method.
Like the direct CMOD method, the CMOD-DDPM method reverses the CMOD function to acquire the wind speed matrix first. Then, we mask the matrix by a threshold of 15 m/s. With speeds under and above 15 m/s, different strategies are applied to improve the performance of wind retrieval. For speed values under 15 m/s, NRCS is denoised to decrease the error of the CMOD source. For speed values beyond 15 m/s, which belong to high-wind-speed regions/TC regions, the DDPM is responsible for reconstruction based on the retrieval result in low–medium-wind-speed regions, denoised NRCS, and original NRCS in high-speed regions. After combining the retrieved wind speed in these two cases, the wind field information in the whole SAR image is obtained.
The network utilized for both tasks follows a U-net [32] architecture, which is illustrated in Figure 5. The U-net architecture follows a symmetric U-shape encoder–decoder structure and incorporates skip connections between corresponding layers in the encoder and decoder to enhance the gradient flow. There are 15 blocks in the network, which consist of convolutional residual blocks, attention blocks, and downsampling blocks. First, the original image and the image in timestep t are concatenated and input into the model through the convolutional layer. Timestep t after the transformer sinusoidal positional encoding [33] is transferred to the embedding . Additionally, self-attention blocks like those in [26] at multiple resolutions are utilized, and upsampling and downsampling are achieved by BigGAN residual blocks [34]. Eventually, the noise at timestep t − 1 can be predicted after the convolution layer in the network.
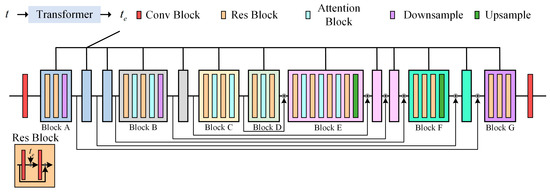
Figure 5.
Overview of U-net network architecture used in CMOD-DDPM.
Referring to the position of the DDPMs related to the CMOD function, they can be divided into the front-placed DDPM and the posterior-placed DDPM.
Portabella et al. [35] concluded that wind retrieval errors come from the observation error and the background error from the maximum likelihood estimate. When the wind speed is low, the error is expressed as the former.
where the observation NRCS equals the sum of the reference NRCS and the error . The main task of the front-placed DDPM is to recalibrate close to . We used the ECMWF wind-speed matrix as the input of the forward CMOD function to obtain a reference NRCS as the training target, so that after DDPM recalibration becomes , which is close to , achieving a more precise retrieval result .
Signal noise manifests as “speckle”-like points with abrupt changes in wind speed retrieval tasks. The front-placed DDPM is utilized for despeckling to address challenges posed by signal noise. The front-placed DDPM is predicated upon a forward and reverse diffusion process, characterized by a T-step diffusion progression, as elucidated in Figure 6. During the forward process, the reference image is gradually converted into the observed NRCS by gradually introducing Gaussian noise. The essence of the training regimen lies in refining the parameters of the noise predictor , thereby enhancing its efficacy in delineating the inverse mapping from the observed image space back to the pristine reference domain.
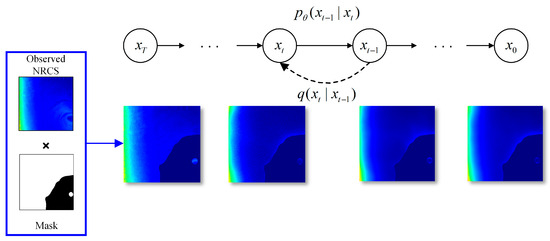
Figure 6.
Overview of forward and reverse diffusion process of front-placed DDPM.
Algorithm 1 summarizes the training and inference procedure of the front-placed DDPM. During the training stage, the masked observed images and their reference image are concatenated to train the front-placed DDPM in T diffusion steps. During the inference stage, the U-net noise predictor according to time step t determines the noise in every diffusion step, thus recovering the reference image.
| Algorithm 1: Training and inference of front-placed DDPM |
| Training stage Input: Observed image and reference image pairs |
|
Input: Observed image
|
After wind retrieval in the region below 15 m/s, the posterior-placed DDPM is responsible for reconstructing the wind field above 15 m/s, a task that proves ineffective for GMF methods, as shown in Figure 1. When the wind speed exceeds 15 m/s, the error source in wind retrieval emanates from the background, i.e., the retrieval method itself. The DDPM, being a general method with demonstrated efficacy in image synthesis and reconstruction, is employed to address this challenge. To mitigate the variability inherent in filling large uncertain regions, diverse information inputs are integrated into the network. Specifically, we concatenate SAR imagery with calibrated wind speeds (below 15 m/s) to furnish additional prior information, rather than treating these elements in isolation. Furthermore, the network is trained to discern the relationship between the recalibrated NRCS and the already retrieved regions, thereby extending the retrieval pattern of the CMOD series of methods to higher wind speeds. As it is analogous to the front-placed DDPM (with only input and output distinctions), the detailed algorithmic flow of the posterior-placed DDPM is not enumerated herein. It is worth mentioning that the front-placed DDPM and the posterior-placed DDPM do not share parameters and are trained separately. The various utilization modes of the network are delineated in below Figure 7.
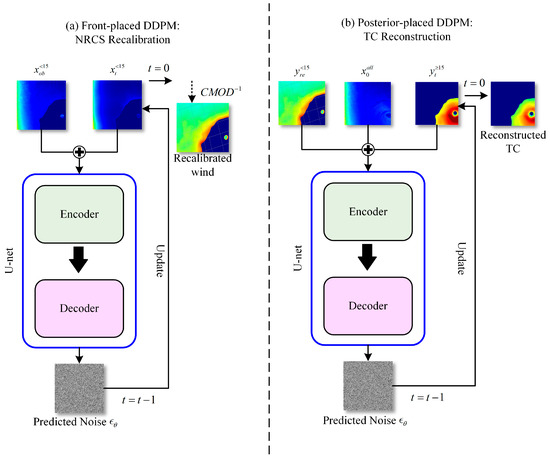
Figure 7.
The comparison of U-net’s inputs and outputs for (a) front-placed DDPM and (b) posterior-placed DDPM.
4. Experimental Results
4.1. Evaluation Metric
We chose commonly used evaluation indicators for image quality to compare the performance between traditional CMOD series methods and the proposed CMOD-DDPM algorithm. These indicators, including the structural similarity index metric (SSIM), the peak signal-to-noise ratio (PSNR), the root mean square error (RMSE), and the correlation coefficient (R), can both evaluate the retrieval quality of low–medium-range wind and TC reconstruction quality.
The SSIM can be used to evaluate the degree of similarity between real wind-speed vectors and wind vectors after the retrieval method has been applied. The metric compares two images from the perspectives of luminance, contrast, and structure [36]. The closer it is to 1, the better the inversion of the wind-speed matrix. The SSIM is formulated as follows:
The PSNR measures the ratio between the maximum possible signal and corrupting noise, and the RMSE indicates the difference between the corresponding values predicted by a model and the actual values.
where MAX is the maximum value in image x. Before calculating these indicators, the values in the image are normalized. Apart from the above indicators, R is used to measure the degree of linear correlation:
4.2. Experimental Configuration
Our experiments were carried out on a server with two NVIDIA RTX3060 GPUs, with a total memory of 32 GB, Python 3.8, and CUDA 11.2. The network was trained for 25 k iterations, and the weights were initialized with pre-trained ImageNet weights from [26].
For the DDPMs, we set the total number of timesteps T = 1000. During the model training stage, 450 SAR images and collocated wind field images were split into training and validation sets, in a ratio of 0.8 to 0.2. Additionally, we added slight random gamma noise in the NRCS image to avoid overfitting and improve the robustness of the model facing more noise. The learning rates for both the front-placed DDPM and the posterior-placed DDPM were set to 1 × 10−4. The values after convergence dropped to 1 × 10−5 to fine-tune models with better performance.
4.3. Front-Placed DDPM
To investigate the performance of the CMOD-DDPM method at different wind speeds, we first performed an analysis of the front-placed DDPM in a TC case study with wind speeds below 15 m/s. As mentioned in Section 3.1, the principle of the front-placed DDPM is to recalibrate NRCS in VV polarization to increase the precision of wind retrieval. We compare the NRCS before and after recalibration with the reference NRCS, which is visualized in Figure 8a–c. In Figure 8b, the observed NRCS has disturbing noise which is the main reason for the drop in CMOD series methods’ wind retrieval precision. After calibration, these noise speckles disappear, and the distribution of NRCS intensity is very close to the reference NRCS. Figure 8d,e compare the NRCS before and after recalibration with the reference NRCS in the form of scatterplots. The number of off-axis data points decreases significantly, and the data points diverging around the diagonal are also converging more tightly.
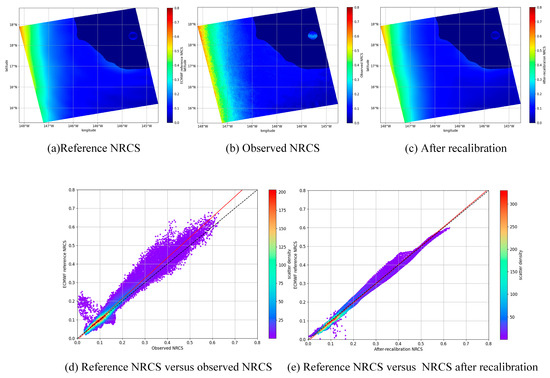
Figure 8.
(a) The reference NRCS from the ECMWF wind matrix after the CMOD5.N forward function has been applied; (b) the observed NRCS; (c) the observed NRCS after recalibration by Front-DDPM; (d) scatterplot between the reference NRCS and the observed NRCS; (e) scatterplot between the reference NRCS and NRCS after recalibration.
After recalibration using the front-placed DDPM, we conducted a validation of the recalibrated results obtained with CMOD5.N, comparing them with the ECMWF wind matrix. Figure 9a–c illustrate the CMOD wind retrieval results, the ECMWF wind matrix, and the wind matrix after front-placed DDPM calibration, respectively. While the CMOD series methods achieve a certain level of precision in wind retrieval, it is evident that noise speckles introduce disturbances, resulting in an inability to reconstruct the eye of the storm. Conversely, the front-placed DDPM component of the proposed method effectively enhances the low-quality SAR data and aligns the wind retrieval results more closely with those of the ECMWF. However, some details of the wind field may remain incompletely inverted.
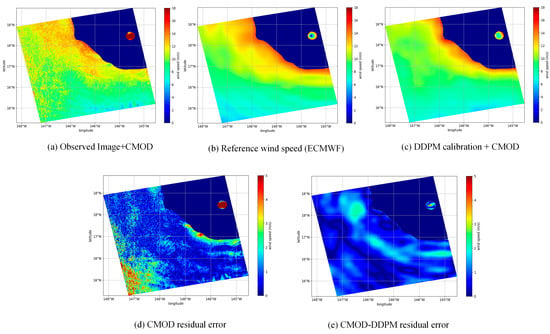
Figure 9.
The comparison between the retrieval results of the original SAR image and those of the DDPM-recalibrated SAR image at low wind speeds (below 15 m/s). (a) The observed image input to CMOD directly; (b) the ECMWF reference wind speed; (c) the observed image after the front-placed DDPM has been applied; (d) the residual between the retrieval result of the original image and the ECWMF reference wind speed; (e) the residual between the retrieval result of CMOD-DDPM and the ECMWF reference wind speed.
The front-placed DDPM is trained by the loss in Formula (8), learning to recalibrate NRCS as the input of CMOD. The metrics to evaluate the recalibration performance include RMSE, PSNR, SSIM, and R, as mentioned in Section 4.1. The metrics comparison using the traditional CMOD5.N before and after the front-placed DDPM on the validation set is shown in Table 1. With the recalibration of the front-placed DDPM, the retrieval results for speeds below 15 m/s are significantly improved.

Table 1.
Comparison of results obtained by using CMOD before and after front-placed DDPM has been applied. ↑: higher is better. ↓: lower is better.
4.4. Posterior-Placed DDPM
In this section, we directly output and visualize not only the posterior-placed DDPM wind speeds for wind speeds above 15 m/s but also the retrieval wind-speed results in the whole region obtained by the CMOD-DDPM method. The results of the proposed method in four cases are shown in Figure 10. Referring to the results of four cases, CMOD5.N’s retrieval results in low-speed regions are relatively convincing without considering noise speckles, but when the wind speed is above 15 m/s, the method becomes ineffective. In comparison, the proposed method predicts the wind speeds with high precision, and the TC features can be reconstructed accurately by the posterior-placed DDPM learning from the training set. In addition, due to the design of the input of the posterior-placed DDPM, the masked wind matrix in the low-speed region and NRCS provide adequate prior information for reconstruction, avoiding the discontinuity between the low-speed region and the high-speed region simultaneously.
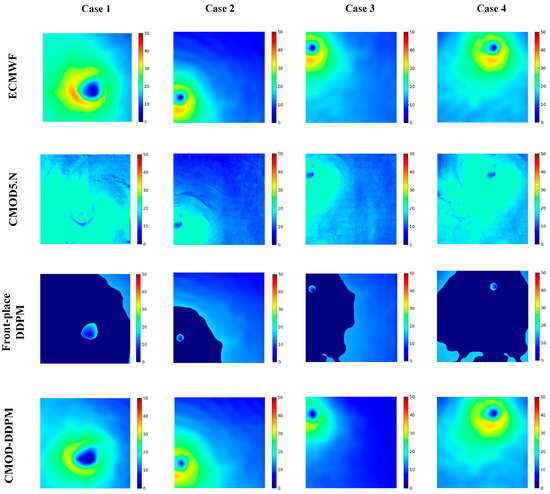
Figure 10.
Comparisons of CMOD-DDPM-reconstructed Sentinel 1 SAR wind speeds with ECMWF and CMOD wind speeds. From top to bottom: ECMWF, CMOD5.N retrieval result, front-placed DDPM retrieval result, and final CMOD-DDPM wind speeds. From left to right: four cases.
Table 2 summarizes the metrics of the above four cases using the traditional CMOD method and the proposed CMOD-DDPM. In all four cases, the indicators show improvement to different degrees after the introduction of the DDPM.

Table 2.
Comparison of metrics using CMOD directly and using CMOD-DDPM method.↑: higher is better. ↓: lower is better.
5. Discussion
The proposed model combines CMOD and the DDPM to address wind retrieval across a wide range of wind speeds. The DDPM is utilized to handle both observation disturbances and background residuals in the wind retrieval process. In our experiment, we gathered 450 SAR images and the corresponding wind-speed matrices for tropical cyclones (TCs) and normal conditions to train the DDPMs. The results from Section 4 demonstrate that applying the front-placed DDPM to low-speed regions leads to a significant improvement in the PSNR (24.2%) and the SSIM (29.2%) after recalibration. However, traditional CMOD methods become less accurate with wind speeds above 15 m/s and ineffective with speeds beyond 20 m/s. In contrast, posterior-placed DDPM reconstruction achieves precise wind field reconstruction with a PSNR of 27.20 and an SSIM of 0.936.
This paper underscores the effectiveness of the DDPM in SAR image recalibration and synthesis through step-by-step denoising. Additionally, CMOD-DDPM successfully integrates traditional GMF models with data-driven DDPM methods to solve complex, multi-element retrieval problems. Leveraging prior knowledge from GMFs alongside the generation and recalibration capabilities of deep learning methods contributes to this success. However, there are areas for improvement. Addressing the underestimation of strong TCs in the ERA5 product [37,38], we intend to incorporate more Soil Moisture Active and Passive (SMAP) [39] samples into the dataset. Furthermore, enlarging the dataset to fine-tune the DDPM and utilizing dual polarization as supplementary input data can enhance the precision and robustness of wind retrieval methods. Finally, due to another two inference stages in our method, it takes about 46 s more for a 256 × 256 SAR image by using CMOD-DDPM for wind retrieval compared with traditional CMOD functions. The time complexity needs to be reduced in the future by decreasing the diffusion steps.
6. Conclusions
In conclusion, we have proposed a pioneering model, CMOD-Diffusion, representing the first diffusion-based approach for wind retrieval in SAR imagery, with the primary objective of enhancing the robustness and precision of SAR wind retrieval methodologies. By amalgamating the traditional GMF method with a data-driven approach, our hybrid methodology capitalizes on the respective strengths of each, thereby ensuring both physical interpretability and robustness. Furthermore, we have implemented distinct strategies tailored to different wind-speed regimes to uphold precision effectively. Specifically, for wind speeds below 15 m/s, the wind-speed scale CMOD method exhibits notable precision. Any errors in wind retrieval in this regime primarily stem from disturbances and low-quality data. To mitigate these issues, the front-placed DDPM is utilized to recalibrate the NRCS to the reference domain, thereby enhancing the quality of wind retrieval input. Conversely, as wind speeds surpass 15 m/s, the efficacy of the CMOD approach diminishes gradually. In such instances, the DDPM emerges as a viable solution, facilitating wind field reconstruction in high-speed regions, including TC areas, by leveraging NRCS input and wind-speed data from the low-speed range. Consequently, the proposed CMOD-Diffusion model achieves precise wind retrieval across all wind-speed ranges, showcasing its versatility and efficacy in SAR applications.
The DDPM in the proposed method is based on a U-net architecture, with an encoder–decoder design to extract the features and generate reconstruction results. The network plays the role of a noise predictor to gradually denoise the image to obtain the desired image. In the experiment, we use ERA5 and Sentinel-1 images to collocate and build a dataset. Additionally, ERA5, through the forward CMOD function, generates a reference SAR image to train the model’s capability of recalibration. When the DDPM is applied to recalibrate the low-wind-speed region, the model achieves an RMSE of 0.630 m/s, an R of 0.989, an SSIM of 0.983, and a PSNR of 25.51 for a model-unfamiliar case, achieving an improvement in all matrices compared with the traditional CMOD method in a low-wind-speed situation. When the posterior DDPM is applied to the reconstruction wind field in TCs, it showcases an RMSE of 2.39 m/s and an SSIM of 0.979. To sum up, the proposed hybrid CMOD-Diffusion model is a promising method of wind retrieval in large-wind-speed scales with high precision.
More SAR images will be trained and validated by the proposed method to fine-tune our model in the future. Moreover, dual-polarization wind retrieval will be considered to improve the precision of wind retrieval further.
Author Contributions
Conceptualization, Q.Z. and H.C.; data curation, H.C.; formal analysis, Q.Z.; funding acquisition, X.L. and H.C.; investigation, Q.Z.; methodology, Q.Z.; project administration, H.C.; resources, H.C. and X.L.; software. Q.Z.; supervision, X.L. and H.C.; validation, Q.Z. and H.C.; visualization, Q.Z.; writing—original draft, Q.Z.; writing—review and editing, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the LuTan-1 L-Band Spaceborne Bistatic SAR data processing program, grant number E0H2080702.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Horstmann, J.; Schiller, H.; Schulz-Stellenfleth, J.; Lehner, S. Global Wind Speed Retrieval From SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2277–2286. [Google Scholar] [CrossRef]
- Ye, X.; Lin, M.; Zheng, Q.; Yuan, X.; Liang, C.; Zhang, B.; Zhang, J. A Typhoon Wind-Field Retrieval Method for the Dual-Polarization SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1511–1515. [Google Scholar] [CrossRef]
- Li, X.; Pichel, W.G.; He, M.; Wu, S.Y.; Zhao, C. Observation of hurricane-generated ocean swell refraction at the Gulf Stream north wall with the RADARSAT-1 synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2131–2142. [Google Scholar]
- Shao, W.; Jiang, X.; Sun, Z.; Hu, Y.; Marino, A.; Zhang, Y. Evaluation of wave retrieval for Chinese Gaofen-3 synthetic aperture radar. Geo-Spat. Inf. Sci. 2022, 25, 229–243. [Google Scholar] [CrossRef]
- Shao, W.; Hu, Y.; Jiang, X.; Zhang, Y. Wave retrieval from quad-polarized Chinese Gaofen-3 SAR image using an improved tilt modulation transfer function. Geo-Spat. Inf. Sci. 2023, 1–19. [Google Scholar] [CrossRef]
- Jiang, T.; Shao, W.; Yuyi, H.; Gang, Z.; Wei, S. L-Band Analysis of the Effects of Oil Slicks on Sea Wave Characteristics. J. Ocean Univ. China 2023, 22, 9–20. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y.; Li, X.; Zhang, Z.; Cao, Y.; Cheng, Y. Impact of Ships and Ocean Fronts on Coastal Sea Surface Wind Measurements from the Advanced Scatterometer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2162–2169. [Google Scholar] [CrossRef]
- Stoffelen, A.; Anderson, D. Scatterometer data interpretation: Estimation and validation of the transfer function CMOD4. J. Geophys. Res. 1997, 102, 5767–5780. [Google Scholar] [CrossRef]
- Hersbach, H. Comparison of C-band scatterometer CMOD5.N equivalent neutral winds with ECMWF. J. Atmos. Ocean. Technol. 2010, 27, 721–736. [Google Scholar] [CrossRef]
- Stoffelen, A.; Verspeek, J.; Vogelzang, J.; Verhoef, A. The CMOD7 Geophysical Model Function for ASCAT and ERS Wind Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2123–2134. [Google Scholar] [CrossRef]
- Vachon, P.W.; Wolfe, J. C-band cross-polarization wind speed retrieval. IEEE Geosci. Remote Sens. Lett. 2011, 8, 456–459. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W. Cross-polarized synthetic aperture radar: A new potential measurement technique for hurricanes. Bull. Amer. Meteorol. Soc. 2012, 93, 531–541. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; Zhang, J.; Uhlhorn, E.; He, Y. High-Resolution Hurricane Vector Winds from C-Band Dual-Polarization SAR Observations. J. Atmos. Ocean. Technol. 2014, 31, 272–286. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Perrie, W.; Hwang, P.A.; Zhang, B.; Yang, X. A Hurricane Wind Speed Retrieval Model for C-Band RADARSAT-2 Cross-Polarization ScanSAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4766–4774. [Google Scholar] [CrossRef]
- Mouche, A.A.; Chapron, B.; Zhang, B.; Husson, R. Combined Co- and Cross-Polarized SAR Measurements under Extreme Wind Conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
- Boussioux, L.; Zeng, C.; Guénais, T.; Bertsimas, D. Hurricane forecasting: A novel multimodal machine learning framework. Weather Forecast 2022, 37, 817–831. [Google Scholar] [CrossRef]
- Carmo, A.R.; Longépé, N.; Mouche, A.; Amorosi, D.; Cremer, N. Deep Learning Approach for Tropical Cyclones Classification Based on C-Band Sentinel-1 SAR Images. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3010–3013. [Google Scholar]
- Li, X.M.; Qin, T.; Wu, K. Retrieval of sea surface wind speed from spaceborne SAR over the Arctic marginal ice zone with a neural network. Remote Sens. 2020, 12, 3291. [Google Scholar] [CrossRef]
- Funde, K.; Joshi, J.; Damani, J.; Jyothula, V.R.; Pawar, R. Tropical Cyclone Intensity Classification Using Convolutional Neural Networks On Satellite Imagery. In Proceedings of the 2022 International Conference on Industry 4.0 Technology (I4Tech), Pune, India, 23–24 September 2022; pp. 1–5. [Google Scholar]
- Yu, P.; Xu, W.; Zhong, X.; Johannessen, J.A.; Yan, X.H.; Geng, X.; He, Y.; Lu, W. A Neural Network Method for Retrieving Sea Surface Wind Speed for C-Band SAR. Remote Sens. 2022, 14, 2269. [Google Scholar] [CrossRef]
- Mu, S.; Li, X.; Wang, H. The Fusion of Physical, Textural and Morphological Information in SAR Imagery for Hurricane Wind Speed Retrieval Based on Deep Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Han, X.; Li, X.; Yang, J.; Wang, J.; Zheng, G.; Ren, L.; Chen, P.; Fang, H.; Xiao, Q. Dual-Level Contextual Attention Generative Adversarial Network for Reconstructing SAR Wind Speeds in Tropical Cyclones. Remote Sens. 2023, 15, 2454. [Google Scholar] [CrossRef]
- Chierchia, G.; Cozzolino, D.; Poggi, G.; Verdoliva, L. Sar image despeckling through convolutional neural networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5438–5441. [Google Scholar]
- Perera, M.V.; Bandara, W.G.C.; Valanarasu, J.M.J.; Patel, V.M. SAR Despeckling Using Overcomplete Convolutional Networks. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 401–404. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Nice, France, 2020; Volume 33, pp. 6840–6851. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. In Advances in Neural Information Processing Systems; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Nice, France, 2021; Volume 34, pp. 8780–8794. [Google Scholar]
- Perera, M.V.; Nair, N.G.; Bandara, W.G.C.; Patel, V.M. SAR despeckling using a denoising diffusion probabilistic model. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.D.; de Haan, S. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
- Zhao, X.B.; Shao, W.Z.; Zhao, L.B.; Gao, Y.; Hu, Y.Y.; Yuan, X.Z. Impact of rain on wave retrieval from Sentinel-1 synthetic aperture radar images in tropical cyclones. Adv. Space Res. 2021, 67, 3072–3086. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Y.; Wang, W. A New Approach for Ocean Surface Wind Speed Retrieval Using Sentinel-1 Dual-Polarized Imagery. Remote Sens. 2023, 15, 4267. [Google Scholar] [CrossRef]
- Hersbach, H. CMOD5. N: A C-Band Geophysical Model Function for Equivalent Neutral Wind; ECMWF: Reading, UK, 2008. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the MICCAI, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.U.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Nice, France, 2017; Volume 30. [Google Scholar]
- Brock, A.; Donahue, J.; Simonyan, K. Large scale GAN training for high fidelity natural image synthesis. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Portabella, M.; Stoffelen, A.; Johannessen, J.A. Toward an optimal inversion method for synthetic aperture radar wind retrieval. J. Geophys. Res. Ocean. 2002, 107, 1-1–1-13. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Li, X.; Yang, J.; Wang, J.; Han, G. Evaluation and Calibration of Remotely Sensed High Winds from the HY-2B/C/D Scatterometer in Tropical Cyclones. Remote Sens. 2022, 14, 4654. [Google Scholar] [CrossRef]
- Li, X.; Yang, J.; Han, G.; Ren, L.; Zheng, G.; Chen, P.; Zhang, H. Tropical Cyclone Wind Field Reconstruction and Validation Using Measurements from SFMR and SMAP Radiometer. Remote Sens. 2022, 14, 3929. [Google Scholar] [CrossRef]
- Njoku, E.; Entekhabi, D.; Kellogg, K.; O’Neill, P. The Soil Moisture Active and Passive (SMAP) Mission. Earth Obs. Water Cycle Sci. 2009, 674, 2. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).