On Unsupervised Multiclass Change Detection Using Dual-Polarimetric SAR Data
Abstract
1. Introduction
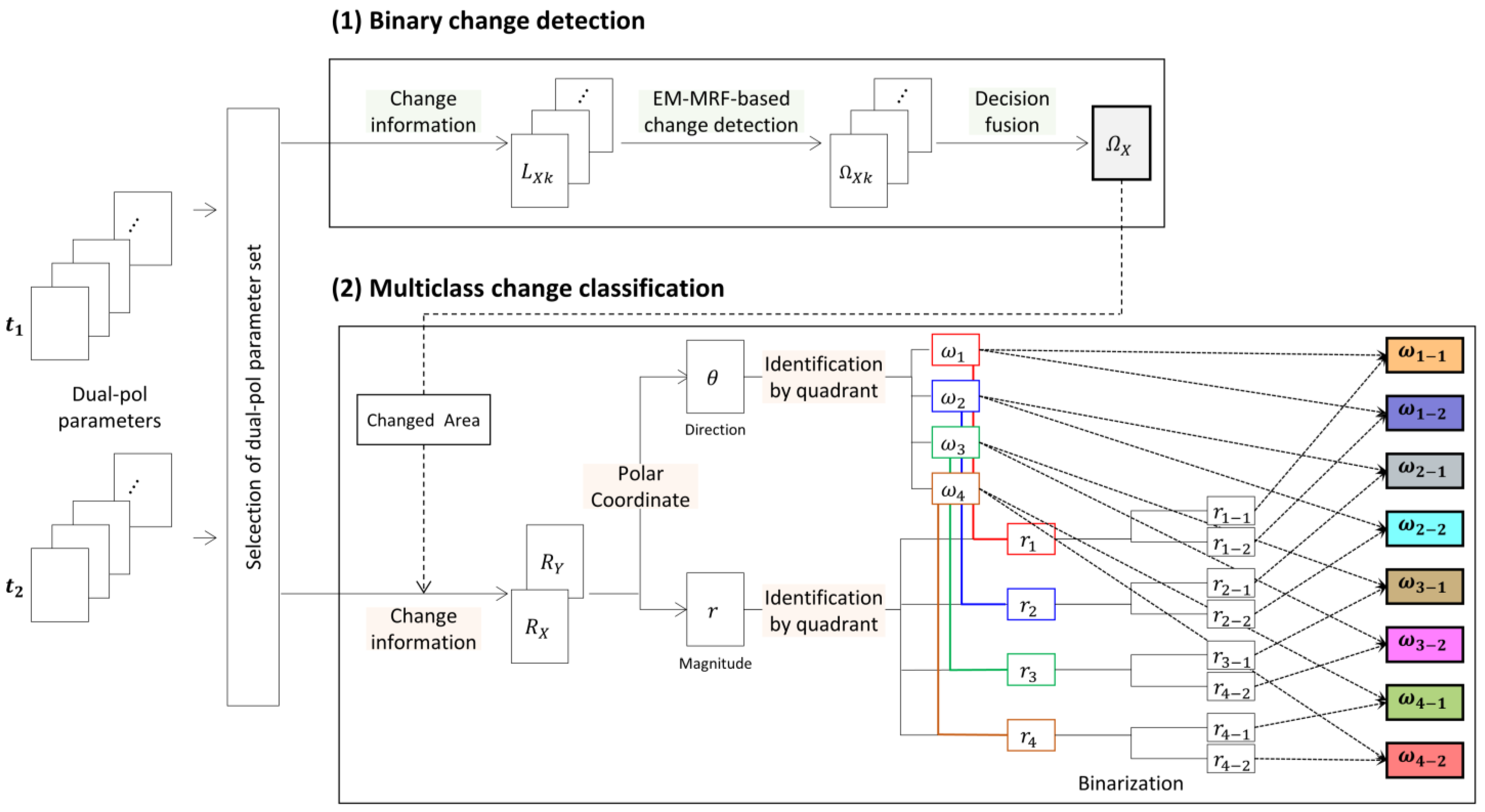
2. Dual-Pol Multiclass Change Detection
2.1. Dual-Pol Parameters
2.2. Dual-Pol Change Detection
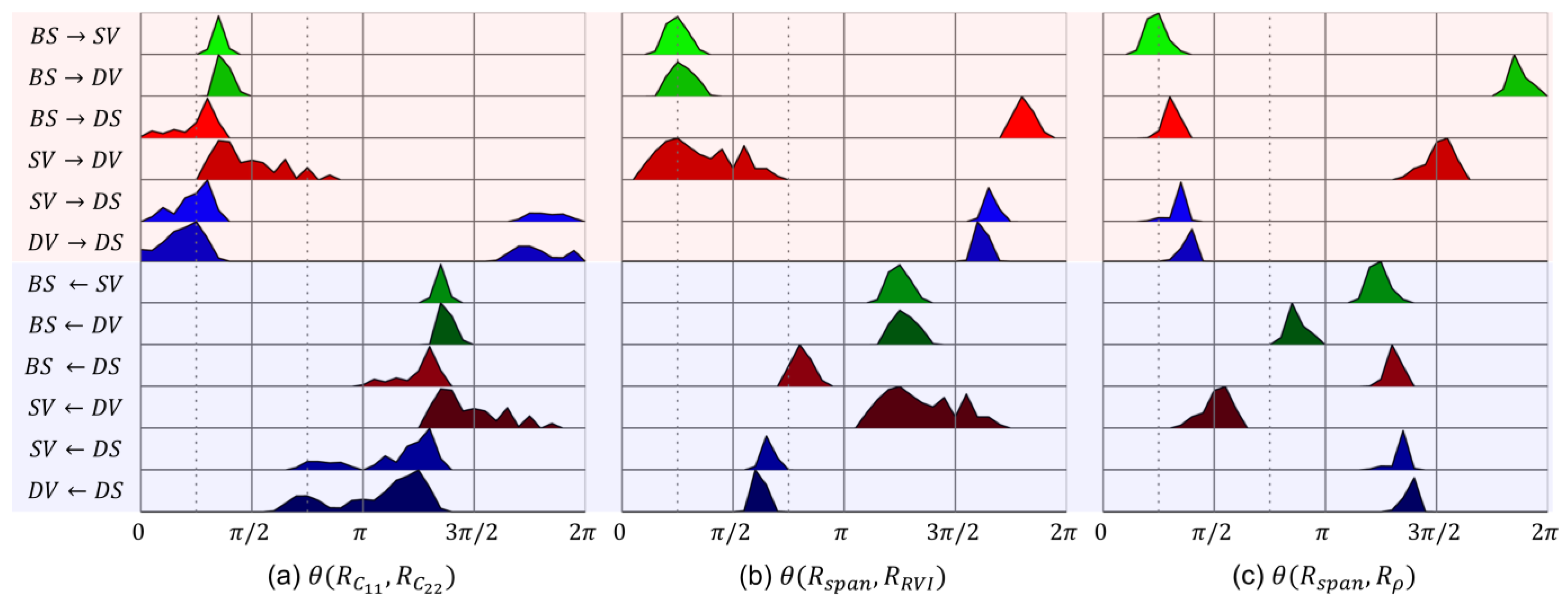
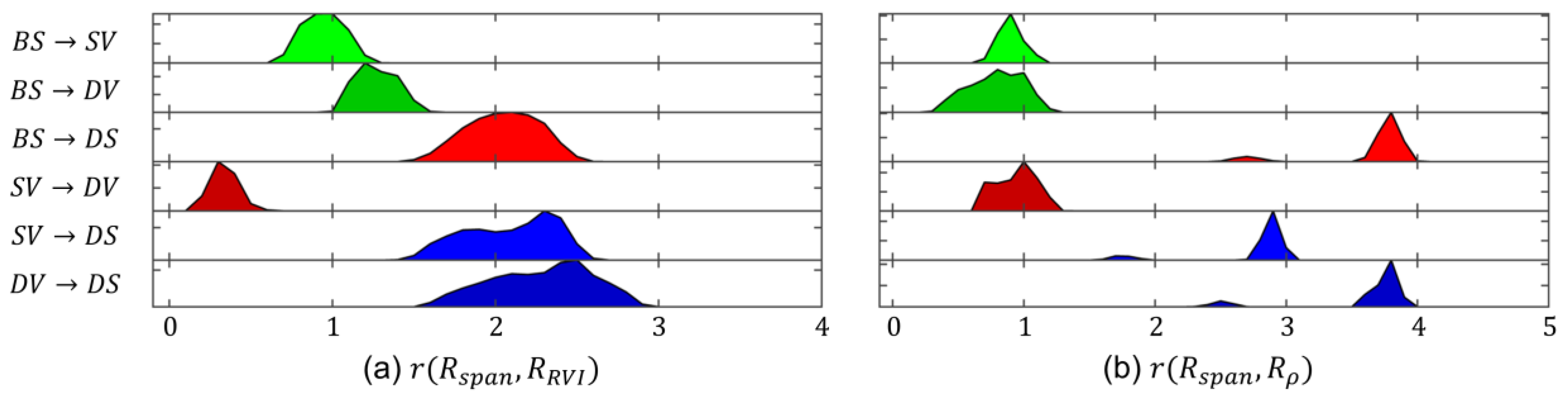
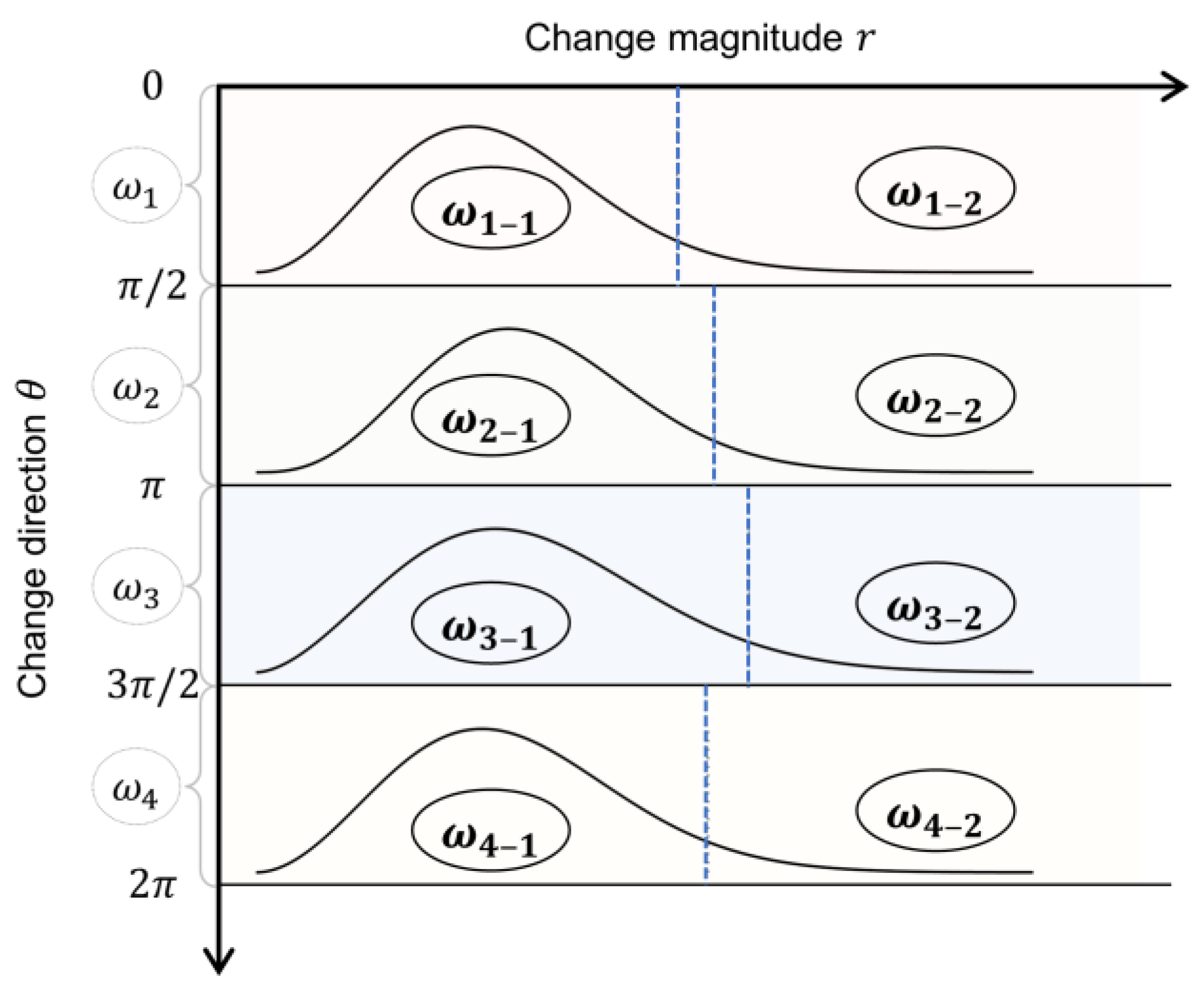
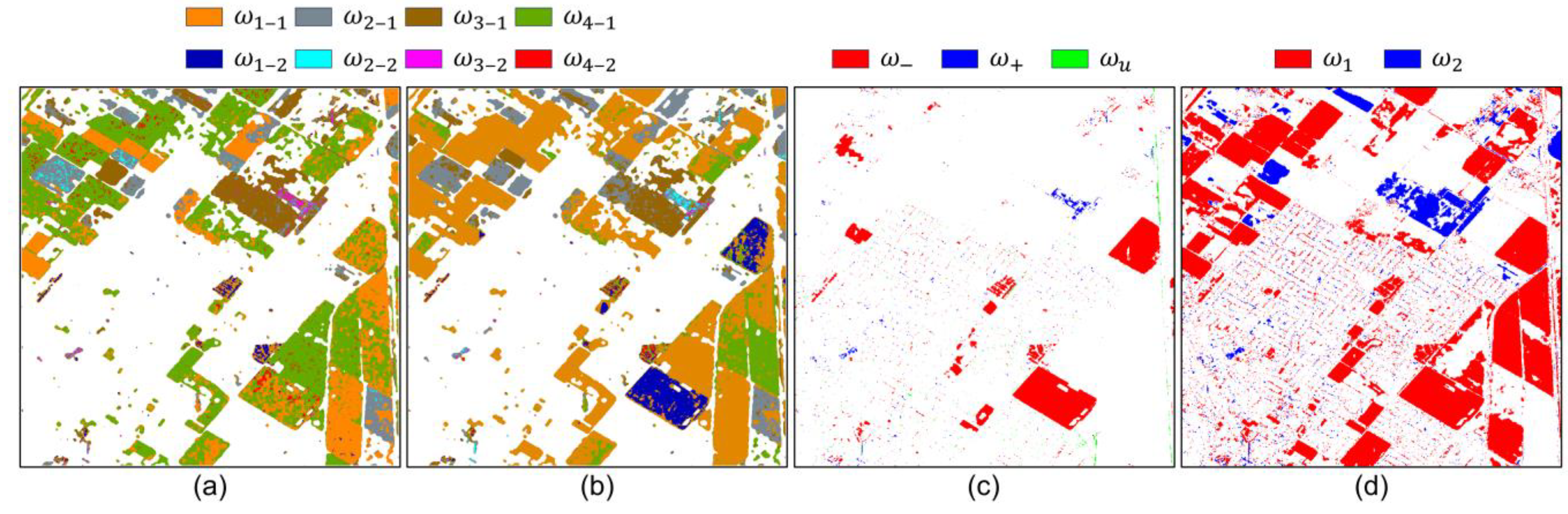
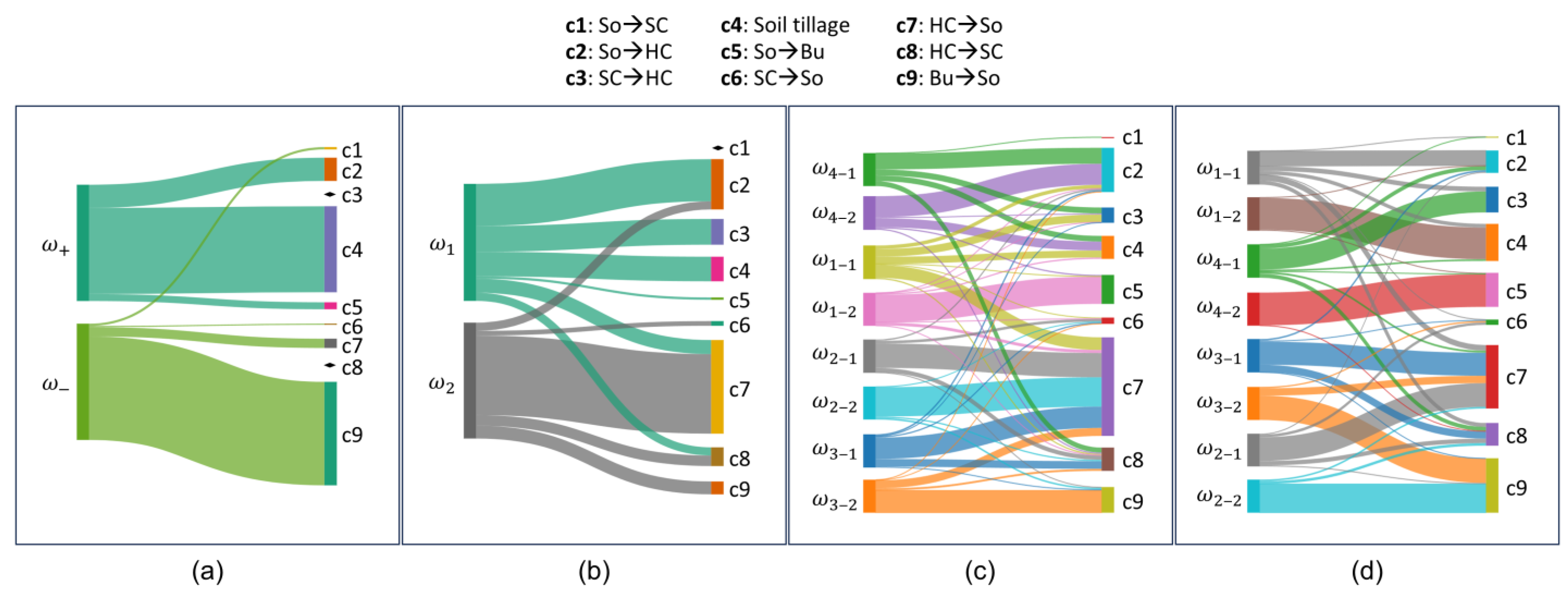
2.3. Dual-Pol Multiclass Change Classification
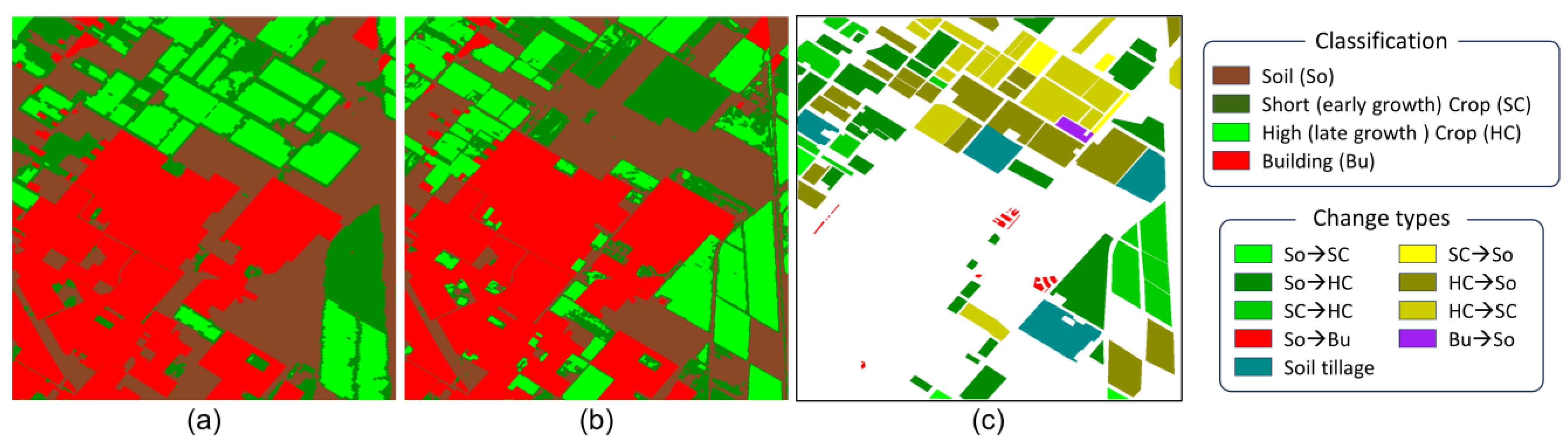
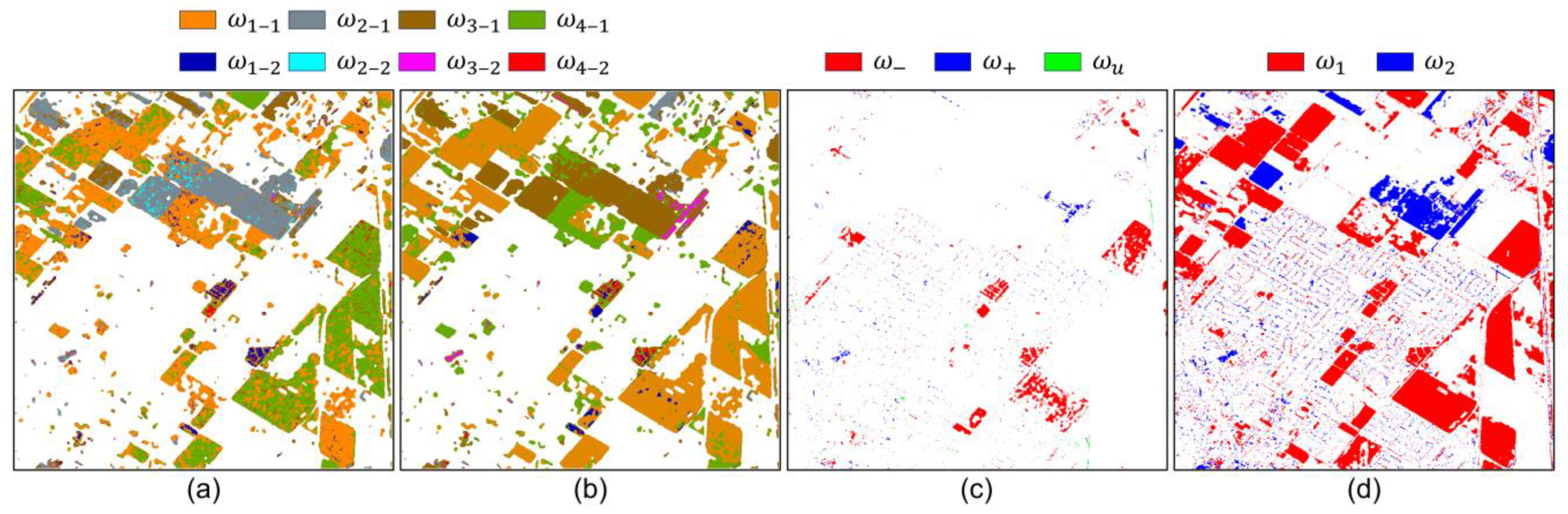
3. Experimental Results
3.1. Data Set for Experiments
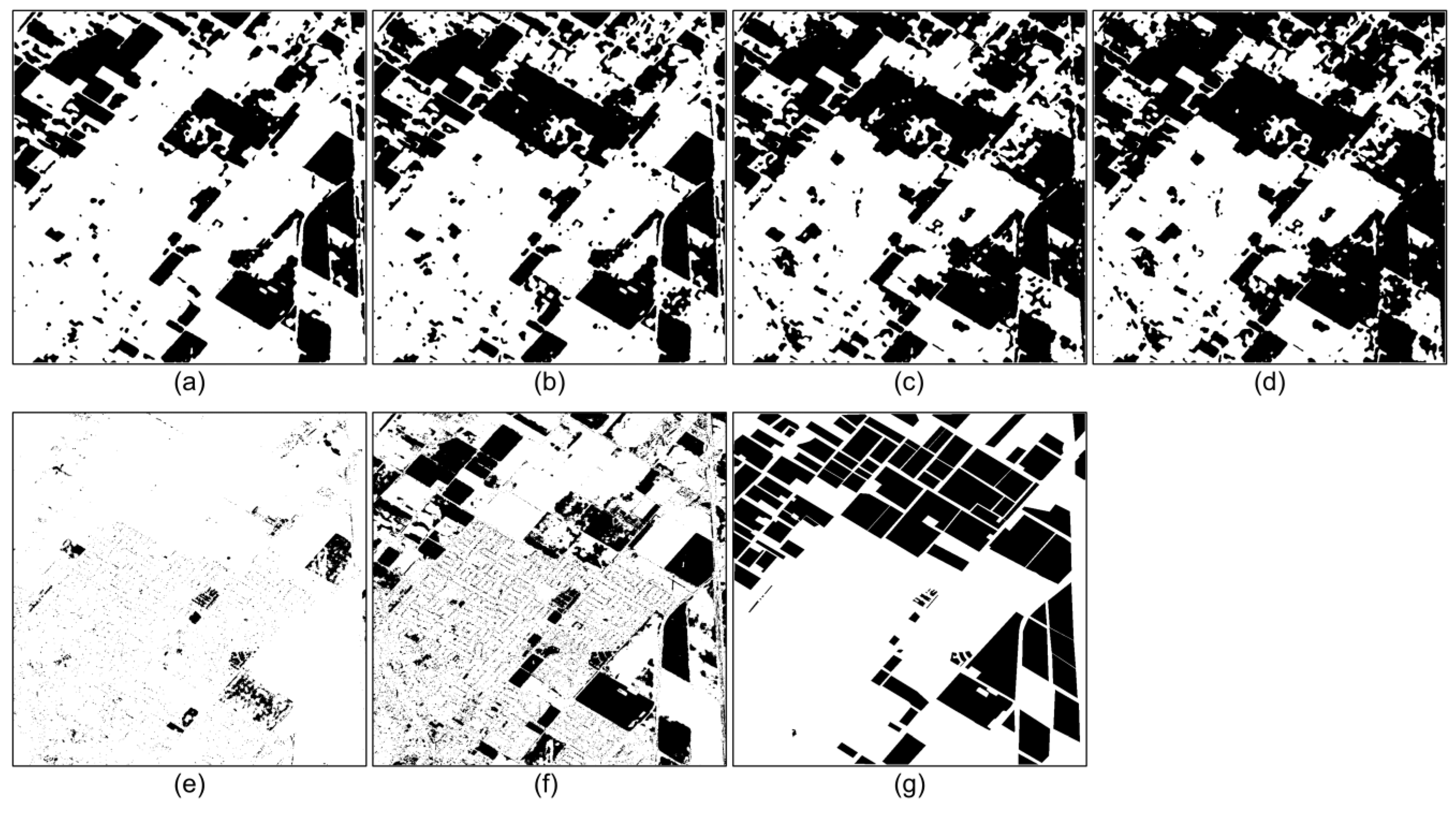
3.2. Results of Change Detection
- Intensities: ;
- Intensities and coherence: ;
- Intensities and depolarization: ;
- Intensities, coherence, and depolarization: .
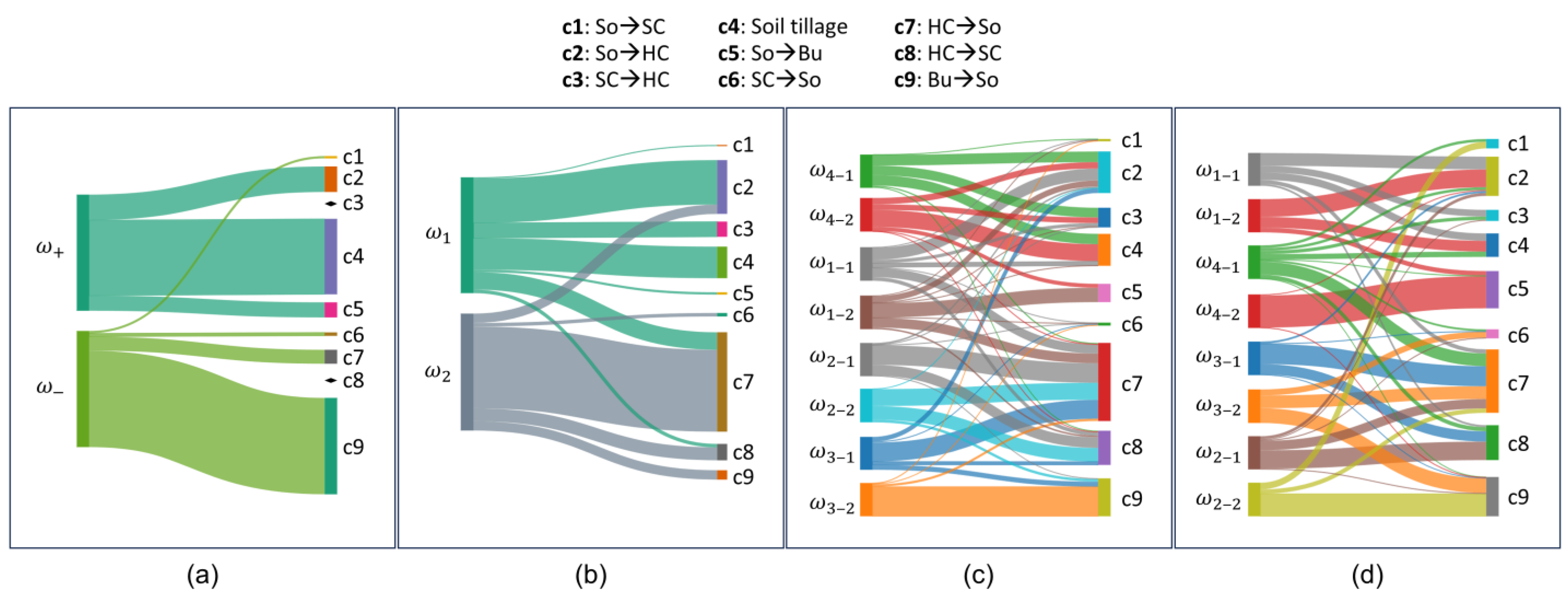
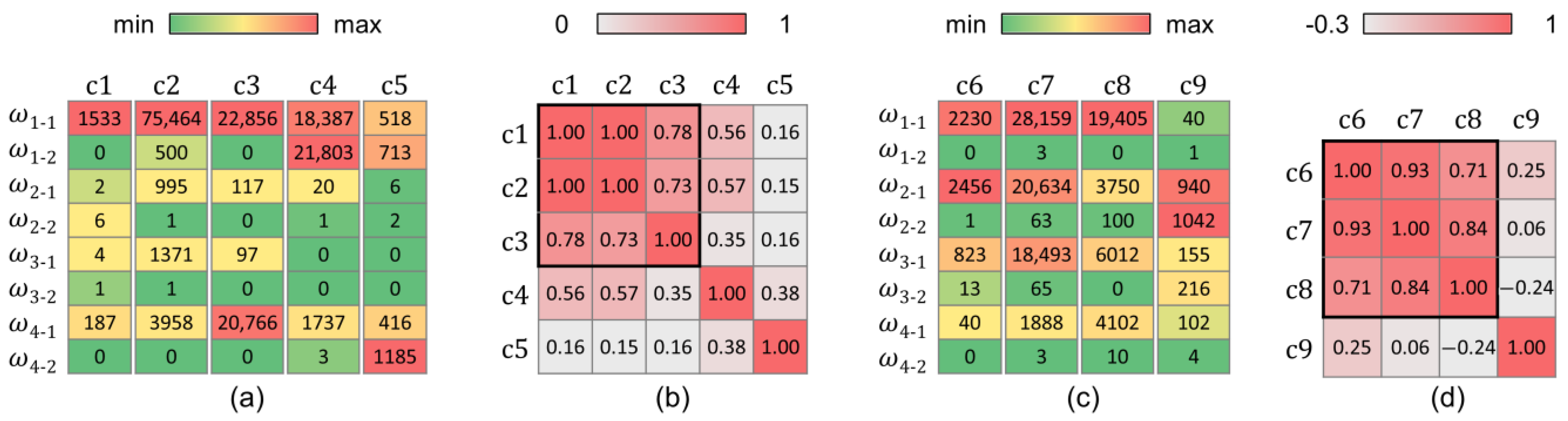
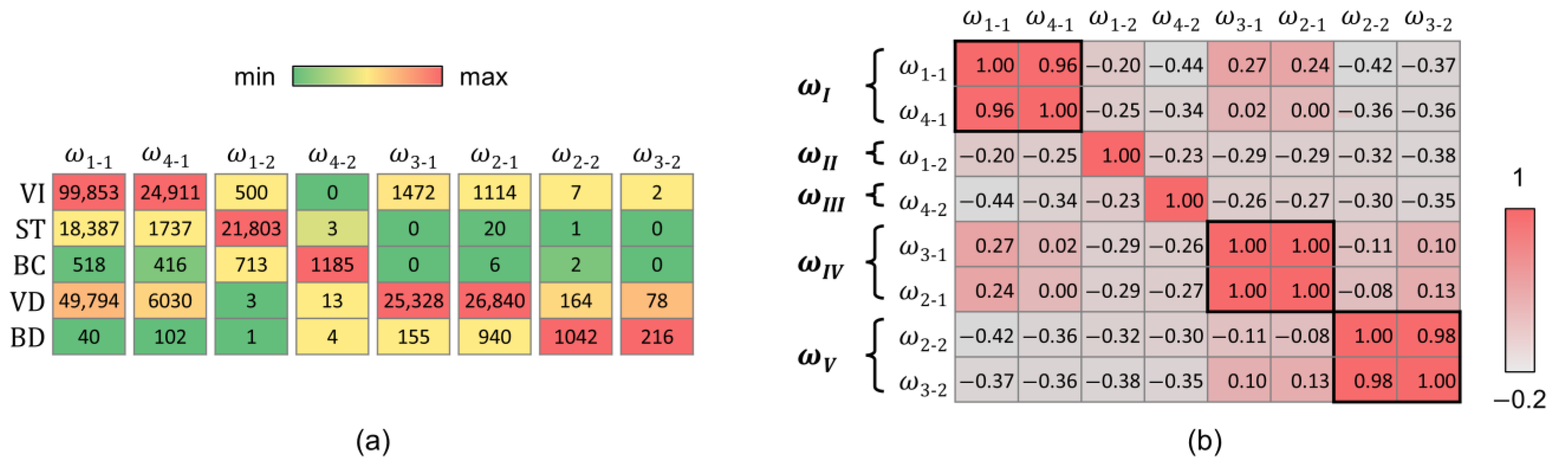
3.3. Results of Multiclass Change Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rignot, E.J.; Van Zyl, J.J. Change detection techniques for ERS-1 SAR data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 896–906. [Google Scholar] [CrossRef]
- Bazi, Y.; Bruzzone, L.; Melgani, F. An unsupervised approach based on the generalized Gaussian model to automatic change detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 874–887. [Google Scholar] [CrossRef]
- Gong, M.; Cao, Y.; Wu, Q. A neighborhood-based ratio approach for change detection in SAR images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 307–311. [Google Scholar] [CrossRef]
- Ban, Y.; Yousif, O.A. Multitemporal spaceborne SAR data for urban change detection in China. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2012, 5, 1087–1094. [Google Scholar] [CrossRef]
- Hou, B.; Wei, Q.; Zheng, Y.; Wang, S. Unsupervised change detection in SAR image based on Gauss-log ratio image fusion and compressed projection. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 3297–3317. [Google Scholar] [CrossRef]
- Ing Lada, J.; Mercier, G. A new statistical similarity measure for change detection in multitemporal SAR images and its extension to multiscale change analysis. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1432–1445. [Google Scholar] [CrossRef]
- Chatelain, F.; Tourneret, J.Y.; Inglada, J.; Ferrari, A. Bivariate gamma distributions for image registration and change detection. IEEE Trans. Image Process. 2007, 16, 1796–1806. [Google Scholar] [CrossRef]
- Mercier, G.; Moser, G.; Serpico, S.B. Conditional copulas for change detection in heterogeneous remote sensing images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1428–1441. [Google Scholar] [CrossRef]
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake damage assessment of buildings using VHR optical and SAR imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Zoppetti, C. Nonparametric change detection in multitemporal SAR images based on mean-shift clustering. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2022–2031. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S.B. Unsupervised change detection from multichannel SAR data by Markovian data fusion. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2114–2128. [Google Scholar] [CrossRef]
- Pantze, A.; Santoro, M.; Fransson, J.E. Change detection of boreal forest using bi-temporal ALOS PALSAR backscatter data. Remote Sens. Environ. 2014, 155, 120–128. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Conradsen, K.; Skriver, H. Change detection in full and dual polarization, single-and multifrequency SAR data. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 4041–4048. [Google Scholar] [CrossRef]
- Ferrentino, E.; Marino, A.; Nunziata, F.; Migliaccio, M. A dual–polarimetric approach to earthquake damage assessment. Int. J. Remote Sens. 2019, 40, 197–217. [Google Scholar] [CrossRef]
- Ferrentino, E.; Nunziata, F.; Bignami, C.; Graziani, L.; Maramai, A.; Migliaccio, M.; Stramondo, S. On the combination of dual-polarization Sentinel-1 ascending/descending orbiting passes to estimate damage due to the 2016 Central Italy earthquake. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2022, 15, 9509–9518. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Skriver, H.; Conradsen, K. The Loewner order and direction of detected change in Sentinel-1 and Radarsat-2 data. IEEE Geosci. Remote Sens. Lett. 2020, 17, 242–246. [Google Scholar] [CrossRef]
- Malmgren-Hansen, D.; Sohnesen, T.; Fisker, P.; Baez, J. Sentinel-1 change detection analysis for cyclone damage assessment in urban environments. Remote Sens. 2020, 12, 2409. [Google Scholar] [CrossRef]
- Pirrone, D.; Bovolo, F.; Bruzzone, L. A novel framework based on polarimetric change vectors for unsupervised multiclass change detection in dual-pol intensity SAR images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4780–4795. [Google Scholar] [CrossRef]
- Bruzzone, L.; Bovolo, F. A novel framework for the design of change-detection systems for very-high-resolution remote sensing images. Proc. IEEE 2013, 101, 609–630. [Google Scholar] [CrossRef]
- Braun, A.; Offermann, E. Polarimetric information content of Sentinel-1 for land cover mapping: An experimental case study using quad-pol data synthesized from complementary repeat-pass acquisitions. Front. Remote Sens. 2022, 3, 905713. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Velotto, D.; Bentes, C.; Tings, B.; Lehner, S. First comparison of Sentinel-1 and TerraSAR-X data in the framework of maritime targets detection: South Italy case. IEEE J. Ocean. Eng. 2016, 41, 993–1006. [Google Scholar] [CrossRef]
- Park, S.E.; Moon, W.M.; Pottier, E. Assessment of scattering mechanism of polarimetric SAR signal from mountainous forest areas. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4711–4719. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: London, UK, 2009. [Google Scholar]
- Wolf, E. Coherence properties of partially polarized electromagnetic radiation. Nuovo Cim. 1959, 13, 1165–1181. [Google Scholar] [CrossRef]
- Raney, R.K. Hybrid-polarity SAR architecture. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3397–3404. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual polarimetric radar vegetation index for crop growth monitoring using Sentinel-1 SAR data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
- Kim, Y.; Van Zyl, J. Comparison of forest parameter estimation techniques using SAR data. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001. [Google Scholar]
- Chang, J.G.; Shoshany, M.; Oh, Y. Polarimetric radar vegetation index for biomass estimation in desert fringe ecosystems. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7102–7108. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, M.; Hou, Z.; Wu, L.; Guo, Z.; Shen, X.; Zheng, W.; Li, N. Land cover classification of SAR based on 1DCNN-MRF model using improved dual-polarization radar vegetation index. Remote Sens. 2023, 15, 3221. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Machine Intell. 1984, PAMI-6, 721–741. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, Z. An improved MRF-based change detection approach for multitemporal remote sensing imagery. Signal Process. 2013, 93, 163–175. [Google Scholar] [CrossRef]
- Yousif, O.; Ban, Y. Improving SAR-based urban change detection by combining MAP-MRF classifier and nonlocal means similarity weights. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 4288–4300. [Google Scholar] [CrossRef]
- Solarna, D.; Moser, G.; Serpico, S.B. A Markovian approach to unsupervised change detection with multiresolution and multimodality SAR data. Remote Sens. 2018, 10, 1671. [Google Scholar] [CrossRef]
- Besag, J. On the statistical analysis of dirty pictures. J. Roy. Stat. Soc. Ser. B Methodol. 1986, 48, 259–302. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S.B. Generalized minimum-error thresholding for unsupervised change detection from SAR amplitude imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2972–2982. [Google Scholar] [CrossRef]
- Bloch, I. Information combination operators for data fusion: A comparative review with classification. IEEE Trans. Syst. Man Cybern. A Syst. Hum. 1996, 26, 52–67. [Google Scholar] [CrossRef]
- Park, S.E.; Yamaguchi, Y.; Kim, D.J. Polarimetric SAR remote sensing of the 2011 Tohoku earthquake using ALOS/PALSAR. Remote Sens. Environ. 2013, 132, 212–220. [Google Scholar] [CrossRef]
- Park, S.E.; Yamaguchi, Y.; Singh, G.; Yamaguchi, S.; Whitaker, A.C. Polarimetric SAR response of snow-covered area observed by multi-temporal ALOS PALSAR fully polarimetric mode. IEEE Trans. Geosci. Remote Sens. 2014, 52, 329–340. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRS Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Malila, W.A. Change Vector Analysis: An Approach for Detecting Forest Changes with Landsat. In Proceedings of the LARS Symposia, West Lafayette, IN, USA, 3–6 June 1980. [Google Scholar]
- Bovolo, F.; Bruzzone, L. A theoretical framework for unsupervised change detection based on change vector analysis in polar domain. IEEE Trans. Geosci. Remote Sens. 2007, 45, 218–236. [Google Scholar] [CrossRef]
- Lee, J.S.; Wen, J.H.; Ainsworth, T.L.; Chen, K.S.; Chen, A.J. Improved sigma filter for speckle filtering of SAR imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 202–213. [Google Scholar]
- Goutte, C.; Gaussier, E. A probabilistic interpretation of precision, recall and F-score, with implication for evaluation. In Proceedings of the European Conference on Information Retrieval, Santiago de Compostela, Spain, 21–23 March 2005. [Google Scholar]
- Schuler, D.L.; Lee, J.S.; Kasilingam, D.; Nesti, G. Surface roughness and slope measurements using polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 687–698. [Google Scholar] [CrossRef]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- Lee, J.S.; Schuler, D.L.; Ainsworth, T.L. Polarimetric SAR data compensation for terrain azimuth slope variation. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2153–2163. [Google Scholar]
- Kimura, H. Radar polarization orientation shifts in built-up areas. IEEE Geosci. Remote Sens. Lett. 2008, 5, 217–221. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Estimation of forest structure, ground, and canopy layer characteristics from multibaseline polarimetric interferometric SAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1086–1104. [Google Scholar] [CrossRef]


| Bare Surface (BS) | Sparse Volume (SV) | Dense Volume (DV) | Dihedral Structure (DS) | ||
|---|---|---|---|---|---|
| (dB) | min | −19 | −21 | −21 | −23 |
| max | −17 | −19 | −19 | −21 | |
| (dB) | min | −36 | −19 | −26 | −4 |
| max | −34 | −17 | −24 | −2 | |
| (dB) | min | −36 | −16 | −11 | −26 |
| max | −34 | −14 | −9 | −24 | |
| Change Type | ) Class | ) Class |
|---|---|---|
| 1 | Bare Surface (BS) | Sparse Volume (SV) |
| 2 | Bare Surface (BS) | Dense Volume (DV) |
| 3 | Bare Surface (BS) | Dihedral Structure (DS) |
| 4 | Sparse Volume (SV) | Dense Volume (DV) |
| 5 | Sparse Volume (SV) | Dihedral Structure (DS) |
| 6 | Dense Volume (DV) | Dihedral Structure (DS) |
| 7 | Sparse Volume (SV) | Bare Surface (BS) |
| 8 | Dense Volume (DV) | Bare Surface (BS) |
| 9 | Dihedral Structure (DS) | Bare Surface (BS) |
| 10 | Dense Volume (DV) | Sparse Volume (SV) |
| 11 | Dihedral Structure (DS) | Sparse Volume (SV) |
| 12 | Dihedral Structure (DS) | Dense Volume (DV) |
| OA | F1 | Pr | DR | FA | |
|---|---|---|---|---|---|
| WL | 0.5984 | 0.1808 | 0.5662 | 0.1076 | 0.0577 |
| PVA | 0.7013 | 0.5814 | 0.6879 | 0.5034 | 0.1600 |
| Proposed () | 0.7728 | 0.7020 | 0.7634 | 0.6498 | 0.1411 |
| Proposed () | 0.8113 | 0.7703 | 0.7724 | 0.7683 | 0.1586 |
| Proposed () | 0.7747 | 0.7107 | 0.7545 | 0.6716 | 0.1531 |
| Proposed () | 0.8091 | 0.7713 | 0.7616 | 0.7812 | 0.1713 |
| OA | F1 | Pr | DR | FA | |
|---|---|---|---|---|---|
| WL | 0.5924 | 0.0997 | 0.5544 | 0.0548 | 0.0308 |
| PVA | 0.6722 | 0.5128 | 0.6613 | 0.4187 | 0.1502 |
| Proposed () | 0.7458 | 0.6495 | 0.7518 | 0.5717 | 0.1323 |
| Proposed () | 0.7699 | 0.7057 | 0.7460 | 0.6695 | 0.1598 |
| Proposed () | 0.7388 | 0.6913 | 0.6735 | 0.7101 | 0.2412 |
| Proposed () | 0.7478 | 0.7127 | 0.6716 | 0.7592 | 0.2602 |
| VI | ST | BC | VD | BR | |
|---|---|---|---|---|---|
| 124,764 | 20,124 | 934 | 55,824 | 142 | |
| 500 | 21,803 | 713 | 3 | 1 | |
| 0 | 3 | 1185 | 13 | 4 | |
| 2586 | 20 | 6 | 52,168 | 1095 | |
| 9 | 1 | 2 | 242 | 1258 | |
| Overall Accuracy: 71.0% | |||||
| VI | ST | BC | VD | BR | |
|---|---|---|---|---|---|
| 99,815 | 40,033 | 425 | 47,268 | 277 | |
| 2556 | 1565 | 693 | 2 | 5 | |
| 57 | 0 | 1709 | 7 | 9 | |
| 3216 | 0 | 4 | 46,152 | 1208 | |
| 8 | 0 | 0 | 1099 | 863 | |
| Overall Accuracy: 60.8% | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Lee, S.-J.; Park, S.-E. On Unsupervised Multiclass Change Detection Using Dual-Polarimetric SAR Data. Remote Sens. 2024, 16, 2858. https://doi.org/10.3390/rs16152858
Kim M, Lee S-J, Park S-E. On Unsupervised Multiclass Change Detection Using Dual-Polarimetric SAR Data. Remote Sensing. 2024; 16(15):2858. https://doi.org/10.3390/rs16152858
Chicago/Turabian StyleKim, Minhwa, Seung-Jae Lee, and Sang-Eun Park. 2024. "On Unsupervised Multiclass Change Detection Using Dual-Polarimetric SAR Data" Remote Sensing 16, no. 15: 2858. https://doi.org/10.3390/rs16152858
APA StyleKim, M., Lee, S.-J., & Park, S.-E. (2024). On Unsupervised Multiclass Change Detection Using Dual-Polarimetric SAR Data. Remote Sensing, 16(15), 2858. https://doi.org/10.3390/rs16152858






