Comparing Three Freeze-Thaw Schemes Using C-Band Radar Data in Southeastern New Hampshire, USA
Abstract
1. Introduction
2. Methodology
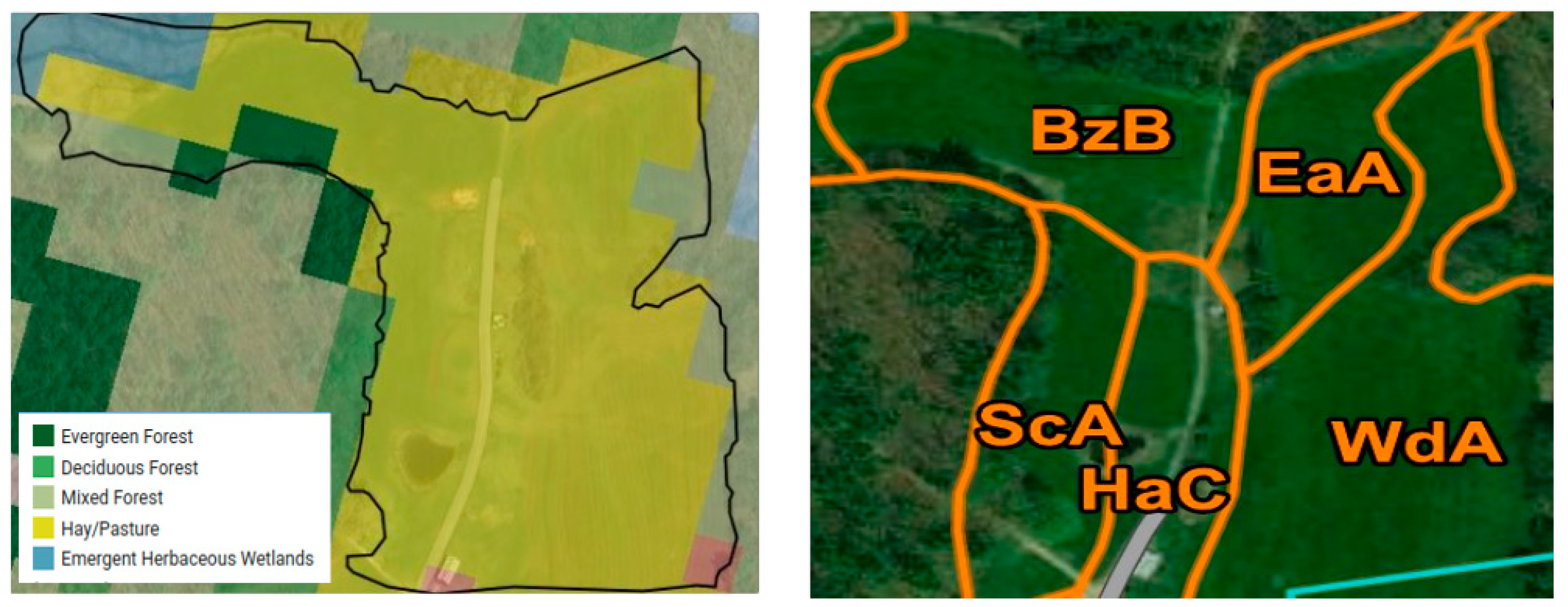
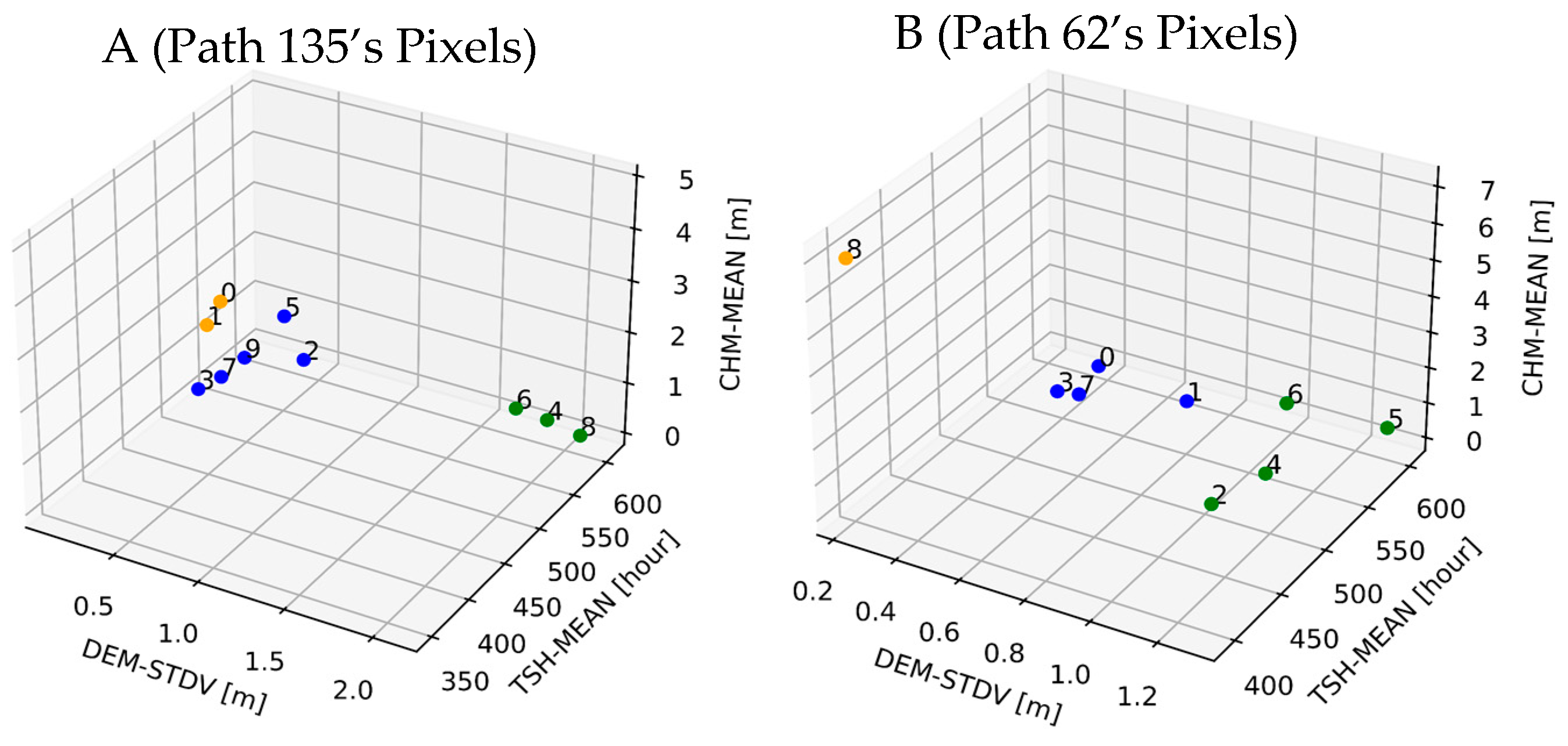
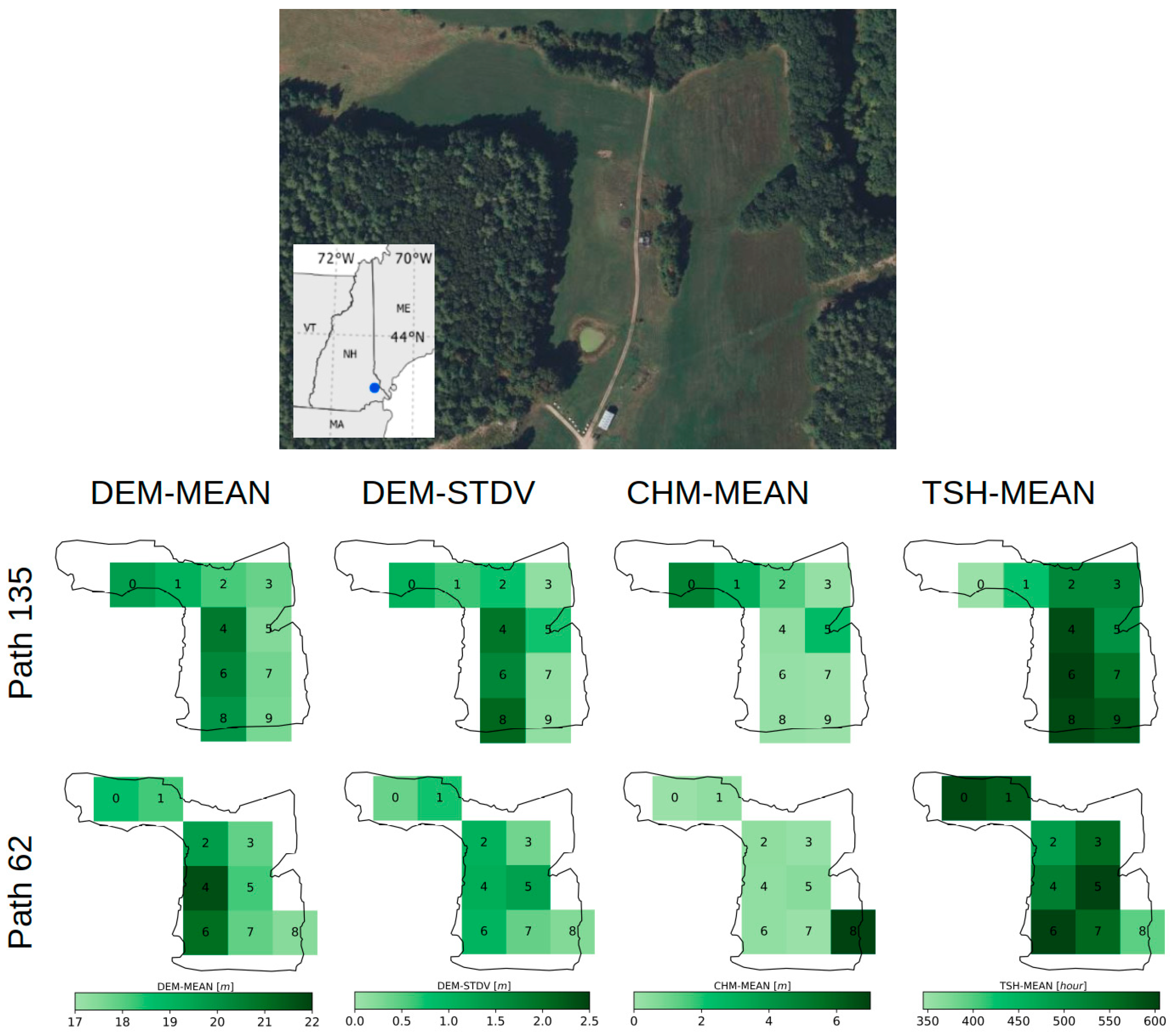
2.1. Study Area
2.2. SAR Data
2.3. RCS and Coherence Product Alignments
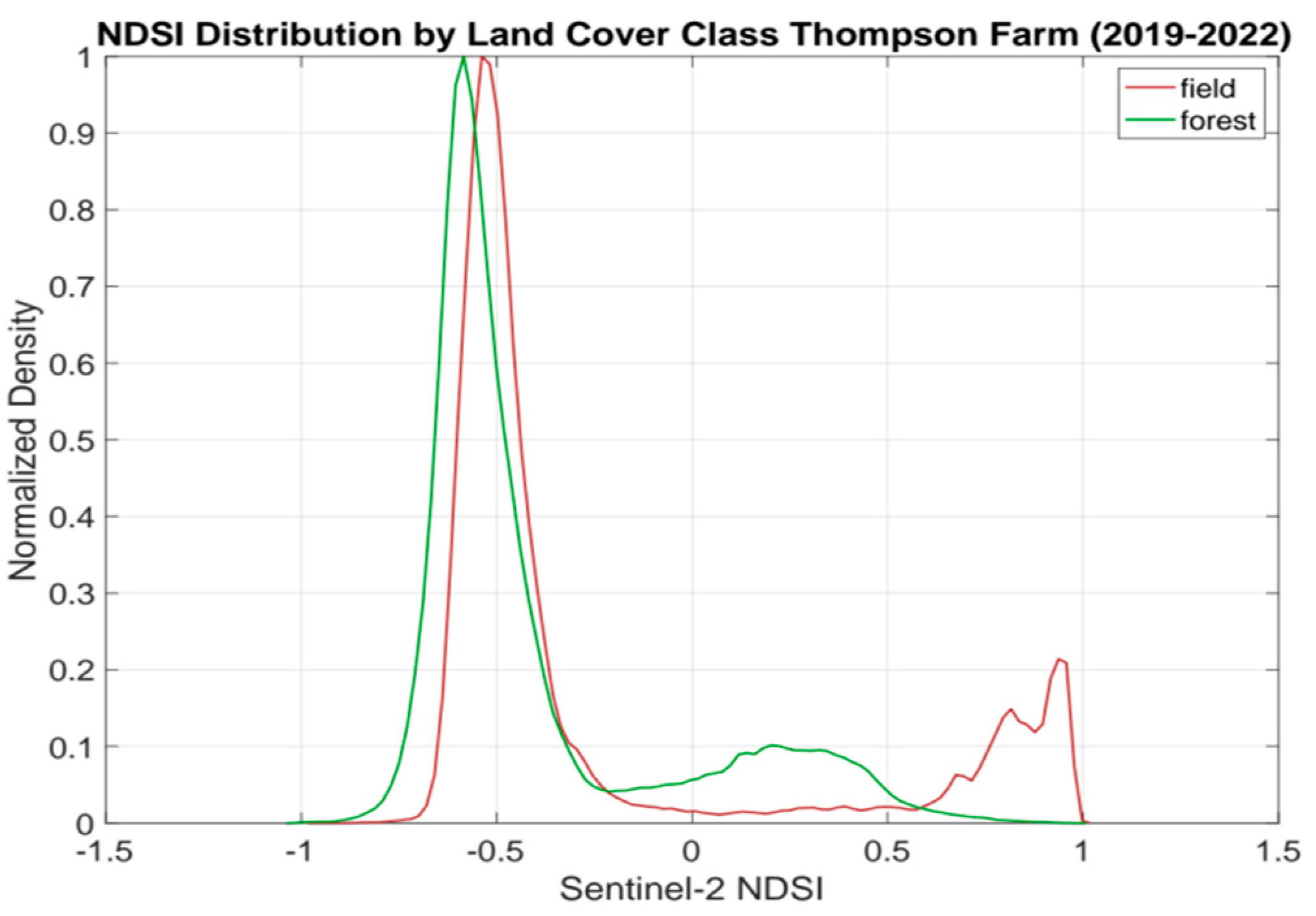
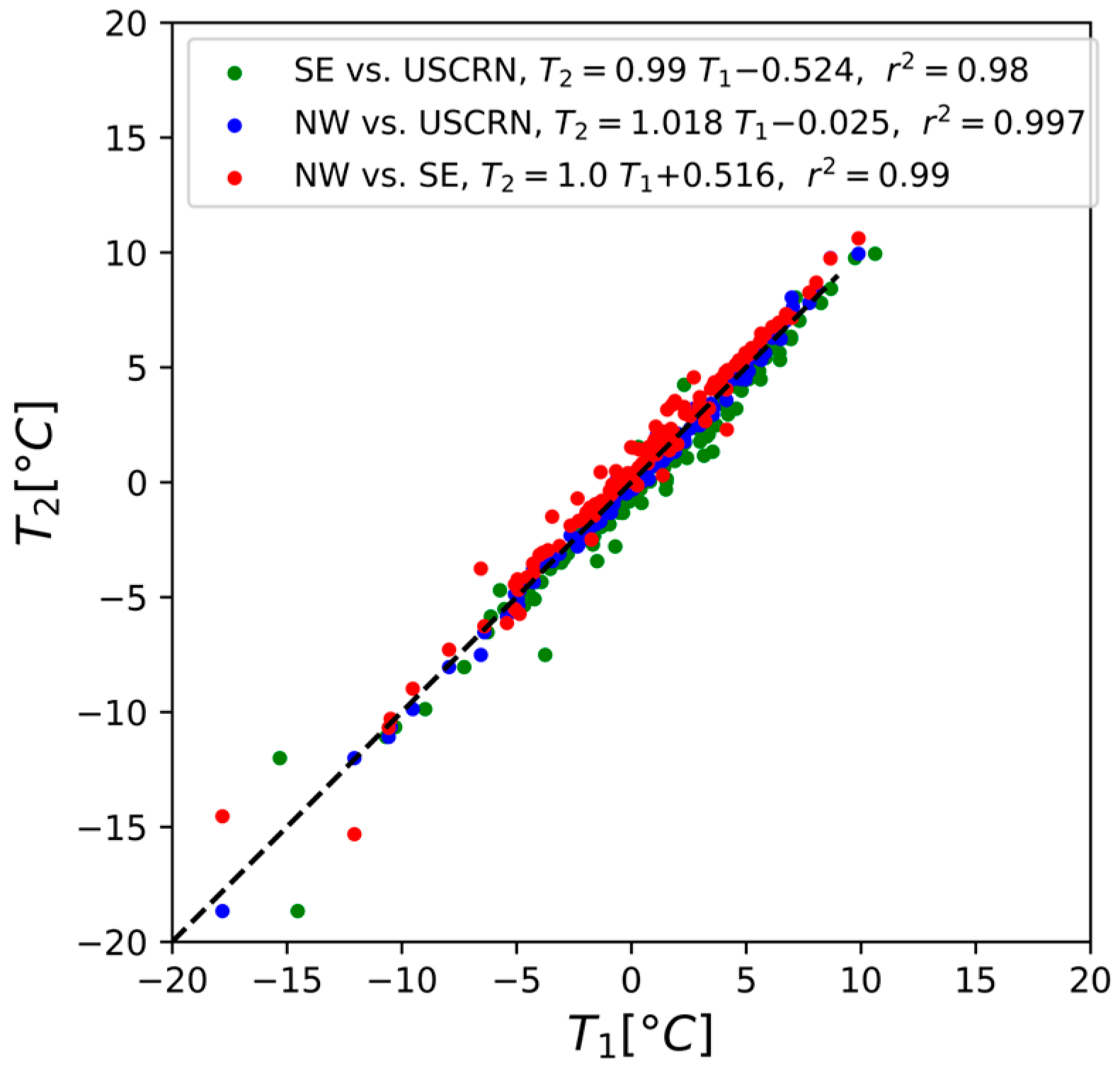
2.4. FT Reference Data
2.5. Ancillary Data
2.6. FT Detection Approaches
2.6.1. Seasonal Threshold Approach
2.6.2. General Threshold Approach
2.6.3. Interferometric Coherence Approach
2.7. Performance Metrics
3. Results
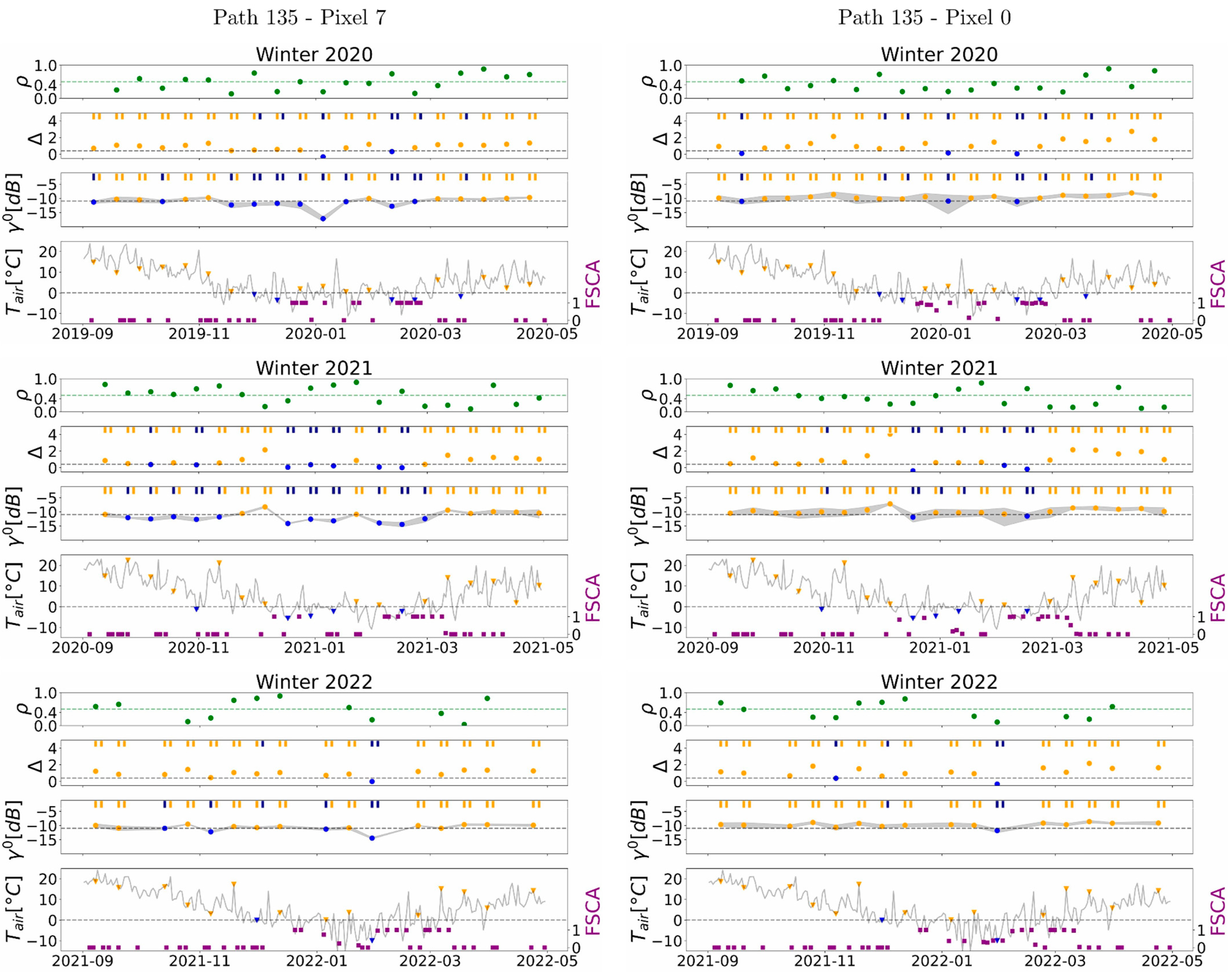
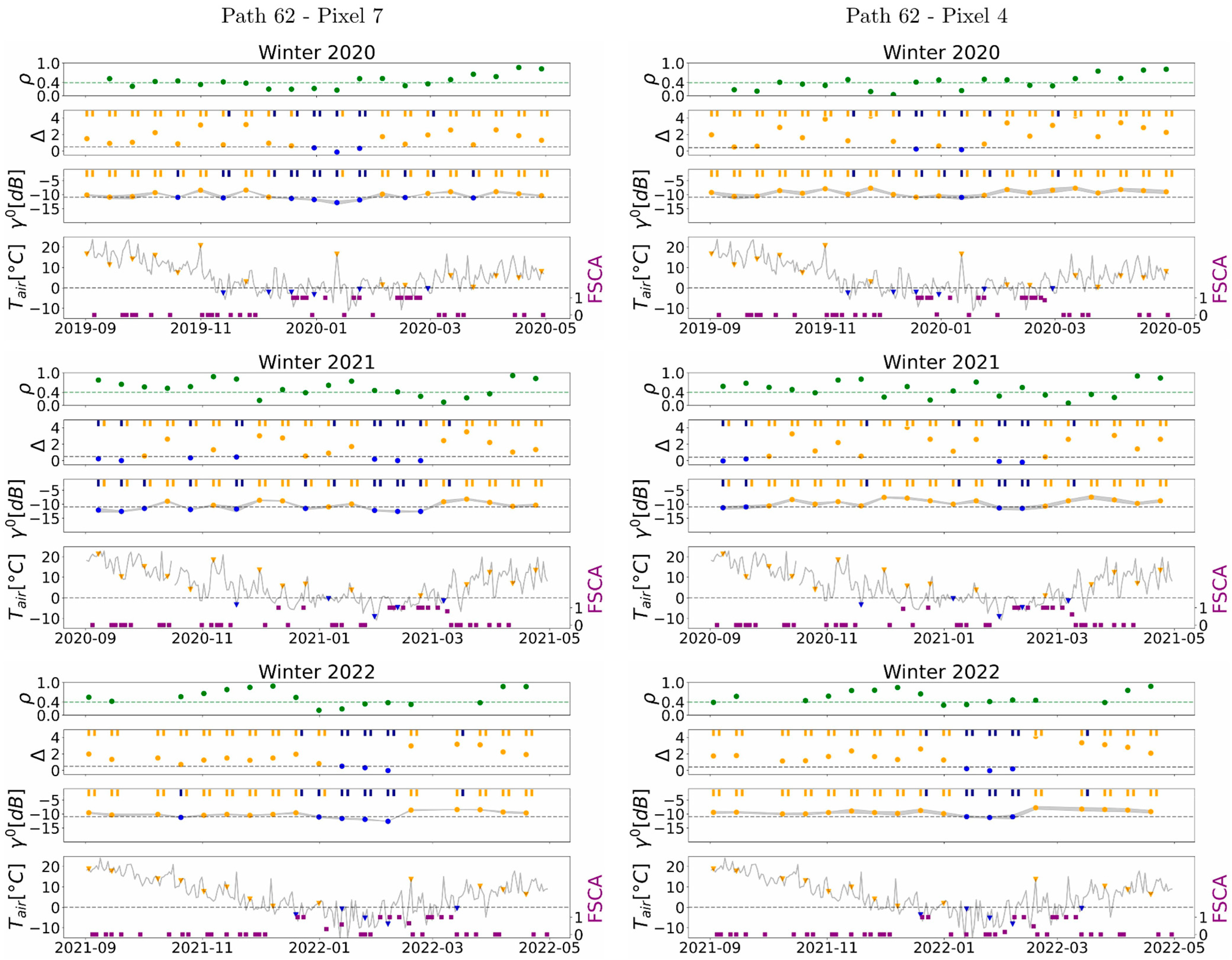
3.1. RCS Time-Series
3.2. Seasonal Threshold Approach
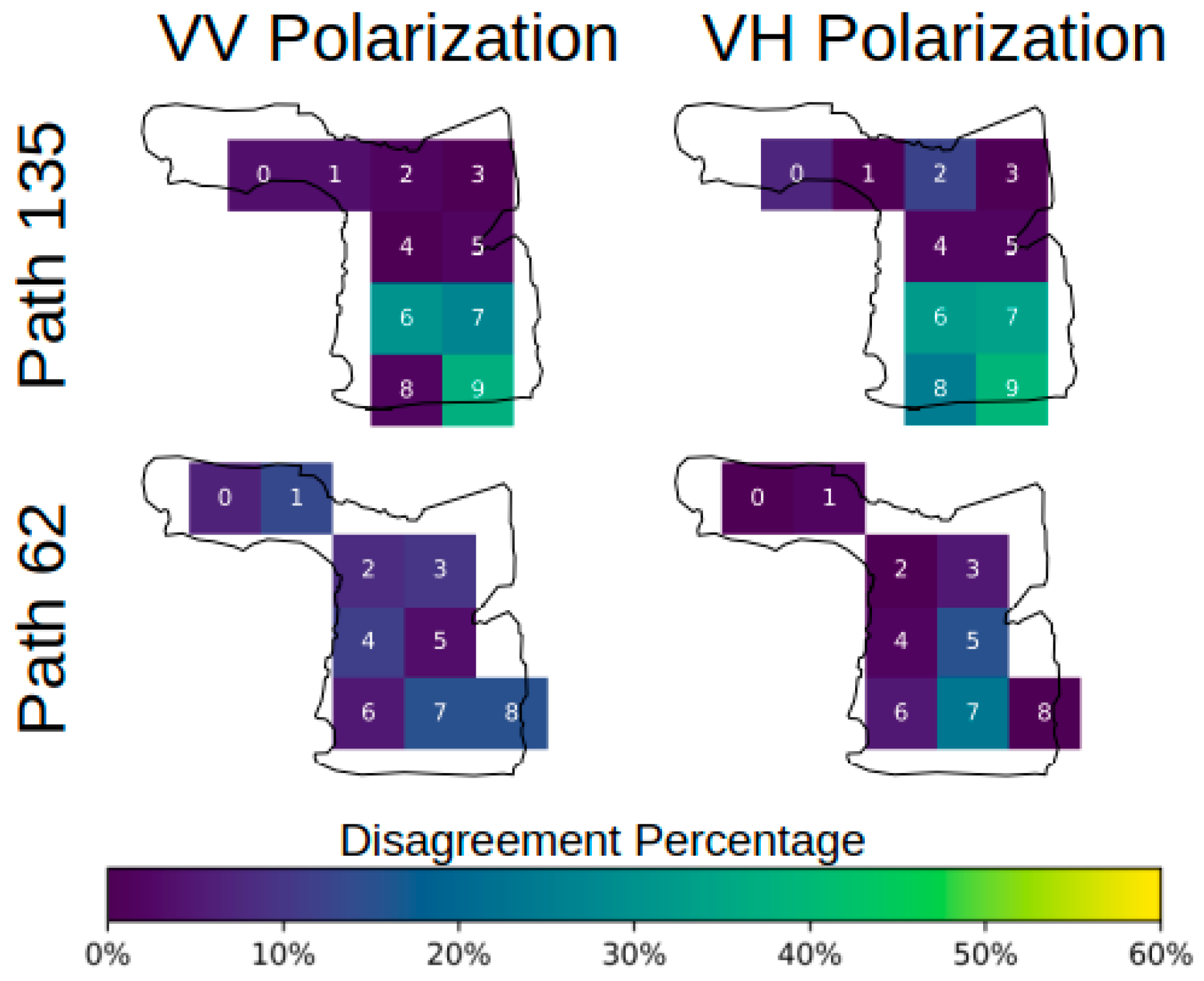
3.3. General Threshold Approach
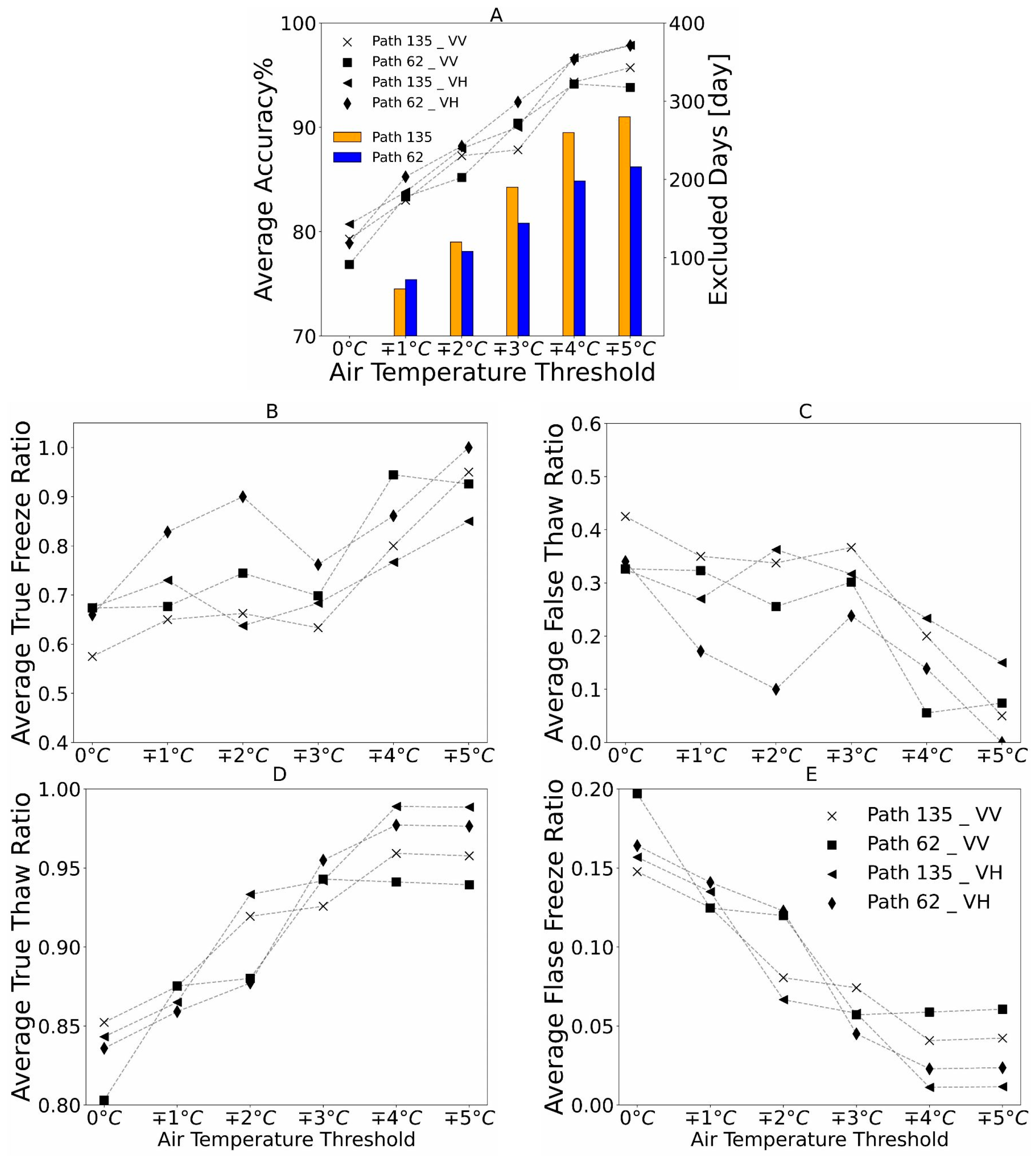
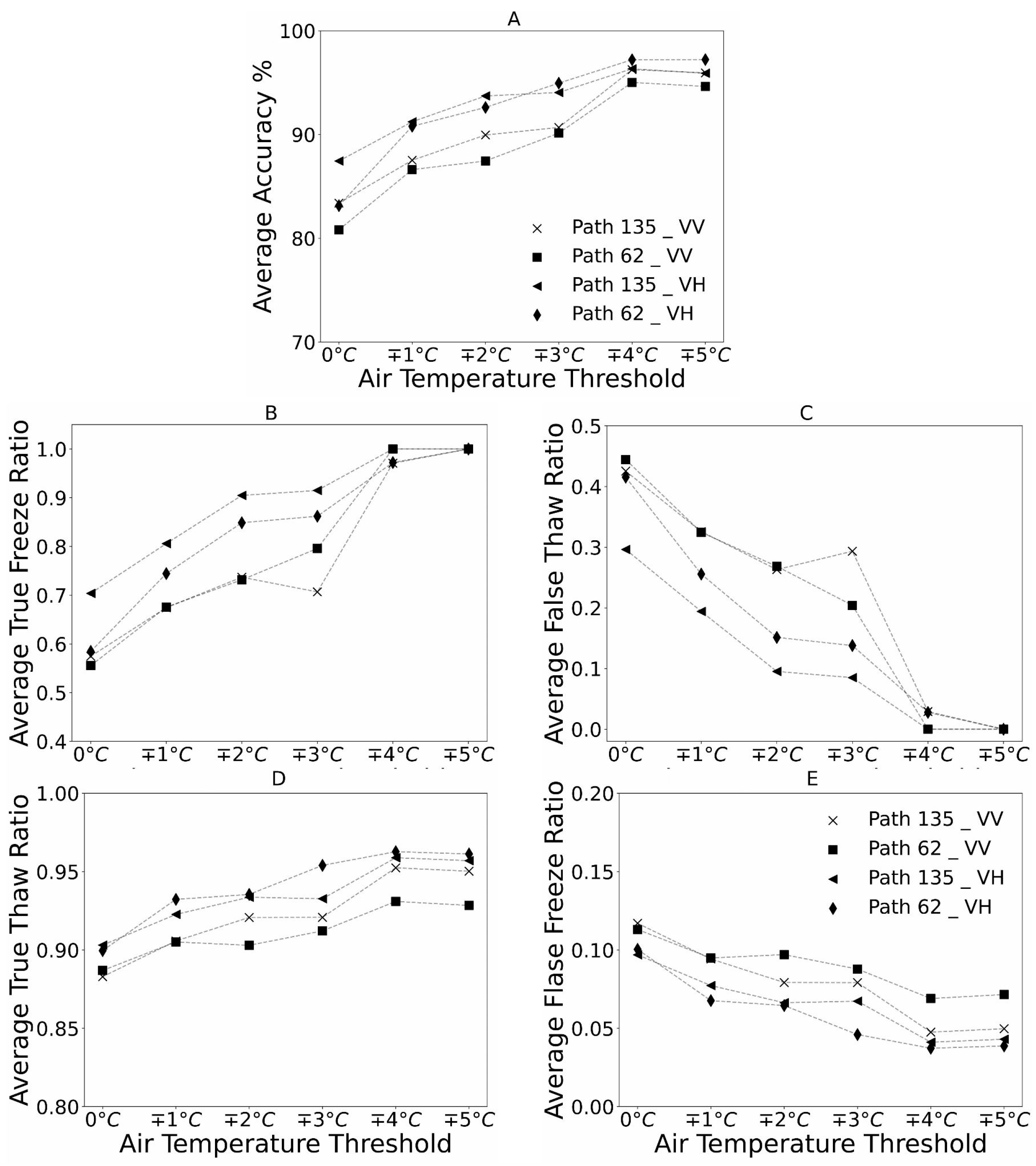
3.4. Impact of Air Temperature Threshold on FT Classification Accuracy
3.5. Coherence Approach
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
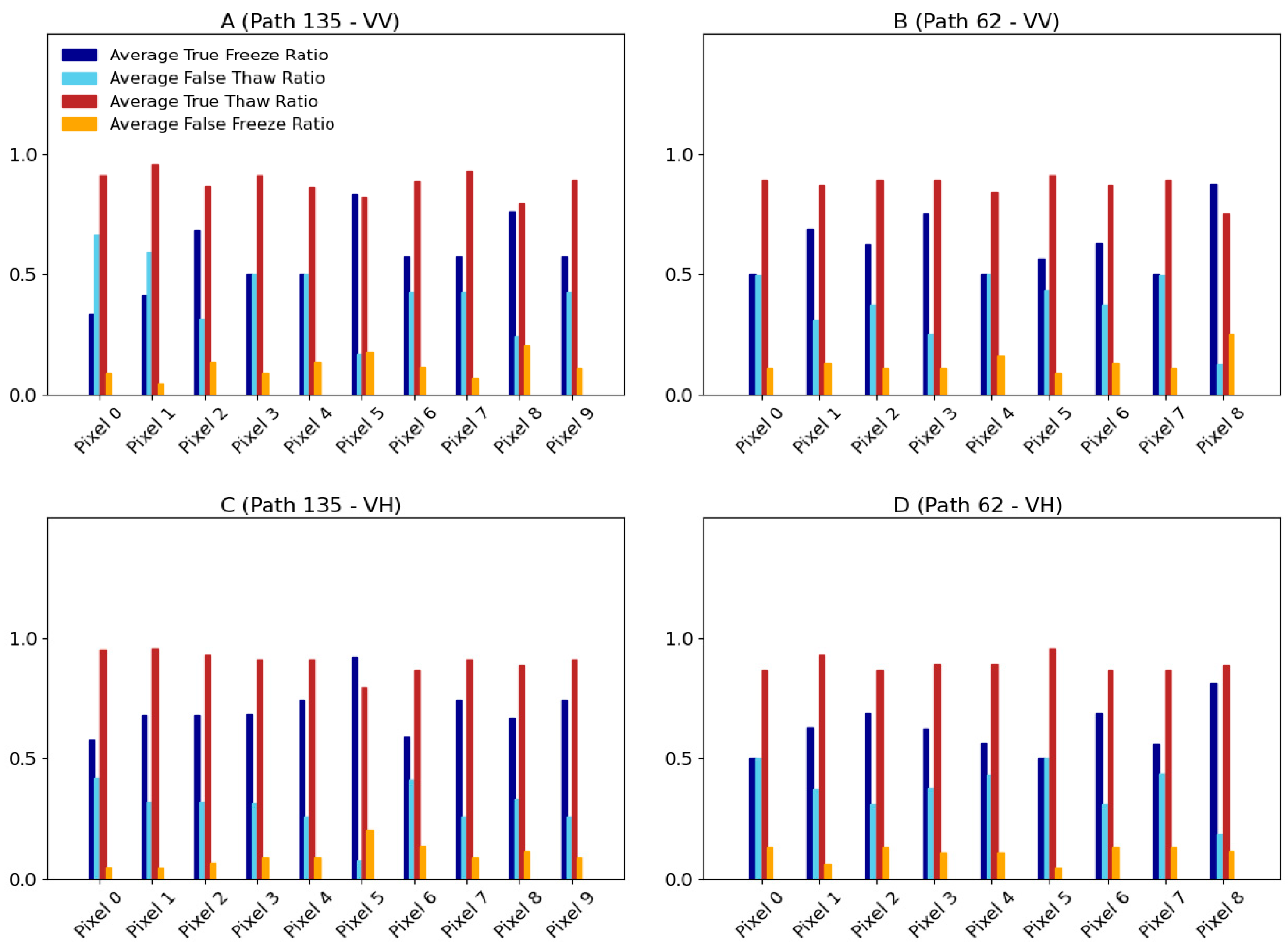
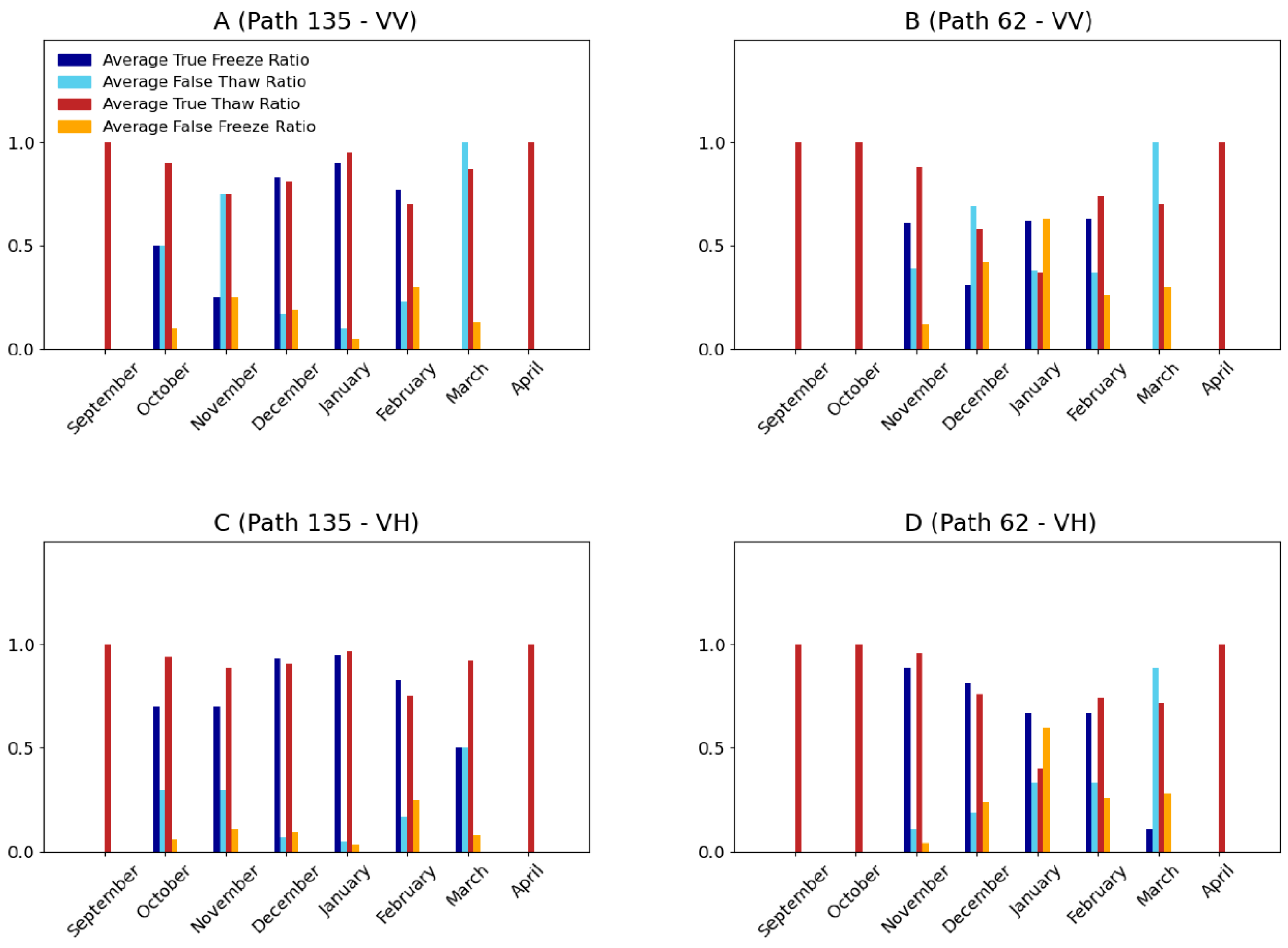
| Threshold (Linear Power) | Threshold [dB] | Kappa | True Freeze Ratio | False Thaw Ratio | True Thaw Ratio | False Freeze Ratio | Accuracy % | ||
|---|---|---|---|---|---|---|---|---|---|
| VV | 135 | 0.065 | 11.87 | 0.36 | 0.39 | 0.61 | 0.92 | 0.08 | 80.9 |
| 0.07 | 11.55 | 0.4 | 0.5 | 0.5 | 0.89 | 0.11 | 80.5 | ||
| 0.075 | 11.25 | 0.41 | 0.58 | 0.43 | 0.85 | 0.15 | 79.3 | ||
| 0.08 | 10.97 | 0.35 | 0.63 | 0.37 | 0.78 | 0.23 | 74.5 | ||
| 0.085 | 10.71 | 0.32 | 0.69 | 0.31 | 0.72 | 0.28 | 71.1 | ||
| 0.09 | 10.46 | 0.3 | 0.77 | 0.23 | 0.65 | 0.35 | 67.5 | ||
| 0.095 | 10.22 | 0.23 | 0.84 | 0.16 | 0.52 | 0.48 | 58.8 | ||
| 0.1 | 10.00 | 0.19 | 0.91 | 0.09 | 0.42 | 0.58 | 52.3 | ||
| 62 | 0.065 | 11.87 | 0.1 | 0.1 | 0.9 | 0.97 | 0.03 | 73.9 | |
| 0.07 | 11.55 | 0.25 | 0.24 | 0.76 | 0.95 | 0.05 | 76.5 | ||
| 0.075 | 11.25 | 0.37 | 0.38 | 0.62 | 0.94 | 0.06 | 78.9 | ||
| 0.08 | 10.97 | 0.39 | 0.47 | 0.53 | 0.89 | 0.11 | 78 | ||
| 0.085 | 10.71 | 0.45 | 0.58 | 0.42 | 0.86 | 0.14 | 78.5 | ||
| 0.09 | 10.46 | 0.45 | 0.67 | 0.33 | 0.8 | 0.2 | 76.9 | ||
| 0.095 | 10.22 | 0.41 | 0.72 | 0.28 | 0.75 | 0.25 | 74.1 | ||
| 0.1 | 10.00 | 0.33 | 0.75 | 0.25 | 0.65 | 0.35 | 67.6 | ||
| VH | 135 | 0.008 | 20.97 | 0.14 | 0.11 | 0.89 | 0.99 | 0.01 | 79.8 |
| 0.01 | 20.00 | 0.25 | 0.22 | 0.78 | 0.97 | 0.03 | 80.9 | ||
| 0.0125 | 19.03 | 0.34 | 0.33 | 0.68 | 0.95 | 0.05 | 82 | ||
| 0.015 | 18.24 | 0.41 | 0.48 | 0.53 | 0.91 | 0.09 | 81.6 | ||
| 0.0175 | 17.57 | 0.48 | 0.68 | 0.33 | 0.84 | 0.16 | 80.7 | ||
| 0.02 | 16.99 | 0.46 | 0.82 | 0.18 | 0.76 | 0.24 | 77.3 | ||
| 0.03 | 15.23 | 0.11 | 1 | 0 | 0.22 | 0.78 | 38.9 | ||
| 0.04 | 13.98 | 0.01 | 1 | 0 | 0.02 | 0.98 | 22.7 | ||
| 62 | 0.008 | 20.97 | 0.04 | 0.03 | 0.97 | 0.99 | 0.01 | 73.7 | |
| 0.01 | 20.00 | 0.1 | 0.08 | 0.92 | 0.99 | 0.01 | 74.8 | ||
| 0.0125 | 19.03 | 0.2 | 0.19 | 0.81 | 0.97 | 0.03 | 76.1 | ||
| 0.015 | 18.24 | 0.35 | 0.34 | 0.66 | 0.95 | 0.05 | 78.9 | ||
| 0.0175 | 17.57 | 0.43 | 0.47 | 0.53 | 0.92 | 0.08 | 79.8 | ||
| 0.02 | 16.99 | 0.48 | 0.66 | 0.34 | 0.84 | 0.16 | 78.9 | ||
| 0.03 | 15.23 | 0.19 | 0.98 | 0.02 | 0.32 | 0.68 | 49.3 | ||
| 0.04 | 13.98 | 0.04 | 1 | 0 | 0.08 | 0.92 | 32.4 |
References
- Nielsen, C.B.; Groffman, P.M.; Hamburg, S.P.; Driscoll, C.T.; Fahey, T.J.; Hardy, J.P. Freezing effects on carbon and nitrogen cycling in northern hardwood forest soils. Soil Sci. Soc. Am. J. 2001, 65, 1723–1730. [Google Scholar] [CrossRef]
- Yang, K.; Wang, C. Water storage effect of soil freeze-thaw process and its impacts on soil hydro-thermal regime variations. Agric. For. Meteorol. 2019, 265, 280–294. [Google Scholar] [CrossRef]
- Zhang, T.; Barry, R.G.; Armstrong, R.L. Application of satellite remote sensing techniques to frozen ground studies. Polar Geogr. 2004, 28, 163–196. [Google Scholar] [CrossRef]
- Bélanger, G.; Castonguay, Y.; Bertrand, A.; Dhont, C.; Rochette, P.; Couture, L.; Drapeau, R.; Mongrain, D.; Chalifour, F.P.; Michaud, R. Winter damage to perennial forage crops in eastern Canada: Causes, mitigation, and prediction. Can. J. Plant Sci. 2006, 86, 33–47. [Google Scholar] [CrossRef]
- Sharratt, B.S. Freeze-thaw and winter temperature of agricultural soils in interior Alaska. Cold Reg. Sci. Technol. 1993, 22, 105–111. [Google Scholar] [CrossRef]
- Sharratt, B.S.; Saxton, K.E.; Radke, J.K. Freezing and thawing of agricultural soils: Implications for soil, water, and air quality. J. Minn. Acad. Sci. 1995, 59, 1–5. [Google Scholar]
- Six, J.; Bossuyt, H.; Degryze, S.; Denef, K. A history of research on the link between (micro) aggregates, soil biota, and soil organic matter dynamics. Soil Tillage Res. 2004, 79, 7–31. [Google Scholar] [CrossRef]
- Chang, X.; Jin, H.; Zhang, Y.; He, R.; Luo, D.; Wang, Y.; Lü, L.; Zhang, Q. Thermal impacts of boreal forest vegetation on active layer and permafrost soils in northern Da Xing’anling (Hinggan) Mountains, Northeast China. Arct. Antarct. Alp. Res. 2015, 47, 267–279. [Google Scholar] [CrossRef]
- Jiang, H.; Yi, Y.; Zhang, W.; Yang, K.; Chen, D. Sensitivity of soil freeze/thaw dynamics to environmental conditions at different spatial scales in the central Tibetan Plateau. Sci. Total Environ. 2020, 734, 139261. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). The 2022 GCOS ECVs Requirements (GCOS 245). 2022. Available online: https://library.wmo.int/viewer/58111/download?file=GCOS-245_2022_GCOS_ECVs_Requirements.pdf&type=pdf&navigator=1 (accessed on 11 January 2023).
- Whitcraft, A.K.; Becker-Reshef, I.; Justice, C.O.; Gifford, L.; Kavvada, A.; Jarvis, I. No pixel left behind: Toward integrating Earth Observations for agriculture into the United Nations Sustainable Development Goals framework. Remote Sens. Environ. 2019, 235, 111470. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Zhang, K.; McDonald, K.C. Satellite detection of increasing Northern Hemisphere non-frozen seasons from 1979 to 2008: Implications for regional vegetation growth. Remote Sens. Environ. 2012, 121, 472–487. [Google Scholar] [CrossRef]
- Kraatz, S.; Jacobs, J.M.; Schröder, R.; Cho, E.; Cosh, M.; Seyfried, M.; Prueger, J.; Livingston, S. Evaluation of SMAP freeze/thaw retrieval accuracy at core validation sites in the contiguous United States. Remote Sens. 2018, 10, 1483. [Google Scholar] [CrossRef]
- Rautiainen, K.; Parkkinen, T.; Lemmetyinen, J.; Schwank, M.; Wiesmann, A.; Ikonen, J.; Derksen, C.; Davydov, S.; Davydova, A.; Boike, J.; et al. SMOS prototype algorithm for detecting autumn soil freezing. Remote Sens. Environ. 2016, 180, 346–360. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, L.; Cui, H.; Wang, G.; Yang, J.; Liu, X.; Su, X. Evaluation and analysis of SMAP, AMSR2 and MEaSUREs freeze/thaw products in China. Remote Sens. Environ. 2020, 242, 111734. [Google Scholar] [CrossRef]
- Livingstone, C.E.; Sikaneta, I.; Gierull, C.; Chiu, S.; Beaulne, P. RADARSAT-2 system and mode description. In Meeting Proceedings; RTO-MP-SCI-150, Paper; RTO: Bangalore, India, 2005; Volume 15. [Google Scholar]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Werninghaus, R.; Buckreuss, S. The TerraSAR-X mission and system design. IEEE Trans. Geosci. Remote Sens. 2009, 48, 606–614. [Google Scholar] [CrossRef]
- Covello, F.; Battazza, F.; Coletta, A.; Lopinto, E.; Fiorentino, C.; Pietranera, L.; Valentini, G.; Zoffoli, S. COSMO-SkyMed an existing opportunity for observing the Earth. J. Geodyn. 2010, 49, 171–180. [Google Scholar] [CrossRef]
- Baghdadi, N.; Abou Chaaya, J.; Zribi, M. Semiempirical calibration of the integral equation model for SAR data in C-band and cross polarization using radar images and field measurements. IEEE Geosci. Remote Sens. Lett. 2010, 8, 14–18. [Google Scholar] [CrossRef]
- Baghdadi, N.; Bazzi, H.; El Hajj, M.; Zribi, M. Detection of frozen soil using Sentinel-1 SAR data. Remote Sens. 2018, 10, 1182. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Bazzi, H.; Zribi, M. Near real-time freeze detection over agricultural plots using Sentinel-1 data. Remote Sens. 2020, 12, 1976. [Google Scholar] [CrossRef]
- Rodionova, N.V. Identification of Frozen/Thawed Soils in the Areas of Anadyr (Chukotka) and Belaya Gora (Sakha) from the Sentinel 1 Radar Data. Izv. Atmos. Ocean. Phys. 2019, 55, 1314–1321. [Google Scholar]
- Entekhabi, D.; Njoku, E.; Houser, P.; Spencer, M.; Doiron, T.; Smith, J.; Girard, R.; Belair, S.; Crow, W.; Jackson, T.; et al. The Hydrosphere State (HYDROS) mission concept: An Earth SystemPathfinder for global mapping of soil moisture and land freeze/thaw. Trans. Geosci. Remote Sens. 2004, 42, 2184–2195. [Google Scholar]
- Chen, Y.; Wang, L.; Bernier, M.; Ludwig, R. Retrieving Freeze/Thaw Cycles Using Sentinel-1 Data in Eastern Nunavik (Québec, Canada). Remote Sens. 2022, 14, 802. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, L.; Rautiainen, K.; Zhang, C.; Xiao, Z.; Li, H.; Yang, J.; Cui, H. Daily High-Resolution Land Surface Freeze/Thaw Detection Using Sentinel-1 and AMSR2 Data. Remote Sens. 2022, 14, 2854. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, Z.; Shen, Q.; Chen, Q.; Liu, X. Identifying soil freeze/thaw states using scattering and coherence time series of high-resolution C-band synthetic aperture radar in the Qinghai-Tibet Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 15, 519–532. [Google Scholar] [CrossRef]
- Cho, E.; Hunsaker, A.G.; Jacobs, J.M.; Palace, M.; Sullivan, F.B.; Burakowski, E.A. Maximum entropy modeling to identify physical drivers of shallow snowpack heterogeneity using unpiloted aerial system (UAS) lidar. J. Hydrol. 2021, 602, 126722. [Google Scholar]
- Jacobs, J.M.; Hunsaker, A.G.; Sullivan, F.B.; Palace, M.; Burakowski, E.A.; Herrick, C.; Cho, E. Snow depth mapping with unpiloted aerial system lidar observations: A case study in Durham, New Hampshire, United States. Cryosphere 2021, 15, 1485–1500. [Google Scholar] [CrossRef]
- Proulx, H.; Jacobs, J.M.; Burakowski, E.A.; Cho, E.; Hunsaker, A.G.; Sullivan, F.B.; Palace, M.; Wagner, C. Brief communication: Comparison of in-situ ephemeral snow depth measurements over a mixed-use temperate forest landscape. Cryosphere Discuss. 2023, 17, 3435–3442. [Google Scholar] [CrossRef]
- Johnston, J.; Jacobs, J.M.; Cho, E. Global Snow Seasonality Regimes from Satellite Records of Snow Cover. J. Hydrometeorol. 2023, 25, 65–88. [Google Scholar]
- Lopes, A.; Touzi, R.; Nezry, E. Adaptive speckle filters and scene heterogeneity. IEEE Trans. Geosci. Remote Sens. 1990, 28, 992–1000. [Google Scholar] [CrossRef]
- Shi, Z.; Fung, K.B. A comparison of digital speckle filters. In Proceedings of the IGARSS’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; IEEE: Piscataway, NJ, USA, 1994; Volume 4, pp. 2129–2133. [Google Scholar]
- Alaska Satellite Facility RTC Guild. Available online: https://hyp3-docs.asf.alaska.edu/guides/rtc_product_guide/ (accessed on 1 August 2023).
- Alaska Satellite Facility InSAR Product Guide. Available online: https://hyp3-docs.asf.alaska.edu/guides/insar_product_guide/ (accessed on 1 August 2023).
- Henry, H.A. Soil freeze–thaw cycle experiments: Trends, methodological weaknesses and suggested improvements. Soil Biol. Biochem. 2007, 39, 977–986. [Google Scholar] [CrossRef]
- Moradi, M.; Cho, E.; Jacobs, J.M.; Vuyovich, C.M. Seasonal soil freeze/thaw variability across North America via ensemble land surface modeling. Cold Reg. Sci. Technol. 2023, 209, 103806. [Google Scholar] [CrossRef]
- Ren, J.; Vanapalli, S.K.; Han, Z. Soil freezing process and different expressions for the soil-freezing characteristic curve. Sci. Cold Arid Reg. 2017, 9, 221–228. [Google Scholar]
- Gascoin, S.; Barrou Dumont, Z.; Deschamps-Berger, C.; Marti, F.; Salgues, G.; López-Moreno, J.I.; Revuelto, J.; Michon, T.; Schattan, P.; Hagolle, O. Estimating fractional snow cover in open terrain from sentinel-2 using the normalized difference snow index. Remote Sens. 2020, 12, 2904. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Appel, I. Estimating fractional snow cover from MODIS using the normalized difference snow index. Remote Sens. Environ. 2004, 89, 351–360. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. Algorithm Theoretical Basis Document (ATBD) for the MODIS Snow and Sea Ice-Mapping Algorithms (Text); 610 WebDev; NASA GSFC: Greenbelt, MD, USA, 2001; Volume 45, pp. 14–28.
- Tong, R.; Parajka, J.; Komma, J.; Blöschl, G. Mapping snow cover from daily Collection 6 MODIS products over Austria. J. Hydrol. 2020, 590, 125548. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Zhang, G.; Che, T.; Yan, W.; Ye, M.; Ma, N. Ground-based evaluation of MODIS snow cover product V6 across China: Implications for the selection of NDSI threshold. Sci. Total Environ. 2019, 651, 2712–2726. [Google Scholar] [CrossRef]
- Schwanghart, W.; Scherler, D. TopoToolbox 2–MATLAB-based software for topographic analysis and modeling in Earth surface sciences. Earth Surf. Dyn. 2014, 2, 1–7. [Google Scholar] [CrossRef]
- Reda, I.; Andreas, A. Solar Position Algorithm for Solar Radiation Applications; National Renewable Energy Laboratory: Golden, CO, USA, 2008.
- Entekhabi, D.; Yueh, S.; De Lannoy, G. SMAP Handbook; NASA: Washington, DC, USA, 2014.
- Podest, E.; McDonald, K.C.; Kimball, J.S. Multisensor microwave sensitivity to freeze/thaw dynamics across a complex boreal landscape. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6818–6828. [Google Scholar] [CrossRef]
- Bakon, M.; Czikhardt, R.; Papco, J.; Barlak, J.; Rovnak, M.; Adamisin, P.; Perissin, D. remotIO: A Sentinel-1 multi-temporal InSAR infrastructure monitoring service with automatic updates and data mining capabilities. Remote Sens. 2020, 12, 1892. [Google Scholar] [CrossRef]
- Cigna, F.; Banks, V.J.; Donald, A.W.; Donohue, S.; Graham, C.; Hughes, D.; McKinley, J.M.; Parker, K. Mapping ground instability in areas of geotechnical infrastructure using satellite InSAR and Small UAV surveying: A case study in Northern Ireland. Geosciences 2017, 7, 51. [Google Scholar] [CrossRef]
- Macchiarulo, V.; Milillo, P.; Blenkinsopp, C.; Reale, C.; Giardina, G. Multi-temporal InSAR for transport infrastructure monitoring: Recent trends and challenges. Proc. Inst. Civ. Eng. Bridge Eng. 2021, 176, 92–117. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.; Dubovyk, O.; Greve, K. The potential of sentinel-1 InSAR coherence for grasslands monitoring in Eastern Cape, South Africa. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102306. [Google Scholar] [CrossRef]
- Nasirzadehdizaji, R.; Cakir, Z.; Sanli, F.B.; Abdikan, S.; Pepe, A.; Calo, F. Sentinel-1 interferometric coherence and backscattering analysis for crop monitoring. Comput. Electron. Agric. 2021, 185, 106118. [Google Scholar] [CrossRef]
- Zalite, K.; Antropov, O.; Praks, J.; Voormansik, K.; Noorma, M. Monitoring of agricultural grasslands with time series of X-band repeat-pass interferometric SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 3687–3697. [Google Scholar] [CrossRef]
- Lu, Z.; Meyer, D.J. Study of high SAR backscattering caused by an increase of soil moisture over a sparsely vegetated area: Implications for characteristics of backscattering. Int. J. Remote Sens. 2002, 23, 1063–1074. [Google Scholar] [CrossRef]
- Moeremans, B.; Dautrebande, S. Soil moisture evaluation by means of multi-temporal ERS SAR PRI images and interferometric coherence. J. Hydrol. 2000, 234, 162–169. [Google Scholar] [CrossRef]
- Zhang, T.; Zeng, Q.; Li, Y.; Xiang, Y. Study on relation between InSAR coherence and soil moisture. In Proceedings of the ISPRS Congress, Beijing, China, 3–11 July 2008; pp. 3–11. [Google Scholar]
- Zwieback, S.; Hensley, S.; Hajnsek, I. Assessment of soil moisture effects on L-band radar interferometry. Remote Sens. Environ. 2015, 164, 77–89. [Google Scholar] [CrossRef]
- Wegmueller, U. Soil Moisture Monitoring with ERS SAR Interferometry; Print; ESA SP: São Paulo, Brazil, 1997; pp. 47–52. [Google Scholar]
- Li, Z.; Guo, H.; Li, X.; Wang, C. SAR Interferometry coherence analysis for snow mapping. In Proceedings of the IGARSS 2001. Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No. 01CH37217), Sydney, NSW, Australia, 9–13 July 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 6, pp. 2905–2907. [Google Scholar]
- Lund, J.; Forster, R.R.; Deeb, E.J.; Liston, G.E.; Skiles, S.M.; Marshall, H.P. Interpreting Sentinel-1 SAR backscatter signals of snowpack surface melt/freeze, warming, and ripening, through field measurements and physically-based SnowModel. Remote Sens. 2022, 14, 4002. [Google Scholar] [CrossRef]
- Singh, G.; Venkataraman, G.; Rao, Y.S.; Kumar, V. InSAR coherence measurement techniques for snow cover mapping in Himalayan region. In Proceedings of the IGARSS 2008-2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 4, pp. IV-1077–IV-1080. [Google Scholar]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Medica Biochem. Medica 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Kraatz, S.; Jacobs, J.M.; Miller, H.J. Spatial and temporal freeze-thaw variations in Alaskan roads. Cold Reg. Sci. Technol. 2019, 157, 149–162. [Google Scholar] [CrossRef]
- Tsai, Y.L.S.; Dietz, A.; Oppelt, N.; Kuenzer, C. Remote sensing of snow cover using spaceborne SAR: A review. Remote Sens. 2019, 11, 1456. [Google Scholar] [CrossRef]
- Mätzler, C. Applications of the interaction of microwaves with the natural snow cover. Remote Sens. Rev. 1987, 2, 259–387. [Google Scholar] [CrossRef]
- Karbou, F.; Veyssière, G.; Coleou, C.; Dufour, A.; Gouttevin, I.; Durand, P.; Gascoin, S.; Grizonnet, M. Monitoring wet snow over an alpine region using Sentinel-1 observations. Remote Sens. 2021, 13, 381. [Google Scholar] [CrossRef]
- Ashcraft, I.S.; Long, D.G. Comparison of methods for melt detection over Greenland using active and passive microwave measurements. Int. J. Remote Sens. 2006, 27, 2469–2488. [Google Scholar] [CrossRef]
- Floricioiu, D.; Rott, H. Seasonal and short-term variability of multifrequency, polarimetric radar backscatter of alpine terrain from SIR-C/X-SAR and AIRSAR data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2634–2648. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Batlivala, P.P.; Dobson, M.C. Microwave backscatter dependence on surface roughness, soil moisture, and soil texture: Part I-bare soil. IEEE Trans. Geosci. Electron. 1978, 16, 286–295. [Google Scholar] [CrossRef]
- Barrett, B.W.; Dwyer, E.; Whelan, P. Soil moisture retrieval from active spaceborne microwave observations: An evaluation of current techniques. Remote Sens. 2009, 1, 210–242. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- McNairn, H.; Brisco, B. The application of C-band polarimetric SAR for agriculture: A review. Can. J. Remote Sens. 2004, 30, 525–542. [Google Scholar] [CrossRef]
- Schmugge, T.J.; Kustas, W.P.; Ritchie, J.C.; Jackson, T.J.; Rango, A. Remote sensing in hydrology. Adv. Water Resour. 2002, 25, 1367–1385. [Google Scholar] [CrossRef]
- Brown, R.J.; Pokier, S.; Manore, M.J. Correlations between X, C and L-band imagery within an agricultural environment. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS’88), Edinburgh, UK, 12–16 September 1988; pp. 1279–1280. [Google Scholar]
- Derksen, C.; Xu, X.; Dunbar, R.S.; Colliander, A.; Kim, Y.; Kimball, J.S.; Black, T.A.; Euskirchen, E.; Langlois, A.; Loranty, M.M.; et al. Retrieving landscape freeze/thaw state from Soil Moisture Active Passive (SMAP) radar and radiometer measurements. Remote Sens. Environ. 2017, 194, 48–62. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Xu, X.; Dunbar, R.S.; Colliander, A.; Derksen, C. Global assessment of the SMAP freeze/thaw data record and regional applications for detecting spring onset and frost events. Remote Sens. 2019, 11, 1317. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Derksen, C.; Brucker, L.; Langlois, A.; Mialon, A.; Kerr, Y.H. Evaluation of spaceborne L-band radiometer measurements for terrestrial freeze/thaw retrievals in Canada. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4442–4459. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Cartus, O.; Lavalle, M.; Magnard, C.; Milillo, P.; Oveisgharan, S.; Osmanoglu, B.; Rosen, P.A.; Wegmüller, U. Global seasonal Sentinel-1 interferometric coherence and backscatter data set. Sci. Data 2022, 9, 73. [Google Scholar] [CrossRef]
- Yun, H.W.; Kim, J.R.; Choi, Y.S.; Lin, S.Y. Analyses of time series InSAR signatures for land cover classification: Case studies over dense forestry areas with L-band SAR images. Sensors 2019, 19, 2830. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J.; Lemmetyinen, J.; Ruiz, J.J.; Rautiainen, K.; Ikonen, J.; Kontu, A.; Pulliainen, J. Detection of soil and canopy freeze/thaw state in the boreal region with L and C Band Synthetic Aperture Radar. Remote Sens. Environ. 2024, 305, 114102. [Google Scholar] [CrossRef]
- Cohen, J.; Rautiainen, K.; Lemmetyinen, J.; Smolander, T.; Vehviläinen, J.; Pulliainen, J. Sentinel-1 based soil freeze/thaw estimation in boreal forest environments. Remote Sens. Environ. 2021, 254, 112267. [Google Scholar] [CrossRef]
- Meyer, F. Spaceborne Synthetic Aperture Radar: Principles, data access, and basic processing techniques. In Synthetic Aperture Radar (SAR) Handbook: Comprehensive Methodologies for Forest Monitoring and Biomass Estimation; NASA: Washington, DC, USA, 2019; pp. 21–64. [Google Scholar]
- Du, J.; Kimball, J.S.; Azarderakhsh, M.; Dunbar, R.S.; Moghaddam, M.; McDonald, K.C. Classification of Alaska spring thaw characteristics using satellite L-band radar remote sensing. IEEE Trans. Geosci. Remote Sens. 2014, 53, 542–556. [Google Scholar]
- Kim, Y.; Kimball, J.S.; Glassy, J.; Du, J. An extended global Earth system data record on daily landscape freeze–thaw status determined from satellite passive microwave remote sensing. Earth Syst. Sci. Data 2017, 9, 133–147. [Google Scholar] [CrossRef]
- Mortin, J.; Schrøder, T.M.; Walløe Hansen, A.; Holt, B.; McDonald, K.C. Mapping of seasonal freeze-thaw transitions across the pan-Arctic land and sea ice domains with satellite radar. J. Geophys. Res. Ocean. 2012, 117, C08004. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Derksen, C.; Rowlandson, T.; Berg, A.; Lemmetyinen, J.; Royer, A.; Tetlock, E.; Helgason, W.; Sonnentag, O. Spatial variability of L-band brightness temperature during freeze/thaw events over a prairie environment. Remote Sens. 2017, 9, 894. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Williamson, M.; Rowlandson, T.; Derksen, C.; Royer, A.; Berg, A.A.; Lemmetyinen, J.; Arnold, L. Response of L-Band brightness temperatures to freeze/thaw and snow dynamics in a prairie environment from ground-based radiometer measurements. Remote Sens. Environ. 2017, 191, 67–80. [Google Scholar] [CrossRef]
- Lyu, H.; McColl, K.A.; Li, X.; Derksen, C.; Berg, A.; Black, T.A.; Euskirchen, E.; Loranty, M.; Pulliainen, J.; Rautiainen, K.; et al. Validation of the SMAP freeze/thaw product using categorical triple collocation. Remote Sens. Environ. 2018, 205, 329–337. [Google Scholar] [CrossRef]





| Path | Threshold (Linear Power) | Threshold [dB] | Kappa | True Freeze Ratio | False Thaw Ratio | True Thaw Ratio | False Freeze Ratio | Accuracy % | |
|---|---|---|---|---|---|---|---|---|---|
| VV | 135 | 0.08 | 10.97 | 0.35 | 0.63 | 0.37 | 0.78 | 0.23 | 74.5 |
| 62 | 0.39 | 0.47 | 0.53 | 0.89 | 0.11 | 78.0 | |||
| VH | 135 | 0.02 | 16.99 | 0.46 | 0.82 | 0.18 | 0.76 | 0.24 | 77.3 |
| 62 | 0.48 | 0.66 | 0.34 | 0.84 | 0.16 | 78.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradi, M.; Kraatz, S.; Johnston, J.; Jacobs, J.M. Comparing Three Freeze-Thaw Schemes Using C-Band Radar Data in Southeastern New Hampshire, USA. Remote Sens. 2024, 16, 2784. https://doi.org/10.3390/rs16152784
Moradi M, Kraatz S, Johnston J, Jacobs JM. Comparing Three Freeze-Thaw Schemes Using C-Band Radar Data in Southeastern New Hampshire, USA. Remote Sensing. 2024; 16(15):2784. https://doi.org/10.3390/rs16152784
Chicago/Turabian StyleMoradi, Mahsa, Simon Kraatz, Jeremy Johnston, and Jennifer M. Jacobs. 2024. "Comparing Three Freeze-Thaw Schemes Using C-Band Radar Data in Southeastern New Hampshire, USA" Remote Sensing 16, no. 15: 2784. https://doi.org/10.3390/rs16152784
APA StyleMoradi, M., Kraatz, S., Johnston, J., & Jacobs, J. M. (2024). Comparing Three Freeze-Thaw Schemes Using C-Band Radar Data in Southeastern New Hampshire, USA. Remote Sensing, 16(15), 2784. https://doi.org/10.3390/rs16152784








