The Preparation Phase of the 2023 Kahramanmaraş (Turkey) Major Earthquakes from a Multidisciplinary and Comparative Perspective
Abstract
1. Introduction
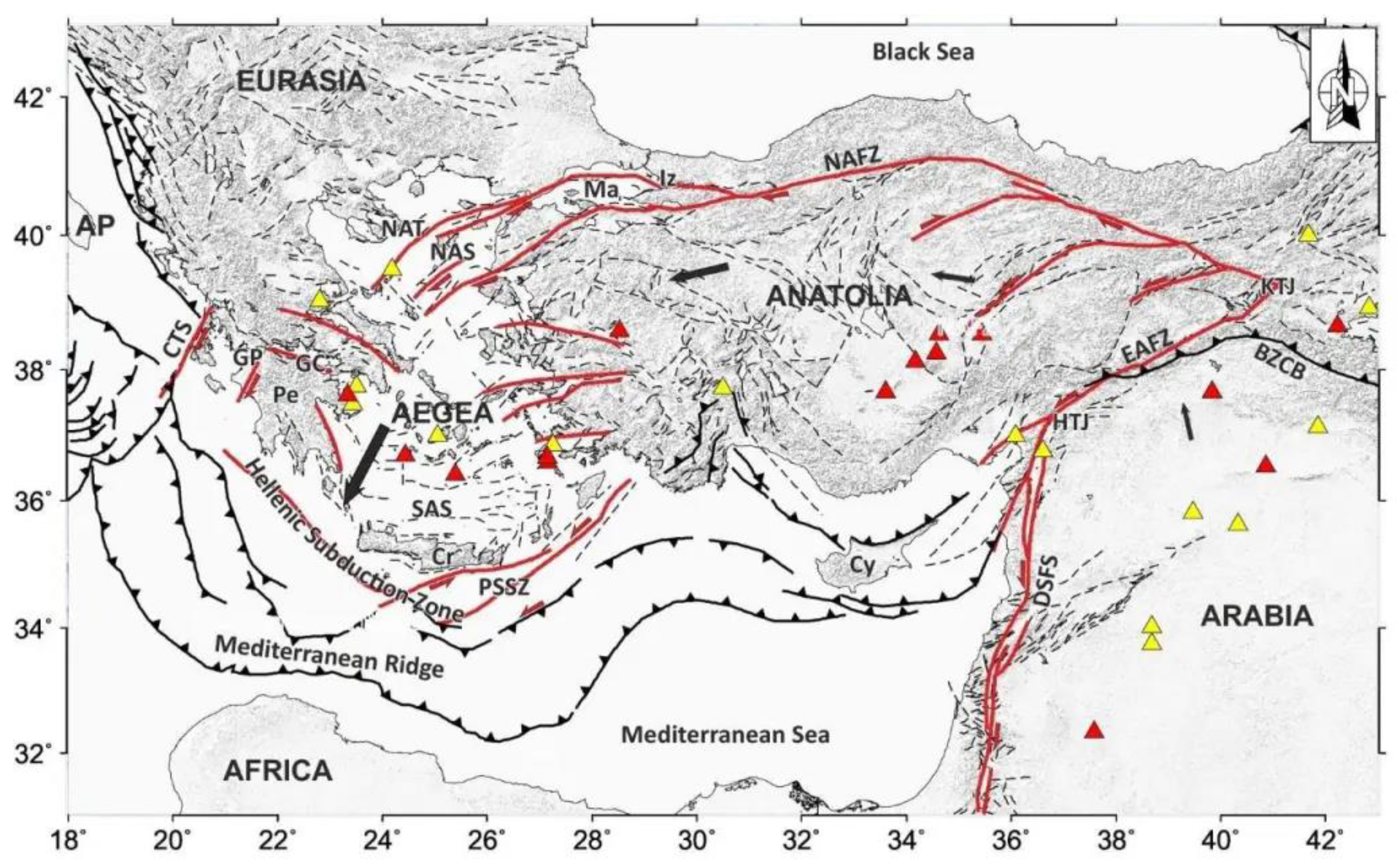
2. Geological and Geodynamic Settings
3. Multidisciplinary Data and Methods
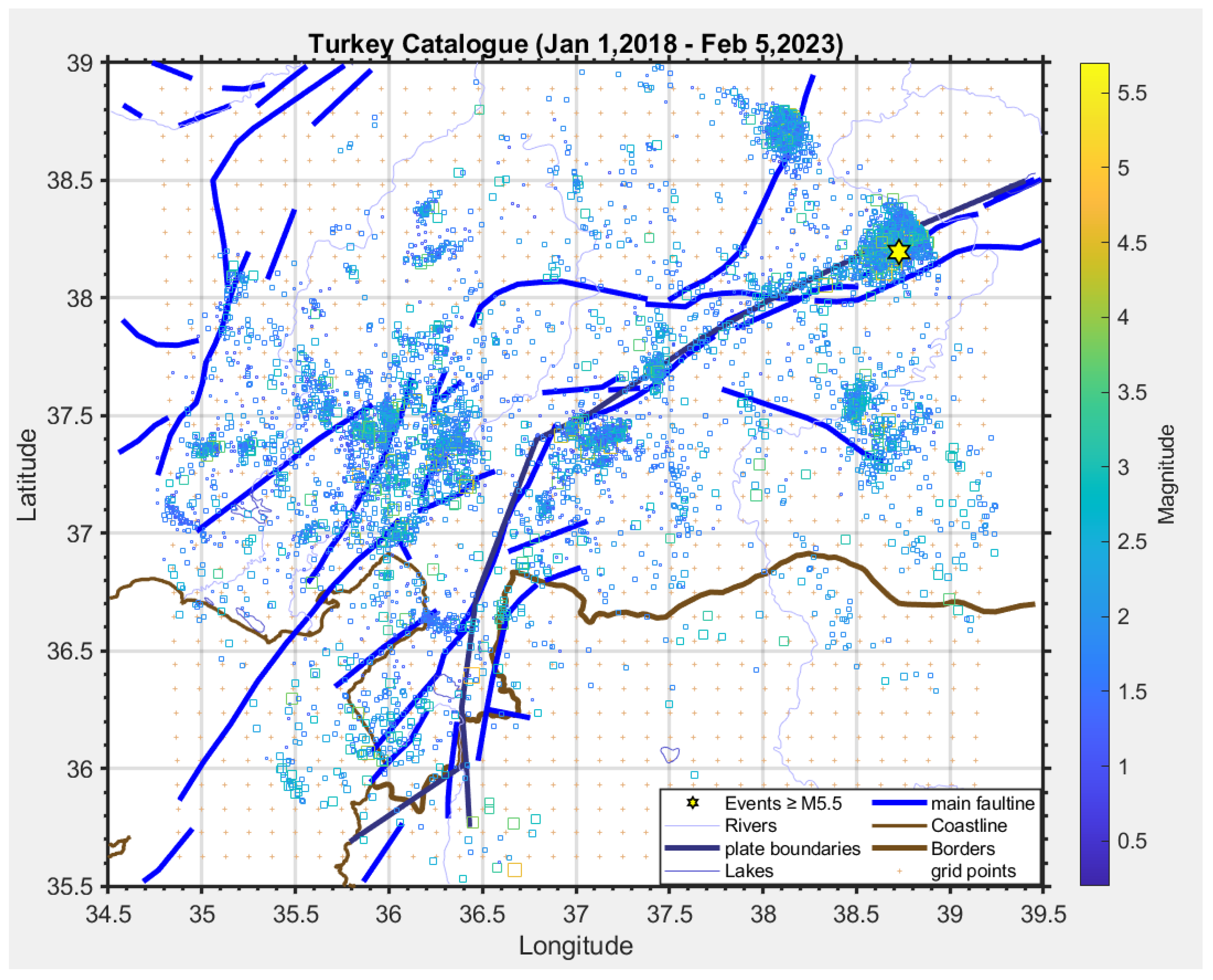
3.1. Earthquake Data Analyses
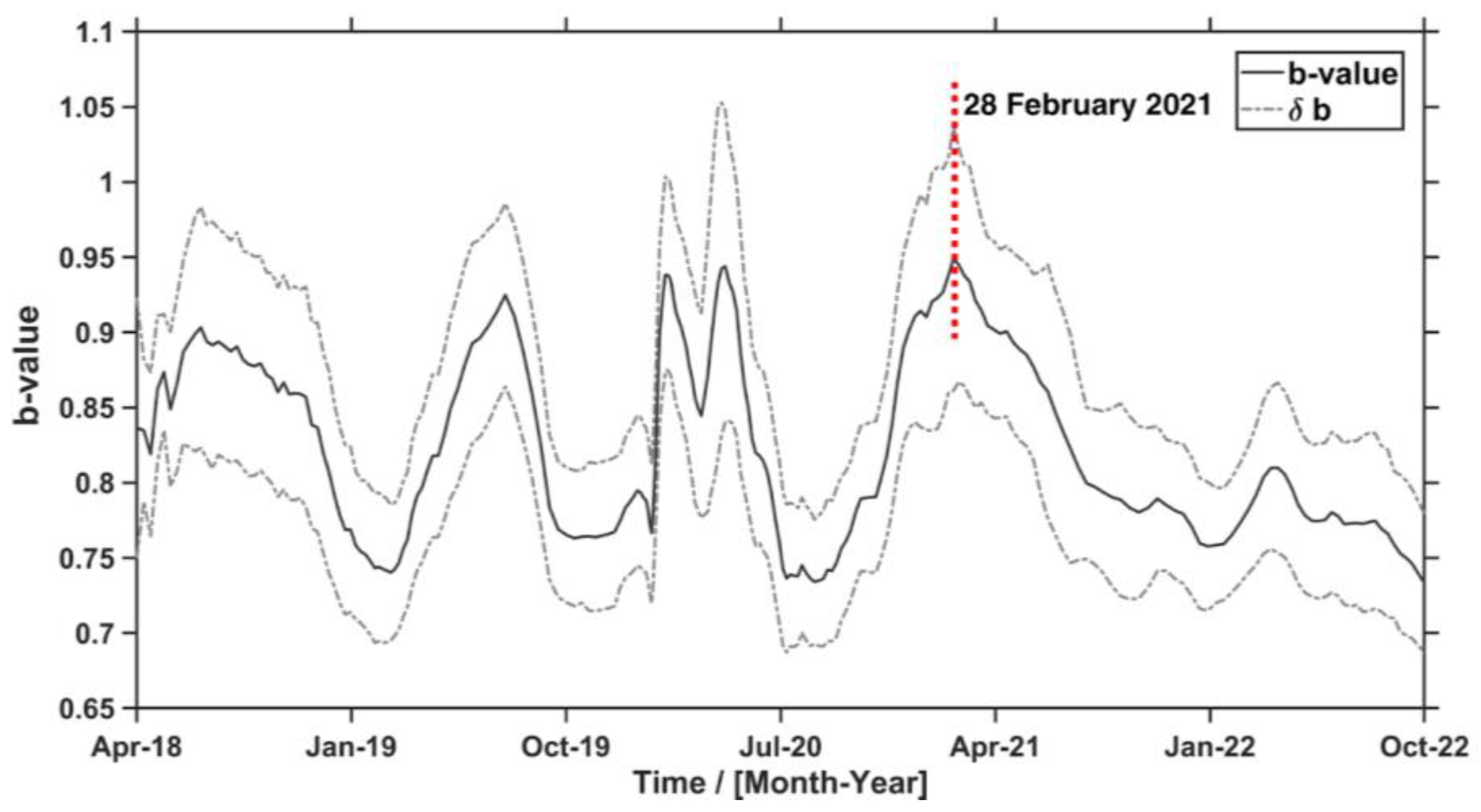
3.1.1. b-Value Analysis
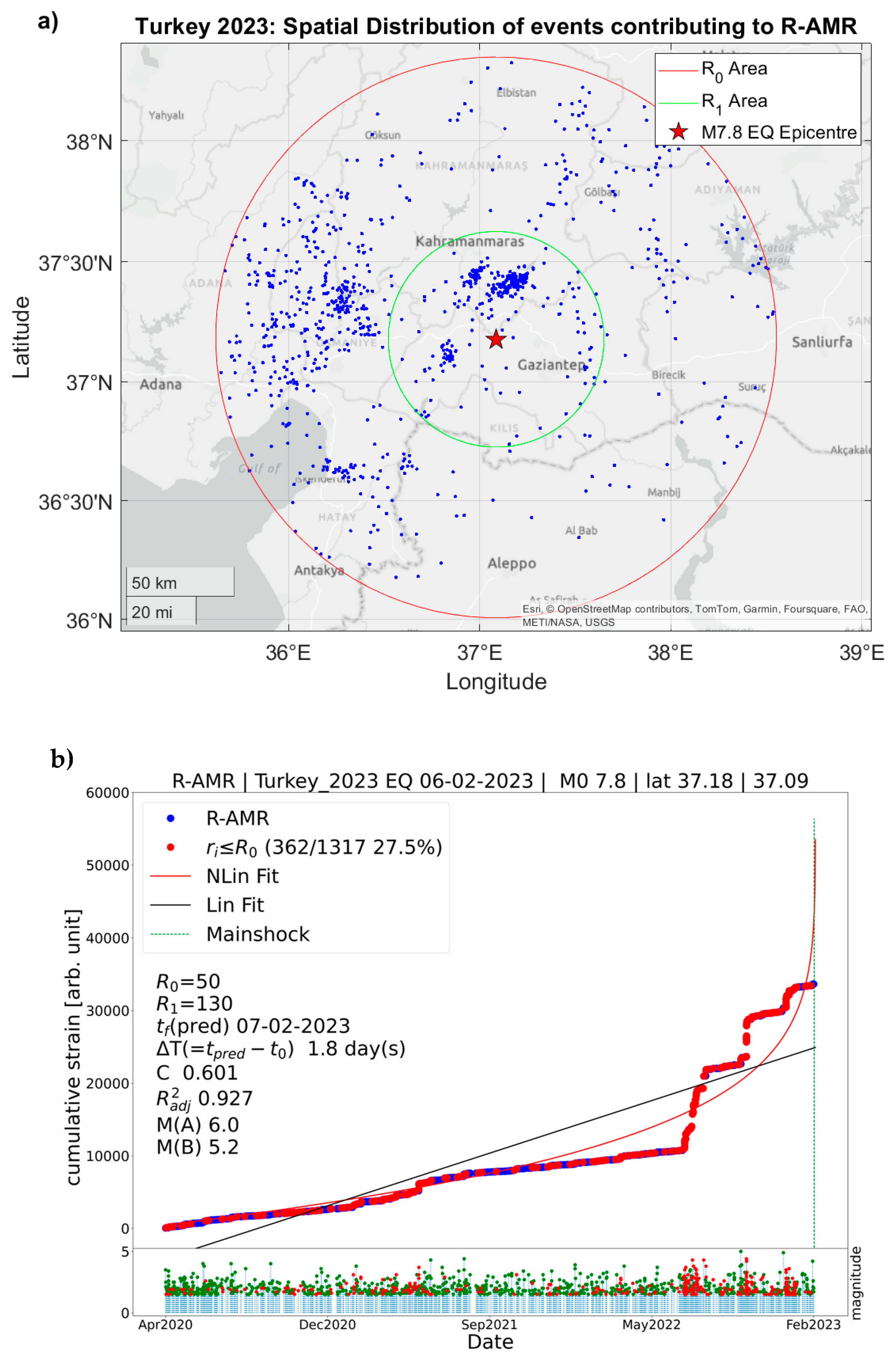
3.1.2. Revised Acceleration Seismic Release (R-AMR)
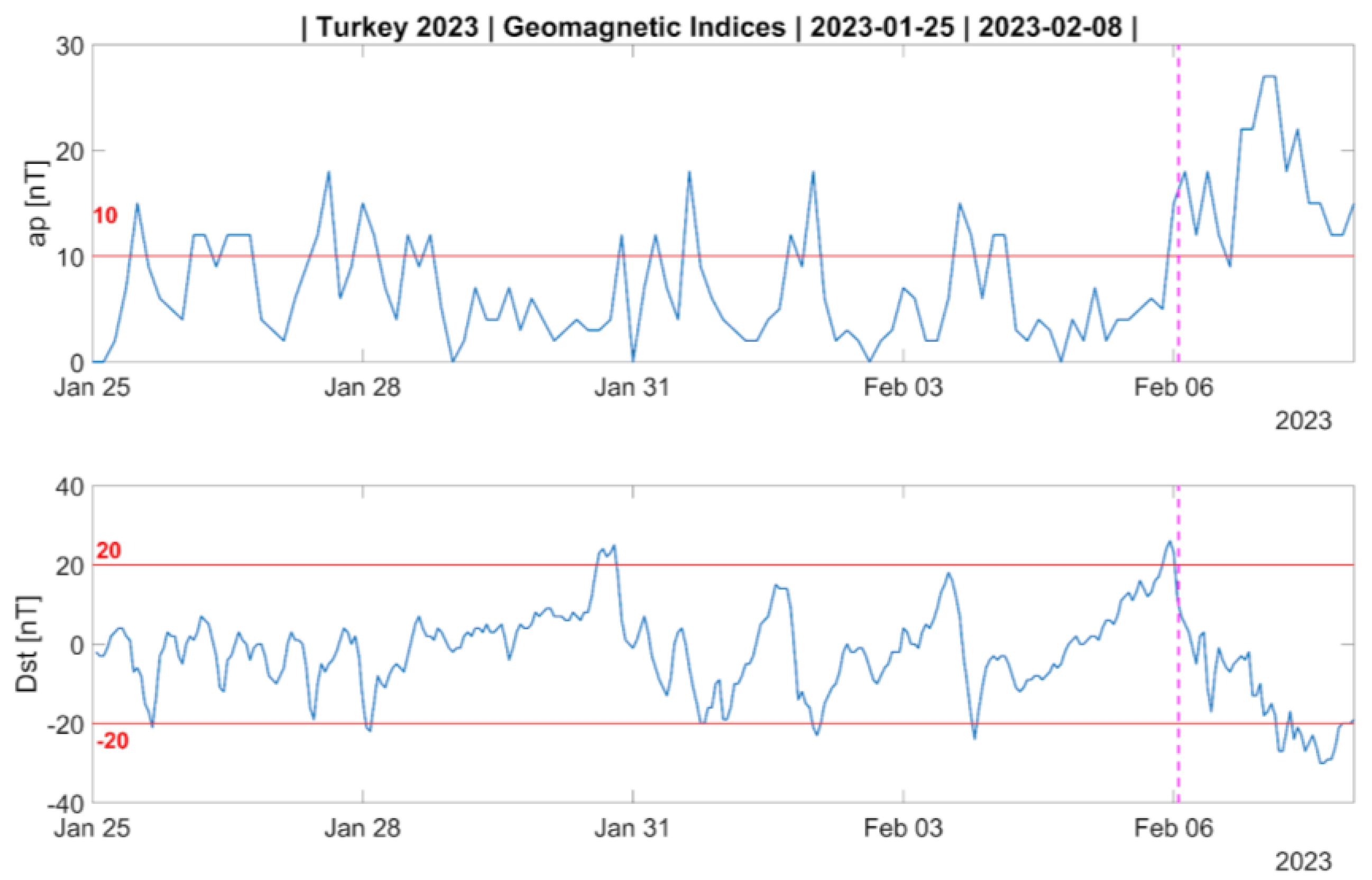
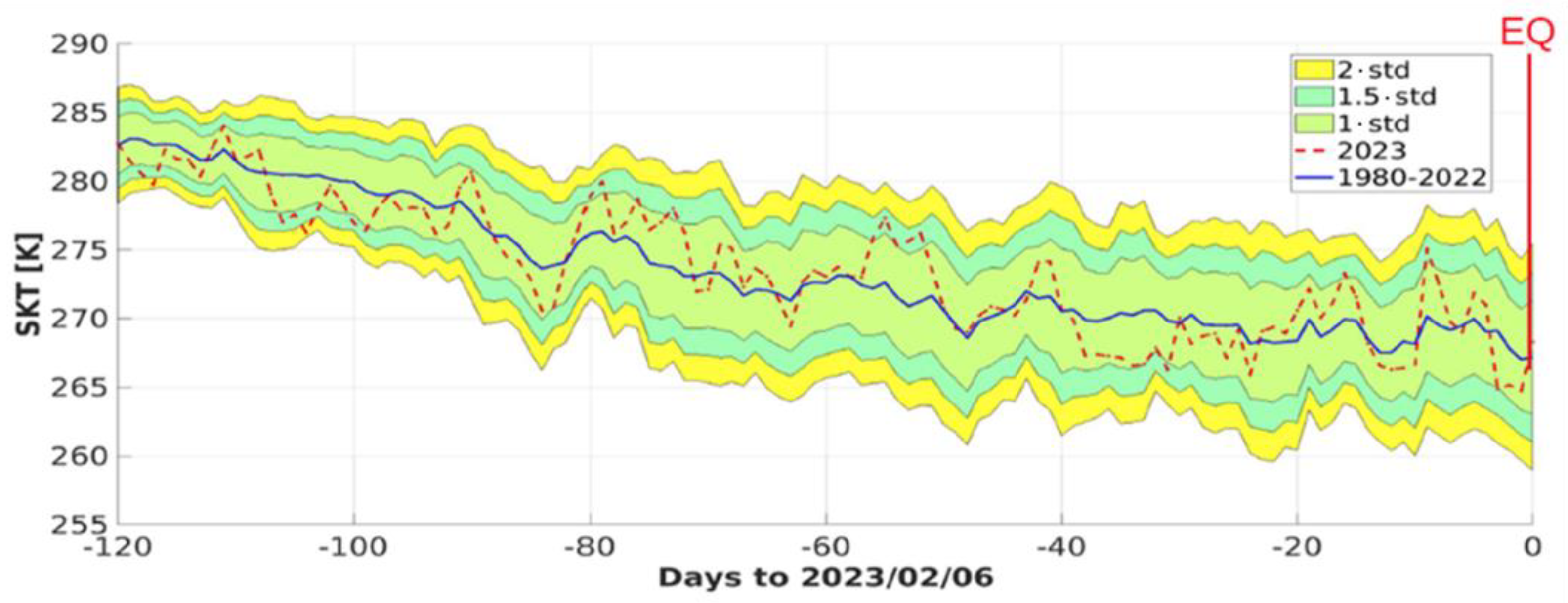
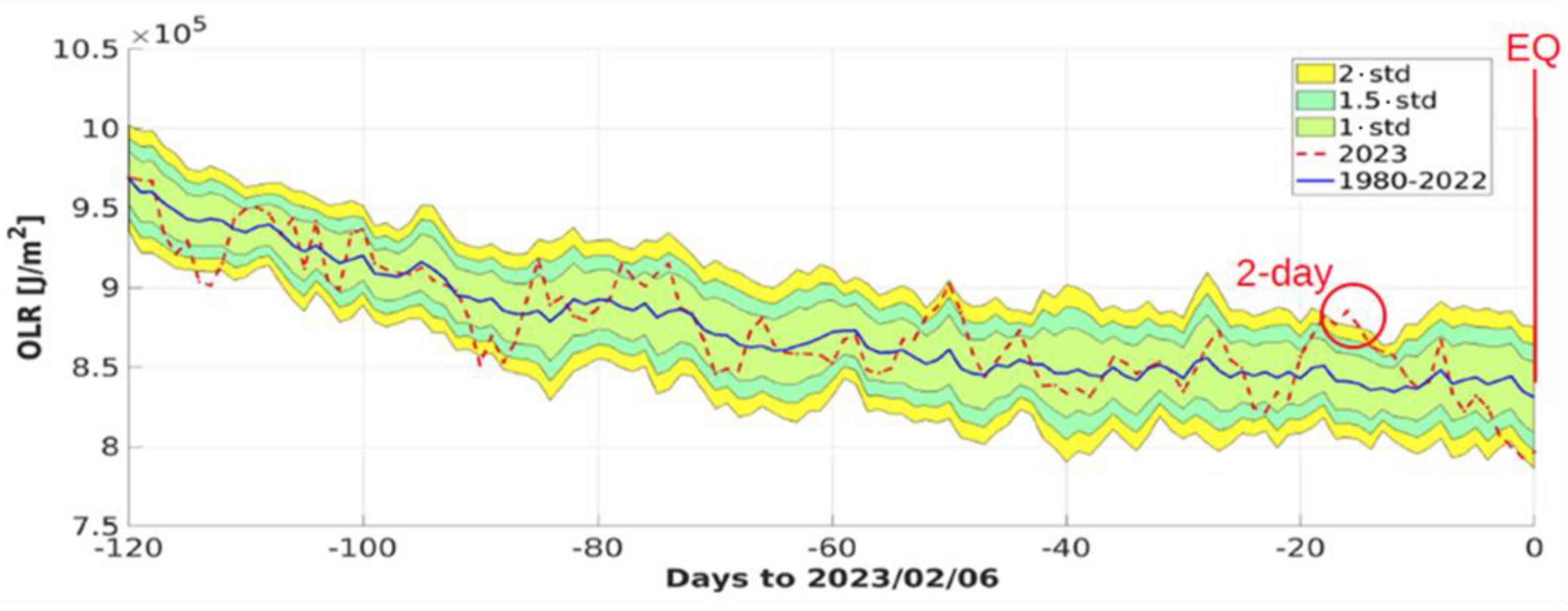
3.2. Atmospheric Data Analysis
3.3. Ionospheric Data Analysis
3.4. Electron Burst Data Analysis
4. Results
4.1. Seismological Analyses
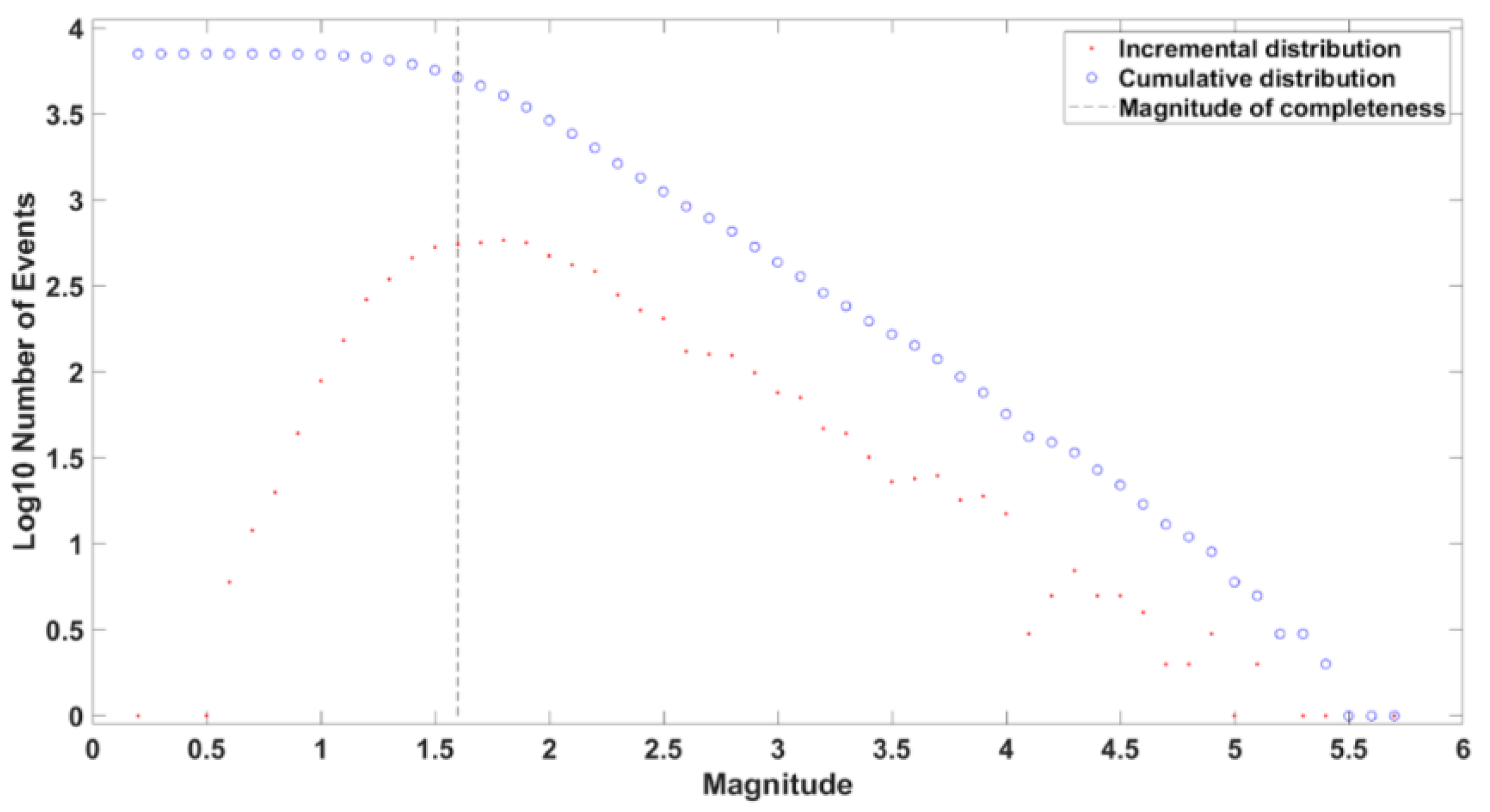
4.1.1. Magnitude of Completeness (Mc) and b-Value
4.1.2. R-AMR Analysis
4.2. Atmospheric Data Analysis
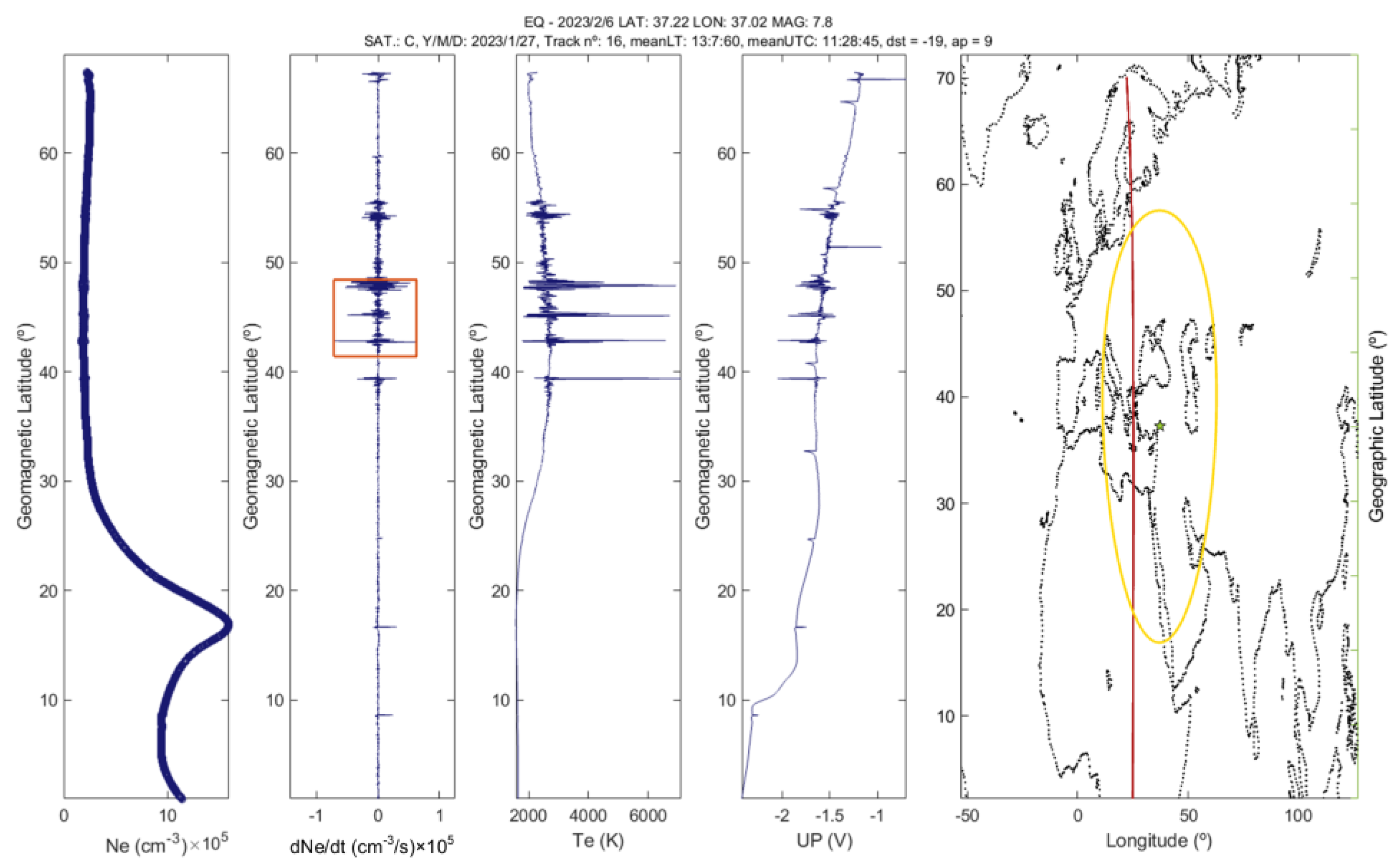
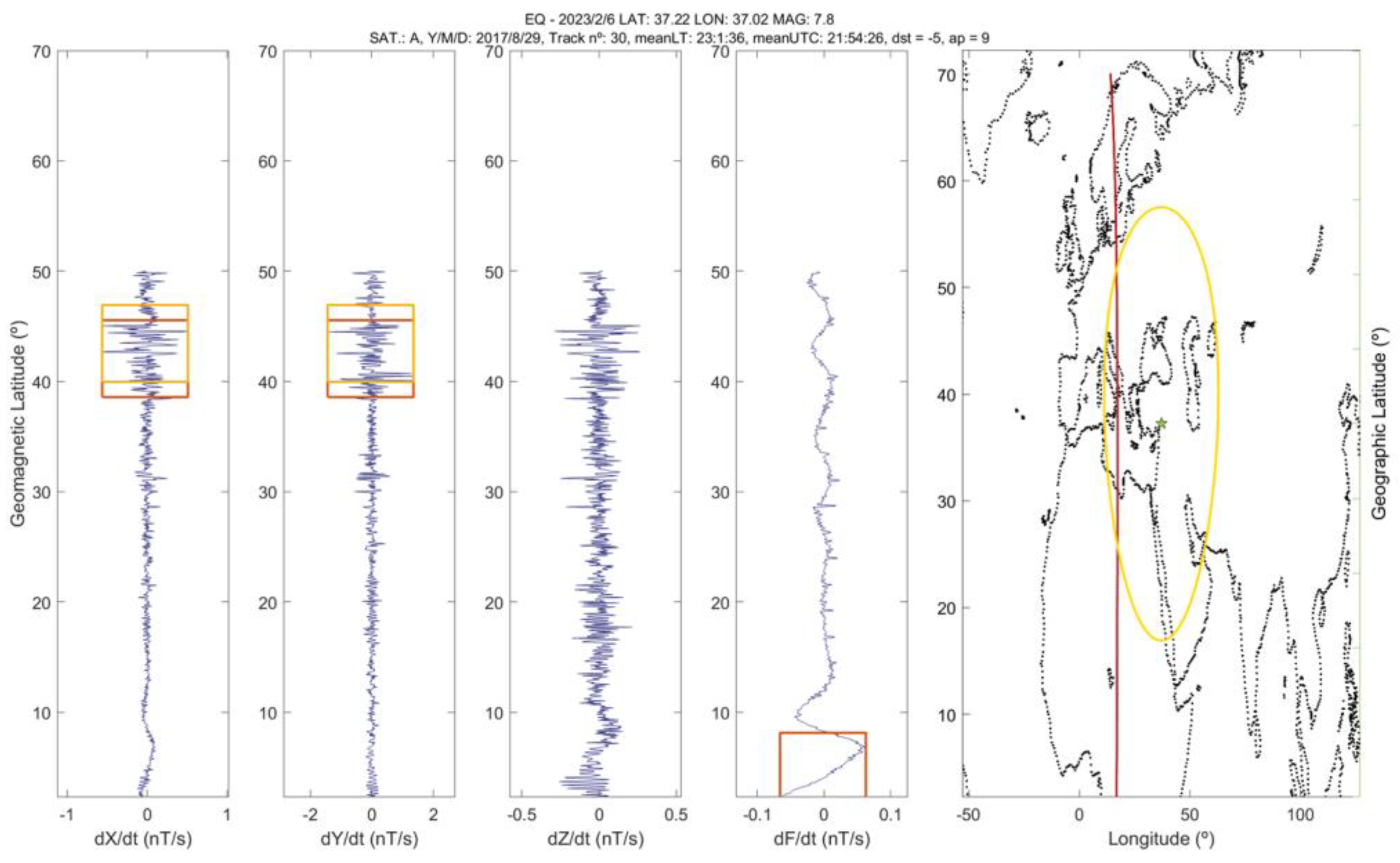
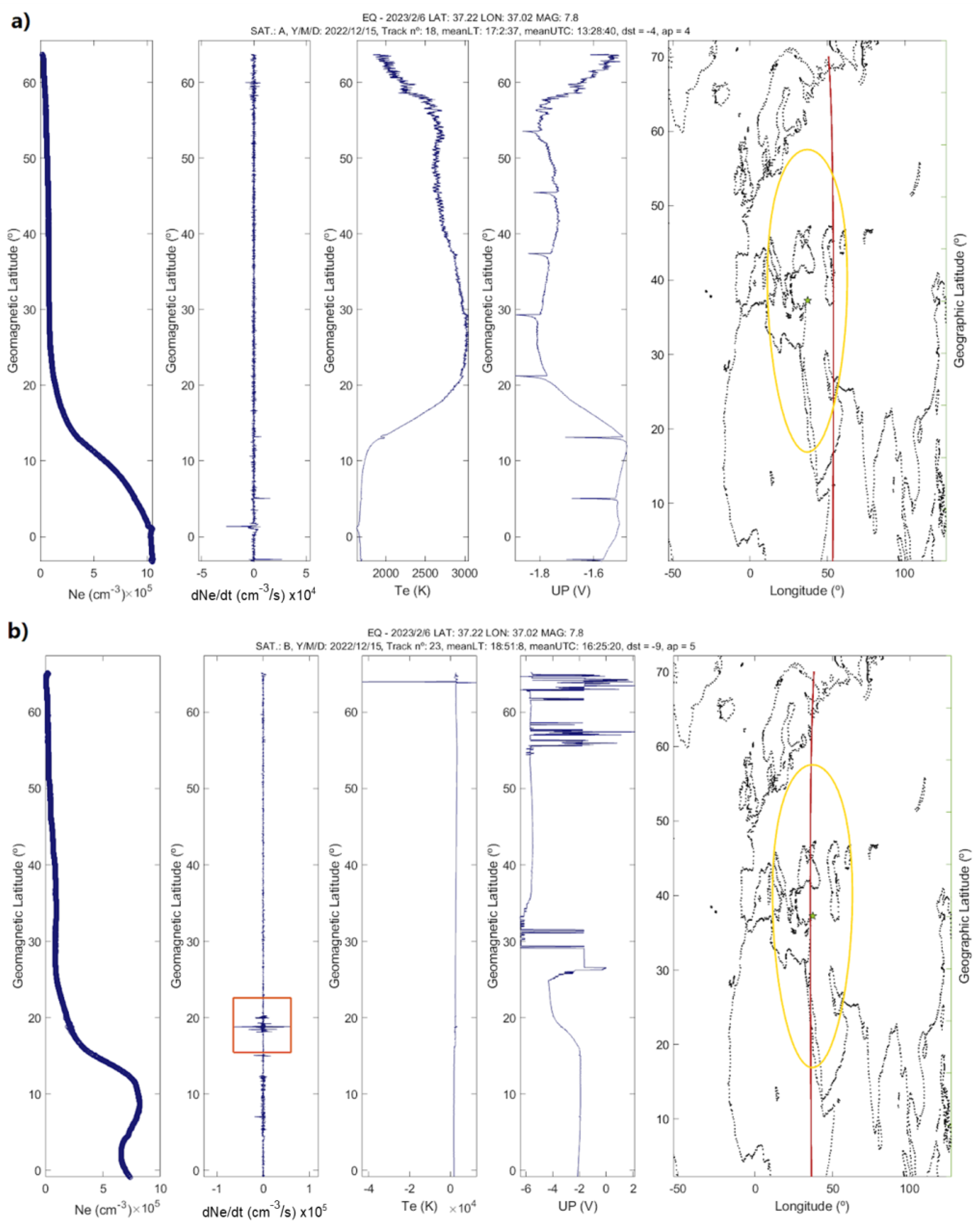
4.3. Swarm and CSES-01 Magnetic and Electron Density Data Analysis
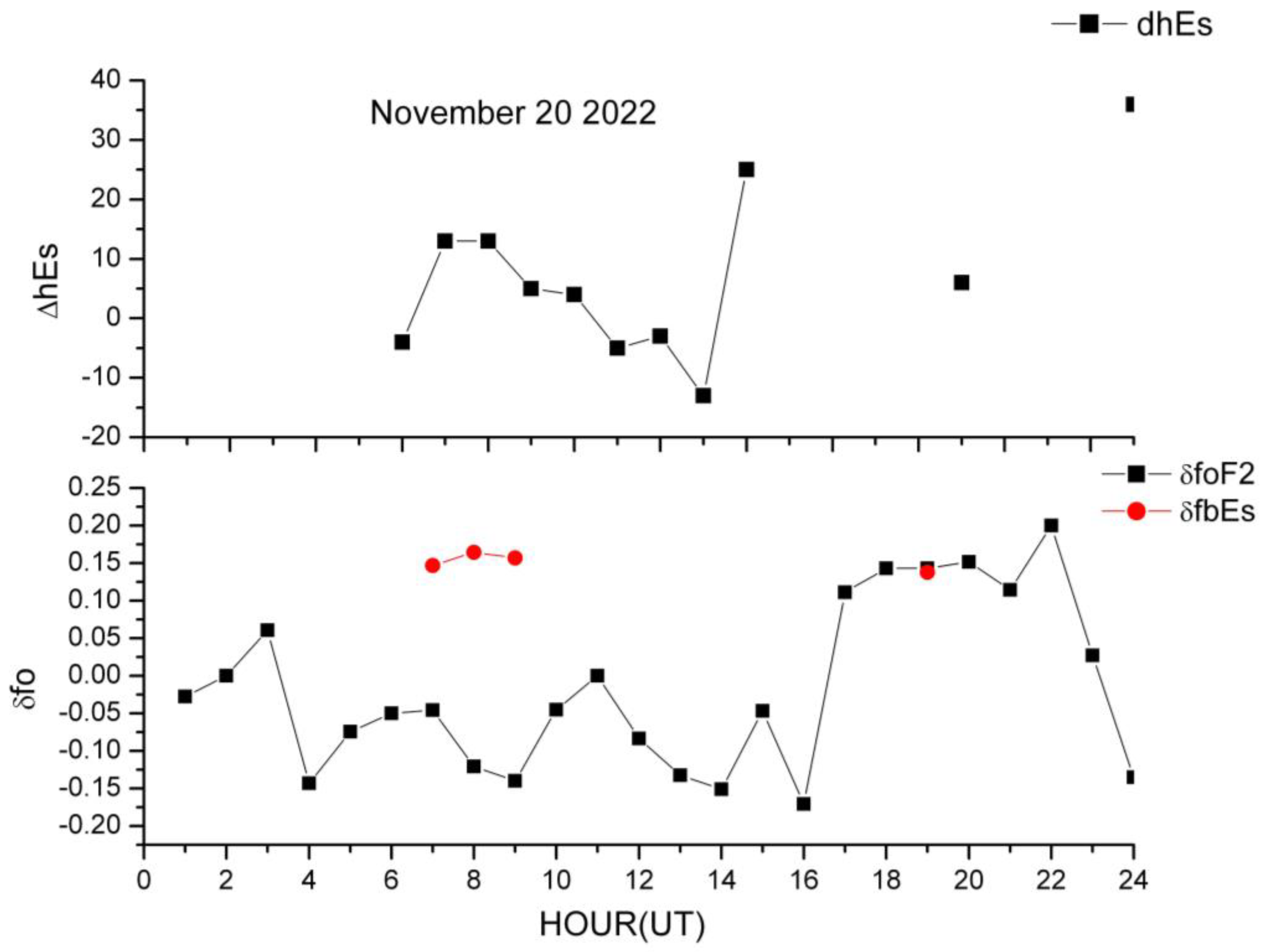
4.4. Analysis of Ionospheric Data from Ionosonde
4.5. Electron Loss Data Analysis
5. Discussion: Comprehensive Analysis of Turkey EQ
- According to the seismic models, the emergence of lithospheric activity (the decreasing of b-value as stress increases) dates back even years before the great seismicity;
- Ionospheric anomalies are much more numerous than atmospheric ones but begin to appear more frequently within a few months to weeks before the mainshock;
- Moreover, some satellite anomalies appear well before atmospheric anomalies so they should be produced with another kind of coupling, which is not the progressive one from the lithosphere to atmosphere and ionosphere, but it is more direct. As in [80], if we remove these anomalies (those indicated in bold in Table 3) from the general trend of Figure 25, this appears with less oscillating parts.
- 1.
- As soon as microcracks develop, the fluid pressure (pore pressure in [20]) drops. Elements solvated in supercritical water separate. Multiphase systems develop with each pure phase as it is similar to a distillation process. Now, each phase is theoretically free to move and to migrate in pre-existing and coalesced fissures or newly created ones, according to their chemical and physical characteristics. The chemical release of elements, free to migrate upward, begins here. The next step is as follows:
- 2.
- Due to the constant tectonic load, the pressure acting on fluids starts to rise again. The fluid density rises again and H2O tends to interact more actively with solids in freshly opened fractures it encounters. CO2 acquires a dipole moment (measured in [83], calculated with quantum chemistry methods by Saharay and Balasubramanian [84], and modelled by Calcara and Caricaterra [85]), and tends to co-ordinate ions, becoming a polar solvent as well [86]—at the same time, free to migrate upward more easily than water can as a result of having a lower density. Being lighter and smaller than CO2, CO follows other paths. In this stage, besides the release and the eventual upward migration, rocks of the nucleation zone become weaker as a result of the chemical action of fluids. The combined action of the water/fluid chemistry and increasing total pressure will lead to the main shock.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pulinets, S.; Ouzounov, D. Lithosphere-atmosphere-ionosphere coupling (LAIC) model-an unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Hayakawa, M. Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes; Terra Scientific Publishing Company: Tokyo, Japan, 1999; p. 996. [Google Scholar]
- Korepanov, V.; Hayakawa, M.; Yampolski, Y.; Lizunov, G. AGW as a seismo–ionospheric coupling responsible agent. Phys. Chem. Earth Parts A/B/C 2009, 34, 485–495. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Boyarchuk, K.A. Ionospheric Precursors of Earthquakes; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Rozhnoi, A.; Solovieva, M.S.; Molchanov, O.A.; Hayakawa, M. Middle latitude LF (40 kHz) phase variations associated with earthquakes for quiet and disturbed geomagnetic conditions. Phys. Chem. Earth 2004, 29, 89–598. [Google Scholar] [CrossRef]
- Astafyeva, E. Ionospheric detection of natural hazards. Rev. Geophys. 2019, 57, 1265–1288. [Google Scholar] [CrossRef]
- Bravo, M.; Benavente, R.; Foppiano, A.; Urra, B.; Ovalle, E. Traveling Ionospheric Disturbances observed over South America after lithospheric events: 2010–2020. J. Geophys. Res. Space Phys. 2022, 127, e2021JA030060. [Google Scholar] [CrossRef]
- Haralambous, H.; Guerra, M.; Chum, J.; Verhulst, T.G.W.; Barta, V.; Altadill, D.; Cesaroni, C.; Galkin, I.; Márta, K.; Mielich, J.; et al. Multi-instrument observations of various ionospheric disturbances caused by the 6 February 2023 Turkey earthquake. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031691. [Google Scholar] [CrossRef]
- Sunil, A.S.; Bagiya, M.S.; Catherine, C.; Rolland, L.; Sharma, N.; Sunil, P.S.; Ramesh, D.S. Dependence of near field co-seismic ionospheric perturbations on surface deformations: A case study based on the April, 25 2015 Gorkha Nepal earthquake. Adv. Space Res. 2017, 59, 1200–1208. [Google Scholar] [CrossRef]
- Reddy, C.D.; Seemala, G.K. Two-mode ionospheric response and Rayleigh wave group velocity distribution reckoned from GPS measurement following Mw 7.8 Nepal earthquake on 25 April 2015. J. Geophys. Res. Space Phys. 2015, 120, 7049–7059. [Google Scholar] [CrossRef]
- Cicerone, R.D.; Ebel, J.E.; Britton, J. A systematic compilation of earthquake precursors. Tectonophysics 2009, 476, 371–396. [Google Scholar] [CrossRef]
- De Santis, A.; Marchetti, D.; Pavón-Carrasco, F.J.; Cianchini, G.; Perrone, L.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; et al. Precursory worldwide signatures of earthquake occurrences on Swarm satellite data. Sci. Rep. 2019, 9, 20287. [Google Scholar] [CrossRef]
- De Santis, A.; Cianchini, G.; Marchetti, D.; Piscini, A.; Sabbagh, D.; Perrone, L.; Campuzano, S.A.; Inan, S. A Multiparametric Approach to Study the Preparation Phase of the 2019 M7.1 Ridgecrest (California, United States) Earthquake. Front. Earth Sci. 2020, 8, 540398. [Google Scholar] [CrossRef]
- D’Arcangelo, S.; Regi, M.; De Santis, A.; Perrone, L.; Cianchini, G.; Soldani, M.; Piscini, A.; Fidani, C.; Sabbagh, D.; Lepidi, S.; et al. A multiparametric-multilayer comparison of the preparation phase of two geophysical events in the Tonga-Kermadec subduction zone: The 2019 M7.2 Kermadec earthquake and 2022 Hunga Ha’apai eruption. Front. Earth Sci. 2023, 11, 1267411. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. Generation of ULF electromagnetic emissions by microfracturing. Geophys. Res. Lett. 1995, 22, 3091–3094. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kawate, R.; Molchanov, O.A.; Yumoto, K. Results of ultra-low-frequency magnetic field measurements during the Guam earthquake of 8 August 1993. Geophys. Res. Lett. 1996, 23, 241–244. [Google Scholar] [CrossRef]
- Piscini, A.; De Santis, A.; Marchetti, D.; Cianchini, G. A Multi-parametric Climatological Approach to Study the 2016 Amatrice–Norcia (Central Italy) Earthquake Preparatory Phase. Pure Appl. Geophys. 2017, 174, 3673–3688. [Google Scholar] [CrossRef]
- Piersanti, M.; Materassi, M.; Battiston, R.; Carbone, V.; Cicone, A.; D’Angelo, G.; Diego, P.; Ubertini, P. Magnetospheric–Ionospheric–Lithospheric Coupling Model. 1: Observations during the 5 August 2018 Bayan Earthquake. Remote Sens. 2020, 12, 3299. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hattori, K.; Ando, Y. Natural electromagnetic phenomena and electromagnetic theory: A review. IEEJ Trans. Fundam. Mater. 2004, 124, 72–79. [Google Scholar] [CrossRef]
- Scholz, C.H.; Sykes, L.R.; Aggarwal, Y.P. Earthquake prediction: A physical basis. Science 1973, 180, 632–641. [Google Scholar] [CrossRef]
- Calcara, M. Chemistry in earthquake: The active chemical role of liquid and supercritical waters in microfracturing at depth. J. Seismol. 2022, 26, 1205–1221. [Google Scholar] [CrossRef]
- Fidani, C. The Conditional Probability of Correlating East Pacific Earthquakes with NOAA Electron Bursts. Appl. Sci. 2022, 12, 10528. [Google Scholar] [CrossRef]
- Perrone, L.; De Santis, A.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Carbone, M.; Cesaroni, C.; Cianchini, G.; De Franceschi, G.; Di Giovambattista, R.; et al. Ionospheric anomalies detected by ionosonde and possibly related to crustal earthquakes in Greece. Ann. Geophys. 2018, 36, 361–371. [Google Scholar] [CrossRef]
- Ni, S.; Sun, H.; Somerville, P.; Yuen, D.A.; Milliner, C.; Wang, H.; Zhou, J.; Cui, Y. Complexities of the Turkey-Syria doublet earthquake sequence. Innovation 2023, 4, 100431. [Google Scholar] [CrossRef]
- Chadha, R.K. An Mw 7.8 Earthquake on 6 February 2023 on the East Anatolian Fault, TurkeyJour. Geol. Soc. India 2023, 99, 449–453. [Google Scholar] [CrossRef]
- Liu, J.; Huang, C.; Zhang, G.; Shan, X.; Korzhenkov, A.; Taymaz, T. Immature characteristics of the East Anatolian Fault Zone from SAR, GNSS and strong motion data of the 2023 Türkiye-Syria earthquake doublet. Sci. Rep. 2024, 14, 10625. [Google Scholar] [CrossRef]
- Okuwaki, R.; Yagi, Y.; Taymaz, T.; Hicks, S.P. Multi-scale rupture growth with alternating directions in a complex fault network during the 2023 south-eastern Türkiye and Syria earthquake doublet. Geophys. Res. Lett. 2023, 50, e2023GL103480. [Google Scholar] [CrossRef]
- Softa, M.; Koçbulut, F.; Akgün, E.; Aksoy, E.; Sözbilir, H.; Tatar, O.; Karabacak, V.; Özkaymak, Ç.; Utku, M.; Özdag, Ö.C.; et al. Surface rupture during the 6th of February 2023 Mw 7.6 Elbistan-Ekinözü (Kahramanmaras) earthquake: Implications for fault rupture dynamics along the northern branch of East Anatolian Fault Zone. Turk. J. Earth Sci. 2023, 32, 1–21. [Google Scholar] [CrossRef]
- Galasso, C.; Opabola, E.A. The 2023 Kahramanmaras Earthquake Sequence: Finding a path to a more resilient, sustainable, and equitable society. Commun. Eng. 2024, 3, 24. [Google Scholar] [CrossRef]
- Sparacino, F.; Galuzzi, B.G.; Palano, M.; Segou, M.; Chiarabba, C. Seismic coupling for the Aegean-Anatolian region. Earth-Sci. Rev. 2022, 228, 103993. [Google Scholar] [CrossRef]
- Jiang, X.; Song, X.; Li, T.; Wu, K. Moment magnitudes of two large Turkish earthquakes on February 6, 2023 from long-period coda. Earthq. Sci. 2023, 36, 169–174. [Google Scholar] [CrossRef]
- Abdelmeguid, M.; Zhao, C.; Yalcinkaya, E.; Gazetas, G.; Elbanna, A.; Rosakis, A. Dynamics of episodic supershear in the 2023 M7.8 Kahramanmaras/Pazarcik earthquake, revealed by near-field records and computational modeling. Commun. Earth Environ. 2023, 4, 456. [Google Scholar] [CrossRef]
- Dal Zilio, L.; Ampuero, J.P. Earthquake doublet in Turkey and Syria. Commun. Earth Environ. 2023, 4, 71. [Google Scholar] [CrossRef]
- Picozzi, M.; Iaccarino, A.G.; Spallarossa, D. The preparatory process of the 2023 Mw7.8 Türkiye earthquake. Sci. Rep. 2023, 13, 17853. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seism. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Kwiatek, G.; Martínez-Garzón, P.; Becker, D.; Dresen, G.; Cotton, F.; Beroza, G.C.; Acarel, D.; Ergintav, S.; Bohnhoff, M. Months-long seismicity transients preceding the 2023 MW 7.8 Kahramanmaras earthquake, Türkiye. Nat. Commun. 2023, 14, 7534. [Google Scholar] [CrossRef]
- Ouzounov, D.; Khachikyan, G. On the impact of geospace weather on the occurrence of M7.8/M7.5 earthquakes on 6 February 2023 (Turkey), possibly associated with the geomagnetic storm of 7 November 2022. Geosciences 2024, 14, 159. [Google Scholar] [CrossRef]
- De Santis, A.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; Cesaroni, C.; Cianchini, G.; De Franceschi, G.; De Santis, A.; et al. Geosystemics View of Earthquakes. Entropy 2019, 21, 412. [Google Scholar] [CrossRef]
- Cianchini, G.; De Santis, A.; Di Giovambattista, R.; Abbattista, C.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; Cesaroni, C.; De Santis, A.; Marchetti, D.; et al. Revised Accelerated Moment Release under test: Fourteen worldwide real case studies in 2014–2018 and simulations. PAGeoph 2020, 177, 4057–4087. [Google Scholar] [CrossRef]
- Fidani, C. West Pacific Earthquake Forecasting Using NOAA Electron Bursts with Independent L-Shells and Ground-Based Magnetic Correlations. Front. Earth Sci. 2021, 9, 673105. [Google Scholar] [CrossRef]
- Emre, Ö.; Duman, T.Y.; Özalp, S.; Şaroğlu, F.; Olgun, Ş.; Elmacı, H.; Çan, T. Active fault database of Turkey. Bull. Earthq. Eng. 2018, 16, 3229–3275. [Google Scholar] [CrossRef]
- Rizaoglu, T.; Parlak, O.; Isler, F. Geochemistry of the Esence Granitoid (Göksun-Kahramanmaras), SE Turkey. Yerbilimleri 2005, 26, 1–13. [Google Scholar]
- Ertürk, M.A.; Kara, H.; Sar, A.; Yilmaz, I.; Aysal, N. Geochronology and petrogenesis of the lower Miocene felsic rocks: New evidence for initiation of post-collisional magmatism in the SW Malatya—Eastern Anatolia (Turkey). Geol. Carpathica 2023, 74, 245–260. [Google Scholar] [CrossRef]
- Naji, D.M.; Akin, M.K.; Cabalar, A.F. A Comparative Study on the VS30 and N30 Based Seismic Site Classification in Kahramanmaras, Turkey. Adv. Civ. Eng. 2020, 2020, 8862827. [Google Scholar] [CrossRef]
- Hacioglu, Ö.; Basokur, A.T.; Çiftçi, E.T. Crustal structure of a young collision zone: The Arabia–Eurasia collision in northeastern Turkey investigated by magnetotelluric data. Earth Planets Space 2018, 70, 161. [Google Scholar] [CrossRef]
- Weiss, J.R.; Walters, R.J.; Morishita, Y.; Wright, T.J.; Lazecky, M.; Wang, H.; Hussain, E.; Hooper, A.J.; Elliott, J.R.; Rollins, C.; et al. High-resolution surface velocities and strain for Anatolia from Sentinel-1 InSAR and GNSS data. Geophys. Res. Lett. 2020, 47, e2020GL087376. [Google Scholar] [CrossRef]
- Kurt, A.I.; Özbakir, A.D.; Cingöz, A.; Semih, E.; Dogan, U.; Seda, Ö. Contemporary Velocity Field for Turkey Inferred from Combination of a Dense Network of Long Term GNSS Observations. Turk. J. Earth Sci. 2000, 32, 4. [Google Scholar] [CrossRef]
- Akin, U.; Ulugergerli, E.U.; Kutlu, S. The assessment of geothermal potential of Turkey by means of heat flow estimation. Bull. Min. Res. Exp. 2014, 149, 201–210. [Google Scholar] [CrossRef][Green Version]
- Wiemer, S.; Wyss, M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seism. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Zúñiga, F.R.; Wyss, M. Inadvertent changes in magnitude reported in earthquake catalogs: Their evaluation through b-value estimates. Bull. Seismol. Soc. Am. 1995, 85, 1858–1866. [Google Scholar] [CrossRef]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Schorlemmer DWiemer, S.; Wyss, M. Earthquake statistics at Parkfield: 1. Stationarity of b values. J. Geophys. Res. 2004, 109, B12307. [Google Scholar] [CrossRef]
- Wiemer, S. A software package to analyze seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Bowman, D.D.; Ouillon, G.; Sammis, C.G.; Sornette, A.; Sornette, D. An observational test of the critical earthquake concept. J. Geophys. Res. Solid Earth 1998, 103, 24359–24372. [Google Scholar] [CrossRef]
- Jaumé, S.C.; Sykes, L.R. Evolution of moderate seismicity in the San Francisco Bay region, 1850 to 1993: Seismicity changes related to the occurrence of large and great earthquakes. J. Geophys. Res. Solid Earth 1996, 101, 765–789. [Google Scholar] [CrossRef]
- Bufe, C.G.; Varnes, D.J. Predictive modeling of the seismic cycle of the greater San Francisco Bay region. J. Geophys. Res. 1993, 98, 9871–9883. [Google Scholar] [CrossRef]
- Mignan, A.; King, G.C.P.; Bowman, D. A mathematical formulation of accelerating moment release based on the stress accumulation model. J. Geophys. Res. 2007, 112, B07308. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1940 to present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2023. Available online: https://doi.org/10.24381/cds.adbb2d47 (accessed on 8 September 2023).
- Ouzounov, D.; Liu, D.; Chunli, K.; Cervone, G.; Kafatos, M.; Taylor, P. Outgoing long wave radiation variability from IR satellite data prior to major earthquakes. Tectonophysics 2007, 431, 211–220. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era retrospective analysis for research and applications, version 2 (MERRA-2), American meteorological society-modern-Era retrospective analysis for research and applications version 2 (MERRA-2) special collection. J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Ippolito, A.; Perrone, L.; De Santis, A.; Sabbagh, D. Ionosonde Data Analysis in Relation to the 2016 Central Italian Earthquakes. Geosciences 2020, 10, 354. [Google Scholar] [CrossRef]
- De Santis, A.; Marchetti, D.; Spogli, L.; Cianchini, G.; Pavón-Carrasco, F.J.; De Franceschi, G.; Di Giovambattista, R.; Perrone, L.; Qamili, E.; Cesaroni, C.; et al. Magnetic field and electron density data analysis from Swarm satellites searching for ionospheric effects by great earthquakes: 12 case studies from 2014 to 2016. Atmosphere 2019, 10, 371. [Google Scholar] [CrossRef]
- Dobrovolsky, I.R.; Zubkov, S.I.; Myachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Fidani, C.; D’Arcangelo, S.; De Santis, A.; Perrone, L.; Soldani, M. Investigating a Possible Correlation between NOAA-Satellite-Detected Electron Precipitations and South Pacific Tectonic Events. Remote Sens. 2024, 16, 1059. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S. Microseismicity data forecasts rupture area. Nature 2005, 434, 1086. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Biswas, R. Spatio-temporal variation in b-value prior to the 26 November 2021 Mizoram earthquake of northeast India. Geol. J. 2022, 57, 5361–5373. [Google Scholar] [CrossRef]
- Xie, W.; Hattori, K.; Han, P. Temporal variation and statistical assessment of the b value off the pacific coast of Tokachi, Hokkaido, Japan. Entropy 2019, 21, 249. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Lyu, Y.; Li, X. Temporal and spatial changes in the b-value prior to the 2021 Luxian MS 6.0 earthquake in Sichuan, China. Geomat. Nat. Hazards Risk 2022, 13, 934–948. [Google Scholar] [CrossRef]
- Tormann, T.; Wiemer, S.; Mignan, A. Systematic survey of high-resolution b value imaging along Californian faults: Inference on asperities. J. Geophys. Res. Solid Earth 2014, 119, 2029–2054. [Google Scholar] [CrossRef]
- Ouzounov, D.; Kalenda, P.; Pulinets, S.; Shen, X.; Yan, R.; Rušajová, J. Multi-parameter precursory patterns associated with the earthquake sequence in Turkey on February 6th, 2023. In Proceedings of the IWEP7 workshop, Chiba University (Nishi-Chiba Campus), Chiba, Japan, 24–25 May 2023. [Google Scholar]
- Rikitake, T. Earthquake precursors. Bull. Seismol. Soc. Am. 1975, 65, 1133–1162. [Google Scholar] [CrossRef]
- Kawai, K.; Shiokawa, K.; Otsuka, Y.; Oyama, S.; Kasaba, Y.; Kasahara, Y.; Tsuchiya, F.; Kumamoto, A.; Nakamura, S.; Matsuoka, A.; et al. First simultaneous observation of a night time medium-scale traveling ionospheric disturbance from the ground and a magnetospheric satellite. J. Geophys. Res. Space Phys. 2021, 126, e2020JA029086. [Google Scholar] [CrossRef]
- Occhipinti, G.; Rolland, L.; Lognonné, P.; Watada, S. From Sumatra 2004 to Tohoku-Oki 2011: The systematic GPS detection of the ionospheric signature induced by tsunamigenic earthquakes. J. Geophys. Res. Space Phys. 2013, 118, 3626–3636. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Xia, H.; Wang, W.; Liu, J.; Zhang, S.; Jin, Y. The Turkey earthquake Induced Equatorial Ionospheric Current Disturbances on 6 February 2023. Remote Sens. 2024, 16, 272. [Google Scholar] [CrossRef]
- Vesnin, A.; Yasyukevich, Y.; Perevalova, N.; Sentürk, E. Ionospheric Response to the 6 February 2023 Turkey–Syria Earthquake. Remote Sens. 2023, 15, 2336. [Google Scholar] [CrossRef]
- Akhoondzadeh, M. Kalman Filter, ANN-MLP, LSTM and ACO Methods Showing Anomalous GPS-TEC Variations Concerning Turkey’s Powerful Earthquake (6 February 2023). Remote Sens. 2023, 15, 3061. [Google Scholar] [CrossRef]
- Salikhov, N.; Shepetov, A.; Pak, G.; Nurakynov, S.; Kaldybayev, A.; Ryabov, V.; Zhukov, V. Investigation of the Pre- and Co-Seismic Ionospheric Effects from the 6 February 2023 M7.8 Turkey Earthquake by a Doppler Ionosonde. Atmosphere 2023, 14, 1483. [Google Scholar] [CrossRef]
- Korsunova, L.P.; Khegai, V.V. Medium-term ionospheric precursors to strong earthquakes. Int. J. Geomagn. Aeron. 2006, 6, GI3005. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; Marchetti, D. Study of the Preparation Phase of Turkey’s Powerful Earthquake (6 February 2023) by a Geophysical Multi-Parametric Fuzzy Inference System. Remote Sens. 2023, 15, 2224. [Google Scholar] [CrossRef]
- Zhang, X.; De Santis, A.; Liu, J.; Campuzano, S.A.; Yang, N.; Cianchini, G.; Ouyang, X.; D’Arcangelo, S.; Yang, M.; De Caro, M.; et al. Pre-earthquake oscillating and accelerating patterns in the Lithosphere Atmosphere Ionosphere coupling (LAIC) before the 2022 Luding (China) Ms6.8 earthquake. Remote Sens. 2024, 16, 2381. [Google Scholar] [CrossRef]
- Sahin, Ü.A.; Kaynak, B. Questioning whether there was a short-term interaction between the 6 February 2023 earthquakes and air quality parameters in Türkiye. Chemosphere 2024, 347, 140616. [Google Scholar] [CrossRef]
- Inan, S.; Çetin, H.; Yakupoglu, N. Spring water anomalies before two consecutive earthquakes (Mw 7.7 and Mw 7.6) in Kahramanmaras (Türkiye) on 6 February 2023. Nat. Hazards Earth Syst. Sci. 2024, 24, 397–409. [Google Scholar] [CrossRef]
- Di Noto, V.; Vezzù, K.; Conti, F.; Giffin, G.A.; Lavina, S.; Bertucco, A. Broadband Electric Spectroscopy at High CO2 Pressure: Dipole Moment of CO2 and Relaxation Phenomena of the CO2–Poly(vinyl chloride) System. J. Phys. Chem. B 2011, 115, 9014–9021. [Google Scholar] [CrossRef] [PubMed]
- Saharay, M.; Balasubramanian, S. Enhanced Molecular Multipole Moments and Solvent Structure in Supercritical Car-bon Dioxide. ChemPhysChem 2004, 5, 1442–1445. [Google Scholar] [CrossRef] [PubMed]
- Calcara, M.; Caricaterra, M. CO2 Dipole Moment: A Simple Model and Its Implications for CO2-Rock Interactions. Minerals 2023, 13, 87. [Google Scholar] [CrossRef]
- Criscenti, L.J.; Cygan, R.T. Molecular Simulations of Carbon Dioxide and Water: Cation Solvation. Environ. Sci. Technol. 2013, 47, 87–94. [Google Scholar] [CrossRef] [PubMed]


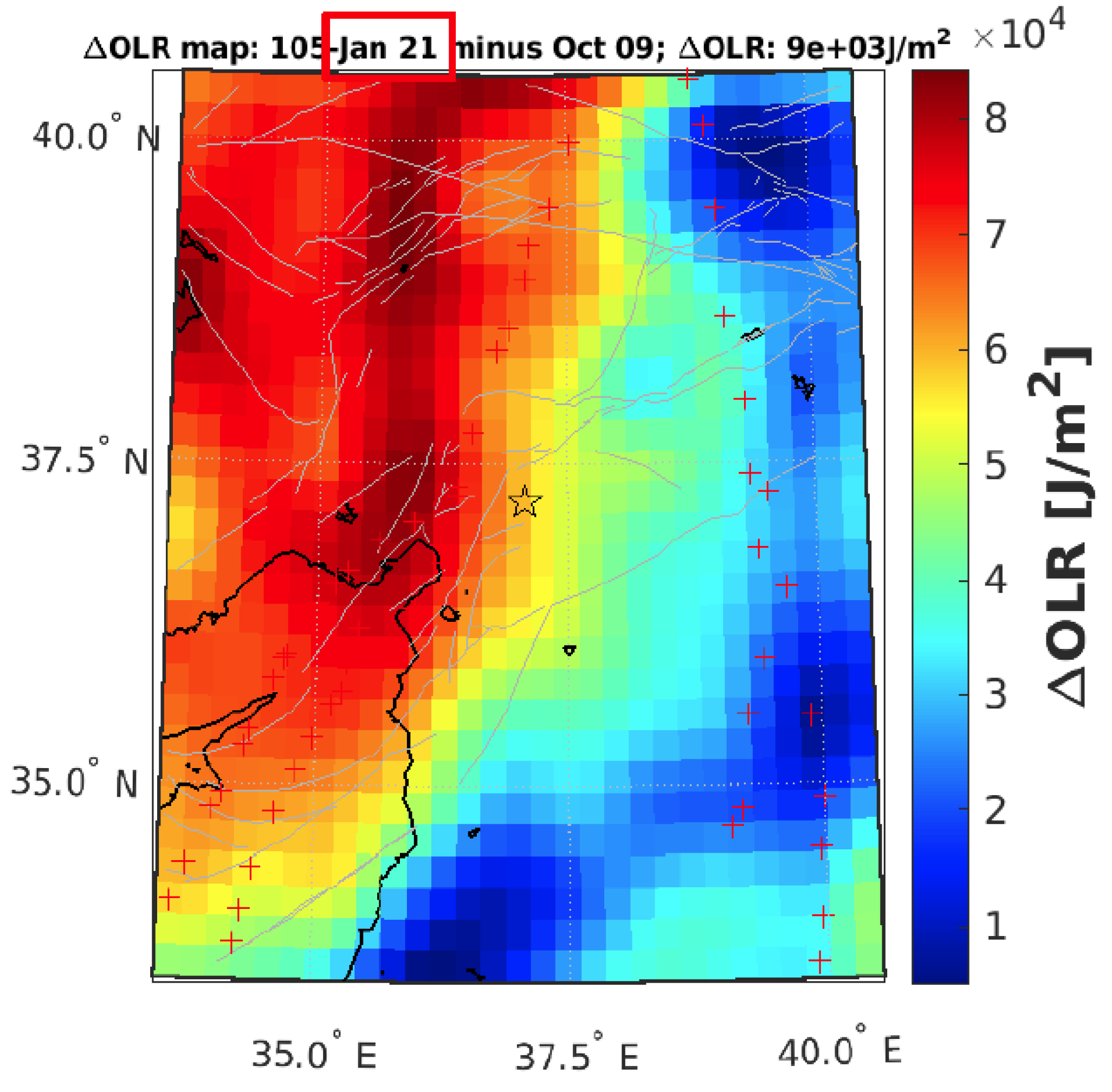
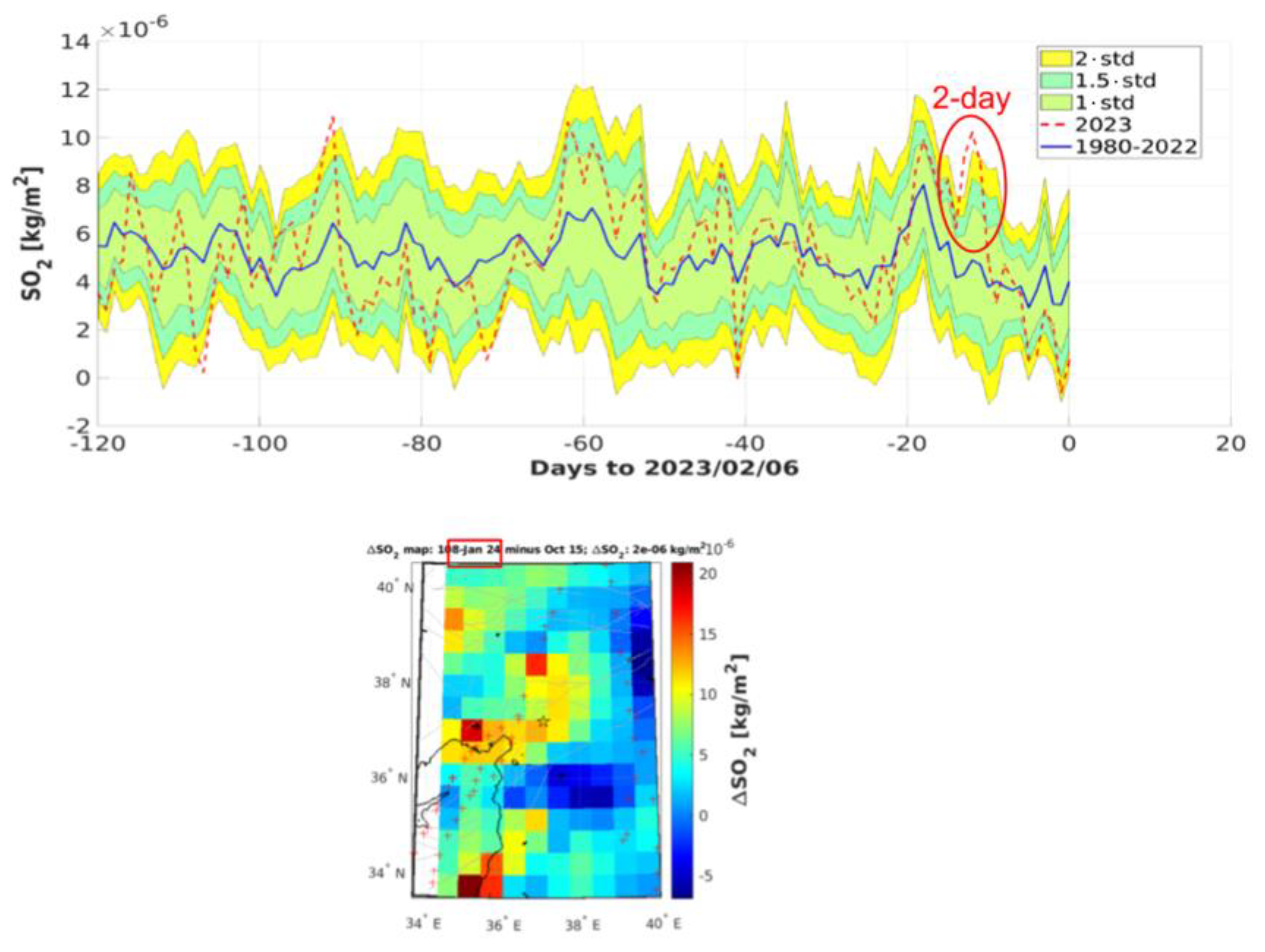
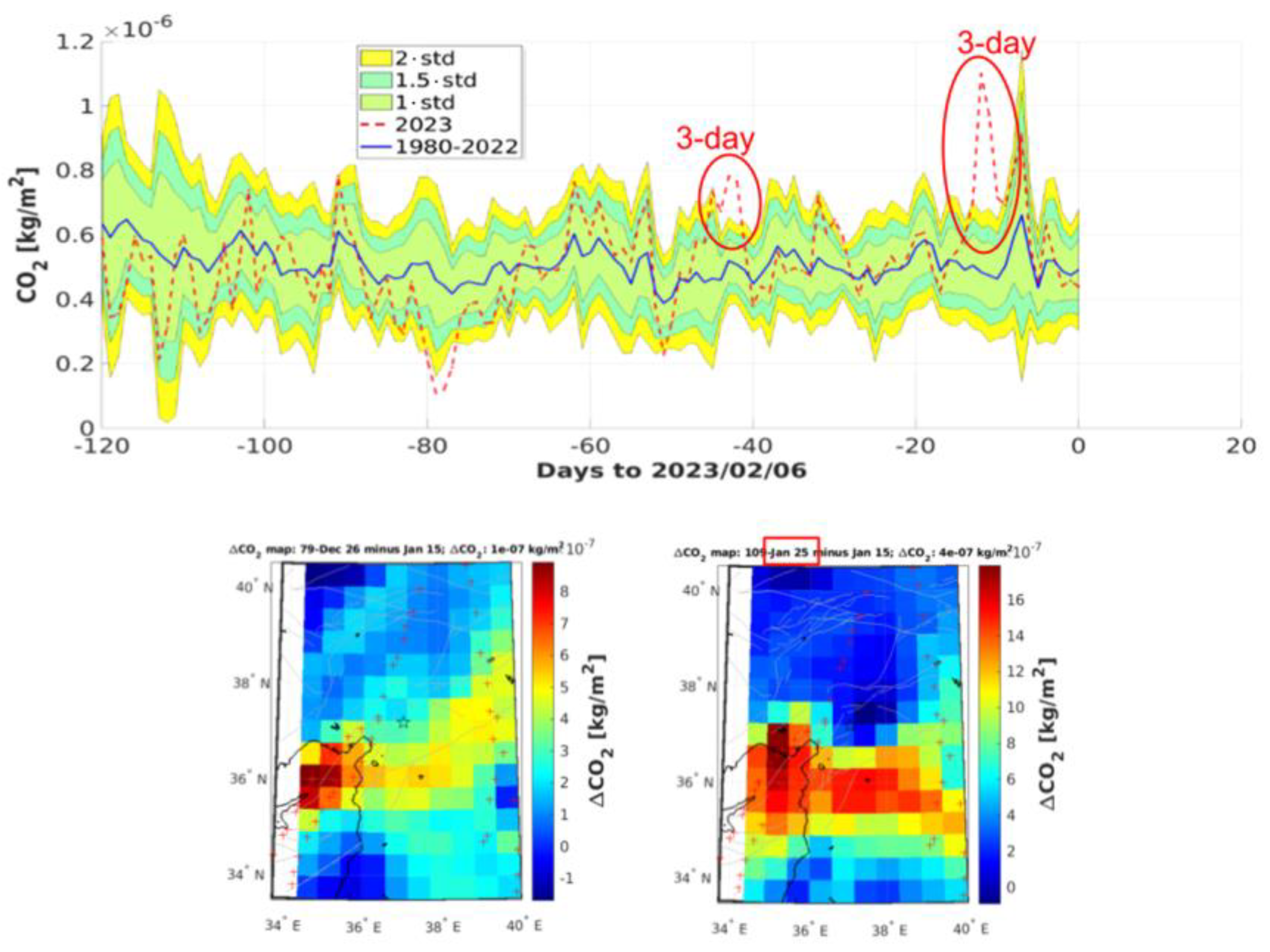

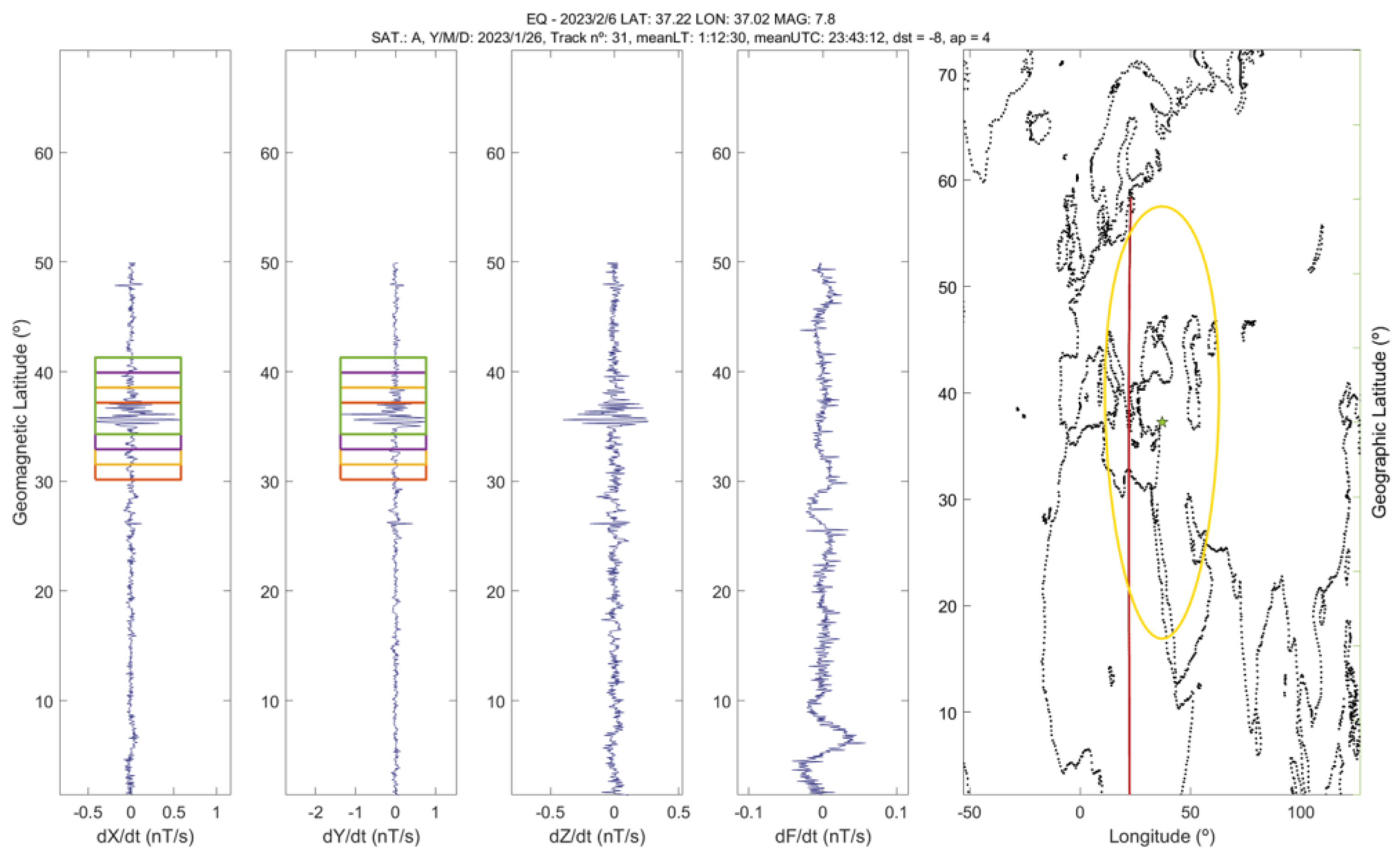




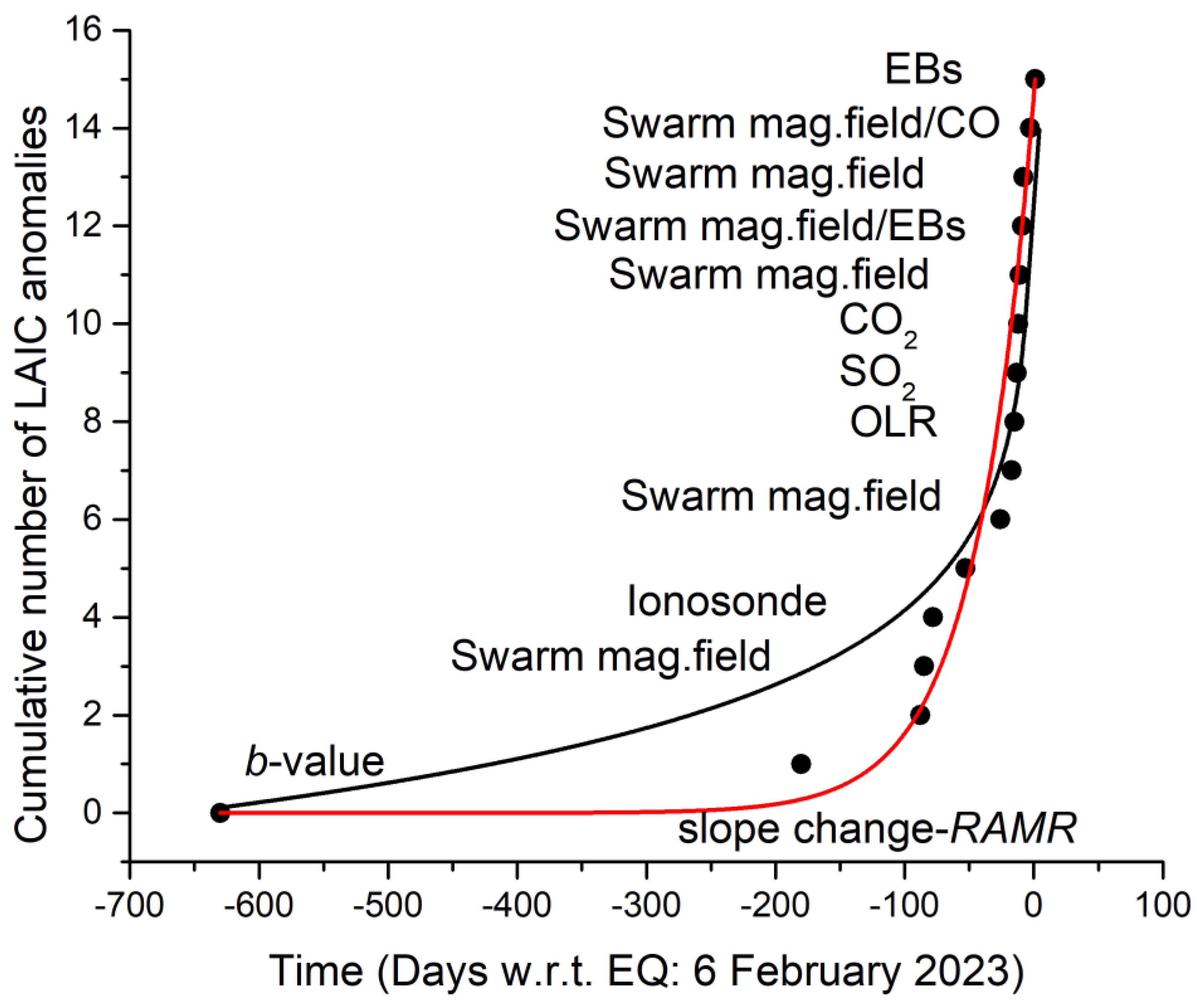
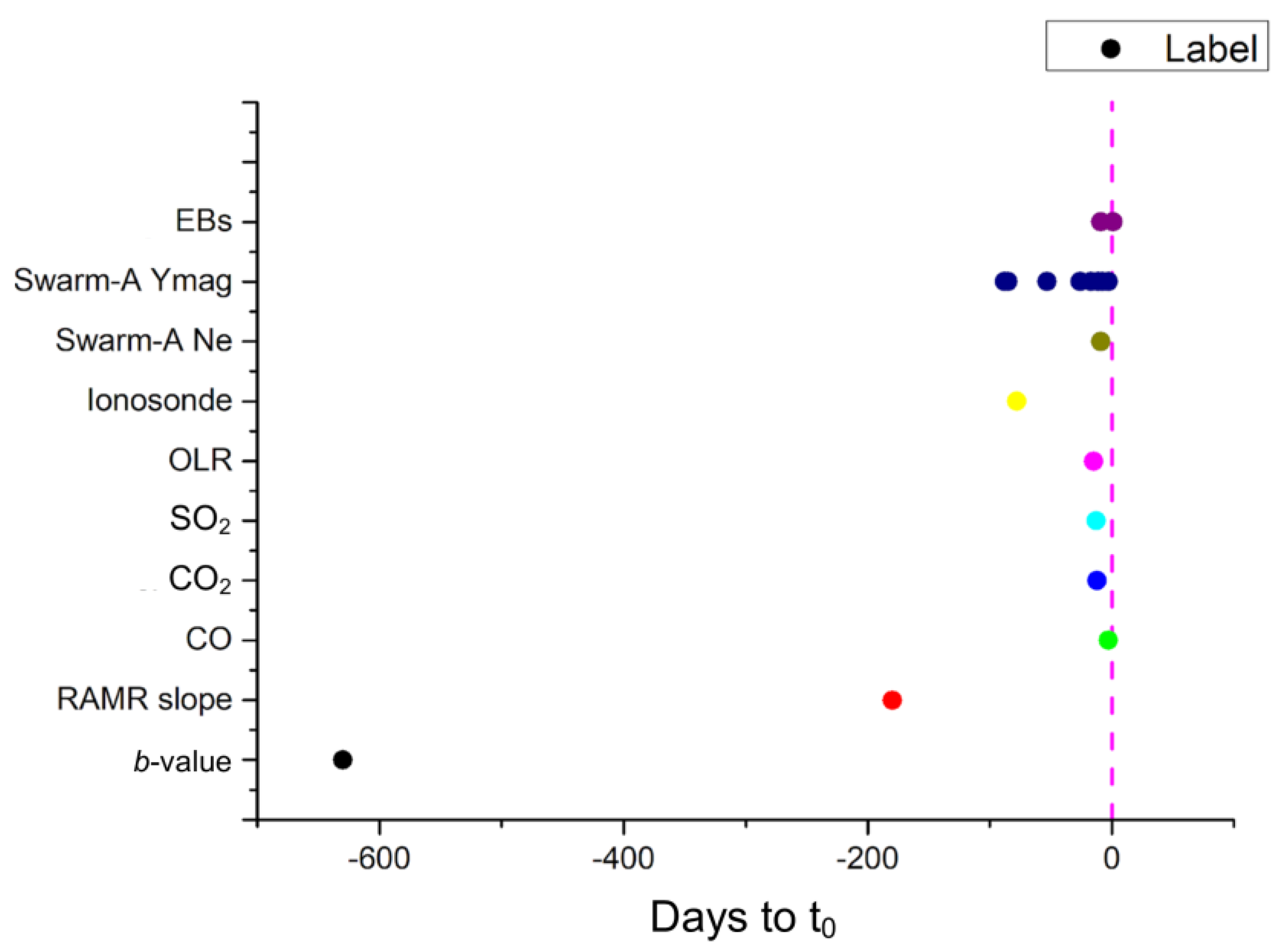
| EQ Date Time (UT) | EQ Location (Lat Lon) | Magnitude [Mw] | Ionosonde | Ionosonde Location (Lat Lon) | R [km] |
|---|---|---|---|---|---|
| 6 February 2023 01:17 | 37.20°N 37.06°E | 7.8 | DPS-4D (Nicosia) | 35.03°N 33.16°E | 425.30 |
| 6 February 2023 10:24 | 38.09°N 37.27°E | 7.6 | 501.16 |
| Date | Hour [UT] | Δh’Es | δfbEs | δfoF2 | ΔT [days] | Ap Index | AE Index |
|---|---|---|---|---|---|---|---|
| 20 November 2022 | 06-07 | 13 | 0.4 | 0.18 | 77.84/78.2 | 5 nT | <100 nT |
| Days to Mainshock | Cumulative Number | Source |
|---|---|---|
| −630 | 1 | b-value descent |
| −180 | 2 | change slope RAMR |
| −88 | 3 | Swarm-A Y mag. field |
| −85 | 4 | Swarm-A Y mag. field |
| −78 | 5 | Ionosonde |
| −53 | 6 | Swarm-A Y mag. field |
| −26 | 7 | Swarm-A Y mag. field |
| −17 | 8 | Swarm-A Y mag. field |
| −15 | 9 | OLR |
| −13 | 10 | SO2 |
| −12 | 11 | CO2 |
| −11 | 12 | Swarm-A Y mag. field |
| −9 | 13 | Swarm-A Ne |
| −9 | 14 | EBs |
| −8 | 15 | Swarm-A Y mag. field |
| −3 | 16 | CO |
| −3 | 17 | Swarm-A Y mag. field |
| 1 | 18 | EBs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cianchini, G.; Calcara, M.; De Santis, A.; Piscini, A.; D’Arcangelo, S.; Fidani, C.; Sabbagh, D.; Orlando, M.; Perrone, L.; Campuzano, S.A.; et al. The Preparation Phase of the 2023 Kahramanmaraş (Turkey) Major Earthquakes from a Multidisciplinary and Comparative Perspective. Remote Sens. 2024, 16, 2766. https://doi.org/10.3390/rs16152766
Cianchini G, Calcara M, De Santis A, Piscini A, D’Arcangelo S, Fidani C, Sabbagh D, Orlando M, Perrone L, Campuzano SA, et al. The Preparation Phase of the 2023 Kahramanmaraş (Turkey) Major Earthquakes from a Multidisciplinary and Comparative Perspective. Remote Sensing. 2024; 16(15):2766. https://doi.org/10.3390/rs16152766
Chicago/Turabian StyleCianchini, Gianfranco, Massimo Calcara, Angelo De Santis, Alessandro Piscini, Serena D’Arcangelo, Cristiano Fidani, Dario Sabbagh, Martina Orlando, Loredana Perrone, Saioa A. Campuzano, and et al. 2024. "The Preparation Phase of the 2023 Kahramanmaraş (Turkey) Major Earthquakes from a Multidisciplinary and Comparative Perspective" Remote Sensing 16, no. 15: 2766. https://doi.org/10.3390/rs16152766
APA StyleCianchini, G., Calcara, M., De Santis, A., Piscini, A., D’Arcangelo, S., Fidani, C., Sabbagh, D., Orlando, M., Perrone, L., Campuzano, S. A., De Caro, M., Nardi, A., & Soldani, M. (2024). The Preparation Phase of the 2023 Kahramanmaraş (Turkey) Major Earthquakes from a Multidisciplinary and Comparative Perspective. Remote Sensing, 16(15), 2766. https://doi.org/10.3390/rs16152766










