Missing Region Completion Network for Large-Scale Laser-Scanned Point Clouds: Application to Transparent Visualization of Cultural Heritage
Abstract
1. Introduction
2. Related Works
2.1. Deep Learning-Based Point Cloud Shape Completion
2.2. Dense Point Cloud Reconstruction for Sparse Regions
2.3. Transparent Visualization for Large-Scale Point Clouds
3. Proposed Method for Missing Region Reconstruction
3.1. Overview
3.2. Centroid-Aware Feature Extraction
3.3. Transformer Block
3.4. Dense Point Cloud Generation
3.5. Loss Functions
4. Experiments
4.1. Datasets and Implementation Details
4.2. Synthetic Dataset Completion Results
4.3. Results on Real Scanned Point Cloud Datasets
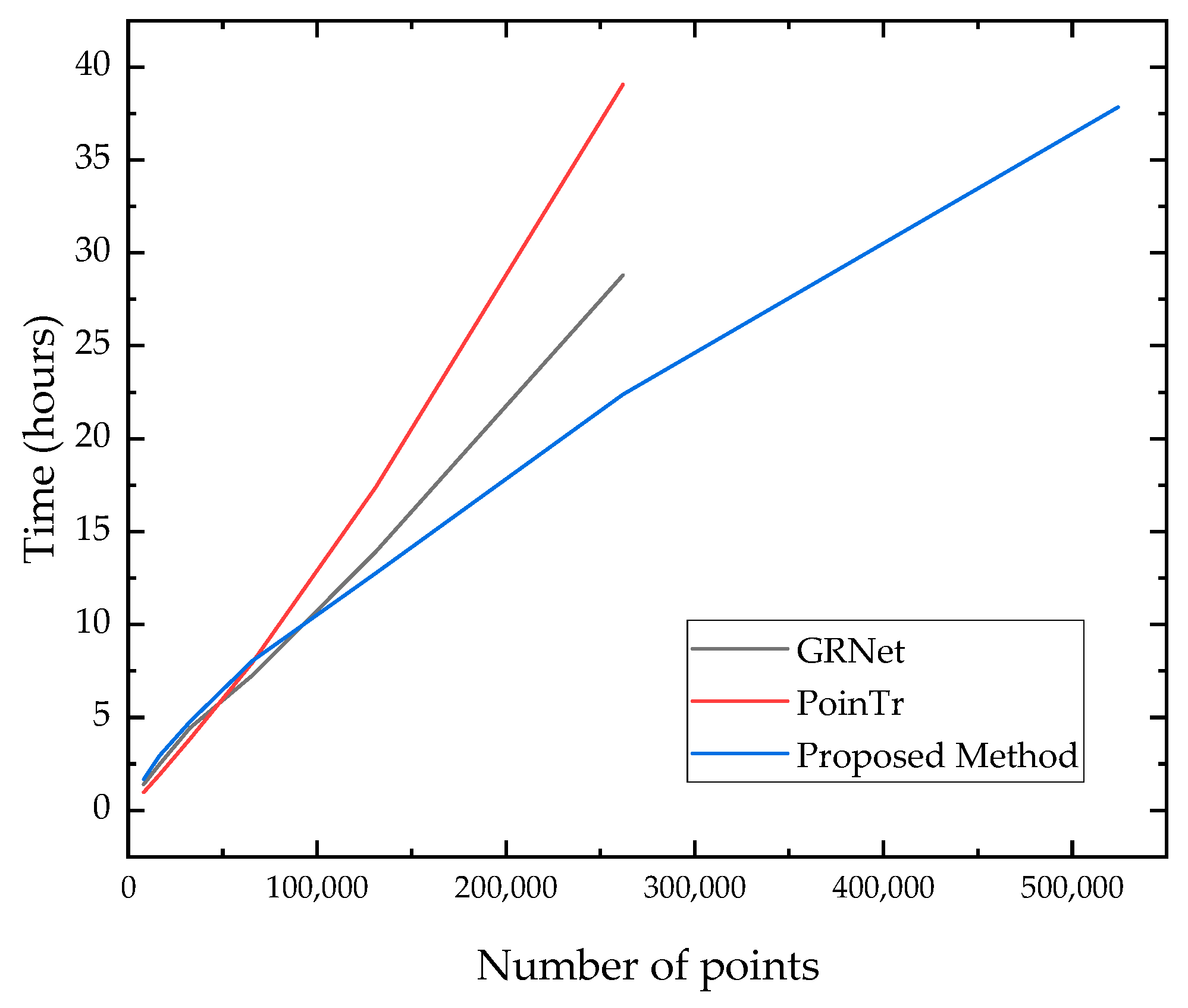
4.4. Application to Large-Scale Cultural Heritage Scanning Data
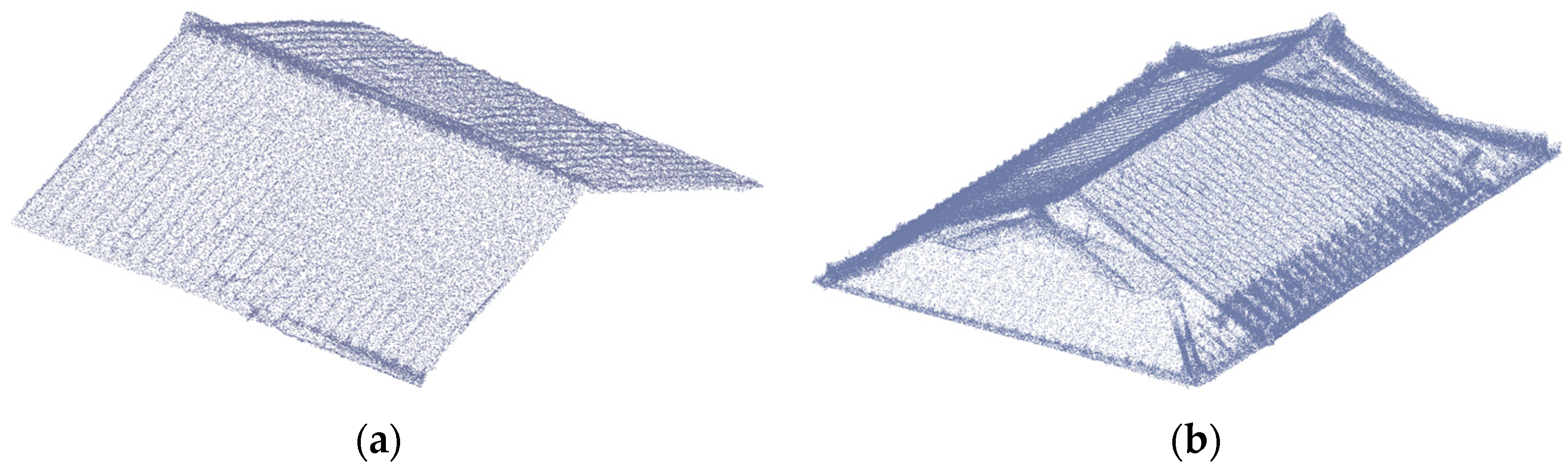
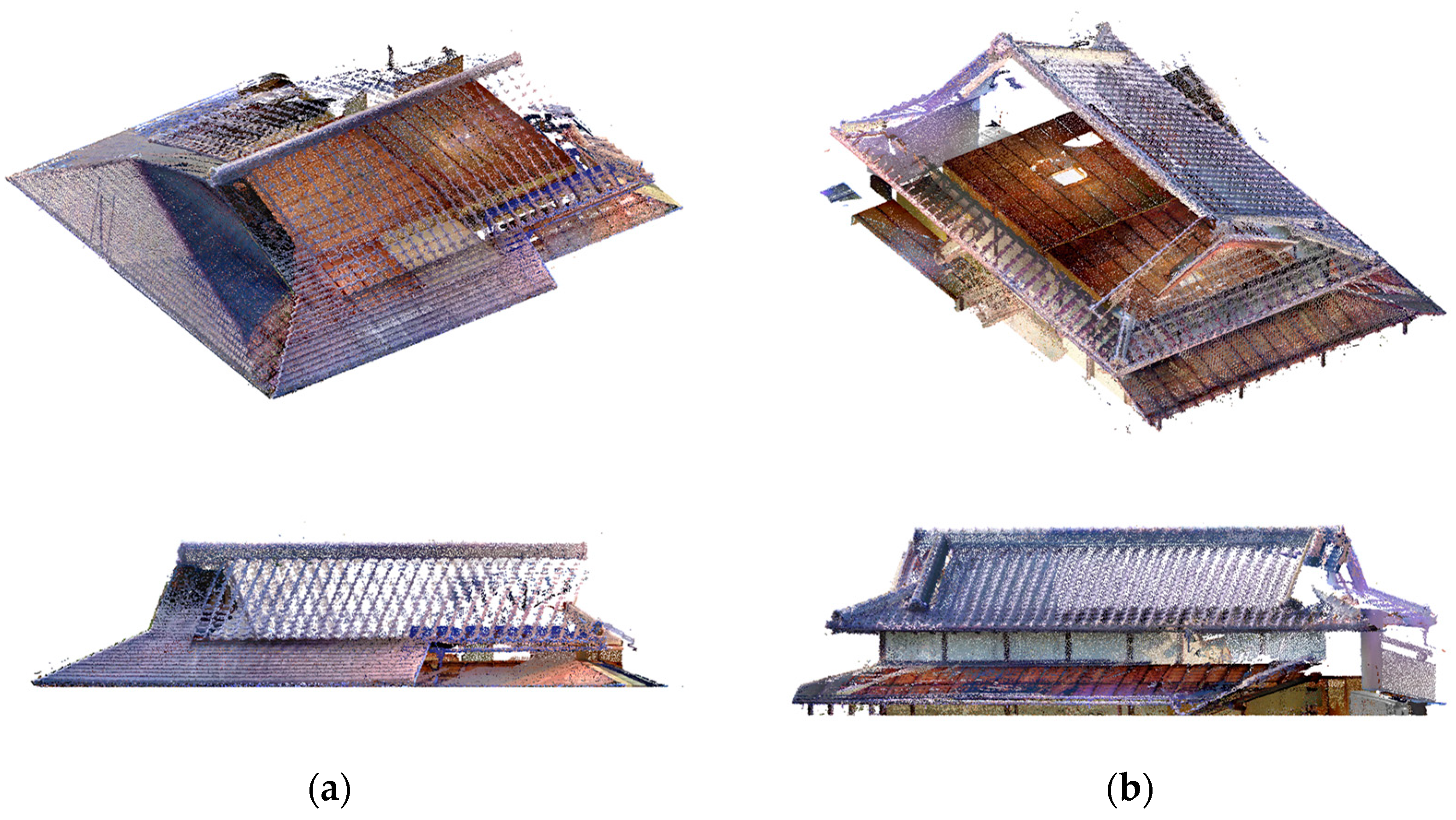
4.4.1. Results of Completion and Visualization for Waraku-an
4.4.2. Results of Completion and Visualization for Zuiganji Temple
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gomes, L.; Bellon, O.R.P.; Silva, L. 3D reconstruction methods for digital preservation of cultural heritage: A survey. Pattern Recognit. Lett. 2014, 50, 3–14. [Google Scholar] [CrossRef]
- Stanco, F.; Battiato, S.; Gallo, G. Digital imaging for cultural heritage preservation. In Analysis, Restoration, and Reconstruction of Ancient Artworks; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3D.net: A new Large-scale Point Cloud Classification Benchmark. arXiv 2017, arXiv:1704.03847. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Huang, Z.; Yu, Y.; Xu, J.; Ni, F.; Le, X. Pf-net: Point fractal network for 3d point cloud completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7662–7670. [Google Scholar]
- Wen, X.; Li, T.; Han, Z.; Liu, Y.-S. Point cloud completion by skip-attention network with hierarchical folding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1939–1948. [Google Scholar]
- Xie, H.; Yao, H.; Zhou, S.; Mao, J.; Zhang, S.; Sun, W. Grnet: Gridding residual network for dense point cloud completion. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 365–381. [Google Scholar]
- Yu, X.; Rao, Y.; Wang, Z.; Liu, Z.; Lu, J.; Zhou, J. Pointr: Diverse point cloud completion with geometry-aware transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 12498–12507. [Google Scholar]
- Pan, L.; Chen, X.; Cai, Z.; Zhang, J.; Zhao, H.; Yi, S.; Liu, Z. Variational relational point completion network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 8524–8533. [Google Scholar]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C.T. Computing and rendering point set surfaces. IEEE Trans. Vis. Comput. Graph. 2003, 9, 3–15. [Google Scholar] [CrossRef]
- Lipman, Y.; Cohen-Or, D.; Levin, D.; Tal-Ezer, H. Parameterization-free projection for geometry reconstruction. ACM Trans. Graph. (ToG) 2007, 26, 22-es. [Google Scholar] [CrossRef]
- Huang, H.; Li, D.; Zhang, H.; Ascher, U.; Cohen-Or, D. Consolidation of unorganized point clouds for surface reconstruction. ACM Trans. Graph. (TOG) 2009, 28, 1–7. [Google Scholar] [CrossRef]
- Qin, Z.; Yu, H.; Wang, C.; Guo, Y.; Peng, Y.; Xu, K. Geometric transformer for fast and robust point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11143–11152. [Google Scholar]
- Bai, X.; Luo, Z.; Zhou, L.; Chen, H.; Li, L.; Hu, Z.; Fu, H.; Tai, C.-L. Pointdsc: Robust point cloud registration using deep spatial consistency. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 15859–15869. [Google Scholar]
- Zhang, Y.; Rabbat, M. A graph-cnn for 3d point cloud classification. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 6279–6283. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8895–8904. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-scale point cloud semantic segmentation with superpoint graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Lai, X.; Liu, J.; Jiang, L.; Wang, L.; Zhao, H.; Liu, S.; Qi, X.; Jia, J. Stratified transformer for 3d point cloud segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8500–8509. [Google Scholar]
- Yu, L.; Li, X.; Fu, C.-W.; Cohen-Or, D.; Heng, P.-A. Pu-net: Point cloud upsampling network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2790–2799. [Google Scholar]
- Yifan, W.; Wu, S.; Huang, H.; Cohen-Or, D.; Sorkine-Hornung, O. Patch-based progressive 3d point set upsampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5958–5967. [Google Scholar]
- Li, R.; Li, X.; Fu, C.-W.; Cohen-Or, D.; Heng, P.-A. Pu-gan: A point cloud upsampling adversarial network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 7203–7212. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Qian, Y.; Hou, J.; Kwong, S.; He, Y. PUGeo-Net: A geometry-centric network for 3D point cloud upsampling. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 752–769. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H. Shapenet: An information-rich 3d model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Yin, T.; Zhou, X.; Krähenbühl, P. Multimodal virtual point 3d detection. Adv. Neural Inf. Process. Syst. 2021, 34, 16494–16507. [Google Scholar]
- Gross, M.; Pfister, H. Point-Based Graphics; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Aicardi, I.; Chiabrando, F.; Lingua, A.M.; Noardo, F. Recent trends in cultural heritage 3D survey: The photogrammetric computer vision approach. J. Cult. Herit. 2018, 32, 257–266. [Google Scholar] [CrossRef]
- Kersten, T.P.; Keller, F.; Saenger, J.; Schiewe, J. Automated generation of an historic 4D city model of Hamburg and its visualisation with the GE engine. In Proceedings of the Progress in Cultural Heritage Preservation: 4th International Conference, EuroMed 2012, Limassol, Cyprus, 29 October–3 November 2012; Proceedings 4. pp. 55–65. [Google Scholar]
- Dylla, K.; Frischer, B.; Müller, P.; Ulmer, A.; Haegler, S. Rome reborn 2.0: A case study of virtual city reconstruction using procedural modeling techniques. In Proceedings of the Computer Applications and Quantitative Methods in Archaeology, Williamsburg, VA, USA, 22–26 March 2010; pp. 62–66. [Google Scholar]
- Tanaka, S.; Hasegawa, K.; Okamoto, N.; Umegaki, R.; Wang, S.; Uemura, M.; Okamoto, A.; Koyamada, K. See-through imaging of laser-scanned 3D cultural heritage objects based on stochastic rendering of large-scale point clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 73–80. [Google Scholar] [CrossRef]
- Tanaka, S.; Hasegawa, K.; Shimokubo, Y.; Kaneko, T.; Kawamura, T.; Nakata, S.; Ojima, S.; Sakamoto, N.; Tanaka, H.T.; Koyamada, K. Particle-Based Transparent Rendering of Implicit Surfaces and its Application to Fused Visualization. In Proceedings of the EuroVis (Short Papers), Vienna, Austria, 5–8 June 2012; pp. 25–29. [Google Scholar]
- Uchida, T.; Hasegawa, K.; Li, L.; Adachi, M.; Yamaguchi, H.; Thufail, F.I.; Riyanto, S.; Okamoto, A.; Tanaka, S. Noise-robust transparent visualization of large-scale point clouds acquired by laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 161, 124–134. [Google Scholar] [CrossRef]
- Choy, C.; Gwak, J.; Savarese, S. 4d spatio-temporal convnets: Minkowski convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3075–3084. [Google Scholar]
- Park, C.; Jeong, Y.; Cho, M.; Park, J. Fast point transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16949–16958. [Google Scholar]
- Bello, I.; Zoph, B.; Vaswani, A.; Shlens, J.; Le, Q.V. Attention augmented convolutional networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3286–3295. [Google Scholar]
- Yuan, W.; Khot, T.; Held, D.; Mertz, C.; Hebert, M. Pcn: Point completion network. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 728–737. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. Foldingnet: Point cloud auto-encoder via deep grid deformation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 206–215. [Google Scholar]
- Li, W.; Hasegawa, K.; Li, L.; Tsukamoto, A.; Tanaka, S. Deep Learning-Based Point Upsampling for Edge Enhancement of 3D-Scanned Data and Its Application to Transparent Visualization. Remote Sens. 2021, 13, 2526. [Google Scholar] [CrossRef]
- Fan, H.; Su, H.; Guibas, L.J. A point set generation network for 3d object reconstruction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 605–613. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference Learn Represent (ICLR), San Diego, CA, USA, 5–8 May 2015. [Google Scholar]
- Tchapmi, L.P.; Kosaraju, V.; Rezatofighi, H.; Reid, I.; Savarese, S. Topnet: Structural point cloud decoder. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 383–392. [Google Scholar]
- Berger, M.; Levine, J.A.; Nonato, L.G.; Taubin, G.; Silva, C.T. A benchmark for surface reconstruction. ACM Trans. Graph. (TOG) 2013, 32, 1–17. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (NZ). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]














| Table | Bottle | Airplane | Bathtub | Bed | Lamp | Piano | Sofa | Overall | |
|---|---|---|---|---|---|---|---|---|---|
| GRNet | 3.86 | 4.53 | 5.87 | 3.41 | 5.63 | 4.85 | 2.89 | 3.51 | 3.06 |
| PoinTr | 0.95 | 2.03 | 3.16 | 1.14 | 2.84 | 1.58 | 0.74 | 1.29 | 1.36 |
| Ours | 1.24 | 2.38 | 2.97 | 1.30 | 3.05 | 1.81 | 1.12 | 1.62 | 1.57 |
| Method | () | ||||
|---|---|---|---|---|---|
| 0.4% | 0.6% | 0.8% | 1.0% | 1.2% | |
| GRNet | 42.71 | 44.59 | 47.35 | 48.91 | 51.22 |
| PoinTr | 16.83 | 17.28 | 18.39 | 20.47 | 21.30 |
| Ours | 13.03 | 13.11 | 13.84 | 14.58 | 15.21 |
| Data_1 | Data_2 | Data_3 | Overall | Data_1 | Data_2 | Data_3 | Overall | Data_1 | Data_2 | Data_3 | Overall | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PoinTr | 2.59 | 2.19 | 1.93 | 3.01 | 4.79 | 8.67 | 2.97 | 7.26 | 4.29 | 3.68 | 2.58 | 4.14 |
| Ours | 2.67 | 2.93 | 2.07 | 3.13 | 3.54 | 6.24 | 1.06 | 5.11 | 4.81 | 5.05 | 2.91 | 4.43 |
| Method | |||||
|---|---|---|---|---|---|
| 0.4% | 0.6% | 0.8% | 1.0% | 1.2% | |
| PoinTr | 5.33 | 5.61 | 5.82 | 6.17 | 6.42 |
| Ours | 4.75 | 4.92 | 5.11 | 5.40 | 5.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Pan, J.; Hasegawa, K.; Li, L.; Tanaka, S. Missing Region Completion Network for Large-Scale Laser-Scanned Point Clouds: Application to Transparent Visualization of Cultural Heritage. Remote Sens. 2024, 16, 2758. https://doi.org/10.3390/rs16152758
Li W, Pan J, Hasegawa K, Li L, Tanaka S. Missing Region Completion Network for Large-Scale Laser-Scanned Point Clouds: Application to Transparent Visualization of Cultural Heritage. Remote Sensing. 2024; 16(15):2758. https://doi.org/10.3390/rs16152758
Chicago/Turabian StyleLi, Weite, Jiao Pan, Kyoko Hasegawa, Liang Li, and Satoshi Tanaka. 2024. "Missing Region Completion Network for Large-Scale Laser-Scanned Point Clouds: Application to Transparent Visualization of Cultural Heritage" Remote Sensing 16, no. 15: 2758. https://doi.org/10.3390/rs16152758
APA StyleLi, W., Pan, J., Hasegawa, K., Li, L., & Tanaka, S. (2024). Missing Region Completion Network for Large-Scale Laser-Scanned Point Clouds: Application to Transparent Visualization of Cultural Heritage. Remote Sensing, 16(15), 2758. https://doi.org/10.3390/rs16152758






