Construction of High-Precision and Complete Images of a Subsidence Basin in Sand Dune Mining Areas by InSAR-UAV-LiDAR Heterogeneous Data Integration
Abstract
1. Introduction
2. Materials and Methods
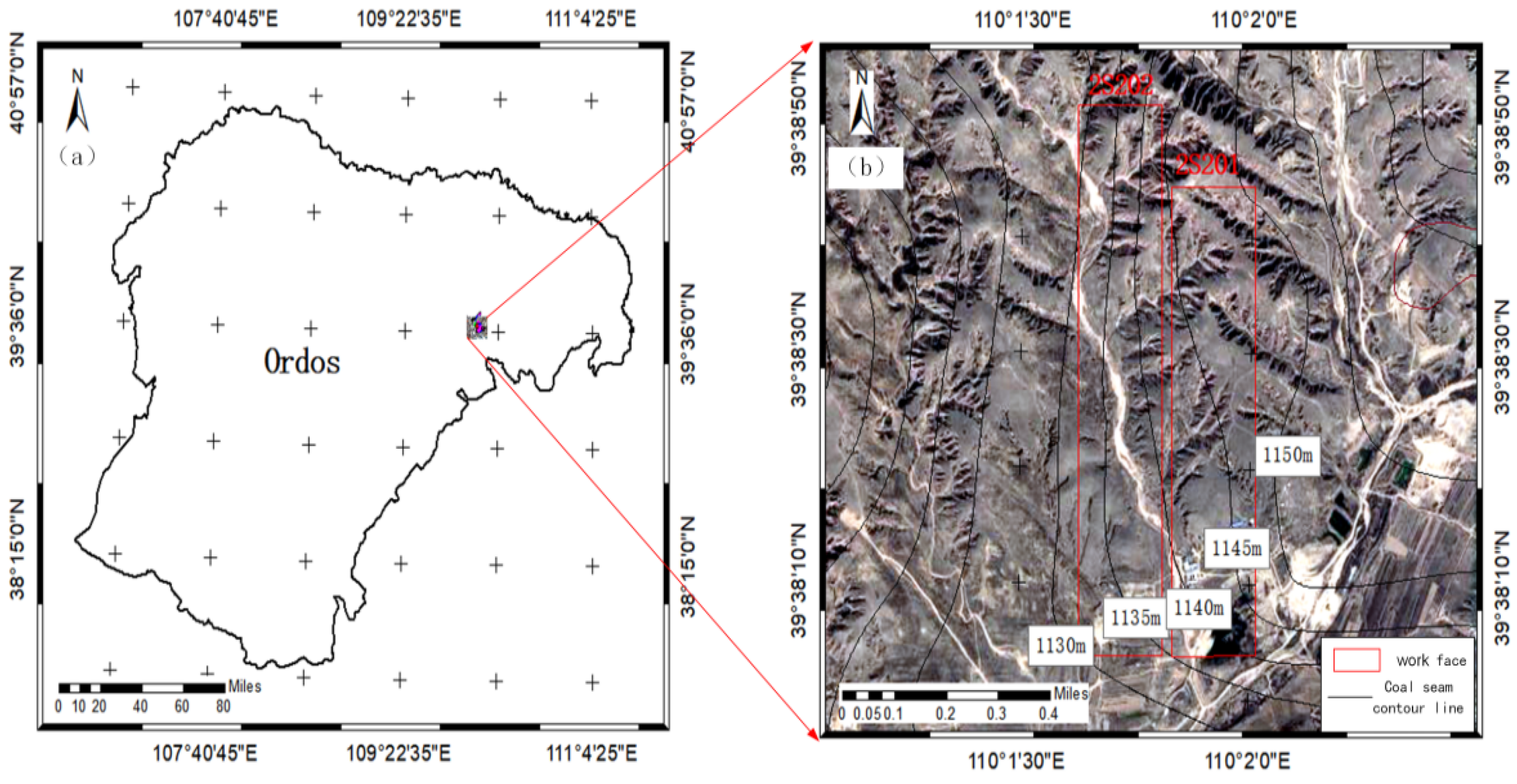
2.1. Study Area and Data
2.2. Data Acquisition
- (1)
- InSAR data
- (2)
- UAV data
- (3)
- LiDAR data
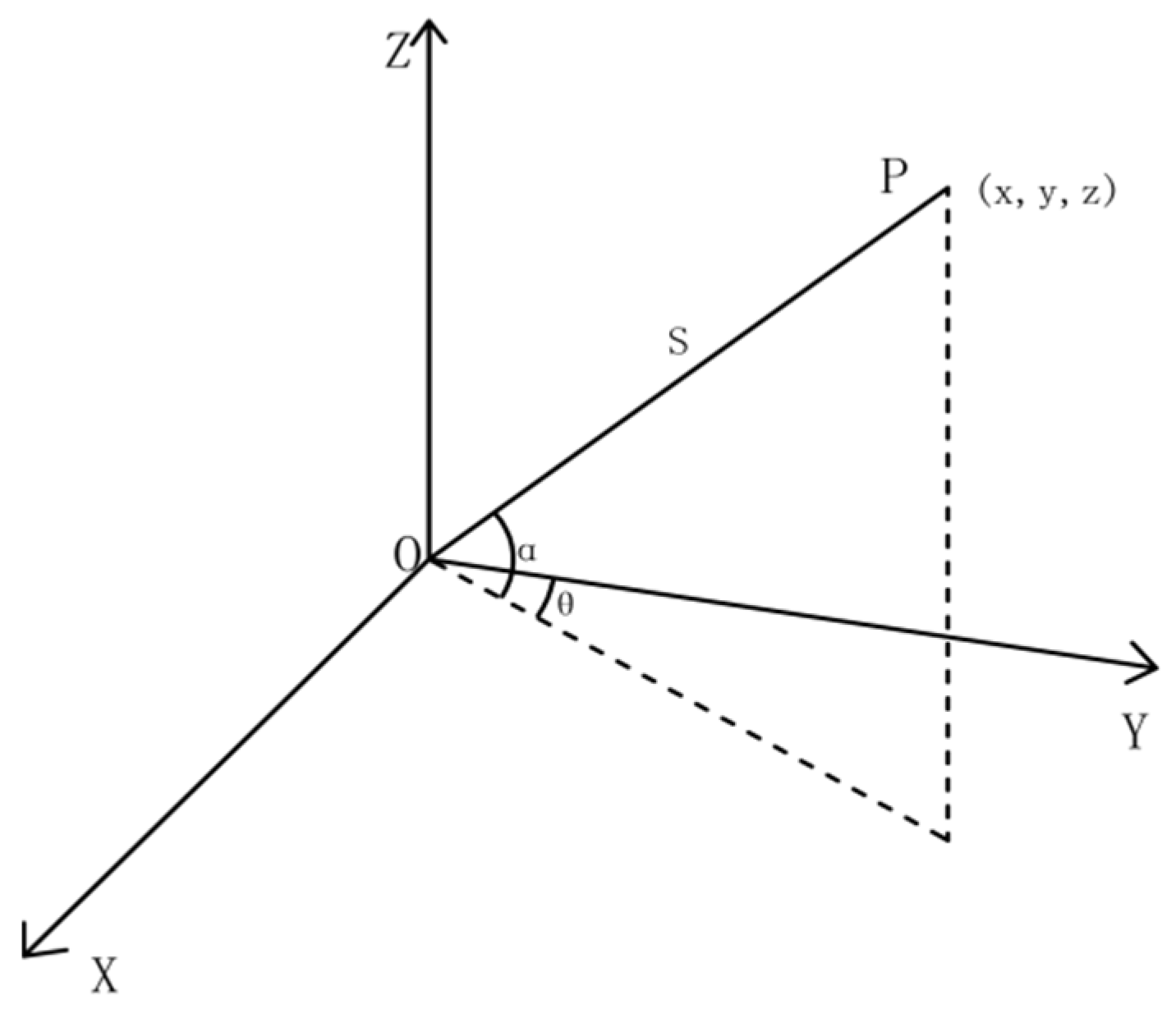
2.3. Principle of SBASInSAR Technology
2.4. Principle of UAV Technology
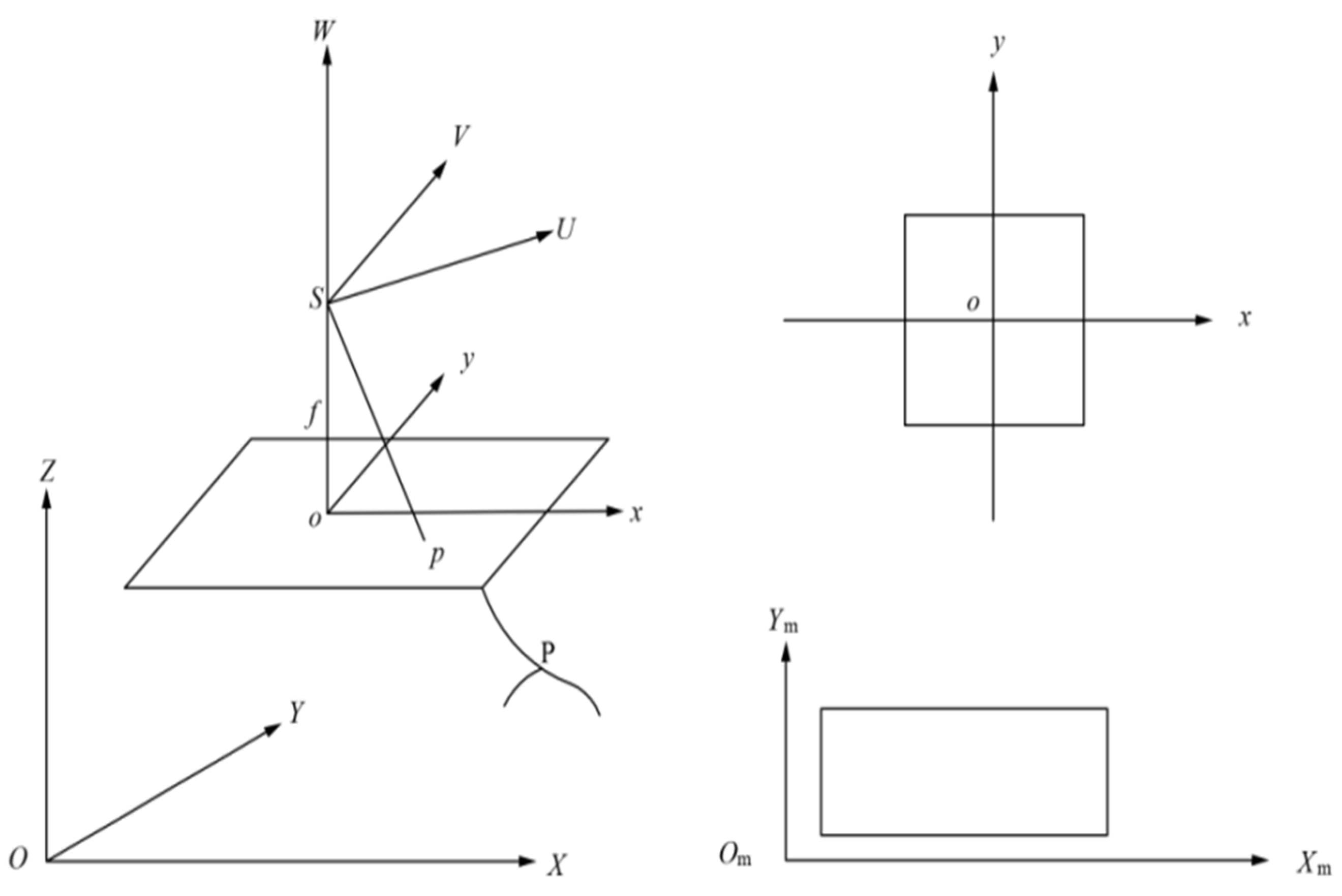
2.5. Principle of LiDAR Technology
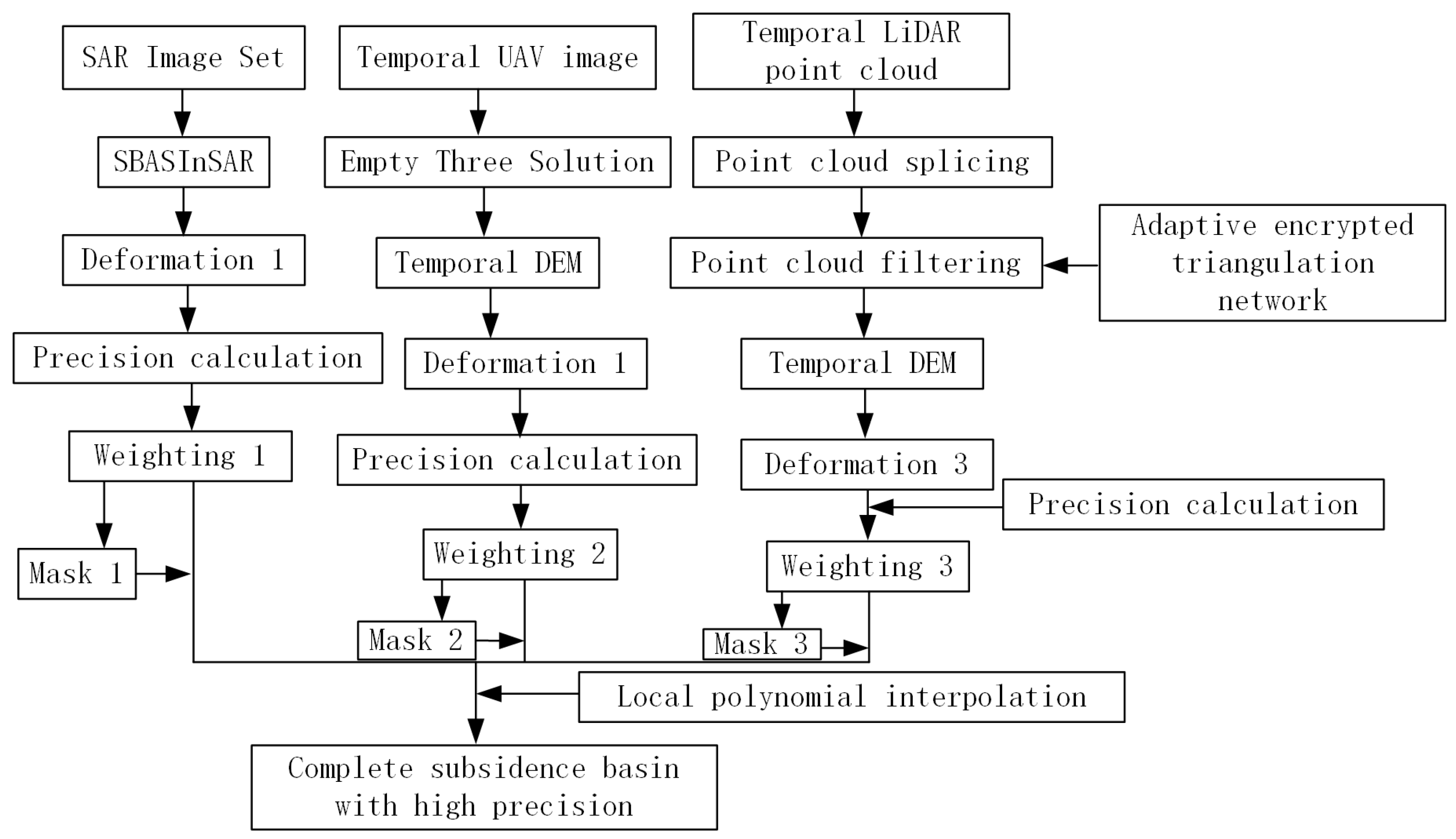
2.6. Data Fusion Theory
3. Results
3.1. Results of SBASInSAR
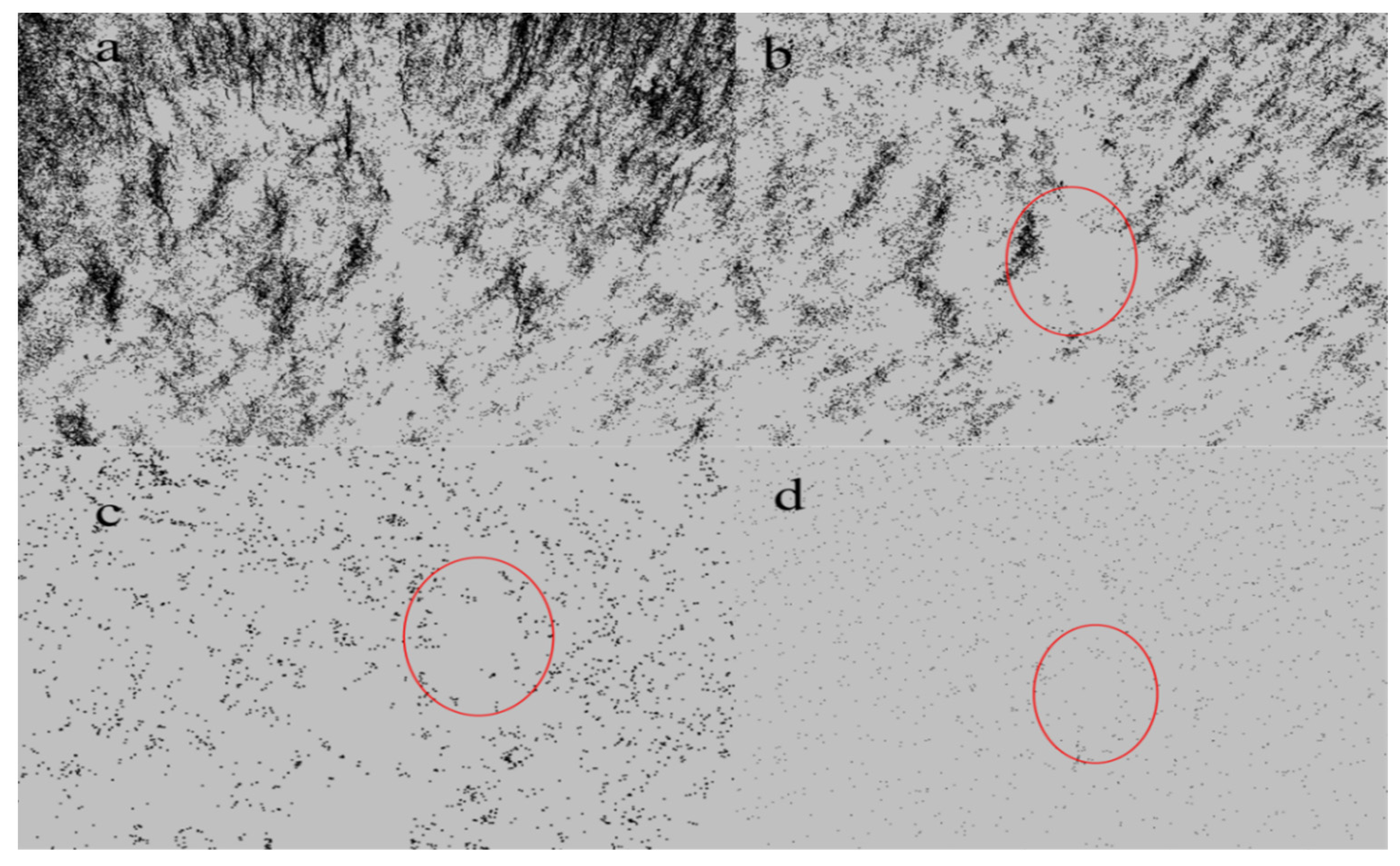
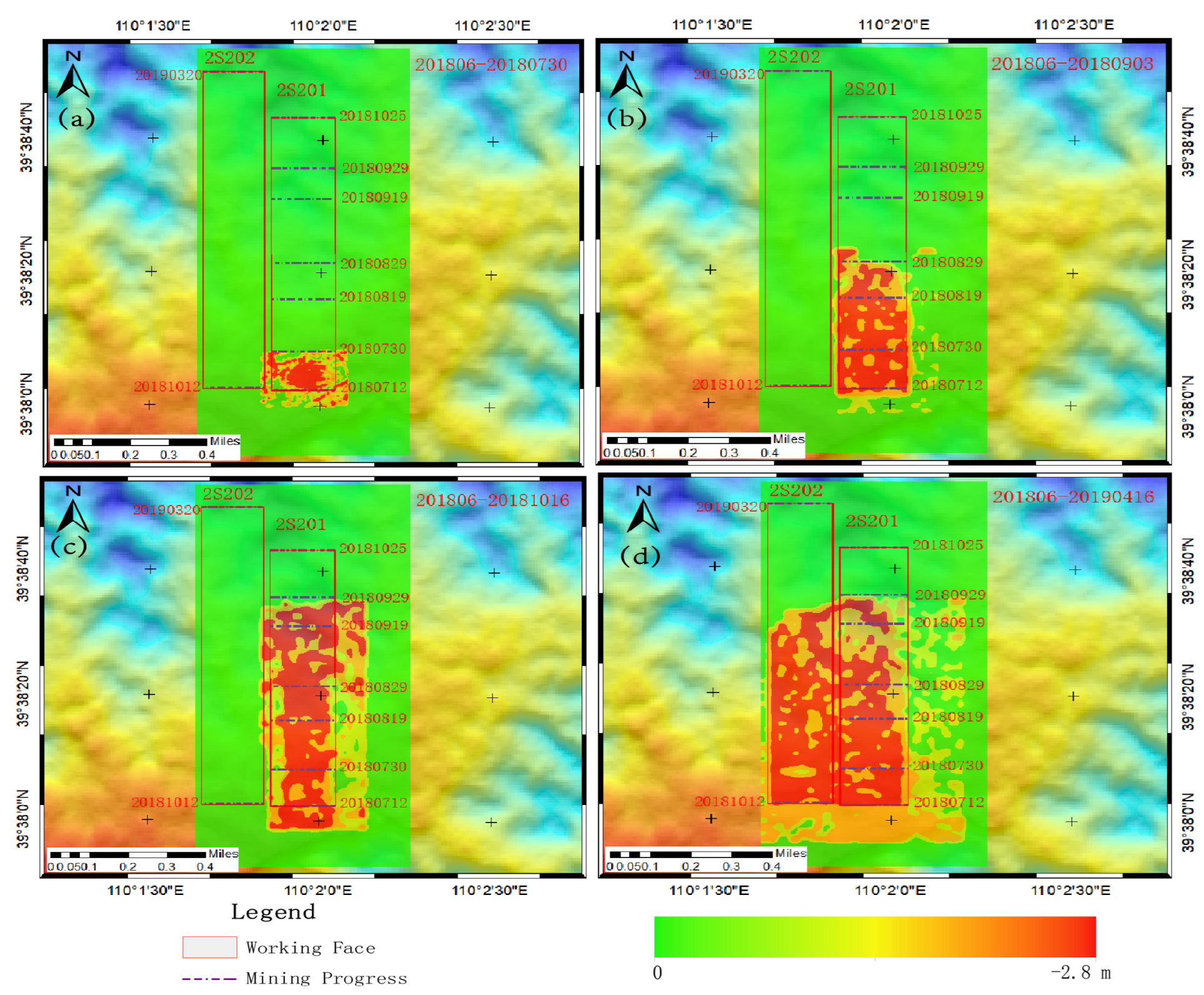
3.2. UAV Results and Accuracy Analysis
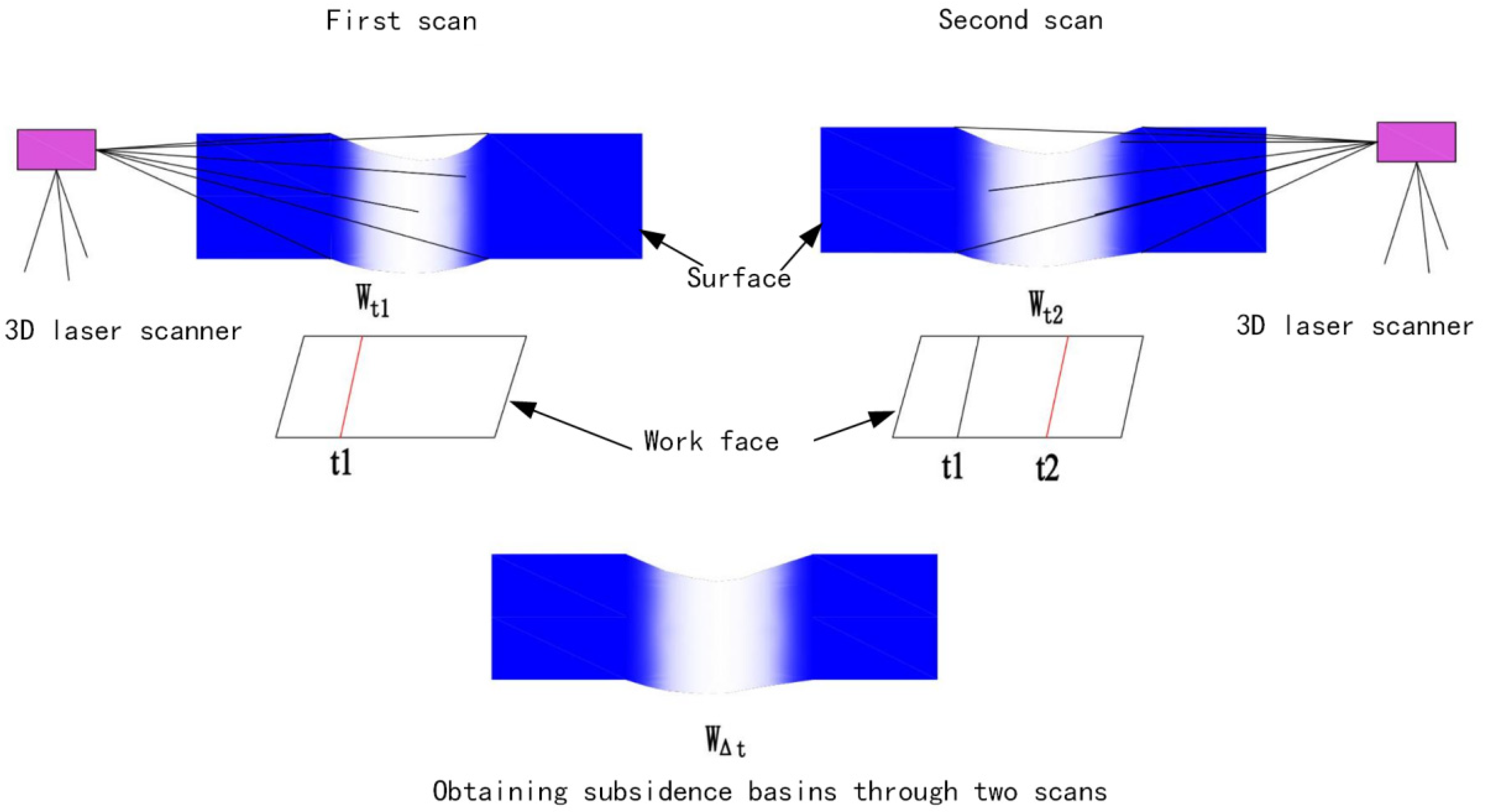
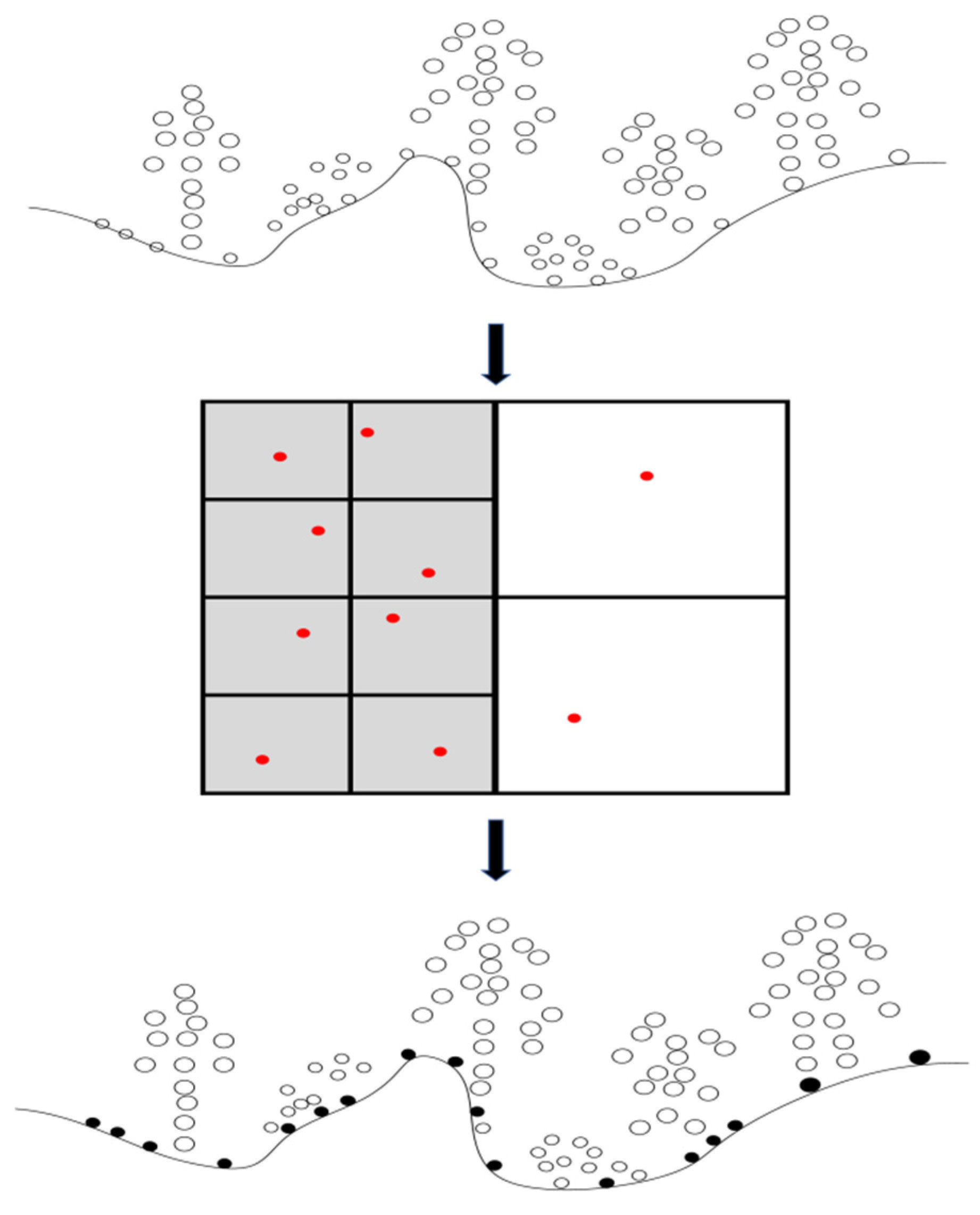
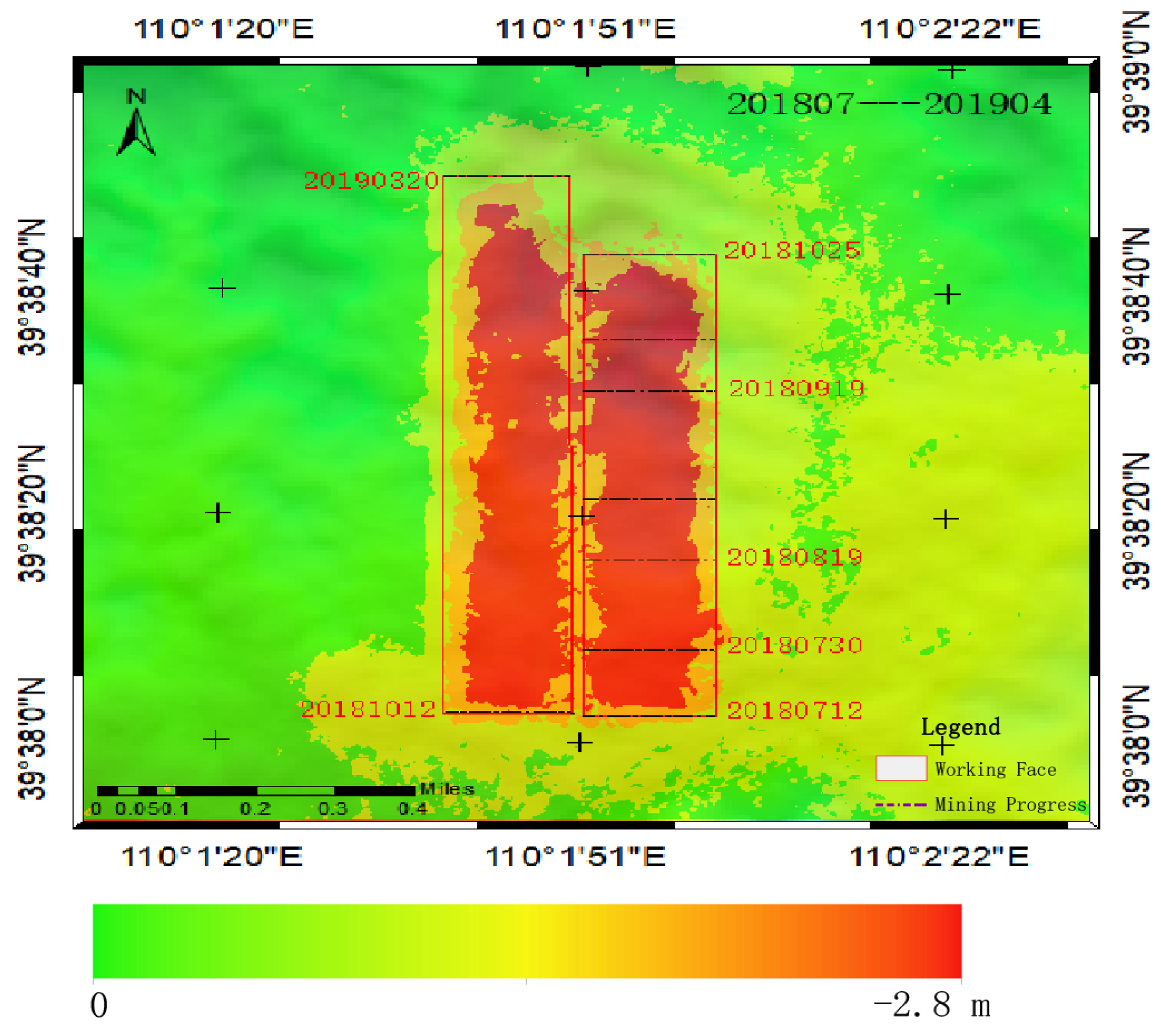
3.3. LiDAR Results and Accuracy Analysis
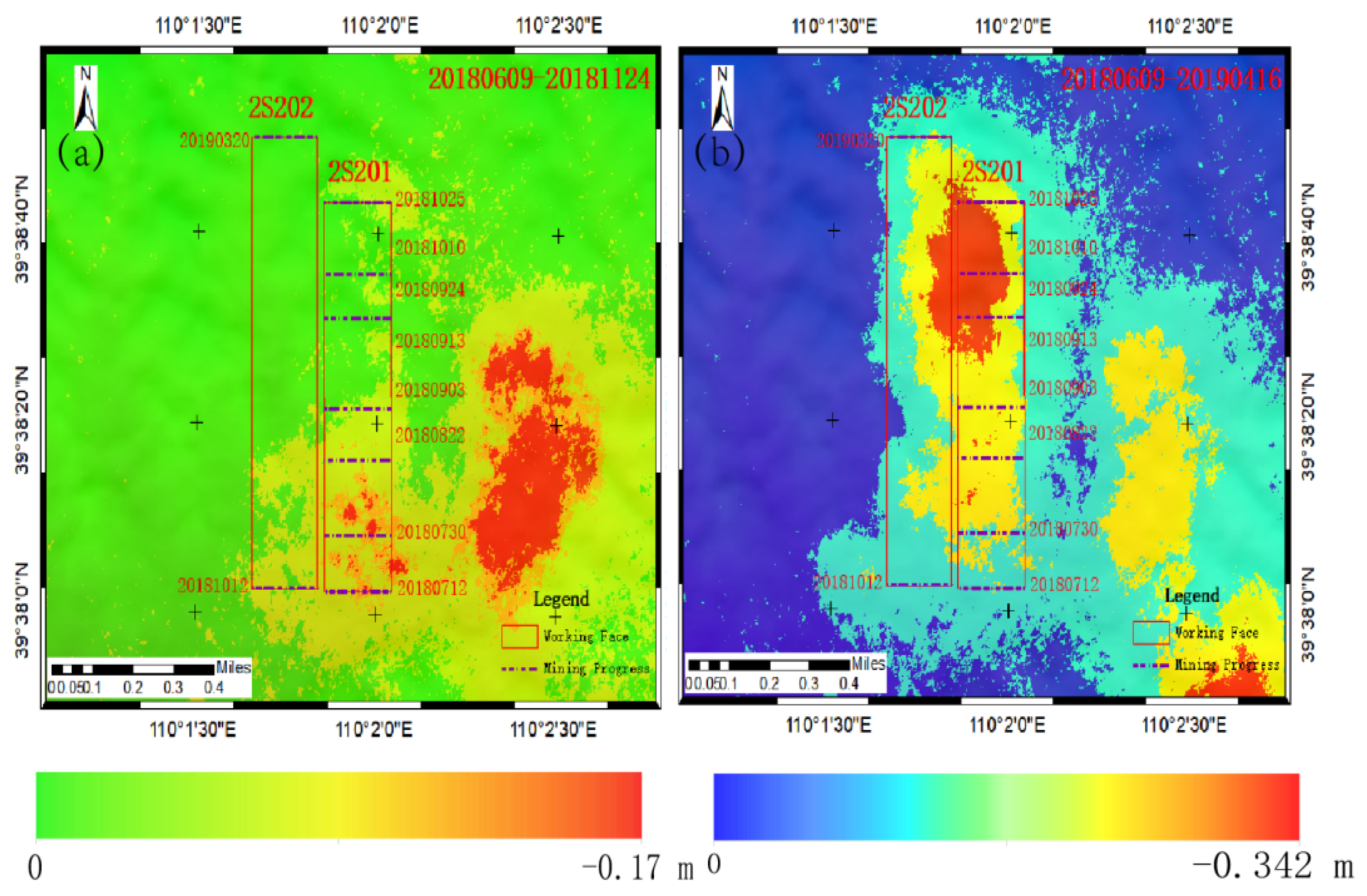
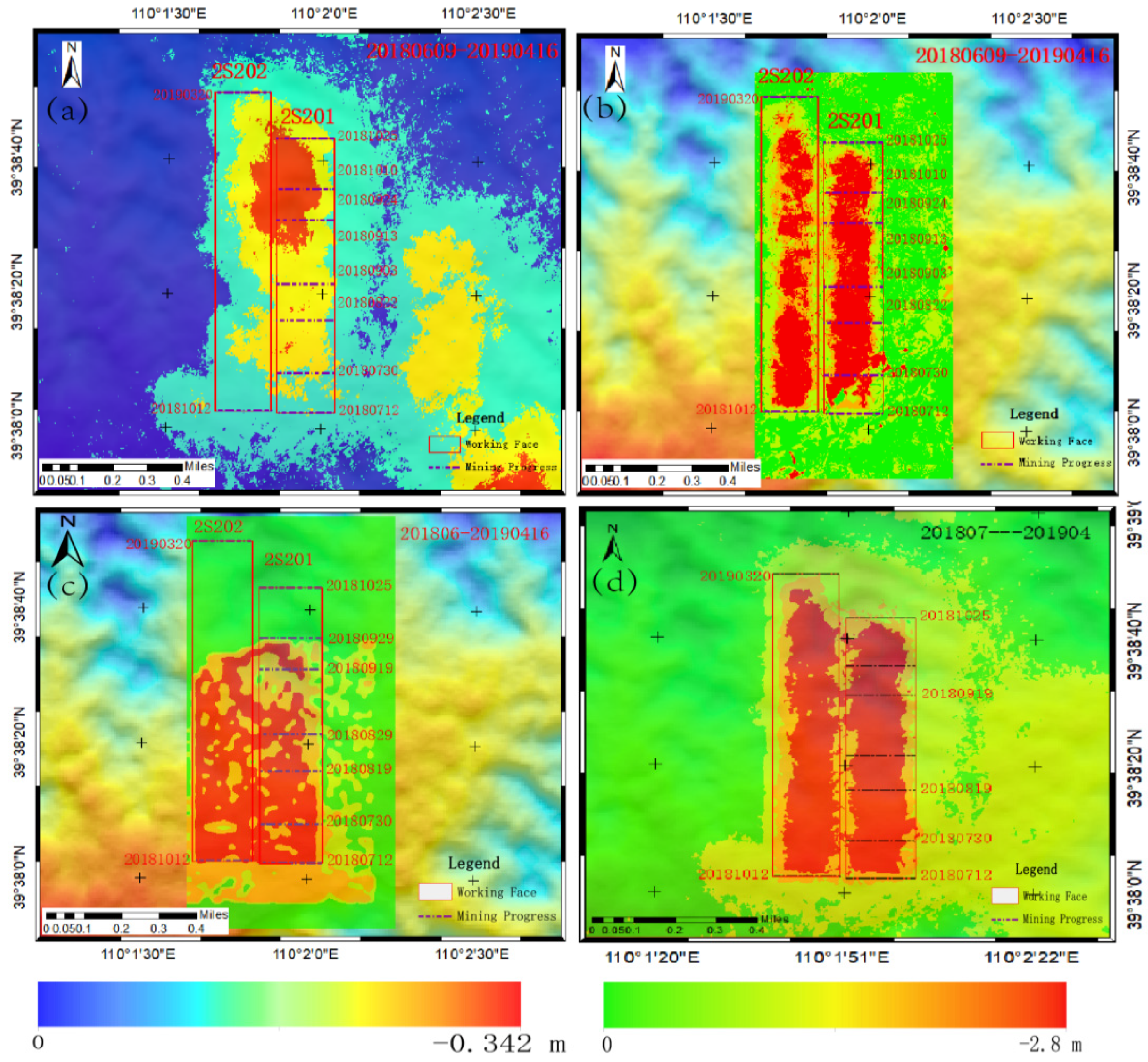
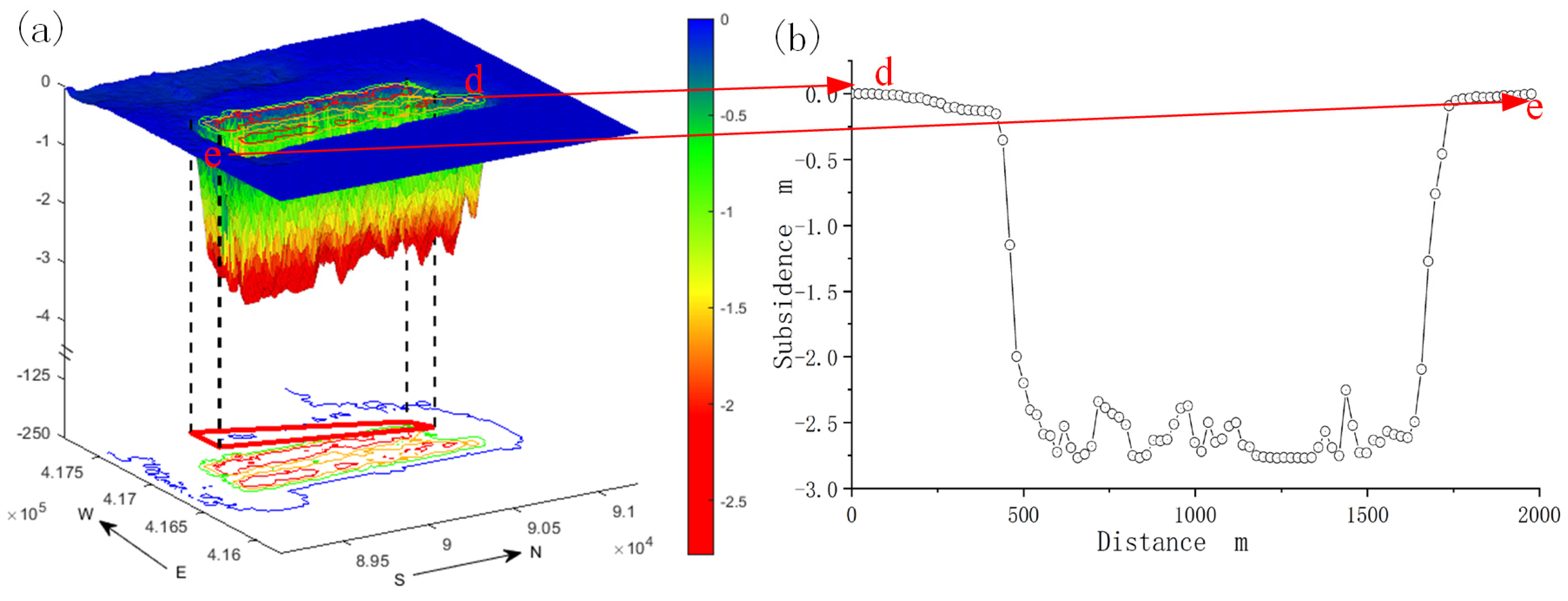
3.4. Fusion Results of Space–Sky–Surface Integrated Monitoring Data
4. Discussion
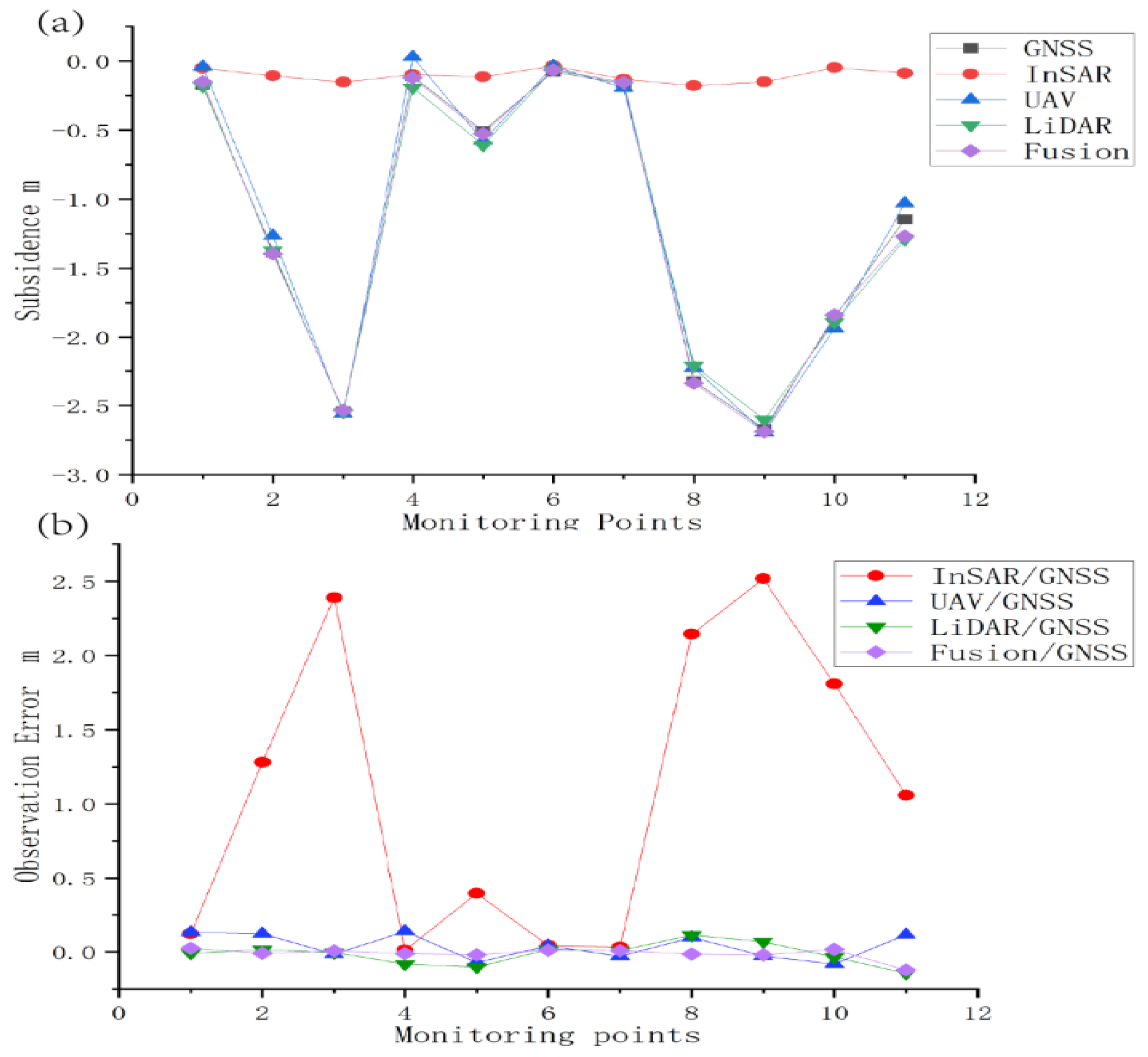
Comparative Analysis of Data Obtained from InSAR, UAV, LiDAR, and GNSS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rui, W.; Shuang, W.; Kan, W.; Huang, S.; Wu, R.; Liu, B.; Lin, M.; Li, L.; Zhou, D.; Diao, X. Estimation and spatial analysis of heavy metals in metal tailing pond based on improved PLS with multiple factors. IEEE Access 2021, 9, 64880–64894. [Google Scholar] [CrossRef]
- Ferrentino, E.; Nunziata, F.; Bignami, C.; Graziani, L.; Maramai, A.; Migliaccio, M. Multi-polarization C-band SAR imagery to quantify damage levels due to the Central Italy earthquake. Int. J. Remote Sens. 2021, 42, 5969–5984. [Google Scholar] [CrossRef]
- An, Q.; Feng, G.; He, L.; Xiong, Z.; Lu, H.; Wang, X.; Wei, J. Three-Dimensional Deformation of the 2023 Turkey Mw 7.8 and Mw 7.7 Earthquake Sequence Obtained by Fusing Optical and SAR Images. Remote Sens. 2023, 15, 2656. [Google Scholar] [CrossRef]
- Spaans, K.; Hooper, A. InSAR processing for volcano monitoring and other near-real time applications. J. Geophys. Res. Solid Earth 2016, 121, 2947–2960. [Google Scholar] [CrossRef]
- Parker, A.L.; Biggs, J.; Lu, Z. Investigating long-term subsidence at Medicine Lake Volcano, CA, using multitemporal InSAR. Geophys. J. Int. 2014, 199, 844–859. [Google Scholar] [CrossRef]
- Shaobo, S.; Tao, C. A review of research on snow cover monitored with synthetic aperture radar (SAR). J. Glaciol. Geocryol. 2013, 35, 636–647. [Google Scholar]
- Xue, F.; Lv, X.; Dou, F.; Yun, Y. A Review of Time-Series Interferometric SAR Techniques: A Tutorial for Surface Deformation Analysis. IEEE Geosci. Remote Sens. Mag. 2020, 8, 22–42. [Google Scholar] [CrossRef]
- Hu, J.; Ding, X.; Li, Z.; Zhang, L.; Zhu, J.; Sun, Q.; Gao, G. Vertical and horizontal displacements of Los Angeles from InSAR and GPS time series analysis: Resolving tectonic and anthropogenic motions. J. Geodyn. 2016, 99, 27–38. [Google Scholar] [CrossRef]
- Shih, P.T.-Y.; Wang, H.; Li, K.-W.; Liao, J.-J.; Pan, Y.-W. Landslide monitoring with interferometric SAR in Liugui, a vegetated area. TAO Terr. Atmos. Ocean. Sci. 2019, 30, 521–530. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Borkowski, A. Integration of DInSAR and SBAS Techniques to determine mining-related deformations using sentinel-1 data: The case study of Rydułtowy mine in Poland. Remote Sens. 2020, 12, 242. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, Q.; Hu, J. Potential of TCPInSAR in monitoring linear infrastructure with a small dataset of SAR images: Ap-plication of the Donghai Bridge, China. Appl. Sci. 2018, 8, 425. [Google Scholar] [CrossRef]
- Bateson, L.; Cigna, F.; Boon, D.; Sowter, A. The application of the Intermittent SBAS (ISBAS) InSAR method to the South Wales Coalfield, UK. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 249–257. [Google Scholar] [CrossRef]
- Xu, Y.; Li, T.; Tang, X.; Zhang, X.; Fan, H.; Wang, Y. Research on the applicability of DInSAR, stacking-InSAR and SBAS-InSAR for mining region subsidence detection in the datong coalfield. Remote Sens. 2022, 14, 3314. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.; Lu, Z. Modeling PSInSAR time series without phase unwrap. IEEE Trans. Geosci. Remote Sens. 2010, 49, 547–556. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Wu, H.; Lu, Z.; Guangtong, S. Monitoring of urban subsidence with SAR interferometric point target analysis: A case study in Suzhou, China. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 812–818. [Google Scholar] [CrossRef]
- Ou, D.; Tan, K.; Du, Q.; Chen, Y.; Ding, J. Decision fusion of D-InSAR and pixel offset tracking for coal mining deformation monitoring. Remote Sens. 2018, 10, 1055. [Google Scholar] [CrossRef]
- Huang, J.; Deng, K.; Fan, H.; Lei, S.; Yan, S.; Wang, L. An Improved Adaptive Template Size Pixel-Tracking Method for Monitoring Large-Gradient Mining Subsidence. J. Sens. 2017, 2017, 3059159. [Google Scholar] [CrossRef]
- Wang, L.; Deng, K.; Zheng, M. Research on ground deformation monitoring method in mining areas using the probability integral model fusion D-InSAR, sub-band InSAR and offset-tracking. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101981. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, L.; Deng, K.; Wang, M.; Xu, Y.; Zheng, M.; Luo, Q. An Adaptive Offset-Tracking Method Based on Deformation Gradients and Image Noises for Mining Deformation Monitoring. Remote Sens. 2021, 13, 2958. [Google Scholar] [CrossRef]
- Huang, J.; Deng, K.; Fan, H.; Yan, S. An improved pixel-tracking method for monitoring mining subsidence. Remote Sens. Lett. 2016, 7, 731–740. [Google Scholar] [CrossRef]
- Kenner, R.; Bühler, Y.; Delaloye, R.; Ginzler, C.; Phillips, M. Monitoring of high alpine mass movements combining laser scan-ning with digital airborne photogrammetry. Geomorphology 2014, 206, 492–504. [Google Scholar] [CrossRef]
- Salvini, R.; Francioni, M.; Riccucci, S.; Bonciani, F.; Callegari, I. Photogrammetry and laser scanning for analyzing slope stability and rock fall runout along the Domodossola-Iselle railway, the Italian Alps. Geomorphology 2013, 185, 110–122. [Google Scholar] [CrossRef]
- Puniach, E.; Gruszczyński, W.; Ćwiąkała, P.; Matwij, W. Application of UAV-based orthomosaics for determination of hor-izontal displacement caused by underground mining. ISPRS J. Photogramm. Remote Sens. 2021, 174, 282–303. [Google Scholar] [CrossRef]
- Stupar, D.I.; Rošer, J.; Vulić, M. Investigation of Unmanned Aerial Vehicles-Based Photogrammetry for Large Mine Subsidence Monitoring. Minerals 2020, 10, 196. [Google Scholar] [CrossRef]
- Ćwiąkała, P.; Gruszczyński, W.; Stoch, T.; Puniach, E.; Mrocheń, D.; Matwij, W.; Matwij, K.; Nędzka, M.; Sopata, P.; Wójcik, A. UAV applications for de-termination of land deformations caused by underground mining. Remote Sens. 2020, 12, 1733. [Google Scholar] [CrossRef]
- Khan, S.D.; Huang, Z.; Karacay, A. Study of ground subsidence in northwest Harris county using GPS, LiDAR, and InSAR techniques. Nat. Hazards 2014, 73, 1143–1173. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Liu, F.; Wang, J. A New Data Processing Method for High-Precision Mining Subsidence Measurement Using Airborne LiDAR. Front. Earth Sci. 2022, 10, 858050. [Google Scholar] [CrossRef]
- Zheng, J.; Yao, W.; Lin, X.; Ma, B.; Bai, L. An Accurate Digital Subsidence Model for Deformation Detection of Coal Mining Areas Using a UAV-Based LiDAR. Remote Sens. 2022, 14, 421. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, W.; Lian, X.; Xu, X. Monitoring Mining Surface Subsidence with Multi-Temporal Three-Dimensional Unmanned Aerial Vehicle Point Cloud. Remote Sens. 2023, 15, 374. [Google Scholar] [CrossRef]
- Wang, R.; Wu, K.; He, Q.; He, Y.; Gu, Y.; Wu, S. A Novel Method of Monitoring Surface Subsidence Law Based on Probability Integral Model Combined with Active and Passive Remote Sensing Data. Remote Sens. 2022, 14, 299. [Google Scholar] [CrossRef]
- Deren, L.I.; Zhang, L.; Xia, G. Automatic analysis and mining of remote sensing big data. Acta Geod. Cart. Graph. Sin. 2014, 43, 1211. [Google Scholar]





| No. | Product | Beam Model | Polarization | Resolution/(m) | Acquisition Date | Pixel Center | Mean Incident Angle (°) |
|---|---|---|---|---|---|---|---|
| (Rng × Az) | Lat–Lng (°) | ||||||
| 1 | SLC | Wide Multi-look Fine | HH | 2.6 × 2.4 | 9 June 2018 | 39.5841–110.5944 | 35.2230 |
| 2 | 27 July 2018 | 39.5852–110.5950 | 35.2232 | ||||
| 3 | 20 August 2018 | 39.5851–110.5961 | 35.2224 | ||||
| 4 | 24 November 2018 | 39.591–110.5977 | 35.2128 | ||||
| 5 | 11 January 2019 | 39.5892–110.5969 | 35.2129 | ||||
| 6 | 4 February 2019 | 39.5627–110.5903 | 35.2124 | ||||
| 7 | 28 February 2019 | 39.5729–110.5952 | 35.2165 | ||||
| 8 | 24 March 2019 | 39.5899–110.5995 | 35.2207 | ||||
| 9 | 17 April 2019 | 39.5880–110.5955 | 35.2223 |
| No. | UAV | Camera | Course Overlap% | Lateral Overlap% | Ground Resolution (m) | Row Height (m) | Collection Date |
|---|---|---|---|---|---|---|---|
| 1 | Trimble UX5 | SONY A5100 | 80 | 80 | 0.06 | 230 | 9 June 2018 |
| 2 | 4 September 2018 | ||||||
| 3 | 16 October 2018 | ||||||
| 4 | 16 April 2019 |
| Date | 20180609 | 20180904 | 20181015 | 20190416 | Mean Squared Error in Average Observation (m) |
|---|---|---|---|---|---|
| Mean Square Error of Observation (m) | 0.101 | 0.118 | 0.109 | 0.091 | 0.105 |
| Data | 20180904 | 20181015 | 20190416 | Mean Square Error |
|---|---|---|---|---|
| Error in settlement (m) | 0.091 | 0.098 | 0.091 | 0.093 |
| Data | 20180730 | 20180903 | 20181016 | 20190416 | Mean Square Error |
|---|---|---|---|---|---|
| Error in subsidence basin (m) | 0.066 | 0.065 | 0.068 | 0.077 | 0.069 |
| Point Mark | GNSS (m) | InSAR (m) | UAV (m) | LiDAR (m) | Fusion (m) | GNSS/ InSAR (m) | GNSS/UAV (m) | GNSS/ LiDAR (m) | GNSS/ Fusion (m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | −0.174 | −0.051 | −0.041 | −0.182 | −0.15 | 0.123 | 0.133 | −0.008 | 0.024 |
| 2 | −1.387 | −0.106 | −1.265 | −1.372 | −1.395 | 1.281 | 0.122 | 0.015 | −0.008 |
| 3 | −2.542 | −0.152 | −2.558 | −2.545 | −2.535 | 2.39 | −0.016 | −0.003 | 0.007 |
| 4 | −0.11 | −0.098 | 0.029 | −0.191 | −0.121 | 0.012 | 0.139 | −0.081 | −0.011 |
| 5 | −0.507 | −0.113 | −0.579 | −0.609 | −0.526 | 0.394 | −0.072 | −0.102 | −0.019 |
| 6 | −0.077 | −0.034 | −0.036 | −0.060 | −0.065 | 0.043 | 0.041 | 0.017 | 0.012 |
| 7 | −0.164 | −0.131 | −0.193 | −0.155 | −0.155 | 0.033 | −0.029 | 0.009 | 0.009 |
| 8 | −2.323 | −0.178 | −2.227 | −2.210 | −2.337 | 2.145 | 0.096 | 0.113 | −0.014 |
| 9 | −2.668 | −0.150 | −2.695 | −2.600 | −2.688 | 2.518 | −0.027 | 0.068 | −0.02 |
| 10 | −1.856 | −0.047 | −1.937 | −1.890 | −1.839 | 1.809 | −0.081 | −0.034 | 0.017 |
| 11 | −1.146 | −0.087 | −1.03 | −1.290 | −1.269 | 1.059 | 0.116 | −0.144 | −0.123 |
| Mean square error | 1.442 | 0.09 | 0.072 | 0.040 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Huang, S.; He, Y.; Wu, K.; Gu, Y.; He, Q.; Yan, H.; Yang, J. Construction of High-Precision and Complete Images of a Subsidence Basin in Sand Dune Mining Areas by InSAR-UAV-LiDAR Heterogeneous Data Integration. Remote Sens. 2024, 16, 2752. https://doi.org/10.3390/rs16152752
Wang R, Huang S, He Y, Wu K, Gu Y, He Q, Yan H, Yang J. Construction of High-Precision and Complete Images of a Subsidence Basin in Sand Dune Mining Areas by InSAR-UAV-LiDAR Heterogeneous Data Integration. Remote Sensing. 2024; 16(15):2752. https://doi.org/10.3390/rs16152752
Chicago/Turabian StyleWang, Rui, Shiqiao Huang, Yibo He, Kan Wu, Yuanyuan Gu, Qimin He, Huineng Yan, and Jing Yang. 2024. "Construction of High-Precision and Complete Images of a Subsidence Basin in Sand Dune Mining Areas by InSAR-UAV-LiDAR Heterogeneous Data Integration" Remote Sensing 16, no. 15: 2752. https://doi.org/10.3390/rs16152752
APA StyleWang, R., Huang, S., He, Y., Wu, K., Gu, Y., He, Q., Yan, H., & Yang, J. (2024). Construction of High-Precision and Complete Images of a Subsidence Basin in Sand Dune Mining Areas by InSAR-UAV-LiDAR Heterogeneous Data Integration. Remote Sensing, 16(15), 2752. https://doi.org/10.3390/rs16152752






