Abstract
Proper documentation is fundamental to providing structural health monitoring, damage identification and failure assessment for Cultural Heritage (CH). Three-dimensional models from photogrammetric and laser scanning surveys usually provide 3D point clouds that can be converted into meshes. The point clouds usually contain noise data due to different causes: non-cooperative material or surfaces, bad lighting, complex geometry and low accuracy of the instruments utilized. Point cloud denoising has become one of the hot topics of 3D geometric data processing, removing these noise data to recover the ground-truth point cloud and adding smoothing to the ideal surface. These cleaned point clouds can be converted in volumes with different algorithms, suitable for different uses, mainly for structural analysis. This paper aimed to analyse the geometric accuracy of algorithms available for the conversion of 3D point clouds into volumetric models that can be used for structural analyses through the FEA process. The process is evaluated, highlighting problems and difficulties that lie in poor reconstruction results of volumes from denoised point clouds due to the geometric complexity of the objects.
1. Introduction
Reality-based models can be obtained from photogrammetry [1], laser scanning [2] or the integration of both [3]. The process is now straightforward and well-established, and it has become easier thanks to the development of computer vision algorithms for photogrammetric purposes and relatively low-cost scanners [4]. The most appropriate technique depends on different factors such as the object surveyed, the area where it is placed, the user experience, the budget, the time available and the goals of the research. Fundamental to heritage conservation is accurate documentation, which can be used, for example, for structural analysis after proper data post-processing. The passage from an unorganized 3D point cloud to surface reconstruction (3D mesh) is a tough issue, especially for applications related to the digitization of architectural sites, virtual environments, reverse engineering for the creation of CAD models [5], and sensing and geospatial analysis. With the developments of instruments, mainly scanner technology, it is possible to acquire dense 3D point clouds consisting of millions of points. The results obtained through the 3D survey are usually affected by different circumstances, such as non-cooperative material or surfaces, bad lighting, complex geometry and the low accuracy of the instruments utilized that can bring noise data. The first step for the conservation of Cultural Heritage is the knowledge of their geometrical complexity. It is a difficult task since the objects surveyed and analysed have been changed through the centuries, showing reparations, changes and reconstructions. All these modifications may have caused cracks and damages, which are usually very difficult to identify and understand. The diagnosis that permits the identification and interpretation of the crack patterns on Cultural Heritage objects and buildings is fundamental if the point is to identify the structural behaviour of the artefact for further interventions. Usually, this is a visual process that is not always possible. When it is not possible to perform this process, the other possibility is quantitative damage diagnostics approaches [6].
Hence, it is mandatory to find the best pipeline to obtain results as close as possible to reality. Another issue that has to be taken into consideration and that will be addressed in the following parts of the research is the segmentation of 3D models into the main part characterizing the object surveyed. The mapping of different parts can be useful for segmenting the object considering its different materials, so it will be easier to apply the correct parameters in the FEA process [7].
1.1. Three-Dimensional Reality-Based Modelling and Structural Analysis
Finite element analysis (FEA) is commonly used as a normal procedure in engineering for structural analyses. It was initially developed for structural mechanics and then applied to solve other kinds of problems, such as dynamic and thermal problems. When dealing with ancient structures, the best result from FEA is derived from the analysis of 3D volumetric models. To avoid the potential propagation of error, a possibility is to directly model a volume from an unorganized 3D point cloud from a 3D survey. The main issue is the accuracy of the model created for FEA, which must be as close as possible to the initial one. The uncertainty and accuracy errors that may occur during the overall process (from surveying to post-processing of 3D models) would be better referred to the identification and modelling of cracks in FEA models; hence, the geometry would be the most important data to be considered. Unfortunately, most of the time, it is not possible to perform a complete and accurate survey of cracks and failures, so it is usually better to refer to a sub-centimetre error considering the entire geometry surveyed; hence, material model and failure data are taken into consideration.
The defined methodology uses Non-Uniform Rational B-splines (NURBS) surfaces to characterize the shape of the object to be simulated. Applying this process to 3D models of CH may introduce a high level of approximation leading to wrong simulation results. Preliminary experiments were carried out on Cultural Heritage [8] for simulating stress behaviour and predicting critical damages. The approaches used are different: (a) drawing a new surface from the 3D mesh [9]; (b) creating a volume directly from the 3D point cloud [10]; (c) using the 3D model for a BIM/HBIM for FEA [11]; (d) using the 3D mesh simplified with retopology [12]. Using HBIM processes to provide FEA of Cultural Heritage is becoming more and more common in research. As well described in [13], BIM was created to support new construction projects, so it has to be modified to adapt it to more complex situations regarding structures built in the past. A BIM project starts from simple details to a more complex structure as the project progresses. With HBIM, on the other hand, the different levels refer not to different complexity from one level to another but rather to parallel levels from a single model related to different details or accuracy connected to different scopes of the project. Therefore, the use of HBIM is useful for the structural investigation of buildings starting from reality-based models, but the point is still the loss of details and accuracy that geometric models present compared to direct 3D survey models. Since the process to obtain a model for structural analysis implies approximation, which must be summed to one of the meshing processes from a sparse 3D point cloud and the one to create a volume, the main issue is to start with the most accurate data possible, which can guarantee the geometrical accuracy and the least possible loss in details. The main problems while dealing with this process regard the following:
- The way to obtain a volume is not yet clearly defined and may greatly influence the result.
- The balance between the geometric resolution and confidence level of the simulated results is often not compliant with the shape of a volume originated by a 3D acquisition process.
Topology refers to the study of geometrical properties and spatial relations between the polygons of a mesh, independent of a continuous variation of their shape and size. Any abrupt change in this relationship is considered a topological error, like the flip of the normal in two adjacent polygons. The reconstruction of surfaces from the oriented point cloud is rather difficult. The point sampling is often non-uniform, and the positions and normal are generally noisy due to sampling inaccuracy and scan misregistration. Starting from these assumptions, the meshing part of the process supposes the topology fits the noisy data accurately and fills holes reasonably. The reconstruction of meshes from a 3D point cloud is usually made of triangles, which barycentre describes as a linear surface representation. While triangles are the most popular reality-based modelling primitive, quads elements are frequently used during the modelling stage. A model with a triangle-based topology can produce sharp angles that can affect the design of a mesh. With quads, it is easier to add or manipulate edge loops to obtain a smoother deformation.
Quad-based topology is formed by polygons that have four vertices and four edges used as essential components in 3D modelling and in computer graphics to specify the geometry and surfaces of three-dimensional objects. They offer a quick and effective way to explain intricate forms and surfaces having intrinsic regularity and symmetry, leading to smoother surface interpolation and more realistic-looking curves. This is the reason why they are mostly used to represent biological things like people, animals and items with curved surfaces. One of the benefits is the control of topology and the management of edge loops, which are continuous lines of edges that flow around the surface of a model. Fixing edge loops carefully results in softer deformations, effective rigging and smoother animation. To pass from a triangular to a quadrangular mesh, the process used is called retopology. It samples the original mesh at a spatial resolution lower than the original with a degree of accuracy higher, it conserves the overall geometry of the original mesh, redefining from scratch its topological structure. This method allows the generation of an accurate and simplified 3D model of a real artefact starting from a 3D image and range-based one, maintaining its accuracy.
There are different solutions to turn a 3D mesh into a volume suitable for FEA:
- (a)
- The creation of a new topology with retopology [14] without losing the initial accuracy of the models even when creating a NURBS.
- (b)
- Use voxels, 3D pixels, to model a 3D point cloud into a volume. In the process called voxelization, points in the point cloud that fall in certain voxels are maintained, while all others are either discarded or zeroed out to obtain a sculpted representation of the object.
The use of retopology implies different passages, which leads to possible inaccuracies and approximations. Of course, the level of approximation depends on how strong the interventions on the mesh were and on the complexity of the object analysed:
- From point cloud to mesh;
- Post-processing of the mesh (closing holes and check topology);
- Retopology (smoothing);
- Closing holes and check topology;
- NURBS.
Both processes allow obtaining volumes that can be imported into FEA software Ansys 19.2 to provide structural analysis, and both present advantages and disadvantages, as in Table 1.

Table 1.
Pro and cons of retopology and voxelization of 3D point clouds.
1.2. Voxel and Denoising
Voxelization is certainly faster than the retopology process for the creation of NURBS, but the parameters have to be chosen wisely since strong smoothing is often added to the model. This process seems, however, the most promising in terms of time-saving and accuracy since it avoids all the problems related to the different steps needed when dealing with a 3D mesh and its transformation. No studies have now compared volumetric models obtained with different techniques and procedures to identify the best in terms of precision and accuracy. Most of the related works apply voxelization to object detection [15,16,17,18,19,20], especially for autonomous driving or the detection of elements for the segmentation of 3D point clouds. There is a huge application of voxel-based modelling in the medical field [21,22,23,24,25]. There have been some tests on the use of voxels for FEA, for example, for calculating ballistic impacts on ceramic–polymer composite panels [26], where voxel-based micro-modelling allowed to build of a parametrical model made of composite structure. Another study used voxel modelling of caves to predict roof collapses. Using this technique allowed us to overcome difficulties in the reconstruction of the geometry of the caves and the limitation of FEM software Ansys 19.2 [27]. Then, to improve the accuracy of FEA, since using voxels reduces the time in mesh generation but there is a lack of accuracy when dealing with curved surfaces, refs. [28,29] present a homogenization method for the voxel elements.
The problem when dealing with complex geometries, such as the ones of Cultural Heritage artefacts, is that the voxelization algorithms present too much simplification.
A strong algorithm to process voxel is [30]. Unfortunately, the starting point is a mesh, and it was decided to start from the point cloud to create voxel grids. So, it was decided to test the Open3D open-source library [31] with the voxel_down_sample (self, voxel_size) function that permits down sampling the input point cloud into an output point cloud with a voxel. Normals and colours are averaged if they exist.
- PARAMETERS:
- voxel_size (float)–Voxel size to downsample into.
- RETURNS:
- open3d.geometry.PointCloud
To improve the accuracy of the 3D point cloud, a denoising algorithm can be used. Point cloud denoising aims at removing undesirable noises from a specified noisy dense cloud. Over the past few years, diverse algorithms have been proposed for 3D point cloud cleaning to make them more geometrically close to real objects. Bilateral filtering [32] is a nonlinear technique to smooth an image. This concept has been extended to denoising point clouds [33]. These denoising methods apply the bilateral filter directly to point clouds based on point position, point normal and point colour [34]. The guided filter [35] is an image filter that can serve as an edge-preserving smoothing operator [36]. Recently, most filter-based algorithms employ the normal of the points as guidance signals. The points are then iteratively filtered and updated to match the estimated normal. There are then graph-based point cloud denoising methods that first interpret the input point cloud as a graph signal and then perform denoising via chosen graph filters [37]. The patch-based graph builds the graph on surface patches of point clouds where each patch is defined as a node [38]. Optimization-based denoising methods look for a denoised point cloud that can best fit the input point cloud [39]. Finally, deep learning algorithms have been applied to point cloud processing [40]. The denoising of point clouds starts from the noisy inputs to learn a map to be superimposed on the ground-truth data in an offline stage. Deep learning-based methods can be categorized into two types: supervised denoising methods as PointNet-based [41] and unsupervised denoising methods [36]. The algorithm used in this paper is proposed in [42] and was analysed by comparing the point clouds of different objects to underline its usefulness. It consists of a point cloud score-based denoiser in a three-dimensional space. The technique simulates an intelligent smoothing operation on potential surfaces based on a majority voting (or density/magnitude of points) approach.
In this paper, raw point clouds and denoised ones have been compared to test the usefulness of a denoising algorithm [37] for the geometric accuracy of point clouds and meshes for volumetric modelling for structural analysis. The aim of the paper does not include a discussion about the capability of the methodology to generate an ideal shape but tries to understand if a denoising algorithm could be helpful in interpretative processes. Thus, the quality of the denoiser could be partially responsible for the obtained results in the study. Then, the rough 3D point clouds and the denoised ones have been processed to create direct voxel grids. The pipeline then followed two steps: (i) creation of voxel models from voxel grids; (ii) creation of mesh, retopology and creation of NURBS from voxel grids. These models have been compared to NURBS models obtained through the process that uses retopology from reality-based 3D models. The idea is to see if it is possible to use direct voxel models created from 3D point clouds in FEA software for structural analysis.
2. Materials and Methods
Three-dimensional meshes of six different objects have been considered for this study:
- A portion of the wall of the Solimene factory in Vietri (Figure 1a).
 Figure 1. The test objects of this paper: (a) Solimene’s factory; (b) statue of Moses; (c) portion of the façade of Solimene’s factory; (d) car’s suspension; (e) medieval pillar; (f) scorpionide (copy of a Roman throwing machine).
Figure 1. The test objects of this paper: (a) Solimene’s factory; (b) statue of Moses; (c) portion of the façade of Solimene’s factory; (d) car’s suspension; (e) medieval pillar; (f) scorpionide (copy of a Roman throwing machine). - The statue of Moses from the tomb of Julius II in Rome (Figure 1b).
- Several amphorae of the same wall (Figure 1c).
- A suspension of a car, chosen for its simple geometry (Figure 1d).
- A pillar of a medieval cloister (Figure 1e).
- A replica of a Roman throwing weapon (scorpionide) (Figure 1f).
The objects have been surveyed with photogrammetry, with an APS-C Canon 60D camera coupled with a 20 mm lens. Parameters like ISO and f-stop have been set according to the environmental light and GSD. Agisoft Metashape 2.1.1 was chosen for the creation of the 3D models, using high parameters for the alignment of the images and the creation of point clouds and different numbers of elements for each mesh, depending on the number of points in the dense cloud. These meshes have been then post-processing in different ways:
- For retopology, Instant Meshes have been used, while, for the creation of NURBS, the automatic tool in Rhinoceros has been used.
- For voxelization of meshes and point clouds, the algorithm voxel_down_sample(self, voxel_size) and the voxel process in Blender and Meshmixer 3.5.474 volume creator were tested.
- For denoising the point cloud, score-based point cloud denoising algorithm has been used since it is one of the latest and most stable by now [35].
2.1. Retopology and NURBS
For the creation of 3D simplified meshes through retopology, InstantMeshes open source software has been used [42,43]. It automatically calculates the more suitable number of elements in the final, simplified model, starting from the number of elements in the high-resolution one. The operator can always change it approximately with a sliding tool, but the result is not always satisfactory: sometimes, holes and missing parts are largely visible (Figure 2a–d).

Figure 2.
Retopologised models of (a) Moses’s statue; (b) Solimene’s factory; (c) portion of the wall of Solimene’s factory; (d) suspension of car.
The process was quite straightforward except for the portion of the Solimene’s façade, which counted more than 5 million polygons. The simplified models had 530 K polygons, still too many for the mesh to be converted to a volumetric model. The retopologised models have then been transformed in NURBS to export a volumetric model. A mesh represents 3D surfaces with a series of discreet faces, closer in likeness as pixels form an image. NURBS, on the contrary, are mathematical surfaces, able to represent complex shapes with no granularity as in the mesh. The conversion from a mesh to a NURBS is implemented in CAD software or similar (e.g., 3DMax, Blender, Rhinoceros, Maya, Grasshopper), and it transforms a mesh composed of polygons or faces to a faceted NURBS surface. In detail, it creates one NURBS surface for each face of the mesh and then merges everything into a single polysurface.
Depending on the mesh, the conversion works in different ways:
- If the starting point is a triangular mesh, and while, by definition, triangles are plane, the conversion creates trimmed or untrimmed planar patches. The degree of the patches is 1 × 1, and the surface is trimmed in the middle to form a triangle.
- If the starting point is a quadrangular mesh, the conversion creates a 4-sided untrimmed degree1 NURBS patches, meaning that the edges of the mesh are the same as the outer boundaries of the patches.
2.2. Denoising Algorithm
Original and denoised point clouds have been compared with the CloudCompare 2.13.2 software’s tool. As known, comparison systems can be performed using shapes or clouds as references [24]. Considering the Gaussian distribution for both mean and standard deviation along with the C2C (Cloud-to-Cloud) signed distances, it just looks for the nearest points and makes a comparison (Figure 3a–e). The portion of Solimene’s façade failed during the denoising process, probably because the dense cloud was heavy and presented more than 22 million points. These settings have been chosen because the denoising algorithm basically takes the noisy points far from a target surface (aka where the majority of points lay) and moves them onto this reference surface.
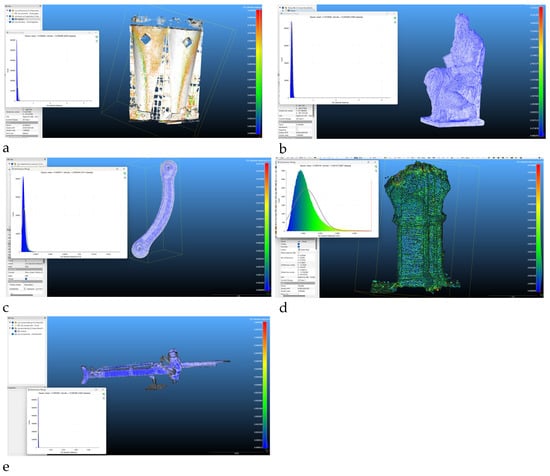

Figure 3.
The comparison of raw data and denoised ones: (a) Solimene factory; (b) Moses’s statue; (c) car suspension; (d) medieval pillar; (e) scorpionide.
| Object | Mean (mm) | Standard deviation (mm) |
| Fabbrica Solimene | 0.034662 | 0.001625 |
| Mosè | 0.072848 | 0.034495 |
| Suspensions | 0.000471 | 0.000344 |
| Masonry pillar | 0.002318 | 0.001413 |
| Scorpionide | 0.0002883 | 0.000284 |
For a simple test regarding the better geometrical reproduction of the real object, the denoising algorithm was applied to the statue of Moses, which presents a complex geometry and the cleanest and most accurate 3D point cloud. Then, the mesh from the initial point clouds and the denoised ones have been compared (Figure 4).

Figure 4.
Topological analysis of the Moses’ meshes: not denoised (a); denoised (b); retopologised not denoised (c); retopologised denoised (d). Red dots in the images indicates the errors and the holes in the models.
The purpose was to analyse how the geometric approximation in the meshing process can be influenced by the denoising algorithm, so the geometrical accuracy of the point cloud can then be an added value to the process. The first passage was to investigate the topological errors in the meshes: the one derived from the raw data showed many topological errors while the denoised one did not any (Figure 4a,b), meaning that the algorithm helped in adjusting the geometrical accuracy of the data. After the meshing process, the models were then simplified using retopology. The meshes showed few topological errors, the denoised one less than the other (Figure 4c,d). As a plus, both retopologised meshes were then converted into NURBS to check the accuracy of the volumetric model, and the one obtained from the raw point cloud failed in the construction, meaning that the data were too noisy and too dense for the tool.
2.3. Voxel
Point clouds and triangle meshes are very flexible but irregular geometry types. The voxel grid is a geometry type, the 3D counterpart of 2D pixels in images, defined on a regular grid. The creation of the voxel models has been completed with the use of 2 software, Blender 4.1 and Meshmixer 3.5.474, that automatically create a voxel model from the input mesh and an open source library, Open3D. It was decided to test these tools to understand how the automatic transposition works without using Python coding. The test was performed on retopologised meshes because they are lighter than the high-resolution models and because the quad elements are more adaptable to geometry. The operator can decide the accuracy and the number of elements.
Blender showed the most straightforward process; the only parameter the operator can control is the number of the elements approximated, indicating the resolution or the amount of detail the remeshed mesh will have. The value is used to define the size, in object space, of the voxel. These voxels are assembled around the mesh and are used to determine the new geometry. For example, a value of 0.5 m will create topological patches that are about 0.5 m. Lower values preserve finer details but will result in a mesh with a much denser topology.
Meshmixer creates a watertight solid from mesh surfaces by recomputing the object into a voxel representation. The process is easy, the only parameter the operator can change is the solid type, if fast or accurate, the solid accuracy with a sliding tool that gives a certain number and the mesh density. These numbers are not correlated to the final number of polygons of the volume.
Open3D (Figure 5) supports rapid development of software that deals with 3D data. Core features of Open3D include (i) 3D data structures, (ii) 3D data processing algorithms, (iii) scene reconstruction, (iv) surface alignment, (v) 3D visualization.
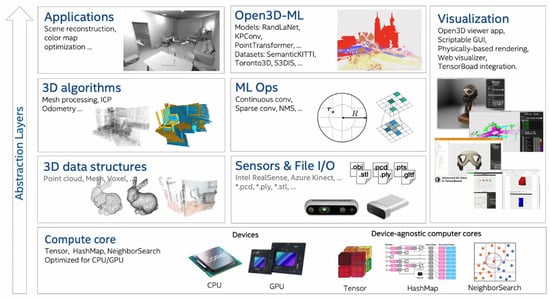
Figure 5.
Schema regarding the functions of Open3D (taken from https://www.open3d.org/docs/release/introduction.html, accessed on 15 February 2024).
Open3D has the geometry type VoxelGrid that can be used to work with voxel grids.
It works on both meshes and point clouds. From triangle mesh, using the “create_from_triangle_mesh”, it creates a voxel grid where all voxels that are intersected by a triangle are set to 1, and all others are set to 0. Using the argument “voxel_size”, Open3D defines the resolution of the voxel grid. Starting from point cloud, the voxel grid can be created using the method “create_from_point_cloud” that determines that a voxel is occupied if at least one point of the point cloud is within the voxel. The colour of the voxel is the average of all the points within the voxel. Also, in this case, the “voxel_size” defines the resolution of the voxel grid.
3. Results
The volumes obtained with the Blender and Meshmixer software have been compared with the high-resolution models to analyse the mean Gaussian deviation and the standard deviation. The mean distribution, expressly the normal or Gaussian distribution, is a sort of continuous probability distribution for a real-valued random variable. The mean of a distribution gives a general idea about the value around which the data points are centred. The standard deviation is a measure of the total of variants of a random variable expected about its mean. A low standard deviation signifies that the values veer to be close to the mean, while a high standard deviation indicates that the values are extended over a wider range. It tells how close the data points are to the mean of the distribution. If the standard deviation is small, it tells that most of the datapoints are close to the mean of the distribution. The tool used was the cloud-to-mesh comparison in the open software CloudCompare, which searches for the nearest triangle in the reference mesh and only computes the distances from the vertices of the meshes. The first model analysed was the statue of Moses (Figure 6a–c).
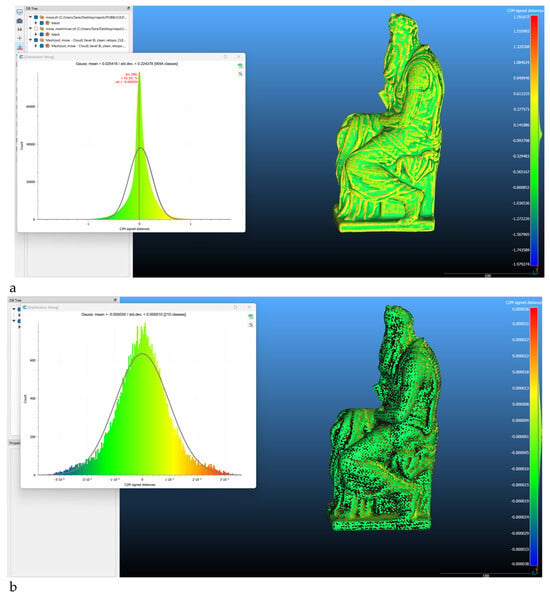
Figure 6.
Comparison of the high-resolution models of the statue of Moses with (a) volume in blender and (b) volume in Meshmixer.
The statue was a perfect test object given its geometrical complexity, a cooperative material. In this case, the creation of a closed volume was an easy task because the starting point was a 3D closed mesh. Nevertheless, the results gave an error of a centimetre, probably due to the smoothing added in the voxelization process.
Solimene’s factory’s mesh offered a different problem (Figure 7a,b). The geometry has a different level of complexity due to the presence of the bottle’s bases composing the façade and because the mesh is not closed, which bought the voxelization process to randomly compose the mesh to create the volumes. The results are then not satisfactory at all, giving the erroneous shape of the model in the back, with a maximum standard deviation of 49 m.
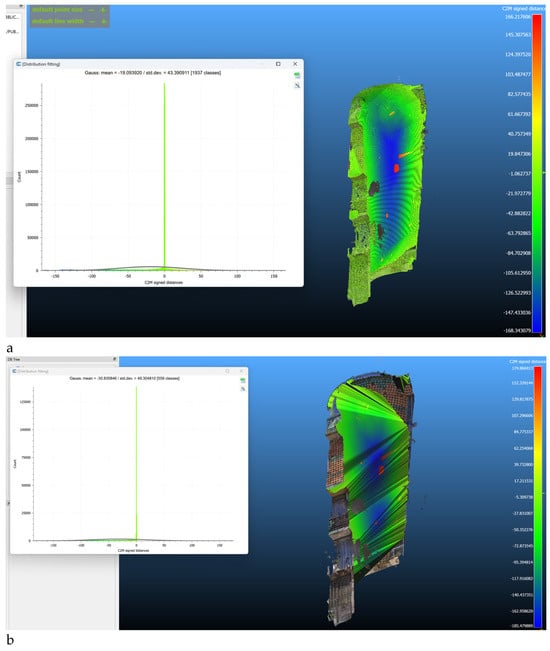
Figure 7.
Comparison of the high-resolution models of Solimene’s façade with (a) volume in blender and (b) volume in Meshmixer.
With the portion of the wall of Solimene’s factory (Figure 8a,b), the problem in the results for each software was that the volume was randomly closed following the profile of the mesh, creating an abstract surface with no geometrical references with the reality. The errors are clearly visible in Figure 6a–c. As in the façade of Solimene’s Factory, the closing of the model does not follow the real geometry of the object surveyed.
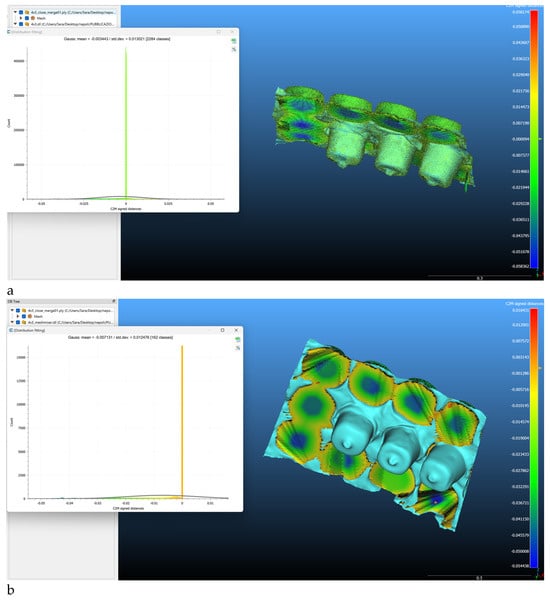
Figure 8.
Comparison of the high-resolution models of the portion of Solimene’s wall with (a) volume in blender and (b) volume in Meshmixer.
The suspension, even though it has a simple geometry, presented some problems in the distribution of the errors along the model. This can be explained because of the presence of holes and the roughness of the surface due to the non-cooperative material that caused reflections (Figure 9a,b).
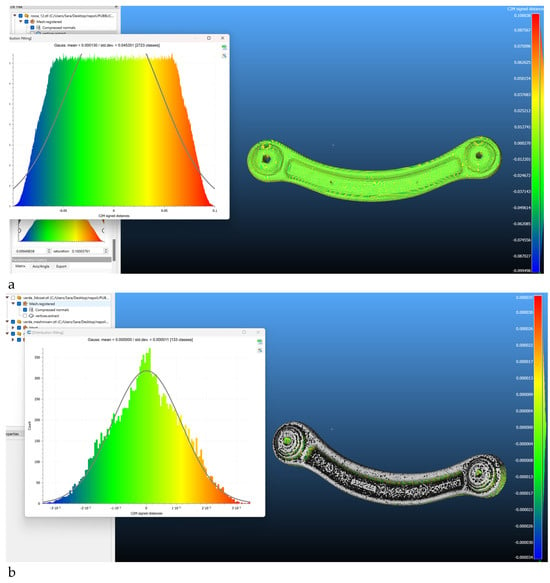
Figure 9.
Comparison of the high-resolution models of the suspension with (a) volume in blender and (b) volume in Meshmixer.
The model of the pillar, even though not the most complex or heavy in terms of the number of elements, failed to be converted in Blender (Figure 10a). The reason probably lies in the fact that the original photogrammetric model is open on the bottom, a hole that the software is not able to close automatically. MeshMixer, on the contrary, was able to create a volume from the 3D mesh (Figure 10b). The results of the comparison of the high-res models with the voxelised ones with both software are summarised in Table 2 (the standard deviation value) and Table 3 (the Gaussian distribution value).
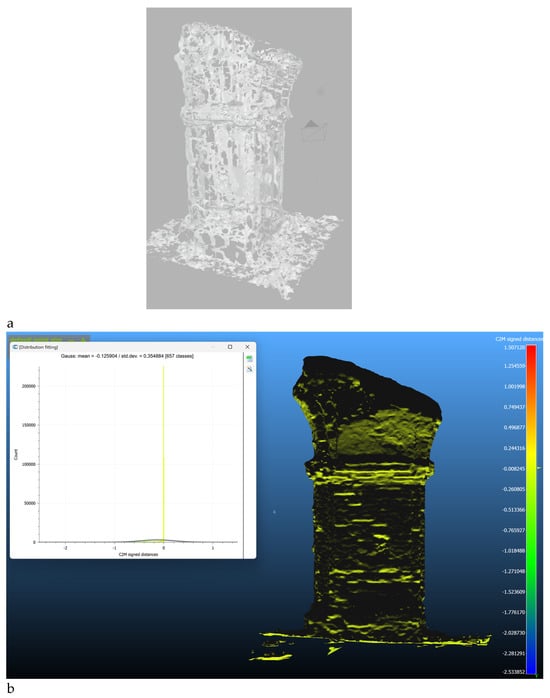
Figure 10.
Comparison of the high-resolution models of the pillar with (a) error while creating the volume in blender and (b) volume in Meshmixer.

Table 2.
Results of standard deviation from the comparison of high-resolution meshes and volumes.

Table 3.
Results of normal or Gaussian distribution from the comparison of high-resolution meshes and volumes.
Both Blender and Meshmixer software failed to convert the model into a voxel also for the scorpionide. In this case, beyond the fact that the 3D model was not closed, the complexity of the geometry with small and tiny parts may have influenced the results.
The graph of the Gaussian distribution depends on two factors: the mean and the standard deviation. The mean determines the location of the centre of the graph, and the standard deviation determines its height and width. The height is determined by the scaling factor and the width by the factor in the power of the exponential. When the standard deviation is large, the curve is short and wide; when it is small, the curve is tall and narrow. Analysing the data and the distribution of the Gaussian curve, if the standard deviation is greater than the mean, a high variation between values is present, hence an abnormal distribution for data. If the curve is high and narrow, the bulk of the data is in an average area, and the standard deviation is small (at most a vertical straight line of infinite height); otherwise, it will be lower and wider, and the standard deviation will be large (at most flat). The larger the standard deviation, the lower and flatter the curve, which is not a good thing.
This is highly visible for the volumes of the Moses by Blender, all the volumes for Solimene’s factory, the models for the portion of the façade and the models of the suspension by Blender. The meaning of this result can be analysed first considering the algorithm used in Blender for the creation of the volume: the specification of the dimension of the voxel cannot be set autonomously but is channelled inside pre-sets. This means that the density of voxels is a lot lower than the density of the elements composing the meshes. This is why even a closed mesh such as that of Moses presents a high standard deviation considering the comparison with the mean value.
For the Open3D results, the voxel grids, denoised and not denoised (Figure 11a–f and Figure 12a–e), have been compared to the relative point cloud used for their creation; hence, they are non-denoised and denoised point clouds, respectively (Figure 13a–k).

Figure 11.
The voxel grid originated from the denoised point cloud: (a) Mosè, (b) pillar, (c) Solimene, (d) portion of Solimene’s wall, (e) scorpionide, (f) suspension.

Figure 12.
The voxel grid originated from the not-denoised point cloud: (a) pillar, (b) Solimene, (c) scorpionide, (d) suspension, (e) portion of Solimene’s wall.
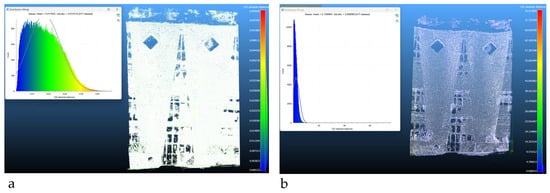
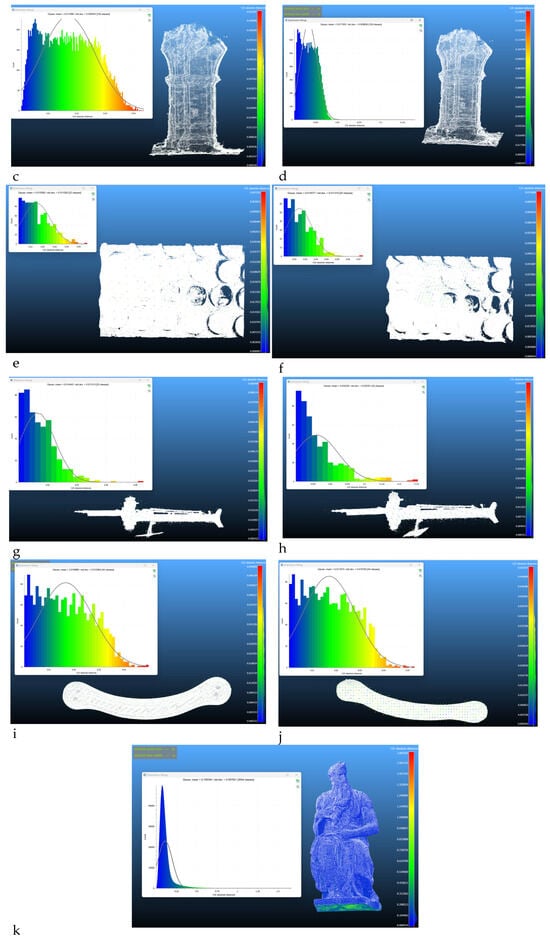
Figure 13.
Comparison of the high-resolution 3D point cloud with the voxel grids originated from them. Column on the left, original not denoised point clouds; column on the right, denoised point clouds: (a,b) Solimene, (c,d) pillar (e,f) portion of Solimene’s wall (g,h) scorpionide (i,j) suspension, (k) Moses.
A first consideration, examining the voxel grids obtained, is that for some point clouds (e.g., the scorpionide and the portion of the Solimene’s wall), the algorithm strongly simplified the shape (it is almost impossible to identify the geometry of the real object surveyed, leading to a loss of a big amount of data and, hence, geometric information and accuracy.
The only point cloud that could not possibly convert in the voxel grid was the Moses not denoised, probably because it was too heavy and too complex.
The results, expressed in meters, are summarised in Table 4 for both the standard deviation and the normal distribution.

Table 4.
Results of standard deviation and normal or Gaussian distribution in meters from the comparison of voxel grids with relative point clouds.
As it can be easily highlighted by the table, the results are almost the same in the denoised and not denoised voxel grid, except for the scorpionide, which has a higher deviation in the denoised comparison and Moses, even if it is slightly different. What is most striking is the enormous deviation (more than 2 m) in the denoised comparison of the Solimene model. It is not completely clear why this happened; the guess is that the voxel grid derived from the denoised mesh was probably strongly simplified in terms of geometric accuracy.
The voxel grids were then used to create voxel models. The results (Figure 14a–e) were not satisfactory at all. The problem can be pinpointed to the extreme complexity of the object surveyed and analysed or probably to the difficulty of the Open3D library to process grids made of many details.

Figure 14.
The voxel models of (a) pillar, (b) Solimene, (c) scorpionide, (d) suspension, (e) portion of Solimene’s wall.
The resolution of the voxels is very low and not sufficient nor satisfactory for the use of these models in FEA software for structural analyses since the approximation is too strong. The point to be investigated is if the algorithm used is not suitable for managing models of Cultural Heritage objects (but also whether the model of the suspension that has a simple geometry is not enough for FEA) or if the accuracy of reality-based models is too high for this kind of algorithm. So, it was decided to use the voxel grid for the creation of a mesh (using both screened Poisson filter in Meshlab and the Open3D mesh processing algorithm) on which retology was used and then NURBS, so volumetric models were exported. For models such as Moses or the Pillar that are complete and well organised, the process worked fine with Meshlab but not with Open3D, as for all the other models (Figure 15a–l).

Figure 15.
The meshes reconstructed from the voxel grid with Meshlab (on the left) and with Open3D (on the right) of (a,b) Moses, (c,d) pillar, (e,f) Solimene, (g,h) portion of Solimene’s wall, (i,k) scorpionide (j,l) suspension.
4. Discussion and Future Work
The volumetric models useful for structural analysis software are the result of several subsequent passages, each one of which adds a sort of approximation to the different results. From the unorganized point cloud to the mesh, the approximation derives from the 3D surface reconstruction. The simplification through retopology adds smoothing to the surface even if it has proved to maintain a high accuracy [43]. The creation of NURBS applies patches equal to the number of superficial elements of the mesh and approximates the shape of the object. Considering all these passages, starting with less-accurate data (point cloud) leads to a less-accurate result, and since the structural analysis through FEA adds another approximation, summing all these passages, the results will be far from reality. The use of the denoising algorithm proved its usefulness in terms of geometrical accuracy and geometrical reconstruction. The better distribution of the points in the cloud showed that the mesh resulted in a geometry with fewer topological errors, avoiding geometric inaccuracy with a high concentration of noisy points. This led to a less noised mesh, with no intersecting elements or spikes that modify the surface geometry of the model. This geometric alteration, if on a mesh to be used for visualization or virtual applications, does not substantially influence the results; in structural finite element analyses, it can lead, at best, to a further approximation of the results if not even a failure in the process. The present work aimed at analysing the factuality of using precompiled tools and available libraries for the creation of volumes from 3D reality-based models of objects of different shapes, geometrical complexity, size and material. The main problems are related firstly to the input data, which, for these software, need to be a mesh, while, for the algorithm, are both meshes and 3D point clouds. If the object is a closed 3D shape, turning its mesh into volume does not add too many approximations, even with automatic tools. On the other hand, if the result is just a surface, the volume needs the thickness of the model to close it properly. This is not something available on custom software. It seems, considering the results obtained, that the automatic tools are not useful for the creation of accurate volumes if the initial mesh is not a full 3D.
The test of the Open3D library gave optimal results in the creation of the voxel grid from 3D point clouds that are geometrically well-defined and correctly structured, while it simplified too many point clouds that presented complex geometry or tiny details. On the other hand, the algorithm was able to voxelise the grids created from point clouds closing the volume although with poor results in terms of details because of the strong approximation of the grid with particularly complex shapes. The same problem was encountered while creating a mesh from the voxel grid with the algorithm. The reason lies in the Open3D voxelization function “voxel_down_sample”, which sometimes seems to suffer from some issues that clearly show a plane that passes through the figure. This artifact seems to be a well-known issue of the library and contributes to providing a bad result in the output of the algorithm. The issue could be related to the calculated normals of the input point cloud, and further investigations will be performed in the future.
Future work will concentrate, analyse and discuss the possible reasons why the results in the voxel modelling were so mediocre. The intention is to test different algorithms and use point clouds of a great variety of objects that are different in shape, geometric complexity and dimensions to see if there is an algorithm or a tool that permits using volumes in FEA for structural analysis starting directly from 3D reality-based point clouds without increasing the intrinsic approximation of the process. The hope is that testing different algorithms will lead to a better comprehension of the improvements needed to write a script more adaptable to the geometric complexity of the models analysed. It seems that there is no script, algorithm or software that is able to provide the level of accuracy needed for the pipeline proposed. Another possibility is to previously segment the point clouds and then apply the voxelisation to create a more suitable model for FEA (subdivided into its specific characteristics of material properties). This process, on the other hand, can add other problems and inaccuracy due to the modelling of single parts instead of the complexity of the object as a unique body.
Furthermore, as expected, this procedure works better on a single object, such as statues, because they can be modelled as a closed volume, filling the inside with voxels. Buildings need a more careful and complex survey step to acquire both the outside and the inside; the cleaning of the point cloud is longer and has to be performed carefully to have a proper, complete and accurate 3D reproduction of the structure. Only from this kind of data will it be possible to start the voxelization process.
Author Contributions
Conceptualization, S.G.B., M.R.M., S.G.M. and A.R.; methodology, S.G.B. and M.R.M.; software, S.G.B. and M.R.M.; validation, S.G.B., M.R.M., S.G.M. and A.R.; formal analysis, S.G.B. and M.R.M.; investigation, S.G.B. and M.R.M.; resources, S.G.B., M.R.M., S.G.M. and A.R. data curation, S.G.B. and M.R.M.; writing—original draft preparation, S.G.B. and M.R.M.; writing—review and editing, S.G.B., M.R.M., S.G.M. and A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Höllig, K. Finite Element Methods with B-Splines; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Alfio, V.S.; Costantino, D.; Pepe, M.; Restuccia Garofalo, A. A Geomatics Approach in Scan to FEM Process Applied to Cultural Heritage Structure: The Case Study of the “Colossus of Barletta”. Remote Sens. 2022, 14, 664. [Google Scholar] [CrossRef]
- Brune, P.; Perucchio, R. Roman Concrete Vaulting in the Great Hall of Trajan’s Markets: A Structural Evaluation. J. Archit. Eng. 2012, 18, 332–340. [Google Scholar] [CrossRef]
- Castellazzi, G.; Altri, A.M.D.; Bitelli, G.; Selvaggi, I.; Lambertini, A. From Laser Scanning to Finite Element Analysis of Complex Buildings by Using a Semi-Automatic Procedure. Sensors 2015, 15, 18360–18380. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, V.; Tsukanov, I.; Grishin, A. Geometric Issues in Computer Aided Design/Computer Aided Engineering Integration. J. Comput. Inf. Sci. Eng. 2011, 11, 21005. [Google Scholar] [CrossRef]
- D’Altri, A.M.; de Miranda, S.; Castellazzi, G.; Glisic, B. Numerical modelling-based damage diagnostics in cultural heritage structures. J. Cult. Herit. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Marton, Z.; Soos, A.; Beetz, M. Towards 3D object maps for autonomous household robots. In International Conference on Intelligent Robots and Systems; IEEE: Piscateway, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Karanikoloudis, G.; Lourenço, P.B.; Alejo, L.E.; Mendes, N. Lessons from Structural Analysis of a Great Gothic Cathedral: Canterbury Cathedral as a Case Study. Int. J. Archit. Herit. 2021, 15, 1765–1794. [Google Scholar] [CrossRef]
- Erkal, A.; Ozhan, H.O. Value and vulnerability assessment of a historic tomb for conservation. Sci. World J. 2014, 2014, 357679. [Google Scholar] [CrossRef] [PubMed]
- Riveiro, B.; Caamaño, J.C.; Arias, P.; Sanz, E. Photogrammetric 3D modelling and mechanical analysis of masonry arches: An approach based on a discontinuous model of voussoirs. Autom. Constr. 2011, 20, 380–388. [Google Scholar] [CrossRef]
- Milani, G.; Casolo, S.; Naliato, A.; Tralli, A. Seismic assessment of a medieval masonry tower in northern Italy by limit, non-linear static and full dynamic analyses. Int. J. Archit. Herit. 2012, 6, 489–524. [Google Scholar] [CrossRef]
- Zvietcovich, F.; Castaneda, B.; Perucchio, R. 3D solid model updating of complex ancient monumental structures based on local geometrical meshes. Digit. Appl. Archaeol. Cult. Herit. 2014, 2, 12–27. [Google Scholar] [CrossRef]
- Brumana, R.; Banfi, F.; Cantini, L.; Previtali, M.; Della Torre, S. Hbim level of detail-geometry-accuracy and survey analysis for architectural preservation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 293–299. [Google Scholar] [CrossRef]
- Gonizzi Barsanti, S.; Guidi, G. A geometric processing workflow for transforming reality-based 3D models in volumetric meshes suitable for FEA. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 331–338. [Google Scholar] [CrossRef]
- Sun, J.; Ji, Y.M.; Wu, F.; Zhang, C.; Sun, Y. Semantic-aware 3D-voxel CenterNet for point cloud object detection. Comput. Electr. Eng. 2022, 98, 107677. [Google Scholar] [CrossRef]
- He, C.; Li, R.; Li, S.; Zhang, L. Voxel set transformer: A set-to-set approach to 3D object detection from point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8417–8427. [Google Scholar]
- Mahmoud, A.; Hu, J.S.; Waslander, S.L. Dense voxel fusion for 3D object detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 663–672. [Google Scholar]
- Shrout, O.; Ben-Shabat, Y.; Tal, A. GraVoS: Voxel Selection for 3D Point-Cloud Detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 21684–21693. [Google Scholar]
- Deng, J.; Shi, S.; Li, P.; Zhou, W.; Zhang, Y.; Li, H. Voxel r-cnn: Towards high performance voxel-based 3D object detection. Proc. AAAI Conf. Artif. Intell. 2021, 35, 1201–1209. [Google Scholar] [CrossRef]
- He, C.; Zeng, H.; Huang, J.; Hua, X.S.; Zhang, L. Structure Aware Single-Stage 3D Object Detection from Point Cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11870–11879. [Google Scholar]
- Lv, C.; Lin, W.; Zhao, B. Voxel Structure-Based Mesh Reconstruction From a 3D Point Cloud. IEEE Trans. Multimed. 2022, 24, 1815–1829. [Google Scholar] [CrossRef]
- Sas, A.; Ohs, N.; Tanck, E.; van Lenthe, G.H. Nonlinear voxel-based finite element model for strength assessment of healthy and metastatic proximal femurs. Bone Rep. 2020, 12, 100263. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.Y.; Weng, T.L.; Lin, C.H.; Sun, Y.N. Interactive voxel surface rendering in medical applications. Comput. Med. Imaging Graph. 1999, 23, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Han, G.; Li, J.; Wang, S.; Wang, L.; Zhou, Y.; Liu, Y. A comparison of voxel- and surface-based cone-beam computed tomography mandibular superimposition in adult orthodontic patients. J. Int. Med. Res. 2021, 49, 0300060520982708. [Google Scholar] [CrossRef] [PubMed]
- Goto, M.; Abe, O.; Hagiwara, A.; Fujita, S.; Kamagata, K.; Hori, M.; Aoki, S.; Osada, T.; Konishi, S.; Masutani, Y.; et al. Advantages of Using Both Voxel- and Surface-based Morphometry in Cortical Morphology Analysis: A Review of Various Applications, Magnetic Resonance. Med. Sci. 2022, 21, 41–57. [Google Scholar] [CrossRef]
- Babich, M.; Kublanov, V. Voxel Based Finite Element Method Modelling Framework for Electrical Stimulation Applications Using Open-Source Software. In Proceedings of the Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 25–26 April 2019; pp. 127–130. [Google Scholar]
- Sapozhnikov, S.B.; Shchurova, E.I. Voxel and Finite Element Analysis Models for Ballistic Impact on Ceramic-polymer Composite Panels. Procedia Eng. 2017, 206, 182–187. [Google Scholar] [CrossRef]
- Doğan, S.; Güllü, H. Multiple methods for voxel modeling and finite element analysis for man-made caves in soft rock of Gaziantep. Bull. Eng. Geol. Environ. 2022, 81, 23. [Google Scholar] [CrossRef]
- Watanabe, K.; Iijima, Y.; Kawano, K.; Igarashi, H. Voxel Based Finite Element Method Using Homogenization. IEEE Trans. Magn. 2012, 48, 543–546. [Google Scholar] [CrossRef]
- Baert, J. Cuda Voxelizer: A Gpu-Accelerated Mesh Voxelizer. 2017. Available online: https://github.com/Forceflow/cuda_voxelizer (accessed on 2 February 2024).
- Zhou, Q.Y.; Park, J.; Koltun, V. Open3D: A modern library for 3D data processing. arXiv 2018, arXiv:1801.09847. [Google Scholar]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the IEEE Sixth International Conference on Computer Vision, Bombay, India, 7 January 1998; pp. 839–846. [Google Scholar]
- Chen, H.; Shen, J. Denoising of point cloud data for computer-aided design, engineering, and manufacturing. Eng. Comput. 2018, 34, 523–541. [Google Scholar] [CrossRef]
- Digne, J.; Franchis, C.D. The bilateral filter for point clouds. Image Process. Online 2017, 7, 278–287. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Jin, J.S.; Wang, M.; Jiang, W. Guided 3D point cloud filtering. Multimed. Tools Appl. 2018, 77, 17397–17411. [Google Scholar] [CrossRef]
- Irfan, M.A.; Magli, E. Exploiting color for graph-based 3d point cloud denoising. J. Vis. Commun. Image Represent. 2021, 75, 103027. [Google Scholar] [CrossRef]
- Dinesh, C.; Cheung, G.; Bajić, I.V. Point cloud denoising via feature graph Laplacian regularization. IEEE Trans. Image Process. 2020, 29, 4143–4158. [Google Scholar] [CrossRef]
- Xu, Z.; Foi, A. Anisotropic denoising of 3D point clouds by aggregation of multiple surface-adaptive estimates. IEEE Trans. Vis. Comput. Graph. 2021, 27, 2851–2868. [Google Scholar] [CrossRef]
- Rakotosaona, M.J.; La Barbera, V.; Guerrero, P.; Mitra, N.J.; Ovsjanikov, M. Pointcleannet: Learning to denoise and remove outliers from dense point clouds. Comput. Graph. Forum 2021, 39, 185–203. [Google Scholar] [CrossRef]
- Shitong, L.; Hu, W. Score-based point cloud denoising. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 4563–4572. [Google Scholar]
- Jakob, W.; Tarini, M.; Panozzo, D.; Sorkine-Hornung, O. Instant field-aligned meshes. ACM Trans. Graph. 2015, 34, 189:1–189:15. [Google Scholar] [CrossRef]
- Gonizzi Barsanti, S.; Guagliano, M.; Rossi, A. 3D Reality-Based Survey and Retopology for Structural Analysis of Cultural Heritage. Sensors 2022, 22, 9593. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).