Predicting Grapevine Physiological Parameters Using Hyperspectral Remote Sensing Integrated with Hybrid Convolutional Neural Network and Ensemble Stacked Regression
Abstract
1. Introduction
2. Materials and Methods
2.1. Site and Experimental Design
2.2. Directly Measured Physiological Attributes
2.3. Hyperspectral Data Acquisition and Preprocessing
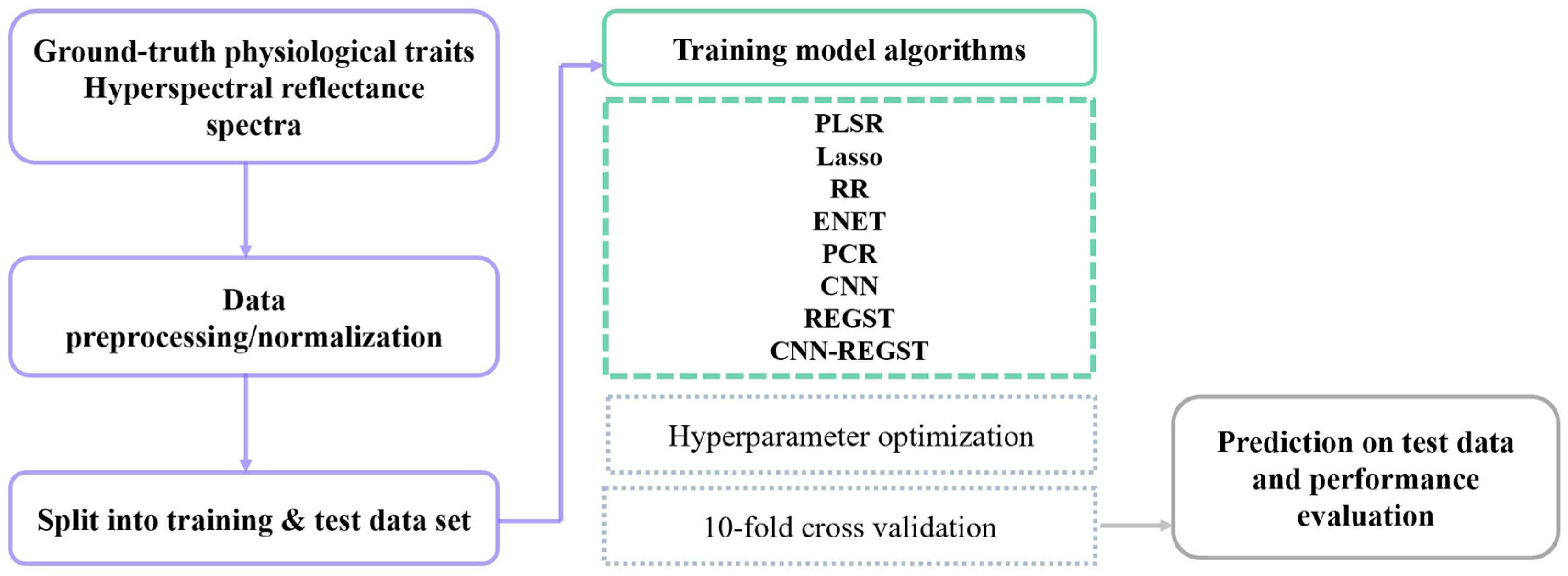
2.4. Modeling Assessment
2.4.1. Model Algorithm Selection
2.4.2. Modeling Pipeline and Hyperparameter Optimization
2.4.3. Evaluation Metrics
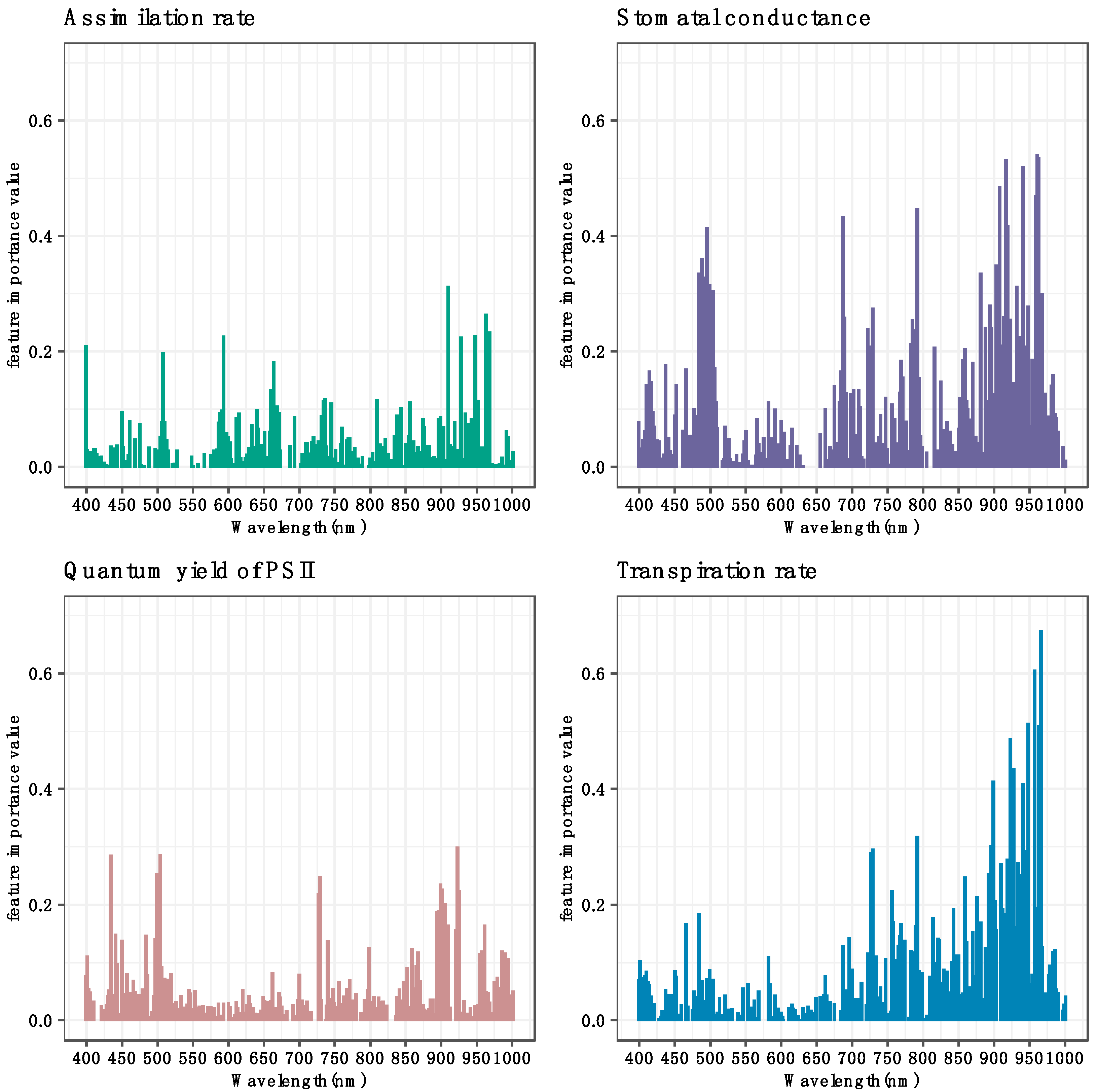
2.4.4. Permutation-Based Feature Importance Score
3. Results
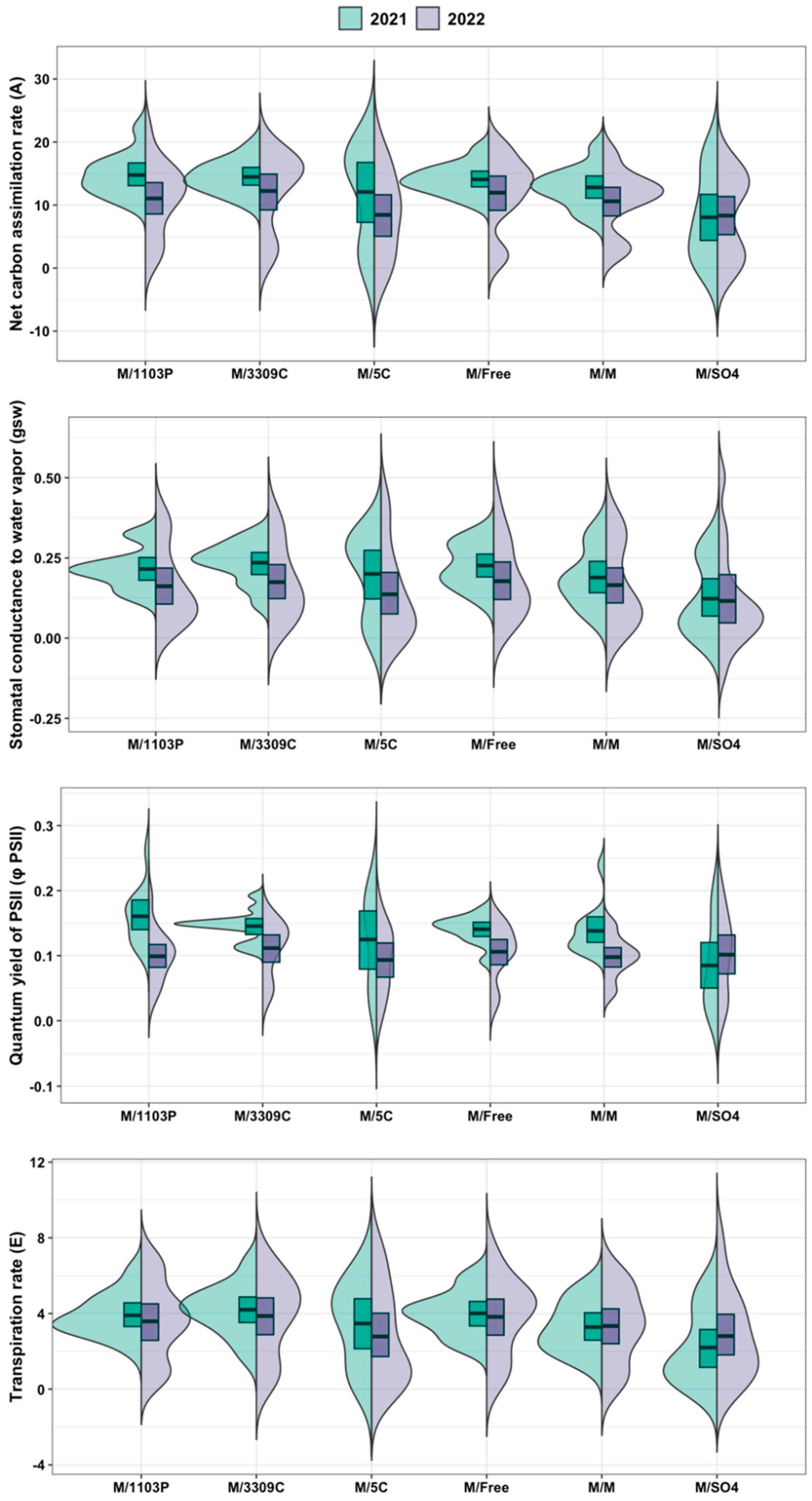
3.1. Directly Measured Leaf Mesophyll Traits and Physiology
3.2. Relationship of Directly Measured Vine Traits with Hyperspectral Features
3.3. Performance of Different Modeling Algorithms
3.4. Important Hyperspectral Features in Modeling Algorithm
4. Discussion
4.1. Rootstock Has Significant Impact on Physiology of Scion
4.2. Aerial Hyperspectral Data Have a Positive Correlation with Actual Ground-Truth Physiology Parameters of Vines
4.3. Ensemble Stacked Regression (REGST) Model Outperformed Individual Base Models
4.4. Both REGST and Hybrid CNN-REGST Models Had Similar Predictive Performances
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martínez de Toda, F.; Balda, P. Delaying berry ripening through manipulating leaf area to fruit ratio. J. Grapevine Res. 2013, 52, 171–176. [Google Scholar]
- Martinez de Toda, F.; Sancha, J.C.; Balda, P. Reducing the sugar and pH of the grape (Vitis vinifera L. cvs. ’Grenache’ and ’Tempranillo’) through a single shoot trimming. S. Afr. J. Enol. Vitic. 2013, 34, 246–251. [Google Scholar]
- Keller, M.; Tarara, J.; Mills, L. Spring temperatures alter reproductive development in grapevines. Aust. J. Grape Wine Res. 2010, 16, 445–454. [Google Scholar] [CrossRef]
- Parker, A.K.; De Cortazar-Atauri, I.G.; Van Leeuwen, C.; Chuine, I. General phenological model to characterise the timing of flowering and veraison of Vitis vinifera L. Aust. J. Grape Wine Res. 2011, 17, 206–216. [Google Scholar] [CrossRef]
- Ruml, M.; Korać, N.; Vujadinović, M.; Vuković, A.; Ivanišević, D. Response of grapevine phenology to recent temperature change and variability in the wine-producing area of Sremski Karlovci, Serbia. J. Agric. Sci. 2016, 154, 186–206. [Google Scholar] [CrossRef]
- Schultz, H.; Hofmann, M. The ups and downs of environmental impact on grapevines: Future challenges in temperate viticulture. In Grapevine in a Changing Environment: A Molecular and Ecophysiological Perspective; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015; pp. 18–37. [Google Scholar]
- Arrizabalaga-Arriazu, M.; Morales, F.; Irigoyen, J.J.; Hilbert, G.; Pascual, I. Growth performance and carbon partitioning of grapevine Tempranillo clones under simulated climate change scenarios: Elevated CO2 and temperature. J. Plant Physiol. 2020, 252, 153226. [Google Scholar] [CrossRef]
- Galet, P. Phylloxera galls on Vitis vinifera L. [Grapes]. Prog. Agric. Vitic. 1983, 100, 155–162. [Google Scholar]
- Ordish, G. The Great Wine Blight; J.M. Dent & Sons Ltd.: London, UK, 1972. [Google Scholar]
- Pouget, R. Histoire de la Lutte Contre le Phylloxéra de la Vigne en France; INRA: Paris, France, 1990; pp. 1–168. [Google Scholar]
- Corso, M.; Bonghi, C. Grapevine rootstock effects on abiotic stress tolerance. Plant Sci. Today 2014, 1, 108–113. [Google Scholar] [CrossRef]
- Warschefsky, E.J.; Klein, L.L.; Frank, M.H.; Chitwood, D.H.; Londo, J.P.; von Wettberg, E.J.; Miller, A.J. Rootstocks: Diversity, domestication, and impacts on shoot phenotypes. Trends Plant Sci. 2016, 21, 418–437. [Google Scholar] [CrossRef]
- Pou, A.; Rivacoba, L.; Portu, J.; Mairata, A.; Labarga, D.; García-Escudero, E.; Martín, I. How Rootstocks Impact the Scion Vigour and Vine Performance of Vitis vinifera L. cv. Tempranillo. Aust. J. Grape Wine Res. 2022, 2022, 9871347. [Google Scholar] [CrossRef]
- Mantilla, S.M.O.; Collins, C.; Iland, P.G.; Kidman, C.M.; Ristic, R.; Boss, P.K.; Jordans, C.; Bastian, S.E. Shiraz (Vitis vinifera L.) berry and wine sensory profiles and composition are modulated by rootstocks. Am. J. Enol. Vitic. 2018, 69, 32–44. [Google Scholar] [CrossRef]
- Keller, M. Developmental physiology. In The Science of Grapevines: Anatomy and Physiology; Academic Press: Cambridge, MA, USA, 2010; pp. 169–225. [Google Scholar]
- Padgett-Johnson, M.; Williams, L.; Walker, M.A. The influence of Vitis riparia rootstock on water relations and gas exchange of Vitis vinifera cv. Carignane scion under non-irrigated conditions. Am. J. Enol. Vitic. 2000, 51, 137–143. [Google Scholar] [CrossRef]
- Soar, C.J.; Dry, P.R.; Loveys, B. Scion photosynthesis and leaf gas exchange in Vitis vinifera L. cv. Shiraz: Mediation of rootstock effects via xylem sap ABA. Aust. J. Grape Wine Res. 2006, 12, 82–96. [Google Scholar] [CrossRef]
- Marguerit, E.; Brendel, O.; Lebon, E.; Van Leeuwen, C.; Ollat, N. Rootstock control of scion transpiration and its acclimation to water deficit are controlled by different genes. New Phytol. 2012, 194, 416–429. [Google Scholar] [CrossRef]
- Suarez, D.L.; Celis, N.; Anderson, R.G.; Sandhu, D. Grape Rootstock Response to Salinity, Water and Combined Salinity and Water Stresses. Agronomy 2019, 9, 321. [Google Scholar] [CrossRef]
- Domingues Neto, F.J.; Pimentel Junior, A.; Modesto, L.R.; Moura, M.F.; Putti, F.F.; Boaro, C.S.F.; Ono, E.O.; Rodrigues, J.D.; Tecchio, M.A. Photosynthesis, Biochemical and Yield Performance of Grapevine Hybrids in Two Rootstock and Trellis Height. Horticulturae 2023, 9, 596. [Google Scholar] [CrossRef]
- Prinsi, B.; Simeoni, F.; Galbiati, M.; Meggio, F.; Tonelli, C.; Scienza, A.; Espen, L. Grapevine rootstocks differently affect physiological and molecular responses of the scion under water deficit condition. Agronomy 2021, 11, 289. [Google Scholar] [CrossRef]
- Ghule, V.; Zagade, P.; Bhor, V.; Somkuwar, R. Rootstock affects graft success growth and physiological parameters of grape varieties (Vitis vinifera L.). Int. J. Curr. Microbiol. App. Sci 2019, 8, 799–805. [Google Scholar] [CrossRef]
- Edwards, E.; Betts, A.; Clingeleffer, P.; Walker, R. Rootstock-conferred traits affect the water use efficiency of fruit production in Shiraz. Aust. J. Grape Wine Res. 2022, 28, 316–327. [Google Scholar] [CrossRef]
- Bianchi, D.; Ricciardi, V.; Pozzoli, C.; Grossi, D.; Caramanico, L.; Pindo, M.; Stefani, E.; Cestaro, A.; Brancadoro, L.; De Lorenzis, G. Physiological and Transcriptomic Evaluation of Drought Effect on Own-Rooted and Grafted Grapevine Rootstock (1103P and 101-14MGt). Plants 2023, 12, 1080. [Google Scholar] [CrossRef]
- Peccoux, A.; Loveys, B.; Zhu, J.; Gambetta, G.A.; Delrot, S.; Vivin, P.; Schultz, H.R.; Ollat, N.; Dai, Z. Dissecting the rootstock control of scion transpiration using model-assisted analyses in grapevine. Tree Physiol. 2017, 38, 1026–1040. [Google Scholar] [CrossRef] [PubMed]
- Maimaitiyiming, M.; Sagan, V.; Sidike, P.; Maimaitijiang, M.; Miller, A.J.; Kwasniewski, M. Leveraging very-high spatial resolution hyperspectral and thermal UAV imageries for characterizing diurnal indicators of grapevine physiology. Remote Sens. 2020, 12, 3216. [Google Scholar] [CrossRef]
- Yang, Z.; Tian, J.; Wang, Z.; Feng, K. Monitoring the photosynthetic performance of grape leaves using a hyperspectral-based machine learning model. Eur. J. Agron. 2022, 140, 126589. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Catalina, A.; González, M.; Martín, P. Relationships between net photosynthesis and steady-state chlorophyll fluorescence retrieved from airborne hyperspectral imagery. Remote Sens. Environ. 2013, 136, 247–258. [Google Scholar] [CrossRef]
- Pôças, I.; Rodrigues, A.; Gonçalves, S.; Costa, P.M.; Gonçalves, I.; Pereira, L.S.; Cunha, M. Predicting grapevine water status based on hyperspectral reflectance vegetation indices. Remote Sens. 2015, 7, 16460–16479. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, J.R.; Riaño, D.; Carlisle, E.; Ustin, S.; Smart, D.R. Evaluation of hyperspectral reflectance indexes to detect grapevine water status in vineyards. Am. J. Enol. Vitic. 2007, 58, 302–317. [Google Scholar] [CrossRef]
- Mariotto, I.; Thenkabail, P.S.; Huete, A.; Slonecker, E.T.; Platonov, A. Hyperspectral versus multispectral crop-productivity modeling and type discrimination for the HyspIRI mission. Remote Sens. Environ. 2013, 139, 291–305. [Google Scholar] [CrossRef]
- Aneece, I.; Thenkabail, P. Accuracies achieved in classifying five leading world crop types and their growth stages using optimal earth observing-1 hyperion hyperspectral narrowbands on google earth engine. Remote Sens. 2018, 10, 2027. [Google Scholar] [CrossRef]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Wu, J.; Bernacchi, C. Estimating photosynthetic traits from reflectance spectra: A synthesis of spectral indices, numerical inversion, and partial least square regression. Plant Cell Environ. 2020, 43, 1241–1258. [Google Scholar] [CrossRef]
- Serbin, S.P.; Dillaway, D.N.; Kruger, E.L.; Townsend, P.A. Leaf optical properties reflect variation in photosynthetic metabolism and its sensitivity to temperature. J. Exp. Bot. 2012, 63, 489–502. [Google Scholar] [CrossRef]
- Wold, H. Systems under indirect observation using, P.L.S. In A Second Generation of Multivariate Analysis: Methods; Praeger: Westport, CT, USA, 1982. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Jolliffe, I.T. A note on the use of principal components in regression. J. R. Stat. Soc. Ser. C Appl. Stat. 1982, 31, 300–303. [Google Scholar] [CrossRef]
- Gomes, V.; Rendall, R.; Reis, M.S.; Mendes-Ferreira, A.; Melo-Pinto, P. Determination of sugar, pH, and anthocyanin contents in port wine grape berries through hyperspectral imaging: An extensive comparison of linear and non-linear predictive methods. Appl. Sci. 2021, 11, 10319. [Google Scholar] [CrossRef]
- Yang, Y.; Nan, R.; Mi, T.; Song, Y.; Shi, F.; Liu, X.; Wang, Y.; Sun, F.; Xi, Y.; Zhang, C. Rapid and nondestructive evaluation of wheat chlorophyll under drought stress using hyperspectral imaging. Int. J. Mol. Sci. 2023, 24, 5825. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Marquardt, D.W.; Snee, R.D. Ridge regression in practice. Am. Stat. 1975, 29, 3–20. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Bernacchi, C.J. Hyperspectral leaf reflectance as proxy for photosynthetic capacities: An ensemble approach based on multiple machine learning algorithms. Front. Plant Sci. 2019, 10, 454448. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Unlersen, M.F.; Sonmez, M.E.; Aslan, M.F.; Demir, B.; Aydin, N.; Sabanci, K.; Ropelewska, E. CNN–SVM hybrid model for varietal classification of wheat based on bulk samples. Eur. Food Res. Technol. 2022, 248, 2043–2052. [Google Scholar] [CrossRef]
- Tanwar, V.; Lamba, S.; Sharma, B. Deep learning-based hybrid model for severity prediction of leaf smut sugarcane infection. In Proceedings of the 2023 Third International Conference on Artificial Intelligence and Smart Energy (ICAIS), Coimbatore, India, 2–4 February 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Gavrishchaka, V.; Yang, Z.; Miao, R.; Senyukova, O. Advantages of hybrid deep learning frameworks in applications with limited data. Int. J. Mach. Learn. Comput. 2018, 8, 549–558. [Google Scholar]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Gillies, S. Rasterio Documentation; MapBox: San Francisco, CA, USA, 2019; Volume 23. [Google Scholar]
- Press, W.H.; Teukolsky, S.A. Savitzky-Golay smoothing filters. Comput. Phys. 1990, 4, 669–672. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Berrar, D. Cross-Validation. In Reference Module in Life Sciences Encyclopedia of Bioinformatics and Computational Biology; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Altmann, A.; Tolosi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Raschka, S. MLxtend: A Python Library for Machine Learning Extensions. Available online: https://sebastianraschka.com/pdf/software/mlxtend-latest.pdf (accessed on 1 May 2023).
- Bica, D.; Gay, G.; Morando, A.; Soave, E. Effects of rootstock and Vitis vinifera genotype on photosynthetic parameters. In Proceedings of the V International Symposium on Grapevine Physiology 526, Jerusalem, Israel, 25–30 May 1997. [Google Scholar]
- Alsina, M.M.; Smart, D.R.; Bauerle, T.; De Herralde, F.; Biel, C.; Stockert, C.; Negron, C.; Save, R. Seasonal changes of whole root system conductance by a drought-tolerant grape root system. J. Exp. Bot. 2011, 62, 99–109. [Google Scholar] [CrossRef]
- Romero, P.; Botía, P.; Navarro, J.M. Selecting rootstocks to improve vine performance and vineyard sustainability in deficit irrigated Monastrell grapevines under semiarid conditions. Agric. Water Manag. 2018, 209, 73–93. [Google Scholar] [CrossRef]
- Lovisolo, C.; Perrone, I.; Carra, A.; Ferrandino, A.; Flexas, J.; Medrano, H.; Schubert, A. Drought-induced changes in development and function of grapevine (Vitis spp.) organs and in their hydraulic and non-hydraulic interactions at the whole-plant level: A physiological and molecular update. Funct. Plant Biol. 2010, 37, 98–116. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Lehmeier, C.; Pajor, R.; Lundgren, M.R.; Mathers, A.; Sloan, J.; Bauch, M.; Mitchell, A.; Bellasio, C.; Green, A.; Bouyer, D. Cell density and airspace patterning in the leaf can be manipulated to increase leaf photosynthetic capacity. Plant J. 2017, 92, 981–994. [Google Scholar] [CrossRef] [PubMed]
- Peñuelas, J.; Filella, I. Visible and near-infrared reflectance techniques for diagnosing plant physiological status. Trends Plant Sci. 1998, 3, 151–156. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Huang, W.; Zhao, C.; Zhang, B.; Tong, Q. Estimating winter wheat plant water content using red edge parameters. Int. J. Remote Sens. 2004, 25, 3331–3342. [Google Scholar] [CrossRef]
- Tilling, A.K.; O’Leary, G.J.; Ferwerda, J.G.; Jones, S.D.; Fitzgerald, G.J.; Rodriguez, D.; Belford, R. Remote sensing of nitrogen and water stress in wheat. Field Crops Res. 2007, 104, 77–85. [Google Scholar] [CrossRef]
- Gamon, J.; Penuelas, J.; Field, C. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Gamon, J.; Serrano, L.; Surfus, J. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Peñuelas, J.; Llusia, J.; Pinol, J.; Filella, I. Photochemical reflectance index and leaf photosynthetic radiation-use-efficiency assessment in Mediterranean trees. Int. J. Remote Sens. 1997, 18, 2863–2868. [Google Scholar] [CrossRef]
- Suarez, L.; González-Dugo, V.; Camino, C.; Hornero, A.; Zarco-Tejada, P.J. Physical model inversion of the green spectral region to track assimilation rate in almond trees with an airborne nano-hyperspectral imager. Remote Sens. Environ. 2021, 252, 112147. [Google Scholar] [CrossRef]
- Hikosaka, K.; Tsujimoto, K. Linking remote sensing parameters to CO2 assimilation rates at a leaf scale. J. Plant Res. 2021, 134, 695–711. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical properties and nondestructive estimation of anthocyanin content in plant leaves. Photochem. Photobiol. 2001, 74, 38–45. [Google Scholar] [CrossRef] [PubMed]
- Berger, B.; Parent, B.; Tester, M. High-throughput shoot imaging to study drought responses. J. Exp. Bot. 2010, 61, 3519–3528. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.-T.; Yang, D.-C.; Guan, Z.; He, Y.-H. Chlorophyll-catalyzed visible-light-mediated synthesis of tetrahydroquinolines from N,N-dimethylanilines and maleimides. J. Org. Chem. 2017, 82, 1888–1894. [Google Scholar] [CrossRef] [PubMed]
- Slaton, M.R.; Hunt, E.R., Jr.; Smith, W.K. Estimating near-infrared leaf reflectance from leaf structural characteristics. Am. J. Bot. 2001, 88, 278–284. [Google Scholar] [CrossRef] [PubMed]
- Clinton, N.; Yu, L.; Gong, P. Geographic stacking: Decision fusion to increase global land cover map accuracy. ISPRS J. Photogramm. Remote Sens. 2015, 103, 57–65. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Hughes, M.J.; Kennedy, R.E. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Huang, X.; Guan, H.; Bo, L.; Xu, Z.; Mao, X. Hyperspectral proximal sensing of leaf chlorophyll content of spring maize based on a hybrid of physically based modelling and ensemble stacking. Comput. Electron. Agric. 2023, 208, 107745. [Google Scholar] [CrossRef]
- Furbank, R.T.; Silva-Perez, V.; Evans, J.R.; Condon, A.G.; Estavillo, G.M.; He, W.; Newman, S.; Poiré, R.; Hall, A.; He, Z. Wheat physiology predictor: Predicting physiological traits in wheat from hyperspectral reflectance measurements using deep learning. Plant Methods 2021, 17, 108. [Google Scholar] [CrossRef]
- Ghimire, S.; Nguyen-Huy, T.; Deo, R.C.; Casillas-Perez, D.; Salcedo-Sanz, S. Efficient daily solar radiation prediction with deep learning 4-phase convolutional neural network, dual stage stacked regression and support vector machine CNN-REGST hybrid model. Sustain. Mater. Technol. 2022, 32, e00429. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. A review of the use of convolutional neural networks in agriculture. J. Agric. Sci. 2018, 156, 312–322. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Bai, J.; Al-Sabaawi, A.; Santamaría, J.; Albahri, A.; Al-dabbagh, B.S.N.; Fadhel, M.A.; Manoufali, M.; Zhang, J.; Al-Timemy, A.H. A survey on deep learning tools dealing with data scarcity: Definitions, challenges, solutions, tips, and applications. J. Big Data 2023, 10, 46. [Google Scholar] [CrossRef]



| Model Name | Model Hyperparameters |
|---|---|
| PLSR | n_components |
| Lasso | alpha, fit_intercept |
| RR | alpha, fit_intercept |
| ENET | alpha, fit_intercept, l1_ratio |
| PCR | n_components |
| RF | max_depth, min_samples_leaf, min_samples_split, n_estimators |
| CNN | Learning rate, batch_size, epochs, activation function |
| Genotypes | A | gsw | ϕ PSII | E |
|---|---|---|---|---|
| M/1103P | 12.64 a ± 0.95 | 0.18a ± 0.01 | 0.12 ± 0.009 | 3.72ab ± 0.31 |
| M/3309C | 13.19 a ± 0.92 | 0.20a ± 0.01 | 0.12 ± 0.007 | 4.01a ± 0.33 |
| M/5C | 09.83 ab ± 1.45 | 0.16ab ± 0.02 | 0.10 ± 0.012 | 3.04ab ± 0.48 |
| M/Freedom | 12.87 a ± 0.88 | 0.19a ± 0.01 | 0.12 ± 0.007 | 3.90ab ± 0.31 |
| M/M | 11.54 ab ± 0.82 | 0.17a ± 0.02 | 0.11 ± 0.007 | 3.31ab ± 0.31 |
| M/SO4 | 08.21 b ± 1.22 | 0.11b ± 0.02 | 0.09 ± 0.012 | 2.53b ± 0.40 |
| i. Performance results for net assimilation rate (A) | ||||||
| Training performance (n = 114) | Test Performance (n = 49) | |||||
| Model name | MAE | RMSE | R2 | MAE | RMSE | R2 |
| PLSR | 2.18 | 2.84 | 0.72 | 2.74 | 3.95 | 0.58 |
| Lasso | 2.24 | 2.93 | 0.70 | 2.88 | 4.16 | 0.53 |
| RR | 2.07 | 2.69 | 0.74 | 2.76 | 3.81 | 0.61 |
| ENET | 2.22 | 2.92 | 0.70 | 2.89 | 4.14 | 0.53 |
| PCR | 2.18 | 2.87 | 0.71 | 2.81 | 3.90 | 0.59 |
| REGST | 2.01 | 2.51 | 0.81 | 2.70 | 3.51 | 0.64 |
| CNN | 3.04 | 3.89 | 0.61 | 3.07 | 3.89 | 0.51 |
| CNN-REGST | 2.41 | 2.95 | 0.71 | 2.68 | 3.55 | 0.65 |
| ii. Performance results for stomatal conductance to water vapor (gsw) | ||||||
| Training performance (n = 114) | Test Performance (n = 49) | |||||
| Model name | MAE | RMSE | R2 | MAE | RMSE | R2 |
| PLSR | 0.04 | 0.05 | 0.72 | 0.06 | 0.08 | 0.57 |
| Lasso | 0.04 | 0.05 | 0.71 | 0.06 | 0.08 | 0.55 |
| RR | 0.03 | 0.05 | 0.77 | 0.07 | 0.09 | 0.55 |
| ENET | 0.04 | 0.05 | 0.71 | 0.06 | 0.09 | 0.55 |
| PCR | 0.05 | 0.06 | 0.62 | 0.07 | 0.09 | 0.49 |
| REGST | 0.04 | 0.05 | 0.74 | 0.06 | 0.08 | 0.58 |
| CNN | 0.06 | 0.09 | 0.42 | 0.06 | 0.08 | 0.37 |
| CNN-REGST | 0.05 | 0.06 | 0.62 | 0.06 | 0.08 | 0.61 |
| iii. Performance results for quantum yield of PSII (ϕ PSII) | ||||||
| Training performance (n = 114) | Test Performance (n = 49) | |||||
| Model name | MAE | RMSE | R2 | MAE | RMSE | R2 |
| PLSR | 0.02 | 0.02 | 0.68 | 0.03 | 0.04 | 0.46 |
| Lasso | 0.02 | 0.02 | 0.68 | 0.02 | 0.04 | 0.52 |
| RR | 0.02 | 0.02 | 0.67 | 0.03 | 0.04 | 0.51 |
| ENET | 0.02 | 0.03 | 0.60 | 0.03 | 0.04 | 0.48 |
| PCR | 0.02 | 0.02 | 0.67 | 0.03 | 0.04 | 0.46 |
| REGST | 0.02 | 0.02 | 0.69 | 0.02 | 0.04 | 0.54 |
| CNN | 0.02 | 0.03 | 0.39 | 0.03 | 0.04 | 0.33 |
| CNN-REGST | 0.02 | 0.02 | 0.65 | 0.02 | 0.04 | 0.55 |
| iv. Performance results for transpiration rate (E) | ||||||
| Training performance (n = 114) | Test Performance (n = 49) | |||||
| Model name | MAE | RMSE | R2 | MAE | RMSE | R2 |
| PLSR | 0.81 | 0.99 | 0.70 | 1.13 | 1.39 | 0.55 |
| Lasso | 0.75 | 0.92 | 0.74 | 1.07 | 1.32 | 0.59 |
| RR | 0.75 | 0.91 | 0.75 | 0.96 | 1.21 | 0.65 |
| ENET | 0.75 | 0.92 | 0.74 | 0.98 | 1.23 | 0.64 |
| PCR | 0.85 | 1.06 | 0.66 | 1.13 | 1.41 | 0.53 |
| REGST | 0.68 | 0.87 | 0.77 | 0.91 | 1.19 | 0.67 |
| CNN | 0.93 | 1.17 | 0.60 | 1.35 | 1.63 | 0.38 |
| CNN-REGST | 0.80 | 0.98 | 0.71 | 0.98 | 1.19 | 0.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, P.; Villegas-Diaz, R.; Fennell, A. Predicting Grapevine Physiological Parameters Using Hyperspectral Remote Sensing Integrated with Hybrid Convolutional Neural Network and Ensemble Stacked Regression. Remote Sens. 2024, 16, 2626. https://doi.org/10.3390/rs16142626
Sharma P, Villegas-Diaz R, Fennell A. Predicting Grapevine Physiological Parameters Using Hyperspectral Remote Sensing Integrated with Hybrid Convolutional Neural Network and Ensemble Stacked Regression. Remote Sensing. 2024; 16(14):2626. https://doi.org/10.3390/rs16142626
Chicago/Turabian StyleSharma, Prakriti, Roberto Villegas-Diaz, and Anne Fennell. 2024. "Predicting Grapevine Physiological Parameters Using Hyperspectral Remote Sensing Integrated with Hybrid Convolutional Neural Network and Ensemble Stacked Regression" Remote Sensing 16, no. 14: 2626. https://doi.org/10.3390/rs16142626
APA StyleSharma, P., Villegas-Diaz, R., & Fennell, A. (2024). Predicting Grapevine Physiological Parameters Using Hyperspectral Remote Sensing Integrated with Hybrid Convolutional Neural Network and Ensemble Stacked Regression. Remote Sensing, 16(14), 2626. https://doi.org/10.3390/rs16142626







