Abstract
Aerosol research is important for the protection of the ecological environment, the improvement of air quality, and as a response to climate change. In this study, a random forest (RF) estimation model of aerosol optical depth (AOD) and extinction coefficient vertical profiles was, respectively, established using Orbiting Carbon Observatory-2 (OCO-2) oxygen-A band (O2 A-band) data from China and its surrounding areas in 2016, combined with geographical information (longitude, latitude, and elevation) and viewing angle data. To address the high number of OCO-2 O2 A-band channels, principal component analysis (PCA) was employed for dimensionality reduction. The model was then applied to estimate the aerosol extinction coefficients for the region in 2017, and its validity was verified by comparing the estimated values with the Cloud-Aerosol Lidar Infrared Pathfinder Satellite Observations (CALIPSO) Level 2 extinction coefficients. In the comprehensive analysis of overall performance, an AOD model was initially constructed using variables, achieving a correlation coefficient (R) of 0.676. Subsequently, predictions for aerosol extinction coefficients were generated, revealing a satisfactory agreement between the predicted and the actual values in the vertical direction, with an R of 0.535 and a root mean square error (RMSE) of 0.107 km−1. Of the four seasons of the year, the model performs best in autumn (R = 0.557), while its performance was relatively lower in summer (R = 0.442). Height had a significant effect on the model, with both R and RMSE decreasing as height increased. Furthermore, the accuracy of aerosol profile inversion shows a dependence on AOD, with a better accuracy when AOD is less than 0.3 and RMSE can be less than 0.06 km−1.
1. Introduction
With the acceleration of industrialization, the issue of air quality has become increasingly prominent, posing severe challenges to both human habitation and ecological environments [1]. Particle pollution poses a serious threat to human health [2]. Regions, especially urban areas, frequently experience widespread smoggy weather, leading to a sharp reduction in visibility due to particle pollution. Consequently, improving air quality has become a focal point of urgent concern across society [3].
Atmospheric aerosols are multiphase systems composed of tiny solid or liquid particles suspended in the air along with a gaseous carrier, with sizes ranging from a few nanometers to several tens of micrometers [4,5,6]. They can consist of a variety of substances, including dust, particulate matter, sulfates, nitrates, organic compounds, black carbon, and sea salt [7,8,9]. They can be introduced into the atmosphere through natural sources (e.g., volcanic eruptions, marine aerosols, and biogenic emissions) or anthropogenic activities (e.g., industrial emissions and vehicular exhaust) [10].
As a vital constituent of the atmosphere, aerosols play a crucial role in the radiation balance of the Earth–atmosphere system [11]. They not only directly absorb and scatter solar radiation, but also indirectly influence the formation and distribution of clouds and precipitation [12]. However, due to the complex composition and sources of atmospheric aerosols, their impact exhibits considerable variability [13,14]. Research indicates that three widely recognized factors determine the positive or negative radiative effects of aerosols in the atmosphere—aerosol type, information on aerosol vertical profiles, and surface albedo. Among these factors, extracting information on aerosol profiles is the most challenging aspect [15].
Various methods, including ground-based monitoring, balloon-borne aerosol counters, model simulations, and remote sensing, are currently utilized for detecting aerosol information [16,17,18,19]. Ground-based observations can provide high-precision aerosol concentration data but are limited by sparse station distribution, offering aerosol information only for specific regions [20,21]. Consequently, this method cannot reflect aerosol gradients in a given area and it is impractical for continuous global observation. While balloon observations effectively provide information on aerosol concentration and distribution in the upper atmosphere, they are significantly affected by weather conditions and are limited by the balloon’s flight path and altitude, resulting in data constraints [22,23,24]. Model simulation methods can be employed using a specific approach, but they typically offer limited spatial and temporal resolution and cannot capture micro-scale aerosol variations [25]. Satellite technology, among others, facilitates the acquisition of extensive aerosol distribution information with global coverage, enabling researchers to obtain continuous time series data and conveniently observe global aerosol change trends [26,27]. The utilization of satellite-borne lidar allows for the retrieval of relatively accurate profile information and is currently recognized as one of the most direct and accurate means of information retrieval [28,29]. However, it is constrained by significant energy loss, lengthy detection cycles, and challenges in achieving global coverage within a short timeframe [30,31,32].
In 1908, Mie G. [33] proposed a computational method for the scattering and absorption of spherical particles, laying the foundation for the study of aerosol optics. In order to obtain high-precision aerosol retrieval information, as early as the 1980s, Soviet scientists Badaev and Malkevich [34] first attempted to utilize the 0.76 μm oxygen A-band (O2 A-band) for aerosol optical measurements. They derived inversion formulas and established the vertical profile of atmospheric aerosol optical thickness. Subsequently, Gabella et al. [35] demonstrated the feasibility of retrieving aerosol profiles using a linearly constrained inversion method and applied this method based on the O2 A-band, confirming that the O2 A-band contains sufficient aerosol information even at low resolutions. In 2006, Corradini et al. [36] retrieved aerosol extinction profiles using the Scanning Imaging Absorption Spectrometer for Atmospheric Chartography, proposing a multiple scattering retrieval method for passive remote sensing instruments to invert aerosol extinction coefficient profiles and assess errors within the O2 A-band.
Malladi et al. [37] obtained altitude-varying extinction-to-backscatter ratio profiles using a pre-established aerosol model in 2010. However, the aerosol model exhibits significant differences across different regions, thus lacking universal applicability. O.M. and Holz. R. [38] improved the pre-assigned extinction-to-backscatter ratio in Cloud-Aerosol Lidar Infrared Pathfinder Satellite Observations (CALIPSO) products using MODIS data, yet inversion errors due to aerosol type matching still persist. In 2011, Zhang Yan et al. [39] proposed an algorithm that introduced correction factors and validated its effectiveness in retrieving aerosol profiles in the O2 A-band constrained by optical thickness. Sanders [40] investigated a general aerosol retrieval algorithm based on the O2 A-band for retrieving aerosol parameters in vegetated areas. In 2015, Geddes et al. [41] discussed the potential of retrieving tropospheric aerosol layer height from the O2 A-band using simulated data based on next-generation satellite instruments such as the Greenhouse Gases Observing Satellite (GOSAT), the Orbiting Carbon Observatory-2 (OCO-2), and the Tropospheric Ozone Monitor (TROPOMI). Ding et al. [42] analyzed the sensitivity and information content of aerosol vertical profiles using polarized remote sensing in the O2 A-band and O2 B-band in 2016. In recent years, Zeng and Chen et al. [43] employed spectral classification methods, utilizing the solar absorption spectra within the OCO-2 O2 A-band to constrain aerosol vertical structure. The authors of [44] also utilized machine learning to retrieve aerosol optical depth (AOD) and aerosol layer height (ALH) information from the spectra, aiding in the retrieval of aerosol profiles. In summary, progress has been made in aerosol retrieval methods based on the O2 A-band, ranging from initial theoretical explorations to the validation and application of various retrieval techniques. These methods have shown great potential in improving retrieval accuracy and applicability, providing essential tools for atmospheric aerosol research. However, current research on aerosol profiles is primarily theoretical, with only a few individuals obtaining aerosol information with extensive vertical height distribution. Utilizing data from new-generation high spectral resolution satellite instruments, further improvements in retrieval accuracy and regional applicability are necessary to better serve atmospheric science research and environmental monitoring needs.
In general, oxygen (O2) is a gas that is present in the atmosphere in stable and uniform concentrations and serves as the sole strong absorber within absorption bands [6]. Therefore, the O2 A-band represents an ideal retrieval channel containing aerosol information. Moreover, CALIPSO and OCO-2 are instruments within the A-Train series, and until September 2018, both instruments operated in nearly synchronized orbits, offering the possibility of extracting aerosol profile information [45]. In this study, the extinction coefficient data from CALIPSO was used as the true value. Primarily utilizing OCO-2 O2 A-band data, supplemented by the weak carbon dioxide (CO2) band and strong CO2 band, and integrating geographical and observational geometrical information, a random forest (RF) model was constructed for China and its surrounding areas (16.9–54.9°N, 72–136°E). This model estimates the inversion of atmospheric aerosol extinction coefficient profiles, and the results were comprehensively evaluated from multiple perspectives. This approach offers new methodological support for acquiring aerosol information and monitoring atmospheric environmental conditions.
In this study, the dataset of CALIPSO and OCO-2, data processing methods, and model construction approaches are introduced in Section 2. In Section 3, the results of AOD retrieval using the RF model are discussed. This discussion highlights the feasibility provided by these results for the subsequent estimation of aerosol extinction coefficient profiles. Section 3.2, Section 3.3, Section 3.4 and Section 3.5 include the validation of CALIPSO extinction coefficient data and the estimated coefficients concerning overall, seasonal, altitude, and various AOD aspects. Furthermore, in Section 3.2 a comparison of aerosol extinction coefficient profiles for individual observation points is presented. Finally, the discussion and conclusions section is provided in Section 4.
2. Materials and Methods
2.1. Data
In this study, OCO-2 Level 1B data (i.e., the O2 A-band, the weak CO2 band, and strong CO2 band) for China and its surrounding regions (16.9–54.9°N, 72–136°E) were utilized for the years 2016 and 2017. Additionally, CALIPSO Level 2 data were employed, including AOD and aerosol extinction coefficient profile data, for modeling and validating aerosol information retrieval. Furthermore, it was found that the distribution of aerosols is influenced by spatiotemporal factors and observational geometry [46,47]. Hence, auxiliary data such as longitude, latitude, altitude, solar zenith angle, and satellite zenith angle were also incorporated in this study.
2.1.1. CALIPSO Data
The CALIPSO, jointly developed by the National Aeronautics and Space Administration (NASA) of the United States and the Centre National d‘Études Spatiales (CNES) of France, was launched in April 2006 [48,49]. CALIPSO integrates an active lidar instrument with passive infrared and visible imagers [50]. The Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP) serves as the primary instrument, operating at two wavelengths (i.e., 532 nm and 1064 nm) [51,52]. It emits laser pulses and measures the scattered signals returned to acquire information on the vertical distribution, morphology, and optical properties of clouds and aerosols in the atmosphere [38].
This study is based on the CALIPSO standard Level 2–5 km aerosol profile data product (CAL_LID_L2_05 km APro-Standard-V4-51). This product provides detailed observational results regarding the vertical distribution of aerosols in the atmosphere. We selected key parameters, including positional information, altitude distribution, and a 532 nm aerosol extinction coefficient and AOD, for analysis and research.
Based on the selected CALIPSO aerosol extinction coefficients for the region, we analyzed the two-dimensional histogram of extinction coefficients with height and the relationship between height-averaged extinction coefficients and standard deviation, as shown in Figure 1. The aerosol extinction coefficients in the study area are primarily distributed between 0 and 0.3 km−1 (Figure 1a). The extinction coefficient exceeds 0.4 km−1 with a height < 2 km. It is noteworthy that the maximum boundary value of extinction coefficients for each layer exhibits exponential decay with height, reflecting the trend in aerosol profile variations in the vertical structure of the atmosphere. In Figure 1b, the red shaded area represents the uncertainty range of the extinction coefficient at each height, where a wider shaded area indicates a greater variability in the extinction coefficient at that height. From the figure, it can be observed that around 0.7 km above ground level, there is a characteristic of maximum dispersion and high aerosol concentration, indicating a significant dynamic range of aerosol variability at this height.
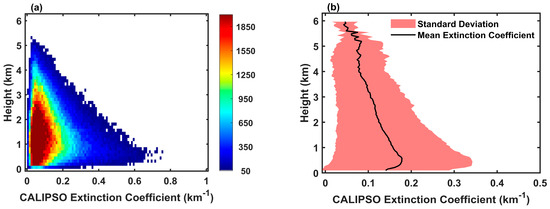
Figure 1.
Variation of CALIPSO extinction coefficient with height for China and neighboring regions (16.9–54.9°N, 72–136°E) in 2017. (a) Two-dimensional histogram of extinction coefficients with height; (b) the relationship figure of mean extinction coefficient and standard deviation with height.
2.1.2. OCO-2 Data
The OCO-2 was launched in July 2014 as an Earth observation mission initiated by the NASA with the objective of quantifying column-averaged atmospheric dry air mole fractions of carbon dioxide (XCO2) to better understand the Earth’s carbon cycle processes [53,54]. Equipped with an imaging grating spectrometer, the instrument collects high-resolution spectra of reflected sunlight at the O2 A-band centered at 0.765 μm, the weak CO2 absorption band at 1.61 μm, and the strong CO2 absorption band at 2.06 μm [54,55]. The O2 A-band spectra exhibit high sensitivity to changes in the light path, providing valuable information for detecting surface pressure, aerosol optical thickness, and the vertical distribution of aerosols. In this study, calibrated and geolocated Level 1B data (Version 11r OCO2_L1B_Science) provided by NASA were utilized, selecting variables such as radiance of three absorption bands, solar zenith angle, satellite zenith angle, and location information for analysis.
2.2. Methods
2.2.1. Data Processing
Prior to September 2018, CALIPSO was flying in the A-Train, approximately 7 min behind OCO-2. In this study, the nearest-neighbor method was used to perform spatiotemporal matching on CALIPSO and OCO-2 data. Specifically, we considered data points within a 1.3 km (0.0012°) range of longitude and latitude differences and with a temporal difference of approximately 7 min at neighborhood points around each target grid point for analysis. The CALIPSO Level 2 aerosol data were derived from Level 1 data through algorithmic preprocessing and calibration steps. There were uncertainties in the algorithms, so clouds or other factors needed to be excluded before using aerosol extinction coefficients and AOD data as real data in order to obtain scientifically reliable data.
CALIPSO extinction coefficient data consists of 399 vertical layers at each latitude and longitude point. In our study, we selected the extinction coefficient data from layers 277 to 390, comprising a total of 114 layers (heights below 6.8 km from the ground). According to the CALIPSO product data description manual (https://ntrs.nasa.gov (accessed on 28 April 2024)), parameters such as extinction coefficient uncertainty, cloud-aerosol discrimination score (CAD Score), and atmospheric volume description (AVD) were utilized for data filtering. Initially, all values below locations with extinction coefficients exceeding 10 km−1 were excluded. The CAD Score serves as an indicator to assess the discriminative ability between clouds and aerosols in remote sensing observations, where negative values represent aerosols and positive values represent clouds. Consequently, data with negative values in both upper and lower adjacent layers were identified as reliable aerosol extinction coefficient data. Additionally, AVD comprises two sets of data, serving as indicators for distinguishing feature classifications. A set of data were deemed to be aerosol if the first three bits resulted in a value of 3 after a specific calculation. Finally, profiles with effective values greater than 10 layers in the vertical direction were retained, while other invalid values were set to null. Figure 2 illustrates the trajectory of the 2016 and 2017 data after matching processing between CALIPSO and OCO-2 satellites. In the Qinghai-Tibet Plateau region, most of the CALIPSO aerosol extinction coefficient data were invalid, resulting in data gaps after processing and screening.
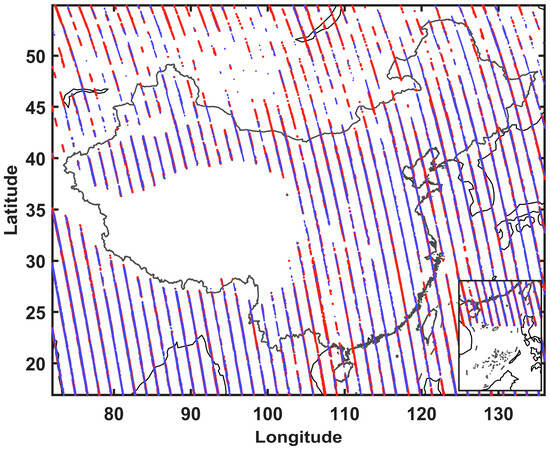
Figure 2.
Trajectories of matched data for Cloud-Aerosol Lidar with Orthogonal Polarization (CALIPSO) and Orbiting Carbon Observatory-2 (OCO-2) in 2016 (red) and 2017 (blue) using the nearest-neighbor method.
2.2.2. Principal Component Analysis
Principal component analysis (PCA) is a common multivariate statistical technique used to reveal inherent relationships among variables or samples in multivariate datasets [56]. It aims to reduce data dimensionality to extract the most relevant information efficiently [57]. It constitutes a linear transformation aimed at achieving dimensionality reduction by projecting the data onto a new coordinate system. In this novel coordinate system, the primary principal component encapsulates the greatest variance of the data projection, followed by the second principal component, and so forth. This conversion is designed to preserve the features within the original dataset that contribute the most to the variance, while reducing dimensionality. Through PCA, the original dataset is reconfigured and transformed into a set of new mutually uncorrelated variables.
The workflow of this method is as follows:
Assuming there are m satellite sample data and n channels per satellite detector, the complete satellite radiance dataset is denoted by the matrix Xmn:
(1) Compute the correlation coefficient matrix
Calculate the correlation coefficient between variables and () in dataset to derive the correlation coefficient matrix.
(2) Calculate eigenvalues and eigenvectors
Firstly, obtain the characteristic equation through the following:
resulting in eigenvalues , which are then arranged in descending order, i.e., ; subsequently, compute the eigenvectors corresponding to each eigenvalue .
(3) Calculate the contribution rate of each value in principal component analysis.
(4) Compute the principal component coefficients.
In light of the observational data from OCO-2 regarding the O2 A-band, weak CO2 band, and strong CO2 band, PCA can be employed to reduce the dimensionality of a large number of channel observations, preserving the primary components to simplify input variables. Given that OCO-2 encompasses over 3000 channels for the O2 A-band and CO2 absorption bands, PCA was utilized to reduce the dimensionality of these variables. Subsequently, we conducted principal component analysis on the OCO-2 observational spectra, examining the feasibility of aerosol vertical profile inversion using the principal component threshold method.
This study conducted PCA on the observed spectra of three absorption bands from 2016 and 2017, totaling 73,978 datasets. PCA is a statistical method that uses the idea of dimensionality reduction to transform multiple variables into a small number of unrelated composite variables, usually expressed as a linear combination of the original variables. Table 1 presents the characteristic vectors, contribution rates, and cumulative contribution rates of the top 10 principal components of the O2 A-band observed spectra. The contribution rate and cumulative contribution rate are utilized to depict the extent to which the principal components explain the total variance of the original variables. Based on the findings, we selected 10 principal components for the O2 A-band, 10 for the weak CO2 band, and 20 for the strong CO2 band for analysis. Each principal component is a linear combination of all channels in the O2 and CO2 absorption bands, and the individual principal components are uncorrelated. The results indicate that the cumulative contribution rate of the principal components selected for each band exceeds 99.99%. It is evident that the selected principal components can extract the majority of the information from the original spectra, further validating the effectiveness of PCA.

Table 1.
Principal component analysis information of oxygen A-band (O2 A-Band) spectrum.
2.2.3. Random Forest Model
The RF algorithm, proposed by Breiman [58], is an ensemble method that integrates multiple basic decision trees to address single prediction problems and achieve regression goals [59]. Compared to other methods, RF regression is widely applied in high-dimensional and large-scale data studies due to its robustness. It performs well in capturing nonlinear data fitting relationships, reducing root mean square error (RMSE), and further improving the predictive accuracy of the model [60].
The explanation of the RF model can be articulated by assuming an independent distribution relationship between the independent variable and the dependent variable Y. By randomly sampling in the (, ) space to construct the training set , the model predicts the outcomes in the form of . When evaluating the model performance, we employ the mean square error as a metric to gauge the average degree of squared deviation between the predicted values and the true values, where the RMSE can be defined as follows:
The steps of the RF model are as follows:
The model predicts the outcome as the average of predictions from decision trees. When ,
The left side of the equation represents the RMSE of the average prediction of decision trees, denoted as . When , the RMSE of a single decision tree is denoted as ·satisfies
where is the correlation coefficient between the residuals, and satisfies:
The final expression of the RF model is given by the following equation:
In this study, an RF model was utilized for estimating the AOD and extinction coefficient. The input variables included 40 principal components of the O2 A-band, weak CO2 band, and strong CO2 band, as well as solar zenith angle, satellite zenith angle, and geolocation information (i.e., latitude, longitude, and altitude). The output consisted of extinction coefficients for each layer of CALIPSO data. The data from 2016 were employed as the training set for the model, while the data from 2017 served as the validation set. Since RF supports only multi-input single-output mode, a total of 114 RF models were constructed for predicting aerosol vertical distribution. Figure 3 illustrates the workflow of the RF model for estimating aerosol profiles for a single layer. During the model construction process, the number of decision trees (numTrees) was incrementally increased from 100 to 360, with increments of 20. The RF was trained and validated at each step, and the performance stabilized when the number of decision trees reached 300 layers.
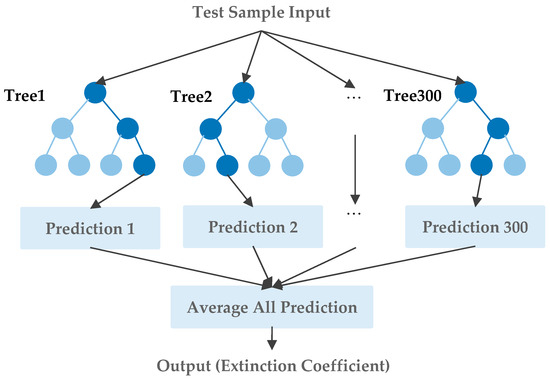
Figure 3.
Flowchart of the single-layer extinction coefficient random forest (RF) estimation model.
2.2.4. Statistical Metrics
In this study, we selected three error evaluation metrics—correlation coefficient (R), RMSE, and bias—to evaluate the aerosol prediction results. The formulas for these three statistical metrics are presented below:
where X and Y are RF estimates and CALIPSO extinction coefficients, respectively.
3. Results
3.1. Evaluation of AOD Accuracy
Figure 4 presents a two-dimensional histogram comparing the AOD estimated using the RF algorithm with CALIPSO AOD. It is evident that the inversion results obtained using the RF algorithm exhibit good agreement with CALIPSO AOD, with an R of 0.676, an RMSE of 0.168, and a bias of 0.01. The densely populated data points are distributed near the 1:1 line, particularly concentrated when AOD is less than 0.2. These results demonstrate the feasibility of predicting aerosols using OCO-2 data.
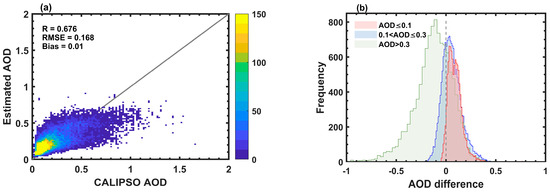
Figure 4.
(a) Two-dimensional histogram for CALIPSO aerosol optical depth (AOD) versus estimated AOD; (b) distribution of errors in AOD estimated using CALIPSO and RF for different AOD ranges.
Figure 4b presents a histogram depicting the errors between AOD estimated using CALIPSO and RF for different AOD ranges. AOD is stratified into three categories delineated by thresholds at 0.1 and 0.3, with errors being color-coded according to their respective AOD values. The results indicate that for AOD values equal to or less than 0.3, there is a propensity for AOD overestimation, with errors primarily centered around 0.05. Conversely, when AOD surpasses 0.3, it tends to be underestimated, with errors primarily concentrated around −0.15. Overall, the absolute errors for 74.51% of observation points are less than 0.15. Furthermore, an analysis of the relative errors in estimated AOD reveals that 24.25% of observation points exhibit relative errors below 20%, and 12.14% have relative errors below 10%.
3.2. The Overall Accuracy of Aerosol Profile Retrieval and Assessment at Individual Observation Points
Figure 5 presents a detailed examination of the correlation and accuracy between the aerosol extinction profiles derived from the RF estimation model and those from CALIPSO. It is evident from the figure that the predicted results exhibit a commendable alignment with the CALIPSO extinction profiles, displaying an R of 0.535, indicative of a moderate correlation (i.e., 0.3–0.7) with the CALIPSO extinction profiles. The RMSE and bias stand at 0.107 km−1 and 0.01 km−1, respectively. This suggests that leveraging the RF model based on OCO-2 O2 A-band observation data enables the extraction of valuable aerosol profile information. Figure 5 shows that the error increases with the CALIPSO extinction coefficient. This may be related to the larger dynamic range of CALIPSO extinction coefficient profiles in the vertical direction, while the profiles retrieved using the RF method are relatively smoother. In addition, with an increasing CALIPSO extinction coefficient, the negative bias increases. This could be attributed to the fact that the output data of the model trained in this study is predominantly concentrated below 0.3 km−1 (constituting 90.77% of the total samples), potentially limiting the model’s ability to accurately capture intricate variations under higher extinction coefficient conditions. But the color gradient in the figure shifts gradually with escalating extinction coefficients, with a reduced density of data points in regions characterized by higher extinction coefficients, predominantly concentrated in areas where the extinction coefficient is less than 0.2 km−1.
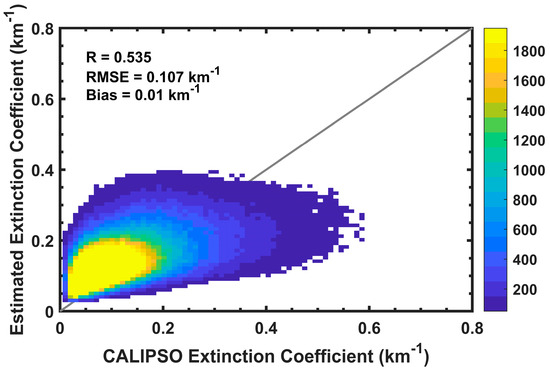
Figure 5.
Two-dimensional histogram of the 2017 CALIPSO extinction coefficient versus the estimated extinction coefficient (the color bar on the right represents the density of the data points, with densities ranging from 50 to 2000).
Figure 6 displays the distributions of aerosol extinction coefficients estimated using CALIPSO and the RF model for the validation dataset, comprising 37,537 cases. The figures offer a visual comparison between the predicted values from RF and the measured values from CALIPSO, demonstrating a notable agreement in the vertical aerosol profiles across various locations and altitudes. Additionally, the figures reveal that the extinction coefficients in this region during 2017 are primarily concentrated below 3 km, consistent with the findings obtained in Figure 1.
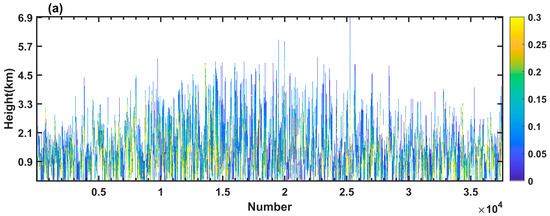
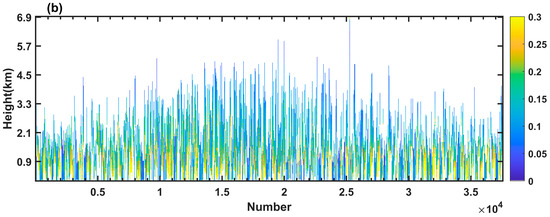
Figure 6.
(a) Distribution of CALIPSO extinction coefficients; (b) distribution of estimated extinction coefficients (the colors of the bars represent the magnitude of the extinction coefficient).
Figure 7 shows a comparison of RF estimates and CALIPSO aerosol extinction coefficient vertical profiles for a single observation point, where the extinction coefficients are primarily in the range of 0.1–0.3 km−1 and the profile is relatively complete, with more than 30 layers. The comparative analysis indicates variations in the range and distribution of aerosol extinction coefficient profiles across different locations and times. However, the overall trends are similar to the characteristics depicted in Figure 1, with higher aerosol extinction coefficients observed near the surface. It is evident from the figure that, vertically, there is a notable consistency between the aerosol vertical profiles estimated using RF and the observed values from CALIPSO. At vertical heights, there is a good agreement between the RF-estimated aerosol vertical profiles and CALIPSO, with most of the estimated and true values at the same height having an error of less than 0.05 km. In essence, the results demonstrate a favorable agreement between the OCO-2 O2 A-band estimations and CALIPSO across most altitude layers, highlighting the capability of the RF method in estimating aerosol vertical profiles.
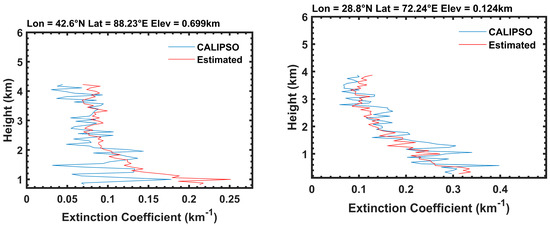
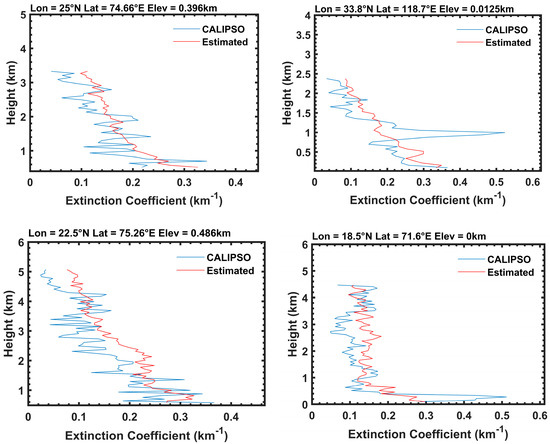
Figure 7.
Comparison figure of RF estimates and CALIPSO aerosol extinction coefficient profiles as a function of height for individual observations (the CALIPSO aerosol extinction coefficients are primarily concentrated within the range of 0.1–0.3 km−1, with the total number of layers exceeding 30).
3.3. Seasonal Dependence
Aerosol characteristics exhibit variations across different seasons [61]. In this study, an analysis of the mean aerosol extinction coefficient profiles was conducted for the four seasons (i.e., spring, summer, autumn, and winter). Characteristic metrics comparing the true values and predicted values for each season were calculated, as illustrated in Figure 8 and Table 2.
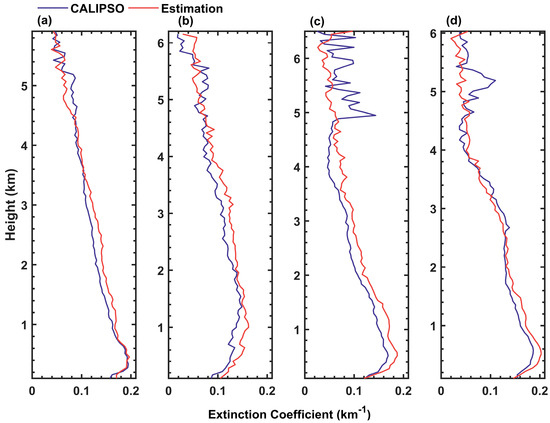
Figure 8.
Quarterly averaged CALIPSO aerosol extinction coefficient profiles and estimated aerosol extinction coefficient profiles over China and surrounding areas for 2017 ((a) spring (March–May), (b) summer (June–August), (c) autumn (September–November), (d) winter (December–February)).

Table 2.
Seasonal average statistical analysis of correlation coefficient (R), root mean square error (RMSE), and bias between CALIPSO and estimated aerosol extinction coefficients.
The aerosol extinction coefficients generally decrease with height in each season. In autumn, the vertical distribution of atmospheric aerosols appears non-uniform across different height levels, particularly with multiple peaks observed at higher heights. This phenomenon may be attributed to the pronounced vertical atmospheric motions during autumn, where the boundary layer tends to be elevated, facilitating the upward dispersion of aerosols from the lower atmosphere [62]. Overall, the trends in the average aerosol extinction coefficient predictions for each season closely align with those of CALIPSO extinction coefficients, with errors typically below 0.02 at each altitude level. Combined with Table 2, it is observed that the correlation is strongest in autumn (R = 0.557) and weakest in summer (R = 0.442), though still maintaining a moderate correlation. Additionally, the RMSE of the average extinction coefficients for all four seasons is approximately 0.1 km−1. The bias is minimal in spring (0.009 km−1) and maximal in autumn (0.017 km−1), once again underscoring the reliability of the aerosol vertical profile estimations in this study.
3.4. Height Dependency
In this study, a statistical analysis was conducted on the aerosol extinction coefficients retrieved using CALIPSO and predicted using the RF model at intervals of 0.5 km within the height range of 0 to 6 km, as illustrated in Figure 9. The figure presents the variations of the R, RMSE, and bias with height. With increasing height, all three statistical metrics exhibit discernible trends. Specifically, the maximum RMSE (0.585 km−1) is observed within the range of 0−0.5 km, while the minimum RMSE (0.098 km−1) occurs between 5.5 and 6 km. The RMSE decreases with height, likely due to lower aerosol concentrations at higher heights. When height < 4.5 km, it remains positive, indicating an overall positive bias in predictions. The maximum positive bias value of 0.0155 km−1 is observed at heights between 1 and 1.5 km. Conversely, when height > 4.5 km, it becomes negative, indicating an overall negative bias in predictions. Furthermore, within the height range of 0 to 6 km, the R demonstrates fluctuations but generally decreases with height. Notably, within the height range of 0 to 0.5 km, the R can reach a value of 0.585, indicating a notable correlation.
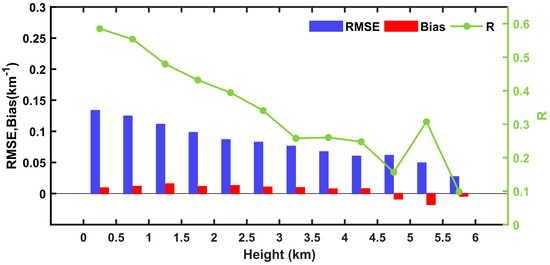
Figure 9.
Within the height range of 0–6 km (categorized every 0.5 km), a comparative analysis of CALIPSO aerosol extinction coefficients and estimated extinction coefficients (R, RMSE, and bias) is conducted at different heights over China and surrounding areas for 2017.
3.5. Accuracy of Aerosol Profile for Different AODs
To assess the disparities between estimated data and CALIPSO actual data under different AOD conditions, this study categorized the data into three models—Condition 1 (AOD ≤ 0.1), Condition 2 (0.1 < AOD ≤ 0.3), and Condition 3 (AOD > 0.3). Subsequently, the RMSE was computed for each model, as depicted in Figure 10. It is evident that the median values of RMSE for all three scenarios are lower than their respective means. The results reveal a positive correlation between RMSE and AOD, with RMSE values predominantly clustering around 0.04 km−1, 0.06 km−1, and 0.08 km−1 for condition- s 1, 2, and 3, respectively. Notably, all conditions exhibit outliers in RMSE. When AOD > 0.3, the violin plot shows a flat and elongated distribution, indicating a greater dispersion in RMSE values and an increased variability and fluctuation of prediction errors under high AOD conditions. Conversely, when AOD ≤ 0.3, the distribution is narrower, indicating relatively stable errors under low-to-moderate AOD conditions. Additionally, the total RMSE for models 1 and 2 is 0.04 km−1 less than that of model 3, with RMSE values being more concentrated and having fewer outliers.
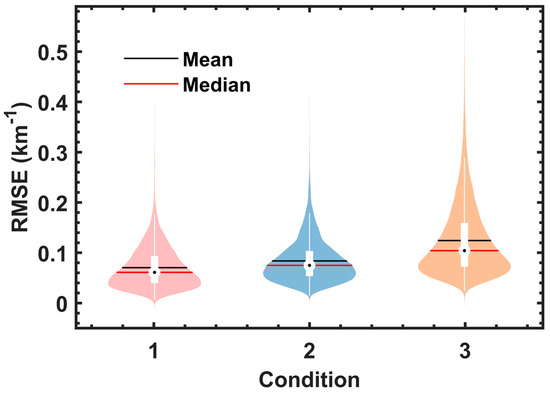
Figure 10.
Violin plots of CALIPSO aerosol extinction coefficients versus predicted extinction coefficients RMSE at different AOD concentrations (Condition 1: AOD ≤ 0.1, Condition 2: 0.1 < AOD ≤ 0.3, Condition 3: AOD > 0.3).
4. Discussion and Conclusions
This study utilized the O2 A-band, weak CO2 band, and strong CO2 band information from the OCO-2 satellite over China and its surrounding regions in 2016, along with geographical parameters such as longitude, latitude, and altitude, as well as solar zenith angle and satellite zenith angle, as input data for the model. The CALIPSO Level 2 aerosol extinction coefficient data were used as the output data for model training. An RF model was established and trained using these data, which was subsequently applied to aerosol data from the same region in 2017. By comparing the retrieved inversion estimates with CALIPSO Level 2 aerosol extinction coefficient data under various seasonal, altitudinal, and AOD conditions, the feasibility of this approach has been demonstrated.
In the comprehensive performance analysis, we initially analyze the selected variables to construct the AOD prediction model. The RF model for AOD yields an R value of 0.676, indicating the effectiveness of retrieving aerosol information. Subsequently, a new RF model was established to invert aerosol extinction coefficients. The results showed a favorable consistency between the predicted results and the true values in the vertical direction across different regions, with an R value of 0.535, indicating a moderate correlation. Additionally, we analyze the vertical aerosol extinction coefficient profiles at individual geographic coordinates, visually demonstrating the fitting degree achieved using this method. Furthermore, comparisons are made between the predicted values for all four seasons and the average extinction coefficient profiles from CALIPSO, showing a general agreement in the trend with height. The proposed model performs best in autumn (R = 0.557) and slightly less well in summer (R = 0.442). Height has a certain impact on the model, with both R and RMSE generally increasing with decreasing height. Specifically, the correlation is highest near the ground level, reaching 0.585 at heights between 0 and 0.5 km. This indicates that the model’s accuracy in estimating aerosol extinction coefficients is higher near the ground level, which may be related to the more reliable and abundant data in this region. When the height is less than 4.5 km, the estimated values exhibit a positive bias, with the aerosol extinction coefficients being overestimated. Conversely, when the height is greater than 4.5 km, a negative bias is observed, with the aerosol extinction coefficients being underestimated. Finally, the influence of different AOD conditions on the predicted results varies. When AOD > 0.3, the predicted results are relatively unstable, with a wider range of RMSE values, but they are still predominantly concentrated around 0.08 km−1. Compared to traditional physical inversion estimation methods, we employ machine learning techniques such as RF to autonomously learn features and patterns within the data. Through a straightforward analysis of O2 A-band data, we identify and utilize latent features and their associations with aerosol profiles, thereby obtaining relevant information. The CO2 satellites are uniformly equipped with O2 A-band observation instruments, so the results of this study are of great significance for improving CO2 inversion algorithms. Moreover, aerosols influence cloud formation and properties, affecting precipitation patterns. Examining aerosol profiles can enhance climate prediction model accuracy. Passive remote sensing satellites offer extensive spatial coverage and frequent revisit times. OCO-2, in a sun-synchronous orbit, performs continuous and systematic Earth observations, covering regions from the equator to the poles, with global coverage every 16 days. Therefore, the proposed approach has the potential to enable current and future passive remote sensing missions to retrieve global vertical profiles of aerosol extinction coefficients.
In the future, we will continue to optimize the aerosol extinction coefficient profile prediction model by exploring other ensemble learning algorithms and incorporating additional relevant input variables (e.g., surface reflectance). Additionally, in this study, we conducted a classification-based validation of the results according to AOD ranges. Future work can evaluate aerosol extinction coefficient profiles according to aerosol types and develop separate machine learning models for different aerosol types. Furthermore, geographical data could be organized into groups based on spatial locations to predict and assess data across diverse geographic regions and terrains, ensuring the applicability of the models to varying terrain types.
Author Contributions
Conceptualization, X.-Q.Z. and H.-L.L.; methodology, X.-Q.Z.; software, X.-Q.Z.; validation, X.-Q.Z. and H.-L.L.; formal analysis, X.-Q.Z.; investigation, M.-Z.D.; resources, M.-Z.D. and B.C.; data curation, X.-Q.Z.; writing—original draft preparation, X.-Q.Z.; writing—review and editing, X.-Q.Z. and H.-L.L.; visualization, S.-L.Z.; supervision, B.C.; project administration, H.-L.L.; funding acquisition, H.-L.L. All authors have read and agreed to the published version of this manuscript.
Funding
This study is supported by the National Natural Science Foundation of China, grant number 42030107 and 42175150.
Data Availability Statement
In this study, CALIPSO aerosol products are available at https://subset.larc.nasa.gov/calipso/ (last access: 28 April 2024). OCO-2 Level 1 product data are available at https://search.earthdata.nasa.gov/search (last access: 28 April 2024).
Acknowledgments
The authors thank the CALIPSO and OCO-2 teams for providing the data used in this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ogunkunle, O.; Ahmed, N.A. Overview of Biodiesel Combustion in Mitigating the Adverse Impacts of Engine Emissions on the Sustainable Human-Environment Scenario. Sustainability 2021, 13, 28. [Google Scholar] [CrossRef]
- Baker, E.; Barlow, C.F.; Daniel, L.; Morey, C.; Bentley, R.; Taylor, M.P. Mental health impacts of environmental exposures: A scoping review of evaluative instruments. Sci. Total Environ. 2024, 912, 9. [Google Scholar] [CrossRef] [PubMed]
- Mohan, M.; Payra, S. Influence of aerosol spectrum and air pollutants on fog formation in urban environment of megacity Delhi, India. Environ. Monit. Assess. 2009, 151, 265–277. [Google Scholar] [CrossRef] [PubMed]
- Pöschl, U. Atmospheric Aerosols: Composition, Transformation, Climate and Health Effects. Angew. Chem. Int. Ed. 2006, 44, 7520–7540. [Google Scholar] [CrossRef]
- Shiraiwa, M.; Ueda, K.; Pozzer, A.; Lammel, G.; Kampf, C.J.; Fushimi, A.; Enami, S.; Arangio, A.M.; Fröhlich-Nowoisky, J.; Fujitani, Y.; et al. Aerosol Health Effects from Molecular to Global Scales. Environ. Sci. Technol. 2017, 51, 13545–13567. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.X.; Sun, X.B.; Huang, H.L.; Ti, R.F.; Liu, X.; Fan, Y.Z. Study on Influencing Factors of the Information Content of Satellite Remote-Sensing Aerosol Vertical Profiles Using Oxygen A-Band. Remote Sens. 2023, 15, 948. [Google Scholar] [CrossRef]
- Charlson, R.J.; Schwartz, S.E.; Hales, J.M.; Cess, R.D.; Coakley, J.A., Jr.; Hansen, J.E.; Hofmann, D.J. Climate forcing by anthropogenic aerosols. Science 1992, 255, 423–430. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Xu, X.G.; Zhou, M.; Zhang, H.X.; Garcia, L.C.; Colarco, P.R.; Janz, S.J.; Yorks, J.; McGill, M.; et al. First retrieval of absorbing aerosol height over dark target using TROPOMI oxygen B band: Algorithm development and application for surface particulate matter estimates. Remote Sens. Environ. 2021, 265, 112674. [Google Scholar] [CrossRef]
- Xue, W.H.; Zhang, J.; Qiao, Y.; Wei, J.; Lu, T.W.; Che, Y.F.; Tian, Y.L. Spatiotemporal variations and relationships of aerosol-radiation-ecosystem productivity over China during 2001–2014. Sci. Total Environ. 2020, 741, 140324. [Google Scholar] [CrossRef]
- Chen, Q.X.; Huang, C.L.; Dong, S.K.; Lin, K.F. Satellite-Based Background Aerosol Optical Depth Determination via Global Statistical Analysis of Multiple Lognormal Distribution. Remote Sens. 2024, 16, 20. [Google Scholar] [CrossRef]
- Cai, H.K.; Yang, Y.; Luo, W.; Chen, Q.L. City-level variations in aerosol optical properties and aerosol type identification derived from long-term MODIS/Aqua observations in the Sichuan Basin, China. Urban Clim. 2021, 38, 100886. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, Y.; Gu, Y.; Liou, K.N.; Jiang, J.H.; Fan, J.W.; Liu, X.H.; Huang, L.; Yung, Y.L. Ice nucleation by aerosols from anthropogenic pollution. Nat. Geosci. 2019, 12, 602–607. [Google Scholar] [CrossRef] [PubMed]
- Bran, S.H.; Jose, S.; Srivastava, R. Investigation of optical and radiative properties of aerosols during an intense dust storm: A regional climate modeling approach. J. Atmos. Sol.-Terr. Phys. 2018, 168, 21–31. [Google Scholar] [CrossRef]
- Andreae, M.O. Natural and anthropogenic aerosols and their effects on clouds, precipitation and climate. Geochim. Cosmochim. Acta 2009, 73, A42. [Google Scholar]
- Wang, F.; Li, Z.Q.; Jiang, Q.; Ren, X.R.; He, H.; Tang, Y.H.; Dong, X.B.; Sun, Y.L.; Dickerson, R.R. Comparative Analysis of Aerosol Vertical Characteristics over the North China Plain Based on Multi-Source Observation Data. Remote Sens. 2024, 16, 1425. [Google Scholar] [CrossRef]
- Nzeffe, F.; Joseph, E.; Min, Q.L. Surface-based observation of aerosol indirect effect in the Mid-Atlantic region. Geophys. Res. Lett. 2008, 35, L22841. [Google Scholar] [CrossRef]
- Jethva, H.; Satheesh, S.K.; Srinivasan, J.; Levy, R.C. Improved retrieval of aerosol size-resolved properties from moderate resolution imaging spectroradiometer over India: Role of aerosol model and surface reflectance. J. Geophys. Res.-Atmos. 2010, 115, D18213. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Sendra, C. Algorithm for automatic atmospheric corrections to visible and near-IR satellite imagery. Int. J. Remote Sens. 1988, 9, 1357–1381. [Google Scholar] [CrossRef]
- Sinha, P.R.; Nagendra, N.; Manchanda, R.K.; Ojha, D.K.; Kumar, B.S.; Koli, S.K.; Trivedi, D.B.; Lodha, R.K.; Sahu, L.K.; Sreenivasan, S. Development of balloon-borne impactor payload for profiling free tropospheric aerosol. Aerosol Sci. Technol. 2019, 53, 231–243. [Google Scholar] [CrossRef]
- De Tomasi, F.; Perrone, M.R. Lidar measurements of tropospheric water vapor and aerosol profiles over southeastern Italy. J. Geophys. Res.-Atmos. 2003, 108, 4286. [Google Scholar] [CrossRef]
- Chazette, P.; Raut, J.C.; Dulac, F.; Berthier, S.; Kim, S.W.; Royer, P.; Sanak, J.; Loaëc, S.; Grigaut-Desbrosses, H. Simultaneous observations of lower tropospheric continental aerosols with a ground-based, an airborne, and the spaceborne CALIOP lidar system. J. Geophys. Res.-Atmos. 2010, 115, 15. [Google Scholar] [CrossRef]
- Hofmann, D.J. Twenty years of balloon-borne tropospheric aerosol measurements at Laramie, Wyoming. J. Geophys. Res. Atmos. 1993, 98, 12753–12766. [Google Scholar] [CrossRef]
- Deshler, T.; Hofmann, D.J.; Johnson, B.J.; Rozier, W.R. Balloonborne measurements of the Pinatubo aerosol size distribution and volatility at Laramie, Wyoming during the summer of 1991. Geophys. Res. Lett. 2013, 19, 199–202. [Google Scholar] [CrossRef]
- Kiran, V.R.; Ratnam, M.V.; Fujiwara, M.; Russchenberg, H.; Wienhold, F.G.; Madhavan, B.L.; Raman, M.R.; Nandan, R.; Raj, S.T.A.; Kumar, A.H.; et al. Balloon-borne aerosol-cloud interaction studies (BACIS): Field campaigns to understand and quantify aerosol effects on clouds. Atmos. Meas. Tech. 2022, 15, 4709–4734. [Google Scholar] [CrossRef]
- Tegen, I.; Neubauer, D.; Ferrachat, S.; Siegenthaler-Le Drian, C.; Bey, I.; Schutgens, N.; Stier, P.; Watson-Parris, D.; Stanelle, T.; Schmidt, H.; et al. The global aerosol-climate model ECHAM6.3-HAM2.3-Part 1: Aerosol evaluation. Geosci. Model Dev. 2019, 12, 1643–1677. [Google Scholar] [CrossRef]
- Pan, H.L.; Huang, J.P.; An, L.L.; Zhang, J.X.; Kumar, K.R. The CALIPSO retrieved spatiotemporal and vertical distributions of AOD and extinction coefficient for different aerosol types during 2007–2019: A recent perspective over global and regional scales. Atmos. Environ. 2022, 274, 118986. [Google Scholar] [CrossRef]
- He, Y.P.; Xu, X.Q.; Gu, Z.L.; Chen, X.H.; Li, Y.M.; Fan, S.J. Vertical distribution characteristics of aerosol particles over the Guanzhong Plain. Atmos. Environ. 2021, 255, 118444. [Google Scholar] [CrossRef]
- Winker, D.M.; Pelon, J.; Coakley, J.A.; Ackerman, S.A.; Charlson, R.J.; Colarco, P.R.; Flamant, P.; Fu, Q.; Hoff, R.M.; Kittaka, C.; et al. The calipso mission A Global 3D View of Aerosols and Clouds. Bull. Amer. Meteorol. Soc. 2010, 91, 1211–1229. [Google Scholar] [CrossRef]
- Sugimoto, N.; Lee, C.H. Characteristics of dust aerosols inferred from lidar depolarization measurements at two wavelengths. Appl. Opt. 2006, 45, 7468–7474. [Google Scholar] [CrossRef]
- Zeng, Z.L.; Wang, Z.M.; Zhang, B.J. An Adjustment Approach for Aerosol Optical Depth Inferred from CALIPSO. Remote Sens. 2021, 13, 3085. [Google Scholar] [CrossRef]
- Ntwali, D.; Dubache, G.; Ogou, F.K. Vertical Profile Comparison of Aerosol and Cloud Optical Properties in Dominated Dust and Smoke Regions over Africa Based on Space-Based Lidar. Atmos. Clim. Sci. 2022, 12, 588–602. [Google Scholar] [CrossRef]
- Baars, H.; Ansmann, A.; Engelmann, R.; Althausen, D. Continuous monitoring of the boundary-layer top with lidar. Atmos. Chem. Phys. 2008, 8, 7281–7296. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Badaev, V.V.; Malkevich, M.S. On the possibility of determining the vertical profiles of aerosol attenuation using satellite measurements of reflected radiation in the 0.76 micron oxygen band. Akad. Nauk. SSSR Fiz. Atmos. Okeana 1979, 14, 1022–1030. [Google Scholar]
- Gabella, M.; Guzzi, R.; Kisselev, V.; Perona, G. Retrieval of aerosol profile variations in the visible and near infrared: Theory and application of the single-scattering approach. Appl. Opt. 1997, 36, 1328–1336. [Google Scholar] [CrossRef] [PubMed]
- Corradini, S.; Cervino, M. Aerosol extinction coefficient profile retrieval in the oxygen A-band considering multiple scattering atmosphere. J. Quant. Spectrosc. Radiat. Transf. 2006, 97, 354–380. [Google Scholar] [CrossRef]
- Malladi, S.; Radha, R.S.; Pillai, V.P.M.; Sangipillai, V.; Bhargavan, P.; Vinjanampaty, M.; Karnam, R. Laser radar characterization of atmospheric aerosols in the troposphere and stratosphere using range dependent lidar ratio. J. Appl. Remote Sens. 2010, 4, 20. [Google Scholar] [CrossRef]
- Oo, M.; Holz, R. Improving the CALIOP aerosol optical depth using combined MODIS-CALIOP observations and CALIOP integrated attenuated total color ratio. J. Geophys. Res.-Atmos. 2011, 116, D14201. [Google Scholar] [CrossRef]
- Yan, Z.; Minzheng, D.; Daren, L. Retrieving aerosol extinction profile with high spectral resolution radiance in Oxygen A-band and Simulation research. Remote Sens. Technol. Appl. 2012, 27, 208–219. [Google Scholar]
- Sanders, A.F.J.; de Haan, J.F. Retrieval of aerosol parameters from the oxygen A band in the presence of chlorophyll fluorescence. Atmos. Meas. Tech. 2013, 6, 2725–2740. [Google Scholar] [CrossRef]
- Geddes, A.; Bösch, H. Tropospheric aerosol profile information from high-resolution oxygen A-band measurements from space. Atmos. Meas. Tech. 2015, 8, 859–874. [Google Scholar] [CrossRef]
- Ding, S.G.; Wang, J.; Xu, X.G. Polarimetric remote sensing in oxygen A and B bands: Sensitivity study and information content analysis for vertical profile of aerosols. Atmos. Meas. Tech. 2016, 9, 2077–2092. [Google Scholar] [CrossRef]
- Zeng, Z.C.; Chen, S.; Natraj, V.; Le, T.; Xu, F.; Merrelli, A.; Crisp, D.; Sander, S.P.; Yung, Y.L. Constraining the vertical distribution of coastal dust aerosol using OCO-2 O2 A-band measurements. Remote Sens. Environ. 2020, 236, 111494. [Google Scholar] [CrossRef]
- Chen, S.H.; Natraj, V.; Zeng, Z.C.; Yung, Y.L. Machine learning-based aerosol characterization using OCO-2 O2 A-band observations. J. Quant. Spectrosc. Radiat. Transf. 2022, 279, 108049. [Google Scholar] [CrossRef]
- L’Ecuyer, T.S. Touring the atmosphere aboard the A-Train. Phys. Today 2011, 64, 245–256. [Google Scholar]
- Meng, F.; Cao, C.Y.; Shao, X. Spatio-temporal variability of Suomi-NPP VIIRS-derived aerosol optical thickness over China in 2013. Remote Sens. Environ. 2015, 163, 61–69. [Google Scholar] [CrossRef]
- Natraj, V.; Spurr, R.J.D.; Boesch, H.; Jiang, Y.B.; Yung, Y.L. Evaluation of errors from neglecting polarization in the forward modeling of O2 A band measurements from space, with relevance to CO2 column retrieval from polarization-sensitive instruments. J. Quant. Spectrosc. Radiat. Transf. 2007, 103, 245–259. [Google Scholar] [CrossRef]
- Shikwambana, L.; Sivakumar, V. Global distribution of aerosol optical depth in 2015 using CALIPSO level 3 data. J. Atmos. Sol.-Terr. Phys. 2018, 173, 150–159. [Google Scholar] [CrossRef]
- Pan, B.W.; Liu, D.T.; Kumar, K.R.; Wang, M.; Devi, N. Global distribution of maritime low clouds with an emphasis on different aerosol types and meteorological parameters inferred from multi-satellite and reanalysis data during 2007–2016. Atmos. Environ. 2021, 246, 118082. [Google Scholar] [CrossRef]
- Nanda, S.; de Graaf, M.; Veefkind, J.P.; Sneep, M.; ter Linden, M.; Sun, J.Y.T.; Levelt, P.F. A first comparison of TROPOMI aerosol layer height (ALH) to CALIOP data. Atmos. Meas. Tech. 2020, 13, 3043–3059. [Google Scholar] [CrossRef]
- Mehta, M.; Singh, N.; Anshumali. Global trends of columnar and vertically distributed properties of aerosols with emphasis on dust, polluted dust and smoke—Inferences from 10-year long CALIOP observations. Remote Sens. Environ. 2018, 208, 120–132. [Google Scholar] [CrossRef]
- Wang, F.; Guo, J.P.; Zhang, J.H.; Huang, J.F.; Min, M.; Chen, T.M.; Liu, H.; Deng, M.J.; Li, X.W. Multi-sensor quantification of aerosol-induced variability in warm clouds over eastern China. Atmos. Environ. 2015, 113, 1–9. [Google Scholar] [CrossRef]
- Eldering, A.; Wennberg, P.O.; Crisp, D.; Schimel, D.S.; Gunson, M.R.; Chatterjee, A.; Liu, J.; Schwandner, F.M.; Sun, Y.; O’Dell, C.W.; et al. The Orbiting Carbon Observatory-2 early science investigations of regional carbon dioxide fluxes. Science 2017, 358, eaam5745. [Google Scholar] [CrossRef] [PubMed]
- O’Dell, C.W.; Eldering, A.; Wennberg, P.O.; Crisp, D.; Gunson, M.R.; Fisher, B.; Frankenberg, C.; Kiel, M.; Lindqvist, H.; Mandrake, L.; et al. Improved retrievals of carbon dioxide from Orbiting Carbon Observatory-2 with the version 8 ACOS algorithm. Atmos. Meas. Tech. 2018, 11, 6539–6576. [Google Scholar] [CrossRef]
- Richardson, M.; Lebsock, M.D.; McDuffie, J.; Stephens, G.L. A new Orbiting Carbon Observatory 2 cloud flagging method and rapid retrieval of marine boundary layer cloud properties. Atmos. Meas. Tech. 2020, 13, 4947–4961. [Google Scholar] [CrossRef]
- Liu, X.; Smith, W.L.; Zhou, D.K.; Larar, A. Principal component-based radiative transfer model for hyperspectral sensors: Theoretical concept. Appl. Opt. 2006, 45, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Yang, Q.G.; Li, H.; Jin, Z.H.; Wu, W.; Kizer, S.; Zhou, D.K.; Yang, P. Development of a fast and accurate PCRTM radiative transfer model in the solar spectral region. Appl. Opt. 2016, 55, 8236–8247. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Huang, Y.; Bao, Y.S.; Petropoulos, G.P.; Lu, Q.F.; Huo, Y.F.; Wang, F. Precipitation Estimation Using FY-4B/AGRI Satellite Data Based on Random Forest. Remote Sens. 2024, 16, 1267. [Google Scholar] [CrossRef]
- Zhu, W.D.; Li, Y.Q.; Luan, K.F.; Qiu, Z.E.; He, N.Y.; Zhu, X.L.; Zou, Z.Y. Forest Canopy Height Retrieval and Analysis Using Random Forest Model with Multi-Source Remote Sensing Integration. Sustainability 2024, 16, 1735. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Huang, G.; Zhang, S. Comprehensive Assessment and Analysis of the Current Global Aerosol Optical Depth Products. Remote Sens. 2024, 16, 1425. [Google Scholar] [CrossRef]
- Sun, T.Z.; Che, H.Z.; Qi, B.; Wang, Y.Q.; Dong, Y.S.; Xia, X.G.; Wang, H.; Gui, K.; Zheng, Y.; Zhao, H.J.; et al. Characterization of vertical distribution and radiative forcing of ambient aerosol over the Yangtze River Delta during 2013–2015. Sci. Total Environ. 2019, 650, 1846–1857. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).