Abstract
The integrated detection and jamming system employs integrated signals devoid of typical radar signal characteristics for detection and jamming. This allows for the sharing of resources such as waveform, frequency, time, and aperture, significantly enhancing the overall utilization rate of system resources. However, to achieve effective interference, the integrated waveform must overlap with the adversary radar signal within the frequency band. Consequently, the detection echoes are susceptible to the strong co-frequency direct wave generated by the adversary signals. This paper proposes a co-frequency direct wave interference suppression algorithm based on 2D generalized smoothed- norm sparse recovery. The algorithm exploits a joint dictionary comprising our integrated signals and adversary signals, along with the sparsity of 2D range-Doppler maps. The direct solution of the sparse decomposition optimization problem, formulated for the entire echo matrix, enhances the target detection performance for integrated signals even in the presence of robust co-frequency direct wave interference. Furthermore, the proposed method achieves robustness to interference of varying intensities through the adaptive updating and adjustment of relevant parameters. The effectiveness of the proposed method is validated through simulation and experimental results.
1. Introduction
With the rapid development of software and hardware technologies, the operational modes of radars in electronic warfare (EW) [1,2] have evolved from the combination of independent devices to modular and integrated systems [3,4]. Scholars have shown a growing interest in the integrated detection and jamming system [5], whose signal can eliminate typical radar signal characteristics, enhancing detection concealment [6]. Simultaneously, the sharing of resources between detection and jamming contributes to the overall efficiency of system resource utilization. However, a critical issue persists within the integrated detection and jamming system: strong co-frequency direct wave interference degrades the detection performance [7]. Traditional radar signal processing methods are unable to address this issue effectively. Current studies on integrated detection and jamming predominantly focus on the design of multifunctional integrated waveforms [8], with limited exploration of waveform optimization processes like interference suppression [9,10,11]. This paper aims to address this gap by proposing a novel co-frequency direct wave interference suppression method for integrated detection and jamming signal processing.
The most typical waveform among radar transmission signals is the linear frequency modulation (LFM) [12] signal. In waveform design, operations like convolution and modulation applied to the LFM signal could result in the generation of integrated detection and jamming signals [13]. An example of such a signal is the minimum shift keying-linear frequency modulation (MSK-LFM) signal [14]. Additionally, some scholars have proposed a cooperative detection and localization technique based on noise frequency modulation (NFM) jamming signals [5,15], which could be utilized to design integrated detection and interference signals waveforms. From a resource perspective, orthogonal LFM multiplexing synthetic waveforms [16] can also function as integrated waveforms. They demonstrate high-resolution target detection performance under appropriate signal-processing protocols [17]. Although there are many existing integrated waveform design methods, further waveform optimization is required to achieve detection functionality, particularly in the presence of strong co-frequency direct wave interference. At present, there are relatively few effective optimization methods available to tackle this challenge.
In an integrated radar and communication system, diverse digital self-interference cancellation methods [18,19] can be employed to tackle the problem of co-frequency self-interference. In the integrated detection and jamming system, the detected target echoes will include the adversary transmission signal that shares the same frequency band. Traditional radar signal processing methods, such as matched filtering (MF) [20], are unable to address this issue.Ref. [21] proposed a receiving and processing method based on prior information to identify and suppress adversary LFM signals from the time-domain pulses of signal echoes. Transforming the echoes of the integrated signal into the fractional Fourier (FRFT) [22,23] domain is also effective in identifying and suppressing LFM direct wave interference [24]. Building on this approach, we previously proposed a de-slope filtering and sparse recovery method [25]. The adversary’s LFM slope can be estimated using FRFT, and the adversary signals can then be filtered through frequency filtering. In cases where the interference energy is exceptionally strong and results in the loss of useful integrated signals, further restoration can be achieved through sparse recovery [26] based on the smoothed- (SL0) algorithm [27]. For interference with moderate intensity, employing time-varying filtering (TVF) [28,29,30] in the echo domain can yield favorable outcomes. However, these methods do not fully exploit the known prior information and solely process each pulse repetition interval (PRI) from the time dimension. The optimization problem only incorporates the sparsity of the range dimension as a constraint during solving. Detecting targets becomes challenging when facing strong co-frequency direct wave interference.
In this paper, a new co-frequency direct wave interference suppression method is proposed for integrated detection and jamming signal processing. In contrast to the traditional approach of processing signals for each PRI separately, the proposed method directly processes the entire echo matrix based on the sparsity of the range-Doppler domain. Initially, we leverage prior information to design a joint delay dictionary incorporating both our integrated signals and adversary signals. Combining the joint delay dictionary with the Doppler dictionary allows us to construct a signal model that correlates with both the echo matrix and the range-Doppler matrix. Subsequently, we derive the 2D sparse recovery optimization problem [31] for interference suppression. Utilizing the two-dimensional sparsity of targets, we solve the 2D sparse recovery problem employing the 2D generalized smoothed- (2DGSL0) algorithm [32,33], directly yielding the range-Doppler map results. Additionally, manually adjusting algorithm parameters such as iteration step size and threshold according to different situations, along with an adaptive regularization parameter, can enhance the algorithm’s robustness to varying interference intensities. Different from traditional approaches, the proposed method leverages prior information and directly processes the entire echo matrix based on the sparsity of the range-Doppler domain. This approach demonstrates superior sparse recovery performance compared to existing methods, and can further suppress range sidelobes and mitigate the effects of strong co-frequency direct wave interference.
The contributions of this article can be outlined as follows: (1) proposing a novel method to suppress co-frequency direct wave interference, addressing a significant problem within the integrated detection and jamming system. (2) exploiting prior information to construct the joint delay dictionary and establishing the 2D received integrated signal model along with the sparse recovery optimization problem based on the 2D generalized smoothed- (2DGSL0) algorithm. (3) utilizing simulation and experimentation to explore the integrated detection and jamming working scenarios and verify the feasibility of the algorithm.
This paper is organized as follows. Section 2 discusses the working scenario and the receiving signal model of the detection and jamming integrated system. Section 3 presents the limitations of the one-dimensional traditional approach that we have proposed in the past. The joint dictionary signal model and two-dimensional sparse recovery based on the 2D generalized smoothed- (2DGSL0) algorithm are introduced in Section 4. Simulation and experimental results to verify the superior performance of the proposed method are demonstrated in Section 5 and Section 6. Finally, Section 7 summarizes this paper and discusses limitations and prospects.
2. Problem Formulation
2.1. Scene Description
In the context of electronic warfare confrontation [34], there are various forms of adversarial interference between devices. As an illustration, consider the adversary radar transmitting the typical linear frequency modulation (LFM) signal. To attain both detection and jamming capabilities, our integrated device chooses a noise frequency modulation (NFM) signal within the same frequency band for target detection while concurrently interfering with the adversary radar. Then the working scenario of the integrated system considered in this paper is shown in Figure 1. In this scenario, since our signal and the adversary signal are on the same frequency to achieve the interference effect, the echo received during detection will contain the adversary radar signal. This will cause strong direct waves to affect our detection, thus reducing our detection performance. Therefore, the signal received by our integrated device includes not only the echoes reflected from the target for detection but also the direct wave impact formed by the adversary radar transmission signal. As for the adversary radar, the received signal includes the echoes reflected from our device and the interference caused by our device’s integrated signal transmission.
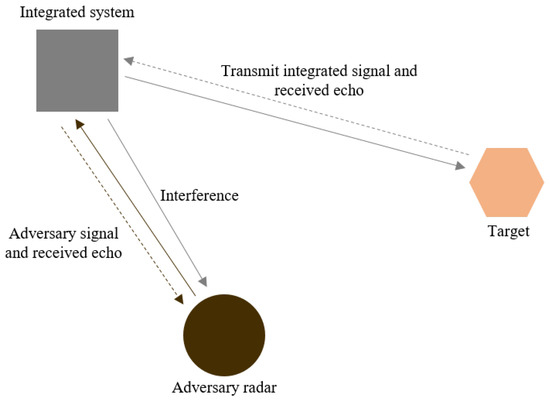
Figure 1.
The working scene of the detection and jamming integrated system.
In this scenario, the signal processing of our integrated device needs to ensure effective interference with the adversary radar while minimizing the impact of the adversary radar signal on our detection. This guarantees the detection capability of our integrated system. Hence, in the operational context of the integrated detection and jamming system, it becomes imperative to mitigate the co-frequency interference created by the adversary radar signal through suitable signal processing methods. This should be achieved while preserving the inherent detection and jamming capabilities of our integrated signal. This approach is crucial for gaining a distinct advantage in electronic warfare confrontations.
2.2. Signal Model
When our integrated detection and jamming system transmits the integrated signal for detection and interference, the total received signal under the mth pulse repetition interval (PRI) can be expressed as the superposition of the clean integrated signal echo reflected from the detected target, the co-frequency direct wave of the adversary radar transmission signal , and the additive noise :
where , is the PRI. The target echo is the cleanly integrated signal echo, where is the target scatter amplitude, is the time delay of the target, is the NFM detection and jamming integrated signal transmitted by our integrated device which can be expressed as:
where represents the carrier frequency, represents the amplitude of the NFM integrated signal, and can be expressed as:
where the modulation noise signal is a zero-mean and wide-sense stationary Gaussian random process, and represents the frequency modulation slope for frequency modulation.
Assuming the sampling rate of the received signal is , and each PRI contains equidistant sampling points. Therefore, Equation (1) can be expressed after sampling as:
Therefore, the signal transmitted from the adversary radar is composed of one or more time-varying components, and after sampling, it can be expressed as:
where and represent the time-varying amplitude and phase of the ith component, respectively. Considering the typical LFM signal transmitted by the adversary radar, is the discrete form of the LFM signal.
Supposing the pulse repetition intervals number during one observation time is M, the total echo can be expressed discretely as where . Similarly, each component in the echo can also be represented in a matrix. Therefore the echo matrix can be expressed as:
where and denote the integrated signal echo matrix and the adversary radar direct wave matrix respectively. Matrix denotes the additive noise. Suppose the potential ranges and Doppler frequencies of targets within the detection region of interest are respectively divided into range bins and Doppler bins. In that case, the matrix [31] corresponding to the signal received by our integrated device, as depicted in Figure 2, can be expressed as:
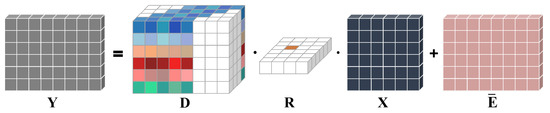
Figure 2.
Schematic diagram of the integrated signal echo model (7). (M = 6, = 8, = 4, and one target exists in the schematic with the delay and Doppler frequency of ).
The matrix denotes the delay dictionary, and denotes the Doppler dictionary respectively. Matrix stands for the additive interference including the adversary direct wave and the noise. The delay dictionary consists of M sub-dictionaries, where the matrix represents the delay sub-dictionary for the emitted signal in mth PRI. The column can be represented as
where denotes the resolution of the delay sub-dictionary. The Doppler dictionary X can be represented as
where the Doppler resolution can be represented as . The matrix is the range-Doppler map. indicates that the position bin is , and the Doppler bin is . The integrated signal echo model is illustrated in Figure 2.
Assuming that the echo does not contain the direct wave transmitted by the adversary radar and additive noise. The mth PRI clean target echo of our integrated signal can be represented as a linear combination of the echoes from all scattering points of the target:
where represents the scattering coefficient of the target during the mth PRI. Therefore the mth PRI echo can also be represented as (Figure 3):
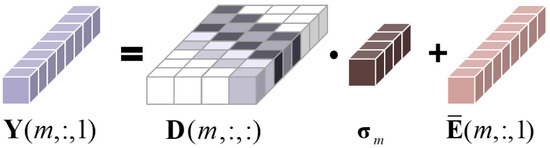
Figure 3.
Schematic diagram of mth PRI echo model (3). ( = 8, = 4).
In conventional processing, direct pulse compression (PC) processing of the total echo will be affected by the transmitted signal s from the adversary radar which may result in higher side lobes or false targets appearing in the detection range. Therefore, before further signal processing and data analysis, it is necessary to propose a suppression scheme to mitigate the impact of the adversary co-frequency direct wave signal and extract the pure echo signal of our integrated system to achieve better detection performance.
3. Traditional Methodology
To suppress co-frequency interference caused by direct waves emitted by adversary radar during integrated system detection, we have proposed a De-slope filtering and sparse recovery method in the past [25]. The De-slope frequency domain filtering (DSFF) processing was applied for each PRI, followed by sparse recovery based on the smoothed- (SL0) algorithm. This step aimed to further reconstruct the pure integrated signal echo and compensate for the useful signal part lost during filtering. After processing by the De-slope frequency domain filtering and smoothed- based sparse recovery (DSFF-SL0) method, matched filtering can be applied to conduct pulse compression for each PRI. Subsequently, coherent integration among different PRIs can yield results of range-Doppler maps. The schematic diagram of the traditional DSFF-SLO method is shown in Figure 4.
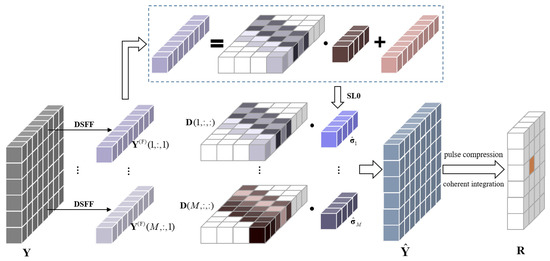
Figure 4.
Schematic diagram of the traditional DSFF-SLO method. (M = 6, = 8, = 4, and one target exists in the schematic with the delay and Doppler frequency of ).
Due to the continuous linear frequency variation of the LFM signal, the Fractional Fourier Transform (FRFT) can be used for the detection and parameter estimation [35,36] of the LFM signal. After obtaining the frequency modulation slope of the LFM signal, the slope removal method [37] is applied to convert the LFM signal into a manageable single-frequency signal. Finally, the frequency domain filtering method is used to suppress the influence of the LFM signal on the target signal.
The mth PRI echo is and then the FRFT of signal is defined as follows:
where is the order of the FRFT, which can be any real number, and . represents the FRFT operator symbol, and is the FRFT kernel.
When the adversary radar transmits an LFM signal, the direct wave signal received by our integrated system can be expressed as:
where represents the matrix envelope. is the starting frequency. is the signal amplitude and is the pulse width. k is the frequency modulation slope. represents the time delay of the direct wave from the adversary radar to our integrated system.
Due to the different energy concentrations of the LFM signal in different FRFT domains. We can estimate the slope of the adversary signal and remove it to obtain the de-sloped signal [25]. Further through frequency domain filtering and inverse de-sloping operations , the final purified result of our integrated system echo after removing the LFM direct wave interference is obtained as:
where and are the NFM integrated signal echo and the LFM direct wave signal respectively after the DSFF processing.
In situations with strong interference energy, the DSFF method might not completely mitigate the impact of co-frequency interference and could lose certain useful signal echoes. To extract the pure integrated signal echoes, further processing can be performed using sparse recovery methods.
Unfortunately, the output signal after the de-slope filtering will no longer be represented in the dictionary . As part of the echo containing the information from our transmitted integrated signal is lost and cannot be expressed as a linear combination of delayed transmitted pulses. For each echo pulse contaminated by the adversary signals, the dictionary must be constructed based on the characteristics of the signal after DSFF processing.
According to Equation (14), the mth PRI signal echo can be expressed in another form based on the linear characteristics of the DSFF processing:
Combining with Equation (10), can be written as:
where represents the ith row of the sub-dictionary , is the ith element of the vector . is the adaptive dictionary for the current echo pulse. In practical implementation, the processing results for other atoms can be represented as time-shifted forms of corresponding atoms, allowing the storage of DSFF results for specific atoms in memory to reduce computational complexity. Based on Equations (16) and (15) can be written as:
where represents the residual equivalent noise composed of the direct adversary signal after the DSFF processing and additive noise:
By further transforming this problem into an optimization problem, and using the and norms to enforce sparsity constraints [38], we can obtain the sparse coefficients to solve the following sparse decomposition denoising problem [39]:
where denotes the residual errors which represent the one-dimensional sparsity level of the scene. The sparse recovery model of this type of one-dimensional vector can be solved by smoothed- (SL0) algorithm [27] or orthogonal matching pursuit (OMP) [40,41].
Assuming is the solution to the optimization problem in Equation (19), the extracted mth PRI pure integrated signal echo can be represented as:
Subsequently, processing the signal of each PRI through the DSFF-SL0 method enables the suppression of co-frequency interference across all pulses. Following this preprocessing step, matched filtering can be employed for pulse compression in each PRI, and coherent integration across different PRIs can be conducted to obtain the range-Doppler map result.
Since our integrated signal is constructed based on intercepted adversary signal parameters, the known prior information is not fully utilized during the dictionary construction. Additionally, this method employs de-sloping filtering and one-dimensional sparse recovery for each PRI, utilizing only the sparsity of the range dimension as a constraint during solving. In situations with strong co-frequency direct wave interference, it has difficulty effectively suppressing the interference background in the detection results.
4. Co-Frequency Interference Suppression Based on Joint Dictionary and 2D Sparse Recovery
In this section, we propose a method for suppressing co-frequency direct wave interference. This method involves constructing a signal model using a joint dictionary and performing sparse recovery based on the 2D generalized smoothed- (2DGSL0) algorithm [31,33]. No longer is the signal processing performed on each PRI individually, instead, the entire echo matrix is directly processed based on the sparsity in the two-dimensional domain of range and Doppler. By utilizing a joint delay dictionary derived from the transmitted signal of both parties and a Doppler dictionary, the sparse decomposition problem is solved directly to obtain the range-Doppler map results. This method demonstrates superior sparse recovery performance in comparison to the one-dimensional approach across PRI. It enables more effective suppression of range sidelobes and mitigates the impact of strong co-frequency direct wave interference, thereby enhancing the target detection capability of the integrated signal.
The schematic diagram of the joint dictionary integrated signal echo model is shown in Figure 5.
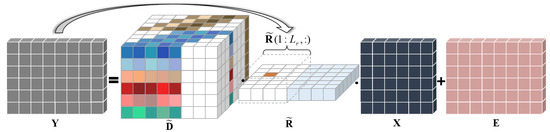
Figure 5.
Schematic diagram of the joint dictionary integrated signal echo model (24). (M = 6, = 8, = 4, and one target exists in the schematic with the delay and Doppler frequency of ).
4.1. Jiont Dictionary Signal Model
According to the signal model (7) in section II. The echo received by our integrated system can be expressed as
Similar to the integrated signal echo matrix , the adversary radar’s co-frequency direct wave matrix can also be represented by the delay and Doppler dictionaries, that is
where the matrix is the delay sub-dictionary for the adversary transmitted signal in mth PRI. Let be the signal transmitted by adversary radar, the column can be represented as
where represents the resolution of the delay sub-dictionary. The matrix is the range-Doppler map obtained through the processing of the transmitted signal of the adversary radar. After combining the range-Doppler map of our signal and the adversary direct wave, it can be represented by a joint delay dictionary. Then the total echo can be expressed as
where the matrix denotes the joint delay dictionary. The mth PRI subdictionary can be represented as
The joint range-Doppler map . The direct wave signal emitted by the adversary radar does not contain target information, so the range-Doppler map has weak sparseness. However, the targets’ range-Doppler map through processing the integrated signal is sparse. Therefore, as a combination of a sparse matrix and a non-sparse matrix, the joint range-Doppler map still has a certain degree of sparseness. To capture the 2D sparsity of matrix , the cost function can be defined as
where the indicator function is
Subsequently, the joint range-Doppler map can be reconstructed through solving the 2D sparse recovery optimization problem:
4.2. Sparse Recovery Based on 2D Generalized Smoothed- (2DGSL0) Algorithm
To solve the sparse decomposition optimization problem (28), we use the JD-2DGSL0 method [31] based on the joint dictionary signal model (24) and the 2D generalized smoothed- algorithm [33]. Considering that the norm of a matrix is a discontinuous indicator function, which is highly sensitive to noise during the search [27]. Thus, a continuous cost function is established to approximate the discontinuous indicator function in this context. Contemplate a Gaussian function:
Subsequently, the indicator function can be approximated by
For ease of expression, we construct a functional expression:
Then, the continuous smoothed- cost function to approximate the discontinuous norm can be represented as
Although the minimization of is equivalent to the minimization of when is small, at this point, contains many local minima. On the flip side, becomes smoother with the increase of . To prevent falling into local minima, we can address the optimization problem through iterations, gradually decreasing the value of . Further considering that each pulse of the integrated waveform is different, the problem model (28) can be expressed as
where denotes the joint range profile matrix. The is minimized through gradient descent steps under the constraints of the to enhance sparsity and the projection steps to improve accuracy. During the gradient descend step, we seek a matrix that minimizes by
where represents the step size and is the gradient of . The element at the index in can be represented as
In the projection step, the matrix , which has undergone sparse optimization, needs to be projected into the feasible set to guarantee the accuracy of recovery. Sparse recovery within each PRI pulse can be achieved by a range profile projection, while 2D accuracy is ensured by a 2D range-Doppler map projection. The mth PRI range profile projection can be viewed as an optimization problem:
where is the range profile matrix corresponding to the optimized in the gradient descend step. is an adaptive regularization parameter employed to maintain an acceptable recovery accuracy level, and the resulting solution closely aligns with that obtained through the steepest descent step. The application of this regularization term markedly improves the algorithm’s robustness to interference intensity and noise [42]. We write Equation (36) as . Therefore, to obtain this minimum value, the derivative of is derived in .
Let , the optimization problem (36) has an analytical solution:
where represents the matrix inversion operator. After the projection of the range profile, the joint range-Doppler map projection [33] can be obtained by solving:
Then we can obtain the pure integrated signal’s range-Doppler map . The whole steps of the proposed JD-2DGSL0 method are shown in Algorithm 1.
To facilitate the algorithm’s rapid convergence towards an initial solution close to the actual minimizer, an initial configuration is set with a sufficiently large value of , which is gradually decreased during iterations. The gradual reduction of is implemented to approach the actual minimum sparse solution, preventing the algorithm from becoming trapped in local minima. This ensures accuracy in sparse recovery in the range-Doppler domain.
| Algorithm 1 Joint Dictionary and 2D Generalized Smoothed- Algorithm (JD-2DGSL0) |
|
4.3. Discussion on the Selection of Regularization Parameter
The performance of the proposed JD-2DGSL0 method is closely related to the selection of regularization parameter . It can be seen from (36) that the approximate solution obtained by the steepest descent step and the approximate solution fitted to the received data in the optimizer can be balanced by . The steepest descent step is intended to produce a sparse solution, so the choice of is a trade-off between data fidelity and sparsity. Due to the varying proportions of sparsity and residual in different steps of the algorithm [42], we design an adaptive regularization parameter updating method to achieve a balance during the iteration. An optimized should satisfy the equation that , and according to the Equation (37) we have
From the previous analysis, we know that the solver of this equation is . Then (40) can be expressed as
Taking the Frobenius norm on both sides of the equation, then can be written as:
Since the of the current iteration loop step is unknown, we substitute it with the known optimizer solution of the previous inner loop, which is , then can be estimated by:
4.4. Complexity Analysis
In this section, we analyze the computational complexity of the proposed method. As demonstrated in Algorithm 1, the main complexity lies in the update of and . Updating requires the calculation of and . The complexity of them are and respectively, and the multiplication of them with a total complexity of . The complexity to update is . Therefore, the complexity at each iteration step is approximately . Suppose the numbers of external and internal loops are and respectively, we can obtain the total complexity of the proposed method is . The complexity of the traditional method DSFF-SLO is . Compared with the traditional method, the proposed method has slightly more computational complexity due to the consideration of the joint dictionary and Doppler characteristics. Fortunately the Doppler dictionary is known a prior and remains unchanged, the term in can be computed off-line in advance and then be cached in the iterations. The term can also be computed off-line, since our transmit integrated waveforms and the intercepted adversary waveforms are known in advance. With these techniques to accelerate the proposed method, the complexity can be reduced to .
5. Simulation Results
In this section, we showcase the performance of the proposed method within the working scenario of the integrated equipment. The adversary radar is configured to transmit an LFM signal, and our integrated device transmits a detection and interference integrated signal based on the NFM signal. The parameters in the simulation are shown in Table 1. Each range bin corresponds to a distance of 1 m, and each Doppler bin corresponds to a velocity of 1 m/s. We continuously adjust the algorithm’s iteration step size, termination threshold, and other parameters based on variations in signal and noise interference intensity to achieve optimal results. We first briefly describe the detection and interference performance of the integrated signal, then focus on the analysis of the detection effect after co-frequency interference suppression.

Table 1.
The Simulation Parameters.
5.1. Detection and Interference Performance Demonstration of Integrated Signal
To demonstrate the detection and interference performance of the integrated signal, we compare the range-Doppler maps of the adversary radar and our integrated device before and after being disturbed by the opponent’s transmitting signal. During the simulation, the Gaussian noise is added to the echoes of both parties with −10 dB signal-to-noise ratios (SNR). On the other hand, our transmitting NFM integrated signal and the adversary transmitting LFM signal are added to the opponent’s echoes respectively as direct wave interference, where the interference-to-signal ratios (ISR) are both set to 40 dB.
The interference performance of our integrated signal can be seen in the first row of Figure 6. When the adversary radar performs detection, the range-Doppler map result without interference is shown in Figure 6a and We see that the target is well detected. Figure 6b shows the range-Doppler map result of the adversary radar after our device transmitted the integrated signal. Since the target is completely covered by interference, our detection and interference integrated signal can effectively interfere with the detection of the adversary radar.
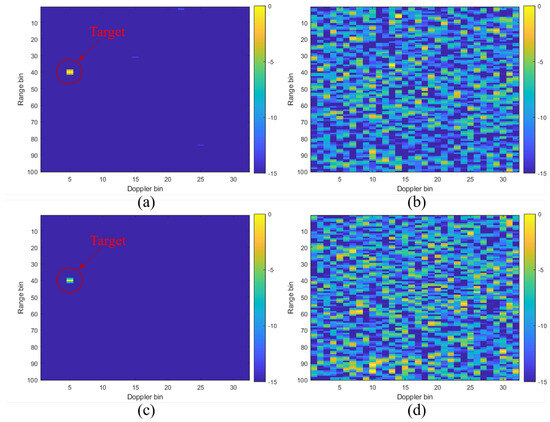
Figure 6.
The range-Doppler maps before and after interference for our system and adversary radar. (a) Our range-Doppler map without interference. (b) Our range-Doppler map after interference. (c) adversary range-Doppler map without interference. (d) adversary range-Doppler map after interference.
The detection performance of our integrated signal is demonstrated in the second row of Figure 6. When not affected by the adversary signal, our NFM integrated signal can realize the detection function very well which can be seen in Figure 6c. However, when the echoes are mixed with the adversary direct wave signal, as depicted in Figure 6d, the target cannot be detected. Considering the impact of the adversary direct wave on our integrated equipment during detection, the method proposed in this paper can effectively suppress the co-frequency interference from the adversary radar and extract the pure integrated signal echoes.
5.2. Performance Demonstration under Varied Co-Frequency Interference Intensities
We showcase the efficacy of the proposed method by comparing it with six other approaches, including the matched filtering (MF) [20] method, the time-varying filtering (TVF) [29] method, the orthogonal matching pursuit (OMP) [40] and SLO [27] method based on the one-dimensional sequential model (11), the traditional methods [25] previously proposed (i.e., the DSFF method shown as model (14) and DSFF-SLO method based on the optimization model (19)) which ignores the Doppler dimension property and the dictionary of adversary direct wave.
To analyze the improvement of the detection performance of our integrated signal by various methods under the co-frequency direct wave interference, we evaluate the performance of each method from a qualitative perspective and a quantitative perspective. The parameters of our NFM integrated signal, the adversary LFM signal, and the target are still shown in Table 1. Utilizing various methods to process simulated disturbed echoes of our integrated signal for obtaining the range-Doppler maps. This process aims to subsequently observe whether the simulated target point can be successfully detected for qualitative analysis. Based on the range-Doppler maps’ results in various scenarios, we derive the main-to-sidelobe ratios of the target points across different dimensions. Subsequently, we calculate the errors by comparing them to the ideal results, free from interference, to quantitatively assess the outcomes.
5.2.1. Qualitative Analysis
The range-Doppler maps of different methods are obtained by processing the echoes of our integrated signal interfered by the adversary direct wave in four examples. The four scenarios correspond to varying intensities of adversary direct wave interference in the simulation environment, including I. no noise and no interference, II. SNR of −15 dB with ISR of 20 dB, III. SNR of −15 dB with ISR of 40 dB, IV. SNR of −15 dB with ISR of 60 dB. The performance is demonstrated based on the confrontation scene between the integrated signal and the adversary direct wave during the detection process. Therefore, a fixed intensity noise is set and the analysis is mainly considered from different adversary direct wave interference intensities.
In the ideal situation of no noise and no adversary direct wave interference, the range-Doppler maps obtained after processing the echo of our integrated signal through various methods serve as a reference for subsequent analysis of other situations. The results are shown in Figure 7, and the target can be successfully detected only by the basic MF processing in the radar signal processing. The results obtained by further processing of the TVF and DSFF methods are almost identical to the results of the MF processing. Since each pulse of our integrated signal is not the same, higher side lobes will be formed in the range dimension after pulse compression processing. Some traditional methods (i.e., OMP, SL0, and DSFF-SL0) and the proposed JD-2DGSL0 method can further suppress the range dimension side lobe of the target point to obtain better detection performance even under ideal conditions without noise and interference.
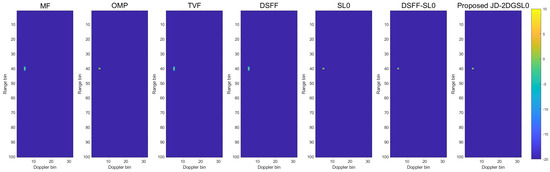
Figure 7.
The range-Doppler maps corresponding to different methods. (No noise, no co-frequency interference).
In the other three examples where the integrated signal echoes are contaminated by noise and the adversary direct wave interference, the proposed JD-2DGSL0 method outperforms the other methods which can be seen in Figure 8, Figure 9 and Figure 10. As Figure 8 shows, in a noisy environment with an SNR of −15 dB and when the intensity of adversary direct wave interference is small (i.e., ISR = 20 dB), the basic MF method and the OMP method cannot suppress the interference and noise to detect the target. Although the TVF and SL0 methods are sufficient to suppress direct wave interference to a certain extent, the target still cannot be observed. The DSFF and DSFF-SL0 methods can extract the target very well, but the range dimension side lobe processed by the proposed method is smaller. In Figure 9 and Figure 10, the basic MF processing and the traditional OMP and SL0 methods have little effect on strong adversary direct wave interference so that the target is still completely covered. Although the TVF method can filter out the strong interference, the target will also be removed at the same time. The methods of exclusively processing echoes within the echo domain without considering the Doppler dimension sparsity can slightly suppress the adversary’s direct wave interference (i.e., DSFF and DSFF-SL0), and they have almost no effect or even leave strong interference components in the Doppler dimension When the ISR reaches 60 dB. Compared with other methods, the proposed method can successfully mitigate interference on 2D range-Doppler maps under various levels of adversary direct wave interference. This provides a significant advantage to the integrated signal in adversarial scenarios to detect the target.
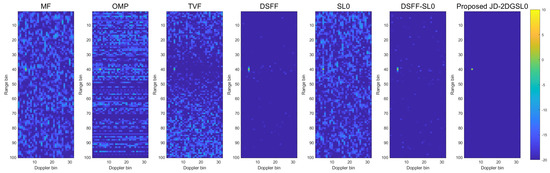
Figure 8.
The range-Doppler maps corresponding to different methods. (SNR = −15 dB, ISR = 20 dB).
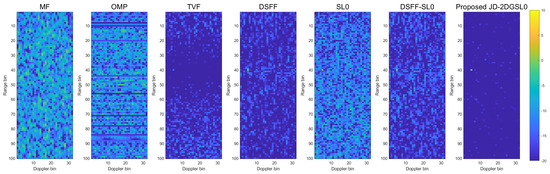
Figure 9.
The range-Doppler maps corresponding to different methods. (SNR = −15 dB, ISR = 40 dB).
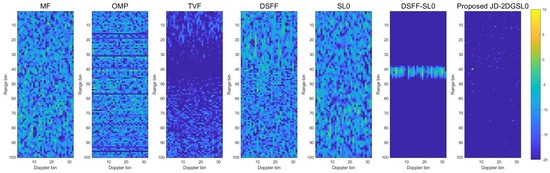
Figure 10.
The range-Doppler maps corresponding to different methods. (SNR = −15 dB, ISR = 60 dB).
5.2.2. Quantitative Analysis
To demonstrate the robustness of various methods, we quantitatively assess the results by calculating the main-to-sidelobe ratios (MSRs) of the target point and the root mean square errors (RMSEs). After obtaining the range-Doppler maps through various methods, we take the range-dimensional vector and the Doppler-dimensional vector of the target respectively to calculate the MSRs. The RMSEs between the range-Doppler maps processed by various methods and the ground truth are calculated with varying intensities of adversary direct wave interference. Both MSRs and RMSEs are obtained by Monte Carlo simulations with 100 independent runs.
Figure 11a shows the range-dimensional main-to-sidelobe ratios (RMSRs) as the ISRs vary from 0 dB to 60 dB and Figure 11b corresponds to the Doppler-dimensional main-to-sidelobe ratios (DMSRs). When the ISR is small, all methods have higher MSRs which can be greater than 10 dB in both the range and Doppler dimensions. However, as the ISR increases, the traditional methods (i.e., MF, OMP, SLO, and TVF) are all rapidly declining towards 0 dB, and even the TVF method is already less than 0 dB. The DSFF and DSFF-SL0 methods can maintain an MSR of about 25 dB when the direct wave intensity is small, but when the interference is large, the filtering in DSFF will lose more useful signals and lead to the deterioration of MSRs. In the distance dimension, SL0 can restore part of the useful signal to a certain extent, while it has no effect in the Doppler dimension. Compared with other methods, the proposed JD-2DGSL0 method can consistently maintain RMSR and DMSR greater than 30 dB, demonstrating strong robustness against adversary direct wave interference.
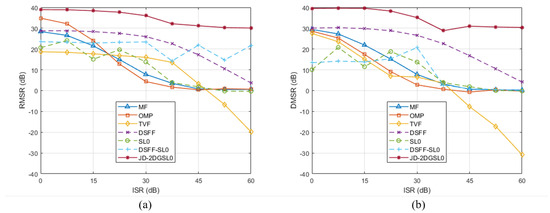
Figure 11.
The main-to-sidelobe ratios (MSRs) curves of different methods as ISRs vary from 0 dB to 60 dB. (a) The range-dimensional main-to-sidelobe ratios (RMSRs) curves. (b) The Doppler-dimensional main-to-sidelobe ratios (DMSRs) curves.
Root mean square errors (RMSEs) can provide a visual representation of the disparities between the range-Doppler maps generated by processing the echoes with interference and the ideal range-Doppler maps that are free from direct wave interference and noise. The RMSE curves for each method are shown in Figure 12 where RMSEs are in logarithm form [i.e., ()]. It is evident that, among all the methods, the proposed JD-2DGSL0 method consistently maintains the RMSE at or below 0 dB, showing an improvement of over an order of magnitude compared to other methods.
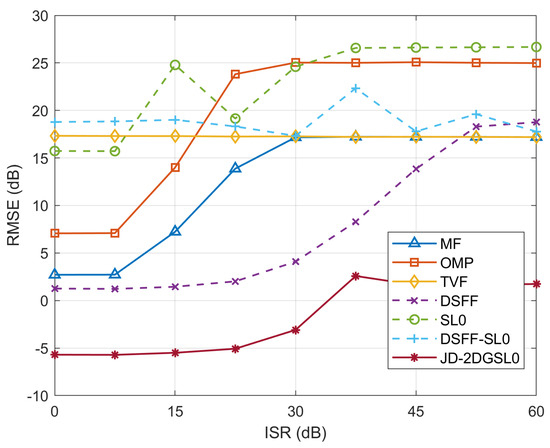
Figure 12.
The root mean square errors (RMSEs) curves of different methods as ISRs vary from 0 dB to 60 dB.
6. Experimental Results
In this section, we use real measured data to demonstrate the performance of the proposed method. Following the work scenario described in the section II, we set up an experimental validation system as illustrated in Figure 13. The experimental system consists of a set of adversary radar equipment and a set of our integrated system. Both the adversary and our equipment are located within the beam range of each other’s transmitting and receiving antennas. During the detection process, the transmitted signals from each side interfere with the equipment on the other side. In the experiment, we used an electric bicycle as the moving target to be detected. When the bicycle moved into the beam range of the equipment’s transmitting antenna, both sides’ equipment could detect it. The adversary radar employed an LFM signal for detection. Based on the parameters of the adversary radar’s LFM signal, our integrated system transmits an NFM integrated signal within the same frequency range. The pulse width and bandwidth of the NFM integrated signal are the same as the adversary signal, achieving target detection while simultaneously interfering with the adversary radar. The specific signal parameters and target motion parameters in the experiment are provided in Table 2. The sampling frequency used for analog-to-digital conversion in signal generation and echo processing is 40 MHz.
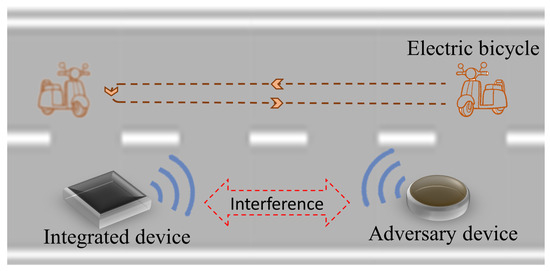
Figure 13.
The schematic diagram of the experimental scene.

Table 2.
The Experimental Parameters.
The adversary radar system employs the fundamental MF method for processing the received signal and generating range-Doppler maps. The result under the interference of our transmitted integrated signal is shown in Figure 14. Our integrated signal achieved a significant interference suppression effect, with real targets in the adversary equipment’s detection results being submerged within our interference.
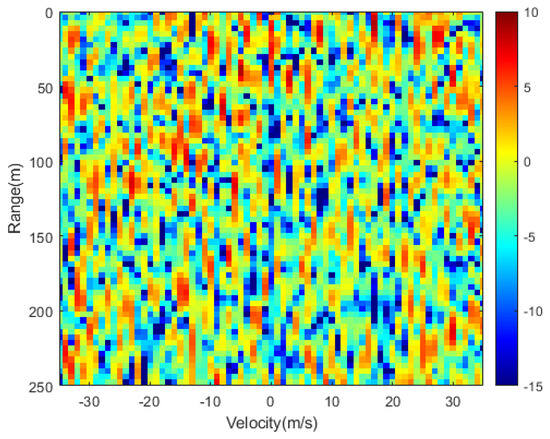
Figure 14.
The adversary range-Doppler maps after interference.
The signal received by our integrated system is processed by the basic MF method, the DSFF-SL0 method, and the proposed JD-2DGSL0 method, respectively. From Figure 15a, it is evident that our integrated system, when exposed to interference from the adversary radar’s co-frequency direct waves, fails to suppress the interference adequately for target detection through the basic matched filtering method. The range-Doppler maps obtained after processing with the DSFF-SL0 method and the proposed JD-2DGSL0 method are shown in Figure 15b,c, the interference can be successfully suppressed. However, it is worth noting that the DSFF-SL0 method still retains significant interference, which can impact the detection performance. Further analysis of the imaging results in the range and velocity dimensions for the target cells is presented. The results of the target’s main-to-sidelobe ratios under different processing methods are shown in Table 3. It can be observed in the presence of interference from the adversary direct wave, the basic matched filtering method exhibits significantly low main-to-sidelobe ratios, making it incapable of accurately extracting the target range and velocity information [see Figure 15d,g]. After processing with the DSFF-SL0 method, the main-to-sidelobe ratio in the range dimension increased by 6.86 dB, and the velocity dimension increased by 8.63 dB. However, there remains a significant amount of relatively high sidelobes, which can be seen in Figure 15e,h. After applying the proposed JD-2DGSL0 method, there is a significant improvement in the main-to-sidelobe ratios, with an increase of 21.44 dB in the range dimension and 20.51 dB in the velocity dimension. As a result, the high sidelobe interference is effectively suppressed, allowing for the accurate retrieval of target range and velocity information.
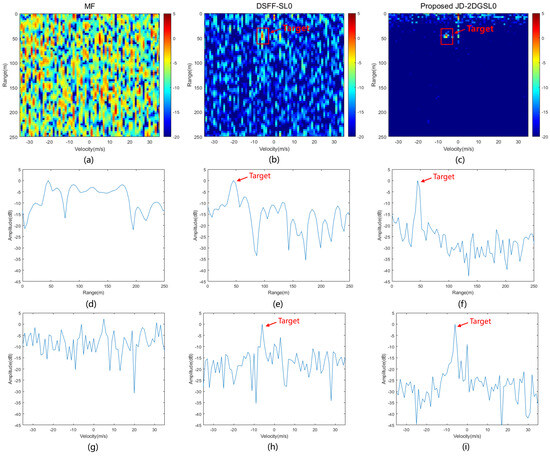
Figure 15.
The experimental data results corresponding to different methods. (a–c) The range-Doppler maps corresponding to different methods. (d–f) The range-dimension results corresponding to different methods. (g–i) The velocity-dimension results corresponding to different methods.

Table 3.
The MSRs for Measured Data.
7. Discussion
This paper addresses the co-frequency direct wave interference problem in integrated detection and jamming systems. A 2D generalized smoothed- norm based sparse recovery method is proposed to process the received integrated signal echos. We utilize prior information to construct a joint delay dictionary comprising our integrated signals and adversary radar signals. Leveraging the two-dimensional sparse characteristics of the targets, we formulate a sparse recovery optimization problem. The solution to this problem is directly derived from the entire echo matrix, resulting in the 2D range-Doppler map results. Taking the example of the typical LFM radar signal emitted by the adversary radar, our integrated system constructs an NFM integrated signal with the same waveform parameters and transmits it in the same frequency band. The proposed method effectively suppresses the co-frequency direct wave interference caused by the adversary transmission signal, ensuring that our integrated signal maintains excellent target detection performance while interfering with the adversary radar. Benefiting from the introduction of regularization parameters, the proposed method exhibits robustness to varying intensities of co-frequency direct wave interference. Both the target side-lobe levels and the errors in the ideal range-Doppler map are superior compared to traditional radar signal processing methods and the DSFF-SL0 method that we proposed in the past. Simulation and experimental results verify the superior performance of the proposed method.
The interference suppression method proposed in this paper still has some limitations. To simultaneously achieve detection and interference functions, there will inevitably be a certain degree of correlation between our integrated waveform and the adversary radar signal. Although constructing a joint dictionary significantly reduces the impact of the opposing signal on the transmission signal’s delay dictionary, there may still be some influence. In future research, we will consider methods related to dictionary learning to further minimize this impact. On the other hand, some parameters in the optimization algorithm need to be manually set based on various situations during experiments, which can be time-consuming. To address this parameter tuning process, future work could integrate approaches from the field of deep learning, attempting to learn parameter settings from large datasets to save time on experimental parameter tuning.
Author Contributions
S.Z. conceived and simulated the algorithm and wrote the paper; X.L. improved the algorithm and designed experiments; K.T. and H.Y. conducted experiments and data analysis; J.Y. and Z.D. provided valuable suggestions to improve this study; H.G. contributed analysis tools and laboratory equipment. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by National Natural Science Foundation of China under Grant 62001229, Grant 62101264, and Grant 62101260; Natural Science Foundation of Jiangsu Province under Grant BK20210334 and Grant BK20230915; China Postdoctoral Science Foundation under Grant 2020M681604; and Jiangsu Province Postdoctoral Science Foundation under Grant 2020Z441.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Zhang, C.; Wang, L.; Jiang, R.; Hu, J.; Xu, S. Radar jamming decision-making in cognitive electronic warfare: A review. IEEE Sens. J. 2023, 23, 11383–11403. [Google Scholar] [CrossRef]
- Park, S.R.; Nam, I.; Noh, S. Modeling and simulation for the investigation of radar responses to electronic attacks in electronic warfare environments. Secur. Commun. Netw. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Xiong, G.; Li, Y.; Li, P.; Chen, C. Design and performance analysis of an integrated detection-jamming shared waveform based on PNFM-LFM composite modulation. Acta Aeronaut. Astronaut. Sin. 2021, 42, 525821. [Google Scholar]
- Wang, Y.; Cao, Y.; Yeo, T.S.; Cheng, Y.; Zhang, Y. Sparse reconstruction-based joint signal processing for MIMO-OFDM-IM integrated radar and communication systems. Remote Sens. 2024, 16, 1773. [Google Scholar] [CrossRef]
- Orlando, D. A novel noise jamming detection algorithm for radar applications. IEEE Signal Process. Lett. 2017, 24, 206–210. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L. Radar detection and parameter estimation of high-speed target based on MART-LVT. IEEE Sens. J. 2018, 19, 1478–1486. [Google Scholar] [CrossRef]
- Lei, Z.; Chen, H.; Zhang, Z.; Dou, G.; Wang, Y. A cognitive beamforming method via range-doppler map features for skywave radar. Remote Sens. 2022, 14, 2879. [Google Scholar] [CrossRef]
- Liu, G.; Huang, Z.; Zhang, Q.; Mu, B.; Guo, H. Joint radar jamming and communication system design based on universal filtered multicarrier chirp waveform. Remote Sens. 2024, 16, 1383. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Li, J.; Chen, Z.; Yang, X. Reweighted tensor factorization method for SAR narrowband and wideband interference mitigation using smoothing multiview tensor model. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3298–3313. [Google Scholar] [CrossRef]
- Tao, M.; Su, J.; Huang, Y.; Wang, L. Mitigation of radio frequency interference in synthetic aperture radar data: Current status and future trends. Remote Sens. 2019, 11, 2438. [Google Scholar] [CrossRef]
- Tao, M.; Li, J.; Su, J.; Wang, L. Characterization and removal of RFI artifacts in radar data via model-constrained deep learning approach. Remote Sens. 2022, 14, 1578. [Google Scholar] [CrossRef]
- Kim, E.; Sohn, S.; Moon, H.; Choi, J.H.; Lee, K. Linear frequency modulation and orthogonal code modulation for co-located multiple-input multiple-output high-frequency surface wave radar. Remote Sens. 2024, 16, 104. [Google Scholar] [CrossRef]
- Li, C.; Wu, G.; Li, G.; Xue, H. Shared waveform design for integrated detection and jamming signal based on smart noise jamming of convolution modulation. In Proceedings of the 2023 8th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 8–10 July 2023; pp. 564–569. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H. The design of integrated waveform based on MSK-LFM signal. In Proceedings of the 2020 15th IEEE International Conference on Signal Processing (ICSP), Beijing, China, 6–9 December 2020; Volume 1, pp. 565–569. [Google Scholar] [CrossRef]
- Pralon, L.; Pompeo, B.; Fortes, J.M. Stochastic analysis of random frequency modulated waveforms for noise radar systems. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1447–1461. [Google Scholar] [CrossRef]
- Huan, S.; Chen, W.; Peng, Y.; Yang, C. Orthogonal chirp division multiplexing waveform for mmWave joint radar and communication. In Proceedings of the IET Conference Proceedings, Online, 4–6 November 2020; pp. 1222–1226. [Google Scholar] [CrossRef]
- Wang, S.; He, F.; Dong, Z. A novel intrapulse beamsteering sar imaging mode based on ofdm-chirp signals. Remote Sens. 2024, 16, 126. [Google Scholar] [CrossRef]
- Chu, J.; Tang, Y.; Zhou, Y. Digital domain self-interference cancellation based on modified variable step-size LMS algorithm. In Proceedings of the 2023 5th International Conference on Communications, Information System and Computer Engineering (CISCE), Guangzhou, China, 14–16 April 2023; pp. 9–14. [Google Scholar] [CrossRef]
- Lu, Y.; Qiao, G.; Yang, C.; Zhao, Y.; Yang, G.; Li, H. A real-time digital self interference cancellation method for in-band full-duplex underwater acoustic communication based on improved VSS-LMS algorithm. Remote Sens. 2022, 14, 2924. [Google Scholar] [CrossRef]
- Sack, M.; Ito, M.; Cumming, I. Application of efficient linear FM matched filtering algorithms to synthetic aperture radar processing. Proc. Inst. Elect. Eng. 1985, 132, 45–57. [Google Scholar] [CrossRef]
- Li, C.; Wu, G. A shared waveform design and processing method for integrated radar detection and coherent jamming signal. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; Volume 10, pp. 373–380. [Google Scholar] [CrossRef]
- Sejdić, E.; Djurović, I.; Stanković, L. Fractional fourier transform as a signal processing tool: An overview of recent developments. Signal Process. 2011, 91, 1351–1369. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L. Detection of maneuvering target with complex motions based on ACCF and FRFT. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 0017–0020. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, J. Wideband LFM interference suppression based on fractional Fourier transform and projection techniques. Circuits Syst. Signal Process. 2014, 33, 613–627. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, X.; Yu, W.; Wu, Y.; Yan, H.; Wu, M.; Gu, H. Direct wave suppression technology based on de-slope filtering and sparse recovery of integrated detection and jamming system. J. Signal Process. 2023, 39, 221–234. [Google Scholar] [CrossRef]
- Lu, X.; Yang, J.; Yu, W.; Su, W.; Gu, H.; Yeo, T.S. Enhanced LRR-based RFI suppression for SAR imaging using the common sparsity of range profiles for accurate signal recovery. IEEE Geosci. Remote Sens. Lett. 2020, 59, 1302–1318. [Google Scholar] [CrossRef]
- Mohimani, H.; Babaie-Zadeh, M.; Jutten, C. A fast approach for overcomplete sparse decomposition based on smoothed l0 norm. IEEE Trans. Signal Process. 2009, 57, 289–301. [Google Scholar] [CrossRef]
- Lu, X.; Yang, J.; Ma, C.; Gu, H.; Su, W. Wide-band interference mitigation algorithm for SAR based on time-varying filtering and sparse recovery. Electron. Lett. 2018, 54, 165–167. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, X.; Yang, J.; Su, W.; Gu, H. Enhanced signal processing method for integrated detection and jamming system considering the complex environment. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 2233–2237. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Yang, X.; Chen, Z.; Liu, J.; Li, J.; Hong, W. An efficient graph-based algorithm for time-varying narrowband interference suppression on SAR system. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8418–8432. [Google Scholar] [CrossRef]
- Lu, X.; Xu, B.; Yeo, T.S.; Su, W.; Gu, H. Co-located MIMO radar target detection in cluttered and noisy environment based on 2D block sparse recovery. IEEE Trans. Signal Process. 2021, 69, 3431–3445. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, B. Hyperspectral anomaly detection based on low-rank representation and learned dictionary. Remote Sens. 2016, 8, 289. [Google Scholar] [CrossRef]
- Lu, X.; Gu, H.; Su, W. Noise radar range doppler imaging via 2D generalized smoothed-l0. Electron. Lett. 2021, 57, 448–450. [Google Scholar] [CrossRef]
- Zhang, K.D.; Zhou, Q.S.; Wang, J.; Zhang, J.Y.; Li, Z.H. A method for jamming waveform design in precision electronic warfare scenarios. IET Signal Process. 2022, 16, 562–574. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, H.; Wei, G.; Ji, F.; Chen, F. Parameter estimation of wideband underwater acoustic multipath channels based on fractional Fourier transform. IEEE Trans. Signal Process. 2016, 64, 5396–5408. [Google Scholar] [CrossRef]
- Deng, B.; Luan, J.B.; Cui, S.Q. Analysis of parameter estimation using the sampling-type algorithm of discrete fractional Fourier transform. Def. Technol. 2014, 10, 321–327. [Google Scholar] [CrossRef]
- Zhou, B. Distributed coherent radar LFM wideband stretch parameter estimation method. J. Electron. Inf. Technol. 2020, 42, 1566–1572. [Google Scholar]
- Ma, C.; Yeo, T.S.; Ng, B.P. Multiple input multiple output radar imaging based on multidimensional linear equations and sparse signal recovery. IET Radar Sonar Navig. 2018, 12, 3–10. [Google Scholar] [CrossRef]
- Hu, X.; Tong, N.; Zhang, Y.; Huang, D. MIMO radar imaging with nonorthogonal waveforms based on joint-block sparse recovery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5985–5996. [Google Scholar] [CrossRef]
- Cai, T.T.; Wang, L. Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Wang, J.; Kwon, S.; Shim, B. Generalized orthogonal matching pursuit. IEEE Trans. Signal Process. 2012, 60, 6202–6216. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Y.; Jin, L.; Li, J.; Zhu, Y. An adaptive regularized smoothed l0 norm algorithm for sparse signal recovery in noisy environments. Signal Process. 2017, 135, 153–157. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).