Abstract
Since Neural Radiation Field (NeRF) was first proposed, a large number of studies dedicated to them have emerged. These fields achieved very good results in their respective contexts, but they are not sufficiently practical for our project. If we want to obtain novel images of satellites photographed in space by another satellite, we must face problems like inaccurate camera focal lengths and poor image texture. There are also some small structures on satellites that NeRF-like algorithms cannot render well. In these cases, the NeRF’s performance cannot sufficiently meet the project’s needs. In fact, the images rendered by the NeRF will have many incomplete structures, while the MipNeRF will blur the edges of the structures on the satellite and obtain unrealistic colors. In response to these problems, we proposed STs-NeRF, which improves the quality of the new perspective images through an encoding module and a new network structure. We found a method for calculating poses that are suitable for our dataset and that enhance the network’s input learning effect by recoding the sampling points and viewing directions through a dynamic encoding (DE) module. Then, we input them into our layer-by-layer normalized multi-layer perceptron (LLNMLP). By simultaneously inputting points and directions into the network, we avoid the mutual influence between light rays, and through layer-by-layer normalization, we ease the model’s overfitting from a training perspective. Since real images should not be made public, we created a synthetic dataset and conducted a series of experiments. The experiments showed that our method achieves the best results in reconstructing captured satellite images, compared with the NeRF, the MipNeRF, the NeuS and the NeRF2Mesh, and improves the Peak Signal-to-Noise Ratio (PSNR) by 19%. We have also tested on public datasets, and our NeRF can still render acceptable images on datasets with better textures.
1. Introduction
In recent years, novel view synthesis based on two-dimensional (2D) images has been a hot topic with important applications in many fields. Many classical methods, such as Structure from Motion (SFM) [1], open Multiple View Geometry (openMVG) [2], etc., have seen preliminary progress in some contexts. Recently, the NeRF [3] has been used to implicitly describe scenes through neural networks, achieving some stunning view synthesis effects. Therefore, a large amount of research based on the NeRF [3] has emerged.
The representation of three-dimensional (3D) scenes can be divided into two types: explicit and implicit. Explicit expression methods, like Multi-view Stereo Net (MVSNet) [4], Fast Multi-view Stereo Net (FastMVSNet) [5], and Self-supervised-CVP-MVSNet [6], describe objects or scenes through point clouds, voxels, grids, etc. Their advantages are easy editing, fast computer processing speeds, and the fact that explicit expression is supported by software. However, explicit expression usually involves extracting features through the network and then learning the relationship between the features and the known depth. Therefore, this method cannot meet our needs. Firstly, the texture of our image is very poor, which makes obtaining enough feature points difficult. Secondly, it is also difficult for us to obtain accurate depth images, since the distance between the two satellites exceeds the measuring range of the sensors. Thirdly, our dataset is not sufficiently large; we do not have a enough satellite models to make our dataset. Even if we did have enough modules, other factors, such as lighting, would have an effect. To sum up, the explicit method is not suitable for us.
The implicit representation of 3D scenes uses a function to describe the geometric shape of objects. It only needs us to provide the images and the corresponding poses and can thus effectively avoid the problems caused by poor texture in explicit expression methods. However, it is difficult to obtain accurate internal and external parameters. Before the introduction of the NeRF [3], it was difficult to synthesize realistic virtual views with implicit expressions. Unlike Signed Distance Functions [7] and Occupancy Fields [8], the NeRF [3] uses neural networks to simulate the radiation field of objects and performs novel view synthesis through volume rendering [9]. The images rendered by the NeRF [3] thus look like real photos.
Since our project requires obtaining a satellite model, we can know from the above discussion that it is difficult to obtain a point cloud or grid of a satellite through explicit expression methods. So we chose to obtain a satellite model described using an implicit method, and the quality of the rendered new perspective image becomes the evaluation criterion for this model.
There are already some NeRF-based works for processing satellite images, such as Sat-NeRF [10]. However, our work is significantly different from these methods. Existing works are mainly dedicated to processing geomorphic images taken by geosynchronous satellites. The characteristics of these data are that the same location is photographed for a long time, describing the radiation field of the location that changes over time. The scene has a larger range and a longer shooting distance. The scene is more complex, including transient objects and Lambertian surfaces. We are committed to reconstructing satellite models through satellite images taken by satellites, mainly dealing with the characteristics of satellite images such as low texture, illumination changes and circular shooting trajectories.
Since real images are difficult to obtain and should not be made public, we designed a synthetic dataset to simulate real data based on the features mentioned above. It is worth noting that our camera on another satellite is fixed, and it takes pictures of the rotating satellite. It just looks like the satellite is not rotating and the camera is orbiting it. In fact, the synthetic data are still different from the real data. In the face of some other potential challenges, we do not think it is suitable to use NeRF-based methods to solve them. For example, in the face of low resolution, some super-resolution reconstruction methods [11] can be used, and in the face of image distortion caused by the camera, there are also some distortion correction methods [12].
Although the NeRF [3] can render realistic novel views, it is not practical enough for our purposes. When we want to synthesize a new perspective image of a captured satellite photographed by another satellite in space. We do not know the camera focal length that can be used in the algorithm because the satellite images undergo a series of post-processing. At the same time, the texture of the image is very poor, and thus, we cannot estimate it through a traditional method like SFM [1]. In addition, there are some small structures on satellites that cannot be reconstructed well by the NeRF [3]. Although the current State-of-the-Art (SOTA) method for reconstructing objects, MipNeRF [13], performs well on its own dataset, it cannot achieve good results on our low-texture datasets. The MipNeRF [13] replaces rays with cones, which allows it to obtain more accurate colors under certain conditions. However, in our dataset, the gray value of a pixel experiences interference from nearby pixels. Therefore, the color and structure of the image rendered by the MipNeRF [13] are not sufficiently accurate. All in all, it is still possible to improve the image quality. One can achieve a more detailed Figure 1; the satellite in the right figure is noticeably blurrier than that in the left one and has some structural defects. The NeRF-W [14] handles illumination changes between images by optimizing the input embedding and learning a shared appearance representation across the entire image set. However, it is more suitable for reconstructing scenes in the wild, mainly targeting illumination changes and transient objects in the scene.

Figure 1.
Illustration showing that the NeRF [3] and its variations are still lacking in terms of image quality, and that the reconstruction of some small structures is not good enough [13].
In this paper, we solve these problems by proposing STs-NeRF. We hope to use this algorithm to synthesize new perspective images of satellites photographed in space when only their relative rotation angles are known. In fact, since the satellite rotates at a constant speed under normal working conditions, we can obtain this information through the shooting time.
Based on the above analysis of existing methods and our needs, we chose to complete our task by improving the NeRF [3], since the MipNeRF’s main innovation, the view frustum, has no use for us. First, we calculated the internal and external parameters based on the relative rotation angle of the satellite and the shape of the image; the internal and external parameters have a decisive influence on the reconstruction results of the NeRF [3]. Then, we added a DE module to make the network more effective in learning the features of the inputted data. The biggest challenge with sparse input perspectives is the overfitting of the neural network from the input perspective. This results in the deformation of objects in new perspectives. In order to avoid this problem, we added some regularization layers to the network. We simultaneously input points and directions into LLNMLP, which could improve the reconstruction effect of some satellites and avoid missing parts.
We conducted a series of experiments on these data to evaluate the effectiveness of our algorithm. These experiments included hyperparameter experiments, ablation experiments, and comparison experiments, all of which showed that our STs-NeRF can achieve better reconstruction results on our dataset compared with existing methods like the NeRF [3], the MipNeRF [13], the NeuS [15] and the NeRF2Mesh [16]. We also tested our algorithm on a public dataset. Although our method only performed better in some scenes, it also shows that our NeRF can still obtain acceptable results on data with better texture.
2. Related Works
2.1. NeRF and NeRF Variants
The NeRF [3] is an advanced method for novel view synthesis. It learns the radiation field of the scene through a neural network and achieves stunning results. Therefore, a large number of works based on NeRF [3] have emerged in recent years.
Although the NeRF [3] provides a way to render realistic new perspective images, there is still huge room for improvement. It can be extended to other scenes, such as aliasing caused by different focal lengths, reconstructing shiny objects, etc. Many authors have carried out a lot of work in these aspects.
For example, Mip-NeRF, proposed by Barron, JT, and others [13], is based on the NeRF [3]. In order to handle input views with different resolutions, the view cone replaces rays, which, to a certain extent, solves the problem of different picture resolutions due to the varying distances between the camera and the scene. This caused an aliasing problem. They also introduced integrated position coding, which performs well at lower resolutions; their Mip-NeRF360 [17], based on the Mip-NeRF, proposes a method similar to Kalman filtering, which can provide highly complex boundary-less real-world scenes, generating realistic synthetic views and detailed depth maps.
Mildenhall, B et al. [18] proposed the RawNeRF, which directly trains the radiation field on the original image in a raw format, and can reconstruct the scene well on darkly illuminated and extremely noisy data sets.
Verbin, D et al. [19] solved the problem that the NeRF [3] cannot reconstruct smooth surfaces well by introducing the Ref-NeRF. The Ref-NeRF replaces the NeRF’s view-related outgoing radiation parameterization with a reflection radiation representation and uses a series of spatially varying scene properties to construct this function, significantly improving the realism and accuracy of specular reflections.
Martin, B et al. [14] proposed the NeRF-W, which uses the weight of multi-layer perceptrons to model the density and color of the scene as a function of three-dimensional coordinates, solving the problem of variable illumination or instantaneous occlusions and making NeRF adaptable to real-world environments.
NeRFactor, by Zhang et al. [20], enables the rendering of novel object views under arbitrary lighting and the editing of object material properties.
The SRes-NeRF, as proposed by Dai, SF et al. [21], introduces a representation method composed of a density voxel grid and enhanced MLP for complex view-related appearance and model acceleration, which can obtain more specular details and faster training speeds.
Hwang, I et al. [22] proposed the Ev-NeRF. The Ev-NeRF is not the assumed image of the original NeRF but the sensor movement’s accompanying event measurement. Utilizing a loss function that reflects the sensor measurement model, the Ev-NeRF creates a synthetic neural body that summarizes unstructured sparse data points captured in approximately 2–4 s. The generated neural volumes also generate new perspective intensity images with reasonable depth estimation, which can serve as high-quality inputs for a variety of vision-based tasks. The results show that the Ev-NeRF achieves highly competitive performance in intensity image reconstruction under the conditions of extreme noise and high dynamic range imaging.
Some researchers have reduced the number of input views required by the NeRF [3]. For example, the PixelNeRF, as proposed by Yu, A et al. [23], introduces a CNN-based encoder to learn scene priors. With a limited number of input images (at least one is required), this method performed well.
The surface quality reconstructed by the NeRF [3] is not good. NeuS, as proposed by Wang, P et al. [15], solves this problem. It is a new neural surface reconstruction method based on the NeRF. They represent the surface as a signed distance function, so that there is no accurate surface reconstruction that can also be achieved under mask supervision.
The training and rendering of the NeRF [3] are very time-consuming, and there has also been some work focusing on acceleration, such as Chen and AP [24]’s tensoRF. Their radiation field is modeled as a 4D tensor, and CP and VM decomposition are introduced to obtain better rendering effects. Training time and model size are reduced. The FastNeRF, as proposed by Garbin, SJ et al. [25], is 3000 times faster than a NeRF [3]. Instant-NGP, as proposed by Thomas M et al. [26], uses a multi-resolution hash encoding scheme, which greatly speeds up NeRF [3] rendering.
The NeRF [3] can only train the radiation field for a set of data and lacks generalization. The MVSNeRF, as proposed by Chen, AP and others [27], solves this problem. Their algorithm can synthesize new views across scenes with only three input images.
The NoPe-NeRF proposed by Wenjing Bian et al. [28] can train the neural radiation field in advance without an accurate pose, reducing the NeRF’s dependence on accurate pose input. The pose obtained through software such as ColMap is used a priori and can be optimized to adapt to more challenging camera trajectories.
The scene radiation field obtained by the NeRF [3] is difficult to edit, so there has been some work on improving editability, such as the work of Liu, S et al. [29], in which they proposed an EC-NeRF. They proposed a conditional radiation field that can convert rough Broadcast 2D graffiti into 3D space. Yuan, YJ et al. [30] proposed a method that establishes correspondence between the extracted explicit grid representation and the implicit neural representation of the target scene. This allows users to perform controllable shape deformations on an implicit scene representation and synthesizes new view images of the edited scene without retraining the network.
The Control-NeRF was proposed by Lazova, V et al. [31]. To explore controllable scene representations for novel view synthesis, the model combines learned scene-specific 3D feature volumes with a general NeRF [3] rendering network. By simply optimizing the three-dimensional feature quantities of a specific scene while keeping the parameters of the rendering network fixed, it can be generalized to new scenes.
Researchers have also chosen to focus on converting the radiation field into a point cloud to represent the scene. For example, the Point-NeRF proposed by Xu, QG et al. [32] uses neural three-dimensional point clouds and related neural features to simulate the radiation field. In ray-based rendering, points can be efficiently rendered by aggregating neural point features near the scene surface. nerf2mesh, as proposed by Tang, JX and others [16], is also a method that uses neural radiation fields to obtain point clouds.
There have also been some works on stylization, such as Zhang, K et al. [33]’s ARF, which can transfer the artistic features of any picture style to three-dimensional scenes.
There are other works based on the NeRF [3], such as that of Sünderhauf, N et al. [34], which reduce the uncertainty of NeRFs based on density. Liu, JL et al. [35]. proposed NeRF-Loc, a new visual relocalization method based on directly matching implicit 3D descriptors and 2D images. The X-NeRF proposed by Zhu, HY et al. [36] can train a method that can represent multiple scenes and 360° views and models with insufficient RGB-D images. The VT-NeRF prposed by Hao, FY et al. [37] can learn the neural radiation field of the dynamic human body. The CM-NeRF method proposed by Kim, H et al. [38] is more effective in real-life scenarios involving challenging and complex camera motions. Qiu, JX et al. [39]’s RD-NeRF is more suitable for dense view synthesis with free movement in indoor scenes, while Klenk, S et al. [40]’s E-NeRF is the first to estimate, in NeRF form, fast-moving camera methods for volumetric scene representation.
The following figure, Figure 2, shows some typical implicit expression methods in chronological order. In fact, after NeRF was proposed in 2020 and due to the realistic images it synthesized, it aroused people’s interest and a large number of works based on NeRFs emerged.
Figure 2.
Some typical algorithms in chronological order.
2.2. Remote Sensing Novel View Synthesis
As the most advanced method for new view synthesis, there has also been some work on the NeRF in the field of remote sensing, as can be seen with RS-NeRF [41], which proposes a new method of satellite-to-Earth photogrammetry that can quickly generate novel views and provide accurate altitude predictions. NeRF-HRRS [42] proposes an attention mechanism and frequency-weighted coding strategy, which can perform new view synthesis on high-resolution remote sensing images with limited viewing angles and scarcity.
3. Methodology
3.1. Preliminaries on NeRF
Our method is based on the NeRF [3]. The NeRF [3] uses a neural network to describe an object. By training on a dataset of input views and corresponding poses, the neural radiation field of the object can be obtained. Then, according to the poses of the new perspective through volume rendering [9] technology, new images are obtained. Specifically, NeRFs work by obtaining realistic views from new perspectives that can be divided into two parts:
(1) Obtaining an object’s neural radiation field.
(2) Using the radiation field to obtain pictures from new perspectives through volume rendering.
In the first stage, the spatial points sampled, according to the poses and the observation angle , are inputted into the MLP network to learn the neural radiation field of the object,
and obtain the body density and the color c of the object. In the second stage, the author obtains the pictures from the new perspective through volume rendering.
where , and calculating the probability that the ray from to does not collide with any sampling point.
3.2. Overall Architecture
The NeRF-like algorithm relies on accurate internal and external parameters, but our conditions are limited. We can only calculate an alternative parameter based on the existing data and can only generate the spatial coordinates and observation direction of the sampling point based on these parameters. This is at least better than using the SFM class parameters the method generates. The coordinates of these sampling points and the vector of the observation direction are encoded and input into the encoding module. The output of the encoding module is superimposed onto the original data and input into our modified MLP network to obtain the volume density and color. In fact, our process is similar to a NeRF. The basic process of our algorithm is as follows: segment the image -> process internal and external parameters -> encode -> input data into MLP for training.
3.3. Our NeRF
3.3.1. Segment the Images
Because the background is black, we use the threshold method to segment. We count the point set with a pixel gray value greater than 0 on the ith picture and obtain the maximum and minimum values of the coordinates, , so , ,
where h is the height and width of the image. The reason why we do this is that a large number of black areas do not need to be learned, which can reduce the training time.
3.3.2. Process Internal and External Parameters
In our dataset, the space target rotates around the x-axis. This is actually to simulate the situation where the satellite and the satellite-borne camera are relatively stationary and the satellite rotates. The rotation axis of the satellite is assumed to be the x-axis. We also take into account the different lighting conditions of each image. Please see Figure 3 below for more details.

Figure 3.
The six images from our dataset to illustrate how satellites are photographed.
The height and width of the picture are h, f is the focal length, and are the coordinates of the center of the satellite in the image coordinate system. Their units are in pixels, so the internal parameter is
The above internal parameter is not suitable for the NeRF [3] to reconstruct spatial targets in our dataset. In order to concentrate the sampling points within a certain area, we change the internal parameter to
Since we cannot obtain the focal length in the actual project, here . In the NeRF [3], the focal length f actually affects the relative distance between the object and the camera, which actually affects the null visibility distribution of the sampling points inputted to the network. This may affect the reconstruction effect to a certain extent. Here, is just a way to determine the internal parameters of the camera. Readers can learn more in Section 3.3.3 and Figure 4.
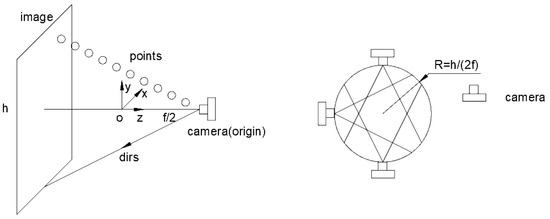
Figure 4.
Some details of generating sampling points. In the left figure, point o is the center of the object. In the right figure, the sector formed by the arc and the two line segments starting from the camera is the range of sampling points generated from this perspective.
As for the external parameters, we assume that the rotation angle of the space target around the x-axis is . We also assume that the distance from the camera to the object is , so that the trajectory of the camera is in a circle with the object as the center and with a radius of . Readers can learn more in Section 3.3.3 and Figure 4. The pose is
3.3.3. Generate Rays and Samples and Encode
The coordinates of the sampling points and dirs are
where are the coordinates of the camera’s center, is the ray direction, and t is a scaling factor.
where N represents the number of sampling points on a ray, while is used to describe the range of the sampling points on the ray.
where are grid points uniformly taken within the range on the plane. Readers can find further details in Figure 4. From the above content, we know that the value of f is not important. What is important is that . The value of f only affects the spatial range of the sampling points. It may have some impact on the final algorithm effect, but we will not discuss this issue in this study.
Since the matrix dimension of sampling points is low and is quite different from the number of channels in our network, we encoded the matrix to increase the dimension. The encoder is
where L is used to control the data dimension obtained after encoding. From encoding Formula (7), we can see that this encoding method is continuous, which means that the change in the volume density of the object is a gradual process. However, this is based on the premise that the image has good geometric consistency. When objects are occluded, the effect will be lacking. Thus, the and encoded by will be inputted into the DE module for re-coding. Since the radiation field is only a physical explanation, what the network actually learns is the relationship between the encoded sampling point coordinates, observation angle, and color. Therefore, when this relationship does not correspond accurately, the NeRF [3] cannot achieve good rendering results. In order to improve this shortcoming, we designed a dynamic encoding module, which consists of a linear layer, dropout layer, and maxpool layer. It adjusts the encoded inputs in real time and randomly zeroes the neurons to improve the network’s generalizability. In the Dropout layer, a probability value p is usually used to represent the probability of each neuron being retained. Assume that the input of the neuron is x. After passing through a Dropout layer, the calculation formula of the output y is , where r is a Bernoulli random variable with a value of 1. The probability is p, and the probability of the value 0 is .
As for the MaxPool layer, assuming that the input sequence is and the pooling window size is k, then the output , where i represents the index of the output position. Readers can see the structure of the module in Figure 5.

Figure 5.
The structure of the dynamic encoder.
Fourier coding increases the dimensionality of the inputs, but it does not enable the network to achieve the best learning effect. So, we designed this module to re-encode the inputs in order to further improve the network’s performance. The DE module actually blurs the difference in encoded coordinates through the Dropout layer and then extracts the blurred encoded features through MaxPool, making use of some additional points to improve better learning results. However, when the perspective consistency between this kind of structural knowledge and the image is not good, it will actually reduce the learning effect when the image has good perspective consistency.
3.3.4. Network Structure
We also use volume rendering technology to synthesize novel views but with some modifications. The color is as follows:
where , calculating the probability that the ray from to does not collide with any sampling points. We simultaneously input encoded and into the network to avoid the insufficient results caused by different camera shooting angles. We believe that the probability of the existence of a sampling point is a function related to the viewing direction; a point shows different opacity in different viewing directions. This approach is necessary when there is planar symmetry in the input perspective. Taking photos from the upper and lower plane symmetrical positions of the satellite, it is obvious that the difference in the images is large. However, if the opacity of the sampling points is same but the directions are opposite, it will obviously affect the learning effect. At the same time, pure MLP has a better learning effect for centrally symmetric objects. Our satellites are basically planar symmetrical, so this change improves the image quality of novel view synthesis for some satellites.
We added Layer Normalization (LN) layers to the network. An LN layer is a common hidden layer; the reader can get more details from the Formula (9). Let be the vector representation of an input of size H to normalization layers. LayerNorm re-centers and re-scales input as
where is the output of a LayerNorm layer, and ⊙ is a dot production operation. and are the mean and standard deviation of input. Bias and gain are parameters with the same dimension H.
Due to the difference in inputs during training and rendering, the rendering effect is poor, which can actually be understood as the network’s overfitting of the training data. We normalize the inputs of each layer through the LN layer, which reduces the sensitivity of the model to overfitting, thereby improving its robustness. As the number of network layers increases, the output of each layer will deviate more and more from the inputs. However, what is meaningful to network learning is the relationship between the data, so normalizing them can effectively improve the quality of the network’s rendered images.
The LN layer adjusts the input and variance. By subtracting the mean, the tensors are centered, eliminating the overall bias in the data, so that they are consistent on the mean. Then, they are divided by the standard deviation to unify the scale of the data, so that the fluctuation range of the data are relatively fixed. In this way, the data are transformed into a relatively standard distribution state with similar characteristics. Under this processing, it becomes more comparable and standardized, thereby the instability factors caused by excessive differences in data distribution can be reduced. This method is commonly used and can improve network performance in many fields. Readers can find more details about the network structure in Figure 6.

Figure 6.
The structure of the neural network.
4. Experiments and Results
In this section, we first present the experimental details of the method and introduce the dataset and the common evaluation metrics. Then, experiments are used to evaluate our algorithm, including ablation studies, hyperparameter results, quantitative and qualitative comparisions, and so on. The experimental results strongly illustrate that our method outperforms existing methods.
4.1. Experimental Details
We implement our model on the basis of the NeRF [3] and use a similar MLP architecture (ReLU activation). Our NeRF is trained on a single Nvidia 3090 GPU with the RMSProp optimizer starting with a learning rate of . The batch size is 1024 rays and each ray is discretized into 8192 uniformly distributed 3D points. We train the module with iterations of 17 epochs. In the experiment on our dataset, we set . The training loss is Mean Square Error (MSE):
where I is the novel view and G is the ground truth. We use common quantitative metrics to evaluate the quality of the rendered novel views, Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM), and Learned Perceptual Image Patch Similarity (LPIPS) in order to evaluate image quality.
4.2. Datasets and Metrics
In this section, we introduce the two datasets that we used to test our algorithms, including the public dataset Blender [3] and the synthetic dataset we created, Ciomp_SAT_89. This set is different from the Blender dataset [3], readers can get more details in Table 1. Additionally, we used three quantitative metrics to evaluate the quality of the rendered novel views: PSNR, SSIM, and LPIPS.

Table 1.
The table is used to show the difference between our data and previous data.
4.2.1. Datasets
Real Synthetic Dataset: Although our NeRF is more suitable for our dataset, we also tested it on Blender’s real synthetic dataet and compared it with previous algorithms in order to prove that our algorithm also works well on public datasets. There are 100 images in the training set and 100 images in the test set, the resolution of which is . The images of the eight objects in the Blender dataset are not actually of the same type, so our method only performed better on some of them.
Ciomp_SAT_89: We designed a synthetic dataset to simulate real-world conditions. First, we found eight satellite models so that the images have the basic structure of space targets. The space target is located in the center of the image, which is an ideal situation for satellite images. The texture of the space target is poor, which actually takes into account the poor quality of the images due to the long shooting distance. The illumination between the images of the space target is different, which is to simulate the different lighting conditions when taking images of the space target. We use a fixed camera to photograph rotating space targets, which is mainly to consider the rotation of the space target during shooting.
In this dataset, we have a total of eight satellites, the textures and shapes of which are different. We took orbital shots of the satellites and captured 89 images. These were photographed from different angles to ensure that different situations can be simulated. The size of the image depends on the size of the satellite.
In the experiment, starting from the first image, every eighth image was selected for the test set. There were 12 images in total and the remaining 77 images were used as the training set. This dataset was used to test the ability of our NeRF to synthesize novel views when the input views are rich. With this dataset, our NeRF achieved good reconstruction results. The rendered images are relatively clear, and the structure of the satellite is also complete.
4.2.2. Quality Assessment Metrics
Novel view synthesis by the NeRF and variants thereof commonly use visual quality assessment metrics for benchmarks, such as the Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM), and Learned Perceptual Image Patch Similarity (LPIPS). The PSNR is a no-reference quality assessment metric to evaluate image quality. The PSNR, between novel view, I, and ground truth, G, is given by
where MAX(I) is the maximum possible pixel value of image I, and MSE(I, G) is the mean squared error of image I and image G.
SSIM is a metric commonly used for measuring the structural similarity between two images. It takes into account the perception of local structural changes in an image and quantifies its properties in terms of luminance, contrast, and structure. The SSIM values range from 0 to 1, with larger values indicating greater similarity between the images. If two images are identical, the SSIM value is 1. When calculating SSIM for a novel view image (I) and a ground truth image (G), the formula is as follows:
where and are the means of I and G to estimate luminance, and the contrast is estimated by variance and . Moreover, is the covariance of I and G used to estimate the structural similarity. and are two constants used to maintain stability, where and . L is the dynamic range of pixels, and by the origin work.
LPIPS is a full reference quality assessment metric which uses learned neural network features. LPIPS is given by a weighted pixel-wise MSE of feature maps over multiple layers
where and are the features of novel views and the ground truth at pixel width w, height h, and layer l. and are the height and width of the feature maps. The original LPIPS used several networks such as VGG, AlexNet, etc., as the feature extraction backbone.
4.3. Ablation Studies
In this section, we tested all aspects of our algorithm in the Ciomp_SAT_89, including the effect of our improvements and the impact of hyperparameters. Due to the different shapes and shooting angles of each satellite, the effect of each change and hyperparameter is actually different.
4.3.1. Effect of Improvements
Our improvements to the algorithm are mainly the dynamic encoder (de) and layer-by-layer normalization (lln). The original intention of these two modules was to improve the generalization of the model. We simultaneously input points and dirs into the network (pd). Through these experiments, we found that they have different performances with different data. Readers can find more details in Table 2. The subscripts in the lower right corner represent the changes we made based on the NeRF [3]. Their specific meanings can be found above. We used this pyramid-shaped experiment to illustrate the impact of each of our changes on the final effect.

Table 2.
Evaluation on the Ciomp_SAT_89 dataset.
From Table 2, we can know the impact of each improvement on the performance of the algorithm. Layer normalization is used to avoid deviations during gradient propagation based on the NeRF [3], it improves PSNR by 4.7%. In some cases, if the network is not deep, this deviation may not need to be considered. However, there are some relatively small parts on the satellite that the original NeRF cannot describe. This can be seen in Figure 7.

Figure 7.
It can be seen from this perspective that some small structures were not reconstructed until was added to the network [3].
We believe that the dynamic encoder can compensate for the lack of level and consistency from the input perspective. When some structures are not represented in enough images, the module can use sampling points at other positions to compensate for the structure, so that the object is at least complete in the image. This only provides a significant improvement for the PSNR of three satellites; the other five satellites see a smaller improvement. In fact, due to random zeroing, the results may be somewhat uncertain.
As for , although it can only improve the reconstruction quality of some satellites in terms of evaluation indicators, it will actually bring improvements visible to the naked eye. When the satellite’s solar panels are turned to a certain angle, they will disappear or break. According to the original network structure, the opacity of the sampling point is only related to its coordinates, which means that the opacity is the same no matter which direction it is viewed from. However, when there are plane symmetrical perspectives in the training set, because their viewing directions are opposite but the color values are very close, the final value learned by the network will only be close to zero. We believe that the opacity of the sampling point is related to both the coordinates and the viewing direction, thus avoiding the above problem. Of course, this also reduces the amount of parameters related to coordinates, resulting in a decrease in rendering effects. Readers can find more details in Figure 8.

Figure 8.
When inputting points and dirs into the network at the same time for novel view rendering, we can see that the images in the middle are missing; however, in Figure (e), they are complete.
The achieved improvement in SSIM is very small, only about 3%. In particular, and actually have little impact on SSIM, but at least they do not reduce SSIM. reduce LPIPS, but and both increase LPIPS. Overall, the improvements we have made to the NeRF [3], at least in the reconstruction of some satellites, can improve the learning effect of the network. The loss function we used is MSE, which is directly related to PSNR, so there was a significant improvement. Meanwhile, SSIM relies more on the volume rendering formula, so the impact is not significant at the beginning. However, when we input points and dirs together into the network, SSIM will drop slightly. As for LPIPS, we believe that the network structure and volume rendering formula will have an impact on this. When we simultaneously add a Dropout layer to the network and input points and dirs into the network, LPIPS will increase.
4.3.2. Results of Hyperparameters
We conducted experiments on two hyperparameters, including the width of the network and the scale of Dropout. The width of the network affects the number of network parameters. When the data are not elegant and accurate, they are very sensitive to the number of network parameters. The same is true for the proportion of the Dropout layer. After several experiments, we found that the final reconstruction effect had a certain mathematical relationship with the two hyperparameters, which we fitted. Readers can see Figure 9 and Figure 10 for more details. From Figure 9, we know that, when the input perspectives are rich enough, the novel view effect is basically positively related to the number of network parameters. However, when the number of channels exceeds a certain fixed value, the curve becomes flat and the improvement in rendering effect is lessened. From the above Figure 10, we know that when the input perspective is rich enough, the Dropout on a small part of the input can slightly improve the reconstruction effect. This ratio is actually somewhat accidental and will show different effects on different satellites.
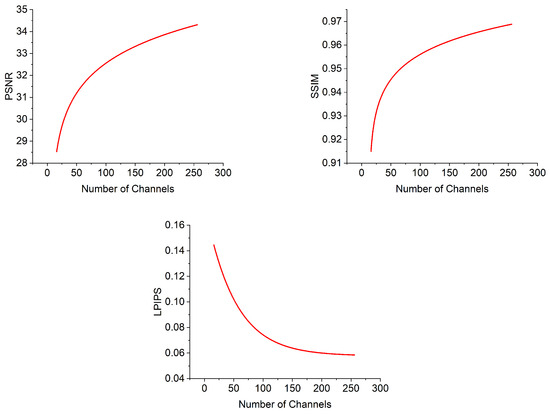
Figure 9.
Effect of channel number on reconstruction effect.
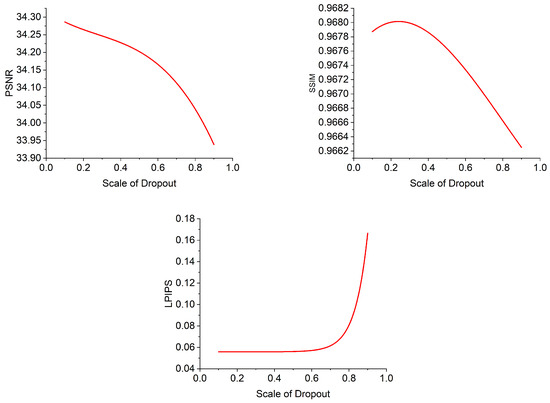
Figure 10.
Effect of scale of dropout on reconstruction effect.
4.4. Comparisons with the State-of-the-Art (SOTA) Methods
In this section, we compare our NeRF with existing algorithms on public and homemade datasets. Our experiments showed that, in certain scenarios with public datasets, our NeRF can achieve better reconstruction results. On our autonomous dataset, our NeRF is the existing SOTA method.
Evaluation of the Blender Dataset: Table 3 shows a comparison between ours and some existing methods with the Blender Dataset. Although our method is not designed for these kinds of data, we can still reconstruct good results. Our novel view rendering of the ship and drums actually looks better. To a certain extent, our NeRF can alleviate the situation where the correspondence between the pose and color is inaccurate. However, when this correspondence is more accurate, the image displays diffuse color, less reflection, opacity, and is unobstructed. In this case, the reconstruction effect is reduced. This is a necessary trade-off, which is why our NeRF is worse than existing methods in some contexts. This also shows that the performance of our NeRF in data with better texture is relatively ordinary.

Table 3.
Evaluation on the Blender dataset.
Evaluation on our Dataset: This dataset cna be used to test the reconstruction effect of our NeRF when the input views are rich. Our experiments showed that our NeRF can reconstruct good, new perspective images of spatial objects in this case. We tested SOTA methods such as the MipNeRF [13], the NeuS [15] and the NeRF2Mesh [16]. The comparison results with the NeRF [3] and MipNeRF [13], etc., can be seen in Table 4 and Figure 11. We can see that the NeRF [3] only presents the problem of missing or blurred structures at certain angles. For most images, there is not much visual difference with the images rendered by our NeRF. As for the MipNeRF [13], there is a clear change in color, some small holes in the structure are filled in, and the edges become blurred. The limitation of the frustum application designed with the MipNeRF [13] lies in the texture of the image. When the texture of the image is poor, it cannot correctly judge the color weights of adjacent pixels, resulting in color inaccuracies. This is also the reason that this algorithm fills any small holes in the object structure. The images rendered by NeuS [15] look of good quality, with no obvious flaws in color or structure. The effect of NeRF2Mesh [16] is worse, which may be due to the presence of planar symmetrical perspectives in the training set.

Table 4.
Comparison between NeRF [3], MipNeRF [13], NeuS [15] and NeRF2Mesh [16] on the Ciomp_SAT_89 dataset.
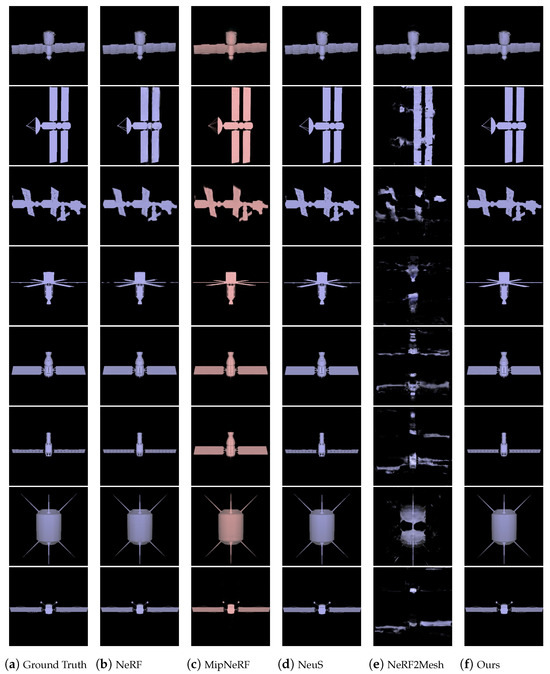
Figure 11.
Comparison between NeRF [3], MipNeRF [13], NeuS [15] and NeRF2Mesh [16] on the Ciomp_SAT_89 dataset.
5. Conclusions
Based on the need of our project to obtain a satellite model, we chose to use implicit expressions to describe the satellite and use the quality of the new perspective image rendered by the model to judge the quality of the model. We selected several disadvantages that may be encountered in practice and made a synthetic dataset based on them. We also created several improvements to obtain better images with this dataset. We conducted multiple sets of experiments on the number of parameter channels and the scale of dropout in order to choose more appropriate parameters. We tested the model both with a public dataset and with our own dataset, and the STs-NeRF achieved the best rendering effect with the latter.
Author Contributions
Conceptualization, K.M.; methodology, K.M.; validation, K.M. and P.L.; formal analysis, K.M.; investigation, K.M. and P.L.; resources, P.L.; data curation, K.M.; writing—original draft preparation, K.M.; writing—review and editing, K.M., H.S., J.T. and P.L.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jilin Provincial Science and Technology Development Program Key R&D Project, grant number No. 20220201148GX, and the Changchun Science and Technology Development Program Projects, grant number Nos. 23JQ01, 23YQ14.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Schonberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 4104–4113. [Google Scholar]
- Moulon, P.; Monasse, P.; Perrot, R.; Marlet, R. OpenMVG: Open Multiple View Geometry. In Proceedings of the International Workshop on Reproducible Research in Pattern Recognition, Cancun, Mexico, 4 December 2016; pp. 60–74. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. In Proceedings of the European Conference on Computer Vision, Online, 23–28 August 2020. [Google Scholar]
- Yao, Y.; Luo, Z.X.; Li, S.W.; Fang, T.; Quan, L. MVSNet: Depth Inference for Unstructured Multi-view Stereo. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 785–801. [Google Scholar]
- Yu, Z.H.; Gao, S.H. Fast-MVSNet: Sparse-to-Dense Multi-View Stereo with Learned Propagation and Gauss–Newton Refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1946–1955. [Google Scholar]
- Yg, J.Y.; Alvarez, J.M.; Liu, M.M. Self-supervised Learning of Depth Inference for Multi-view Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 19–25 June 2021; pp. 7522–7530. [Google Scholar]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Lone Beach, CA, USA, 16–20 June 2019; pp. 165–174. [Google Scholar]
- Mescheder, L.; Oechsle, M.; Niemeyer, M.; Nowozin, S.; Geiger, A. Occupancy Networks: Learning 3D Reconstruction in Function Space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Lone Beach, CA, USA, 16–20 June 2019; pp. 4455–4465. [Google Scholar]
- Kajiya, J.T.; Von Herzen, B.P. Ray tracing volume densities. ACM SIGGRAPH Comput. Graph. 1984, 18, 165–174. [Google Scholar] [CrossRef]
- Mari, R.; Facciolo, G.; Ehret, T. Sat-NeRF: Learning multi-view satellite photogrammetry with transient objects and shadow modeling using rpc cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 1311–1321. [Google Scholar]
- Hsu, C.-H.; Lin, C.-H. Dual Reconstruction with Densely Connected Residual Network for Single Image Super-Resolution. In Proceedings of the International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Li, X.; Zhang, B.; Sander, P.V.; Liao, J. Blind Geometric Distortion Correction on Images Through Deep Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Lone Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Barron, J.T.; Mildenhall, B.; Tancik, M.; Hedman, P.; Martin-Brualla, R.; Srinivasan, P.P. Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields. In Proceedings of the IEEE/CVF Conference on on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 5835–5844. [Google Scholar]
- Martin-Brualla, R.; Radwan, N.; Sajjadi, M.S.M.; Barron, J.T.; Dosovitskiy, A.; Duckworth, D. NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 19–25 June 2021; pp. 3206–7215. [Google Scholar]
- Wang, P.; Liu, L.J.; Liu, Y.; Theobalt, C.; Komura, T.; Wang, W.P. NeuS: Learning Neural Implicit Surfaces by Volume Rendering for Multi-view Reconstruction. In Proceedings of the Neural Information Processing Systems, Electr Network, Online, 6–14 December 2021. [Google Scholar]
- Tang, J.; Zhou, H.; Chen, X.; Hu, T.; Ding, E.; Wang, J.; Zeng, G. Delicate Textured Mesh Recovery from NeRF via Adaptive Surface Refinement. arXiv 2022, arXiv:2303.02091. [Google Scholar]
- Barron, J.T.; Mildenhall, B.; Verbin, D.; Srinivasan, P.P.; Hedman, P. Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 5460–5469. [Google Scholar]
- Mildenhall, B.; Hedman, P.; Martin-Brualla, R.; Srinivasan, P.P.; Barron, J.T. NeRF in the Dark: High Dynamic Range View Synthesis from Noisy Raw Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 16169–16178. [Google Scholar]
- Verbin, D.; Hedman, P.; Mildenhall, B.; Zickler, T.; Barron, J.T.; Srinivasan, P.P. Ref-NeRF: Structured View-Dependent Appearance for Neural Radiance Fields. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 5481–5490. [Google Scholar]
- Zhang, X.M.; Srinivasan, P.P.; Deng, B.Y.; Debevec, P.; Freeman, W.T.; Barron, J.T. NeRFactor: Neural Factorization of Shape and Reflectance Under an Unknown Illumination. Acm Trans. Graph. 2021, 40, 1–18. [Google Scholar] [CrossRef]
- Dai, S.; Cao, Y.; Duan, P.; Chen, X. SRes-NeRF: Improved Neural Radiance Fields for Realism and Accuracy of Specular Reflections. In Proceedings of the International Conference on MultiMedia Modeling, Bergen, Norway, 9–12 January 2023; pp. 306–317. [Google Scholar]
- Hwang, I.; Kim, J.; Kim, Y.M. Ev-NeRF: Event Based Neural Radiance Field. In Proceedings of the Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–7 January 2023; pp. 837–847. [Google Scholar]
- Yu, A.; Ye, V.; Tancik, M.; Kanazawa, A. pixelNeRF: Neural Radiance Fields from One or Few Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 19–25 June 2021; pp. 4576–4585. [Google Scholar]
- Chen, A.P.; Xu, Z.X.; Geiger, A.; Yu, J.Y.; Su, H. TensoRF: Tensorial Radiance Fields. In Proceedings of the European Conference on Computer Vision, Tel-Aviv, Israel, 23–24 October 2022; pp. 333–350. [Google Scholar]
- Garbin, S.J.; Kowalski, M.; Johnson, M.; Shotton, J.; Valentin, J. FastNeRF: High-Fidelity Neural Rendering at 200FPS. In Proceedings of the IEEE/CVF Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 14326–14335. [Google Scholar]
- Muller, T.; Evans, A.; Schied, C.; Keller, A. Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. Acm Trans. Graph. 2022, 41, 1–15. [Google Scholar] [CrossRef]
- Chen, A.P.; Xu, Z.X.; Zhao, F.Q.; Zhang, X.S.; Xiang, F.B.; Yu, J.Y.; Su, H. MVSNeRF: Fast Generalizable Radiance Field Reconstruction from Multi-View Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 14104–14113. [Google Scholar]
- Bian, W.; Wang, Z.; Li, K.; Bian, J. Victor Adrian Prisacariu NoPe-NeRF: Optimising Neural Radiance Field with No Pose Prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 5428–5438. [Google Scholar]
- Liu, S.; Zhang, X.M.; Zhang, Z.T.; Zhang, R.; Zhu, J.Y.; Russell, B. Editing Conditional Radiance Fields. In Proceedings of the IEEE/CVF Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 5753–5763. [Google Scholar]
- Yuan, Y.J.; Sun, Y.T.; Lai, Y.K.; Ma, Y.W.; Jia, R.F.; Gao, L. NeRF-Editing: Geometry Editing of Neural Radiance Fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 18332–18343. [Google Scholar]
- Lazova, V.; Guzov, V.; Olszewski, K.; Tulyakov, S.; Pons-Moll, G. Control-NeRF: Editable Feature Volumes for Scene Rendering and Manipulation. In Proceedings of the Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–7 January 2023; pp. 4329–4339. [Google Scholar]
- Xu, Q.G.; Xu, Z.X.; Philip, J.; Bi, S.; Shu, Z.X.; Sunkavalli, K.; Neumann, U. Point-NeRF: Point-based Neural Radiance Fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 5428–5438. [Google Scholar]
- Zhang, K.; Kolkin, N.; Bi, S.; Luan, F.J.; Xu, Z.X.; Shechtman, E.; Snavely, N. ARF: Artistic Radiance Fields. In Proceedings of the European Conference on Computer Vision, Tel-Aviv, Israel, 23–24 October 2022; pp. 717–733. [Google Scholar]
- Sunderhauf, N.; Abou-Chakra, J.; Miller, D. Density-aware NeRF Ensembles: Quantifying Predictive Uncertainty in Neural Radiance Fields. In Proceedings of the International Conference on Robotics and Automation, London, UK, 29 May–2 June 2023; pp. 9370–9376. [Google Scholar]
- Liu, J.; Nie, Q.; Liu, Y.; Wang, C. NeRF-Loc: Visual Localization with Conditional Neural Radiance Field. In Proceedings of the International Conference on Robotics and Automation, London, UK, 29 May–2 June 2023; pp. 9385–9392. [Google Scholar]
- Zhu, H. Density-aware X-NeRF: Explicit Neural Radiance Field for Multi-Scene 360. Insufficient RGB-D Views. In Proceedings of the Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–7 January 2023; pp. 5755–5764. [Google Scholar]
- Hao, F.; Shang, X.; Li, W.; Zhang, L.; Lu, B. VT-NeRF: Neural radiance field with a vertex-texture latent code for high-fidelity dynamic human-body rendering. IET Comput. Vis. 2023; early view. [Google Scholar] [CrossRef]
- Kim, H.; Lee, D.; Kang, S.; Kim, P. Complex-Motion NeRF: Joint Reconstruction and Pose Optimization with Motion and Depth Priors. IEEE Access 2023, 11, 97425–97434. [Google Scholar] [CrossRef]
- Qiu, J.; Zhu, Y.; Jiang, P.-T.; Cheng, M.-M.; Ren, B. RDNeRF: Relative depth guided NeRF for dense free view synthesis. Vis. Comput. 2023, 40, 1485–1497. [Google Scholar] [CrossRef]
- Klenk, S.; Koestler, L.; Scaramuzza, D.; Cremers, D. E-NeRF: Neural Radiance Fields from a Moving Event Camera. IEEE Robot. Autom. Lett. 2023, 8, 1587–1594. [Google Scholar] [CrossRef]
- Xie, S.L.; Zhang, L.; Jeon, G.; Yang, X.M. Remote Sensing Neural Radiance Fields for Multi-View Satellite Photogrammetry. Remote Sens. 2023, 15, 3808. [Google Scholar] [CrossRef]
- Lv, J.W.; Guo, J.Y.; Zhang, Y.T.; Zhao, X.; Lei, B. Neural Radiance Fields for High-Resolution Remote Sensing Novel View Synthesis. Remote Sens. 2023, 15, 3920. [Google Scholar] [CrossRef]
- Zhang, K.; Luan, F.; Wang, Q.; Bala, K.; Snavely, N. PhySG: Inverse rendering with spherical gaussians for physics-based material editing and relighting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Online, 19–25 June 2021. [Google Scholar]
- Yariv, L.; Gu, J.; Kasten, Y.; Lipman, Y. Volume rendering of neural implicit surfaces. In Proceedings of the Thirty-fifth Annual Conference on Neural Information Processing Systems, Online, 6–14 December 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
