Estimation of Anthocyanins in Winter Wheat Based on Band Screening Method and Genetic Algorithm Optimization Models
Abstract
1. Introduction
2. Materials and Methods
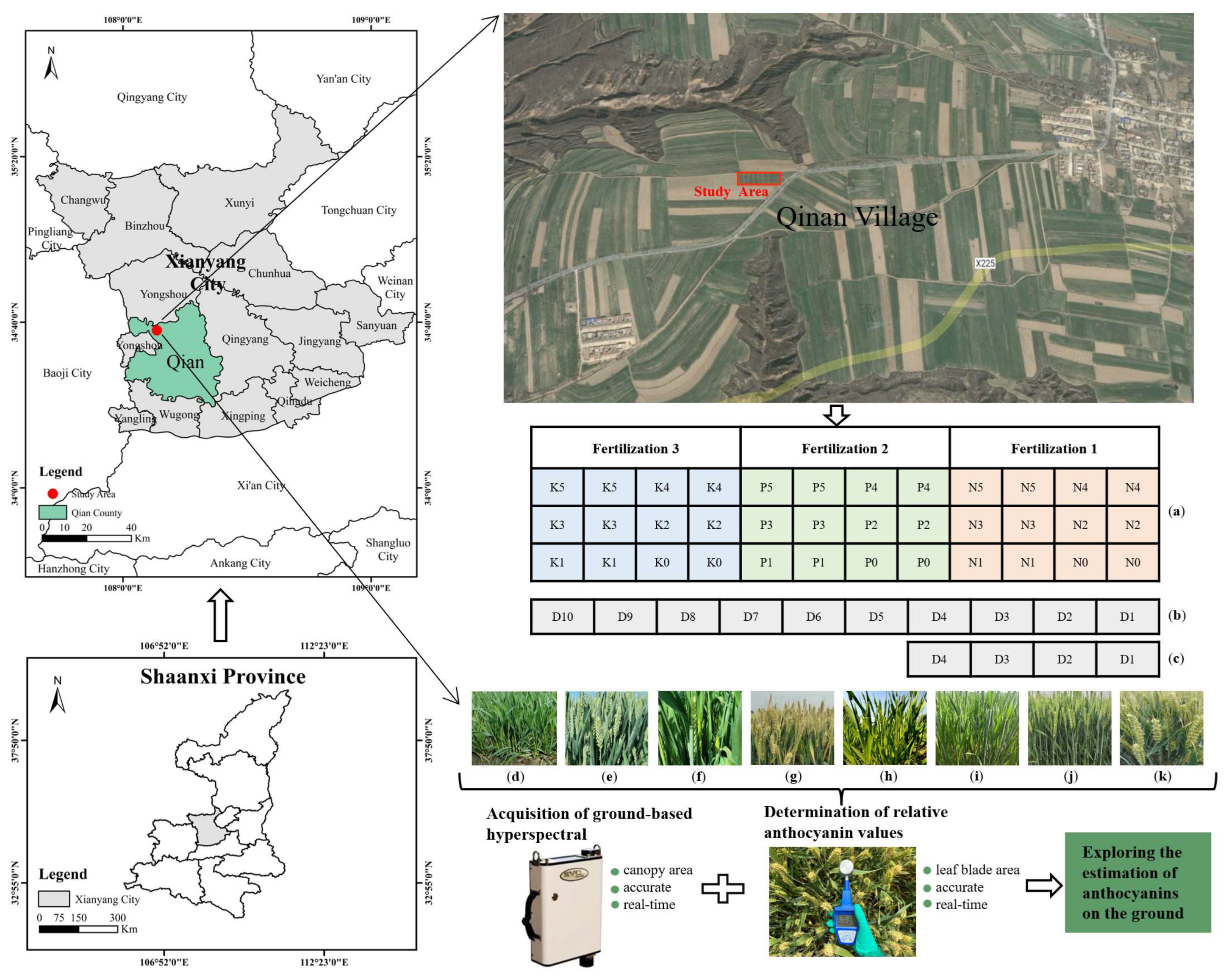
2.1. Overview of the Experimental Design
2.2. Data Acquisition
2.2.1. Hyperspectral Data Acquisition and Preprocessing
2.2.2. Determination of Relative Anthocyanin Values
2.3. Methods and Models
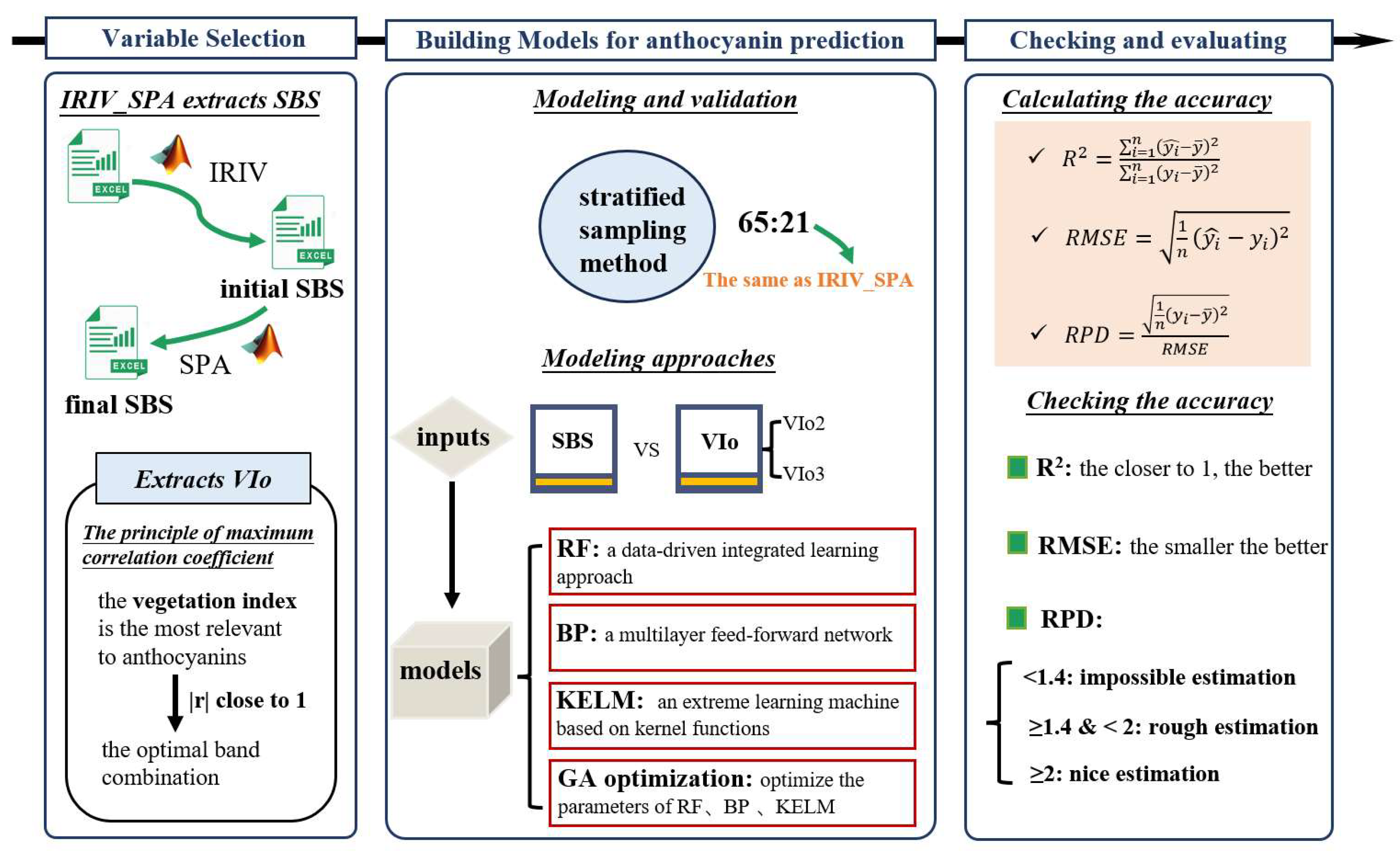
2.3.1. Variable Selection Method
2.3.2. Modeling and Verification
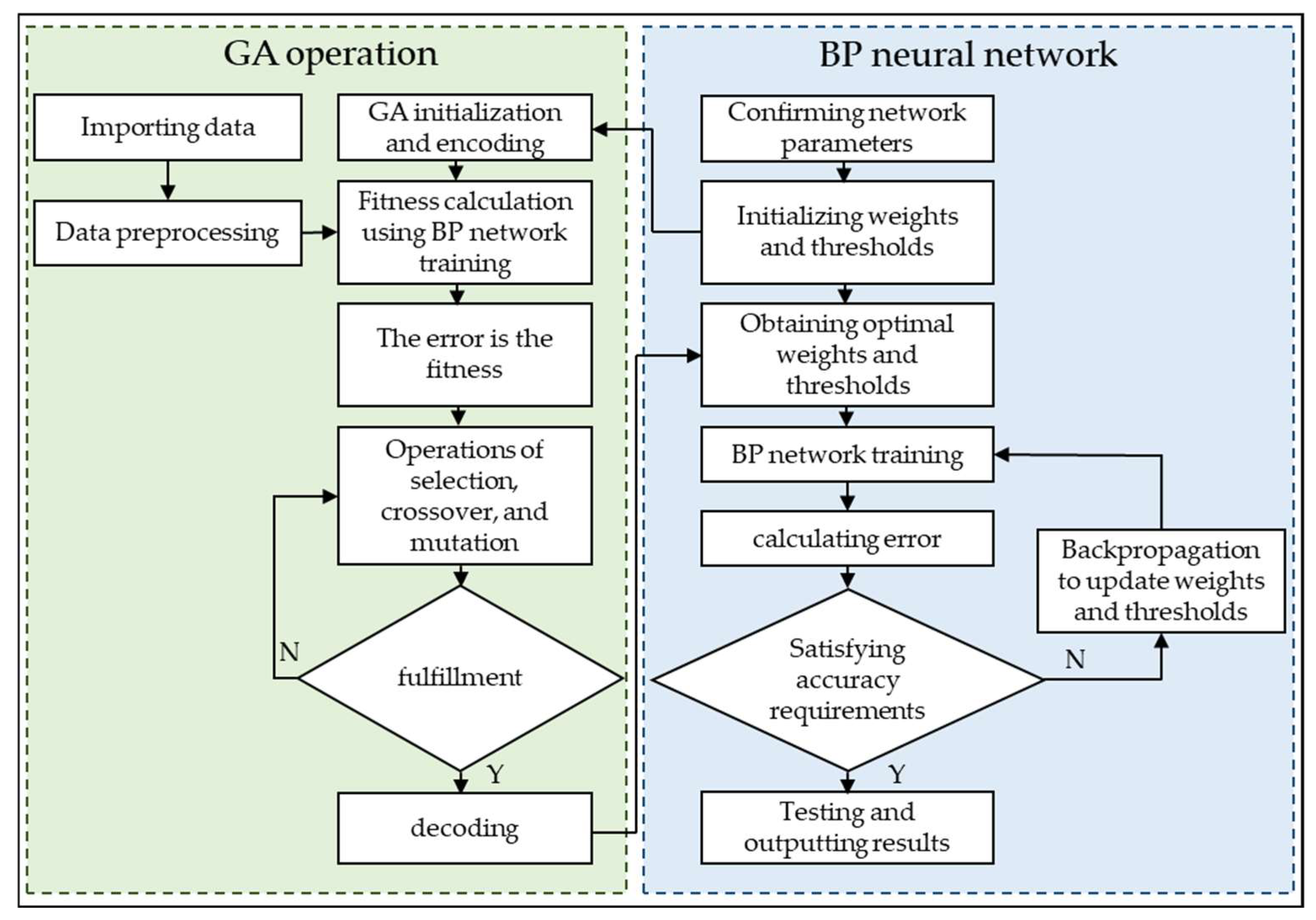
2.3.3. Modeling Approaches
2.3.4. Checking the Accuracy of Models
3. Results
3.1. Characterizations of Spectrum and Correlation between Anthocyanin and Spectrum
3.2. Selection of SBS and VIo
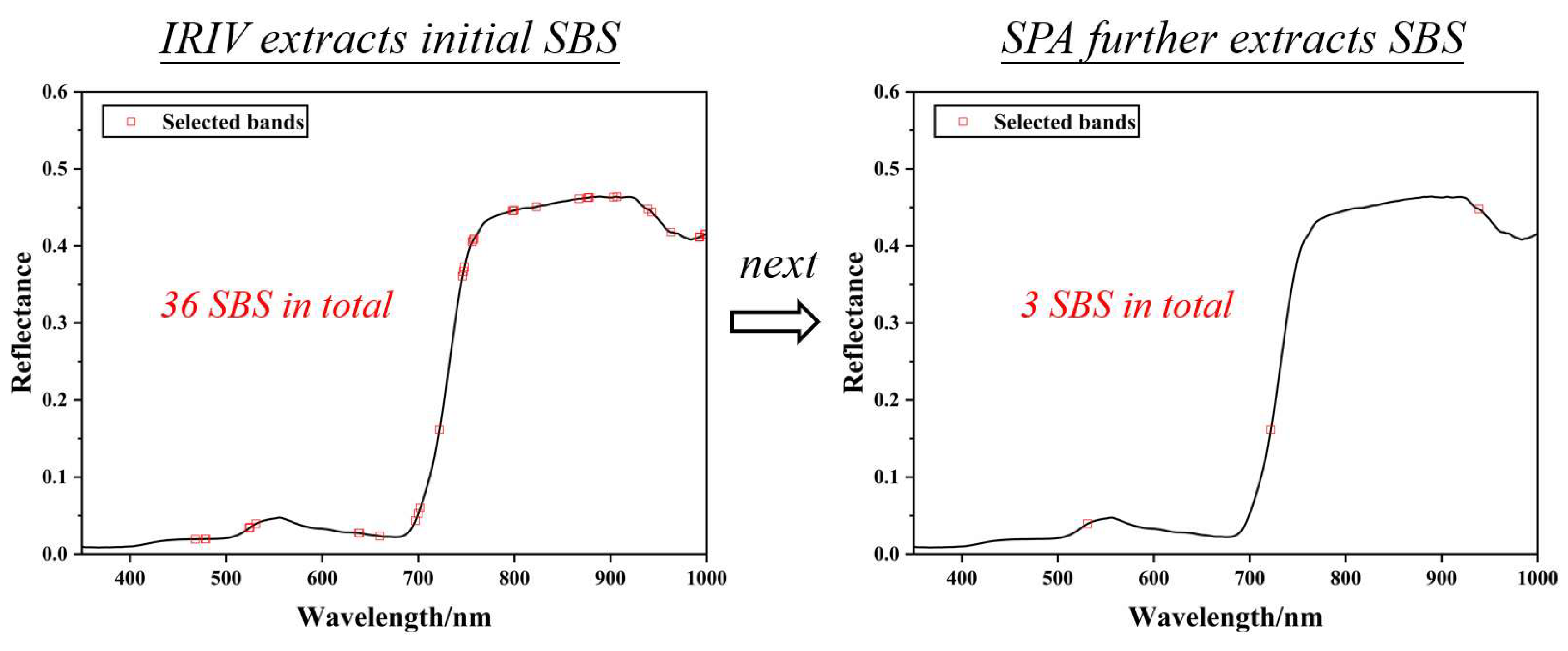
3.2.1. Selection of SBS Based on IRIV_SPA
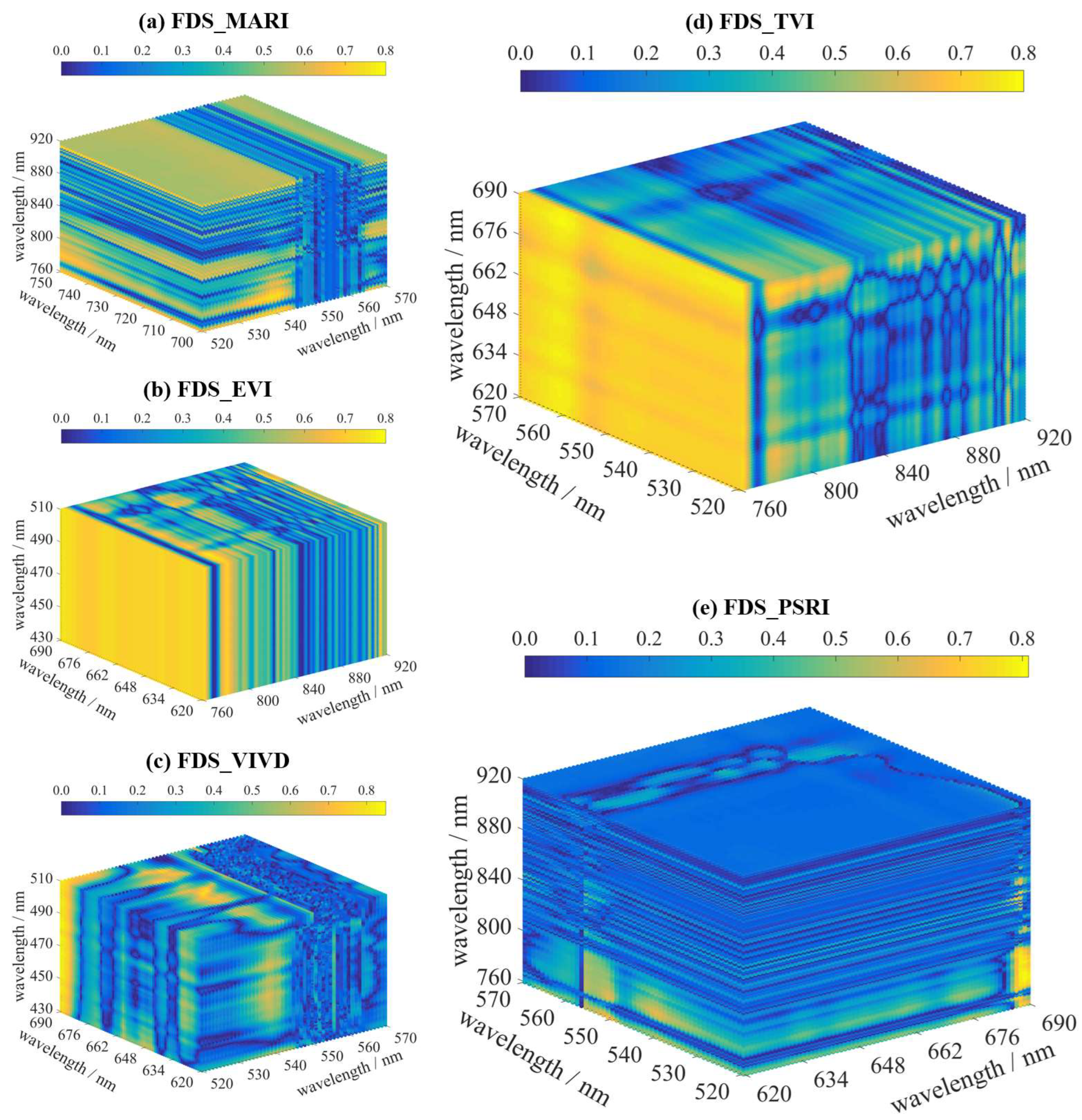
3.2.2. Selection of VIo Based on the Principle of Maximum Relevance
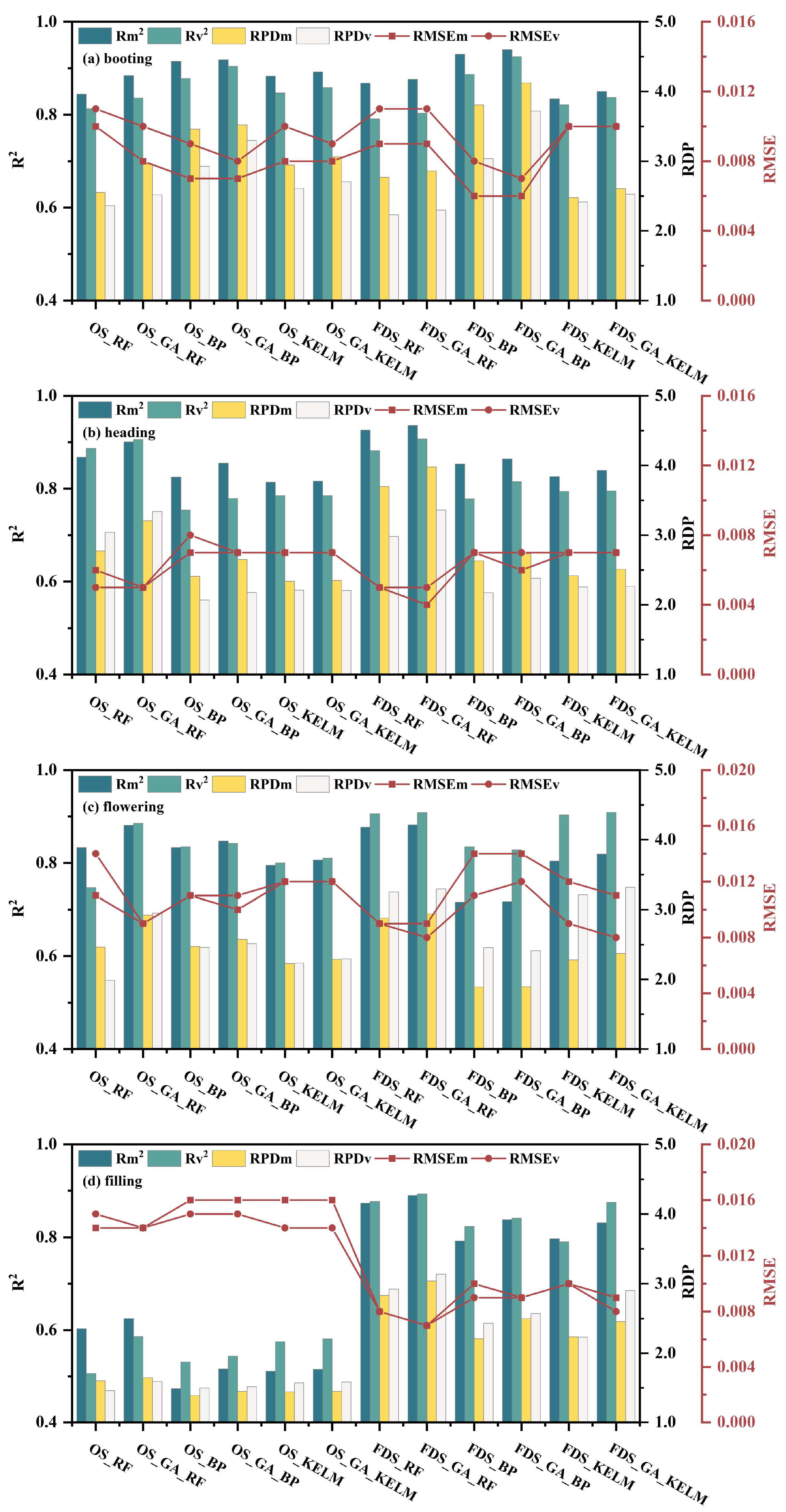
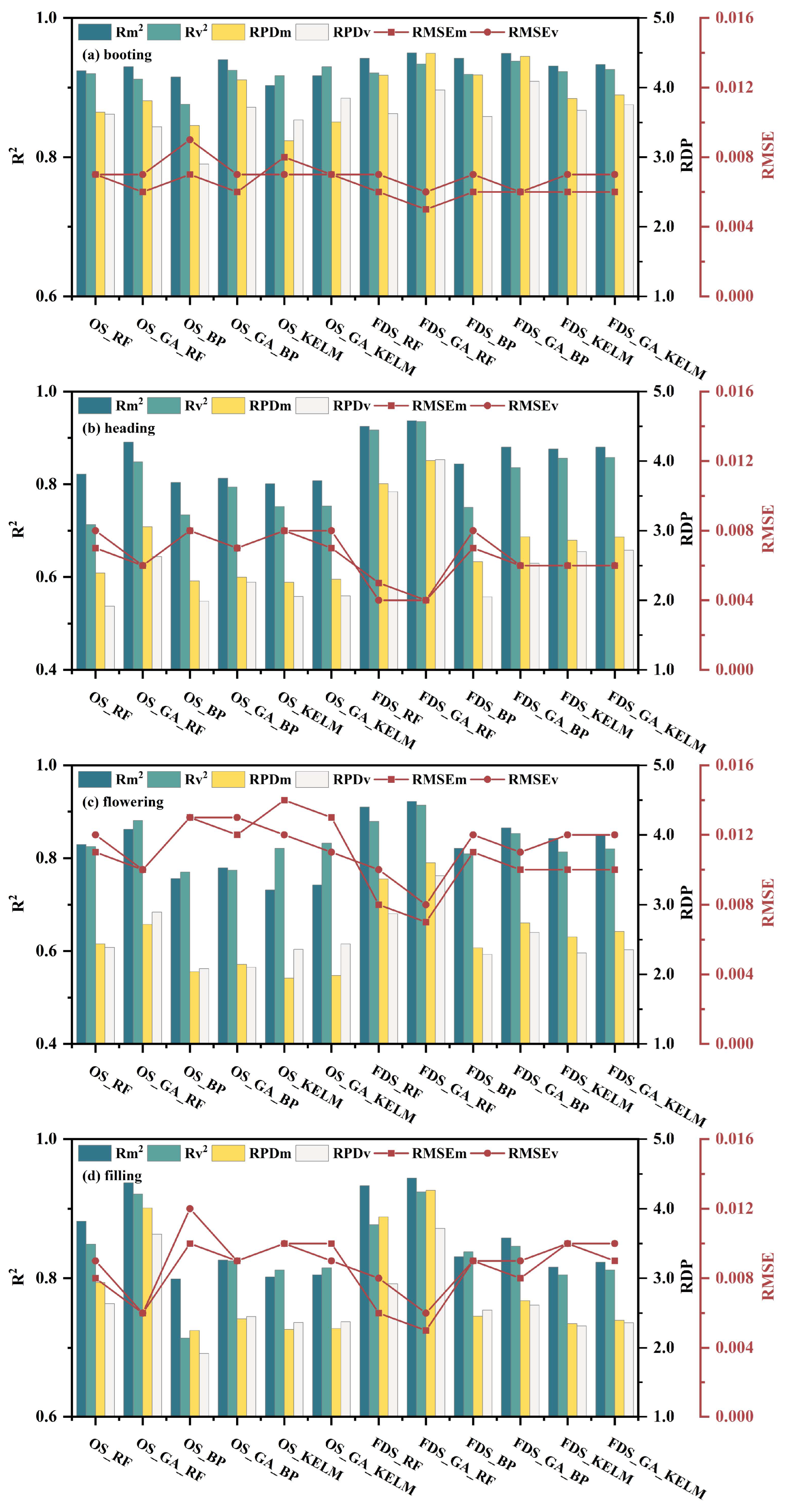
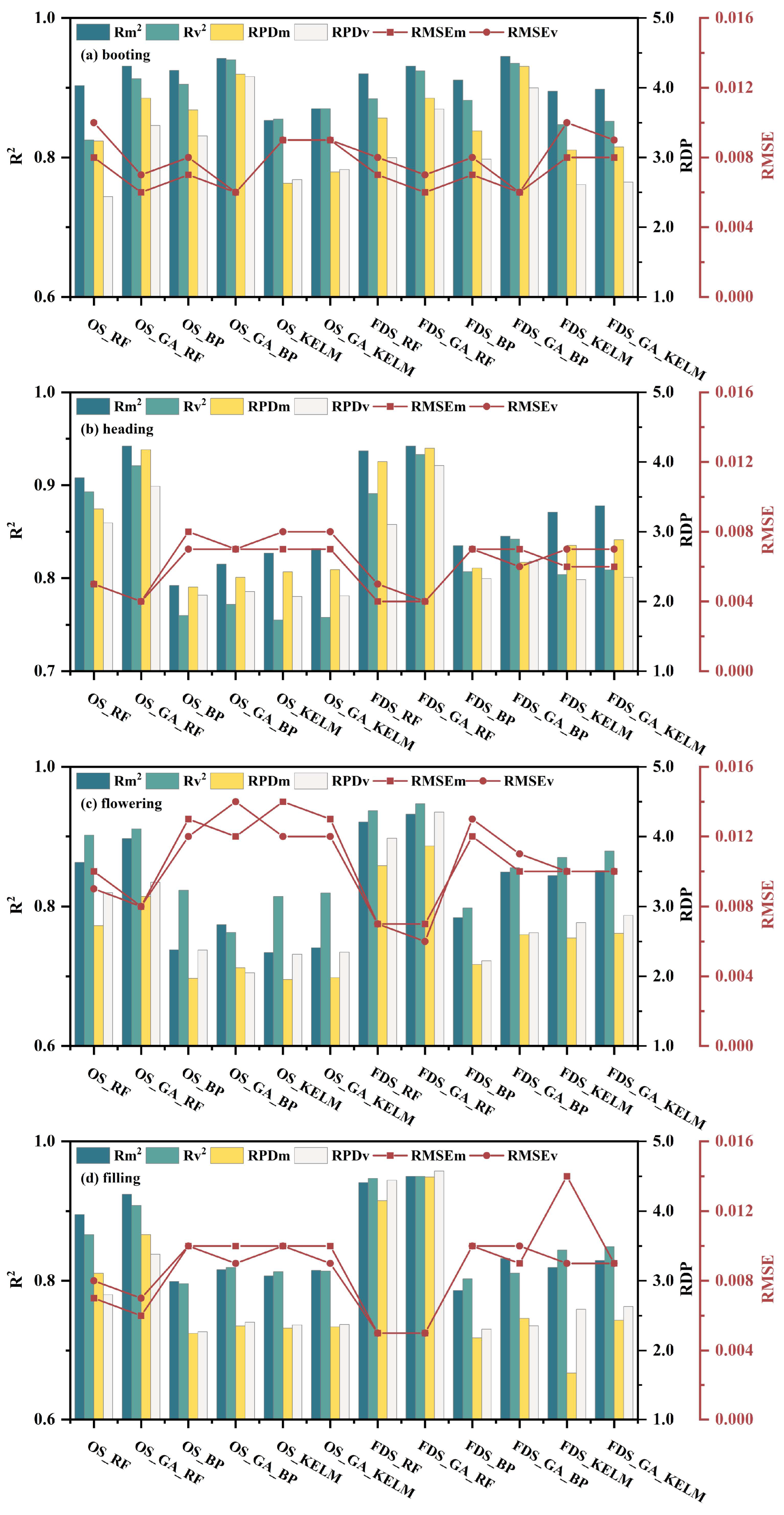
3.3. Anthocyanin Estimation Based on Models and GA Optimization
4. Discussion
4.1. BSM: Screening for Optimal Sensitive Bands and Band Combinations
4.2. Predictive Accuracy of Anthocyanin and Its Influencing Factors
4.3. Optimizing RF, BP, and KELM with GA
5. Conclusions
- (1)
- Among the models, the GA_RF model was consistently excellent, and VIo3 was remarkable for estimating anthocyanin values. The model GA_RF of FDS data based on VIo3 during the filling stage had the best performance (Rv2 = 0.950, RMSEv = 0.005, RPDv = 4.575) among all the models.
- (2)
- The first-order differential processing can effectively improve the correlation between anthocyanin and SBS, VIo2, and VIo3. The model performances of the FDS were better than that of OS on the whole, and the Rv2 values of the optimal models of FDS were all greater than 0.89.
- (3)
- The GA-optimized models showed an overall increase of 0.00% to 18.93% in the explanation of anthocyanins.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, L.; Lu, Y.; Zhou, Y.; Hao, X.; Chen, W. Functional Analysis of a Methyltransferase Involved in Anthocyanin Biosynthesis from Blueberries (Vaccinium corymbosum). J. Agric. Food Chem. 2022, 70, 16253–16262. [Google Scholar] [CrossRef] [PubMed]
- Ceferino, C.; María José, A.-G.; Monika, V.; Marta, F.-G.; Gerardo, F.B. A Novel Ultrasound-Assisted Extraction Method for the Analysis of Anthocyanins in Potatoes (Solanum tuberosum L.). Antioxidants 2021, 10, 1375. [Google Scholar] [CrossRef] [PubMed]
- Averina, N.; Savina, S.; Dremuk, I.; Yemelyanava, H.; Pryshchepchyk, Y.; Usatov, A. Influence of 5-aminolevulinic acid on physiological and biochemical characteristics of winter wheat varieties with different levels of anthocyanins in coleoptiles. Proc. Natl. Acad. Sci. Belarus Biol. Ser. 2022, 67, 135–146. [Google Scholar] [CrossRef]
- Bhatt, V.; Sendri, N.; Swati, K.; Devidas, S.; Bhandari, P. Identification and quantification of anthocyanins, flavonoids and phenolic acids in flowers of Rhododendron arboreum and evaluation of their antioxidant potential. J. Sep. Sci. 2022, 45, 2555–2565. [Google Scholar] [CrossRef] [PubMed]
- Chandra Singh, M.; Price, W.; Kelso, C.; Arcot, J.; Probst, Y. Measuring the anthocyanin content of the Australian fruit and vegetables for the development of a food composition database. J. Food Compos. Anal. 2022, 112, 104697. [Google Scholar] [CrossRef]
- Nitasaka, E.; Hoshino, A. Anthocyanin mutants of Japanese and common morning glories exhibit normal proanthocyanidin accumulation in seed coats. Plant Biotechnol. 2018, 35, 259–266. [Google Scholar] [CrossRef]
- Gitelson, A.; Keydan, G.; Merzlyak, M.; Gitelson, C. Three-Band Model for Noninvasive Estimation of Chlorophyll Carotenoids and Anthocyanin Contents in Higher Plant Leaves. Geophys. Res. Lett. 2006, 33, L11402. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Guo, D.; Xiong, X.; Chang, L.; Niu, Q.; Huang, D. Measuring and evaluating anthocyanin in lettuce leaf based on color information. IFAC-PapersOnLine 2016, 49, 96–99. [Google Scholar] [CrossRef]
- Duan, D.; Zhao, C.; Li, Z.; Yang, G.; Yang, W. Estimating total leaf nitrogen concentration in winter wheat by canopy hyperspectral data and nitrogen vertical distribution. J. Integr. Agric. 2019, 18, 1562–1570. [Google Scholar] [CrossRef]
- Yin, Q.; Zhang, Y.; Li, W.; Wang, J.; Wang, W.; Ahmad, I.; Zhou, G.; Huo, Z. Estimation of Winter Wheat SPAD Values Based on UAV Multispectral Remote Sensing. Remote Sens. 2023, 15, 3595. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, T.; Cui, J.; Shi, X.; Chen, J.; Wang, H. Non-destructive estimation of winter wheat leaf moisture content using near-ground hyperspectral imaging technology. Acta Agric. Scand. Sect. B-Soil Plant Sci. 2020, 70, 294–306. [Google Scholar] [CrossRef]
- Yang, C.; Xu, J.; Feng, M.; Bai, J.; Sun, H.; Song, L.; Wang, C.; Yang, W.; Xiao, L.; Zhang, M.; et al. Evaluation of Hyperspectral Monitoring Model for Aboveground Dry Biomass of Winter Wheat by Using Multiple Factors. Agronomy 2023, 13, 983. [Google Scholar] [CrossRef]
- Luo, L.; Chang, Q.; Gao, Y.; Jiang, D.; Li, F. Combining Different Transformations of Ground Hyperspectral Data with Unmanned Aerial Vehicle (UAV) Images for Anthocyanin Estimation in Tree Peony Leaves. Remote Sens. 2022, 14, 2271. [Google Scholar] [CrossRef]
- Jiang, S.; Chang, Q.; Wang, X.; Zheng, Z.; Zhang, Y.; Wang, Q. Estimation of Anthocyanins in Whole-Fertility Maize Leaves Based on Ground-Based Hyperspectral Measurements. Remote Sens. 2023, 15, 2571. [Google Scholar] [CrossRef]
- Gutiérrez, S.; Tardaguila, J.; Fernández-Novales, J.; Diago, M.-P. On-the-go hyperspectral imaging for the in-field estimation of grape berry soluble solids and anthocyanin concentration: Hyperspectral imaging for in-field grape estimation. Aust. J. Grape Wine Res. 2018, 25, 127–133. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, H. Hyperspectral characteristic analysis for leaf nitrogen content in different growth stages of winter wheat. Appl. Opt. 2016, 55, D151. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, H.; Wang, P. Quantitative modelling for leaf nitrogen content of winter wheat using UAV-based hyperspectral data. Int. J. Remote Sens. 2016, 38, 2117–2134. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, H.; Xu, Y.; Guijun, Y. UAV-based hyperspectral analysis and spectral indices constructing for quantitatively monitoring leaf nitrogen content of winter wheat. Appl. Opt. 2018, 57, 7722. [Google Scholar] [CrossRef]
- Chen, X.; Lv, X.; Ma, L.; Chen, A.; Zhang, Q.; Zhang, Z. Optimization and Validation of Hyperspectral Estimation Capability of Cotton Leaf Nitrogen Based on SPA and RF. Remote Sens. 2022, 14, 5201. [Google Scholar] [CrossRef]
- Shu, M.; Zhu, J.; Yang, X.; Gu, X.; Li, B.; Ma, Y. A spectral decomposition method for estimating the leaf nitrogen status of maize by UAV-based hyperspectral imaging. Comput. Electron. Agric. 2023, 212, 108100. [Google Scholar] [CrossRef]
- Hu, Y.; Kang, Z. The Rapid Non-Destructive Detection of Adulteration and Its Degree of Tieguanyin by Fluorescence Hyperspectral Technology. Molecules 2022, 27, 1196. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, T.; Su, R.; Hu, C.; Chen, F.; Cheng, J. Quantitative Evaluation of Color, Firmness, and Soluble Solid Content of Korla Fragrant Pears via IRIV and LS-SVM. Agriculture 2021, 11, 731. [Google Scholar] [CrossRef]
- Zhang, L.; Nie, P.; Zhang, S.; Zhang, L.; Sun, T. Research on Defect Detection in Kubo Peach Based on Hyperspectral Imaging Technology Combined with CARS-MIV-GA-SVM Method. Foods 2023, 12, 3593. [Google Scholar] [CrossRef] [PubMed]
- Sudu, B.; Rong, G.; Guga, S.; Li, K.; Zhi, F.; Guo, Y.; Zhang, J.; Bao, Y. Retrieving SPAD Values of Summer Maize Using UAV Hyperspectral Data Based on Multiple Machine Learning Algorithm. Remote Sens. 2022, 14, 5407. [Google Scholar] [CrossRef]
- Liang, K.; Liu, Q.; Pan, L.; Chen, M. Detection of soluble solids content in ‘Korla fragrant pear’ based on hyperspectral imaging and CARS-IRIV algorithm. J. Nanjing Agric. Univ. 2018, 41, 760–766. [Google Scholar]
- Zhang, J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.; Xie, Y.; Ma, X. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 49. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.; Man, W.; Liu, M.; Zhang, Y.; Chen, X.; Li, X.; He, J.; Tian, D. Leaf Area Index Inversion of Spartina alterniflora Using UAV Hyperspectral Data Based on Multiple Optimized Machine Learning Algorithms. Remote Sens. 2023, 15, 4465. [Google Scholar] [CrossRef]
- Deng, J.; Wang, R.; Yang, L.; Lv, X.; Yang, Z.; Zhang, K.; Zhou, C.; Pengju, L.; Wang, Z.; Abdullah, A.; et al. Quantitative Estimation of Wheat Stripe Rust Disease Index Using Unmanned Aerial Vehicle Hyperspectral Imagery and Innovative Vegetation Indices. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Fei, S.; Hassan, M.; Xiao, Y.; Su, X.; Chen, Z.; Cheng, Q.; Duan, F.; Chen, R.; Ma, Y. UAV-based multi-sensor data fusion and machine learning algorithm for yield prediction in wheat. Precis. Agric. 2022, 24, 187–212. [Google Scholar] [CrossRef]
- Xu, M.; Zhao, Y.; Zhang, G.; Gao, P.; Yang, R. Method for forecasting winter wheat first flowering stage based on machine learning algorithm. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2021, 37, 162–171. [Google Scholar] [CrossRef]
- Yadav, M.; Rengma, N.S. A Generic Machine Learning-Based Framework for Predictive Modeling of Land Surface Temperature. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-4/W2-2022, 95–102. [Google Scholar] [CrossRef]
- Andrade, C.; Moura-Bueno, J.; Comin, J.; Brunetto, G. Grape Yield Prediction Models: Approaching Different Machine Learning Algorithms. Horticulturae 2023, 9, 1294. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, X.; Cheng, Q.; Fei, S.; Chen, Z. A Machine-Learning Model Based on the Fusion of Spectral and Textural Features from UAV Multi-Sensors to Analyse the Total Nitrogen Content in Winter Wheat. Remote Sens. 2023, 15, 2152. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Wang, Q.; Shen, H. Winter Wheat SPAD Value Inversion Based on Multiple Pretreatment Methods. Remote Sens. 2022, 14, 4660. [Google Scholar] [CrossRef]
- Ziheng, F.; Guan, H.; Yang, T.; He, L.; Duan, J.; Song, L.; Wang, C.; Feng, W. Estimating the canopy chlorophyll content of winter wheat under nitrogen deficiency and powdery mildew stress using machine learning. Comput. Electron. Agric. 2023, 211, 107989. [Google Scholar] [CrossRef]
- Ziheng, F.; Zhang, H.; Duan, J.; He, L.; Yuan, X.; Gao, Y.; Liu, W.; Li, X.; Feng, W. Improved Spectral Detection of Nitrogen Deficiency and Yellow Mosaic Disease Stresses in Wheat Using a Soil Effect Removal Algorithm and Machine Learning. Remote Sens. 2023, 15, 2513. [Google Scholar] [CrossRef]
- Adami, M.; Rudorff, B.; Breunig, F.; Ponzoni, F.; Galvao, L.; Moreira, M.; Freitas, J.; Sala, V. Effect of Nitrogen and Endophytic Bacteria on Biophysical and Spectral Parameters of Wheat Canopy. Agron. J. 2010, 102, 544–552. [Google Scholar] [CrossRef]
- Shabnam, R.; Tarek, M.; Iqbal, M. Understanding phosphorus dynamics in wheat plant and growth response in a split-root system in acidic soil. Agric. Nat. Resour. 2018, 52, 259–265. [Google Scholar] [CrossRef]
- Guo, J.; Jia, Y.; Chen, H.; Zhang, L.; Yang, J.; Zhang, J.; Hu, X.; Ye, X.; Li, Y.; Zhou, Y. Growth, photosynthesis, and nutrient uptake in wheat are affected by differences in nitrogen levels and forms and potassium supply. Sci. Rep. 2019, 9, 1248. [Google Scholar] [CrossRef]
- Pfündel, E.; Ben Ghozlen, N.; Meyer, S.; Cerovic, Z. Investigating UV screening in leaves by two different types of portable UV fluorimeter reveals in vivo screening by anthocyanins and carotenoids. Photosynth. Res. 2007, 93, 205–221. [Google Scholar] [CrossRef]
- Hagen, S.; Solhaug, K.A.; Bengtsson, G.; Borge, G.I.; Bilger, W. Chlorophyll fluorescence as a tool for non-destructive estimation of anthocyanins and total flavonoids in apples. Postharvest Biol. Technol. 2006, 41, 156–163. [Google Scholar] [CrossRef]
- Altuner, F.; Tuncturk, R.; Oral, E.; Tuncturk, M. Evaluation of pigment, antioxidant capacity and bioactive compounds in microgreens of wheat landraces and cereals. Chil. J. Agric. Res. 2021, 81, 643–654. [Google Scholar] [CrossRef]
- Ji, R.; Chen, X.; Liu, S.; Rao, L.; Wang, Z. Nondestructive Testing of Volatile Oil of Zanthoxylum Bungeanum Based on Hyperspectral Technique and IRIV-FOA-ELM Algorithm. Laser Optoelectron. Prog. 2020, 57, 394–400. [Google Scholar] [CrossRef]
- Ding, D.; Yu, H.; Yin, Y.; Yuan, Y.; Li, Z.; Li, F. Determination of Chlorophyll and Hardness in Cucumbers by Raman Spectroscopy with Successive Projections Algorithm (SPA)—Extreme Learning Machine (ELM). Anal. Lett. 2022, 56, 1216–1228. [Google Scholar] [CrossRef]
- Yun, Y.-H.; Wang, W.-T.; Tan, M.-L.; Liang, Y.-Z.; Li, H.-D.; Cao, D.-S.; Lu, H.-M.; Xu, Q. A strategy that iteratively retains informative variables for selecting optimal variable subset in multivariate calibration. Anal. Chim. Acta 2014, 807, 36–43. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, T.; Zhu, Y.; Zhou, Y.; Xia, T.; Nie, Y. Determination of soybean leaf SPAD value using characteristic wavelength variables preferably selected by IRIV algorithm. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2018, 34, 148–154. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Peng, F.; Liu, J.; Han, G. Non-destructive prediction and visualization of anthocyanin content in mulberry fruits using hyperspectral imaging. Front. Plant Sci. 2023, 14, 1137198. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2021, 45, 5–32. [Google Scholar] [CrossRef]
- Qian, C.; Du, T.; Sun, S.; Liu, W.; Zheng, H.; Wang, J. An integrated learning algorithm for early prediction of melon harvest. Sci. Rep. 2022, 12, 18199. [Google Scholar] [CrossRef]
- Yang, S.; Hu, L.; Wu, H.; Qiao, H.; Li, P.; Fan, W. Integration of Crop Growth Model and Random Forest for Winter Wheat Yield Estimation From UAV Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6253–6269. [Google Scholar] [CrossRef]
- Deng, T. Effect of the Number of Hidden Layer Neurons on the Accuracy of the Back Propagation Neural Network. Highlights Sci. Eng. Technol. 2023, 74, 462–468. [Google Scholar] [CrossRef]
- Leema, N.; Khanna, H.N.; Elgin Christo, V.R.; Kannan, A. Evaluation of Parameter Settings for Training Neural Networks Using Backpropagation Algorithms. In Research Anthology on Artificial Neural Network Applications; IGI Global: Hershey, PA, USA, 2022. [Google Scholar] [CrossRef]
- Chunhao, L.; Guangyuan, P.; Dongming, S.; Zhi, Y. Air Quality Index Forecasting via Genetic Algorithm-Based Improved Extreme Learning Machine. IEEE Access 2023, 11, 67086–67097. [Google Scholar] [CrossRef]
- Chen, Q.; Wei, H.; Rashid, M.; Cai, Z. Kernel extreme learning machine based hierarchical machine learning for multi-type and concurrent fault diagnosis. Measurement 2021, 184, 109923. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic Algorithm—A Literature Review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019. [Google Scholar]
- Yasojima, C.; Araujo, T.; Meiguins, B.; Neto, N.; Morais, J. A Comparison of Genetic Algorithms and Particle Swarm Optimization to Estimate Cluster-Based Kriging Parameters. In Proceedings of the EPIA Conference on Artificial Intelligence, Vila Real, Portugal, 3–6 September 2019. [Google Scholar]
- Ao, D.; Yang, J.; Ding, W.; An, S.; He, H. Review of 54 Vegetation Indices. J. Anhui Agric. Sci. 2023, 51, 13–21+28. [Google Scholar]
- Liu, X.; Liu, C.; Wu, S.; Shi, Z.; Chang, Q. Nondestructive Inversion of Anthocyanins Content in Maize Leaves Using Hyperspectral Remote Sensing. Remote Sens. Inf. 2018, 33, 1–8. [Google Scholar]
- Zhang, J.; Sun, B.; Yang, C.; Wang, C.; You, Y.; Zhou, G.; Liu, B.; Chufeng, W.; Kuai, J.; Xie, J. A novel composite vegetation index including solar-induced chlorophyll fluorescence for seedling rapeseed net photosynthesis rate retrieval. Comput. Electron. Agric. 2022, 198, 107031. [Google Scholar] [CrossRef]
- Xing, N.; Huang, W.; Xie, Q.; Shi, Y.; Ye, H.; Dong, Y.; Wu, M.; Sun, G.; Jiao, Q. A Transformed Triangular Vegetation Index for Estimating Winter Wheat Leaf Area Index. Remote Sens. 2019, 12, 16. [Google Scholar] [CrossRef]
- Jiang, D.; Chang, Q.; Zhang, Z.; Liu, Y.; Zhang, Y.; Zheng, Z. Monitoring the Degree of Mosaic Disease in Apple Leaves Using Hyperspectral Images. Remote Sens. 2023, 15, 2504. [Google Scholar] [CrossRef]
- Haboudane, D.; John, R.M.; Pattey, E.; Pablo, J.Z.-T.; Ian, B.S. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Ren, S.; Chen, X.; An, S. Assessing plant senescence reflectance index-retrieved vegetation phenology and its spatiotemporal response to climate change in the Inner Mongolian Grassland. Int. J. Biometeorol. 2016, 61, 601–612. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y. Soil Heavy Metals Estimation based on Hyprspectral in Urban Residential. Remote Sens. Technol. Appl. 2019, 34, 540–546. [Google Scholar]
- Pasquini, C. Near Infrared Spectroscopy: A mature analytical technique with new perspectives—A review. Anal. Chim. Acta 2018, 1026, 8–36. [Google Scholar] [CrossRef]
- Tang, R.; He, Y.; Fan, K. Recent advances in stability improvement of anthocyanins by efficient methods and its application in food intelligent packaging: A review. Food Biosci. 2023, 56, 103164. [Google Scholar] [CrossRef]
- Silva, P.; Paulo, L.; Barbafina, A.; Eisei, F.; Quina, F.; Macanita, A. Photoprotection and the Photophysics of Acylated Anthocyanins. Chem.–A Eur. J. 2012, 18, 3736–3744. [Google Scholar] [CrossRef]
- Houghton, A.; Appelhagen, I.; Martin, C. Natural Blues: Structure Meets Function in Anthocyanins. Plants 2021, 10, 726. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, J.; Meng, P.; Li, Y.; Wang, H.; Li, C. Improvement of algorithm used for extraction hyperspectral feature bands of vegetation. Trans. Chin. Soc. Agric. Eng. 2015, 31, 179–185. [Google Scholar] [CrossRef]
- Curran, P.; Dungan, J.; Macler, B.; Plummer, S.; Peterson, D. Reflectance spectroscopy of fresh whole leaves for the estimation of chemical concentration. Remote Sens. Environ. 1992, 39, 153–166. [Google Scholar] [CrossRef]
- Yu, K.; Li, F.; Gnyp, M.L.; Miao, Y.; Bareth, G.; Chen, X. Remotely detecting canopy nitrogen concentration and uptake of paddy rice in the Northeast China Plain. ISPRS J. Photogramm. Remote Sens. 2013, 78, 102–115. [Google Scholar] [CrossRef]
- Kong, Y.R.; Wang, L.J.; Feng, H.K.; Xu, Y.; Liang, L.; Xu, L.; Yang, X.D.; Zhang, Q.Q. Leaf Area Index Estimation Based on UAV Hyperspectral Band Selection. Spectrosc. Spectr. Anal. 2022, 42, 933–939. [Google Scholar] [CrossRef]
- Li, F.; Elsayed, S.; Hu, Y.; Schmidhalter, U. Passive reflectance sensing using optimized two-and three-band spectral indices for quantifying the total nitrogen yield of maize. Comput. Electron. Agric. 2020, 173, 105403. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Huang, T.; Wang, J.; Lin, L.; Wang, L.; Yang, M. Estimation of Leaf Nitrogen Content in Wheat Using New Hyperspectral Indices and a Random Forest Regression Algorithm. Remote Sens. 2018, 10, 1940. [Google Scholar] [CrossRef]
- Qiao, H.; Xia, B.; Ma, X.; Cheng, D.; Zhou, Y. Identification of Damage by Diseases and Insert Pests in Winter Wheat. J. Triticeae Crops 2010, 30, 770–774. [Google Scholar]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Jiang, J.; Johansen, K.; Stanschewski, C.S.; Wellman, G.; Mousa, M.A.; Fiene, G.M.; Asiry, K.A.; Tester, M.; McCabe, M.F. Phenotyping a diversity panel of quinoa using UAV-retrieved leaf area index, SPAD-based chlorophyll and a random forest approach. Precis. Agric. 2022, 23, 961–983. [Google Scholar] [CrossRef]
- Tang, Z.; Guo, J.; Xiang, Y.; Lu, X.; Wang, Q.; Wang, H.; Cheng, M.; Wang, H.; Wang, X.; An, J.; et al. Estimation of Leaf Area Index and Above-Ground Biomass of Winter Wheat Based on Optimal Spectral Index. Agronomy 2022, 12, 1729. [Google Scholar] [CrossRef]
- Shi, H.; Guo, J.; An, J.; Tang, Z.; Wang, X.; Li, W.; Zhao, X.; Jin, L.; Xiang, Y.; Li, Z.; et al. Estimation of Chlorophyll Content in Soybean Crop at Different Growth Stages Based on Optimal Spectral Index. Agronomy 2023, 13, 663. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Pu, Y.; Zhang, Y.; Tang, Z.; Fu, J.; Xu, W.; Xiang, Y.; Zhang, F. Estimation of the Leaf Area Index of Winter Rapeseed Based on Hyperspectral and Machine Learning. Sustainability 2023, 15, 12930. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, Y.; Cheng, M.; Sun, C. Comprehensive Growth Index (CGI): A Comprehensive Indicator from UAV-Observed Data for Winter Wheat Growth Status Monitoring. Agronomy 2023, 13, 2883. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, J.; Huang, S.; Tian, S.; Liu, Y.; Lu, L.; Zhang, Y.; Huang, Y.; Wang, X. Development of chemometric modelling in the applcation of NIR to the quality control of Chinese herbal medicine: Literature review and future perspectives. Chem. Ind. Eng. Prog. 2016, 35, 1627–1645. [Google Scholar] [CrossRef]
- Sebastian, R. Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
- Delaney, J.T.; Larson, D.M. Using explainable machine learning methods to evaluate vulnerability and restoration potential of ecosystem state transitions. Conserv. Biol. 2024, 38, e14203. [Google Scholar] [CrossRef] [PubMed]
- Qiao, H. The Measurement and Analysis of Canopy Hyperspectral Character on Winter Wheat Damaged by Aphids and Wheat Powdery Mildew. Master’s Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2004. [Google Scholar]
- Sourabh, K.; Sumit Singh, C.; Vijay, K. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2020, 80, 8091–8126. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, J.; Chen, Z. Predicting the effect of silver nanoparticles on soil enzyme activity using the machine learning method: Type, size, dose and exposure time. J. Hazard. Mater. 2023, 457, 131789. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Su, Z.; Zhou, H.; Jia, X.; Ye, G.; Cai, C. Application of GA-BP model based on principal component analysis to urban water demand prediction. South-to-North Water Transf. Water 2017, 15, 39–44. [Google Scholar] [CrossRef]
- Atefeh, M.; Masoomeh, Z.; Leila, N. Optimization of Tree-Based Machine Learning Models to Predict the Length of Hospital Stay Using Genetic Algorithm. J. Healthc. Eng. 2023, 2023, 9673395. [Google Scholar] [CrossRef]
- Shi, M.; Jing, X.; Shi, X. Inversion of winter wheat chlorophyll content based on hyperspectral and GA-BP neural network model. Jiangsu Agric. Sci. 2022, 50, 56–62. [Google Scholar] [CrossRef]
- Zheng, G.; Hua, W.; Qiu, Z.; Gong, Z. Detecting Water Depth from Remotely Sensed Imagery Based on ELM and GA-ELM. J. Indian Soc. Remote Sens. 2021, 49, 947–957. [Google Scholar] [CrossRef]
- Seo, Y.; Choi, Y.; Choi, J. River Stage Modeling by Combining Maximal Overlap Discrete Wavelet Transform, Support Vector Machines and Genetic Algorithm. Water 2017, 9, 525. [Google Scholar] [CrossRef]
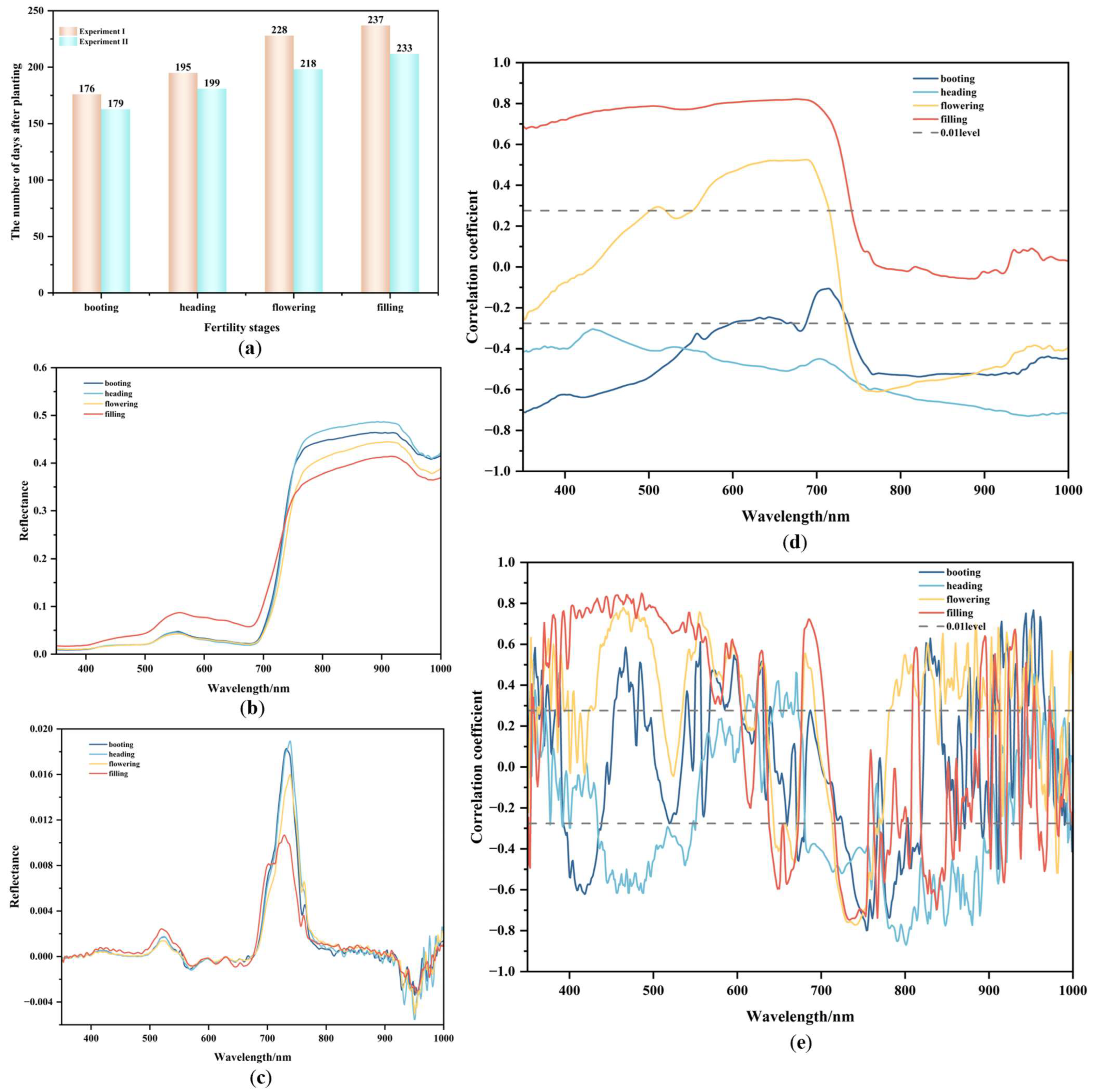

| Experiments | Variety | N Rate (Kg/hm2) | P Rate (Kg/hm2) | K Rate (Kg/hm2) |
|---|---|---|---|---|
| Experiment I (2016–2017) | Xiaoyan 22 | 0, 30, 60, 90, 120, 150 | 0, 30, 60, 90, 120, 150 | 0, 22.5, 45, 67.5, 90, 112.5 |
| Experiment II (2017–2018) | Xiaoyan 22 | 0, 30, 60, 90, 120, 150 | 0, 22.5, 45, 67.5, 90, 112.5 | 0, 22.5, 45, 67.5, 90, 112.5 |
| Dataset | Growth Stage | Sample Numbers | Min | Max | Mean | Standard Deviation | Kurtosis Zscore | Skewness Zscore | Coefficient of Variation/% |
|---|---|---|---|---|---|---|---|---|---|
| Modeling set | booting | 65 | 0.04 | 0.12 | 0.09 | 0.03 | 3.02 | 0.54 | 28.58% |
| heading | 65 | 0.07 | 0.13 | 0.11 | 0.02 | 2.08 | 1.40 | 16.12% | |
| flowering | 65 | 0.04 | 0.13 | 0.09 | 0.03 | 2.39 | 1.14 | 30.56% | |
| filling | 65 | 0.06 | 0.16 | 0.09 | 0.02 | 0.03 | 2.16 | 24.10% | |
| Verification set | booting | 21 | 0.04 | 0.11 | 0.08 | 0.03 | 1.78 | 0.34 | 29.88% |
| heading | 21 | 0.08 | 0.13 | 0.11 | 0.02 | 1.56 | 0.50 | 14.51% | |
| flowering | 21 | 0.04 | 0.12 | 0.08 | 0.03 | 1.73 | 0.20 | 34.60% | |
| filling | 21 | 0.06 | 0.14 | 0.09 | 0.02 | 0.23 | 1.40 | 24.16% |
| Growth Stage | Data | Sensitive Bands |
|---|---|---|
| booting | OS_IRIV_SPA | 722 nm 531 nm 939 nm |
| FDS_IRIV_SPA | 741 nm 732 nm 446 nm 761 nm | |
| heading | OS_IRIV_SPA | 770 nm 900 nm 852 nm 968 nm 353 nm |
| FDS_IRIV_SPA | 803 nm 896 nm | |
| flowering | OS_IRIV_SPA | 763 nm 1000 nm 720 nm |
| FDS_IRIV_SPA | 742 nm 356 nm 959 nm | |
| filling | OS_IRIV_SPA | 843 nm 834 nm |
| FDS_IRIV_SPA | 729 nm 394 nm 948 nm 979 nm |
| Title | VI | Equations | References |
|---|---|---|---|
| 2 bands | ARI | [14] | |
| MGRVI | [59] | ||
| R/G | [14] | ||
| RDVI | [60] | ||
| OSAVI | [61] | ||
| 3 bands | MARI | [62] | |
| EVI | [27] | ||
| VDVI | [57] | ||
| TVI | [60] | ||
| PSRI | [63] |
| Growth Stage | OS | FDS | ||
|---|---|---|---|---|
| Bands Combination | Correlation Coefficient | Bands Combination | Correlation Coefficient | |
| booting | ARI (532 nm 706 nm) | 0.85 ** | ARI (520 nm 700 nm) | 0.86 ** |
| MGRVI (520 nm 620 nm) | 0.47 ** | MGRVI (520 nm 690 nm) | 0.85 ** | |
| RG (620 nm 520 nm) | 0.44 ** | RG (690 nm 520 nm) | 0.84 ** | |
| RDVI (821 nm 632 nm) | 0.49 ** | RDVI (761 nm 640 nm) | 0.75 ** | |
| OSAVI (821 nm 632 nm) | 0.41 ** | OSAVI (782 nm 629 nm) | 0.77 ** | |
| heading | ARI (535 nm 703 nm) | 0.57 ** | ARI (568 nm 700 nm) | 0.61 ** |
| MGRVI (520 nm 620 nm) | 0.63 ** | MGRVI (554 nm 668 nm) | 0.67 ** | |
| RG (620 nm 520 nm) | 0.62 ** | RG (647 nm 568 nm) | 0.55 ** | |
| RDVI (915 nm 679 nm) | 0.64 ** | RDVI (791 nm 671 nm) | 0.81 ** | |
| OSAVI (920 nm 679 nm) | 0.55 ** | OSAVI (801 nm 622 nm) | 0.89 ** | |
| flowering | ARI (535 nm 700 nm) | 0.76 ** | ARI (542 nm 700 nm) | 0.80 ** |
| MGRVI (520 nm 620 nm) | 0.81 ** | MGRVI (557 nm 669 nm) | 0.86 ** | |
| RG (620 nm 520 nm) | 0.80 ** | RG (651 nm 569 nm) | 0.82 ** | |
| RDVI (760n m 620 nm) | 0.75 ** | RDVI (760 nm 688 nm) | 0.61 ** | |
| OSAVI (760 nm 620 nm) | 0.77 ** | OSAVI (884 nm 669 nm) | 0.76 ** | |
| filling | ARI (557 nm 744 nm) | 0.82 ** | ARI (533 nm 704 nm) | 0.87 ** |
| MGRVI (530 nm 620 nm) | 0.83 ** | MGRVI (568 nm 657 nm) | 0.79 ** | |
| RG (620 nm 530 nm) | 0.83 ** | RG (686 nm 525 nm) | 0.78 ** | |
| RDVI (783 nm 690 nm) | 0.76 ** | RDVI (767 nm 687 nm) | 0.83 ** | |
| OSAVI (882 nm 620 nm) | 0.82 ** | OSAVI (767 nm 686 nm) | 0.82 ** | |
| Growth Stage | OS | FDS | ||
|---|---|---|---|---|
| Bands Combination | Correlation Coefficient | Bands Combination | Correlation Coefficient | |
| booting | MARI (557 nm 750 nm 821 nm) | 0.41 ** | MARI (541 nm 750 nm 782 nm) | 0.77 ** |
| EVI (822 nm 632 nm 451 nm) | 0.57 ** | ESI (782 nm 629 nm 430 nm) | 0.77 ** | |
| VDVI (570 nm 680 nm 434 nm) | 0.54 ** | VDVI (520 nm 690 nm 484 nm) | 0.85 ** | |
| TVI (821 nm 520 nm 632 nm) | 0.53 ** | TVI (915 nm 554 nm 668 nm) | 0.80 ** | |
| PSRI (620 nm 520 nm 760 nm) | 0.40 ** | PSRI (689 nm 520 nm 782 nm) | 0.80 ** | |
| heading | MARI (544 nm 700 nm 914 nm) | 0.78 ** | MARI (568 nm 700 nm 802 nm) | 0.87 ** |
| EVI (915 nm 680 nm 510 nm) | 0.66 ** | ESI (801 nm 622 nm 439 nm) | 0.89 ** | |
| VDVI (520 nm 620 nm 510 nm) | 0.61 ** | VDVI (535 nm 642 nm 489 nm) | 0.70 ** | |
| TVI (915 nm 570 nm 680 nm) | 0.69 ** | TVI (800 nm 555 nm 669 nm) | 0.88 ** | |
| PSRI (620 nm 522 nm 920 nm) | 0.74 ** | PSRI (654 nm 570 nm 806 nm) | 0.70 ** | |
| flowering | MARI (570 nm 741 nm 760 nm) | 0.80 ** | MARI (550 nm 720 nm 761 nm) | 0.77 ** |
| EVI (760 nm 620 nm 430 nm) | 0.75 ** | ESI (884 nm 669 nm 501 nm) | 0.76 ** | |
| VDVI (520 nm 620 nm 510 nm) | 0.79 ** | VDVI (539 nm 636 nm 451 nm) | 0.84 ** | |
| TVI (760 nm 520 nm 620 nm) | 0.70 ** | TVI (845 nm 560 nm 670 nm) | 0.84 ** | |
| PSRI (620 nm 521 nm 914 nm) | 0.75 ** | PSRI (670 nm 558 nm 845 nm) | 0.86 ** | |
| filling | MARI (570 nm 750 nm 882 nm) | 0.77 ** | MARI (543 nm 722 nm 831 nm) | 0.81 ** |
| EVI (881 nm 690 nm 430 nm) | 0.75 ** | EVI (767 nm 686 nm 444 nm) | 0.82 ** | |
| VDVI (521 nm 620 nm 510 nm) | 0.82 ** | VDVI (523 nm 686 nm 433 nm) | 0.83 ** | |
| TVI (783 nm 520 nm 690 nm) | 0.58 ** | TVI (767 nm 523 nm 686 nm) | 0.82 ** | |
| PSRI (620 nm 520 nm 920 nm) | 0.83 ** | PSRI (649 nm 556 nm 822 nm) | 0.84 ** | |
| Discussion Items |
|---|
| Point 1 BSM: Screening for Optimal Bands and Band Combinations |
| 1. Screening for Optimal Bands |
| (1) The bands screened in all stages were mainly concentrated at 720-1000 nm. |
| (2) Certain near-infrared bands have some sensitivity to the anthocyanin values of winter wheat. |
| 2. Screening for Band Combinations |
| (1) Seeking VIo can play a terrific role in VIs and improve prediction. |
| (2) Different band combinations were selected for the same vegetation index in OS and FDS data. |
| (3) The band combinations selected for the same vegetation index were not identical for different wheat growth stages. |
| (4) The consequences of band combinations of MGRVI, RG, RDVI, and OSAVI showed that the bands selected for VIs in the same band range were divergent. |
| (5) VIo was more suitable for estimating anthocyanin values than SBS. |
| Point 2 Predictive Accuracy of Anthocyanin and Its Influencing Factors |
| (1) The GA_RF model behaved both stably and marvelously in the four stages. |
| (2) It is essential to calibrate and evaluate competitive estimation models based on specific experimental datasets. |
| (3) It is crucial to compare transformation treatments and multiple methods based on different data periods and input variables. |
| Point 3 Optimizing RF, BP, and KELM with GA |
| (1) GA can optimize the parameters of RF, BP, and KELM. |
| (2) GA can improve the accuracy of the modeling. |
| (3) GA can effectively emphasize the effects of distinct models. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, H.; Chen, X.; Guo, Y.; Wang, Q.; Zhang, R.; Chang, Q. Estimation of Anthocyanins in Winter Wheat Based on Band Screening Method and Genetic Algorithm Optimization Models. Remote Sens. 2024, 16, 2324. https://doi.org/10.3390/rs16132324
Miao H, Chen X, Guo Y, Wang Q, Zhang R, Chang Q. Estimation of Anthocyanins in Winter Wheat Based on Band Screening Method and Genetic Algorithm Optimization Models. Remote Sensing. 2024; 16(13):2324. https://doi.org/10.3390/rs16132324
Chicago/Turabian StyleMiao, Huiling, Xiaokai Chen, Yiming Guo, Qi Wang, Rui Zhang, and Qingrui Chang. 2024. "Estimation of Anthocyanins in Winter Wheat Based on Band Screening Method and Genetic Algorithm Optimization Models" Remote Sensing 16, no. 13: 2324. https://doi.org/10.3390/rs16132324
APA StyleMiao, H., Chen, X., Guo, Y., Wang, Q., Zhang, R., & Chang, Q. (2024). Estimation of Anthocyanins in Winter Wheat Based on Band Screening Method and Genetic Algorithm Optimization Models. Remote Sensing, 16(13), 2324. https://doi.org/10.3390/rs16132324









