Seasonal–Longitudinal Variability of Equatorial Plasma Bubbles Observed by FormoSat-7/Constellation Observing System for Meteorology Ionosphere and Climate II and Relevant to the Rayleigh–Taylor Instability

Abstract

The FormoSat-7/Constellation Observing System for Meteorology, Ionosphere, and Climate II (FS7/COSMIC2) program has acquired over three hundred thousand equatorial plasma bubble (EPB) observations from 2019 to 2023 in the equatorial and near low-latitude regions. The huge FS7/COSMIC2 database offers an opportunity to perform statistical inspections of the proposed hypothesis on seasonal versus longitudinal variability of EPB occurrence rates relevant to the Rayleigh–Taylor (R-T) instability. The detected EPBs are distributed along the magnetic equator with a half width of ~20° in geomagnetic latitude. The obtained EPB occurrence rates in local time (LT) rose rapidly after sunsets, and could be deconstructed into two overlapped Gaussian distributions resembling a major peak around 23:00 LT and a minor peak around 20:20 LT. The two groups of Gaussian-distributed EPBs in LT were classified as first- and second-type EPBs, which could be caused by different mechanisms such as sporadic E (Es) instabilities and pre-reversal enhancement (PRE) fields. The obtained seasonal–longitudinal distributions of both types of EPBs presented two diffused traces of high occurrence rates, which happened near the days and longitudes when and where the angle between the two lines of magnetic declination and solar terminator at the magnetic equator was equal to zero. Finally, we analyzed the climatological and seasonal–longitudinal variability of EPB occurrences and compared the results with the physical R-T instability model controlled by Es instabilities and/or PRE fields.

1. Introduction

Ionospheric plasma density irregularities could induce radio-signal phase and amplitude scintillations in the receiving transionospheric radio wave. It is well-known that such transionospheric radio signal scintillations are caused by a scattering mechanism as radio waves propagate through random electron density (N_e) fluctuations, especially within the F-region ionosphere where the irregularity layer is sufficiently thick [1]. Previous analyses [2] have shown that when radio phase fluctuations (i.e., phase scintillations) reach a certain limiting value, the intensity of amplitude scintillation ceases to increase. Ref. [3] demonstrated that ionospheric scintillation effects are most intense in the equatorial and low-latitude regions, moderate at high latitudes, and minimum at middle latitudes. Specifically, equatorial plasma bubbles (EPBs) refer to irregular plasma density depletions observed by satellites and ground-based backscattering radar and distributed around magnetic equatorial and low-latitude regions after sunsets [4,5]. Another phenomenon, termed equatorial spread F (ESF), stems from the “spread” of ionospheric echoes in recorded ionograms obtained with ground-based high-frequency sounding radars, and is also due to the spectral distribution of ionospheric N_e irregularities.

A basic understanding of EPB causality can be evaluated according to the growth rate γ of generalized Rayleigh–Taylor (R-T) instabilities [6,7,8,9]. Based on earlier investigations [6,10], Ref. [9] derived a formula for generalized R-T growth rate at the magnetic equator as follows:

$$\gamma =\frac{{\Sigma }_p^F}{{\Sigma }_p^E+{\Sigma }_p^F}\left(V_p-U_n^p-\frac{g_L}{{\nu }_{in}^{eff}}\right)\frac{1}{L_n}-R_T,$$

(1)

where Σ_p^E and Σ_p^F are the flux-tube integrated Pederson conductivities at the E- and F-region ionosphere, respectively; V_p is the vertical component of plasma drift due to the zonal component of the electric field E at the magnetic equator; U_n^p is the Pederson conductivity-weighted neutral wind velocity perpendicular to the magnetic field B; g_L represents the altitude-corrected gravity acceleration; ν_in^eff is the effective ion-neutral collision frequency; L_n is the scale length of the vertical gradient of plasma densities in the bottomside F-region ionosphere; and R_T is the flux-tube integrated recombination rate of electrons and ions. We note that L_n is positive in the bottomside of the F layer. An eastward E, downward U_n^p, or downward g_L could contribute to a positive growth rate γ. Equation (1) also indicates that EPBs could grow rapidly at longitudes where the zonal gradients of Σ_p^E at the dusk meridian are strong. Ref. [11] established that the steepest gradients in Σ_p^E occur where magnetic flux tubes align with the sunset terminator, and the maximum rate of EPB should occur near the days and longitudes when and where the angle α between the two lines of magnetic declination and solar terminator at the magnetic equator is close to zero. The general features of Tsunoda’s hypothesis for seasonal versus longitudinal variability on EPB occurrences have been demonstrated by [12,13,14,15].

Equation (1) indicates that γ should grow with the vertical plasma drift V_p, defined as E × B/B², with the zonal component of the electric field E and the geomagnetic field B at the magnetic equator. Ref. [16] showed that the vertical plasma drifts after and near local sunsets are characterized by an enhanced eastward electric field, called pre-reversal enhancement (PRE), due to the zonal neutral wind and conductivity gradient developed by the solar terminator interaction. As a result, the ionosphere moves upward and develops steep density gradients and large-scale plasma depletions in the bottomside F region where it becomes unstable to trigger the R-T instability.

In this study, we aim to deduce trends in the overall occurrence and quiet-time variability of EPBs, rather than examining the characteristics of isolated events. There are several studies on the structures, movements, and other characteristics of recent EPB events [17,18,19,20]. Furthermore, low-latitude ionospheric N_e irregularities can also be dictated by solar transients, such as magnetic storms [21], which are not discussed in this paper. Many investigations [22,23,24,25,26,27] have presented identifiable seeding mechanisms that produce turbulence which can then be amplified into an EPB by the R-T instability mechanism. The physical properties of specific seed perturbations are important in understanding EPB development, onset criteria, and developed EPB characteristics. However, it can be argued that if the R-T growth rate γ is high enough, one small perturbation will cause a plasma bubble; meanwhile, if γ is low, no perturbation will be able to cause a plasma bubble. Thus, the first problem of EPB predictability could be reduced to the estimation of the R-T instability growth rate of the specific ambient background ionosphere. We note that Tsunoda’s hypothesis does attempt to explain the appearance of differences in EPB occurrence rate distributed near the days and longitudes when and where the magnetic field declinations closely align with the sunset terminator. It seems that Tsunoda’s hypothesis itself is not sufficient to explain the intensities and extents of EPB distributions that are subject to seasonal, longitudinal, and solar cycle variability, as well as other geophysical factors.

This paper presents seasonal–longitudinal trends of EPB occurrences, lending support to the physical R-T instability model controlled by PRE fields and/or Es instabilities. In the following section, we introduce the GNSS-LEO RO amplitude and excess phase data sets from the FS7/COSMIC2 mission and derive amplitude scintillation index and N_e profiles to identify EPB events. We also describe the statistical analyses on EPB distributions versus local time and classify the obtained EPBs into two types at different Gaussian-distributed mean times. In Section 3, we present the seasonal–longitudinal variability of both types of EPB occurrences obtained by FS7/COSMIC2. In Section 4, we simulate the seasonal–longitude trend of R-T instability growth rate depending on PRE fields and compare it with that of the post-sunset (i.e., second-type) EPB occurrences. In Section 5, we discuss the Es instability mechanism of EPB development and compare the seasonal–longitude trend of nighttime equatorial Es instabilities with that of the first-type EPB occurrences. In the conclusion section, we summarize the studied results and point out several problems to be addressed in future studies.

2. EPB Observations from FS7/COSMIC2

Since June of 2019, the Taiwanese–American FS7/COSMIC2 program has executed GPS/GLONASS RO observations of the Earth’s neutral atmosphere and ionosphere using low Earth orbiting (LEO) satellites. Similar to the prior mission, FS3/COSMIC, the FS7/COSMIC2 program is a six-LEO-satellite constellation mission but orbits at 24° inclination and ~550 km altitudes (~720 km altitudes for parking orbits). It can simultaneously receive both L1- and L2-band signals from GPS and GLONASS satellites and provide more than 5000 RO observations per day within the region between the geographic latitudes of ±40°. The completed FS7/COSMIC2 RO observations can be used to retrieve GNSS-LEO limb-viewing N_e and dual-band scintillation index (S4) files at altitudes from the LEO satellite orbits to the Earth’s surface. We note that the scintillation index S4 is most often used to estimate amplitude scintillation and is defined as a normalized variance of the signal intensity A²:

$$S4=\frac{\sqrt{〈A^4〉-{〈A^2〉}^2}}{〈A^2〉}.$$

(2)

Refs. [28,29] showed that a GPS RO scintillation observation is complete when the sampling spatial scale is less than the first Fresnel zone (i.e., the sampling frequency is higher than the Fresnel frequency). Otherwise, undersampling occurs and the derived S4 value is underestimated. 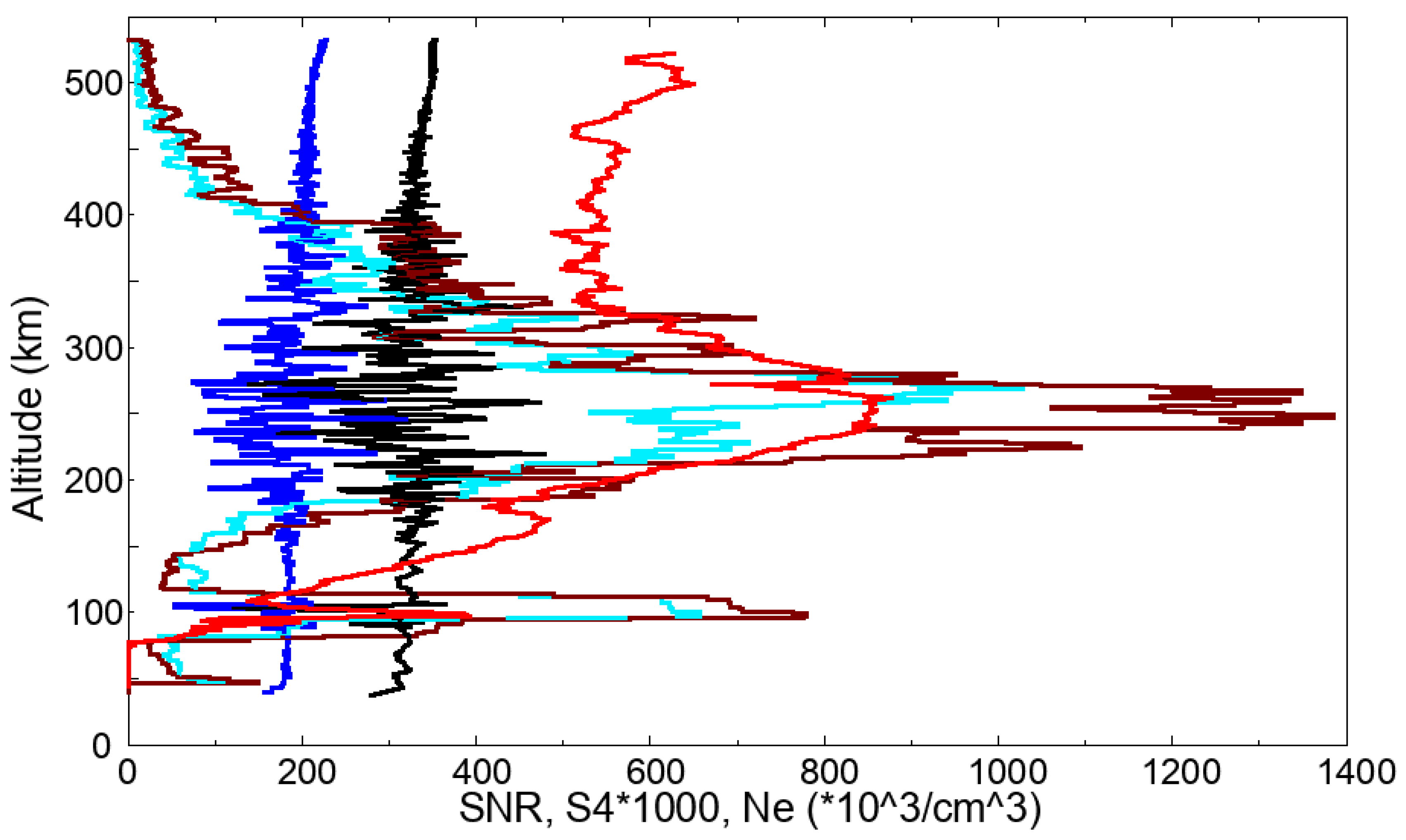Applicable to the complete and oversampled S4 profiles, a criterion of 0.3 for the maximum L1-band S4 value (S4L1max) at F-region altitudes was selected for identifying scintillation and/or EPB events, as used in former investigations [28,30]. An identified EPB example from an FS7/COSMIC2 RO observation is shown as Figure 1. The corresponding signal-to-noise ratio (SNR) and the raw excess phase and scintillation index data are available from the Taiwan Analysis Center for COSMIC (TACC, http://tacc.cwa.gov.tw/data-service/ (accessed on 10 January 2024)) and the COSMIC Data Analysis and Archive Center (CDAAC, http://cdaac-www.cosmic.ucar.edu/ (accessed on 10 January 2024)). More details about the diagnostics of F-layer scintillation observations using FS3/COSMIC RO data are presented in [28,29].

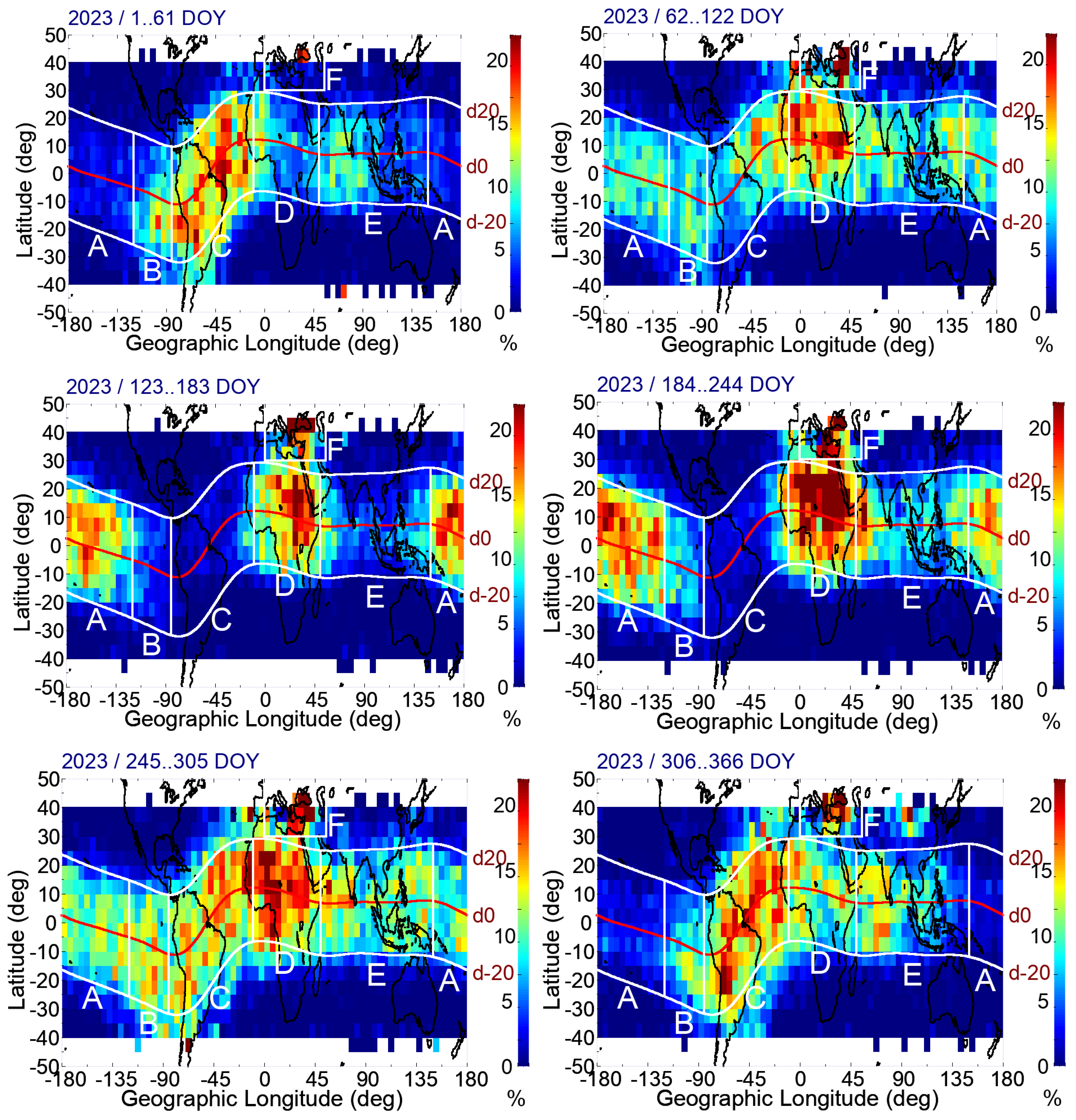
From 2019 to 2023, the FS7/COSMIC2 program acquired over 7,500,000 complete ionospheric RO observations at the equatorial and near low-latitude regions, and around 300,000 (i.e., 4%) of these observations are identified as EPB events. Figure 2 shows six bimonthly geographical occurrence distributions of EPB or F-layer scintillation events in 2023. The EPB (or F-layer scintillation) occurrence rates are defined as the ratios of EPB (or F-layer scintillation) event numbers to complete RO observation numbers and are expressed as a percentage within every 5° by 5° in the geographic bin and during every sixty-one days (approximately two months), excluding disturbed days with an averaged geomagnetic activity index Kp > 3. The other bimonthly geographical occurrences of EPBs from 2020 to 2022 showed similar distributions but lower rates, while solar activities were weaker than those in 2023. The details of daily EPB occurrence rates will be presented and discussed in the following paragraphs. We note that the detected EPBs distributed along the magnetic equator with a half width of ~20° in geomagnetic latitude. Five low-latitude zones were identified as Zone A (the Central Pacific area), B (the East Pacific area), C (the South American area), D (the African area), and E (the South Asian area), as shown in Figure 2, which showed different seasonal scintillation characteristics. We also identified Zone F located in the Mediterranean and South European areas for “mid-latitude” irregularities, but we did not further study and discuss this issue. We note that the EPB distributions comprised an equatorial and low-latitude region within the 20° and −20° geomagnetic latitudes, which roughly agreed with the ionospheric N_e irregularity occurrence distributions observed by the in situ Ionospheric Plasma and Electrodynamics Instrument (IPEI) during the ROCSAT1 mission from 1999 to 2004 [31].

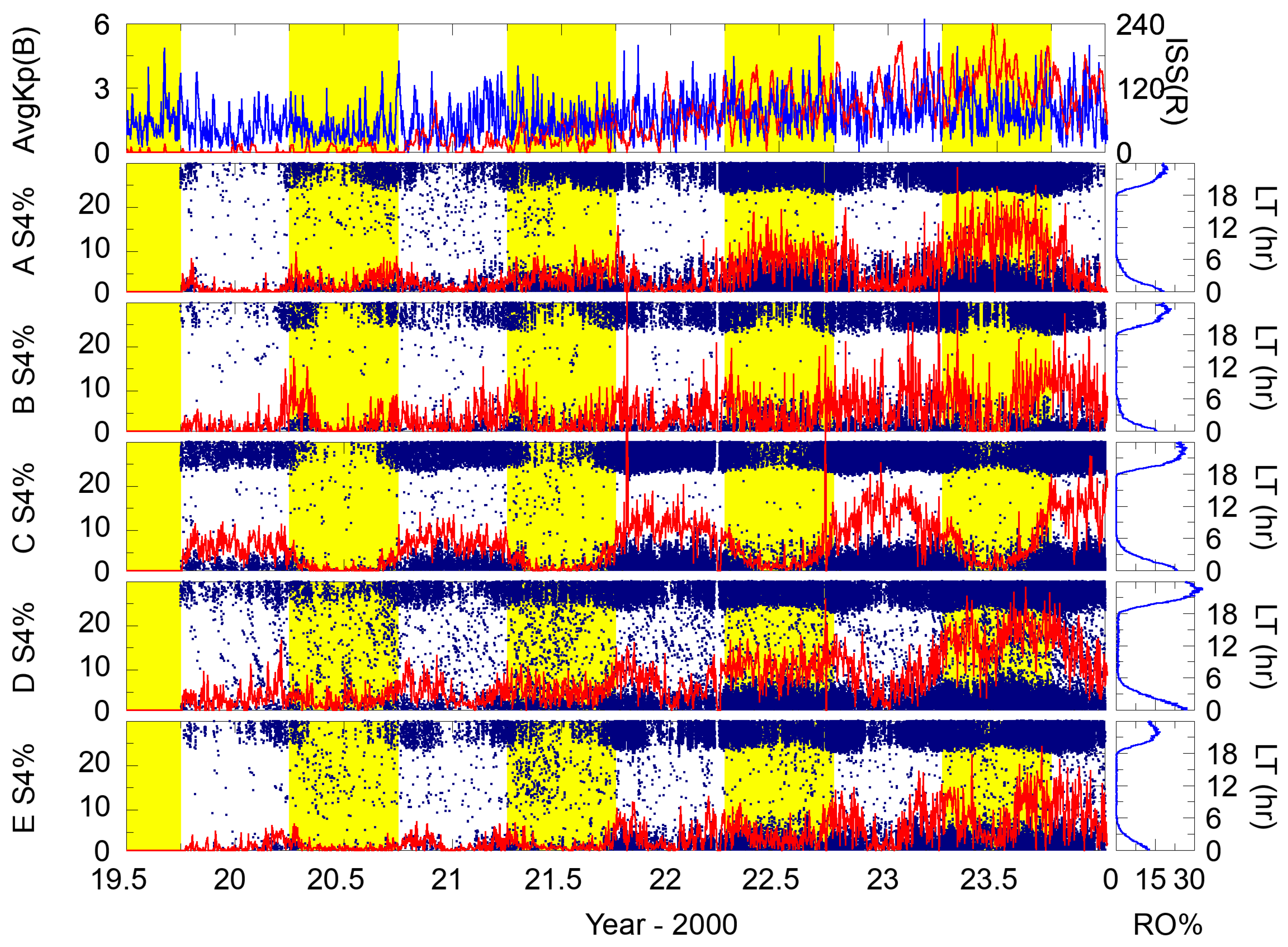
We examined the EPB occurrence characteristics of the five identified low-latitude zones as related to season, local time, magnetic activity, and solar activity. Figure 3 shows the temporal profiles of daily averaged geomagnetic activity index (Kp), international sunspot number (ISS), and zonal EPB occurrence rates from mid-2019 to the end of 2023. Some typical RO scintillation occurrence characteristics were found and should be noticed. We note that solar activities increased yearly from 2019 to 2023, and the averaged EPB occurrence rates of the five identified zones also increased yearly from 2019 to 2023. There were a few strong geomagnetic disturbances from 2019 to 2023. However, in this study, we focused on the relatively quiet geomagnetic conditions when geomagnetic activity was limited by daily averaged Kp values of less than 3. We also note that the zonal EPBs and/or scintillations were significantly lower during daytime. Furthermore, Zones A and D (i.e., the Central Pacific area and the African area) had similar seasonal trends in EPB occurrences, which showed a diffuse maximum from April to September and a diffuse minimum from October to March. The seasonal EPB occurrence trends of Zone C (the South American area) were almost opposite to those of Zones A and D. Zones B and E (i.e., the East Pacific area and the South Asian area) had transitional EPB occurrence trends, which showed stronger rates in equinoctial months (i.e., February, March, April, August, September, and October) and weaker rates in solstice months. On average, such EPB events were most intense in the South American and African areas, moderate in the Central Pacific area, and minimum in the East Pacific and South Asian areas.

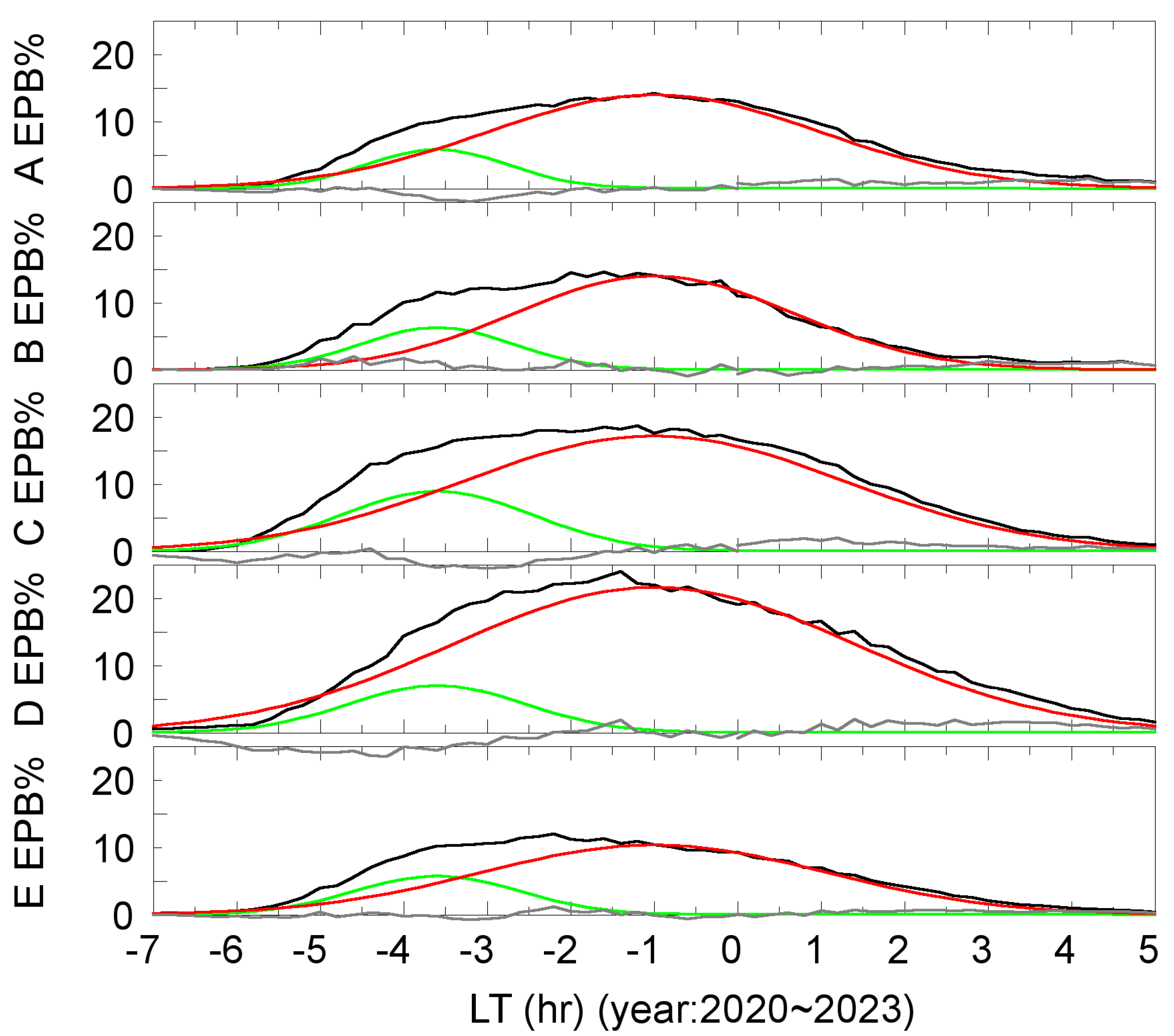
For all five identified low-latitude zones, almost all the observed EPBs occurred at nighttime. As illustrated in the five right subpanels of Figure 3, the EPB occurrence rates (defined as the ratios of zonal EPB event numbers to complete RO observation numbers as a function of local time in 0.2 h resolution) rose rapidly after local sunsets and peaked at around 23:00 LT. However, using the least-squares fitting technique, statistical analyses of zonal EPB occurrence rates versus local time could be implemented to deconstruct the obtained occurrence rates into two overlapped Gaussian distributions. Based on the FS7/COSMIC2 data from 2020 to 2023, Figure 4 shows the deconstructed Gaussian distributions resembling a major peak around 23:00 LT and a minor peak around 20:20 LT for Zones A to E separately. We note that the yearly zonal EPB occurrence rates could also be deconstructed into two overlapped Gaussian distributions in local time similar to those shown in Figure 4, and the resulting Gaussian-distributed peak rates were highly correlative with solar activities.

3. Seasonal–Longitudinal Variability of EPB Occurrences Observed by FS7/COSMIC2

Based on the statistical distribution analyses of zonal EPB occurrence rates versus local time, as shown in Figure 4, the two groups of Gaussian-distributed EPBs in LT could be caused by different mechanisms and be classified into first- and second-type EPBs with different mean LTs at 23:00 and 20:20. Many earlier investigations also presented different characteristics of ESF events observed by ground-based ionosondes and VHF radars. Referring to the second-type EPBs, the post-sunset ESFs were observed from irregular traces of range-type equatorial spread F in ionograms [32,33]. On the other hand, the first-type EPBs can refer to post-midnight ESFs which were observed as frequency-type spread F [32,33,34] due to weak field-aligned irregularities [35]. For all the five identified zones, the first-type EPBs had higher peaks and wider widths of occurrence rate distributions in local time than the second-type EPBs. We estimated the daily occurrence rates of the first-type EPBs to be approximately double the accumulated rates from the experimental mean (23:00 LT) to a rough end (e.g., 4:00 LT) of the distribution in a targeted zone, and those of the second-type EPBs to be one and a half times the accumulated rates from local sunsets to the corresponding experimental mean (20:20 LT) of the distribution. 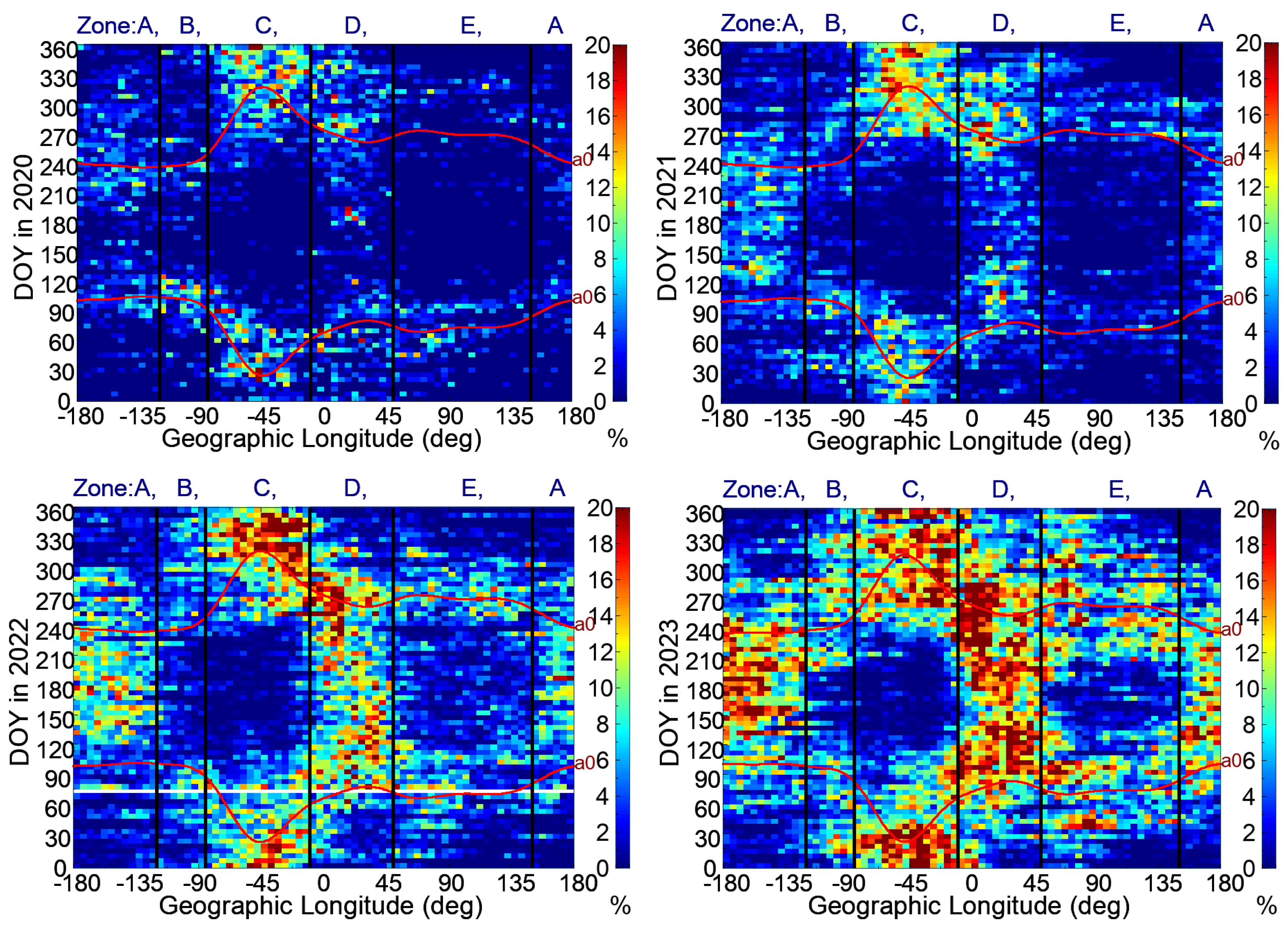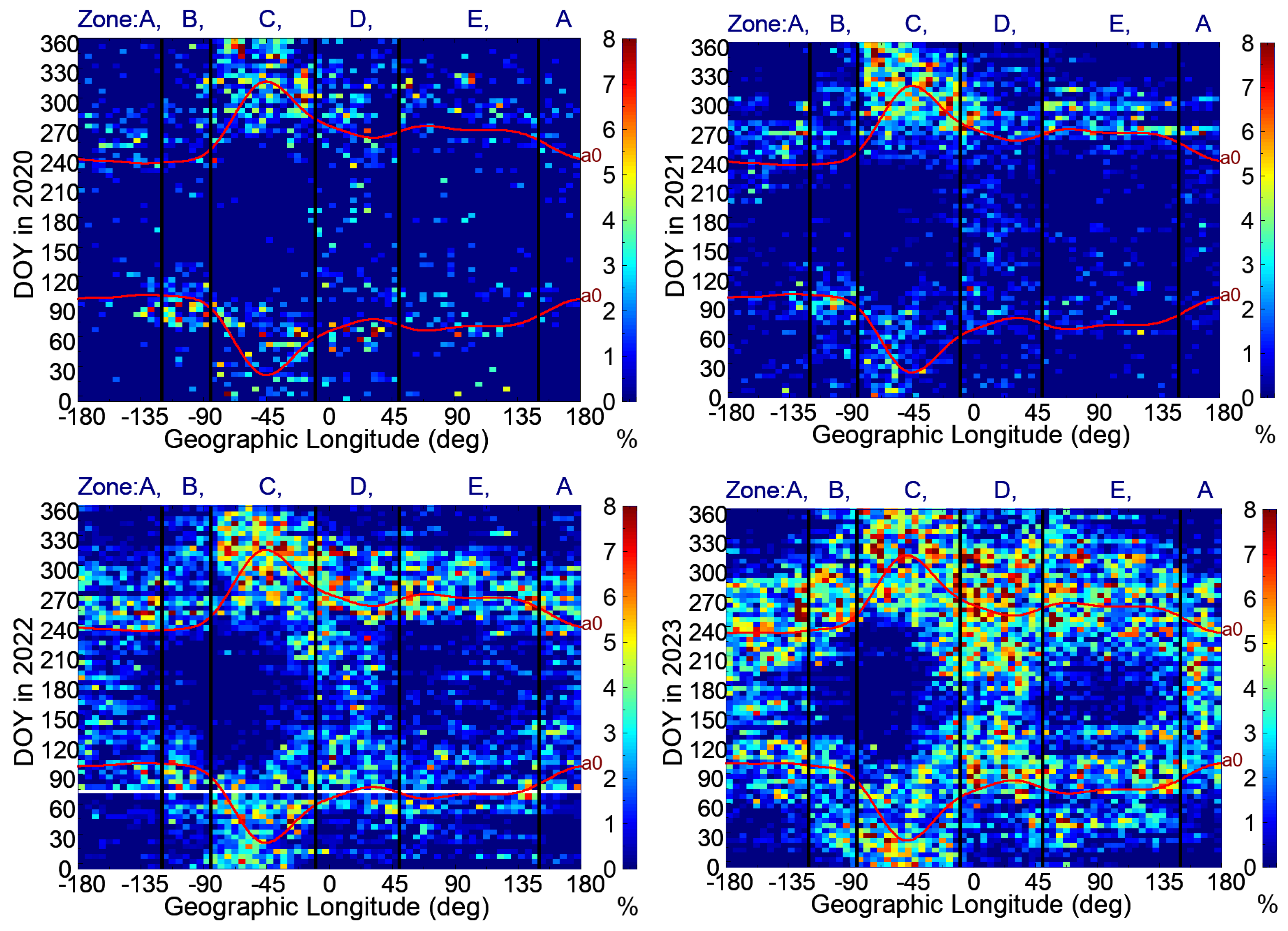Figure 5 and Figure 6 show the yearly distribution maps of the first- and second-type EPB occurrence rates, respectively, as a function of DOY (day of year) and geographic longitude based on the FS7/COSMIC2 RO observations from 2020 to 2023. The EPB occurrence rates were determined within every bin of 5 days by 5° geographic longitudes and within ± 20° geomagnetic latitudes.

In general, the averaged occurrence rates of both first- and second-type EPBs increased yearly with solar activities from 2020 to 2023. The yearly seasonal–longitudinal occurrence trends of both types of EPBs were similar, but the occurrence rates of the first-type EPBs were approximately double to triple those of the second-type EPBs. Furthermore, we note that there were two diffused seasonal–longitudinal traces of intense EPB events, which happened near the days and longitudes when and where the angle α between the two lines of magnetic declination and solar terminator at the magnetic equator was equal to zero. However, as shown in Figure 5 and Figure 6, the intense EPB days expanded from the seasonal–longitudinal curves of α = 0 were different in different zones. The seasonal–longitudinal EPB occurrence trends of Zones A and D (i.e., the Central Pacific area and the African area) had more intense EPB days from April to September. The seasonal–longitudinal EPB occurrence trends of Zone C (the South American area) had more intense EPB days from October to March and were almost opposite to those of Zones A and D. Zones B and E (i.e., the East Pacific area and the South Asian area) had more or less 30 intense EPB days expanded from the curves of α = 0, which happened in equinoctial months (i.e., February, March, April, August, September, and October). We note that from the ESF observations by the ground-based ionosonde of the station Fortaleza (38°W, 4°S) [32], the observed range-type ESFs occurred mostly at post-sunset hours and have similar seasonal variation as that shown in this study, and the observed frequency-type ESFs occurred at around midnight hours but have different seasonal variation. From the topside sounding results obtained by the Ionosphere Sounding Satellite b (ISS-b) in 1978–1980 [36], the observed ESFs were identified as pre-midnight (18~24 LT) and post-midnight (0~6 LT) events, which had similar activities and seasonal–longitudinal variability as that shown in this study. Furthermore, the solar activity correlations and the seasonal–longitudinal patterns of both first- and second-type EPB occurrence rates highly agree with those of EPB observations obtained by Defense Meteorological Satellite Program (DMSP) satellites from 1989 to 2004 [14,15].

4. Predictability of R-T Instability Growth Rate Due to PRE Electric Fields

Observations using VHF radars [4,37] present close connections between the vertical movements of the equatorial evening ionosphere and the occurrences of plasma depletion and irregularity. A theoretical study [38] has also demonstrated the coupling between the E and F regions and its effect on F-region drift. It is well known that the daytime upward plasma drift and its reversal at nighttime are caused by eastward and westward electric fields in the equatorial F region, respectively. Apart from this, a zonal thermospheric wind U, blowing eastward from the dayside to the nightside of the F-region ionosphere, produces a downward electric field, Ez = −U × B, at sunset hours. This vertical polarization electric field projects to an equatorward field in the E layer, which tends to drive a westward Hall current and then produces negative charges and zonal electric fields crossing the sunset terminator. The resulting zonal electric field projects back to the F layer [16,39]. Thus, the eastward electric field E in the F region is enhanced after and near local sunsets and produces upward plasma movements Vz due to the E × B drift. This phenomenon is called pre-reversal enhancement (PRE). Ref. [40] showed that Vz enhancements also start after and near local sunsets, but approach the maxima a couple hours after sunsets.

Due to the PRE electric field and its induced upward E × B drift, the R-T instability growth rate factor of EPB development in the bottomside F region has been proposed by [8]:

$$\gamma =\left(\frac{E\times B}{B^2}-\frac{g_L}{{\nu }_{in}^{eff}}\right)·\frac{\nabla N_e}{N_e},$$

(3)

which is similar to the first term of Equation (1) but excludes the impacts of flux-tube integrated Pederson conductivities and vertically neutral winds. In this equation, the two parameters are the vertical plasma drift E × B/B² and the vertical component of bottomside F-layer N_e gradient ratio. We assumed the enhanced eastward electric field E$\propto$Ez = −U × B $\propto \left(\cos \alpha \right)B$ and approximated the vertical bottomside N_e gradient ratio to be the reciprocal of the F-layer scale height H. A relative R-T instability growth rate γ_r can be defined using the following equation:

$${\gamma }_r\propto \frac{{\cos }^2\alpha }{H},$$

(4)

where α is the angle between the two lines of magnetic declination and sunset terminator at the magnetic equator.

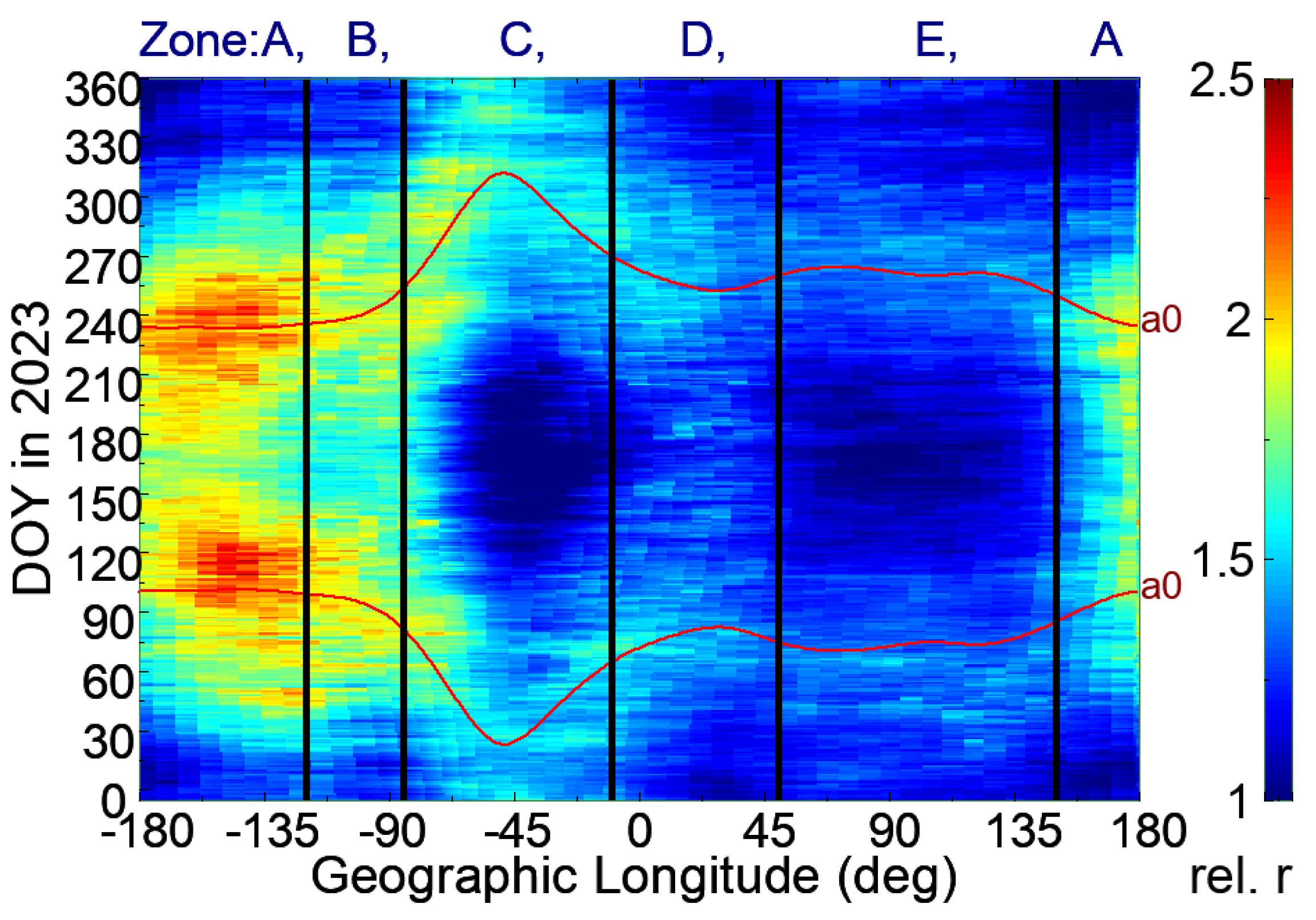
We evaluated the impacts of the angle α on the R-T instability growth rates and EPB occurrences. Figure 7 shows the α map of DOY versus geographic longitude (i.e., seasonal–longitudinal map of the angle α) in 2023. The other yearly seasonal–longitudinal maps of the angle α from 2020 to 2022 are almost the same as Figure 7. In this study, the values of the solar terminator were calculated based on the equations from [41], and the values of the magnetic fields and their declinations were derived based on the International Geomagnetic Reference Field (IGRF) model [42]. As shown in Figure 7, the two red curves represent the days and longitudes when and where α = 0°, and at every geographic longitude, the α values as a function of DOY are almost symmetric with respect to the mid of the year. The seasonal–longitudinal pattern of the angle α when it is less than 15°, which is zoned by the four white curves, is like that of the high second-type EPB occurrence rates shown in Figure 6, except for Zone D. We note that the seasonal–longitudinal zone of |α| $\le$ 15° in Zone D (i.e., the African area) has approximately 30 days only when expanded from the curves of α = 0° and is different to those for the high second-type EPB occurrence rates in most of the days from May to July.

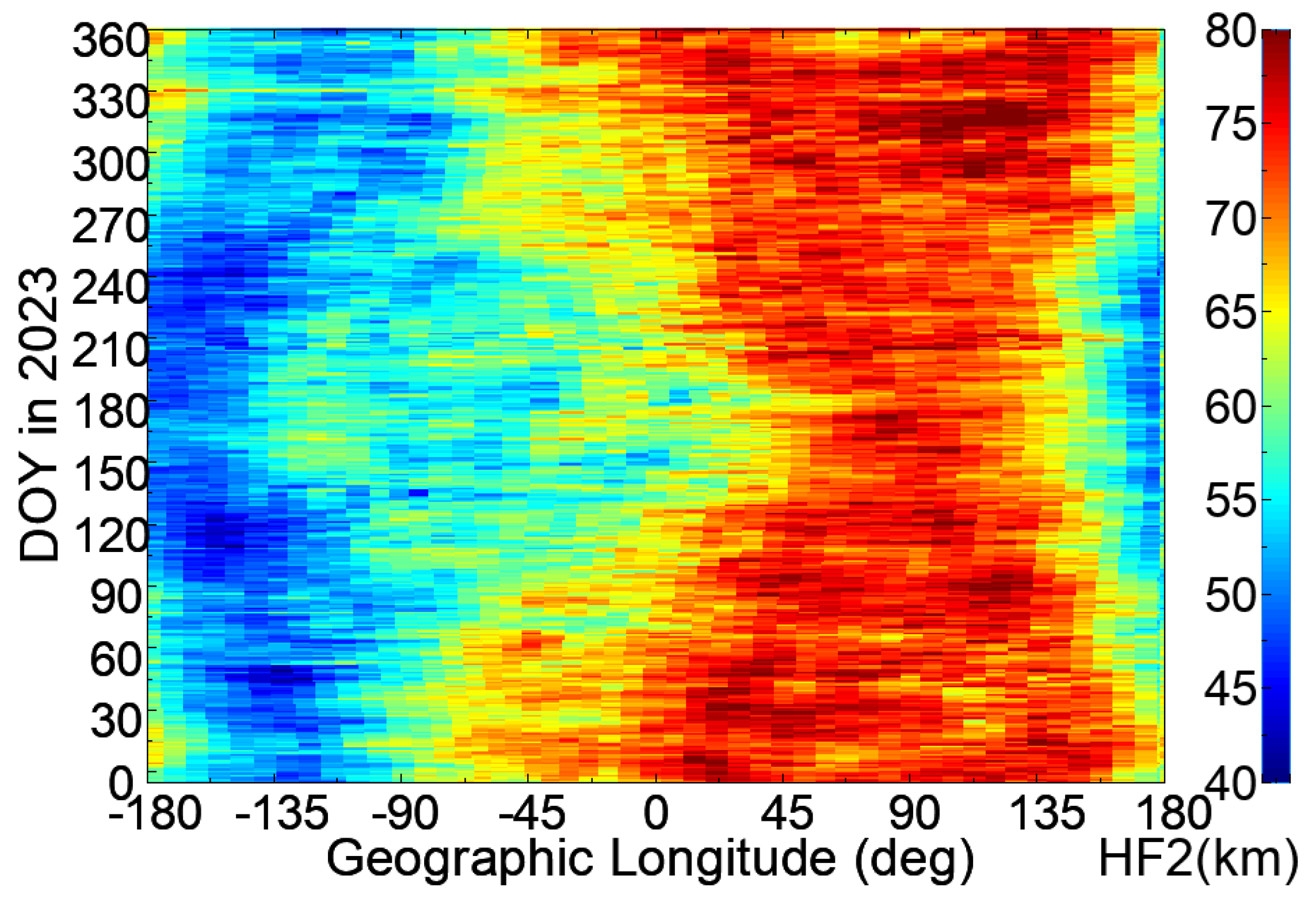
To evaluate the impacts of the bottomside F-layer scale height H on the R-T instability growth rates and EPB occurrences, we estimated the H values based on a three-dimensional N_e model named the TaiWan Ionospheric Model (TWIM) [43]. The TWIM is a global numerical N_e model in half-hour resolution and is constructed from windowed (10 days in season and one hour in universal time) and weighted vertical N_e profiles, with approximately 2500 profiles, retrieved from FS7/COSMIC2 GNSS RO measurements. The TWIM exhibits vertically fitted Chapman layers, with distinct F2, F1, E, and D layers, and surface spherical harmonic approaches for the fitted Chapman-layer parameters, including layered peak density, peak density height, and scale height. Detailed evaluations of the TWIM’s performance are presented in [44,45]. We note that the TWIM exhibits vertically fitted Chapman layers, and the corresponding vertical component of the bottomside F-layer N_e gradient ratio is proportional to the reciprocal of the F-layer scale height H.

Figure 8 shows the seasonal–longitudinal map of the F-layer scale height H from the TWIM at the magnetic equator and at the local time of 20:20 LT in 2023. The H values at 20:20 LT were used because the second-type EPBs reached a peak around 20:20 LT as shown in Figure 4. There is a process from the initiation of EPBs to the peak occurrence, which needs around one or more hours. The second-type EPB mean time at 20:20 LT also matches the time of observed maximum Vz values presented in [40]. After applying Equation (4), we present the seasonal–longitudinal map of the relative R-T instability growth rates due to PRE electric fields in 2023 in Figure 9. Compared to the seasonal–longitudinal pattern of |α| $\le$ 15° shown in Figure 7, the seasonal–longitudinal zone of high relative R-T instability growth rates in Zone D was better matched to those for high second-type EPB occurrence rates shown in Figure 6 in most of the days from May to July. However, the relative R-T instability growth rates of the five identified low-latitude zones were most intense in Zone A (the Central Pacific area), moderate in Zones B and C (the East Pacific area and the South American area), and minimum in Zones D and E (the African area and the South Asian area), and were different to the results of zonal EPB occurrence rates. In this study, we assumed a constant bottomside F-layer N_e gradient ratio in height. A more detailed and accurate evaluation of bottomside F-layer N_e gradient and its impacts on R-T instability growth rates and EPB occurrences is necessary in future studies.

5. Predictability of R-T Instability Growth Rates Due to Nighttime Es Instability

Ref. [46] was the first study to propose that large-scale wave structures (LSWSs) in the bottomside F layer correlatively appear with EPB occurrences and can be a reliable precursor of EPB occurrences. Refs. [24,47] further suggested that an Es-layer instability situated at a zonal velocity–shear node can generate a polarization electric field Ep. This Es-induced Ep extends along geomagnetic field lines to the base of the equatorial F layer, where it produces a westward and upward Ep × B motion. Ref. [47] derived the upward component of Ep × B drift as follows:

$$V_z\propto {\Sigma }_H^{Es}{U}_x{\cos }^2\delta ,$$

(5)

where ${\Sigma }_H^{Es}$ is Es-layer field-line integrated Hall conductivity, U_x is the zonal component of a neutral wind, and δ is the complement of the magnetic azimuth in the plane transverse to B. The Ep × B motion produces local and regional upwelling and can modulate the ionospheric N_e in the form of an LSWS, which then gives rise to EPBs from its crests.

As mentioned in the previous sections, the FS7/COSMIC2 program also provides 50 Hz signal-to-noise ratio amplitude and excess phase measurements (i.e., the “atmPhs” data from CDAAC and/or TACC) for atmospheric RO observations with GNSS-LEO tangent point altitudes from below the Earth’s surface to around 130 km. Such 50 Hz RO observations could also be used to retrieve L1-band scintillation index (S4L1), normalized L1-band amplitude standard deviation (SDL1), and relative electron density N_e profiles in the E-region ionosphere and detect the Es layer successfully. Based on earlier investigations [29,48,49], an SDL1max criterion of 0.2, which is almost the same as an S4L1max criterion of 0.4, was used to identify an Es event in this study. We note that the reason for using different criteria of 0.3 and 0.4 for S4L1max for identifying EPB events and Es events, respectively, was because we were following the criteria used in previous investigations [28,30,48,49]. 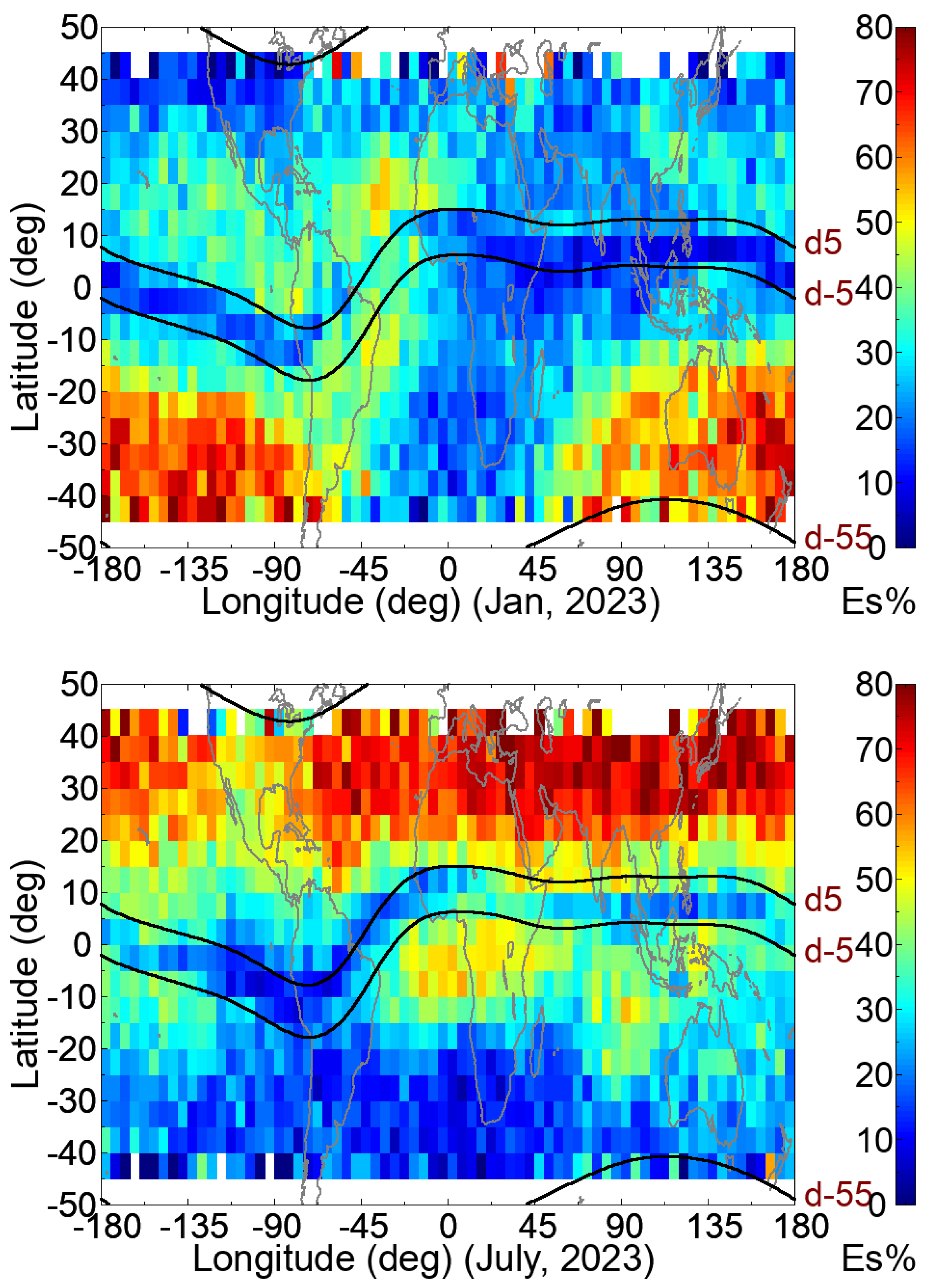Figure 10 shows two example monthly occurrence rate distributions of Es events observed from FS7/COSMIC2 in January and July of 2023. The coded colors represent the Es occurrence rates from zero to eighty percent within every 5° by 5° in the geographic bin, and white bins at geographic latitudes higher than around 40° are not considered as they indicate fewer than ten complete ionospheric RO observations located within each bin area.

As shown in Figure 10, three typical regions, including a geomagnetic equatorial region (Region X: −5° < magnetic latitude (ML) < 5°) and two extended geomagnetic mid-latitude regions (Region Y: 5° < ML < 55°, and Region Z: −55° < ML < −5°), were identified to have different Es climatology; that is, variations within each identified region due to altitude, season, and local time. We found that both extended mid-latitude regions (i.e., Regions Y and Z) had maximum Es activities of around 80%, which occurred during hemispheric summer seasons, as shown in the two example distributions in Figure 10. Meanwhile, there were two areas showing Es occurrence depression during hemispheric summer seasons. One was located around the South Atlantic and African areas (the longitude sector of 40°W–50°E), where the Es occurrence rates were approximately 60% lower than the maximum Es occurrence rate in Region Z, as shown in the upper panel of Figure 10. The other was located around the American area (the longitude sector of 70°~120°W), where the Es occurrence rates were approximately 30% lower than the maximum Es occurrence rate in Region Y, as shown in the lower panel of Figure 10. These Es occurrence depression results can be explained by the wind shear theory [50], which suggests a connection with the horizontal component of the Earth’s magnetic field, leading to distinctive depressions in the two areas.

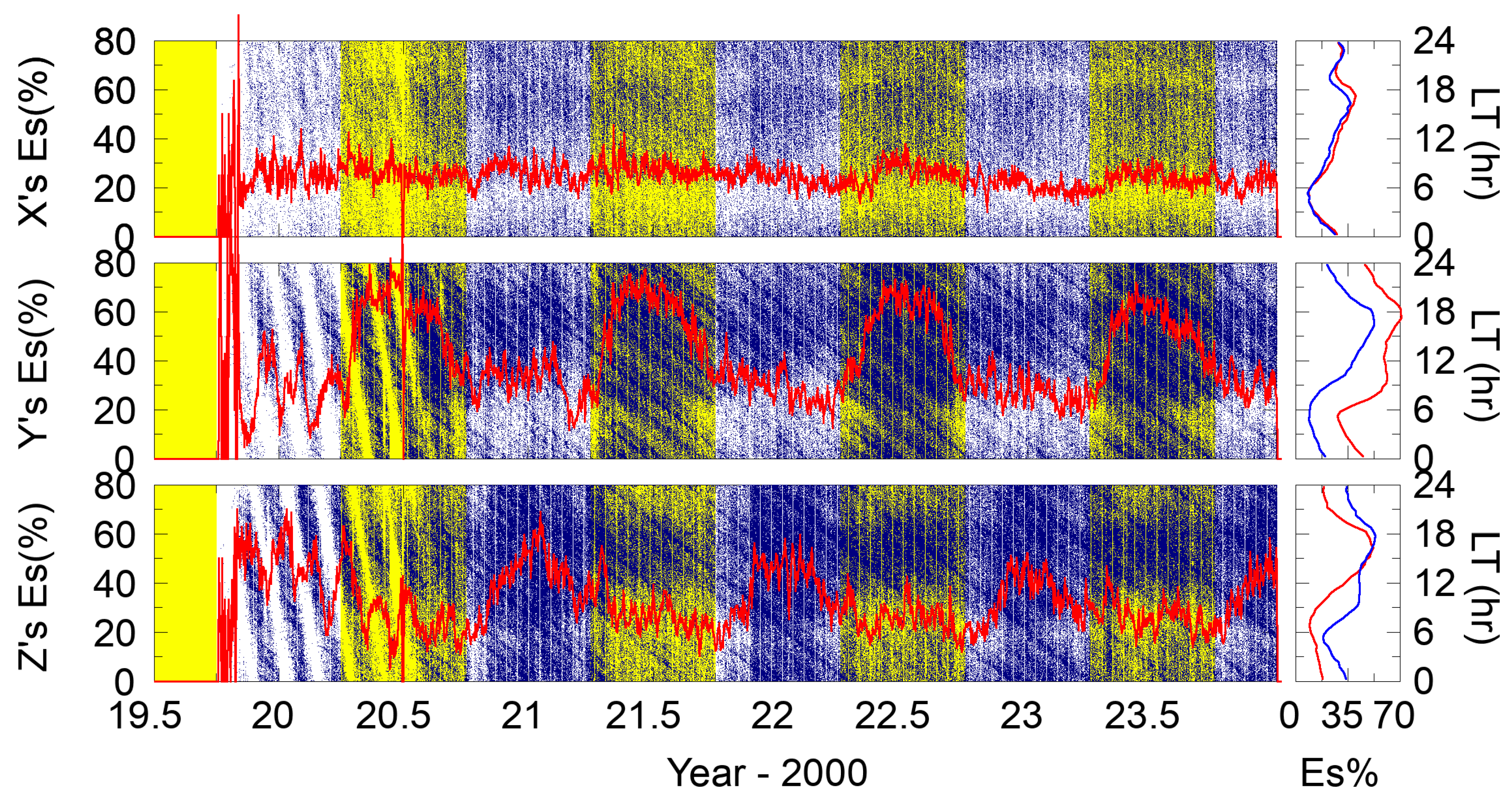
Some detailed regional Es occurrence characteristics related to season and local time are presented in Figure 11. In the figure, the temporal profiles of daily Es occurrence rates and local times of Es occurrences in the three identified regions are presented separately based on the FS7/COSMIC2 “atmPhs” data from 2019 to 2023. In each left panel, the yellow background denotes the “yellow” seasons from April to September, including the northern hemispheric summers, annually, and the white background denotes the “white” seasons from October to March, including the southern hemispheric summers. We note that the obtained zonal Es events were not completely distributed in days, especially in the days of the first year of the FS7/COSMIC2 mission. This is because the FS7/COSMIC2 spacecraft were integrated and launched together, whereupon the six LEO satellites awaited at adjacent parking orbits of ~720 km altitude and were then separated and transferred to orbits from 720 km to 550 km during the earlier phase of the FS7/COSMIC2 program. As mentioned above, both extended mid-latitude regions (i.e., Regions Y and Z) had much higher Es occurrence rates during hemispheric summer seasons. We note that solar activities increased yearly from 2019 to 2023, and there were no significant correlations between the three regional Es occurrence rates and solar activities. The three right subpanels in Figure 11 depict the corresponding regional Es occurrence rates as a function of local time in red and blue lines for “yellow” and “white” seasons, respectively. It is evident that in Regions Y and Z, semidiurnal behavior of Es occurrences was dominant during hemispheric summers, but diurnal behavior was prevalent during hemispheric winters. In subsequent analyses, we focused on the predictability of R-T instability growth rates due to nighttime equatorial Es instability. Other details about the diagnostics of Es-layer observations and morphologies using FS3/COSMIC RO data have already been presented in [48,49].

As shown in the upper-left panel of Figure 11, the temporal profile of daily Es occurrence rate in the geomagnetic equatorial region (Region X) shows more or less than 25% during the days from 2019 to 2023. There was no clear seasonal variation, but the temporal profile shows small diffuse maxima approaching 35% in the mid of 2022 and 2023 with higher solar activities. Furthermore, as illustrated in the upper-right panel showing the Es occurrence rates of Region X as a function of local time, the diurnal occurrence behavior was prevalent and similar during both “yellow” and “white” seasons, and Es occurrences were more active during daytime than nighttime. Es activity had a minimum occurrence rate of ~7% that occurred around local sunrise (i.e., 6 LT), increased steadily afterwards, and approached a maximum of ~40% around local sunset (i.e., 18 LT). After sunset, Es activity decreased to 20% within a couple of hours, increased and approached a minor maximum of ~30% at around 23 LT, and then decreased again slowly to reach a minimum occurrence rate of 7% at sunrise. We note that the minor peak of Es occurrence rates occurring at 23 LT is well matched to the statistical analysis result of the occurrence peak around 23 LT for the first-type EPBs.

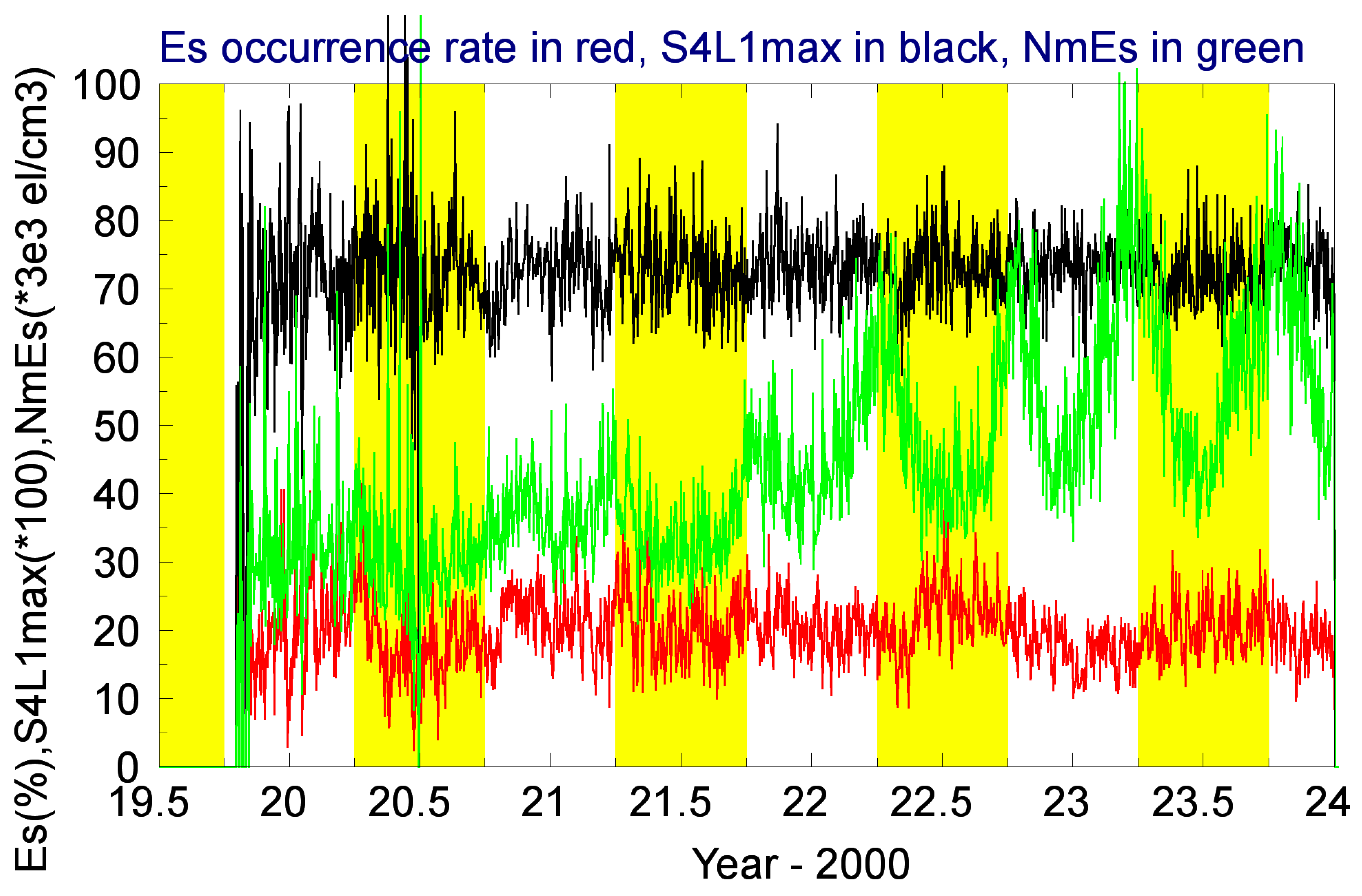
We then examined the nighttime FS7/COSMIC2 RO observations in the magnetic equatorial region (i.e., Region X) only. Figure 12 presents the daily Es occurrence rates, the daily averaged S4L1max values, and the relative N_e values (NmEs) at the Es-layer peaks observed during nighttime (19:00~5:00 LT) for the period from mid-2019 to the end of 2023. As shown in the figure, there was no clear seasonal variation in Es occurrence rates and averaged S4L1max values of the observed nighttime Es layers. However, the daily averaged NmEs values of the observed nighttime Es layers exhibited local maxima during spring and autumn equinoxes, and these seasonal maximum values increased yearly in the same way as solar activities. In this study, the vertical N_e profiles in the E regions were first retrieved using the Abel integral transform through relative GNSS-LEO total electron contents and then calibrated based on an assumed N_e value of zero at an E-layer base of 70 km altitude [49]. Thus, the NmEs values were relative N_es, and the corresponding biases or errors caused by the Abel inversion assumptions were assumed to be mostly calibrated out and, thus, could be ignored.

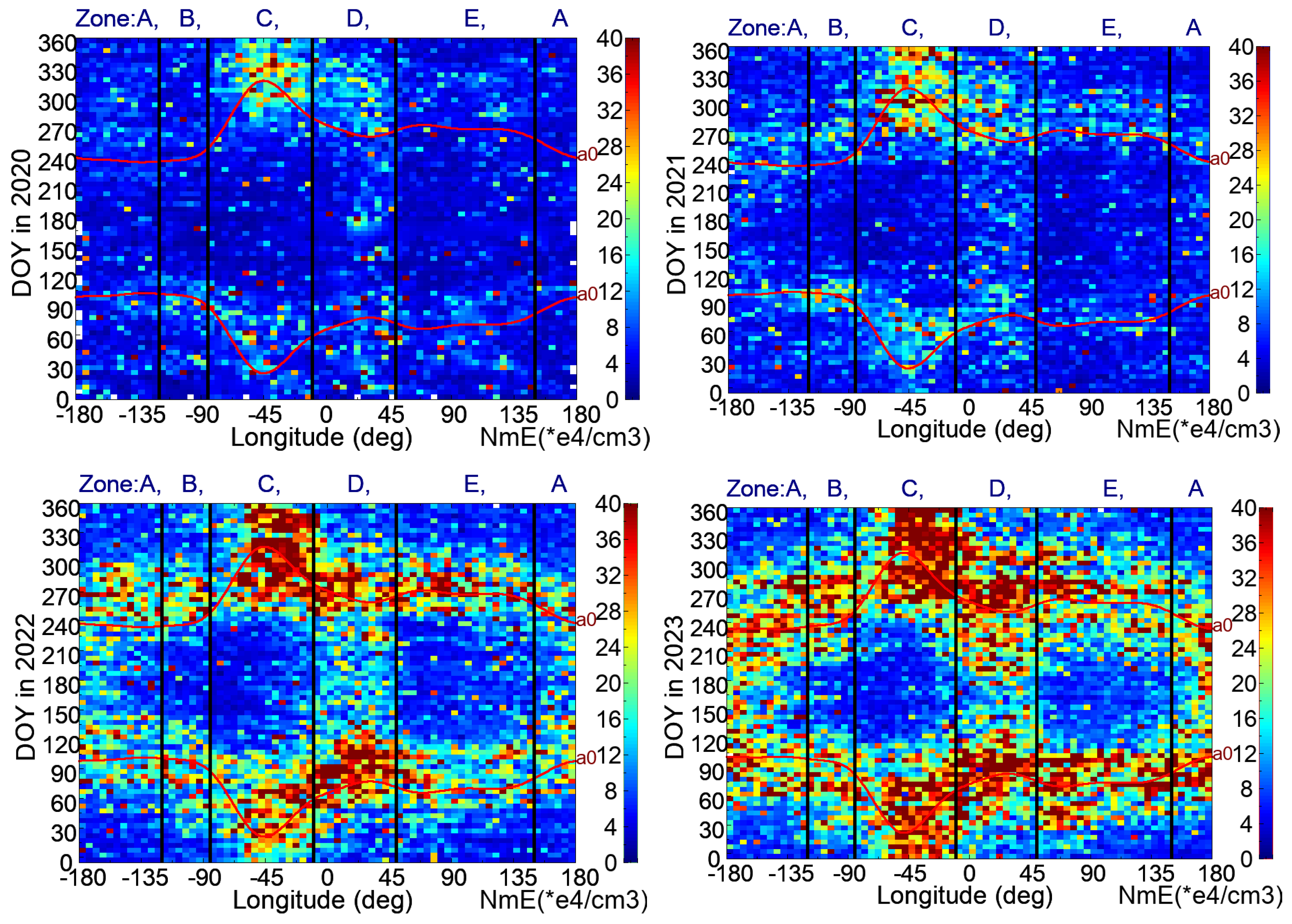
Further analysis was conducted, and the results are shown in Figure 13, which presents the yearly seasonal–longitudinal distribution maps of the averaged nighttime (21:00~01:00 LT) N_e values (NmE) at the E- and Es-layer peaks in Region X from 2020 to 2023. The reason for choosing the nighttime E-layer data from 21:00 LT to 01:00 LT was to examine those seeding the first-type EPBs. To characterize the corresponding seasonal–longitudinal distribution patterns, these maps present the averaged E-layer peak N_e values, which were calculated as the averaged peak N_e (NmE) values of both groups of normal E layers and abnormal Es layers and are usually close to zero at nighttime without Es feature. As shown in the figure, the maximum averaged NmE values increased yearly in the same way as solar activities from 2020 to 2023. Meanwhile, the high NmE distribution patterns of the four yearly seasonal–longitudinal NmE maps are similar. There were two diffused seasonal–longitudinal traces of high NmE values, which happened near the days and longitudes when and where the angle α between the two lines of magnetic declination and solar terminator at the magnetic equator was equal to zero. The two diffused seasonal–longitudinal traces of high NmE values also answer why the daily averaged NmEs values of the nighttime equatorial Es layers had local maxima during spring and autumn equinoxes, as shown in Figure 12.

We note that the high-NmE-spreading days shown in the seasonal–longitudinal curves of α = 0 were different in different identified zones (Zones A to E) and were similar to the seasonal–longitudinal occurrence trends of first-type EPBs shown in Figure 5. Furthermore, on average, such Es events were most intense in the South American and African areas, moderate in the Central Pacific area, and minimum in the East Pacific and South Asian areas. These nighttime NmEs distribution results support the EPB seeding mechanism proposed by the authors of [24,47]. These results confirm that some EPB occurrences, e.g., the first-type EPBs in this study, would likely be controlled by a polarization electric field Ep and induced bottomside F-layer upwelling generated from Es instabilities. Higher NmEs values will produce higher Es-layer field-line integrated Hall conductivities and generate stronger Ep × B drifts and the corresponding upward components, as defined by Equation (5). The implication is that polarization electric fields occur at the base of the F layer or even in the E-F valley region, which must be generated based on Hall polarization processes and driven by Es instabilities, rather than other processes, in the F region. However, Ref. [47] defined the upward component of Ep × B drift as a function of δ (i.e., the complement of the magnetic azimuth in the plane transverse to B), and not α. Further detailed and accurate inspections of the polarization electric field Ep and Ep × B drift induced by Es instabilities depending on the solar terminator are necessary in future studies.

6. Conclusions

In analyzing the climatological variability of EPB occurrences, this study aimed to evaluate the physical and/or experimental predictability of R-T instability. Several analyses were simulated and experimented to gain quantitative understanding of the seasonal–longitudinal trends of R-T instability growth rates controlled by PRE electric fields and Es instabilities. The main results of this study are summarized as follows: (1) Almost all of the EPB events observed by FS7/COSMIC2 occurred after local sunsets and during nighttime and were distributed along the magnetic equator with a half width of ~20° in geomagnetic latitude. (2) The EPB occurrences versus local time were analyzed and deconstructed into two overlapped Gaussian distributions with different peaks at 20:20 and 23:00 LT. (3) Compared with the ground-based ionosonde observations with less post-midnight ESFs, a higher percentage of EPBs occurred at around midnight than post-sunset based on FS7/COSMIC2 GNSS RO observations. (4) Strong seasonal–longitudinal variability characterizes both types of EPB occurrence rates in the same way that the predictability of R-T instability growth rates depends on PRE fields and Es instabilities separately. (5) The seasonal–longitudinal trends of intense EPB occurrences are more or less 30 days expanded from when and where α = 0° but have more intense EPB days during southern (northern) hemispheric summers in the South American area (the Central Pacific area and the Africa area). (6) As shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 12, and Figure 13, the averaged occurrence rates of both types of EPBs as well as the averaged NmEs values of the nighttime equatorial Es layers increased yearly from 2020 to 2023, and were highly correlative with solar activities.

We note that the EPBs occurred at around and post-midnight are initiated during a period when the background electric field is westward. In this condition, the Rayleigh–Taylor instability does not grow. The Es layer instability can compensate the negative background condition for the Rayleigh–Taylor instability, and could contribute to the plasma bubble generation around midnight. Further detailed and accurate inspections of the polarization electric field Ep and Ep × B drift induced by Es instabilities depending on the solar terminator are necessary for better understanding of EPB development. The ultimate goal would be to search and identify the seeding mechanisms and improve the predictive model to the level when and where night-to-night EPB predictability becomes practical.