Ionosphere-Weighted Network Real-Time Kinematic Server-Side Approach Combined with Single-Differenced Observations of GPS, GAL, and BDS
Abstract
1. Introduction
2. Materials and Methods
2.1. Brief Review of VRS Technology Principles and Server-Side Data Processing Flows
2.2. GNSS Observation Equations
2.3. Full-Rank Single-Differenced Ionosphere-Weighted Functional Model
2.4. Stochastic Model
2.5. Ambiguity Closure Check
2.6. Virtual Observation Generation
3. Results
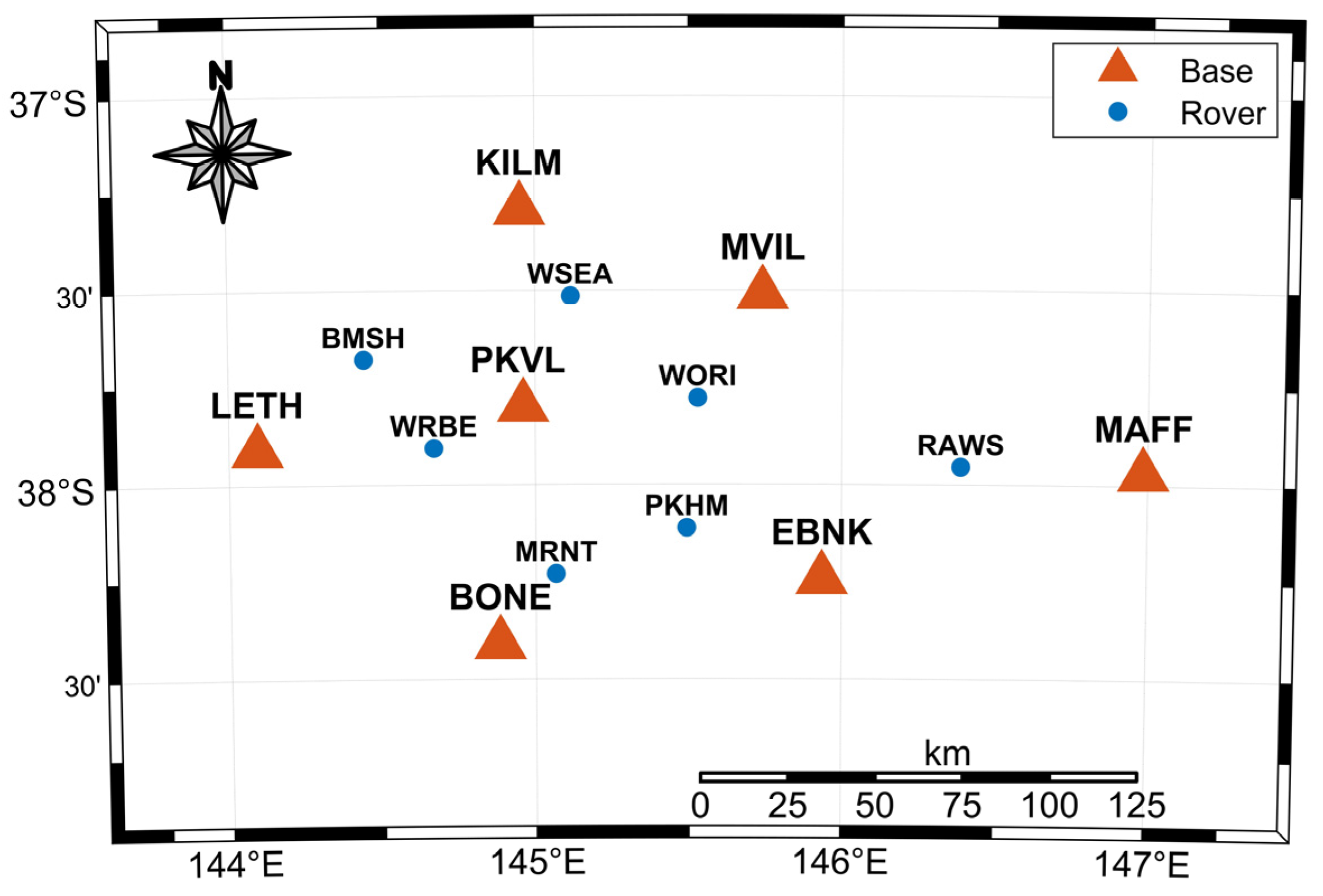
3.1. GNSS Data Collection and Processing Strategy
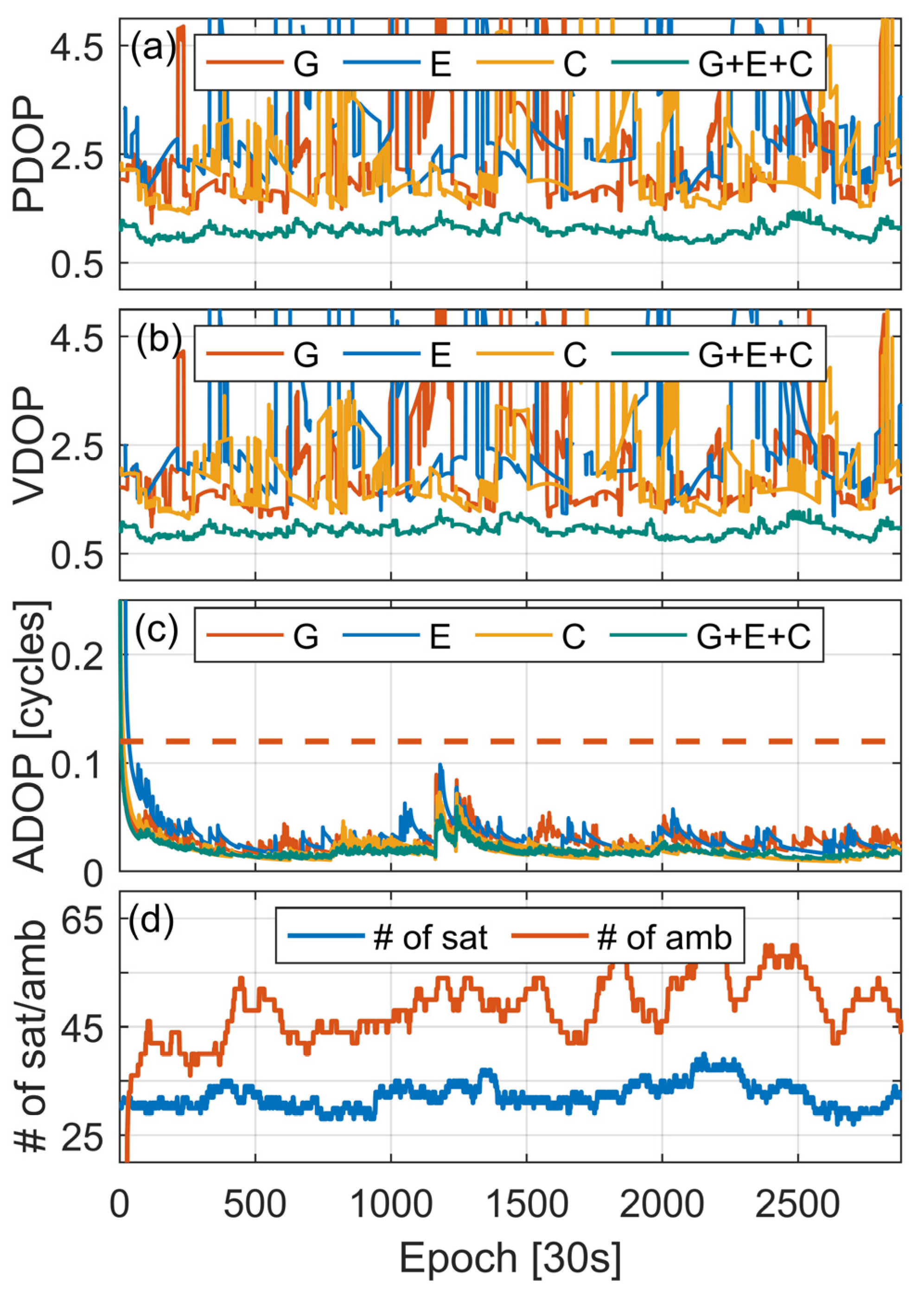
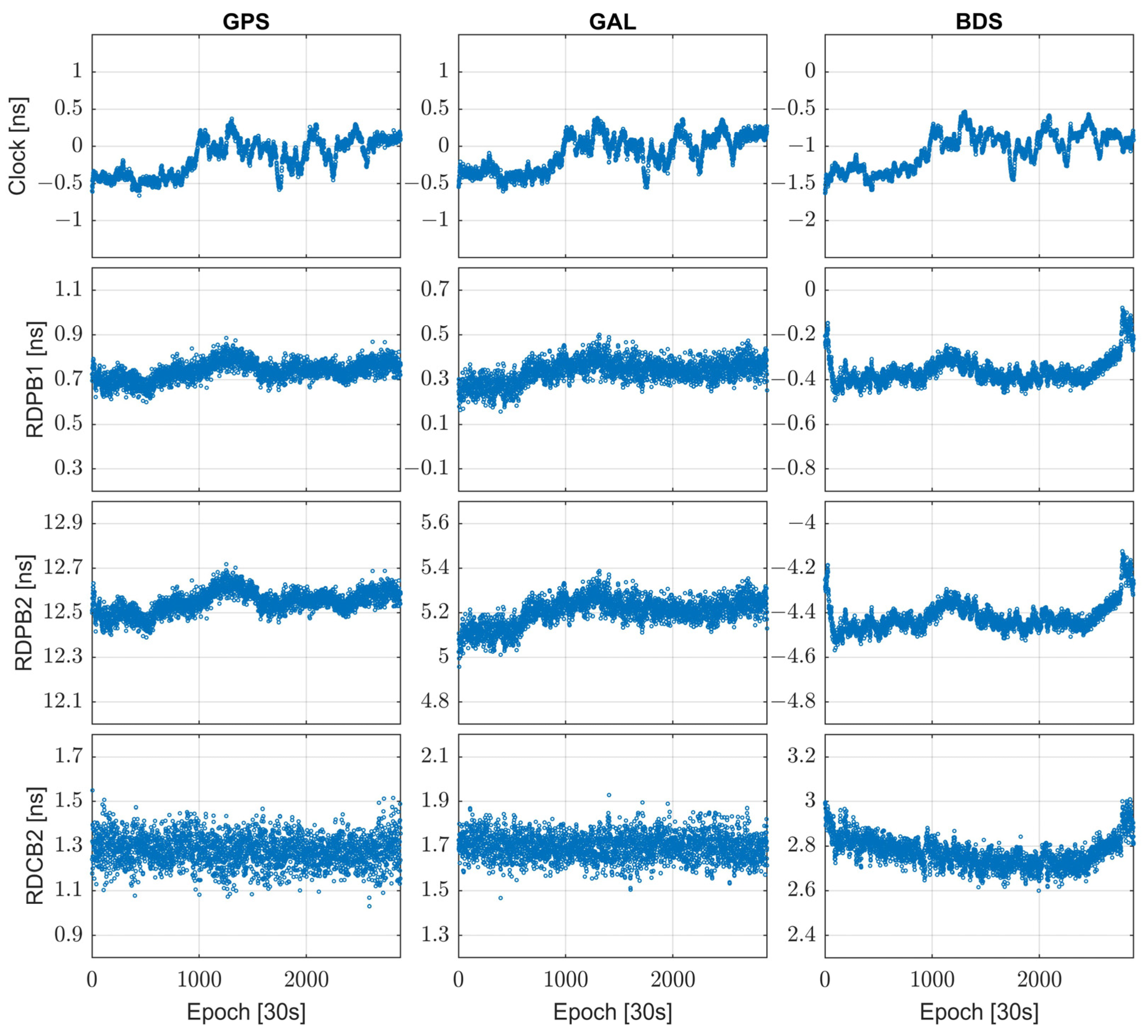
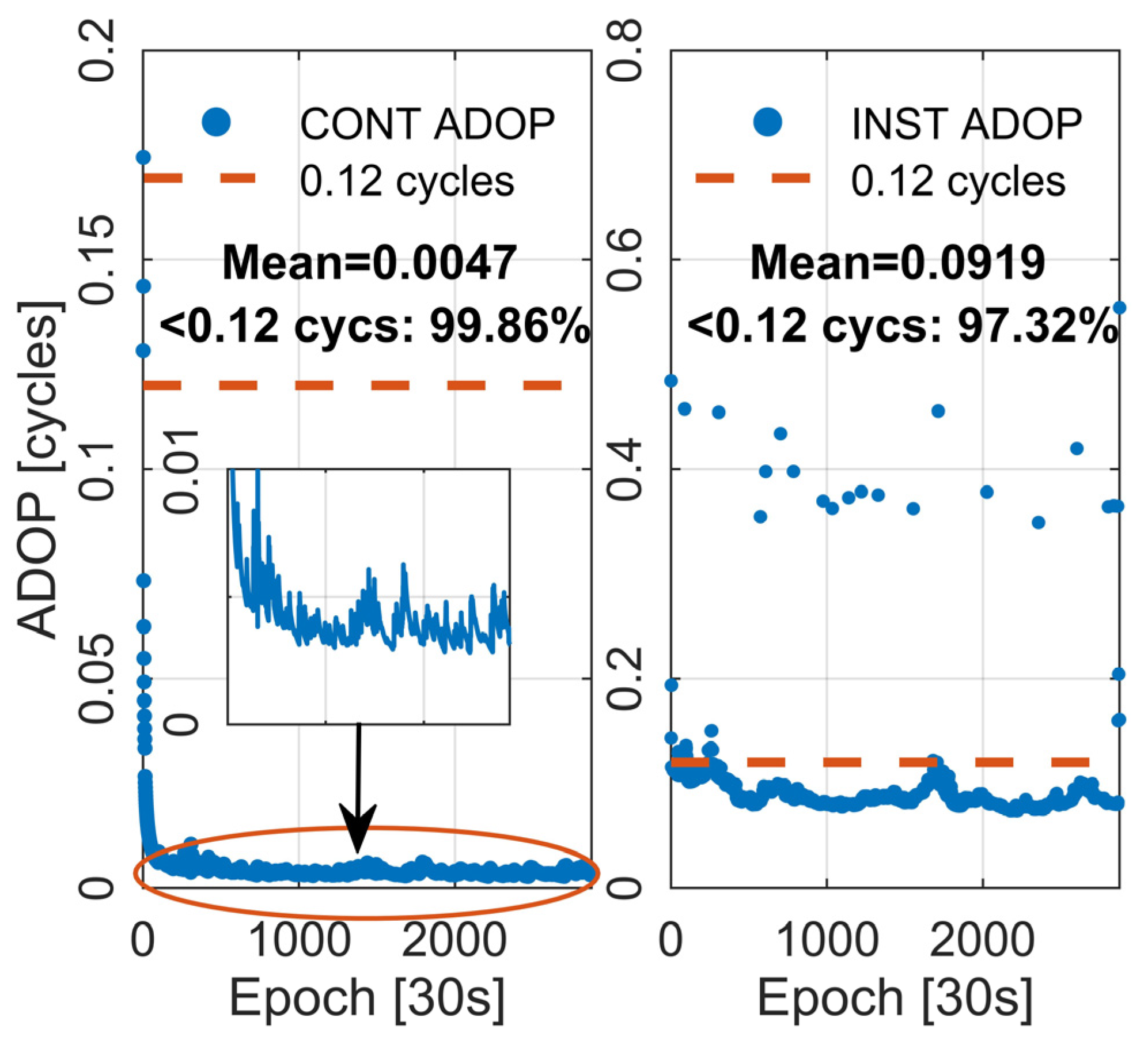
3.2. Server-Side Test Results and Analysis
- Float ambiguities pass bootstrapped success rate test with threshold greater than 99.99%;
- Ambiguities successfully fixed, and the integer DD ambiguity closure error is strictly zero for each subnet;
- The number of available satellites is greater than 15, and the VRS observations of the three systems are all available.
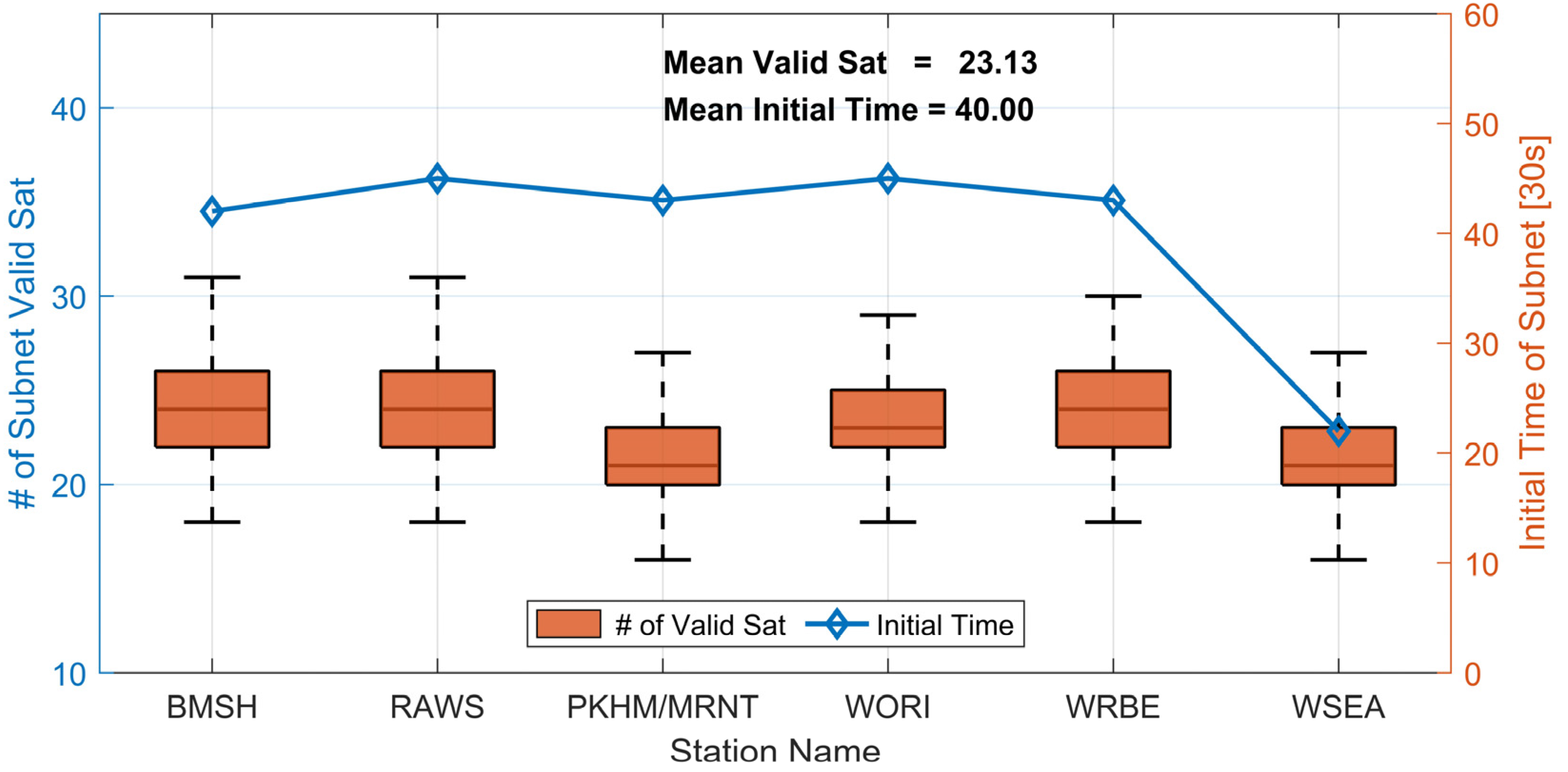
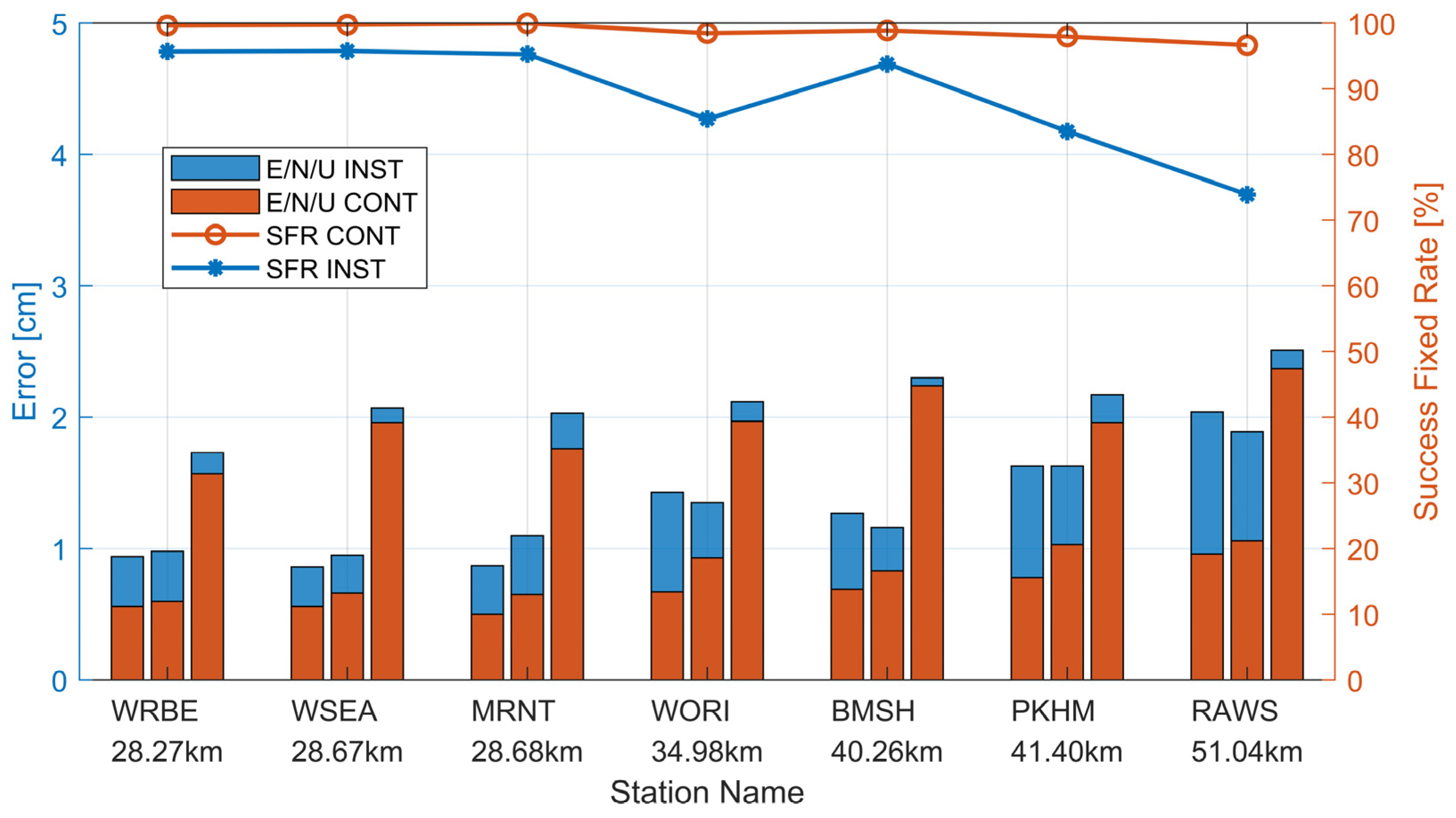
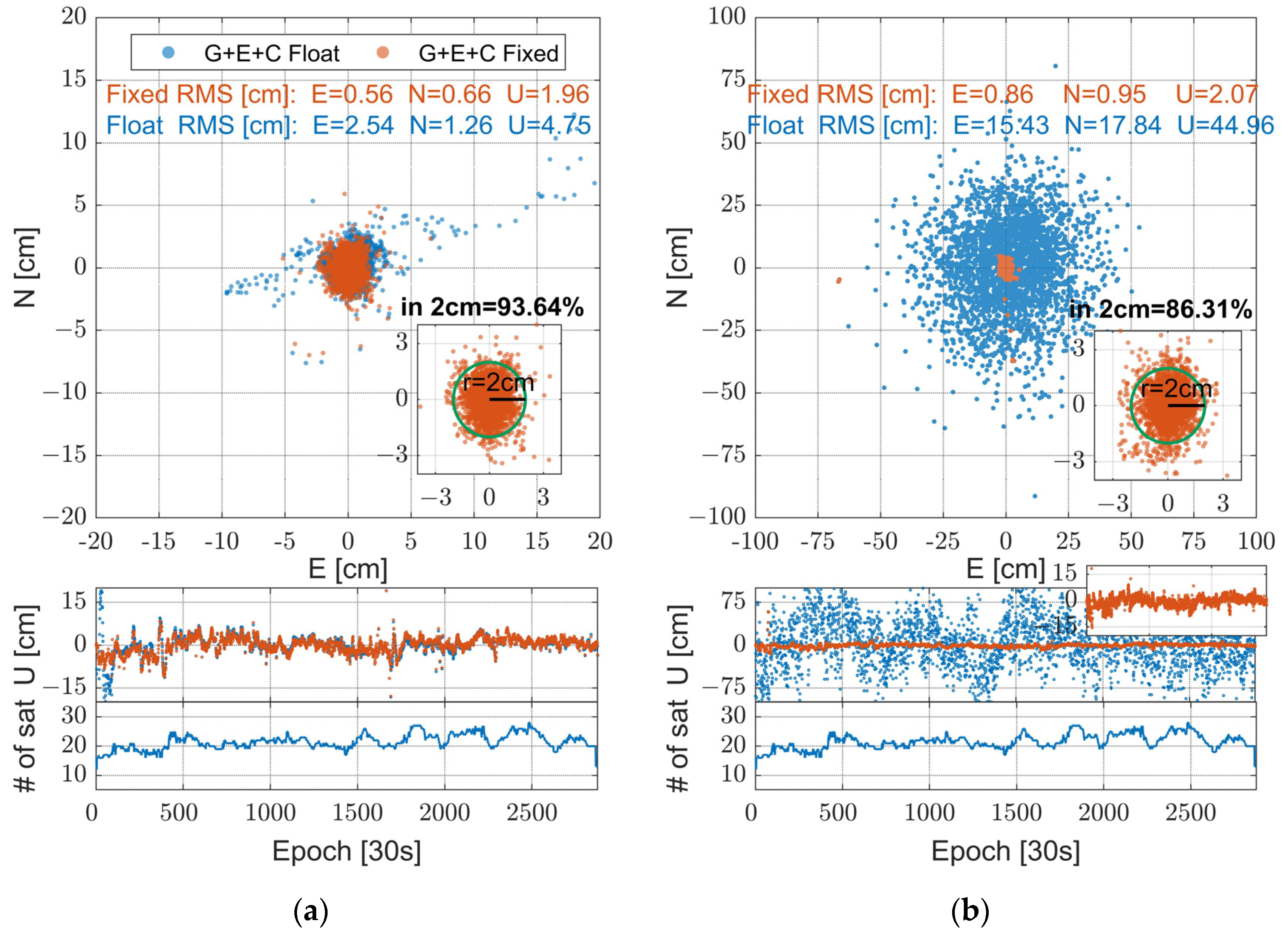
3.3. User-End Test Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dang, Y.; Jiang, T.; Yang, Y.; Sun, H.; Jiang, W.; Zhu, J.; Xue, S.; Zhang, X.; Yu, B.; Luo, Z.; et al. Research Progress of Geodesy in China (2019–2023). Acta Geod. Cartogr. Sin. 2023, 52, 1419. [Google Scholar]
- Li, G.; Geng, J.; Chu, B. High-Precision Velocity Determination Using Mass-Market Android GNSS Measurements in the Case of Anomalous Clock Variations. GPS Solut. 2023, 27, 98. [Google Scholar] [CrossRef]
- Naciri, N.; Bisnath, S. RTK-Quality Positioning with Global Precise Point Positioning Corrections. Navig. J. Inst. Navig. 2023, 70, 3. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, F.; Li, G.; Geng, J. Single-Frequency Multi-GNSS PPP-RTK for Smartphone Rapid Centimeter-Level Positioning. IEEE Sens. J. 2023, 18, 21553–21561. [Google Scholar] [CrossRef]
- Gu, S.; Dai, C.; Mao, F.; Fang, W. Integration of Multi-GNSS PPP-RTK/INS/Vision with a Cascading Kalman Filter for Vehicle Navigation in Urban Areas. Remote Sens. 2022, 14, 4337. [Google Scholar] [CrossRef]
- Huang, G.; Du, S.; Wang, D. GNSS Techniques for Real-Time Monitoring of Landslides: A Review. Satell. Navig. 2023, 4, 5. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.; Odijk, D. A Novel Un-Differenced PPP-RTK Concept. J. Navig. 2011, 64, S180–S191. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Yuan, Y. PPP-RTK Based on Undifferenced and Uncombined Observations: Theoretical and Practical Aspects. J. Geod. 2019, 93, 1011–1024. [Google Scholar] [CrossRef]
- Zhu, F.; Chen, X.; Liu, W.; Wang, Y.; Zhang, X. Connecting Integer Ambiguities to Avoid Reinitialization and Keep VRS Seamless Switching for Virtual Grid-Based NRTK. GPS Solut. 2023, 27, 133. [Google Scholar] [CrossRef]
- Dardanelli, G.; Maltese, A.; Pipitone, C.; Pisciotta, A.; Lo Brutto, M. NRTK, PPP or Static, That Is the Question. Testing Different Positioning Solutions for GNSS Survey. Remote Sens. 2021, 13, 1406. [Google Scholar] [CrossRef]
- Pehlivan, H.; Bezcioglu, M.; Yilmaz, M. Performance of Network RTK Correction Techniques (FKP, MAC and VRS) under Limited Sky View Condition. Int. J. Eng. Geosci. 2019, 4, 492496. [Google Scholar] [CrossRef]
- Wanninger, L. Improved Ambiguity Resolution by Regional Differential Modelling of the Ionosphere. In Proceedings of the 8th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1995), Palm Springs, CA, USA, 12–15 September 1995; pp. 55–62. [Google Scholar]
- Wanninger, L. Real-Time Differential GPS Error Modelling in Regional Reference Station Networks. In Proceedings of the Advances in Positioning and Reference Frames; Brunner, F.K., Ed.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 86–92. [Google Scholar]
- Zhang, S. The GPS/GLONASS Integrated CORS Network Atmosphere Modeling and RTK Algorithm Implementation; Wuhan University: Wuhan, China, 2010. [Google Scholar]
- Wübbena, G.; Bagge, A.; Seeber, G.; Böder, V.; Hankemeier, P. Reducing Distance Dependent Errors for Real−Time Precise DGPS Applications by Establishing Reference Station Networks; Institute of Navigation: Garbsen, Germany, 1996. [Google Scholar]
- Euler, H.J.; Keenan, C.R.; Zebhause, B.E. Study of a Simplified Approach in Utilizing Information from Permanent Reference Station Arrays. In Proceedings of the 14th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2001), Salt Lake City, UT, USA, 11–14 September 2001; pp. 379–391. [Google Scholar]
- Gao, Y.; Li, Z.; McLellan, J.F. Carrier Phase Based Regional Area Differential GPS for Decimeter-Level Positioning and Navigation. In Proceedings of the 10th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1997), Kansas City, MO, USA, 16–19 September 1997; pp. 1305–1313. [Google Scholar]
- Li, Z.; Gao, Y. Improving Ambiguity Resolution for a Regional Area DGPS System Using Multiple Days of Data. In Proceedings of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998), Nashville, TN, USA, 15–18 September 1998; pp. 399–406. [Google Scholar]
- Sun, H.; Cannon, M.E.; Melgard, T.E. Real-Time GPS Reference Network Carrier Phase Ambiguity Resolution. In Proceedings of the 1999 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 25–27 January 1999; pp. 193–199. [Google Scholar]
- Han, S. Carrier Phase-Based Long-Range GPS Kinematic Positioning. Ph.D. Thesis, UNSW Sydney, Sydney, Australia, 1997. [Google Scholar]
- Tang, W.; LIU, J.; Shi, C.; Lou, Y. Three Steps Method to Determine Double Difference Ambiguities Resolution of Network RTK Reference Station. Geomat. Inf. Sci. Wuhan Univ. 2007, 32, 305–308. [Google Scholar]
- Zhu, H.Z.; Liu, J.N.; Tang, W.M.; Gao, X.W. The Algorithm of Single-Epoch Integer Ambiguity Resolution between Long-Range Network RTK Base Stations. Acta Geod. Cartogr. Sin. 2012, 41, 359–365. [Google Scholar]
- Tang, W.; Meng, X.; Shi, C.; Liu, J. Algorithms for Sparse Network-Based RTK GPS Positioning and Performance Assessment. J. Navig. 2013, 66, 335–348. [Google Scholar] [CrossRef][Green Version]
- Feng, J.; Yuan, Y.; Zhang, T.; Zhang, Z.; Meng, D. Analysis of Ionospheric Anomalies before the Tonga Volcanic Eruption on 15 January 2022. Remote Sens. 2023, 15, 4879. [Google Scholar] [CrossRef]
- Yuan, Y. Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Ionosphere Based on GPS; Institute of Geodesy and Geophysics Chinese Academy of Sciences: Wuhan, China, 2002. [Google Scholar]
- Hu, G.; Abbey, D.A.; Castleden, N.; Featherstone, W.E.; Earls, C.; Ovstedal, O.; Weihing, D. An Approach for Instantaneous Ambiguity Resolution for Medium- to Long-Range Multiple Reference Station Networks. GPS Solut. 2005, 9, 1–11. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Feng, Y.; Gao, W.; Yang, L. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK. J. Geod. 2014, 88, 99–112. [Google Scholar] [CrossRef]
- Teunissen, P. The Ionosphere-Weighted GPS Baseline Precision in Canonical Form. J. Geod. 1998, 72, 107–111. [Google Scholar] [CrossRef]
- Odijk, D. Weighting Ionospheric Correction to Improve Fast GPS Positioning Over Medium Distances. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000. [Google Scholar]
- Mi, X.; Zhang, B.; Yuan, Y. Multi-GNSS RTK Positioning with Integer Ambiguity Resolution: From Double-Differenced to Single-Differenced. J. Glob. Position. Syst. 2021, 17, 151–163. [Google Scholar] [CrossRef]
- Mi, X.; Zhang, B.; Odolinski, R.; Yuan, Y. On the Temperature Sensitivity of Multi-GNSS Intra- and Inter-System Biases and the Impact on RTK Positioning. GPS Solut. 2020, 24, 112. [Google Scholar] [CrossRef]
- Hou, P.; Zha, J.; Liu, T.; Zhang, B. LS-VCE Applied to Stochastic Modeling of GNSS Observation Noise and Process Noise. Remote Sens. 2022, 14, 258. [Google Scholar] [CrossRef]
- Hou, P.; Zhang, B.; Yuan, Y. Analysis of the Stochastic Characteristics of GPS/BDS/Galileo Multi-Frequency Observ-ables with Different Types of Receivers. J. Spat. Sci. 2021, 66, 49–73. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y. On the Short-Term Temporal Variations of GNSS Receiver Differential Phase Biases. J. Geod. 2017, 91, 563–572. [Google Scholar] [CrossRef]
- Gu, S.; Gan, C.; He, C.; Lyu, H.; Hernandez-Pajares, M.; Lou, Y.; Geng, J.; Zhao, Q. Quasi-4-Dimension Ionospheric Modeling and Its Application in PPP. Satell. Navig. 2022, 3, 24. [Google Scholar] [CrossRef]
- Odolinski, R.; Odijk, D.; Teunissen, P. Combined GPS and BeiDou Instantaneous RTK Positioning. Navigation 2014, 61, 135–148. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined GPS+ BDS for Short to Long Baseline RTK Positioning. Meas. Sci. Technol. 2015, 26, 045801. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.; Odijk, D. First Combined COMPASS/BeiDou-2 and GPS Positioning Results in Australia. Part II: Single- and Multiple-Frequency Single-Baseline RTK Positioning. J. Spat. Sci. 2014, 59, 25–46. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Low-Cost, 4-System, Precise GNSS Positioning: A GPS, Galileo, BDS and QZSS Ionosphere-Weighted RTK Analysis. Meas. Sci. Technol. 2017, 28, 125801. [Google Scholar] [CrossRef]
- Odijk, D. Fast Precise GPS Positioning in the Presence of Ionospheric Delays. Publ. Geod. 2002, 52. Available online: https://www.researchgate.net/publication/27348975_Fast_Precise_GPS_Positioning_in_the_Presence_of_Ionospheric_Delays (accessed on 4 June 2024).
- Morton, Y.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021; Volume 1. [Google Scholar]
- Teunissen, P.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS Network-Based PPP with Integer Ambiguity Resolution. J. Aeronaut. Astronaut. Aviat. Ser. A 2010, 42, 223–230. [Google Scholar]
- Hou, P.; Zhang, B.; Yuan, Y. Combined GPS+BDS Instantaneous Single- and Dual-Frequency RTK Positioning: Stochastic Modelling and Performance Assessment. J. Spat. Sci. 2021, 66, 3–26. [Google Scholar] [CrossRef]
- Miao, W.; Li, B.; Zhang, Z.; Zhang, X. Combined BeiDou-2 and BeiDou-3 Instantaneous RTK Positioning: Stochastic Modeling and Positioning Performance Assessment. J. Spat. Sci. 2020, 65, 7–24. [Google Scholar] [CrossRef]
- Han, S.; Rizos, C. An Instantaneous Ambiguity Resolution Technique for Medium-Range GPS Kinematic Positioning. Navigation 2000, 47, 17–31. [Google Scholar] [CrossRef]
- Tang, W.; Liu, J.; Liu, H.; Bai, Q. A Modified Combined Bias Interpolation Method for GNSS Network RTK. Geomat. Inf. Sci. Wuhan Univ. 2007, 32, 1156–1159. [Google Scholar]
- Zha, J.; Zhang, B.; Liu, T.; Hou, P. Ionosphere-Weighted Undifferenced and Uncombined PPP-RTK: Theoretical Models and Experimental Results. GPS Solut. 2021, 25, 135. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. A Canonical Theory for Short GPS Baselines. J. Geod. 1997, 71, 389–401. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P.J.G. ADOP in Closed Form for a Hierarchy of Multi-Frequency Single-Baseline GNSS Models. J. Geod. 2008, 82, 473–492. [Google Scholar] [CrossRef]
- Teunissen, P.; De Jonge, P.; Tiberius, C. The Volume of the GPS Ambiguity Search Space and Its Relevance for Integer Ambiguty Resolution. In Proceedings of the 9th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1996), Kansas City, MO, USA, 17–20 September 1996; Volume 9, pp. 889–898. [Google Scholar]
- Gao, R.; Liu, Z.; Zhang, B. Ionosphere-Weighted Post-Processing Kinematic for Airborne Positioning with Refined Modeling of Receiver Phase Biases and Tropospheric Zenith Wet Delays. GPS Solut. 2022, 26, 113. [Google Scholar] [CrossRef]
- Zhu, F. GNSS/SINS/Vision Multi-Sensors Integration for Precise Positioning and Orientation Determination. Ph.D. Thesis, Wuhan University, Wuhan, China, 2019. [Google Scholar]
- Li, B.; Verhagen, S.; Teunissen, P.J.G. Robustness of GNSS Integer Ambiguity Resolution in the Presence of Atmospheric Biases. GPS Solut. 2014, 18, 283–296. [Google Scholar] [CrossRef]


| Symbol | Definition | Description |
|---|---|---|
| Expectation operator | ||
| Observed-minus-computed code and phase observations (O-C) | ||
| Epoch of observations | ||
| Receiver indicator | ||
| Satellite indicator | ||
| * | System indicator, with G for GPS, E for Galileo, C for BeiDou | |
| Wavelength of frequency and its ambiguities | ||
| Mapping function of the tropospheric wet components | ||
| Zenith tropospheric wet delays | ||
| Coefficient of ionospheric delays | ||
| Slant ionospheric delays | ||
| Receiver and satellite code biases | ||
| Receiver and satellite phase biases |
| Parameter | Estimable Form | Description | Condition |
|---|---|---|---|
| Between-receiver clock with code bias on | |||
| Between-receiver zenith tropospheric wet delays | |||
| Between-receiver slant ionospheric delays | |||
| Between-receiver code bias | |||
| Between-receiver phase bias | |||
| Double-differenced integer ambiguities |
| Indicator | Baseline | Receiver Type | Antenna Type | Length |
|---|---|---|---|---|
| BL01 | PKVL–BONE | ALOY–PL5X | AT01–AT01 | 68.16 km |
| BL02 | PKVL–EBNK | ALOY–ALOY | AT01–AT02 | 98.64 km |
| BL03 | PKVL–MVIL | ALOY–PL5X | AT01–AT02 | 75.37 km |
| BL04 | PKVL–KILM | ALOY–ALOY | AT01–AT02 | 56.45 km |
| BL05 | PKVL–LETH | ALOY–ALOY | AT01–AT01 | 77.19 km |
| BL06 | KILM–LETH | ALOY–ALOY | AT02–AT01 | 102.24 km |
| BL07 | KILM–MVIL | ALOY–PL5X | AT02–AT02 | 73.82 km |
| BL08 | LETH–BONE | ALOY–PL5X | AT01–AT01 | 88.52 km |
| BL09 | EBNK–BONE | ALOY–PL5X | AT02–AT01 | 93.76 km |
| BL10 | EBNK–MVIL | ALOY–PL5X | AT02–AT02 | 83.32 km |
| BL11 | EBNK–MAFF | ALOY–ALOY | AT02–AT02 | 96.63 km |
| BL12 | MVIL–MAFF | PL5X–PL5X | AT02–AT02 | 120.89 km |
| Receiver Type: ALOY: TRIMBLE ALLOY; PL5X: SEPT PLOAR5X. | ||||
| Antenna Type: AT01: TRM115000.00; AT02: TRM57971.00. | ||||
| Items | Models/Strategies |
|---|---|
| Observations | GPS, BDS, and GAL code and phase observations |
| Frequency | GPS L1 and L2, BDS B1I and B3I, GAL E1 and E5b |
| Estimator | Kalman filter |
| Elevation cutoff angle | 10° |
| Weighting strategy | Elevation-dependent weighting, for raw data: Code: Phase: |
| Slant ionospheric delays | Network: estimated as white noise User: without estimation |
| Zenith tropospheric delay | A priori value provided by the UNB3m model; estimated as random-walk noise (); GMF is used for mapping function |
| Phase ambiguities | Estimated as float constants for each arc |
| Station coordinates | Network: Known constants User: Estimate each epoch as an unknown |
| Inter-system bias | Not estimated |
| Station Name | WRBE | WSEA | MRNT | WORI | PKHM | BMSH | RAWS | |
|---|---|---|---|---|---|---|---|---|
| Length to MSTA [km] | 28.27 | 28.67 | 28.68 | 34.98 | 40.26 | 41.40 | 51.04 | |
| GPS | Mean [cm] | 0.01 | −0.02 | 0.03 | 0.03 | 0.02 | 0.06 | 0.14 |
| STD [cm] | 2.41 | 1.60 | 2.08 | 3.07 | 3.01 | 3.11 | 4.16 | |
| GAL | Mean [cm] | −0.14 | −0.02 | 0.15 | −0.05 | −0.16 | 0.36 | −0.07 |
| STD [cm] | 2.36 | 1.5 | 2.09 | 2.93 | 2.83 | 3.00 | 3.57 | |
| BDS | Mean [cm] | 0.04 | 0.03 | 0.01 | −0.03 | 0.11 | 0.01 | −0.05 |
| STD [cm] | 2.35 | 1.72 | 1.95 | 3.23 | 2.95 | 3.12 | 3.67 | |
| Station Name | WRBE | WSEA | MRNT | WORI | PKHM | BMSH | RAWS | |
|---|---|---|---|---|---|---|---|---|
| Length to MSTA [km] | 28.27 | 28.67 | 28.68 | 34.98 | 40.26 | 41.40 | 51.04 | |
| Height Difference from MSTA [m] | 35.00 | 150.00 | −42.00 | 158.00 | 300.00 | 150.00 | −448.00 | |
| CONT Mode | East RMS [cm] | 0.56 | 0.56 | 0.50 | 0.67 | 0.69 | 0.78 | 0.96 |
| North RMS [cm] | 0.60 | 0.66 | 0.65 | 0.93 | 0.83 | 1.03 | 1.06 | |
| Up RMS [cm] | 1.57 | 1.96 | 1.76 | 1.97 | 2.24 | 1.96 | 2.37 | |
| CONT SFR [%] | 99.65 | 99.76 | 99.97 | 98.48 | 98.88 | 97.95 | 96.65 | |
| INST Mode | East RMS [cm] | 0.94 | 0.86 | 0.87 | 1.43 | 1.27 | 1.63 | 2.04 |
| North RMS [cm] | 0.98 | 0.95 | 1.10 | 1.35 | 1.16 | 1.63 | 1.89 | |
| Up RMS [cm] | 1.73 | 2.07 | 2.03 | 2.12 | 2.30 | 2.17 | 2.51 | |
| INST SFR [%] | 95.68 | 95.76 | 95.27 | 88.99 | 93.80 | 83.53 | 73.90 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Xu, H.; Wang, Y.; Yuan, Y.; Chen, X.; Dai, Z.; Ai, Q. Ionosphere-Weighted Network Real-Time Kinematic Server-Side Approach Combined with Single-Differenced Observations of GPS, GAL, and BDS. Remote Sens. 2024, 16, 2269. https://doi.org/10.3390/rs16132269
Ma Y, Xu H, Wang Y, Yuan Y, Chen X, Dai Z, Ai Q. Ionosphere-Weighted Network Real-Time Kinematic Server-Side Approach Combined with Single-Differenced Observations of GPS, GAL, and BDS. Remote Sensing. 2024; 16(13):2269. https://doi.org/10.3390/rs16132269
Chicago/Turabian StyleMa, Yi, Hongjin Xu, Yifan Wang, Yunbin Yuan, Xingyu Chen, Zelin Dai, and Qingsong Ai. 2024. "Ionosphere-Weighted Network Real-Time Kinematic Server-Side Approach Combined with Single-Differenced Observations of GPS, GAL, and BDS" Remote Sensing 16, no. 13: 2269. https://doi.org/10.3390/rs16132269
APA StyleMa, Y., Xu, H., Wang, Y., Yuan, Y., Chen, X., Dai, Z., & Ai, Q. (2024). Ionosphere-Weighted Network Real-Time Kinematic Server-Side Approach Combined with Single-Differenced Observations of GPS, GAL, and BDS. Remote Sensing, 16(13), 2269. https://doi.org/10.3390/rs16132269






