Abstract
Individual-tree-based models (IBMs) have emerged to provide finer-scale operational simulations of stand dynamics by accommodating and/or representing tree-to-tree interactions and competition. Like stand-level growth model development, IBMs need an array of detailed data from individual trees in any stand through repeated measurement. Conventionally, these data have been collected through forest mensuration by establishing permanent sample plots or temporary measurement plots. With the evolution of remote sensing technology, it is now possible to efficiently collect more detailed information reflecting the heterogeneity of the whole forest stand than before. Among many techniques, airborne laser scanning (ALS) has proved to be reliable and has been reported to have potential to provide unparallel input data for growth models. This study utilized repeated ALS data to develop a model to project the annualized individual tree height increment (ΔHT) in a conifer plantation by considering spatially explicit competition through a mixed-effects modelling approach. The ALS data acquisition showed statistical and biological consistency over time in terms of both response and important explanatory variables, with correlation coefficients ranging from 0.65 to 0.80. The height increment model had high precision (RMSE = 0.92) and minimal bias (0.03), respectively, for model fitting. Overall, the model showed high integrity with the current biological understanding of individual tree growth in a monospecific Pinus radiata plantation. The approach used in this study provided a robust model of annualized individual tree height growth, suggesting such an approach to modelling will be useful for future forest management.
1. Introduction
The growth of forest trees presents a phenomenon of considerable ecophysiological intricacy, moderated by edaphic and climatic factors, and competitive interactions [1,2]. In any forest stand, the organizational structure of individual trees manifests as a mosaic wherein the majority of interactions transpire in a close proximal zone of influence, facilitating the exploitation of available growth resources and space [3,4,5]. As the trees grow, they engender modifications in their surroundings, exerting influence over (1) the general environment, (2) micro-environmental and genetic parameters and (3) the spatial and temporal dynamics of neighboring entities [6]. Consequently, the resultant degree of competitive interaction among the trees assumes a paramount role in steering the growth dynamics of any given forest stand [7], emerging as a salient feature within forest ecosystems [8,9].
The comprehension and projection of forest growth dynamics pose a formidable yet indispensable challenge in the strategic selection of management schemes and the allocation of financial resources to ensure optimized output. Forest growth and yield models serve as quantitative generalizations of these dynamics, offering a means to narrow the uncertainty gap through precise predictions [2], and provide crucial insights for effective forest management [10,11]. Amidst the diverse array of forest growth and yield models, individual tree growth models have emerged as refined simulations operating at a finer scale to provide flexible stand dynamics predictions [12]. Generally, individual-tree-level models aspire to forecast stand growth dynamics by encapsulating inter-tree interactions, including one- or two-sided competition and facilitation [2,13,14]. The representation of these interactions may involve a plethora of potential competition indices [6,14,15,16]. These indices can be broadly classified into two categories based on their consideration of location. Spatially implicit or distance-independent indices quantify competitive interaction solely through the size of the competitors, whereas spatially explicit or distance-dependent indices incorporate the distance of the competitors into account [6,17,18]. The latter indices, while offering enhanced precision through more nuanced mathematical representations, introduce additional complexity into the modelling framework [6,18]. However, it is imperative to note that the efficacy of such models is contingent upon the availability of detailed individual tree data. In recent research, Pont et al. [19] demonstrated using mixed-effects models to incorporate site and competition effects to successfully estimate tree height, diameter and total stem volume. Their potential for broader application, including tree growth modelling, was suggested, emphasizing the need to test, extend and apply a generalized mixed-effects approach to remotely acquired datasets.
The quantification of forest tree growth involves the systematic utilization of repeated observations, which facilitate the comprehensive capture of morphological changes through various methodologies, including (1) individual stem analysis, (2) temporary plots and (3) permanent plots [2]. Conventional forest mensuration practices employ ground-based tools, including diameter tape and relascopes, to record fundamental metrics, such as diameter at breast height (DBH), tree height and height of the crown base [1,2]. The evolution of remote sensing technology has ushered in a more practical operational dimension to forest mensuration [20,21], effectively bridging the extant gaps in this domain. For example, measuring tree crown dimensions is crucial to assessing light interception, gas exchange and transpiration [22]. This aspect, although pivotal, poses inherent challenges when measured through traditional field mensuration techniques. Consequently, the integration of remote sensing methodologies significantly broadens the avenues for effortlessly collecting a diverse array of indispensable data [23,24].
Among many techniques, White et al. [25] reported four specific tools, namely (i) airborne laser scanning (ALS), (ii) terrestrial laser scanning (TLS), (iii) digital aerial photogrammetry (DAP) and (iv) high/very high-spatial-resolution (HSR/VHSR) optical imagery, with the greatest potential. The utility of light detection and ranging (lidar) through ALS technologies and its applicability to forest inventory are well established [25,26,27,28]. In particular, it has proved effective in adequately characterizing tree structures at both the stand [29,30,31,32] and individual tree scales [33,34,35,36]. Numerous studies have demonstrated the efficiency and accuracy of using ALS in estimating various forest and tree morphological features, encompassing tree height [37,38,39], crown base height [40,41,42], crown area, crown volume [43,44,45], canopy cover [46], above-ground biomass [32,47,48] and basal area [49]. Prior research has also demonstrated the feasibility of utilizing ALS point cloud-derived tree and competition metrics to elucidate variations in tree growth [19,33]. Additionally, ALS data hold an advantageous position over traditional in situ measurements, as they efficiently estimate forest competition over expansive areas [50]. Nonetheless, most individual-tree-level studies employing ALS lidar have predominantly focused on mature forests, where the competition among trees exhibits a degree of homogeneity through the application of spatially implicit approaches or is limited to refining various competition metrices. While spatially implicit approaches with restricted competition yield greater predictive precision, they often fall short in providing insights into the organizational intricacies of individual entities within space. Furthermore, Fassnacht et al. [21] advocate for a shift in remote sensing-based forestry research towards addressing ‘real-world’ problems. Hence, there exists a pertinent scientific imperative to delve into enhancing the practical utility of data obtained through remote sensing, particularly leveraging advanced techniques such as lidar.
Therefore, this study aims to evaluate spatially explicit modelling of individual tree growth utilizing bi-temporal ALS point clouds. The objectives of the study in particular are to (1) scrutinize the consistency of morphometric change detection for different tree-level attributes and (2) demonstrate the applicability of spatially explicit mixed modelling approaches in the context of individual tree height growth increments. This study seeks to address these objectives in order to advance our current understanding of the intricacies associated with individual tree growth dynamics through refining and optimizing ALS.
2. Materials and Methods
2.1. Study Site and Experimental Area
The study site was situated within the confines of Puruki Experimental Forest (PEF), which is located at the southern end of the Paeroa range in the central North Island (CNI) of New Zealand. Characterized by a topography that oscillates between easy-rolling hills and steep slopes (>12–38°), the elevation of the sites spans from 480 to 650 m above sea level (Figure 1) [51]. The prevailing soil composition at PEF aligns with the predominant plantation forest soil in the CNI, primarily featuring free-draining pumice soils. Climatically, the region experiences an average monthly temperature fluctuating between 5 °C and 15 °C. The average temperature surpasses 10 °C for a significant duration of six months annually, coupled with a general scarcity of frosty days. The distribution of precipitation exhibits an even temporal spread throughout the month, contributing to a yearly average of 1500 mm [51,52].
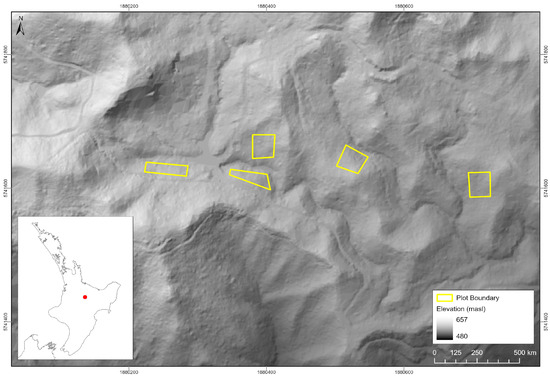
Figure 1.
Study site and experimental plots.
Puruki Experimental Forest consists of a total of five experimental trials, as described in Beets et al. [53]. For the purposes of this study, data were sourced exclusively from Trial 5. This trial comprised twenty plots, each planted with a single genotype at an initial planting density of 1000 stems per hectare. The plots were mostly 40 × 40 m square (a 30 × 30 m measurement area with two buffer rows of trees), and a few of the five plots used in this study were quadrilateral in shape due to the terrain [51]. Additionally, approximately 400 stems per hectare were pruned to a nominal height of 6.5 m in 2004. A detailed description is provided in Supplementary Materials (Table S1).
2.2. Field and Lidar Data Acquisition
Permanent sample plots (PSPs) were established in 1997 and tree measurements carried out, including individual tree stem diameter at breast height (DBH at 1.4 m), total height (HT) and crown height of all trees and age classes, as well as counting all the live trees.
Airborne lidar data were captured from 1200 m over PEF on 16 and 17 August 2006 and 13 March 2010 using an Optech ALTM 3100EA system from New Zealand Aerial Mapping. Detailed specification of the lidar acquisition and accuracy estimates was presented in Beets et al. [53]. The data acquisition parameters are provided in Table 1.

Table 1.
Lidar data acquisition parameters. * From 2 passes combined.
2.3. ALS Processing for Individual Trees and Competition Metrics
The 2006 and 2010 lidar datasets were processed to create canopy height models of a 0.25 m resolution and pits removed using a closed image processing method. Individual trees were detected, their crown boundaries were determined on crown height model (CHM) images using the calibrated tree detection method from Pont et al. [54] and individual tree heights were considered by taking the highest point of each CHM segment. This method was previously used in watershed segmentation with operator calibration to determine the level of image smoothing and has been shown to provide a tree detection accuracy of 95% for radiata pine plantations across a range of stand densities and crown sizes.
The two lidar images and associated detected tree locations were loaded into ArcGIS (ArcMap 10.8, Redland, CA, USA [55]) and ground tree numbers assigned manually to each detected tree using the ground plot sequential tree numbering and ground measurement data as a guide (Figure 2). In this way, a total of 4915 trees were matched for different lidar acquisitions and subsequent ground measurements. Trees where there was uncertainty in matching between the two lidar sets or to the ground were coded and excluded from the subsequent focal tree analyses but incorporated into the competition metric calculation. This approach ensured certainty in the linkages between the ground measurements and the two lidar datasets.

Figure 2.
Matching treetops detected in lidar with ground tree numbers.
Crown height model (CHM)-based generalized competition metrics were extracted by using the bounded neighborhood (NB) method (see [19,56]). With this method, only trees sharing a segmented boundary with the focal tree were included in the final competition metric calculation, crown intersection boundness (CIB, Equation (1)). Then, individual tree competition metrics (Table 2) were calculated for individual focal trees in each neighborhood.
where CIB = crown intersection boundness, ci = crown metric for reference tree i, cj = crown metric for competitor tree j, Lij = distance between reference tree i and competitor j.

Table 2.
Individual tree crown competition metrics. Additional description provided in Supplementary Materials.
2.4. Statistical Analyses
All the statistical analyses were carried out in the R statistical environment (Version 4.3.1; [58]) through RStudio as an integrated development environment [59]. In addition to the base R packages, the tidyverse [60], lme4 [61] and Metrics [62] packages were used subsequently for organization, model development and testing.
The statistical analyses started with an exploratory analysis by checking the correlation between tree growth and the calculated competition metrics. Then, two lidar scans were compared with simple difference metrics and the distribution of their time series measurements.
2.5. Model Development and Validation
Model development started with multi-collinearity checking among the response and dependent variables. This was carried out by checking the variance inflation factor (VIF) and employing the procedures outlined in Cook and Weisberg [63] by comparing the contribution of the most strongly correlated variables towards their residuals. Highly multi-colinear variables with less contribution were excluded from the final model building.
Both field measurement and lidar data acquisition occurred at different temporal intervals, which is a common phenomenon for growth modelling datasets. Therefore, to homogenize the variance at a finer scale, the growth increments were annualized according to simple linear expansion [2].
Annualized individual tree height increments (ΔHT) were regressed against independent explanatory competition indices. The simple traditional mathematical approach of augmenting the competition indices was applied with an ordinary least square (OLS) approach. A two-parameter Schumacher equation (Equation (2)) was chosen due to its simple yet robust nature [1,64].
where Y is the annualized height (ΔHT) at time T, and α and β are the model parameters. The model parameters were extended linearly to accommodate individual tree competition variables (v), following Woollons et al. [65] (Equations (3) and (4)).
Furthermore, as the dataset had a hierarchical and unbalanced non-normal structure, with individual trees nested in a neighborhood, a generalized linear mixed-effects model (GLMM) [66,67] was employed for ΔHT by partitioning the unexplained variance, assuming a gamma distribution of errors. A restricted maximum likelihood (REML) method was used to estimate the GLMM parameters. The GLMM has the following general form:
where yij is the response for the jth observation in the cluster i; xij is a p × 1 vector of covariates associated with that response; β is the vector of regression coefficients that are of interest; zij is a q × 1 subset of xij with random coefficients; bi is a q × 1 vector of random effects as follows a normal distribution with unknown variance D; and εij is the error with variance σ2ij.
The final models were initially selected based on simplicity, biological realism and mathematical consistency [68,69], namely the corrected Akaike information criterion (AICc), mean error (Bias), root mean square error (RMSE) and the coefficient of determination (R2) [70,71]. However, the final models need to be tested for compatibility and reliability. Hence, model validation is a central aspect, as it attempts to assess the appropriateness of any particular model specification and to appreciate the strength of the drawn conclusions [72]. In this study, an independent dataset was built by sub-setting and matching the ground tree measurements with the lidar-segmented and measured trees, which was left out of the model development datasets. This independent dataset was used as the validation dataset only with the selected final model. Similar to the final model selection, mean error (Bias), root mean square error (RMSE) and the coefficient of determination (R2) were computed for model evaluation and validation using the predicted and observed data.
3. Results
3.1. Bi-Temporal Data Consistency
The two lidar acquisitions showed significant consistency and biologically meaningful representations for different important tree morphological attributes, i.e., total individual height (HT), crown height (CH), total individual tree crown volume (CVF) and crown surface area (CS) (Figure 3). On average, all the measured attributes increased from ALS1 to ALS2 with significant correlations (Figure 3). In addition, the growth differences also resembled the biological patterns of different attributes.
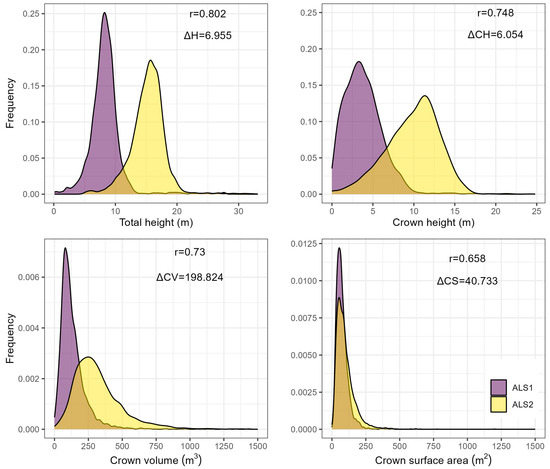
Figure 3.
Distributions of tree height (HT), crown height (CH), crown volume (CVF) and surface area (CS) from ALS1 and ALS2. The mean values of changes (Δ) and bi-temporal correlations (r) are also labelled.
3.2. Modelling Annualized Height Increments
Comparing the two different approaches, the mixed-effect modelling approach showed greater precision (RMSE, 0.92) and minimal bias (Bias, 0.03) for height increments (Table 3). The augmented empirical models with competition indices produced reasonable results with a greater margin of errors. Moreover, the residual plots of the final models confirmed their consistency within the range, with minimal biases at the extreme ends (Figure 4).

Table 3.
Model’s goodness-of-fit statistics for two modelling approaches for annualized tree height.
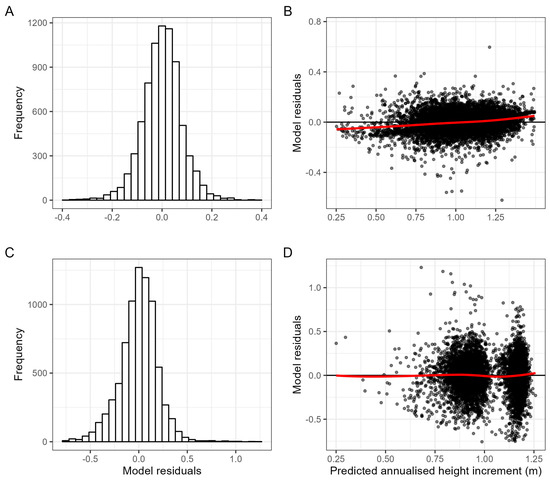
Figure 4.
Residual distribution and residuals against predicted plots for generalized mixed-effects model (GLMM) (A,B) and augmented empirical model (C,D). Red lines show the models fitting trend.
During validation of the final model, with the GLMM approach only, overall precision and bias were affected, but within relatively smaller limits (Table 4). While using the validation datasets, the models showed better agreement with the observed height increments: the coefficient of determination for height increments was 0.82.

Table 4.
Model validation goodness-of-fit statistics.
3.3. Competition Indices Modulate Height Increments
Annualized individual height growth was significantly influenced by the individual tree crown volume (CVF) and neighborhood stem density (SD) based on neighborhood competition interaction (Figure 5). Height growth was influenced positively by individual CVF, negatively by SD and negatively by their interaction (Table 5). So, when an individual tree with a larger crown volume happened to be present in a high-density neighborhood, a negative effect on tree height growth was experienced. However, the neighborhood tree density (SD) effect marginalized with an increasing crown volume.
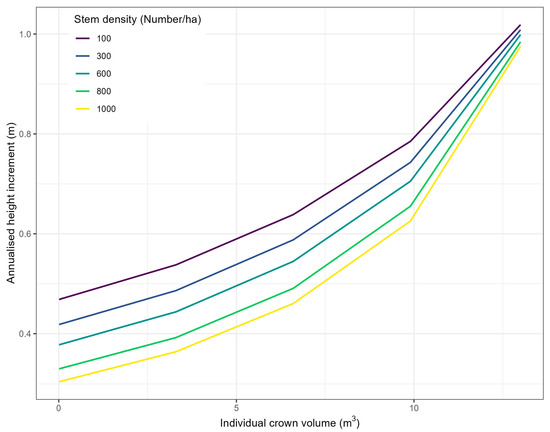
Figure 5.
Effect of spatially explicit competition indices (i.e., crown volume and neighborhood stem density) on annualized height.

Table 5.
Model coefficients of annualized height increment.
4. Discussion
4.1. Tree Attributes Related to Growth
Individual tree growth is fundamentally shaped by the attributes of the subject tree and its neighboring companions. Prior research has consistently noted that individual tree growth is influenced by internal factors, such as the size of the subject tree, while concurrently being impacted by external tree competition. This external competition hinges on resource utilization efficiency and partitioning, with particular regard to factors like moisture and light availability [2,73]. The observed changes in individual tree HTs over time exhibited distinct patterns compared to the crown attributes. Initially, the dominance in HTs was concentrated among a few prominent trees, and this number expanded over time. Consequently, the density distribution evolved, leading to a flattening and spreading of the pattern at ALS2, the last ALS acquisition. Ideally, the crown growth increment of a vigorous tree should be proportional to its initial crown size, considering a similar elongation of the main stem and branches, as posited by Pretzsch [74]. However, this ideal scenario is contingent upon the availability of space and resources among the trees, highlighting the complex interplay between competition and growth dynamics within forest ecosystems.
4.2. The Spatially Explicit Individual-Tree-Based Mixed-Effects Model
Individual tree height increment (ΔHT) is critical for forest growth and yield models, as accurate predictions of height increments can be used to precisely estimate higher-order tree attributes, including individual tree volume and basal area. Given the pivotal role of ΔHT, precise predictions are imperative, as errors at this level can compound and lead to greater uncertainty when scaling up to stand-level metrics, such as total standing volume [75]. Previous studies using similar datasets have typically employed multivariate regression with ordinary least square (OLS), as demonstrated by Ma et al. [33]. However, the current study uses multi-temporal lidar returns with a nested stochastic structure. Nested stochastic structures occur when multiple measurements are combined across sampling units [76]. As trees interact and thus compete locally [9], it is important to consider neighborhood effects within the modelling framework. It is often challenging to fully incorporate the variation in sampling residuals through OLS because it violates the regression assumption of independent residuals and results in biased estimates [77,78]. When a similar approach was trialed in the current study by augmenting non-linear OLS, the results provided inadequate precision of the annualized ΔHT predictions. In addition, this conventional approach does not consider complex individual-tree-level interactions adequately [2,18]. Often, the inadequacies of OLS are addressed through a two-step generalized least square approach, offering flexibility to the nested structure and enabling valid inferences to residual variance [79]. Meanwhile, the current study adopts a straightforward, flexible and innovative approach to modelling annualized ΔHT from lidar inputs, treating each neighborhood as a random effect.
Since its inception, mixed modelling methodology has provided a statistically flexible framework for explicitly modelling a nested structure and is increasingly used in forest biometry. This includes the incorporation of nested stochastic structures into individual tree growth models [80,81,82]. For instance, Penner et al. [82] used a mixed model to explicitly emphasize the flexibility to integrate complex errors into individual tree height growth models for Norway spruce and Scots pine. In addition, Pont et al. [19] employed a similar approach to quantify interactions among genotype, the environment and management practices for radiata pine, showed a substantial reduction in residual variance. Similarly, Hao et al. [34] compared mixed-effect modelling with other contemporary and traditional approaches to modelling individual-tree DBHs of Larix olgensis, with a significant improvement in the goodness of fit. Ogana et al. [83] in Sweden and Patrício et al. [84] in Portugal applied an approach with a generalized term for the optimized height–diameter relationship from long-term mensuration data. In contrast to these, this study aimed to model the annualized height growth change with a generalized term in the model and obtained a greater precision in the model estimates and minimum bias in the variance distribution from bi-temporal lidar data.
4.3. Crown-Based Individual Tree Competition Indices
The existing body of literature has predominantly focused on the development and evaluation of individual-tree-size-based competition indices [1,2]. Many of these indices have been developed from different formulations of Hegyi [17]’s index. However, Biging and Dobbertin [15] introduced the notion that crown-based competition indices might be more informative than their DBH-based counterparts, especially when the spatial organization of the trees is known. There is enough evidence that trees with a greater crown volume and/or surface area receive a greater amount of light [85,86,87]. This empirical observation provides a plausible explanation for the better performance of crown-based measures for growth modelling. Consequently, the results of this study, highlighting the impact of crown volume (CVF) and neighborhood stem density (SD) on ΔHT, align with this rationale. The crown attributes and spatial organization of the trees were related to the individual-tree-level competition dynamics by explaining the light interception and space utilization within the forest stand. Interestingly, stand-level tree density is most often used to describe stand-level competition [88]; however, Bella [89] showed the implications of tree density induced competition at the individual tree level. It is considered an important factor and has been reported to improve model prediction during the implementation of spatially explicit individual tree growth modelling [88,90]. This may be due to its high correlation and indication with resource use efficiency, such as water use dynamics and nitrogen supply [91].
4.4. Limitations and Future Directions
Even though this study presented a complete modelling approach for the total individual tree height change, it is important to acknowledge certain limitations. Firstly, this study does not address diameter at breast height (DBH), mortality and recruitment, which are crucial components of individual-tree-based growth models [92,93]. To simulate individual tree growth over time in a spatially explicit manner, it is necessary to quantify the presence and occurrence of individual trees in a particular space. Secondly, the study utilized the best available lidar data at the time of collection; however, these data are now considered to have a relatively low point density. This relatively low point density may have inhibited the detection of the forest structure and therefore negatively affected the final outcome. Also, a considerable number of works have reported on using different quantile metrics for the tree morphometric features to be evaluated from lidar point clouds [43,48]. Therefore, it may be prudent to use different point collections fused together or to combine remotely sensed data with field measurements. Coops et al. [26] proposed combining field measurement with lidar acquisitions, presenting a promising strategy to tackle such shortcomings. Additionally, combining terrestrial laser scanning and multispectral imagery has shown potential to better characterize tree morphometrics [94,95,96].
5. Conclusions
This study enhances our understanding and highlights a plausible approach to modelling total individual tree height increments. Height is one of the foundational attributes for any tree growth modelling framework. The demonstrated efficacy of lidar-derived individual tree measurements and estimated competition indices underscores their applicability to obtaining precise predictions through an appropriate approach.
The approach outlined described in this study is one of the few so far that can adequately explain individual tree growth by taking crown-based neighborhood competition indices into account, so it has wider applicability, especially in the ever-changing and expanding landscape of remote sensing. Furthermore, the outlined approach can statistically and appropriately partition variance and result in greater precision. Its demonstrated accuracy and robustness ensure that this is easily transferable and applicable to large-area tree growth quantification, as well as providing an ingenious tool for forest management.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/rs16132270/s1. Table S1. Field measurements description values range. SPH = stems per hectare; MTH = mean top height; Mean CrHT = Mean crown height; Table S2. Generalized mixed-effect models’ goodness-of-fit comparison.
Author Contributions
S.S.: Conceptualization, methodology, investigation, data curation, formal analysis, visualization, project administration, funding acquisition, writing—original draft, writing—review and editing; D.P.: conceptualization, methodology, data acquisition and processing, data curation, writing—review and editing, visualization, project administration, funding acquisition; Y.D.: conceptualization, methodology, writing—review and editing, project administration, funding acquisition; S.A.: data processing and curation, visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Scion’s Strategic Science Investment Fund and the Forest Growers Levy Trust through the Resilient Forest Programme for the financial year 2023–2024.
Data Availability Statement
The underlying data are privately owned and not available.
Acknowledgments
The authors thank the forest owners of the site for providing the data and acknowledge and thank Loretta Garrett, Peter Clinton and Steven Dovey for providing initial comments to improve this manuscript. They are also grateful to the anonymous reviewers and editor for their constructive suggestions on improving this manuscript.
Conflicts of Interest
The authors are empoyed at Scion Ltd. The authors declare no known competing interests or personal relationships that could have appeared to influence the work reported in this study.
References
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A., Jr.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Pretzsch, H. Forest dynamics, growth, and yield. In Forest Dynamics, Growth and Yield: From Measurement to Model; Pretzsch, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–39. [Google Scholar]
- Munro, D.D. Forest Growth Models—A Prognosis; Royal College of Forestry: Stockholm, Sweden, 1974; pp. 7–21. [Google Scholar]
- Gillet, F. Plant competition. In Encyclopedia of Ecology; Jorgensen, S.E., Fath, B.D., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 2783–2793. [Google Scholar]
- Tomé, M.; Burkhart, H.E. Distance-dependent competition measures for predicting growth of individual trees. For. Sci. 1989, 35, 816–831. [Google Scholar] [CrossRef]
- Curtis, R.O. Stand density measures: An interpretation. For. Sci. 1970, 16, 403–414. [Google Scholar]
- Oliver, C.D.; Larson, B.C. Forest Stand Dynamics; Updated ed.; Yale School of the Environment; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Thorpe, H.C.; Astrup, R.; Trowbridge, A.; Coates, K.D. Competition and tree crowns: A neighborhood analysis of three boreal tree species. For. Ecol. Manag. 2010, 259, 1586–1596. [Google Scholar] [CrossRef]
- Twery, M.J.; Weiskittel, A.R. Forest-management modelling. In Environmental Modelling; John Wiley and Sons: Hoboken, NJ, USA, 2013; pp. 379–398. [Google Scholar] [CrossRef]
- Pretzsch, H.; Grote, R.; Reineking, B.; Rötzer, T.; Seifert, S. Models for forest ecosystem management: A European perspective. Ann. Bot. 2007, 101, 1065–1087. [Google Scholar] [CrossRef] [PubMed]
- Vospernik, S. Possibilities and limitations of individual-tree growth models—A review on model evaluations. Die Bodenkult. J. Land Manag. Food Environ. 2017, 68, 103–112. [Google Scholar] [CrossRef][Green Version]
- Weiner, J. Asymmetric competition in plant populations. Trends Ecol. Evol. 1990, 5, 360–364. [Google Scholar] [CrossRef] [PubMed]
- Soares, P.; Tomé, M. Distance-dependent competition measures for Eucalyptus plantations in Portugal. Ann. For. Sci. 1999, 56, 307–319. [Google Scholar] [CrossRef]
- Biging, G.S.; Dobbertin, M. Evaluation of competition indices in individual tree growth models. For. Sci. 1995, 41, 360–377. [Google Scholar] [CrossRef]
- Berger, U.; Piou, C.; Schiffers, K.; Grimm, V. Competition among plants: Concepts, individual-based modelling approaches, and a proposal for a future research strategy. Perspect. Plant Ecol. Evol. Syst. 2008, 9, 121–135. [Google Scholar] [CrossRef]
- Hegyi, F. A simulation model for managing jack-pine stands simulation. R. Coll. For. Res. Notes 1974, 30, 74–90. [Google Scholar]
- Kuehne, C.; Weiskittel, A.R.; Waskiewicz, J. Comparing performance of contrasting distance-independent and distance-dependent competition metrics in predicting individual tree diameter increment and survival within structurally-heterogeneous, mixed-species forests of Northeastern United States. For. Ecol. Manag. 2019, 433, 205–216. [Google Scholar] [CrossRef]
- Pont, D.; Dungey, H.S.; Suontama, M.; Stovold, G.T. Spatial models with inter-tree competition from airborne laser scanning improve estimates of genetic variance. Front. Plant Sci. 2021, 11, 596315. [Google Scholar] [CrossRef] [PubMed]
- Coops, N.C. Characterizing forest growth and productivity using remotely sensed data. Curr. For. Rep. 2015, 1, 195–205. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; White, J.C.; Wulder, M.A.; Næsset, E. Remote sensing in forestry: Current challenges, considerations and directions. For. Int. J. For. Res. 2023, 97, 11–37. [Google Scholar] [CrossRef]
- Hardiman, B.S.; Gough, C.M.; Halperin, A.; Hofmeister, K.L.; Nave, L.E.; Bohrer, G.; Curtis, P.S. Maintaining high rates of carbon storage in old forests: A mechanism linking canopy structure to forest function. For. Ecol. Manag. 2013, 298, 111–119. [Google Scholar] [CrossRef]
- Lechner, A.M.; Foody, G.M.; Boyd, D.S. Applications in remote sensing to forest ecology and management. One Earth 2020, 2, 405–412. [Google Scholar] [CrossRef]
- Maltamo, M.; Næsset, E.; Vauhkonen, J. Forestry Applications of Airborne Laser Scanning, 1st ed.; Springer: Dordrecht, The Netherlands, 2014; Volume 27, p. 460. [Google Scholar]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling lidar-derived estimates of forest attributes over space and time: A review of approaches and future trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; White, J.C.; Goodbody, T.R.H.; Hennigar, C.R.; Wulder, M.A.; Socha, J.; Woods, M.E. Estimating changes in forest attributes and enhancing growth projections: A review of existing approaches and future directions using airborne 3D point cloud data. Curr. For. Rep. 2021, 7, 1–24. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Becknell, J.M.; Keller, M.; Piotto, D.; Longo, M.; Nara dos-Santos, M.; Scaranello, M.A.; Bruno de Oliveira Cavalcante, R.; Porder, S. Landscape-scale lidar analysis of aboveground biomass distribution in secondary Brazilian Atlantic Forest. Biotropica 2018, 50, 520–530. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Gregoire, T.G.; Næsset, E.; Øyen, B.-H. Detection of biomass change in a Norwegian mountain forest area using small footprint airborne laser scanner data. Stat. Methods Appl. 2012, 22, 113–129. [Google Scholar] [CrossRef]
- Dalponte, M.; Liu, S.; Gianelle, D. Detection of forest changes with multi-temporal Lidar data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 9011–9013. [Google Scholar]
- Økseter, R.; Bollandsås, O.M.; Gobakken, T.; Næsset, E. Modeling and predicting aboveground biomass change in young forest using multi-temporal airborne laser scanner data. Scand. J. For. Res. 2015, 30, 458–469. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Tao, S.; Guo, Q. Quantifying individual tree growth and tree competition using bi-temporal airborne laser scanning data: A case study in the Sierra Nevada Mountains, California. Int. J. Digit. Earth 2018, 11, 485–503. [Google Scholar] [CrossRef]
- Hao, Y.; Widagdo, F.R.A.; Liu, X.; Quan, Y.; Dong, L.; Li, F. Individual tree diameter estimation in small-scale forest inventory using UAV laser scanning. Remote Sens. 2021, 13, 24. [Google Scholar] [CrossRef]
- Hill, S.; Latifi, H.; Heurich, M.; Müller, J. Individual tree- and stand-based development following natural disturbance in a heterogeneously structured forest: A LiDAR-based approach. Ecol. Inform. 2017, 38, 12–25. [Google Scholar] [CrossRef]
- Lo, C.-S.; Lin, C. Growth-competition-based stem diameter and volume modeling for tree-level forest inventory using airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2216–2226. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using lidar remote sensing at La Selva, Costa Rica. J. Geophys. Res. Biogeosci. 2010, 115, 1–17. [Google Scholar] [CrossRef]
- Duncanson, L.; Dubayah, R. Monitoring individual tree-based change with airborne lidar. Ecol. Evol. 2018, 8, 5079–5089. [Google Scholar] [CrossRef]
- Vega, C.; St-Onge, B. Height growth reconstruction of a boreal forest canopy over a period of 58 years using a combination of photogrammetric and lidar models. Remote Sens. Environ. 2008, 112, 1784–1794. [Google Scholar] [CrossRef]
- Holmgren, J. Estimation of Forest Variables Using Airborne Laser Scanning; Swedish University of Agricultural Sciences: Umeå, Sweden, 2003. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Scrivani, J.A. Fusion of small-footprint Lidar and multispectral data to estimate plot-level volume and biomass in deciduous and pine forests in Virginia, USA. For. Sci. 2004, 50, 551. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Q.; Luo, P.; Ye, Q.; Duan, G.; Sharma, R.P.; Zhang, H.; Wang, G.; Fu, L. Prediction of individual tree diameter and height to crown base using nonlinear simultaneous regression and airborne LiDAR data. Remote Sens. 2020, 12, 2238. [Google Scholar] [CrossRef]
- Nakajima, T. Estimating tree growth using crown metrics derived from LiDAR data. J. Indian Soc. Remote Sens. 2015, 44, 217–223. [Google Scholar] [CrossRef]
- Pont, D. Assessment of Individual Trees Using Aerial Laser Scanning in New Zealand Radiata Pine Forests; University of Canterbury: Christchurch, New Zealand, 2016. [Google Scholar]
- Pont, D. Analyses of basic crown-stem growth relationship in Radiata pine. In Proceedings of the 4th International Workshop on Functional-Structural Plant Models (FSPM), Montpellier, France, 7–11 June 2004; pp. 105–109. [Google Scholar]
- Tompalski, P.; White, J.C.; Coops, N.C.; Wulder, M.A.; Leboeuf, A.; Sinclair, I.; Butson, C.R.; Lemonde, M.-O. Quantifying the precision of forest stand height and canopy cover estimates derived from air photo interpretation. For. Int. J. For. Res. 2021, 94, 611–629. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Jones, S.; Soto-Berelov, M.; Haywood, A.; Hislop, S. Estimate forest biomass dynamics using multi-temporal lidar and single date inventory data. In Proceedings of the GARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium 2019, Yokohama, Japan, 28 July–2 August 2019; pp. 7338–7341. [Google Scholar] [CrossRef]
- Poudel, K.; Flewelling, J.; Temesgen, H. Predicting volume and biomass change from multi-temporal lidar sampling and remeasured field inventory data in Panther creek watershed, Oregon, USA. Forests 2018, 9, 28. [Google Scholar] [CrossRef]
- Silva, C.A.; Klauberg, C.; Hudak, A.T.; Vierling, L.A.; Fennema, S.J.; Corte, A.P.D. Modeling and mapping basal area of Pinus taeda L. plantation using airborne LiDAR data. An. Acad. Bras. Ciências 2017, 89, 1895–1905. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, R.Ø.; Bollandsås, O.M.; Gobakken, T.; Næsset, E. Deriving individual tree competition indices from airborne laser scanning. For. Ecol. Manag. 2012, 280, 150–165. [Google Scholar] [CrossRef]
- Beets, P.N.; Brownlie, R.K. Puruki experimental catchment: Site, climate, forest management and research. N. Z. J. For. Sci. 1987, 17, 137–156. [Google Scholar]
- Garrett, L.; Wakelin, S.A.; Pearce, S.H.; Wakelin, S.J.; Barnard, T. Puruki experimental forest—Half a century of forestry research. N. Z. J. For. 2021, 66, 3–10. [Google Scholar]
- Beets, P.N.; Reutebuch, S.; Kimberley, M.O.; Oliver, G.R.; Pearce, S.H.; McGaughey, R.J. Leaf area index, biomass carbon and growth rate of radiata pine genetic types and relationships with LiDAR. Forests 2011, 2, 637–659. [Google Scholar] [CrossRef]
- Pont, D.; Kimberley, M.O.; Brownlie, R.K.; Sabatia, C.O.; Watt, M.S. Calibrated tree counting on remotely sensed images of planted forests. Int. J. Remote Sens. 2015, 36, 3819–3836. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Realease 10.8; ESRI: Redlands, CA, USA, 2021. [Google Scholar]
- Suarez-Minguez, J.C. An Analysis of the Consequences of Stand Variability in Sitka Spruce Plantations in Britain Using a Combination of Airborne LiDAR Analysis and Models; University of Sheffield: Sheffield, UK, 2010. [Google Scholar]
- Chen, Q.; Gong, P.; Baldocchi, D.; Tian, Y.Q. Estimating basal area and stem volume for individual trees from LiDAR data. Photogramm. Eng. Remote Sens. 2007, 73, 1355–1365. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing, 4.3.1; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- RStudio Team. RStudio: Integrated Development for R, RStudio; PBC: Boston, MA, USA, 2023. [Google Scholar]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Bates, D.; Achler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using—lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Hamner, B.; Frasco, M. Metrics: Evaluation Metrics for Machine Learning; R Package Version 0.1.4; R Package Team: Vienna, Austria, 2018. [Google Scholar]
- Cook, R.D.; Weisberg, S. Applied Regression Including Computing and Graphics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Schumacher, F.X. A new growth curve and its application to timber yield studies. J. For. 1939, 37, 819–820. [Google Scholar]
- Woollons, R.C.; Snowdon, P.; Mitchell, N.D. Augmenting empirical stand projection equations with edaphic and climatic variables. For. Ecol. Manag. 1997, 98, 267–275. [Google Scholar] [CrossRef]
- Bolker, B.M.; Brooks, M.E.; Clark, C.J.; Geange, S.W.; Poulsen, J.R.; Stevens, M.H.H.; White, J.S.S. Generalized linear mixed models: A practical guide for ecology and evolution. Trends Ecol. Evol. 2009, 24, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Schall, R. Estimation in generalized linear models with random effects. Biometrika 1991, 78, 719–727. [Google Scholar] [CrossRef]
- Robinson, A.P.; Monserud, R.A. Criteria for comparing the adaptability of forest growth models. For. Ecol. Manag. 2003, 172, 53–67. [Google Scholar] [CrossRef]
- Vanclay, J.K.; Skovsgaard, J.P. Evaluating forest growth models. Ecol. Model. 1997, 98, 1–12. [Google Scholar] [CrossRef]
- Cavanaugh, J.E. Unifying the derivations for the Akaike and corrected Akaike information criteria. Stat. Probab. Lett. 1997, 33, 201–208. [Google Scholar] [CrossRef]
- Onyutha, C. From R-squared to coefficient of model accuracy for assessing “goodness-of-fits”. Geosci. Model Dev. Discuss. 2020, 1–25. [Google Scholar] [CrossRef]
- Salciccioli, J.D.; Crutain, Y.; Komorowski, M.; Marshall, D.C. Sensitivity analysis and model validation. In Secondary Analysis of Electronic Health Records, Data; MIT Critical Data., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 263–271. [Google Scholar]
- Aakala, T.; Fraver, S.; D’Amato, A.W.; Palik, B.J. Influence of competition and age on tree growth in structurally complex old-growth forests in northern Minnesota, USA. For. Ecol. Manag. 2013, 308, 128–135. [Google Scholar] [CrossRef]
- Pretzsch, H. Canopy space filling and tree crown morphology in mixed-species stands compared with monocultures. For. Ecol. Manag. 2014, 327, 251–264. [Google Scholar] [CrossRef]
- Willson, D.; Monleon, V.J.; Weiskittel, A.R. Quantification and incorporation of uncertainty in forest growth and yield projections using a Bayesian probabilistic framework: A demonstration for plantation coastal Douglas-fir in the Pacific Northwest, USA. Math. Comput. For. Nat. Resour. Sci. 2019, 11, 264–285. [Google Scholar]
- West, P.W.; Ratkowsky, D.A.; Davis, A.W. Problems of hypothesis testing of regressions with multiple measurements from individual sampling units. For. Ecol. Manag. 1984, 7, 207–224. [Google Scholar] [CrossRef]
- West, P.W.; Davis, A.W.; Ratkowsky, D.A. Approaches to regression analysis with multiple measurements from individual sampling units. J. Stat. Comput. Simul. 1986, 26, 149–175. [Google Scholar] [CrossRef]
- Schabenberger, O.; Gregoire, T.G. A conspectus on estimating function theory and its applicability to recurrent modeling issues in forest biometry. Silva Fenn. 1995, 29, 4–70. [Google Scholar] [CrossRef]
- Fox, J.C.; Ades, P.K.; Bi, H. Stochastic structure and individual-tree growth models. For. Ecol. Manag. 2001, 154, 261–276. [Google Scholar] [CrossRef]
- Lappi, J. Calibration of height and volume equations with random parameters. For. Sci. 1991, 37, 781–801. [Google Scholar] [CrossRef]
- Lappi, J.; Bailey, R.L. A height prediction model with random stand and tree parameters: An alternative to traditional site index methods. For. Sci. 1988, 34, 907–927. [Google Scholar] [CrossRef]
- Penner, M.; Hökkä, H.; Penttilä, T. A method for using random parameters in analyzing permanent sample plots. Silva Fenn. 1995, 29, 287–296. [Google Scholar] [CrossRef]
- Ogana, F.N.; Holmström, E.; Sharma, R.P.; Langvall, O.; Nilsson, U. Optimizing height measurement for the long-term forest experiments in Sweden. For. Ecol. Manag. 2023, 532, 120843. [Google Scholar] [CrossRef]
- Patrício, M.S.; Dias, C.R.G.; Nunes, L. Mixed-effects generalized height-diameter model: A tool for forestry management of young sweet chestnut stands. For. Ecol. Manag. 2022, 514, 120209. [Google Scholar] [CrossRef]
- Coonen, E.J.; Sillett, S.C. Separating effects of crown structure and competition for light on trunk growth of Sequoia sempervirens. For. Ecol. Manag. 2015, 358, 26–40. [Google Scholar] [CrossRef]
- Di Salvatore, U.; Marchi, M.; Cantiani, P. Single-tree crown shape and crown volume models for Pinus nigra J. F. Arnold in central Italy. Ann. For. Sci. 2021, 78, 76. [Google Scholar] [CrossRef]
- Zhu, Z.; Kleinn, C.; Nölke, N. Assessing tree crown volume—A review. For. Int. J. For. Res. 2020, 94, 18–35. [Google Scholar] [CrossRef]
- Uhl, E.; Biber, P.; Ulbricht, M.; Heym, M.; Horváth, T.; Lakatos, F.; Gál, J.; Steinacker, L.; Tonon, G.; Ventura, M.; et al. Analysing the effect of stand density and site conditions on structure and growth of Oak species using Nelder trials along an environmental gradient: Experimental design, evaluation methods, and results. For. Ecosyst. 2015, 2, 17. [Google Scholar] [CrossRef]
- Bella, I.E. A new competition model for individual trees. For. Sci. 1971, 17, 364–372. [Google Scholar]
- Fraver, S.; D’Amato, A.W.; Bradford, J.B.; Jonsson, B.G.; Jönsson, M.; Esseen, P.-A. Tree growth and competition in an old-growth Picea abies forest of boreal Sweden: Influence of tree spatial patterning. J. Veg. Sci. 2014, 25, 374–385. [Google Scholar] [CrossRef]
- Paligi, S.S.; Lichter, J.; Kotowska, M.; Schwutke, R.L.; Audisio, M.; Mrak, K.; Penanhoat, A.; Schuldt, B.; Hertel, D.; Leuschner, C. Water status dynamics and drought tolerance of juvenile European beech, Douglas fir and Norway spruce trees as dependent on neighborhood and nitrogen supply. Tree Physiol. 2024, 44, tpae044. [Google Scholar] [CrossRef] [PubMed]
- Salas-Eljatib, C.; Weiskittel, A.R. On studying the patterns of individual-based tree mortality in natural forests: A modelling analysis. For. Ecol. Manag. 2020, 475, 118369. [Google Scholar] [CrossRef]
- Vanderwel, M.C.; Lyutsarev, V.S.; Purves, D.W. Climate-related variation in mortality and recruitment determine regional forest-type distributions. Glob. Ecol. Biogeogr. 2013, 22, 1192–1203. [Google Scholar] [CrossRef]
- Ali, S.S.; Dare, P.; Jones, S.D. Fusion of remotely sensed multispectral imagery and LiDAR data for forest structure assessment at the tree level. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 28 August–1 September 2021. [Google Scholar]
- Åkerblom, M.; Kaitaniemi, P. Terrestrial laser scanning: A new standard of forest measuring and modelling? Ann. Bot. 2021, 128, 653–662. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).