Non-Destructive Monitoring of Peanut Leaf Area Index by Combing UAV Spectral and Textural Characteristics
Abstract
1. Introduction
- (1)
- An exhaustive and meticulous correlation analysis between the spectral/textural characteristics and peanut LAI is carried out using a feature variable screening technique to determine the optimal feature combination in estimating the peanut LAI.
- (2)
- Several key parameters for calculating GLCM-derived statistical measures from the high-resolution UAV remote sensing data are investigated to evaluate the effect on the performance of the peanut LAI estimation model.
- (3)
- Different combinations of both spectral and textural characteristics are systematically compared and evaluated using six frequently used regression methods, including ULR, SVR, RR, DTR, PLSR, and RFR, to determine the optimal estimation of peanut LAI.
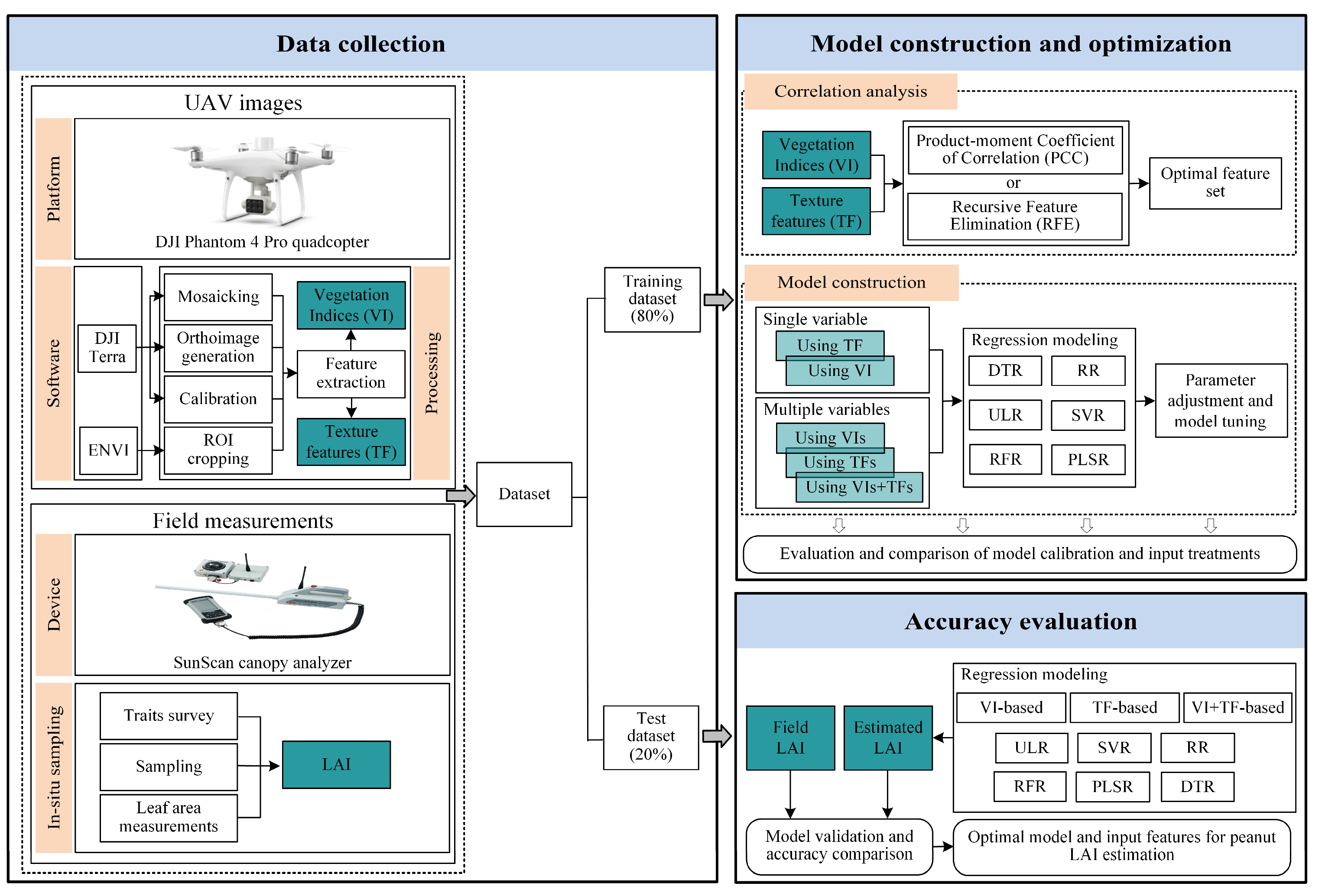
2. Material and Methods
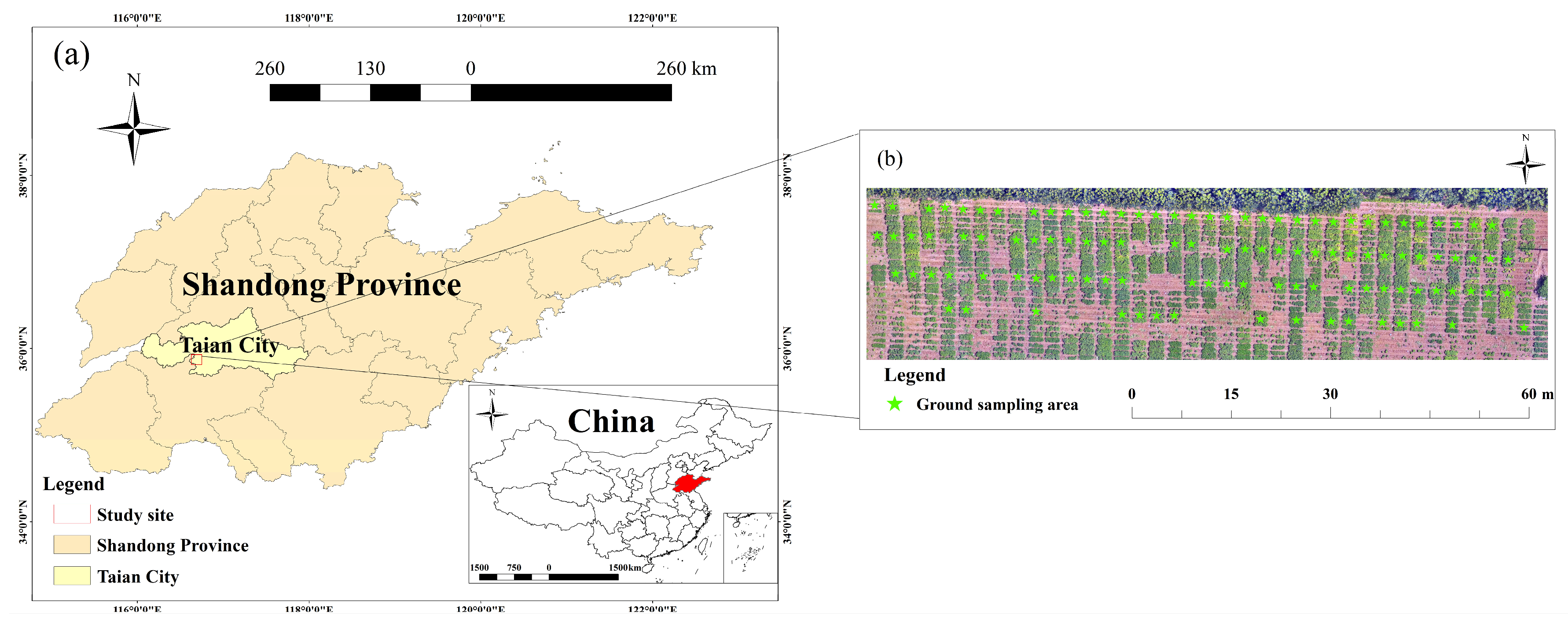
2.1. Description of Study Site
2.2. Field Data Collection
2.3. UAV Imagery Acquisition
2.4. Methods
2.4.1. Calculation of Spectral Characteristics
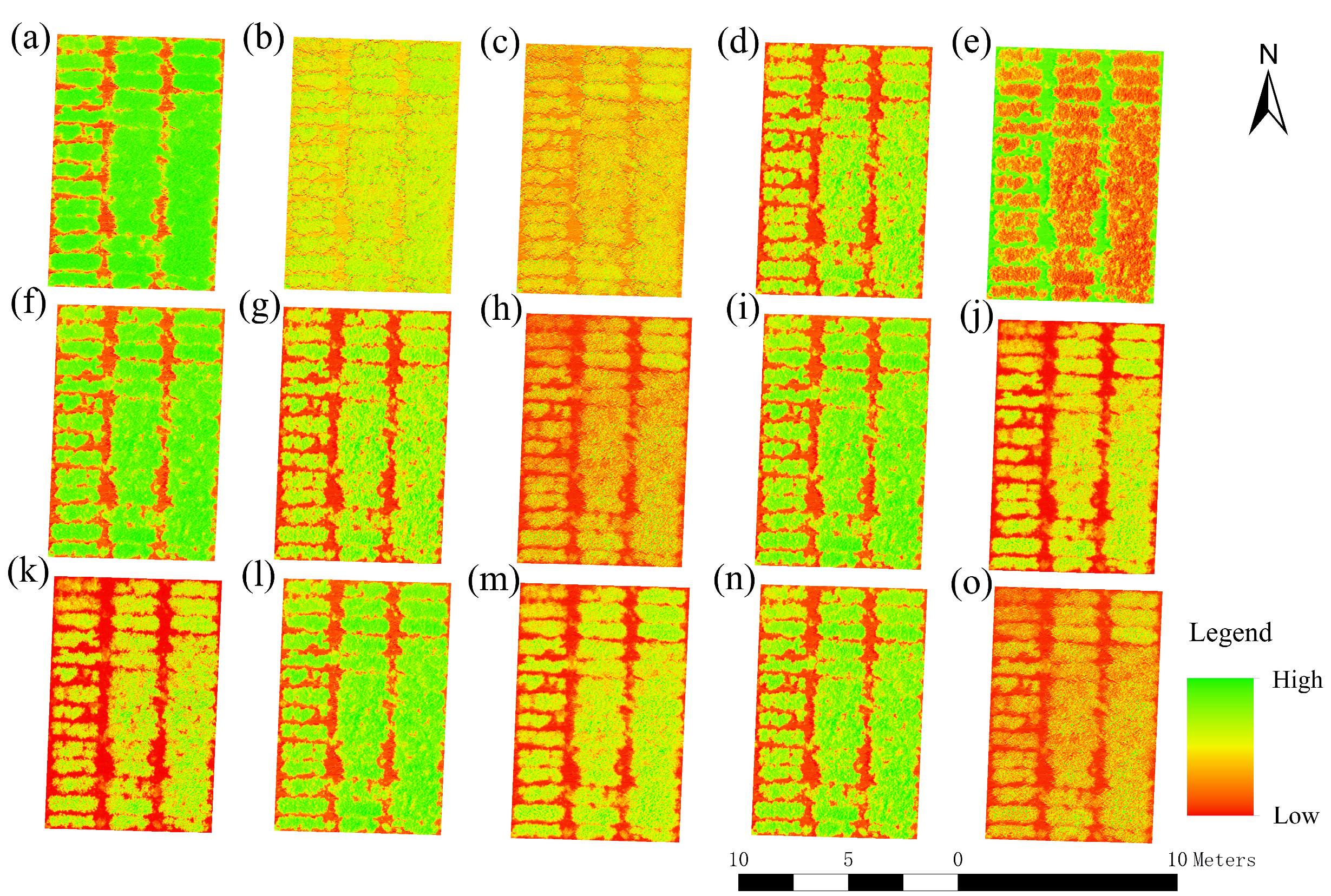
2.4.2. Calculation of Texture Characteristics
2.4.3. Screening of Spectral and Texture Characteristics
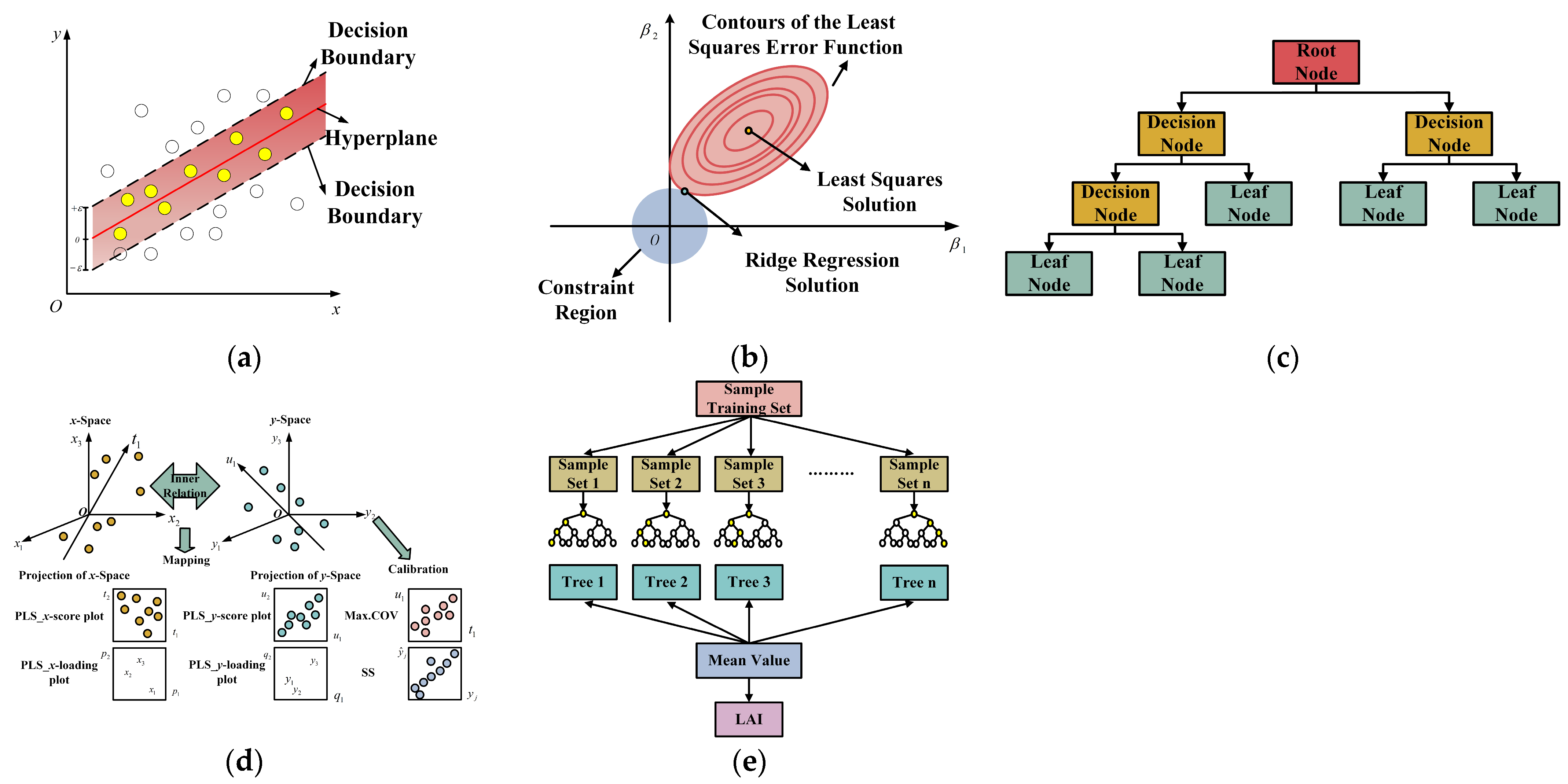
2.4.4. Construction of Regression Models
2.4.5. Assessment of Regression Models
3. Result and Analysis
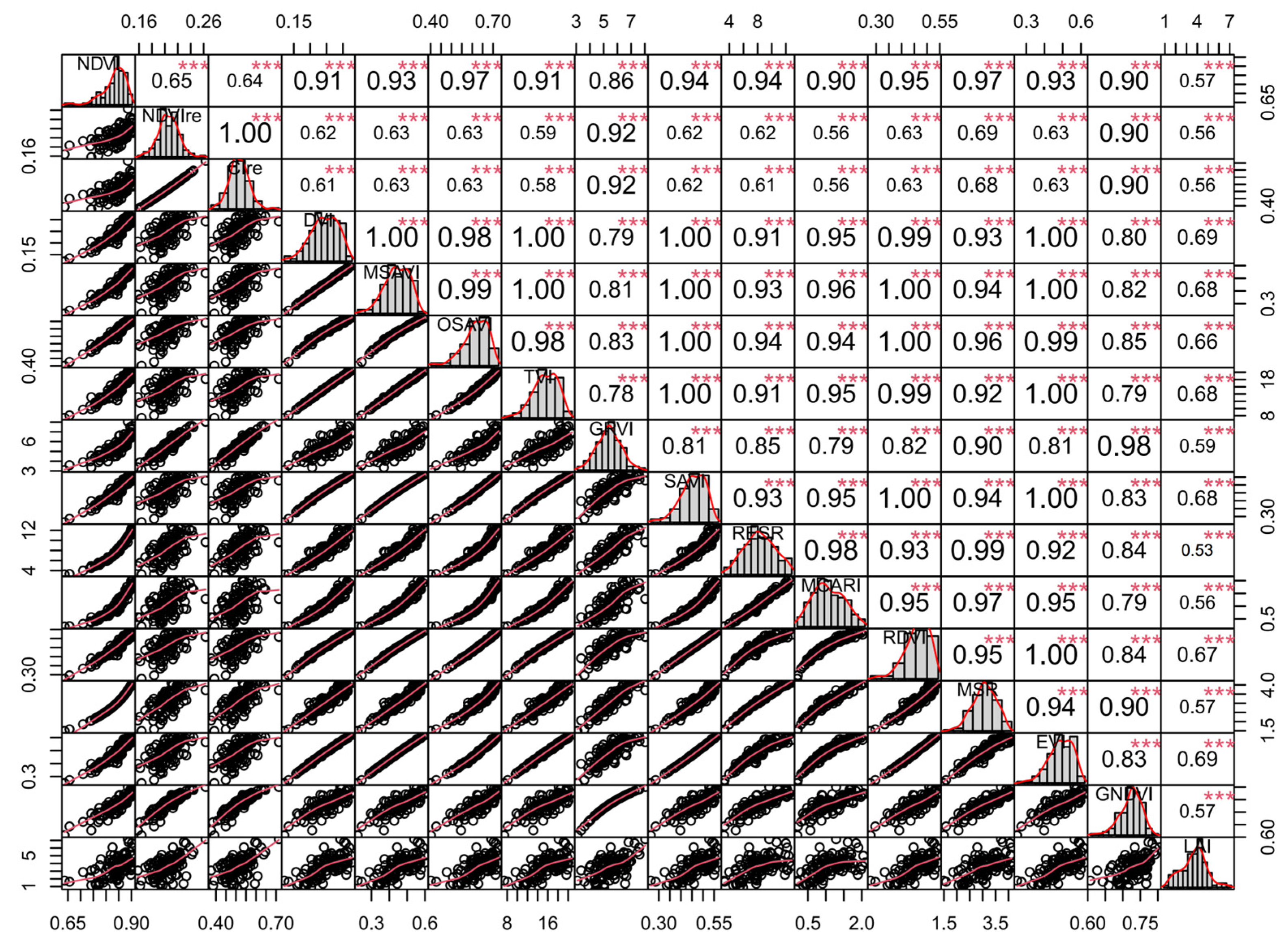
3.1. Correlation Analysis between LAI and Vegetation Indices
3.2. Correlation Analysis between LAI and Texture Features
3.3. RFE Processing for Feature Selection
3.4. Estimation of Peanut LAI with Texture Features
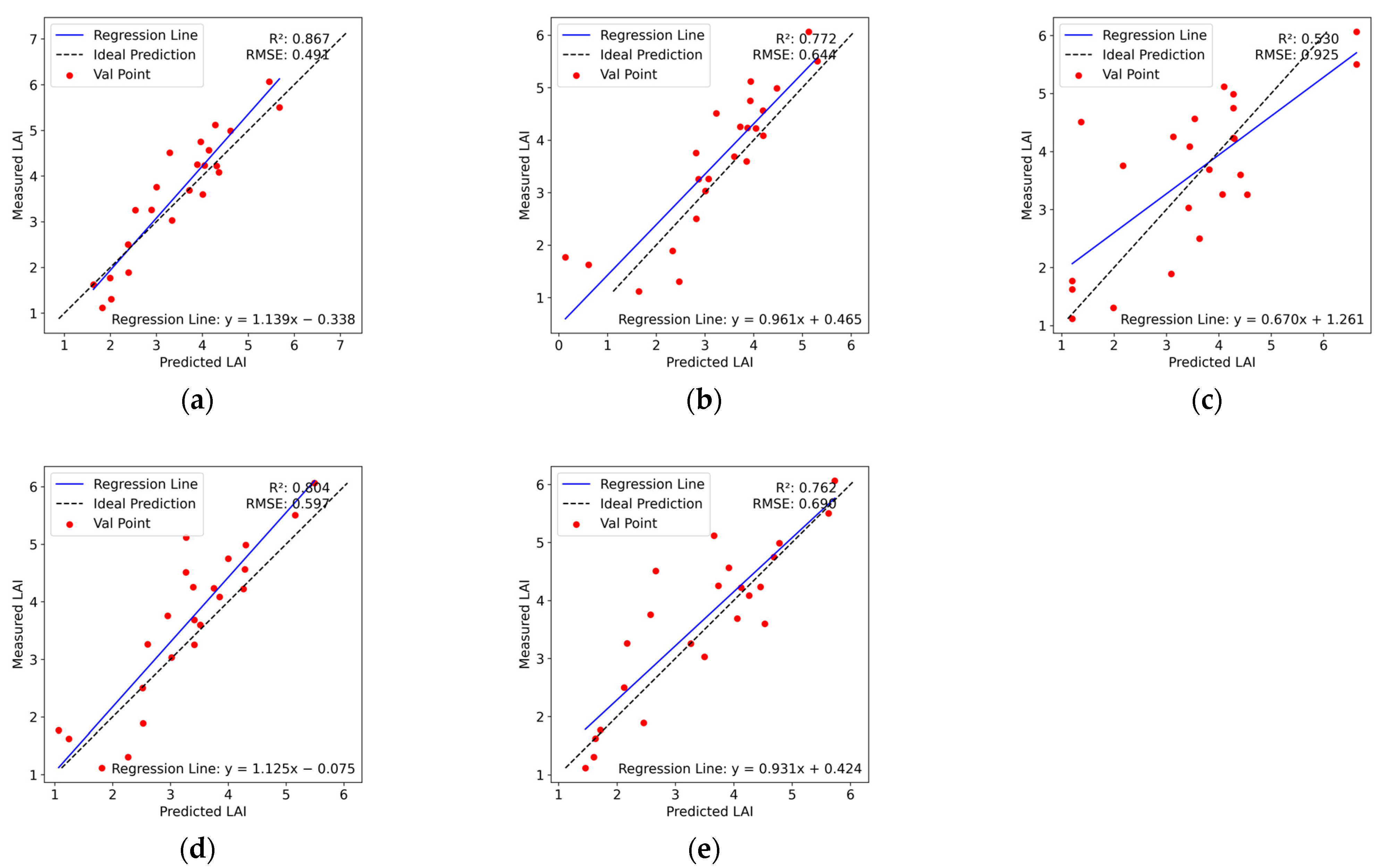
3.5. LAI Estimation Based on Different Characteristics
3.6. Comparison of Various Multivariate Regression Methods
4. Discussion
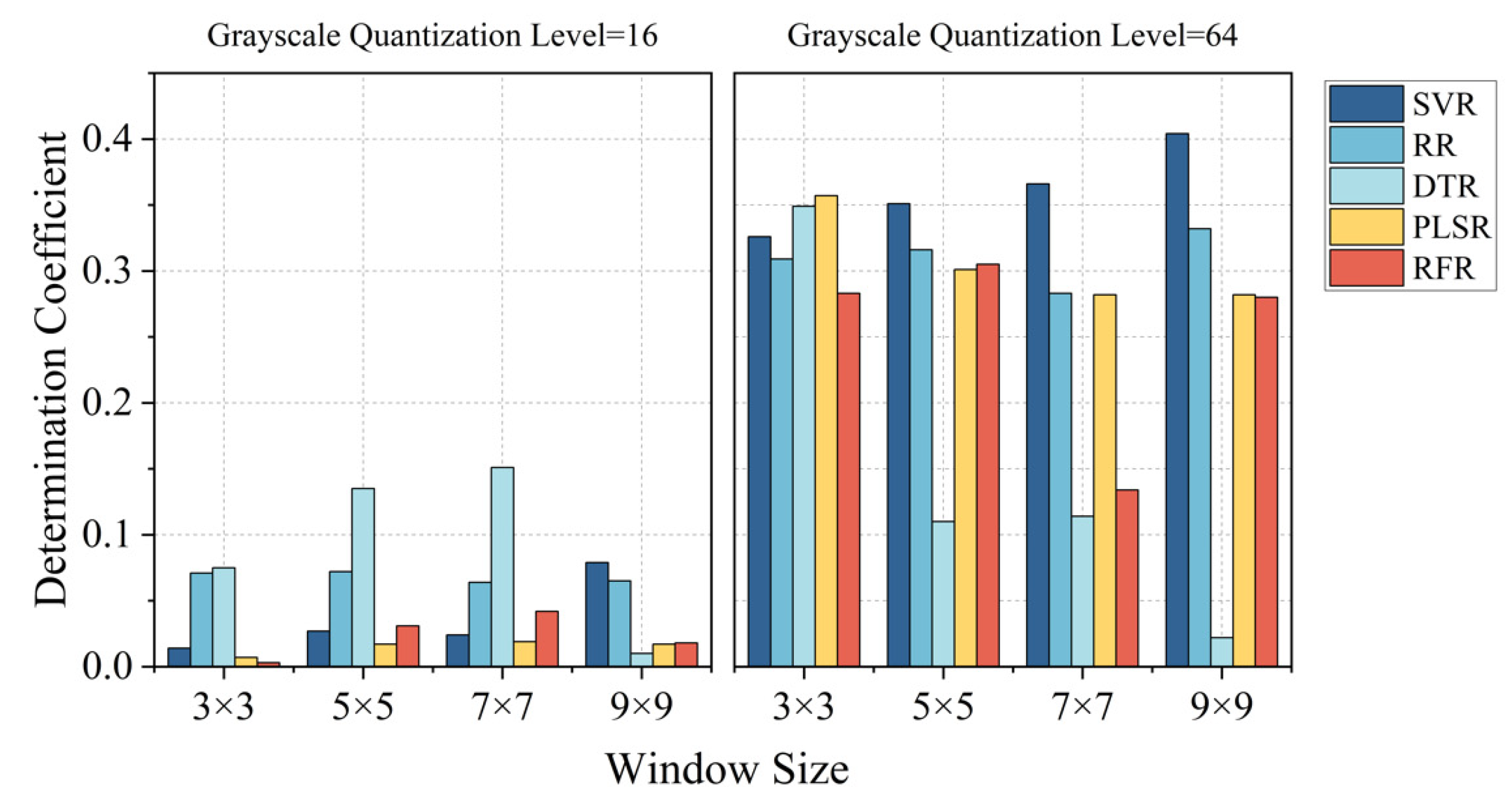
4.1. Effects of GLCM Parameters on the Performance of LAI Estimation
4.2. Advantages and Limitations of the Developed LAI Estimation Model
5. Conclusions
- (1)
- The integration of two feature selection methods, PCC and RFE, was used to identify 9 useful spectral and textural characteristics that contribute significantly to peanut LAI, including 3 vegetation indices (GRVI, MCARI, and TVI) and 6 texture features (blue-MEA, NIR-SEC, NIR-HOM, NIR-DIS, RE-DIS, and RE-VAR).
- (2)
- The parameter settings when extracting texture features have an impact on the estimation results. For high-resolution images obtained using drones, the smaller the size of the moving window and the higher the grayscale quantization level are, the higher the accuracy of the estimation of peanut LAI.
- (3)
- The estimation model that combines VI and TF effectively enhances the accuracy of LAI prediction, achieving an R2 of 0.867 and an RMSE of 0.491.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- National Bureau of Statistics of China. China Statistical Yearbook; China Statistics Press: Beijing, China, 2023. [Google Scholar]
- Bonan, G.B. Importance of leaf area index and forest type when estimating photosynthesis in boreal forests. Remote Sens. Environ. 1993, 43, 303–314. [Google Scholar] [CrossRef]
- Al-Kaisi, M.; Brun, L.J.; Enz, J.W. Transpiration and evapotranspiration from maize as related to leaf area index. Agric. For. Meteorol. 1989, 48, 111–116. [Google Scholar] [CrossRef]
- Albaugh, T.J.; Allen, H.L.; Dougherty, P.M.; Kress, L.W.; King, J.S. Leaf area and above-and belowground growth responses of loblolly pine to nutrient and water additions. For. Sci. 1998, 44, 317–328. [Google Scholar] [CrossRef]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and indirect estimation of leaf area index, fAPAR, and net primary production of terrestrial ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Bréda, N.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Van Wijk, M.T.; Williams, M. Optical instruments for measuring leaf area index in low vegetation: Application in arctic ecosystems. Ecol. Appl. 2005, 15, 1462–1470. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, R. Unmanned aerial vehicle remote sensing for field-based crop phenotyping: Current status and perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef]
- Colombo, R.; Bellingeri, D.; Fasolini, D.; Marino, C.M. Retrieval of leaf area index in different vegetation types using high resolution satellite data. Remote Sens. Environ. 2003, 86, 120–131. [Google Scholar] [CrossRef]
- Green, E.; Mumby, P.; Edwards, A.; Clark, C.; Ellis, A.C. The assessment of mangrove areas using high resolution multispectral airborne imagery. J. Coast. Res. 1998, 14, 433–443. [Google Scholar]
- Herwitz, S.; Johnson, L.; Dunagan, S.; Higgins, R.; Sullivan, D.; Zheng, J.; Lobitz, B.; Leung, J.; Gallmeyer, B.; Aoyagi, M.; et al. Imaging from an unmanned aerial vehicle: Agricultural surveillance and decision support. Comput. Electron. Agric. 2004, 44, 49–61. [Google Scholar] [CrossRef]
- Bicheron, P.; Leroy, M. A method of biophysical parameter retrieval at global scale by inversion of a vegetation reflectance model. Remote Sens. Environ. 1999, 67, 251–266. [Google Scholar] [CrossRef]
- Lin, L.; Yu, K.; Yao, X.; Deng, Y.; Hao, Z.; Chen, Y.; Wu, N.; Liu, J. UAV based estimation of forest leaf area index (LAI) through oblique photogrammetry. Remote Sens. 2021, 13, 803. [Google Scholar] [CrossRef]
- Vélez, S.; Poblete-Echeverría, C.; Rubio, J.A.; Barajas, E. Estimation of Leaf Area Index in vineyards by analysing projected shadows using UAV imagery. OENO ONE 2021, 55, 159–180. [Google Scholar] [CrossRef]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Ke, L.; Zhou, Q.; Wu, W.; Tian, X.; Tang, H. Estimating the crop leaf area index using hyperspectral remote sensing. J. Integr. Agric. 2016, 15, 475–491. [Google Scholar]
- Cao, Y.; Li, G.L.; Luo, Y.K.; Pan, Q.; Zhang, S.Y. Monitoring of sugar beet growth indicators using wide-dynamic-range vegetation index (WDRVI) derived from UAV multispectral images. Comput. Electron. Agric. 2020, 171, 105331. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Ilniyaz, O.; Kurban, A.; Du, Q. Leaf area index estimation of pergola-trained vineyards in arid regions based on UAV RGB and multispectral data using machine learning methods. Remote Sens. 2022, 14, 415. [Google Scholar] [CrossRef]
- Zhou, C.; Gong, Y.; Fang, S.; Yang, K.; Peng, Y.; Wu, X.; Zhu, R. Combining spectral and wavelet texture features for unmanned aerial vehicles remote estimation of rice leaf area index. Front. Plant Sci. 2022, 13, 957870. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, Y.; Chen, P.; Yang, Y.; Fu, H.; Yang, F.; Raza, M.A.; Guo, C.; Shu, C.; Sun, Y.; et al. Estimation of rice aboveground biomass by combining canopy spectral reflectance and unmanned aerial vehicle-based red green blue imagery data. Front. Plant Sci. 2022, 13, 903643. [Google Scholar] [CrossRef]
- Zhang, J.; Qiu, X.; Wu, Y.; Zhu, Y.; Cao, Q.; Liu, X.; Cao, W. Combining texture, color, and vegetation indices from fixed-wing UAS imagery to estimate wheat growth parameters using multivariate regression methods. Comput. Electron. Agric. 2021, 185, 106138. [Google Scholar] [CrossRef]
- Liu, Y.; An, L.; Wang, N.; Tang, W.; Liu, M.; Liu, G.; Sun, H.; Li, M.; Ma, Y. Leaf area index estimation under wheat powdery mildew stress by integrating UAV-based spectral, textural and structural features. Comput. Electron. Agric. 2023, 213, 108169. [Google Scholar] [CrossRef]
- Wang, X.; Yan, S.; Wang, W.; Liubing, Y.; Li, M.; Yu, Z.; Chang, S.; Hou, F. Monitoring leaf area index of the sown mixture pasture through UAV multispectral image and texture characteristics. Comput. Electron. Agric. 2023, 214, 108333. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Zhang, J.; Guo, Y.; Yang, X.; Yu, G.; Bai, X.; Chen, J.; Chen, Y.; Shi, L.; et al. Improving estimation of maize leaf area index by combining of UAV-based multispectral and thermal infrared data: The potential of new texture index. Comput. Electron. Agric. 2023, 214, 108294. [Google Scholar] [CrossRef]
- Yuan, W.; Meng, Y.; Li, Y.; Ji, Z.; Kong, Q.; Gao, R.; Su, Z. Research on rice leaf area index estimation based on fusion of texture and spectral information. Comput. Electron. Agric. 2023, 211, 108016. [Google Scholar] [CrossRef]
- Zhou, J.; Yan Guo, R.; Sun, M.; Di, T.T.; Wang, S.; Zhai, J.; Zhao, Z. The Effects of GLCM parameters on LAI estimation using texture values from Quickbird Satellite Imagery. Sci. Rep. 2017, 7, 7366. [Google Scholar] [CrossRef] [PubMed]
- Bian, M.; Chen, Z.; Fan, Y.; Ma, Y.; Liu, Y.; Chen, R.; Feng, H. Integrating Spectral, Textural, and Morphological Data for Potato LAI Estimation from UAV Images. Agronomy 2023, 13, 3070. [Google Scholar] [CrossRef]
- Yu, T.; Zhou, J.; Fan, J.; Wang, Y.; Zhang, Z. Potato Leaf Area Index Estimation Using Multi-Sensor Unmanned Aerial Vehicle (UAV) Imagery and Machine Learning. Remote Sens. 2023, 15, 4108. [Google Scholar] [CrossRef]
- Luo, P.; Liao, J.; Shen, G. Combining spectral and texture features for estimating leaf area index and biomass of maize using Sentinel-1/2, and Landsat-8 data. IEEE Access 2020, 8, 53614–53626. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, K.; Sun, Y.; Zhao, Y.; Zhuang, H.; Ban, W.; Chen, Y.; Fu, E.; Chen, S.; Liu, J.; et al. Combining spectral and texture features of UAS-based multispectral images for maize leaf area index estimation. Remote Sens. 2022, 14, 331. [Google Scholar] [CrossRef]
- Zhou, M.; Zheng, H.; He, C.; Liu, P.; Awan, G.M.; Wang, X.; Cheng, T.; Zhu, Y.; Cao, W.; Yao, X. Wheat phenology detection with the methodology of classification based on the time-series UAV images. Field Crops Res. 2023, 292, 108798. [Google Scholar] [CrossRef]
- Rouse Jr, J.W.; Haas, R.H.; Deering, D.; Schell, J.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation. NASA/GSFC Type III Final Report, Greenbelt, Md 371; NASA: Washington, DC, USA, 1974; p. E75-10354. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N.; Lichtenthaler, H.K. Detection of red edge position and chlorophyll content by reflectance measurements near 700 nm. J. Plant Physiol. 1996, 148, 501–508. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.J. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Daughtry, C.S.; Walthall, C.; Kim, M.; De Colstoun, E.B.; McMurtrey Iii, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the enhanced vegetation index (EVI) and normalized difference vegetation index (NDVI) to topographic effects: A case study in high-density cypress forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Sedgwick, P. Pearson’s correlation coefficient. BMJ 2012, 345, e4483. [Google Scholar] [CrossRef]
- Granitto, P.M.; Furlanello, C.; Biasioli, F.; Gasperi, F. Recursive feature elimination with random forest for PTR-MS analysis of agroindustrial products. Chemom. Intell. Lab. Syst. 2006, 83, 83–90. [Google Scholar] [CrossRef]
- Kurtz, A.K.; Mayo, S.T.; Kurtz, A.K.; Mayo, S.T. Pearson product moment coefficient of correlation. Stat. Methods Educ. Psychol. 1979, 192–277. [Google Scholar] [CrossRef]
- Obilor, E.I.; Amadi, E.C. Test for significance of Pearson’s correlation coefficient. Int. J. Innov. Math. Stat. Energy Policies 2018, 6, 11–23. [Google Scholar]
- Zhang, J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.; Xie, Y.; Ma, X. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 49. [Google Scholar] [CrossRef]
- Sun, X.; Yang, Z.; Su, P.; Wei, K.; Wang, Z.; Yang, C.; Wang, C.; Qin, M.; Xiao, L.; Yang, W.; et al. Non-destructive monitoring of maize LAI by fusing UAV spectral and textural features. Front. Plant Sci. 2023, 14, 1158837. [Google Scholar] [CrossRef]
- Duan, M.; Zhang, X. Using remote sensing to identify soil types based on multiscale image texture features. Comput. Electron. Agric. 2021, 187, 106272. [Google Scholar] [CrossRef]
- Kiala, Z.; Odindi, J.; Mutanga, O.; Peerbhay, K. Comparison of partial least squares and support vector regressions for predicting leaf area index on a tropical grassland using hyperspectral data. J. Appl. Remote Sens. 2016, 10, 036015. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Zhao, Z.; Zhao, J.; Zhao, Q.; Wang, F.; Wang, H. A comparison of three methods for estimating the LAI of black locust (Robinia pseudoacacia L.) plantations on the Loess Plateau, China. Int. J. Remote Sens. 2014, 35, 171–188. [Google Scholar] [CrossRef]
- Franklin, S.; Wulder, M.; Gerylo, G.R. Texture analysis of IKONOS panchromatic data for Douglas-fir forest age class separability in British Columbia. Int. J. Remote Sens. 2001, 22, 2627–2632. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Zhou, C.; Yin, L.; Feng, X. Urban forest monitoring based on multiple features at the single tree scale by UAV. Urban For. Urban Green. 2021, 58, 126958. [Google Scholar] [CrossRef]
- Clausi, D.A. An analysis of co-occurrence texture statistics as a function of grey level quantization. Can. J. Remote Sens. 2002, 28, 45–62. [Google Scholar] [CrossRef]
- Xie, Q.; Huang, W.; Zhang, B.; Chen, P.; Song, X.; Pascucci, S.; Pignatti, S.; Laneve, G.; Dong, Y. Estimating winter wheat leaf area index from ground and hyperspectral observations using vegetation indices. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 771–780. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved forest biomass estimates using ALOS AVNIR-2 texture indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
- Xu, W.; Chen, P.; Zhan, Y.; Chen, S.; Zhang, L.; Lan, Y. Cotton yield estimation model based on machine learning using time series UAV remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102511. [Google Scholar] [CrossRef]
- Cheng, Q.; Ding, F.; Xu, H.; Guo, S.; Li, Z.; Chen, Z. Quantifying corn LAI using machine learning and UAV multispectral imaging. Precis. Agric. 2024, 1–23. [Google Scholar] [CrossRef]
- Gao, L.; Yang, G.; Li, H.; Li, Z.; Feng, H.; Wang, L.; Dong, J.; He, P. Winter wheat LAI estimation using unmanned aerial vehicle RGB-imaging. Chin. J. Eco-Agric. 2016, 24, 1254–1264. [Google Scholar]
- Chen, C.; Wang, E.; Yu, Q. Modeling wheat and maize productivity as affected by climate variation and irrigation supply in North China Plain. Agron. J. 2010, 102, 1037–1049. [Google Scholar] [CrossRef]




| Band Number | Band Name | Center Wavelength/nm | Band Width/nm |
|---|---|---|---|
| B1 | Blue | 450 | 16 |
| B2 | Green | 560 | 16 |
| B3 | Red | 650 | 16 |
| B4 | Red Edge | 730 | 16 |
| B5 | Near-Infrared Red | 840 | 26 |
| Number | Index | Acronym | Formula | Reference |
|---|---|---|---|---|
| (a) | Normalized Difference Vegetation Index | NDVI | [33] | |
| (b) | Red-Edge Normalized Difference Vegetation Index | NDVIre | [34] | |
| (c) | Red-Edge Chlorophyll Index | CIre | [35] | |
| (d) | Difference Vegetation Index | DVI | [36] | |
| (e) | Modified Soil-Adjusted Vegetation Index | MSAVI | [37] | |
| (f) | Optimized Soil-Adjusted Vegetation Index | OSAVI | [38] | |
| (g) | Triangular Vegetation Index | TVI | [39] | |
| (h) | Green Ratio Vegetation Index | GRVI | [40] | |
| (i) | Soil-Adjusted Vegetation Index | SAVI | [41] | |
| (j) | Red Edge Simple Ratio | RESR | [42] | |
| (k) | Modified Chlorophyll Absorption Ratio Index | MCARI | [40] | |
| (l) | Renormalized Difference Vegetation Index | RDVI | [43] | |
| (m) | Modified Simple Ratio | MSR | [42] | |
| (n) | Enhanced Vegetation Index | EVI | [44] | |
| (o) | Green Normalized Difference Vegetation Index | GNDVI | [40] |
| Number | Texture Feature | Acronym | Formula | Description |
|---|---|---|---|---|
| (a) | Mean | MEA | Average of the texture | |
| (b) | Variance | VAR | Variation of the texture change | |
| (c) | Homogeneity | HOM | Homogeneity of the local texture | |
| (d) | Contrast | CON | Clarity of the texture | |
| (e) | Dissimilarity | DIS | Similarity of the texture | |
| (f) | Entropy | ENT | Non-uniformity or complexity of the texture in the image | |
| (g) | Second Moment | SEC | Gray distribution uniformity and texture thickness in the image | |
| (h) | Correlation | COR | Consistency of the texture |
| Texture Feature | Correlation Coefficient | ||||
|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | |
| CON | 0.021 | 0.200 * | 0.200 * | 0.170 * | 0.085 |
| COR | −0.270 ** | −0.210 * | −0.210 * | −0.370 ** | −0.330 ** |
| DIS | 0.091 | 0.190 * | 0.190 * | 0.230 ** | 0.097 |
| ENT | 0.160 * | 0.190 * | 0.190 * | 0.270 ** | 0.095 |
| HOM | −0.150 | −0.190 * | −0.190 * | −0.270 ** | −0.096 |
| MEA | 0.610 ** | 0.160 | 0.160 * | 0.570 ** | 0.610 ** |
| SEC | −0.190 * | −0.190 * | −0.190 * | −0.270 ** | −0.120 |
| VAR | −0.032 | 0.210 * | 0.210 * | 0.160 * | 0.014 |
| Model Input | Model Formula | R2 | RMSE |
|---|---|---|---|
| MCARI | LAI = 1.569 MCARI + 1.889 | 0.323 | 0.940 |
| GRVI | LAI = 0.742 GRVI − 0.482 | 0.519 | 0.792 |
| TVI | LAI = 0.293 TVI − 0.979 | 0.545 | 0.770 |
| LAI = 2.391 + 3.031 | 0.093 | 1.088 | |
| LAI = 0.685 + 3.388 | 0.225 | 1.005 | |
| LAI= 3.318 + 2.205 | 0.274 | 0.973 | |
| LAI = −1.542 + 4.376 | 0.271 | 0.975 | |
| LAI = −2.576 + 4.056 | 0.309 | 0.950 |
| Combination of Different Characteristics | Model | ||||
|---|---|---|---|---|---|
| SVR | RR | DTR | PLSR | RFR | |
| VI | 0.812 | 0.708 | 0.397 | 0.666 | 0.601 |
| TF | 0.326 | 0.309 | 0.349 | 0.357 | 0.283 |
| VI + TF | 0.867 | 0.772 | 0.530 | 0.804 | 0.762 |
| Parameter Setting | TF | VI + TF | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Patch Size | Grayscale | SVR | RR | DTR | PLSR | RFR | SVR | RR | DTR | PLSR | RFR |
| 3 × 3 | 16 | 0.014 | 0.071 | 0.075 | 0.007 | 0.003 | 0.826 | 0.735 | 0.443 | 0.647 | 0.609 |
| 64 | 0.326 | 0.309 | 0.349 | 0.357 | 0.283 | 0.867 | 0.772 | 0.530 | 0.804 | 0.762 | |
| 5 × 5 | 16 | 0.027 | 0.072 | 0.135 | 0.017 | 0.031 | 0.826 | 0.734 | 0.385 | 0.637 | 0.622 |
| 64 | 0.351 | 0.316 | 0.110 | 0.301 | 0.305 | 0.860 | 0.767 | 0.567 | 0.771 | 0.779 | |
| 7 × 7 | 16 | 0.024 | 0.064 | 0.151 | 0.019 | 0.042 | 0.824 | 0.730 | 0.375 | 0.624 | 0.650 |
| 64 | 0.366 | 0.283 | 0.114 | 0.282 | 0.134 | 0.865 | 0.766 | 0.575 | 0.759 | 0.746 | |
| 9 × 9 | 16 | 0.076 | 0.065 | 0.010 | 0.017 | 0.018 | 0.823 | 0.730 | 0.302 | 0.646 | 0.591 |
| 64 | 0.404 | 0.332 | 0.022 | 0.282 | 0.280 | 0.832 | 0.725 | 0.489 | 0.647 | 0.748 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, D.; Yang, J.; Bai, B.; Li, G.; Wang, J.; Li, Z.; Liu, J.; Liu, J. Non-Destructive Monitoring of Peanut Leaf Area Index by Combing UAV Spectral and Textural Characteristics. Remote Sens. 2024, 16, 2182. https://doi.org/10.3390/rs16122182
Qiao D, Yang J, Bai B, Li G, Wang J, Li Z, Liu J, Liu J. Non-Destructive Monitoring of Peanut Leaf Area Index by Combing UAV Spectral and Textural Characteristics. Remote Sensing. 2024; 16(12):2182. https://doi.org/10.3390/rs16122182
Chicago/Turabian StyleQiao, Dan, Juntao Yang, Bo Bai, Guowei Li, Jianguo Wang, Zhenhai Li, Jincheng Liu, and Jiayin Liu. 2024. "Non-Destructive Monitoring of Peanut Leaf Area Index by Combing UAV Spectral and Textural Characteristics" Remote Sensing 16, no. 12: 2182. https://doi.org/10.3390/rs16122182
APA StyleQiao, D., Yang, J., Bai, B., Li, G., Wang, J., Li, Z., Liu, J., & Liu, J. (2024). Non-Destructive Monitoring of Peanut Leaf Area Index by Combing UAV Spectral and Textural Characteristics. Remote Sensing, 16(12), 2182. https://doi.org/10.3390/rs16122182







