Research on Calculation Method of On-Orbit Instrumental Line Shape Function for the Greenhouse Gases Monitoring Instrument on the GaoFen-5B Satellite
Abstract
1. Introduction
2. GMI Payload Overview and Ground-Based ILSF Testing
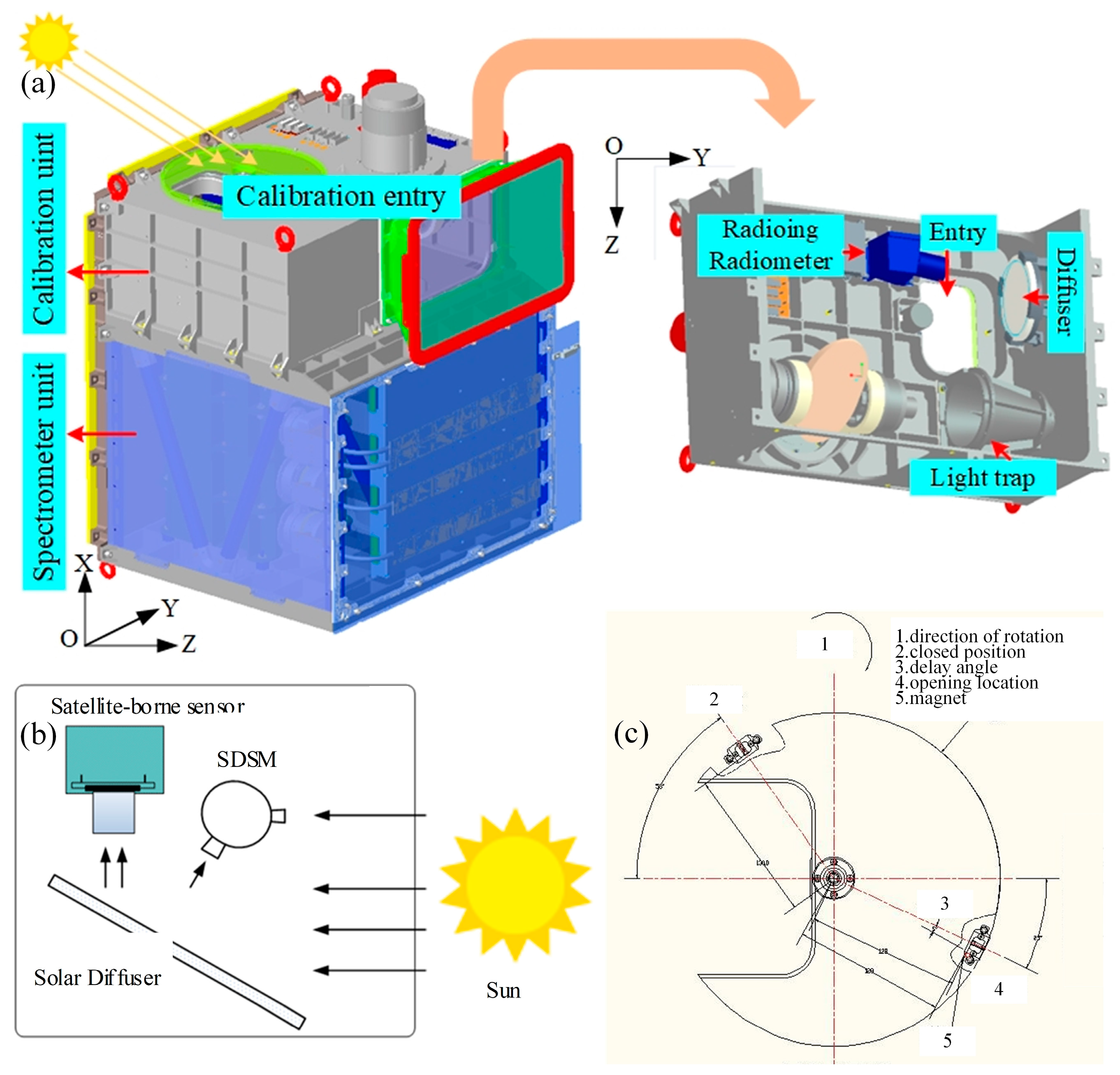
2.1. Overview of the GMI Payload
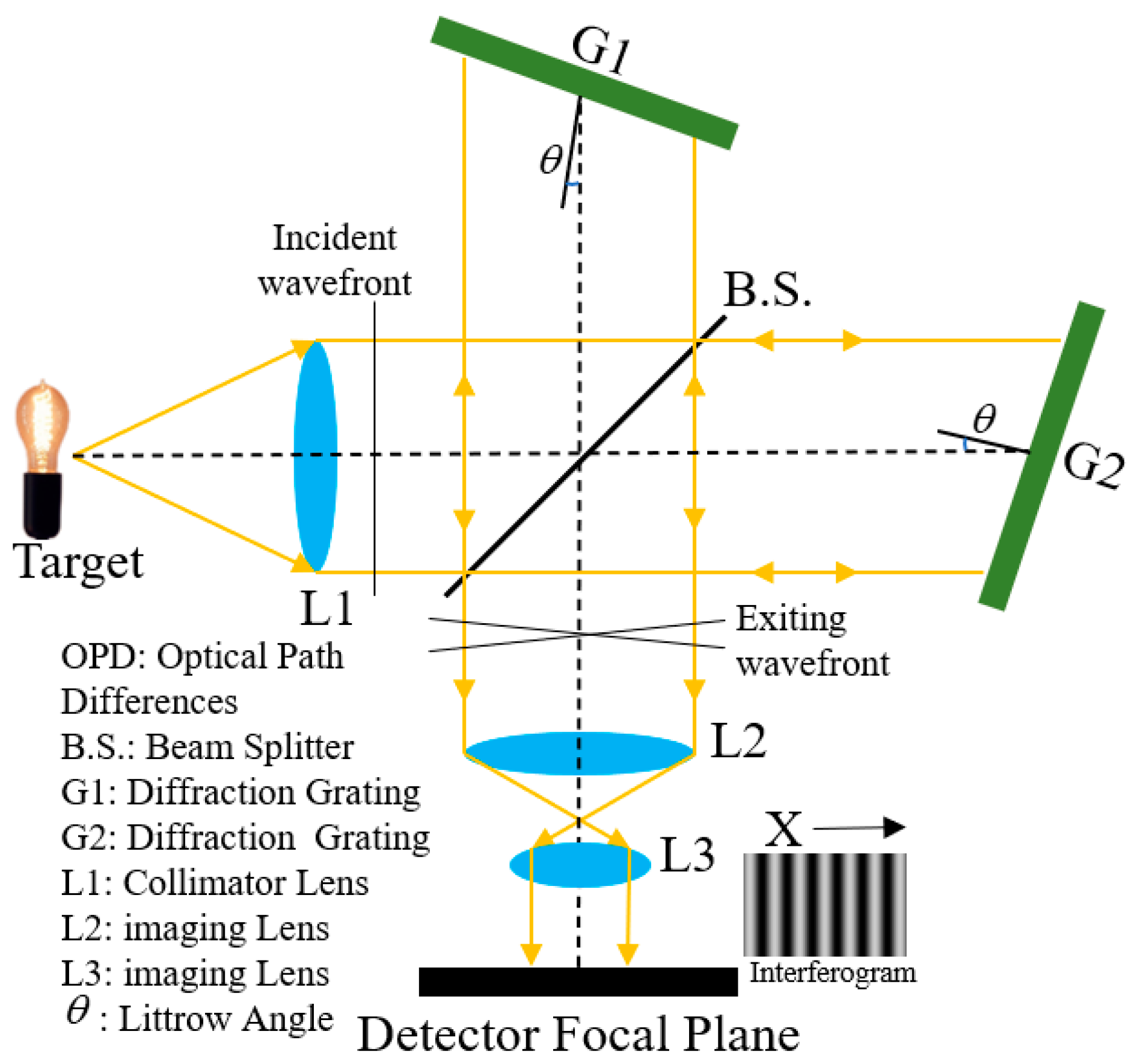
2.2. The ILSF Model and Laboratory Testing
2.2.1. Ideal Measurement Model
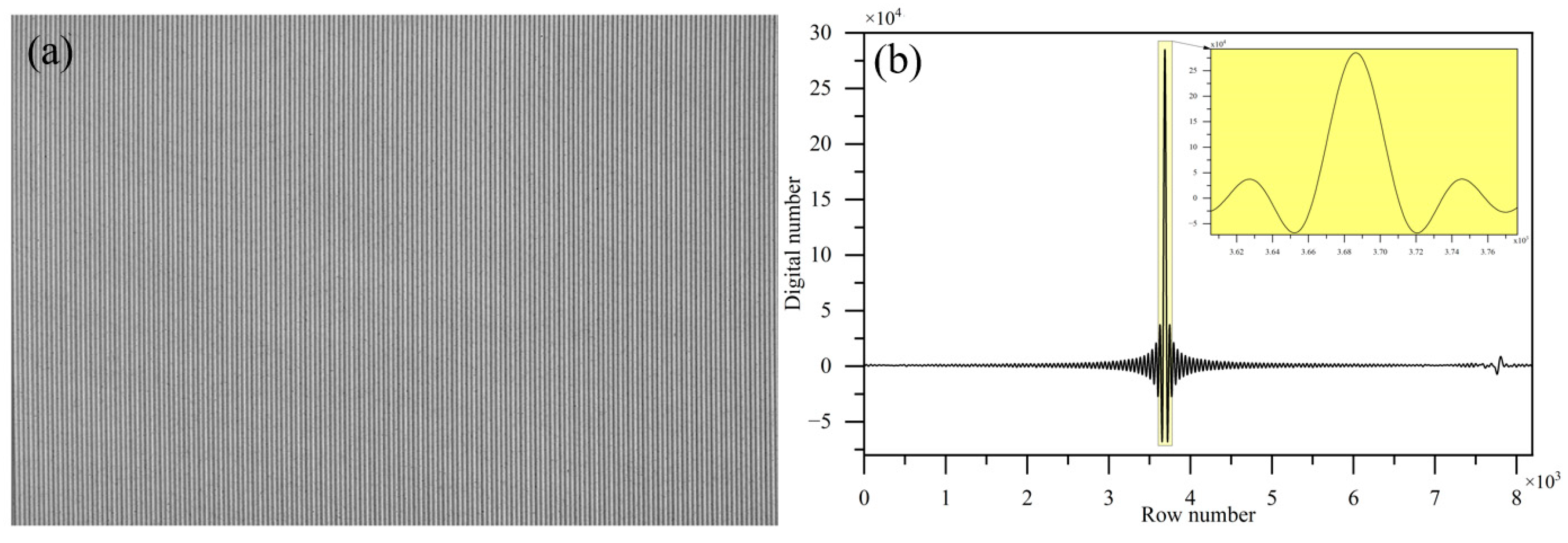
2.2.2. The Laboratory ILSF Experiment
2.2.3. The ILSF Absorption Cell Test Validation
3. On-Orbit ILSF Status Analysis
3.1. On-Orbit Calibration Scheme
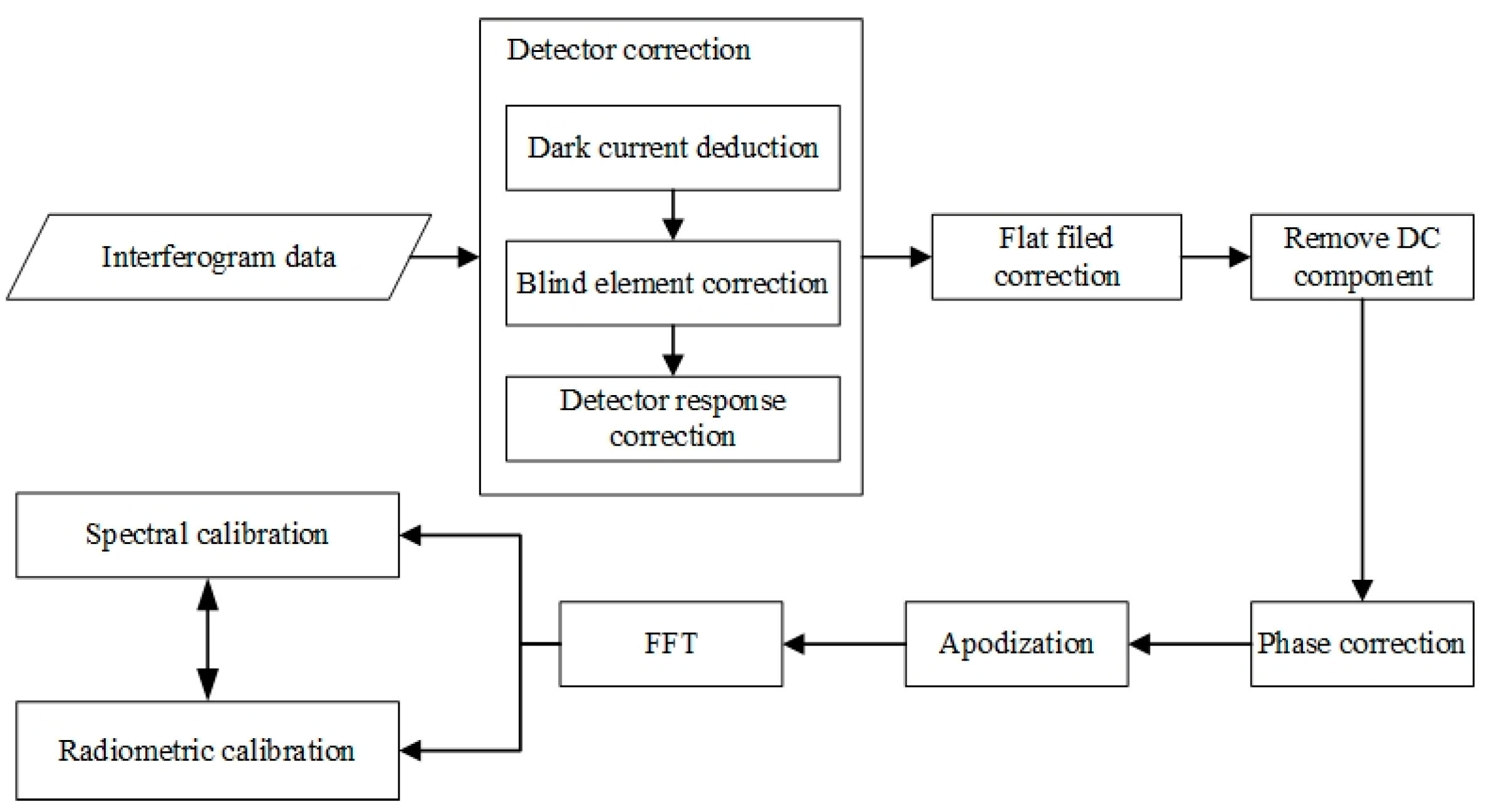
3.2. Theoretical Spectral Processing
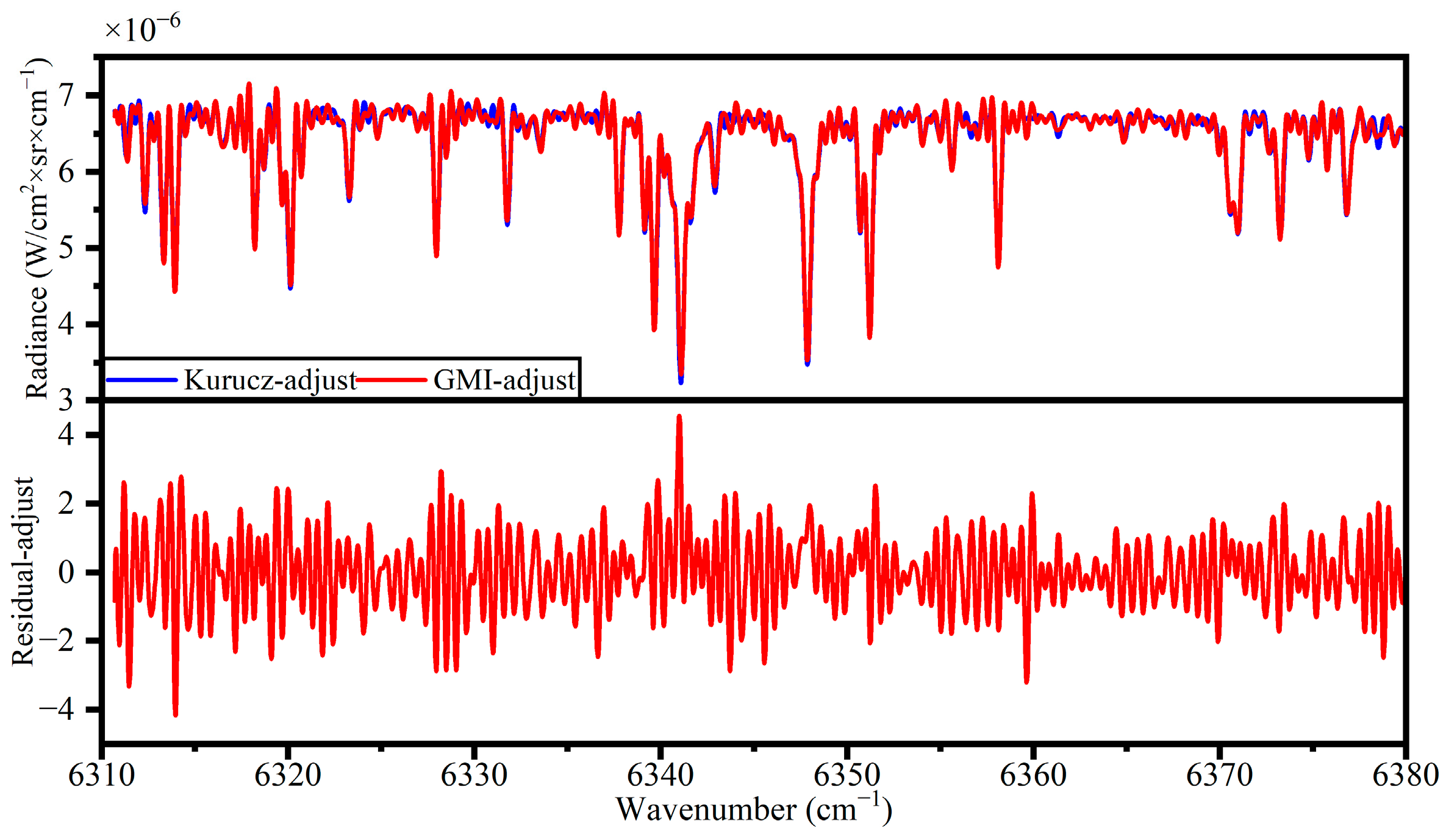
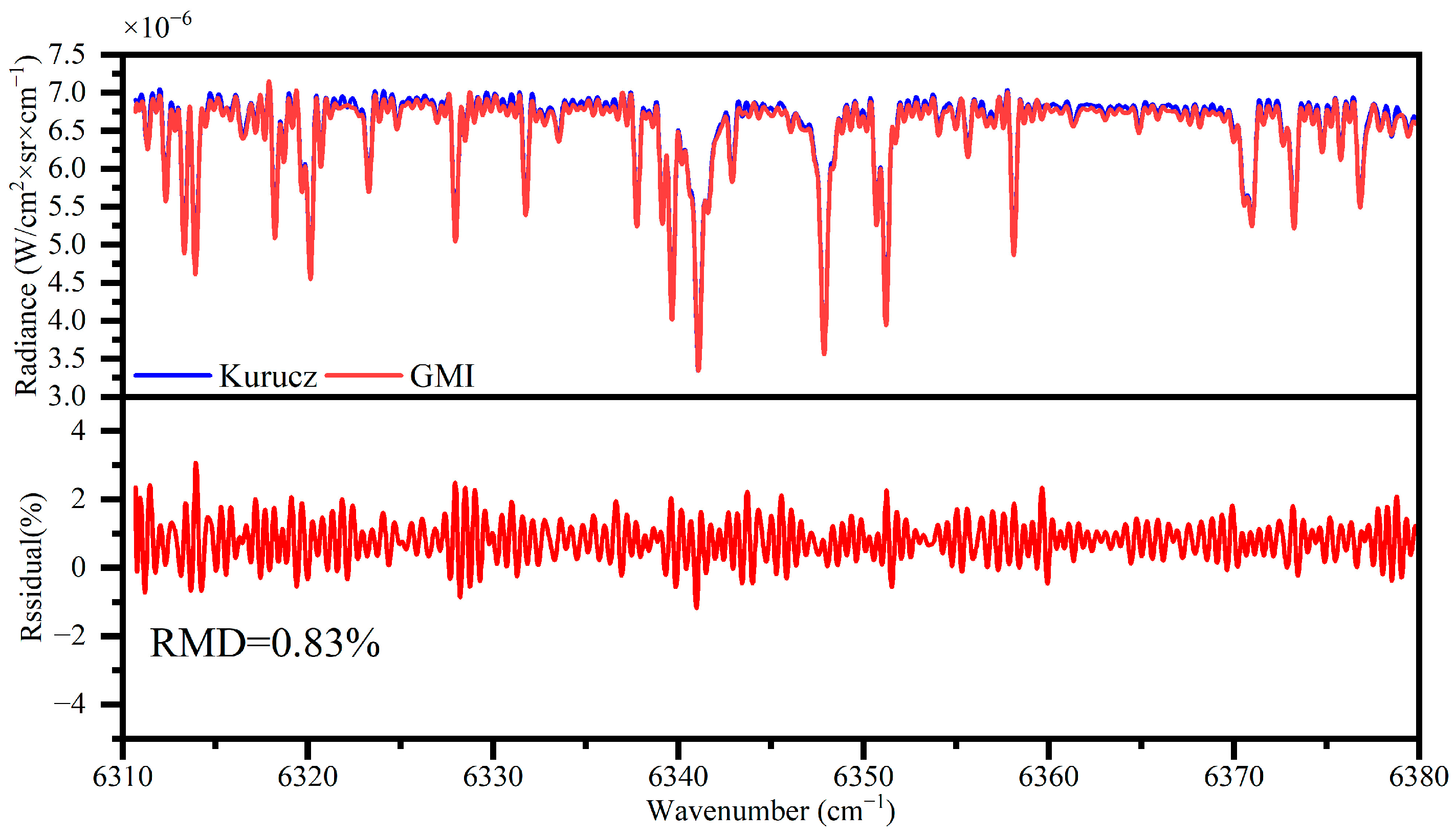
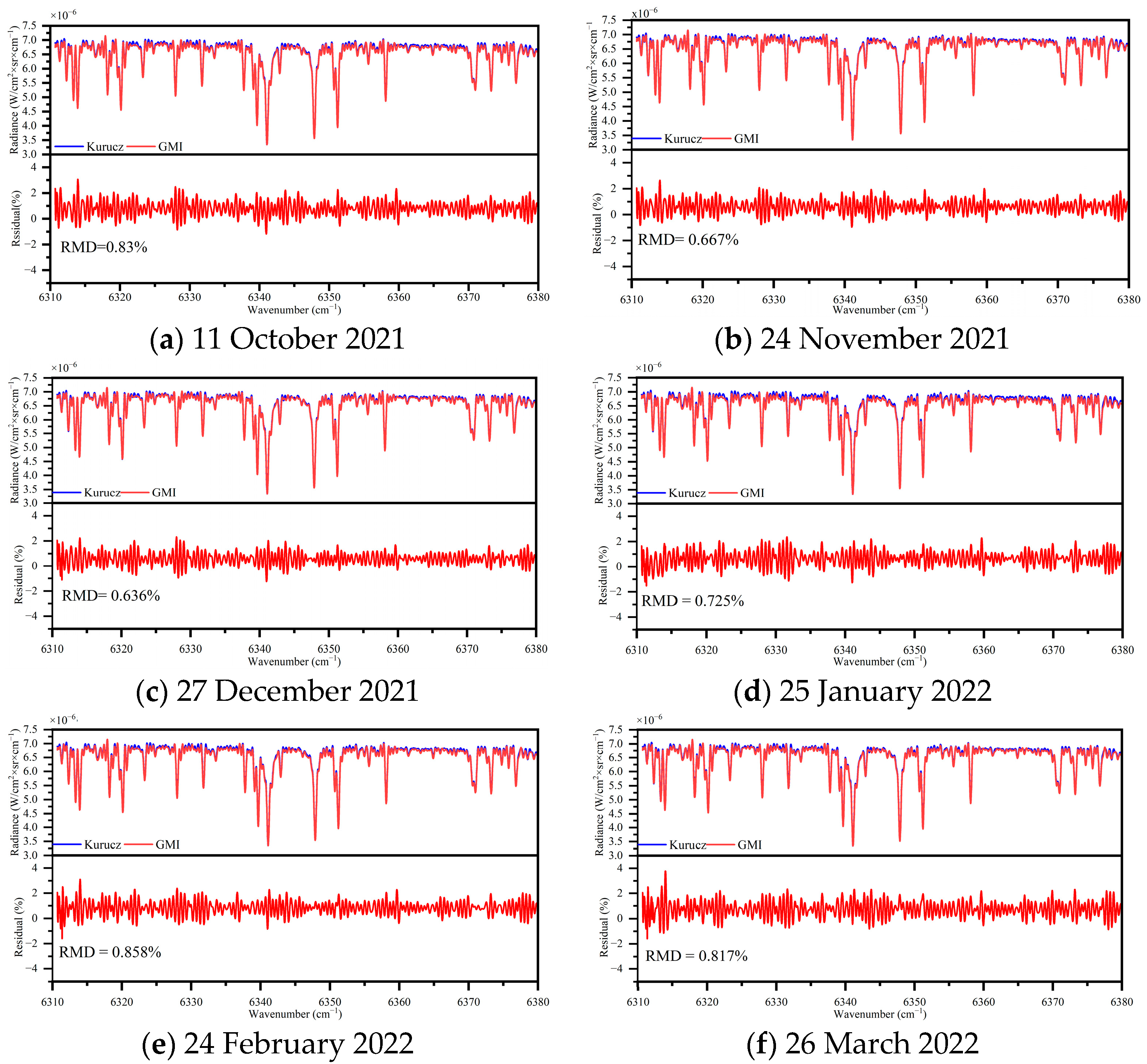
3.3. Solar Calibration Spectrum Processing
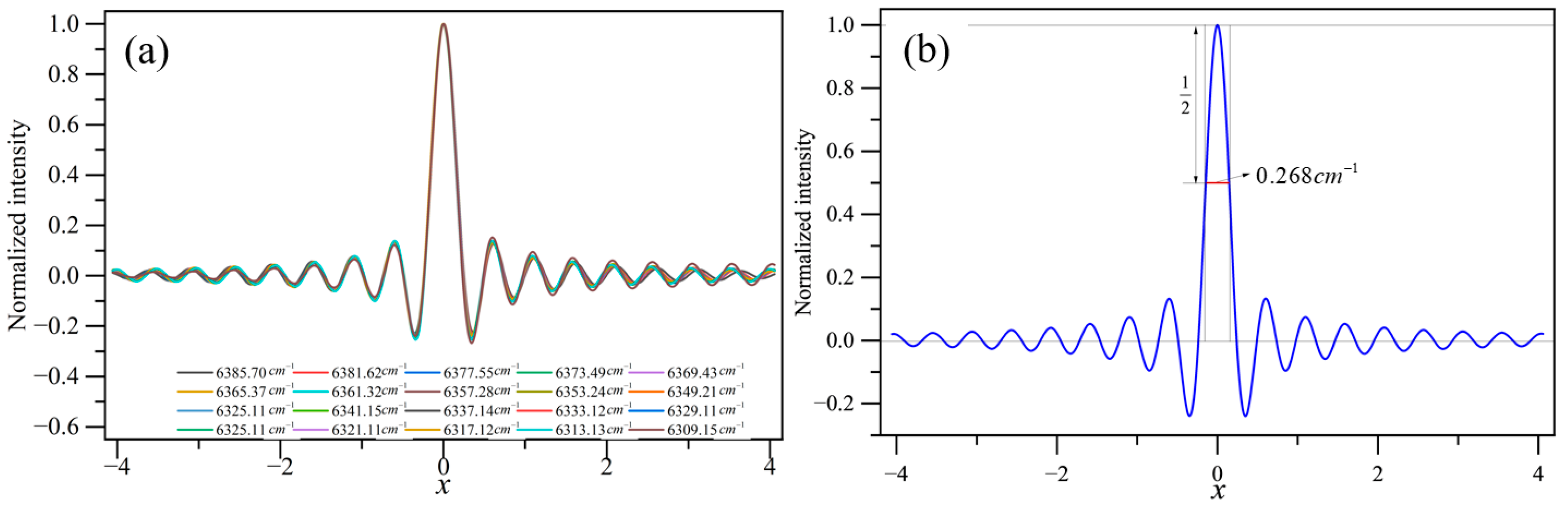
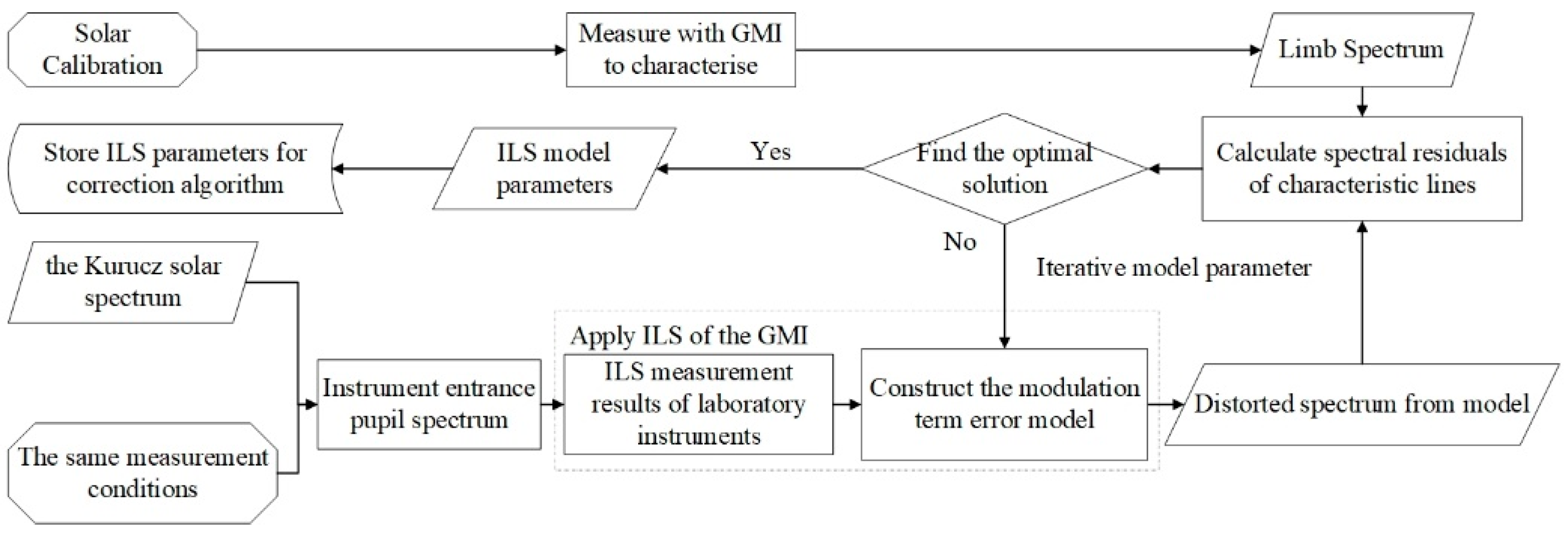
4. On-Orbit ILSF Iterative Model Algorithm
4.1. Error Function Model
4.2. Construction of an Error Model for the Modulation Term
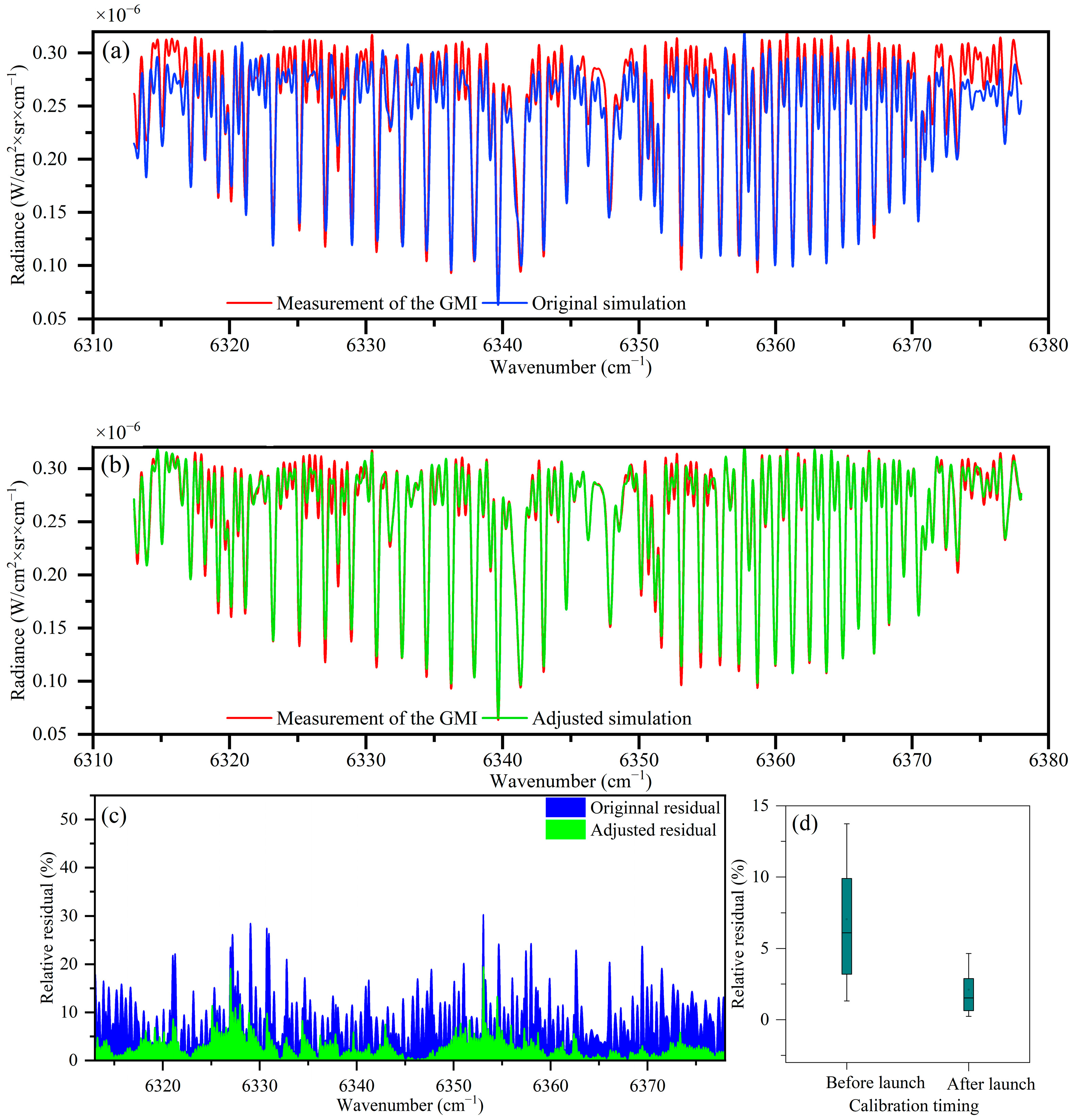
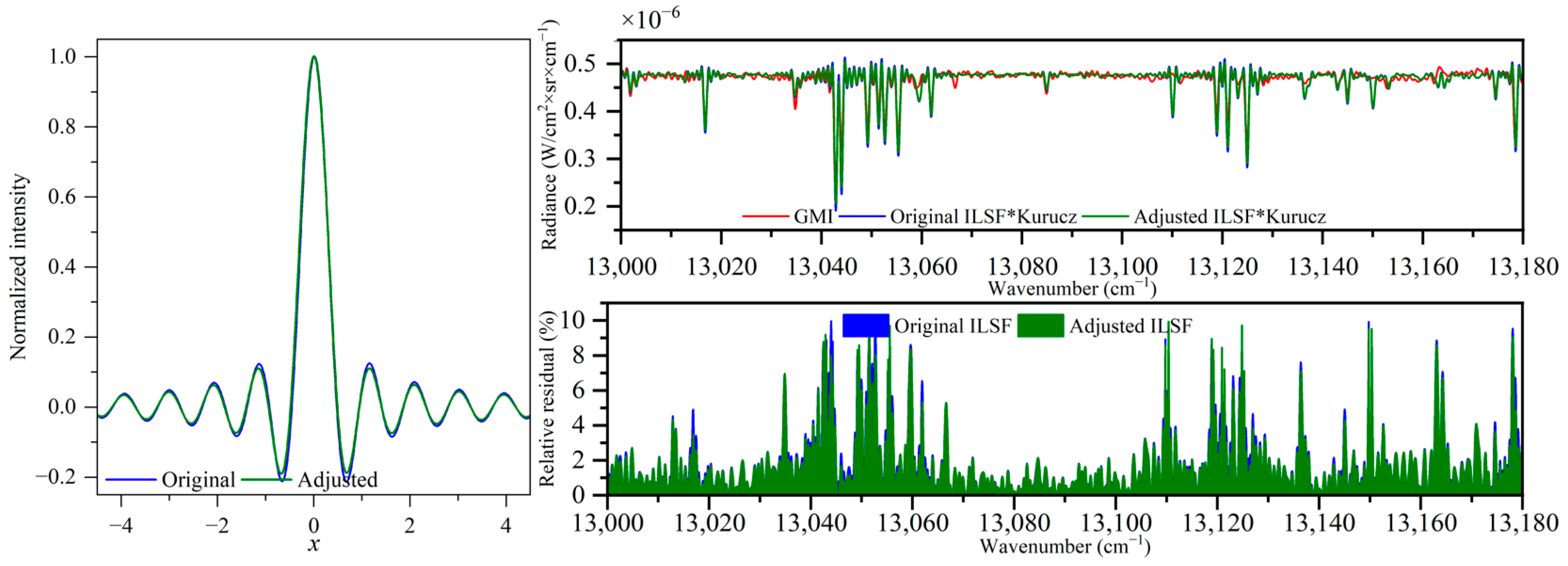
4.3. The ILSF Modulation Term Error Correction
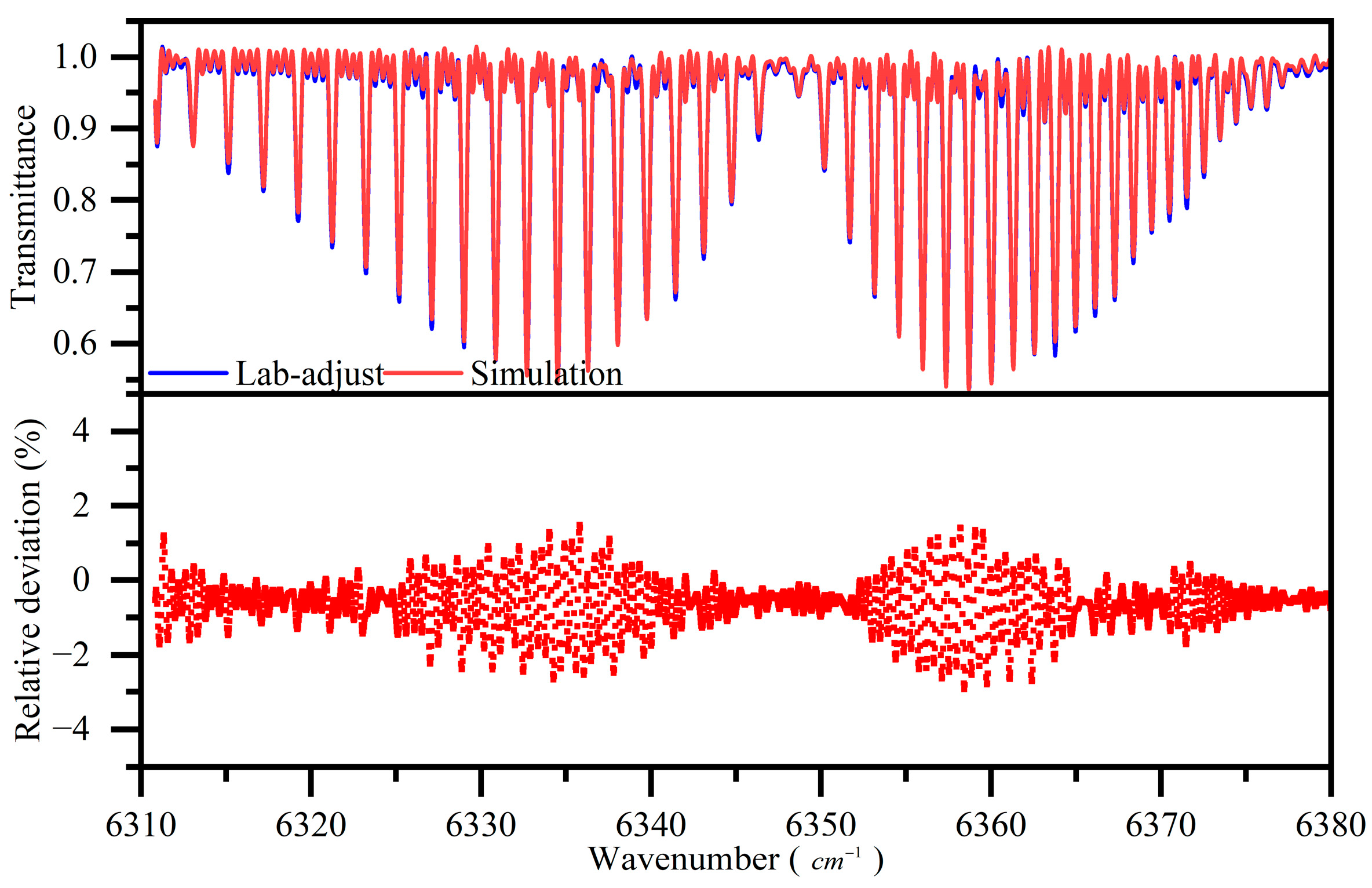
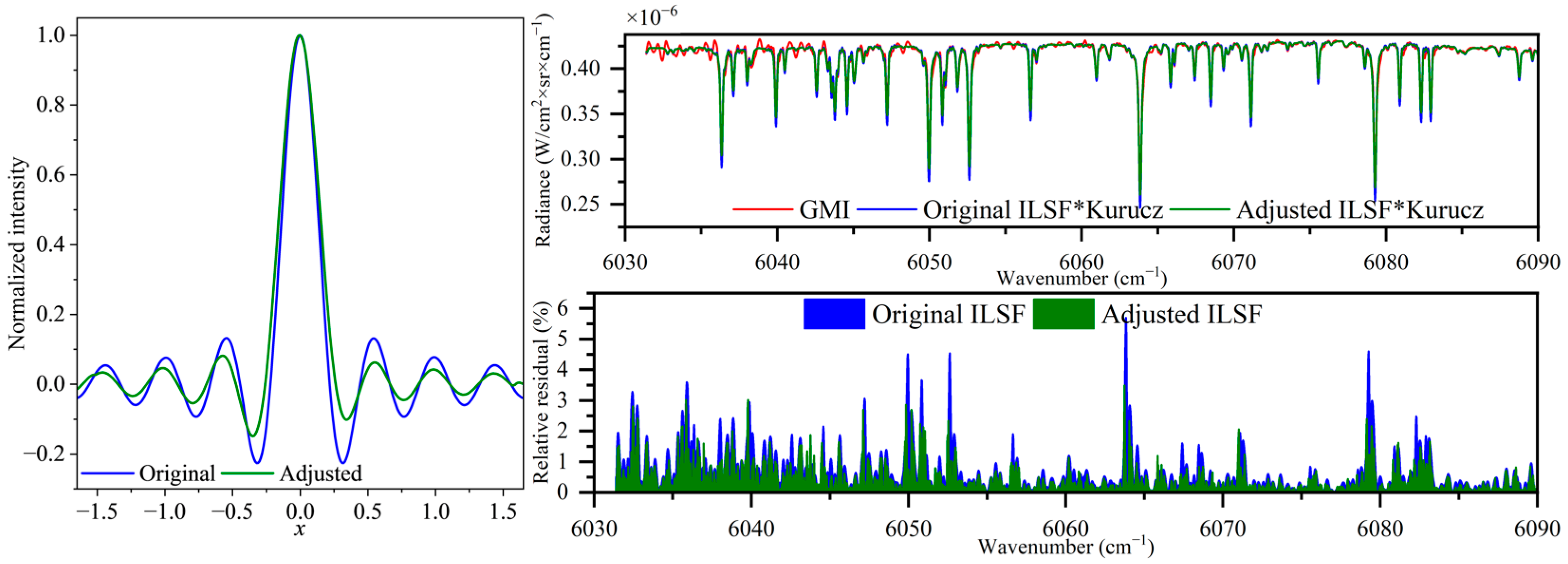
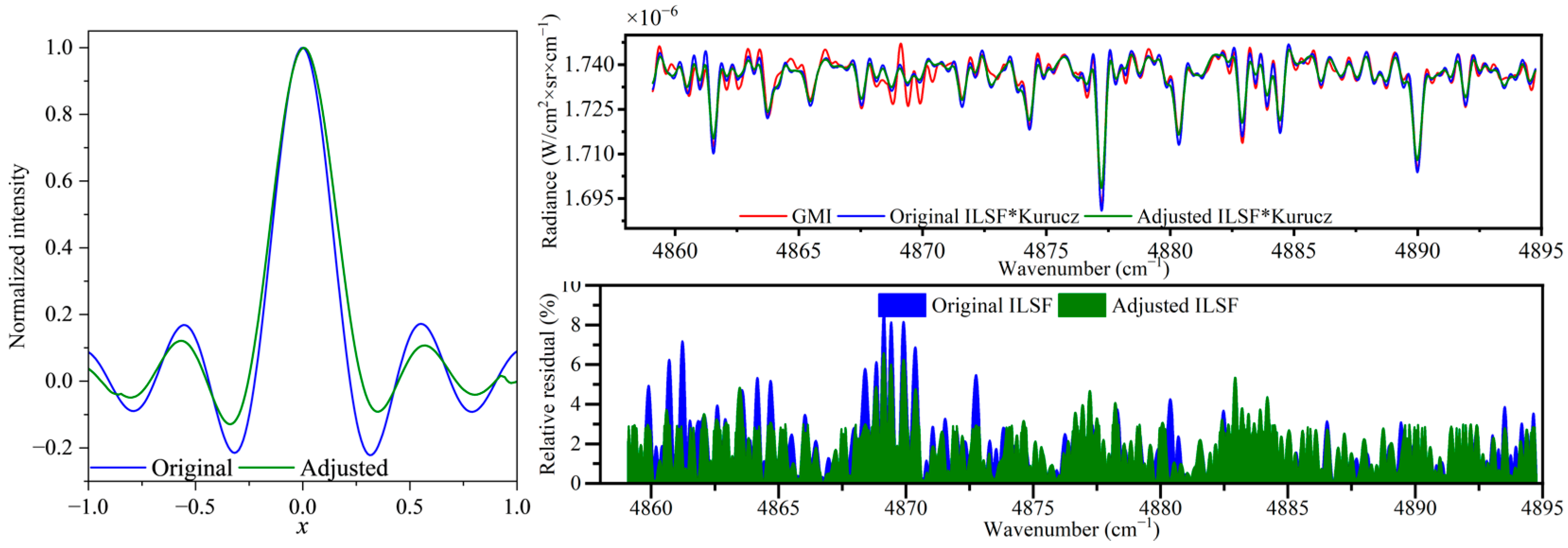
5. Experiment and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, M.; Wen, Y.; Sun, L.; Li, Y. Overview and Application of GaoFen 5-02 Satellite. Aerosp. China 2022, 12, 9–15. [Google Scholar]
- Bruhwiler, L.; Basu, S.; Butler, J.H.; Chatterjee, A.; Dlugokencky, E.; Kenney, M.A.; McComiskey, A.; Montzka, S.A.; Stanitski, D. Observations of greenhouse gases as climate indicators. Clim. Chang. 2021, 165, 12. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Kawa, S.R. Sensitivity studies for space-based measurement of atmospheric total column carbon dioxide by reflected sunlight. Appl. Opt. 2004, 43, 914–927. [Google Scholar] [CrossRef] [PubMed]
- Rayner, P.J.; O’Brien, D.M. The utility of remotely sensed CO2 concentration data in surface source inversions. Geophys. Res. Lett. 2001, 28, 175–178. [Google Scholar] [CrossRef]
- Harlander, J.M.; Roesler, F.L. Spatial heterodyne spectroscopy: A novel interferometric technique for ground-based and space astronomy. In Instrumentation in Astronomy VII; Proc. SPIE 1235; SPIE (Society of Photo-Optical Instrumentation Engineers): Tucson, AZ, USA, 1990. [Google Scholar] [CrossRef]
- Smith, B.W.; Harlander, J.M. Imaging spatial heterodyne spectroscopy: Theory and practice. In Infrared Technology and Applications XXV; Proc. SPIE 3698; SPIE (Society of Photo-Optical Instrumentation Engineers): Tucson, AZ, USA, 1999. [Google Scholar] [CrossRef]
- Hamazaki, T.; Kaneko, Y.; Kuze, A.; Kondo, K. Fourier transform spectrometer for Greenhouse Gases Observing Satellite (GOSAT). In Enabling Sensor and Platform Technologies for Spaceborne Remote Sensing; Proc. SPIE 5659; SPIE (Society of Photo-Optical Instrumentation Engineers): Tucson, AZ, USA, 2005. [Google Scholar] [CrossRef]
- Frankenberg, C.; Pollock, R.; Lee, R.A.M.; Rosenberg, R.; Blavier, J.-F.; Crisp, D.; O’Dell, C.W.; Osterman, G.B.; Roehl, C.; Wennberg, P.O.; et al. The Orbiting Carbon Observatory (OCO-2): Spectrometer performance evaluation using pre-launch direct sun measurements. Atmos. Meas. Tech. 2015, 8, 301–313. [Google Scholar] [CrossRef]
- Crisp, D.; Fisher, B.M.; O’Dell, C.; Frankenberg, C.; Basilio, R.; Bösch, H.; Brown, L.R.; Castano, R.; Connor, B.; Deutscher, N.M.; et al. The ACOS CO2 retrieval algorithm—Part II: Global XCO2 data characterization. Atmos. Meas. Tech. 2012, 5, 687–707. [Google Scholar] [CrossRef]
- Li, Z.; Xiong, W.; Shi, H.; Wang, X.; Ye, H.; Wei, Q.; Qiao, Y. Study on Laboratory Calibration of Spatial Heterodyne Spectrometer. Acta Opt. Sin. 2014, 34, 0430002. [Google Scholar]
- Xiong, W.; Shi, H.L.; Yu, N.H. Study on a new method for instrumental line shape measurement of spatial heterodyne interference spectrometer. Spectrosc. Spectr. Anal. 2015, 35, 267–271. [Google Scholar] [PubMed]
- Sun, K.; Liu, X.; Nowlan, C.R.; Cai, Z.; Chance, K.; Frankenberg, C.; Lee RA, M.; Pollock, R.; Rosenberg, R.; Crisp, D. Characterization of the OCO-2 instrument line shape functions using on-orbit solar measurements. Atmos. Meas. Tech. 2017, 10, 939–953. [Google Scholar] [CrossRef]
- Han, Y.; Shi, H.; Li, Z.; Luo, H.; Ding, Y.; Xiong, W.; Hu, Z. Greenhouse gas monitoring instrument on the GF-5 satellite-II: On-orbit spectral calibration. Appl. Opt. 2023, 62, 5839–5849. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.; Fang, Y.; Xiong, W.; Shi, H.; Qiao, Y. Abilitiy Analysis of Spatial Heterodyne Spectrometer in Atmospheric CO2 Detection. Acta Opt. Sin. 2011, 31, 0101001. [Google Scholar]
- Genest, J.; Tremblay, P. Instrument Line Shape of Fourier Transform Spectrometers: Analytic Solutions for Nonuniformly Illuminated Off-axis Detectors. Appl. Opt. 1999, 38, 5438–5446. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, N.C.; Wilson, S.H.S. Measurement of interferometer instrument line shape. In Remote Sensing—A Scientific Vision for Sustainable Development, Proceedings of the IGARSS’97. 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings, Singapore, 3–8 August 1997; IEEE: Singapore, 1997; Volume 4, pp. 2011–2014. [Google Scholar] [CrossRef]
- Xiong, W. Hyperspectral Greenhouse Gases Monitor Instrument (GMI) for Spaceborne Payload. Spacecr. Recovery Remote Sens. 2018, 39, 14–24. [Google Scholar]
- Gero, P.J.; Dykema, J.A.; Anderson, J.G.; Leroy, S.S. On-orbit Characterization of Blackbody Emissivity and Spectrometer Instrument Line Shape Using Quantum Cascade Laser Based Reflectometry. In Proceedings of the SPIE—Earth Observing Systems XIII, San Diego, CA, USA, 11–13 August 2008; SPIE: San Diego, CA, USA, 2008; Volume 7081. [Google Scholar]
- Shiomi, K.; Kina, T.; Kawakami, S.; Mitomi, Y.; Yoshida, M.; Higuchi, R.; Sekio, N.; Kataoka, F. Status of GOSAT Post-launch Calibration. In Proceedings of the ESA Atmospheric Science Conference 2009, Barcelona, Spain, 7–11 September 2009. [Google Scholar]
- Shiomi, K.; Kina, T.; Kawakami, S.; Takeshima, T. Calibration of operational GOSAT Level 1 products. In Sensors, Systems, and Next-Generation Satellites XIV; Proc. SPIE 7826; SPIE (Society of Photo-Optical Instrumentation Engineers): Toulouse, France, 2010; p. 782605. [Google Scholar] [CrossRef]
- Lin, C.L.; Wang, Y.M.; Zheng, Y.Q. Preflight Spectral Calibration of Hyperspectral Carbon Dioxide Spectrometer of TanSat. Opt. Precis. Eng. 2017, 25, 2064–2075. [Google Scholar]
- Harlander, J.M. Spatial Heterodyne Spectroscopy: Interferometric Performance at Any Wavelength without Scanning. Ph.D. Thesis, University of Wisconsin, Madison, WI, USA, 1991; p. 0903. [Google Scholar]
- Li, B.; Li, M.; Xu, P. High Precision On-board Calibration for Spaceborne Atmospheric Monitoring Spectrometer. Spacecr. Recovery Remote Sens. 2018, 39, 60–69. [Google Scholar] [CrossRef]
- Chamberlain, J. The Principles of Interferometric Spectroscopy; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Xu, Q.; Zheng, X.; Zhang, W.; Wang, X. Advanced Calibration Method for Sun Radiometers. Acta Opt. Sin. 2010, 30, 1337. [Google Scholar]
- Zhai, W.; Li, J.; Zheng, X.; Li, Z.; Meng, B.; Zhang, W.; Wang, X. Research on Method of Calibrating Sun Channels of Sun Radiometers. Acta Opt. Sin. 2012, 32, 0412004. [Google Scholar] [CrossRef]
- Li, Z.; Xiong, W.; Luo, H.; Qiao, Y. Study on Asymmetric Spatial Heterodyne Spectroccopy. Spectrosc. Spectr. Anal. 2016, 36, 2291–2295. [Google Scholar]
- Shen, J.; Xiong, W.; Shi, H.; Luo, H.; Li, Z.; Hu, G.; Fang, X.; Xu, B. Absolute Phase Drift Analysis and Correction of Asymmetric Spatial Heterodyne Interferometer for Wind Detection. Acta Opt. Sin. 2017, 37, 0430003. [Google Scholar] [CrossRef]
- Swinehart, D.F. The Beer-Lambert Law. J. Chem. Educ. 1962, 39, 333. [Google Scholar] [CrossRef]
- Kenneth Rideout, M.S. Barron’s AP Physics; Barron’s Educational Series: Hauppauge, NY, USA, 2015; p. 313. [Google Scholar]
- Gordon, I.; Rothman, L.; Hargreaves, R.; Hashemi, R.; Karlovets, E.; Skinner, F.; Conway, E.; Hill, C.; Kochanov, R.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Kurucz, R.L.; Furenlid, I.; Brault, J.; Testerman, L. Solar Flux Atlas from 296 to 1300 nm, National Solar Observatory, Sunspot, New Mexico, 1984. Available online: http://kurucz.harvard.edu/sun/fluxatlas/ (accessed on 11 June 2024).
- Meroni, M.; Busetto, L.; Guanter, L.; Cogliati, S.; Crosta, G.F.; Migliavacca, M.; Panigada, C.; Rossini, M.; Colombo, R. Characterization of fine resolution field spectrometers using solar Fraunhofer lines and atmospheric absorption features. Appl. Opt. 2010, 49, 2858–2871. [Google Scholar] [CrossRef]
- Chateauneuf, F.J.; Fortin, S.Y.; Buijs, H.L.; Soucy, M.-A.A. On-orbit performance of the ACE-FTS instrument. In Earth Observing Systems IX; Proc. SPIE 5542; SPIE: Denver, CO, USA, 2004. [Google Scholar] [CrossRef]
- Kostkowski, H.J.; Bass, A.M. Slit Function Effects in the Direct Measurement of Absorption Line Half-Widths and Intensities*†. J. Opt. Soc. Am. 1956, 46, 1060–1064. [Google Scholar] [CrossRef]
- Wang, J.; Ye, H.; Yi, W.; Chen, Z.; Fang, X.; Du, L. Research on the method of updating instrument line shape function of on-orbit Fourier ultrahigh resolution spectrometer. J. Infrared Millim. Waves 2018, 37, 613. [Google Scholar]
- Ye, S.; Xiong, W.; Qiao, Y.; Hong, J.; Fang, Y. Data Processing for Interferogram of Spatial Heterodyne Spectrometer. Spectrosc. Spectr. Anal. 2009, 29, 848–852. [Google Scholar]
- Luo, H.; Ye, Q.; Xiong, W.; Li, Z.; Li, S.; Shi, H. Study on the interferogram modulation efficiency of Spatial Heterodyne Spectrometer. Acta Opt. Sin. 2016, 36, 0712003. [Google Scholar]
- Genest, J.; Tremblay, P. Impact of the optical aberrations on the line shape of Fourier-transform spectrometers. Vib. Spectrosc. 2002, 29, 3–13. [Google Scholar] [CrossRef]
- Jozwicki, R.; Kosycarz, M. Influence of optical aberrations on the accuracy of Fourier transform infrared spectrometer. In Proceedings of the Tenth Polish-Czech-Slovak Optical Conference: Wave and Quantum Aspects of Contemporary Optics, Karpacz, Poland, 16–20 September 1996; Proc. SPIE 3320. SPIE: Karpacz, Poland, 1998. [Google Scholar] [CrossRef]
- Wawrzyniuk, L. Influence of collimator aberrations on the instrument line shape of a Fourier transform spectrometer. Appl. Opt. 2021, 60, 8792–8801. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Huang, Y.; Cao, Z.; Lu, X.; Liu, X. The Influence of Instrumental Line Shape Degradation on Gas Retrievals and Observation of Greenhouse Gases in Maoming, China. Atmosphere 2021, 12, 863. [Google Scholar] [CrossRef]
- Chance, K.; Kurucz, R.L. An improved high-resolution solar reference spectrum for earth’s atmosphere measurements in the ultraviolet, visible, and near infrared. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1289–1295. [Google Scholar] [CrossRef]
- Smith, G.W. Modulation Effects in Magnetic Resonance: Widths and Amplitudes for Lorentzian and Gaussian Lines. J. Appl. Phys. 1964, 35, 1217–1221. [Google Scholar] [CrossRef]





| Parameters | Technical Indicators | |||
|---|---|---|---|---|
| O2 | CO2-1 | CH4 | CO2-2 | |
| Central Wavelength/μm | 0.765 | 1.575 | 1.65 | 2.05 |
| Spectral Range/μm | 0.765~0.769 | 1.568~1.583 | 1.642~1.658 | 2.043~2.058 |
| Spectral Resolution/cm−1 | 0.6 | 0.27 | 0.27 | 0.27 |
| SNR (Albedo = 0.3; Sun Elevation = 30°) | 300 | 250 | ||
| Radiometric Calibration | Absolute Accuracy: 5%; Relative Accuracy: 2% | |||
| Field of View (FOV) | 14.6 mrad (10.3 km@705 km) | |||
| Observation Mode | Nadir Observation Mode: 1, 5, 7, 9 Points (Default 5 Points) Solar Observation Mode: Calibration Observation | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Shi, H.; Luo, H.; Li, Z.; Ye, H.; Li, C.; Ding, Y.; Wu, S.; Wang, X.; Xiong, W.; et al. Research on Calculation Method of On-Orbit Instrumental Line Shape Function for the Greenhouse Gases Monitoring Instrument on the GaoFen-5B Satellite. Remote Sens. 2024, 16, 2171. https://doi.org/10.3390/rs16122171
Han Y, Shi H, Luo H, Li Z, Ye H, Li C, Ding Y, Wu S, Wang X, Xiong W, et al. Research on Calculation Method of On-Orbit Instrumental Line Shape Function for the Greenhouse Gases Monitoring Instrument on the GaoFen-5B Satellite. Remote Sensing. 2024; 16(12):2171. https://doi.org/10.3390/rs16122171
Chicago/Turabian StyleHan, Yunfei, Hailiang Shi, Haiyan Luo, Zhiwei Li, Hanhan Ye, Chao Li, Yi Ding, Shichao Wu, Xianhua Wang, Wei Xiong, and et al. 2024. "Research on Calculation Method of On-Orbit Instrumental Line Shape Function for the Greenhouse Gases Monitoring Instrument on the GaoFen-5B Satellite" Remote Sensing 16, no. 12: 2171. https://doi.org/10.3390/rs16122171
APA StyleHan, Y., Shi, H., Luo, H., Li, Z., Ye, H., Li, C., Ding, Y., Wu, S., Wang, X., Xiong, W., & Hou, C. (2024). Research on Calculation Method of On-Orbit Instrumental Line Shape Function for the Greenhouse Gases Monitoring Instrument on the GaoFen-5B Satellite. Remote Sensing, 16(12), 2171. https://doi.org/10.3390/rs16122171







