Agricultural Drought Monitoring Using an Enhanced Soil Water Deficit Index Derived from Remote Sensing and Model Data Merging
Abstract
1. Introduction
2. Data and Study Area
2.1. ESA CCI Soil Moisture
2.2. VIC Soil Moisture
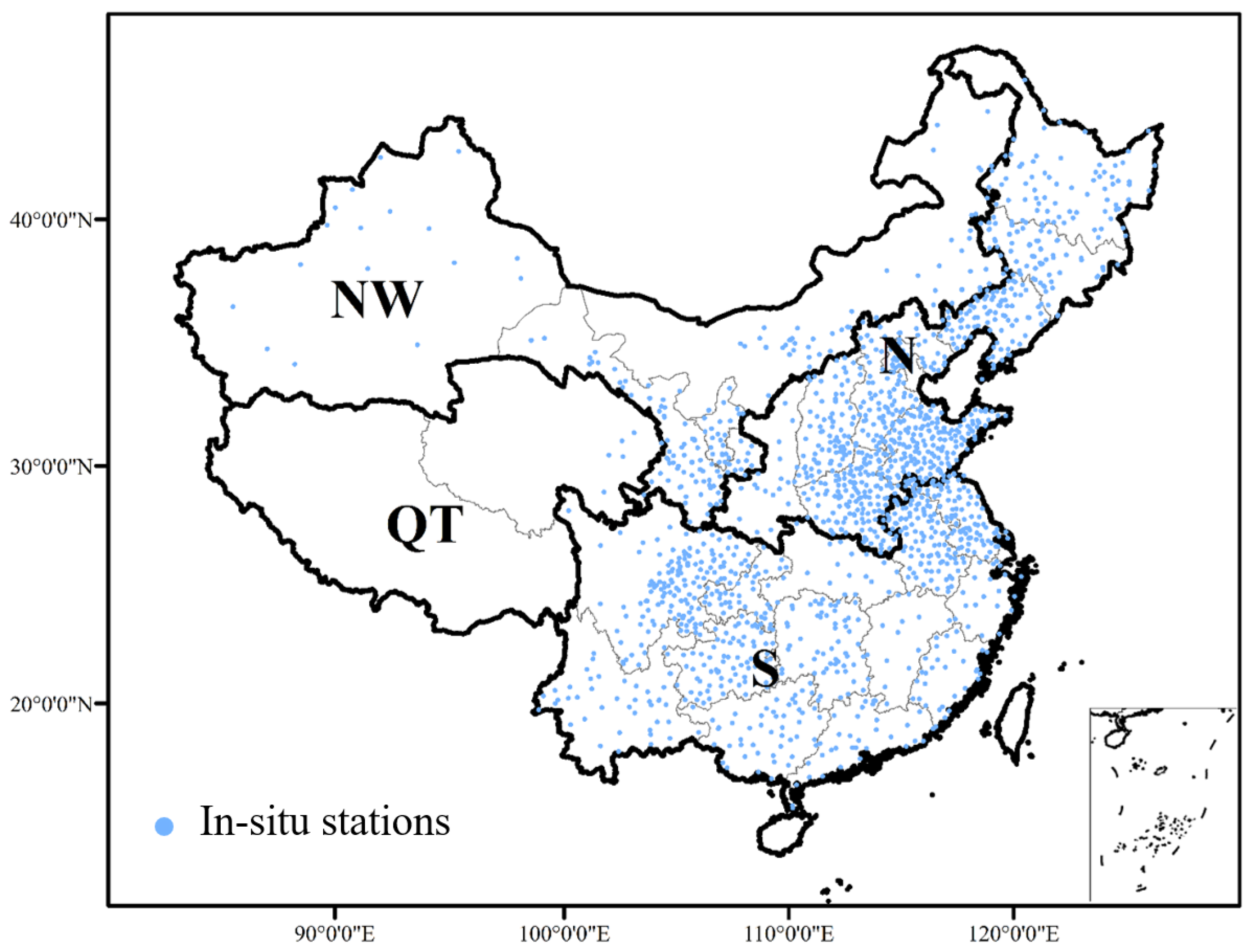
2.3. In Situ Soil Moisture
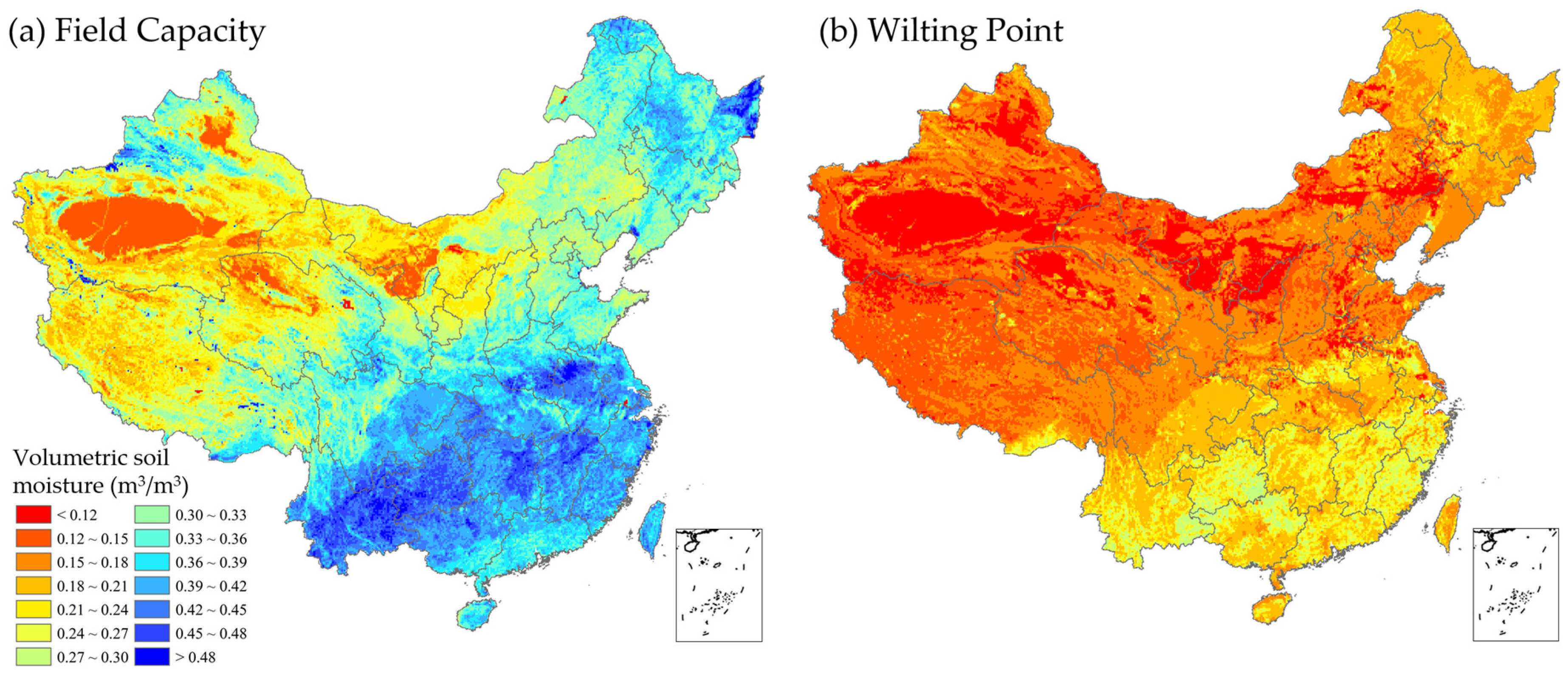
2.4. Field Capacity
2.5. SoilGrids
2.6. Precipitation and Evapotranspiration
2.7. Drought-Affected Crop Area
2.8. Auxiliary Data
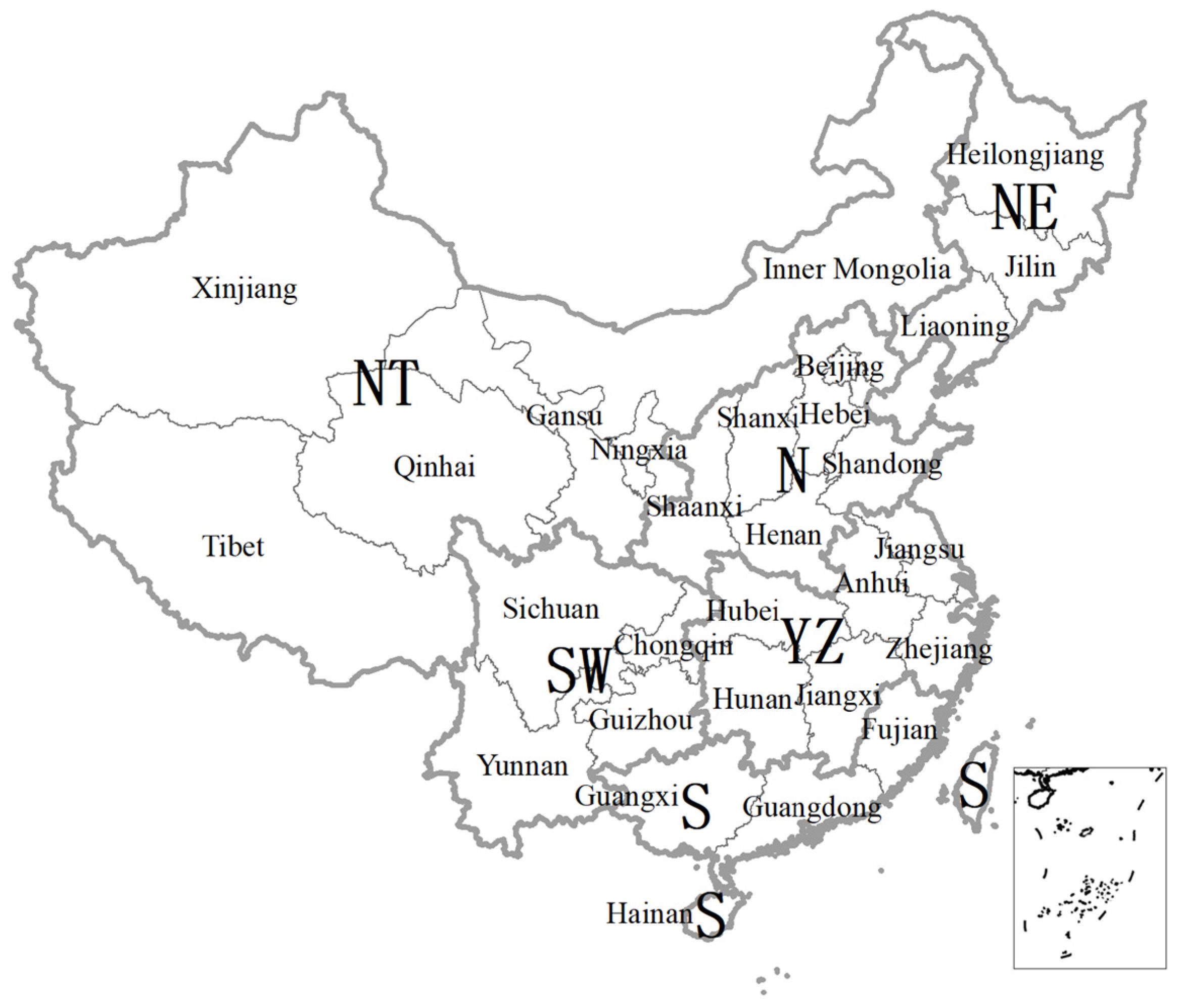
2.9. Study Area
3. Methods
3.1. Extended Triple Collocation
3.2. Pedotransfer Functions
3.3. Soil Water Deficit Index
3.4. Other Drought Indexes
3.4.1. SMI
3.4.2. SMAPI
3.4.3. AWD
3.4.4. SPI
3.4.5. Categories of Each Drought Index
3.5. Validation Metrics
3.5.1. Correlation Coefficient
3.5.2. Probability of Detection
3.5.3. Matching Index
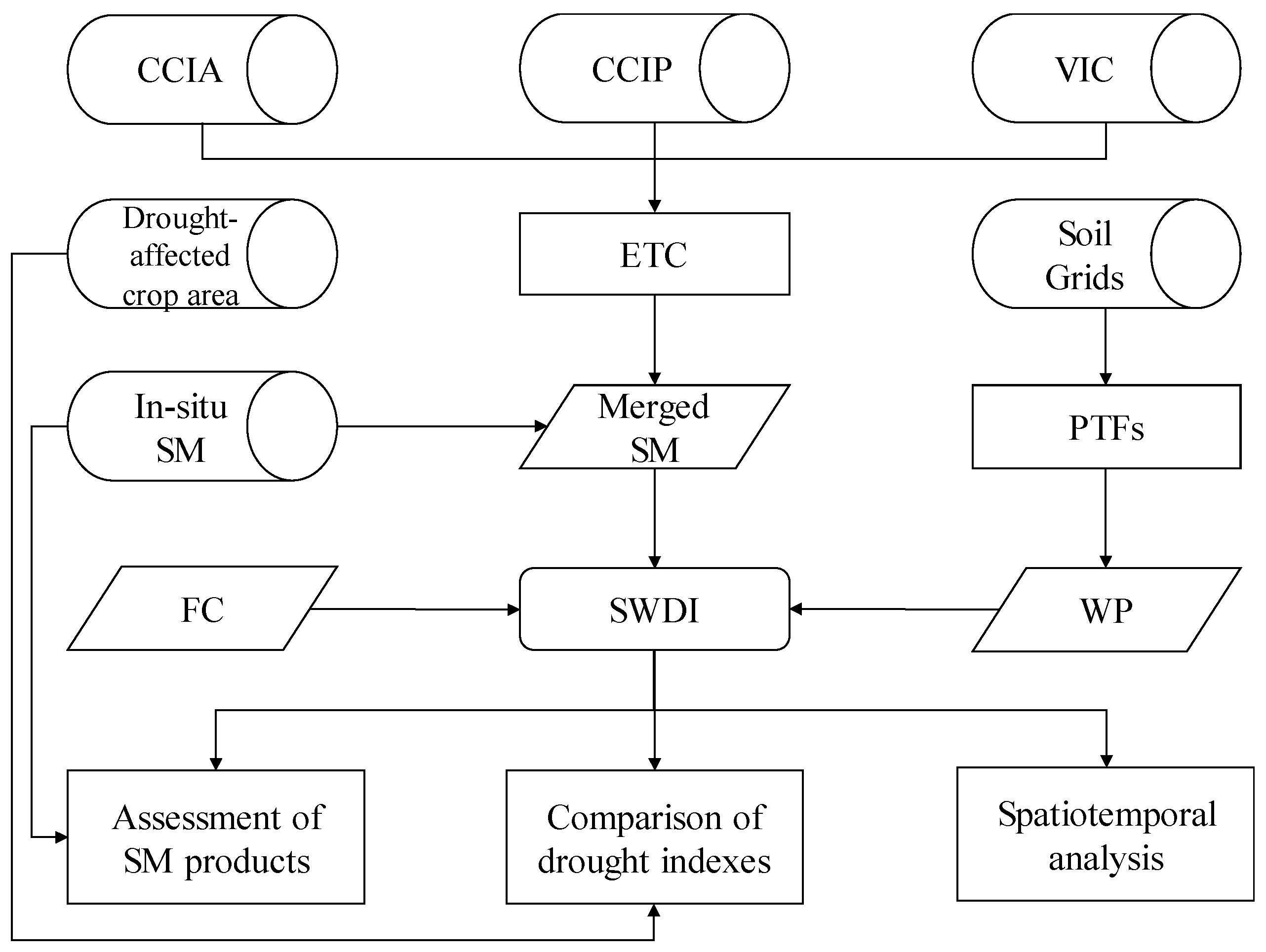
3.6. Data Processing Method
3.7. Technical Framework for the Drought Index Development and Results Analysis
4. Results and Discussion
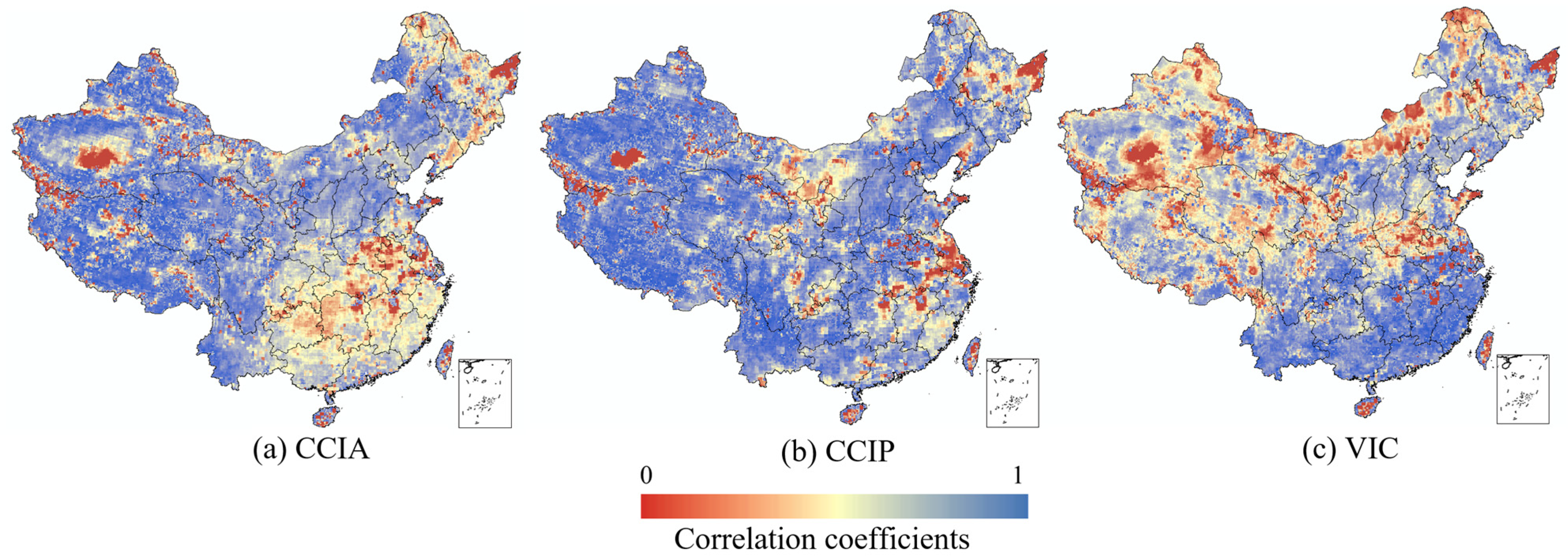
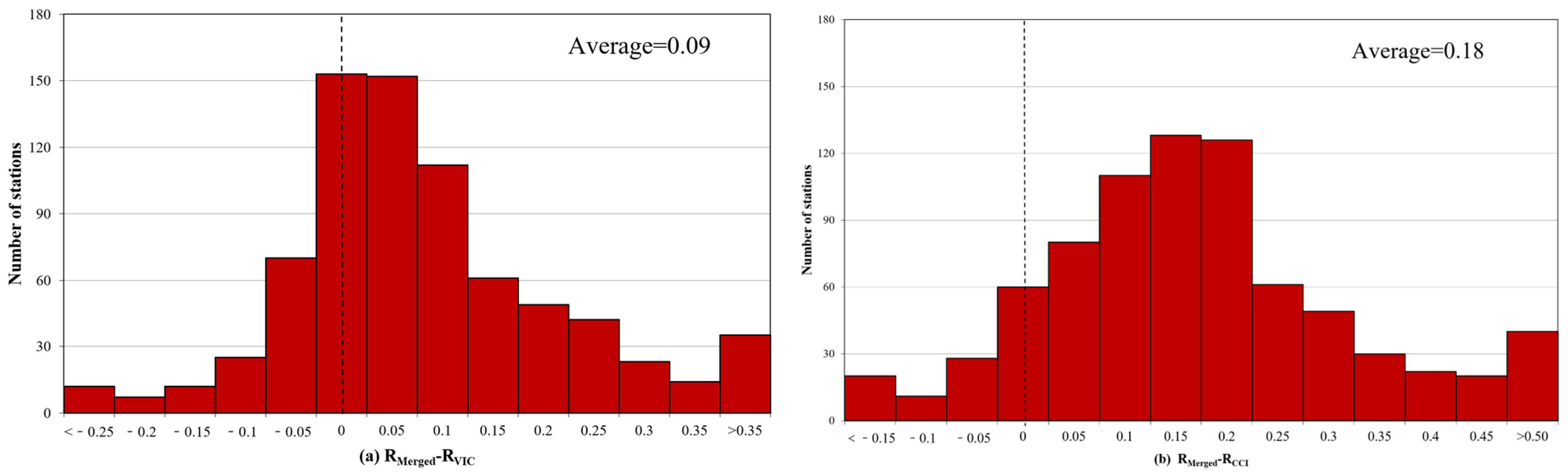
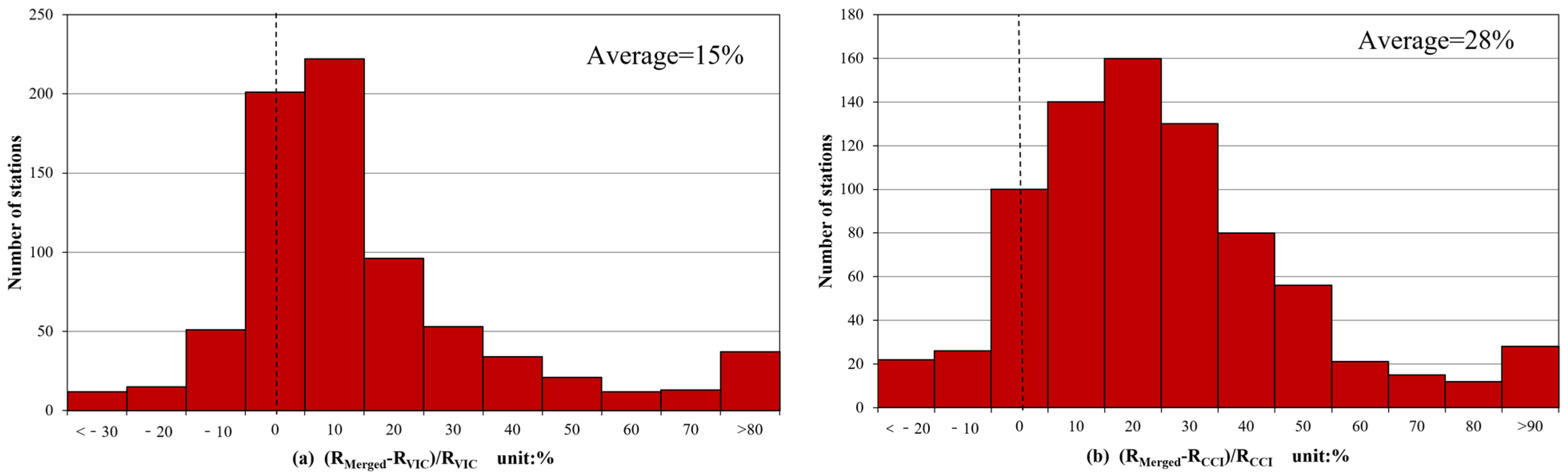
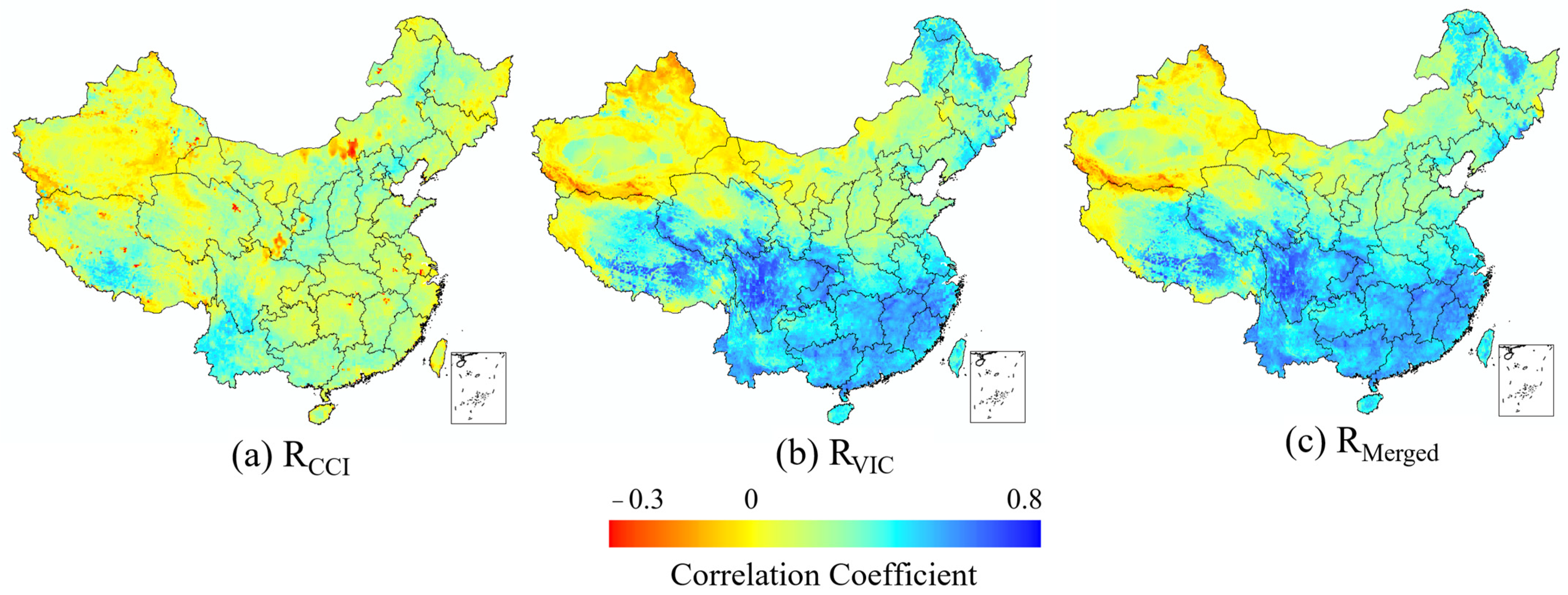
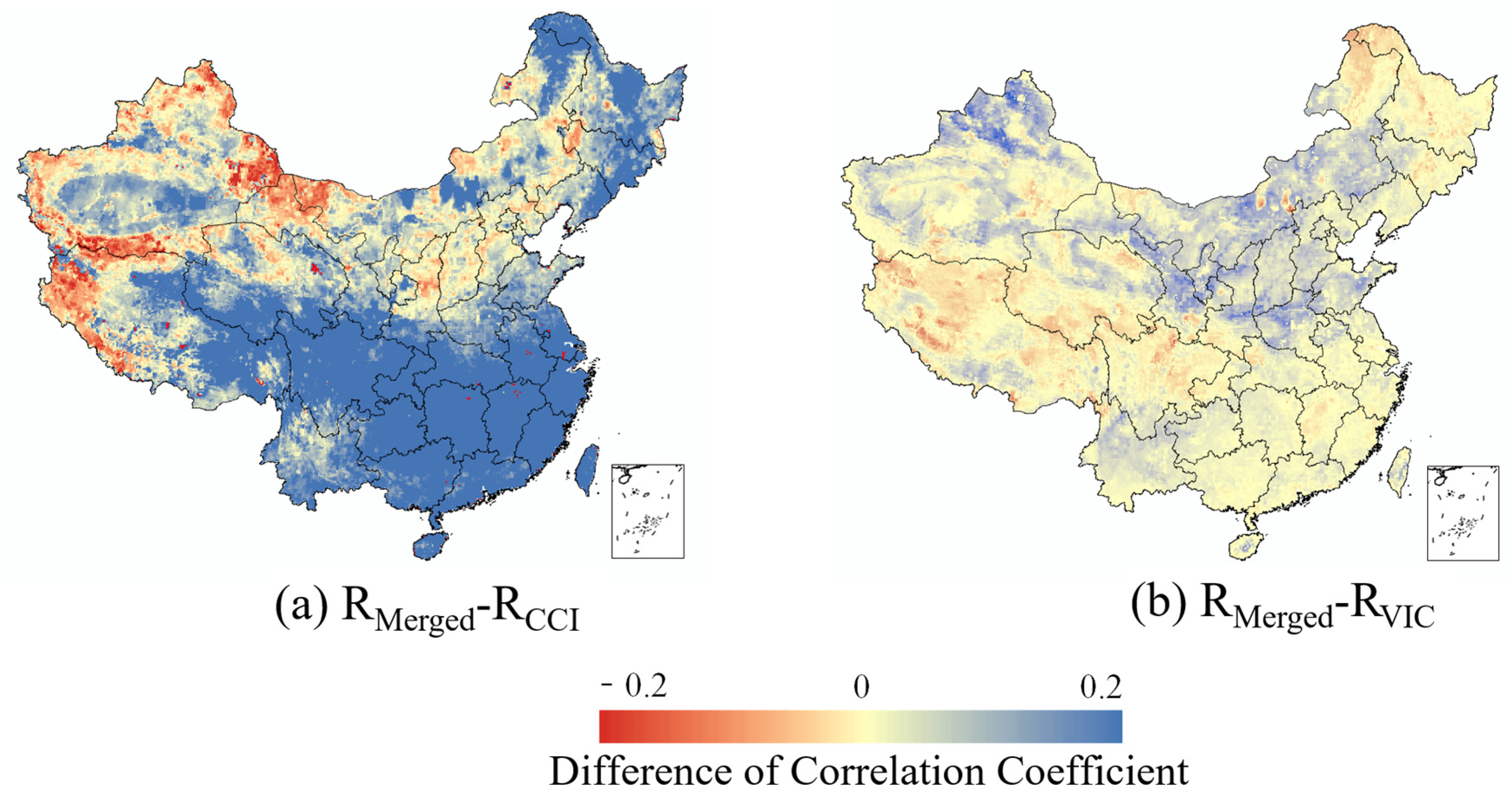
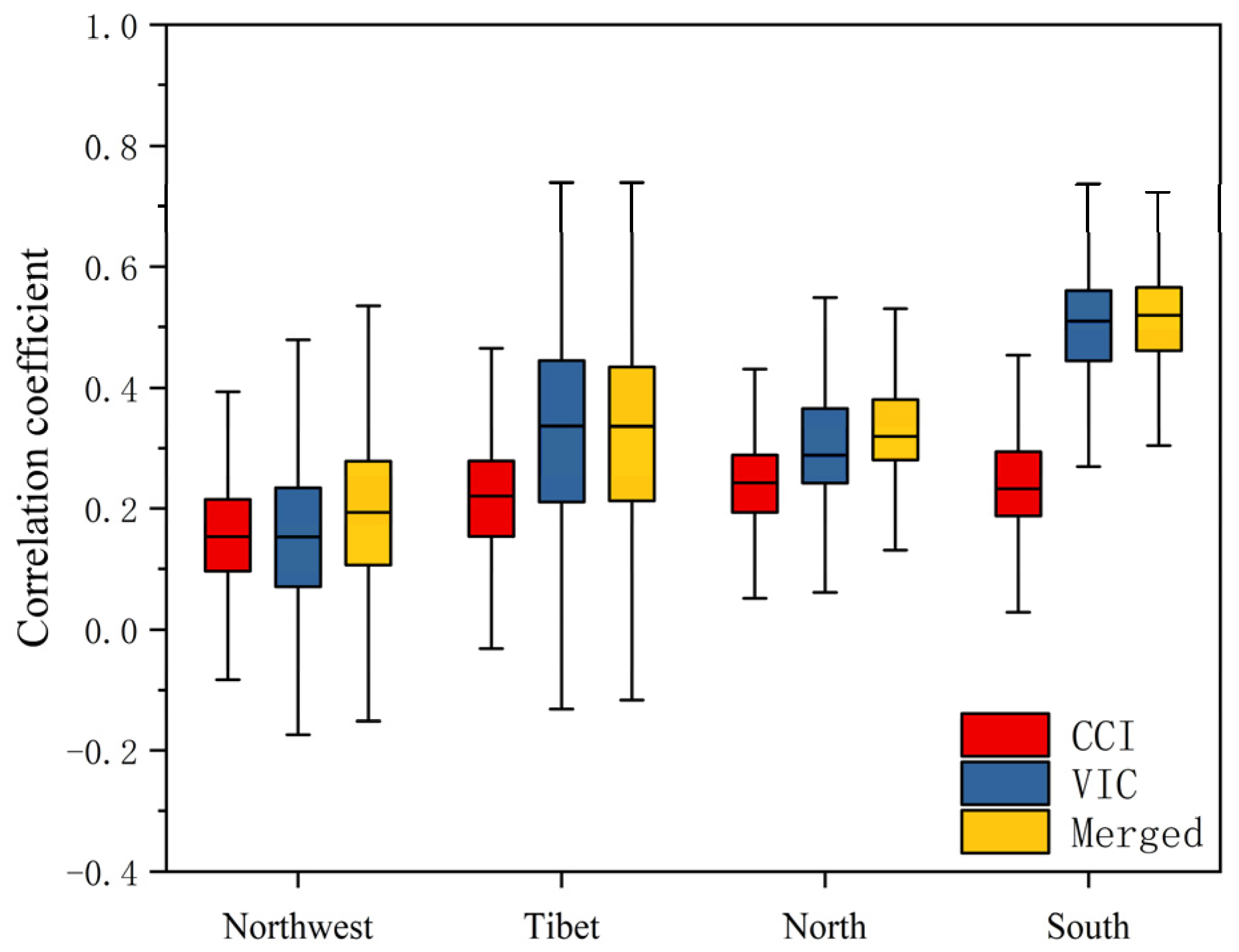
4.1. ETC-Based Soil Moisture Data Merging and Validation
4.2. Assessment of Various Soil Moisture Products in Drought Monitoring
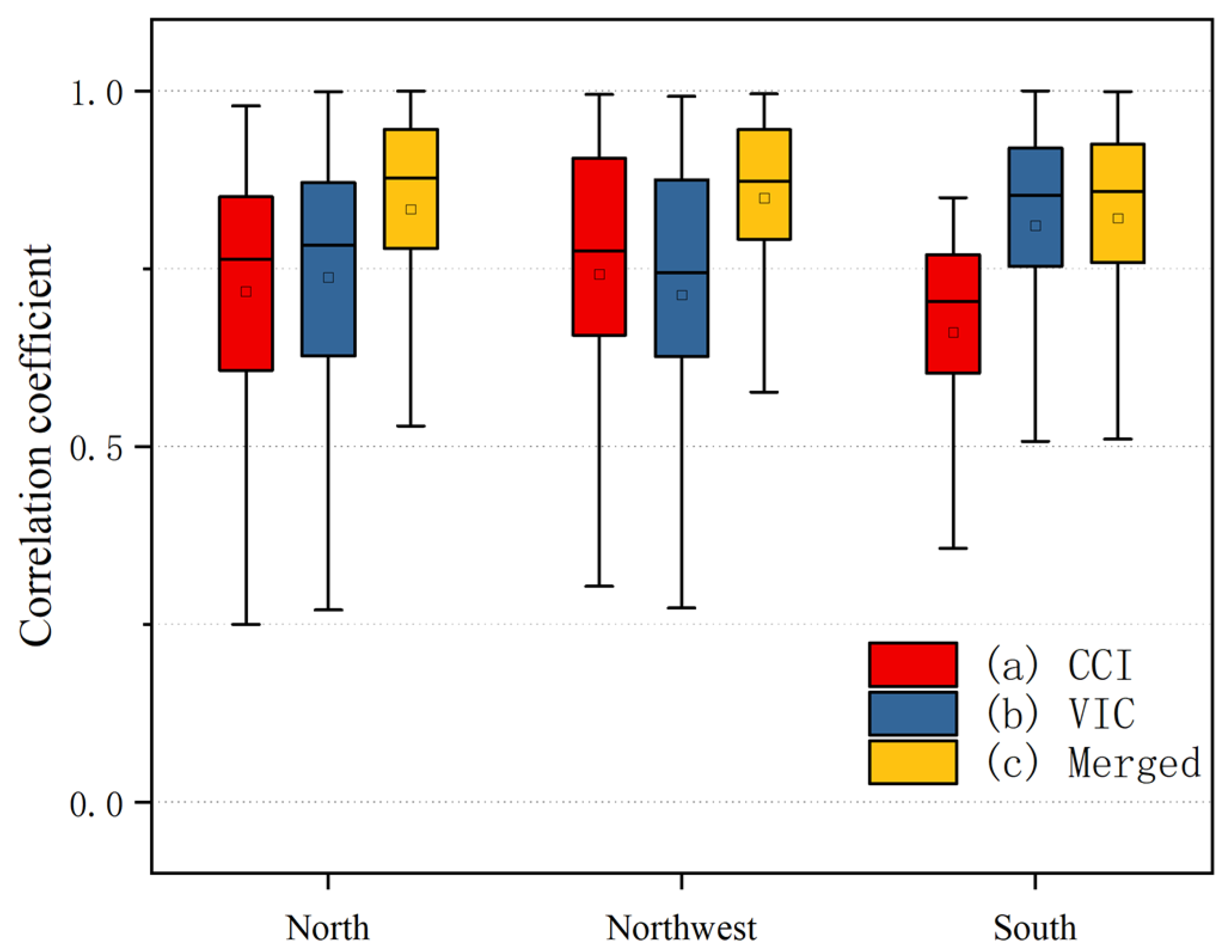
4.3. Spatiotemporal Characteristics Analysis of Drought Monitoring Accuracy
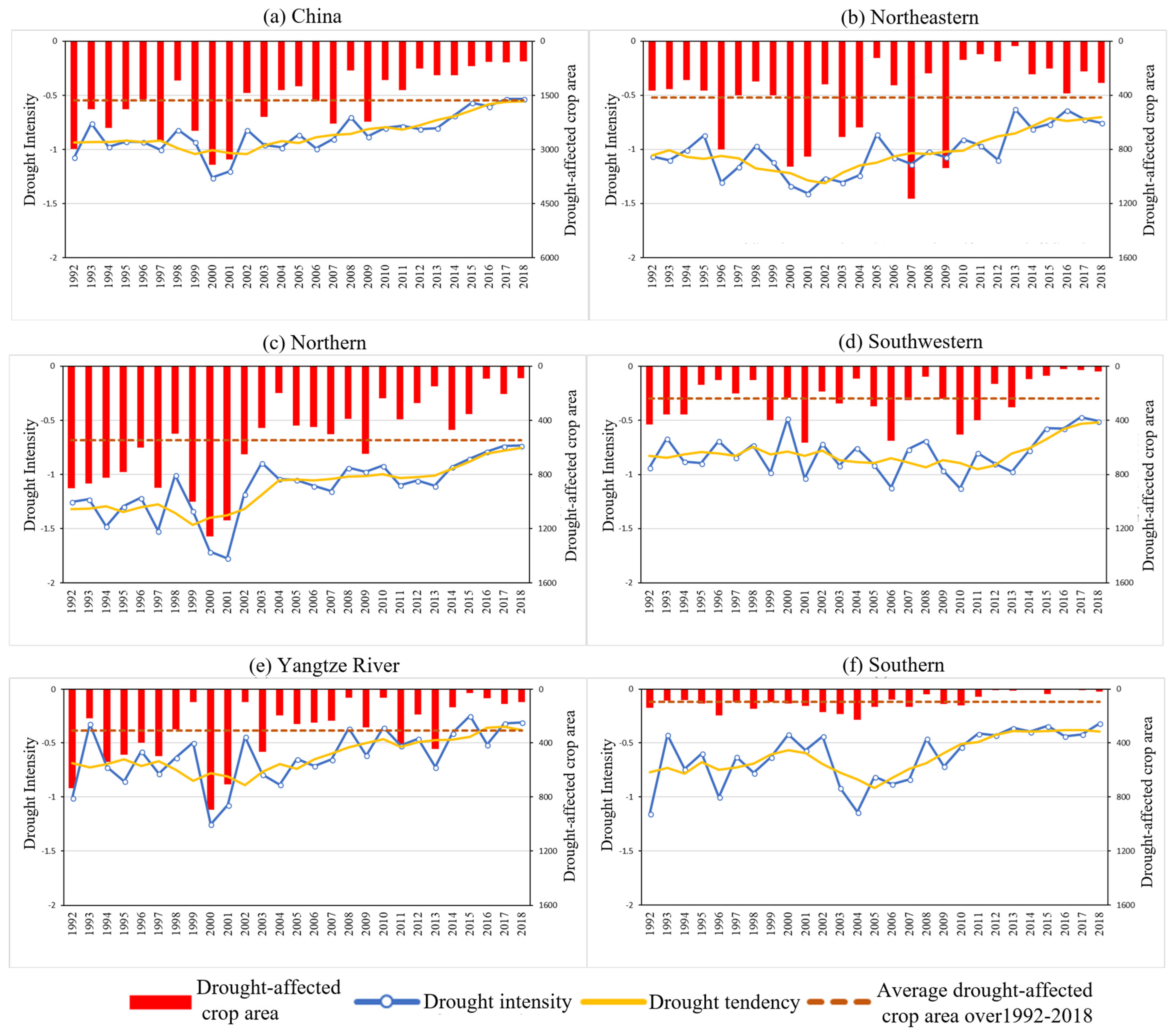
4.4. Drought Evolution Analysis and Drought Indexes Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| AWD | Atmospheric Water Deficit |
| CCI | Climate Change Initiative |
| CCIA | Climate Change Initiative Active |
| CCIP | Climate Change Initiative Passive |
| CDF | Cumulative Density Function |
| ET | Evapotranspiration |
| ETC | Extended Triple Collocation |
| FC | Field Capacity |
| MI | Matching Index |
| POD | Probability of Detection |
| PTFs | Pedotransfer Functions |
| R | Correlation Coefficient |
| SM | Soil Moisture |
| SMAP | Soil Moisture Active Passive |
| SMAPI | Soil Moisture Anomaly Percentage Index |
| SMI | Soil Moisture Index |
| SMOS | Soil Moisture and Ocean Salinity |
| SPI | Standardized Precipitation Index |
| TC | Triple Collocation |
| VIC | Variable Infiltration Capacity |
| WP | Wilting Point |
References
- Ault, T.R. On the essentials of drought in a changing climate. Science 2020, 6488, 256–260. [Google Scholar] [CrossRef] [PubMed]
- Trenberth, K.E.; Dai, A.; Schrier, G.V.D.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Food and Agriculture Organization. The Impact of Disasters and Crises on Agriculture and Food Security, 2017; Food and Agriculture Organization of the United Nations: Rome, Italy, 2018. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Zeng, J.; Li, J.; Lu, X.; Wei, Z.; Shangguan, W.; Zhang, S.; Dai, Y.; Zhang, S. Assessment of global meteorological, hydrological and agricultural drought under future warming based on CMIP6. Atmos. Ocean. Sci. Lett. 2022, 15, 7. [Google Scholar] [CrossRef]
- Wen, W.; Ertsen, M.W.; Svoboda, M.D.; Mohsin, H. Propagation of Drought: From Meteorological Drought to Agricultural and Hydrological Drought. Adv. Meteorol. 2016, 2016, 6547209. [Google Scholar] [CrossRef]
- Crocetti, L.; Forkel, M.; Fischer, M.; Jureka, F.; Dorigo, W. Earth Observation for agricultural drought monitoring in the Pannonian Basin (southeastern Europe): Current state and future directions. Reg. Environ. Chang. 2020, 20, 123. [Google Scholar] [CrossRef]
- Grayson, M. Agriculture and drought. Nature 2013, 501, S1. [Google Scholar] [CrossRef] [PubMed]
- Duan, K.; Mei, Y. Comparison of Meteorological, Hydrological and Agricultural Drought Responses to Climate Change and Uncertainty Assessment. Water Resour. Manag. 2014, 28, 5039–5054. [Google Scholar] [CrossRef]
- Javed, T.; Li, Y.; Rashid, S.; Li, F.; Hu, Q.; Feng, H.; Chen, X.; Ahmad, S.; Liu, F.; Pulatov, B. Performance and relationship of four different agricultural drought indices for drought monitoring in China’s mainland using remote sensing data—ScienceDirect. Sci. Total Environ. 2020, 759, 143530. [Google Scholar] [CrossRef]
- Mao, Y.; Wu, Z.; He, H.; Lu, G.; Xu, H.; Lin, Q. Spatio-temporal analysis of drought in a typical plain region based on the soil moisture anomaly percentage index. Sci. Total Environ. 2017, 576, 752–765. [Google Scholar] [CrossRef]
- Hou, M.; Yao, N.; Li, Y.; Liu, F.; Biswas, A.; Pulatov, A.; Hassan, I. Better Drought Index between SPEI and SMDI and the Key Parameters in Denoting Drought Impacts on Spring Wheat Yields in Qinghai, China. Agronomy 2022, 12, 1552. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A. A soil water based index as a suitable agricultural drought indicator. J. Hydrol. 2015, 522, 265–273. [Google Scholar] [CrossRef]
- Pablos, M.; Gonz Alez-Zamora, A.; Anchez, S.N.; Mart I Nez-Fern Andez, J. Assessment of SMADI and SWDI agricultural drought indices using remotely sensed root zone soil moisture. Proc. Int. Assoc. Hydrol. Sci. 2018, 380, 55–66. [Google Scholar] [CrossRef][Green Version]
- Chatterjee, S.; Desai, A.R.; Zhu, J.; Townsend, P.A.; Huang, J. Soil moisture as an essential component for delineating and forecasting agricultural rather than meteorological drought. Remote Sens. Environ. 2022, 269, 112833. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Miralles, D.G.; Reichle, R.H.; Dorigo, W.A.; Hahn, S.; Sheffield, J.; Karthikeyan, L.; Balsamo, G.; Parinussa, R.M.; et al. Evaluation of 18 satellite- and model-based soil moisture products using in situ measurements from 826 sensors. Hydrol. Earth Syst. Sci. 2021, 25, 17–40. [Google Scholar] [CrossRef]
- Dorigo, W.; Himmelbauer, I.; Aberer, D.; Schremmer, L.; Petrakovic, I.; Zappa, L.; Preimesberger, W.; Xaver, A.; Annor, F.; Ard O, J.; et al. The International Soil Moisture Network: Serving Earth system science for over a decade. Hydrol. Earth Syst. Sci. 2021, 25, 5749–5804. [Google Scholar] [CrossRef]
- Liu, H.; Jia, Y.; Niu, C.; Su, H.; Wang, J.; Du, J.; Khaki, M.; Hu, P.; Liu, J. Development and validation of a physically-based, national-scale hydrological model in China. J. Hydrol. 2020, 590, 125431. [Google Scholar] [CrossRef]
- Li, Z.; Leng, P.; Zhou, C.; Chen, K.; Zhou, F.; Shang, G. Soil moisture retrieval from remote sensing measurements: Current knowledge and directions for the future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar] [CrossRef]
- Fang, B.; Lakshmi, V.; Bindlish, R.; Jackson, T.J.; Liu, P. Evaluation and validation of a high spatial resolution satellite soil moisture product over the Continental United States. J. Hydrol. 2020, 588, 125043. [Google Scholar] [CrossRef]
- Mishra, A.; Vu, T.; Veettil, A.V.; Entekhabi, D. Drought monitoring with soil moisture active passive (SMAP) measurements. J. Hydrol. 2017, 552, 620–632. [Google Scholar] [CrossRef]
- Wu, X.; Lu, G.; Wu, Z.; He, H.; Scanlon, T.; Dorigo, W. Triple Collocation-Based Assessment of Satellite Soil Moisture Products with In Situ Measurements in China: Understanding the Error Sources. Remote Sens. 2020, 12, 2275. [Google Scholar] [CrossRef]
- Gruber, A.; Scanlon, T.; van der Schalie, R.; Wagner, W.; Dorigo, W. Evolution of the ESA CCI Soil Moisture climate data records and their underlying merging methodology. Earth Syst. Sci. Data 2019, 11, 717–739. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50, 2. [Google Scholar] [CrossRef]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef]
- Wei, S. A China data set of soil properties for land surface modeling. J. Adv. Model. Earth Syst. 2013, 5, 212–224. [Google Scholar] [CrossRef]
- Dai, Y.; Shangguan, W.; Duan, Q.; Liu, B.; Fu, S.; Niu, G. Development of a China Dataset of Soil Hydraulic Parameters Using Pedotransfer Functions for Land Surface Modeling. J. Hydrometeorol. 2013, 14, 869–887. [Google Scholar] [CrossRef]
- Zhao, C.; Shao, M.A.; Jia, X.; Nasir, M.; Zhang, C. Using pedotransfer functions to estimate soil hydraulic conductivity in the Loess Plateau of China. Catena 2016, 143, 1–6. [Google Scholar] [CrossRef]
- Wu, X.; Lu, G.; Wu, Z.; He, H.; Zhou, J.; Liu, Z. An Integration Approach for Mapping Field Capacity of China Based on Multi-Source Soil Datasets. Water 2018, 10, 728. [Google Scholar] [CrossRef]
- Ray, R.L.; Fares, A.; Risch, E. Effects of Drought on Crop Production and Cropping Areas in Texas. Agric. Environ. Lett. 2018, 3, 170037. [Google Scholar] [CrossRef]
- Dietz, K.J.; Zörb, C.; Geilfus, C.M. Drought and crop yield. Plant Biol. 2021, 23, 881–893. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Wang, G.Q.; Zhang, J.Y.; Jin, J.L.; Pagano, T.C.; Calow, R.; Bao, Z.X.; Liu, C.S.; Liu, Y.L.; Yan, X.L. Assessing water resources in China using PRECIS projections and a VIC model. Hydrol. Earth Syst. Sci. 2012, 16, 231–240. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, G.; Zhang, J.; Yang, Y. Simulation of Daily Soil Moisture Using VIC Model. Sci. Geogr. Sin. 2007, 27, 359–364. [Google Scholar]
- Hengl, T.; De Jesus, J.M.; MacMillan, R.A.; Batjes, N.H.; Heuvelink, G.B.; Ribeiro, E.; Samuel-Rosa, A.; Kempen, B.; Leenaars, J.G.; Walsh, M.G.; et al. SoilGrids1km—Global Soil Information Based on Automated Mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef]
- Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotic, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil. Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Tomasella, J.; Hodnett, M. Estimating soil water retention characteristics from limited data in Brazilian Amazonia. Soil. Sci. 1998, 163, 190–202. [Google Scholar] [CrossRef]
- Rawls, W.J.; Pachepsky, Y.A.; Ritchie, J.C.; Sobecki, T.M.; Bloodworth, H. Effect of soil organic carbon on soil water retention. Geoderma 2003, 116, 61–76. [Google Scholar] [CrossRef]
- Wosten, H.; Pachepsky, Y.; Rawls, W.J. Pedotransfer functions: Bridging the gap between available basic soil data and missing soil hydraulic characteristics. J. Hydrol. 2001, 251, 123–150. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J.; Romberger, J.S.; Papendick, R.I. Estimating Generalized Soil-water Characteristics from Texture. Soil. Sci. Soc. Am. J. 1986, 50, 1031–1036. [Google Scholar] [CrossRef]
- Bagarello, V.; Castellini, M.; Di Prima, S.; Iovino, M. Soil hydraulic properties determined by infiltration experiments and different heights of water pouring. Geoderma 2014, 213, 492–501. [Google Scholar] [CrossRef]
- Hodnett, M.G.; Tomasella, J. Marked differences between van Genuchten soil water-retention parameters for temperate and tropical soils: A new water-retention pedo-transfer functions developed for tropical soils. Geoderma 2002, 108, 155–180. [Google Scholar] [CrossRef]
- Hunt, E.D.; Hubbard, K.G.; Wilhite, D.A.; Arkebauer, T.J.; Dutcher, A.L. The development and evaluation of a soil moisture index. Int. J. Climatol. 2010, 29, 747–759. [Google Scholar] [CrossRef]
- Pan, X.; QIU, Q.; Li, J.; Wang, J.; He, Q.; Su, Y.; Ma, J.; Du, K. Physiological indexes of six plant species from the tibetan plateau under drought stress. Acta Ecol. Sin. 2014, 34, 3558–3567. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, L.; Liu, M.; Zhang, J.; Leng, S.; Diao, C. Establishing and assessing the Integrated Surface Drought Index (ISDI) for agricultural drought monitoring in mid-eastern China. Int. J. Appl. Earth Obs. 2013, 23, 397–410. [Google Scholar] [CrossRef]
- An, X.; Wu, J. Assessing the relative soil moisture for agricultural drought monitoring in Northeast China. Geogr. Res-Aust. 2017, 36, 837–849. [Google Scholar]
- Xu, Z.; Wu, Z.; He, H.; Guo, X.; Zhang, Y. Comparison of soil moisture at different depths for drought monitoring based on improved soil moisture anomaly percentage index. Water Sci. Eng. 2021, 14, 171–183. [Google Scholar] [CrossRef]
- Laimighofer, J.; Laaha, G. How standard are standardized drought indices? Uncertainty components for the SPI & SPEI case. J. Hydrol. 2022, 613, 128385. [Google Scholar] [CrossRef]
- Bhardwaj, K.; Mishra, V. Drought detection and declaration in India. Water Secur. 2021, 14, 100104. [Google Scholar] [CrossRef]


| AWD | SPI | SWDI | SMI | SMAPI | ||
|---|---|---|---|---|---|---|
| No drought | >0 | >−0.5 | >0 | >60 | >−0.05 | |
| Drought | Light | ≤0 | −1.0~−0.5 | −2~0 | 50~60 | −0.15~−0.05 |
| Moderate | −1.5~−1.0 | −5~−2 | 40~50 | −0.20~−0.15 | ||
| Severe | −2.0~−1.5 | −10~−5 | 30~40 | −0.25~−0.20 | ||
| Extreme | ≤−2.0 | ≤−10 | ≤30 | ≤−0.25 | ||
| POD | Northwest | North | South |
|---|---|---|---|
| Merged | 0.95 | 0.96 | 0.93 |
| VIC | 0.81 | 0.87 | 0.83 |
| SMAP | 0.89 | 0.92 | 0.86 |
| SMOS | 0.76 | 0.81 | 0.73 |
| CCI | 0.83 | 0.89 | 0.84 |
| MI | Northwest | North | South |
|---|---|---|---|
| Merged | 0.31 | 0.39 | 0.29 |
| VIC | 0.18 | 0.26 | 0.22 |
| SMAP | 0.36 | 0.27 | 0.28 |
| SMOS | 0.18 | 0.15 | 0.23 |
| CCI | 0.18 | 0.25 | 0.22 |
| |R| | China | Northeastern | Northern | Southwestern | Yangtze River | Southern |
|---|---|---|---|---|---|---|
| SWDI | 0.88 | 0.69 | 0.88 | 0.75 | 0.89 | 0.76 |
| SMI | 0.83 | 0.69 | 0.85 | 0.74 | 0.85 | 0.74 |
| SMAPI | 0.81 | 0.69 | 0.82 | 0.73 | 0.79 | 0.75 |
| SPI | 0.51 | 0.13 | 0.43 | 0.63 | 0.32 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Xu, H.; He, H.; Wu, Z.; Lu, G.; Liao, T. Agricultural Drought Monitoring Using an Enhanced Soil Water Deficit Index Derived from Remote Sensing and Model Data Merging. Remote Sens. 2024, 16, 2156. https://doi.org/10.3390/rs16122156
Wu X, Xu H, He H, Wu Z, Lu G, Liao T. Agricultural Drought Monitoring Using an Enhanced Soil Water Deficit Index Derived from Remote Sensing and Model Data Merging. Remote Sensing. 2024; 16(12):2156. https://doi.org/10.3390/rs16122156
Chicago/Turabian StyleWu, Xiaotao, Huating Xu, Hai He, Zhiyong Wu, Guihua Lu, and Tingting Liao. 2024. "Agricultural Drought Monitoring Using an Enhanced Soil Water Deficit Index Derived from Remote Sensing and Model Data Merging" Remote Sensing 16, no. 12: 2156. https://doi.org/10.3390/rs16122156
APA StyleWu, X., Xu, H., He, H., Wu, Z., Lu, G., & Liao, T. (2024). Agricultural Drought Monitoring Using an Enhanced Soil Water Deficit Index Derived from Remote Sensing and Model Data Merging. Remote Sensing, 16(12), 2156. https://doi.org/10.3390/rs16122156





