Abstract
Light Detection and Ranging systems serve as robust tools for creating three-dimensional representations of the Earth’s surface. These representations are known as point clouds. Point cloud scene segmentation is essential in a range of applications aimed at understanding the environment, such as infrastructure planning and monitoring. However, automating this process can result in notable challenges due to variable point density across scenes, ambiguous object shapes, and substantial class imbalances. Consequently, manual intervention remains prevalent in point classification, allowing researchers to address these complexities. In this work, we study the elements contributing to the automatic semantic segmentation process with deep learning, conducting empirical evaluations on a self-captured dataset by a hybrid airborne laser scanning sensor combined with two nadir cameras in RGB and near-infrared over a 247 km2 terrain characterized by hilly topography, urban areas, and dense forest cover. Our findings emphasize the importance of employing appropriate training and inference strategies to achieve accurate classification of data points across all categories. The proposed methodology not only facilitates the segmentation of varying size point clouds but also yields a significant performance improvement compared to preceding methodologies, achieving a mIoU of 94.24% on our self-captured dataset.
1. Introduction
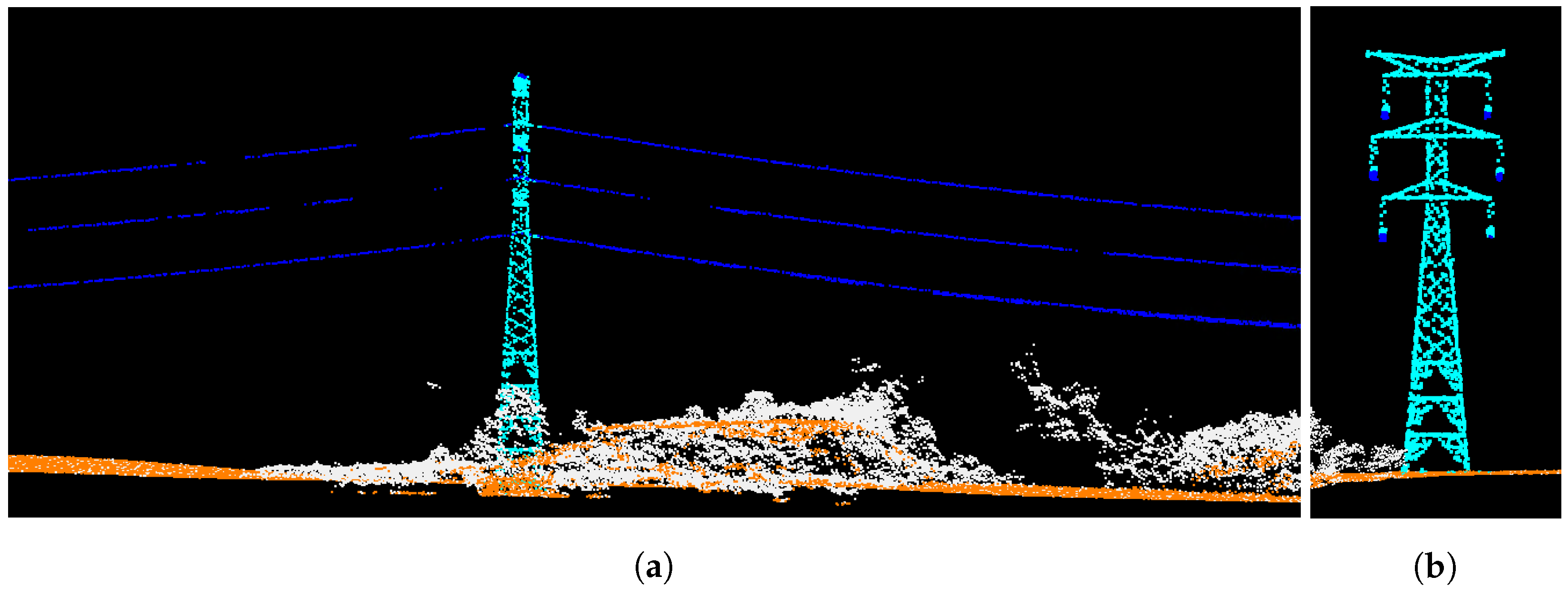
Topographic Light Detection and Ranging (LiDAR) systems technology can be used to create highly detailed three-dimensional (3D) maps. This technology uses pulses of light to scan the Earth’s surface, capturing a vast amount of data, which are stored as point clouds. In regional-scale applications, an Airborne Laser Scanning (ALS) platform is commonly utilized for land cover classification [1], forest inventory [2], or archaeology [3]. This platform involves mounting the LiDAR system on an aircraft, allowing for a broader coverage area and the ability to capture data from a bird’s-eye view. The main strength of LiDAR technology, in contrast to other 3D mapping techniques that rely on aerial photogrammetry [4], lies in its principle of active measurement, which allows us to penetrate small gaps in foliage to reveal objects within and beneath the canopy. As a result, LiDAR provides accurate data pertaining to the ground, the vertical structure of forests, as well as the buildings and objects above it, as depicted in Figure 1.

Figure 1.
Labeled LiDAR point cloud of a scene with power lines where each color represents a different class. The point cloud was obtained by an ALS platform and exhibits a mean density of 27 points per square meter. The precision of LiDAR data is evidenced by their ability to capture the geometric structure of the scene.
Determining how to segment and classify objects within the 3D data is essential for proper analysis of the captured surface. There have been remarkable advances in deep learning techniques for point cloud understanding. The pioneering work for directly processing point clouds was PointNet [5], which uses Multi-Layer Perceptrons (MLPs) to learn per-point features and a symmetric function to obtain a representation of the point cloud. In a subsequent study, Qi et al. [6] extended the capabilities of PointNet by incorporating local geometric information through a hierarchical architecture, which resulted in PointNet++. Inspired by the mentioned networks, new studies [7,8,9] focus on augmenting features, especially local relationships among points. These include PointCNN [10], KPConv [11], RandLa-Net [12], and Point Transformer [13], all of which demonstrate significantly better performance than PointNet++, suggesting that its simplicity may limit its capacity to effectively learn intricate point cloud representations.
Nevertheless, recent works [14,15] reveal that a significant portion of performance gain observed in state-of-the-art models is caused by many factors beyond architecture design, which receive comparatively less attention. These include improved training strategies, data augmentation and different inference strategies. For instance, employing label smoothing [16] into training procedures enhances the performance of tasks such as point cloud classification and semantic segmentation on some datasets [14,17]. Furthermore, augmentation techniques such as point resampling and height appending contribute significantly to improve performance of shape classification [14,18].
Point cloud data can vary significantly in terms of density, size, and attributes influenced by both the acquisition system and the flight plan, which will align with the specific requirements of the intended application. Hence, a one-fits-all approach is unsuitable for all scenarios. It is essential to consider the characteristics of the point cloud data. ALS point cloud data, in particular, pose unique challenges arising from the variability caused by the flight specifications, such as the flight date and height. The flight date determines the state of most trees’ foliage, directly impacting the vegetation shape. The flight height, which also depends on the terrain’s topography, directly influences the point cloud density. Elevated regions typically have a higher concentration of points because they are closer to the sensor, while lower areas tend to have fewer points, resulting in a broad spectrum of density variations within the same category. Additionally, different object categories exhibit a diverse range of sizes, extending from thin and long power lines to 200-m-tall wind turbines. This variability in size further contributes to the complexity of automatic segmenting multiple categories within a point cloud. Existing approaches for point cloud processing have limitations in terms of the point cloud size they can handle, being confined to either small point clouds ( points) [5,6] or large-scale point clouds ( points) [12]. Therefore, there is a need to explore segmentation techniques that can effectively handle point clouds of varying sizes.
Segmenting objects in forestry scenes serves as the initial step for several tasks, including fire risk monitoring, environmental analysis, resource management, and ecosystem understanding [19,20,21]. The goal of this work is to propose a methodology for a robust semantic segmentation of cluttered scenes, with specific emphasis on training and evaluation factors independent of network architecture. We use a self-captured airborne dataset with manually labeled objects, such as transmission towers, power line facilities and wind turbines, across diverse terrains, including flat lands, hilly zones, and forestry areas. Each terrain exhibits unique density distributions and shapes due to different types of vegetation and buildings. Therefore, we require a method that not only performs effectively with a specific data distribution but generalizes well to different surrounding environments.
In this work, we present a set of efficient strategies that, when combined with PointNet++, result in a substantial improvement in performance, outperforming state-of-the-art architectures subsequent to PointNet++, such as KPConv. Our contributions are summarized as follows:
- (I)
- We introduce a pipeline for point classification of outdoor scenes characterized by varying point cloud sizes. Our experiments demonstrate the effectiveness of this pipeline on a diverse dataset, with point cloud sizes ranging from to points.
- (II)
- We study the training and inference strategies independent of network architecture and show that they have a large impact on semantic segmentation performance, resulting in an increase of +21.7% Intersection over Union (IoU).
- (III)
- We propose a novel inference strategy based on prediction uncertainty, which demonstrates a performance improvement of +2.9% IoU on minority classes, while also exhibiting greater efficiency than the voting strategy.
This article is organized as follows: Section 2 provides an overview of the deep learning processing methods for point clouds, as well as the modern training strategies. Section 3 describes the proposed methodology for semantic segmentation of point cloud scenes. The experimental settings, dataset, and evaluation of our method are discussed in Section 4. Quantitative and qualitative results are presented in Section 5. Finally, Section 6 summarizes the main conclusions derived from this study.
2. Related Work
2.1. Deep Learning Methods
LiDAR data are characterized by their irregular and unordered distribution, which is a result of the laser emission technique employed during data collection. The emitted pulses of light reflect off objects within the beam’s range, resulting in the formation of scattered data points that lack a regular pattern. Consequently, traditional deep learning methods that work very well in computer vision, such as Convolution Neural Networks (CNN), cannot be directly applied to analyze point clouds. To address this, several representations of point clouds have been explored. The most common include multi-view projections [15,22,23], voxel grids [24,25,26], point clouds [5,6,10,11], as well as combinations of them [27,28].
Multi-view methods employ two-dimensional (2D) projections, offering a fast and efficient approach. However, these methods exhibit limitations in terms of accuracy and robustness, as they compromise the preservation of spatial information. For this reason, they are mainly employed for shape classification. In contrast, voxel grids convert irregular data into a 3D grid, facilitating the application of 3D CNNs. Nevertheless, the use of voxel grids entails significant computational resources and highly dense point clouds need to be quantized to match the desired size. For this reason, they are usually restricted to much lower-resolution point clouds.
Rather than projecting irregular point clouds onto regular grids, point-based networks directly process point clouds. PointNet [5] was the pioneering work that directly processed point sets. This approach uses permutation-invariant operators to independently process individual points, followed by a global aggregation through max-pooling to generate a point cloud representation. In a subsequent study, PointNet++ [6], the authors extended the approach by incorporating hierarchical feature learning with PointNet layers, aiming to capture local geometric structures. Since then, more point-based methods have been proposed, focusing on the design of local modules to capture 3D geometries with more complex architectures. The Structural Relational Network [29] leverages MLPs to learn structural relational features between parts of objects. Some works have proposed extending regular grid CNN to irregular point clouds. PointCNN [10] introduces an X-transformation to the input points, enabling the application of a CNN to the representation. RSCNN [30] proposes a relation-shape convolution operator to encode the geometric relation of points. Wang et al. [31] propose an EdgeConv operator for dynamic graphs, which facilitates point cloud learning by recovering local topology. KPConv [11] introduces a flexible convolution operator for point clouds that adapts to point density. The Critical Points Layer [32] learns to reduce the number of points in a point cloud. These methods are primarily developed and evaluated on small-scale or subsampled point clouds and directly applying them to large-scale point clouds heavily increases the computation demand.
Recently, several works have tackled the challenge of semantic segmentation for large-scale point clouds. In SPG [33] the authors suggest a representation of points as a collection of interconnected shapes using graphs. However, its approach of processing point clouds as super graphs prior to applying neural networks results in a computationally intensive method. In contrast, RandLA-Net [12] proposes a local feature aggregation module to capture geometric features. This approach enhances efficiency by employing random sampling and shared MLPs. Nevertheless, it is designed to work at a single scale, causing the duplication of points in smaller point clouds that introduce notable noise. Considering the success observed in transformers across various domains [34,35], recent methods leverage attention mechanisms to extract local features. Several 3D Transformer backbones have been proposed for point cloud segmentation [13,36,37]. Transformers offer distinct advantages over CNNs; in particular, their ability to model long-term dependencies. Furthermore, the attention mechanism is permutation-invariant, and the attention map dynamically adjusts based on input during inference, showcasing greater adaptability than MLPs with fixed weight matrices. However, transformers can be computationally expensive, especially for large point clouds. The self-attention mechanism has a quadratic complexity with respect to the input size, which can be a limiting factor for high-density point clouds. Additionally, while transformers excel at capturing global context, they might struggle with capturing fine-grained local information. This could be a drawback for tasks that heavily rely on detailed local structures. A descriptive summary table is provided in Table 1 with the principal limitations and characteristics of each method.

Table 1.
Descriptive summary table of state-of-the-art methods for point cloud segmentation. The second column outlines the characteristics of the input data each method is designed to handle. The third column highlights the methods’ adaptability to varying point cloud sizes. The fourth column delves into the improved strategies incorporated by each method. Note that not all the strategies are included in the table, only the most relevant. The last column quantifies the network sizes in terms of parameters, providing insights into the model’s complexity.
The aim of this study is to address the limitations of current methods by designing a methodology capable of processing LiDAR scenes defined by small and large point clouds while minimizing computational complexity. Our focus is not centered on designing local modules; rather, we explore all aspects beyond architecture. We believe that the performance of a method relies heavily on various factors, including data augmentation, point cloud subsampling approaches, optimization techniques, and inference strategies.
2.2. Training Strategies
Recent works have highlighted the significant influence of training strategies on neural network performance for point cloud classification and segmentation. SimpleView [15] adopts DGCNN [31] training strategies and compares the performance of several methods for point cloud classification. The findings reveal that auxiliary factors such as different evaluation schemes, data augmentation strategies, and loss functions, which are independent of the model architecture, significantly affect performance. In a systematic study, PointNeXt [14] quantifies the impact of data augmentation and optimization techniques. The authors propose a set of training strategies that enhance the performance of PointNet++ for semantic segmentation of the S3DIS indoor dataset [38]. It is noteworthy that none of these studies address airborne LiDAR data, which pose specific challenges due to their varying density and scale. Given the absence of a standard training procedure for 3D scene segmentation, we examine the strategies employed in recent studies.
2.2.1. Sampling Approaches
Modern airborne LiDAR systems produce dense point clouds of up to 50 points per square meter, representing a significant increase in density compared to existing point cloud benchmarks. Consequently, a common approach is to down-sample point clouds before fitting them into the network. In the work describing RandLa-Net [12], the authors identify random sampling as by far the most suitable component for large-scale point cloud processing, as it is fast and scales efficiently. During random sampling, arbitrary points are filtered from the original point cloud. While this approach maintains the distribution of the original set of points and is computationally efficient, with time complexity of , it may discard crucial points by chance. Alternative methods that address the limitations of random sampling include Farthest Point Sampling (FPS), Inverse Density Importance Sampling (IDIS), Grid Subsampling, and Constrained Sampling (CS). FPS [6] involves selecting the points that are furthest away from each other in the point cloud, obtaining good coverage of the entire point set. Hence, it has been used in several works [10,13,39]. However, its computational complexity is too heavy for large-scale point clouds ( points). IDIS [40] defines the inverse density importance of a point by adding up all distances between the center point and its neighbors, and then it samples points whose sum values are smaller. Compared to FPS, IDIS is more efficient (), but it is also more sensitive to outliers. Grid Subsampling [11] projects the point cloud into a grid, retaining only one point per voxel. The density and detail of the resulting point cloud are specified by the voxel size. Constrained sampling [41] is an efficient technique with low computational complexity that selectively removes points based on their heights. Nevertheless, this method is susceptible to task-specific bias, as the optimal height ranges may differ across tasks.
Overall, FPS and IDIS are computationally expensive when applied to large-scale point clouds. Grid subsampling requires the specification of a grid size, and in cluttered point clouds it can result in the loss of fine details. CS is restricted to a specific task in which the parameters need to be specified in advance. Random sampling emerges as a computationally efficient alternative, which is particularly well suited for handling extensive point cloud datasets. However, it may potentially exclude crucial points when applied to small point clouds. In this work, we address and mitigate these limitations through effective strategies to ensure accurate data representation.
2.2.2. Data Augmentation
In the point cloud domain, data augmentation is an important strategy to address the challenges posed by limited labeled data. It involves transforming and expanding existing point cloud data to enhance model robustness and mitigating overfitting. PointNet++ proposed a range of data augmentations including random rotation, scaling, translation, and jittering, across diverse benchmarks [6], which are conventionally used. Recent studies have introduced modern augmentations, such as random dropping of colors during training [11], point resampling [18], and the introduction of noise by randomly modifying a small portion of points’ coordinates [42]. Advanced augmentation methods like PointMixup [43] generate new samples through interpolation between examples, while PointWOLF [44] employs locally weighted transformations to produce smoothly varying non-rigid deformations.
2.2.3. Optimization Techniques
The effectiveness of a neural network is heavily influenced by optimization techniques, including factors such as loss functions, optimizers, learning rate schedulers, and hyperparameters. The first few works employed CrossEntropy loss, Adam [45] optimizer, exponential learning rate decay, and uniform hyperparameters. Advancements in machine learning have led to the exploration of superior optimizers, such as AdamW [46] as an improvement over Adam, learning-rate schedulers, and more sophisticated loss functions like CrossEntropy with label smoothing [16].
3. Method
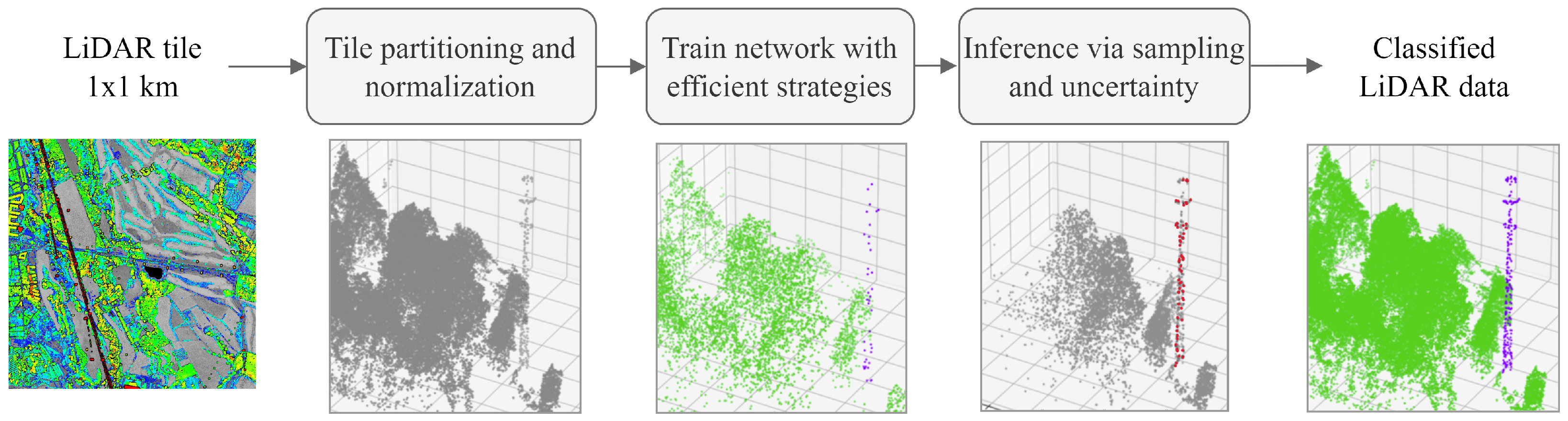
The aim of this study is to develop a method that effectively classifies the points of both small and large objects in cluttered scenes, ensuring accurate and efficient segmentation in LiDAR-based applications. In order to define a pipeline for segmenting varying density point cloud scenes from LiDAR data, we define the methodology depicted in Figure 2. This involves (I) tile partitioning and heights normalization; (II) training the neural network with efficient strategies; and (III) Inference through sampling and uncertainty.
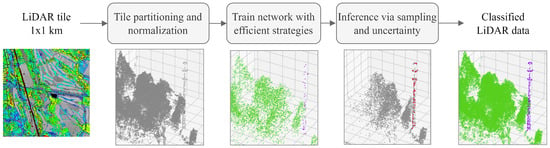
Figure 2.
Overview of the LiDAR semantic segmentation pipeline: Each LiDAR tile undergoes a multi-step process, beginning with partitioning into subtiles and normalization of heights. Then, a supervised point-based neural network is trained using efficient strategies for point cloud segmentation. During inference, the method employs sampling techniques that consider point classification uncertainty, resulting in a robust point classification.
3.1. Tile Partitioning and Normalization
In the pre-processing stage of our point cloud segmentation pipeline, we employ heights normalization and tile partitioning to facilitate the network training. These pre-processing steps are recommended when possible for effective management of the high-density ALS point cloud data.
1. Heights Normalization. Given the variability of surface altitude across our dataset, heights are normalized by subtracting the ground’s elevation (the topographic ground map is provided by ICGC) to all points, obtaining height above ground. This transformation ensures that heights are represented as distances above ground level with the intention of enhancing the model’s comprehension of features related to height.
2. Tile Partitioning. In order to handle the abundance of points in raw ALS tiles, we implement a tile partitioning process. The dimensions of the subtiles are selected based on the point cloud density and the size of objects within the dataset. The subtile size must be large enough to ensure that the objects are adequately represented, but not so large that the number of points becomes unmanageable. We have established subtiles of m with a 50 m overlap, considering that our target object sizes range from 30 to 120 m and our mean point density is between 13 and 27 ppm2. This configuration ensures that subtiles are manageable in terms of the number of points while effectively capturing the necessary detail.
3.2. Training the Network with Improved Strategies
We investigate the impact of sampling, data augmentation, and optimization techniques employed in recent neural networks when processing LiDAR data, and we study the effect of each strategy for semantic segmentation of point cloud scenes.
1. Point Cloud Sampling. The initial choices to be made when processing point cloud data are the determination of the sampling technique and the point cloud size to be used in training. These factors are particularly pertinent given the dense nature of point cloud scenes with numerous points that do not offer valuable information. In accordance with previous works [6,11], we set the training size to 4096. Regarding the sampling technique, we limited the study to random sampling due to its speed, minimal computational requirements, and straightforward simplicity. We start our study by comparing training with a fixed set of points, where the model encounters the same set of points throughout the entire training period, versus resampling during the training process. Resampling allows the network to see a broader range of point configurations, enhancing its ability to generalize across diverse scenes. Section 4.2 presents and analyzes the revealed discoveries.
2. Data augmentation. Next, we delve into quantifying the performance improvement associated with each data augmentation technique during training. We conduct experimentation with a set of augmentations that, according to our assessment, have the potential to enhance the model’s capacity for generalization. Our initial augmentation involves incorporating rotation, as suggested by PointNet++. While rotation is commonly believed to be beneficial, its application has demonstrated a performance drop on the S3DIS dataset, as documented in [14]. Subsequently, we introduce color dropout, a technique proposed by KPConv, which involves randomly removing color channels of a point cloud during training. The purpose of the dropout process is to guide the model to prioritize spatial coordinates, discouraging it from memorizing color-specific details, which promotes a better overall performance on unseen data.
3. Optimization Strategies. In optimizing model performance, several key strategies are explored. Firstly, we analyze the learning-rate decay during training; specifically, we compare the step decay with the cosine scheduler, which has demonstrated advantages in recent works [14]. Additionally, we experiment with label smoothing, a technique that is known to be advantageous for refining classification tasks by introducing controlled uncertainty into ground truth labels. Furthermore, we incorporate weighted cross-entropy loss during training by assigning distinct weights to address potential imbalances within the dataset. This technique ensures that the model places more emphasis on correctly classifying instances from under-represented classes, contributing to a more equitable training process. Finally, we replace the conventional Adam optimization algorithm with AdamW, a widely employed optimization algorithm in modern neural networks [46]. The study, which is described in detail in Section 4.2, comprehensively analyzes the impacts of these optimization strategies on each category, dataset, and overall performance.
3.3. Inference Strategies
Conventionally, the standard inference procedure involves feeding all points into the model to obtain predictions. Given the variable density across LiDAR point clouds, we hypothesize that the size of the point cloud may impact the obtained predictions. In this section, we contrast the conventional approach with different inference strategies: feeding a batch of random samplings and utilizing a voting approach, and we propose a novel strategy that uses point predictions uncertainty to make predictions. The practical implications of each inference strategy are comprehensively explored in the subsequent sections.
3.3.1. Batch of Random Samplings
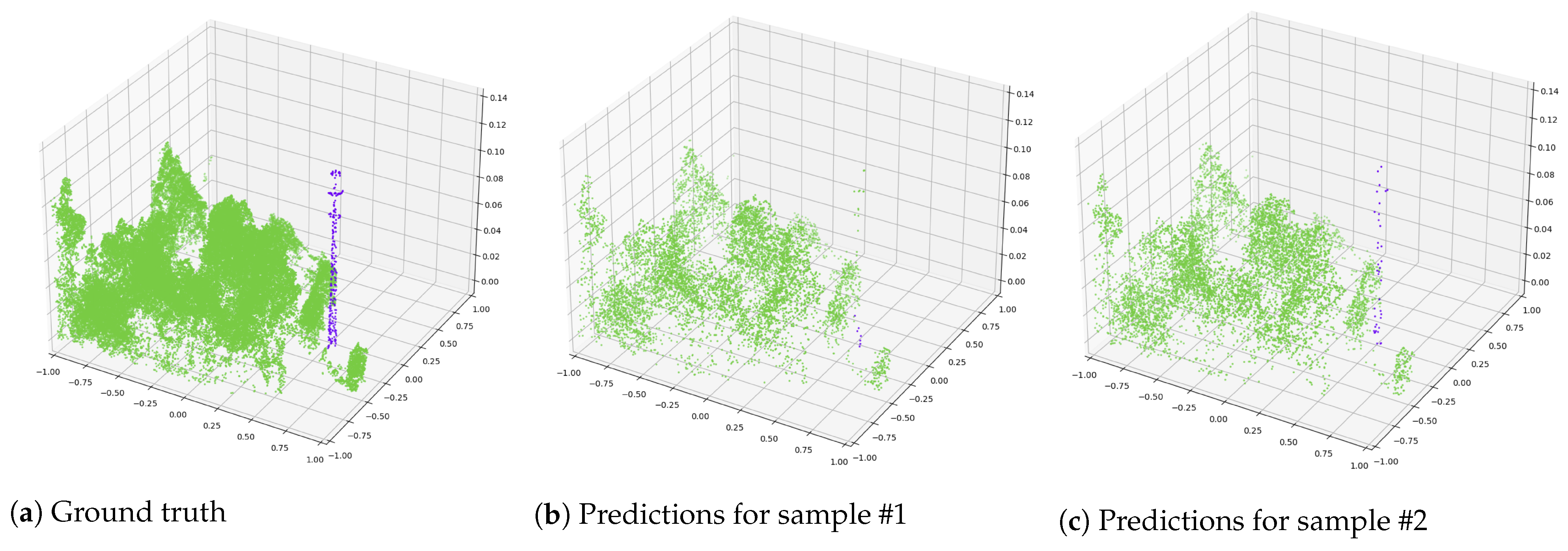
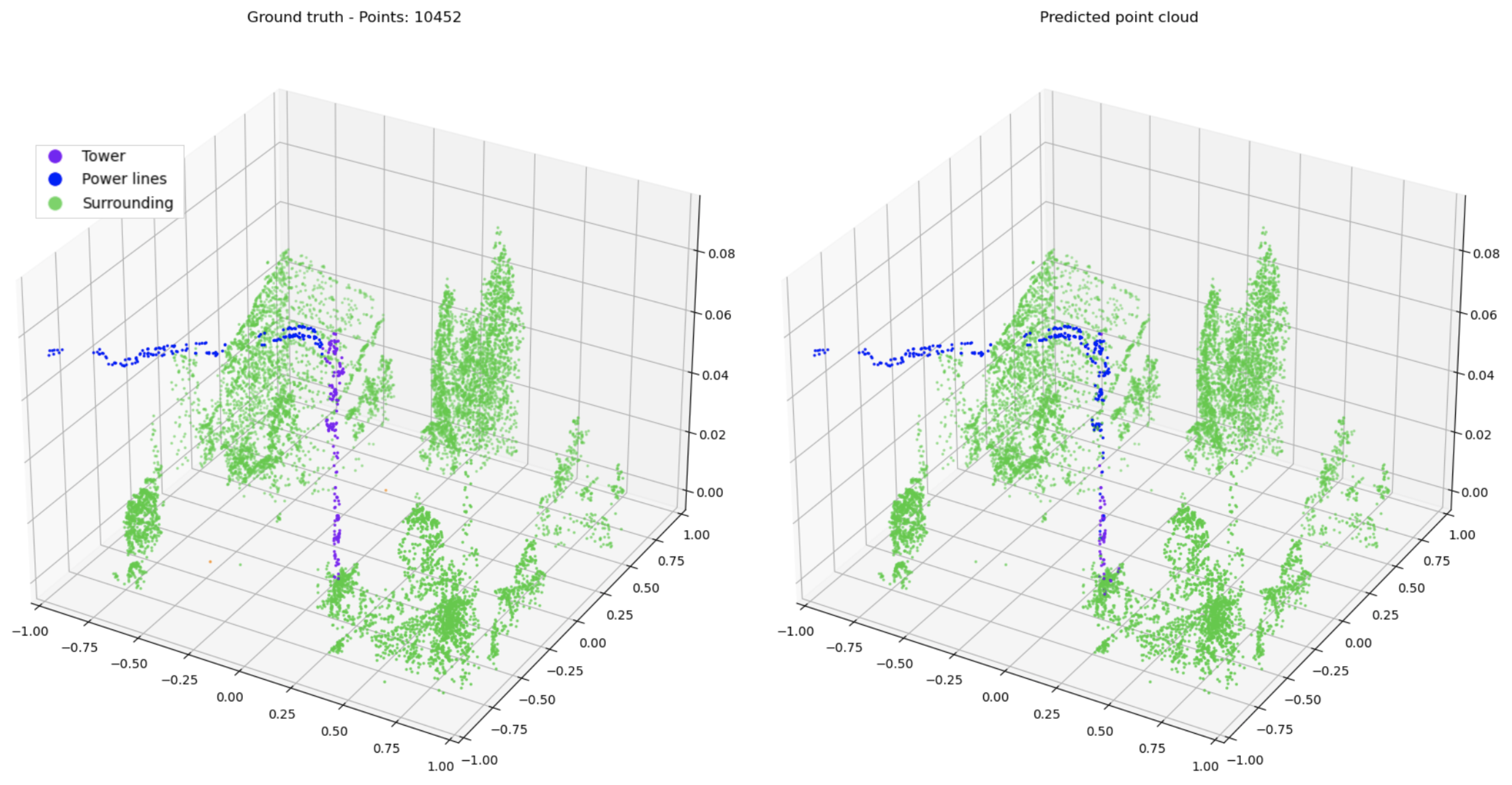
During the inference process, each point cloud is reshaped into a batch of n sampled point clouds. n is determined by dividing the total number of points in the input point cloud by p, which represents the desired number of points per sample. We experiment with different values of p; specifically, 8 K and 16 K. Since the point cloud size may not align perfectly with multiples of p, partially filled point clouds are supplemented with duplicated points. This batch of samples is then fed into the network to generate predictions. Our intuition is that maintaining a point cloud size similar to the training data (4096 points) would result in improved performance. There is a potential risk of object points being dispersed across batches and incorrectly predicted, as exemplified in Figure 3, which can be mitigated through the use of voting mechanisms. Nevertheless, as detailed in Section 4.3, adopting inference on random samplings instead of feeding all points not only reduces the inference time but also contributes to an overall enhancement in performance.
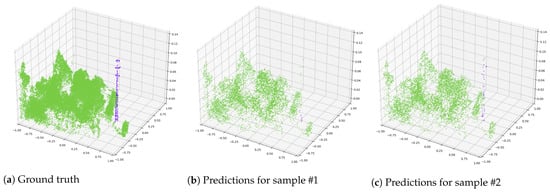
Figure 3.
Full ground truth point cloud with 59,694 points and predictions for two different random samples of 8000 points. Green points represent the surrounding category, and purple points represent towers. Predictions vary due to different sampled points. In (b), some points are misclassified as vegetation, while (c) accurately classifies both categories.
3.3.2. Voting
The voting technique combines multiple predictions of the same point to achieve a more robust and accurate classification. The final label is determined by the prediction that occurs most frequently through majority voting. This technique is beneficial in scenarios where some points may be uncertain for the model, and combining predictions from different contexts helps mitigate errors. However, this comes at the cost of increasing the inference time, whose duration is directly proportional to the number of votes employed. Determining the optimal number of votes remains unclear, and our objective is to explore and determine the most effective value. In Section 4.3 we quantify the increase in IoU as well as the computation time corresponding to the number of votes.
3.3.3. Uncertainty-Based Sampling
Certain points exhibit higher prediction uncertainty compared to others. We believe that points with greater uncertainty should undergo the voting process, whereas points that are already highly certain might not benefit from voting. To leverage this distinction, we propose obtaining two predictions for each point using two different randomly sampled point clouds. Then, we compare both predictions, and if they are identical then we move on to the next sample. However, if there is entropy in the obtained predictions, we employ the uncertainty-based sampling technique. Entropy measures the uncertainty in a distribution and it is defined in Equation (1), where is the probability of the i-th possible prediction of x.
Our goal is to obtain more robust predictions for uncertain points. Applying K-Nearest Neighbors (KNN) sampling using uncertain points as query points would be an option, but it alters the data distribution by creating point clouds with a sphere shape. To address this, we employ an exponential probability distribution on squared distances between uncertain points and all other points, each point defined by x and y coordinates, which results in a smooth KNN sampling, defined as follows:
here, is the i-th query point, represented as a vector in , is the j-th reference point, represented as a vector in , and is a scaling factor that controls the rate at which the probability decays with distance.
The resampling process aims to select uncertain points and their neighbors with higher probability, while distant points still have a chance of being included with a lower probability. The process is showcased in Figure 4, with uncertain points highlighted in red. The number of sampled point clouds used is a parameter that can be adjusted. As the number increases, the results become more robust, at the cost of higher GPU memory requirements.
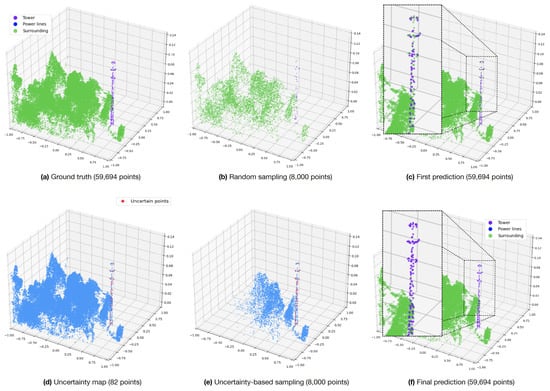
Figure 4.
Inference process illustrated from left to right, utilizing uncertainty-based sampling. (a) The complete labeled point cloud is initially presented. (b) The point cloud is transformed into 8000-point samples. (c) Predictions from all samples are obtained and merged. (d) Examination for uncertain points is conducted, identifying points with different predictions marked in red. (e) The point cloud is resampled using uncertainty-based sampling. (f) Final predictions.
4. Experiments
We evaluate our methodology by applying it to our collected dataset to determine its accuracy, efficiency and computational cost. We begin by describing the dataset used in our experiments, as well as the considered parameters. We then elaborate on the experimental design and provide a thorough analysis of the obtained results in which we study the effects of each strategy with an ablation study.
4.1. Experimental Settings
This section involves a description of the experimental setup, including the datasets used, training and test splits, evaluation procedure, and the implementation details used for all experiments.
4.1.1. Dataset
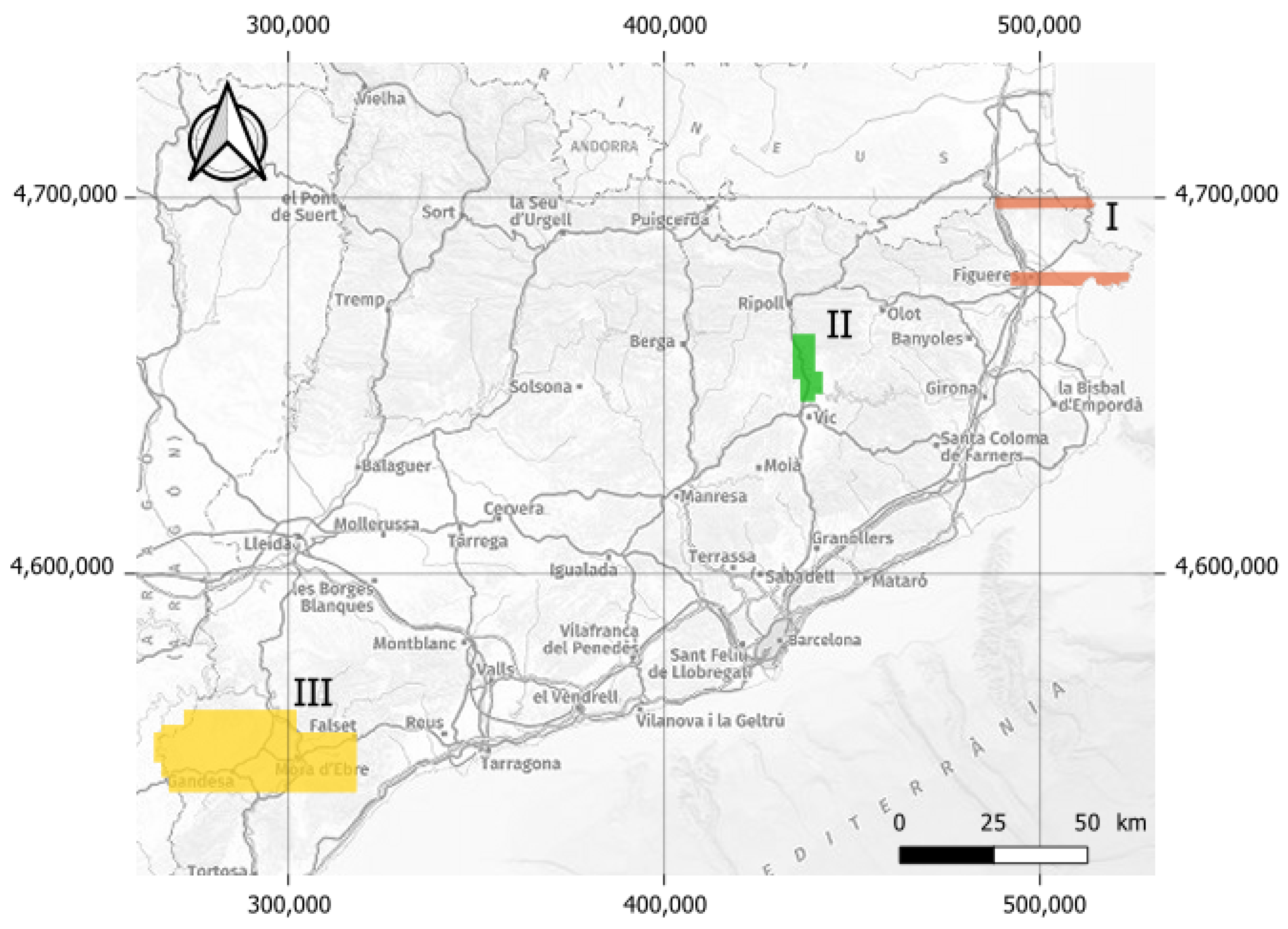
The study area is composed of three different areas of Catalonia, Spain: Alt Empordà, Ribera del Ter, and Terra Alta, as depicted in Figure 5. The surface area, point density, and date of flight of each region are outlined in Table 2.
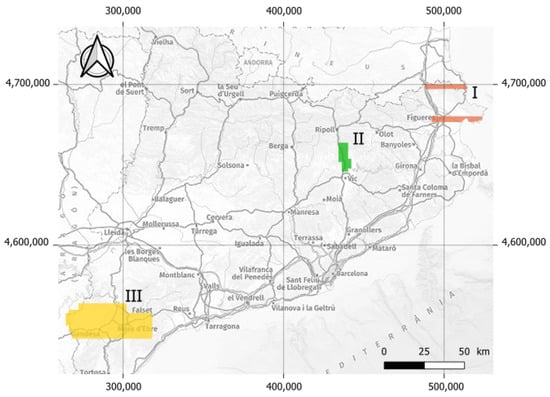
Figure 5.
Scanned areas of Catalonia. Alt Empordà (I), Ribera del Ter (II), and Terra Alta (III). The reference system of the indicated coordinates is ETRS89 and it is projected in UTM zone 31N.

Table 2.
Mapped areas.
The experimental dataset was collected by a Terrain Mapper 2, which combines a LiDAR sensor with two nadir cameras in RGB and NIR (Near-InfraRed), provided by the ICGC (Cartographic and Geological Institute of Catalonia). The system scans in a circular pattern, obtaining a constant oblique FOV (Field Of View) of 40° with even point distribution. Areas I and III (Alt Empordà and Terra Alta) belong to the third Catalan LiDAR coverage (LIDARCAT3) and were flown at a maximum AGL (Above-Ground Level) of 2100 m with a minimum sidelap of 20 percent. The pulse rate is nearly 2 million Hz. Overlapping points are filtered during the classification process to achieve a homogeneous density of 10 pts/m² at average terrain height. Area II (Ribera del Ter) was flown at a maximum AGL of 2150 m with a minimum sidelap of 60 per cent. The pulse rate is about 700,000 Hz. It was planned to obtain a minimum point density of 4 pts/m² in a single strip and a homogeneous density of 8 pts/m² using the overlapping points. The cameras maximum GSD (Ground Sample Distance) is approximately 11 cm in all areas. The system produces points in the Euclidean space with a lateral placement accuracy of 5–25 cm and vertical placement accuracy of 9–20 cm.
Photogrammetric images and LiDAR point clouds are generated using Leica HxMap 3.3 software. This process mainly involves a data quality check, strip orientation, radiometric adjustment of images, LIDAR bundle block adjustment, noise filtering, and color assignment from the images to the point clouds. Then, Terrasolid 021.001 software is employed to classify both ground and overlapping points, with the latter being subsequently removed from the dataset. The overlapping points are only classified in areas I and III, since in area II, these points are used to achieve a consistent density of 8 pts/m2. Terrasolid is also used to calculate the height of each point above ground. The resulting average point density for the last and only returns varies from 8 to 11 pts/m2. Each point is defined by several attributes; the most significant ones are coordinates, class, intensity, height above ground, RGB, and NIR.
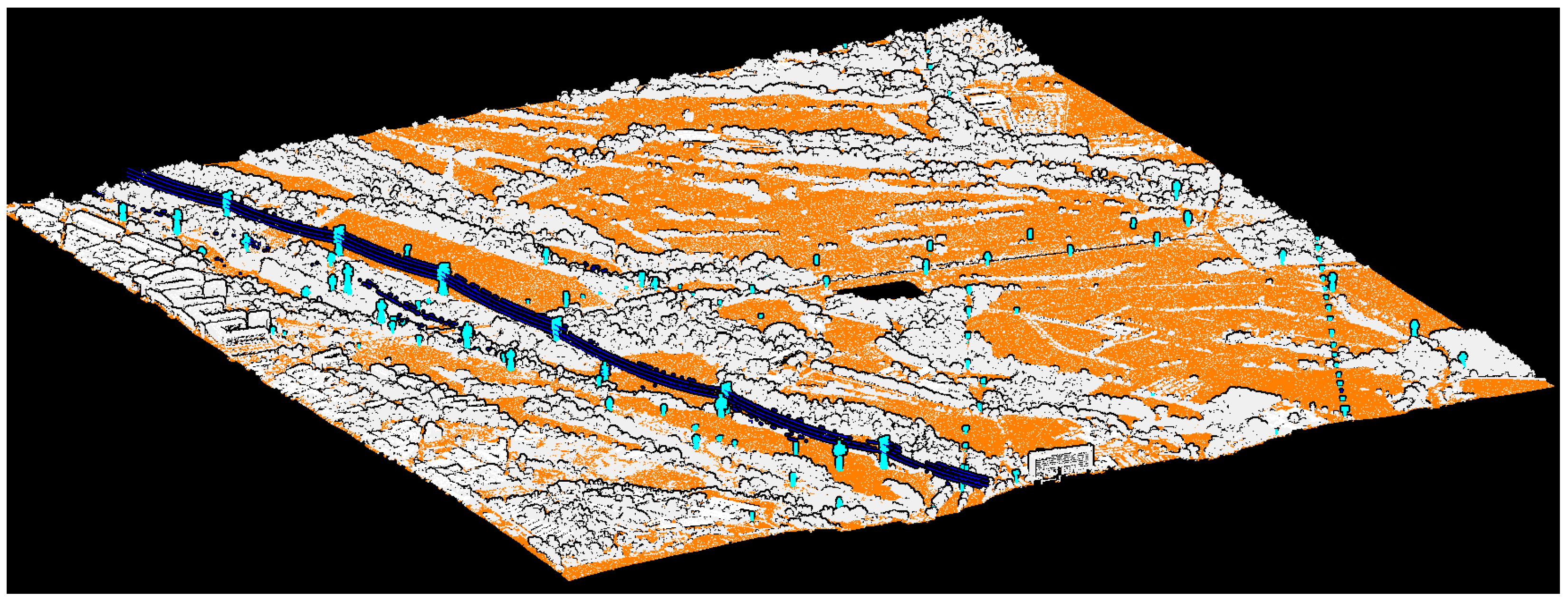
The landscape of each area differs significantly. Alt Empordà is characterized by hilly terrain and dense forests, while Ribera del Ter features riparian vegetation. Terra Alta, being the largest scanned area, presents flat fields with wind farms as well as mountainous zones with electrical facilities. These areas contain power lines, transmission towers, wind turbines, vegetation, and different types of buildings and infrastructures.
Objects are manually labeled into their respective categories using Terrassolid software. Initially, some wind turbines and high voltage towers and lines are identified from the ICGC topographic base 1:5000. To ensure accurate classification, sections are created and point clouds are visualized from various profiles. Transmission lines are traced and classified accordingly. Finally, other transmission towers, lines, and wind turbines are added to the classification by examining the surrounding points, coloring them by height above ground and visualizing profiles and isometric views. The remaining points, which include vegetation, buildings and various infrastructures, are assigned to the same category named “surrounding environment”.
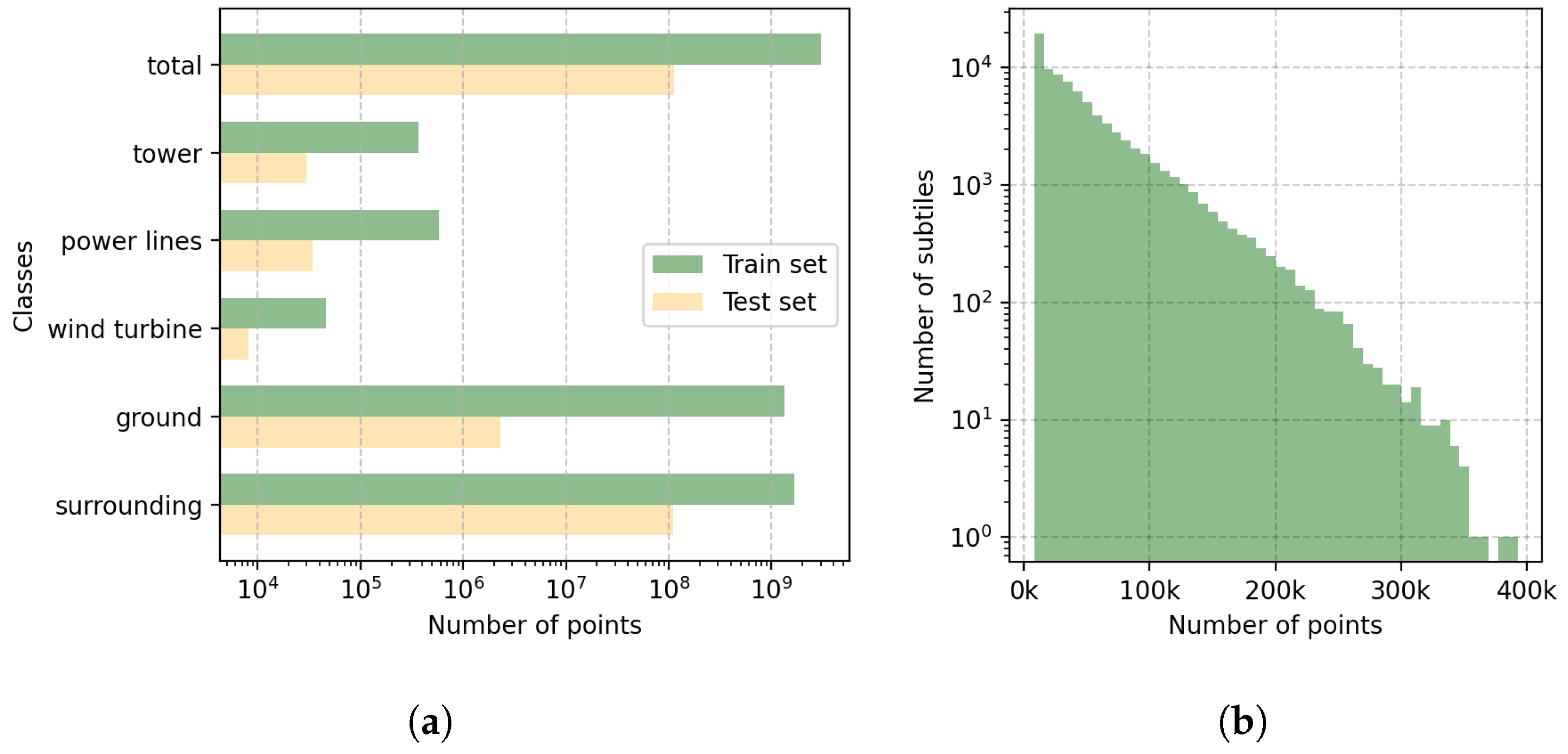
This dataset poses significant challenges due to incomplete objects, considerable variation in shapes and densities within categories, and a high class imbalance. The number of points pertaining to each class is presented in Table 3. Examples of categories are showcased in Figure 6.

Table 3.
Number of points per category and its relative percentage.
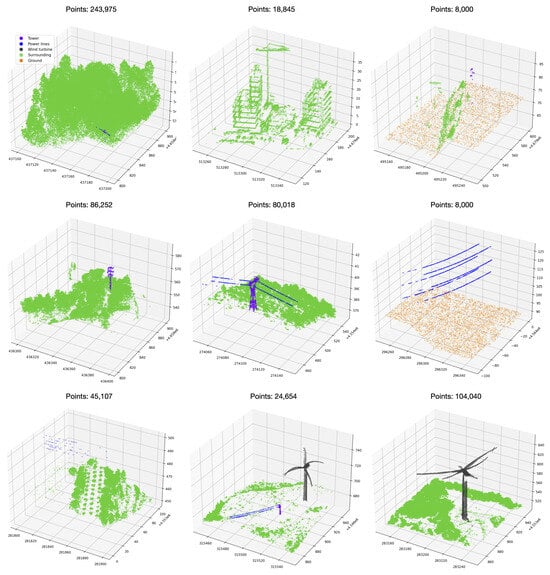
Figure 6.
A variety of m subtile instances displaying different classes within the dataset. This selection provides a glimpse into the rich diversity of object sizes and shapes present in the dataset.
4.1.2. Training Setup
Initially, each dataset is split into training and test sets, comprising a total of 242 tiles for training and 29 tiles for testing. Given the extensive size of each tile (1 × 1 km), all tiles are divided into subtiles measuring 100 × 100 m, with 50 m of overlap for training and 20 m for testing. Table 4 presents the number of tiles and subtiles per dataset. Subsequently, ground filtering is performed. Eliminating normalized ground points () to reduce the overall number of points is a common practice in ALS data processing [4], as ground points often provide minimal valuable information compared to object points for semantic segmentation. Specifically, we filter ground points out when the size of the tile exceeds the defined number of input points to the network; otherwise, they are retained. This approach ensures that tiles with an excessive ground presence are effectively managed, contributing to a more efficient representation of the objects within the point cloud. Simultaneously, isolated objects on flat ground are preserved, along with their contextual information.

Table 4.
Number of tiles ( Km) and subtiles ( m) per dataset.
The distribution of points per subtile is illustrated in Figure 7b, revealing variability in the density of points across samples in the dataset. The majority of samples have less than 50,000 points; however, we encounter point clouds with up to 400,000 points. Examples of subtiles are showcased in Figure 6.
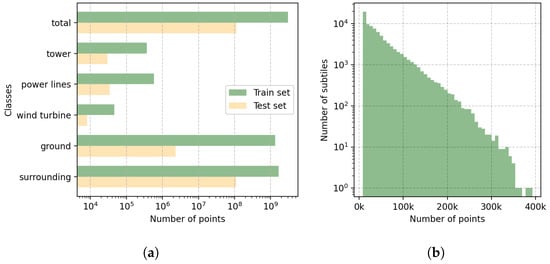
Figure 7.
Descriptive histograms depicting the distributions of classes in (a) and the number of points in (b) within m overlapping subtiles.
As detailed in the dataset Section 4.1.1, points are characterized by eight attributes: coordinates , intensity , three color channels , and . In addition to these attributes, we incorporate the Normalized Difference Vegetation Index (), which is used in remote sensing [47] to indicate whether or not the target being observed contains live green vegetation, as depicted in Figure 8. is obtained from Red (R) and channels, as shown in Equation (3):

Figure 8.
The same point cloud is visualized through: (a) RGB representation, and (b) NDVI colorization. In the latter (b), points are only colorized if they surpass the threshold of 0.2.
Coordinates are normalized in the range [−1, 1] and features are normalized in the range of [0, 1]. Per-point labels are used for supervised training and validation.
4.1.3. Out-of-Domain Data
To evaluate the robustness and generalization capacity of our model, we test how effectively our model extrapolates its learned patterns to an unfamiliar terrain. The data consist of four tiles of km (Figure 9) from a different geographical location to the training dataset, characterized by distinct landscape features, such as a different vegetation distribution and structural elements. The surface area and mean point density are outlined in Table 5.
Figure 9.
Isometric view of the out-of-domain data, comprising four tiles of LiDAR data.

Table 5.
Out-of-domain data properties.
4.1.4. Evaluation Procedure
During the training process, no feedback from the test set is utilized, ensuring the model’s independence from the evaluation data. For evaluation metrics, we use the mean Intersection over Union (mIoU), which is calculated as follows:
where C corresponds to the total number of classes and the subscript i identifies each individual class. TP denotes the number of true positives, where the model correctly identifies a point as belonging to an object. FP is the number of false positives, occurring when the model identifies a point as part of an object when it actually belongs to the background. Similarly, FN is the number of false negatives, indicating instances where the model fails to recognize a point as part of an object when it truly is.
mIoU is particularly suitable for imbalanced datasets, as it considers the intersection of predicted and ground truth masks relative to the union for each of the classes. We calculate IoU across classes (per-class IoU), across datasets (dataset mIoU), and using all test points (global mIoU). This evaluation approach allows us to compare the model’s performance across classes and datasets, each of which is characterized by unique attributes and challenges. We evaluate our method across all classes except for the ground class, which is filtered from the point cloud before being fed into the network, as explained in Section 4.1.1. To compute the global mIoU, we use test points from all classes and datasets. The number of points for each dataset is summarized in following Table 6.

Table 6.
Number of points per class in the test set.
We do not use overall accuracy because it can be misleading in the context of imbalanced datasets, as it computes the ratio of correctly classified samples to the total number of samples without distinguishing between different classes.
We benchmark our approach against KPConv [11], which is the state of the art on the Dayton Annotated Laser Earth Scan (DALES) dataset [48] for semantic segmentation. DALES is an aerial LiDAR dataset spanning 10 square kilometers of an area characterized by urban, rural, and commercial scenes. We trained KPConv using the recommended parameters provided by the authors.
4.1.5. Implementation Details
The experimental program is built using the PyTorch deep learning framework, version 1.8, utilizing CUDA 11.7. For optimization, we employ the Adam optimizer and set the initial learning rate to 0.01, with a cosine decay scheduler, unless otherwise specified. Models are trained for 100 epochs with early stopping on the validation loss. The loss used in all networks is the cross-entropy [49]. As for the batch size, it is set to 64. Batch normalization layers are used to normalize the output of each linear layer. Dropout is used to regularize the network. The system used for the experiments has the following configuration: (i) CPU: Intel Xeon Silver 4210, (ii) RAM: 128GB, (iii) GPU: NVIDIA RTX A6000-48 GB, and (iv) OS: Ubuntu 20.04.
4.2. Experimental Insights of Training Strategies
Table 7 and Table 8 present a detailed analysis of the effectiveness of the proposed training strategies for each category across all datasets, as well as for each dataset when considering all categories. We use PointNet++ as the backbone architecture, with the baseline comprising PointNet++ trained with step decay, Adam optimizer, and no augmentations during training.

Table 7.
Additive study of sequentially applying training strategies for semantic segmentation. The metric used is IoU (%) per category across datasets and the backbone architecture is PointNet++. Global mIoU (%) is mIoU using all test points. is the increment of the performance from the best obtained result after adding a strategy. Baseline without any specific strategy yields initial IoU percentages; subsequent strategies showcase their impact.

Table 8.
Additive study of sequentially applying training strategies for semantic segmentation. The metric used is mIoU (%) per dataset using PointNet++ as backbone architecture.
To assess the efficacy of each training strategy, we measure per-class IoU, the overall mIoU across all test points, and dataset mIoU. Referring to Table 7, it is noteworthy that point cloud resampling is the most effective strategy, significantly boosting the global mIoU by 31.8%. This significant improvement is partially explained by the performance increase in the wind turbine class, which initially goes undetected, and then attains a remarkable IoU of 96.54% after this strategy is implemented. This can be attributed to the limited number of wind turbine instances in the dataset, and resampling facilitates the model’s ability to generalize the characteristic patterns associated with them.
Cosine decay, color dropout, and weighted loss contribute positively to the global mIoU, resulting in increments around 1% mIoU, showcasing their beneficial influence on overall performance. While rotation has a modest effect on global mIoU, it notably enhances IoU on the Alt Empordà dataset by 3.66%, which is the dataset with fewer samples. We chose to incorporate rotation into our training strategies with the expectation that it will effectively augment less common samples.
Additionally, strategies such as label smoothing and AdamW optimization demonstrate different behavior over specific categories and dataset regions, as illustrated in Table 7. For instance, label smoothing exhibits positive effects on wind turbines (+2.5%) while decreasing IoU in tower and power lines categories. AdamW optimization improves mIoU over Alt Empordà dataset but results in less accurate predictions for the other regions with different characteristics. The surrounding category remains unaffected by any of the employed training strategies.
We conclude that data augmentation techniques such as rotation, resampling, and color dropout are advantageous, as they contribute to the model’s generalization ability. Using cosine decay results in a notable 1.7% increase in the global mIoU. Nevertheless, the benefits of label smoothing and AdamW are not clear in our dataset, leading us to abstain from their utilization. Finally, given the pronounced imbalance in our datasets, we observe that employing weighted loss improves IoU on all minority categories. In summary, the effectiveness of each training strategy depends on the specific characteristics of the dataset. Therefore, we adopt the strategies that improve the performance on our test set.
4.3. Experimental Insights of Inference Strategies
To explore the effectiveness of inference strategies, we first compare the performance and inference time between feeding all points into the network against feeding a batch of sampled point clouds, and the results of this comparison are analyzed in Section 4.3.1. Then, in Section 4.3.2, we use the best inference strategy to evaluate the mIoU increase by varying the numbers of votes. Finally, in Section 4.3.3, we analyze the experiments and results obtained with our proposed uncertainty-based inference strategy.
4.3.1. Feeding All Points vs. Feeding Sampled Point Clouds
Table 9 presents the results obtained by the top-performing model using two different inference strategies. We compare the effectiveness between feeding the network with full point clouds and feeding batches of sampled point clouds, with sample sizes of 8 K and 16 K points. mIoU is obtained for each dataset: Alt Empordà, Ribera de Ter, and Terra Alta. Our findings indicate that optimal performance is achieved when utilizing sampled point clouds comprising 8 K points, as opposed to providing all points.

Table 9.
mIoU (%) results of different inference strategies implemented on the optimal trained network, which employs PointNet++ as a backbone. The best results are marked in bold.
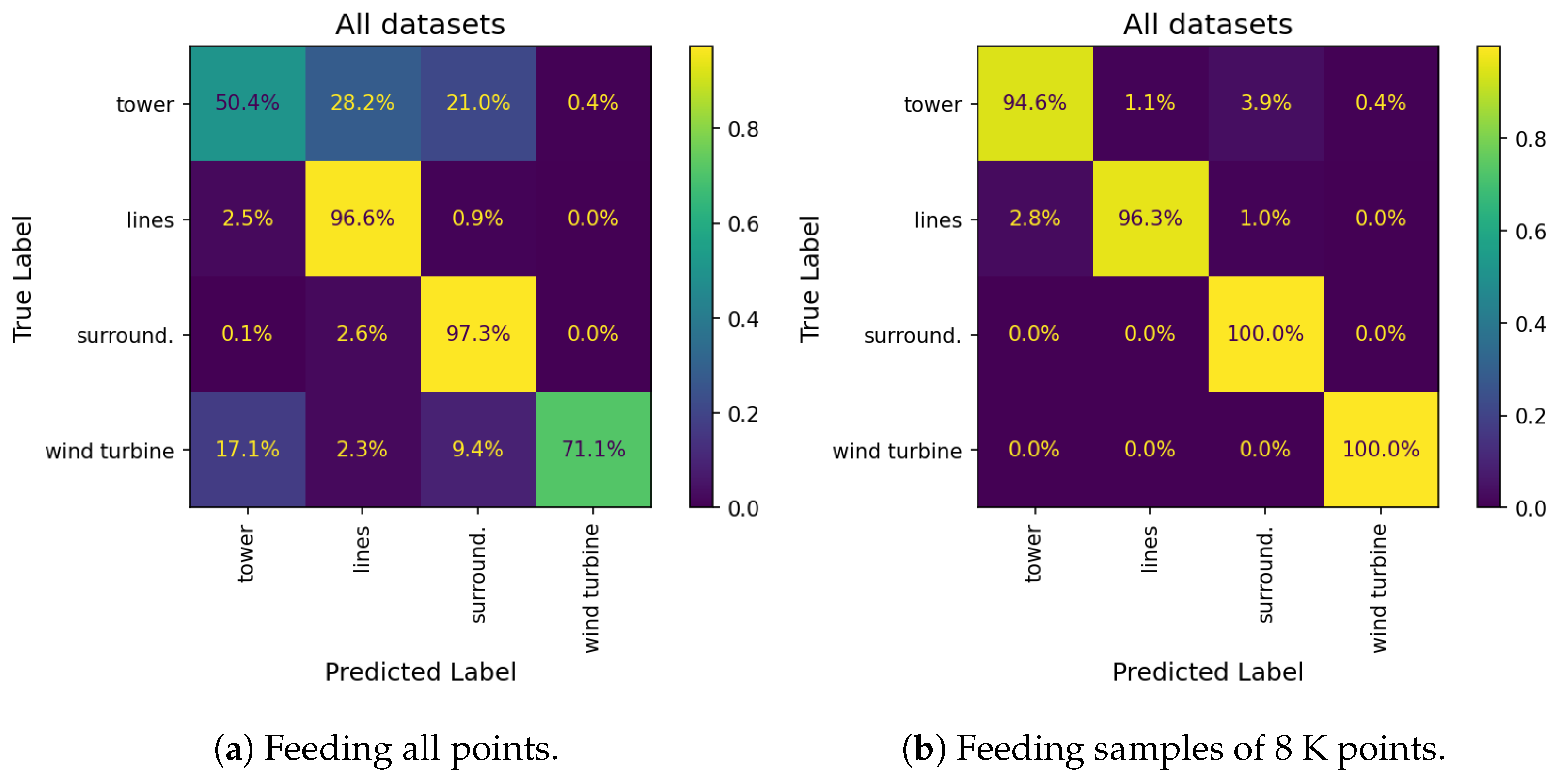
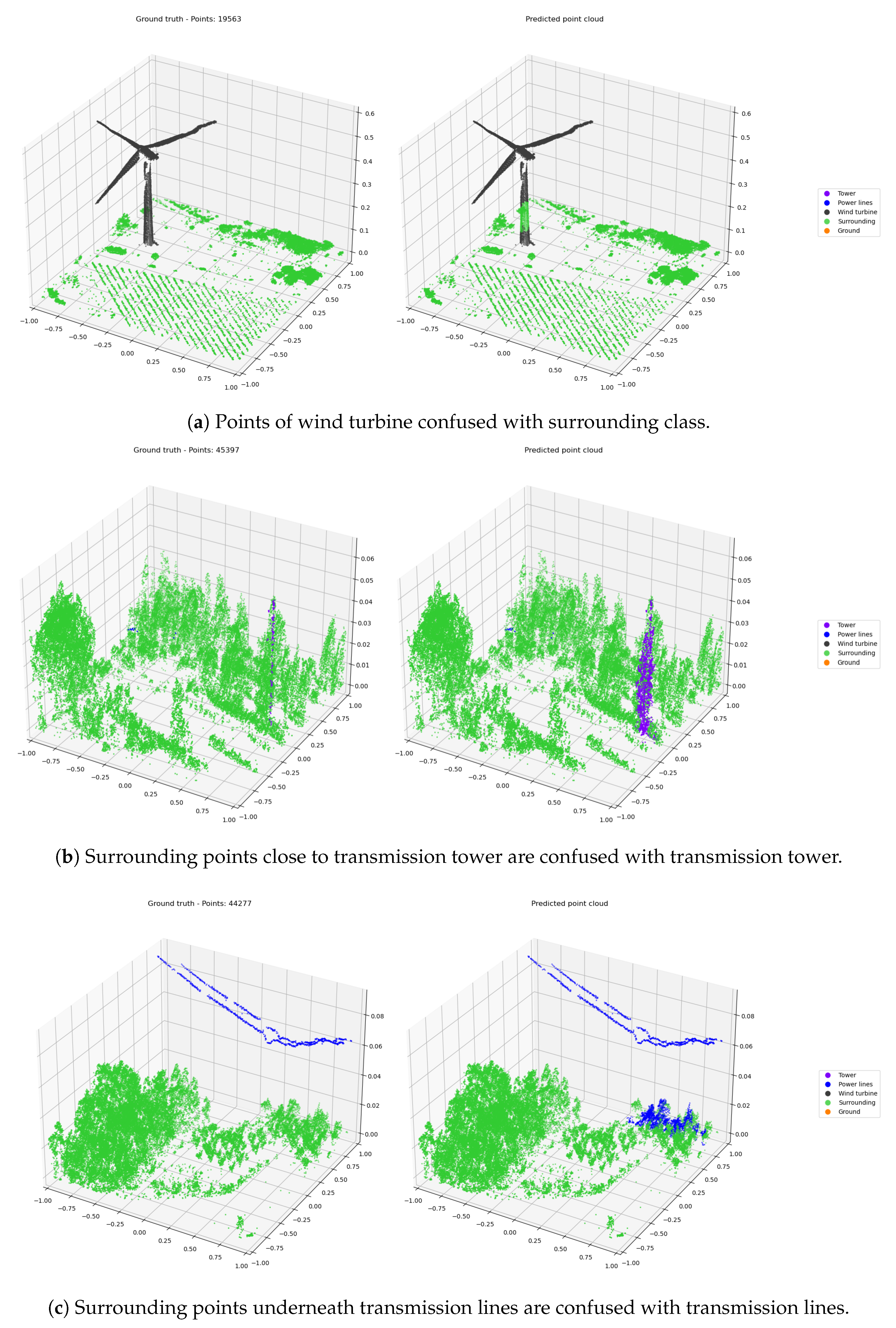
To gain insights into these results, we examine the confusion matrices presented in Figure 10, which compare predictions from feeding both full point clouds and 8000-point sampled clouds across all datasets. We notice a significant reduction in confusion among instances of vertical objects, such as wind turbines, transmission towers, and vegetation, when utilizing 8000-point samples compared to feeding the full point cloud. Specifically, misclassifications in which towers and wind turbines are predicted as surrounding elements are mitigated by 17.1% and 9.4%, respectively. We see that the percentage of correctly detected lines is diminished as some of lines points are detected as towers due to the proximity between botch classes; however, lines decrease by 0.3% and tower prediction improves by 44.2%. Upon closer examination of specific errors (refer to Figure 11), it becomes clear that inaccuracies arise from the misprediction of dense objects. This could be attributed to the elevated point cloud density associated with vegetation. We conclude that utilizing 8000-point samples in inference successfully reduces confusion across all categories.
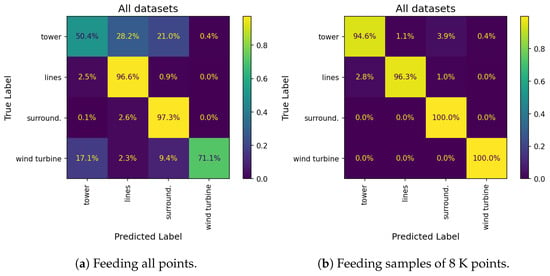
Figure 10.
Comparison of normalized confusion matrices obtained by performing inference on all points against 8000-point samplings across the three regions.
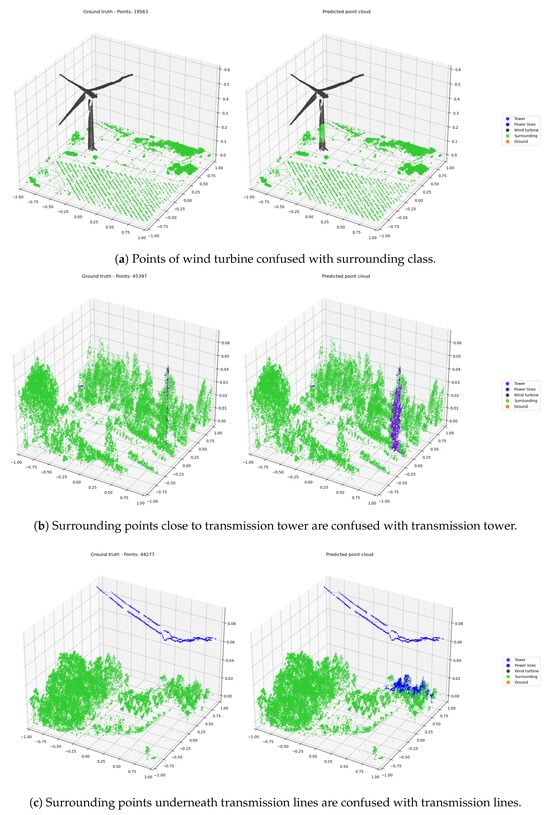
Figure 11.
Left: Ground truth|Right: Predictions. Errors arise when all points are fed into the network, causing confusion between objects and surrounding, especially in areas with high point density.
4.3.2. Inference on Sampled Point Clouds with Voting
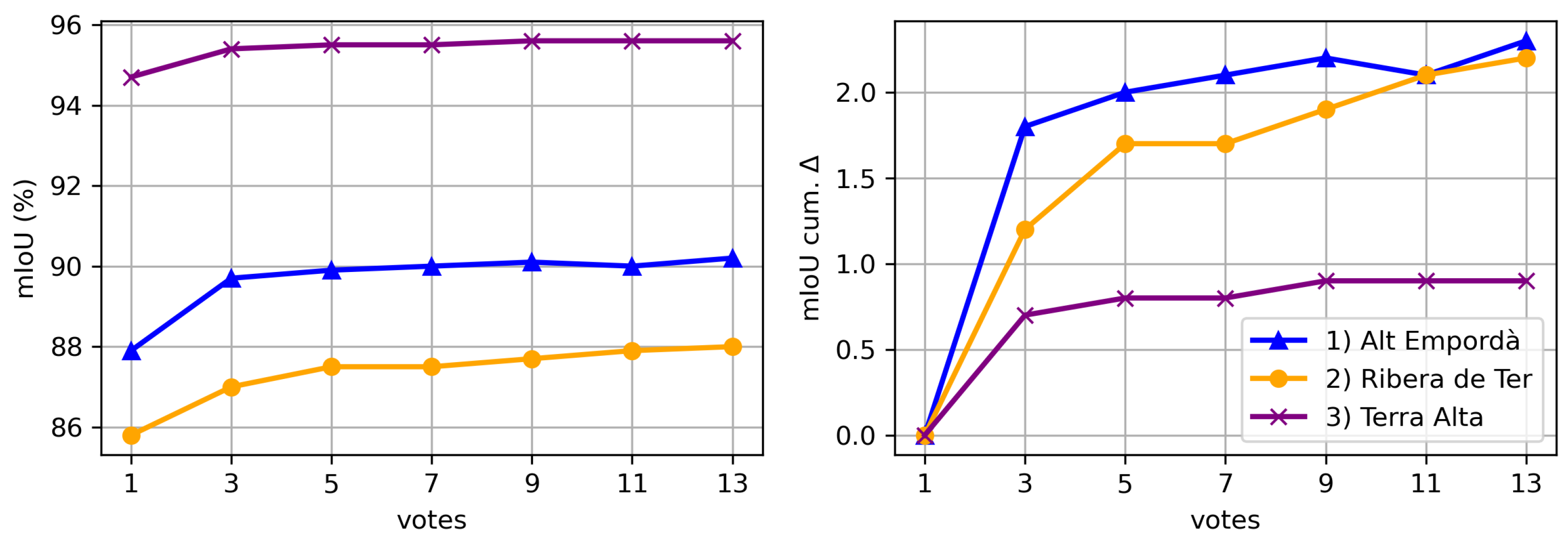
Figure 12 and Figure 13 illustrate the impact of varying the number of votes during point cloud segmentation on the resulting IoU. We can see that the influence of the voting strategy is more pronounced in the initial votes and gradually diminishes with additional votes.
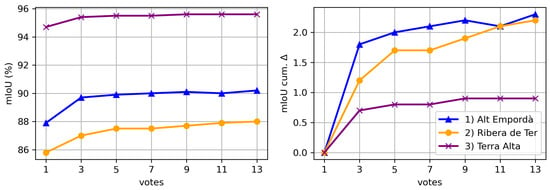
Figure 12.
mIoU (%) and cumulative mIoU gain per number of votes for each dataset. The “votes” axis represents the number of votes considered, ranging from 1 to 13. The mIoU value signifies the mean Intersection over Union across all classes for each dataset, while the cumulative mIoU indicates the incremental increase in mIoU per dataset with the addition of votes.
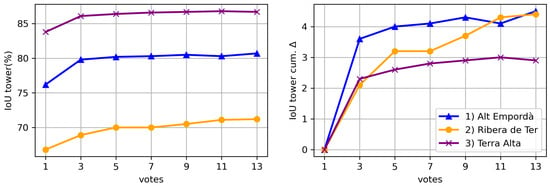
Figure 13.
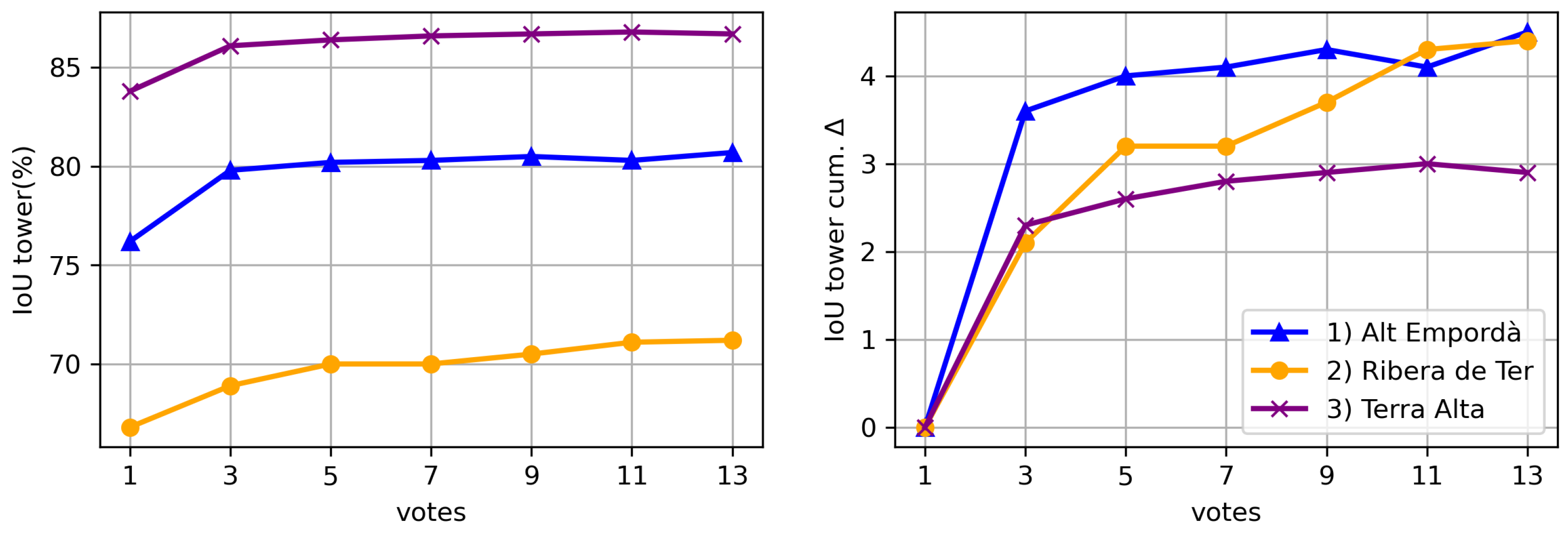
IoU tower (%) and cumulative IoU tower gain per number of votes for each dataset.
When focusing on the tower category (Figure 13), which is present in all utilized datasets, we see a considerable variability of IoU across datasets. This disparity may be attributed to the higher density and increased object detail in the Terra Alta dataset, which makes shapes more easily distinguishable compared to other datasets. In addition, the datasets exhibiting lower IoU experience greater benefit from the voting strategy.
4.3.3. Inference with Uncertainty-Based Sampling
We present a quantitative comparison of results obtained from voting against uncertainty-based sampling, focusing on mIoU per dataset, global mIoU, and execution time detailed in Table 10. The evaluation is conducted using sampled point clouds consisting of 8000 points. The voting strategy with 13 votes achieves the highest score on global mIoU (94.3%). However, this comes at a significant cost in terms of time, requiring 455 min for complete inference. In contrast, uncertainty-based sampling offers competitive mIoU scores with ten times lower inference time. Hence, if inference time is a priority, uncertainty-based sampling emerges as the optimal choice.

Table 10.
Quantitative comparison of mIoU (%) and execution time (minutes) obtained by different amount of votes versus using uncertainty-based sampling. All models are tested with sampled point clouds of 8 K points.
5. Results
In this section, we show the semantic segmentation results using the best training and inference strategies.
5.1. Quantitative Results
The IoU results across categories are presented in Table 11, comparing KPConv [11] against PointNet ++ [6] trained with improved training strategies and employing different inference methods specified by column "Inference Strategy". When all points are fed into PN++, the results are adversely affected by high-density objects, as discussed in the Section 4. Performance significantly improves when 8000-point sampled clouds are used. Additionally, as discussed in earlier sections, increasing the number of votes further raises IoU at the expense of longer inference times. To achieve the best balance of performance and practical inference time, PN++ with uncertainty-based sampling proves to be the optimal approach.

Table 11.
Comparison of IoU (%) per category and global mIoU (%) between KPConv and PN++ using different inference strategies.
Table 12 presents per-class IoU for each dataset using PN++ with uncertainty-based inference strategy. The class tower exhibits the lowest IoU, which can be attributed to the high variability in shapes and densities within this class. In contrast, the wind turbine class, which has far fewer points in the training and testing data, achieves a high IoU of 98.33 %, possibly due to its characteristic shape and size, making it easily distinguishable from other elements. Regarding mIoU across datasets, there are significant variations, with Ribera de Ter achieving the lowest score (88.13%) and Terra Alta attaining the highest (95.43%).

Table 12.
IoU scores (%) per category using uncertainty-based inference strategy and computation time in minutes per squared kilometer.
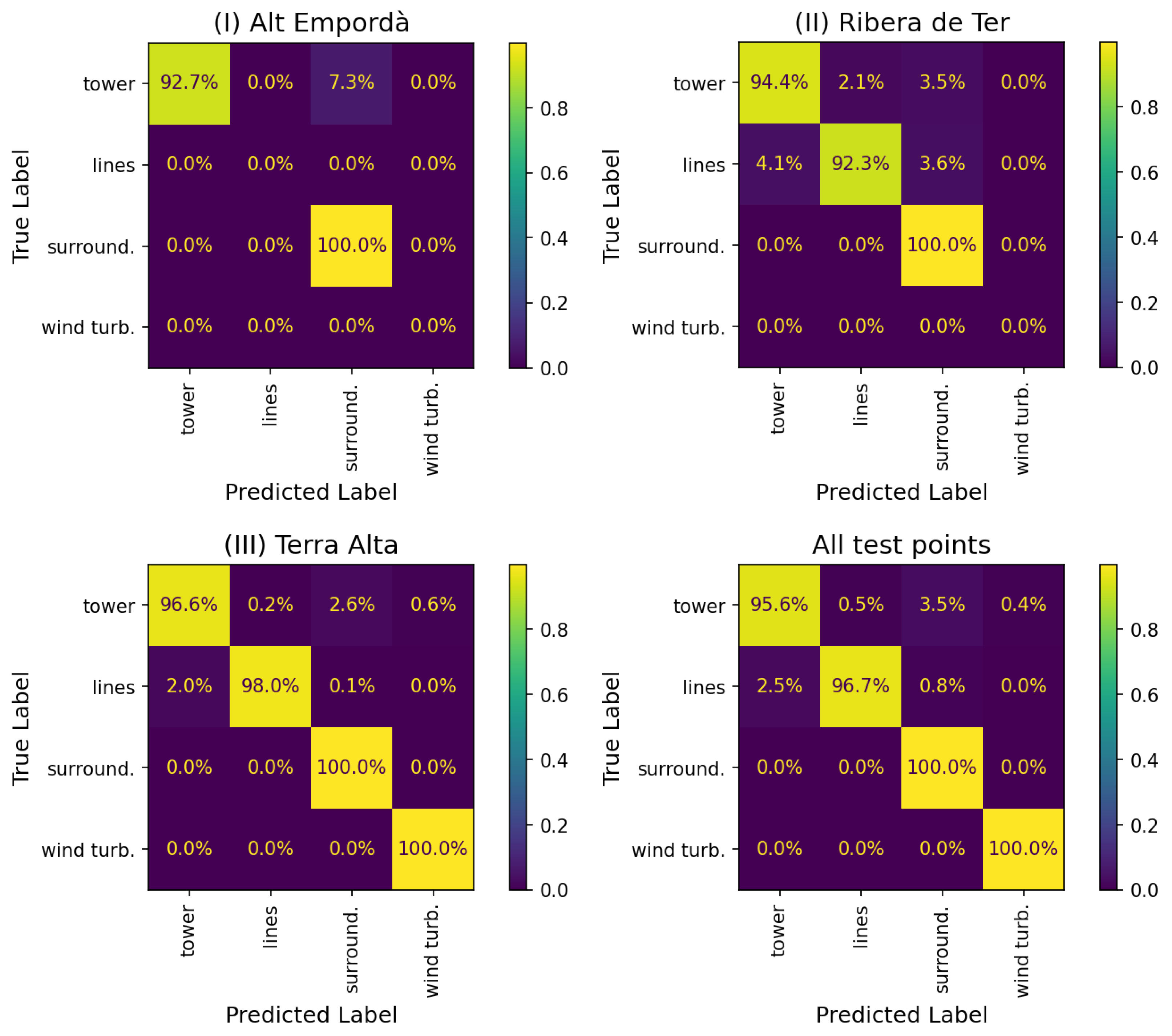
By looking at the normalized confusion matrices of Figure 14, we see that for the Alt Empordà dataset, some of the tower points are misclassified as vegetation, possibly due to the lower density of this dataset. Additionally there are no false positives of lines and wind turbines. For the Ribera de Ter dataset, which contains a lot of vegetation and lines with gaps resulting from the noise filtering process, we see confusion between towers, power lines, and vegetation. As expected, the Terra Alta dataset, which provides more detailed data, yields the best results.
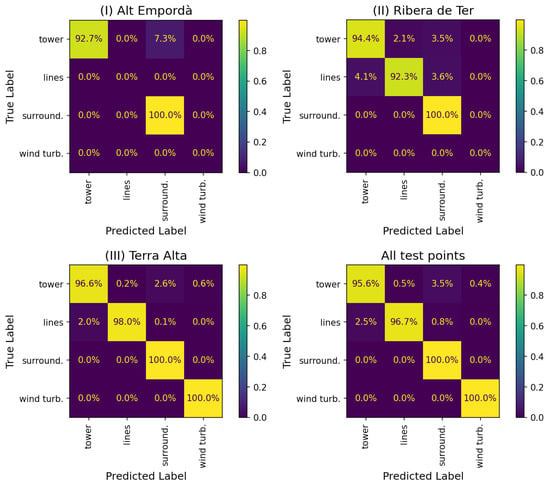
Figure 14.
Normalized confusion matrices using PN++ with uncertainty-based inference for each test dataset and across all test points.
5.2. Qualitative Results
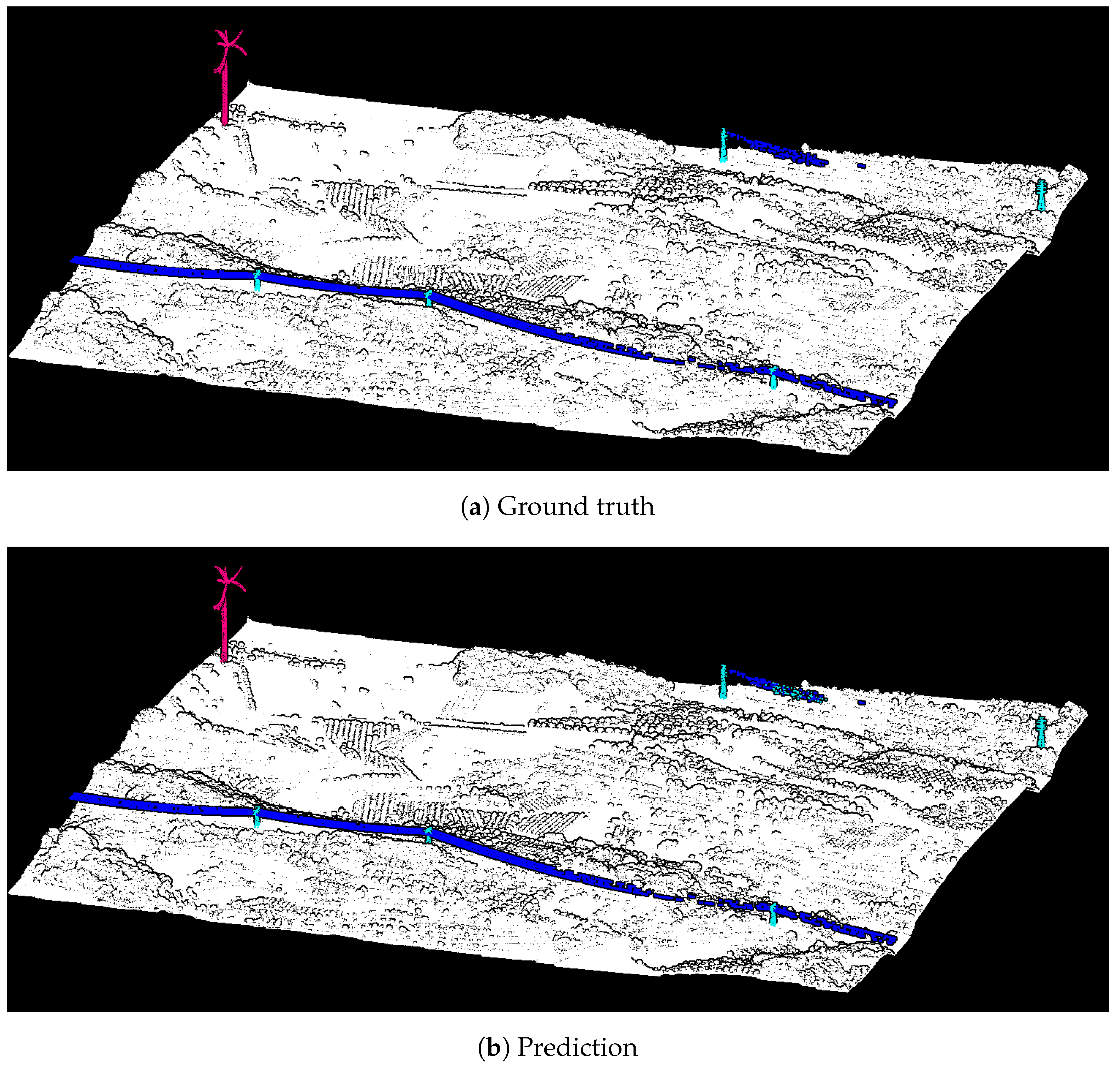
Figure 15 illustrates the ground truth and prediction for a LiDAR tile example from Terra Alta dataset, where each color represents a different class. The tower, wind turbine and surrounding classes are accurately classified. While most power lines are correctly identified, there are some points misclassified as towers. However, no false-positive points are detected within the vegetation.
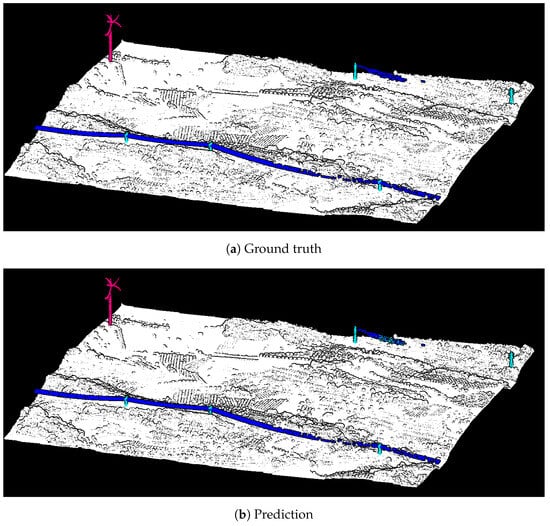
Figure 15.
Ground truth and predicted labels for a scene from Terra Alta dataset. Different colors identify different classes.
In Figure 16, we observe an example of a scene in RGB along with the corresponding predicted point cloud. Despite the absence of visible lines between towers and their small size compared to high-voltage towers, the model has successfully detected them, showcasing its robustness across a diverse range of scenarios.
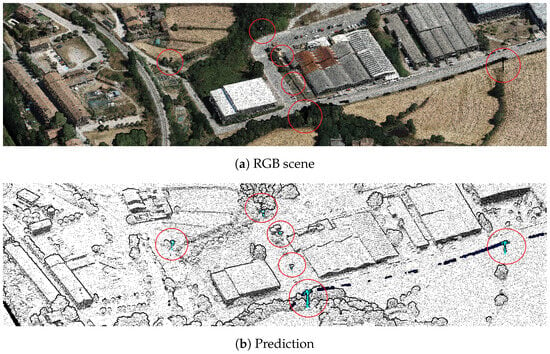
Figure 16.
Point cloud scene from Ribera de Ter dataset, colorized by RGB, along with its corresponding semantic segmentation predictions. Towers classified by the model are highlighted and marked with a red circle for easy identification.
Next, we illustrate the failure cases identified in our method. Figure 17 showcases the model’s limitation in accurately distinguishing between towers and power lines for the given instance, resulting in some tower points being misclassified as power lines. This misclassification can be attributed to the structural similarities and spatial proximity of towers and power lines, which can confuse the model. Such a limitation should be taken into account, particularly if the final task requires precise delineation of power lines.
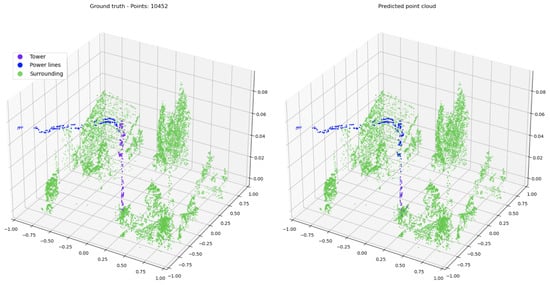
Figure 17.
Ground truth (left) and model predictions (right), illustrating the challenge in distinguishing between towers and power lines due to shared structural characteristics and close spatial proximity. Note that the cables are not straight because z is normalized to height above ground.
We identify false positives of towers, as shown in Figure 18, which can occur due to objects with similar attributes to towers, such as comparable height, shape, or reflective properties. For example, vertical structures like poles might be incorrectly identified as towers.
Figure 18.
Detection of a false positive resembling a pole within the tower class.
Finally, Figure 19 presents an instance of a transmission tower that has not been fully classified. Upon deeper inspection, we determine that this is caused by high NDVI values on misclassified points. The issue arises from the fact that towers and lines are not fully captured in the photogrammetric images, which is attributed to the size of the elements to be detected and the GSD obtained in the aerial survey, as well as potential occlusions and shadows from other objects. Consequently, during the process of assigning color information from the photogrammetric images to the corresponding LiDAR points, values from the surrounding vegetation may be mistakenly assigned to the location of the object. To provide visual clarity, Figure 20 showcases a point cloud colorized by NDVI. The central structure in the point cloud contains a tower with low NDVI values, as expected for non-vegetative structures. Surrounding the tower are points colored in shades of green, indicating the presence of vegetation. Nevertheless, the cross-arms of the transmission tower also show high NDVI values, likely due to the color assignment process.
Figure 19.
Illustration of a transmission tower that remains incompletely classified due to high NDVI values on misclassified points.

Figure 20.
Visualization of a point cloud colorized by NDVI, highlighting points that exceed the threshold of 0.2 in green. The transmission tower surrounded by vegetation exhibits low NDVI values, which are consistent with non-vegetative structures, contrasted with elevated NDVI values on the tower’s cross-arms, likely due to the color assignment process.
5.3. Results on Out-of-Domain Data
This section presents quantitative and qualitative results obtained from an OOD area that was not part of the training dataset. This area includes towers and power lines and is surrounded by vegetation and buildings. The IoU for each class is shown in Table 13. The tower category achieves an IoU of 89.48%, indicating robust classification accuracy in vegetated environments. Similarly, the power lines exhibit outstanding performance with an IoU of 97.55%, demonstrating the effectiveness of our approach in accurately delineating fine structures against diverse backgrounds. In addition, Figure 21 illustrates the predicted labels of a scene containing a transmission line. Despite some gaps in the transmission line and close vegetation around the tower, both the tower and cables are accurately classified. The ground class is predicted but is not included in the evaluation.

Table 13.
Iou scores (%) per category obtained using the uncertainty-based inference strategy on OOD data, along with the computation time in minutes per square kilometer.
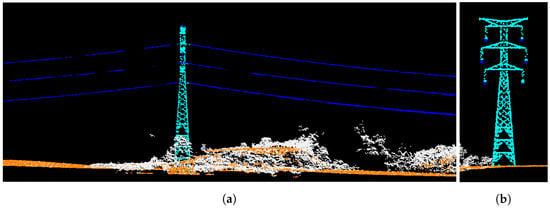
Figure 21.
Longitudinal (a) and transversal (b) profiles of a point cloud with a power line from OOD data, displaying predicted labels with different colors.
6. Conclusions
Our study advances the field of semantic segmentation for ALS data, presenting two key scientific contributions to address the complexities of outdoor environments characterized by imbalanced data distributions. Our first contribution focuses on refining training and inference strategies to boost the performance of point classification networks like PointNet++. The study involves several experiments conducted on a 247 km2 manually labeled airborne LiDAR dataset, which is characterized by both densely forested and urban environments with distinct labeled objects. Our findings indicate that utilizing improved training techniques and feeding sampled point clouds into the network significantly outperforms the common approach of processing entire point clouds. This approach not only reduces the computational load but also mitigates confusion between closely located objects.
Our second contribution introduces an uncertainty-based inference strategy to enhance network robustness, particularly for objects in cluttered environments. This approach has been rigorously tested across three distinct geographical sites, each with unique attributes, improving the IoU for minority classes up to +2.9%. The obtained mean IoU across datasets is 94.24%, with specific scores of 82.66% IoU for transmission towers, 95.97% IoU for power lines, and 98.33% IoU for wind turbines. Additionally, the robustness of the model is validated on out-of-domain data, maintaining a high mean IoU of 94.33% despite varying conditions.
Overall, these advancements result in significant improvements both quantitatively and qualitatively in the segmentation of ALS data, suggesting valuable applications in areas such as infrastructure monitoring and urban planning. The presented strategies could be applied to other architectures, offering potential advancements in classification methodologies for real-world scenarios.
The source code in PyTorch as well as the trained models are available at https://github.com/marionacaros/Strategies-for-Point-Classification-in-LiDAR-Scenes (accessed on 1 June 2024).
Author Contributions
Conceptualization, M.C., A.J., S.S. and J.V.; software, M.C.; validation, M.C. and A.J.; data curation, M.C. and A.J.; writing—original draft preparation, M.C.; writing—review and editing, M.C., A.J., S.S. and J.V.; visualization, M.C.; supervision, A.J., S.S. and J.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by an Industrial Doctorate grant 2021DI41 of AGAUR (Generalitat de Catalunya) between Universitat de Barcelona and Institut Cartogràfic i Geològic de Catalunya and PID2022-136436NB-I00, 2021SGR01104 grants. The LiDARCAT3 project, which involves data acquisition, was funded through the European Next-Generation funds as part of the Recovery, Transformation, and Resilience Plan, which is affiliated with the Ministerio para la Transición Ecológica y el Reto Demográfico (MITECO), and coordinated by the IGN (Instituto Geográfico Nacional).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study will be available on request from the ICGC for research purposes.
Acknowledgments
The authors acknowledge “Doctorats Industrials” for the financial support and ICGC for providing the data. M. Carós expresses gratitude to D. Santos and S. Valverde for their meticulous manual labeling of the LiDAR data and E. Delgado for their expertise in geoprocessing. Additionally, sincere appreciation is extended to L. Carós and A. Bozal for their technical support and insightful feedback.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 2D | Two-dimensional. |
| 3D | Three-dimensional. |
| ALS | Airborne Laser Scanning. |
| CNN | Convolution Neural Network. |
| CS | Constrained Sampling. |
| DALES | Dayton Annotated LiDAR Earth Scan. |
| FN | False Negatives. |
| FP | False Positives. |
| FPS | Farthest Point Sampling. |
| GSD | Ground Sample Distance. |
| ICGC | Cartographic and Geological Institute of Catalonia. |
| IDIS | Inverse Density Importance Sampling. |
| IoU | Intersection Over Union. |
| KNN | K-Nearest Neighbors. |
| LiDAR | Light Detection and Ranging. |
| mIoU | mean Intersection Over Union. |
| MLP | Multi-Layer Perceptron. |
| NIR | Near InfraRed. |
| NDVI | Normalized Difference Vegetation Index. |
| OOD | Out-of-Domain. |
| OA | Overall Accuracy. |
| RGB | Red Green Blue. |
| TP | True Positives. |
References
- Megahed, Y.; Shaker, A.; Yan, W.Y. Fusion of airborne LiDAR point clouds and aerial images for heterogeneous land-use urban mapping. Remote Sens. 2021, 13, 814. [Google Scholar] [CrossRef]
- Michałowska, M.; Rapiński, J. A review of tree species classification based on airborne LiDAR data and applied classifiers. Remote Sens. 2021, 13, 353. [Google Scholar] [CrossRef]
- Štular, B.; Lozić, E.; Eichert, S. Airborne LiDAR-derived digital elevation model for archaeology. Remote Sens. 2021, 13, 1855. [Google Scholar] [CrossRef]
- Mandlburger, G.; Wenzel, K.; Spitzer, A.; Haala, N.; Glira, P.; Pfeifer, N. Improved topographic models via concurrent airborne LiDAR and dense image matching. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 259–266. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Xie, Y.; Tian, J.; Zhu, X.X. Linking points with labels in 3D: A review of point cloud semantic segmentation. IEEE Geosci. Remote Sens. Mag. 2020, 8, 38–59. [Google Scholar] [CrossRef]
- Chen, J.; Kakillioglu, B.; Velipasalar, S. Background-aware 3-D point cloud segmentation with dynamic point feature aggregation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5703112. [Google Scholar] [CrossRef]
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Deep learning on 3D point clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 16259–16268. [Google Scholar]
- Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.; Elhoseiny, M.; Ghanem, B. Pointnext: Revisiting pointnet++ with improved training and scaling strategies. Adv. Neural Inf. Process. Syst. 2022, 35, 23192–23204. [Google Scholar]
- Goyal, A.; Law, H.; Liu, B.; Newell, A.; Deng, J. Revisiting point cloud shape classification with a simple and effective baseline. In Proceedings of the International Conference on Machine Learning. PMLR, Virtual Event, 18–24 July 2021; pp. 3809–3820. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. arXiv 2015, arXiv:1512.00567. [Google Scholar]
- Müller, R.; Kornblith, S.; Hinton, G.E. When does label smoothing help? Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-bert: Pre-training 3d point cloud transformers with masked point modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 19313–19322. [Google Scholar]
- Kankare, V.; Vastaranta, M.; Holopainen, M.; Räty, M.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Viitala, R. Retrieval of forest aboveground biomass and stem volume with airborne scanning LiDAR. Remote Sens. 2013, 5, 2257–2274. [Google Scholar] [CrossRef]
- Martín-Alcón, S.; Coll, L.; De Cáceres, M.; Guitart, L.; Cabré, M.; Just, A.; González-Olabarría, J.R. Combining aerial LiDAR and multispectral imagery to assess postfire regeneration types in a Mediterranean forest. Can. J. For. Res. 2015, 45, 856–866. [Google Scholar] [CrossRef]
- Tanhuanpää, T.; Vastaranta, M.; Kankare, V.; Holopainen, M.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Raisio, J. Mapping of urban roadside trees–A case study in the tree register update process in Helsinki City. Urban For. Urban Green. 2014, 13, 562–570. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and multi-view cnns for object classification on 3d data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5648–5656. [Google Scholar]
- Roveri, R.; Rahmann, L.; Oztireli, C.; Gross, M. A network architecture for point cloud classification via automatic depth images generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4176–4184. [Google Scholar]
- Graham, B.; Van der Maaten, L. Submanifold sparse convolutional networks. arXiv 2017, arXiv:1706.01307. [Google Scholar]
- Wang, P.S.; Liu, Y.; Guo, Y.X.; Sun, C.Y.; Tong, X. O-cnn: Octree-based convolutional neural networks for 3d shape analysis. Acm. Trans. Graph. 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Tang, H.; Liu, Z.; Zhao, S.; Lin, Y.; Lin, J.; Wang, H.; Han, S. Searching efficient 3d architectures with sparse point-voxel convolution. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 685–702. [Google Scholar]
- Liu, Z.; Tang, H.; Lin, Y.; Han, S. Point-voxel cnn for efficient 3d deep learning. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Hu, J.S.; Kuai, T.; Waslander, S.L. Point density-aware voxels for lidar 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8469–8478. [Google Scholar]
- Duan, Y.; Zheng, Y.; Lu, J.; Zhou, J.; Tian, Q. Structural relational reasoning of point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 949–958. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8895–8904. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Nezhadarya, E.; Taghavi, E.; Razani, R.; Liu, B.; Luo, J. Adaptive hierarchical down-sampling for point cloud classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 12956–12964. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-scale point cloud semantic segmentation with superpoint graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Feng, M.; Zhang, L.; Lin, X.; Gilani, S.Z.; Mian, A. Point attention network for semantic segmentation of 3D point clouds. Pattern Recognit. 2020, 107, 107446. [Google Scholar] [CrossRef]
- Park, C.; Jeong, Y.; Cho, M.; Park, J. Fast point transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16949–16958. [Google Scholar]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D semantic parsing of large-scale indoor spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar]
- Wu, W.; Qi, Z.; Fuxin, L. Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9621–9630. [Google Scholar]
- Groh, F.; Wieschollek, P.; Lensch, H.P. Flex-Convolution: Million-scale point-cloud learning beyond grid-worlds. In Asian Conference on Computer Vision; Springer: Cham, Switzerland, 2018; pp. 105–122. [Google Scholar]
- Caros, M.; Just, A.; Segui, S.; Vitria, J. Object Segmentation of Cluttered Airborne LiDAR Point Clouds. Artif. Intell. Res. Dev. 2022, 356, 259–268. [Google Scholar]
- Carós, M.; Just, A.; Seguí, S.; Vitrià, J. Self-Supervised Pre-Training Boosts Semantic Scene Segmentation on LiDAR data. In Proceedings of the 2023 18th International Conference on Machine Vision and Applications (MVA), Hamamatsu, Japan, 23–25 July 2023; pp. 1–6. [Google Scholar]
- Chen, Y.; Hu, V.T.; Gavves, E.; Mensink, T.; Mettes, P.; Yang, P.; Snoek, C.G. Pointmixup: Augmentation for point clouds. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part III 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 330–345. [Google Scholar]
- Kim, S.; Lee, S.; Hwang, D.; Lee, J.; Hwang, S.J.; Kim, H.J. Point cloud augmentation with weighted local transformations. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual Conference, 11–17 October 2021; pp. 548–557. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Pettorelli, N. The Normalized Difference Vegetation Index; Oxford University Press: Oxford, MI, USA, 2013. [Google Scholar]
- Varney, N.; Asari, V.K.; Graehling, Q. DALES: A large-scale aerial LiDAR data set for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 186–187. [Google Scholar]
- Zhang, Z.; Sabuncu, M. Generalized cross entropy loss for training deep neural networks with noisy labels. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).