Enhancing Seasonal PM2.5 Estimations in China through Terrain–Wind–Rained Index (TWRI): A Geographically Weighted Regression Approach
Abstract
1. Introduction
2. Materials and Method
2.1. Materials
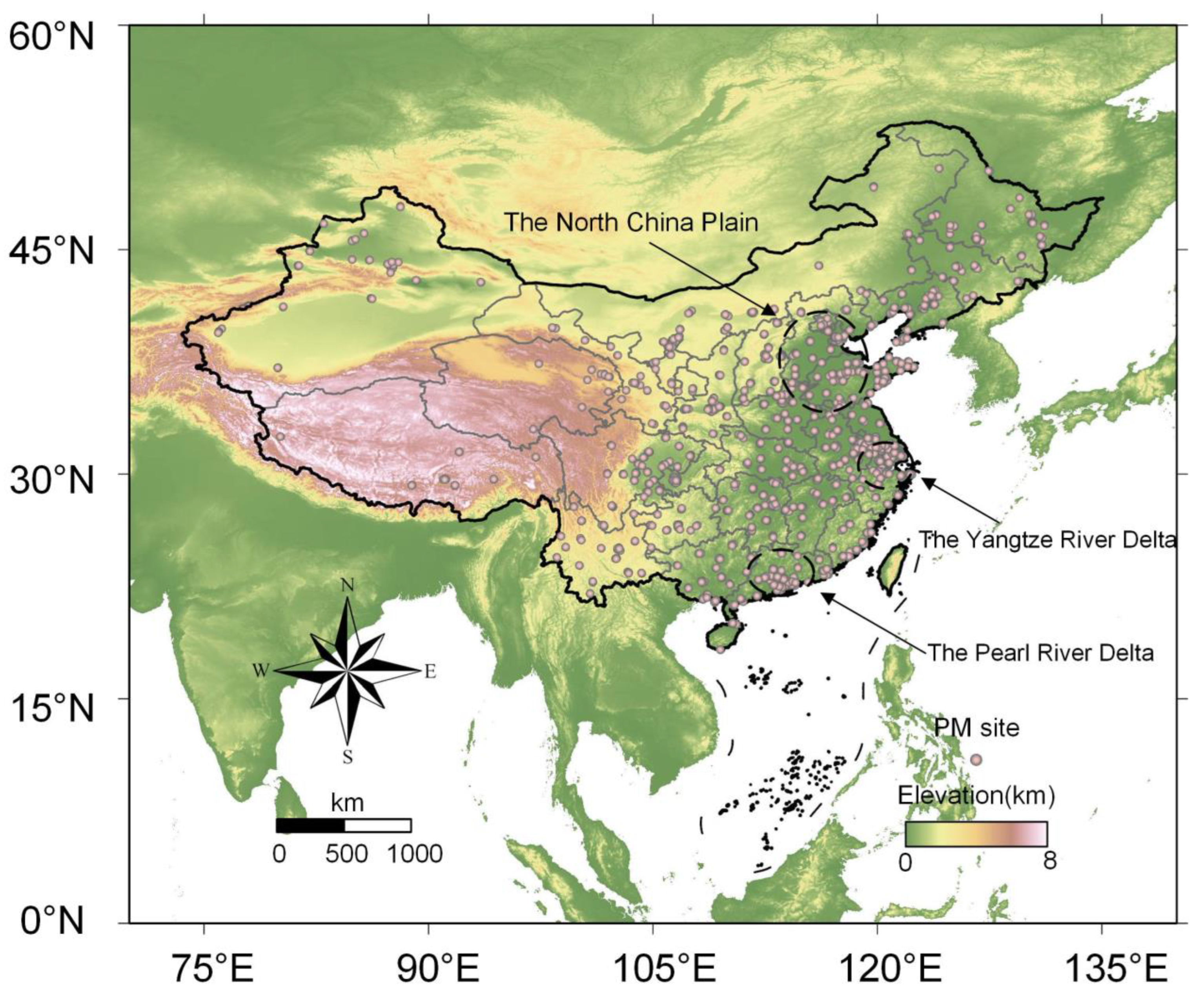
2.1.1. Site-Based PM2.5 Levels
2.1.2. MODIS AOD
2.1.3. Meteorological Factors
2.1.4. Digital Elevation Model
2.1.5. Data Processing
2.2. Method
2.2.1. The Construction of TWRI
2.2.2. Geographically Weighted Regression Model (GWR)
3. Results
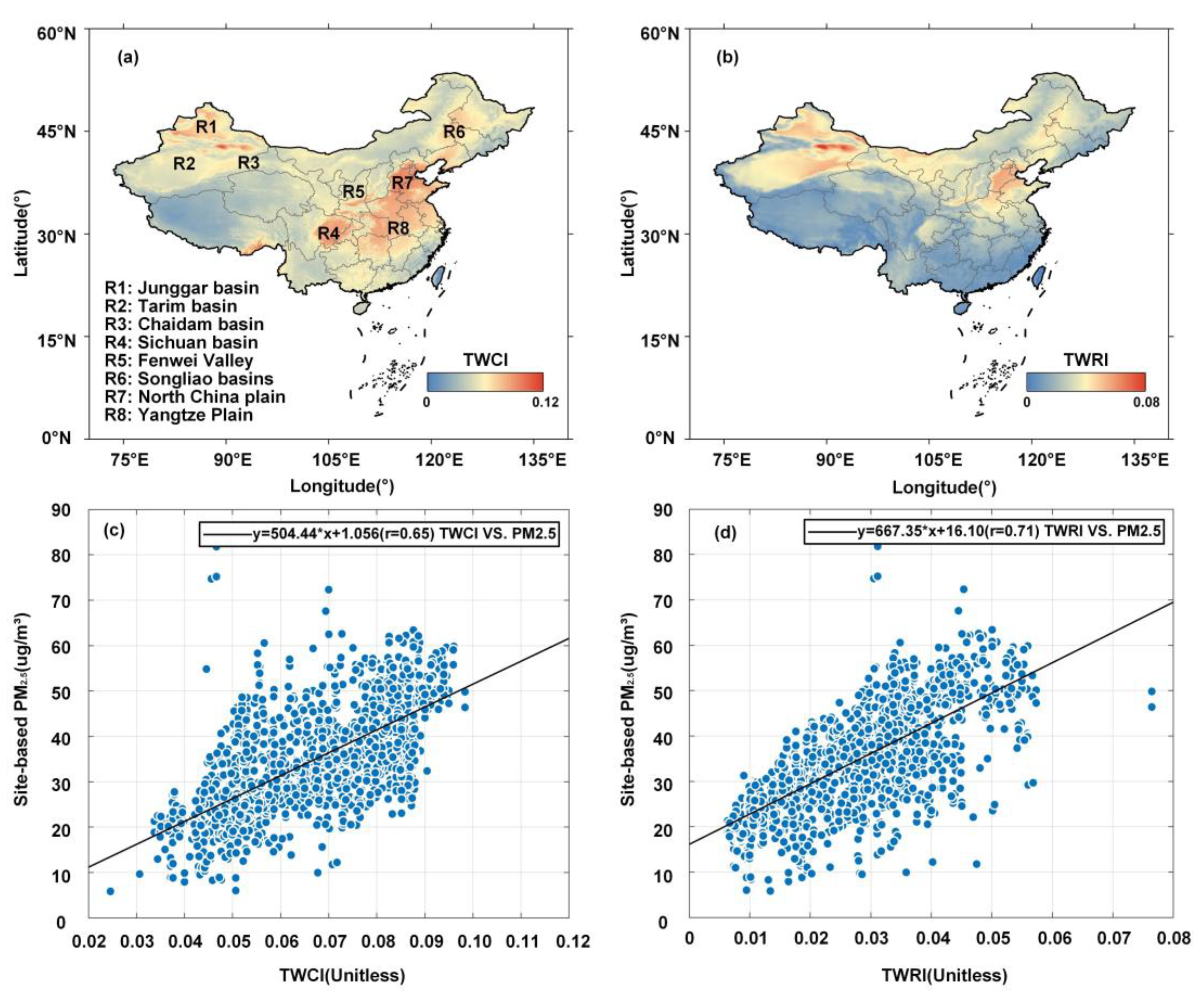
3.1. Comparison between TWRI and TWCI
3.1.1. Comparison between Annual TWRI and TWCI
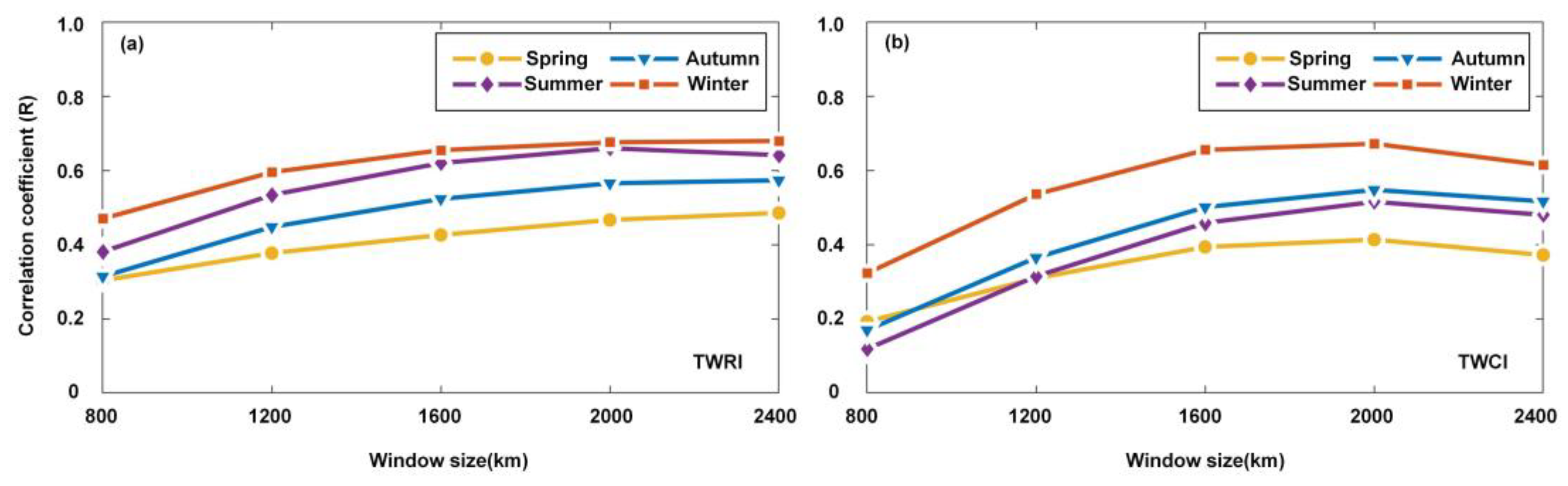
3.1.2. Comparison between Seasonal TWRI and TWCI
3.2. PM2.5 Estimation
3.2.1. Descriptive Statistics
3.2.2. Model Fitting and Validation
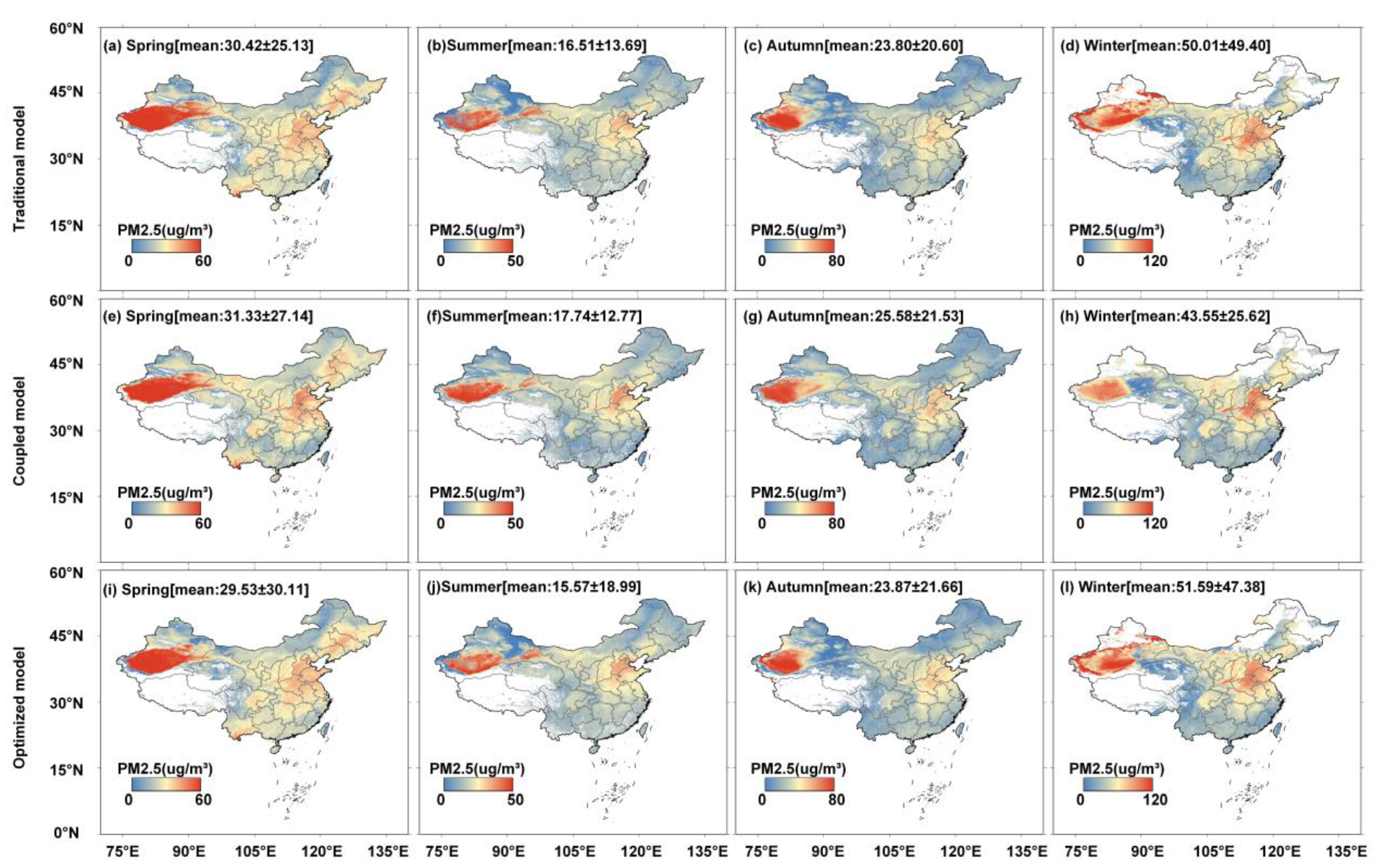
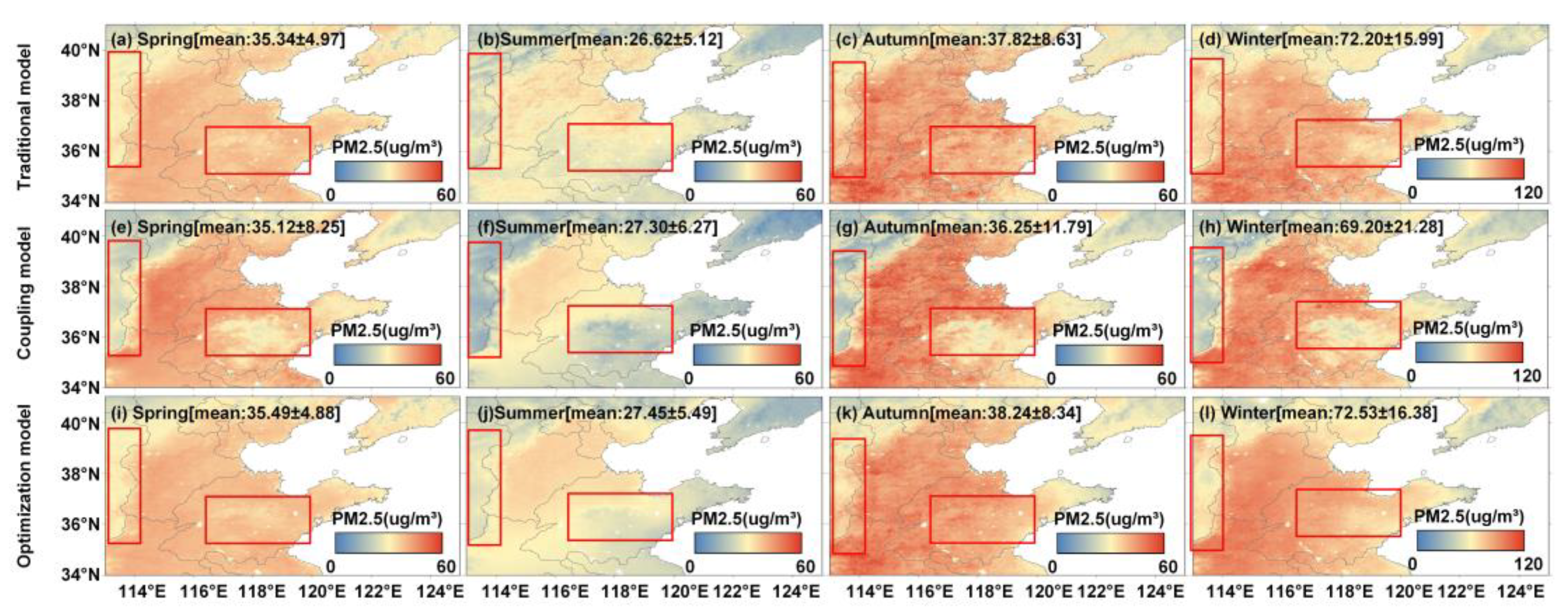
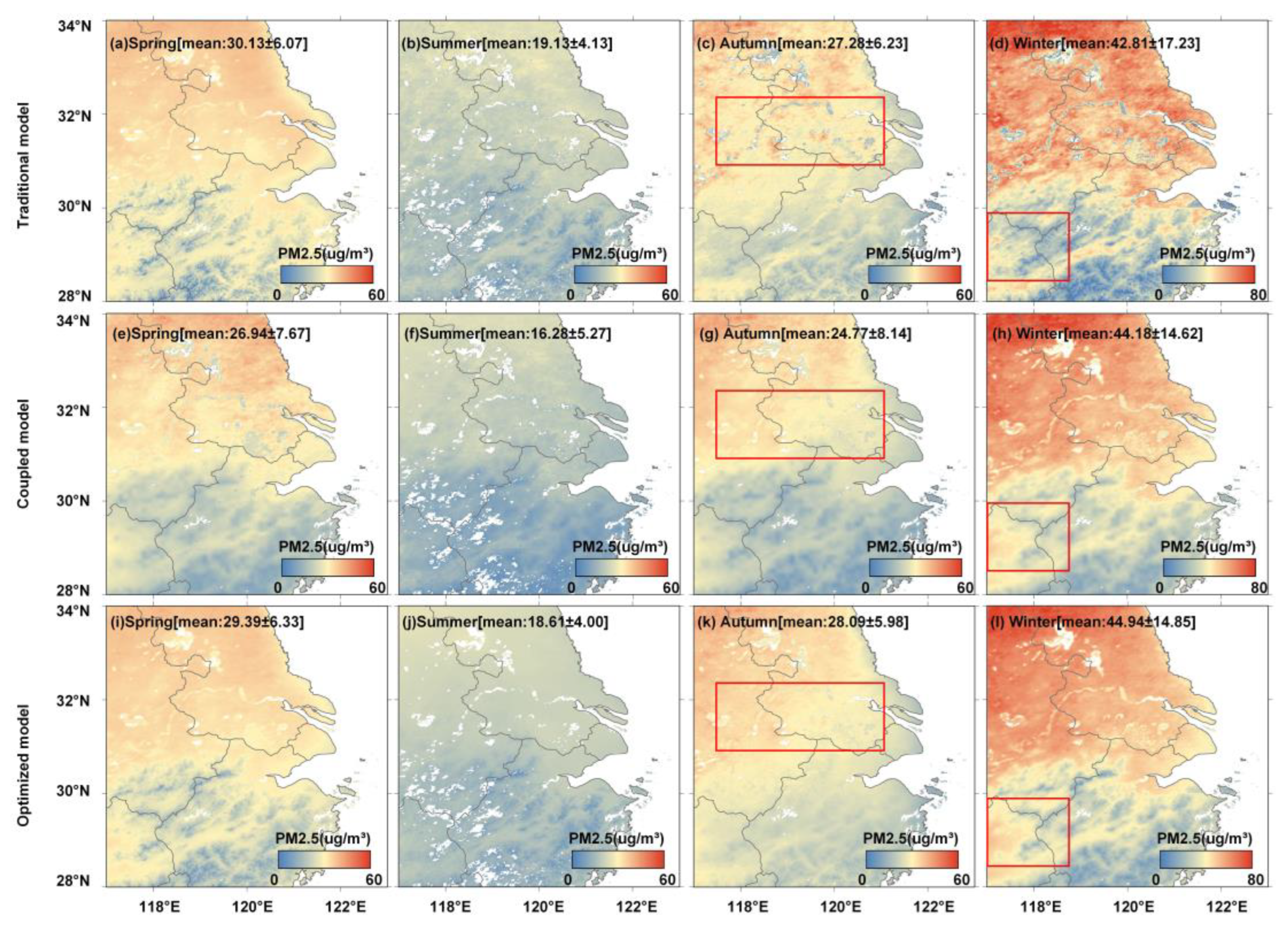
3.2.3. PM2.5 Spatial Distribution
3.2.4. Regional PM2.5
- (1)
- North China Plain
- (2)
- Pearl River Delta
- (3)
- Yangtze River Delta
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yin, P.; Brauer, M.; Cohen, A.J.; Wang, H.D.; Li, J.; Burnett, R.T.; Stanaway, J.D.; Causey, K.; Larson, S.; Godwin, W.; et al. The effect of air pollution on deaths, disease burden, and life expectancy across China and its provinces, 1990-2017: An analysis for the Global Burden of Disease Study 2017. Lancet Planet. Health 2020, 4, E386–E398. [Google Scholar] [CrossRef] [PubMed]
- Steffen, W.; Richardson, K.; Rockström, J.; Cornell, S.E.; Fetzer, I.; Bennett, E.M.; Biggs, R.; Carpenter, S.R.; de Vries, W.; de Wit, C.A.; et al. Planetary boundaries: Guiding human development on a changing planet. Science 2015, 347, 1259855. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R.; et al. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef] [PubMed]
- Dominici, F.; Peng, R.D.; Bell, M.L.; Pham, L.; McDermott, A.; Zeger, S.L.; Samet, J.M. Fine particulate air pollution and hospital admission for cardiovascular and respiratory diseases. JAMA-J. Am. Med. Assoc. 2006, 295, 1127–1134. [CrossRef]
- Liu, C.; Hu, H.; Zhou, S.; Chen, X.L.; Hu, Y.T.; Hu, J.L. Change of Composition, Source Contribution, and Oxidative Effects of Environmental PM2.5 in the Respiratory Tract. Environ. Sci. Technol. 2023, 57, 11605–11611. [Google Scholar] [CrossRef] [PubMed]
- Shu, Z.; Zhao, T.; Liu, Y.; Zhang, L.; Ma, X.; Kuang, X.; Li, Y.; Huo, Z.; Ding, Q.; Sun, X.; et al. Impact of deep basin terrain on PM(2.5) distribution and its seasonality over the Sichuan Basin, Southwest China. Environ. Pollut. 2022, 300, 118944. [Google Scholar] [CrossRef] [PubMed]
- Qi, L.; Zheng, H.; Ding, D.; Ye, D.; Wang, S. Effects of Meteorology Changes on Inter-Annual Variations of Aerosol Optical Depth and Surface PM2.5 in China—Implications for PM2.5 Remote Sensing. Remote Sens. 2022, 14, 2762. [Google Scholar] [CrossRef]
- Zhai, S.X.; Jacob, D.J.; Wang, X.; Shen, L.; Li, K.; Zhang, Y.Z.; Gui, K.; Zhao, T.L.; Liao, H. Fine particulate matter (PM2.5) trends in China, 2013–2018: Separating contributions from anthropogenic emissions and meteorology. Atmos. Chem. Phys. 2019, 19, 11031–11041. [Google Scholar] [CrossRef]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.T.; Zhang, M.; Qian, X.Y.; Li, C.R.; Chen, S.; Wang, W.W. Using the geographical detector technique to explore the impact of socioeconomic factors on PM2.5 concentrations in China. J. Clean. Prod. 2019, 211, 1480–1490. [Google Scholar] [CrossRef]
- Liu, B.; Ma, X.; Ma, Y.; Li, H.; Jin, S.; Fan, R.; Gong, W. The relationship between atmospheric boundary layer and temperature inversion layer and their aerosol capture capabilities. Atmos. Res. 2022, 271, 106121. [Google Scholar] [CrossRef]
- Chen, X.; Ye, J. When the wind blows: Spatial spillover effects of urban air pollution in China. J. Environ. Plan. Manag. 2018, 62, 1359–1376. [Google Scholar] [CrossRef]
- Liu, B.Y.; Wang, L.L.; Zhang, L.; Bai, K.X.; Chen, X.F.; Zhao, G.N.; Yin, H.T.; Chen, N.; Li, R.; Xin, J.Y.; et al. Evaluating urban and nonurban PM2.5 variability under clean air actions in China during 2010-2022 based on a new high-quality dataset. Int. J. Digit. Earth 2024, 17, 2310734. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, Y.X.; Tong, D.; Shao, M.; Wang, S.X.; Zhang, Y.H.; Xu, X.D.; Wang, J.N.; He, H.; Liu, W.Q.; et al. Drivers of improved PM2.5 air quality in China from 2013 to 2017. Proc. Natl. Acad. Sci. USA 2019, 116, 24463–24469. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-L.; Cao, F. Fine particulate matter (PM2.5) in China at a city level. Sci. Rep. 2015, 5, 14884. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.M.; Zdanski, C.; Farkas, D.; Bang, J.; Williams, H. Evaluation of Aerosol Optical Depth (AOD) and PM2.5 associations for air quality assessment. Remote Sens. Appl.-Soc. Environ. 2020, 20, 100396. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Q.; Yue, L.; Li, T.; Shen, H.; Zhang, L. The relationships between PM2.5 and aerosol optical depth (AOD) in mainland China: About and behind the spatio-temporal variations. Environ. Pollut. 2019, 248, 526–535. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Wang, W.; Wang, N.; Chen, B. A New Algorithm for Himawari-8 Aerosol Optical Depth Retrieval by Integrating Regional PM₂.₅ Concentrations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4106711. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Q.; Yue, L.; Li, T. Investigation of the spatially varying relationships of PM2.5 with meteorology, topography, and emissions over China in 2015 by using modified geographically weighted regression. Environ. Pollut. 2020, 262, 114257. [Google Scholar] [CrossRef] [PubMed]
- Hammer, M.S.; van Donkelaar, A.; Li, C.; Lyapustin, A.; Sayer, A.M.; Hsu, N.C.; Levy, R.C.; Garay, M.J.; Kalashnikova, O.V.; Kahn, R.A.; et al. Global Estimates and Long-Term Trends of Fine Particulate Matter Concentrations (1998–2018). Environ. Sci. Technol. 2020, 54, 7879–7890. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.T.; Tang, J.Y.; Zhou, X.L.; Li, P.; Liu, Z.L.; Zhang, C.C.; Zou, Z.Y.; Li, T.; Peng, C.H. Research progress, challenges, and prospects of PM2.5 concentration estimation using satellite data. Environ. Rev. 2023, 31, 605–631. [Google Scholar] [CrossRef]
- Wang, W.; Mao, F.; Du, L.; Pan, Z.; Gong, W.; Fang, S. Deriving Hourly PM2.5 Concentrations from Himawari-8 AODs over Beijing–Tianjin–Hebei in China. Remote Sens. 2017, 9, 858. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, L.; Qin, K.; Zhang, Y.; Shen, Y.; Zhou, Y. A Geographically and Temporally Weighted Regression Model for Ground-Level PM2.5 Estimation from Satellite-Derived 500 m Resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef]
- He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Song, S.; Gao, M.; Xu, W.; Sun, Y.; Worsnop, D.R.; Jayne, J.T.; Zhang, Y.; Zhu, L.; Li, M.; Zhou, Z.; et al. Possible heterogeneous chemistry of hydroxymethanesulfonate (HMS) in northern China winter haze. Atmos. Chem. Phys. 2019, 19, 1357–1371. [Google Scholar] [CrossRef]
- Ning, G.; Wang, S.; Ma, M.; Ni, C.; Shang, Z.; Wang, J.; Li, J. Characteristics of air pollution in different zones of Sichuan Basin, China. Sci. Total Environ. 2018, 612, 975–984. [Google Scholar] [CrossRef] [PubMed]
- Karle, N.N. Studies of the Planetary Boundary Layer and their Impact on Air Pollution in a Semi-Arid Region with Complex Terrain; The Unisversity of Texas: El Paso, TX, USA, 2021. [Google Scholar]
- Tang, Y.; Xie, S.; Huang, L.; Liu, L.; Wei, P.; Zhang, Y.; Meng, C. Spatial Estimation of Regional PM2.5 Concentrations with GWR Models Using PCA and RBF Interpolation Optimization. Remote Sens. 2022, 14, 5626. [Google Scholar] [CrossRef]
- Ding, W.; Zhu, Y. Prediction of PM2.5 Concentration in Ningxia Hui Autonomous Region Based on PCA-Attention-LSTM. Atmosphere 2022, 13, 1444. [Google Scholar] [CrossRef]
- Zhang, T.; Zang, L.; Wan, Y.; Wang, W.; Zhang, Y. Ground-level PM2.5 estimation over urban agglomerations in China with high spatiotemporal resolution based on Himawari-8. Sci. Total Environ. 2019, 676, 535–544. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Xie, B.; Wang, W. Quantifying the impact of terrain–wind–governed close-effect on atmospheric polluted concentrations. J. Clean. Prod. 2022, 367, 132995. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y. MCD19A2 MODIS/Terra+Aqua Land Aerosol Optical Depth Daily L2G Global 1 km SIN Grid V006. [Dataset], NASA EOSDIS Land Processes DAAC, 2018. Available online: https://lpdaac.usgs.gov/products/mcd19a2v006/ (accessed on 9 June 2024).
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Schnell, J.L.; Naik, V.; Horowitz, L.W.; Paulot, F.; Mao, J.; Ginoux, P.; Zhao, M.; Ram, K. Exploring the relationship between surface PM2.5 and meteorology in Northern India. Atmos. Chem. Phys. 2018, 18, 10157–10175. [Google Scholar] [CrossRef]
- Liu, S.; Xing, J.; Sahu, S.K.; Liu, X.; Liu, S.; Jiang, Y.; Zhang, H.; Li, S.; Ding, D.; Chang, X. Wind-blown dust and its impacts on particulate matter pollution in Northern China: Current and future scenarios. Environ. Res. Lett. 2021, 16, 114041. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, X.; Zhao, T.; Gong, S.; Xu, X.; Li, Y.; Luo, L.; Gui, K.; Wang, H.; Zheng, Y.; et al. A modelling study of the terrain effects on haze pollution in the Sichuan Basin. Atmos. Environ. 2019, 196, 77–85. [Google Scholar] [CrossRef]
- Oshan, T.M.; Smith, J.P.; Fotheringham, A.S. Targeting the spatial context of obesity determinants via multiscale geographically weighted regression. Int. J. Health Geogr. 2020, 19, 11. [Google Scholar] [CrossRef]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]





| Variable Name | Source | Spatial Resolution | Temporal Resolution | Unit |
|---|---|---|---|---|
| Wind speed | ERA5 | 0.25° × 0.25° | 1 month | m/s |
| Wind direction | ERA5 | 0.25° × 0.25° | 1 month | ° |
| Boundary layer height | ERA5 | 0.25° × 0.25° | 1 month | m |
| Relative humidity | ERA5 | 0.25° × 0.25° | 1 month | % |
| DEM | USGS | 90 m | - | m |
| MODIS-AOD | MODIS | 0.01° × 0.01° | 1 day | - |
| Ground-level PM2.5 | CNEMC | - | 1 h | μg/m3 |
| Grid-level PM2.5 | WUSTL | 0.01° × 0.01° | 1 month | μg/m3 |
| Season | PM2.5 (μg/m3) | AOD | RH (%) | PBLH (km) | WS (m/s) | TWRI × 1000 | DEM (m) | |
|---|---|---|---|---|---|---|---|---|
| Spring | Min | 7.18 | 0 | 20.25 | 0.22 | 0.16 | 6.27 | 0 |
| N = 1484 | Max | 187.28 | 0.37 | 85.72 | 1.42 | 3.40 | 74.98 | 4101 |
| Mean | 55.27 | 0.12 | 58.99 | 0.58 | 0.97 | 28.01 | 426 | |
| Std. | 23.51 | 0.07 | 15.36 | 0.16 | 0.52 | 12.07 | 725 | |
| Summer | Min | 4.00 | 0 | 22.17 | 0.21 | 0.17 | 5.46 | - |
| N = 1486 | Max | 83.35 | 0.27 | 90.50 | 1.16 | 4.34 | 69.73 | - |
| Mean | 19.95 | 0.04 | 73.67 | 0.51 | 1.17 | 28.40 | - | |
| Std. | 7.86 | 0.03 | 10.75 | 0.13 | 0.62 | 13.08 | - | |
| Autumn | Min | 5.40 | 0 | 27.34 | 0.17 | 0.22 | 6.53 | - |
| N = 1481 | Max | 82.92 | 0.24 | 87.28 | 0.90 | 5.72 | 82.54 | - |
| Mean | 31.39 | 0.08 | 66.34 | 0.44 | 1.30 | 26.42 | - | |
| Std. | 11.15 | 0.05 | 10.63 | 0.09 | 0.77 | 11.65 | - | |
| Winter | Min | 7.18 | 0 | 17.67 | 0.07 | 0.19 | 6.38 | - |
| N = 1447 | Max | 187.28 | 0.27 | 87.09 | 1.28 | 5.16 | 94.18 | - |
| Mean | 55.27 | 0.10 | 64.69 | 0.38 | 1.31 | 28.87 | - | |
| Std. | 23.51 | 0.06 | 10.97 | 0.10 | 0.74 | 14.22 | - |
| Season/R | AOD | RH (%) | PBLH (km) | WS (m/s) | TWRI | DEM |
|---|---|---|---|---|---|---|
| Spring | 0.5888 | −0.2975 | 0.1129 | −0.2502 | 0.4603 | −0.2553 |
| Summer | 0.7258 | −0.2917 | 0.0201 | −0.3296 | 0.6577 | −0.2123 |
| Autumn | 0.7540 | −0.4059 | −0.3159 | −0.4138 | 0.5667 | −0.2829 |
| winter | 0.5684 | −0.3480 | −0.4571 | −0.5077 | 0.6950 | −0.2906 |
| Model | Model Fitting | Model Validation | ||||||
|---|---|---|---|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| GWR (traditional model) | R2 = 0.78 | R2 = 0.77 | R2 = 0.78 | R2 = 0.78 | R2 = 0.75 | R2 = 0.74 | R2 = 0.76 | R2 = 0.76 |
| RMSE = 4.71 | RMSE = 3.81 | RMSE = 5.24 | RMSE = 10.97 | RMSE = 5.04 | RMSE = 3.99 | RMSE = 5.51 | RMSE = 11.61 | |
| MAE = 3.57 | MAE = 2.90 | MAE = 3.95 | MAE = 7.95 | MAE = 3.78 | MAE = 3.04 | MAE = 4.16 | MAE = 8.35 | |
| GWR (coupled model) | R2 = 0.68 | R2 = 0.70 | R2 = 0.72 | R2 = 0.74 | R2 = 0.66 | R2 = 0.68 | R2 = 0.71 | R2 = 0.73 |
| RMSE = 5.95 | RMSE = 4.57 | RMSE = 6.16 | RMSE = 11.99 | RMSE = 6.13 | RMSE = 4.67 | RMSE = 6.30 | RMSE = 12.40 | |
| MAE = 4.53 | MAE = 3.55 | MAE = 4.74 | MAE = 8.47 | MAE = 4.66 | MAE = 3.63 | MAE = 4.84 | MAE = 8.69 | |
| GWR (optimized model) | R2 = 0.80 | R2 = 0.80 | R2 = 0.82 | R2 = 0.84 | R2 = 0.76 | R2 = 0.78 | R2 = 0.79 | R2 = 0.82 |
| RMSE = 4.47 | RMSE = 3.52 | RMSE = 4.80 | RMSE = 9.52 | RMSE = 4.90 | RMSE = 3.73 | RMSE = 5.12 | RMSE = 10.12 | |
| MAE = 3.32 | MAE = 2.67 | MAE = 3.60 | MAE = 6.61 | MAE = 3.56 | MAE = 2.83 | MAE = 3.84 | MAE = 7.00 | |
| Model | Model Validation | |||
|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | |
| Traditional model | R2 = 0.6038 | R2 = 0.4951 | R2 = 0.7209 | R2 = 0.6391 |
| MAE = 3.1961 | MAE = 4.2243 | MAE = 4.5146 | MAE = 9.2194 | |
| RMSE = 4.3009 | RMSE = 5.2480 | RMSE = 5.8526 | RMSE = 13.5801 | |
| Coupled model | R2 = 0.4812 | R2 = 0.4205 | R2 = 0.6480 | R2 = 0.5728 |
| MAE = 4.3503 | MAE = 4.4136 | MAE = 5.4437 | MAE = 10.4857 | |
| RMSE = 5.4718 | RMSE = 5.5517 | RMSE = 6.8394 | RMSE = 15.031 | |
| Optimized model | R2 = 0.6459 | R2 = 0.6028 | R2 = 0.7932 | R2 = 0.7078 |
| MAE = 3.0781 | MAE = 3.7031 | MAE = 3.9485 | MAE = 8.0193 | |
| RMSE = 4.1251 | RMSE = 4.5989 | RMSE = 5.0712 | RMSE = 12.231 | |
| Model | Model Validation | |||
|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | |
| Traditional model | R2 = 0.4199 | R2 = 0.5901 | R2 = 0.3351 | R2 = 0.3779 |
| MAE = 2.7604 | MAE = 1.8302 | MAE = 2.6256 | MAE = 4.6836 | |
| RMSE = 3.3114 | RMSE = 2.3255 | RMSE = 3.1117 | RMSE = 6.1177 | |
| Coupled model | R2 = 0.2936 | R2 = 0.1852 | R2 = 0.1782 | R2 = 0.2816 |
| MAE = 2.5943 | MAE = 2.6615 | MAE = 3.3697 | MAE = 3.3234 | |
| RMSE = 3.3598 | RMSE = 3.5591 | RMSE = 4.5965 | RMSE = 4.0667 | |
| Optimized model | R2 = 0.5299 | R2 = 0.6287 | R2 = 0.4757 | R2 = 0.4363 |
| MAE = 1.8325 | MAE = 1.7368 | MAE = 2.0630 | MAE = 2.7679 | |
| RMSE = 2.3227 | RMSE = 2.2703 | RMSE = 2.7055 | RMSE = 3.4448 | |
| Model | Model Validation | |||
|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | |
| Traditional model | R2 = 0.4622 | R2 = 0.2722 | R2 = 0.5203 | R2 = 0.5852 |
| MAE = 3.4077 | MAE = 2.6890 | MAE = 3.7955 | MAE = 7.7003 | |
| RMSE = 4.4071 | RMSE = 3.3348 | RMSE = 5.1042 | RMSE = 9.6655 | |
| Coupled model | R2 = 0.4520 | R2 = 0.2011 | R2 = 0.5909 | R2 = 0.7595 |
| MAE = 3.8866 | MAE = 3.5427 | MAE = 3.8037 | MAE = 5.3997 | |
| RMSE = 5.0530 | RMSE = 4.4939 | RMSE = 4.8866 | RMSE = 7.2528 | |
| Optimized model | R2 = 0.5317 | R2 = 0.3492 | R2 = 0.6337 | R2 = 0.7713 |
| MAE = 3.1902 | MAE = 2.5069 | MAE = 3.3545 | MAE = 5.3192 | |
| RMSE = 4.1344 | RMSE = 3.1245 | RMSE = 4.3711 | RMSE = 7.1304 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, B.; Xie, B.; Wang, W.; Wu, L. Enhancing Seasonal PM2.5 Estimations in China through Terrain–Wind–Rained Index (TWRI): A Geographically Weighted Regression Approach. Remote Sens. 2024, 16, 2145. https://doi.org/10.3390/rs16122145
Peng B, Xie B, Wang W, Wu L. Enhancing Seasonal PM2.5 Estimations in China through Terrain–Wind–Rained Index (TWRI): A Geographically Weighted Regression Approach. Remote Sensing. 2024; 16(12):2145. https://doi.org/10.3390/rs16122145
Chicago/Turabian StylePeng, Boqi, Busheng Xie, Wei Wang, and Lixin Wu. 2024. "Enhancing Seasonal PM2.5 Estimations in China through Terrain–Wind–Rained Index (TWRI): A Geographically Weighted Regression Approach" Remote Sensing 16, no. 12: 2145. https://doi.org/10.3390/rs16122145
APA StylePeng, B., Xie, B., Wang, W., & Wu, L. (2024). Enhancing Seasonal PM2.5 Estimations in China through Terrain–Wind–Rained Index (TWRI): A Geographically Weighted Regression Approach. Remote Sensing, 16(12), 2145. https://doi.org/10.3390/rs16122145







