Deep-Learning-Based Daytime COT Retrieval and Prediction Method Using FY4A AGRI Data
Abstract
1. Introduction
- A daytime COT retrieval model based on CNN (CM4CR) has been designed, which enhances the neural network’s feature extraction capability by employing the CBAM module. Additionally, two matching methods, single-point matching, and multi-point average matching, have significantly reduced errors during data matching. Experimental results demonstrate that CM4CR achieves satisfactory retrieval performance.
- A COT prediction model CPM based on a video prediction model was developed. We incorporate a time embedding module to enhance its ability to learn from different time intervals and utilize Charbonnier Loss and Edge Loss during the training phase to improve the prediction of detailed information. We also explore how varying lengths of COT input sequences and the time intervals between adjacent COT frames affect prediction performance.
2. Related Works
2.1. Retrieval of COT
2.2. Prediction in the Field of Meteorology
3. Data
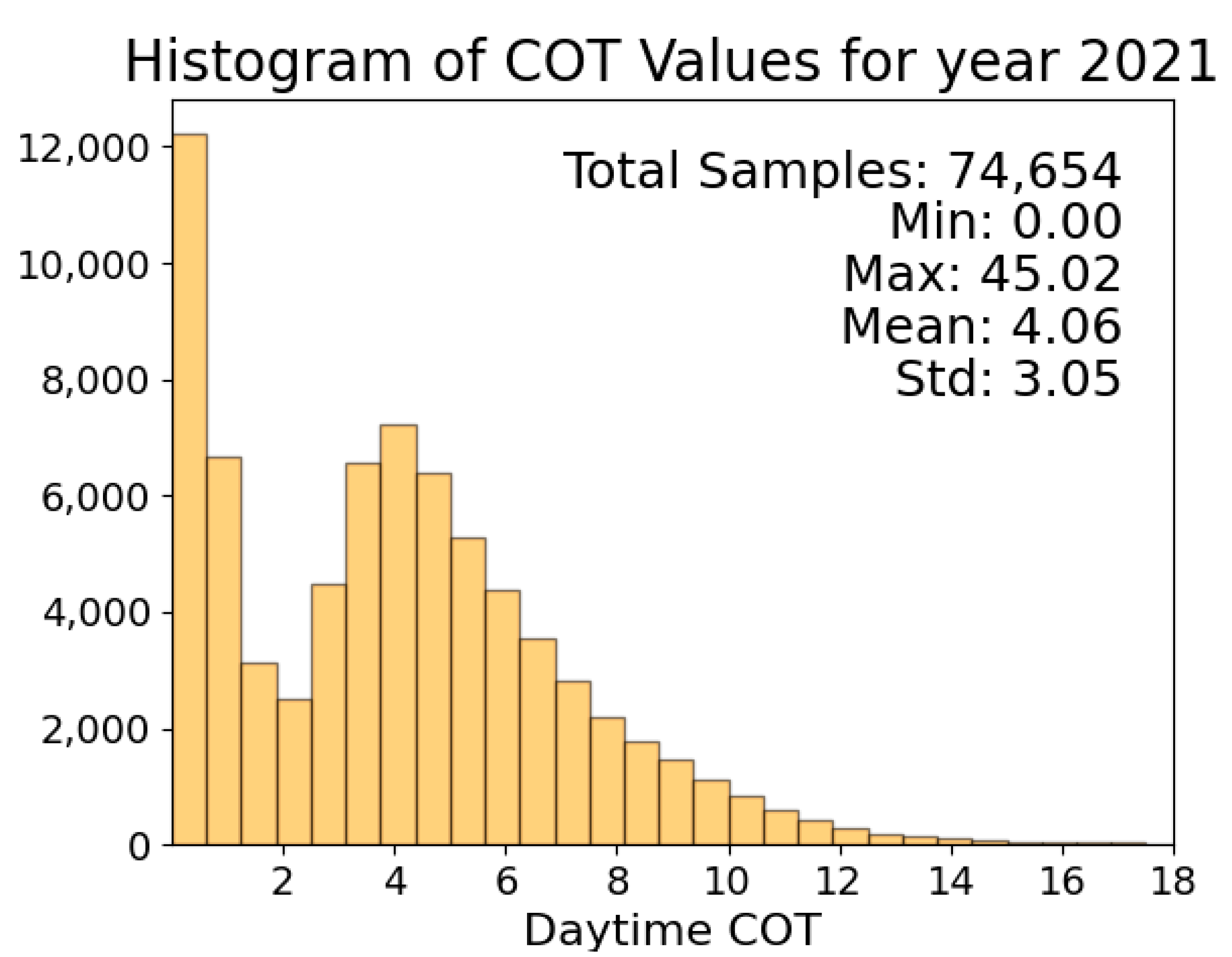
3.1. Data Introduction
3.2. Data Processing
3.2.1. Single-Point Data Matching
- (a)
- Based on the observation time of each element in the CALIPSO dataset, we locate the corresponding FY4A AGRI file for the respective period. Then, using the nominal formulas for converting between row and column numbers and geographical coordinates, we calculate the row and column numbers corresponding to the latitude and longitude of CALIPSO (rounded to the nearest integer).
- (b)
- We read the latitude and longitude information of the corresponding position from FY4A based on the row and column numbers. Then, using the Pyproj library, we calculate the distance d between the two points based on their latitude and longitude information. Afterward, we compute the time difference t between the observations of the two points.
- (c)
- If and , then we consider the two points as matched.
- (d)
- For each matched AGRI data point, we create a grid slice centered at its spatial position, which is used for training the regression model.where denotes a matched AGRI data point, represents the two-dimensional plane coordinates of this matched point, and denotes the grid slice created centered at this AGRI matched point.
3.2.2. Multiple-Point Averaging Matching
4. Methodology
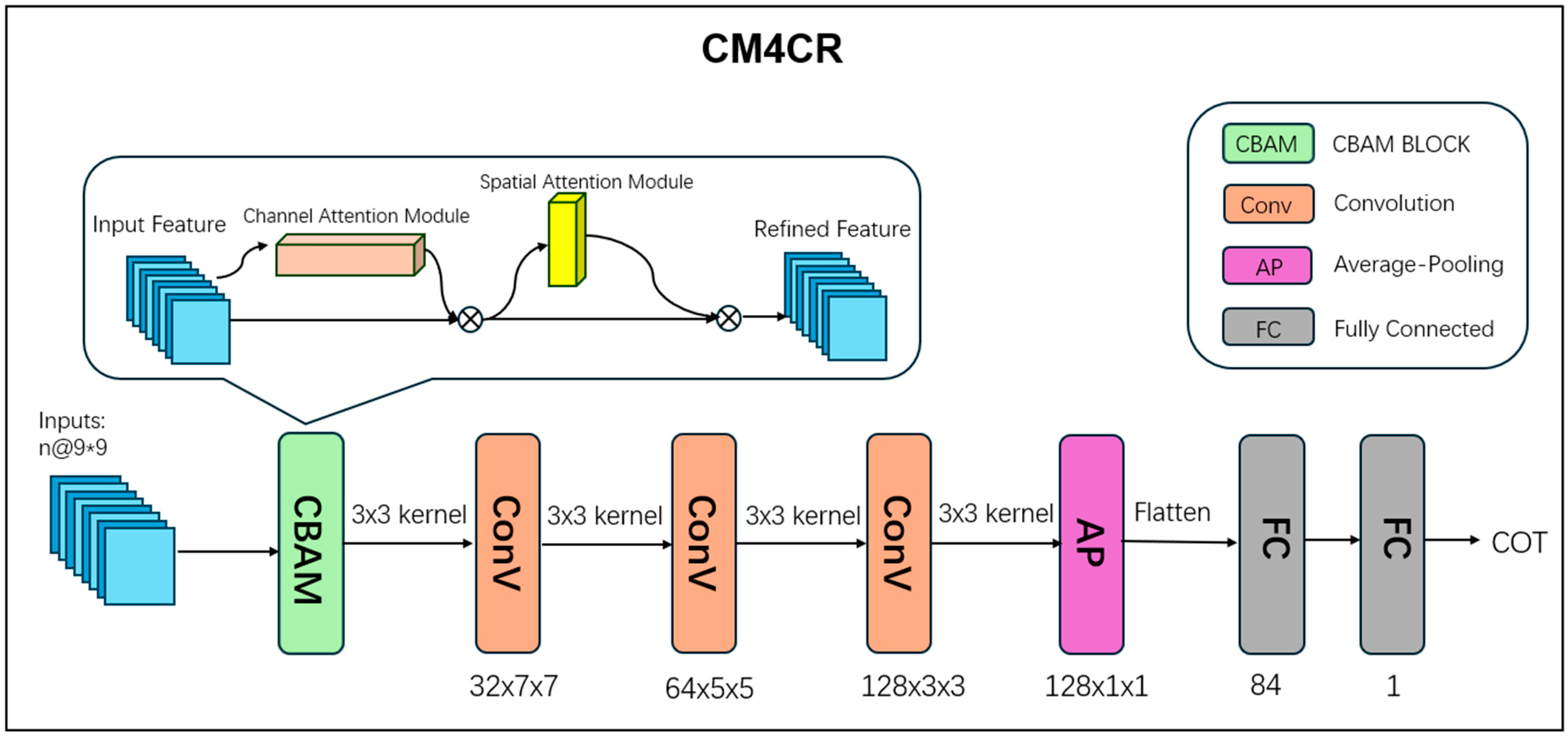
4.1. Retrieval Model
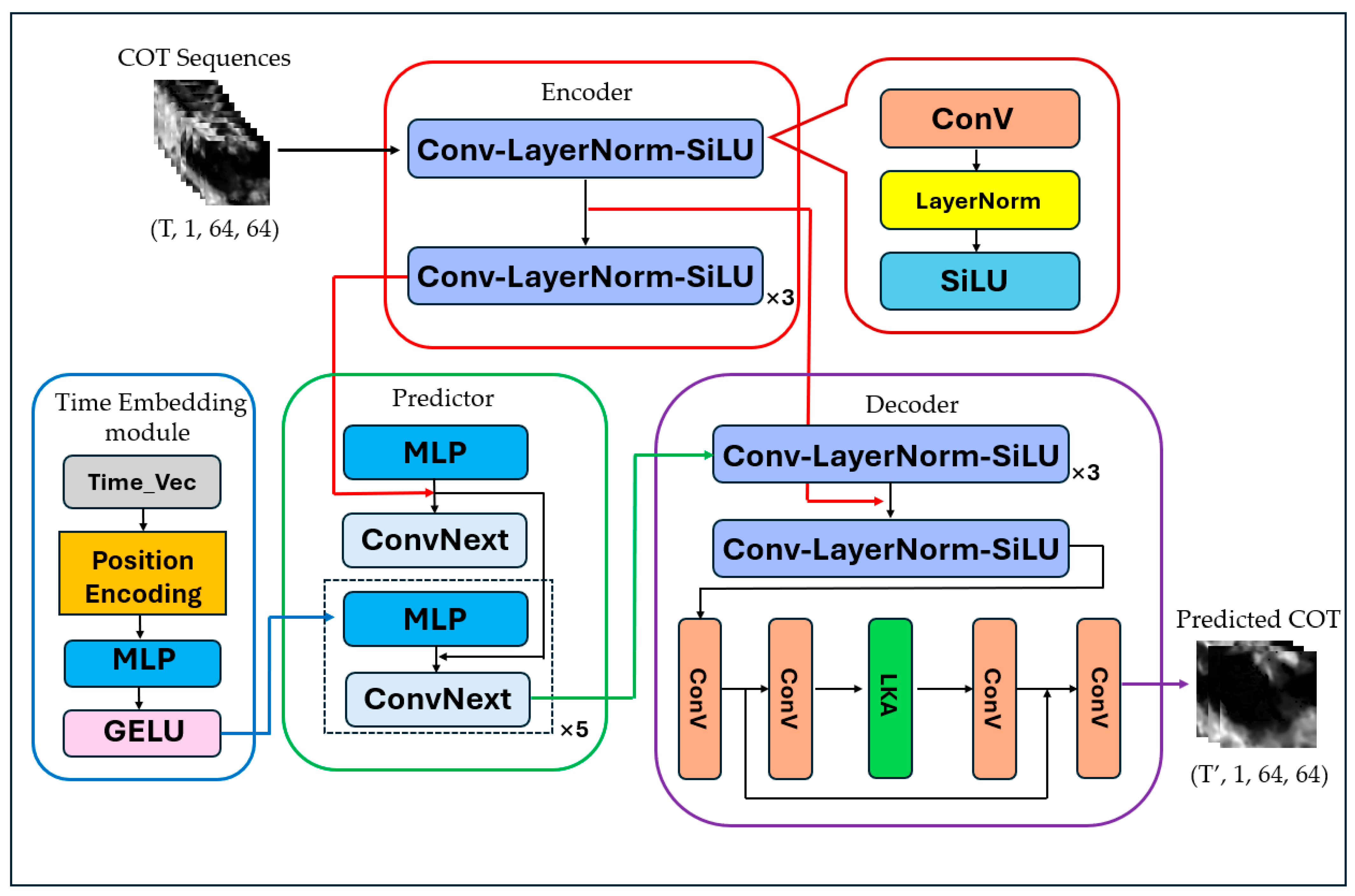
4.2. Prediction Model
4.2.1. Encoder
4.2.2. Predictor
4.2.3. Decoder
5. Experiments
5.1. Setup
5.2. Metrics
5.2.1. Root Mean Square Error (RMSE)
5.2.2. Mean Absolute Error (MAE)
5.2.3. The Coefficient of Determination ()
5.2.4. Structural Similarity Index (SSIM)
5.2.5. Structural Similarity Index (SSIM)
5.3. COT Retrieval Experiment Results
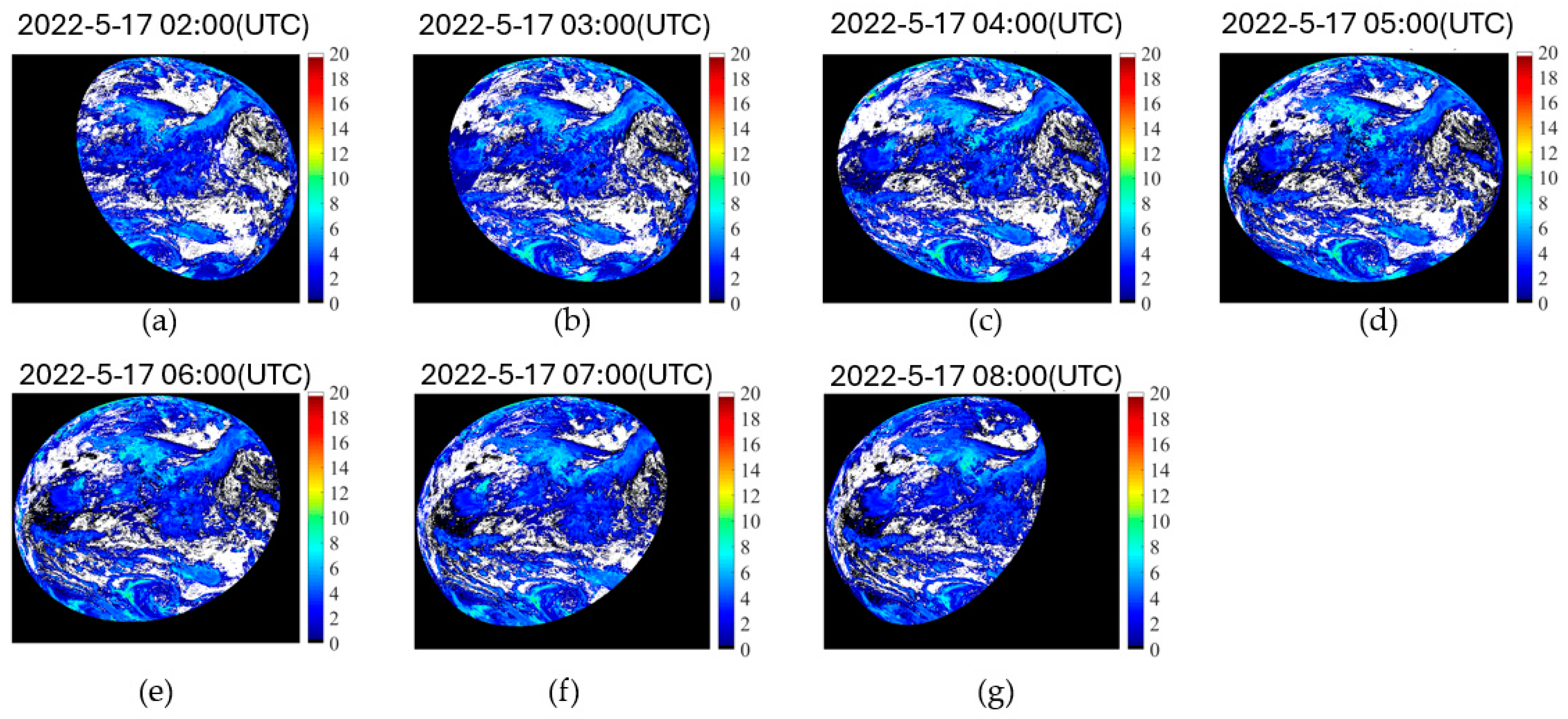
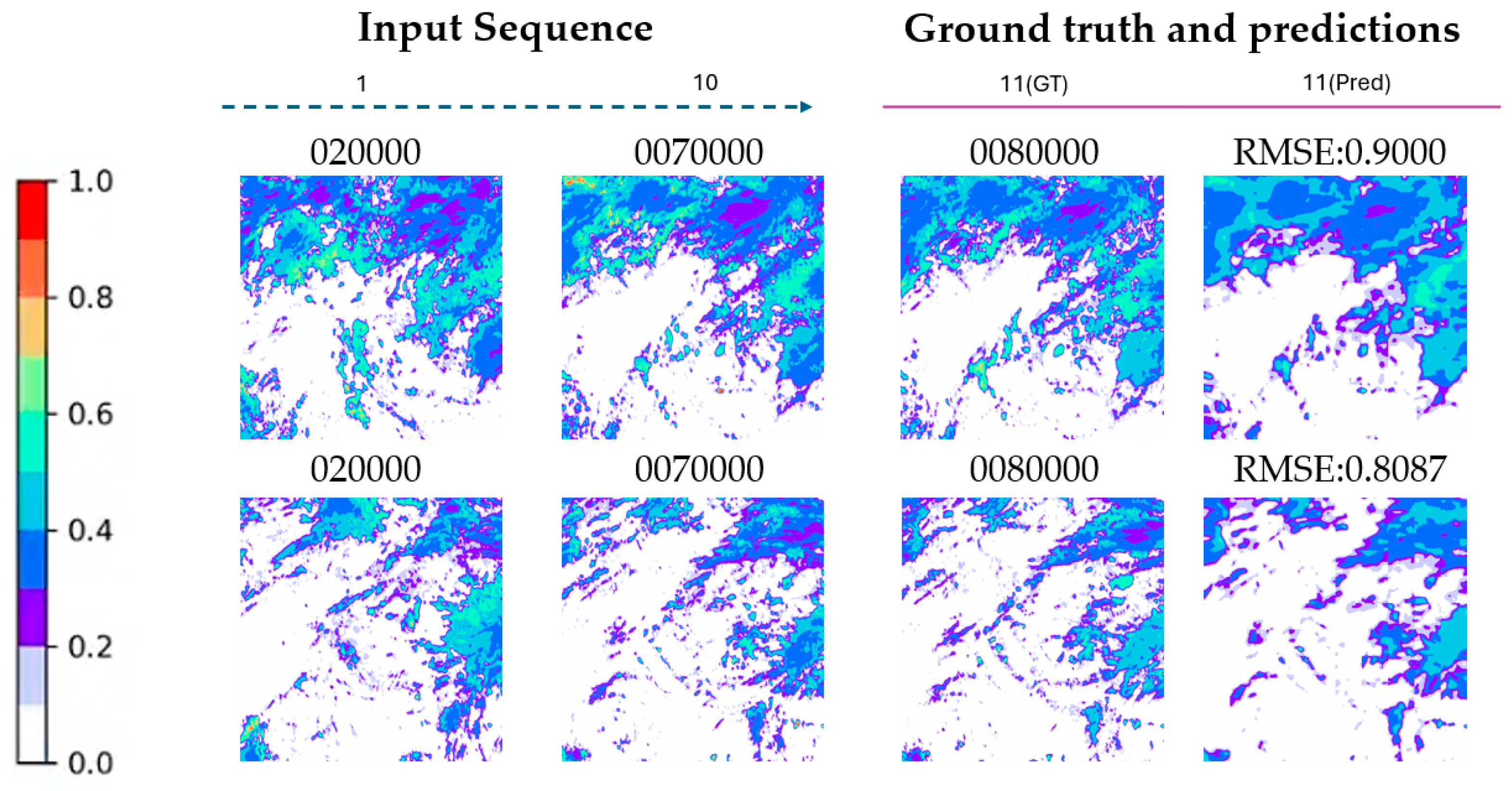
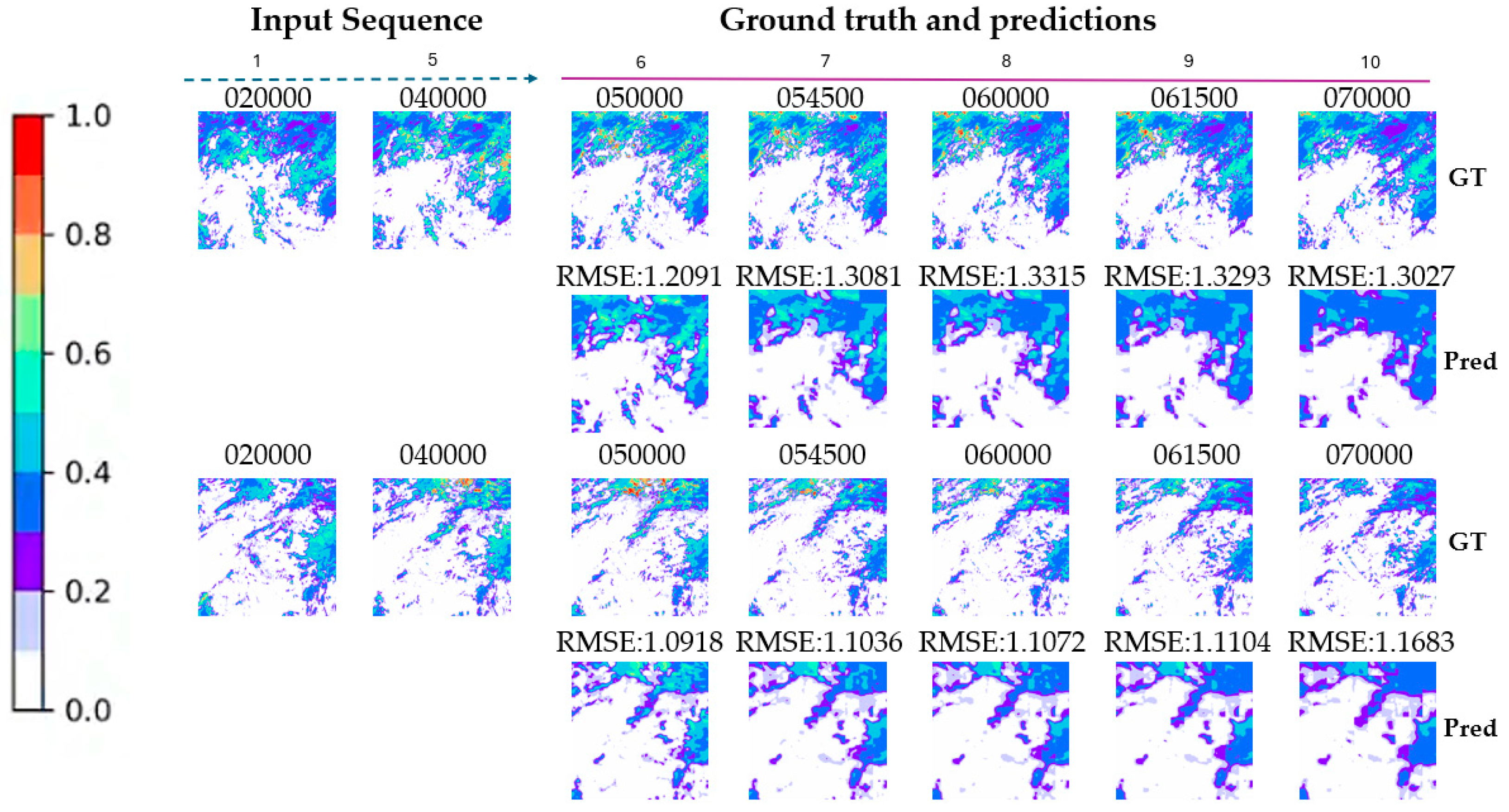
5.4. COT Prediction Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khain, A.; Rosenfeld, D.; Pokrovsky, A. Aerosol impact on precipitation from convective clouds. In Measuring Precipitation from Space: EURAINSAT and the Future; Springer: Dordrecht, The Netherlands, 2007; pp. 421–434. [Google Scholar]
- Jensen, E.J.; Kinne, S.; Toon, O.B. Tropical cirrus cloud radiative forcing: Sensitivity studies. Geophys. Res. Lett. 1994, 21, 2023–2026. [Google Scholar] [CrossRef]
- Roeckner, E.; Schlese, U.; Biercamp, J.; Loewe, P. Cloud optical depth feedbacks and climate modelling. Nature 1987, 329, 138–140. [Google Scholar] [CrossRef]
- Mitchell, J.F.B.; Senior, C.A.; Ingram, W.J. C02 and climate: A missing feedback? Nature 1989, 341, 132–134. [Google Scholar] [CrossRef]
- Stephens, G.L.; Webster, P.J. Clouds and climate: Sensitivity of simple systems. J. Atmos. Sci. 1981, 38, 235–247. [Google Scholar] [CrossRef]
- Nakajima, T.Y.; Uchiyama, A.; Takamura, T.; Nakajima, T. Comparisons of warm cloud properties obtained from satellite, ground, and aircraft measurements during APEX intensive observation period in 2000 and 2001. J. Meteorol. Soc. Japan Ser. II 2005, 83, 1085–1095. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, X.; Wang, H.; Yeung, D.-Y.; Woo, W.; Wong, W.-K. Deep learning and the weather forecasting problem: Precipitation nowcasting. In Deep Learning for the Earth Sciences: A Comprehensive Approach to Remote Sensing, Climate Science, and Geosciences; John Wiley & Sons, Ltd.: Chichester, UK, 2021; pp. 218–239. [Google Scholar]
- Chen, S.; Zhang, X.; Shao, D.; Shu, X. SASTA-Net: Self-attention spatiotemporal adversarial network for typhoon prediction. J. Electron. Imaging 2022, 31, 053020. [Google Scholar] [CrossRef]
- Wang, R.; Teng, D.; Yu, W.; Zhang, X.; Zhu, J. Improvement and Application of a GAN Model for Time Series Image Prediction—A Case Study of Time Series Satellite Cloud Images. Remote Sens. 2022, 14, 5518. [Google Scholar] [CrossRef]
- Letu, H.; Yang, K.; Nakajima, T.Y.; Ishimoto, H. High-resolution retrieval of cloud microphysical properties and surface solar radiation using Himawari-8/AHI next-generation geostationary satellite. Remote Sens. Environ. 2020, 239, 111583. [Google Scholar] [CrossRef]
- Liu, C.; Song, Y.; Zhou, G.; Teng, S.; Li, B.; Xu, N.; Lu, F.; Zhang, P. A cloud optical and microphysical property product for the advanced geosynchronous radiation imager onboard China’s Fengyun-4 satellites: The first version. Atmos. Ocean. Sci. Lett. 2023, 16, 100337. [Google Scholar] [CrossRef]
- Kox, S.; Bugliaro, L.; Ostler, A. Retrieval of cirrus cloud optical thickness and top altitude from geostationary remote sensing. Atmos. Meas. Tech. 2014, 7, 3233–3246. [Google Scholar] [CrossRef]
- Minnis, P.; Hong, G.; Sun-Mack, S.; Smith, W.L.; Chen, Y.; Miller, S.D. Estimating nocturnal opaque ice cloud optical depth from MODIS multispectral infrared radiances using a neural network method. J. Geophys. Res. Atmos. 2016, 121, 4907–4932. [Google Scholar] [CrossRef]
- Wang, X.; Iwabuchi, H.; Yamashita, T. Cloud identification and property retrieval from Himawari-8 infrared measurements via a deep neural network. Remote Sens. Environ. 2022, 275, 113026. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, C.; Zhuge, X.; Liu, C.; Weng, F.; Wang, M. Retrieval of cloud properties from thermal infrared radiometry using convolutional neural network. Remote Sens. Environ. 2022, 278, 113079. [Google Scholar] [CrossRef]
- Li, J.; Zhang, F.; Li, W.; Tong, X.; Pan, B.; Li, J.; Lin, H.; Letu, H.; Mustafa, F. Transfer-learning-based approach to retrieve the cloud properties using diverse remote sensing datasets. In Proceedings of the IEEE Transactions on Geoscience and Remote Sensing, Pasadena, CA, USA, 13 October 2023. [Google Scholar]
- Curran, R.J.; Wu, M.L.C. Skylab near-infrared observations of clouds indicating supercooled liquid water droplets. J. Atmos. Sci. 1982, 39, 635–647. [Google Scholar] [CrossRef]
- Platnick, S.; King, M.D.; Ackerman, S.A.; Menzel, W.P.; Baum, B.A.; Riédi, J.C.; Frey, R.A. The MODIS cloud products: Algorithms and examples from Terra. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–473. [Google Scholar] [CrossRef]
- Letu, H.; Nagao, T.M.; Nakajima, T.Y.; Riedi, J.; Ishimoto, H.; Baran, A.J.; Shang, H.; Sekiguchi, M.; Kikuchi, M. Ice cloud properties from Himawari-8/AHI next-generation geostationary satellite: Capability of the AHI to monitor the DC cloud generation process. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3229–3239. [Google Scholar] [CrossRef]
- Greenwald, T.J.; Pierce, R.B.; Schaack, T.; Otkin, J.A.; Rogal, M.; Bah, K.; Lenzen, A.J.; Nelson, J.P.; Li, J.; Huang, H.-L. Real-time simulation of the GOES-R ABI for user readiness and product evaluation. Bull. Am. Meteorol. Soc. 2016, 97, 245–261. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.-S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Gao, Z.; Tan, C.; Wu, L.; Li, S.Z. Simvp: Simpler yet better video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 3170–3180. [Google Scholar]
- Seo, M.; Lee, H.; Kim, D.; Seo, J. Implicit stacked autoregressive model for video prediction. arXiv 2023, arXiv:2303.07849. [Google Scholar]
- Oprea, S.; Martinez-Gonzalez, P.; Garcia-Garcia, A.; Castro-Vargas, J.A.; Orts-Escolano, S.; Garcia-Rodriguez, J.; Argyros, A. A review on deep learning techniques for video prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2806–2826. [Google Scholar] [CrossRef]
- Hsieh, J.T.; Liu, B.; Huang, D.A.; Li, F.-F.; Niebles, J.C. Learning to decompose and disentangle representations for video prediction. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Byeon, W.; Wang, Q.; Srivastava, R.K.; Koumoutsakos, P. Contextvp: Fully context-aware video prediction. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 753–769. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.-H.; Shao, L. Multi-stage progressive image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14821–14831. [Google Scholar]
- Barnard, J.C.; Long, C.N. A simple empirical equation to calculate cloud optical thickness using shortwave broadband measurements. J. Appl. Meteorol. 2004, 43, 1057–1066. [Google Scholar] [CrossRef]
- Kikuchi, N.; Nakajima, T.; Kumagai, H.; Kamei, A.; Nakamura, R.; Nakajima, T.Y. Cloud optical thickness and effective particle radius derived from transmitted solar radiation measurements: Comparison with cloud radar observations. J. Geophys. Res. Atmos. 2006, 111, D07205. [Google Scholar] [CrossRef]
- Gong, K.; Ye, D.L.; Ge, C.H. A method for geostationary meteorological satellite cloud image prediction based on motion vector. J. Image Graph. 2000, 50, 5. [Google Scholar]
- Lorenz, E.; Hammer, A.; Heinemann, D. Short term forecasting of solar radiation based on satellite data. In EUROSUN2004 (ISES Europe Solar Congress); PSE Instruments GmbH, Solar Info Center: Freiburg, Germany, 2004. [Google Scholar]
- Yang, J.; Lv, W.T.; Ma, Y.; Yao, W.; Li, Q. An automatic groundbased cloud detection method based on local threshold interpolation. Acta Meteorol. Sin. 2010, 68, 1007–1017. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems 2015, Montreal, QC, Canada, 7–12 December 2015; Volume 28. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Yeung, D.-Y. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Requena-Mesa, C.; Benson, V.; Reichstein, M.; Runge, J.; Denzler, J. EarthNet2021: A large-scale dataset and challenge for Earth surface forecasting as a guided video prediction task. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1132–1142. [Google Scholar]
- Yu, Z.; Ma, S.; Han, D.; Li, G.; Yan, W.; Liu, J. Physical and optical properties of clouds in the southwest Vortex from FY-4A cloud retrievals. J. Appl. Meteorol. Climatol. 2022, 61, 1123–1138. [Google Scholar] [CrossRef]
- Lai, R.; Teng, S.; Yi, B.; Letu, H.; Min, M.; Tang, S.; Liu, C. Comparison of cloud properties from Himawari-8 and FengYun-4A geostationary satellite radiometers with MODIS cloud retrievals. Remote Sens. 2019, 11, 1703. [Google Scholar] [CrossRef]
- Krebs, W.; Mannstein, H.; Bugliaro, L.; Mayer, B. A new day-and night-time Meteosat Second Generation Cirrus Detection Algorithm MeCiDA. Atmos. Chem. Phys. 2007, 7, 6145–6159. [Google Scholar] [CrossRef]
- Li, Q.; Sun, X.; Wang, X. Reliability evaluation of the joint observation of cloud top height by FY-4A and Himawari-8. Remote Sens. 2021, 13, 3851. [Google Scholar] [CrossRef]
- Xu, X.; Zeng, Y.; Yu, X.; Liu, G.; Yue, Z.; Dai, J.; Feng, Q.; Liu, P.; Wang, J.; Zhu, Y. Identification of Supercooled Cloud Water by FY-4A Satellite and Validation by CALIPSO and Airborne Detection. Remote Sens. 2022, 15, 126. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; Jensen, M.P.; Toto, T.; Foster, M.J.; Long, C.N. A Comparison of Multiscale Variations of Decade-Long Cloud Fractions from Six Different Platforms over the Southern Great Plains in the United States. Geophys. Res. Atmos. 2014, 119, 3438–3459. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, T.; Liu, D.; Wang, Z. Spatial scales of altocumulus clouds observed with collocated CALIPSO and CloudSat measurements. Atmos. Res. 2014, 149, 58–69. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Guo, M.H.; Lu, C.Z.; Liu, Z.N.; Cheng, M.M.; Hu, S.M. Visual attention network. Comput. Vis. Media 2023, 9, 733–752. [Google Scholar] [CrossRef]





| Channel Number | Channel Type | Central Wavelength (µm) | Spectral Bandwidth (µm) | Spatial Resolution (km) |
|---|---|---|---|---|
| 1 | Visible light and near infrared | 0.47 | 0.45~0.49 | 1 |
| 2 | 0.65 | 0.55~0.75 | 0.5~1 | |
| 3 | 0.825 | 0.75~0.90 | 1 | |
| 4 | Shortwave infrared | 1.375 | 1.36~1.39 | 2 |
| 5 | 1.61 | 1.58~1.64 | 2 | |
| 6 | 2.25 | 2.10~2.35 | 2 | |
| 7 | Medium wave infrared | 3.75 | 3.5~4.0 (high) | 4 |
| 8 | 3.75 | 3.5~4.0 (low) | 4 | |
| 9 | Water vapor | 6.25 | 5.8~6.7 | 4 |
| 10 | 7.1 | 6.9~7.3 | 4 | |
| 11 | Long wave infrared | 8.5 | 8.0~9.0 | 4 |
| 12 | 10.7 | 10.3~11.3 | 4 | |
| 13 | 12.0 | 11.5~12.5 | 4 | |
| 14 | 13.5 | 13.2~13.8 | 4 |
| Variable | Data Source | Spatial Resolution | Temporal Resolution | |
|---|---|---|---|---|
| Daytime Input | 0.65, 0.825, 8.5, 10.7 µm | FY-4A/AGRI | 4 km | 15 min |
| T8.5 µm–T10.7 µm | FY-4A/AGRI | 4 km | 15 min |
| Layer | Sub Layer | Input | Output |
|---|---|---|---|
| Encoder | Conv-LayerNorm-SiLU Conv-LayerNorm-SiLU (×3) | COT Sequences: (T, 1, 64, 64) Enc_1 | Enc_1: (T, 128, 64, 64) Enc_2: (T, 128, 16, 16) |
| Time Embedding Module | Position Encoding Linear GELU Linear | Time_Vec: (T) Time_Vec (T, 64) Time_Vec (256) Time_Vec (256) | Time_Vec: (T, 64) Time_Vec: (256) Time_Vec: (256) Time_Vec: (64) |
| Predictor | Reshape | hyper-parameter: (T, 128, 16, 16) Enc_2 | Prediction: (2560, 16, 16) |
| ConvNeXt | Prediction | Prediction: (1280, 16, 16) | |
| Linear | Time_Vec | Time_emb: (128) | |
| Add | Prediction, Time_emb | Prediction: (1280, 16, 16) | |
| ConvNeXt | Prediction | Prediction: (1280, 16, 16) | |
| Linear | Time_Vec | Time_emb: (128) | |
| Add | Prediction, Time_emb | Prediction: (1280, 16, 16) | |
| ConvNeXt | Prediction | Prediction: (1280, 16, 16) | |
| Linear | Time_Vec | Time_emb: (128) | |
| Add | Prediction, Time_emb | Prediction: (1280, 16, 16) | |
| Linear | Time_Vec | Time_emb: (128) | |
| ConvNeXt | Prediction | Prediction: (1280, 16, 16) | |
| Linear | Time_Vec | Time_emb: (128) | |
| Add | Prediction, Time_emb | Prediction: (1280, 16, 16) | |
| ConvNeXt | Prediction | Prediction: (1280, 16, 16) | |
| Linear | Time_Vec | Time_emb: (128) | |
| Add | Prediction, Time_emb | Prediction: (1280, 16, 16) | |
| Reshape | Prediction | Prediction: (T, 128, 16, 16) | |
| Decoder | Transposed Conv-LayerNorm-SiLU | Prediction | Dec: (T, 128, 16, 16) |
| Transposed Conv-LayerNorm-SiLU | Dec | Dec: (T, 128, 32, 32) | |
| Transposed Conv-LayerNorm-SiLU | Dec | Dec: (T, 128, 64, 64) | |
| Add | Dec, Enc_1 | Dec: (T, 256, 64, 64) | |
| Transposed Conv-LayerNorm-SiLU | Dec | Dec: (T, 128, 64, 64) | |
| Reshape | Dec | Dec: (1280, 64, 64) | |
| 2D Convolution (1 × 1) | Dec | Dec: (64, 64, 64) | |
| Large Kernel Attention | Dec | Dec: (64, 64, 64) | |
| 2D Convolution (1 × 1) | Dec | Output: (T′, 64, 64) |
| Dataset | Original Input | Additional Bands (µm) |
|---|---|---|
| 1 | null | |
| 2 | 0.47, 1.61, 1.21 | |
| 3 | 1.37, 1.61, 2.22 | |
| 4 | 1.61, 1.22. |
| Input | Matching Method | RMSE | R2 |
|---|---|---|---|
| Single-Point Data Matching | 1.99 | 0.57 | |
| Multiple-Point Averaging | 1.37 | 0.71 | |
| Multiple-Point Averaging | 1.26 | 0.75 |
| Sequence Length | Input Sequence | Output Sequence |
|---|---|---|
| Model | RMSE↓ | MAE↓ | SSIM↑ | PSNR↑ | RMSE′↓ | R2↑ |
|---|---|---|---|---|---|---|
| ConvLSTM | 1.114 | 0.889 | 0.2994 | 19.0386 | 1.3480 | 0.48 |
| SimVP | 0.882 | 0.626 | 0.4396 | 29.2083 | 1.2758 | 0.53 |
| CPM (ours) | 0.878 | 0.560 | 0.5197 | 29.9403 | 1.2670 | 0.54 |
| Sequence Length | RMSE at Different Time Points: Δt(Frame Number) | ||||||
|---|---|---|---|---|---|---|---|
| 60(6) | 45(7) | 15(8) | 15(9) | 45(10) | 60(11) | Total | |
| T = 5, T′ = 5 | 1.232 | 1.348 | 1.345 | 1.335 | 1.315 | null | 1.315 |
| T = 8, T′ = 3 | Input | Input | Input | 0.611 | 0.914 | 1.078 | 0.868 |
| T = 8, T′ = 2 | Input | Input | Input | Input | 0.827 | 1.067 | 0.947 |
| T = 10, T′ = 1 | Input | Input | Input | Input | Input | 0.878 | 0.878 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, F.; Song, B.; Chen, J.; Guan, R.; Zhu, R.; Liu, J.; Qiu, Z. Deep-Learning-Based Daytime COT Retrieval and Prediction Method Using FY4A AGRI Data. Remote Sens. 2024, 16, 2136. https://doi.org/10.3390/rs16122136
Xu F, Song B, Chen J, Guan R, Zhu R, Liu J, Qiu Z. Deep-Learning-Based Daytime COT Retrieval and Prediction Method Using FY4A AGRI Data. Remote Sensing. 2024; 16(12):2136. https://doi.org/10.3390/rs16122136
Chicago/Turabian StyleXu, Fanming, Biao Song, Jianhua Chen, Runda Guan, Rongjie Zhu, Jiayu Liu, and Zhongfeng Qiu. 2024. "Deep-Learning-Based Daytime COT Retrieval and Prediction Method Using FY4A AGRI Data" Remote Sensing 16, no. 12: 2136. https://doi.org/10.3390/rs16122136
APA StyleXu, F., Song, B., Chen, J., Guan, R., Zhu, R., Liu, J., & Qiu, Z. (2024). Deep-Learning-Based Daytime COT Retrieval and Prediction Method Using FY4A AGRI Data. Remote Sensing, 16(12), 2136. https://doi.org/10.3390/rs16122136






