Lossy Compression of Single-channel Noisy Images by Modern Coders
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
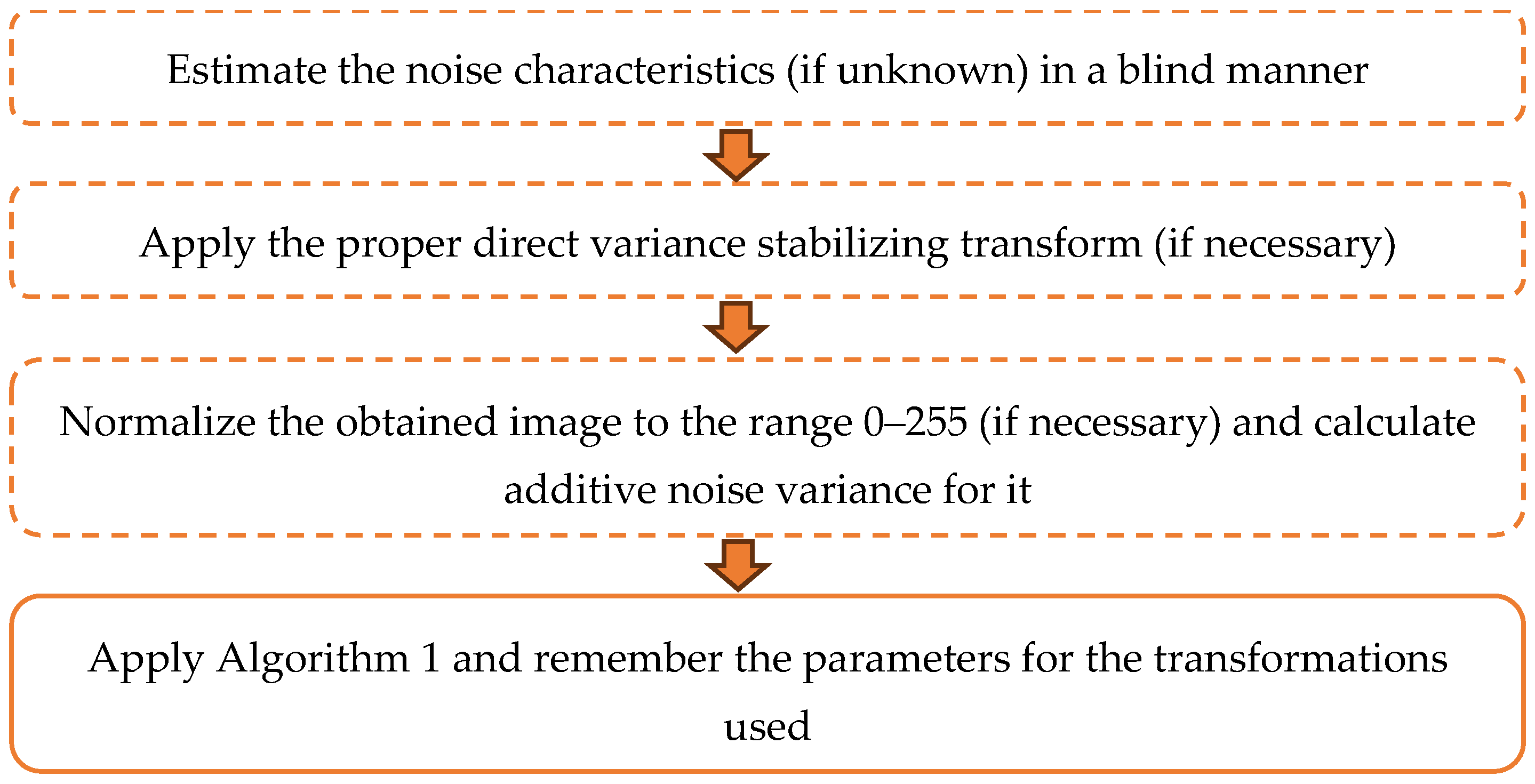
- (1)
- Suppose that σ2 is known in advance; if it is unknown, estimate it;
- (2)
- Set a starting QFst for a used coder according to the observations given above (see also the data in Table 4);
- (3)
- Compress and decompress a considered image using QFst and calculate MSEnc;
- (4)
- If 0.9σ2 ≤ MSEnc ≤ 1.1σ2, retain the compressed image obtained at Step 3 as the final one; if MSEnc ≤ 0.9σ2, decrease QF by 2 and continue; if MSEnc > 1.1σ2, increase QF by 2 and continue;
- (5)
- For the new QF, compress and decompress the image, calculate MSEnc, and continue checking the validity of 0.9σ2 ≤ MSEnc ≤ 1.1σ2 as in Step 4; stop when it is valid and retain the last obtained compressed image as the final one.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bondžulić, B.; Stojanović, N.; Lukin, V.; Stankevich, S.A.; Bujaković, D.; Kryvenko, S. Target Acquisition Performance in the Presence of JPEG Image Compression. Def. Technol. 2023, 33, 30–41. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Kolotii, A.; Skakun, S.; Rakoid, O.; Shumilo, L. A workflow for Sustainable Development Goals indicators assessment based on high-resolution satellite data. Int. J. Digit. Earth 2020, 13, 309–321. [Google Scholar] [CrossRef]
- Mielke, C.; Boshce, N.K.; Rogass, C.; Segl, K.; Gauert, C.; Kaufmann, H. Potential Applications of the Sentinel-2 Multispectral Sensor and the ENMAP hyperspectral Sensor in Mineral Exploration. EARSeL eProc. 2014, 13, 93–102. [Google Scholar] [CrossRef]
- Khorram, S.; van der Wiele, C.F.; Koch, F.H.; Nelson, S.A.C.; Potts, M.D. Future Trends in Remote Sensing. In Principles of Applied Remote Sensing; Springer International Publishing: Cham, Switzerland, 2016; pp. 277–285. ISBN 978-3-319-22559-3. [Google Scholar]
- Pillai, D.K. New Computational Models for Image Remote Sensing and Big Data. In Big Data Analytics for Satellite Image Processing and Remote Sensing; IGI Global: Hershey, PA, USA, 2018; pp. 1–21. [Google Scholar]
- Chow, K.; Tzamarias, D.E.O.; Blanes, I.; Serra-Sagristà, J. Using Predictive and Differential Methods with K2-Raster Compact Data Structure for Hyperspectral Image Lossless Compression. Remote Sens. 2019, 11, 2461. [Google Scholar] [CrossRef]
- Radosavljevic, M.; Brkljac, B.; Lugonja, P.; Crnojevic, V.; Trpovski, Ž.; Xiong, Z.; Vukobratovic, D. Lossy Compression of Multispectral Satellite Images with Application to Crop Thematic Mapping: A HEVC Comparative Study. Remote Sens. 2020, 12, 1590. [Google Scholar] [CrossRef]
- Yu, G.; Vladimirova, T.; Sweeting, M.N. Image compression systems on board satellites. Acta Astronaut. 2009, 64, 988–1005. [Google Scholar] [CrossRef]
- Li, F.; Kryvenko, S.; Lukin, V. Remote Sensing Image Lossy Compression Based on JPEG with Controlled Visual Quality. In Proceedings of the 7th International Symposium of Space Optical Instruments and Applications, Beijing, China, 21–23 October 2023; Urbach, H.P., Jiang, H., Eds.; Springer Proceedings in Physics. Springer Nature Singapore: Singapore, 2023; Volume 295, pp. 8–19, ISBN 978-981-9940-97-4. [Google Scholar]
- Abramov, S.K.; Abramova, V.V.; Lukin, V.V.; Egiazarian, K.O. Denoising of multichannel images with nonlinear transformation of reference image. Telecom. Rad. Eng. 2018, 77, 769–786. [Google Scholar] [CrossRef]
- Abramov, S.; Uss, M.; Lukin, V.; Vozel, B.; Chehdi, K.; Egiazarian, K. Enhancement of Component Images of Multispectral Data by Denoising with Reference. Remote Sens. 2019, 11, 611. [Google Scholar] [CrossRef]
- Christophe, E. Hyperspectral Data Compression Tradeoff. In Optical Remote Sensing; Prasad, S., Bruce, L.M., Chanussot, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 9–29. ISBN 978-3-642-14211-6. [Google Scholar]
- Chen, Z.; Hu, Y.; Zhang, Y. Effects of Compression on Remote Sensing Image Classification Based on Fractal Analysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4577–4590. [Google Scholar] [CrossRef]
- Yang, K.; Jiang, H. Optimized-SSIM Based Quantization in Optical Remote Sensing Image Compression. In Proceedings of the 2011 Sixth International Conference on Image and Graphics, Hefei, China, 12–15 August 2011; IEEE: New York, NY, USA, 2011; pp. 117–122. [Google Scholar]
- Li, F.; Lukin, V.; Ieremeiev, O.; Okarma, K. Quality Control for the BPG Lossy Compression of Three-Channel Remote Sensing Images. Remote Sens. 2022, 14, 1824. [Google Scholar] [CrossRef]
- Bondžulić, B.; Stojanović, N.; Petrović, V.; Pavlović, B.; Miličević, Z. Efficient Prediction of the First Just Noticeable Difference Point for JPEG Compressed Images. Acta Polytech. Hungarica. 2021, 18, 201–220. [Google Scholar] [CrossRef]
- BPG Image Format. Available online: https://bellard.org/bpg/ (accessed on 22 April 2024).
- Kovalenko, B.; Lukin, V.; Vozel, B. BPG-Based Lossy Compression of Three-Channel Noisy Images with Prediction of Optimal Operation Existence and Its Parameters. Remote Sens. 2023, 15, 1669. [Google Scholar] [CrossRef]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; Optical Science and Engineering; CRC Press: Boca Raton, FL, USA, 2009; ISBN 978-1-4200-5497-2. [Google Scholar]
- Mullissa, A.G.; Persello, C.; Tolpekin, V. Fully Convolutional Networks for Multi-Temporal SAR Image Classification. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6635–6638. [Google Scholar]
- Zhong, P.; Wang, R. Multiple-Spectral-Band CRFs for Denoising Junk Bands of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2260–2275. [Google Scholar] [CrossRef]
- Hassanzadeh, S.; Karami, A. Compression and Noise Reduction of Hyperspectral Images Using Non-Negative Tensor Decomposition and Compressed Sensing. Eur. J. Remote Sens. 2016, 49, 587–598. [Google Scholar] [CrossRef]
- Wang, W.; Zhong, X.; Su, Z. On-Orbit Signal-to-Noise Ratio Test Method for Night-Light Camera in Luojia 1-01 Satellite Based on Time-Sequence Imagery. Sensors 2019, 19, 4077. [Google Scholar] [CrossRef]
- Wei, D.; Odegard, J.E.; Guo, H.; Lang, M.; Burrus, C.S. Simultaneous noise reduction and SAR image data compression using best wavelet packet basis. In Proceedings of the IEEE International Conference on Image Processing, Washington, DC, USA, 23–26 October 1995; pp. 200–203. [Google Scholar]
- Odegard, J.E.; Guo, H.; Burrus, C.S.; Baraniuk, R.G. Joint compression and Speckle Reduction of SAR Images Using Embedded Zero-tree Models. In Proceedings of the Workshop on Image and Multidimensional Signal Processing, Belize City, Belize; 1996; pp. 80–81. Available online: https://repository.rice.edu/items/e04d67f2-5e85-41a6-8989-40e0f49af097 (accessed on 22 April 2024).
- Chang, S.G.; Yu, B.; Vetterli, M. Image Denoising via Lossy Compression and Wavelet Thresholding. In Proceedings of the International Conference on Image Processing, Santa Barbara, CA, USA, 26–29 October 1997; Volume 1, pp. 604–607. [Google Scholar]
- Al-Shaykh, O.K.; Mersereau, R.M. Lossy Compression of Noisy Images. IEEE Trans. Image Process. 1998, 7, 1641–1652. [Google Scholar] [CrossRef] [PubMed]
- Wallace, G. The JPEG Still Picture Compression Standard. Commun. ACM. 1991, 34, 30–44. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Silvestri, F.; Egiazarian, K.; Carli, M.; Astola, J.; Lukin, V. On Between-Coefficient Contrast Masking of DCT Basis Functions. In Proceedings of the Third International Workshop on Video Processing and Quality Metrics for Consumer Electronics, Scottsdale, AZ, USA, 25–26 January 2007; 4p. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale Structural Similarity for Image Quality Assessment. In Proceedings of the ty-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1398–1402. [Google Scholar]
- Taubman, D.S.; Marcellin, M.W. JPEG2000: Image Compression Fundamentals, Standards, and Practice; Kluwer Academic Publishers: Boston, MA, USA, 2002; p. 779. [Google Scholar]
- Ponomarenko, N.; Lukin, V.; Zriakhov, M.; Egiazarian, K.; Astola, J. Lossy Compression of Images with Additive Noise. In Advanced Concepts for Intelligent Vision Systems; Blanc-Talon, J., Philips, W., Popescu, D., Scheunders, P., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3708, pp. 381–386. ISBN 978-3-540-29032-2. [Google Scholar]
- Ponomarenko, N.; Zriakhov, M.; Lukin, V.V.; Astola, J.T.; Egiazarian, K.O. Estimation of Accessible Quality in Noisy Image Compression. In Proceedings of the 2006 14th European Signal Processing Conference, Florence, Italy, 4–8 September 2006; pp. 1–4. [Google Scholar]
- Zemliachenko, A.N.; Abramov, S.K.; Lukin, V.V.; Vozel, B.; Chehdi, K. Lossy Compression of Noisy Remote Sensing Images with Prediction of Optimal Operation Point Existence and Parameters. J. Appl. Remote Sens. 2015, 9, 095066. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Lukin, V.; Egiazarian, K.; Astola, J. DCT Based High Quality Image Compression. In Image Analysis; Kalviainen, H., Parkkinen, J., Kaarna, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3540, pp. 1177–1185. ISBN 978-3-540-26320-3. [Google Scholar]
- Ponomarenko, N.N.; Egiazarian, K.O.; Lukin, V.V.; Astola, J.T. High-Quality DCT-Based Image Compression Using Partition Schemes. IEEE Signal Process. Lett. 2007, 14, 105–108. [Google Scholar] [CrossRef]
- Kovalenko, B.; Lukin, V.; Kryvenko, S.; Naumenko, V.; Vozel, B. BPG-Based Automatic Lossy Compression of Noisy Images with the Prediction of an Optimal Operation Existence and Its Parameters. Appl. Sci. 2022, 12, 7555. [Google Scholar] [CrossRef]
- Makarichev, V.; Kovalenko, B.; Lukin, V. Preliminary Analysis of Noisy Image Lossy Compression by Discrete Atomic Transform-Based Coder. Aktt 2023, 67–74. [Google Scholar] [CrossRef]
- Alves De Oliveira, V.; Chabert, M.; Oberlin, T.; Poulliat, C.; Bruno, M.; Latry, C.; Carlavan, M.; Henrot, S.; Falzon, F.; Camarero, R. Satellite Image Compression and Denoising with Neural Networks. IEEE Geosci. Remote Sensing Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X. FLLIC: Functionally Lossless Image Compression. arXiv 2024, arXiv:2401.13616. [Google Scholar]
- Zemliachenko, A.; Kozhemiakin, R.; Uss, M.; Abramov, S.; Ponomarenko, N.; Lukin, V.; Vozel, B.; Chehdi, K. Lossy compression of hyperspectral images based on noise parameters estimation and variance stabilizing transform. J. Appl. Remote Sens. 2014, 8, 25. [Google Scholar] [CrossRef]
- Yee, D.; Soltaninejad, S.; Hazarika, D.; Mbuyi, G.; Barnwal, R.; Basu, A. Medical Image Compression Based on Region of Interest Using Better Portable Graphics (BPG). In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 216–221. [Google Scholar]
- Chen, Y.; Mukherjee, D.; Han, J.; Grange, A.; Xu, Y.; Parker, S.; Chen, C.; Su, H.; Joshi, U.; Chiang, C.-H.; et al. An Overview of Coding Tools in AV1: The First Video Codec from the Alliance for Open Media. APSIPA Trans. Signal Inf. Process. 2020, 9, e6. [Google Scholar] [CrossRef]
- Lainema, J.; Hannuksela, M.M.; Vadakital, V.K.M.; Aksu, E.B. HEVC Still Image Coding and High Efficiency Image File Format. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 71–75. [Google Scholar]
- Barman, N.; Martini, M.G. An Evaluation of the Next-Generation Image Coding Standard AVIF. In Proceedings of the 2020 Twelfth International Conference on Quality of Multimedia Experience (QoMEX), Athlone, Ireland, 26–28 May 2020; pp. 1–4. [Google Scholar]
- Hanhart, P.; Rerabek, M.; Korshunov, P.; Ebrahimi, T. Subjective Evaluation of HEVC Intra Coding for Still Image Compression. In Proceedings of the Seventh International Workshop on Video Processing and Quality Metrics for Consumer Electronics (VPQM-2013), Scottsdale, AZ, USA, 30 January–1 February 2013; pp. 1–6. [Google Scholar]
- Colom, M.; Buades, A.; Morel, J.-M. Nonparametric Noise Estimation Method for Raw Images. J. Opt. Soc. Am. A 2014, 31, 863–871. [Google Scholar] [CrossRef] [PubMed]
- Uss, M.L. Maximum Likelihood Estimation of Spatially Correlated Signal-Dependent Noise in Hyperspectral Images. Opt. Eng. 2012, 51, 111712. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2008; ISBN 9780131687288 013168728X/9780135052679 013505267X. [Google Scholar]
- Sendur, L.; Selesnick, I.W. Bivariate Shrinkage with Local Variance Estimation. IEEE Signal Process. Lett. 2002, 9, 438–441. [Google Scholar] [CrossRef]
- Chatterjee, P.; Milanfar, P. Is Denoising Dead? IEEE Trans Image Process. 2010, 19, 895–911. [Google Scholar] [CrossRef] [PubMed]
- Pogrebnyak, O.; Lukin, V.V. Wiener Discrete Cosine Transform-Based Image Filtering. J. Electron. Imaging 2012, 21, 043020. [Google Scholar] [CrossRef]
- Kozhemiakin, R.; Abramov, S.; Lukin, V.; Djurović, I.; Vozel, B. Peculiarities of 3D Compression of Noisy Multichannel Images. In Proceedings of the MECO, Budva, Montenegro, 14–18 June 2015; pp. 331–334. [Google Scholar]
- Zhang, B.; Fadili, M.J.; Starck, J.-L. Multi-Scale Variance Stabilizing Transform for Multi-Dimensional Poisson Count Image Denoising. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Toulouse, France, 14–19 May 2006; 4p. [Google Scholar] [CrossRef]
- Choi, H.; Jeong, J. Speckle Noise Reduction Technique for SAR Images Using Statistical Characteristics of Speckle Noise and Discrete Wavelet Transform. Remote Sens. 2019, 11, 1184. [Google Scholar] [CrossRef]
- ISO/IEC 23008-12:2022; Information technology—High efficiency coding and media delivery in heterogeneous environments, Part 12: Image File Format. International Organization for Standardization: Geneva, Switzerland, 2022.
- Báscones, D.; González, C.; Mozos, D. An FPGA Accelerator for Real-Time Lossy Compression of Hyperspectral Images. Remote Sens. 2020, 12, 2563. [Google Scholar] [CrossRef]





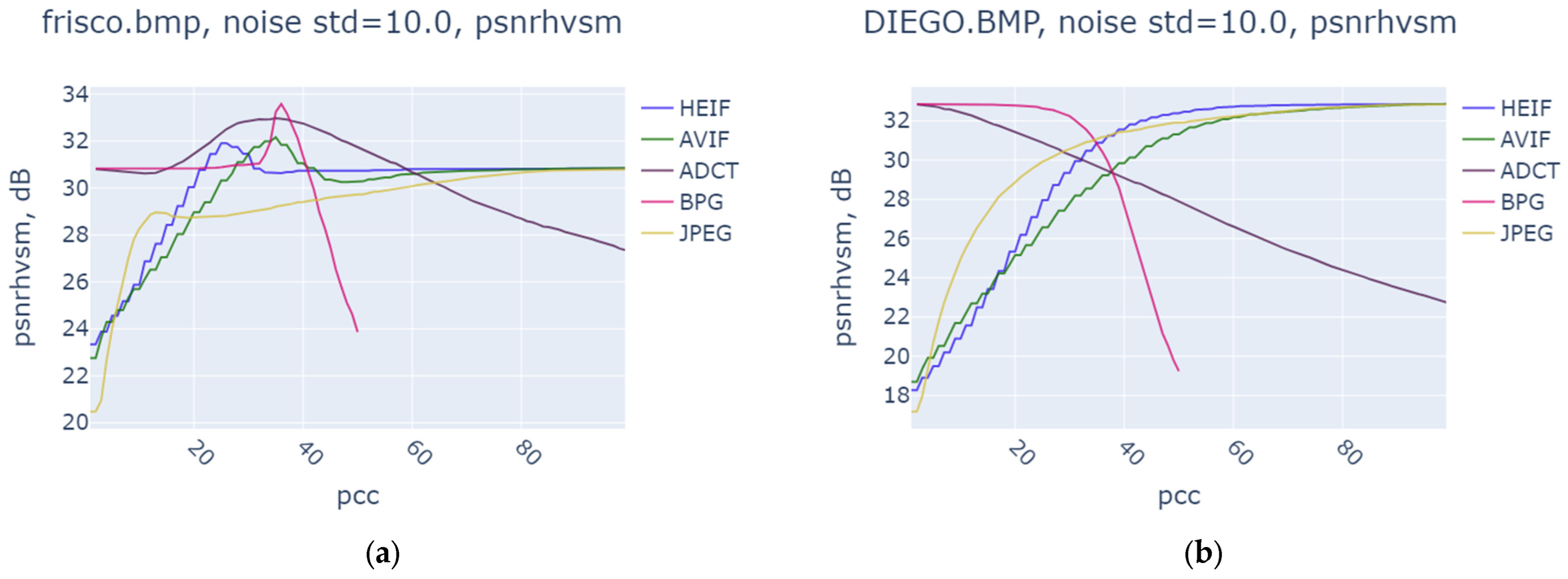
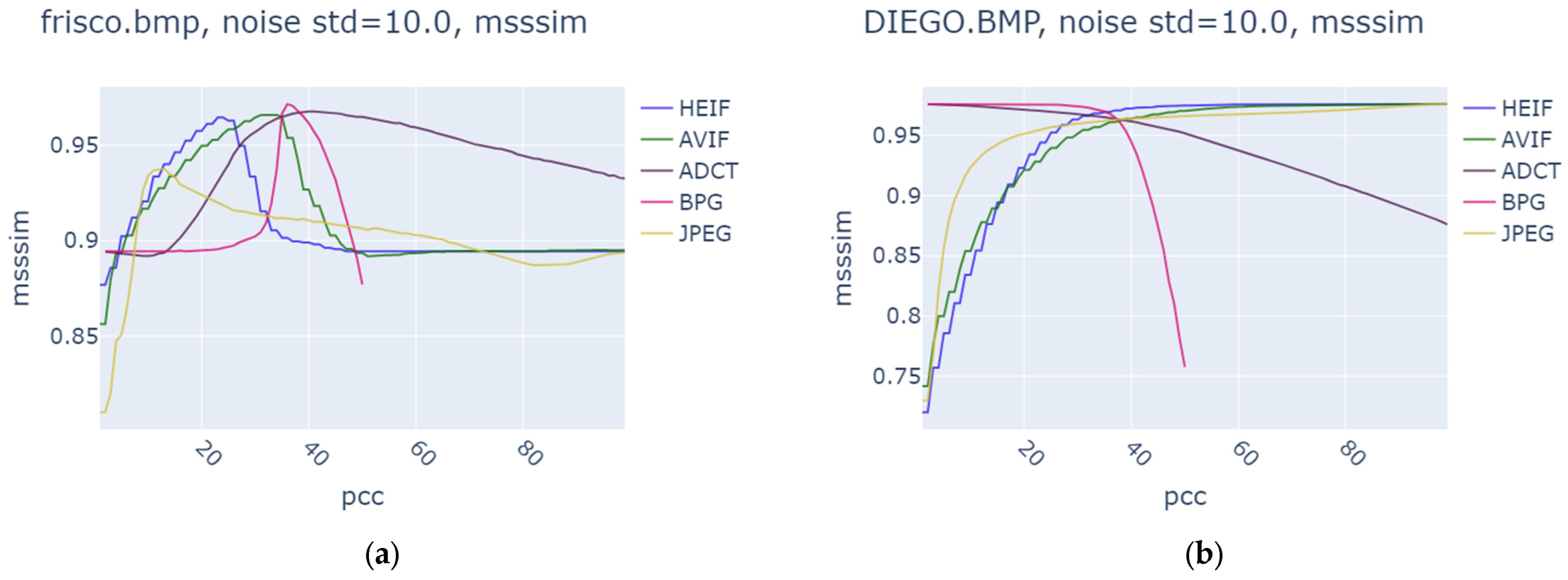
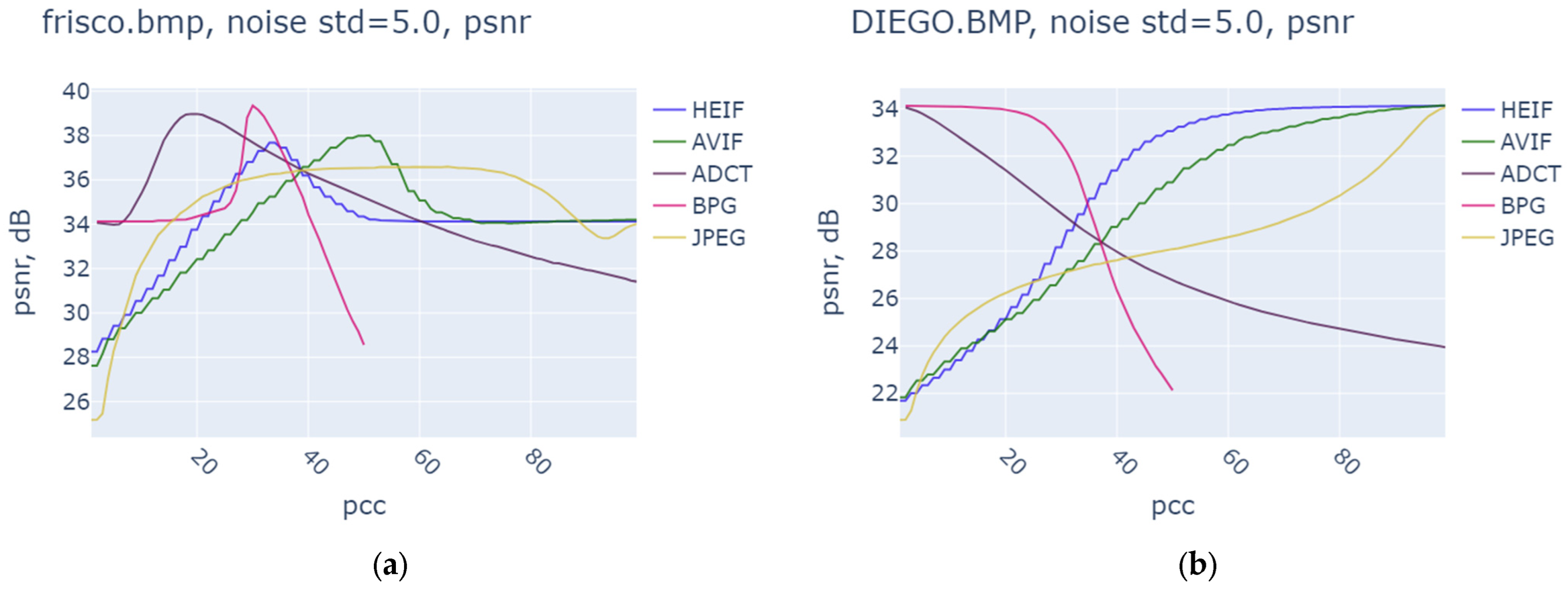
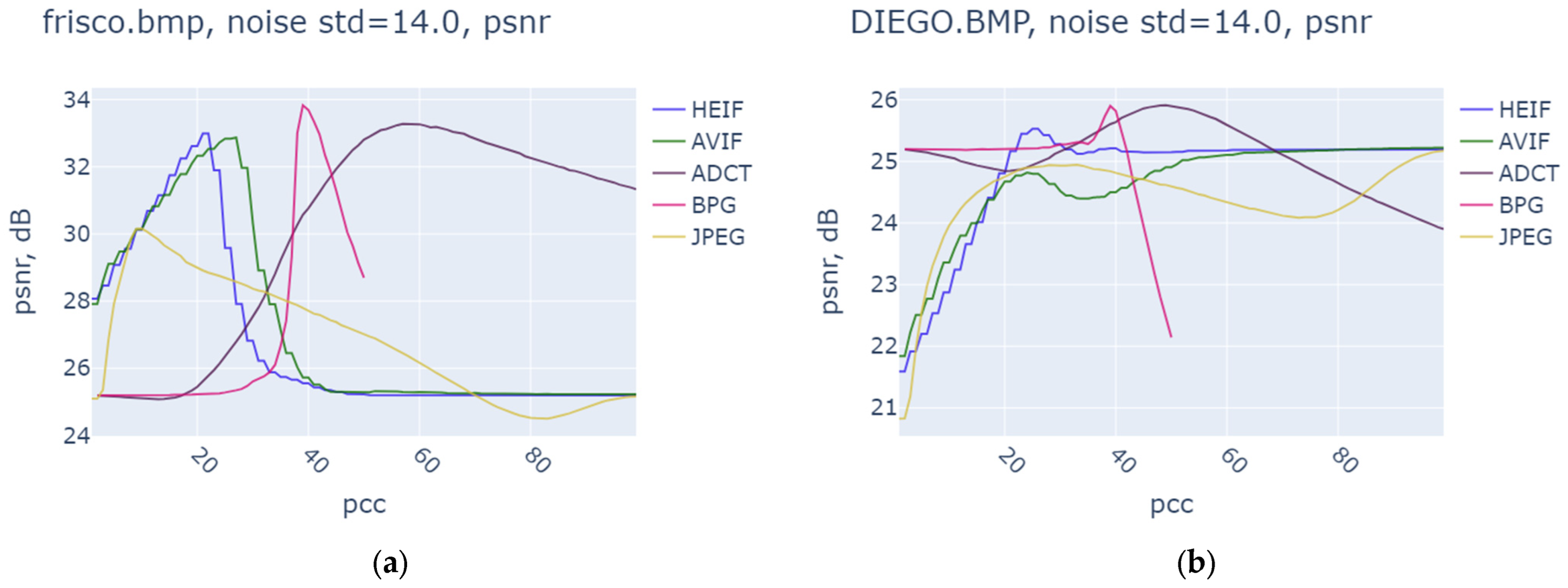

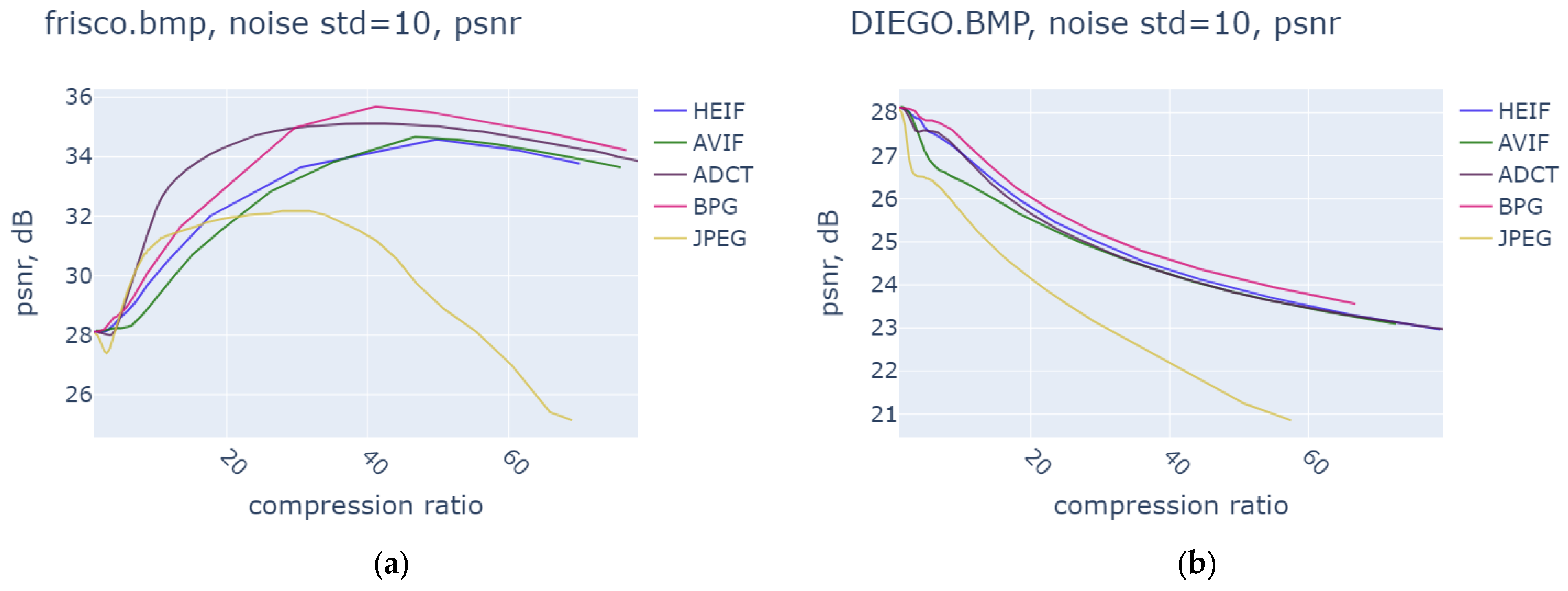
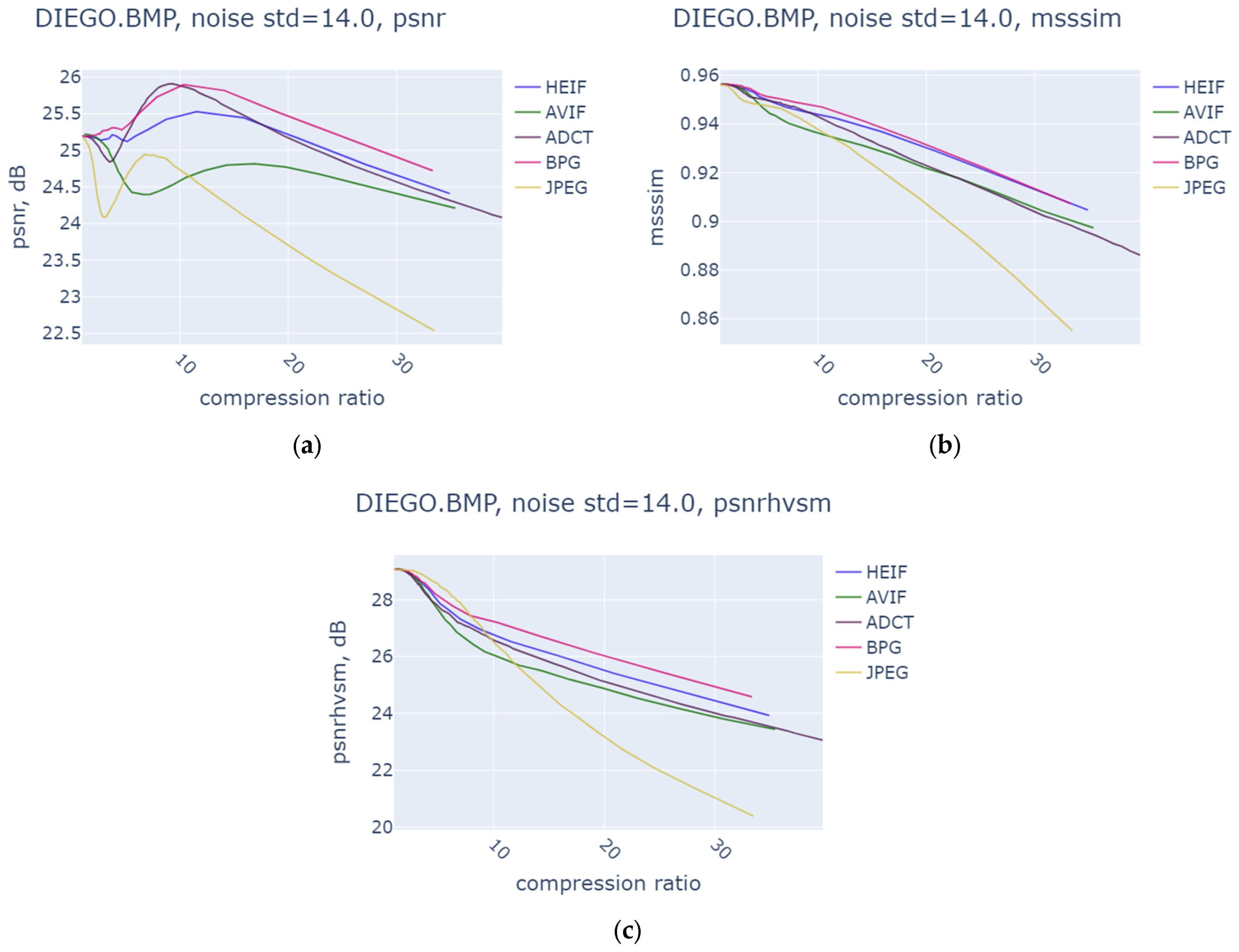

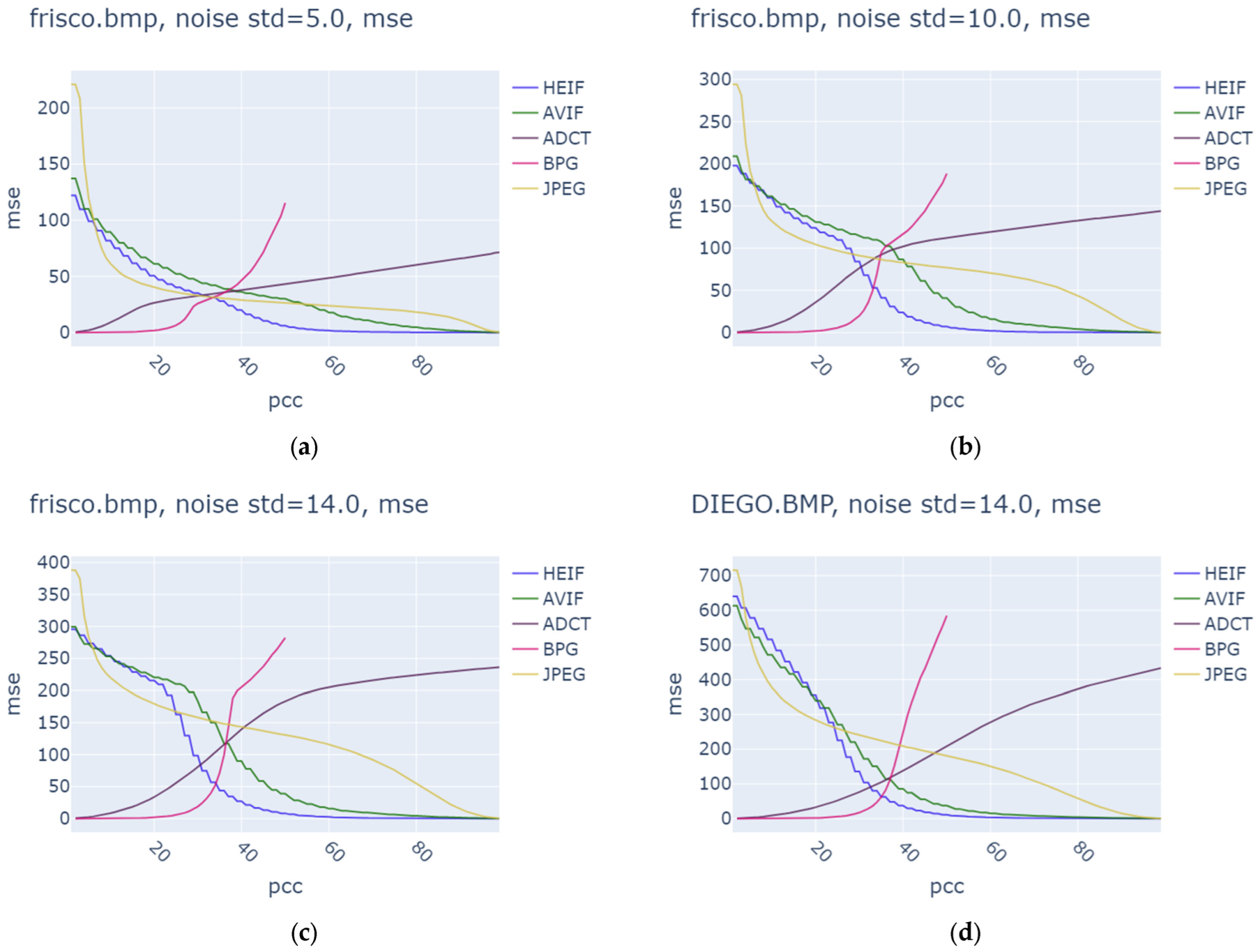



| Noise Variance | JPEG | AVIF | HEIF | BPG | ||||
|---|---|---|---|---|---|---|---|---|
| PSNRmax | CR | PSNRmax | CR | PSNRmax | CR | PSNRmax | CR | |
| 25 | 36.5 (QF = 48) | 13.2 | 38.0 (QF = 51) | 26.5 | 37.7 (QF = 33) | 31.6 | 39.3 (Q = 30) | 22.4 |
| 100 | 32.2 (QF = 14) | 29.8 | 34.7 (QF = 35) | 46.8 | 34.6 (QF = 25) | 49.8 | 35.7 (Q = 36) | 41.2 |
| 196 | 30.2 (QF = 10) | 34.7 | 32.9 (QF = 27) | 61.2 | 33.0 (QF = 21) | 66.0 | 33.8 (Q = 39) | 56.6 |
| Noise Variance | JPEG | AVIF | HEIF | BPG | ||||
|---|---|---|---|---|---|---|---|---|
| MS-SSIMmax | CR | MS-SSIMmax | CR | MS-SSIMmax | CR | MS-SSIMmax | CR | |
| 25 | 0.9743 (QF = 33) | 18.3 | 0.9814 (QF = 49) | 30.2 | 0.9815 (QF = 33) | 31.6 | 0.9856 (Q = 30) | 22.4 |
| 100 | 0.9738 (QF = 13) | 31.7 | 0.9659 (QF = 33) | 57.8 | 0.9645 (QF = 23) | 61.1 | 0.9716 (Q = 36) | 41.2 |
| 196 | 0.9002 (QF = 7) | 45.3 | 0.9526 (QF = 25) | 69.3 | 0.9508 (QF = 21) | 66.0 | 0.9601 (Q = 39) | 56.6 |
| Noise Variance | JPEG | AVIF | HEIF | BPG | ||||
|---|---|---|---|---|---|---|---|---|
| PSNRmax | CR | PSNRmax | CR | PSNRmax | CR | PSNRmax | CR | |
| 196 | 24.9 (QF = 28) | 7.6 | 24.8 (QF = 24 *) | 16.9 | 25.5 (QF = 25) | 11.5 | 25.9 (Q = 39) | 10.4 |
| σ2 | 20–30 | 31–44 | 45–64 | 65–90 | 91–130 | 131–180 | >180 |
| QFst for AVIF | 50 | 45 | 41 | 37 | 33 | 30 | 25 |
| QFst for HEIF | 33 | 31 | 29 | 27 | 26 | 25 | 24 |
| Image | Encoder | PCC | Compression Time | Decompression Time |
|---|---|---|---|---|
| Frisco.bmp | BPG | 2 | 0.69 | 0.19 |
| Frisco.bmp | BPG | 40 | 0.24 | 0.12 |
| DIEGO.BMP | BPG | 2 | 0.74 | 0.24 |
| DIEGO.BMP | BPG | 40 | 0.36 | 0.19 |
| fr02.bmp | BPG | 2 | 0.73 | 0.22 |
| fr02.bmp | BPG | 40 | 0.34 | 0.18 |
| frisco.bmp | HEIF | 98 | 0.37 | 0.04 |
| frisco.bmp | HEIF | 30 | 0.15 | 0.02 |
| DIEGO.BMP | HEIF | 98 | 0.4 | 0.06 |
| DIEGO.BMP | HEIF | 30 | 0.23 | 0.04 |
| fr02.bmp | HEIF | 98 | 0.44 | 0.06 |
| fr02.bmp | HEIF | 30 | 0.2 | 0.04 |
| frisco.bmp | AVIF | 98 | 0.23 | 0.05 |
| frisco.bmp | AVIF | 30 | 0.09 | 0.02 |
| DIEGO.BMP | AVIF | 98 | 0.34 | 0.07 |
| DIEGO.BMP | AVIF | 30 | 0.17 | 0.03 |
| fr02.bmp | AVIF | 98 | 0.31 | 0.06 |
| fr02.bmp | AVIF | 30 | 0.21 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kryvenko, S.; Lukin, V.; Vozel, B. Lossy Compression of Single-channel Noisy Images by Modern Coders. Remote Sens. 2024, 16, 2093. https://doi.org/10.3390/rs16122093
Kryvenko S, Lukin V, Vozel B. Lossy Compression of Single-channel Noisy Images by Modern Coders. Remote Sensing. 2024; 16(12):2093. https://doi.org/10.3390/rs16122093
Chicago/Turabian StyleKryvenko, Sergii, Vladimir Lukin, and Benoit Vozel. 2024. "Lossy Compression of Single-channel Noisy Images by Modern Coders" Remote Sensing 16, no. 12: 2093. https://doi.org/10.3390/rs16122093
APA StyleKryvenko, S., Lukin, V., & Vozel, B. (2024). Lossy Compression of Single-channel Noisy Images by Modern Coders. Remote Sensing, 16(12), 2093. https://doi.org/10.3390/rs16122093








