Identifying Plausible Labels from Noisy Training Data for a Land Use and Land Cover Classification Application in Amazônia Legal
Abstract
1. Introduction
Learning with Noisy Labels
2. Materials and Methods
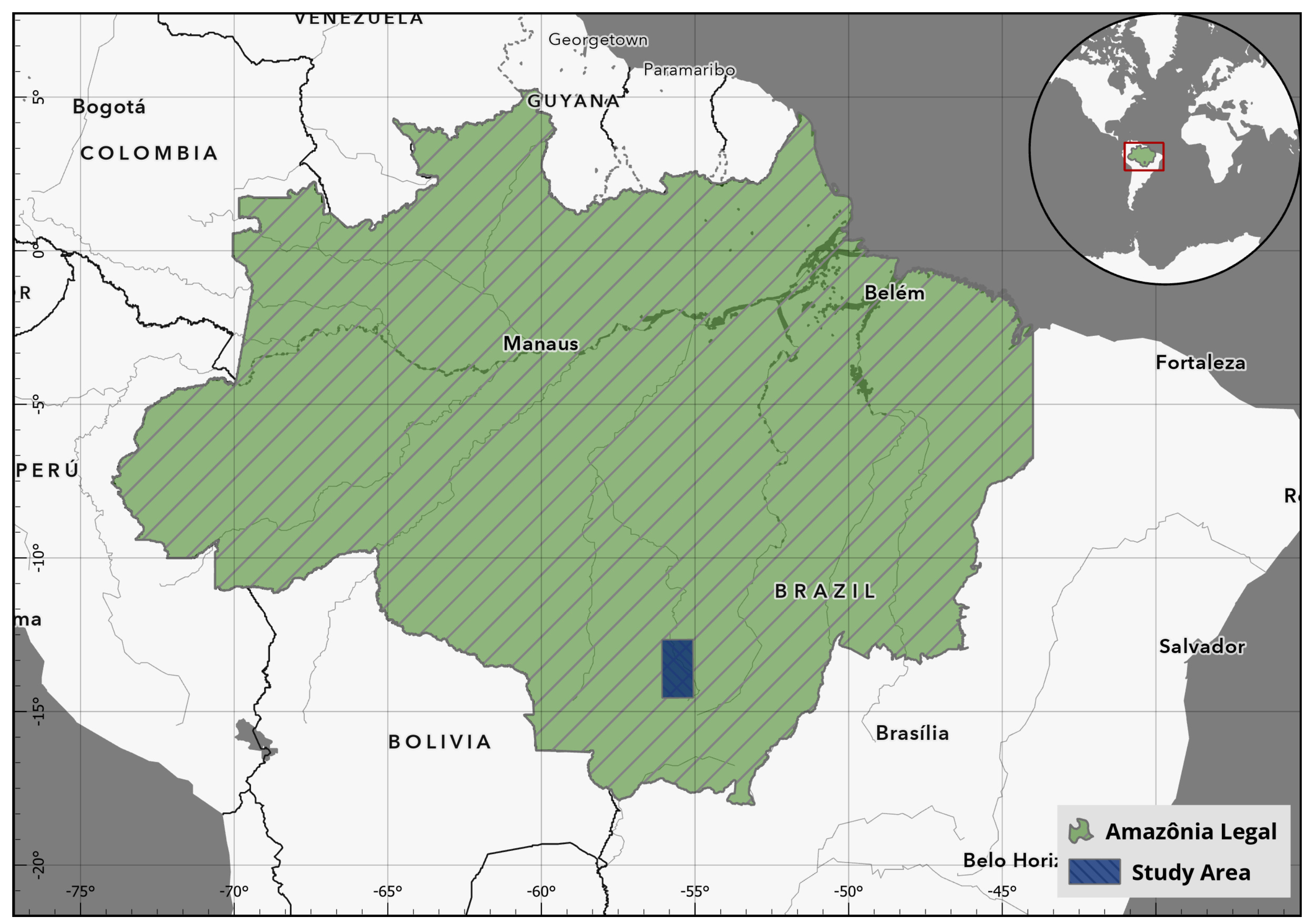
2.1. Study Area and Data
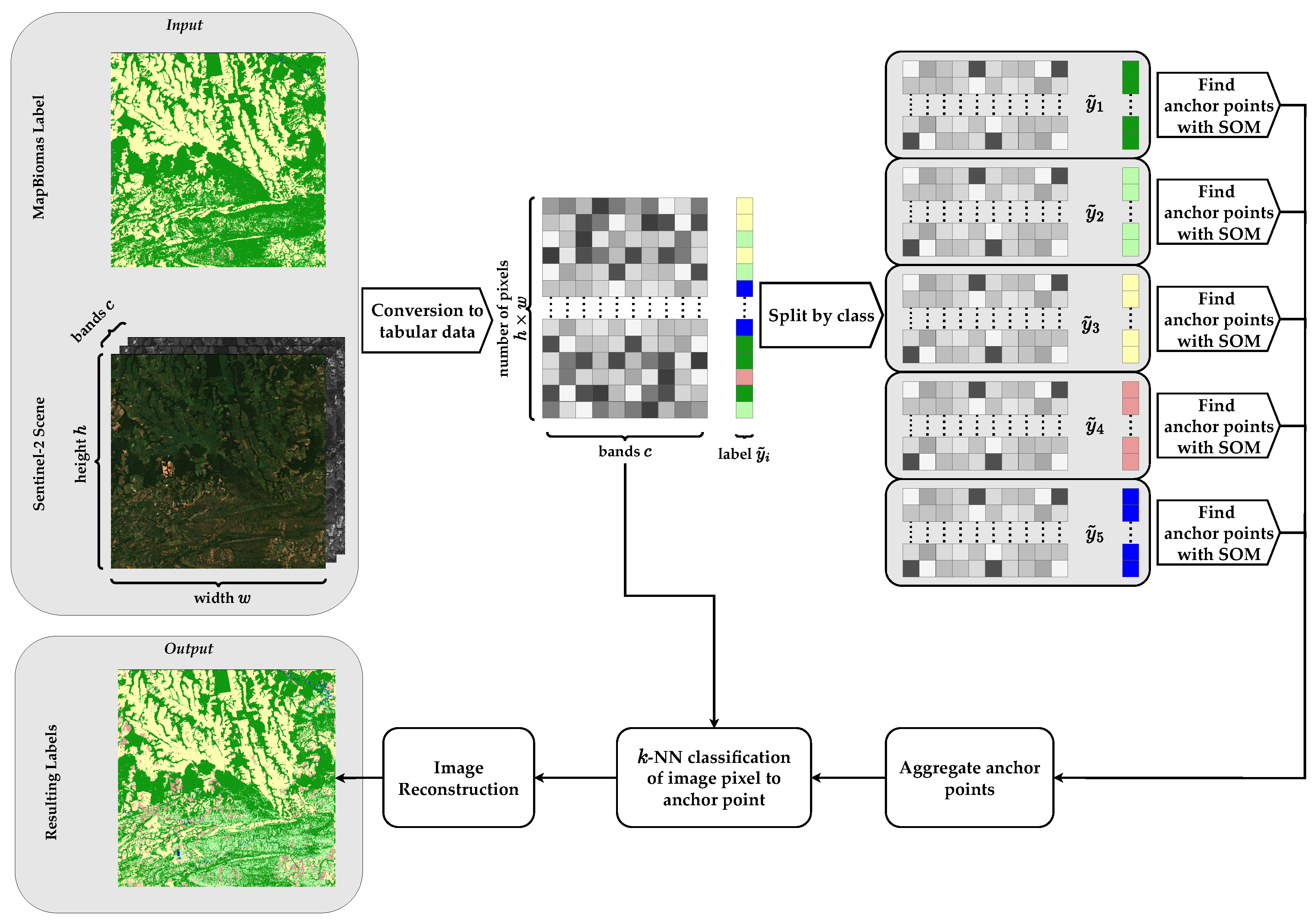
2.2. Identification of Noisy Labels
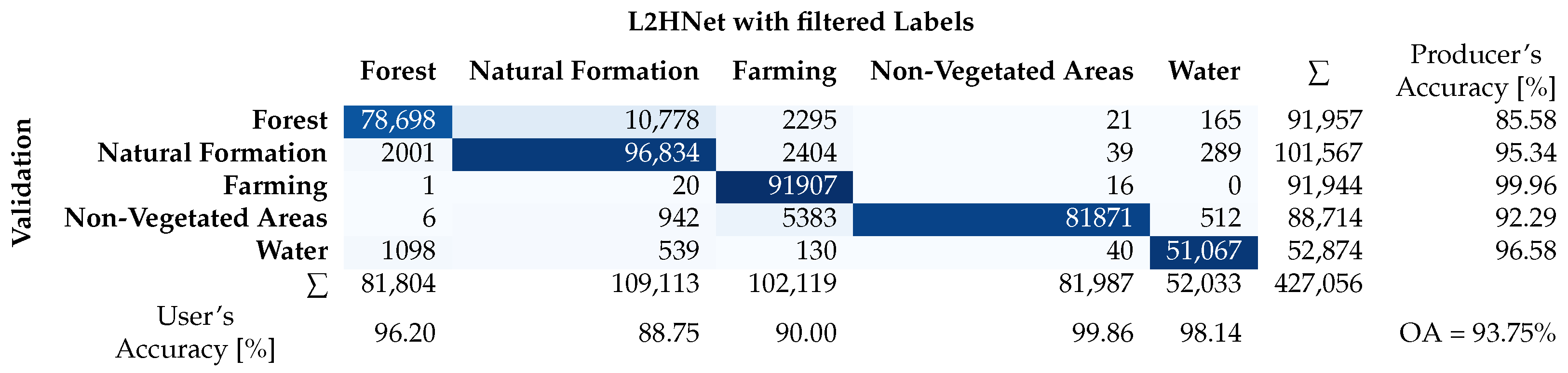
2.3. Validation
2.4. Comparison to Supervised Classification Methods
2.5. Performance Evaluation of L2HNet Using Filtered Labels
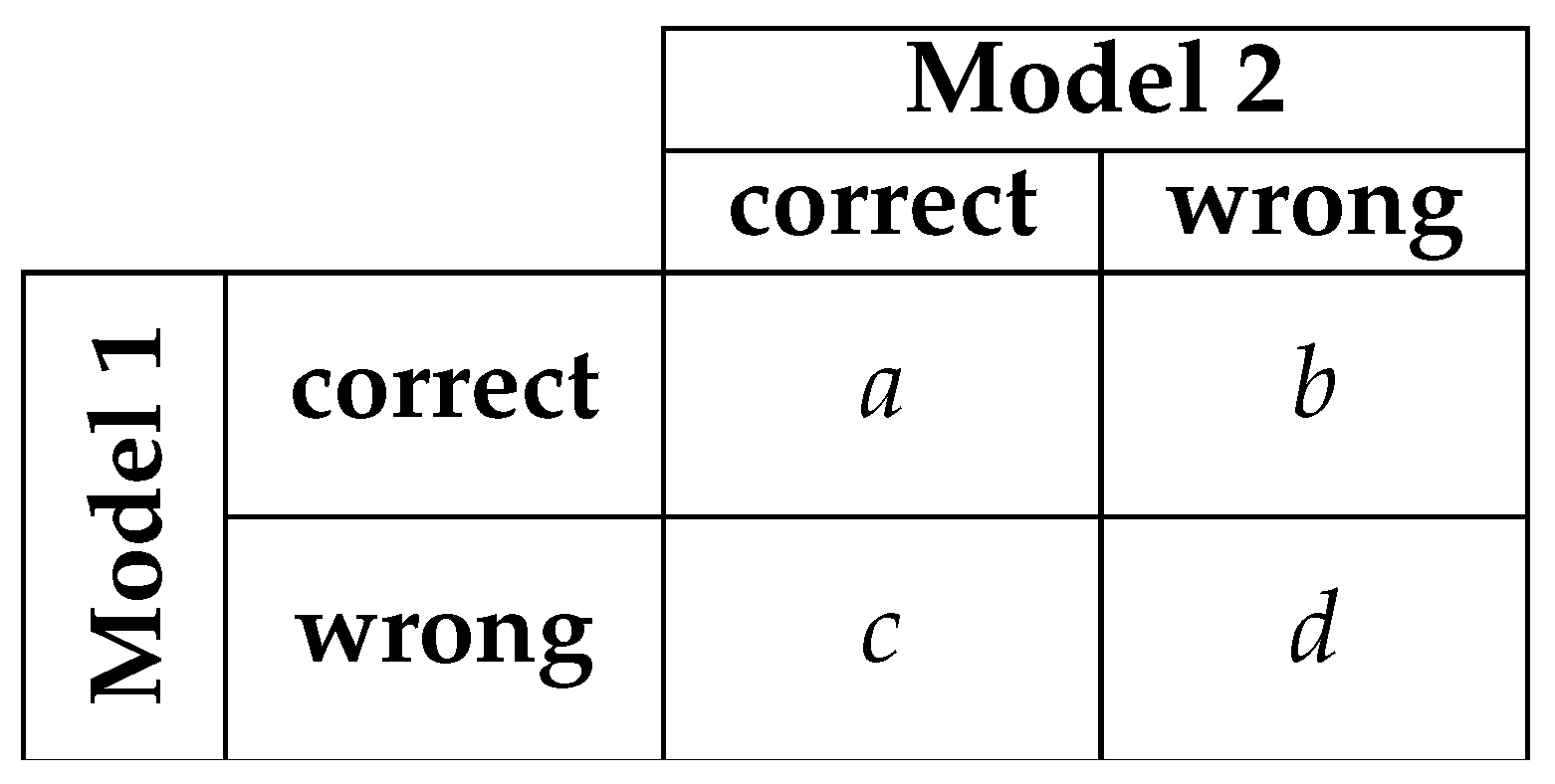
Statistical Significance Tests
3. Results
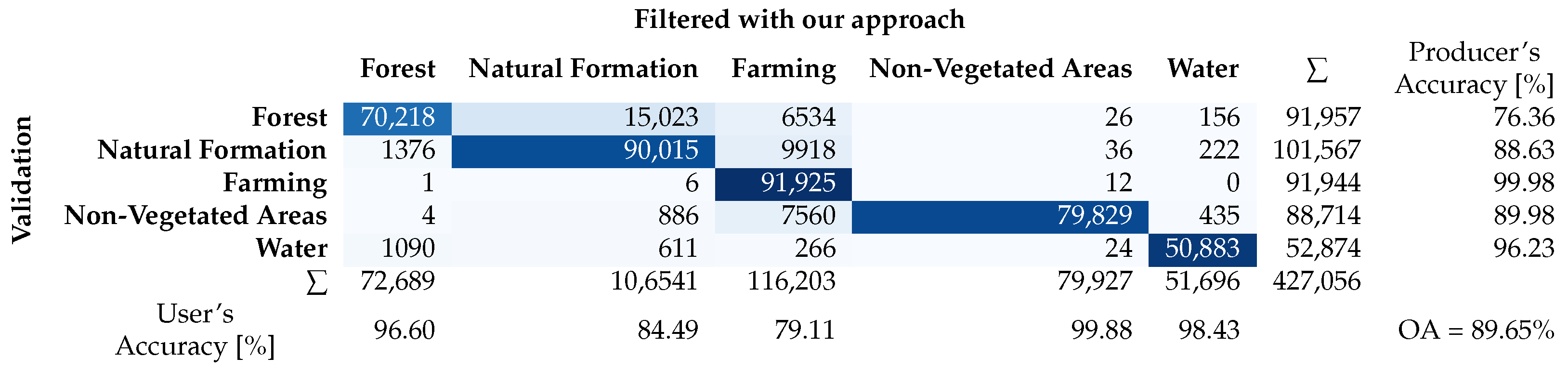
3.1. Quantitative Assessment
3.2. Qualitative Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LULC | Land Use and Land Cover |
| SOM | Self-organizing map |
| OA | Overall Accuracy |
| PA | Producer’s Accuracy |
| UA | User’s Accuracy |
Appendix A

References
- The Nature Conservancy. The Amazon is Our Planet’s Greatest Life Reserve and Our World’s Largest Tropical Rainforest; The Nature Conservancy: Arlington, VA, USA, 2020. [Google Scholar]
- Baer, H.A.; Singer, M. The Anthropology of Climate Change: An Integrated Critical Perspective, 2nd ed.; Routledge: London, UK, 2018. [Google Scholar] [CrossRef]
- de Area Leão Pereira, E.J.; Silveira Ferreira, P.J.; de Santana Ribeiro, L.C.; Sabadini Carvalho, T.; de Barros Pereira, H.B. Policy in Brazil (2016–2019) threaten conservation of the Amazon rainforest. Environ. Sci. Policy 2019, 100, 8–12. [Google Scholar] [CrossRef]
- Carvalho, T.S.; Domingues, E.P.; Horridge, J.M. Controlling deforestation in the Brazilian Amazon: Regional economic impacts and land-use change. Land Use Policy 2017, 64, 327–341. [Google Scholar] [CrossRef]
- PRODES—Coordenação—Geral de Observação da Terra. Available online: http://www.obt.inpe.br/OBT/assuntos/programas/amazonia/prodes (accessed on 2 February 2024).
- Souza, C.M., Jr.; Z. Shimbo, J.; Rosa, M.R.; Parente, L.L.; A. Alencar, A.; Rudorff, B.F.T.; Hasenack, H.; Matsumoto, M.; G. Ferreira, L.; Souza-Filho, P.W.M.; et al. Reconstructing Three Decades of Land Use and Land Cover Changes in Brazilian Biomes with Landsat Archive and Earth Engine. Remote Sens. 2020, 12, 2735. [Google Scholar] [CrossRef]
- Berenguer, E.; Armenteras, D.; Lees, A.C.; Smith, C.C.; Fearnside, P.; Nascimento, N.; Alencar, A.; Almeida, C.; Aragão, L.E.O.; Barlow, J.; et al. Chapter 19: Drivers and ecological impacts of deforestation and forest degradation. In Amazon Assessment Report 2021, 1st ed.; Nobre, C., Encalada, A., Anderson, E., Roca Alcazar, F.H., Bustamante, M., Mena, C., Peña-Claros, M., Poveda, G., Rodriguez, J.P., Saleska, S., et al., Eds.; United Nations Sustainable Development Solutions Network: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Cherif, E.; Hell, M.; Brandmeier, M. DeepForest: Novel Deep Learning Models for Land Use and Land Cover Classification Using Multi-Temporal and -Modal Sentinel Data of the Amazon Basin. Remote Sens. 2022, 14, 5000. [Google Scholar] [CrossRef]
- Zhou, Z.H. A brief introduction to weakly supervised learning. Natl. Sci. Rev. 2018, 5, 44–53. [Google Scholar] [CrossRef]
- Han, J.; Luo, P.; Wang, X. Deep Self-Learning From Noisy Labels. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5138–5147. [Google Scholar]
- Feng, W.; Long, Y.; Wang, S.; Quan, Y. A review of addressing class noise problems of remote sensing classification. J. Syst. Eng. Electron. 2023, 34, 36–46. [Google Scholar] [CrossRef]
- Hickey, R.J. Noise modelling and evaluating learning from examples. Artif. Intell. 1996, 82, 157–179. [Google Scholar] [CrossRef]
- Brodley, C.E.; Friedl, M.A. Identifying Mislabeled Training Data. J. Artif. Intell. Res. 1999, 11, 131–167. [Google Scholar] [CrossRef]
- Nettleton, D.F.; Orriols-Puig, A.; Fornells, A. A study of the effect of different types of noise on the precision of supervised learning techniques. Artif. Intell. Rev. 2010, 33, 275–306. [Google Scholar] [CrossRef]
- Liu, Y. Understanding Instance-Level Label Noise: Disparate Impacts and Treatments. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 6725–6735, ISSN 2640-3498. [Google Scholar]
- Lachenbruch, P.A. Discriminant Analysis When the Initial Samples Are Misclassified. Technometrics 1966, 8, 657. [Google Scholar] [CrossRef]
- Zhu, Z.; Dong, Z.; Liu, Y. Detecting Corrupted Labels without Training a Model to Predict. In Proceedings of the 39th International Conference on Machine Learning, PMLR, Baltimore, ML, USA, 17–23 July 2022; pp. 27412–27427, ISSN 2640-3498. [Google Scholar]
- Frenay, B.; Verleysen, M. Classification in the Presence of Label Noise: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 845–869. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Herrera, F. Dealing with Noisy Data. In Data Preprocessing in Data Mining; García, S., Luengo, J., Herrera, F., Eds.; Intelligent Systems Reference Library; Springer International Publishing: Cham, Switzerland, 2015; pp. 107–145. [Google Scholar] [CrossRef]
- Teng, C.M. Correcting Noisy Data. In Proceedings of the Sixteenth International Conference on Machine Learning; ICML ’99; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1999; pp. 239–248. [Google Scholar]
- Verbaeten, S.; Van Assche, A. Ensemble Methods for Noise Elimination in Classification Problems. In Proceedings of the Multiple Classifier Systems; Windeatt, T., Roli, F., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; pp. 317–325. [Google Scholar] [CrossRef]
- Ghosh, A.; Manwani, N.; Sastry, P.S. Making Risk Minimization Tolerant to Label Noise. Neurocomputing 2015, 160, 93–107. [Google Scholar] [CrossRef]
- Gao, W.; Wang, L.; Li, Y.F.; Zhou, Z.H. Risk Minimization in the Presence of Label Noise. Proc. AAAI Conf. Artif. Intell. 2016, 30, 10293. [Google Scholar] [CrossRef]
- Thulasidasan, S.; Bhattacharya, T.; Bilmes, J.; Chennupati, G.; Mohd-Yusof, J. Combating Label Noise in Deep Learning Using Abstention. arXiv 2019, arXiv:1905.10964. [Google Scholar] [CrossRef]
- Hao, D.; Zhang, L.; Sumkin, J.; Mohamed, A.; Wu, S. Inaccurate Labels in Weakly-Supervised Deep Learning: Automatic Identification and Correction and Their Impact on Classification Performance. IEEE J. Biomed. Health Inform. 2020, 24, 2701–2710. [Google Scholar] [CrossRef]
- Patrini, G.; Rozza, A.; Krishna Menon, A.; Nock, R.; Qu, L. Making Deep Neural Networks Robust to Label Noise: A Loss Correction Approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1944–1952. [Google Scholar]
- Tanaka, D.; Ikami, D.; Yamasaki, T.; Aizawa, K. Joint Optimization Framework for Learning with Noisy Labels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5552–5560. [Google Scholar]
- Bahri, D.; Jiang, H.; Gupta, M. Deep k-NN for Noisy Labels. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 540–550, ISSN 2640-3498. [Google Scholar]
- Northcutt, C.; Jiang, L.; Chuang, I. Confident Learning: Estimating Uncertainty in Dataset Labels. J. Artif. Intell. Res. 2021, 70, 1373–1411. [Google Scholar] [CrossRef]
- Lee, K.H.; He, X.; Zhang, L.; Yang, L. CleanNet: Transfer Learning for Scalable Image Classifier Training with Label Noise. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June2018; pp. 5447–5456. [Google Scholar]
- Lu, Z.; Fu, Z.; Xiang, T.; Han, P.; Wang, L.; Gao, X. Learning from Weak and Noisy Labels for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 486–500. [Google Scholar] [CrossRef]
- Thyagarajan, A.; Snorrason, E.; Northcutt, C.; Mueller, J. Identifying Incorrect Annotations in Multi-Label Classification Data. arXiv 2022, arXiv:2211.13895. [Google Scholar] [CrossRef]
- Kim, Y.; Yim, J.; Yun, J.; Kim, J. NLNL: Negative Learning for Noisy Labels. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 101–110. [Google Scholar]
- Wilson, D.R.; Martinez, T.R. Instance Pruning Techniques. In Machine Learning: Proceedings of the Fourteenth International Conference; Morgan Kaufmann Publishers: Nashville, TN, USA, 1997. [Google Scholar]
- Wilson, D.R. Reduction Techniques for Instance-Based Learning Algorithms; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Peikari, M.; Salama, S.; Nofech-Mozes, S.; Martel, A.L. A Cluster-then-label Semi-supervised Learning Approach for Pathology Image Classification. Sci. Rep. 2018, 8, 7193. [Google Scholar] [CrossRef]
- Zhu, Z.; Song, Y.; Liu, Y. Clusterability as an Alternative to Anchor Points When Learning with Noisy Labels. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 12912–12923, ISSN 2640-3498. [Google Scholar]
- Tu, B.; Kuang, W.; He, W.; Zhang, G.; Peng, Y. Robust Learning of Mislabeled Training Samples for Remote Sensing Image Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5623–5639. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Zhu, Z. Learning Deep Networks under Noisy Labels for Remote Sensing Image Scene Classification. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3025–3028, ISSN 2153-7003. [Google Scholar] [CrossRef]
- Kang, J.; Fernandez-Beltran, R.; Kang, X.; Ni, J.; Plaza, A. Noise-Tolerant Deep Neighborhood Embedding for Remotely Sensed Images with Label Noise. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2551–2562. [Google Scholar] [CrossRef]
- Aksoy, A.K.; Ravanbakhsh, M.; Demir, B. Multi-Label Noise Robust Collaborative Learning for Remote Sensing Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef]
- Burgert, T.; Ravanbakhsh, M.; Demir, B. On the Effects of Different Types of Label Noise in Multi-Label Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Y.; Ghamisi, P. Complementary Learning-Based Scene Classification of Remote Sensing Images with Noisy Labels. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Tu, B.; Zhang, X.; Kang, X.; Zhang, G.; Li, S. Density Peak-Based Noisy Label Detection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1573–1584. [Google Scholar] [CrossRef]
- Bahraini, T.; Azimpour, P.; Yazdi, H.S. Modified-mean-shift-based noisy label detection for hyperspectral image classification. Comput. Geosci. 2021, 155, 104843. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.; Lu, F.; Xue, R.; Yang, G.; Zhang, L. Breaking the resolution barrier: A low-to-high network for large-scale high-resolution land-cover mapping using low-resolution labels. ISPRS J. Photogramm. Remote Sens. 2022, 192, 244–267. [Google Scholar] [CrossRef]
- MapBiomas. Em 38 Anos o Brasil Perdeu 15% de Suas Florestas Naturais; MapBiomas: Sao Paulo, Brazil, 2023. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- MapBiomas. MapBiomas General “Handbook” Algorithm Theoretical Basis Document (ATBD) Collection 8; Technical Report; MapBiomas: Sao Paulo, Brazil, 2023. [Google Scholar]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Chang, C.L. Finding Prototypes For Nearest Neighbor Classifiers. IEEE Trans. Comput. 1974, C-23, 1179–1184. [Google Scholar] [CrossRef]
- Wittek, P.; Gao, S.C.; Lim, I.S.; Zhao, L. Somoclu: An Efficient Parallel Library for Self-Organizing Maps. J. Stat. Softw. 2017, 78, 1–21. [Google Scholar] [CrossRef]
- Theodoridis, S.; Koutroumbas, K. Chapter 5—Feature Selection. In Pattern Recognition, 4th ed.; Theodoridis, S., Koutroumbas, K., Eds.; Academic Press: Boston, MA, USA, 2009; pp. 261–322. [Google Scholar] [CrossRef]
- Windrim, L.; Ramakrishnan, R.; Melkumyan, A.; Murphy, R.J.; Chlingaryan, A. Unsupervised Feature—Learning for Hyperspectral Data with Autoencoders. Remote Sens. 2019, 11, 864. [Google Scholar] [CrossRef]
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef]
- Kumar, P.; Prasad, R.; Choudhary, A.; Mishra, V.N.; Gupta, D.K.; Srivastava, P.K. A statistical significance of differences in classification accuracy of crop types using different classification algorithms. Geocarto Int. 2017, 32, 206–224. [Google Scholar] [CrossRef]
- Edwards, A.L. Note on the “correction for continuity” in testing the significance of the difference between correlated proportions. Psychometrika 1948, 13, 185–187. [Google Scholar] [CrossRef]






| Class Name | Macro Class | Number of Pixels | Proportion of Study Area | ||
|---|---|---|---|---|---|
| Forest Formation | Forest | 56,666,057 | 56,666,057 | 24.60% | 24.60% |
| Savanna Formation | Natural Formation | 47,971,701 | 50,118,662 | 20.82% | 21.75% |
| Grassland | 57,437 | 0.02% | |||
| Wetland | 2,089,524 | 0.91% | |||
| Pasture | Farming | 11,936,233 | 121,651,497 | 5.18% | 52.80% |
| Soybean | 103,705,267 | 45.01% | |||
| Other Temporary Crop | 1,739,405 | 0.76% | |||
| Forest Plantation | 198,954 | 0.09% | |||
| Mosaic of Uses | 4,071,638 | 1.77% | |||
| Urban Area | Non-Vegetated Areas | 354,163 | 1,351,900 | 0.15% | 0.59% |
| Other Non-Vegetated Area | 997,737 | 0.43% | |||
| River, Lake, Ocean | Water | 594,244 | 594,244 | 0.26% | 0.26% |
| 230,382,360 | |||||
| MapBiomas | Denoised | Random Forest | L2HNet | L2HNet (Filtered) | |
|---|---|---|---|---|---|
| Forest | 79.50% | 85.30% | 92.99% | 90.70% | 90.58% |
| Natural Formation | 91.63% | 86.51% | 89.68% | 87.01% | 91.93% |
| Farming | 83.78% | 88.33% | 92.35% | 67.08% | 94.72% |
| Non-Vegetated Areas | 41.55% | 94.67% | 93.65% | 13.62% | 95.92% |
| Water | 90.64% | 97.32% | 96.25% | 96.40% | 97.36% |
| (a) Fisher’s discriminant ratio of the MapBiomas classes (level 1) with the Sentinel-2 data. | ||||
| Water | Non-Vegetated Area | Farming | Natural Formation | |
| Forest | 1.48 | 1.97 | 0.89 | 0.89 |
| Natural Formation | 1.65 | 0.88 | 0.84 | |
| Farming | 2.67 | 1.12 | ||
| Non-Vegetated Area | 2.18 | |||
| (b) Fisher’s discriminant ratio of the corrected labels with the Sentinel-2 data. | ||||
| Water | Non-Vegetated Area | Farming | Natural Formation | |
| Forest | 1.30 | 4.25 | 2.24 | 2.90 |
| Natural Formation | 1.99 | 1.78 | 1.89 | |
| Farming | 3.25 | 2.38 | ||
| Non-Vegetated Area | 3.75 | |||
| Classifier 1 | Classifier 2 | a | b | c | d | -Test | p-Value |
|---|---|---|---|---|---|---|---|
| MapBiomas | L2HNet | 303,274 | 37,749 | 14,069 | 71,964 | 10,820.47 | |
| MapBiomas | L2HNet filtered | 323,554 | 17,469 | 76,823 | 9210 | 37,360.31 | |
| L2HNet | L2HNet filtered | 305,642 | 11,701 | 94,735 | 14,978 | 64,775.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hell, M.; Brandmeier, M. Identifying Plausible Labels from Noisy Training Data for a Land Use and Land Cover Classification Application in Amazônia Legal. Remote Sens. 2024, 16, 2080. https://doi.org/10.3390/rs16122080
Hell M, Brandmeier M. Identifying Plausible Labels from Noisy Training Data for a Land Use and Land Cover Classification Application in Amazônia Legal. Remote Sensing. 2024; 16(12):2080. https://doi.org/10.3390/rs16122080
Chicago/Turabian StyleHell, Maximilian, and Melanie Brandmeier. 2024. "Identifying Plausible Labels from Noisy Training Data for a Land Use and Land Cover Classification Application in Amazônia Legal" Remote Sensing 16, no. 12: 2080. https://doi.org/10.3390/rs16122080
APA StyleHell, M., & Brandmeier, M. (2024). Identifying Plausible Labels from Noisy Training Data for a Land Use and Land Cover Classification Application in Amazônia Legal. Remote Sensing, 16(12), 2080. https://doi.org/10.3390/rs16122080







