Abstract
Addressing the formidable challenges posed by multiple jammers jamming multiple radars, which arise from spatial discretization, many degrees of freedom, numerous model input parameters, and the complexity of constraints, along with a multi-peaked objective function, this paper proposes a cooperative jamming resource allocation method, based on evolutionary reinforcement learning, that uses joint multi-domain information. Firstly, an adversarial scenario model is established, characterizing the interaction between multiple jammers and radars based on a multi-beam jammer model and a radar detection model. Subsequently, considering real-world scenarios, this paper analyzes the constraints and objective function involved in cooperative jamming resource allocation by multiple jammers. Finally, accounting for the impact of spatial, frequency, and energy domain information on jamming resource allocation, matrices representing spatial condition constraints, jamming beam allocation, and jamming power allocation are formulated to characterize the cooperative jamming resource allocation problem. Based on this foundation, the joint allocation of the jamming beam and jamming power is optimized under the constraints of jamming resources. Through simulation experiments, it was determined that, compared to the dung beetle optimizer (DBO) algorithm and the particle swarm optimization (PSO) algorithm, the proposed evolutionary reinforcement learning algorithm based on DBO and Q-Learning (DBO-QL) offers 3.03% and 6.25% improvements in terms of jamming benefit and 26.33% and 50.26% improvements in terms of optimization success rate, respectively. In terms of algorithm response time, the proposed hybrid DBO-QL algorithm has a response time of 0.11 s, which is 97.35% and 96.57% lower than the response times of the DBO and PSO algorithms, respectively. The results show that the method proposed in this paper has good convergence, stability, and timeliness.
1. Introduction
With the advancements in electronic warfare and technologies such as artificial intelligence (AI), radar and jamming systems endowed with cognitive capabilities have made significant progress [1,2,3,4,5,6]. These emerging technologies have transformed the traditional paradigms of electronic warfare engagement, shifting away from the conventional “one-to-one”, “one-to-many”, or “many-to-one” configurations to the more complex “many-to-many” engagement [7,8,9]. Consequently, conventional electronic warfare methods have proven incapable of adapting to the evolving dynamics of modern battlefields. The concept of cognitive electronic warfare has thus been introduced and is gradually emerging as a new developmental trend, poised to play a crucial role in future warfare scenarios [10,11,12]. In the context of “many-to-many” scenarios, the jamming entities now contend with multiple radars or networked radar systems as opposed to a single radar. Taking a networked radar system as an example, it possesses the ability to gather, integrate, and leverage the resources and information advantages of various radars, rendering the traditional approach of employing a single jamming system less effective. Consequently, the cooperative jamming technique, involving multiple jammers and characterized by its broad jamming range, low hardware requirements, high system flexibility, and coordinated control of jamming beams, has become a focal point of current research [13,14,15].
As the complexity of real battlefield environments continues to increase, the efficient allocation of jamming resources, enabling jammers to maximize their jamming effectiveness with limited resources, has become a central challenge in the field of electronic warfare and related domains. Jamming resource allocation represents one manifestation of resource allocation in the domain of electronic warfare, and various resource allocation methods across different domains offer opportunities for mutual cross-fertilization. In recent years, research on communication resource allocation in the context of cognitive communication has yielded rich results, encompassing aspects such as time [16], space [17], spectra [18,19,20], and energy [20,21,22]. These achievements provide valuable references for the investigation of radar-jamming resource allocation.
Numerous scholars have conducted research on the problem of cooperative jamming resource allocation for multiple jammers. Zou [23], Wu [24], Jiang [25], and others have made improvements to the PSO algorithm to enhance its optimization probability and stability when dealing with cooperative jamming resource allocation. Lu et al. [26] employed detection and targeting probability to characterize the jamming effectiveness of a networked radar system in search and tracking modes, constructed a dual-factor jamming effectiveness assessment function, established a non-convex optimization model for cooperative jamming in a networked radar system, and utilized the dynamic adaptive discrete cuckoo search algorithm (DADCS), featuring improved path update strategies and the introduction of a global learning mechanism, to solve the model. This approach achieved the cooperative jamming resource allocation for aircraft formation in a networked radar system. Xing et al. [27] evaluated jamming suppression effects using a constant false-alarm rate detection model for networked radar, established a cooperative control model for multiple jammers involving jamming beams and transmission power levels, and utilized an enhanced improved artificial bee colony (IABC) algorithm to derive optimized allocation solutions for different operational scenarios. Yao et al. [28] developed a jamming resource allocation model considering factors such as jamming beams and jamming power, and solved the model using an improved genetic algorithm (GA), allowing for jamming resource allocation in networked radar systems with any number of nodes under conditions of limited jamming resources. Xing et al. [29] quantified target threat levels through fuzzy comprehensive evaluation, constructed a jamming resource allocation model based on the jamming efficiency matrix, and proposed an improved firefly algorithm (FA) to solve the model, ensuring both the rationality of task assignments and the stability of the algorithm. While these research achievements provide insights into addressing the problem of cooperative jamming resource allocation for multiple jammers, most of the established models are relatively simplistic. Additionally, the three dimensions of the spatial, frequency, and energy domains have not been comprehensively considered together. Moreover, as the scale of jamming resource allocation expands, existing algorithms are becoming increasingly prone to problems such as dimension explosion in solving, decreased convergence speed, reduced optimization probability, and longer algorithm response times. Consequently, obtaining an optimal solution becomes challenging and may not meet practical application requirements.
In recent years, reinforcement learning (RL) technology has been developed and deepened, with its ability to learn strategies that maximize rewards through the interaction of the agent with the environment [30] providing an effective solution for perceptual decision-making problems in complex systems. Nowadays, RL is widely applied in various prominent fields such as autonomous driving, game AI, and robot control. Since 2014, the Google DeepMind team has been applying RL technology to Atari games, and this trained game AI can surpass the highest levels achieved by human players [31]. RL has also been applied in natural language processing, significantly enhancing its capabilities in semantic association, logical reasoning, and sentence generation [32]. Therefore, applying RL technology to the problem of jamming resource allocation is a direction worth exploring. Li et al. [33] modeled the breach process using a Markov decision process, and employed proximal policy optimization algorithms to learn the optimal sequential actions composed of jamming power allocation matrices and waypoints. The reward function defined depends on the distance to the target and the success or failure of the breach. The simulation experiments showed that this model could jointly learn the optimal path and jamming power allocation strategy, effectively completing the breach. Yue et al. [34] decoupled the coordination decision-making problem of a heterogeneous drone swarm for a suppression of enemy air defense mission divided into two sub-problems and solved them using a hierarchical multi-agent reinforcement learning approach. However, the current application of reinforcement learning in cooperative-jamming resource allocation for multiple jammers still faces challenges such as modeling difficulties and complex reward function design, resulting in poor adaptability to complex adversarial scenarios.
The development of evolutionary reinforcement learning (ERL) [35], which combines traditional evolutionary algorithms with reinforcement learning algorithms in order to enhance the speed and effectiveness of convergence, has provided a new perspective for solving the resource allocation problem. Xue et al. [36] proposed a hybrid algorithm combining deep Q networks (DQN) and GA for a resource-scheduling problem involving parallelism and subtask dependency. This algorithm generates the initial population of GA using DQN, improving its own convergence speed and optimization effect. Asghari et al. [37] used a coral reef algorithm to allocate resources to tasks and then used reinforcement learning to avoid falling into local optimums, by using this hybrid algorithm to improve resource allocation efficiency. Zhang et al. [38] addressed the problem of cluster-coordinated jamming decisions, improved the Q-learning algorithm by the ant colony algorithm, and a radar-jamming decision model was constructed, wherein each jammer in the cluster was mapped as an intelligent ant seeking the optimal path. Multiple jammers interacted to exchange information. This method enhanced the convergence speed and stability of the algorithm while reducing the hardware and power resource requirements for jammers.
Based on the above research findings, this paper further investigates the problem of cooperative jamming resource allocation based on multi-domain information. Combined with the idea of evolutionary reinforcement learning, this paper proposes a two-layer model for cooperative jamming resource allocation that integrally considers information in three dimensions: spatial, frequency, and energy domains. The jamming beam allocation matrix and jamming power allocation matrix were optimized using the outer DBO algorithm and the inner Q-learning algorithm, respectively. This method transforms the complex two-dimensional decision problem of the joint optimization of jamming beam allocation and jamming power allocation into two one-dimensional decision problems. The smaller dimensions of the solution space effectively prevent the algorithm from becoming trapped in a locally optimal solution and, at the same time, reduce the response time of the algorithm and ensure its stability.
In summary, the main contributions of this paper can be outlined as follows:
- A model containing a spatial condition constraint matrix, a jamming beam allocation matrix, and a jamming power allocation matrix was constructed to address the cooperative-jamming resource allocation problem. The model integrates information from the spatial, frequency, and energy domains to formulate constraints and an objective function, making its results more aligned with the complex real-world environment.
- In order to better solve the constructed model, an evolutionary reinforcement learning method called the hybrid DBO-QL algorithm was proposed. This method adopts a hierarchical selection and joint optimization strategy for jamming beam and power allocation, greatly reducing the response time of the algorithm while providing good convergence and stability.
The rest of this paper is organized as follows. Section 2 introduces the adversarial scenario model and formulates the constraints and objective function for cooperative jamming resource allocation among multiple jammers. Section 3 provides a detailed explanation of the DBO algorithm, Q-learning algorithm, and the proposed hybrid DBO-QL algorithm. Section 4 presents the simulation experiments and results’ analysis for the three algorithms. Finally, the conclusions drawn from this study are presented in Section 5.
2. System Model
Section 2 describes the modelling of an adversarial scenario for cooperative jamming resource allocation and the design of the constraints and an objective function based on the model.
2.1. Adversarial Scenario Model
This paper considers a “many-to-many” adversarial scenario model, as illustrated in Figure 1. In the spatial adversarial scenario, multiple multi-beam jamming aircraft (jammers) collaborate to perform coordinated jamming tasks against multiple ground radars. The multi-beam jamming systems of each aircraft can simultaneously generate multiple jamming beams to jam multiple radars in different directions. The resources, such as the pointing direction, quantity, and transmission power of the jamming beams, can be flexibly controlled. The radar side detects targets based on the received signal-to-jamming ratio (SJR). Due to the limited jamming power that each jamming aircraft can provide, it is necessary to reasonably allocate the attitude of each jamming aircraft and the transmission power of different beams based on real-time battlefield situation information to improve the utilization of jamming resources. This allocation method is designed to achieve the highest possible jamming benefit using limited jamming resources.
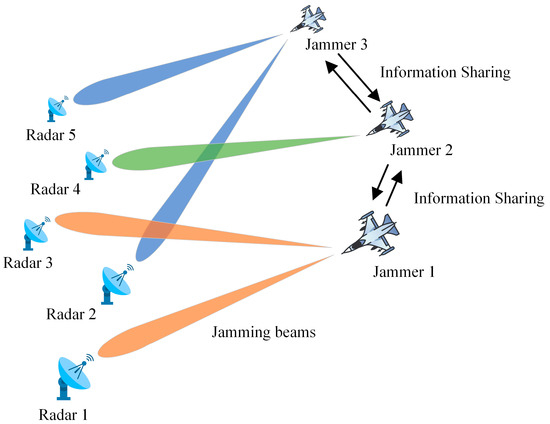
Figure 1.
Schematic diagram of the adversarial scenario.
2.2. Constraints and Objective Function for Cooperative Jamming Resource Allocation Using Multiple Jammers
From a mathematical perspective, the problem of cooperative jamming resource allocation using multiple jammers can be formulated as a multi-choice problem under multi-dimensional constraints. The objective is to minimize the detection performance of enemy radars under the constraint of limited jamming resources. In light of this, the present study integrates information from the spatial, frequency, and energy domains to consider and formulate the constraints and objective function for the cooperative-jamming resource allocation problem.
Assume there are M jammers and N radars in the adversarial scenario. To maximize jamming benefit, it is necessary to optimize the two jamming resources of the cooperative jamming system, namely, the jamming beam directions from jammers to radars and the transmission power of different jamming beams. For this purpose, a binary variable matrix K was defined to characterize the allocation relationship of jamming beam directions from jammers to radars, as shown in Equation (1).
Here, is a binary variable that can only assume values of ‘0’ or ‘1’. denotes that jammer m allocates jamming beams to radar n, while indicates that jammer m does not allocate jamming beams to radar n.
In terms of the allocation of transmission power for different jamming beams, a jamming power allocation matrix P was defined to quantify the distribution of power resources in the cooperative jamming system. The corresponding formulation is provided in Equation (2).
Here, represents the transmission power of the jamming beam assigned by jammer m to radar n.
Therefore, the objective of the cooperative-jamming resource allocation problem for multiple jammers is to solve for the optimal jamming beam allocation matrix K and jamming power allocation matrix P under multiple constraints. In this regard, the aim is to achieve optimal jamming performance in situations where system-jamming resources are limited. Furthermore, considering the constraints in cooperative-jamming resource allocation for multiple jammers, this paper designed an objective function that accurately quantifies the jamming benefit obtained from cooperative-jamming resource allocation. By solving the optimization problem, the best configuration for the system’s jamming resource variables is sought to maximize the jamming benefit characterized by the objective function.
2.2.1. Constraints
Setting the constraints for jamming resource allocation adequately and reasonably is beneficial for quickly finding the optimal jamming resource allocation strategy based on the actual battlefield situation, thereby enhancing the efficiency of jammer utilization. In this regard, this paper considers constraints for the system model based on the following five aspects:
- Spatial condition constraint. When allocating jamming resources, considering the practical situation, not all jammers can be assigned to jam a specific target radar. An essential prerequisite for such an assignment is that the jammer must be within the beam coverage area of that radar. Therefore, this paper defined a binary variable matrix Q to characterize the spatial relationship between jammers and radars, as shown in Equation (3).
- 2.
- Jamming beam allocation quantity constraint. Constrained by the payload capacity of the jammer itself, it is assumed that each jammer can simultaneously allocate a maximum of l jamming beams to jam multiple radars, as follows:
- 3.
- Jamming resource utilization constraint. A single jamming beam emitted by a multi-beam jammer can effectively jam one radar. In practice, the number of radars to be jammed may be several times the number of jammers. To enhance the efficiency of jamming resources and avoid wastage, it is stipulated that each radar can be assigned a maximum of one jamming beam, as follows:
- 4.
- Jamming power allocation constraint. Each targeted radar must be allocated jamming power. Assume that the SJR at the radar end is greater than 14 dB indicates that the jamming provided by the jammers is completely ineffective for the radar in question. An SJR less than 3 dB indicates that the radar has been effectively jammed, and further jamming power allocation beyond this range would result in a waste of jamming resources, as follows:
- 5.
- Total jamming power constraint. Constrained by the payload capacity of the jammer itself, the sum of the jamming power allocated to all jamming beams of a multi-beam jammer should not exceed the maximum jamming power it can provide, as follows:
2.2.2. Objective Function
The purpose of multi-jammer cooperative-jamming resource allocation is to minimize the detection probability of a radar system by optimizing the allocation of the jamming beam and power resources of the multi-jammer cooperative-jamming system while satisfying the working frequency matching between the jammers and the radars. Therefore, the objective function designed in this paper consists of the following four evaluation factors:
- Spectral alignment.
The spectral alignment factor for jammer m with radar n, denoted as (), is used to describe the alignment of jamming frequency with radar operating frequency. A spectral targeting benefit factor, , was defined to assess the overall spectral targeting degree of the current jamming resource allocation scheme and its impact on jamming effectiveness. A larger indicates a higher overall spectral targeting degree in the current jamming resource allocation scheme, leading to better jamming effectiveness.
Assuming the jamming frequency range for jammer m is [] and the operating frequency range for radar n is [], the spectral overlap between the jammer’s jamming frequency and the radar’s operating frequency in the frequency domain is illustrated in Figure 2.
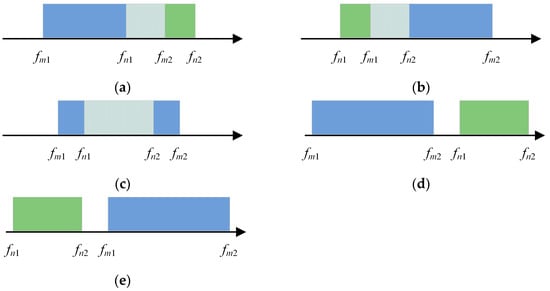
Figure 2.
Spectral overlap between the jammer and radar in the frequency domain: (a) ; (b) ; (c) ; (d) ; (e) .
From Figure 2, it can be observed that when there are three scenarios (a), (b), and (c) depicting the spectral overlap between the jammer’s jamming frequency and the radar’s operating frequency, the overlapping region in the figure can be represented using Equation (8).
When the jammer’s jamming frequency coincides with the radar’s operating frequency in scenarios (d) and (e), it can be observed that there is no overlapping region in the figure. In this case, the spectral overlap degree should be 0. However, if Equation (8) is used for calculation, will be a negative number, which is inaccurate. Therefore, this paper introduced the function , whose value is defined as follows:
Therefore, a formula satisfying all the situations depicted in Figure 2 for the spectral overlap degree can be defined using Equation (10).
where represents the operating bandwidth of the radar. Furthermore, the frequency-domain targeting benefit factor is expressed by Equation (11).
where is a normalization factor, and represents the frequency-domain overlap between jammer m and radar n.
- 2.
- Signal-to-jamming ratio at the radar receiver.
The detection probability on the radar side is closely associated with the SJR at its receiving end. The objective of cooperative-jamming resource allocation among multiple jammers is to appropriately determine the jamming power for jammers, thereby reducing the SJR at the radar end. Consequently, the SJR at the radar end serves as an evaluative metric for the jamming effectiveness at a given jamming power.
In the system model established in this paper, the jammers jam the radars to conceal themselves from detection by said radars. Therefore, the distance between the radar and the target is assumed to be equal to the distance between the radar and the jammer. Consequently, based on the radar equation, the SJR obtained by the radar can be expressed as follows:
where represents the target’s radar cross section area; and denote the transmission power of the radar signal and jamming signal, respectively; is the distance between the radar and the jammer; and are the power gains of the radar and jammer antennas, respectively; and is the polarization matching loss coefficient between the jamming signal and the radar signal.
Similarly, the SJR obtained by the jammer can be derived as follows:
where represents the wavelength of the transmitted signal.
The ratio between the SJR obtained by the radar and that obtained by the jammer can be obtained using the following formula:
Hence, the jammer can estimate the SJR at the radar receiver based on the SJR obtained by its own platforms. To assess the jamming effect of jammer m transmitting a jamming signal with power on radar n, the variable was defined to measure the effectiveness of the jamming, as expressed in Equation (15).
where is a scaling factor, and since this paper conventionally sets the minimum SJR to 3 dB, during the simulation experiments, was set to 3.
A radar receiver SJR benefit-factor, denoted as , was defined to evaluate the jamming effectiveness of the current jamming resource allocation scheme, as follows:
where is a normalization factor and represents the jamming effectiveness of jammer m with respect to radar n.
- 3.
- Distance between jammers and radars.
According to Equation (12), under the condition of maintaining a constant SJR at the radar end, the jamming power required to jam a radar is inversely proportional to the square of the distance between the radar and the jammer. In other words, the greater the distance between the jammer and the radar being jammed, the less jamming power required to jam the radar. This enables greater jamming effectiveness with reduced jamming power consumption.
Assuming the position of jammer m is denoted as and the position of radar n is denoted as , the distance between them can be expressed as follows:
An overall distance benefit factor was defined to evaluate the jamming effectiveness of the current jamming resource allocation scheme, as follows:
where is a normalization factor and represents the distance between jammer m and radar n.
- 4.
- Number of jammed radars.
In practical scenarios, the number of radars that can be jammed may be constrained by factors such as the quantity of jammers, payload limitations, and constraints in the spatial, frequency, and energy domains. Consequently, not all detected radars can be jammed by the jammers. The objective of cooperative-jamming resource allocation involving multiple jammers is to maximize the jamming coverage over the detected radars. To assess the jamming effectiveness of the current resource allocation scheme, a benefit factor for the number of jammed radars was defined as follows:
where is a normalization factor.
Employing a linear weighting method to balance the weights of the four evaluation factors mentioned above, these factors can be integrated into the following unified objective function:
where , , , and are weighting factors and .
J represents the jamming benefit, and a larger value indicates more effective jamming of the entire cooperative jamming system with respect to the radars. The magnitude of J can be used to gauge the rationality of jamming resource allocation, thereby enhancing the utilization efficiency of jamming resources.
3. Evolutionary Reinforcement Learning Method Based on the DBO and Q-Learning Algorithms
An evolutionary reinforcement learning method called the hybrid DBO-QL algorithm was developed for the cooperative-jamming resource allocation model involving the complex constraints constructed in Section 2. The principle of the proposed algorithm is elaborated in detail below.
3.1. DBO Algorithm
The DBO algorithm, introduced by Xue et al. [39] in 2022, is a novel metaheuristic swarm intelligence optimization algorithm and a type of evolutionary algorithm. It draws inspiration from the rolling, dancing, foraging, stealing, and reproductive behaviors of dung beetles. This algorithm simultaneously considers global and local exploitation, endowing it with fast convergence and high accuracy. It can effectively address complex optimization problems.
In the DBO algorithm, each dung beetle’s position corresponds to a solution. There are five behaviors exhibited by the dung beetles when foraging in this algorithm: rolling a ball, utilizing celestial cues such as the sun for navigation, thus allowing the ball to be rolled in a straight line; dancing, which allows a dung beetle to reposition itself; reproduction, a natural behavior in which dung beetles roll fecal balls to a secure location, where they hide and use the balls as a breeding ground; foraging, in which some adult dung beetles emerge from the ground to search for food; and stealing, in which certain dung beetles, known as thieves, steal fecal balls from other beetles.
Therefore, the dung beetle population in the algorithm is divided into four categories, namely, the ball-rolling dung beetle, the brood ball, the small dung beetle, and the thief, as shown in Figure 3. The population is divided into the different roles in a ratio of 6:6:7:11. In other words, according to the population size in Figure 3, out of 30 individuals, six dung beetles are assigned to engage in ball-rolling behavior. These ball-rolling dung beetles adjust their running direction based on various natural environmental influences, initially searching for a safe location for foraging. Another six dung beetles are designated as beetles engaging in reproductive behavior, and the reproduction balls will be placed in a known safe area. Seven dung beetles are defined as small dung beetles, which forage in the optimal foraging area. The remaining eleven dung beetles are classified as thieves, and thief dung beetles search for food based on the positions of other dung beetles and the optimal foraging area.

Figure 3.
The partitioning rules for the population.
3.1.1. Dung Beetle Ball Rolling
The conditions for ball rolling carried out by dung beetles can be categorized into two scenarios: obstacle-free conditions and conditions involving obstacles.
- The scenario without obstacles
When there are no obstacles along the path of the dung beetle’s progression, the ball-rolling dung beetle employs the sun as a navigation reference to ensure its dung-ball rolls along a straight trajectory. Natural factors can affect the beetle’s path during ball rolling. The position-updating mechanism for the dung beetle during the ball-rolling process is represented by Equation (21) as follows:
where t denotes the current iteration number; represents the position of the ith dung beetle in the population in the tth iteration; denotes the deflection coefficient, a constant value; represents a constant value; is a natural coefficient indicating whether there is a deviation from the original direction, assigned a value of 1 or −1 based on a probability method, with 1 indicating no deviation and −1 indicating a deviation from the original direction; represents the worst position in the current population; and is utilized to simulate changes in light intensity.
- 2.
- The scenario with obstacles
When dung beetles encounter obstacles that hinder their progression, they need to adjust their direction through a dancing mechanism. The formula defining the position update during a ball-rolling dung beetle’s dance is as follows:
where represents the deflection angle. When equals 0, , or , is either 0 or meaningless. Therefore, it is stipulated that when equals 0, , or , the dung beetle’s position will not be updated.
3.1.2. Dung Beetle Reproduction
In dung beetle reproduction, a boundary selection strategy is used to simulate the oviposition area for female dung beetles. The definition of the oviposition area is expressed in the following Equation (23):
where , with T representing the maximum iteration count; Lb and Ub are the lower and upper bounds of the optimization problem, respectively; and denotes the global optimal position of the current population.
The DBO algorithm defines the lower bound and upper bound of the oviposition area with each iteration. In other words, the region where dung beetles lay eggs changes dynamically as the iteration count progresses. Once the female dung beetle determines the oviposition area, it proceeds to lay eggs within that region. Each female dung beetle generates only one dung ball in each iteration. Since the oviposition area dynamically adjusts with the iteration count, the position of the dung ball is also dynamically adjusted during the iteration process, which is defined as follows:
where represents the position of the ith dung ball in the tth iteration; and denote two independent random vectors with a size of ; and D represents the dimensionality of the optimization problem.
3.1.3. Dung Beetle Foraging
Guide dung beetle larvae to search for food and simulate their foraging behavior by establishing an optimal foraging area, which is defined in Equation (25).
Here, R remains consistent with the previous definition and represents the local optimal position of the current population.
The DBO algorithm defines the lower bound and upper bound for the foraging area of the small dung beetles. The position update process for the small dung beetles is expressed in Equation (26), as follows:
where is a random number following a normal distribution, and is a random vector with a size of belonging to .
3.1.4. Dung Beetle Stealing
Within the dung beetle population, there will be some that steal dung balls from other dung beetles. The position update process for the thieving dung beetles is expressed in Equation (27), as follows:
where g represents a random vector of size following a normal distribution and denotes a constant value.
A flowchart of the DBO algorithm is shown in Figure 4, which primarily consists of the following six steps:
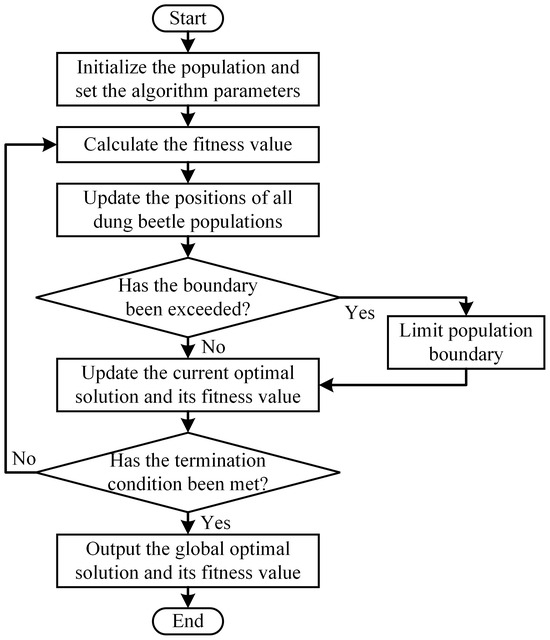
Figure 4.
DBO algorithm flow chart.
- Initialize the dung beetle populations and set the parameters of the DBO algorithm;
- Calculate the fitness values for all dung beetle positions based on the objective function;
- Update the positions of all dung beetle populations according to the set rule;
- Check whether each updated dung beetle has exceeded the boundaries;
- Update the current optimal solution and its fitness value;
- Repeat the above steps, and after the iteration count t reaches the maximum iteration count, output the global optimal value and its corresponding solution.
3.2. Q-Learning Algorithm
As a value-function-based algorithm, Q-learning is a typical temporal difference (TD) algorithm [40] used within the realm of reinforcement learning. This algorithm engages with the environment through a trial-and-error approach, adjusting the next action based on environmental feedback. Through multiple interactions, Q-learning can effectively solve optimal decision-making problems under model-free conditions.
The Q-learning algorithm updates the value function based on the immediate reward obtained from the next state and the estimated value of the value function. Thus, at time , the update of the value function is expressed as follows:
Hence, the update function can be expressed as follows:
where is the action-value function at the current time step, while is the action-value function at the next time step; is the learning rate; is the discount factor, ; and is the reward value.
When the agent selects an action, to avoid falling into local optima, the choice of strategy typically involves a trade-off between “exploration and exploitation”. The greedy algorithm () is a commonly used method for this purpose, where represents the exploration factor, . In this algorithm, exploitation is performed with a probability of , and exploration is performed with a probability of . The specific expression is as follows:
The optimization process of the Q-learning algorithm is an exploration–exploitation process. After reaching the maximum iteration count, a convergent state–action two-dimensional table, known as the Q-table, is obtained.
3.3. The Proposed Hybrid DBO-QL Algorithm
Since the “many-to-many” adversarial scenario model proposed in Section 2 has numerous input parameters, complex constraints, and a multi-peaked objective function, commonly used metaheuristic swarm intelligence algorithms for solving optimization problems often exhibit slow convergence and unsatisfactory convergence results. On the other hand, it is difficult to apply reinforcement learning algorithms with good convergence results and high efficiency in situations with multiple inputs and complex constraints. To address this, this paper proposes a combination of the DBO algorithm, which is an evolutionary algorithm, and the classical Q-Learning algorithm from reinforcement learning. Through this evolutionary reinforcement learning method, this paper aims to tackle the jamming resource allocation problem in a scenario where multiple jammers are jamming multiple radars.
Assuming the adversarial process between the jammers and radars involves a total of U adversarial rounds at a certain time, the process of cooperative jamming resource allocation with joint multi-domain information proceeds as follows.
In the uth adversarial round, the friendly side acquires information about jammers and radars through situational awareness and electromagnetic spectrum sensing in the external environment. Using radar–signal–deinterleaving technology, it determines the quantity, positions, and parameters of the radar radiation sources. Subsequently, based on the received information about the parameters of jammers and radar radiation sources, and with specific constraints in mind, the outer layer of the DBO algorithm is employed to assess which radars can be jammed by the jamming beams of the same jammer. This process generates the jamming beam allocation matrix K. Furthermore, the inner layer of the Q-learning algorithm, utilizing the jamming beam allocation matrix K as a foundation, allocates the transmission power for each jamming beam. This generates the jamming power allocation matrix P, completing the cooperative jamming resource allocation for multiple jammers in the adversarial round. The process then proceeds to the (u + 1)th adversarial round. The method for cooperative jamming resource allocation with joint multi-domain information is illustrated in Figure 5.
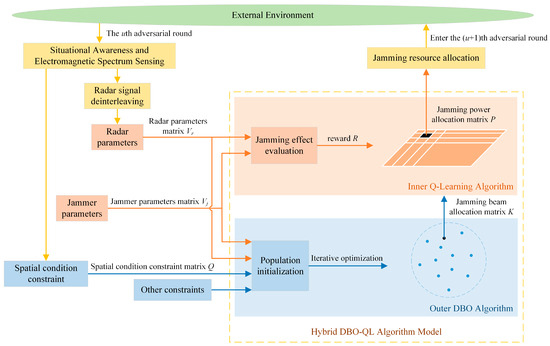
Figure 5.
Cooperative jamming resource allocation with joint multi-domain information.
The objective of the outer-layer DBO algorithm is to find the optimal jamming beam allocation matrix K while satisfying constraints (3), (4), and (5). The objective function of the outer-layer DBO algorithm should incorporate Equations (11), (18), and (19). Therefore, the objective function of the outer-layer DBO algorithm is defined as follows:
where , , and are all weighting factors and . These factors can be configured based on the specific emphasis of the criteria during utilization.
The inner-layer Q-learning algorithm’s objective is to make decisions about the optimal jamming power allocation matrix P under the guidance of the optimal jamming beam allocation matrix K. This process is aimed at achieving cooperative jamming resource allocation with multiple jammers. Therefore, the design approach for the inner-layer Q-learning algorithm is as follows:
(1) The state set consists of matrices representing jamming power allocations. The initial state is randomly selected from the set of jamming power allocation matrices. When the agent takes action in the current state, the transition to the next state transpires.
(2) The action set consists of jamming power values. Adhering to the constraints outlined in Equation (6), the jamming power range is reasonably partitioned into h discrete values. The initial action is randomly selected from these h discrete values, and subsequent actions are chosen according to the policy from Q-learning.
(3) The value of the reward, denoted by , is determined based on the effectiveness of jamming as defined in Equation (15). The specific definition is provided below:
Thus, the jamming effect of the jamming power allocation matrix P, determined by the decision of the inner-layer Q-learning algorithm, can be assessed using the radar receiver SJR benefit factor defined by Equation (16), as follows:
Therefore, for the proposed hybrid DBO-QL algorithm in this paper, the jamming benefit, as defined by Equation (20), can be expressed as follows:
where and both represent weighting factors and .
The pseudo-code of the hybrid DBO-QL algorithm proposed in this paper is Algorithm 1.
| Algorithm 1 Pseudo-Code of the hybrid DBO-QL algorithm |
| Input: Radar parameter matrix ; jamming parameter matrix ; spatial condition constraint matrix Q; weighting factors ; and the parameters for the DBO algorithm include the maximum number of iterations and the population size , while the Q-Learning algorithm involves the maximum number of iterations , initial learning rate , initial exploration factor , and discount factor . |
| Output: Jamming beam allocation matrix K, jamming power allocation matrix P. |
| 1: Initialize the population and parameters for the DBO algorithm. |
| 2: ) do |
| 3: do |
| 4: if i == ball-rolling dung beetle then |
| 5: = rand(1); |
| 6: if < 0.9 then |
| 7: = rand(1); |
| 8: ) then |
| 9: = 1; |
| 10: else |
| 11: = −1; |
| 12: end if |
| 13: Update the ball-rolling dung beetle’s position using Equation (21); |
| 14: else |
| 15: Update the ball-rolling dung beetle’s position using Equation (22); |
| 16: end if |
| 17: end if |
| 18: if i == brood ball then |
| 19: |
| 20: (the brood ball number) do |
| 21: Update the brood ball’s position using Equation (24); |
| 22: for j = 1:D do |
| 23: then |
| 24: |
| 25: end if |
| 26: then |
| 27: |
| 28: end if |
| 29: end for |
| 30: end for |
| 31: end if |
| 32: if i == small dung beetle then |
| 33: Update the small dung beetle’s position using Equation (26); |
| 34: end if |
| 35: if i == thief then |
| 36: Update the thief’s position using Equation (27); |
| 37: end if |
| 38: end for |
| 39: if the newly generated position is better than before then |
| 40: Update it; |
| 41: end if |
| 42: t = t + 1; |
| 43: end while |
| 44: |
| 45: matrix and the parameters for the Q-learning algorithm. |
| 46: for k do |
| 47: Obtain the initial state s; |
| 48: Use the –greedy policy to select an action a in the current state s based on Q; |
| 49: from the environment; |
| 50: by using Equation (29); |
| 51: Update the next state s by using ; |
| 52: end for |
| 53: |
4. Simulation Experiments and Results Analysis
To highlight the effectiveness, superiority, and timeliness of the proposed hybrid DBO-QL algorithm with respect to the joint optimization problem of jamming beam and jamming power allocation, this paper conducted simulation experiments concerning a complex scenario involving “multiple jammers against multiple radars”. Within the same simulation environment, the hybrid DBO-QL algorithm was compared with the DBO algorithm and the PSO algorithm in terms of jamming benefit, algorithm response time, and optimization success rate. To ensure accuracy and fairness in the comparison, all the operational parameters of the jammers and radars were maintained consistently.
4.1. Simulation Parameter Configuration
Assuming that at a certain moment, there are a total of M = 4 jammers conducting cooperative jamming tasks against N = 10 radars in the adversarial space, the radar parameter information and jammer parameter information sets during the simulation are presented in Table 1 and Table 2, respectively.

Table 1.
Radar parameter information.

Table 2.
Jammer parameter information.
The spatial relationship between the jammers and radars is illustrated in Figure 6.
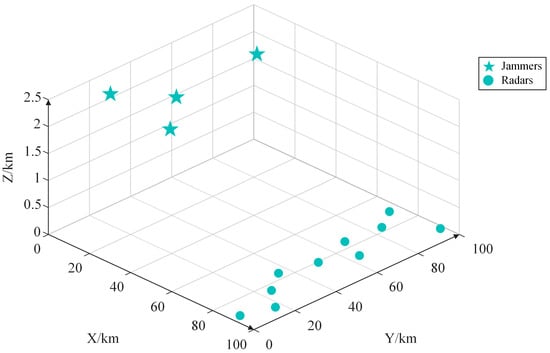
Figure 6.
Visualization of the adversarial scenario.
The spatial condition constraint matrix at this moment is presented in Table 3.

Table 3.
Spatial condition constraint matrix.
Other parameter settings for the adversarial scenario are provided in Table 4.

Table 4.
Other parameter settings for the adversarial scenario.
The specific parameter settings for each algorithm are as follows:
For the hybrid DBO-QL algorithm, weighting factors , , , , and were set to 0.35, 0.25, 0.4, 0.65, and 0.35, respectively. For the outer-layer DBO algorithm, the maximum iteration count corresponded to , and the population size corresponded to ; for the inner-layer Q-learning algorithm, the maximum iteration count corresponded to , and the discount factor corresponded to . An adaptive strategy was employed for the learning rate and exploration factor in this paper. In the initial stages of the algorithm, where exploration is emphasized, relatively larger learning rates and exploration factors are used to enable the algorithm to explore the solution space rapidly. As the training progresses, the learning rate and exploration factor gradually decrease, provoking the transition of the algorithm into the exploitation phase, where smaller values of these parameters facilitate convergence to the optimal result. The definitions of the learning rate and exploration factor in this paper are provided in Equations (35) and (36), and their function plots are shown in Figure 7. The initial learning rate was set to 0.7, and the initial exploration factor was set to 0.9.
where is the initial learning rate and is the decay factor. The decay factor is related to the maximum iteration count , and in the simulation experiments in this paper, was set to 9.
where is the initial exploration factor and the definition and value of are the same as those in Equation (35).
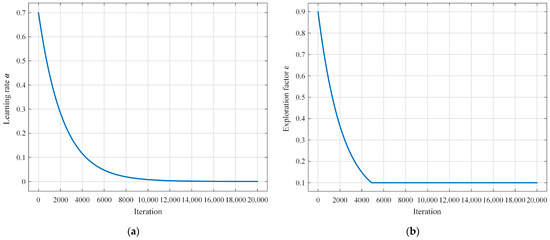
Figure 7.
Function plots of learning rate and exploration factor : (a) function plot of learning rate ; (b) function plot of exploration factor .
The parameter settings for the DBO algorithm are as follows: weighting factors , , , and were set to 0.25, 0.35, 0.15, and 0.25, respectively. The maximum iteration count corresponded to , and population size corresponded to .
The parameter settings for the PSO algorithm are as follows: Weighting factors , , , and were set the same as they were in the DBO algorithm. The maximum iteration count corresponded to , and population size corresponded to . The learning factor has a minimum value of and a maximum value of . The inertia factor has a minimum value of and a maximum value of . Particle velocity has a minimum value of and a maximum value of .
4.2. Experimental Results and Analysis
The convergence results for the hybrid DBO-QL algorithm are illustrated in Figure 8. It can be observed that the outer-layer DBO algorithm reached convergence around the 10th iteration, while the inner-layer Q-learning algorithm achieved convergence around the 9000th iteration.
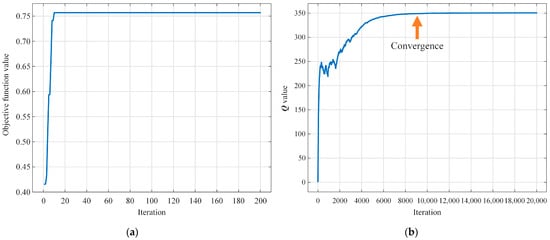
Figure 8.
Convergence curve of the hybrid DBO-QL algorithm: (a) the convergence curve of the outer-layer DBO algorithm; (b) the convergence curve of the inner-layer Q-learning algorithm.
When the algorithm converged, the jamming beam allocation matrix K and the jamming power allocation matrix P are presented in Table 5 and Table 6, respectively.

Table 5.
Jamming beam allocation matrix.

Table 6.
Jamming power allocation matrix (Unit: kW).
The jamming beam allocation matrix and jamming power allocation matrix shown in Table 5 and Table 6 represent the optimal cooperative jamming resource allocation scheme output by the algorithm. According to this scheme, out of the 10 radars in the adversarial scenario, 9 were allocated jamming beams for jamming. Taking the first jammer as an example, it was assigned to jam the sixth and tenth radars, with both jamming beams having a transmission power of 0.10 kW. Moreover, from Table 6, it can be observed that only the ninth radar was not assigned a jamming beam for jamming. This is due to the spatial condition constraint matrix (Table 3), wherein only the third jammer can be assigned to jam the ninth radar. However, referring to the radar parameter information and jammer parameter information in Table 1 and Table 2, it is evident that the operating frequency range of the ninth radar does not overlap with the jamming frequency range of the third jammer. Their frequency domain intersection is 0, indicating that the third jammer cannot effectively jam the ninth radar. Hence, no allocation is made, reflecting a scenario that may occur in practical situations.
To provide a more intuitive display of the results of cooperative jamming resource allocation with multiple jammers, the outputs of the outer-layer DBO algorithm and the inner-layer Q-learning algorithm are depicted separately in Figure 9 and Figure 10.
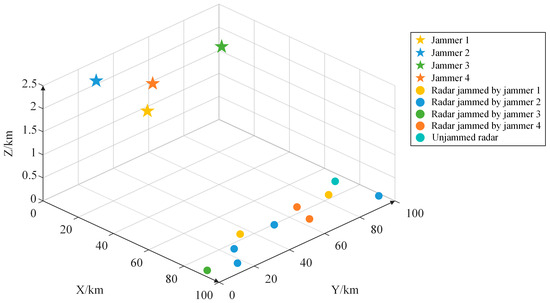
Figure 9.
Visualization of DBO algorithm output.
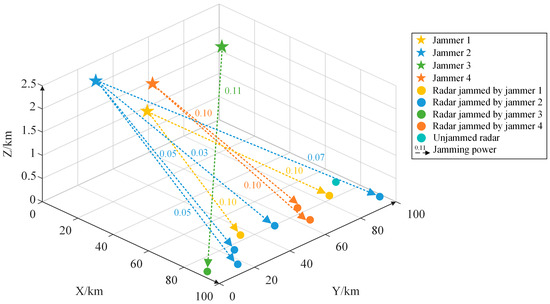
Figure 10.
Visualization of Q-learning algorithm output.
In order to evaluate the stability and adaptability of the algorithm with respect to solving the optimization problem with complex constraints, the optimization success rate is defined in Equation (37) as follows:
where is the number of times the algorithm converges to the optimum and is the total number of experiments.
Under the same simulation scenario, model parameters, and hardware conditions, 200 Monte Carlo experiments were conducted on the hybrid DBO-QL algorithm, DBO algorithm, and PSO algorithm to obtain the optimal jamming benefit, average algorithm response time, and the optimization success rate, as shown in Table 7. The algorithm response time is calculated as follows: For swarm intelligence optimization algorithms, it constitutes the time elapsed from the start of the algorithm to reaching the convergence state. For the Q-learning algorithm, it consists of the time that has elapsed since the algorithm reached the convergence state, ranging from the next state input to the corresponding action output by the agent.

Table 7.
The evaluation results of different algorithms.
The simulation results validated the effectiveness, superiority, and timeliness of the proposed hybrid DBO-QL algorithm. Compared with the DBO and PSO algorithms, the proposed hybrid DBO-QL algorithm improved the jamming benefit by 3.03% and 6.25%, reduced the algorithm response time by 97.35% and 96.57%, and improved the optimization success rate by 26.33% and 50.26%, respectively. This is because, for the DBO algorithm and PSO algorithm, the increase in constraints entails an increase in algorithm optimization difficulty, so when facing problems with complex constraints, these algorithms often need to expand the number of populations to increase their own optimization success rates, but the expansion of the number of populations will bring about the prolongation of the algorithm response time; therefore, it is necessary to balance the relationship between the algorithm response time and the optimization success rate when using these algorithms. A benefit is provided by the hybrid DBO-QL algorithm’s unique model, where the outer-layer DBO algorithm has a discrete solution space with only two values (0 and 1) for each dimension. This significantly simplified the optimization difficulty, resulting in improved convergence and stability and reduced time consumption. For the inner-layer Q-learning algorithm, once the agent is trained, it can rapidly select the optimal action for a given input state at different times based on the trained policy. Unlike the other two swarm intelligence optimization algorithms, the Q-learning algorithm does not require repetitive computations for each iteration, leading to a significant reduction in response time.
Table 7 also reveals that, compared to the PSO algorithm, the DBO algorithm provides a greater jamming benefit but at the cost of a longer response time. This is due to the fact that the DBO algorithm incorporates optimization strategies inspired by the rolling, dancing, foraging, stealing, and reproductive behaviors of dung beetles, which enhance its convergence effectiveness but prolong the algorithm response time.
5. Conclusions
This paper addresses the problem of cooperative jamming resource allocation with multiple jammers in a “many-to-many” scenario, proposing a method based on evolutionary reinforcement learning. This method comprehensively considers information from spatial, frequency, and energy domains to construct constraints and an objective function. It characterizes the jamming resource allocation scheme through the jamming beam allocation matrix and jamming power allocation matrix and optimizes these matrices using the outer-layer DBO algorithm and the inner-layer Q-learning algorithm, respectively. This approach achieves cooperative jamming resource allocation among multiple jammers by leveraging radar parameter information and jammer parameter information. In the simulation experiments, commonly used swarm intelligence optimization algorithms, specifically the DBO algorithm and the PSO algorithm, were selected for comparison in terms of jamming benefit, algorithm response time, and optimization success rate. The results demonstrate that the proposed algorithm outperforms the other two swarm intelligence optimization algorithms, obtaining higher jamming benefits and optimization success rates and showing significant advantages in algorithm response time.
Author Contributions
Conceptualization, Q.X. and T.C.; methodology, Q.X.; software, Q.X.; validation, Q.X., Z.X., and T.C.; formal analysis, Q.X. and Z.X.; investigation, Q.X. and T.C.; resources, T.C.; data curation, Q.X. and Z.X.; writing—original draft preparation, Q.X.; writing—review and editing, Q.X., Z.X., and T.C.; visualization, Q.X.; supervision, T.C.; project administration, T.C.; funding acquisition, T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Shanghai Aerospace Science and Technology Innovation Fund under grant number SAST2022-063.
Data Availability Statement
The data can be obtained by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gurbuz, S.Z.; Griffiths, H.D.; Charlish, A.; Rangaswamy, M.; Greco, M.S.; Bell, K. An overview of cognitive radar: Past, present, and future. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 6–18. [Google Scholar] [CrossRef]
- Haykin, S. New generation of radar systems enabled with cognition. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010; p. 1. [Google Scholar]
- Haykin, S. Cognitive radar: A way of the future. IEEE Signal Process. Mag. 2006, 23, 30–40. [Google Scholar] [CrossRef]
- Darpa, A. Behavioral learning for adaptive electronic warfare. In Darpa-BAA-10-79; Defense Advanced Research Projects Agency: Arlington, TX, USA, 2010. [Google Scholar]
- Haystead, J. DARPA seeks proposals for adaptive radar countermeasures. J. Electron. Def. 2012, 2012, 16–18. [Google Scholar]
- du Plessis, W.P.; Osner, N.R. Cognitive electronic warfare (EW) systems as a training aid. In Proceedings of the Electronic Warfare International: Conference India (EWCI), Bangalore, India, 13–16 February 2018; pp. 1–7. [Google Scholar]
- Wang, X.; Fei, Z.; Huang, J.; Zhang, J.A.; Yuan, J. Joint resource allocation and power control for radar interference mitigation in multi-UAV networks. Sci. China Inf. Sci. 2021, 64, 182307. [Google Scholar] [CrossRef]
- Ren, Y.; Li, B.; Wang, H.; Xu, X. A novel cognitive jamming architecture for heterogeneous cognitive electronic warfare networks. In Information Science and Applications: ICISA 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 97–104. [Google Scholar]
- Xiang, C.-W.; Jiang, Q.-S.; Qu, Z. Modeling and algorithm of dynamic resource assignment for ESJ electronic warfare aircraft. Command Control Simul. 2017, 39, 85–89. [Google Scholar]
- Haigh, K.; Andrusenko, J. Cognitive Electronic Warfare: An Artificial Intelligence Approach; Artech House: London, UK, 2021. [Google Scholar]
- Zhang, C.; Wang, L.; Jiang, R.; Hu, J.; Xu, S. Radar Jamming Decision-Making in Cognitive Electronic Warfare: A Review. IEEE Sens. J. 2023, 23, 11383–11403. [Google Scholar] [CrossRef]
- Zhou, H. An introduction of cognitive electronic warfare system. In Communications, Signal Processing, and Systems: Proceedings of the 2018 CSPS Volume III: Systems 7th, Dalian, China, 14–16 July 2020; Springer: Singapore, 2020; pp. 1202–1210. [Google Scholar]
- Qingwen, Q.; Wenfeng, D.; Meiqing, L.; Yang, Y. Cooperative jamming resource allocation of UAV swarm based on multi-objective DPSO. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 5319–5325. [Google Scholar]
- Gao, Y.; Li, D.-S. Electronic countermeasures jamming resource optimal distribution. In Information Technology and Intelligent Transportation Systems: Volume 2, Proceedings of the 2015 International Conference on Information Technology and Intelligent Transportation Systems ITITS 2015, Xi’an, China, 12–13 December 2015; Springer: Cham, Switzerland, 2017; pp. 113–121. [Google Scholar]
- Liu, X.; Li, D. Analysis of cooperative jamming against pulse compression radar based on CFAR. EURASIP J. Adv. Signal Process. 2018, 2018, 69. [Google Scholar] [CrossRef]
- Xiong, X.; Zheng, K.; Lei, L.; Hou, L. Resource allocation based on deep reinforcement learning in IoT edge computing. IEEE J. Sel. Areas Commun. 2020, 38, 1133–1146. [Google Scholar] [CrossRef]
- Shi, W.; Li, J.; Wu, H.; Zhou, C.; Cheng, N.; Shen, X. Drone-cell trajectory planning and resource allocation for highly mobile networks: A hierarchical DRL approach. IEEE Internet Things J. 2020, 8, 9800–9813. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, J.; Wei, Z.; You, I. A deep reinforcement learning based approach for energy-efficient channel allocation in satellite Internet of Things. IEEE Access 2020, 8, 62197–62206. [Google Scholar] [CrossRef]
- Lei, W.; Ye, Y.; Xiao, M. Deep reinforcement learning-based spectrum allocation in integrated access and backhaul networks. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 970–979. [Google Scholar] [CrossRef]
- He, C.; Hu, Y.; Chen, Y.; Zeng, B. Joint power allocation and channel assignment for NOMA with deep reinforcement learning. IEEE J. Sel. Areas Commun. 2019, 37, 2200–2210. [Google Scholar] [CrossRef]
- Alwarafy, A.; Ciftler, B.S.; Abdallah, M.; Hamdi, M. DeepRAT: A DRL-based framework for multi-RAT assignment and power allocation in HetNets. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Meng, F.; Chen, P.; Wu, L.; Cheng, J. Power allocation in multi-user cellular networks: Deep reinforcement learning approaches. IEEE Trans. Wirel. Commun. 2020, 19, 6255–6267. [Google Scholar] [CrossRef]
- Zou, W.Q.; Niu, C.Y.; Liu, W.; Wang, Y.Y.; Zhan, J.Q. Combination search strategy-based improved particle swarm optimisation for resource allocation of multiple jammers for jamming netted radar system. IET Signal Process. 2023, 17, e12198. [Google Scholar] [CrossRef]
- Wu, Z.; Hu, S.; Luo, Y.; Li, X. Optimal distributed cooperative jamming resource allocation for multi-missile threat scenario. IET Radar Sonar Navig. 2022, 16, 113–128. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Y.; Xu, H. Optimal allocation of cooperative jamming resource based on hybrid quantum-behaved particle swarm optimisation and genetic algorithm. IET Radar Sonar Navig. 2017, 11, 185–192. [Google Scholar] [CrossRef]
- Lu, D.-j.; Wang, X.; Wu, X.-t.; Chen, Y. Adaptive allocation strategy for cooperatively jamming netted radar system based on improved cuckoo search algorithm. Def. Technol. 2023, 24, 285–297. [Google Scholar] [CrossRef]
- Xing, H.; Xing, Q.; Wang, K. A Joint Allocation Method of Multi-Jammer Cooperative Jamming Resources Based on Suppression Effectiveness. Mathematics 2023, 11, 826. [Google Scholar] [CrossRef]
- Yao, Z.; Tang, C.; Wang, C.; Shi, Q.; Yuan, N. Cooperative jamming resource allocation model and algorithm for netted radar. Electron. Lett. 2022, 58, 834–836. [Google Scholar] [CrossRef]
- Xing, H.-x.; Wu, H.; Chen, Y.; Wang, K. A cooperative interference resource allocation method based on improved firefly algorithm. Def. Technol. 2021, 17, 1352–1360. [Google Scholar] [CrossRef]
- Gronauer, S.; Diepold, K. Multi-agent deep reinforcement learning: A survey. Artif. Intell. Rev. 2022, 55, 895–943. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Kottur, S.; Moura, J.M.; Lee, S.; Batra, D. Learning cooperative visual dialog agents with deep reinforcement learning. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2951–2960. [Google Scholar]
- Li, S.; Liu, G.; Zhang, K.; Qian, Z.; Ding, S. DRL-Based Joint Path Planning and Jamming Power Allocation Optimization for Suppressing Netted Radar System. IEEE Signal Process. Lett. 2023, 30, 548–552. [Google Scholar] [CrossRef]
- Yue, L.; Yang, R.; Zuo, J.; Zhang, Y.; Li, Q.; Zhang, Y. Unmanned Aerial Vehicle Swarm Cooperative Decision-Making for SEAD Mission: A Hierarchical Multiagent Reinforcement Learning Approach. IEEE Access 2022, 10, 92177–92191. [Google Scholar] [CrossRef]
- Lü, S.; Han, S.; Zhou, W.; Zhang, J. Recruitment-imitation mechanism for evolutionary reinforcement learning. Inf. Sci. 2021, 553, 172–188. [Google Scholar] [CrossRef]
- Xue, F.; Hai, Q.; Dong, T.; Cui, Z.; Gong, Y. A deep reinforcement learning based hybrid algorithm for efficient resource scheduling in edge computing environment. Inf. Sci. 2022, 608, 362–374. [Google Scholar] [CrossRef]
- Asghari, A.; Sohrabi, M.K. Combined use of coral reefs optimization and reinforcement learning for improving resource utilization and load balancing in cloud environments. Computing 2021, 103, 1545–1567. [Google Scholar] [CrossRef]
- Zhang, C.; Song, Y.; Jiang, R.; Hu, J.; Xu, S. A Cognitive Electronic Jamming Decision-Making Method Based on Q-Learning and Ant Colony Fusion Algorithm. Remote Sens. 2023, 15, 3108. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Clifton, J.; Laber, E. Q-learning: Theory and applications. Annu. Rev. Stat. Its Appl. 2020, 7, 279–301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).