Blind Edge-Retention Indicator for Assessing the Quality of Filtered (Pol)SAR Images Based on a Ratio Gradient Operator and Confidence Interval Estimation

Abstract

Speckle reduction is a key preprocessing approach for the applications of Synthetic Aperture Radar (SAR) data. For many interpretation tasks, high-quality SAR images with a rich texture and structure information are useful. Therefore, a satisfactory SAR image filter should retain this information well after processing. Some quantitative assessment indicators have been presented to evaluate the edge-preservation capability of single-polarization SAR filters, among which the non-clean-reference-based (i.e., blind) ones are attractive. However, most of these indicators are derived based only on the basic fact that the speckle is a kind of multiplicative noise, and they do not take into account the detailed statistical distribution traits of SAR data, making the assessment not robust enough. Moreover, to our knowledge, there are no specific blind assessment indicators for fully Polarimetric SAR (PolSAR) filters up to now. In this paper, a blind assessment indicator based on an SAR Ratio Gradient Operator (RGO) and Confidence Interval Estimation (CIE) is proposed. The RGO is employed to quantify the edge gradient between two neighboring image patches in both the speckled and filtered data. A decision is then made as to whether the ratio gradient value in the filtered image is close to that in the unobserved clean image by considering the statistical traits of speckle and a CIE method. The proposed indicator is also extended to assess the PolSAR filters by transforming the polarimetric scattering matrix into a scalar which follows a Gamma distribution. Experiments on the simulated SAR dataset and three real-world SAR images acquired by ALOS-PALSAR, AirSAR, and TerraSAR-X validate the robustness and reliability of the proposed indicator.

1. Introduction

Nowadays, the Synthetic Aperture Radar (SAR) remote sensing technique has attracted wide attention. As a more advanced form of the traditional single-polarization SAR, fully Polarimetric SAR (PolSAR) sensors can obtain much richer scattering traits of land objects [1]. More and more commercial SAR satellites have been launched in the last decade, making both single-polarization SAR and PolSAR data easier to be accessed and facilitating the various applications of SAR data [2,3]. However, SAR sensors can encounter some image degradation problems. Among these degradation problems, speckle noise is a non-negligible issue, which seriously hinders most image interpretation tasks [4]. Therefore, a speckle reduction approach is required before using SAR data in many applications [5,6]. A number of studies have attempted to design filters for single-polarization SAR or PolSAR data. Generally speaking, traditional single-polarization SAR filters can be categorized into two classes, namely, spatial-domain-based filters and wavelet-domain-based filters [7]. The most typical spatial-domain-based SAR filters are the Lee filter [8] and its refined versions [9,10]. Another popular family of spatial-domain-based SAR filters are the nonlocal-means-based filters [11,12,13]. Among the wavelet-domain-based SAR filters, the 3D-Block-Matching-based SAR (SAR-BM3D) filter [13] has obtained outstanding filtering results. In recent years, deep-learning-based SAR filters have emerged and shown promising performances [14,15]. Most early PolSAR filtering algorithms were developed based on the refined Lee filter [16,17]. In the last decade, nonlocal-means-based PolSAR filtering algorithms [18,19,20] have been widely studied. Moreover, the theories of total variation and sparse coding have also been applied to the filtering of PolSAR images [21,22].

When the user evaluates the despeckling performance of an SAR filter, it will mainly concentrate on two aspects: speckle reduction degree and image detail retention (including edge structures and strong point targets) [23]. For the evaluation of the noise level in filtered SAR images, most researchers have used the equivalent number of looks (ENLs) [4] since it is derived based on the statistical traits of speckle and is easily operated. For the evaluation of strong point targets, the most popular index is the Target-to-Clutter Ratio (TCR) presented by Argenti et al. [23]. For the evaluation of the edge-preservation capability, which is the goal of this paper, some indices have been presented in the literature [24]. Among these indices, the non-clean-reference-based (i.e., blind) indices are often more attractive than the clean-reference-based indices. This is because, in a real case, a clean reference for the observed speckled SAR image is unavailable.

It is well-known that a basic trait of speckle in single-polarization SAR data is that it is a kind of multiplicative noise. SAR data in the intensity format follow a Gamma distribution, while SAR data in the amplitude format follow a Nakagami–Rayleigh distribution [4]. However, the statistical traits of PolSAR data are much more complicated, since speckle not only exhibits in the intensity part but also in the polarimetric phase part [25].

Current blind edge-preservation assessment indicators have some major drawbacks. First, most assessment indicators are derived based on the basic fact of multiplicative noise, and the detailed statistical distribution traits of SAR data have not been utilized. Some are even significantly reliant on the performance of a certain edge detector. These factors make the assessment results of the current indicators not robust and consistent enough for different images with different noise levels or with different scene complexities. Secondly, to our knowledge, there are no specific blind assessment indicators for PolSAR filters up to now. Researchers often directly use the aforementioned single-polarization SAR assessment indicators to evaluate the edge-preservation performance of PolSAR filters in total intensity data, without considering the retention of scattering information in the polarimetric phase part, which makes the assessment results not reliable enough.

In this paper, to obtain robust and logically consistent edge-preservation assessment results, a new blind SAR edge-preservation assessment indicator is presented by fully considering the statistical distribution of speckle. The SAR Ratio Gradient Operator (RGO) is employed to quantify the edge gradient between two neighboring image patches. The main idea of the proposed indicator is that an ideal filter should ensure that the ratio gradient between every two patches in the filtered image is very close to the ratio gradient between the corresponding patches in the clean image. Since the clean image is unobserved, we utilize a Confidence Interval Estimation (CIE) method to make the decision as to whether a ratio gradient value in the filtered image is close to that in the clean image. The proposed indicator is also extended to assess the PolSAR filters by transforming the polarimetric scattering matrix into a scalar that followed a Gamma distribution, which ensures the use of information in both intensity and phase parts.

The main innovations of our work can be summarized as the following two aspects:

(1)

An edge-preservation indicator is proposed to evaluate the quality of SAR images processed by different despeckling methods. The proposal is without the needs of a clean reference image and manual intervention during the assessment process, and it is derived based on the statistical traits of SAR data. Therefore, the proposed indicator can obtain robust and logically consistent assessment results.

(2)

The proposed indicator is extended to evaluate the quality of PolSAR images, which not only consider the intensity information of PolSAR data as most current indicators do, but also consider the phase information of PolSAR data. Therefore, the proposed indicator can obtain reliable results on PolSAR images.

The rest of this paper is organized as follows. The RGO and the proposed RGO-based Blind Assessment Indicator (RGO-BAI) are introduced in Section 2. The basic information about the datasets and some classical indicators used for comparison are described in Section 3. The assessment results obtained on both single-polarization SAR and PolSAR images by the different indicators are shown in Section 4. Finally, we conclude the paper in Section 5.

2. Methodology

2.1. Single-Polarization SAR Ratio Gradient

To quantify the edge gradient between two neighboring pixels or patches in a single-polarization SAR image, the arithmetic difference operator is often used. In [26], Touzi et al. suggested the use of the ratio gradient between the mean values of two neighboring image areas, since the noise component in SAR intensity data is signal-dependent and is of multiplicative nature, and using the ratio operator can eliminate the influence of the signal intensity.

In this study, since the main idea of the proposed indicator is to determine whether the gradients along certain directions are well-kept after filtering but not to simply detect edges in the filtered images, the unbounded conditional Probability Density Function (PDF) is utilized to calculate indicator. Given $u_1$ and $u_2$, which are the mean values of two neighboring patches with N pixels in the unobserved clean image u, we let R be the ratio gradient between the corresponding patches in the speckled image I, the unbounded PDF of the single-polarization SAR ratio gradient is then derived as [26]:

$$f_1(R/u_1,u_2)= \frac{n\Gamma (2NL)}{\Gamma {(NL)}^2}[\frac{{r_0}^{NL}}{{(R^n+r_0)}^{2NL}}]R^{nNL-1}, R\in (0,+\infty )$$

(1)

where $r_0=u_1/u_2$ is the unobserved clean ratio gradient, n = 1 for the image in intensity format, and n = 2 for the image in amplitude format. For a larger N value, the ratio gradient can better alleviate the influence of noise, while, for a smaller N value, the ratio gradient can ensure fine edges of the image to be detected.

In the proposed indicator, to make a compromise between detecting details and high robustness, we use an image patch of 3 × 3 pixels to calculate the ratio gradient, and we focus on the image in intensity format. In such case, N = 9 and n = 1. Thus, the PDF in (1) can be rewritten as:

$$f_1(R/u_1,u_2)=\frac{\Gamma (18L)}{\Gamma {(9L)}^2}[\frac{{r_0}^{9L}}{{(R+r_0)}^{18L}}]R^{9L-1} , R\in (0,+\infty )$$

(2)

In Figure 1, the unbounded PDF curves are plotted for r₀ = 0.5 and r₀ = 2 in the typical cases of L = 1 and L = 4. It can be seen that the distribution of the ratio gradient is a kind of long-tailed distribution. Given a certain noise level, the smaller the r₀ is, the steeper the distribution curve is. Given a certain r₀ value, the less the amount of noise is, the steeper the distribution curve is. The above observations are utilized in the CIE approach presented in the following subsections.

2.2. The Basic Framework of the Proposed Indicator

As mentioned previously, most of the current SAR edge-preservation assessment indices are derived only considering the basic multiplicative nature of speckle, and some are even significantly reliant on the performance of a certain edge detector. To fully exploit the statistical distribution traits of speckle and take advantage of the RGO, an RGO-based Blind Assessment Indicator (RGO-BAI) is presented in this paper. 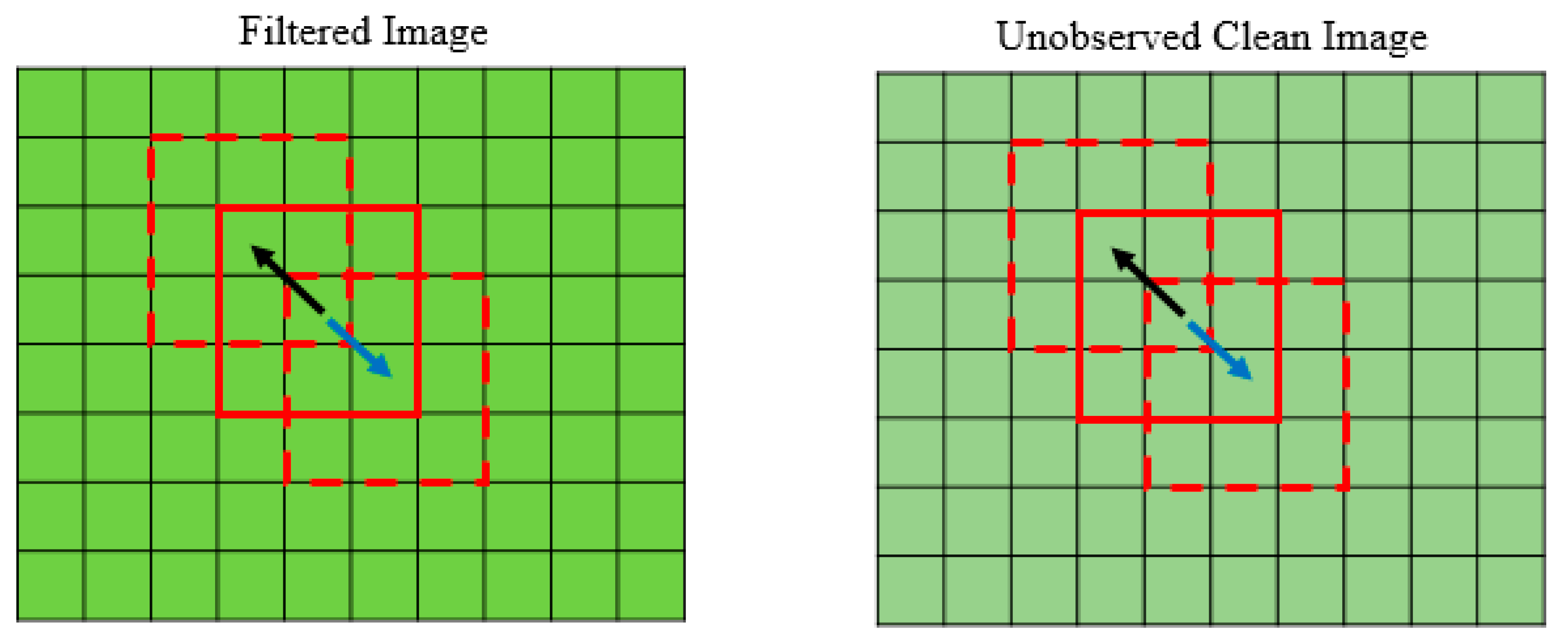As shown in Figure 2, the main idea behind the proposal is that a satisfactory filter should retain the edges in the images well; hence, the ratio gradient between every two neighboring patches in the filtered image should be close to the ratio gradient between the corresponding patches in the clean image.

We let the variable r be the ratio gradient between two filtered patches on opposite sides of a certain pixel; the RGO-BAI is then initially defined as:

$$\mathrm{RGO-BAI}=\frac{1}{M}{\displaystyle \sum _{i=1}^{M}w(i)}$$

(3)

where $w(i)=1$ if $r(i)\approx r_0(i)$; otherwise, $w(i)=0$. In practice, to quantify the gradients in different directions, the RGO along the vertical, horizontal, and oblique directions is calculated. Thus, the RGO-BAI can be rewritten as:

$$\mathrm{RGO-BAI}=\frac{1}{4M}{\displaystyle \sum _{i=1}^M{w}_1(i)}+w_2(i)+w_3(i)+w_4(i)$$

(4)

where the different subscripts of w denote the different directions. The RGO-BAI value ranges from 0 to 1 and is close to 1 for the ideal filtering result. The above expression is simple, but the difficulty is, of course, that we do not have the clean version of the observed image, and, hence, it is impossible to obtain $r_0$. In the next part, we describe the CIE method used to make the decision as to whether r is close to $r_0$.

2.3. Confidence Interval Estimation (CIE) Approach

According to (2), the PDF of the ratio gradient given a filtered image $\widehat{u}$ is:

$$f_1(R/{\widehat{u}}_1,{\widehat{u}}_2)=\frac{\Gamma (18L)}{\Gamma {(9L)}^2}[\frac{r^{9L}}{{(R+r)}^{18L}}]R^{9L-1} , R\in (0,+\infty )$$

(5)

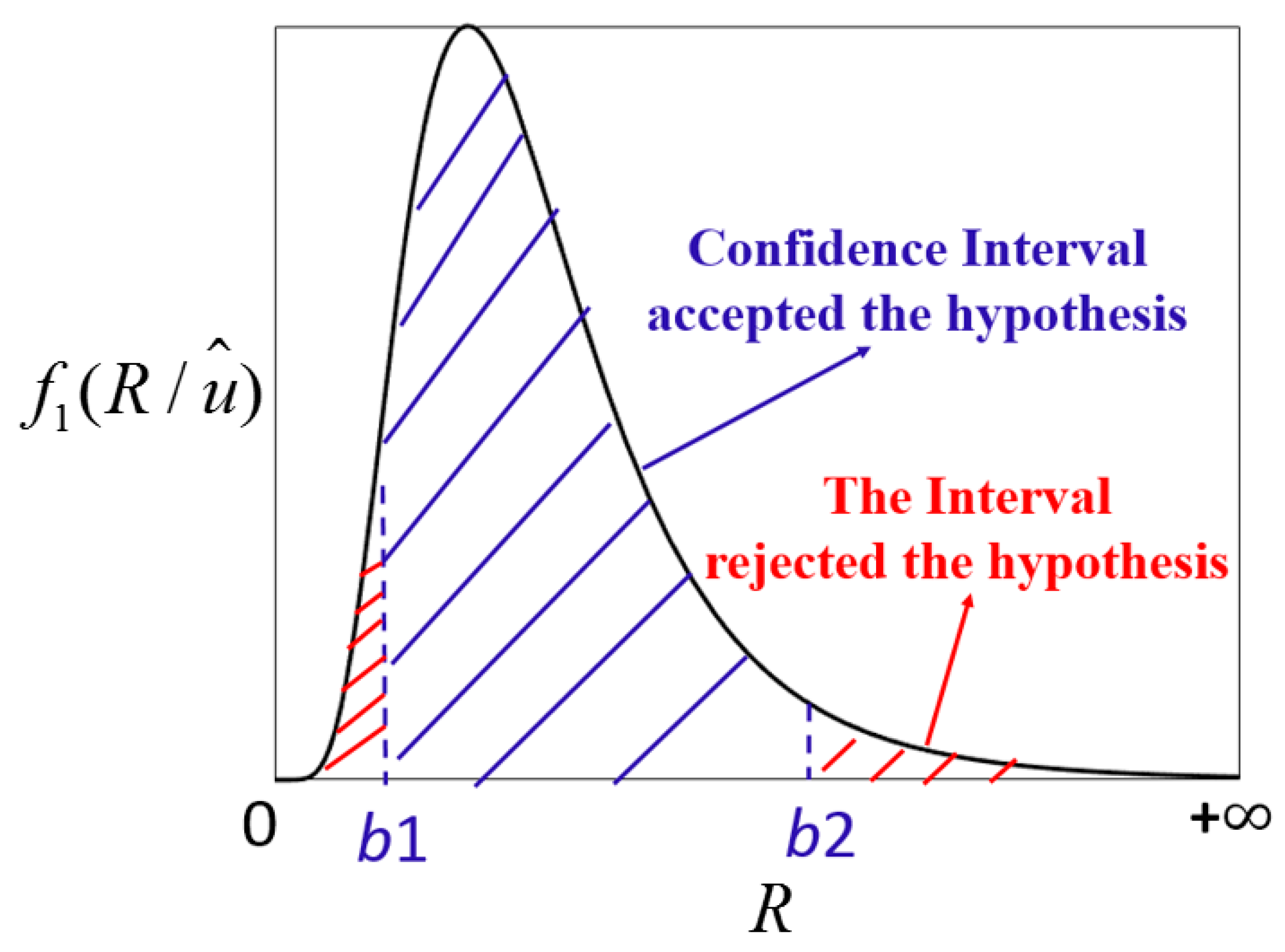
In the rest of this paper, for simplification, we use $f_1(R/\widehat{u})$ to replace $f_1(R/{\widehat{u}}_1,{\widehat{u}}_2)$. As in the example shown in Figure 3, given a lower limit $b_1$ and an upper limit $b_2$, the probability that R is between $b_1$ and $b_2$ (the blue area in Figure 3) can be calculated by:

$$P(R\in [b_1,b_2])=\frac{{\displaystyle {\int }_{b_1}^{b_2}{f}_1(R/\widehat{u}) \mathrm{d}R}}{{\displaystyle {\int }_0^{+\infty }{f}_1(R/\widehat{u}) \mathrm{d}R}}$$

(6)

The basic idea of the CIE method proposed in this paper is that, given a confidence level for $P(R\in [b_1,b_2])$, if the corresponding ratio gradient in the speckled image (i.e., R) is between $b_1$ and $b_2$, then the hypothesis that $r\approx r_0$ is accepted; otherwise, the hypothesis is rejected. Rational setting for confidence level is necessary. On one hand, more robust and reliable assessment results can be obtained if we choose a lower confidence level (a stricter condition), because a stricter condition can ensure that the ratio gradient in the filtered image is more likely to be close to that in the clean image. On the other hand, if we choose a higher confidence level, the numerical searching approach for CIE introduced in the rest of this part can be faster, because $b_1$ is closer to 0 in such case. In this study, by a large number of experiments, we found that, in many cases, good balance between assessment reliability and computational speed was obtained when the confidence level is set as 90%.

The question now comes down to the calculation of the confidence interval $[b_1,b_2]$, which, clearly, should make the following two equations stand:

$$\frac{{\displaystyle {\int }_0^{b_1}{f}_1(R/\widehat{u})} \mathrm{d}R}{{\displaystyle {\int }_0^{+\infty }{f}_1(R/\widehat{u})} \mathrm{d}R}=0.05$$

(7)

and

$$\frac{{\displaystyle {\int }_{b_1}^{b_2}{f}_1(R/\widehat{u})} \mathrm{d}R}{{\displaystyle {\int }_0^{+\infty }{f}_1(R/\widehat{u})} \mathrm{d}R}=0.9$$

(8)

However, due to the high complexity of the PDF in (5), it is not possible for us to directly obtain the mathematical solutions of $b_1$ and $b_2$ by (7) and (8). In the rest of this part, we introduce a numerical searching approach.

For the denominators in (7) and (8), we replace the upper limit $+\infty$ by the large value of 100, because, as previously mentioned, the distribution of the ratio gradient is a kind of long-tailed distribution, and, in real cases, ${\displaystyle {\int }_0^{+\infty }{f}_1(R/\widehat{u})} \mathrm{d}R$ is very close to ${\displaystyle {\int }_0^{100}{f}_1(R/\widehat{u})} \mathrm{d}R$. The next step is to estimate $b_1$ from (7). Setting a very small increment value v₁ and letting $b_1$ be $v_1$ (a small positive value) initially, we check whether the left hand of (7) is very close to 0.05. If it is, we stop finding a new value for $b_1$; otherwise, we let $b_1$ be $2\cdot v_1$ and check the equation again. This process is repeated until we find the approximate solution. An important question here is how to set $v_1$ adaptively. For a very small $v_1$ value, the solution for $b_1$ by the above searching process can be very close to the true solution, but the searching process will be too time-consuming; in contrast, a large $v_1$ can save searching time but may not obtain a close solution. In this study, according to the traits of the PDF curves shown in Figure 1 and large amount of tests, we set $v_1$ as $0.05\cdot r/L$. This means that, for a larger r value and a smaller L value, the PDF curve is gentler, and $v_1$ is adaptively set larger to save computational time without significantly reducing the accuracy of solving $b_1$.

Finally, setting a new increment value $v_2$, we can also obtain the solution of $b_2$ by (8) via the aforementioned searching approach, but with two differences. The first difference is that the searching start of $b_2$ is set as $r+v_2$ rather than $b_1+v_2$, because, apparently, the solution of $b_2$ is larger than r. The second difference is that $v_2$ can be set larger than $v_1$ (for example, $2\cdot r/L$) to save computational time, due to the long-tailed distribution nature of the PDF.

2.4. Consideration of Local Homogeneity

To calculate the proposed RGO-BAI shown in (6), the CIE approach should be used to search for the lower limit $b_1$ and the upper limit $b_2$ for each pixel, as introduced before. However, this makes the assessment procedure relatively time-consuming, even though some adaptive searching strategies are adopted. To further accelerate the computational speed, a direct way is to let the indicator only focus on the areas with high heterogeneity and ignore the homogeneous areas. Therefore, the RGO-BAI in (4) is further refined as:

$$\mathrm{RGO-BAI}=\frac{1}{4M}{\displaystyle \sum _{i=1}^{M}H(i)\left(w_1(i)+w_2(i)+w_3(i)+w_4(i)\right)}$$

(9)

where $H(i)$ denotes the heterogeneity index of a large image patch centered at pixel i. Since the patch size of the ratio gradient is 3 × 3, we set the patch size to calculate $H(i)$ as 7 × 7. $H(i)$ is 1 if the image patch has rich textures; otherwise, it is 0, and the CIE approach will not be used for this pixel. The heterogeneity is measured in the way proposed in the classical Lee filter [7]:

$$\left\{\begin{array}{c}H(i)=0, if \frac{\mathrm{var}(Q(i))-\mathrm{mean}{(Q(i))}^2/L}{(1+1/L)\mathrm{var}(Q(i))}<=0\\ H(i)=1, if \frac{\mathrm{var}(Q(i))-\mathrm{mean}{(Q(i))}^2/L}{(1+1/L)\mathrm{var}(Q(i))}>0\end{array}\right.$$

(10)

where $Q(i)$ denotes the 7 × 7 image patch in intensity format centered at pixel i. Another benefit of considering the local homogeneity is to keep the proposed indicator away from the influence of the block effect exhibited in homogeneous areas, which can be introduced by some filters in some cases.

2.5. Extension to PolSAR Data

By transmitting and receiving the radar waves in different polarization states, PolSAR system can acquire rich scattering information of targets. For each pixel in PolSAR image, the back-scattering polarimetric radar signal can be described by the following Polarimetric Covariance Matrix (PolCM) [27]:

$$\mathit{C}=\mathit{v}\cdot {\mathit{v}}^{\tau }$$

(11)

with

$$\mathit{v}={(S_{\mathrm{HH}},\sqrt{2}{S}_{\mathrm{HV}},S_{\mathrm{VV}})}^T$$

(12)

where T and $\tau$ are the transpose and conjugate transpose operators, respectively; $S_{\mathrm{HV}}$ represents the back-scattering radar signal with vertical transmitting and horizontal receiving states, which is a combination of the amplitude $\left|S_{HV}\right|$ and the phase ${\varphi }_{HV}$: $S_{HV}=|S_{HV}{|\mathrm{e}}^{\mathrm{j}{\varphi }_{HV}}$. Other terms in PolCM have similar definitions.

It is well-known that single-polarization SAR data in intensity (square of amplitude) format follow a Gamma distribution. The statistical traits of PolSAR data are more complicated, since speckle exhibits not only in the intensity part but also in the polarimetric phase part. Studies have found that, given the number of looks L, PolCM can be modelled as the following complex Wishart distribution [28,29]:

$$P(\mathit{C}|\mathit{Z})=\frac{L^{dL}|\mathit{C}{|}^{L-d}\exp (-Ltr({\mathit{Z}}^{-1}\mathit{C}))}{\mathrm{Q}(L,d)|\mathit{Z}{|}^L}$$

(13)

with

$$Q(L,d)={\pi }^{d(d-1)/2}{\displaystyle {\prod }_{i=1}^d\Gamma (L-i+1)}$$

(14)

where d = 3 denotes the dimension of PolCM and $\Gamma (\cdot )$ is the Gamma function.

As aforementioned, current studies often directly use the single-polarization SAR assessment indicators to evaluate the edge-preservation performance of PolSAR filters in total intensity data (sum of the diagonal terms of PolCM shown in (12)) and do not consider the retention of scattering information in the polarimetric phase part, which makes the assessment results not reliable enough. Therefore, it is necessary to take into account the fully polarimetric information when we extend RGO-BAI to assess PolSAR filters. However, it is impossible for us to directly apply the indicator to PolSAR data represented as the form of PolCM.

The study in [30] provides us an idea to accomplish the extension of RGO-BAI by transforming the matrix into a scalar which can utilize the information in all terms of the matrix. The transformation process is as follows:

$$I=\mathrm{tr}({\widehat{\mathit{Z}}}^{-1}{\mathit{C}}_i)$$

(15)

where $\mathrm{tr}(\cdot )$ is matrix trace, and $\widehat{\mathit{Z}}$ is the multi-look estimator by averaging the value of samples $\{{\mathit{C}}_i; i=1,2,\dots ,N\}$. It has been proven in [30] that the transformed data I also follows a Gamma distribution. Specifically, we first calculate the mean value of PolCMs of each image patch; then, the transformation is implemented using this mean value and the matrix of center pixel in the patch by (15); finally, the ratio gradient between two neighboring patches in the transformed image is obtained and the indicator is calculated as described before.

3. Dataset and Processing

3.1. Dataset

In this paper, to demonstrate the reliability of the proposed RGO-BAI, two simulated SAR images and three real SAR images are used.

To simulate SAR images, many studies employ the traditional approach, in which an optical image is chosen as the clean intensity image and the noise component with a Gamma distribution is exerted on the image. However, this simulation approach can introduce significant bias with regard to real-world SAR data. For example, the signal dynamics and geometric characteristics of these simulated data are quite different from those of real SAR data; in addition, the spatial correlation of speckle, which exists in real SAR data, cannot be taken into account by this approach [31,32]. In 2014, a ground-breaking work was published by Martino et al. [33] on how to establish a framework to simulate “near-real” single-polarization SAR images. In their work, some images with typical scenes (for example, buildings and homogeneous areas) were generated by employing a simulation model which considers the complicated physical scattering models of the targets. To generate a clean reference, a multi-look processing step was undertaken through simulating and averaging multiple SAR images of the same scene. In this experiment, we chose the “building” and “homogeneous” image (Figure 4) from the above dataset to evaluate the performance of SAR filters. The building image was generated by placing an isolated building which has high backscattering signals on the homogeneous image.

The first real-world single-polarization SAR image is a single-look image acquired by the L-band ALOS-PALSAR sensor on 18 November 2008 (Figure 5a). The scene of this image is relatively simple, with several high return targets and a river which has clear boundaries. The second real-world single-polarization SAR image is a single-look image acquired by the TerraSAR-X sensor on 15 February 2012 (Figure 5b). The third real-world image is a four-look PolSAR image acquired by the C-band AirSAR system on October 4, 2000 (Figure 5c). This image contains several typical land-cover types, especially urban areas with rich details.

3.2. Classical SAR Filters and Assessment Indicators

In this study, assessments are made on the images processed by some typical SAR filters. For the filtering experiments on single-polarization SAR data, the refined Lee filter [9], the Probabilistic-Patch-Based (PPB) filter [11] and the 3D-Block-Matching-based SAR (SAR-BM3D) filter [13] which combines the ideas of nonlocal and wavelet denoising are chosen. For the filtering experiments on PolSAR data, the PolSAR nonlocal means filter [18], the PolSAR Nonlocal Total Variation (NLTV) method [21], and the PolSAR Nonlinear Guided Filter (PNGF) [34] are chosen.

Two typical indicators which do not resort to the use of a clean reference are deployed for all comparison experiments in this paper. They are the Edge-Preservation Degree (EPD) [35] and the Despeckling Evaluation Index (DEI) [36].

(1) EPD: As a refined version of the Edge-Preservation Index (EPI) proposed in [37], EPD has been widely used for edge-preservation evaluation in many studies. By comparing the difference between a certain pair of adjacent pixels in the filtered data and the same pixels in the original data, the EPI is calculated as follows:

$$\mathrm{EPI}=\frac{{\displaystyle \sum _{i=1}^M|{\widehat{u}}_1(i)-{\widehat{u}}_2(i)|}}{{\displaystyle \sum _{i=1}^M|I_1(i)-I_2(i)|}}$$

(16)

where M is the total pixel number; and $\widehat{u}$ and $I$ denote the despeckled image and the original speckled intensity image, respectively.

In [35], considering the basic fact that speckle is a kind of multiplicative noise, EPI was improved and the EPD was proposed as follows:

$$\mathrm{EPD}=\frac{{\displaystyle \sum _{i=1}^M|{\widehat{u}}_1(i)/{\widehat{u}}_2(i)|}}{{\displaystyle \sum _{i=1}^M|I_1(i)/I_2(i)|}}$$

(17)

Due to the smoothing effect on the image of filters, the numerator is smaller than the denominator in most cases. Clearly, the value range of EPD is between 0 and 1, and, in theory, the EPD value for a filter that retains edges well will be close to 1.

(2) DEI: DEI [36] is used to measure the smoothing degree of the despeckled image and to indirectly evaluate the edge-preservation capability of a filter. The main idea is that, in a large homogeneous area, the minimum of the standard deviation values for all the small image patches located in this area should be very close to the standard deviation of this large area. The DEI is given by:

$$\mathrm{DEI}=\frac{1}{M}{\displaystyle \sum _{i,j}\frac{\underset{|p-i|<s,|q-j|<s}{\min }(\mathrm{std}({\mathrm{W}}_{p,q}^m))}{\mathrm{std}({\mathrm{W}}_{i,j}^s)}}, m<s$$

(18)

where ${\mathrm{W}}_{i,j}^s$ represents the large image patch centered at pixel (i, j) with a size of s × s pixels, and ${\mathrm{W}}_{p,q}^m$ is a small image patch within the above large patch. In theory, a DEI value close to 1 indicates a high image smoothing degree, or, in other words, the edges in the image are more likely to be filtered out. Clearly, the DEI does not utilize any information in the speckled image.

4. Experimental Results

In this section, we describe the experiments conducted with some typical single-polarization SAR and PolSAR filters mentioned in Section 3.2, display the filtering results obtained on four SAR datasets, and report the quantitative assessment values of EPD, DEI, and the proposed RGO-BAI. To help the readers reproduce our work, we have made the source codes of RGO-BAI programmed by MATLAB (version 2018) and some datasets for testing available through the following link: https://github.com/zhilongw/macode, (accessed on 10 February 2024).

4.1. Quantitative Assessment on Simulated SAR Images

Robustness and logical consistency are the basic requirements for an assessment indicator. For example, theoretically, for a given simulated SAR image, the same despeckling method should perform better in preserving image details if we exerted noise of a lower level onto this image. To reveal the robustness and logical consistency of the different indicators, we generated single-look, four-look, and eight-look building images. All the images were then filtered by the refined Lee filter (with 7 × 7 filtering window), the PPB filter (with a patch size of 7 × 7), and the SAR-BM3D filter (with a patch size of 7 × 7).

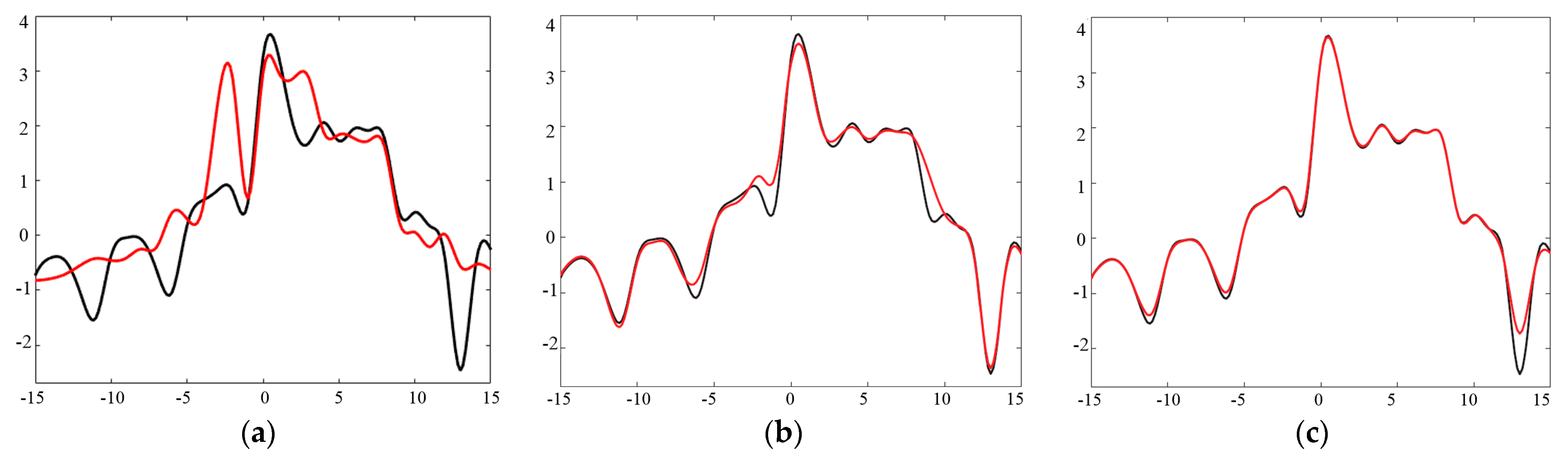
Figure 6 shows the results obtained on the single-look image. To help the readers better judge the edge-preservation capabilities of the different building methods, we chose a line across the building and display the signal intensity of the clean reference and the filtered image along this line in Figure 7. It can be seen that the refined Lee filter blurs the image details notably, while the speckle in the homogeneous area is not effectively suppressed. SAR-BM3D retains the edges and the strong backscattering signals of the building quite well. These observations are supported by Figure 7c, which shows that the line across the clean reference and the SAR-BM3D filtered image are quite close, especially for high returns.

Table 1. Quantitative assessment values for the simulated building image.

		EPD	DEI	RGO-BAI
L = 1	Refined Lee	0.3311	0.0576	0.5756
	PPB	0.2420	0.0599	0.5996
	SAR-BM3D	0.3753	0.0501	0.6330
L = 4	Refined Lee	0.4162	0.0601	0.6002
	PPB	0.3887	0.0652	0.6144
	SAR-BM3D	0.4798	0.0599	0.7201
L = 8	Refined Lee	0.5396	0.0814	0.6655
	PPB	0.5554	0.0820	0.7012
	SAR-BM3D	0.6071	0.0724	0.7993

lists the quantitative values for the images with a different number of looks. It can be seen that, for all the images, the RGO-BAI values follow the aforementioned observations, in that the SAR-BM3D filter performs the best, while the refined Lee filter shows the worst performance. However, for the single-look and four-look images, the EPD deviates from the above facts, as it can be seen that the EPD value of the PPB filtered image is smaller than that of the refined Lee filtered image. The reason is that the EPD value is calculated using all the pixels in the image, while the number of pixels located in the homogeneous area dominate in this image. For the PPB filter, due to the much better smoothing effect compared to the refined Lee filter in the single-look and four-look images, the numerator in EPD is much smaller than the denominator for the large number of pixels located in the homogeneous area, leading to a smaller EPD value. All the EPD and RGO-BAI values for the images with a different number of looks follow the logical consistency that, with the decrease in the noise amount, each individual filter can obtain better results in preserving edges. However, the DEI assessment results are unsatisfactory. We can see that, as L increases, the DEI values become higher, meaning that more edges are smoothed out. Clearly, these values do not reflect the real states. The reason is that the information of the original speckled image is not used at all, and, when the noise level decreases, DEI misjudges that the filters become over-smooth. For DEI, misjudgments also occur between the refined Lee filter and the PPB filter.

To further reveal the robustness and logical consistency of the different indicators, we process the simulated homogeneous single-look SAR image by the simple mean filter with a filtering window size of 3 × 3, 5 × 5 and 7 × 7, respectively. In theory, for the mean filter, more edges tend to be smoothed out with the extension of the filtering size. As displayed in

Table 2. Quantitative assessment values for the simulated homogeneous image.

	EPD	DEI	RGO-BAI
3 × 3 mean filter	0.7070	0.1544	0.9685
5 × 5 mean filter	0.6829	0.1364	0.9101
7 × 7 mean filter	0.5943	0.1380	0.8717

, both EPD and RGO-BAI meet logical consistency, while DEI disobeys logical consistency.

4.2. Quantitative Assessment on Two Real Single-Polarization SAR Images

To test the robustness and logical consistency of the indicators on the filtering results of the ALOS-PALSAR image, we tuned the iteration times (ITs) of the PPB filter. Figure 8 shows the images processed by the refined Lee filter, the PPB filter with IT varied from 2 to 4, and the SAR-BM3D filter. To help the readers better judge the edge-preservation performances of the filters, we also display the corresponding ratio images between the original data and the despeckled data in Figure 8. Correspondingly, the assessments by the different indicators are provided in

Table 3. Quantitative assessment values for the ALOS-PALSAR image.

	EPD	DEI	RGO-BAI
Refined Lee	0.8974	0.0687	0.3695
PPB with IT = 2	0.8938	0.0630	0.9042
PPB with IT = 3	0.8904	0.0559	0.7975
PPB with IT = 4	0.8885	0.0515	0.7208
SAR-BM3D	0.8957	0.0239	0.8409

. The speckle in the SAR intensity image is a kind of multiplicative noise. Therefore, for an ideal filter which does not filter out any edge on the image but only filter out noise, the ratio image should be pure speckle. On the contrary, if a method filters out too many edges on the original image, notable textures will reside on the ratio image.

Once again, the refined Lee filter blurs the details of the image to a large extent, which can be demonstrated by the corresponding ratio image where the boundaries and textures of the river are exhibited quite clearly. SAR-BM3D shows a good compromise between suppressing noise and retaining the profiles of the land objects. Visually, the PPB filter with IT = 2 performs slightly better than the SAR-BM3D filter, in both the judgment from the despeckled images and from the ratio images. It can be seen that, as the IT increases, the PPB filter can better suppress the speckle, but the image becomes over-smooth, and more details of the scene appear in the ratio image.

Basically, the RGO-BAI values are in line with the above observations and judgments: the RGO-BAI value for the refined Lee filter is the lowest; the value for the PPB filter with IT = 2 is the highest; and the value for the SAR-BM3D filter is higher than that for the PPB filter with IT = 3. The EPD also shows good logical consistency for the PPB filter with different IT values, but it misjudges that the refined Lee filter performs the best. For the DEI, the logical inconsistency issue is still apparent as we observed on the simulated SAR datasets.

To test the robustness and logical consistency of the indicators on the filtering results of the TerraSAR-X image, we tuned the block size (BS) of PPB and SAR-BM3D. Normally, for these nonlocal filters, a small block size can ensure better edge-preservation results, while a large block size can ensure better speckle reduction results.

Figure 9 displays the despeckled images for the TerraSAR-X image and

Table 4. Quantitative assessment values for the TerraSAR-X image.

	EPD	DEI	RGO-BAI
Refined Lee	0.1156	0.0340	0.4495
PPB with BS = 5 × 5	0.1551	0.0410	0.6832
PPB with BS = 7 × 7	0.1474	0.0438	0.6453
SAR-BM3D with BS = 5 × 5	0.1294	0.0683	0.8164
SAR-BM3D with BS = 7 × 7	0.1525	0.0682	0.8112

lists the assessment values. As expected, among the three despeckling methods, the refined Lee filter smooths out more image details, resulting in some edges appearing in the ratio image. It can also be seen that using a small block size can indeed help the PPB filter save more image details after processing. Visually, it is difficult to tell whether SAR-BM3D using a small block size performs better in retaining edges than when using a large block size, but it is still apparent that SAR-BM3D outperforms PPB in retaining edges, as was observed in the previous experiment.

Once again, RGO-BAI shows a satisfactory performance as the values are in high agreement with the visual and logical judgments, in that SAR-BM3D is outstanding in retaining edges, followed by PPB, and each individual filter with a small block size has a better edge-preservation capability. In contrast, misjudgments by EPD and DEI are notable. We can also notice some phenomena, such as the value ranges of DEI and RGO-BAI are generally close between the above two single-look SAR datasets, while the value ranges of EPD are dynamic and show uncertainty. Moreover, for each certain filter, the assessments made by RGO-BAI on different images are also generally close.

4.3. Quantitative Assessment on a Real PolSAR Images

Figure 10 shows the filtered results of the AirSAR PolSAR image. As can be seen, the over-smooth issue for the nonlocal means filter is apparent. The PNGF algorithm shows outstanding performance in retaining the structures and edges in urban areas but some details in the forest areas are smoothed out. Visually, the NLTV method keeps most details after filtering. The quantitative assessment values listed in

Table 5. Quantitative assessment values for the AirSAR image.

	EPD	DEI	RGO-BAI
Nonlocal means	0.6715	0.0234	0.9182
PNGF	0.7554	0.0412	0.9684
NLTV	0.8206	0.0377	0.9797
3 × 3 mean filter	0.6476	0.0584	0.9558
5 × 5 mean filter	0.5911	0.0377	0.8214
7 × 7 mean filter	0.5729	0.0308	0.7034
9 × 9 mean filter	0.5650	0.0268	0.6379
11 × 11 mean filter	0.5609	0.0244	0.6055

once again demonstrate that the proposed indicator can better reflect the real states.

To reveal the robustness and logical consistency of the different indicators on this image, we process the image by the simple mean filter with a filtering window size of 3 × 3, 5 × 5, 7 × 7, 9 × 9, and 11 × 11, respectively. As displayed in Table 5, both EPD and RGO-BAI meet logical consistency in that, with the extension of filtering size, more edges are smoothed out. Especially, for RGO-BAI, the decrease rate of the values is generally linearly related to the increase rate of the filtering size. On the contrary, the DEI still encounters logical inconsistency issue.

The proposed indicator involves a numerical searching approach in the implementation process, which introduces an extra computational burden.

Table 6. Computational time (seconds) of the indicators on the three real SAR images.

	EPD	DEI	RGO-BAI
ALOS-PALSAR Image	0.84	1.34	2.17
TerraSAR-X Image	0.82	1.39	6.06
AirSAR Image	0.88	1.48	7.11

showcases the processing time of the different indicators on the three real SAR images which all have the same size of 500 × 500 pixels. As can be seen, EPD has a very high computational efficiency, while RGO-BAI takes more time than EPD and DEI. We notice that the computational time of RGO-BAI on the ALOS-PALSAR image is notably shorter than that on the TerraSAR-X image. The main reason is that the ALOS-PALSAR image has more homogeneous areas; hence, the computational speed of RGO-BAI is accelerated by considering local homogeneity as described in Section 2.4. We can also notice that the computational time of RGO-BAI on the AirSAR PolSAR image is longest, due to the transformation process of PolCM described in Section 2.5.

5. Conclusions

The assessment of the edge-preservation capability for SAR image filters is a challenging task, because, theoretically, we do not have the clean references. Therefore, a reliable and robust blind assessment method is needed. Although several indicators have been presented by researchers to quantify the capability of SAR filters in edge preservation, most are not robust in practical use. The main reason for this lies in the fact that these indicators are normally derived based only on the basic multiplicative nature of speckle, and do not take into account the detailed statistical distribution traits of SAR data.

In this paper, we have proposed the use of SAR RGO instead of the traditional arithmetic difference operator to quantify the edge gradient between two neighboring image patches. CIE is then employed to determine whether the ratio gradient in the filtered image is close to that in the unobserved clean image, based on the statistical distribution traits of the SAR ratio gradient. Finally, the proposed RGO-BAI is derived. In the process of solving the confidence intervals, we introduce a numerical searching approach and deploy some adaptive strategies to accelerate the searching speed. The proposed indicator is also extended to assess the PolSAR filters by transforming the polarimetric scattering matrix into a scalar which follows a Gamma distribution. To validate the reliability of RGO-BAI, we tested the indicator using the filtering results of some typical despeckling algorithms on four datasets. We also tuned the parameters of the different filters to test the robustness and logical consistency of RGO-BAI. The assessment values confirmed the outstanding performance of RGO-BAI from both the aspect of robustness and the aspect of logical consistency. The assessment values of RGO-BAI also have a high goodness of fit compared with the visual inspection on the filtered images. However, we also notice that the computational efficiency of RGO-BAI is relatively low due to the use of a numerical searching approach. In the future, the approaches with a high efficiency need to be studied in order to implement RGO-BAI, and the experiments on more PolSAR images from different sensors need to be conducted to inspect the feasibility of RGO-BAI.