Three-Dimensional Structure of Mesoscale Eddies and Their Impact on Diapycnal Mixing in a Standing Meander of the Antarctic Circumpolar Current
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Mesoscale Eddy Trajectory Atlas Product
2.1.2. Argo Profiles
2.1.3. The Other Data
2.2. Methods
2.2.1. Eddy Composite Analysis
2.2.2. Fine-Scale Strain Parameterization
3. Results
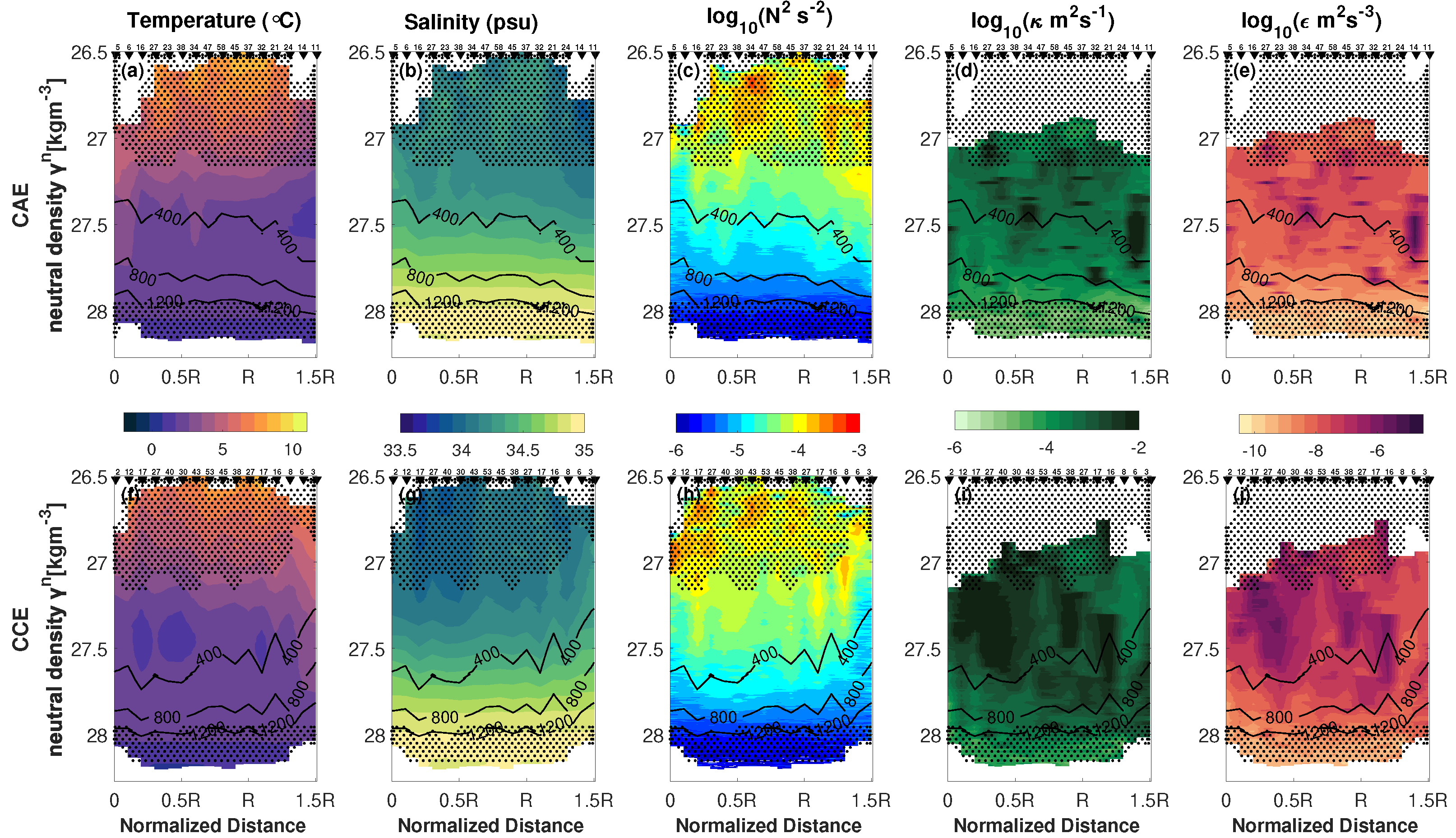
3.1. The Horizontal Structure of Composite Mesoscale Eddies and Their Impact on Mixing
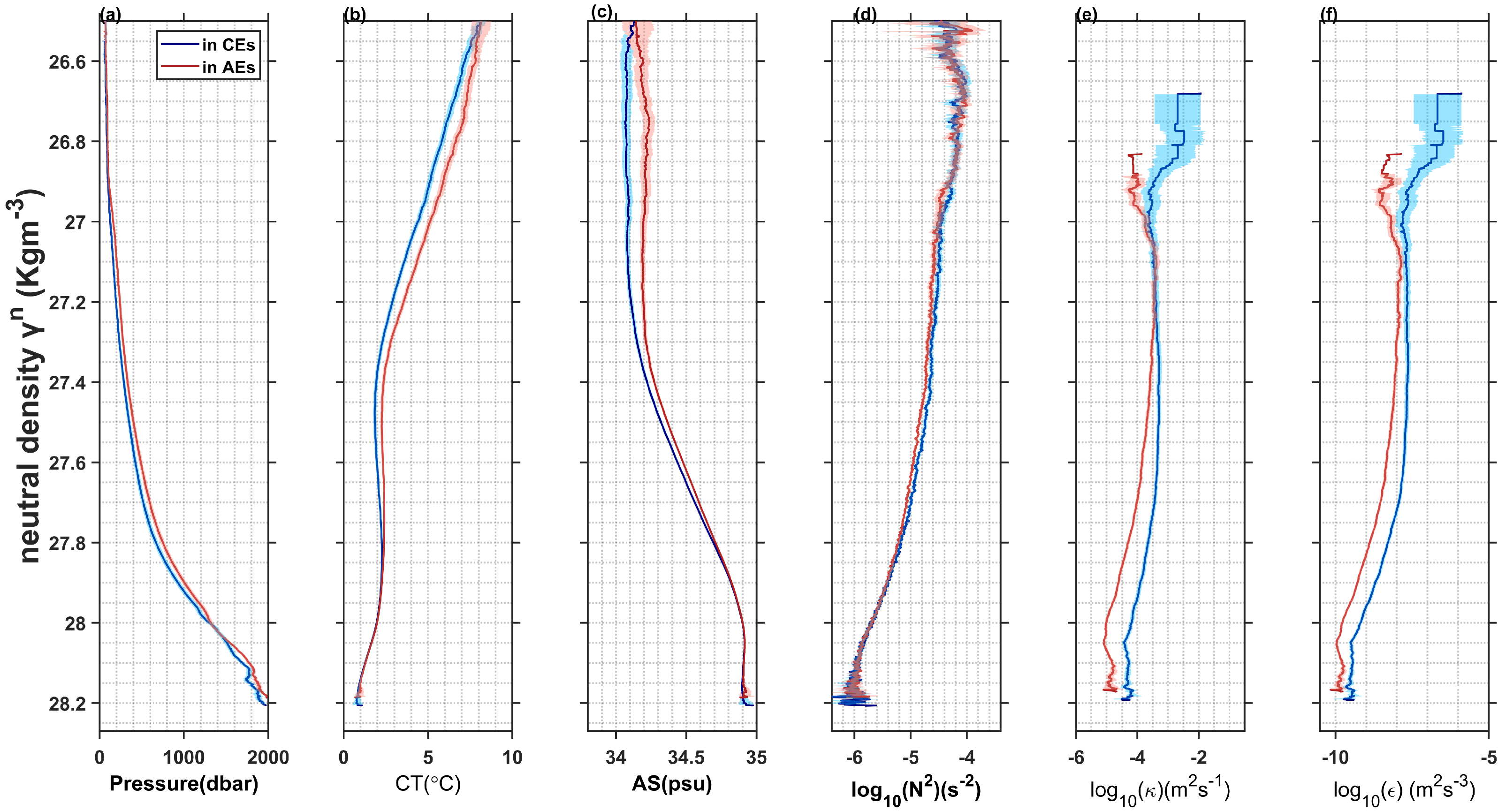
3.2. The Vertical Structure of Composite Mesoscale Eddies and Their Influence on Mixing
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whalen, C.B.; MacKinnon, J.A.; Talley, L.D. Large-scale impacts of the mesoscale environment on mixing from wind-driven internal waves. Nat. Geosci. 2018, 11, 842–847. [Google Scholar] [CrossRef]
- Marshall, J.; Speer, K. Closure of the meridional overturning circulation through Southern Ocean upwelling. Nat. Geosci. 2012, 5, 171–180. [Google Scholar] [CrossRef]
- Rintoul, S.R. The global influence of localized dynamics in the Southern Ocean. Nature 2018, 558, 209–218. [Google Scholar] [CrossRef]
- Frenger, I.; Münnich, M.; Gruber, N.; Knutti, R. Southern Ocean eddy phenomenology. J. Geophys. Res. Ocean. 2015, 120, 7413–7449. [Google Scholar] [CrossRef]
- Waterman, S.; Naveira Garabato, A.C.; Polzin, K.L. Internal Waves and Turbulence in the Antarctic Circumpolar Current. J. Phys. Oceanogr. 2013, 43, 259–282. [Google Scholar] [CrossRef]
- Meyer, A.; Sloyan, B.M.; Polzin, K.L.; Phillips, H.E.; Bindoff, N.L. Mixing Variability in the Southern Ocean. J. Phys. Oceanogr. 2015, 45, 966–987. [Google Scholar] [CrossRef]
- Sheen, K.L.; Garabato, A.C.; Brearley, J.A.; Meredith, M.P.; Polzin, K.L.; Smeed, D.A.; Forryan, A.; King, B.A.; Sallée, J.B.; St. Laurent, L.; et al. Eddy-induced variability in Southern Ocean abyssal mixing on climatic timescales. Nat. Geosci. 2014, 7, 577–582. [Google Scholar] [CrossRef]
- Arzel, O.; de Verdière, A.C. Can we infer diapycnal mixing rates from the world ocean temperature-salinity distribution? J. Phys. Oceanogr. 2016, 46, 3751–3775. [Google Scholar] [CrossRef]
- Dove, L.A.; Thompson, A.F.; Balwada, D.; Gray, A.R. Observational Evidence of Ventilation Hotspots in the Southern Ocean. J. Geophys. Res. Ocean. 2021, 126, e2021JC017178. [Google Scholar] [CrossRef]
- St. Laurent, L.; Naveira Garabato, A.C.; Ledwell, J.R.; Thurnherr, A.M.; Toole, J.M.; Watson, A.J. Turbulence and diapycnal mixing in drake passage. J. Phys. Oceanogr. 2012, 42, 2143–2152. [Google Scholar] [CrossRef]
- Sheen, K.L.; Brearley, J.A.; Naveira Garabato, A.C.; Smeed, D.A.; Waterman, S.; Ledwell, J.R.; Meredith, M.P.; St. Laurent, L.; Thurnherr, A.M.; Toole, J.M.; et al. Rates and mechanisms of turbulent dissipation and mixing in the Southern Ocean: Results from the Diapycnal and Isopycnal Mixing Experiment in the Southern Ocean (DIMES). J. Geophys. Res. Ocean. 2013, 118, 2774–2792. [Google Scholar] [CrossRef]
- Patel, R.S.; Phillips, H.E.; Strutton, P.G.; Lenton, A.; Llort, J. Meridional Heat and Salt Transport Across the Subantarctic Front by Cold-Core Eddies. J. Geophys. Res. Ocean. 2019, 124, 981–1004. [Google Scholar] [CrossRef]
- Cyriac, A.; Phillips, H.E.; Bindoff, N.L.; Polzin, K. Turbulent Mixing Variability in an Energetic Standing Meander of the Southern Ocean. J. Phys. Oceanogr. 2022, 52, 1593–1611. [Google Scholar] [CrossRef]
- Keppler, L.; Cravatte, S.; Chaigneau, A.; Pegliasco, C.; Gourdeau, L.; Singh, A. Observed Characteristics and Vertical Structure of Mesoscale Eddies in the Southwest Tropical Pacific. J. Geophys. Res. Ocean. 2018, 123, 2731–2756. [Google Scholar] [CrossRef]
- Zhan, P.; Krokos, G.; Guo, D.; Hoteit, I. Three-Dimensional Signature of the Red Sea Eddies and Eddy-Induced Transport. Geophys. Res. Lett. 2019, 46, 2167–2177. [Google Scholar] [CrossRef]
- Chaigneau, A.; Le Texier, M.; Eldin, G.; Grados, C.; Pizarro, O. Vertical structure of mesoscale eddies in the eastern South Pacific Ocean: A composite analysis from altimetry and Argo profiling floats. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Liu, C.; Wang, F. Global meridional eddy heat transport inferred from Argo and altimetry observations. Sci. Rep. 2019, 9, 1345. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Qiu, B.; Liu, H.; Zhang, Z. Doubling of surface oceanic meridional heat transport by non-symmetry of mesoscale eddies. Nat. Commun. 2023, 14, 5460. [Google Scholar] [CrossRef]
- Sun, C.; Watts, D.R. Heat flux carried by the Antarctic Circumpolar Current mean flow. J. Geophys. Res. Ocean. 2002, 107, 2-1–2-13. [Google Scholar] [CrossRef]
- Talley, L.D. Closure of the global overturning circulation through the Indian, Pacific, and southern oceans. Oceanography 2013, 26, 80–97. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Jia, F.; Wu, L.; Qiu, B. Seasonal Modulation of Eddy Kinetic Energy and Its Formation Mechanism in the Southeast Indian Ocean. J. Phys. Oceanogr. 2011, 41, 657–665. [Google Scholar] [CrossRef]
- Tamsitt, V.; Drake, H.F.; Morrison, A.K.; Talley, L.D.; Dufour, C.O.; Gray, A.R.; Griffies, S.M.; Mazloff, M.R.; Sarmiento, J.L.; Wang, J.; et al. Spiraling pathways of global deep waters to the surface of the Southern Ocean. Nat. Commun. 2017, 8, 172. [Google Scholar] [CrossRef] [PubMed]
- Foppert, A.; Donohue, K.A.; Watts, D.R.; Tracey, K.L. Eddy heat flux across the Antarctic Circumpolar Current estimated from sea surface height standard deviation. J. Geophys. Res. Ocean. 2017, 122, 6947–6964. [Google Scholar] [CrossRef]
- Patel, R.S.; Llort, J.; Strutton, P.G.; Phillips, H.E.; Moreau, S.; Conde Pardo, P.; Lenton, A. The Biogeochemical Structure of Southern Ocean Mesoscale Eddies. J. Geophys. Res. Ocean. 2020, 125, e2020JC016115. [Google Scholar] [CrossRef]
- Meijer, J.J.; Phillips, H.E.; Bindoff, N.L.; Rintoul, S.R.; Foppert, A. Dynamics of a Standing Meander of the Subantarctic Front Diagnosed from Satellite Altimetry and Along-Stream Anomalies of Temperature and Salinity. J. Phys. Oceanogr. 2022, 52, 1073–1089. [Google Scholar] [CrossRef]
- Cyriac, A.; Phillips, H.E.; Bindoff, N.L.; Mao, H.; Feng, M. Observational estimates of turbulent mixing in the southeast indian ocean. J. Phys. Oceanogr. 2021, 51, 2103–2128. [Google Scholar] [CrossRef]
- Gordon, A.L. An Antarctic oceanographic section along 170°E. Deep-Sea Res. Oceanogr. Abstr. 1975, 22, 357–377. [Google Scholar] [CrossRef]
- Rintoul, S.R.; Sokolov, S.; Williams, M.J.M.; Peña Molino, B.; Rosenberg, M.; Bindoff, N.L. Antarctic Circumpolar Current transport and barotropic transition at Macquarie Ridge. Geophys. Res. Lett. 2014, 41, 7254–7261. [Google Scholar] [CrossRef]
- Pegliasco, C.; Delepoulle, A.; Mason, E.; Morrow, R.; Faugère, Y.; Dibarboure, G. META3.1exp: A new global mesoscale eddy trajectory atlas derived from altimetry. Earth Syst. Sci. Data 2022, 14, 1087–1107. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Wang, W.; Huang, R.X. Universal structure of mesoscale eddies in the ocean. Geophys. Res. Lett. 2013, 40, 3677–3681. [Google Scholar] [CrossRef]
- Sokolov, S.; Rintoul, S.R. Circumpolar structure and distribution of the antarctic circumpolar current fronts: 2. Variability and relationship to sea surface height. J. Geophys. Res. Ocean. 2009, 114, C11019. [Google Scholar] [CrossRef]
- Meijers, A.J.; Bindoff, N.L.; Rintoul, S.R. Frontal movements and property fluxes: Contributions to heat and freshwater trends in the Southern Ocean. J. Geophys. Res. Ocean. 2011, 116, 1–17. [Google Scholar] [CrossRef]
- Meijers, A.J.; Bindoff, N.L.; Rintoul, S.R. Estimating the four-dimensional structure of the southern ocean using satellite altimetry. J. Atmos. Ocean. Technol. 2011, 28, 548–568. [Google Scholar] [CrossRef]
- Orsi, A.H.; Whitworth, T.; Nowlin, W.D. On the meridional extent and fronts of the Antarctic Circumpolar Current. Deep Sea Res. Part I Oceanogr. Res. Pap. 1995, 42, 641–673. [Google Scholar] [CrossRef]
- Sokolov, S.; Rintoul, S.R. Multiple Jets of the Antarctic Circumpolar Current South of Australia. J. Phys. Oceanogr. 2007, 37, 1394–1412. [Google Scholar] [CrossRef]
- Rintoul, S.R.; Bullister, J.L. A late winter hydrographic section from Tasmania to Antarctica. Deep Sea Res. Part I Oceanogr. Res. Pap. 1999, 46, 1417–1454. [Google Scholar] [CrossRef]
- Phillips, H.E.; Rintoul, S.R. Eddy variability and energetics from direct current measurements in the Antarctic Circumpolar Current south of Australia. J. Phys. Oceanogr. 2000, 30, 3050–3076. [Google Scholar] [CrossRef]
- Cressman, G.P. An Operational Objective Analysis System. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Kunze, E.; Firing, E.; Hummon, J.M.; Chereskin, T.K.; Thurnherr, A.M. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. J. Phys. Oceanogr. 2006, 36, 1553–1576. [Google Scholar] [CrossRef]
- Henyey, F.S.; Wright, J.; Flatté, S.M. Energy and action flow through the internal wave field: An eikonal approach. J. Geophys. Res. 1986, 91, 8487. [Google Scholar] [CrossRef]
- Polzin, K.L.; Toole, J.M.; Schmitt, R.W. Finescale Parameterizations of Turbulent Dissipation. J. Phys. Oceanogr. 1995, 25, 306–328. [Google Scholar] [CrossRef]
- Cairns, J.L.; Williams, G.O. Internal wave observations from a midwater float, 2. J. Geophys. Res. 1976, 81, 1943–1950. [Google Scholar] [CrossRef]
- Bray, N.A.; Fofonoff, N.P. Available Potential Energy for MODE Eddies. J. Phys. Oceanogr. 1981, 11, 30–47. [Google Scholar] [CrossRef]
- Gregg, M.C.; D’Asaro, E.A.; Riley, J.J.; Kunze, E. Mixing efficiency in the ocean. Annu. Rev. Mar. Sci. 2018, 10, 443–473. [Google Scholar] [CrossRef]
- Osborn, T.R. Estimates of the Local Rate of Vertical Diffusion from Dissipation Measurements. J. Phys. Oceanogr. 1980, 10, 83–89. [Google Scholar] [CrossRef]
- de Boyer Montégut, C.; Madec, G.; Fischer, A.S.; Lazar, A.; Iudicone, D. Mixed layer depth over the global ocean: An examination of profile data and a profile-based climatology. J. Geophys. Res. Ocean. 2004, 109, 1–20. [Google Scholar] [CrossRef]
- Meyer, A.; Phillips, H.E.; Sloyan, B.M.; Polzin, K.L. Mixing (MX) Oceanographic Toolbox for EM-APEX * Float Data Applying Shear-Strain Finescale Parameterization; University of Tasmania: Tasmania, Australia, 2014. [Google Scholar]
- Cyriac, A.; Meyer, A.; Phillips, H.E.; Bindoff, N.L. Observations of internal wave interactions in a Southern Ocean standing meander. J. Phys. Oceanogr. 2023, 53, 1997–2011. [Google Scholar] [CrossRef]
- Kim, Y.S.; Orsi, A.H. On the variability of antarctic circumpolar current fronts inferred from 1992-2011 altimetry. J. Phys. Oceanogr. 2014, 44, 3054–3071. [Google Scholar] [CrossRef]
- Meredith, M.P.; Meijers, A.S.; Naveira Garabato, A.C.; Brown, P.J.; Venables, H.J.; Abrahamsen, E.P.; Jullion, L.; Messias, M. Circulation, retention, and mixing of waters within the Weddell-Scotia Confluence, Southern Ocean: The role of stratified Taylor columns. J. Geophys. Res. Ocean. 2015, 120, 547–562. [Google Scholar] [CrossRef]
- Perissinotto, R.; Duncombe Rae, C.M. Occurrence of anticyclonic eddies on the Prince Edward Plateau (Southern Ocean): Effects on phytoplankton biomass and production. Deep Sea Res. Part A Oceanogr. Res. Pap. 1990, 37, 777–793. [Google Scholar] [CrossRef]
- Meredith, M.P.; Watkins, J.L.; Murphy, E.J.; Cunningham, N.J.; Wood, A.G.; Korb, R.; Whitehouse, M.J.; Thorpe, S.E.; Vivier, F. An anticyclonic circulation above the Northwest Georgia Rise, Southern Ocean. Geophys. Res. Lett. 2003, 30, 1–5. [Google Scholar] [CrossRef]
- Petersen, M.R.; Williams, S.J.; Maltrud, M.E.; Hecht, M.W.; Hamann, B. A three-dimensional eddy census of a high-resolution global ocean simulation. J. Geophys. Res. Ocean. 2013, 118, 1759–1774. [Google Scholar] [CrossRef]
- Adams, K.A.; Hosegood, P.; Taylor, J.R.; Sallée, J.B.; Bachman, S.; Torres, R.; Stamper, M. Frontal circulation and submesoscale variability during the formation of a southern ocean mesoscale eddy. J. Phys. Oceanogr. 2017, 47, 1737–1753. [Google Scholar] [CrossRef]
- Yang, Q.; Nikurashin, M.; Sasaki, H.; Sun, H.; Tian, J. Dissipation of mesoscale eddies and its contribution to mixing in the northern South China Sea. Sci. Rep. 2019, 9, 556. [Google Scholar] [CrossRef] [PubMed]





| AEs | CEs | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Step 1 | Number of Argo profiles inside corresponding eddies | 782 | 740 | ||||||
| Number of Argo profiles with consistent SLA sign (AVISO) and eddy polarity | 777 (positive) | 579 (negative) | |||||||
| Number of Argo profiles with consistent SLA sign (Argo) and eddy polarity | 753 (positive) | 423 (negative) | |||||||
| Number of Argo profiles with consistent SLA sign (AVISO & Argo) and eddy polarity | 751 (positive) | 405 (negative) | |||||||
| Step 2 | Different DHT range (m) | <0.83 | 0.83∼1.1 | 1.1∼1.6 | 1.6∼1.98 | <0.83 | 0.83∼1.1 | 1.1∼1.6 | 1.6∼1.98 |
| Number of Argo profiles classified by DHT | 88 | 204 | 175 | 282 | 121 | 148 | 127 | 9 | |
| Step 3 | Number of Composite eddy profiles (DHT < 1.6) | 467 | 396 | ||||||
| Number of Composite eddy profiles (Normalized R < 2) | 448 | 388 | |||||||
| Number of Composite eddy profiles (Normalized R < 1.5) | 438 | 384 | |||||||
| CAE Number of Argo Profiles | CCE Number of Argo Profiles | |||
|---|---|---|---|---|
| 0∼0.5R | 77 | 6.62 ± 1.35 | 102 | 46.00 ± 2.25 |
| 0.5R∼1R | 222 | 7.92 ± 0.68 | 214 | 20.00 ± 0.84 |
| R∼1.5R | 128 | 36.00 ± 2.64 | 67 | 28.00 ± 1.05 |
| 1.5R∼2R | 21 | 6.91 ± 1.54 | 5 | 73.00 ± 9.24 |
| Neutral Surface/ (Pressure ± STD/dbar) | 0∼0.5R | 0.5R∼R | R∼1.5R | 1.5R∼2R |
|---|---|---|---|---|
| 27.4 (287 ± 71 dbar) | 4.84 ± 2.18 | 49 ± 72 | 4.56 ± 1.85 | 4.55 ± 1.67 |
| 27.5 (353 ± 84 dbar) | 2.32 ± 0.55 | 9.27 ± 7.51 | 95 ± 150 | 5.74 ± 2.71 |
| 27.6 (430 ± 100 dbar) | 2.64 ± 1.37 | 5.84 ± 2.91 | 109 ± 177 | 5.97 ± 4.44 |
| 27.7 (530 ± 117 dbar) | 2.93 ± 1.23 | 2.88 ± 1.06 | 3.05 ± 1.54 | 2.02 ± 1.05 |
| 27.8 (680 ± 124 dbar) | 1.46 ± 0.60 | 1.56 ± 0.65 | 32 ± 50 | 1.27 ± 1.03 |
| 27.9 (934 ± 134 dbar) | 0.99 ± 0.40 | 0.90 ± 0.27 | 0.69 ± 0.17 | 0.58 ± 0.35 |
| 28 (1273 ± 118 dbar) | 0.56 ± 0.27 | 0.25 ± 0.07 | 0.24 ± 0.09 | 0.11 ± 0.10 |
| Neutral Surface/ (Pressure ± STD/dbar) | 0∼0.5R | 0.5R∼R | R∼1.5R | 1.5R∼2R |
|---|---|---|---|---|
| 27.4 (287 ± 71 dbar) | 24.70 ± 21.6 | 6.50 ± 7.9 | 4.50 ± 5.20 | 2.60 ± 3.20 |
| 27.5 (353 ± 84 dbar) | 13.60 ± 12.90 | 2.20 ± 0.96 | 4.40 ± 5.00 | 1.90 ± 2.80 |
| 27.6 (430 ± 100 dbar) | 5.70 ± 4.60 | 1.60 ± 0.56 | 3.80 ± 3.90 | 1.00 ± 1.50 |
| 27.7 (530 ± 117 dbar) | 1.10 ± 0.59 | 2.70 ± 1.10 | 3.80 ± 2.60 | 13.8 ± 28.4 |
| 27.8 (680 ± 124 dbar) | 0.71 ± 0.40 | 0.95 ± 0.36 | 2.30 ± 1.50 | 2.40 ± 3.50 |
| 27.9 (934 ± 134 dbar) | 0.39 ± 0.27 | 0.54 ± 0.14 | 0.92 ± 0.32 | 11.3 ± 23.0 |
| 28 (1273 ± 118 dbar) | 0.74 ± 0.94 | 0.32 ± 0.12 | 0.70 ± 0.56 | 0.88 ± 3.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Y.; Ma, C.; Luo, Y.; Phillips, H.E.; Cyriac, A. Three-Dimensional Structure of Mesoscale Eddies and Their Impact on Diapycnal Mixing in a Standing Meander of the Antarctic Circumpolar Current. Remote Sens. 2024, 16, 1863. https://doi.org/10.3390/rs16111863
Bao Y, Ma C, Luo Y, Phillips HE, Cyriac A. Three-Dimensional Structure of Mesoscale Eddies and Their Impact on Diapycnal Mixing in a Standing Meander of the Antarctic Circumpolar Current. Remote Sensing. 2024; 16(11):1863. https://doi.org/10.3390/rs16111863
Chicago/Turabian StyleBao, Yanan, Chao Ma, Yiyong Luo, Helen Elizabeth Phillips, and Ajitha Cyriac. 2024. "Three-Dimensional Structure of Mesoscale Eddies and Their Impact on Diapycnal Mixing in a Standing Meander of the Antarctic Circumpolar Current" Remote Sensing 16, no. 11: 1863. https://doi.org/10.3390/rs16111863
APA StyleBao, Y., Ma, C., Luo, Y., Phillips, H. E., & Cyriac, A. (2024). Three-Dimensional Structure of Mesoscale Eddies and Their Impact on Diapycnal Mixing in a Standing Meander of the Antarctic Circumpolar Current. Remote Sensing, 16(11), 1863. https://doi.org/10.3390/rs16111863








