Advancing Physically Informed Autoencoders for DTM Generation

Abstract

The combination of Remote Sensing and Deep Learning (DL) has brought about a revolution in converting digital surface models (DSMs) to digital terrain models (DTMs). DTMs are used in various fields, including environmental management, where they provide crucial topographical data to accurately model water flow and identify flood-prone areas. However, current DL-based methods require intensive data processing, limiting their efficiency and real-time use. To address these challenges, we have developed an innovative method that incorporates a physically informed autoencoder, embedding physical constraints to refine the extraction process. Our approach utilizes a normalized DSM (nDSM), which is updated by the autoencoder to enable DTM generation by defining the DTM as the difference between the DSM input and the updated nDSM. This approach reduces sensitivity to topographical variations, improving the model’s generalizability. Furthermore, our framework innovates by using subtractive skip connections instead of traditional concatenative ones, improving the network’s flexibility to adapt to terrain variations and significantly enhancing performance across diverse environments. Our novel approach demonstrates superior performance and adaptability compared to other versions of autoencoders across ten diverse datasets, including urban areas, mountainous regions, predominantly vegetation-covered landscapes, and a combination of these environments.

1. Introduction

DTMs are a crucial component of geospatial analysis, as they provide foundational information about the earth’s topography without the interference of artificial obstructions. The applications of DTMs are broad and varied, ranging from flood risk assessment [1] to urban planning [2] and environmental conservation [3]. As such, they represent an essential tool for disaster management and sustainable development initiatives [4].

DTMs have traditionally been created using geodetic measurements, which are transformed into a topographic map featuring contour lines. These contour lines are then digitized and gridded to convert the hardcopy map into a digital format called a DTM [5]. However, modern data capture technologies such as Light Detection and Ranging (LiDAR) [6] and remote sensing [7,8] have significantly improved the efficiency and precision of DTM generation [9].

With remote sensing, DTMs can be created from aerial or satellite imagery using the stereoscopic imaging concept. This involves capturing two or more images of the same area from slightly different angles, similar to how human eyes perceive depth [10]. Once these images are analyzed and intersected, they construct three-dimensional representations of the earth’s surface [11], known as a DSM, which can be converted to DTM. On the other hand, a LiDAR point cloud, which contains x, y, and z positional data, is composed of ground points, which reflect the terrain, and nonground points, which represent structures such as buildings and trees. Combining these points forms a DSM [12], which can subsequently be converted into a DTM.

The process of extracting DTMs from DSMs typically involves one of four primary groups of methods: slope-based, morphology-based, interpolation-based, and segmentation-based [13]. Slope-based methods [14,15], which involve filtering based on a predefined slope threshold, are effective in terrains with significant slope variations but are not well-suited for rugged or discontinuous terrain [16]. In contrast, morphology-based methods rely on morphological operators to smooth out irregularities and emphasize significant elements, which aids in isolating and removing objects like buildings and vegetation that are not part of the natural terrain. The accuracy of these methods depends significantly on the size of the structural element [17]. Interpolation-based methods [6], including Triangulated Irregular Networks (TINs) [18] and grid-based techniques like Kriging and Inverse Distance Weighting (IDW), as well as adaptive methods. Ref. [19] play a pivotal role in estimating the height of unmeasured areas based on the elevation of nearby measured locations. However, these methods are limited to interpolation and do not support extrapolation. This means that unknown points that are not surrounded by known points remain without estimable information. Lastly, segmentation-based filters, such as Cloth Simulation Filtering (CSF) [20], are essential for classifying point clouds into ground and nonground points. However, this approach often requires additional methodologies, particularly interpolation-based ones, for refinement and gap-filling. The effectiveness of each method is dependent on the specific terrain characteristics and the intended use of the model [20,21]. Therefore, it is essential to choose the appropriate method based on the specific requirements of the project.

The strategies mentioned earlier do not suffice in addressing intricate terrains comprising mountainous regions, dense low-height foliage, and buildings encompassed by trees. Therefore, there has been a shift towards adopting deep learning technologies, particularly those based on CNNs [22]. DL-based techniques can be broadly classified into point-based [23], voxel-based [24], and depth image-based [16] approaches, each with its unique advantages and challenges [25].

Point-based methods [26,27], which directly manipulate the original geometric configurations of point clouds, offer fidelity to the structural complexities of the data. However, these methods face limitations due to their reliance on the extent of sampling, which can restrict their effectiveness in diverse or expansive environments [28]. The aforementioned task highlights a fundamental challenge in handling large datasets and optimizing computational efficiency, a prevalent theme in discussions surrounding point cloud processing methodologies.

To overcome some of these limitations, voxel-based methods use a 3D grid representation that allows the application of 2D CNNs within 3D spaces. This approach, while mitigating some of the computational burdens associated with point-based methods, still needs significant memory and processing costs [29]. Furthermore, the task of determining the most effective combination of inputs for these methods introduces an additional layer of complexity to their implementation [30].

An alternative approach is a depth image-based deep learning, which shows promise in addressing scalability and efficiency challenges inherent in point and voxel-based methods. This method projects point clouds onto a 2D plane, transforming 3D data into a format that 2D CNN architectures can handle. However, this conversion process is not without its drawbacks, as the simplification from 3D to 2D can lead to a loss of critical geometric information, particularly in settings characterized by complex structures, such as forested areas [25]. However, two key features of image-based methods have captured the interest of researchers, adding to the already complex landscape of point cloud processing. Firstly, the inherently organized nature of input data in image-based methods aligns seamlessly with the requirements of convolutional operators, which stand in contrast to the unstructured format of Point Clouds (PCs). It is important to note that methods relying on PCs often encounter similar issues to those faced by image-based approaches. This is because they typically produce a raster output, and most of their processes, except for the initial stage, are similar to voxel or depth-image-based approaches [23]. Additionally, these methods are more computationally demanding. According to the literature, PC-based methods use either a PointNet network [23] or rasterization [31] to convert 3D point clouds into raster format. After this step, the process becomes similar to image-based methods. For instance, in [31], a two-stage method has been proposed, where the first stage involves rasterizing point clouds before feeding them into a generative network-like image-based one. The above-mentioned challenges related to PC-based methods led us to focus on image-based methods in our research.

This paper addresses the challenges associated with image-based techniques that rely on DSMs as their input [32], with the aid of an introduction of a physically-informed autoencoder. These challenges arise from the need for data processing, ranging from post-processing [22] to sensitivity towards the distribution of training and test datasets [31]. To address these challenges, physical constraints are incorporated into our autoencoder. The proposed autoencoder is designed explicitly for DTM generation and introduces an innovative DL framework that generates DTMs through nDSM. The network itself updates the nDSM, which is then used to generate the DTM via a physical relationship that expresses the DTM as a subtraction of the network’s input, DSM, from the nDSM. This approach reduces the sensitivity of the framework to the earth’s topography, which is often a major obstacle to making these methods more generalizable. To make it more physically equipped, the traditional skip connections, as concatenative ones, are replaced with subtractive ones in our network architecture. This modification enables the network to be better equipped to handle physical variations and, thus, improve the overall performance of the framework.

The contributions of this paper are outlined as follows, each underscoring a significant advancement in the domain of DTM reconstruction:

• Developing an inclusive comparative framework that covers statistical, structural, and geographical characteristics of state-of-the-art benchmarks for DTM reconstruction, which can be utilized to assess and integrate existing methodologies under one cohesive context.
• Compilation and presentation of a large dataset comprising a spectrum of elevation profiles and distributions, thereby providing a comprehensive resource for the evaluation and benchmarking of DTM reconstruction algorithms.
• Introduction of a novel, physically inspired methodology for the derivation of DTM from nDSM, characterized by its enhanced resilience to background noise, thereby improving the accuracy of terrain modeling.
• Development and introduction of a new, physically informed skip connection mechanism, termed ’subtractive skip connection’, tailored for the optimization of DTM reconstruction processes, offering a methodological innovation that enhances the precision and efficiency of terrain modeling.

2. Related Work

Deep learning techniques have improved the accuracy of DTM extraction. This review summarizes studies that integrate topographic knowledge into deep learning and develop new neural network architectures for terrain modeling. In the most relevant task, Ref. [22] presented a method for generating DTMs directly from DSMs without the need for traditional filtering methods to remove nonground pixels. Their approach employs a Hybrid Deep Convolutional Neural Network (HDCNN) that merges the U-net architecture with residual networks, enhanced by a multi-scale fusion strategy for DTM generation. This method excels in complex scenes, outperforming both deep learning-based filters and reference algorithms, particularly in challenging environments.

In a related study, Ref. [32] explored the efficacy of the pix-to-pix model, a conditional GAN framework, for converting DSMs to DTMs in built-up areas without additional data or extensive parameter tuning. This approach simplifies the DTM generation process and demonstrates the model’s versatility across varied topographies and building characteristics, highlighting its potential for flood risk assessment at the building level. Further extending their research, Ref. [32] applied the pix-to-pix model to coastal urban areas of Japan, achieving a high spatial resolution DTM with minimal RMSE, underscoring the model’s capability in handling high and densely built environments. Ref. [31] recently tackled the challenge of extracting DTMs directly from ALS point clouds. To achieve this, they put together a large dataset for training purposes and introduced a new method called DeepTerRa, which is based on deep learning and rasterization. The authors’ work is significant because it not only provides a valuable dataset but also proposes a unified framework for DTM extraction. The proposed method showcases submetric error levels, indicating its potential for end-to-end solutions. In this category, lately, Ref. [33] developed an end-to-end deep learning approach for DTM generation from DSMs, utilizing an EfficientNet-based architecture within a UNet framework. This method, despite its relatively lower parameter count, efficiently discriminates nonground pixels and retains detailed landscape features, offering a significant step forward in preserving the anthropogenic geomorphology of landscapes.

DTMs are generated by removing nonground areas from Digital DSMs and subsequently filling the resultant gaps. This process of gap-filling has been a focal point of numerous research studies due to its importance in creating accurate representations of the Earth’s terrain. Among these, Ref. [34] investigated the use of a Wasserstein Generative Adversarial Network (WGAN) with a fully convolutional architecture and a contextual attention mechanism for filling voids in Digital Elevation Models (DEMs). Utilizing GeoTIFF data from various regions in Norway, provided by the Norwegian Mapping Authority, the study demonstrated the model’s capability to generate semantically plausible data for DEM inpainting. This research showcases the adaptation of image inpainting methodologies to DEM void filling, offering a proof of concept for the application of deep generative models in enhancing remote sensing data.

Further advancing the field, Ref. [35] introduced a multi-attention GAN specifically designed for addressing voids in DEMs, which commonly occur due to instrumentation artifacts and ground occlusion. Their model integrates a multiscale feature fusion generation network for preliminary void filling, followed by a multi-attention network for the recovery of detailed terrain features, and employs a channel-spatial cropping attention mechanism to improve network performance. The discriminator’s convolution layers are enhanced with spectral normalization, and the model’s optimization incorporates a combined loss function that includes both reconstruction and adversarial losses.

Additionally, Ref. [36] presented an innovative approach for DTM data void filling by integrating topographic knowledge into a Conditional Generative Adversarial Network (CGAN), resulting in the Topographic Knowledge-Constrained Conditional Generative Adversarial Network (TKCGAN). This model significantly improves the accuracy of elevation and surface slope in reconstructed DTMs by incorporating topographic constraints into the loss functions.

3. Methodology

3.1. Problem Formulation

This study introduces an autoencoder architecture that incorporates an encoder and a decoder designed to predict DTM from DSM, as illustrated in Figure 1. The encoder is tasked with converting the input DSM into a latent representation within a lower-dimensional space. The DSM is described as 2.5-dimensional geospatial data, where each pixel is characterized by its image coordinates $(x,y)$ in the pixel grid, along with a positive scalar value z denoting elevation. This relationship can be articulated as a mapping from $(x,y)\in {\mathbb{R}}^2$ to $z\in {\mathbb{R}}_{+}$, where ${\mathbb{R}}_{+}$ symbolizes the set of positive real numbers. The encoder generates a latent representation, denoted by $\mathbf{Z}$, existing in a 3D space represented as ${\mathbb{R}}^{d\times p\times q}$. Here, d indicates the depth of the feature space, while p and q represent the reduced spatial dimensions. During training, the encoder’s parameters or weights, ${\theta }_{\mathrm{enc}}$ (Equation (1)), are optimized to efficiently capture the significant features of the DSM in the latent space.

$$\mathbf{Z}=f_{\mathrm{enc}}(\mathrm{DSM};{\theta }_{\mathrm{enc}})$$

(1)

Regarding the decoder, it is tasked with reconstructing the estimated DTM values, denoted by $D_{\mathrm{est}}$. This process involves optimizing the regression decoder parameters, ${\theta }_{\mathrm{reg}}$, as detailed in Equation (2):

$$D_{\mathrm{est}}=f_{\mathrm{reg}}(\mathbf{Z};{\theta }_{\mathrm{reg}})$$

(2)

3.2. Regression Task

The regression autoencoder, as can be seen from Figure 2, is equipped with subtractive skip connections to reconstruct ${\mathbf{D}}_{\mathrm{est}}$. In detail, each layer l in the encoder performs a transformation represented by Equation (3).

$$h_i=f_{\mathrm{enc}}^i\left(h_{i-1}\right),$$

(3)

where $h_0=\mathrm{DSM}$ and $h_{\mathrm{end}}=Z$, as depicted in Figure 2, and $f_{\mathrm{enc}}^i$ is the transformation function at the ith layer. On the other hand, the decoder’s regression branch transforms the latent representation Z into the nDSM. The transformation at each decoder layer of the regression branch i can be represented as:

$${\widehat{h}}_i=f_{\mathrm{reg}}^i\left({\widehat{h}}_{i-1}\right),$$

(4)

where ${\widehat{h}}_0=Z$ is the latent representation, and $f_{\mathrm{regression}}^i$ is the corresponding layer’s transformation function.

In the regression task, we carry out layer-wise operations like subtraction and concatenation. To ensure clarity and precision, we require a formal structure for these operations. The output at the l-th layer of the encoder is denoted by $h_l$, and its corresponding decoder output is denoted by ${\tilde{h}}_l$. The operations are outlined as follows: the subtraction operation at layer l is defined by $S_{\mathrm{sub},l}=h_l-{\tilde{h}}_l$, or the concatenation operation at layer l, denoted by ⊕, is articulated as $C_{\mathrm{concat},l}=h_l\oplus {\tilde{h}}_l$.

This process acts as a filter that highlights the high-frequency elements of the DSM. It produces a high-frequency component represented by $S_{\mathrm{sub}}^l$ in the case of subtractive skip connections. This component can be considered as the difference between DSM and DTM and can be geospatially equivalent to nDSM. This comparison arises because the regression’s loss affects the decoder outputs or ${\tilde{h}}_l$, which measures the deviation between the estimated DTM and the true one. As a result of this fact, the decoders have features that aim to capture the essential qualities of DTM. In contrast, concatenative skip connections strive to provide informed decoder features for their respective details, viewed as high frequency. Finally, in both cases of skip connections, the regressed DTM, $D_{\mathrm{est}}$, is obtained by subtracting nDSM from DSM.

The loss function of this task is designed to minimize the difference between the predicted elevation values and the actual DSM values, facilitating the model’s ability to accurately capture the underlying terrain elevation by adjusting the model parameters. The objective of the regression is to estimate $D_{\mathrm{est}}$ by optimizing the parameters ${\theta }_{\mathrm{enc}}$ and ${\theta }_{\mathrm{reg}}$ through the minimization of the following loss function:

$$L_{reg}({\theta }_{\mathrm{enc}},{\theta }_{\mathrm{reg}})=\sum _{i=1}^N\mathsf{\ell }({\widehat{D}}_i,D_i),$$

(5)

where ℓ represents a loss metric (here, mean absolute error), ${\widehat{D}}_i$ are the estimated elevation values from the regression model, $D_i$ are the actual target DTM values, and N signifies the number of samples.

4. Experiments

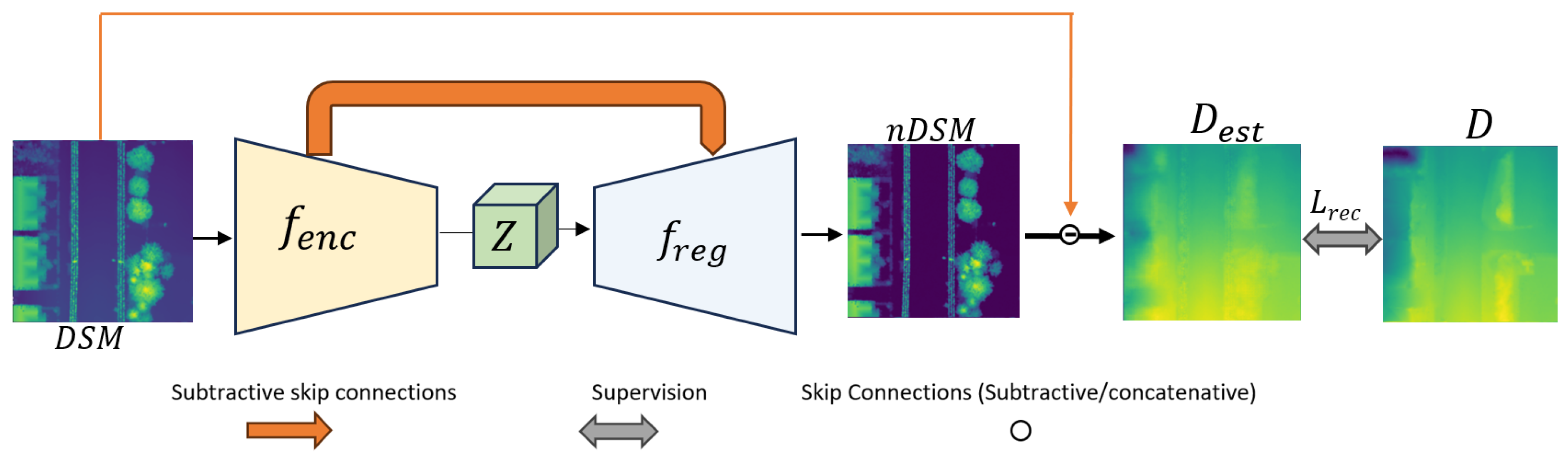
4.1. Characteristics of Datasets

The datasets chosen for evaluating the proposed network’s performance can be categorized into three groups, each of which has been widely adopted as a benchmark for DL-based DTM reconstruction study. Our study aims to comprehensively analyze these datasets and evaluate the performance of our proposed method.

4.1.1. USGS

The present study aims to deliver a comprehensive insight into the USGS datasets [37]. The USGS dataset contains four main subsets with geographical and structural information, tabulated in

Table 1. Structural characteristics of the USGS dataset, where each subset comprises three semantic classes: nonground, ground, and noise.

Dataset	Year	Coverage [${\mathbf{km}}^{\mathbf{2}}$]	Semantics	Density (pts/m2)	Topography Type
SU	2014	45	3	11.93	City, industrial, residential
KA	2005	114	3	2.42	Dense forests, steep mountainous terrain
KW	2020	50	3	7.89	Watershed, landscape response to debris flows
RT	2018	45	3	48.46	Mission River area, post-hurricane landscape

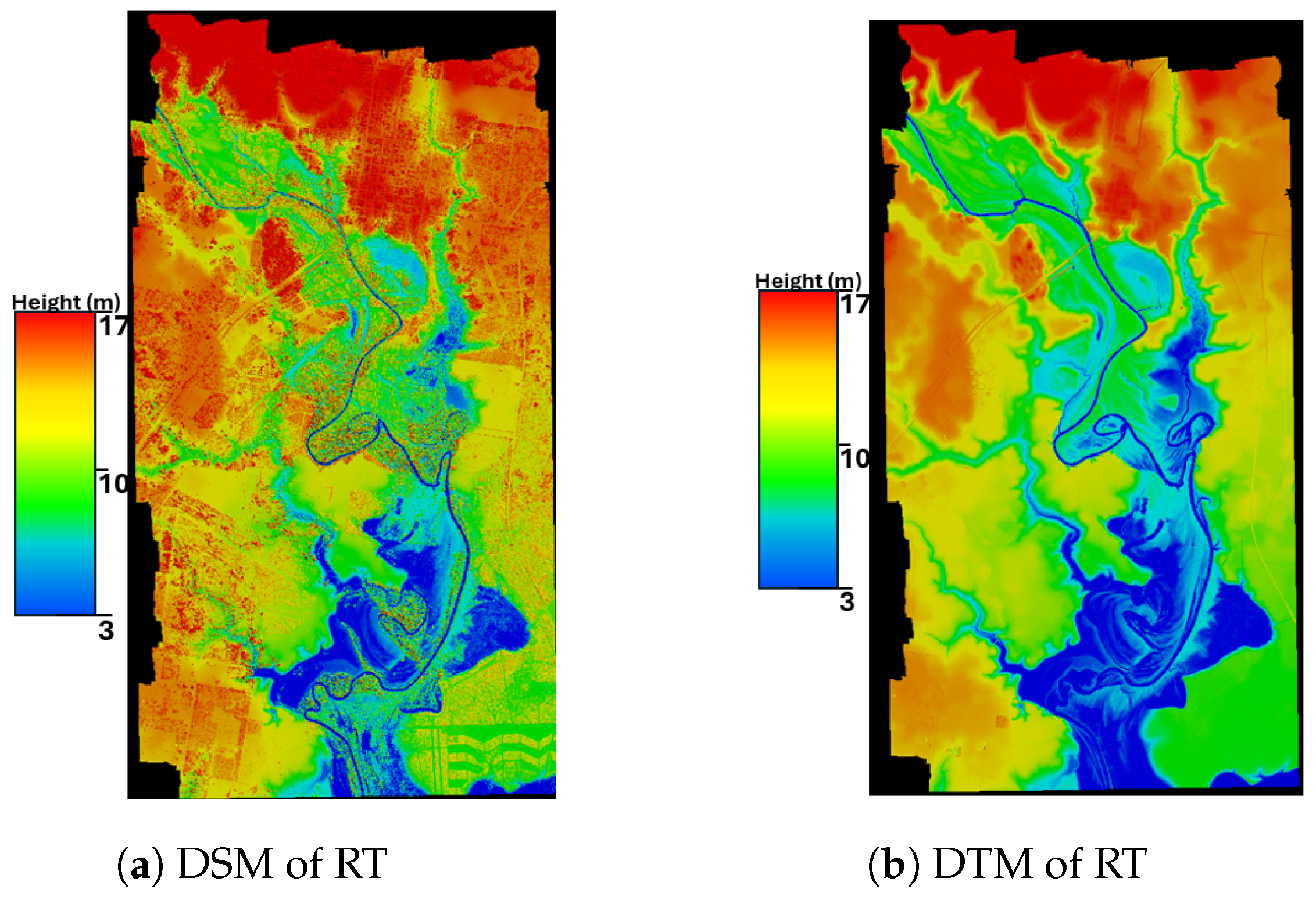
. It is worth noting that SU itself has been divided into three parts: SUI, SUII, and SUIII (Figure 3). Similarly, the KA subset has been separated into two main parts: KAI and KAII (Figure 4). However, RT (Figure 5) and KW (Figure 6) are not divided into smaller parts.

Table 2. Quantitative analysis of statistical features in the USGS dataset (unit: meter).

Dataset	Mean	Std	Max	Min	Median	95th Percentile	5th Percentile
KW-DSM	1611.45	421.81	3111.84	767.34	1559.19	2443.53	1015.90
KW-DTM	1603.88	428.09	3111.84	760.25	1553.54	2443.53	994.72
SUI-DSM	1519.59	160.94	2329.18	1359.07	1463.09	1912.02	1382.29
SUI-DTM	1518.69	160.97	2328.03	1359.07	1461.85	1911.14	1381.52
SUII-DSM	1445.03	86.06	1932.76	1340.83	1424.46	1596.04	1355.61
SUII-DTM	1443.89	86.26	1931.05	1340.82	1423.11	1595.36	1354.51
SUIII-DSM	1699.62	380.30	2664.46	1356.26	1460.83	2430.71	1362.73
SUIII-DTM	1699.03	380.35	2664.46	1356.26	1459.84	2429.83	1362.14
RT-DSM	11.12	4.02	147.50	-0.99	11.34	17.84	3.72
RT-DTM	9.73	3.78	23.52	-0.16	10.27	15.46	3.28
KA-DSM	236.53	132.58	634.49	52.50	187.49	520.96	87.25
KA-DTM	233.09	134.12	634.31	52.43	182.14	520.54	83.27

presents the statistical characteristics of the USGS dataset. In the SUI region, the DSM and DTM datasets show minimal differences in mean and median values, with a mean of around 1519 m for both datasets. This indicates a consistent elevation profile across the region. The maximum values for DSM and DTM are nearly identical, suggesting that the highest elevation points are captured similarly in both models. The 5th and 95th percentile values are very close, indicating a less varied elevation range compared to the KW region.

For the SUII region, there’s a slight decrease in mean elevation values compared to SUI, with the DSM and DTM means around 1445 m and 1443 m, respectively. The standard deviations are lower here, indicating a more uniform elevation profile. The maximum elevation is significantly lower than in the KW and SUI regions, which could suggest a less rugged terrain.

The SUIII region presents higher mean and median values than the previous regions, with means around 1699 m. The high standard deviation indicates a wider range of elevation differences, possibly due to more varied terrain. The maximum elevation is between those of KW and SUI, suggesting a mix of terrain features.

The KA region shows moderate mean elevation values (236.53 m for DSM and 233.09 m for DTM) compared to the other regions. The standard deviations are higher than in RT but lower than in the mountainous regions, indicating a moderate variation in elevation. To provide a better understanding of the position of the network’s input (i.e., DSM) to the network’s output (i.e., DTM), the fitted normal distribution for each subset/region has been illustrated in Figure 7 as well.

For the KW region, the DSM and DTM mean values are closely aligned at 1611.45 m and 1603.88 m, respectively, suggesting a relatively consistent elevation profile between the surface and terrain models. However, the standard deviation is slightly higher for the DTM, indicating more variation in terrain elevation compared to the surface. Notably, both models share the same maximum value of 3111.84 m, pointing to a significant elevation feature present in both datasets. The 95th percentile values are identical for both models, reinforcing the presence of high-elevation features. The RT region stands out with significantly lower mean values (11.12 m for DSM and 9.73 m for DTM), indicating a very flat region. The negative minimum value in the DSM dataset might represent an artifact or, less likely, a below-sea-level feature. The maximum values are notably lower than in other regions, emphasizing the flatness of the area.

These subsets, in total, reveal a rich tapestry of elevation profiles across different regions, from flat terrains in RT to rugged landscapes in KW. The DSM and DTM models consistently capture the elevation characteristics of each region, with slight variations that might be attributed to the models’ inherent differences in representing surface and terrain features.

4.1.2. The OpenGF Dataset

The OpenGF dataset is a comprehensive collection of ground-annotated ALS point clouds, meticulously chosen and processed to support advanced ground filtering methodologies in diverse terrains. Its creation involved selecting only high-quality ground annotations from open-access ALS point clouds, addressing inconsistencies often observed in classification quality [38]. The dataset encompasses point clouds that represent four prime terrain types, each with its unique characteristics and challenges. These terrains include metropolia, small cities, villages, and mountains, each typified by distinct ground and vegetation features (

Table 3. Structural characteristics of the OpenGF dataset, where each subset comprises three semantic classes: nonground, ground, and noise.

Dataset	Year	Coverage (${\mathbf{km}}^{\mathbf{2}}$)	Semantics	Density (pts/m2)	Topography Type
OpenGF (S1)	2022	42	3	11.51	Metropolis with large roofs
OpenGF (S2)	2022	42	3	11.51	Metropolis with dense roofs
OpenGF (S3)	2022	42	3	11.51	Small city with flat ground
OpenGF (S4)	2022	42	3	11.51	Small city with local undulating ground
OpenGF (S5)	2022	42	3	11.51	Small city with rugged ground
OpenGF (S6)	2022	42	3	11.51	Village with scattered roofs
OpenGF (S7)	2022	42	3	11.51	Mountain with gentle slopes and dense vegetation
OpenGF (S8)	2022	42	3	11.51	Mountain with steep slopes and sparse vegetation
OpenGF (S9)	2022	42	3	11.51	Mountain with steep slopes and dense vegetation

). Among these datasets, three tiles (Figure 8) of that, namely S4, S8, and S9, are employed in this study—the features of each of them are shown in

Table 4. Statistical features in the three regions of the OpenGF dataset (unit: meter).

Dataset	Mean	Std	Max	Min	Median	95th Percentile	5th Percentile
S9-DSM	638.30	33.60	753.49	531.59	639.38	690.90	582.38
S9-DTM	630.69	33.88	733.79	523.03	632.43	683.97	573.62
S4-DSM	359.56	4.76	392.04	349.37	359.27	367.93	352.68
S4-DTM	356.78	2.96	366.74	349.31	356.54	360.93	351.64
S8-DSM	365.45	46.41	451.40	235.42	365.58	436.77	286.63
S8-DTM	360.37	49.87	451.37	224.83	360.90	436.18	274.72

.

The selection of benchmark regions—S4, S8, and S9—was guided by the need to address the gaps in existing benchmarks such as USGS and ALS2DTM. The chosen regions were identified as unique based on their distinct geographic and structural characteristics, which are not sufficiently represented in the other benchmarks. The S4 area, characterized by numerous buildings on a flat terrain, offers a unique challenge in urban planning and infrastructure modeling. On the other hand, S8 and S9, representing sparsely covered and fully vegetated mountainous areas, respectively, offer different complexities in terrain navigation and vegetation density analysis. These areas were selected to test the robustness of our models under varied and extreme environmental conditions, ensuring that our research outcomes are broadly applicable in diverse real-world scenarios. Through this approach, we aim to develop models that are effective and applicable to various scenarios, improving the reliability and usefulness of our research.

The S4 datasets exhibit the lowest variability among the presented datasets, as indicated by their standard deviations (4.76 for DSM and 2.96 for DTM). This low variability is beneficial for achieving consistent and reliable measurements. The mean values of DSM (359.56) and DTM (356.78) are relatively close, with the DSM dataset having a slightly higher average. Both datasets’ maximum and minimum values are close, indicating a consistent range of values.

The S8 datasets show significant variability, evident in their standard deviations (46.41 for DSM and 49.87 for DTM). This high variability suggests a diverse set of measurements, which could indicate the heterogeneous nature of the samples or the measurement process itself. The means of the DSM (365.45) and DTM (360.37) datasets are relatively close. However, the DTM dataset shows a slightly lower mean. The ranges of the datasets are broad, emphasizing the spread of values in both cases. Interestingly, the maximum values are nearly identical (451.40 for DSM and 451.37 for DTM). However, the minimum value for DTM (224.83) is significantly lower than that for DSM (235.42).

For the S9 datasets, both DSM and DTM present similar statistical profiles with slight differences. The mean value of the DSM dataset is 638.30, slightly higher than the DTM’s 630.69, indicating a marginally higher average measurement in the DSM dataset. The standard deviation for DSM (33.60) and DTM (33.88) are nearly identical, suggesting a similar level of variability within both datasets. As expected, the maximum value is higher in the DSM dataset (753.49) than in the DTM dataset (733.79). Conversely, the minimum value is slightly lower in the DTM dataset, showing a broader range in the DSM dataset. In Figure 9, the normal distribution that was fitted for each subset/region has been depicted to help comprehend the position of the network’s input (DSM) with regard to the network’s output (DTM).

4.1.3. ALS2DTM Datasets

The ALS2DTM project employs two distinct subsets of ALS point clouds, known as the DALES and NB datasets (see Figure 10). These datasets are integral to the development and evaluation of algorithms for generating DTM from ALS data [31].

The DALES dataset is designed for ongoing research in ALS point clouds and enriched with reference DTM data, thus proving valuable for training CNNs for DTM generation. It represents a uniform terrain type, aiding in the development of models capable of effectively processing ALS point cloud data.

In contrast, the NB dataset, collected from the New Brunswick region, encompasses a wider range of elevations, including urban, rural, forested, and mountainous areas. This diversity introduces additional complexity, crucial for assessing the robustness and adaptability of DTM generation algorithms. The Aerial Laser Scanner (ALS) point clouds in the NB dataset are meticulously produced and processed, ensuring high data integrity and quality.

The characteristics of these datasets are encapsulated in

Table 5. Structural characteristics of the ALS2DTM dataset.

Dataset	Year	Coverage [${\mathbf{km}}^{\mathbf{2}}$]	Semantics	Density (pts/m2)	Topography Type
DALES	2020	10	8	50.5	Urban area
NB	2022	42	11	27.45	Urban and rural areas, forested and mountainous

, while their semantic information is shown in

Table 6. Semantic information of DALES and NB subsets.

Subset	Class Details
DALES	ground (1), vegetation (2), cars (3), trucks (4), power lines (5), fences (6), poles (7), buildings (8)
NB	unclassified (1), ground (2), low vegetation (3), medium vegetation (4), high vegetation (5), buildings (6), low point—noise (7), reserved—model keypoint (8), high noise (18)

.

For the DALES dataset, we observe that the DSM statistics exhibit a slightly higher mean (56.51) compared to the DTM and last-return, which have means of 53.14 and 54.68, respectively. This indicates that, on average, the surface elevation values in the DSM are slightly higher than those in the DTM and last-return datasets. The standard deviation is fairly consistent across all three, suggesting similar variability in elevation values. The maximum value is significantly higher in the DSM (196.89) compared to the DTM, yet it is almost equal to the last-return maximum. The DSM shows a slightly less negative minimum value, which suggests the presence of fewer extremely low elevation values. The minimum values in both cases are within a comparable range. The medians are close, with the DSM’s median being the highest, which aligns with its higher mean. In terms of the 95th and 5th percentiles, the DSM again shows higher values, suggesting that while the bulk of its data is similar to the other two datasets, it has higher extreme values (

Table 7. Statistical analyses of DALES and NB subsets (unit: meter).

Dataset	Mean	Std	Max	Min	Median	95th Percentile	5th Percentile
DALES-DSM	56.51	32.04	196.89	−3.86	62.99	98.46	2.31
DALES-DTM	53.14	31.22	101.81	−2.91	59.63	93.66	1.43
DALES-last-return	54.68	31.73	196.85	−4.50	60.85	95.94	1.85
NB-DTM	136.77	129.64	382.97	−0.21	62.81	340.77	3.27
NB-DSM	144.38	133.79	399.92	−18.02	68.74	352.26	4.32
NB-last-return	137.49	129.72	396.05	−32.65	63.52	341.47	3.44

).

In contrast, the NB dataset shows a different trend. The DSM’s mean (144.38) is notably higher than that of the DTM (136.77) and the last return (137.49), indicating a greater average elevation in the DSM data. The standard deviations are quite high across all datasets, indicating a wide range of elevation values, with the DSM showing the highest variability. The maximum elevation values are again highest for the DSM, reinforcing the idea that it captures higher elevation points more frequently than the DTM and last-return. The minimum values show that the DSM dataset contains an extremely low elevation value (−18.02), which could be an outlier or indicate a wider range of elevation data captured. The median values are relatively close, with the DSM having the highest, aligning with its higher mean and suggesting a higher central tendency in elevation. The 95th and 5th percentiles for the DSM are also the highest among the three datasets, indicating that its elevation values are skewed higher both at the upper and lower ends of the dataset (Table 7).

To have a better understanding of each of the two, the fitted normal distributions of them are illustrated in Figure 11.

4.1.4. Consolidated Analysis of Datasets

In order to gain a comprehensive understanding of the relationship between different datasets, a thorough examination of all datasets is carried out collectively. To facilitate this analysis, Figure 12 and Figure 13 are presented, which graphically illustrate the distribution of DSMs and DTMs of USGS and ALS2DTM datasets, respectively. Figure 14 provides a detailed summary of the mean value of DSM and DTM of all datasets, along with their respective standard deviations. To facilitate a better understanding of the distinction between DSM and DTM, Figure 15 illustrates this difference. Additionally, the distribution of RT and KW datasets, which are different from others, are separately depicted in Figure 16. These illustrations provide a clear and concise overview of the datasets’ characteristics, enabling researchers to draw meaningful conclusions.

4.2. Experimental Setup

To establish a comprehensive benchmark encompassing various terrain features, ranging from flat plains to steep mountains and from urban to forested areas, a balanced dataset is compiled for this study, where the efficacy of basic modules of the proposed method will be assessed. By doing so, we can also ensure that all elevation ranges presented in Figure 14 are covered. To make our comprehensive dataset, from each region/subset, 1000 images are randomly selected as a training without replacement, and 200 images are randomly selected as a test. This selection provides us with a comprehensive benchmark, which can be used to evaluate the performance of the proposed method.

In the preparation of our data, we implemented several key steps to ensure optimal training and results. Initially, DSMs and their corresponding DTMs were divided into images with a 50% overlap, each having a size of $256\times 256$ pixels. These images were then localized and normalized to mitigate the domain shift’s effects [22]. We then applied horizontal and vertical flips as part of our data augmentation strategy to enhance the diversity and robustness of the training set.

The model training parameters were meticulously set, starting with a learning rate of ${10}^{-2}$, gradually reducing to ${10}^{-5}$ every 70 iterations throughout 250 epochs. Finally, during inference, the weights derived from the training dataset were applied to 20% of the comprehensive benchmark, considered as a test.

4.3. Quality Assessment Criteria

Our study employs a widely used framework for quality assessment, which is based on estimated values. This category is central to understanding the accuracy of our predictions. It includes traditional metrics like the Root Mean Squared Error (RMSE), Equation (6), the Mean Absolute Error (MAE), Equation (7), and AbsRel as relative error, Equation (8). RMSE measures the square root of the average squared differences between predictions and actual values, while MAE calculates the average of the absolute differences [39].

$$RMSE=\sqrt{\frac{1}{T}\sum _{i\in T}\Vert d_i-d_i^{gt}{\Vert }^2}$$

(6)

$$MAE=\frac{1}{T}\sum _{i\in T}|d_i-d_i^{gt}|$$

(7)

$$AbsRel=\frac{1}{T}\sum _{i\in T}\frac{|d_i-d_i^{gt}|}{d_i^{gt}}$$

(8)

where T is the total number of observations, and $d_i$ and $d_i^{gt}$ are the predicted and ground truth values, respectively. To offer a comprehensive measure of system performance by integrating key dimensions into a single indicator, a performance index (PI) is used. This index is crucial for evaluating and enhancing the reliability and efficiency of various systems, as it provides a holistic view that incorporates both consistency and accuracy of performance.

To construct the PI, a linear combination of the standard deviation (Std) and the average error (AE) is employed. These two metrics are fundamental in reflecting the system’s stability and accuracy. The standard deviation expresses the consistency of the system’s performance, while the average error highlights the system’s deviation from expected outcomes. This integration offers a balanced perspective on system performance, making the PI a valuable tool for system analysis [40].

The formula for the PI is given by:

$$PI=a·Std+b·AE$$

(9)

where a and b are coefficients that determine the relative importance of the standard deviation and the average error, respectively. These coefficients are adjustable, allowing the performance index to be customized to emphasize either consistency or accuracy based on the system’s specific requirements and objectives.

In contexts where both consistency and accuracy are equally important, setting both a and b to 1 provides a balanced approach. This equal weighting simplifies the PI to a sum of the standard deviation and the average error, offering an effective and straightforward measure of system performance. By adopting this approach, the evaluation ensures that both the system’s variability and accuracy are considered simultaneously, providing a comprehensive overview of the system’s overall stability and efficiency.

4.4. Ablation Study

To show the efficacy of the physically-informed proposed method, five different ablation studies along with our network are considered, the details of which have been tabulated in

Table 8. Summary of ablation studies.

Skip Connections	DTM Reconstruction	Modules	Description
Concatenation	Direct	CNETD	AE equipped with concatenative skip connections that generate the DTM directly, without any intermediate steps affecting the generation process.
Concatenation	Indirect	CNETI	The CNET leads to the generation of the DTM through an indirect process, which involves nDSM.
Subtraction	Direct	SUBNETD	This case refers to the scenario where the SUBNET generates the DTM directly.
Subtraction	Indirect	SUBNETI	Our proposed method.
No Skip-Connection	Direct	TAED	This scenario involves the TAE generating the DTM directly, showcasing a straightforward application of the TAE’s capabilities.
No Skip-Connection	Indirect	TAEI	In this case, the TAE generates the DTM indirectly via nDSM.

. As shown in this table, we designed an ablation study of the proposed network by changing three modules based on the autoencoder (AE) baseline with skip-connection or without skip-connection; with subtractive or concatenative skip-connection; with direct DTM reconstruction (i.e., directly regressing DTM from DSM input) or with indirect DTM reconstruction (i.e., indirectly regressing DTM through subtracting nDSM from DSM input). This combinatorial network architect provides six different networks, including CNETD (Concatenative NETwork with Direct DTM regression), CNETI (Concatenative NETwork with Indirect DTM regression), SUBNETD (SUBtractive NETwork with Direct DTM regression), SUBNETI (SUBtractive NETwork with Indirect DTM regression), TAED (Traditional/Typical Autoencoder with Direct DTM regression), and TAEI (Traditional Autoencoder with Indirect DTM regression) to evaluate their performance.

4.5. Discussion

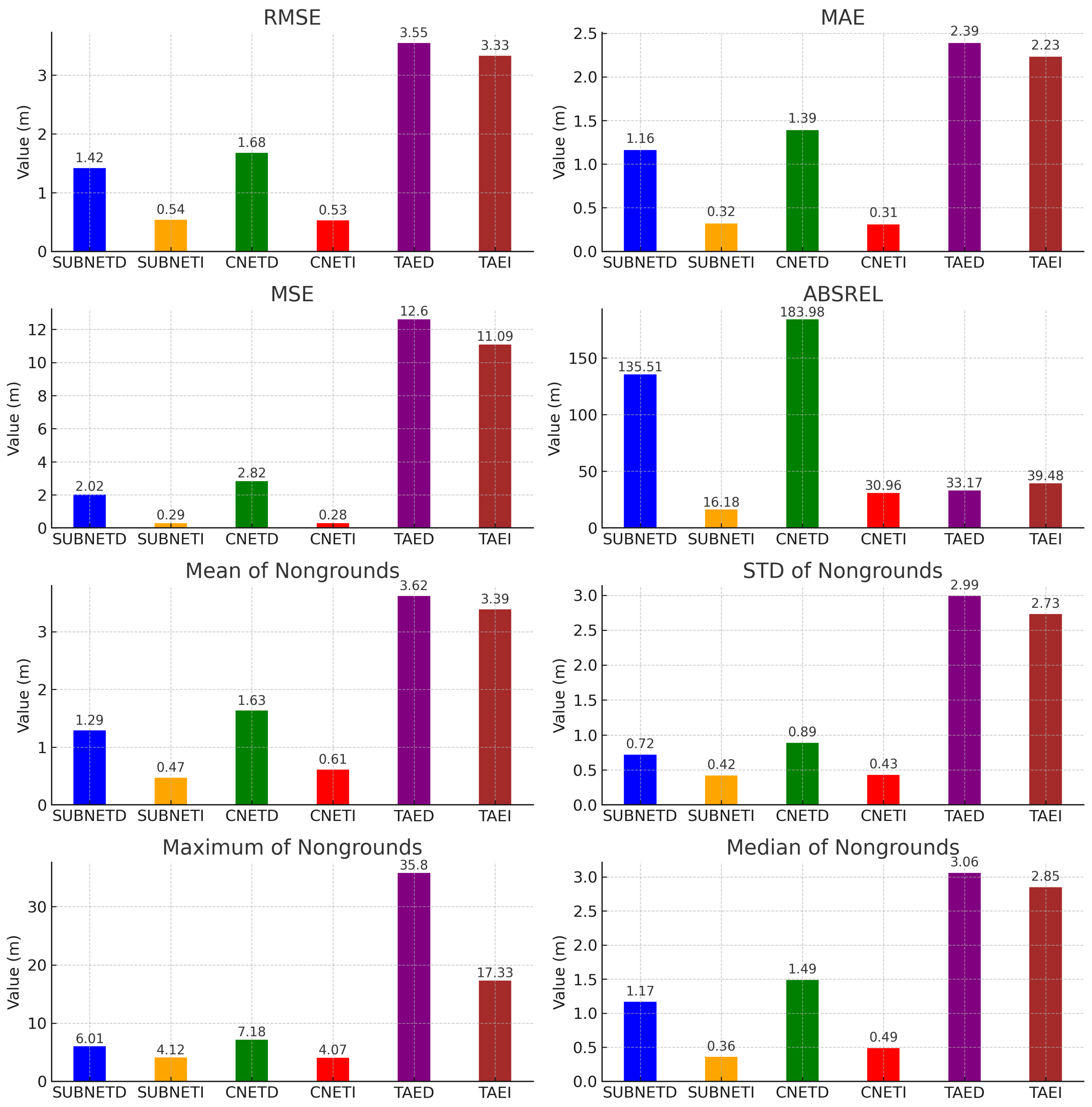
As can be seen from Figure 17, SUBNETI emerges as the standout method, particularly excelling in minimizing RMSE, MAE, MSE, and ABSREL values (See Section 4.3). This superiority can be attributed to its algorithmic efficiency in handling the absolute differences between the output and the target, as highlighted by the provided equations. The ABSREL metric, calculated as the mean of the absolute differences divided by the target, is significantly lower for SUBNETI, indicating its superior performance in relative error reduction. This is crucial because it demonstrates SUBNETI’s ability to maintain accuracy proportionally across varying scales of target values, making it especially reliable in applications where precision relative to the magnitude of the measurement is critical.

Conversely, TAED and TAEI show poorer performance across these metrics, with particularly high values in RMSE, MSE, and ABSREL. The elevated MSE and RMSE values suggest a greater variance in their errors, and the high ABSREL values indicate a pronounced relative error, which could be due to less effective handling of the absolute differences between the output and the target. This inefficiency is further exacerbated in complex scenarios where maintaining a proportional relationship between errors and target values is essential for accuracy.

Regarding nonground area statistics, SUBNETI again leads with the lowest mean, STD, and very competitive median values. These statistics are critical for evaluating the methods’ ability to closely approximate the ground truth in nonground areas, with a particular emphasis on consistency and reliability as reflected by the Std and median values. The superior performance of SUBNETI in these criteria suggests a methodological advantage in minimizing variations and biases in nonground area estimations, likely due to more sophisticated processing of spatial data and an effective balancing of sensitivity to outliers, as evidenced by its optimal maximum of nonground and minimum of nonground values.

CNETI follows SUBNETI in performance, offering a balanced profile that, while not achieving the lowest values in every criterion, demonstrates robustness across both ground and nonground area analyses. This suggests that CNETI, similar to SUBNETI, employs effective strategies for error minimization and consistency in its estimations but may have slight limitations in either its handling of outliers or its adaptability to varying scales of target values, as indicated by its ABSREL performance.

On the other end, TAED’s performance is notably less effective, especially in nonground area statistics, where it records the highest values across mean, STD, and maximum. This indicates a significant deviation from the ground truth, possibly due to the method’s lower sensitivity to fine-grained spatial variations or a propensity to be influenced by outliers, as suggested by its high maximum of nonground values. Such characteristics might stem from algorithmic constraints or less optimized processing techniques for spatial data, leading to increased variability and less accuracy in representing nonground areas.

The analysis underscores the importance of method selection based on specific needs and contexts. For applications requiring high relative accuracy and consistency in both ground and nonground areas, SUBNETI is clearly the preferred choice. However, for contexts where a balance between performance and possibly other considerations, such as computational efficiency or ease of implementation, is needed, CNETI presents a viable alternative. The lesser performance of TAED and TAEI, particularly in nonground area statistics, highlights the challenges in optimizing for both accuracy and consistency, emphasizing the need for further development or application-specific adjustments to these methods.

Following a comparative analysis of various states of our proposed method, this study compares SUBNETI with its competitor, CNETI the results of which have been brought in

Table 9. Comparative performance analysis of the proposed method and its leading competitor, CNETI, across statistical and predictive metrics (unit: meter).

Metric	CNETI Avg	CNETI Std	CNETI PI	SUBNETI Avg	SUBNETI Std	SUBNETI PI	Efficacy
RMSE	0.533	0.043	0.576	0.538	0.028	0.566	SUBNETI
MAE	0.334	0.035	0.369	0.334	0.021	0.355	SUBNETI
MSE	1.513	1.298	2.811	1.375	0.798	2.173	SUBNETI
ABSREL	13.671	10.462	24.133	10.430	6.026	16.456	SUBNETI
Mean	0.496	0.082	0.578	0.469	0.011	0.480	SUBNETI
Std	0.451	0.037	0.488	0.454	0.023	0.477	SUBNETI
Max	4.155	0.204	4.359	4.178	0.213	4.391	CNETI
Median	0.371	0.082	0.453	0.344	0.011	0.355	SUBNETI

. In order to determine the stability of the two methods, a comparison was made between them. To achieve this, a five-fold cross-validation was conducted for both methods, and the results were documented in tables.

The stability of a system can be measured by its Std and the PI values, which is a linear combination of Std and the average error (see Section 4.3). A lower value of Std and PI indicates a more reliable performance. When it comes to stability, SUBNETI outperforms other systems, as it generally exhibits lower Std values for metrics, including RMSE, MAE, MSE, ABSREL, mean, and median.

Efficiency can be inferred from the MSE and RMSE values, metrics that quantify the error magnitude in predictions. SUBNETI and CNETI show comparable performance in terms of MAE. However, SUBNETI edges slightly in RMSE, suggesting it is more efficient at minimizing squared errors, a crucial aspect when high error magnitudes are significantly penalized. The lower PI values for SUBNETI across most metrics further support its efficiency, indicating it performs well on average and does so with more excellent reliability.

Accuracy is often assessed through metrics like RMSE, MAE, and ABSREL, which directly measure error magnitude and relative error. SUBNETI’s marginally better RMSE and significantly better ABSREL values suggest it is more accurate in capturing the actual signal with fewer and less severe errors, particularly in relative terms. This is essential when accuracy relative to the magnitude of the target values is critical, as in many geospatial applications where the range of expected values can vary widely. While SUBNETI and CNETI have almost similar maximum values, the former yields more favorable outcomes overall. This is primarily due to its higher median, mean, and PI values, which indicate a more balanced and consistent performance. Consequently, SUBNETI is deemed to provide better and more reliable results compared to CNETI.

Subsequent analysis entails evaluating each dataset’s performance by comparing the RMSE, maximum error, and distribution of median error between the two. The RMSE comparison plot, Figure 18, immediately highlights the superior performance of SUBNETI across all datasets. This superiority is particularly noteworthy in datasets with high variability, such as S8 and KW, where the standard deviation in both DSM and DTM is significant. The ability of SUBNETI to achieve lower RMSE values in these contexts suggests it is better equipped to handle the complexity introduced by terrain variability. This is crucial in applications where accurate ground-level estimation is paramount, as it indicates a consistent ability to closely match the ground truth DTM, even in challenging environments.

When considering the maximum error comparison plot alongside the dataset characteristics, Figure 19, we gain insight into each method’s ability to manage outliers and extreme values. For example, the S8 dataset, characterized by its high DSM and DTM standard deviations, presents a challenging scenario for DTM estimation. The plot reveals that SUBNETI generally produces lower maximum errors compared to CNETI, indicating its robustness against extreme terrain variations. This aspect of performance is crucial for applications where even rare, extreme errors can have significant consequences, affirming the value of SUBNETI’s approach in maintaining accuracy across various conditions.

The median error along with std, brought in Table 9, provide a representation of the variability and central tendency of errors for both methods. In datasets like RT and SUII, which exhibit lower variability in their DSM and DTM characteristics, SUBNETI not only maintains lower median errors but also demonstrates a tighter distribution of errors, as evidenced by the smaller interquartile ranges and the standard deviation represented by the vertical dashed lines. This tighter error distribution underscores SUBNETI’s precision and reliability, showcasing its effectiveness in providing consistent DTM estimations across different terrains.

Integrating the the above-mentioned results with the DSM and DTM characteristics, highlighted in Figure 14, allows for a more comprehensive assessment of the methods. The variability and complexity captured in the dataset characteristics illuminate why SUBNETI’s performance is particularly commendable. Its ability to handle datasets with high variability (e.g., S8 and KW) while still minimizing RMSE and maximum errors highlights its robustness and adaptability. Conversely, its precision in datasets with lower variability (e.g., RT and SUII) showcases its reliability and consistency, making it a versatile tool for DTM estimation. Moreover, the plots serve as a visual testament to these findings, with the RMSE and Max (m) comparisons directly reflecting SUBNETI’s superior performance across a range of conditions and the box plots for Median (m) with Std Deviation offering a granular view of the methods’ error distributions.

4.6. Comparison to the State-of-the-Art

To demonstrate the effectiveness of SUBNETI, our proposed method, we have conducted a comparative analysis against HDCNN [22], one of the current state-of-the-art methods in this field. To ensure brevity, we have selected a single fold of the dataset for this purpose. By doing so, we aim to provide experimental results that demonstrate the superior performance of our proposed method in comparison to HDCNN.

As can be seen from Figure 20, HDCNN exhibits a higher RMSE at 1.045 compared to SUBNETI’s 0.507, indicating that SUBNETI generally provides predictions that are closer to actual values. For the MAE, HDCNN again shows higher error values (0.775) relative to SUBNETI (0.314), suggesting SUBNETI’s stronger accuracy in predicting outcomes without consideration of error direction. However, in terms of AbsRel, HDCNN performs better with a lower value of 0.50642 compared to SUBNETI’s 1.68990. This metric highlights that, proportionally, HDCNN’s predictions are closer to true values than those of SUBNETI, particularly when normalized against actual magnitudes. Thus, while SUBNETI demonstrates superior performance in minimizing squared and absolute errors, HDCNN provides more accurate relative assessments, offering a mixed view on the superiority of one method over the other depending on the evaluation criteria.

5. Conclusions

This paper concludes by detailing the development and evaluation of a new autoencoder, designed to efficiently generate DTMs from DSMs in a physically-informed manner. The research’s foundation is based on a comparative analysis between the proposed method, SUBNETI, and several rivals, which aim to highlight the effectiveness of the subtractive concept in DTM extraction. A series of ablation studies were conducted to achieve this goal. The first finding of experimental results that draws one’s attention is the fact that the indirect cases for all the methods at hand lead to better results than the direct case. This means generating nDSM as a part of the network and then estimating DTM from that using a physical equation can lead to better results. Experimental results have also definitively underscored the superior capabilities of SUBNETI in terms of accuracy, efficiency, and stability across diverse terrains and conditions, especially compared to CNETI. The only difference between CNETI and the proposed method was its skip connections, which are concatenative compared to subtractive. The comparative stability, efficiency, and accuracy analyses between SUBNETI and CNETI, particularly within the context of a 5-fold cross-validation, reveal SUBNETI’s consistent outperformance. It is the more stable and reliable method, demonstrating lower standard deviation and performance index values across critical metrics. This consistency is paramount in geospatial applications where precision and reliability in DTM estimation can significantly impact environmental monitoring, urban planning, and disaster management strategies. Furthermore, the dataset-specific performance analysis illuminates SUBNETI’s adeptness at managing complex terrain variability. Its ability to consistently achieve lower RMSE and maximum error rates across datasets with high variability, such as S8 and KW, showcases its robustness and adaptability. Additionally, the precision of SUBNETI in datasets with lower variability, like RT and SUII, through tighter error distributions and lower median errors, affirms its reliability and effectiveness in delivering accurate DTM estimations across a spectrum of environmental conditions.

Although SUBNETI is a powerful tool for generating impressive results, it has a limitation that is inherent in all DL-based DTM generations when used as a regressor. This is because it modifies all pixels in DSM, including those associated with the ground, which are highly precise and obtained from LiDAR, leading to a reduction in their accuracy. To address this issue, the authors aim to improve the network’s ability to differentiate between ground and nonground points within DSM in their future work. They plan to accomplish this by introducing a ground segmentation process to the network, which can be customized to regress only nonground points. By doing so, the network can maintain the accuracy and precision of the ground data acquired from LiDAR.