Next Article in Journal
How Representative Are European AERONET-OC Sites of European Marine Waters?
Previous Article in Journal
Constrained Iterative Adaptive Algorithm for the Detection and Localization of RFI Sources Based on the SMAP L-Band Microwave Radiometer
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 16
Issue 10
10.3390/rs16101794
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

An Evaluation of Optimization Algorithms for the Optimal Selection of GNSS Satellite Subsets

by
Abdulaziz Alluhaybi
1,2,
Panos Psimoulis
1,3,* and
Rasa Remenyte-Prescott
3
1
Nottingham Geospatial Institute, University of Nottingham, Nottingham NG7 2TU, UK
2
Department of Civil Engineering, Taibah University, Madinah 42353, Saudi Arabia
3
Department of Civil Engineering, University of Nottingham, Nottingham NG7 2RD, UK
*
Author to whom correspondence should be addressed.
Remote Sens. 2024, 16(10), 1794; https://doi.org/10.3390/rs16101794
Submission received: 7 March 2024 / Revised: 10 May 2024 / Accepted: 15 May 2024 / Published: 18 May 2024
(This article belongs to the Topic Artificial Intelligence in Navigation)
Browse Figures
Review Reports Versions Notes

Abstract

:
Continuous advancements in GNSS systems have led, apart from the broadly used GPS, to the development of other satellite systems (Galileo, BeiDou, GLONASS), which have significantly increased the number of available satellites for GNSS positioning applications. However, despite GNSS satellites’ redundancy, a potential poor GNSS satellite signal (i.e., low signal-to-noise ratio) can negatively affect the GNSS’s performance and positioning accuracy. On the other hand, selecting high-quality GNSS satellite signals by retaining a sufficient number of GNSS satellites can enhance the GNSS’s positioning performance. Various methods, including optimization algorithms, which are also commonly adopted in artificial intelligence (AI) methods, have been applied for satellite selection. In this study, five optimization algorithms were investigated and assessed in terms of their ability to determine the optimal GNSS satellite constellation, such as Artificial Bee Colony optimization (ABC), Ant Colony Optimization (ACO), Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Simulated Annealing (SA). The assessment of the optimization algorithms was based on two criteria, such as the robustness of the solution for the optimal satellite constellation and the time required to find the solution. The selection of the GNSS satellites was based on the weighted geometric dilution of precision (WGDOP) parameter, where the geometric dilution of precision (GDOP) is modified by applying weights based on the quality of the satellites’ signal. The optimization algorithms were tested on the basis of 24 h of tracking data gathered from a permanent GNSS station, for GPS-only and multi-GNSS data (GPS, GLONASS, and Galileo). According to the comparison results, the ABC, ACO, and PSO algorithms were equivalent in terms of selection accuracy and speed. However, ABC was determined to be the most suitable algorithm due it requiring the fewest number of parameters to be set. To further investigate ABC’s performance, the method was applied for the selection of an optimal GNSS satellite subset according to the number of total available tracked GNSS satellites (up to 31 satellites), leading to more than 300 million possible combinations of 15 GNSS satellites. ABC was able to select the optimal satellite subsets with 100% accuracy.

1. Introduction

The Global Navigation Satellite System (GNSS) is a system of satellites that provides positioning, navigation, and timing (PNT) services and consists of GPS (Global Positioning System, USA), GLONASS (Global Navigation Satellite System, Russian), Galileo (European Union), BDS (BeiDou Navigation Satellite System, China), and other regional navigation satellite systems. Due to the recent development in GNSS satellite systems, the number of satellites available in space reached 114 in January 2024: 31 GPS [1], 24 GLONASS, 24 Galileo, and 35 BeiDou satellites [2]. As a result, the number of satellites simultaneously visible from a single location, depending on the geographic location, can reach or exceed 30 [3]. The potential of using such a diverse and large number of GNSS satellites can improve the accuracy and availability of GNSS solutions for positioning, navigation, and timing (PNT) services. However, it also has limitations.
More specifically, the number of computations required for GNSS positioning grows as the number of used GNSS satellites increases. Compared to 10 GNSS satellites, the required time for processing the position based on 20 and 30 GNSS satellites increases by a factor of 3 and 6, respectively [4]. In addition, GNSS positioning accuracy generally increases with the number of available satellites, but practically no further enhancement is achieved after a certain number of satellites [5,6]. This was also revealed by Msaewe et al. [7] using zero-baseline GNSS measurements. The accuracy of GNSS positioning did not improve with the decrease in geometric dilution of precision (GDOP). Moreover, increasing the number of GNSS satellites cannot always guarantee a higher-quality sustained position. The positioning derived from multi-satellite system (multi-GNSS) integration is not of the highest possible accuracy due to introduced errors from various error sources. Some representative examples of error sources are multipath error [8] and inter-system bias [7], even under relative positioning [9]. Also, one of the main requirements in many GNSS monitoring applications is to limit as much as possible the GNSS data size for more sustainable and reliable GNSS data transmission, which makes it important to choose only optimal satellites which will lead to an accurate and reliable GNSS solution. Therefore, GNSS satellite selection is required to not only improve the GNSS’s performance but also to make the application of GNSS technology more sustainable.
GNSS satellite selection is the process of choosing the right GNSS satellite combination from the available GNSS satellites, aiming for better positioning quality with a lower computational load [10]. Various satellite selection criteria have been used for selecting satellites, including satellite elevation angle [11,12,13], satellite signal quality [14,15], GDOP [3,16,17], and weighted GDOP (WGDOP) [18,19]. Since GNSS accuracy is affected by both satellite geometry (i.e., GDOP) and satellite signal quality, the WGDOP, which is based on the satellite signal quality and the satellite geometry (GDOP), can be considered as the most suitable criterion for choosing satellites.
The optimal satellite subset based on WGDOP (for subsets with a specific number of satellites) can be determined simply and accurately by checking the WGDOP value for all possible satellite subsets (of the same number of satellites) and then considering the satellite subset with the lowest WGDOP value as the optimal one. This technique is known as the traditional method (TM). However, due to the required matrix inversion, the TM can be time-consuming as it calculates the WGDOP value of all possible satellite subsets, especially if the number of available tracked GNSS satellites is large. To reduce this computational burden, various techniques including the closed-form solution [18,19], maximum volume [20], artificial neural network (ANN) [21], and optimisation algorithms [22,23] have been used to select optimal satellite subsets based on WGDOP.
The closed-form solution reduces the TM’s computational complexity [16,24]. However, it cannot reduce the number of calculations, so it becomes time-consuming when the number of satellites increases [25]. The maximum volume method is based on maximizing the volume of the tetrahedron or orthogonal projection created between the satellites [22,26]. The WGDOP value decreases (improves) as the tetrahedron volume and maximum orthogonal projection increase. However, the positioning quality obtained with the selected satellites via this method is not guaranteed [25,27], as the method focuses on maximizing the volume of the tetrahedron/orthogonal projection and not on the WGDOP value [22,27], and it is also a time-consuming technique [27]. On the other hand, ANN and optimization algorithms, which are broadly applied in artificial intelligence (AI) problems, can both provide good results in satellite selection [22,28,29]. However, optimization algorithms, contrarily to ANNs and generally to any AI or machine-learning algorithms, do not require any training or, consequently, any large dataset for training [30,31,32], which makes optimization algorithms faster than ANNs. In addition, an ANN-trained model could be difficult to apply due to the varying geometry of tracked satellites due to the different revolution periods of GNSS systems [30,31]. Thus, optimization algorithms are potentially more suitable for the selection of satellites than ANNs and similar AI techniques.
In the current study, we investigated five well-known optimization algorithms, the Artificial Bee Colony (ABC), Ant Colony Optimization (ACO), Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Simulated Annealing (SA), and evaluated which optimization algorithm was the most suitable and reliable for selecting optimal GNSS satellites in a subset from available tracked GNSS satellites. The evaluation of the five optimization algorithms was based on two criteria: (i) the validity of the selected GNSS satellites of each optimization algorithm in terms of high signal quality and optimal geometry (WGDOP) of the satellite subset and (ii) the required computation time of each optimization algorithm for satellite optimization. For the first criterion, we considered the selection of the GNSS satellite subset derived from the TM with the lowest value of WGDOP as the actual truth for the most optimal GNSS satellite subset (for a given number of GNSS satellites in the subset). We compared the WGDOP value of the optimal satellite subset from each optimization algorithm with that of the optimal GNSS satellite subset derived from the TM. We consider an optimization algorithm to be accurate when the WGDOP value of its selected optimal satellite subset exactly matches the WGDOP value of the TM optimal satellite subset, and consequently, the accuracy expresses how closely the WGDOP value of the selected GNSS satellite subset of each optimization algorithm matches that of the TM optimal GNSS satellite subset.
The optimization algorithm with the highest accuracy in the selection of the optimal GNSS satellite subset and the shortest required computation time was considered as the most suitable and reliable. The current study was based on 24 h data of GNSS permanent data, where the optimization algorithms selected the GNSS satellite subset for each epoch and compared against the optimal subset derived for the corresponding epoch from the TM. This study is the first attempt at an overall evaluation of the five optimization algorithms in the problem of selecting an optimal GNSS satellite subset, by (i) examining the accuracy required from each optimization algorithm against the TM based on real GNSS data and (ii) evaluating the impact of functional principles, settings, and parameters on the performance of the optimization algorithms regarding the problem of the optimization of tracked GNSS satellite subsets.

2. GNSS Satellite Constellation Determination

2.1. Weighted Geometric Dilution of Precision (WGDOP)

The accuracy of the obtained GNSS position depends on satellite geometry (GDOP) and user range equivalent error (UERE) [21,22]. The UERE indicates the quality of satellite measurements (pseudo-range), and it is affected by the satellite signal power [33,34], which can be expressed by the value of signal-to-noise ratio (SNR) and carrier-to-noise ratio (CNR) [34]. The value of SNR and CNR increases with the strength of a satellite signal [35]. Since the GNSS’s positioning accuracy relies on GDOP and UERE, satellites should be selected based on them. However, calculating the UERE value can be more complex compared to the values of signal power (SNR/CNR), which are directly calculated by the receiver. Thus, the optimal satellite subsets were selected based on the satellite geometry (GDOP) and signal power (CNR) using WGDOP. Similar to GDOP, the value of WGDOP decreases with the improvement in the geometry of the satellite constellation, and it can be computed as follows:
W G D O P = t r a c e ( H T W H ) − 1
H = c o s E 1 s i n A 1 c o s E 1 c o s A 1 s i n E 1 1 c o s E 2 s i n A 2 c o s E 2 c o s A 2 s i n E 2 1 ⋮ ⋮ ⋮ ⋮ c o s E n s i n A n c o s E n c o s A n s i n E n 1
W = w 1 0 … 0 0 w 2 … 0 … … ⋱ … 0 0 … w n
where H is the geometry matrix determined based on the elevation angle, En, and azimuth, An, of the nth satellite, and W is the weighting matrix, where wn is the weight of the nth satellite. According to Du et al. (2020) [22], the weight wn is defined as the SNR of the nth satellite. However, the CNR was used instead of the SNR in the current study because it was obtained from the receiver. The WGDOP based on the CNR will be called CNR-WGDOP.

2.2. Traditional Method (TM)

The TM is an exhaustive search method to determine optimal GNSS satellite constellations/subsets after checking the quality of all possible GNSS satellite subsets. The TM uses the WGDOP (or GDOP) as a quality criterion. It checks the WGDOP value of all possible GNSS satellite subsets to define the optimal GNSS satellite subset with the lowest WGDOP value [21]. Checking the quality of all possible satellite subsets delivers the optimal satellite combination and, therefore, the TM can be considered the ground truth. However, it becomes time-consuming when the number of satellites increases because the number of possible satellite subsets increases dramatically. For instance, in the cases of 15 and 25 available GNSS satellites, the possible satellite combinations of 10 satellites are about 3 thousand and more than 3 million, respectively.

2.3. Optimization Algorithms

In the current study, five optimization algorithms (ABC, ACO, GA, PSA, SA) were implemented to find the optimal GNSS satellite subset by using the parameter CNR-WGDOP as a cost function, of which the minimum value would indicate the corresponding optimal GNSS satellite subset. In contrast to the TM, optimization algorithms can identify an optimal solution (i.e., the optimal GNSS satellite subset) without checking the quality of all possible solutions, requiring potentially less time. However, the accuracy of the optimal solution of optimization algorithms is subject to their functioning principles, settings, and parameters, which are explained briefly below.

2.3.1. Artificial Bee Colony (ABC)

ABC is an algorithm developed by Karaboga (2005) to simulate the foraging behavior of bees [36]. The algorithm is population-based as it generates multiple numbers of artificial bees. ABC splits these bees into three groups: employed bees, onlooker bees, and scout bees. Each type of bee is assigned to different research tasks. Through sharing information on discovered possible solutions (quality and location in the search space) among the bees (Figure 1), ABC can converge toward the optimal solution. ABC is flexible as it can be used for various types of problems, with the requirement of very few control parameters [37,38], which leads to reliable and robust results. However, ABC is relatively weak in local searching [39].

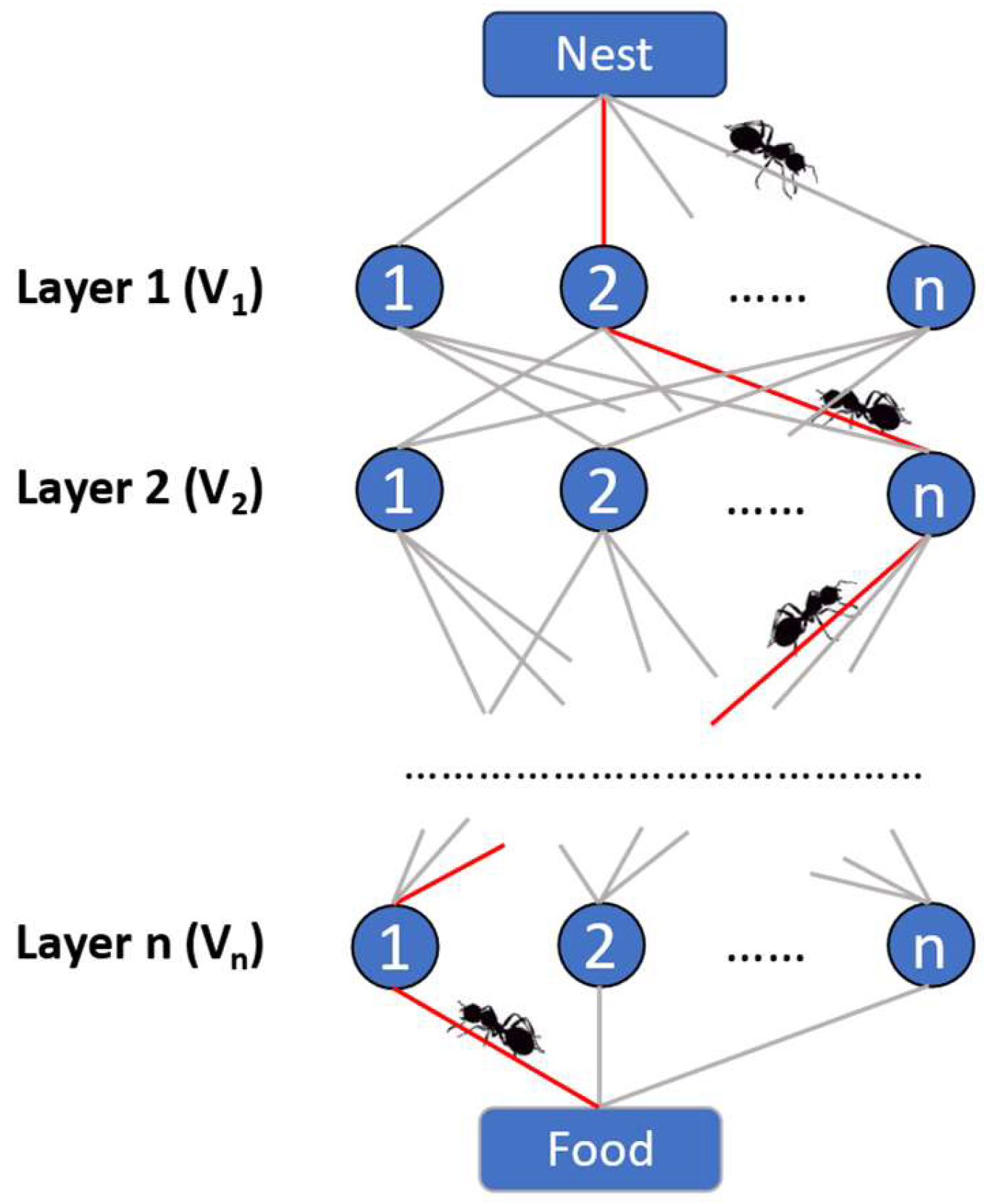
2.3.2. Ant Colony Optimization (ACO)

ACO is an algorithm developed by Marco Dorigo et al. in 1996 [40]. The algorithm simulates the behavior of ants in finding the shortest path between food and their nest. This population-based algorithm generates a number of artificial ants to solve the problem. In ACO, the optimal solution can be found after a number of iterations. At each iteration, each ant creates a new solution (path) that is evaluated by the pheromone rate, which rises as the quality of the solution improves. The pheromone rates on the paths influence the ants’ choice in finding the best path (solution) with the highest pheromone rate, as shown in Figure 2. ACO is a robust and flexible algorithm [41,42] suitable for the path planning problem [42,43], but it has a slow convergence rate [41].

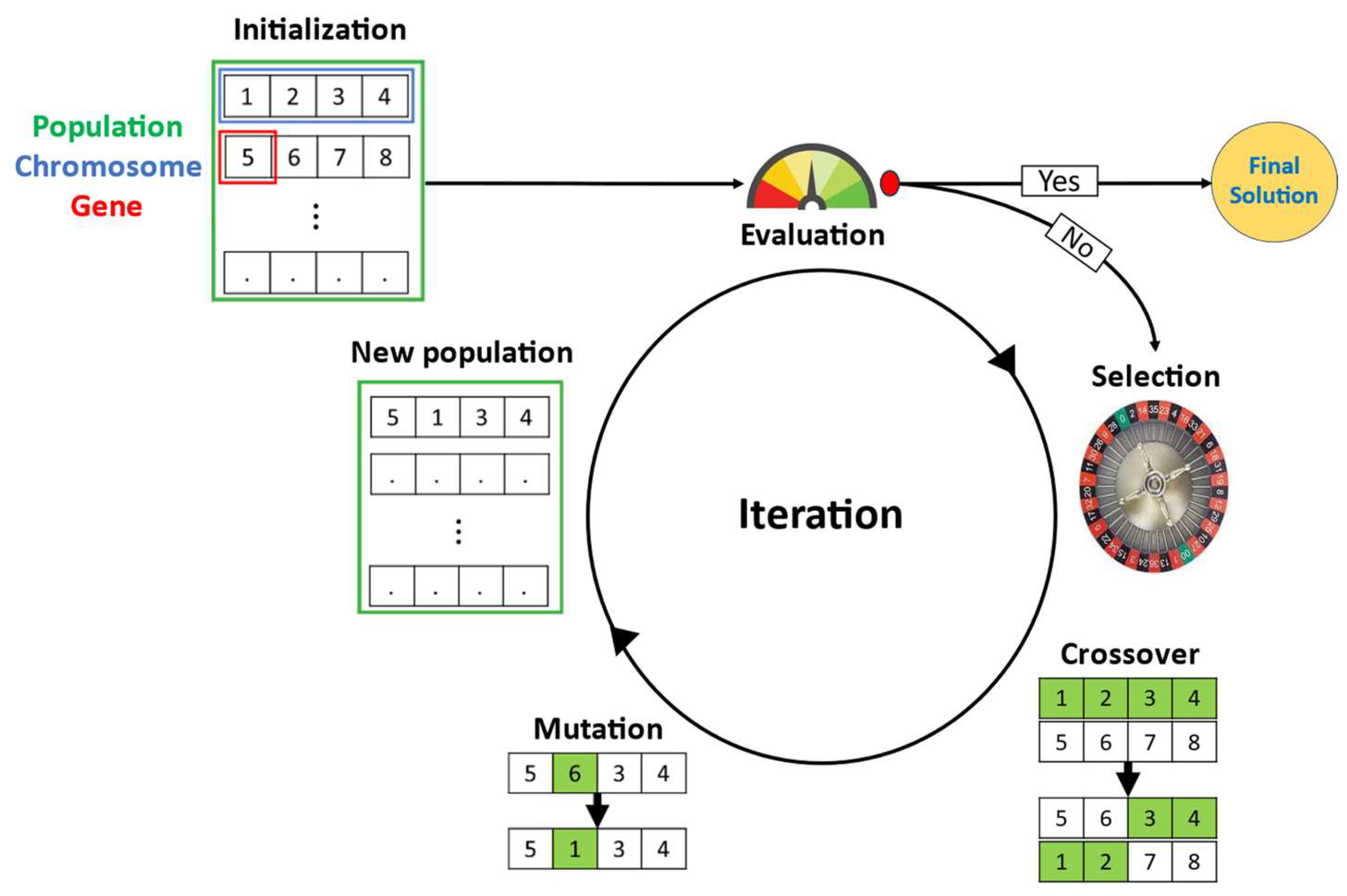
2.3.3. Genetic Algorithm (GA)

GA is an algorithm developed in the 1970s by John Holland et al. [44]. The algorithm mimics Darwin’s concept of evolution and natural selection. GA generates a set of possible solutions. These possible solutions are improved over generations of iterations through selection, crossover, and mutation procedures, as shown in Figure 3. Using the roulette wheel selection technique, the fittest individuals are more likely to be chosen to establish new solutions through crossovers and mutations. GA is a flexible and robust algorithm [45], but it is complex [45,46], sensitive to the value of parameters [45], and dependent on the initial population [46,47].

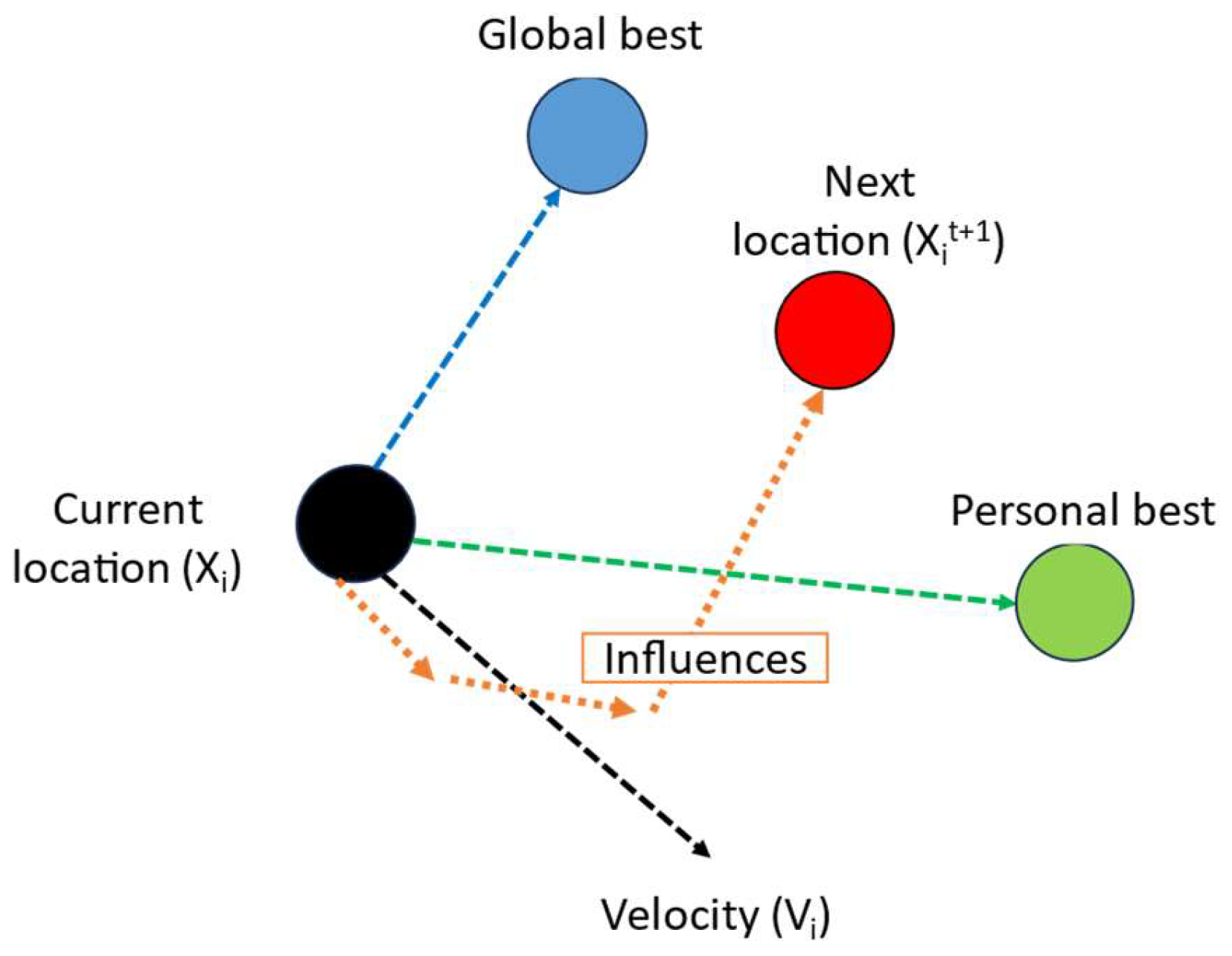
2.3.4. Particle Swarm Optimization (PSO)

PSO is an algorithm that simulates bird/fish foraging behavior, and it was developed by Kennedy and Eberhart (1995) [48]. It is a population-based algorithm in which a number of particles are generated to find the optimal solution in the search space. By sharing information on the discovered possible solutions (quality and location in the search space), particles can converge towards optimal solutions, as shown in Figure 4. PSO is a flexible [45] and simple algorithm and it can be easily implemented compared to other optimization algorithms [45,49]. However, in a high-dimensional search space, PSO slowly converges toward the optimal solution, and the quality of its results decreases [50,51].

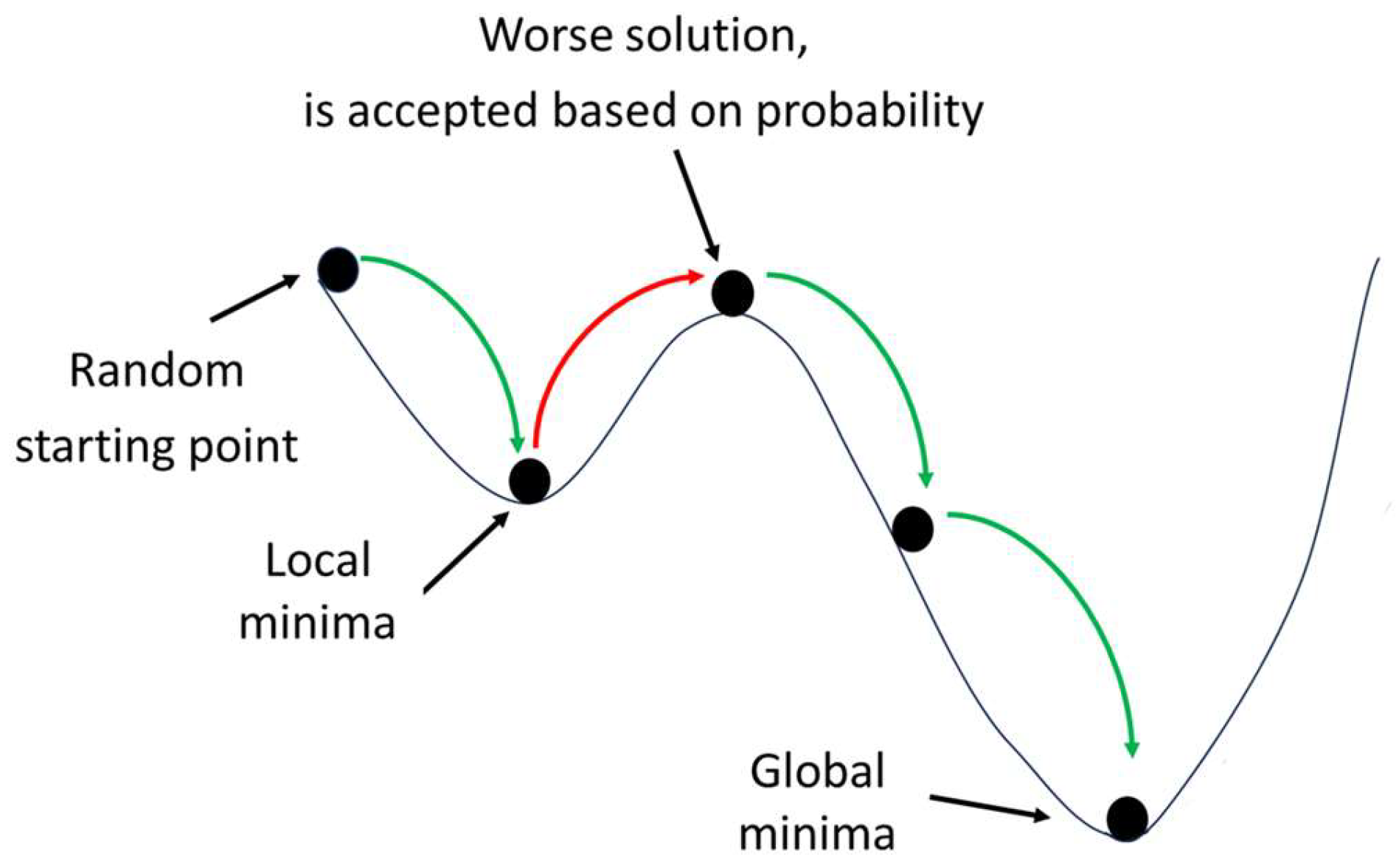
2.3.5. Simulated Annealing (SA)

SA is an algorithm developed by Kirkpatrick et al. (1983) based on metal annealing processes [52]. It starts with a random solution and iteratively explores neighboring solutions to find the best one. Better and worse solutions are accepted to avoid the trap of local optimal solution, as shown in Figure 5. However, the worse solutions are accepted based on probability. As the algorithm progresses, the chance of accepting worse solutions reduces, enabling it to converge towards the best solution. SA is a flexible algorithm [53] with the capacity to avoid the local optima trap by accepting worse solution [45]. However, slow convergence is required in SA to obtain the actual optimal solution [45,46,54]. In addition, it is a single solution-based algorithm, where only one solution is generated and optimized from a local search [45].

3. Methodology of Selecting Tracked GNSS Satellites Based on Optimization Algorithms

To evaluate the performance of the five optimization algorithms (ABC, ACO, GA, PSO, and SA) in the optimization of the satellite subset, the algorithms were modified accordingly to fit the satellite selection problem, while their common parameter values were adjusted and defined uniformly. They were applied in several scenarios of satellite selection for various number of satellites and conditions. In all the cases, the cost function of the five optimization algorithms was the CNR-WGDOP parameter, of which the minimum value would indicate the corresponding optimal GNSS satellite subset. The evaluation of the optimization algorithms was based on comparing the CNR-WGDOP value of their optimal satellite subset with that of the actual optimal satellite subset derived from the TM. The optimization algorithm with the best results in terms of satellite selection accuracy and speed was considered the appropriate algorithm for satellite selection.
Even though GNSS satellite selection is a discrete problem [26], not all of the five optimization algorithms are designed for this type of problem. The five optimization algorithms follow an iterative search process to find the optimal satellite subset. At the end of each iteration, new solution(s) are generated. The ABC and PSO algorithms generate solution(s) with a fractional value as they were designed for continuous problems. However, only an integer is accepted in the satellite selection problem. This issue can be overcome by changing the algorithm design for a discrete problem [26,55,56] or simply rounding solution values [55,57]. To reduce complexity, the generated solutions from ABC and PSO were rounded to the nearest integer in each iteration.
In addition, the four optimization algorithms (apart from ACO) can provide results with duplicate values. In the case of the GNSS satellite problem, this would mean that the same satellite could be chosen twice in the solution of the optimized satellite constellation. To address this problem with less interference in the algorithm design, the algorithm solution was checked at the end of each iteration. If the solution contained a duplicated value, it was rejected, and a new solution was generated without consuming the number of searching iterations.
In this study, the optimal satellite subsets were chosen based on the criterion of minimising the CNR-WGDOP, which indicates the best potential GNSS satellite combination for the given available GNSS satellites. This can be performed without adjustment by all algorithms, except for ACO. ACO was originally designed to simulate the foraging behavior of ants, where ants search for the shortest path to a food source. Due to this, ACO finds the optimal solution based on two criteria: (i) the solution quality and (ii) the distance between solution members [40]. The weight of the two criteria (the solution quality and distance between solution members) on finding the optimal solution can be determined through the values of alpha (α) and beta (β) parameters, respectively. In this problem, the quality of the CNR-WGDOP and the distance between the satellites in a constellation represent the solution quality and the distance between solution members. To select the optimal satellites based on CNR-WGDOP only, the β value was set to zero [40].
The values of the algorithm parameters are critical as they directly affect the algorithm output and performance [58,59]. Choosing the appropriate value for algorithm parameters can be difficult due to their wide range [45,58], whereas homogeneity between these values should be considered [45]. In this study, parameter values were chosen based on their standards and previous studies (Table 1). However, this does not guarantee that the value of these parameters is the best for this problem.
To make an objective comparison of the performance of the five optimization algorithms, the algorithms’ common parameters were standardized. In Table 1, the parameters of the five optimization algorithms are presented, and can be observed that the only common parameters were the searching iteration and population size. The values of both parameters were set to 100, which is considered a reasonable value and consistent with previous studies (Table 1). However, the SA algorithm was originally designed to have a single population size. To make up for this restriction of the population size in the SA algorithm, the number of corresponding iterations was increased with respect to the other four optimization algorithms and defined to 1000 [60]. The number of iterations for the SA algorithm was derived based on tests assessing the performance of the SA algorithm to reach the optimal solution, while also keeping the SA iterations at a similar level of performance to the other four optimization algorithms, as defined by the number of iterations and population size.
To evaluate the five optimization algorithms, they should be applied to a long period of GNSS observation, where (i) the GNSS satellite systems (i.e., GPS, GLONASS, Galileo, etc.), (ii) the number of corresponding GNSS satellites, and (iii) the position of the GNSS satellites (azimuth, elevation) vary with time. Therefore, we used a 24 h period of GNSS observations. The optimization algorithms were applied to select the optimal GNSS satellite subset for specific time intervals where the change in the GNSS satellite position (azimuth and elevation) was adequate to affect the satellite constellation geometry. For the given location of the GNSS station (i.e., Nottingham Geospatial Institute, Nottingham) and available GNSS satellites (i.e., GPS, Galileo, GLONASS), the required time for each GNSS satellite to move on its orbit by one degree was analyzed. Figure 6 displays the required time of each available GNSS satellite to move by one degree, where the maximum required time reaches up to 3 min. In previous studies [23,61], a 10 min satellite selection interval was used. However, in the current study, the satellite selection interval was set to 5 min to reduce the computational load of satellite selection while maintaining a large number of epochs for the satellite selection. Hence, we selected optimal satellite subsets for 288 epochs, corresponding to 1 epoch per 5 min interval, for the 24 h GNSS dataset.
The GNSS satellite selection becomes more challenging as the number of possible satellite combinations increases, which occurs when there is a large number of available GNSS satellites in relation to the number of satellites in the subset. This can be described more clearly with Equation (4):
c r n = n ! r ! n − r !
where c is the number of possible GNSS satellite combinations, expressed as a factorial function of n (the number of available GNSS satellites), and r (the number of GNSS satellites in the subset).
Hence, by increasing the number of available satellites, the number of possible satellite combinations increase dramatically, making the evaluation of the five optimization algorithms more complex. In this study, satellite data were collected from multiple satellite systems (GPS, GLONASS, and Galileo). Therefore, the number of available satellites can easily exceed 20, resulting in a large number of possible satellite combinations, making satellite selection more difficult. Thus, the optimization of the GNSS satellite subset was performed in two stages: (i) for a GPS-only satellite constellation and (ii) for a multi-GNSS satellite constellation (GPS, GLONASS, and Galileo). Based on these two case studies, we evaluated how the performance of the optimization algorithms was affected by the number of GNSS satellites. In the first stage, the performance of the five optimization algorithms was evaluated by optimizing GPS subsets of different sizes to change the selection conditions. Based on the first stage of evaluation, the optimization algorithm with the best performance, in terms of satellite selection accuracy and computation time requirement, was chosen. In the second stage, only the best-performing optimization algorithm was applied and evaluated to optimize different-sized multi-GNSS satellite subsets under more challenging conditions as the number of available GNSS satellites was significantly high, resulting in a large number of possible satellite constellations. In addition, at the second stage, a parametric analysis of the best-performing optimization algorithm was conducted to evaluate the impact of the various settings, such as the number of iterations and the population size, on the performance of the optimization algorithm. In all the tests, the algorithms’ accuracy in satellite selection was evaluated by comparing their selection with the actual optimal satellite subsets, which were identified by TM.
Table 1. The parameter values of the five optimization algorithms.
Table 1. The parameter values of the five optimization algorithms.
AlgorithmNotationMeaningValueReferences
ABCDThe problem dimensions, indicating the satellite constellation size
maxIterThe maximum number of iterations100[26,28,61,62]
pSizeThe population size100[22,26,45,63]
limitThe abandonment limitD × pSize[64]
ACOmaxIterThe maximum number of iterations100
pSizeThe population size100
ρThe evaporation rate0.5[22,40,45]
αThe relative importance of the trail1
βThe relative importance of the visibility0
QThe quantity of trails laid by ants100
GAmaxIterThe maximum number of iterations100
pSizeThe population size 100
PcThe probability of crossover0.8[45,61]
PmThe probability of mutation12
PSOmaxIterThe maximum number of iterations100
pSizeThe population size 100
WmaxThe initial weights0.9[45,62,65]
WminThe final weights0.4
C1The personal acceleration coefficient2
C2The social acceleration coefficient2
SAmaxIterThe maximum number of iterations1000[45,60]
pSizeThe population size 1
T0The initial temperature2000
TfThe final temperature0.01
αThe cooling factor0.975

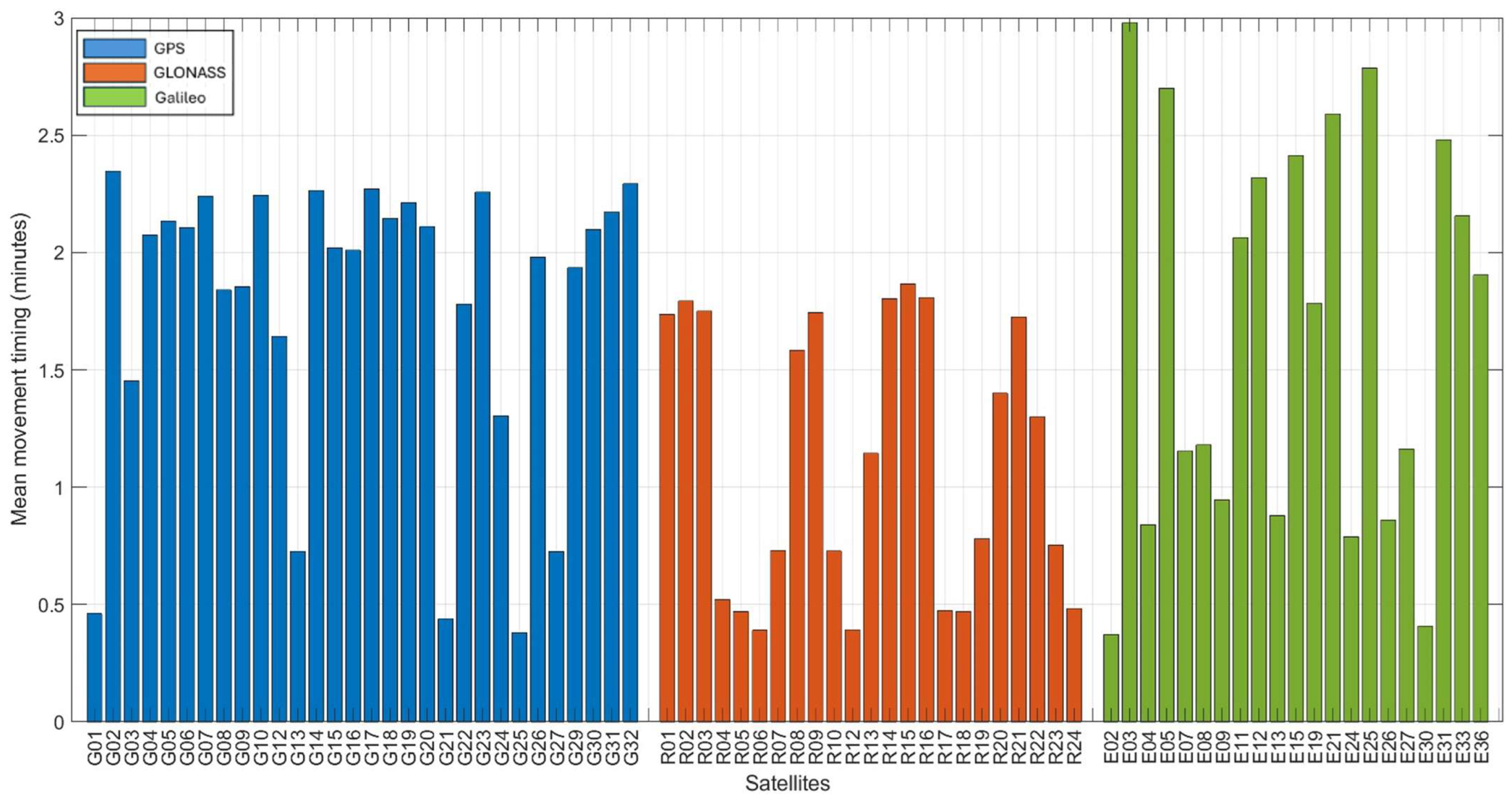
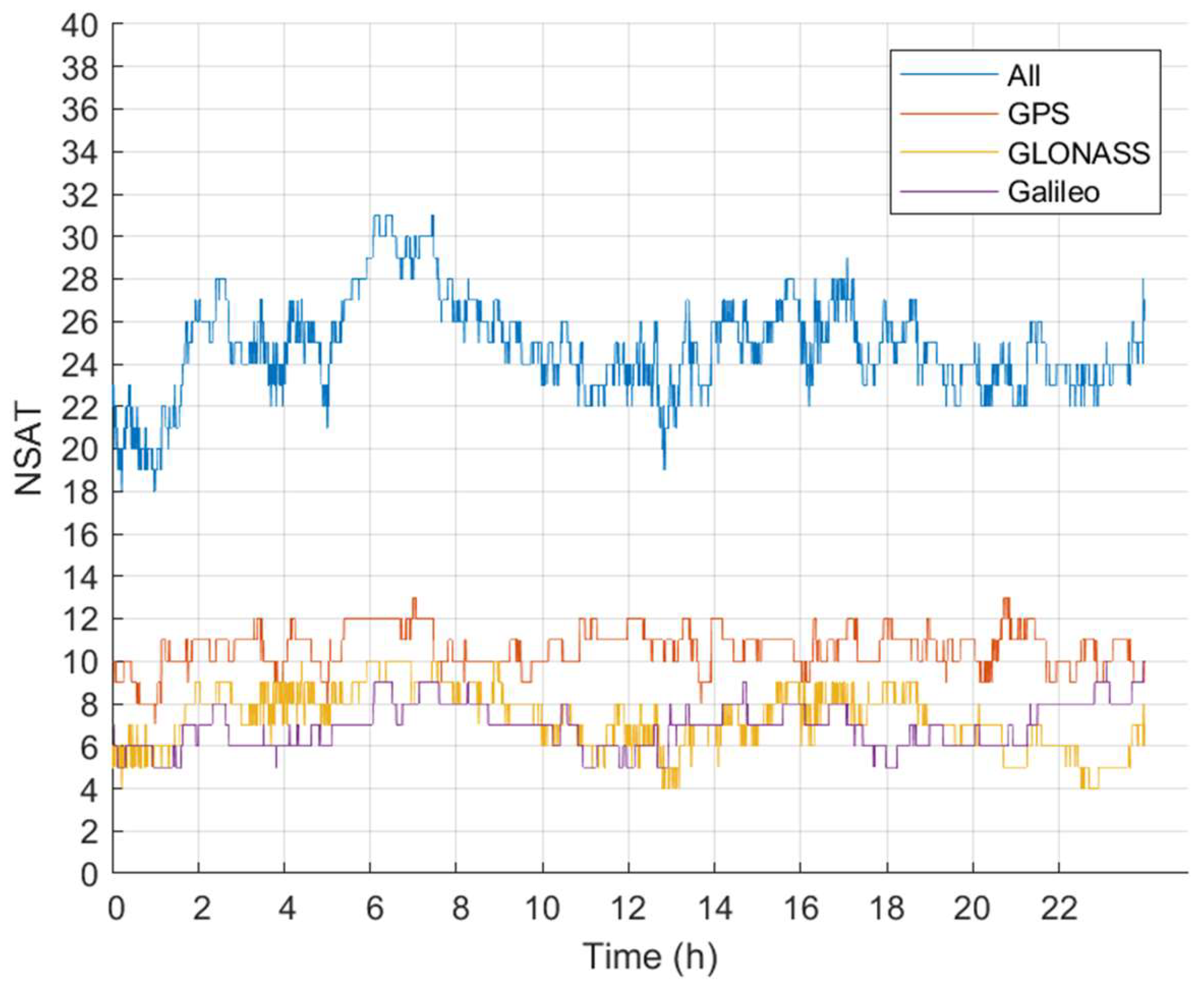
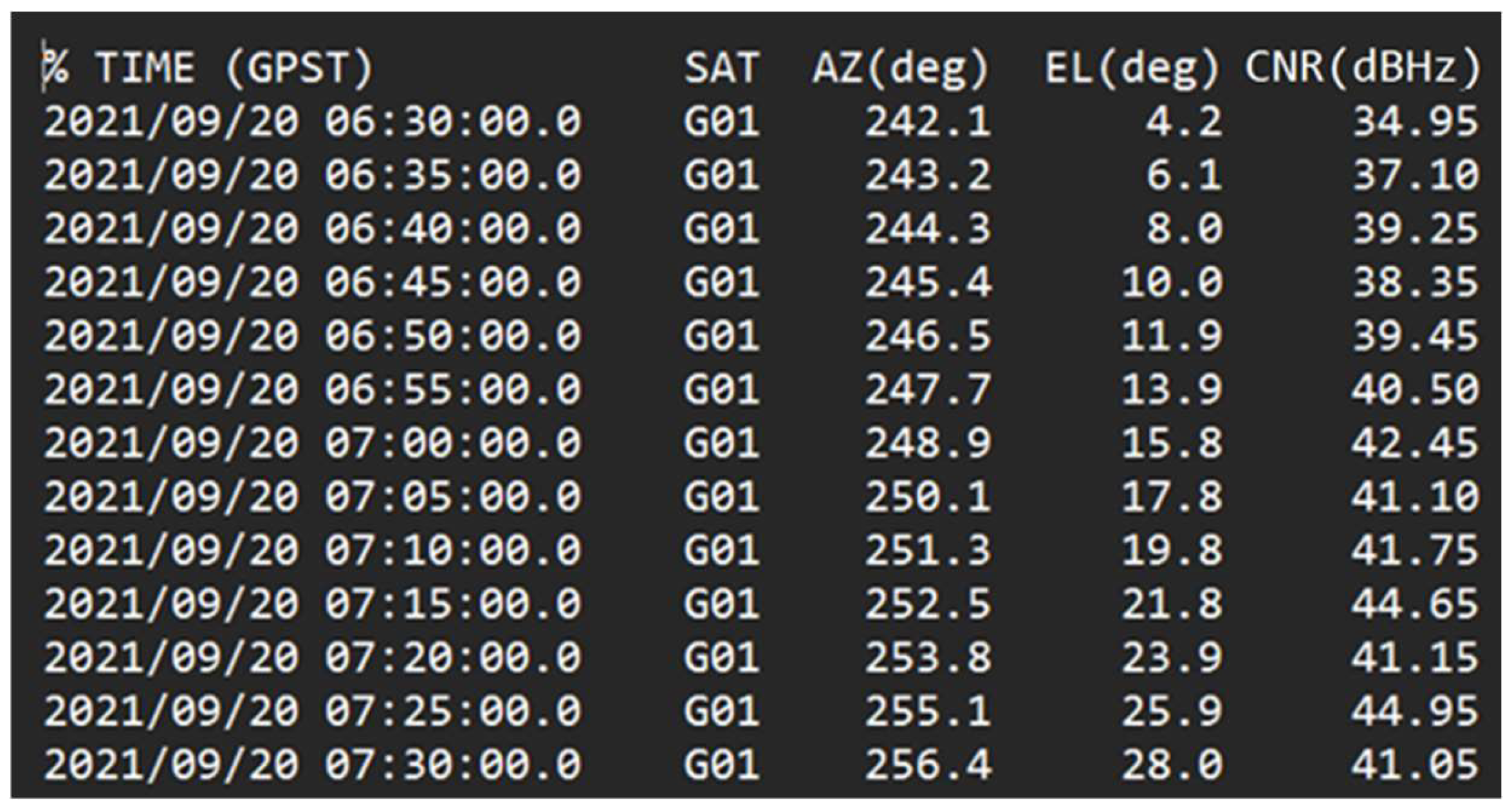
4. GNSS Data

The 24 h GNSS data were obtained from the BIGF (British Isles continuous GNSS Facility) station located on the roof of the Nottingham Geospatial Institute building (Figure 7). The GNSS station is equipped with a Leica AR25.R4 choke ring antenna with strong multipath rejection installed on the pillar of the control point (NGB2) and a Leica GR10 receiver with the capacity to record multi-GNSS signals (GPS, Galileo, GLONASS). On 20 September 2021, GNSS data were collected with a 30 s sampling rate and zero-degree elevation mask. A total of 18–31 satellites were recorded, including 7–13 GPS, 4–10 GLONASS, and 5–10 Galileo satellites (Figure 8).
To choose the satellites based on the CNR-WGDOP, using Equation (1), it was necessary to extract (i) satellite pseudorandom noise (PRN), (ii) the satellite observation time, (iii) elevation angles, (iv) azimuth angles, and (v) the CNR values. The raw satellite data (range observations and navigation data) were introduced into the RTK-LIB (version demo5 b34d) software to define the elevation and azimuth of each satellite, extract the required remaining information (satellite PRN, observation time, and CNR), and save the information in a file, as shown in Figure 9.
The MATLAB (R2022b) software was used to perform the optimal satellite selection by applying the TM and optimization algorithms. The satellite selection was carried out every five minutes. For the examined 24 h GNSS record, the number of GPS satellites ranged from 8 to 13, while the total number of GNSS satellites (GPS, GLONASS, and Galileo) ranged between 18 and 31.
In Figure 10, the number of all possible combinations for a sole GPS constellation and for a multi-GNSS constellation are depicted. The graphs illustrate the potential combinations for a number of given trackable satellites. It is evident that the possible satellite constellation combination increases significantly with the number of available satellites. With 8 GPS satellites available, the maximum number of 4-satellite combinations is 70, whereas in the case of 13 available GPS satellites, the maximum number of combinations is 1716 and occurs for GPS subsets of 6 and 7 satellites. For the case of the multi-GNSS constellation, where the available number of satellites increases, the number of possible combinations increases dramatically. Representative of this is the case of 31 available GNSS satellites, for which the maximum number of possible combinations is 300,540,195 and occurs for multi-GNSS satellite subsets of 15 and 16 satellites.
Based on the methodology described in Section 3, the performance of the five optimization algorithms in optimizing GPS satellite subsets of four, five, six, and seven satellites was examined. The most suitable optimization algorithm was chosen based on its overall performance. It was then tested for optimizing multi-GNSS satellite subsets of 4, 8, 12, and 15 satellites using various algorithm parameter values.

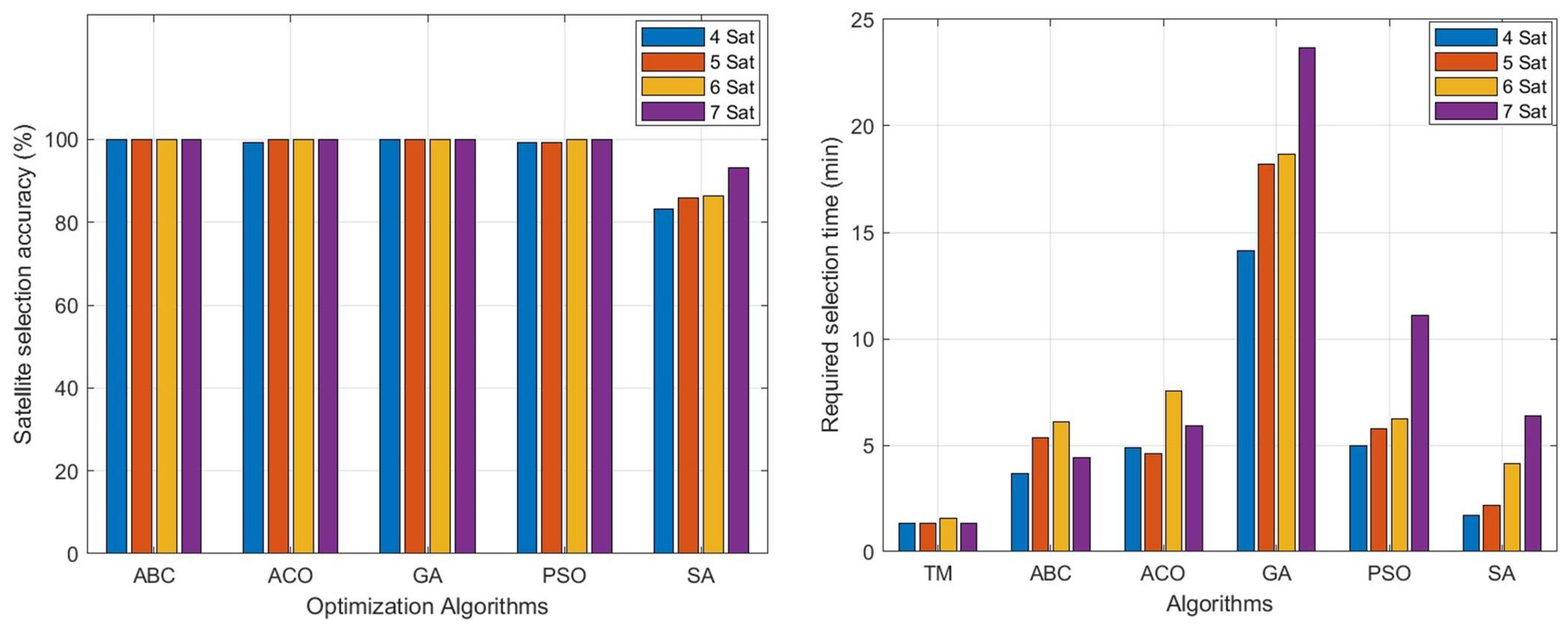
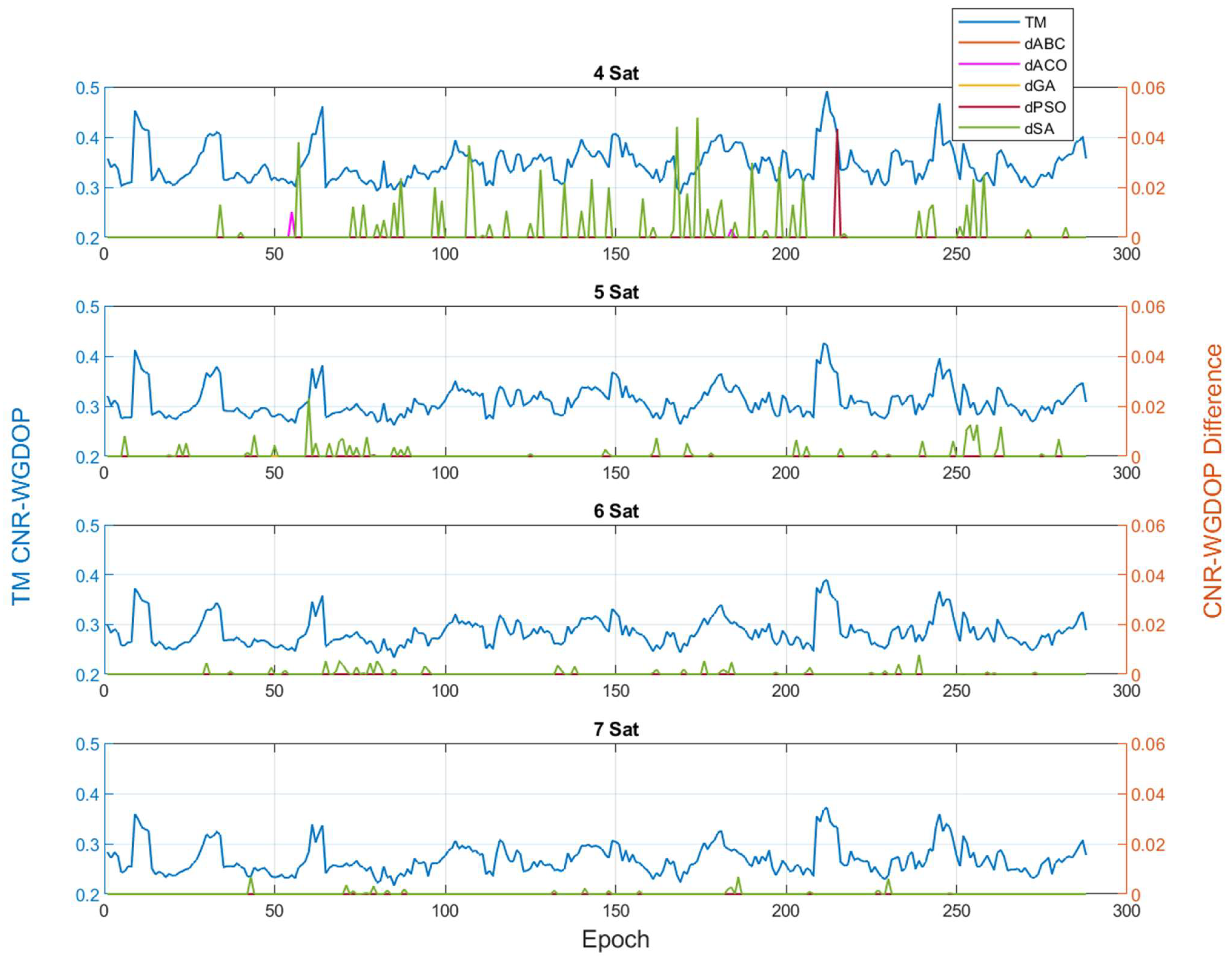
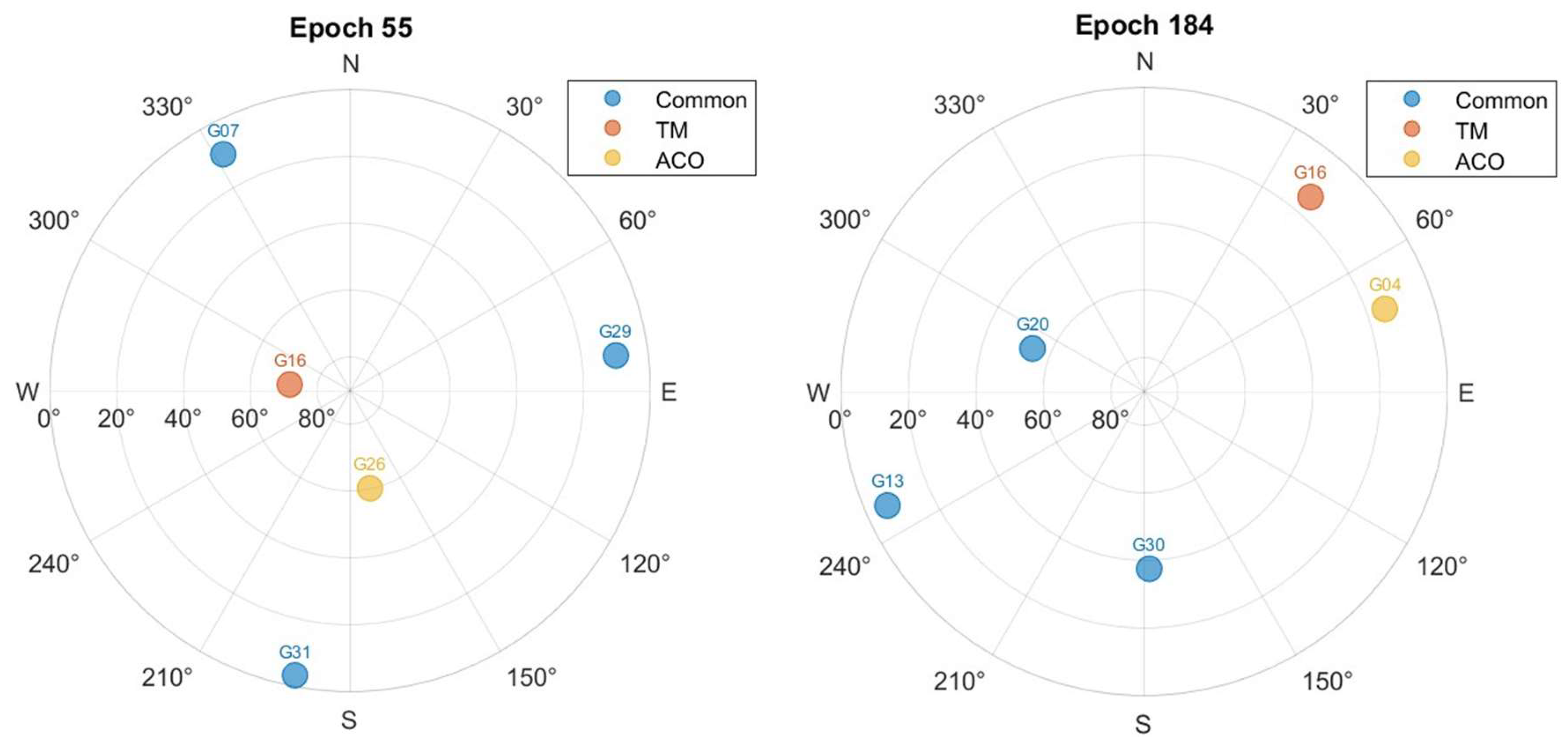
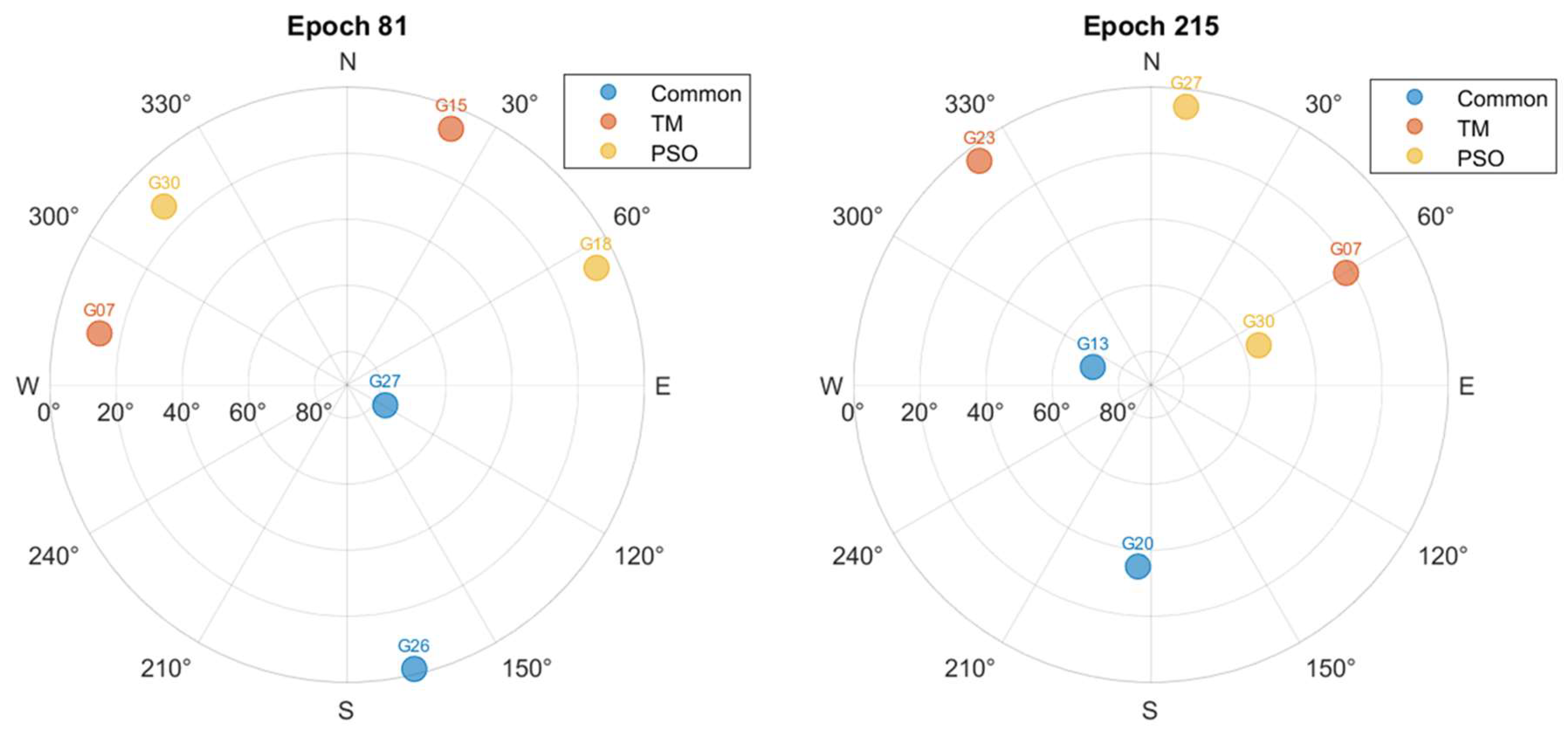
5. Results and Discussion

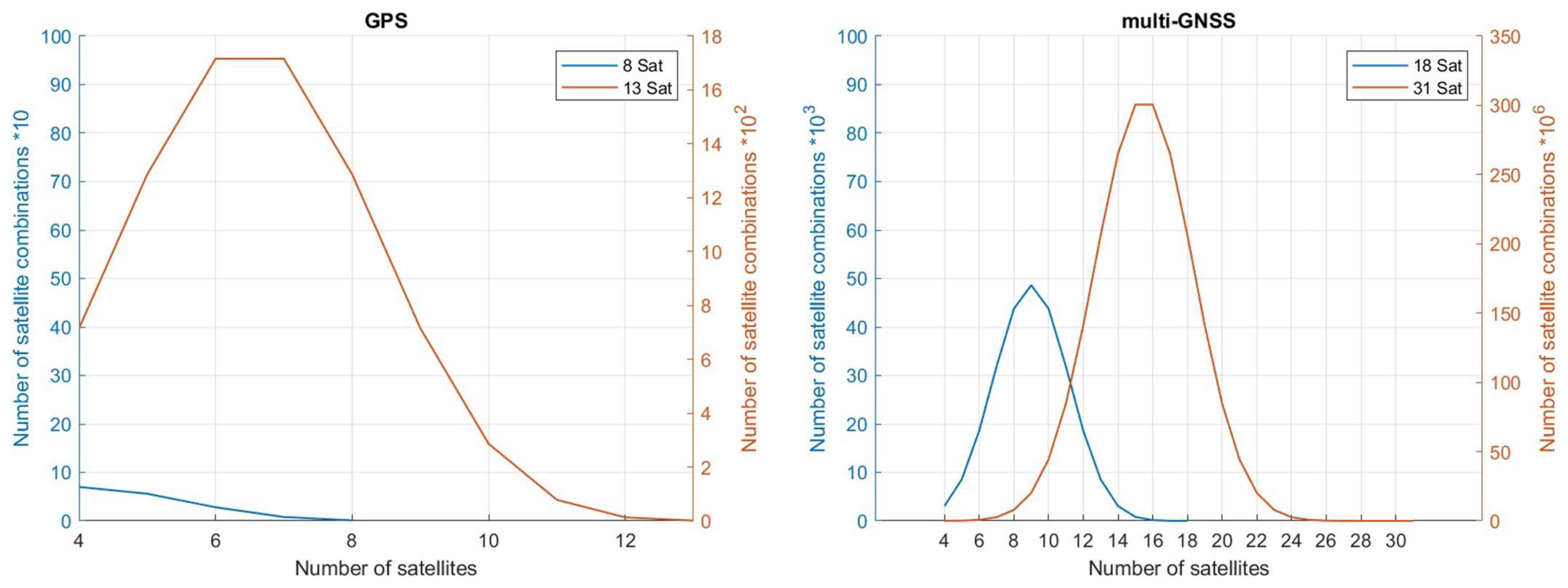
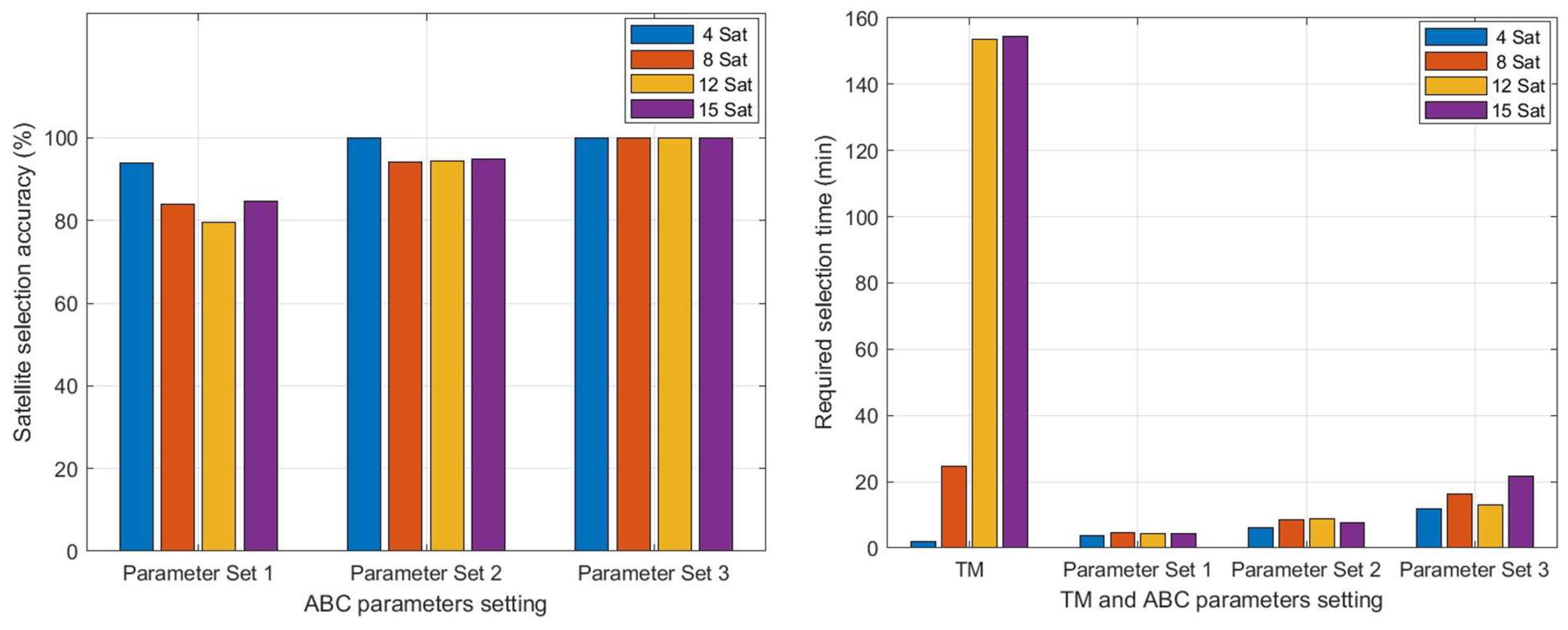
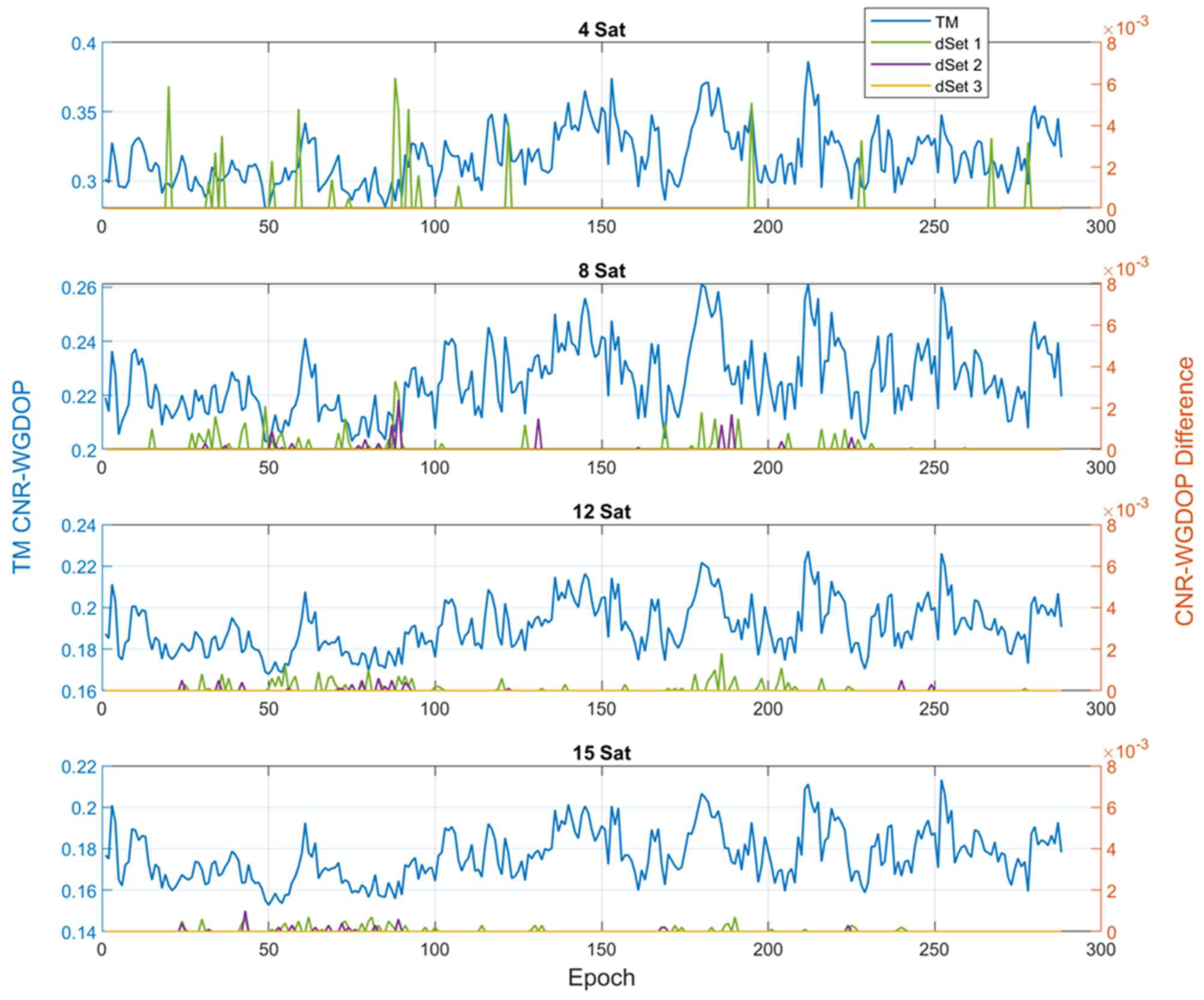
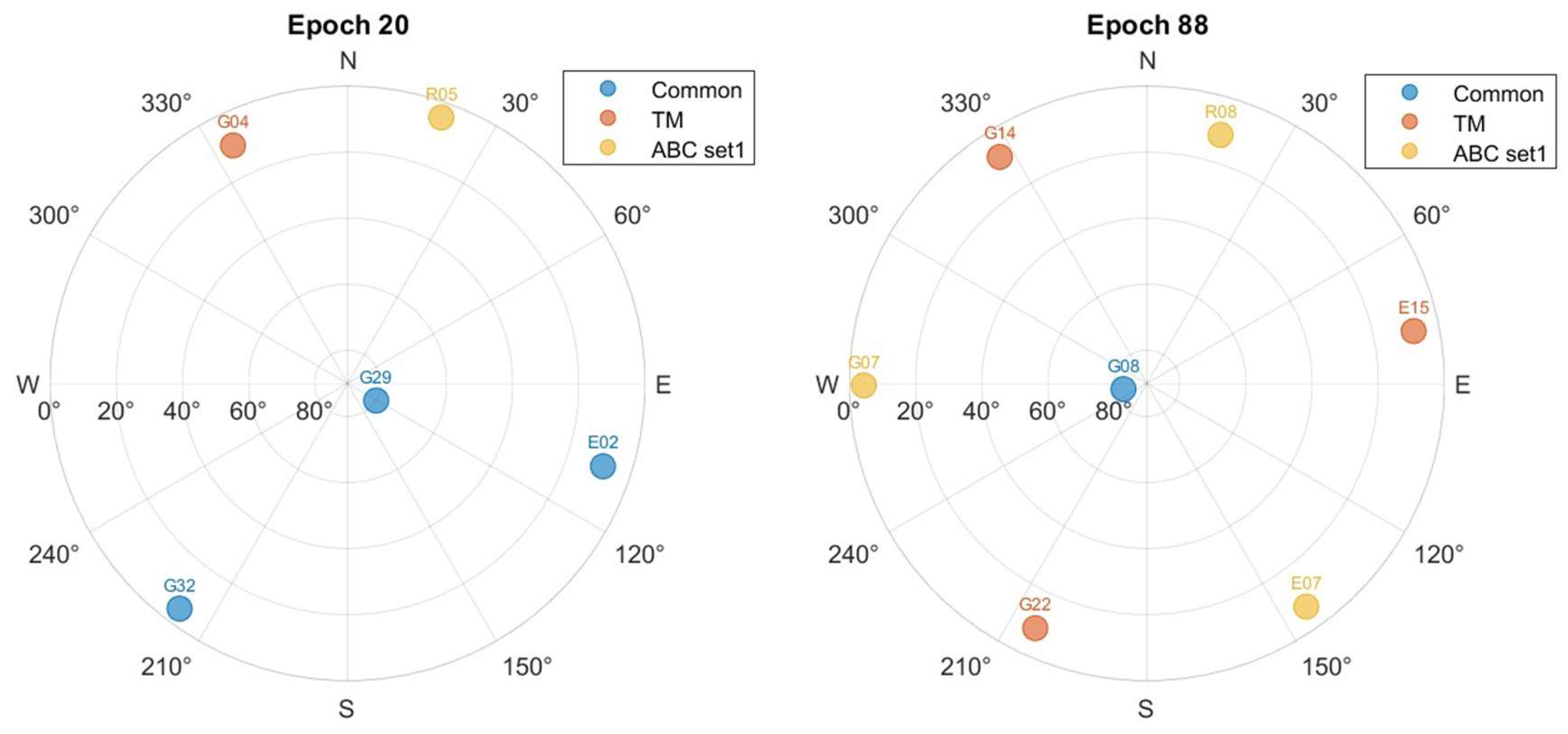
5.1. GPS Optimal Satellites

The five optimization algorithms were applied for the optimization of GPS-only satellite constellations of four, five, six, and seven GPS satellite constellations for the 24 h GPS data. Optimal GPS satellites were selected every five minutes; hence, the optimization algorithms selected the optimal satellite constellation for 288 epochs (i.e., 1 epoch per 5 min) in the 24 h period. Figure 11 shows (i) the matching quality of the GPS satellite subsets selected by the algorithms, which was determined by comparing the satellite selection results of the optimization algorithms with those of the TM, and (ii) the selection time that was taken by the algorithms for the GPS satellite selection over 288 epochs.
According to Figure 11, all the optimization algorithms effectively selected the optimal GPS satellites, except for the SA algorithm. More specifically, for the cases of a GPS satellite constellation of four, five, six, and seven satellites, the four algorithms ABC, ACO, GA, and PSO achieved a GPS satellite selection accuracy of over 99%, with the algorithms ABC and GA achieving the best GPS satellite selection accuracy as they had a 100% match with the optimal GPS satellite constellation as derived by the TM. In contrast, SA had the lowest accuracy in choosing the optimal GPS satellite constellation, with a match ranging between 83% and 93%. However, the SA proved to perform the fastest in satellite selection among the five optimization algorithms, but it was still slower than the TM.
The performance of optimization algorithms, and consequently the quality of their results, can be affected by the value of optimization algorithms’ parameters. However, the main reason for SA’s lower quality in satellite selection is its design, and specifically, the technique of finding the optimal solution. ABC, ACO, GA, and PSO are population-based algorithms, which mean that they use groups of individuals to find the optimal solution [45]. In this project, the population size of these algorithms was set as 100. In contrast, SA was originally designed to find the optimal solution using a single population size. Since increasing the population size can improve the quality of the algorithms’ results [45], the performance of SA was negatively affected by its small population.
On the other hand, it can be seen that the four algorithms (ABC, ACO, GA, and PSO) are equally accurate in selecting satellites. These algorithms achieved more than 99% accuracy in selecting the optimal GPS subsets of four, five, six, and seven satellites. ABC and GA constantly selected the optimal satellites with a quality of 100% in all cases, whereas ACO and PSO exhibited less accurate satellite selection (99.3%) in one and two cases, respectively. Since each case included 288 epochs, the satellite selection accuracy of 99.3% means that the optimal GPS satellite subset was mis-selected in two epochs. When reviewing the selection of satellites in each epoch (Figure 12), no significant difference could be found between the ACO and PSO results and the TM results (actual results). This indicates that ACO and PSO fall into a local optimum that was too close to the best solution (i.e., satellite combination) ever found in the two epochs. ACO and PSO mis-selected the optimal subset of four satellites in two epochs. In Figure 13 and Figure 14, the actual optimal subset of four satellites, derived by the TM, and the satellite combinations selected by ACO and PSO are displayed. The quality of these algorithms may vary from one trial to another, which could be due to the fact that these algorithms start randomly [45], which affects their results [46,47], or because of the chosen values for the different parameters, which can also affect the algorithms’ results. However, the four algorithms (ABC, ACO, GA, and PSO) can generally be considered equally accurate in terms of satellite selection. This aligns with the results presented in [29], where ABC, GA, and PSO provided approximately the same high level of accuracy in GPS satellite selection, while SA provided slightly lower accuracy in selection.
In terms of satellite selection speed, the optimization algorithms were slow in selecting the optimal GPS satellites. Figure 11 presents the time required by the five optimization algorithms and TM to find the optimal GPS satellite selection for all 288 epochs, corresponding to the selection of a GNSS satellite subset of one epoch per 5 min interval, for the 24 h GNSS dataset. According to the figure, the TM, which checks all possible satellite combinations, was faster than the optimization algorithms in finding the optimal satellite subset. TM selected the optimal satellites within about 2 min in all satellite selection cases. In contrast, the five optimization algorithms took more than 2 min in all cases, with the required time varying depending on the number of satellites in the constellation. In general, SA was the fastest algorithm among the five, whereas GA was the slowest. The ABC, ACO, and PSO algorithms were similar in terms of required time (5 min) to complete the satellite optimization.
Unlike the TM, optimization algorithms do not require a complete investigation of possible satellite combinations to determine the optimum. However, the TM was faster in finding the best GPS satellites as the optimization algorithms are computationally heavy for “small” problems due to them following indirect approaches that require additional processing time. For a small number of satellites that can be provided by a single system (e.g., GPS), this additional processing adds an unnecessary burden to the problem. As a result, the TM was faster in finding the optimal GPS satellites, which aligns with the outcome in [22], as the TM is suitable for selecting satellites from one system.
Except for GA, the selection speed of the optimization algorithms was generally comparable. They took about 5 min to choose satellites in all selection cases. However, the GA took much longer, ranging from 14 to 24 min. This contrasts with what was stated in [46], where the GA was a fast algorithm. In addition, it contradicts the results presented by Du et al. [22], who showed that the GA outperformed ACO in terms of satellite selection speed. The GA took only 2 s, while ACO took 4.37 s to complete one selection. Furthermore, in [29], the GA was as fast as ABC and PSO in selecting GPS satellites, completing approximately the same number of search iterations within 1, 1.5, and 2 s. The main reason for this unexpected delay in the speed of GA selection is the algorithm modification. GA finds the optimal solution by iteratively generating better new solutions. However, it may create solutions with a duplicate value, which is unacceptable in satellite selection. Thus, solutions with a duplicate value were rejected and new solutions were generated until no duplicates appeared. Clearly, this is time-consuming. Although the same modification was applied to ABC, PSO, and SA, these algorithms took much less time than the GA. This is because a GA creates new solutions by swapping the variables of two good solutions. As GA solutions converge, two nearly identical solutions are selected to create a new solution, which subsequently leads to more duplication.
Based on Equation (4), the number of possible satellite constellations changes due to the number of available satellites (8 and 13; Figure 10) and the constellation sizes (four, five, six, and seven; Figure 10). Compared to others, the subset of six GPS satellites had the highest number of possible combinations, with a total of 1744. As a result, the TM, which checks all possible satellite combinations, took slightly longer to find the optimal GPS subset of six satellites than the others, as shown in Figure 11. In contrast to the TM, the five optimization algorithms were unaffected by the number of possible satellite combinations as their number of searching iterations is predetermined. Although the five optimization algorithms were executed with the same number of iterations (100) at all satellite constellation sizes (four, five, six, and seven), the selection time for each algorithm varied from one satellite constellation size to another, as shown in Figure 11, due to the adjustment of duplication in the four algorithms (ABC, GA, PSO, and SA). However, the difference in ACO processing time could be due to the number of possible GPS satellite subsets. In ACO, the pheromone rate on the paths influences the ants’ path choice, which is stored in a pheromone matrix containing the pheromone rates of all possible paths. Since the size/burden of the pheromone matrix depends on the number of possible paths, which is equal to the number of possible satellite combinations, the ACO selection time changed with different satellite constellation sizes (four, five, six, seven) as they have different possible satellite constellations.
Among the five optimization algorithms, the most suitable one for satellite selection can be determined based on their satellite selection accuracy and speed. SA and GA are not suitable for satellite selection because of their low selection quality and speed, respectively. On the other hand, ABC, ACO, and PSO showed equivalent levels of selection quality and speed. However, the ABC algorithm was considered to be the most suitable algorithm for satellite selection, as only three parameters have to be determined.

5.2. Multi-GNSS Optimal Satellites

Based on the evaluation of the optimization algorithms for the GPS-only satellite constellation, the ABC algorithm proved to be the most accurate and suitable for the optimization of GNSS satellite subsets. The next step was to apply and evaluate the ABC algorithm for the optimization of the multi-GNSS satellite constellation. The same methodology as that for identifying the GPS-only satellite constellation was followed by selecting the optimal GNSS satellite subset every five minutes. GPS, GLONASS, and Galileo satellites were included for satellite selection, and four cases of satellite subset sizes (4, 8, 12, and 15 satellites) were examined. ABC was applied three times for each size of satellite subset, with different values for the parameters of (i) the number of iterations and (ii) population size (Table 2), to evaluate their impact on algorithm performance and determine which parameters provide the best results.
The ABC algorithm requires the setting of three parameters: the maximum number of iterations (maxIter), population size (pSize), and abandoned limit (limit). In the case of the GPS-only satellite constellation, the maxIter, pSize, and limit values were set to 100, 100, and the product of problem dimensions and population size ( D × p S i z e ), respectively. The value of abandoned limit ( D × p S i z e ) is a dynamic value that automatically adapts to the problem size [64]; hence, it does not need to be adjusted. On the other hand, higher values of population size (pSize) and iteration (maxIter) can lead to better results, but they may cause slow convergence (longer processing times) [45,66]. Increasing the value of both pSize and maxIter could be unnecessary as the algorithm results can be improved with a higher pSize and limited maxIter [66]. Based on previous studies, a pSize of up to 200 is recommended [45]. As a result, pSize and maxIter were set to the values shown in Table 2.
Figure 15 shows the accuracy of the ABC algorithm in the GNSS satellite selection, which was determined by comparing ABC’s optimal GNSS satellite selection with the actual (the TM’s selection), for each satellite subset size (4, 8, 12, and 15) and for each parameter setting. In addition, Figure 15 illustrates the speed of the ABC algorithm and the TM, expressed as the required selection time for the optimal satellite selection of all 288 epochs (GNSS satellite selection per 5 min for the 24 h GNSS dataset). It can be observed that satellite selection becomes more challenging due to the size of the satellite subset, requiring higher parameter values and longer computation time. ABC showed better accuracy in selecting the optimum four GNSS satellite subset compared to the other sizes of satellite constellations (8, 12, 15) using the first two cases of parameter settings. This is due to the significant increase in the possible satellite combinations, which follows the increase in the number of satellites in the constellation (from 4 to 8, 12, and 15) (Figure 10). By increasing the value of the pSize and maxIter to 200, ABC accurately (100%) determined the optimal GNSS satellite subset for all sizes. However, the time required for selection increased by about 3.6 times with respect to the first setting case using 100 for both pSize and maxIter. Therefore, satellite selection becomes more challenging due to constellation size. This requires higher values of population size and iteration, which leads to longer computation time. This is consistent with what was reported in [45,66], as a lower pSize and maxIter prevent achieving the best solution in complex problems, whereas increasing the value of these parameters increases the processing time.
The number of possible satellite combinations of 8- and 12-satellite subsets is less than that for 15 satellites, and consequently, the selection of the optimal satellite constellation should be easier than with 15 satellites. However, ABC was relatively more accurate in selecting the optimal 15 satellites than 8 and 12 satellites using the first parameter setting (Figure 15). The accuracy of choosing the optimal 8-, 12-, and 15-satellite constellations was 84%, 79.5%, and 84.7%, respectively. Since similar parameter values were used for the three satellite constellation sizes, it is the initial randomly generated solution by the ABC algorithm which influences the produced solutions [47].
In terms of speed, the TM required an overall longer processing time to find the optimal satellites than the ABC algorithm, as the required time for the TM increased significantly with the satellite constellation size (which increased from 4 to 15), since the TM checks all possible satellite combinations, which increase with the size of the satellite constellation. It should be noted that in the cases of 12- and 15-GNSS-satellite constellations, the time required by the TM exceeded 150 min (i.e., >30 s per epoch).
On the other hand, the speed of ABC varied based on the parameters’ settings. In the case of the first set of parameters (maxIter and pSize equal to 100), the ABC algorithm required approximately the same processing time (i.e., about 4.3 min; 0.9 s per epoch) for the four cases of satellite constellations (4, 8, 12, and 15), indicating that the number of satellite combinations does not affect the speed of the ABC algorithm. For the other two settings, an increased processing time was observed, caused by the population size/number of iterations, which was increased to 200. However, a slight difference in the required processing time for the various satellite constellations (4, 8, 12, and 15) can be explained by the adjustment of satellite duplication in the solutions.
The total number of GPS, GLONASS, and Galileo satellites reached 31, providing more than 300 million possible satellite combinations (Figure 10). However, ABC provides good results regardless of the setting used. According to Figure 15, ABC achieved a selection accuracy of 100% using setting 3, and its selection accuracy was no less than 80% with other settings. Furthermore, in all cases, the fitness (CNR-WGDOP) of the mis-selected optimal GNSS satellite constellations differed by no more than 0.0063 (i.e., settings and constellation size) from those of the actual optimal GNSS satellite constellations determined by the TM (Figure 16). The largest difference between the quality (i.e., CNR-WGDOP) of ABC satellite selection and the actual selection (TM) occurred in the selection of the four optimal satellites in setting 1. Figure 17 shows the sky plots of the satellites selected by ABC setting 1 and the TM at epochs 20 and 88, which are the epochs with the largest difference in the CNR-WGDOP values between ABC setting 1 and the TM (0.0059 and 0.0063, respectively). In epoch 20, the selection of ABC setting 1 differed from the TM in one satellite; the two different satellites of the ABC and TM are of similar elevation angles and roughly symmetrical with respect to the azimuth. In epoch 88, ABC setting 1 selected three satellites that were different from those of the TM. Similar to epoch 20, the six different satellites of the ABC and TM were of a similar elevation angle and roughly symmetrical with respect to the azimuth. Hence, even for the epochs where ABC’s satellite selection was not actually optimal, its geometry was very close to the actual (as defined by the TM), as shown in Figure 17. As a result, the ABC satellite subset had a very similar CNR-WGDOP value compared to the actual optimal satellite subset.

6. Conclusions

This study focused on the investigation of the performance of five optimization algorithms (ABC, ACO, GA, PSO, and SA) in selecting optimal GNSS satellite subsets and identifying the optimization algorithm with the most reliable, accurate, and cost-efficient features. The importance of this study is (i) the overall evaluation of the performance of the five optimization algorithms against the TM based on a complex optimization function (i.e., CNR-WGDOP) by combining the satellites’ geometry and satellites’ signal quality, (ii) and the investigation of how the algorithms’ principles, settings, and parameters affect their performance.
By comparing against the TM optimal solution, the evaluation for a GPS-only satellite constellation revealed that, generally, the ABC, ACO, and PSO algorithms had the highest accuracy in determining the optimal satellite subset and they were efficient in terms of computation time. However, the ABC algorithm is more practical with the fewest parameters to adjust, making the application of the optimization algorithm suitable for this problem. The evaluation of the ABC algorithm in the more complex problem of a multi-GNSS satellite constellation and even up to 31 available satellites revealed that the satellite selection accuracy of the ABC algorithm improves significantly by increasing (i.e., doubling) the values of population size and number of iterations, although this has an effect on the required computation time. The option of only doubling the population size parameter seems the most efficient as the accuracy of selecting optimal satellites ranged between 93% and 100% for the 24 h GNSS data period, with respect to the TM, without significantly increasing the required processing time. Also, it was shown that the TM is still the most efficient algorithm for selecting the optimal satellite combination from a single satellite system (i.e., GPS-only). However, this is not the case for multi-GNSS constellations with more simultaneously tracked satellites available, making the satellite selection problem too complex and time-consuming for the TM.
Hence, it has been shown that the ABC algorithm can be suitable for optimizing the selection of tracked GNSS satellite constellations, which can be a very useful approach for GNSS technology to contribute to more reliable and accurate GNSS positioning performance. Also, the optimization of the tracked GNSS satellites is aligned with the recent interest in developing sustainable and low-cost GNSS solutions for monitoring applications of civil engineering infrastructure [67] and geohazards [68] by optimizing and limiting the number of required GNSS satellites. This can result in a reduction in the GNSS data size and improve the ease of data transfer. However, further investigation is needed to shed more light on how to make the application of these algorithms to optimizing satellite constellations even more efficient in terms of processing time and performance. Their performance also needs to be evaluated in more complicated satellite selection scenarios where the number of possible satellite subsets exceeds 300 million by increasing the number of tracking satellites to more than 31 when including satellites from other systems, such as BeiDou.

Author Contributions

Methodology, A.A., P.P. and R.R.-P.; investigation, A.A.; software, A.A.; formal analysis, A.A.; supervision, P.P. and R.R.-P.; validation, P.P. and R.R.-P.; writing—original draft preparation, A.A.; writing—review and editing, P.P. and R.R.-P. All authors have read and agreed to the published version of the manuscript.

Funding

Taibah University and Saudi Arabia Cultural Bureau (SACB).

Data Availability Statement

Data can be provided by the authors upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. GPS. GOV Space Segment. Available online: https://www.gps.gov/systems/gps/space/ (accessed on 8 January 2024).
  2. GPS. GOV Other Global Navigation Satellite Systems (GNSS). Available online: https://www.gps.gov/systems/gnss/ (accessed on 8 January 2024).
  3. Yu, Q.; Wang, Y.; Shen, Y. A Fast GNSS Satellite Selection Algorithm for Continuous Real-Time Positioning. GPS Solut. 2022, 26, 68. [Google Scholar] [CrossRef]
  4. Zhang, M.; Zhang, J.; Qin, Y. Satellite Selection for Multi-Constellation. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 1053–1059. [Google Scholar]
  5. Xu, B.; Shao, B. Satellite Selection Algorithm for Combined GPS-Galileo Navigation Receiver. In Proceedings of the 2009 4th International Conference on Autonomous Robots and Agents, Wellington, New Zealand, 10–12 February 2009; pp. 149–154. [Google Scholar]
  6. Nie, Z.; Gao, Y.; Wang, Z.; Ji, S. A New Method for Satellite Selection with Controllable Weighted PDOP Threshold. Surv. Rev.-Dir. Overseas Surv. 2017, 49, 285–293. [Google Scholar] [CrossRef]
  7. Msaewe, H.A.; Hancock, C.M.; Psimoulis, P.A.; Roberts, G.W.; Bonenberg, L.; de Ligt, H. Investigating Multi-GNSS Performance in the UK and China Based on a Zero-Baseline Measurement Approach. Measurement 2017, 102, 186–199. [Google Scholar] [CrossRef]
  8. Lau, L.; Tateshita, H.; Sato, K. Impact of Multi-GNSS on Positioning Accuracy and Multipath Errors in High-Precision Single-Epoch Solutions—A Case Study in Ningbo China Real-Time Kinematic (RTK) Global Positioning System (GPS) Carrier Phase-Based Precise Positioning. J. Navig. 2015, 68, 999–1017. [Google Scholar] [CrossRef]
  9. Takahashi, S.; Kubo, N.; Yamaguchi, N.; Yokoshima, T. Real-Time Monitoring for Structure Deformations Using Hand-Held RTK-GNSS Receivers on the Wall. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; The Institute of Electrical and Electronics Engineers, Inc. (IEEE): Piscataway, NJ, USA, 2017; p. 1. [Google Scholar]
  10. Wang, E.; Sun, C.; Guo, J.; Qu, P.; Pang, T.; Zhang, J. GNSS Receiver Satellite Selection Algorithm Based on Particle Swarm Optimization. In Proceedings of the 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; pp. 985–989. [Google Scholar]
  11. Kiliszek, D.; Kroszczyński, K. Performance of the Precise Point Positioning Method along with the Development of GPS, GLONASS and Galileo Systems. Measurement 2020, 164, 108009. [Google Scholar] [CrossRef]
  12. Kaloop, M.R.; Yigit, C.O.; El-Mowafy, A.; Bezcioglu, M.; Dindar, A.A.; Hu, J.W. Evaluation of Multi-GNSS High-Rate Relative Positioning for Monitoring Dynamic Structural Movements in the Urban Environment. Geomat. Nat. Hazards Risk 2020, 11, 2239–2262. [Google Scholar] [CrossRef]
  13. Psimoulis, P.A.; Stiros, S.C. Experimental Assessment of the Accuracy of GPS and RTS for the Determination of the Parameters of Oscillation of Major Structures. Comput.-Aided Civ. Infrastruct. Eng. 2008, 23, 389–403. [Google Scholar] [CrossRef]
  14. Fang, Y.Y.; Hong, Y.; Zhou, O.G.; Liang, W.; Liu, W. A GNSS Satellite Selection Method Based on SNR Fluctuation in Multipath Environments. Int. J. Control Autom. 2015, 8, 313–324. [Google Scholar] [CrossRef]
  15. Peppa, I.; Psimoulis, P.; Meng, X. Using the Signal-to-Noise Ratio of GPS Records to Detect Motion of Structures. Struct. Control Health Monit. 2018, 25, e2080. [Google Scholar] [CrossRef]
  16. Teng, Y.; Wang, J. A Closed-Form Formula to Calculate Geometric Dilution of Precision (GDOP) for Multi-GNSS Constellations. GPS Solut. 2016, 20, 331–339. [Google Scholar] [CrossRef]
  17. Msaewe, H.A.; Psimoulis, P.A.; Hancock, C.M.; Roberts, G.W.; Bonenberg, L. Monitoring the Response of Severn Suspension Bridge in the United Kingdom Using Multi-GNSS Measurements. Struct. Control Health Monit. 2021, 28, e2830. [Google Scholar] [CrossRef]
  18. Teng, Y.; Wang, J.; Huang, Q.; Liu, B. New Characteristics of Weighted GDOP in Multi-GNSS Positioning. GPS Solut. 2018, 22, 74. [Google Scholar] [CrossRef]
  19. Chen, C.-S. Weighted Geometric Dilution of Precision Calculations with Matrix Multiplication. Sensors 2015, 15, 803–817. [Google Scholar] [CrossRef] [PubMed]
  20. Blanco-delgado, N.; Nunes, F.D. Satellite Selection Based on WDOP Concept and Convex Geometry. In Proceedings of the 2010 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 8–10 December 2010; pp. 1–8. [Google Scholar]
  21. Chen, C.-S.; Lin, J.-M.; Lee, C.-T. Neural Network for WGDOP Approximation and Mobile Location. Math. Probl. Eng. 2013, 2013, 369694. [Google Scholar] [CrossRef]
  22. Du, H.; Hong, Y.; Xia, N.; Zhang, G.; Yu, Y.; Zhang, J. A Navigation Satellites Selection Method Based on ACO with Polarized Feedback. Proc. IEEE Access 2020, 8, 168246–168261. [Google Scholar] [CrossRef]
  23. Meng, X.; Wang, S.; Nie, P.; Niu, Z.; Zhu, B. An Efficient Genetic Algorithm of Multi-Constellation Satellite Selection. In Proceedings of the 2018 IEEE 4th International Conference on Computer and Communications, ICCC 2018, Chengdu, China, 7–10 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2200–2204. [Google Scholar]
  24. Meng, F.; Zhu, B.; Wang, S. A New Fast Satellite Selection Algorithm for BDS-GPS Receivers. In Proceedings of the SiPS 2013 Proceedings, Taipei, Taiwan, 16–18 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 371–376. [Google Scholar]
  25. Jwo, D.-J. Efficient DOP Calculation for GPS with and without Altimeter Aiding. J. Navig. 2001, 54, 269–279. [Google Scholar] [CrossRef]
  26. Hong, Y.; Xu, S. A Navigation Satellite Selection Method Based on Optimized DPSO Algorithm. In Proceedings of the 2020 IEEE 6th Intl Conference on Big Data Security on Cloud (BigDataSecurity), IEEE Intl Conference on High Performance and Smart Computing, (HPSC) and IEEE Intl Conference on Intelligent Data and Security (IDS), Baltimore, MD, USA, 25–27 May 2020; pp. 174–179. [Google Scholar]
  27. Abedi, A.A.; Mosavi, M.R.; Mohammadi, K. A New Recursive Satellite Selection Method for Multi-Constellation GNSS. Surv. Rev. 2020, 52, 330–340. [Google Scholar] [CrossRef]
  28. Xia, J.; Wang, Y.; Li, Y. A Navigation Satellite Selection Method Based on Tabu Search Artificial Bee Colony Algorithm. In Proceedings of the IEEE 3rd International Conference on Electronic Information and Communication Technology (ICEICT), Shenzhen, China, 13–15 November 2020; pp. 421–425. [Google Scholar]
  29. Mosavi, M.R.; Shiroie, M. Efficient Evolutionary Algorithms for GPS Satellites Classification. Arab. J. Sci. Eng. 2012, 37, 2003–2015. [Google Scholar] [CrossRef]
  30. Doong, S.H. A Closed-Form Formula for GPS GDOP Computation. GPS Solut. 2009, 13, 183–190. [Google Scholar] [CrossRef]
  31. Wu, C.H.; Su, W.H. A Comparative Study on Regression Models of GPS GDOP Using Soft-Computing Techniques. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju, Republic of Korea, 20–24 August 2009; pp. 1513–1516. [Google Scholar] [CrossRef]
  32. Habboub, M.; Psimoulis, P.A.; Bingley, R.; Rothacher, M. A Multiple Algorithm Approach to the Analysis of GNSS Coordinate Time Series for Detecting Geohazards and Anomalies. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018104. [Google Scholar] [CrossRef]
  33. Sairo, H.; Akopian, D.; Takala, J. Weighted Dilution of Precision as Quality Measure in Satellite Positioning. IEE Proc. Radar Sonar Navig. 2003, 150, 430–436. [Google Scholar] [CrossRef]
  34. Rost, C.; Wanninger, L. Carrier Phase Multipath Mitigation Based on GNSS Signal Quality Measurements. J. Appl. Geod. 2009, 3, 81–87. [Google Scholar] [CrossRef]
  35. Madonsela, B.; Davidson, I.; Mukubwa, E. The Use of the Carrier to Noise Ratios (C/N0) to Alleviate the Problematic GNSS Phase Multipath. In Proceedings of the 2022 30th Southern African Universities Power Engineering Conference (SAUPEC 2022), Durban, South Africa, 25–27 January 2022; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2022. [Google Scholar]
  36. Karaboga, D. An Idea Based on Honey Bee Swarm For Numerical Optimization. Tech. Rep. TR06 Erciyes Univ. Eng. Fac. Comput. Eng. Dep. 2005, 200, 1–10. [Google Scholar] [CrossRef]
  37. Abu-Mouti, F.S.; El-Hawary, M.E. Overview of Artificial Bee Colony (ABC) Algorithm and Its Applications. In Proceedings of the 2012 IEEE International Systems Conference SysCon 2012, Vancouver, BC, Canada, 19–22 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
  38. Pian, J.; Wang, G.; Li, B. An Improved ABC Algorithm Based on Initial Population and Neighborhood Search. IFAC-Pap 2018, 51, 251–256. [Google Scholar] [CrossRef]
  39. Zhu, G.; Kwong, S. Gbest-Guided Artificial Bee Colony Algorithm for Numerical Function Optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
  40. Dorigo, M.; Maniezzo, V.; Colorni, A. Ant System: Optimization by a Colony of Cooperating Agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
  41. Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLoS ONE 2015, 10, e0122827. [Google Scholar] [CrossRef] [PubMed]
  42. Dai, X.; Long, S.; Zhang, Z.; Gong, D. Mobile Robot Path Planning Based on Ant Colony Algorithm with A∗ Heuristic Method. Front. Neurorobot. 2019, 13, 15. [Google Scholar] [CrossRef]
  43. Wang, W.; Zhao, J.; Li, Z.; Huang, J. Smooth Path Planning of Mobile Robot Based on Improved Ant Colony Algorithm. J. Robot. 2021, 2021, 4109821. [Google Scholar] [CrossRef]
  44. Simon, D. Evolutionary Optimization Algorithms; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013; ProQuest Ebook Central; Available online: https://ebookcentral.proquest.com/lib/nottingham/detail.action?docID=1216196 (accessed on 14 May 2024).
  45. Yang, X.-S. Nature-Inspired Optimization Algorithms, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2014; ProQuest Ebook Central; Available online: https://ebookcentral.proquest.com/lib/nottingham/detail.action?docID=1637335 (accessed on 10 May 2024).
  46. Yang, L.; Yang, X.; Wu, Y.; Liu, X. Applied Research on Distributed Generation Optimal Allocation Based on Improved Estimation of Distribution Algorithm. Energies 2018, 11, 2363. [Google Scholar] [CrossRef]
  47. Li, Q.; Liu, S.Y.; Yang, X.S. Influence of Initialization on the Performance of Metaheuristic Optimizers. Appl. Soft Comput. J. 2020, 91, 106193. [Google Scholar] [CrossRef]
  48. Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
  49. Lee, K.Y.; Park, J.-B. Application of Particle Swarm Optimization to Economic Dispatch Problem: Advantages and Disadvantages. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 188–192. [Google Scholar]
  50. Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
  51. Li, M.; Du, W.; Nian, F. An Adaptive Particle Swarm Optimization Algorithm Based on Directed Weighted Complex Network. Math. Probl. Eng. 2014, 2014, 434972. [Google Scholar] [CrossRef]
  52. Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
  53. Aydin, L.; Artem, H.S. Design and Optimization of Fiber Composites. In Fiber Technology for Fiber-Reinforced Composites; Elsevier: Amsterdam, The Netherlands, 2017; pp. 299–315. ISBN 9780081009932. [Google Scholar]
  54. Austbø, B.; Wahl, P.E.; Gundersen, T. Constraint Handling in Stochastic Optimization Algorithms for Natural Gas Liquefaction Processes. In 23 European Symposium On Computer Aided Process Engineering; Elsevier: Amsterdam, The Netherlands, 2013; Volume 32, pp. 445–450. [Google Scholar]
  55. Strasser, S.; Goodman, R.; Sheppard, J.; Butcher, S. A New Discrete Particle Swarm Optimization Algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016. [Google Scholar] [CrossRef]
  56. Zhao, D.; Cai, C.; Li, L. A Binary Discrete Particle Swarm Optimization Satellite Selection Algorithm with a Queen Informant for Multi-GNSS Continuous Positioning. Adv. Space Res. 2021, 68, 3521–3530. [Google Scholar] [CrossRef]
  57. Chen, Q.; Peng, Y.; Zhang, M.; Yin, Q. Application Analysis on PSO Algorithm in the Discrete Optimization Problems. J. Phys. Conf. Ser. 2021, 2078, 012018. [Google Scholar] [CrossRef]
  58. Eiben, Á.E.; Hinterding, R.; Michalewicz, Z. Parameter Control in Evolutionary Algorithms. IEEE Trans. Evol. Comput. 1999, 3, 124–141. [Google Scholar] [CrossRef]
  59. Krink, T.; Ursem, R.K. Parameter Control Using the Agent Based Patchwork Model. In Proceedings of the 2000 Congress on Evolutionary Computation, CEC 2000, La Jolla, CA, USA, 16–19 July 2000; IEEE Computer Society: Piscataway, NJ, USA, 2000; Volume 1, pp. 77–83. [Google Scholar]
  60. de Andrade, L.N.; Mauri, G.R.; Mendonça, A.S.F. General Multiobjective Model and Simulated Annealing Algorithm for Waste-Load Allocation. J. Water Resour. Plan Manag. 2013, 139, 339–344. [Google Scholar] [CrossRef]
  61. Meng, X.; Nie, P.; Sun, J.; Niu, Z.; Zhu, B. A Novel Satellite Selection Method Based On Genetic Algorithm. In Proceedings of the 2018 11th UK-Europe-China Workshop on Millimeter Waves and Terahertz Technologies (UCMMT), Hangzhou, China, 5–7 September 2018; Volume 1, pp. 1–3. [Google Scholar]
  62. Faisal, S.F.; Beig, A.R.; Thomas, S. Time Domain Particle Swarm Optimization of PI Controllers for Bidirectional VSC HVDC Light System. Energies 2020, 13, 866. [Google Scholar] [CrossRef]
  63. Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. Population Size in Particle Swarm Optimization. Swarm. Evol. Comput. 2020, 58, 100718. [Google Scholar] [CrossRef]
  64. Veček, N.; Liu, S.H.; Črepinšek, M.; Mernik, M. On the Importance of the Artificial Bee Colony Control Parameter ‘Limit’. Inf. Technol. Control 2017, 46, 566–604. [Google Scholar] [CrossRef]
  65. Wang, E.; Sun, C.; Wang, C.; Qu, P.; Huang, Y.; Pang, T. A Satellite Selection Algorithm Based on Adaptive Simulated Annealing Particle Swarm Optimization for the BeiDou Navigation Satellite System/Global Positioning System Receiver. Int. J. Distrib. Sens. Netw. 2021, 17, 155014772110317. [Google Scholar] [CrossRef]
  66. Tsoy, Y.R. The Influence of Population Size and Search Time Limit on Genetic Algorithm. In Proceedings of the 7th Korea-Russia International Symposium on Science and Technology, Proceedings KORUS 2003, (IEEE Cat. No. 03EX737), Ulsan, Republic of Korea, 28 June–6 July 2003; pp. 181–187. [Google Scholar]
  67. Xue, C.; Psimoulis, P.A. Monitoring the Dynamic Response of a Pedestrian Bridge by Using Low-Cost GNSS Receivers. Eng. Struct. 2023, 284, 115993. [Google Scholar] [CrossRef]
  68. Psimoulis, P.A.; Houlié, N.; Habboub, M.; Michel, C.; Rothacher, M. Detection of Ground Motions Using High-Rate GPS Time-Series. Geophys. J. Int. 2018, 214, 1237–1251. [Google Scholar] [CrossRef]
Remotesensing 16 01794 g001
Figure 1. Representation of the ABC searching process and the roles of employed scout and onlooker bees.
Figure 1. Representation of the ABC searching process and the roles of employed scout and onlooker bees.
Remotesensing 16 01794 g001
Remotesensing 16 01794 g002
Figure 2. Schematic representation of the solution building process by ants in ACO.
Figure 2. Schematic representation of the solution building process by ants in ACO.
Remotesensing 16 01794 g002
Remotesensing 16 01794 g003
Figure 3. Representation of the GA processing steps.
Figure 3. Representation of the GA processing steps.
Remotesensing 16 01794 g003
Remotesensing 16 01794 g004
Figure 4. Representation of PSO travelling technique for the solution optimization.
Figure 4. Representation of PSO travelling technique for the solution optimization.
Remotesensing 16 01794 g004
Remotesensing 16 01794 g005
Figure 5. Schematic representation of SA algorithm procedure.
Figure 5. Schematic representation of SA algorithm procedure.
Remotesensing 16 01794 g005
Remotesensing 16 01794 g006
Figure 6. Time period of satellites’ mean movement by one degree, considering satellite azimuth and elevation angles.
Figure 6. Time period of satellites’ mean movement by one degree, considering satellite azimuth and elevation angles.
Remotesensing 16 01794 g006
Remotesensing 16 01794 g007
Figure 7. (Left) View of the roof of NGI building, with the location of control point NGB2 and (right) the GNSS antenna installed on the top of the pillar of NGB2.
Figure 7. (Left) View of the roof of NGI building, with the location of control point NGB2 and (right) the GNSS antenna installed on the top of the pillar of NGB2.
Remotesensing 16 01794 g007
Remotesensing 16 01794 g008
Figure 8. Number of available GNSS satellites at NGB2 GNSS station for a 24 h period on 20 September 2021.
Figure 8. Number of available GNSS satellites at NGB2 GNSS station for a 24 h period on 20 September 2021.
Remotesensing 16 01794 g008
Remotesensing 16 01794 g009
Figure 9. Sample of the file of the GPS data information, which includes (i) date–time, (ii) satellite PRN, (iii) azimuth, (iv) elevation angle, and (v) CNR (in dB-Hz).
Figure 9. Sample of the file of the GPS data information, which includes (i) date–time, (ii) satellite PRN, (iii) azimuth, (iv) elevation angle, and (v) CNR (in dB-Hz).
Remotesensing 16 01794 g009
Remotesensing 16 01794 g010
Figure 10. The possible combinations of satellite constellations for (left) GPS-only in the cases of 8 and 13 available GPS satellites and (right) multi-GNSS satellite constellation in the case of 18 and 31 available GNSS satellites.
Figure 10. The possible combinations of satellite constellations for (left) GPS-only in the cases of 8 and 13 available GPS satellites and (right) multi-GNSS satellite constellation in the case of 18 and 31 available GNSS satellites.
Remotesensing 16 01794 g010
Remotesensing 16 01794 g011
Figure 11. (Left) The quality of match (accuracy) of the selection of the optimal GPS satellite subset by the optimization algorithms with respect to the actual optimal GPS satellite subset derived by the TM. (Right) The time required for the TM and the optimization algorithms to perform optimal GPS satellite subset selection.
Figure 11. (Left) The quality of match (accuracy) of the selection of the optimal GPS satellite subset by the optimization algorithms with respect to the actual optimal GPS satellite subset derived by the TM. (Right) The time required for the TM and the optimization algorithms to perform optimal GPS satellite subset selection.
Remotesensing 16 01794 g011
Remotesensing 16 01794 g012
Figure 12. The comparison of the performance of the optimization algorithms with respect to TM, expressed as the difference between the CNR-WGDOP of the optimal satellite constellation of each optimization algorithm and the corresponding CNR-WDGOP of TM. The results of the four cases of GPS satellite constellations (4, 5, 6, and 7 satellites) are presented. On the left axis, the CNR-WGDOP value of the optimal satellite constellation based on the TM is presented, and on the right axis is the difference between each of the optimization algorithms and the TM.
Figure 12. The comparison of the performance of the optimization algorithms with respect to TM, expressed as the difference between the CNR-WGDOP of the optimal satellite constellation of each optimization algorithm and the corresponding CNR-WDGOP of TM. The results of the four cases of GPS satellite constellations (4, 5, 6, and 7 satellites) are presented. On the left axis, the CNR-WGDOP value of the optimal satellite constellation based on the TM is presented, and on the right axis is the difference between each of the optimization algorithms and the TM.
Remotesensing 16 01794 g012
Remotesensing 16 01794 g013
Figure 13. The sky plots of epoch 55 (left) and epoch 184 (right) presenting the selection of the optimal GPS satellite subset by the ACO and the TM, and showing the satellites commonly selected (blue) by the two methods, but also those that were differently selected by ACO (yellow) and TM (orange).
Figure 13. The sky plots of epoch 55 (left) and epoch 184 (right) presenting the selection of the optimal GPS satellite subset by the ACO and the TM, and showing the satellites commonly selected (blue) by the two methods, but also those that were differently selected by ACO (yellow) and TM (orange).
Remotesensing 16 01794 g013
Remotesensing 16 01794 g014
Figure 14. Same as Figure 13, this figure presents the sky plots for epoch 81 (left) and epoch 215 (right), as well as differences between the selection of the optimal GPS satellite subset for PSO and TM.
Figure 14. Same as Figure 13, this figure presents the sky plots for epoch 81 (left) and epoch 215 (right), as well as differences between the selection of the optimal GPS satellite subset for PSO and TM.
Remotesensing 16 01794 g014
Remotesensing 16 01794 g015
Figure 15. (Left) The accuracy of the selection of the optimal GNSS satellite subset of ABC with respect to TM for the various cases of satellite constellations and parameter settings and (right) the required time of the TM and ABC algorithm to compute the selection of optimal GNSS satellite subset.
Figure 15. (Left) The accuracy of the selection of the optimal GNSS satellite subset of ABC with respect to TM for the various cases of satellite constellations and parameter settings and (right) the required time of the TM and ABC algorithm to compute the selection of optimal GNSS satellite subset.
Remotesensing 16 01794 g015
Remotesensing 16 01794 g016
Figure 16. A comparison of the performance of the ABC algorithm for the three sets of parameter settings with respect to TM, expressed as the difference between the CNR-WGDOP of the optimal satellite constellation of each ABC parameter setting and the corresponding CNR-WDGOP of TM. On the left axis, the CNR-WGDOP value of the optimal satellite constellation based on the TM is presented, and on the right axis is the difference between each of the ABC parameter settings and the TM.
Figure 16. A comparison of the performance of the ABC algorithm for the three sets of parameter settings with respect to TM, expressed as the difference between the CNR-WGDOP of the optimal satellite constellation of each ABC parameter setting and the corresponding CNR-WDGOP of TM. On the left axis, the CNR-WGDOP value of the optimal satellite constellation based on the TM is presented, and on the right axis is the difference between each of the ABC parameter settings and the TM.
Remotesensing 16 01794 g016
Remotesensing 16 01794 g017
Figure 17. Sky plots of epochs 20 (left) and 88 (right), presenting the difference in the selection of optimal GNSS satellite subset between ABC setting 1 and the actual TM, by showing the common satellites (blue) and the differences between ABC’s (yellow) and TM’s (orange) satellite selection.
Figure 17. Sky plots of epochs 20 (left) and 88 (right), presenting the difference in the selection of optimal GNSS satellite subset between ABC setting 1 and the actual TM, by showing the common satellites (blue) and the differences between ABC’s (yellow) and TM’s (orange) satellite selection.
Remotesensing 16 01794 g017
Table 2. ABC parameter values.
Table 2. ABC parameter values.
SettingmaxIterpSizeLimit
1100100D × pSize
2100200D × pSize
3200200D × pSize
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Alluhaybi, A.; Psimoulis, P.; Remenyte-Prescott, R. An Evaluation of Optimization Algorithms for the Optimal Selection of GNSS Satellite Subsets. Remote Sens. 2024, 16, 1794. https://doi.org/10.3390/rs16101794

AMA Style

Alluhaybi A, Psimoulis P, Remenyte-Prescott R. An Evaluation of Optimization Algorithms for the Optimal Selection of GNSS Satellite Subsets. Remote Sensing. 2024; 16(10):1794. https://doi.org/10.3390/rs16101794

Chicago/Turabian Style

Alluhaybi, Abdulaziz, Panos Psimoulis, and Rasa Remenyte-Prescott. 2024. "An Evaluation of Optimization Algorithms for the Optimal Selection of GNSS Satellite Subsets" Remote Sensing 16, no. 10: 1794. https://doi.org/10.3390/rs16101794

APA Style

Alluhaybi, A., Psimoulis, P., & Remenyte-Prescott, R. (2024). An Evaluation of Optimization Algorithms for the Optimal Selection of GNSS Satellite Subsets. Remote Sensing, 16(10), 1794. https://doi.org/10.3390/rs16101794

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop