Evaluation of Satellite-Based Rainfall Estimates against Rain Gauge Observations across Agro-Climatic Zones of Nigeria, West Africa
Abstract
1. Introduction
2. Data and Methods
2.1. Datasets
2.1.1. Satellite-Based Rainfall Estimates (SREs)
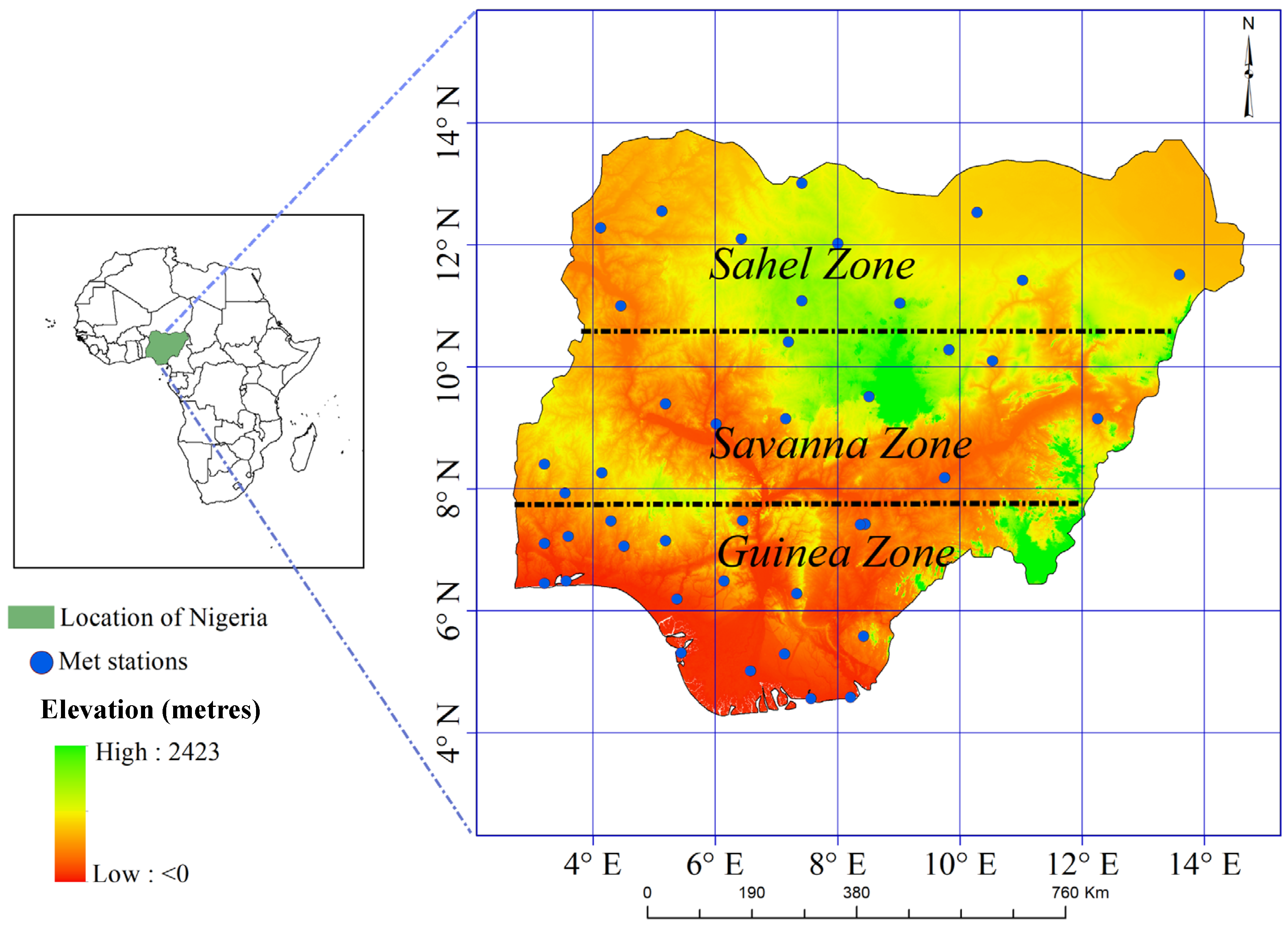
2.1.2. Rain Gauge Observations
2.2. Methodology
2.2.1. Evaluation Metrics
2.2.2. Categorical Skill Metrics
3. Results
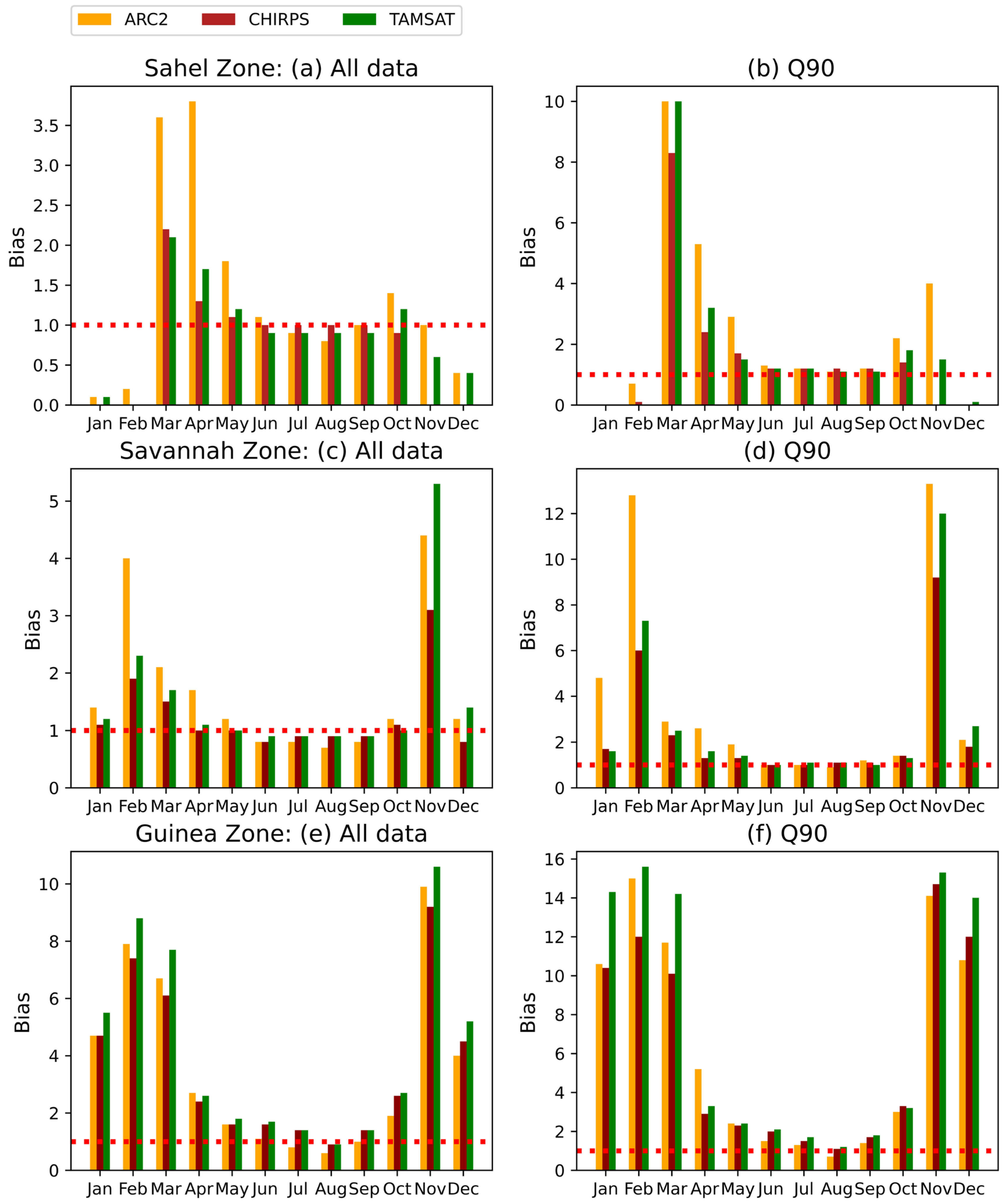
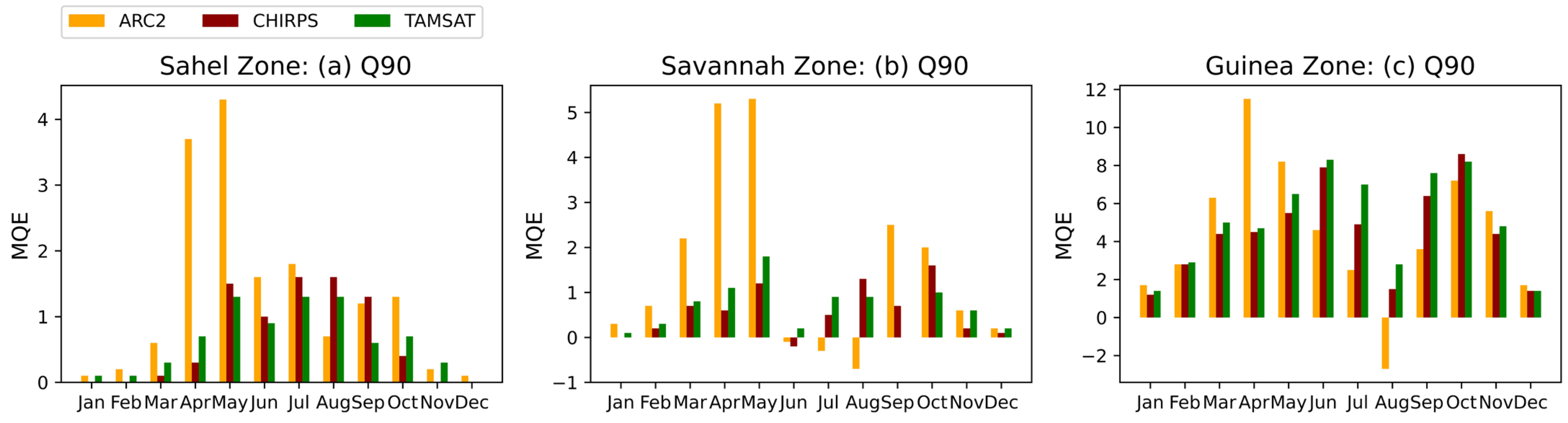
3.1. Evaluation of SREs for Estimating Rainfall
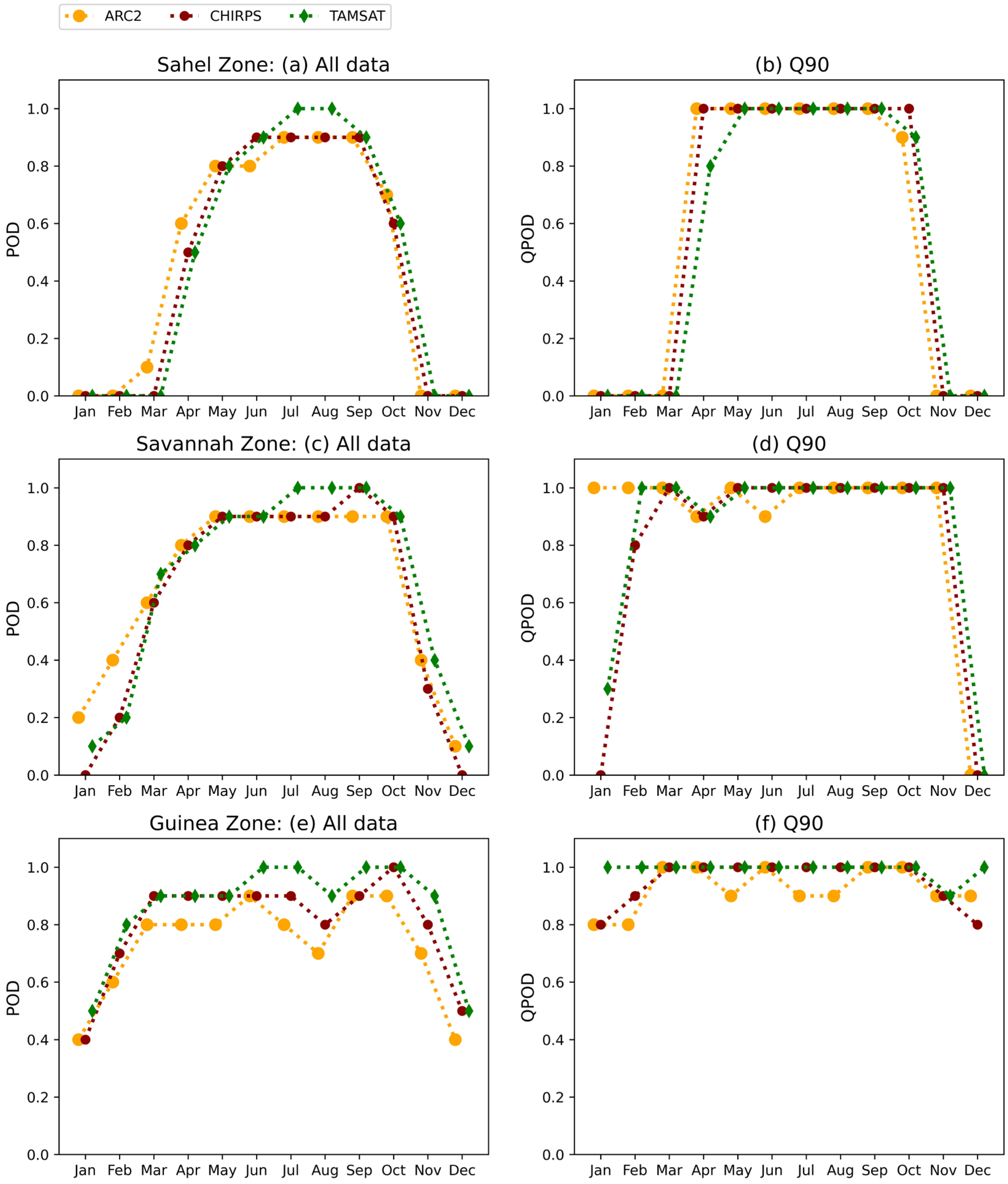
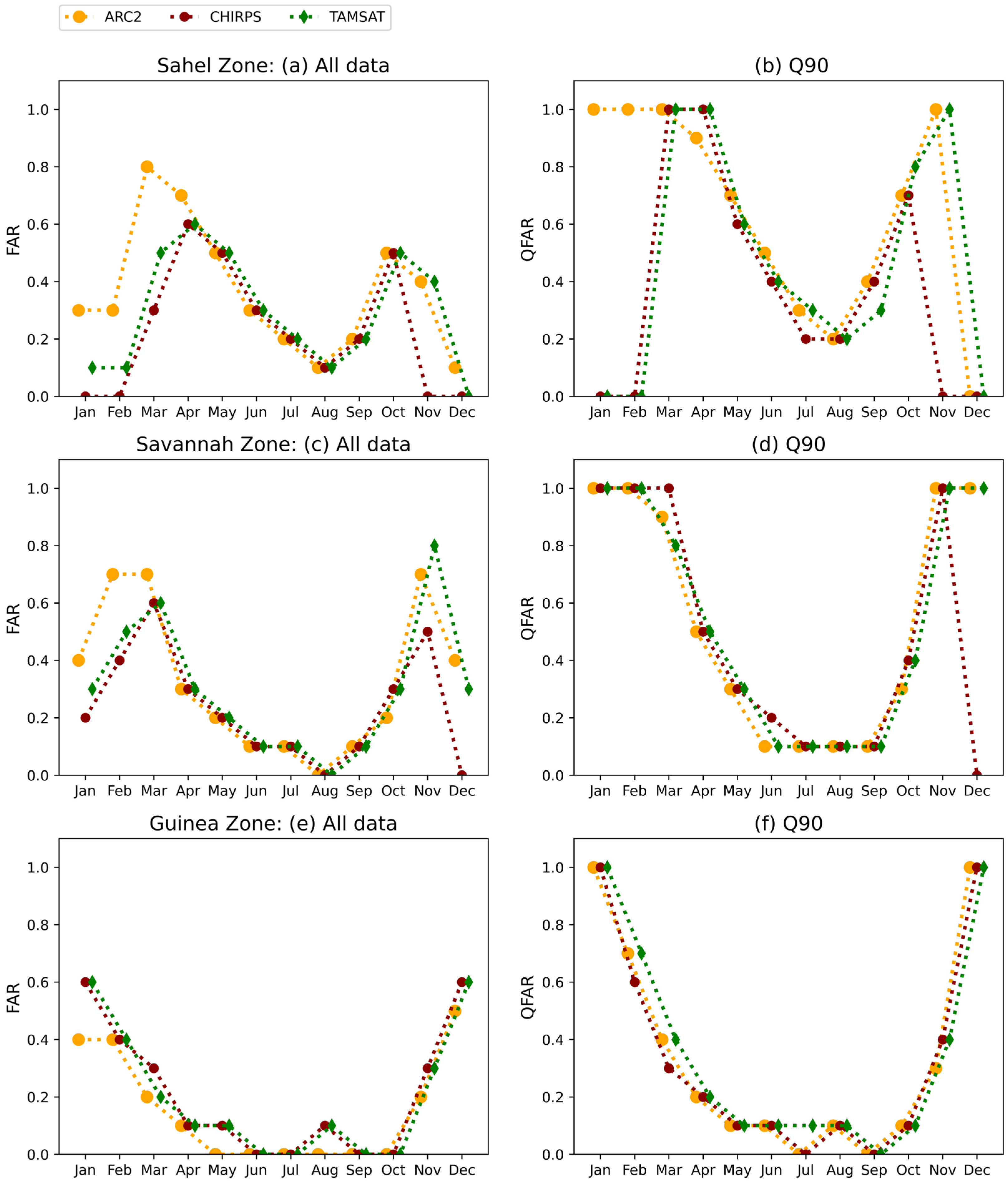
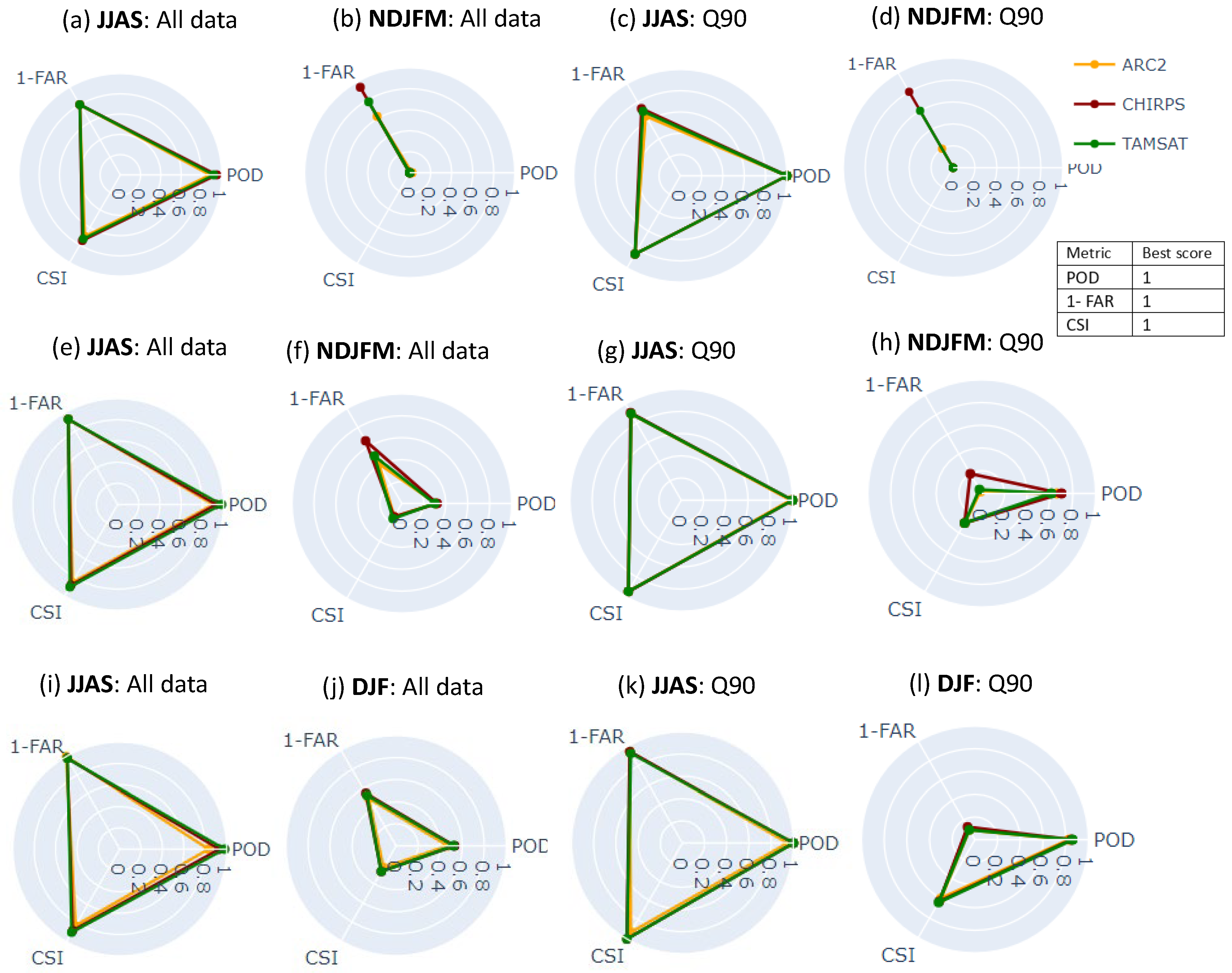
3.2. Performance Evaluation of SREs Detection Capability
Seasonal Variability of Satellite Rainfall Algorithm Skills
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aghakouchak, A.; Behrangi, A.; Sorooshian, S.; Hsu, K.; Amitai, E. Evaluation of Satellite-Retrieved Extreme Precipitation Rates across the Central United States. J. Geophys. Res. Atmos. 2011, 116, D02115. [Google Scholar] [CrossRef]
- Ogbu, K.N.; Hounguè, N.R.; Gbode, I.E.; Tischbein, B. Performance Evaluation of Satellite-Based Rainfall Products over Nigeria. Climate 2020, 8, 103. [Google Scholar] [CrossRef]
- Dembélé, M.; Zwart, S.J. Evaluation and Comparison of Satellite-Based Rainfall Products in Burkina Faso, West Africa. Int. J. Remote Sens. 2016, 37, 3995–4014. [Google Scholar] [CrossRef]
- Fall, C.M.N.; Lavaysse, C.; Drame, M.S.; Panthou, G.; Gaye, A.T. Wet and Dry Spells in Senegal: Evaluation of Satellite-Based and Model Re-Analysis Rainfall Estimates. Nat. Hazards Earth Syst. Sci. 2019, 21, 1051–1069. [Google Scholar] [CrossRef]
- Roehrig, R.; Chauvin, F.; Lafore, J.P. 10-25-Day Intraseasonal Variability of Convection over the Sahel: A Role of the Saharan Heat Low and Midlatitudes. J. Clim. 2011, 24, 5863–5878. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Qin, G.; Huang, Y.; Qi, Y. Evaluation of Satellite-Based Precipitation Products over Complex Topography in Mountainous Southwestern China. Remote Sens. 2023, 15, 473. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Wen, J.; Fan, Z.; Chen, Y.; Scaioni, M.; Wang, J. Evaluation of Satellite-Based Products for Extreme Rainfall Estimations in the Eastern Coastal Areas of China. J. Integr. Environ. Sci. 2019, 16, 191–207. [Google Scholar] [CrossRef]
- Logah, F.Y.; Adjei, K.A.; Obuobie, E.; Gyamfi, C.; Odai, S.N. Evaluation and Comparison of Satellite Rainfall Products in the Black Volta Basin. Environ. Process. 2021, 8, 119–137. [Google Scholar] [CrossRef]
- Polong, F.; Pham, Q.B.; Anh, D.T.; Rahman, K.U.; Shahid, M.; Alharbi, R.S. Evaluation and Comparison of Four Satellite-Based Precipitation Products over the Upper Tana River Basin. Int. J. Environ. Sci. Technol. 2023, 20, 843–858. [Google Scholar] [CrossRef]
- Xie, Z.; Yao, Y.; Tang, Q.; Liu, M.; Fisher, J.B.; Chen, J.; Zhang, X.; Jia, K.; Li, Y.; Shang, K.; et al. Evaluation of Seven Satellite-Based and Two Reanalysis Global Terrestrial Evapotranspiration Products. J. Hydrol. 2024, 630, 130649. [Google Scholar] [CrossRef]
- Mekonnen, K.; Melesse, A.M.; Woldesenbet, T.A. Spatial Evaluation of Satellite-Retrieved Extreme Rainfall Rates in the Upper Awash River Basin, Ethiopia. Atmos. Res. 2021, 249, 105297. [Google Scholar] [CrossRef]
- Romilly, T.G.; Gebremichael, M. Evaluation of Satellite Rainfall Estimates over Ethiopian River Basins. Hydrol. Earth Syst. Sci. 2011, 15, 1505–1514. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Maathuis, B.; Adem, A.A.; Demissie, S.S.; Langan, S.; Steenhuis, T.S. Comparison of Rainfall Estimations by TRMM 3B42, MPEG and CFSR with Ground-Observed Data for the Lake Tana Basin in Ethiopia. Hydrol. Earth Syst. Sci. 2014, 18, 4871–4881. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and Spatial Evaluation of Satellite-Based Rainfall Estimates across the Complex Topographical and Climatic Gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Ribbe, L.; Nauditt, A.; Giraldo-Osorio, J.D.; Thinh, N.X. Temporal and Spatial Evaluation of Satellite Rainfall Estimates over Different Regions in Latin-America. Atmos. Res. 2018, 213, 34–50. [Google Scholar] [CrossRef]
- Mekonnen, K.; Melesse, A.M.; Woldesenbet, T.A. Effect of Temporal Sampling Mismatches between Satellite Rainfall Estimates and Rain Gauge Observations on Modelling Extreme Rainfall in the Upper Awash Basin, Ethiopia. J. Hydrol. 2021, 598, 126467. [Google Scholar] [CrossRef]
- Abiola, S.F.; Mohd-Mokhtar, R.; Ismail, W.; Mohamad, N.; Mandeep, J.S. Categorical Statistical Approach to Satellite Retrieved Rainfall Data Analysis in Nigeria. Sci. Res. Essays 2013, 8, 2123–2137. [Google Scholar] [CrossRef][Green Version]
- Akinyemi, D.F.; Ayanlade, O.S.; Nwaezeigwe, J.O.; Ayanlade, A. A Comparison of the Accuracy of Multi-Satellite Precipitation Estimation and Ground Meteorological Records Over Southwestern Nigeria. Remote Sens. Earth Syst. Sci. 2020, 3, 1–12. [Google Scholar] [CrossRef]
- Nwachukwu, P.N.; Satge, F.; El Yacoubi, S.; Pinel, S.; Bonnet, M.P. From Trmm to GPM: How Reliable Are Satellite-Based Precipitation Data across Nigeria? Remote Sens. 2020, 12, 3964. [Google Scholar] [CrossRef]
- Ogunjo, S.T.; Olusegun, C.F.; Fuwape, I.A. Evaluation of Monthly Precipitation Data from Three Gridded Climate Data Products over Nigeria. Remote Sens. Earth Syst. Sci. 2022, 5, 119–128. [Google Scholar] [CrossRef]
- Salami, A.; Fenta, A.A. Spatio-Temporal Evaluation of Open Access Precipitation Products with Rain Gauge Observations in Nigeria. Arab. J. Geosci. 2022, 15, 1785. [Google Scholar] [CrossRef]
- Usman, M.; Nichol, J.E.; Ibrahim, A.T.; Buba, L.F. A Spatio-Temporal Analysis of Trends in Rainfall from Long Term Satellite Rainfall Products in the Sudano Sahelian Zone of Nigeria. Agric. For. Meteorol. 2018, 260–261, 273–286. [Google Scholar] [CrossRef]
- Guo, H.; Li, M.; Nzabarinda, V.; Bao, A.; Meng, X.; Zhu, L.; Maeyer, P. De Assessment of Three Long-Term Satellite-Based Precipitation Estimates against Ground Observations for Drought Characterization in Northwestern China. Remote Sens. 2022, 14, 828. [Google Scholar] [CrossRef]
- Pan, X.; Wu, H.; Chen, S.; Nanding, N.; Huang, Z.; Chen, W.; Li, C.; Li, X. Evaluation and Applicability Analysis of GPM Satellite Precipitation over Mainland China. Remote Sens. 2023, 15, 2866. [Google Scholar] [CrossRef]
- Zhang, W.; Di, Z.; Liu, J.; Zhang, S.; Liu, Z.; Wang, X.; Sun, H. Evaluation of Five Satellite-Based Precipitation Products for Extreme Rainfall Estimations over the Qinghai-Tibet Plateau. Remote Sens. 2023, 15, 5379. [Google Scholar] [CrossRef]
- Novella, N.S.; Thiaw, W.M. African Rainfall Climatology Version 2 for Famine Early Warning Systems. J. Appl. Meteorol. Climatol. 2013, 52, 588–606. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring. U.S. Geol. Surv. Data Ser. 2014, 832, 4. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations-A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T. Validation of the CHIRPS Satellite Rainfall Estimates over Eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Grimes, D.; Maidment, R.; Black, E.; Allan, R.P.; Stringer, M.; Chadwick, R.; Kayitakire, F. Extension of the TAMSAT Satellite-Based Rainfall Monitoring over Africa and from 1983 to Present. J. Appl. Meteorol. Climatol. 2014, 53, 2805–2822. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A New, Long-Term Daily Satellite-Based Rainfall Dataset for Operational Monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef] [PubMed]
- WMO. Guide to Meteorological Instruments and Methods of Observation; WMO: Geneva, Switzerland, 1983; ISBN 9789263100085. [Google Scholar]
- Ogungbenro, S.B.; Morakinyo, T.E. Rainfall Distribution and Change Detection across Climatic Zones in Nigeria. Weather Clim. Extrem. 2014, 5, 1–6. [Google Scholar] [CrossRef]
- Schepanski, K.; Heinold, B.; Tegen, I. Harmattan, Saharan Heat Low, and West African Monsoon Circulation: Modulations on the Saharan Dust Outflow towards the North Atlantic. Atmos. Chem. Phys. 2017, 17, 10223–10243. [Google Scholar] [CrossRef]
- Gbode, I.E.; Adeyeri, O.E.; Menang, K.P.; Intsiful, J.D.K.; Ajayi, V.O.; Omotosho, J.A.; Akinsanola, A.A. Observed Changes in Climate Extremes in Nigeria. Meteorol. Appl. 2019, 26, 642–654. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; De Roo, A. Validation of Satellite-Based Precipitation Products over Sparsely Gauged African River Basins. J. Hydrometeorol. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.S.; Ashouri, H.; Hsu, K.L.; Sorooshian, S. Trends of Precipitation Extreme Indices over a Subtropical Semi-Arid Area Using PERSIANN-CDR. Theor. Appl. Climatol. 2017, 130, 249–260. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of High-Resolution Satellite Rainfall Products over Complex Terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M.; Ghebremichael, L.T.; Bayissa, Y.A. Evaluation of High-Resolution Satellite Rainfall Products through Streamflow Simulation in a Hydrological Modeling of a Small Mountainous Watershed in Ethiopia. J. Hydrometeorol. 2012, 13, 338–350. [Google Scholar] [CrossRef]
- Reddy, M.V.; Mitra, A.K.; Momin, I.M.; Mitra, A.K.; Pai, D.S. Evaluation and Inter-Comparison of High-Resolution Multi-Satellite Rainfall Products over India for the Southwest Monsoon Period. Int. J. Remote Sens. 2019, 40, 4577–4603. [Google Scholar] [CrossRef]
- Reddy, N.M.; Saravanan, S. Evaluation of the Accuracy of Seven Gridded Satellite Precipitation Products over the Godavari River Basin, India. Int. J. Environ. Sci. Technol. 2023, 20, 10179–10204. [Google Scholar] [CrossRef]
- Perera, H.; Fernando, S.; Gunathilake, M.B.; Sirisena, T.A.J.G.; Rathnayake, U. Evaluation of Satellite Rainfall Products over the Mahaweli River Basin in Sri Lanka. Adv. Meteorol. 2022, 2022, 1926854. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, C.; Yeh, P.J.F.; Li, J.; Hu, B.X.; Feng, P.; Lei, Y. Evaluation of Multi-Satellite Precipitation Products Estimating Precipitation Extremes over Mainland China at Annual, Seasonal and Monthly Scales. Atmos. Res. 2022, 279, 106387. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Mehran, A. Extended Contingency Table: Performance Metrics for Satellite Observations and Climate Model Simulations. Water Resour. Res. 2013, 49, 7144–7149. [Google Scholar] [CrossRef]
- Chidiezie, T.; Shrikant, C. West African Monsoon: Is the August Break “Breaking” in the Eastern Humid Zone of Southern Nigeria ? Clim. Change 2010, 103, 555–570. [Google Scholar] [CrossRef]
- Maranan, M.; Fink, A.H.; Knippertz, P. Rainfall Types over Southern West Africa: Objective Identification, Climatology and Synoptic Environment. Q. J. R. Meteorol. Soc. 2018, 144, 1628–1648. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.L.; Turk, F.J.; Garcia, M.; Zeng, J. Component Analysis of Errors in Satellite-Based Precipitation Estimates. J. Geophys. Res. Atmos. 2009, 114, D24101. [Google Scholar] [CrossRef]
- Kitagawa, M. Stopping Power in a Cylindrical System by the Modified Bessel Function’s Method. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms 2010, 268, 1776–1780. [Google Scholar] [CrossRef]
- Kidd, C.; Bauer, P.; Turk, J.; Huffman, G.J.; Joyce, R.; Hsu, K.L.; Braithwaite, D. Intercomparison of High-Resolution Precipitation Products over Northwest Europe. J. Hydrometeorol. 2012, 13, 67–83. [Google Scholar] [CrossRef]
- Mekonnen, K.; Velpuri, N.M.; Leh, M.; Akpoti, K.; Owusu, A.; Tinonetsana, P.; Hamouda, T.; Ghansah, B.; Paranamana, T.P.; Munzimi, Y. Accuracy of Satellite and Reanalysis Rainfall Estimates over Africa: A Multi-Scale Assessment of Eight Products for Continental Applications. J. Hydrol. Reg. Stud. 2023, 49, 101514. [Google Scholar] [CrossRef]
- Satgé, F.; Defrance, D.; Sultan, B.; Bonnet, M.P.; Seyler, F.; Rouché, N.; Pierron, F.; Paturel, J.E. Evaluation of 23 Gridded Precipitation Datasets across West Africa. J. Hydrol. 2020, 581, 124412. [Google Scholar] [CrossRef]
- Poméon, T.; Jackisch, D.; Diekkrüger, B. Evaluating the Performance of Remotely Sensed and Reanalysed Precipitation Data over West Africa Using HBV Light. J. Hydrol. 2017, 547, 222–235. [Google Scholar] [CrossRef]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of Several Rainfall Products Used for Hydrological Applications over West Africa Using Two High-Resolution Gauge Networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Houngnibo, M.C.M.; Minoungou, B.; Traore, S.B.; Maidment, R.I.; Alhassane, A.; Ali, A. Validation of High-Resolution Satellite Precipitation Products over West Africa for Rainfall Monitoring and Early Warning. Front. Clim. 2023, 5, 1185754. [Google Scholar] [CrossRef]
- Atiah, W.A.; Amekudzi, L.K.; Aryee, J.N.A.; Preko, K.; Danuor, S.K. Validation of Satellite and Merged Rainfall Data over Ghana, West Africa. Atmosphere 2020, 11, 859. [Google Scholar] [CrossRef]
- Garba, J.N.; Diasso, U.J.; Waongo, M.; Sawadogo, W.; Daho, T. Performance Evaluation of Satellite-Based Rainfall Estimation across Climatic Zones in Burkina Faso. Theor. Appl. Climatol. 2023, 154, 1051–1073. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Chavez, E.; Boogaard, H. Sensitivity of an Adapted Water Requirements Satisfaction Index (WRSI) Model to Rainfall. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 77–87. [Google Scholar] [CrossRef]
- Zhang, M.; de Leon, C.; Migliaccio, K. Evaluation and Comparison of Interpolated Gauge Rainfall Data and Gridded Rainfall Data in Florida, USA. Hydrol. Sci. J. 2018, 63, 561–582. [Google Scholar] [CrossRef]



| Rain Gauge | |||
|---|---|---|---|
| Yes (R ) | No () | ||
| SREs | No () | Hits (H) | False alarm (FA) |
| No () | Miss (M) | Correct negatives (CN) | |
| Sahel | Savannah | Guinea | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ARC2 | CHIRPS | TAMSAT | ARC2 | CHIRPS | TAMSAT | ARC2 | CHIRPS | TAMSAT | |
| r | 0.98 | 0.99 | 0.99 | 0.96 | 0.98 | 0.97 | 0.94 | 0.96 | 0.97 |
| Bias | 1.02 | 0.97 | 0.90 | 0.92 | 0.90 | 0.91 | 0.80 | 0.99 | 1.03 |
| ME | 0.75 | −1.17 | −4.0 | 4.86 | −6.52 | −5.47 | 18.82 | −0.85 | 3.08 |
| RMSE | 16.93 | 4.02 | 10.91 | 26.22 | 14.16 | 14.14 | 42.53 | 9.21 | 8.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Datti, A.D.; Zeng, G.; Tarnavsky, E.; Cornforth, R.; Pappenberger, F.; Abdullahi, B.A.; Onyejuruwa, A. Evaluation of Satellite-Based Rainfall Estimates against Rain Gauge Observations across Agro-Climatic Zones of Nigeria, West Africa. Remote Sens. 2024, 16, 1755. https://doi.org/10.3390/rs16101755
Datti AD, Zeng G, Tarnavsky E, Cornforth R, Pappenberger F, Abdullahi BA, Onyejuruwa A. Evaluation of Satellite-Based Rainfall Estimates against Rain Gauge Observations across Agro-Climatic Zones of Nigeria, West Africa. Remote Sensing. 2024; 16(10):1755. https://doi.org/10.3390/rs16101755
Chicago/Turabian StyleDatti, Aminu Dalhatu, Gang Zeng, Elena Tarnavsky, Rosalind Cornforth, Florian Pappenberger, Bello Ahmad Abdullahi, and Anselem Onyejuruwa. 2024. "Evaluation of Satellite-Based Rainfall Estimates against Rain Gauge Observations across Agro-Climatic Zones of Nigeria, West Africa" Remote Sensing 16, no. 10: 1755. https://doi.org/10.3390/rs16101755
APA StyleDatti, A. D., Zeng, G., Tarnavsky, E., Cornforth, R., Pappenberger, F., Abdullahi, B. A., & Onyejuruwa, A. (2024). Evaluation of Satellite-Based Rainfall Estimates against Rain Gauge Observations across Agro-Climatic Zones of Nigeria, West Africa. Remote Sensing, 16(10), 1755. https://doi.org/10.3390/rs16101755





