Estimating the Intensity of Tropical Cyclones from Spiral Signatures Acquired by Spaceborne SAR
Abstract
1. Introduction
- Attenuation due to heavy rain;
- Backscattering from raindrops in the air and ice particles;
- Sea-surface capillary waves induced by rain;
- Damping of sea surface waves by rain-induced turbulence;
- Wind gusts.
2. Data Acquisition and Processing
2.1. Composition of the Dataset
2.2. The Essence of the HLS Assessment
2.2.1. Dependence of the Maximum Wind Speed on HLS Parameters
2.2.2. Logarithmic Component of the HLS and the Crossing Angle
2.3. Data Processing (HLS Approximation)
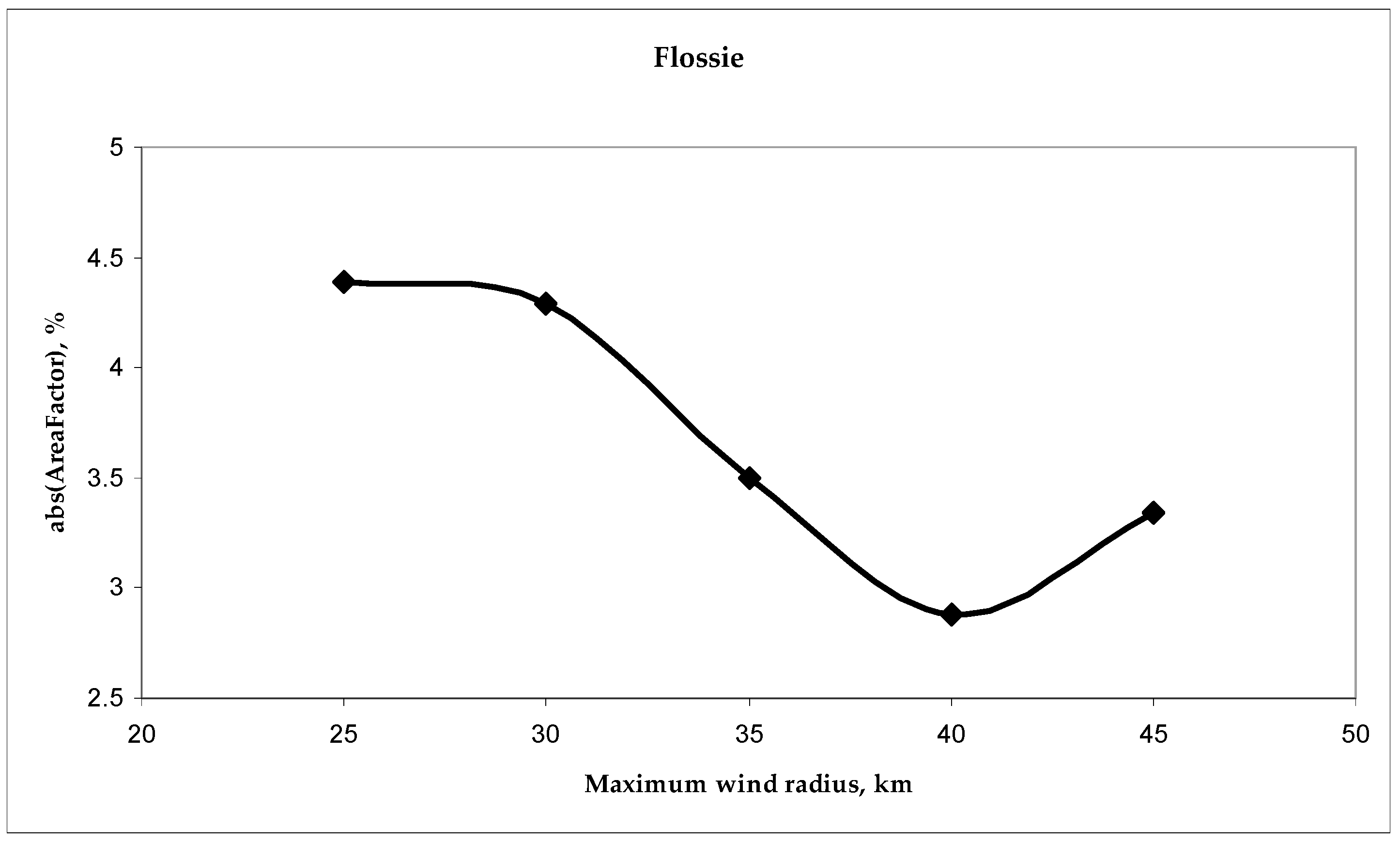
2.4. Estimation of the Radius of Maximum Wind Speed
3. Results
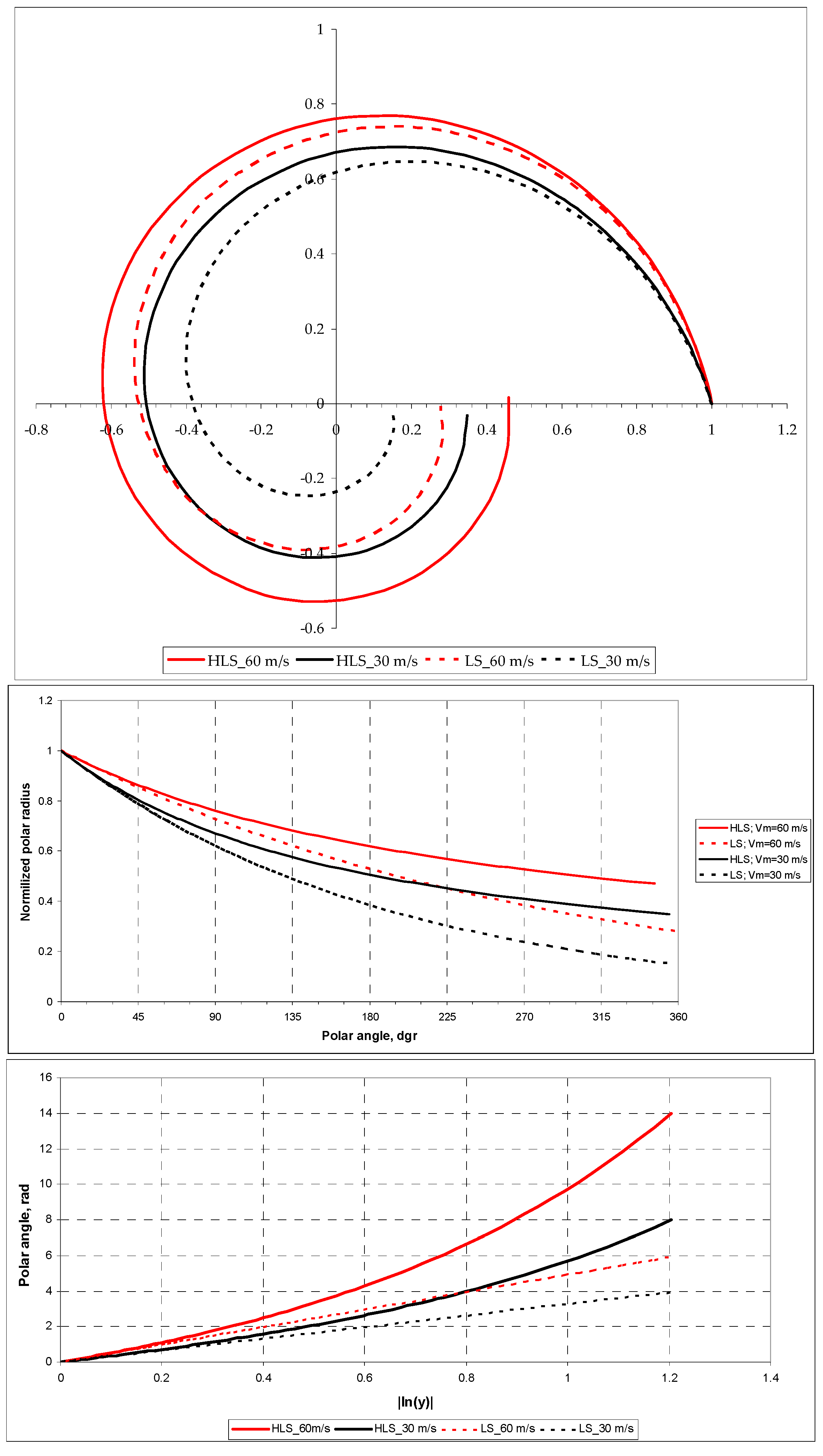
3.1. Results of the HLS Approximation
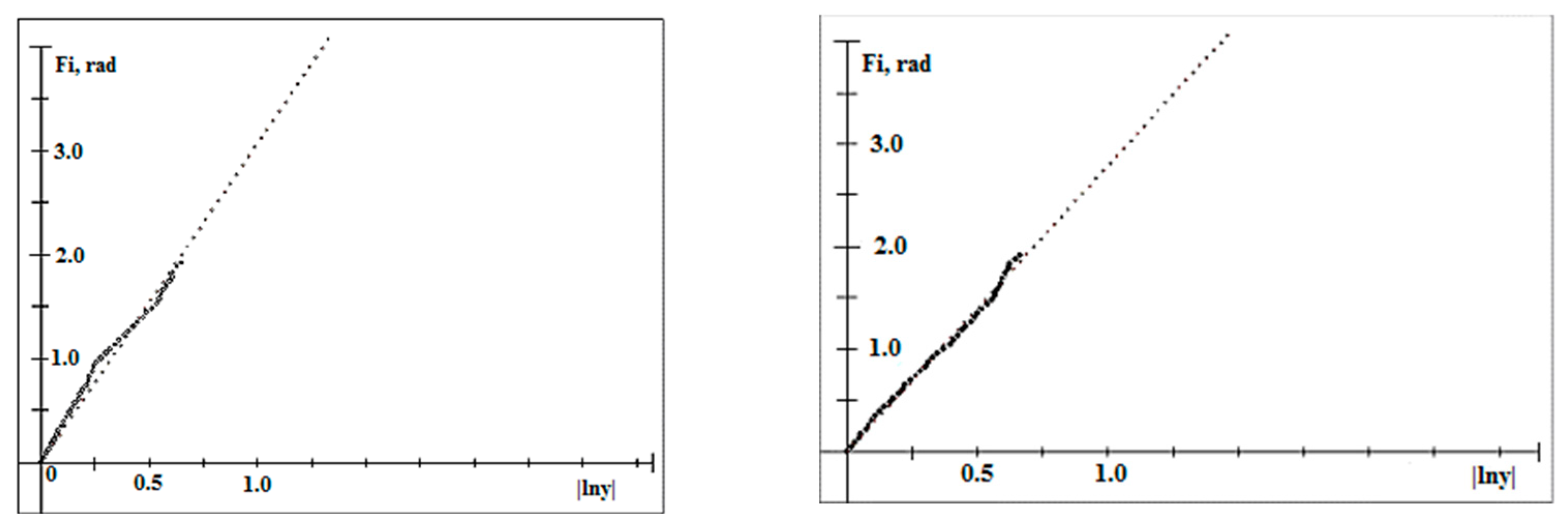
3.2. Logarithmic Approximation of the Edges of Spiral Signatures
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Williams, R.G.; Follows, M.J. Ocean Dynamics and the Carbon Cycle: Principles and Mechanisms; University Press: Cambridge, UK, 2011. [Google Scholar]
- Hasselmann, K.; Raney, R.K.; Plant, W.J.; Alpers, W.; Shuchman, R.A.; Lyzenga, D.A.; Rufenach, C.L.; Tucker, M.J. Theory of Synthetic Aperture Radar ocean imaging: A MARSEN view. J. Geophys. Res. 1985, 90, 4659–4686. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive; Artech House: Reading, MA, USA, 1982; Volume II. [Google Scholar]
- Zhou, X.; Yang, X.F.; Li, Z.W.; Yu, Y.; Bi, H.B.; Ma, S.; Li, X.F. Estimation of Tropical Cyclone Parameters and Wind Fields from SAR Images. Sci. China Earth Sci. 2013, 56, 1977–1987. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.A.; Yang, X.; Pichel, W.G.; DeMaria, M.; Long, D.; Li, Z. Tropical Cyclone Morphology from Spaceborne Synthetic Aperture Radar. Bull. Am. Meteorol. Soc. 2013, 94, 215–230. [Google Scholar] [CrossRef]
- Monaldo, F.M.; Li, X.; Pichel, W.G.; Jackson, C.R. Ocean Wind Speed Climatology from Spaceborne SAR Imagery. Bull. Am. Meteorol. Soc. 2014, 95, 565–569. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Pichel, W.G.; Li, Z. Comparison of Ocean Surface Winds from ENVISAT ASAR, MetOp ASCAT Scatterometer, Buoy Measurements, and NOGAPS Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4743–4750. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W. Cross-Polarized Synthetic Aperture Radar. A New Potential Measurement Technique for Hurricanes. Bull. Am. Meteorol. Soc. 2012, 93, 531–541. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B.; Zhang, B.; Husson, R. Combined Co- and Cross-Polarized SAR Measurements under Extreme Wind Conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B.; Knaff, J.; Zhao, Y.; Zhang, B.; Combot, C. Copolarized and Cross-Polarized SAR Measurements for High-Resolution Description of Major Hurricane Wind Structures: Application to Irma Category 5 Hurricane. J. Geophys. Res. Ocean. 2013, 124, 3905–3922. [Google Scholar] [CrossRef]
- Combot, C.; Mouche, A.; Knaff, J.; Zhao, Y.; Zhao, Y.; Vinour, L.; Quilfen, Y.; Chapron, B. Extensive High-Resolution Synthetic Aperture Radar (SAR) Data Analysis of Tropical Cyclones: Comparison with SFMR Flights and Best Track. Mon. Weather. Rev. 2020, 148, 4545–4563. [Google Scholar] [CrossRef]
- Zhang, G.; Perrie, W.; Yang, J.; He, Y. Monitoring of tropical cyclone structures in ten years of radarsat-2 SAR images. Remote Sens. Environ. 2020, 236, 111449. [Google Scholar] [CrossRef]
- Yu, P.; Xu, W.; Zhong, X.; Johannessen, J.A.; Yan, X.-H.; Geng, X.; He, Y.; Lu, W. A Neural Network Method for Retrieving Sea Surface Wind Speed for C-Band SAR. Remote Sens. 2022, 14, 2269. [Google Scholar] [CrossRef]
- Han, X.; Li, X.; Yang, J.; Wang, J.; Zheng, G.; Ren, L.; Chen, P.; Fang, H.; Xiao, Q. Dual-Level Contextual Attention Generative Adversarial Network for Reconstructing SAR Wind Speeds in Tropical Cyclones. Remote Sens. 2023, 15, 2454. [Google Scholar] [CrossRef]
- Willoughby, H.E. The Dynamics of the Tropical Cyclone Core. Aust. Meteorol. Mag. 1988, 36, 183–191. [Google Scholar]
- Houze, R.A., Jr. Clouds in Tropical Cyclones. Review. Mon. Weather. Rev. 2010, 138, 293–344. [Google Scholar] [CrossRef]
- Yurchak, B.S. Description of cloud-rain bands in a tropical cyclone by a hyperbolic-logarithmic spiral. Russ. Meteorol. Hydrol. 2007, 32, 8–18. [Google Scholar] [CrossRef]
- Yurchak, B.S. The use of a spiral band model to estimate tropical cyclone intensity. In Current Topics in Tropical Cyclone Research; IntechOpen: London, UK, 2019; pp. 1–19. Available online: https://intechopen.com/chapters/68590 (accessed on 14 June 2019). [CrossRef]
- Yurchak, B.S. Estimation of tropical cyclone intensity from the satellite infrared images of its spiral cloud bands. Russ. Meteorol. Hydrol. 2018, 43, 581–590. [Google Scholar] [CrossRef]
- Yurchak, B.S. An estimate of the hurricane’s intensity from radar data using hyperbolic-logarithmic approximation. Int. J. Remote Sens. 2019, 40, 9629–9641. [Google Scholar] [CrossRef]
- Dvorak, V.F. Tropical cyclone intensity analysis and forecasting from satellite imagery. Mon. Weather. Rev. 1975, 103, 420–430. [Google Scholar] [CrossRef]
- Olander, T.L.; Velden, C.S. The advanced Dvorak technique: Continued development of objective scheme to estimate tropical cyclone intensity using geostationary infrared satellite imagery. Weather. Forecast. 2007, 22, 287–298. [Google Scholar] [CrossRef]
- Senn, H.V.; Hiser, H.W.; Low, E.F. Studies of hurricane spiral bands as observed on radar. Final Rep. U.S. Wea. Bur. Contract 1956, 49, Cwb-8735. [Google Scholar]
- Senn, H.V.; Hiser, H.W.; Bourret, R.C. Studies of Hurricane Spiral Bands as Observed on Radar; National Hurricane Research Project Report No. 12; U.S. Weather Bureau: Washington, DC, USA, 1957; 13p. [Google Scholar]
- Senn, H.V.; Hiser, H.W. On the origin of hurricane spiral rain bands. J. Meteorol. 1959, 16, 419–426. [Google Scholar] [CrossRef][Green Version]
- Fernandez, W. Organization and motion of the spiral rainbands in hurricanes. A review. Cienc. Y Technol. 1982, 6, 49–98. [Google Scholar]
- Anthes, R.A. Tropical cyclones. Their evolution, structure and effects. AMS Meteorol. Monogr. 1982, 19, 210. [Google Scholar]
- Lahiri, A. A study of cloud spirals of tropical cyclones. Mausam 1981, 32, 155–158. [Google Scholar] [CrossRef]
- Wong, K.Y.; Yip, C.L.; Li, P.W. A novel algorithm for automatic tropical cyclone fix using Doppler radar data. Meterol. Appl. 2007, 14, 49–59. [Google Scholar] [CrossRef]
- Lajoie, F.; Walsh, K. A diagnostic study of the intensity of three tropical cyclones in the Australian region. Part II: An analytic method for determining the time variation of the intensity of a tropical cyclone. Mon. Wea. Rev. 2010, 138, 22–41. [Google Scholar] [CrossRef]
- Powell, M.D.; Uhlhorn, E.W.; Kepert, J.D. Estimating maximum surface winds from hurricane reconnaissance measurements. Weather Forecast. 2009, 24, 868–883. [Google Scholar] [CrossRef]
- Franklin, J.L. Comments on “Estimating maximum surface winds from hurricane reconnaissance measurements”. Weather Forecast. 2011, 26, 774–776. [Google Scholar] [CrossRef]
- Powell, M.D.; Uhlhorn, E.W.; Kepert, J.D. Reply. Weather Forecast. 2011, 26, 777–779. [Google Scholar] [CrossRef]
- Devore, J.L. Probability and Statistics for Engineering and the Science, 6th ed.; Thomson Learning, Inc.: Toronto, ON, USA, 2004. [Google Scholar]




| # | TC Name | TC Index (YYYYMMDD hhmmss) | Cat. | SAR Scene Center | |
|---|---|---|---|---|---|
| Lat (°N) | Long (°E/−°W) | ||||
| Western Pacific | |||||
| 1 | MEARI | 20040928092545 | I | 29.69 | 128.55 |
| 2 | XANGSANE | 20060930223832 | II | 16.00 | 108.99 |
| 3 | KIROGI | 20051015210400 | III | 24.77 | 132.17 |
| 4 | MAWAR | 20050822203846 | III | 24.81 | 138.48 |
| 5 | EWINIAR | 20060703205345 | III | 14.80 | 133.50 |
| 6 | YAGI | 20060921201753 | V | 23.70 | 143.60 |
| Eastern Pacific | |||||
| 7 | FLOSSIE | 20010830133745 | I | 21.64 | −116.16 |
| 8 | ALMA | 20020530014925 | II | 14.71 | –114.93 |
| 9 | JAVIER | 20040917012033 | III | 21.04 | –108.91 |
| 10 | JOVA | 20050919152220 | III | 15.47 | –143.68 |
| 11 | KENNETH | 20050925032031 | I | 16.69 | –138.41 |
| Atlantic | |||||
| 12 | FRANKLIN | 20050728221603 | TS | 38.20 | –65.43 |
| 13 | KATRINA | 20050828234840 | V | 26.89 | –87.18 |
| 14 | DEAN | 20070819231634 | IV | 14.18 | –61.04 |
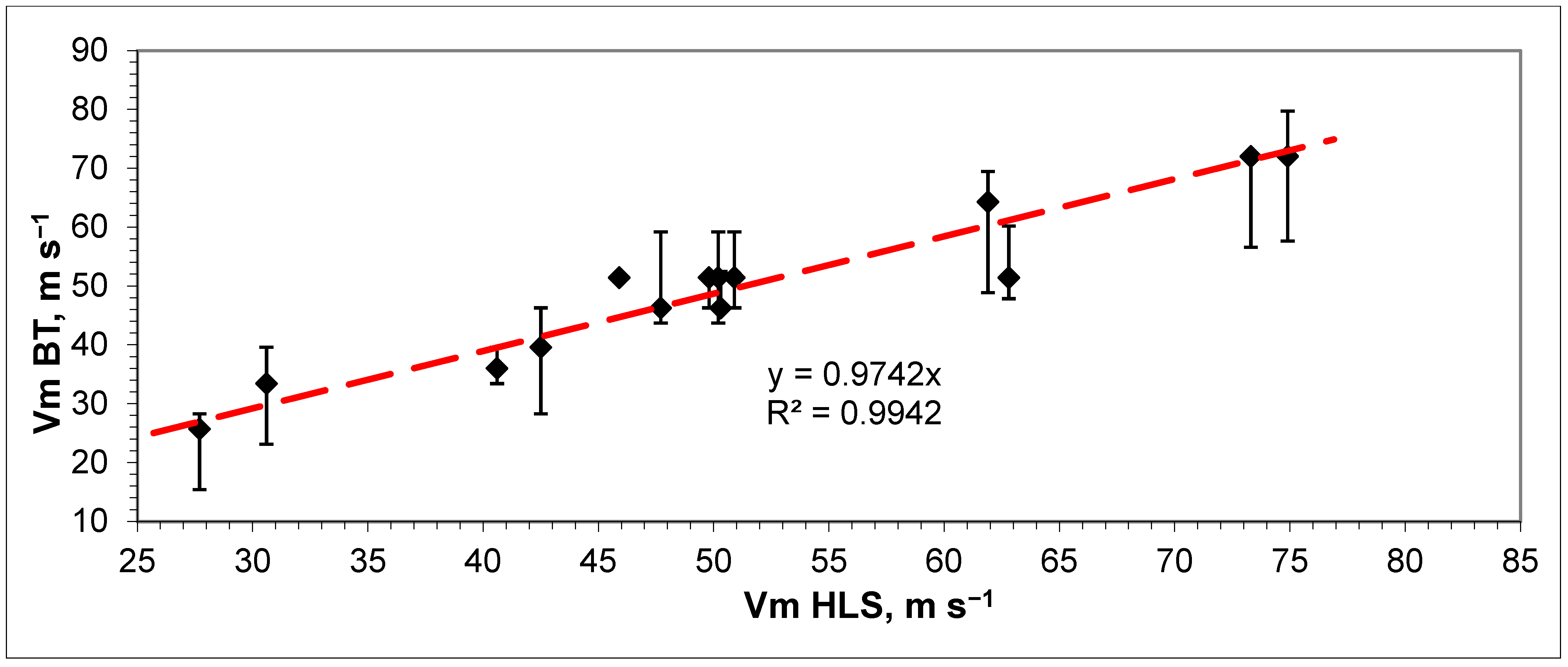
| TC Name | HLS Vm Estimates, m s−1 | Best Tack Vm Estimates, m s−1 | Difference between HLS and BT Estimates of Vm, m s−1 | Optimal Rm, km | |||
|---|---|---|---|---|---|---|---|
| Mean <Vm> | Stdev (Vm) | Vm | ΔVm | ||||
| + | − | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Alma | 50.3 | 20.4 | 46.3 | 6.2 | 0.0 | 4.0 | 30 |
| Dean | 61.9 | 20.0 | 64.3 | 5.1 | 15.4 | −2.4 | 40 |
| Ewiniar | 50.2 | 19.8 | 51.4 | 7.7 | 7.7 | −1.2 | 40 |
| Flossie | 40.6 | 19.6 | 36.0 | 3.6 | 2.6 | 4.6 | 40 |
| Franklin | 27.7 | 13.5 | 25.7 | 2.6 | 2.6 | 2 | 30 |
| Javier | 45.9 | 20.3 | 51.4 | 0.0 | 0.0 | −5.5 | 30 |
| Jova | 49.8 | 20.6 | 51.4 | 0.0 | 5.1 | −1.6 | 35 |
| Katrina | 74.9 | 27.5 | 72.0 | 7.7 | 14.4 | 2.9 | 30 |
| Kenneth | 30.6 | 11.9 | 33.4 | 6.2 | 10.3 | −2.8 | 15 |
| Kirogi | 62.8 | 19.8 | 51.4 | 8.7 | 3.6 | 11.4 * | 30 |
| Mawar | 50.9 | 20.1 | 51.4 | 7.7 | 7.7 | −0.5 | 45 |
| Meary | 42.5 | 20.1 | 39.6 | 6.7 | 11.3 | 2.9 | 50 |
| Xangsane | 57.7 | 18.6 | 46.3 | 12.9 | 2.6 | 1.4 | 30 |
| Yagi | 73.3 | 19.1 | 72.0 | 0.0 | 15.4 | 1.3 | 80 |
| # | TC | HLS Parameters | ym | VC, m s−1 | HLS Equation (11) | Logarithmic Approximation | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| <Vm>, m s−1 | <n> | <B> | ||||||||
| GHLS | GLS | σ | α° | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | Alma | 50.3 | 0.59 | 0.66 | 0.169 | 6.52 | 2.46 | 2.79 | 0.04 | 19.7 |
| 0.143 | 7.7 | 2.04 | 3.07 | 0.09 | 18.0 | |||||
| 2 | Dean | 61.9 | 0.56 | 0.53 | 0.162 | 10.73 | 1.64 | 1.99 | 0.04 | 26.7 |
| 0.149 | 11.71 | 1.50 | 2.82 | 0.03 | 19.5 | |||||
| 3 | Ewiniar | 50.2 | 0.57 | 0.57 | 0.216 | 6.99 | 2.28 | 2.62 | 0.09 | 20.9 |
| 0.191 | 7.91 | 1.98 | 3.2 | 0.07 | 17.4 | |||||
| 4 | Flossie | 40.6 | 0.59 | 1.73 | 0.212 | 10.45 | 4.41 | 4.32 | 0.09 | 13.0 |
| 0.179 | 12.34 | 3.78 | 4.68 | 0.07 | 12.1 | |||||
| 5 | Franklin | 27.7 | 0.59 | 1.3 | 0.163 | 16.41 | 2.05 | 2.15 | 0.04 | 24.9 |
| 0.144 | 18.55 | 1.92 | 2.69 | 0.07 | 20.4 | |||||
| 6 | Javier | 45.9 | 0.56 | 0.54 | 0.141 | 10.9 | 1.30 | 1.46 | 0.06 | 34.4 |
| 0.132 | 11.68 | 1.22 | 1.73 | 0.07 | 30.0 | |||||
| 7 | Jova | 49.8 | 0.56 | 0.56 | 0.197 | 6.82 | 2.19 | 2.52 | 0.02 | 22.4 |
| 0.177 | 7.60 | 1.94 | 3.35 | 0.06 | 17.7 | |||||
| 8 | Katrina | 74.9 | 0.64 | 0.95 | 0.169 | 10.2 | 3.17 | 2.52 | 0.02 | 21.6 |
| 0.148 | 11.66 | 2.73 | 3.35 | 0.06 | 16.6 | |||||
| 9 | Kenneth | 30.6 | 0.59 | 0.45 | 0.378 | 1.63 | 5.20 | 5.14 | 0.23 | 11.0 |
| 0.278 | 2.22 | 3.36 | 6.68 | 0.45 | 8.5 | |||||
| 10 | Kirogi | 62.8 | 0.46 | 0.47 | 0.124 | 14.48 | 1.25 | 1.36 | 0.04 | 36.3 |
| 0.111 | 16.10 | 1.14 | 1.72 | 0.01 | 30.2 | |||||
| 11 | Mawar | 50.9 | 0.57 | 0.7 | 0.244 | 11.47 | 2.09 | 2.6 | 0.04 | 21.0 |
| 0.188 | 14.75 | 1.63 | 3.06 | 0.03 | 18.1 | |||||
| 12 | Meari | 42.5 | 0.58 | 0.77 | 0.246 | 14.60 | 1.77 | 1.79 | 0.05 | 29.2 |
| 0.215 | 16.71 | 1.58 | 2.47 | 0.07 | 22.0 | |||||
| 13 | Xangsane | 47.7 | 0.58 | 0.58 | 0.285 | 4.23 | 3.72 | 3.26 | 0.06 | 17.1 |
| 0.287 | 4.69 | 3.25 | 4.7 | 0.05 | 12.0 | |||||
| 14 | Yagi | 73.3 | 0.57 | 0.79 | 0.290 | 15.68 | 2.62 | 2.75 | 0.04 | 20.0 |
| 0.266 | 17.09 | 2.39 | 4.07 | 0.08 | 13.8 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yurchak, B.S. Estimating the Intensity of Tropical Cyclones from Spiral Signatures Acquired by Spaceborne SAR. Remote Sens. 2024, 16, 1750. https://doi.org/10.3390/rs16101750
Yurchak BS. Estimating the Intensity of Tropical Cyclones from Spiral Signatures Acquired by Spaceborne SAR. Remote Sensing. 2024; 16(10):1750. https://doi.org/10.3390/rs16101750
Chicago/Turabian StyleYurchak, Boris S. 2024. "Estimating the Intensity of Tropical Cyclones from Spiral Signatures Acquired by Spaceborne SAR" Remote Sensing 16, no. 10: 1750. https://doi.org/10.3390/rs16101750
APA StyleYurchak, B. S. (2024). Estimating the Intensity of Tropical Cyclones from Spiral Signatures Acquired by Spaceborne SAR. Remote Sensing, 16(10), 1750. https://doi.org/10.3390/rs16101750







