Implementation of MIMO Radar-Based Point Cloud Images for Environmental Recognition of Unmanned Vehicles and Its Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Frequency Modulated Radar
2.2. Radar System
2.3. Radar Signal Processing
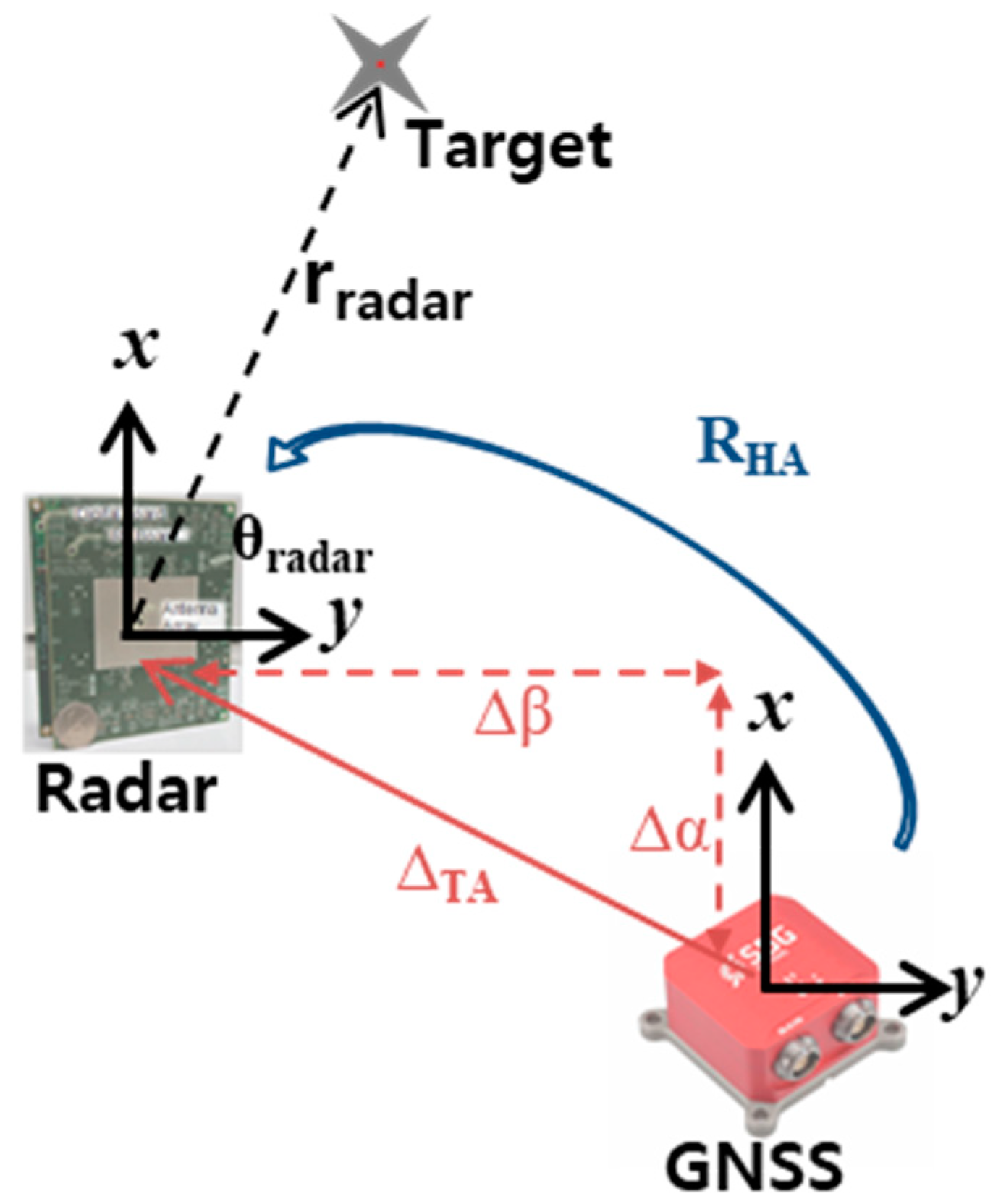
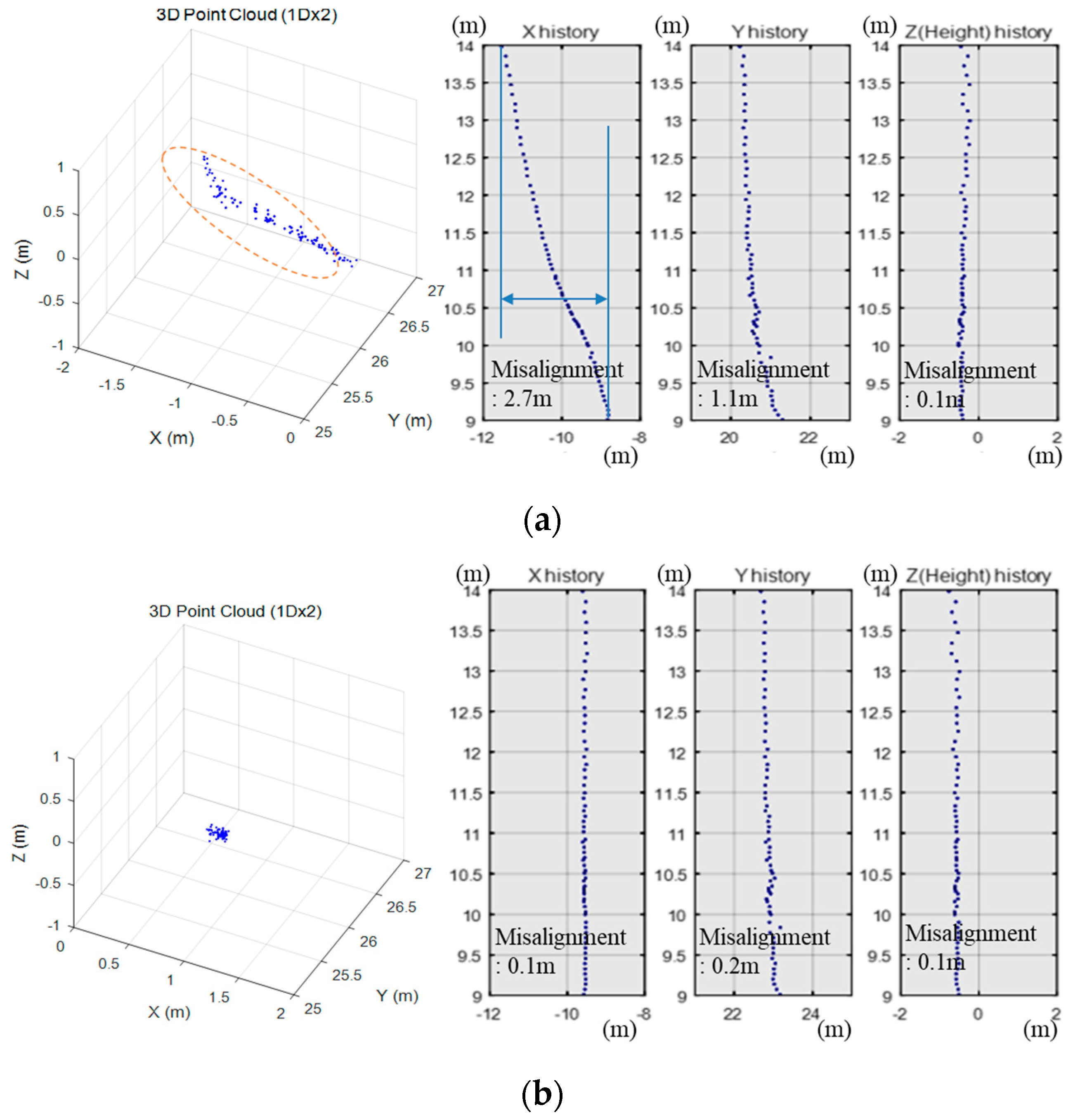
2.4. Misalignment Correction
2.5. Camera-Radar Calibration
3. Results
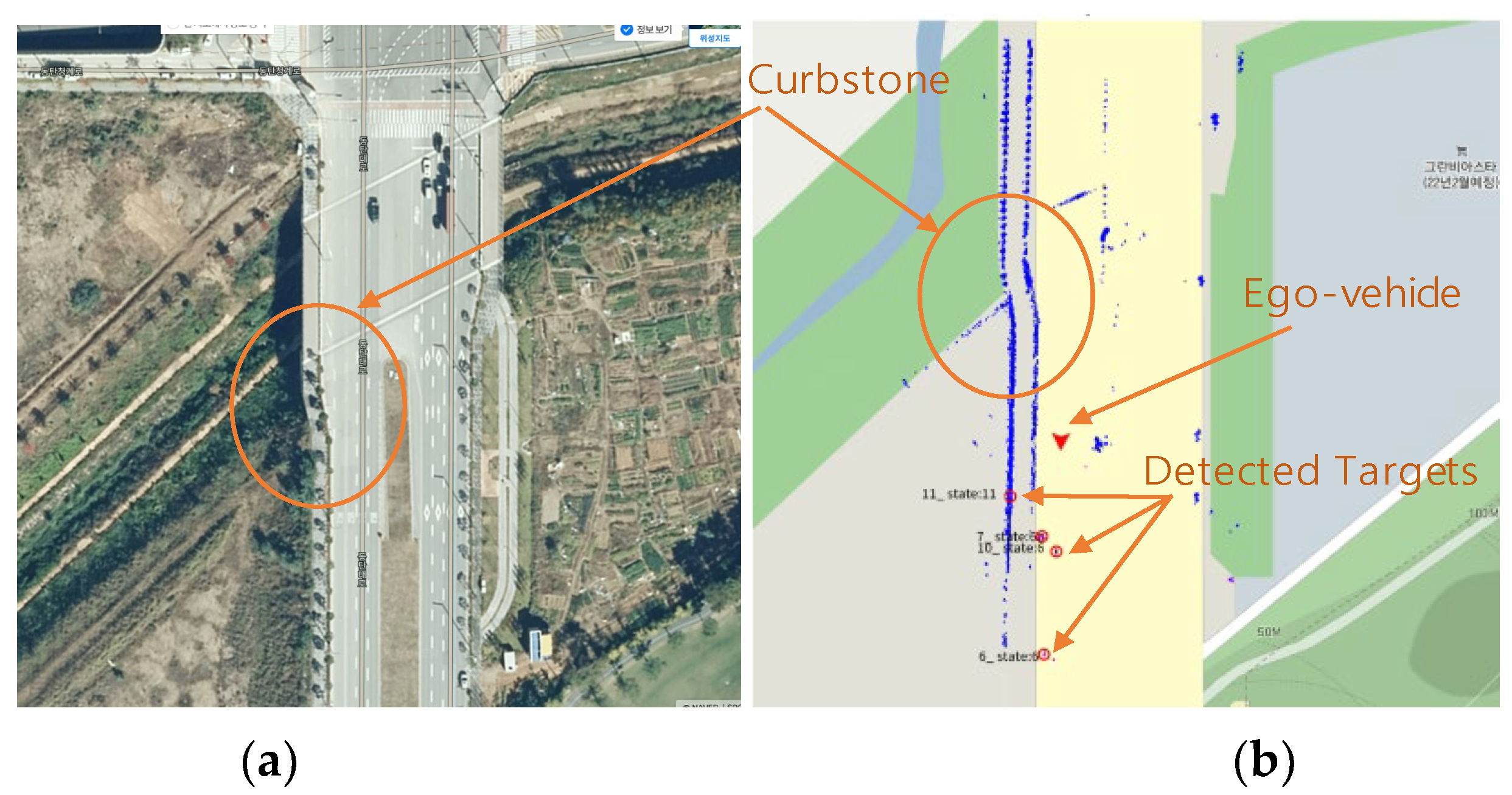
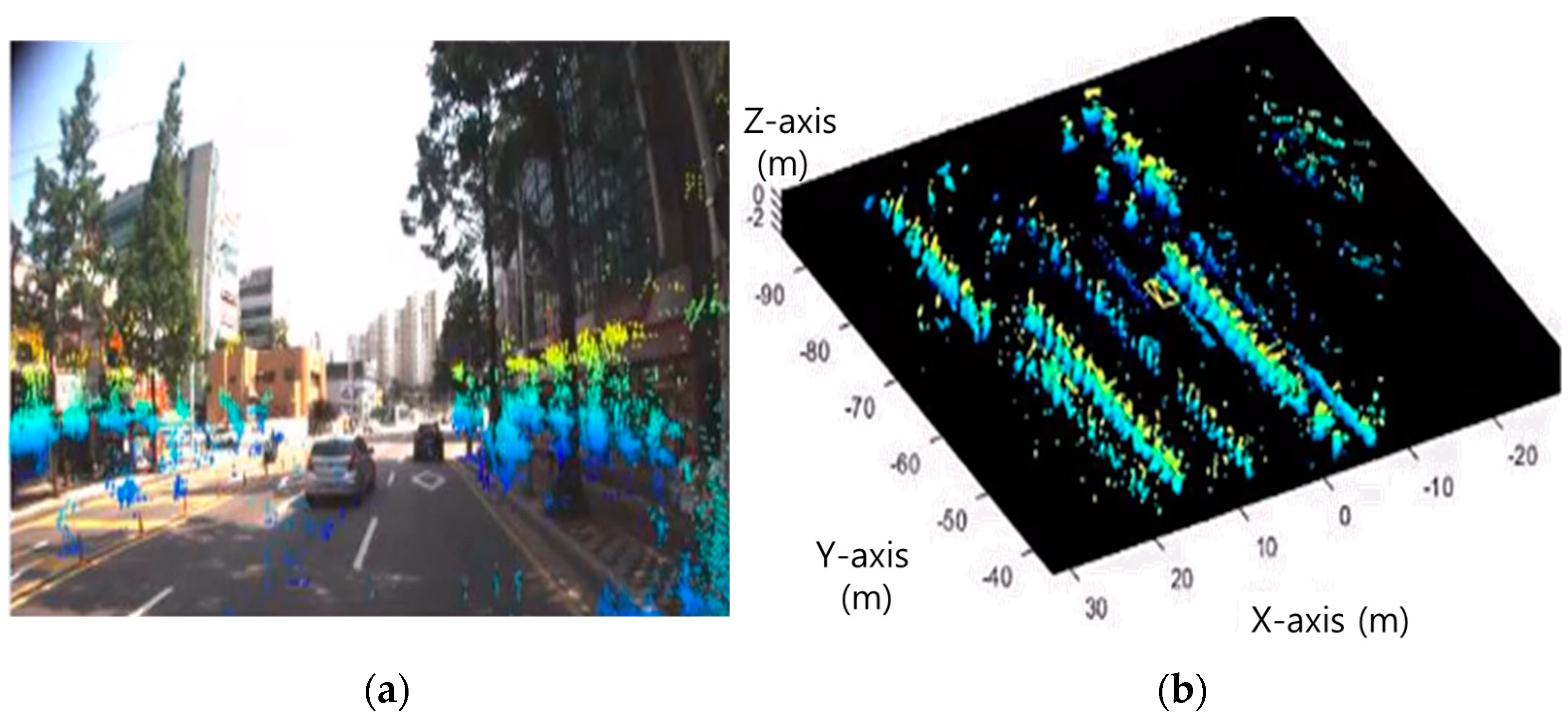
3.1. Point Cloud Image
3.2. A Sensor Fusion Image Based on Camera and Radar
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meinel, H. Evolving Automotive Radar—From the very beginnings into the future. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014; pp. 3107–3114. [Google Scholar] [CrossRef]
- Khalid, F.B.; Nugraha, D.T.; Roger, A.; Ygnace, R.; Bichl, M. Distributed Signal Processing of High-Resolution FMCW MIMO Radar for Automotive Applications. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 513–516. [Google Scholar] [CrossRef]
- Dickmann, J.; Klappstein, J.; Hahn, M.; Appenrodt, N.; Bloecher, H.L.; Werber, K.; Sailer, A. Automotive radar the key technology for autonomous driving: From detection and ranging to environmental understanding. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Rao, R.; Cui, C.; Chen, L.; Gao, T.; Shi, Y. Quantitative Testing and Analysis of Non-Standard AEB Scenarios Extracted from Corner Cases. Appl. Sci. 2024, 14, 173. [Google Scholar] [CrossRef]
- Prophet, R.; Hoffmann, M.; Vossiek, M.; Li, G.; Sturm, C. Parking space detection from a radar based target list. In Proceedings of the 2017 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Nagoya, Japan, 19–21 March 2017; pp. 91–94. [Google Scholar] [CrossRef]
- Wang, M.; Yue, G.; Xiong, J.; Tian, S. Intelligent Point Cloud Processing, Sensing, and Understanding. Sensors 2024, 24, 283. [Google Scholar] [CrossRef] [PubMed]
- Huch, S.; Lienkamp, M. Towards Minimizing the LiDAR Sim-to-Real Domain Shift: Object-Level Local Domain Adaptation for 3D Point Clouds of Autonomous Vehicles. Sensors 2023, 23, 9913. [Google Scholar] [CrossRef]
- Donnet, B.J.; Longstaff, I.D. MIMO Radar, Techniques and Opportunities. In Proceedings of the 2006 European Radar Conference, Manchester, UK, 13–15 September 2006; pp. 112–115. [Google Scholar] [CrossRef]
- Sun, P.; Dai, H.; Wang, B. Integrated Sensing and Secure Communication with XL-MIMO. Sensors 2024, 24, 295. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kim, B.; Choi, S.; Cho, H.; Kim, W.; Eo, M.; Khang, S.; Lee, S.; Sugiura, T.; Nikishov, A.; et al. 79-GHz Four-RFIC Cascading Radar System for Autonomous Driving. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Sit, Y.L.; Li, G.; Manchala, S.; Afrasiabi, H.; Sturm, C.; Lubbert, U. BPSK-based MIMO FMCW Automotive-Radar Concept for 3D Position Measurement. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 289–292. [Google Scholar] [CrossRef]
- Cho, H.W.; Kim, W.S.; Choi, S.D.; Eo, M.S.; Khang, S.T.; Kim, J.S. Guided Generative Adversarial Network for Super Resolution of Imaging Radar. In Proceedings of the 2020 17th European Radar Conference (EuRAD), Utrecht, The Netherlands, 10–15 January 2021; pp. 144–147. [Google Scholar] [CrossRef]
- Kronauge, M.; Rohling, H. New chirp sequence radar waveform. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2870–2877. [Google Scholar] [CrossRef]
- Rohling, H.; Kronauge, M. New radar waveform based on a chirp sequence. In Proceedings of the 2014 International Radar Conference, Lille, France, 13–17 October 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Choi, S.D.; Kim, B.K.; Kim, J.S.; Cho, H. Doppler Coherent Focusing DOA Method for Efficient Radar Map Generation. In Proceedings of the 2019 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Detroit, MI, USA, 15–16 April 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, G.; Geng, X.; Lin, Y.J. Comprehensive mPoint: A Method for 3D Point Cloud Generation of Human Bodies Utilizing FMCW MIMO mm-Wave Radar. Sensors 2021, 21, 6455. [Google Scholar] [CrossRef] [PubMed]
- Abdulla, A.R.; He, F.; Adel, M.; Naser, E.S.; Ayman, H. Using an Unmanned Aerial Vehicle-Based Digital Imaging System to Derive a 3D Point Cloud for Landslide Scarp Recognition. Remote Sens. 2016, 8, 95. [Google Scholar] [CrossRef]
- Tomi, R.; Eija, H. Point Cloud Generation from Aerial Image Data Acquired by a Quadrocopter Type Micro Unmanned Aerial Vehicle and a Digital Still Camera. Sensors 2012, 12, 453–480. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Fu, H.; Liu, B.; Xue, H.Z.; Ren, R.K.; Tu, Z.M. Detailed Analysis on Generating the Range Image for LiDAR Point Cloud Processing. Electronics 2021, 10, 1224. [Google Scholar] [CrossRef]
- Roberto, P.; Marina, P.; Francesca, M.; Massimo, M.; Christian, M.; Eva, S.M.; Emanuele, F.; Andrea, M.L. Point Cloud Semantic Segmentation Using a Deep Learning Framework for Cultural Heritage. Remote Sens. 2020, 12, 1005. [Google Scholar] [CrossRef]
- Lukasz, S.; Katarzyna, F.; Adam, D.; Joanna, D. LiDAR Point Cloud Generation for SLAM Algorithm Evaluation. Sensors 2021, 21, 3313. [Google Scholar] [CrossRef] [PubMed]
- Werber, K.; Rapp, M.; Klappstein, J.; Hahn, M.; Dickmann, J.; Dietmayer, K.; Waldschmidt, C. Automotive radar gridmap representations. In Proceedings of the 2015 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Heidelberg, Germany, 27–29 April 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Point Cloud. Available online: https://en.wikipedia.org/wiki/Point_cloud (accessed on 22 March 2024).
- Wang, J.; Zang, D.; Yu, J.; Xie, X. Extraction of Building Roof Contours from Airborne LiDAR Point Clouds Based on Multidirectional Bands. Remote Sens. 2024, 16, 190. [Google Scholar] [CrossRef]
- Wang, Y.; Han, X.; Wei, X.; Luo, J. Instance Segmentation Frustum–Point Pillars: A Lightweight Fusion Algorithm for Camera–LiDAR Perception in Autonomous Driving. Mathematics 2024, 12, 153. [Google Scholar] [CrossRef]
- Xie, J.; Hsu, Y.; Feris, R.S.; Sun, M. Fine registration of 3D point clouds with iterative closest point using an RGB-D camera. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; pp. 2904–2907. [Google Scholar] [CrossRef]


| Center Frequency (GHz) | Bandwidth (GHz) | Velocity Resolution (ms) | Range Resolution (cm) | Angle Resolution (deg.) | Field of View (deg.) |
|---|---|---|---|---|---|
| 79 | 3.5 | 0.1 | 4.3 | 2.5 | 160 |
| Index | Pixel Value (pixels) | RMSE (m) |
|---|---|---|
| Misalignment | 2.2 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Khang, S.; Choi, S.; Eo, M.; Jeon, J. Implementation of MIMO Radar-Based Point Cloud Images for Environmental Recognition of Unmanned Vehicles and Its Application. Remote Sens. 2024, 16, 1733. https://doi.org/10.3390/rs16101733
Kim J, Khang S, Choi S, Eo M, Jeon J. Implementation of MIMO Radar-Based Point Cloud Images for Environmental Recognition of Unmanned Vehicles and Its Application. Remote Sensing. 2024; 16(10):1733. https://doi.org/10.3390/rs16101733
Chicago/Turabian StyleKim, Jongseok, Seungtae Khang, Sungdo Choi, Minsung Eo, and Jinyong Jeon. 2024. "Implementation of MIMO Radar-Based Point Cloud Images for Environmental Recognition of Unmanned Vehicles and Its Application" Remote Sensing 16, no. 10: 1733. https://doi.org/10.3390/rs16101733
APA StyleKim, J., Khang, S., Choi, S., Eo, M., & Jeon, J. (2024). Implementation of MIMO Radar-Based Point Cloud Images for Environmental Recognition of Unmanned Vehicles and Its Application. Remote Sensing, 16(10), 1733. https://doi.org/10.3390/rs16101733









