Operational Forecasting of Global Ionospheric TEC Maps 1-, 2-, and 3-Day in Advance by ConvLSTM Model
Abstract
1. Introduction
2. Data and Methods
2.1. Data Description
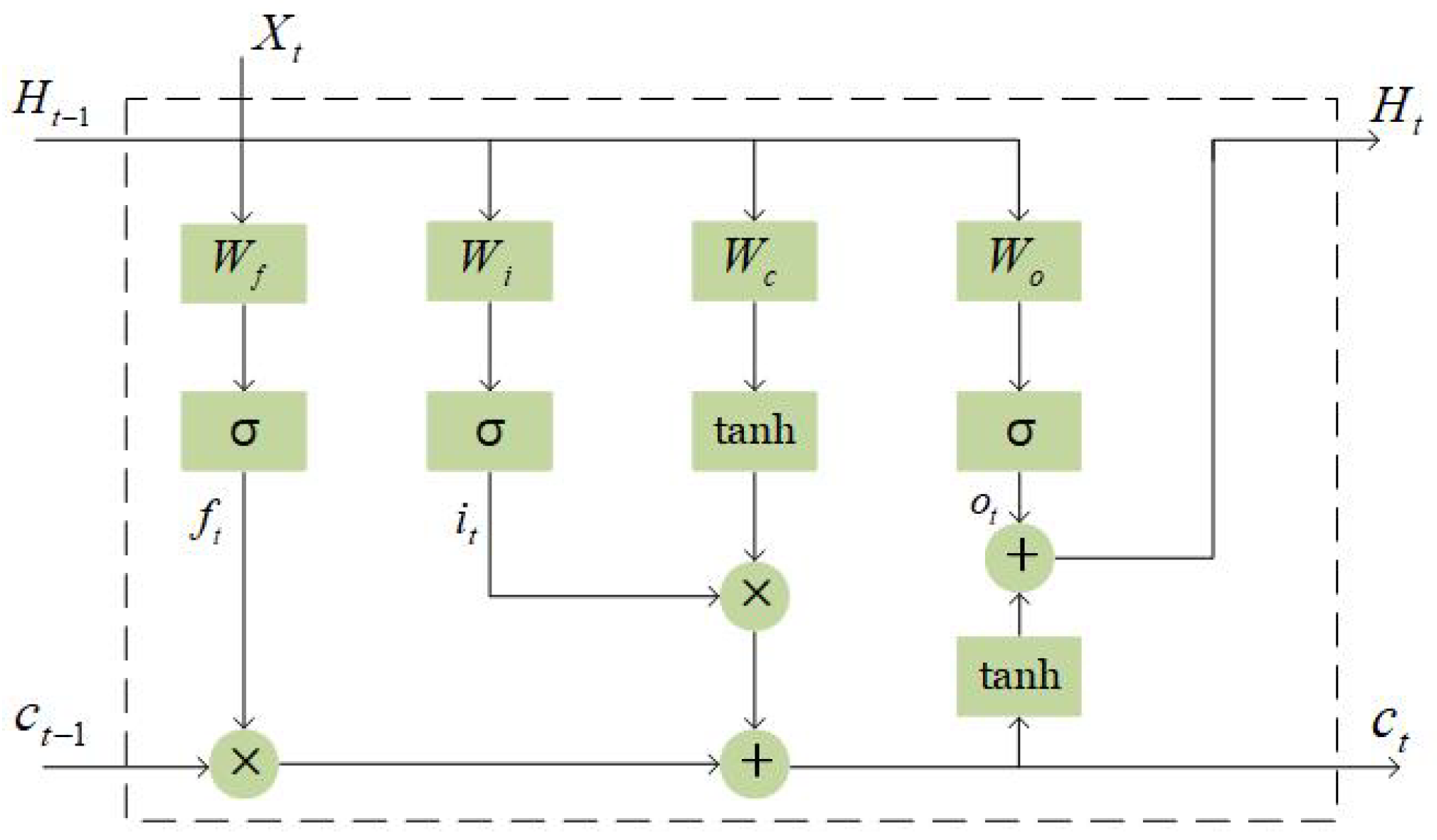
2.2. ConvLSTM Network
2.3. Evaluation Metrics
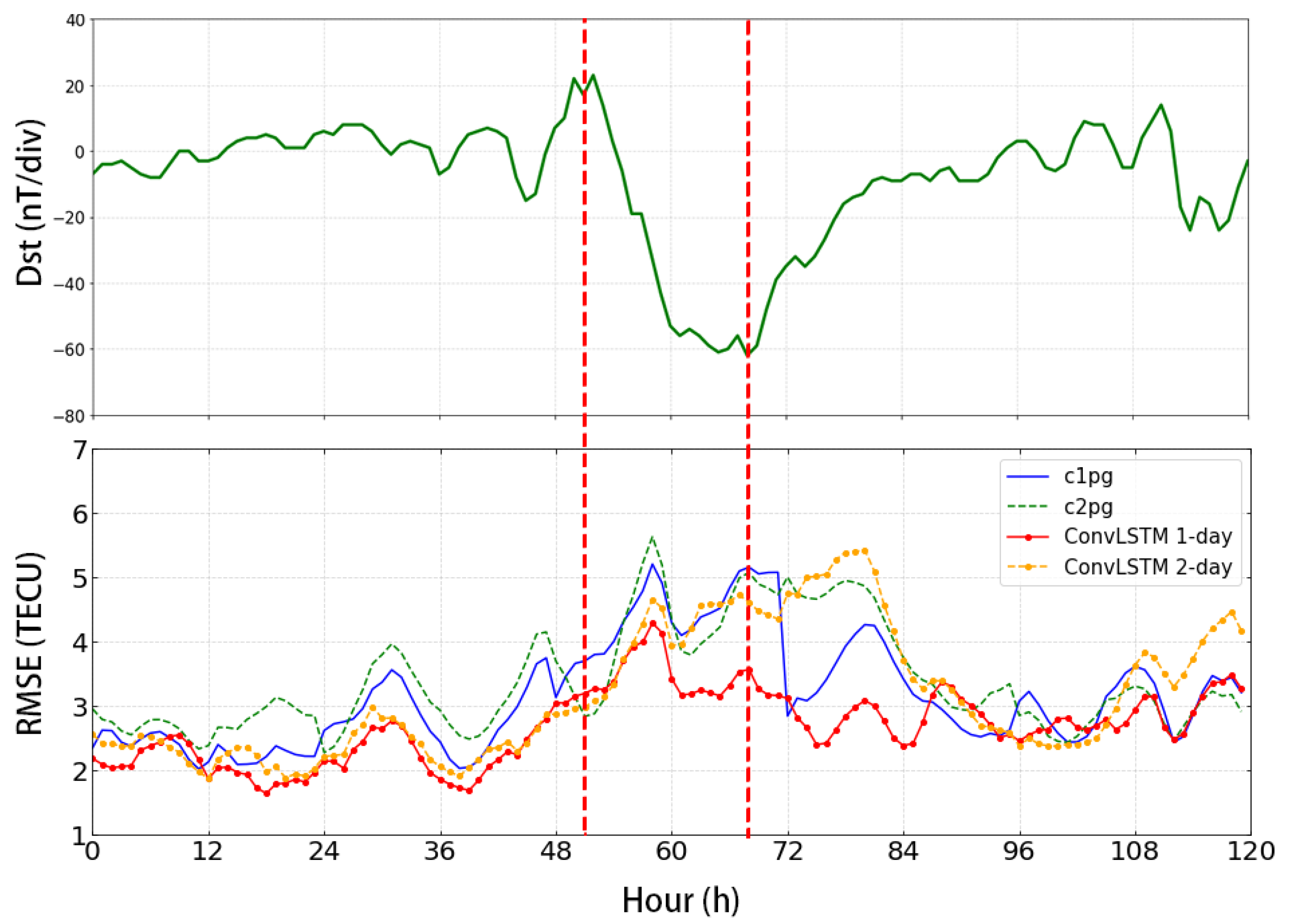
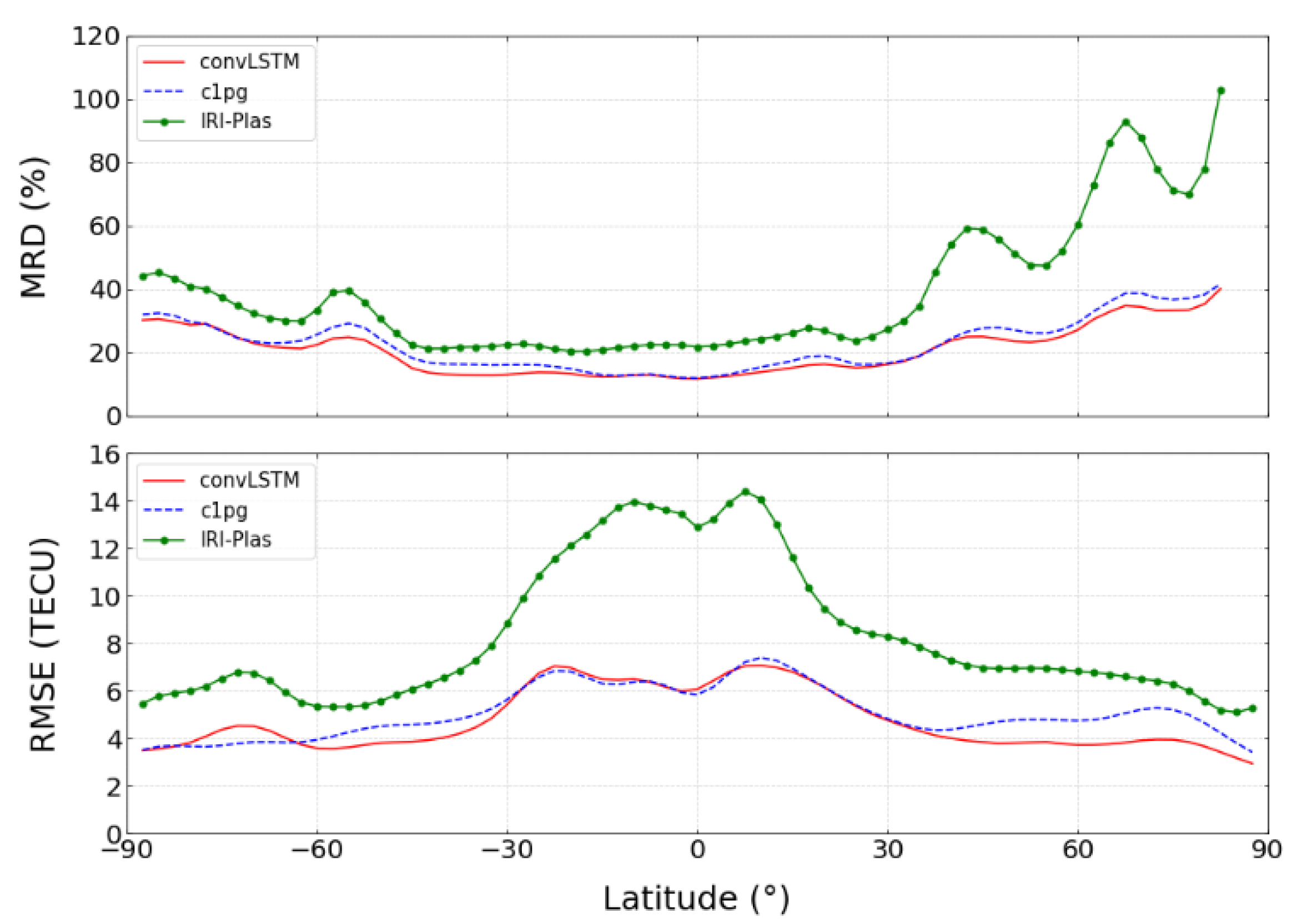
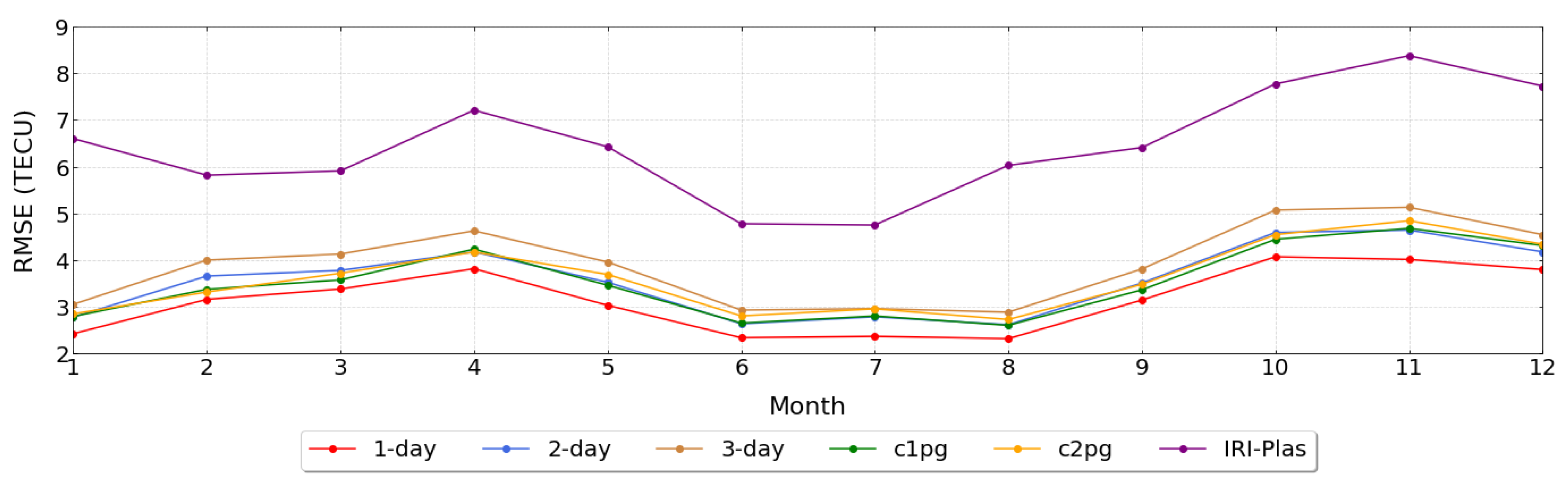
3. Results
4. Conclusions
- The mean RMSE of 1-day prediction in 2022 is 3.17 TECU, and the standard deviation of the error is 0.86 TECU, which shows a relatively stable performance during the geomagnetic quiet and small magnetic storms. The mean RMSE of ConvLSTM 1-day prediction is 2.81 TECU, ConvLSTM 2-day is 3.16 TECU, while the mean RMSE of 3-day prediction is 3.41 TECU;
- Our findings suggest that the ConvLSTM 1-day model outperforms c1pg in situations characterized by geomagnetic quietness and small magnetic storm conditions. However, the performance of our ConvLSTM 2-day model is similar to that of c2pg. Model predictions get worse as the intensity of the storm increases;
- The prediction RMSE of the model gradually increases with the increase of the prediction date.
- In conclusion, the proposed global ionospheric TEC forecasting model in this paper is simple, practical, and has a relatively high forecast accuracy. By only inputting the GIM of the current day, it can forecast the GIM for the next 1, 2, and 3 days, which is convenient for engineering applications. Providing timely, precise, and dependable ionospheric TEC data, along with error correction information, is crucial for scientific research and engineering applications. These datasets find utility in various fields, including satellite navigation, radar imaging, mitigation of radiocommunication issues, aviation purposes, shortwave communication, and more. Geomagnetic perturbations have an important impact on the ionosphere, but forecasting magnetic storms is still a challenging task [46]. With increasing geomagnetic activity, the impacts of energetic particle precipitation on electron production in the ionosphere become more significant [47,48]. Therefore, we did not include geomagnetic indices in our training mainly for the above reasons. In the future, utilizing TEC-measured data, such as MIT’s GNSS-TEC data, can be a promising area of research to enhance the accuracy of global or regional forecasts.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaselimi, M.; Voulodimos, A.; Doulamis, N.; Doulamis, A.; Delikaraoglou, D. A Causal Long Short-Term Memory Sequence to Sequence Model for TEC Prediction Using GNSS Observations. Remote Sens. 2020, 12, 1354. [Google Scholar] [CrossRef]
- Winglee, R.M.; Chua, D.; Brittnacher, M.; Parks, G.K.; Lu, G. Global Impact of Ionospheric Outflows on the Dynamics of the Magnetosphere and Cross-Polar Cap Potential. J. Geophys. Res. Space Phys. 2002, 107, 1237. [Google Scholar] [CrossRef]
- Karpov, I.V.; Karpov, M.I.; Borchevkina, O.P.; Yakimova, G.A.; Koren’kova, N.A. Spatial and Temporal Variations of the Ionosphere during Meteorological Disturbances in December 2010. Russ. J. Phys. Chem. B 2019, 13, 714–719. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Rawer, K.; Bilitza, D.; Ramakrishnan, S. Goals and Status of the International Reference Ionosphere. Rev. Geophys. 1978, 16, 177–181. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From Ionospheric Climate to Real-time Weather Predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Gulyaeva, T.L.; Veselovsky, I.S. Two-phase Storm Profile of Global Electron Content in the Ionosphere and Plasmasphere of the Earth. J. Geophys. Res. 2012, 117, A09324. [Google Scholar] [CrossRef]
- Gulyaeva, T.; Bilitza, D. Towards ISO Standard Earth Ionosphere and Plasmasphere Model. In New Developments in the Standard Model; 39th COSPAR Scientific Assembly; Nova Science Inc.: Mysore, India, 2012; p. 192. [Google Scholar]
- Gulyaeva, T.L.; Arikan, F.; Stanislawska, I. Inter-Hemispheric Imaging of the Ionosphere with the Upgraded IRI-Plas Model during the Space Weather Storms. Earth Planet Space 2011, 63, 929–939. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar]
- Di Giovanni, G.; Radicella, S.M. An Analytical Model of the Electron Density Profile in the Ionosphere. Adv. Space Res. 1990, 10, 27–30. [Google Scholar] [CrossRef]
- Leitinger, R.; Nava, B.; Radicella, S. Electron Density Models for Assessment Studies-New Developments. Acta Geod. Geophys. Hung 2002, 37, 183–193. [Google Scholar] [CrossRef]
- Zhang, D.; Ridley, A.J.; Xiao, Z.; Hao, Y. A global model: Empirical orthogonal function analysis of total electron content 1999–2009 Data. J. Geophys. Res. 2012, 117, A03328. [Google Scholar]
- Aa, E.; Ridley, A.; Huang, W.; Zou, S.; Liu, S.; Coster, A.J.; Zhang, S. An Ionosphere Specification Technique Based on Data Ingestion Algorithm and Empirical Orthogonal Function Analysis Method. Space Weather 2018, 16, 1410–1423. [Google Scholar] [CrossRef]
- Shubin, V.N.; Gulyaeva, T.L.; Deminov, M.G. Aeronomic and Dynamic Correction of the Global Model GTEC for Disturbed Conditions. Geomagn. Aeron. 2022, 62, S74–S86. [Google Scholar] [CrossRef]
- Xiao, Z.; Xiao, R.; Feng, W.; Yu, C. A new method for detection of pre-earthquake ionospheric anomalies. Chin. J. Geophys. 2013, 56, 213–222. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, X.; Wu, F.; Lu, Q. Short-term TEC prediction of ionosphere based on ARIMA model. Acta Geod. Cartogr. Sin. 2014, 43, 118–124. [Google Scholar]
- Inyurt, S.; Hasanpour Kashani, M.; Sekertekin, A. Ionospheric TEC Forecasting Using Gaussian Process Regression (GPR) and Multiple Linear Regression (MLR) in Turkey. Astrophys. Space Sci. 2020, 365, 99. [Google Scholar] [CrossRef]
- Xia, G.; Liu, Y.; Wei, T.; Wang, Z.; Huang, W.; Du, Z.; Zhang, Z.; Wang, X.; Zhou, C. Ionospheric TEC Forecast Model Based on Support Vector Machine with GPU Acceleration in the China Region. Adv. Space Res. 2021, 68, 1377–1389. [Google Scholar] [CrossRef]
- Yuan, T.; Chen, Y.; Liu, S.; Gong, J. Prediction model for ionospheric total electron content based on deep learning recurrent neural network. Chin. J. Space Sci. 2018, 38, 48–57. (In Chinese) [Google Scholar] [CrossRef]
- Cander, L.R.; Lamming, X. Neural Networks in Ionospheric Prediction and Short-Term Forecasting. In Proceedings of the Tenth International Conference on Antennas and Propagation (Conf. Publ. No. 436), Edinburgh, UK, 14–17 April 1997; Volume 2, pp. 27–30. [Google Scholar]
- Habarulema, J.B.; McKinnell, L.-A.; Cilliers, P.J. Prediction of Global Positioning System Total Electron Content Using Neural Networks over South Africa. J. Atmos. Sol. Terr. Phys. 2007, 69, 1842–1850. [Google Scholar] [CrossRef]
- Habarulema, J.B.; McKinnell, L.-A.; Opperman, B.D.L. Regional GPS TEC Modeling; Attempted Spatial and Temporal Extrapolation of TEC Using Neural Networks. J. Geophys. Res. Space Phys. 2011, 116, A4. [Google Scholar] [CrossRef]
- Song, R.; Zhang, X.; Zhou, C.; Liu, J.; He, J. Predicting TEC in China Based on the Neural Networks Optimized by Genetic Algorithm. Adv. Space Res. 2018, 62, 745–759. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Xiong, P.; Zhai, D.; Long, C.; Zhou, H.; Zhang, X.; Shen, X. Long Short-Term Memory Neural Network for Ionospheric Total Electron Content Forecasting Over China. Space Weather 2021, 19, e2020SW002706. [Google Scholar] [CrossRef]
- Liu, L.; Morton, Y.J.; Liu, Y. ML Prediction of Global Ionospheric TEC Maps. Space Weather 2022, 20, e2022SW003135. [Google Scholar] [CrossRef]
- Ren, X.; Yang, P.; Liu, H.; Chen, J.; Liu, W. Deep Learning for Global Ionospheric TEC Forecasting: Different Approaches and Validation. Space Weather 2022, 20, e2021SW003011. [Google Scholar] [CrossRef]
- Ren, X.; Yang, P.; Mei, D.; Liu, H.; Xu, G.; Dong, Y. Global Ionospheric TEC Forecasting for Geomagnetic Storm Time Using a Deep Learning-Based Multi-Model Ensemble Method. Space Weather 2023, 21, e2022SW003231. [Google Scholar] [CrossRef]
- Collado-Villaverde, A.; Muñoz, P.; Cid, C. Neural Networks for Operational SYM-H Forecasting Using Attention and SWICS Plasma Features. Space Weather 2023, 21, e2023SW003485. [Google Scholar] [CrossRef]
- Siciliano, F.; Consolini, G.; Tozzi, R.; Gentili, M.; Giannattasio, F.; De Michelis, P. ForecastingSYM-Hindex: A comparison betweenlong short-term memory andconvolutional neural networks. Space Weather 2021, 19, e2020SW002589. [Google Scholar] [CrossRef]
- Murray, S.A. The Importance of Ensemble Techniques for Operational Space Weather Forecasting. Space Weather 2018, 16, 777–783. [Google Scholar] [CrossRef]
- Zheng, Y.; Macneice, P.; Odstrcil, D.; Mays, M.L.; Rastaetter, L.; Pulkkinen, A.; Taktakishvili, A.; Hesse, M.; Kuznetsova, M.M.; Lee, H.; et al. Forecasting propagation and evolution of CMEs in an operational setting: Whathas been learned. Space Weather 2013, 11, 557–574. [Google Scholar] [CrossRef]
- Merceret, F.J.; O’Brien, T.P.; Roeder, W.P.; Huddleston, L.L.; Bauman, W.H., III; Jedlovec, G.J. Transitioning Research to Operations: Transforming the “Valley of Death” Into a “Valley of Opportunity”. Space Weather 2013, 11, 637–640. [Google Scholar] [CrossRef]
- Posner, A.; Hesse, M.; St. Cyr, O.C. The main pillar: Assessment ofspace weather observational assetperformance supporting nowcasting, forecasting and research to operations. Space Weather 2014, 12, 257–276. [Google Scholar] [CrossRef]
- Turner, H.; Lang, M.; Owens, M.; Smith, A.; Riley, P.; Marsh, M.; Gonzi, S. Solar wind data assimilation in an operational context: Use of near-real-time data and the forecast value of an L5 monitor. Space Weather 2023, 21, e2023SW003457. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Xia, G.; Zhang, F.; Wang, C.; Zhou, C. ED-ConvLSTM: A Novel Global Ionospheric Total Electron Content Medium-Term Forecast Model. Space Weather 2022, 20, e2021SW002959. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. Int. Conf. Learn. Represent. 2014. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System; Institut für Geodäsie und Photogrammetrie, Eidg. Technische Hochschule Zürich: Zurich, Switzerland, 1999. [Google Scholar]
- Gonzalez, W.D.; Joselyn, J.A.; Kamide, Y.; Kroehl, H.W.; Rostoker, G.; Tsurutani, B.T.; Vasyliunas, V.M. What Is a Geomagnetic Storm? J. Geophys. Res. Space Phys. 1994, 99, 5771–5792. [Google Scholar] [CrossRef]
- Mukhtarov, P.; Andonov, B.; Pancheva, D. Global Empirical Model of TEC Response to Geomagnetic Activity. J. Geophys. Res. Space Phys. 2013, 118, 6666–6685. [Google Scholar] [CrossRef]
- Wang, X.; Miao, J.; Aa, E.; Ren, T.; Wang, Y.; Liu, J.; Liu, S. Statistical Analysis of Joule Heating and Thermosphere Response During Geomagnetic Storms of Different Magnitudes. JGR Space Phys. 2020, 125, e2020JA027966. [Google Scholar] [CrossRef]
- Wang, X.; Miao, J.; Lu, X.; Aa, E.; Liu, J.; Wang, Y.; Liu, S. Latitudinal impacts of Joule heating on the high-latitude thermo-spheric density enhancement during geomagnetic storms. JGR Space Phys. 2021, 126, e2020JA028747. [Google Scholar] [CrossRef]
- Wang, X.; Miao, J.; Lu, X.; Aa, E.; Luo, B.; Liu, J.; Hong, Y.; Wang, Y.; Ren, T.; Zeng, R.; et al. Using temporal rela-tionship of thermospheric density with geomagnetic activity indices and Joule heating as calibration for NRLMSISE-00 during geomagnetic storms. Space Weather 2022, 20, e2021SW003017. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The Geomagnetic Kp Index and Derived Indices of Geomagnetic Activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Wang, X.; Cai, L.; Aikio, A.; Vanhamäki, H.; Virtanen, I.; Zhang, Y.; Luo, B.; Liu, S. Ionospheric conductances due to elec-tron and ion precipitations: A comparison between EISCAT and DMSP estimates. JGR Space Phys. 2024, 129, e2023JA032354. [Google Scholar] [CrossRef]
- Shahzad, R.; Shah, M.; Tariq, M.A.; Calabia, A.; Melgarejo-Morales, A.; Jamjareegulgarn, P.; Liu, L. Ionospheric–Thermospheric Responses to Geomagnetic Storms from Multi-Instrument Space Weather Data. Remote Sens. 2023, 15, 2687. [Google Scholar] [CrossRef]



| Storm Level | Dst Range (nT) |
|---|---|
| quiet | Dst ≥ −30 |
| small | −50 ≤ Dst < −30 |
| medium | −100 ≤ Dst <−50 |
| intense | Dst < −100 |
| Events | Minimum Dst (nT) | ConvLSTM 1-Day | ConvLSTM 2-Day | IRI-Plas 2020 | c1pg | c2pg | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MRD | MAE | RMSE | MRD | MAE | RMSE | MRD | MAE | RMSE | MRD | MAE | RMSE | MRD | MAE | ||
| 31 March 2020 02:00 UT | −41 | 1.48 (±0.05) | 19.13 (±0.66) | 1.01 (±0.02) | 1.62 (±0.05) | 21.55 (±0.72) | 1.11 (±0.03) | 6.26 (±0.07) | 75.03 (±2.39) | 4.14 (±0.05) | 1.52 (±0.05) | 18.70 (±0.56) | 1.05 (±0.03) | 1.60 (±0.06) | 18.80 (±0.55) | 1.09 (±0.04) |
| 11 June 2021 11:00 UT | −36 | 1.31 (±0.05) | 23.39 (±0.91) | 0.93 (±0.03) | 1.49 (±0.05) | 26.98 (±1.11) | 1.08 (±0.03) | 4.46 (±0.06) | 114.84 (±4.21) | 3.26 (±0.04) | 1.42 (±0.07) | 21.64 (±0.65) | 1.01 (±0.05) | 1.51 (±0.07) | 24.23 (±0.76) | 1.09 (±0.05) |
| 6 October 2021 17:00 UT | −32 | 2.17 (±0.07) | 18.67 (±0.81) | 1.52 (±0.05) | 2.52 (±0.07) | 20.55 (±0.83) | 1.74 (±0.04) | 7.61 (±0.11) | 61.24 (±2.10) | 5.56 (±0.08) | 2.33 (±0.08) | 20.24 (±0.88) | 1.67 (±0.06) | 2.40 (±0.08) | 20.49 (±0.94) | 1.70 (±0.05) |
| 20 April 2020 12:00 UT | −59 | 1.56 (±0.10) | 26.44 (±1.13) | 1.07 (±0.06) | 1.79 (±0.08) | 30.15 (±1.10) | 1.23 (±0.05) | 6.14 (±0.10) | 96.96 (±3.90) | 4.01 (±0.06) | 1.58 (±0.08) | 22.70 (±0.76) | 1.09 (±0.05) | 1.61 (±0.07) | 23.19 (±0.69) | 1.11 (±0.05) |
| 12 May 2021 14:00 UT | −61 | 1.70 (±0.09) | 25.69 (±1.40) | 1.19 (±0.06) | 1.83 (±0.08) | 27.17 (±1.21) | 1.31 (±0.06) | 5.48 (±0.11) | 105.59 (±6.25) | 3.89 (±0.08) | 1.77 (±0.09) | 28.79 (±2.23) | 1.28 (±0.06) | 1.81 (±0.09) | 27.90 (±1.92) | 1.31 (±0.06) |
| 7 July 2022 22:00 UT | −82 | 2.39 (±0.12) | 23.88 (±1.88) | 1.76 (±0.10) | 2.87 (±0.18) | 27.28 (±2.50) | 2.15 (±0.14) | 4.66 (±0.07) | 77.84 (±6.22) | 3.63 (±0.05) | 2.91 (±0.16) | 26.57 (±2.24) | 2.11 (±0.13) | 3.25 (±0.18) | 30.10 (±1.84) | 2.43 (±0.14) |
| 27 February 2023 12:00 UT | −138 | 6.66 (±0.21) | 24.23 (±1.18) | 4.89 (±0.17) | 7.67 (±0.25) | 28.96 (±1.68) | 5.76 (±0.19) | 11.67 (±0.29) | 32.89 (±1.19) | 8.04 (±0.19) | 7.02 (±0.23) | 26.61 (±1.59) | 5.28 (±0.17) | 7.33 (±0.26) | 29.77 (±2.29) | 5.58 (±0.22) |
| 24 March 2023 02:00 UT | −184 | 7.57 (±0.46) | 30.61 (±2.59) | 5.47 (±0.34) | 8.68 (±0.65) | 39.55 (±4.68) | 6.47 (±0.53) | 12.74 (±0.38) | 44.45 (±2.39) | 8.71 (±0.26) | 8.00 (±0.58) | 34.88 (±3.81) | 6.01 (±0.44) | 8.66 (±0.54) | 41.67 (±4.09) | 6.68 (±0.42) |
| 24 April 2023 05:00 UT | −187 | 6.86 (±0.56) | 39.58 (±5.03) | 4.92 (±0.44) | 7.65 (±0.58) | 47.31 (±5.42) | 5.71 (±0.44) | 9.49 (±0.45) | 70.83 (±6.56) | 7.02 (±0.34) | 7.10 (±0.64) | 39.14 (±5.03) | 5.26 (±0.48) | 8.06 (±0.61) | 46.39 (±4.91) | 6.12 (±0.48) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Huang, W.; Xia, G.; Zhou, C.; Chen, Y. Operational Forecasting of Global Ionospheric TEC Maps 1-, 2-, and 3-Day in Advance by ConvLSTM Model. Remote Sens. 2024, 16, 1700. https://doi.org/10.3390/rs16101700
Yang J, Huang W, Xia G, Zhou C, Chen Y. Operational Forecasting of Global Ionospheric TEC Maps 1-, 2-, and 3-Day in Advance by ConvLSTM Model. Remote Sensing. 2024; 16(10):1700. https://doi.org/10.3390/rs16101700
Chicago/Turabian StyleYang, Jiayue, Wengeng Huang, Guozhen Xia, Chen Zhou, and Yanhong Chen. 2024. "Operational Forecasting of Global Ionospheric TEC Maps 1-, 2-, and 3-Day in Advance by ConvLSTM Model" Remote Sensing 16, no. 10: 1700. https://doi.org/10.3390/rs16101700
APA StyleYang, J., Huang, W., Xia, G., Zhou, C., & Chen, Y. (2024). Operational Forecasting of Global Ionospheric TEC Maps 1-, 2-, and 3-Day in Advance by ConvLSTM Model. Remote Sensing, 16(10), 1700. https://doi.org/10.3390/rs16101700








