Spectral Superresolution Using Transformer with Convolutional Spectral Self-Attention
Abstract
1. Introduction
- (1)
- We propose an SSR network based on a combination of transformers and CNN. The network consists of multiple cascaded encoders and decoders that can efficiently extract spatial texture and spectral contextual features from HSIs.
- (2)
- The proposed CSSA, which combines a CNN and a self-attention mechanism, can compute spatial local self-attention and global spectral self-attention.
- (3)
- The proposed network effectively balances computational complexity with the quality of reconstruction achieved. The superiority of our approach is demonstrated on one remote sensing image dataset and two natural image datasets.
2. Related Works
2.1. CNN-Based SSR Approaches
2.2. Transformer-Based Models
2.3. Architectures Combining CNN and Transformer
3. Proposed Method
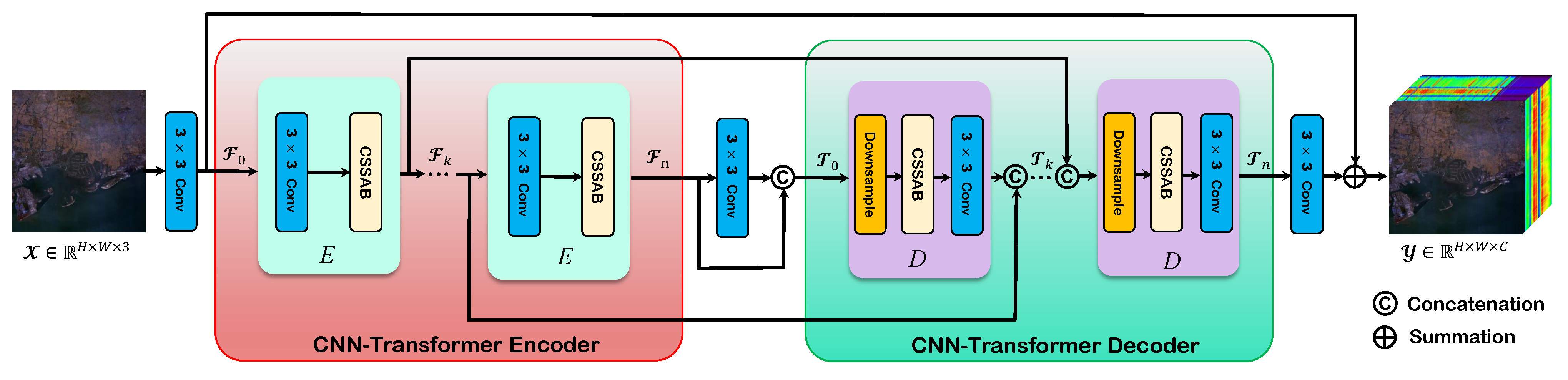
3.1. Architecture of TCSSA
3.1.1. CNN-Transformer Encoder
3.1.2. CNN-Transformer Decoder
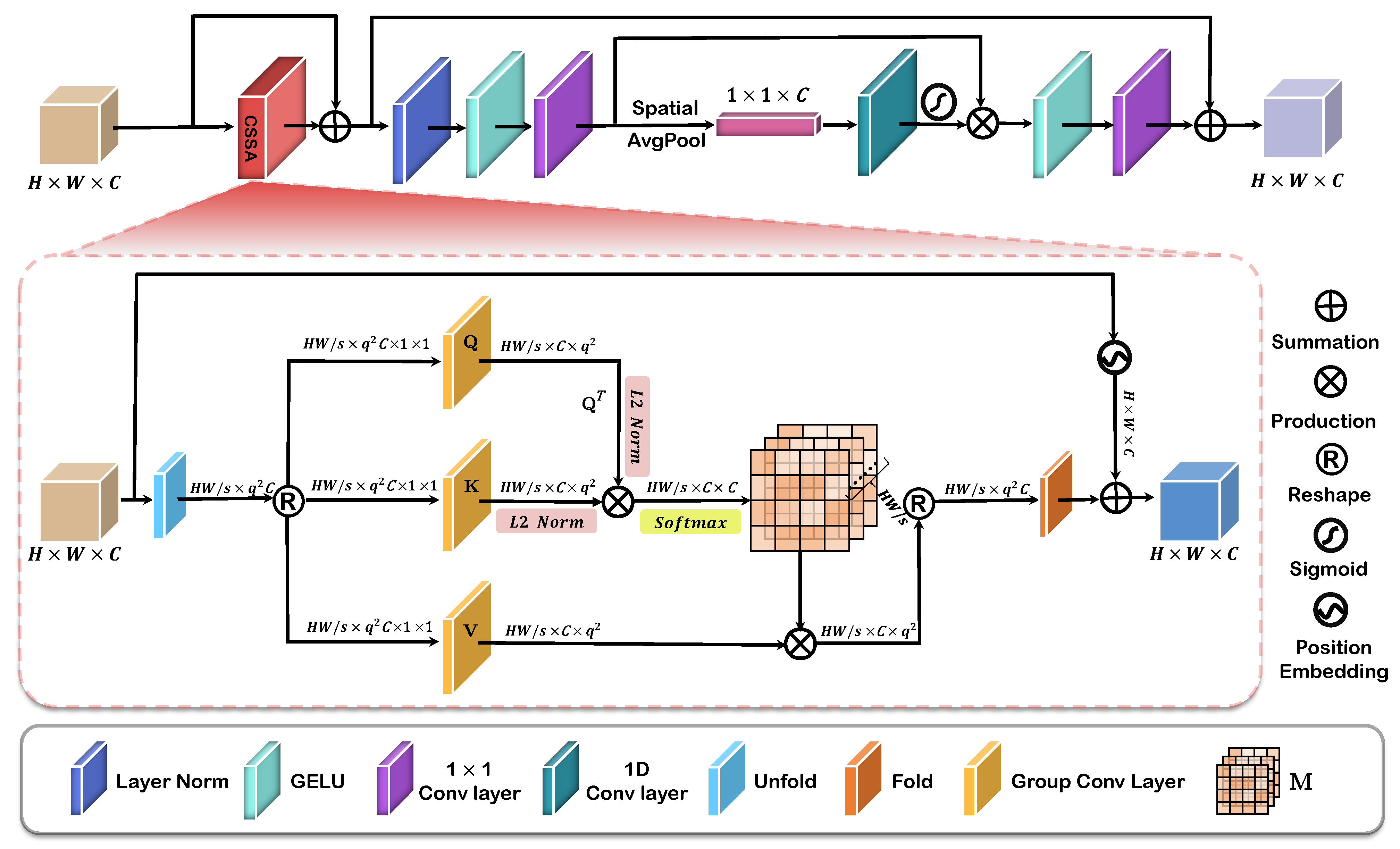
3.2. CSSAB
3.3. CSSA
4. Experiments
4.1. Datasets and Evaluation Metrics
4.1.1. Remote Sensing Image Dataset
4.1.2. Natural Image Datasets
4.1.3. Evaluation Metrics for SSR
4.2. Implementation Settings
4.3. Comparisons With State-of-the-Art Methods
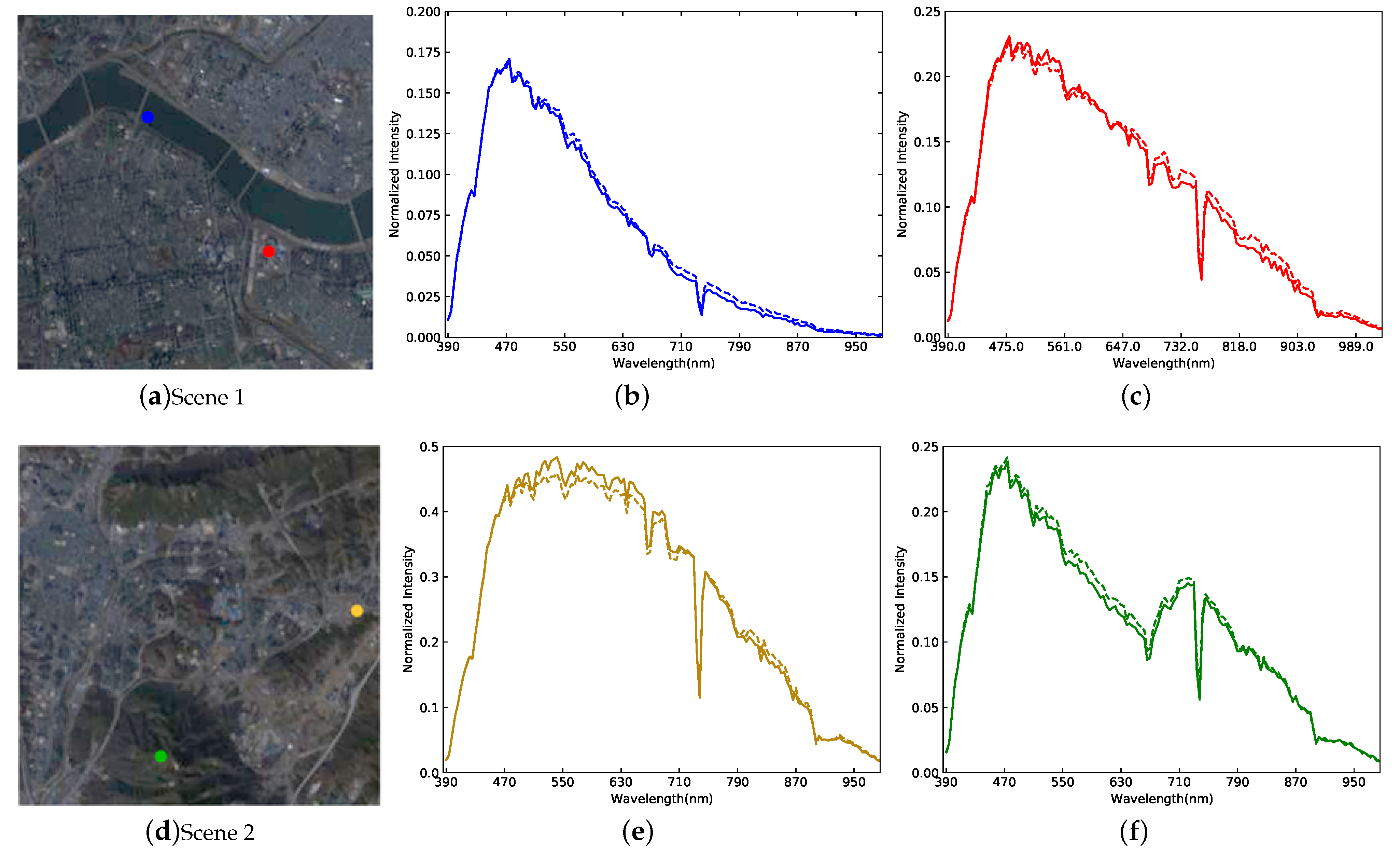
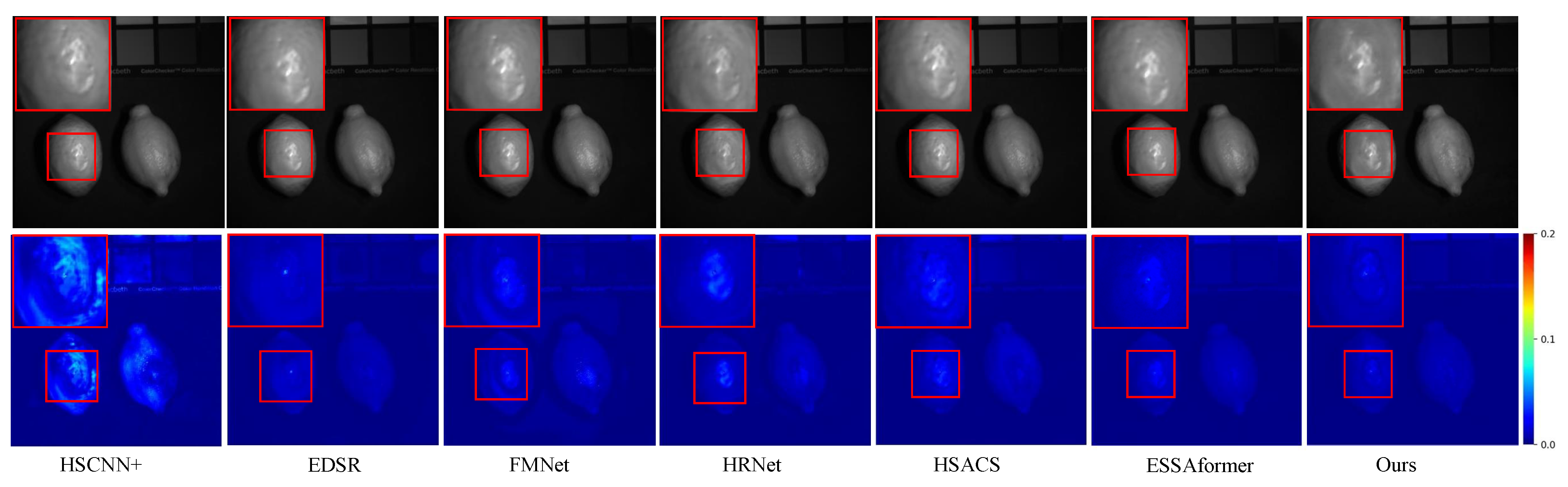
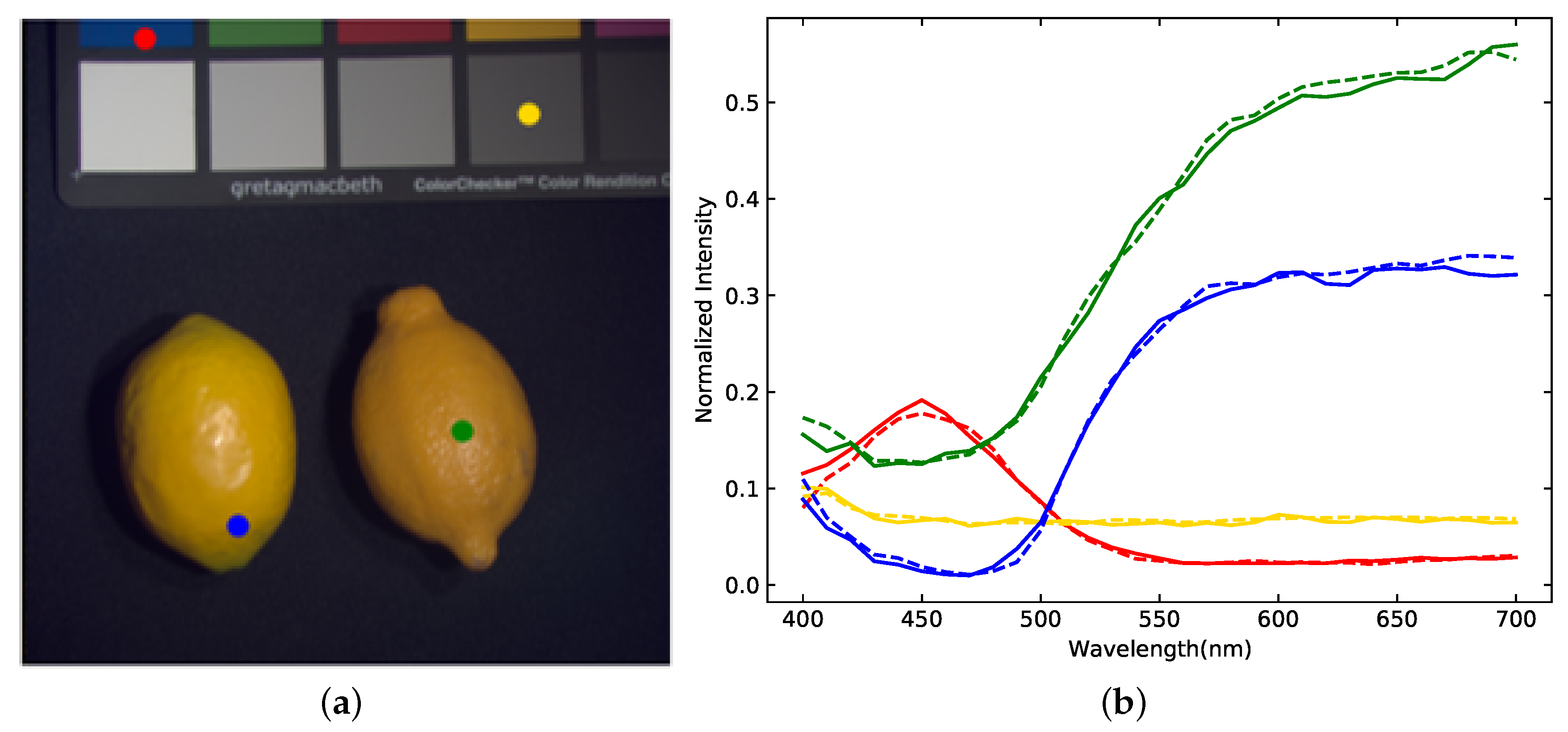
4.3.1. Quantitative and Visual Results Obtained on GF5
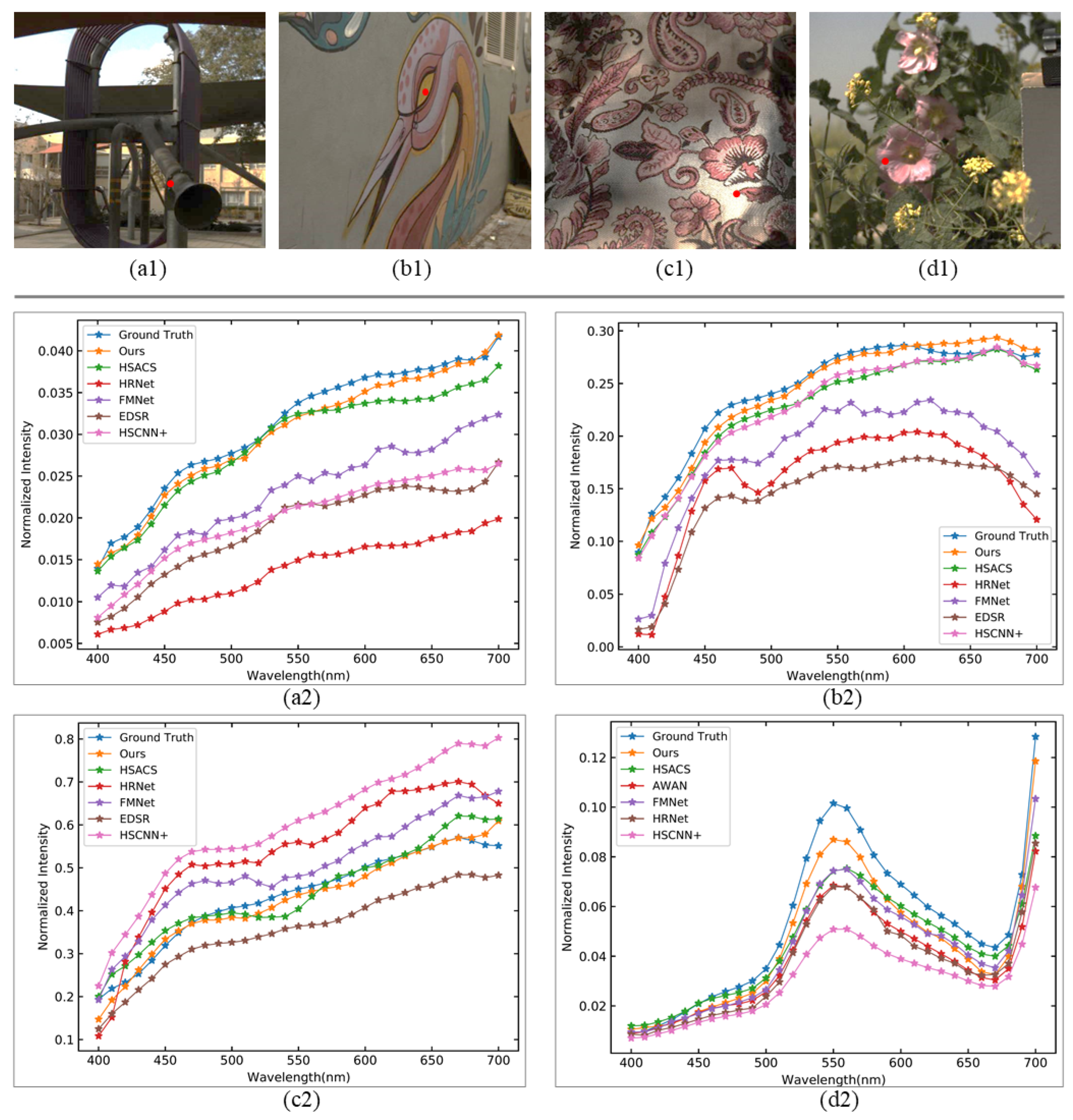
4.3.2. Quantitative and Visual Results Obtained on CAVE and NTIRE2022
4.4. Ablation Analysis
4.4.1. Effectiveness of the CSSA
4.4.2. Effect of Number N
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in Spectral-Spatial Classification of Hyperspectral Images. Proc. IEEE 2012, 101, 652–675. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G. Detection Algorithms For Hyperspectral Imaging Applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–Spatial Hyperspectral Image Segmentation Using Subspace Multinomial Logistic Regression and Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2011, 50, 809–823. [Google Scholar] [CrossRef]
- Ma, Q.; Jiang, J.; Liu, X.; Ma, J. Multi-Task Interaction Learning for Spatiospectral Image Super-Resolution. IEEE Trans. Image Process. 2022, 31, 2950–2961. [Google Scholar] [CrossRef] [PubMed]
- Kaya, B.; Can, Y.B.; Timofte, R. Towards Spectral Estimation from a Single RGB Image in the Wild. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3546–3555. [Google Scholar]
- Zhu, Z.; Liu, H.; Hou, J.; Jia, S.; Zhang, Q. Deep Amended Gradient Descent for Efficient Spectral Reconstruction from Single RGB Images. IEEE Trans. Comput. Imaging 2021, 7, 1176–1188. [Google Scholar] [CrossRef]
- Arad, B.; Ben-Shahar, O. Sparse Recovery of Hyperspectral Signal from Natural RGB Images. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 19–34. [Google Scholar]
- Heikkinen, V. Spectral Reflectance Estimation Using Gaussian Processes and Combination Kernels. IEEE Trans. Image Process. 2018, 27, 3358–3373. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Hong, D.; Yao, J.; Zhang, B.; Gamba, P.; Chanussot, J. Spectral Superresolution of Multispectral Imagery with Joint Sparse and Low-Rank Learning. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2269–2280. [Google Scholar] [CrossRef]
- Akhtar, N.; Mian, A. Hyperspectral Recovery from RGB Images using Gaussian Processes. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 100–113. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Zheng, Y.; Gu, L.; Subpa-Asa, A.; Lam, A.; Sato, Y.; Sato, I. From RGB to Spectrum for Natural Scenes via Manifold-Based Mapping. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4705–4713. [Google Scholar]
- Aeschbacher, J.; Wu, J.; Timofte, R. In Defense of Shallow Learned Spectral Reconstruction from RGB Images. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 471–479. [Google Scholar]
- Timofte, R.; De Smet, V.; Van Gool, L. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 111–126. [Google Scholar]
- Yan, Y.; Zhang, L.; Li, J.; Wei, W.; Zhang, Y. Accurate spectral super-resolution from single RGB image using multi-scale CNN. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Guangzhou, China, 23–26 November 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 206–217. [Google Scholar]
- Wu, C.; Li, J.; Song, R.; Li, Y. Spectral Super-Resolution Using Hybrid 2D-3D Structure Tensor Attention Networks with Camera Spectral Sensitivity Prior. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 17 February 2021; pp. 1857–1860. [Google Scholar]
- Hang, R.; Li, Z.; Liu, Q.; Bhattacharyya, S.S. Prinet: A Prior Driven Spectral Super-Resolution Network. In Proceedings of the 2020 IEEE International Conference on Multimedia and Expo (ICME), London, UK, 6–10 July 2020; pp. 1–6. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Cai, Y.; Lin, J.; Hu, X.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Van Gool, L. Coarse-to-Fine Sparse Transformer for Hyperspectral Image Reconstruction. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; pp. 686–704. [Google Scholar]
- Zhang, M.; Zhang, C.; Zhang, Q.; Guo, J.; Gao, X.; Zhang, J. ESSAformer: Efficient Transformer for Hyperspectral Image Super-resolution. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 23016–23027. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar]
- Shen, Z.; Bello, I.; Vemulapalli, R.; Jia, X.; Chen, C.H. Global Self-Attention Networks for Image Recognition. arXiv 2020, arXiv:2010.03019. [Google Scholar]
- Zhang, K.; Zuo, W.; Gu, S.; Zhang, L. Learning Deep CNN Denoiser Prior for Image Restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3929–3938. [Google Scholar]
- Asgari Taghanaki, S.; Abhishek, K.; Cohen, J.P.; Cohen-Adad, J.; Hamarneh, G. Deep Semantic Segmentation of Natural and Medical Images: A Review. Artif. Intell. Rev. 2021, 54, 137–178. [Google Scholar] [CrossRef]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Learning Enriched Features for Real Image Restoration and Enhancement. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 492–511. [Google Scholar]
- Galliani, S.; Lanaras, C.; Marmanis, D.; Baltsavias, E.; Schindler, K. Learned Spectral Super-Resolution. arXiv 2017, arXiv:1703.09470. [Google Scholar]
- Xiong, Z.; Shi, Z.; Li, H.; Wang, L.; Liu, D.; Wu, F. HSCNN: CNN-Based Hyperspectral Image Recovery from Spectrally Undersampled Projections. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 518–525. [Google Scholar] [CrossRef]
- Shi, Z.; Chen, C.; Xiong, Z.; Liu, D.; Wu, F. HSCNN+: Advanced CNN-Based Hyperspectral Recovery from RGB Images. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1052–10528. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, T.; Zheng, Y.; Zhang, D.; Huang, H. Joint Camera Spectral Response Selection and Hyperspectral Image Recovery. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 256–272. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 2480–2495. [Google Scholar] [CrossRef]
- Zhao, Y.; Po, L.M.; Yan, Q.; Liu, W.; Lin, T. Hierarchical Regression Network for Spectral Reconstruction from RGB Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 422–423. [Google Scholar]
- Bu, L.; Dai, D.; Zhang, Z.; Yang, Y.; Deng, M. Hyperspectral super-resolution reconstruction network based on hybrid convolution and spectral symmetry preservation. Remote Sens. 2023, 15, 3225. [Google Scholar] [CrossRef]
- Zhang, L.; Lang, Z.; Wang, P.; Wei, W.; Liao, S.; Shao, L.; Zhang, Y. Pixel-aware Deep Function-mixture Network for Spectral Super-Resolution. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12821–12828. [Google Scholar]
- Li, J.; Wu, C.; Song, R.; Xie, W.; Ge, C.; Li, B.; Li, Y. Hybrid 2-D–3-D Deep Residual Attentional Network With Structure Tensor Constraints for Spectral Super-Resolution of RGB Images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2321–2335. [Google Scholar] [CrossRef]
- Li, J.; Du, S.; Song, R.; Wu, C.; Li, Y.; Du, Q. HASIC-Net: Hybrid Attentional Convolutional Neural Network With Structure Information Consistency for Spectral Super-Resolution of RGB Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522515. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A Review on the Attention Mechanism of Deep Learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Song, R.; Li, Y.; Liu, F. Adaptive Weighted Attention Network with Camera Spectral Sensitivity Prior for Spectral Reconstruction from RGB Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 462–463. [Google Scholar]
- Li, J.; Wu, C.; Song, R.; Li, Y.; Xie, W.; He, L.; Gao, X. Deep Hybrid 2-D-3-D CNN Based on Dual Second-Order Attention With Camera Spectral Sensitivity Prior for Spectral Super-Resolution. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 623–634. [Google Scholar] [CrossRef]
- He, J.; Li, J.; Yuan, Q.; Shen, H.; Zhang, L. Spectral Response Function-Guided Deep Optimization-Driven Network for Spectral Super-Resolution. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4213–4227. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, T.; Wang, L.; Huang, H. Coded Hyperspectral Image Reconstruction Using Deep External and Internal Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3404–3420. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Yuan, L.; Chen, Y.; Wang, T.; Yu, W.; Shi, Y.; Jiang, Z.; Tay, F.E.H.; Feng, J.; Yan, S. Tokens-to-Token ViT: Training Vision Transformers from Scratch on ImageNet. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 538–547. [Google Scholar] [CrossRef]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in Transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training Data-Efficient Image Transformers & Distillation Through Attention. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 10347–10357. [Google Scholar]
- Xu, W.; Xu, Y.; Chang, T.; Tu, Z. Co-Scale Conv-Attentional Image Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 9981–9990. [Google Scholar]
- d’Ascoli, S.; Touvron, H.; Leavitt, M.L.; Morcos, A.S.; Biroli, G.; Sagun, L. ConViT: Improving Vision Transformers with Soft Convolutional Inductive Biases. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 2286–2296. [Google Scholar]
- Duan, S.; Li, J.; Song, R.; Li, Y.; Du, Q. Unmixing-Guided Convolutional Transformer for Spectral Reconstruction. Remote Sens. 2023, 15, 2619. [Google Scholar] [CrossRef]
- Wu, H.; Xiao, B.; Codella, N.; Liu, M.; Dai, X.; Yuan, L.; Zhang, L. CvT: Introducing Convolutions to Vision Transformers. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 22–31. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, K.; Cao, J.; Timofte, R.; Van Gool, L. LocalViT: Bringing Locality to Vision Transformers. arXiv 2021, arXiv:2104.05707. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. PVT v2: Improved Baselines with Pyramid Vision Transformer. Comput. Vis. Media 2022, 8, 415–424. [Google Scholar] [CrossRef]
- Yang, C.; Wang, Y.; Zhang, J.; Zhang, H.; Wei, Z.; Lin, Z.; Yuille, A. Lite Vision Transformer with Enhanced Self-Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11998–12008. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient Transformer for High-Resolution Image Restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 5728–5739. [Google Scholar]
- Maaz, M.; Shaker, A.; Cholakkal, H.; Khan, S.; Zamir, S.W.; Anwer, R.M.; Khan, F.S. EdgeNeXt: Efficiently Amalgamated CNN-Transformer Architecture for Mobile Vision Applications. arXiv 2022, arXiv:2206.10589. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. Supplementary Material for ‘ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13–19. [Google Scholar]
- Peng, Z.; Huang, W.; Gu, S.; Xie, L.; Wang, Y.; Jiao, J.; Ye, Q. Conformer: Local Features Coupling Global Representations for Visual Recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–147 October 2021; pp. 367–376. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Chakrabarti, A.; Zickler, T. Statistics of Real-World Hyperspectral Images. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 193–200. [Google Scholar]
- Arad, B.; Timofte, R.; Yahel, R.; Morag, N.; Bernat, A.; Cai, Y.; Lin, J.; Lin, Z.; Wang, H.; Zhang, Y.; et al. NTIRE 2022 Spectral Recovery Challenge and Data Set. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; pp. 862–880. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- De Carvalho, O.A.; Meneses, P.R. Spectral Aorrelation Mapper (SCM): An Improvement on the Spectral Angle Mapper (SAM). In Summaries of the 9th JPL Airborne Earth Science Workshop; JPL Publication 00-18; JPL Publication; Pasadena, CA, USA, 2000; Volume 9. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]



| Models | GF5 (Validation) | GF5 (Test) | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE (↓) | PSNR (↑) | SAM (↓) | SSIM (↑) | RMSE (↓) | PSNR (↑) | SAM (↓) | SSIM (↑) | |
| HSCNN+ [27] | 0.0369 | 30.72 | 3.53 | 0.9115 | 0.0349 | 30.12 | 3.29 | 0.9112 |
| EDSR [62] | 0.0244 | 32.76 | 3.60 | 0.9274 | 0.0278 | 31.69 | 3.46 | 0.9216 |
| FMNet [32] | 0.0227 | 33.45 | 3.21 | 0.9333 | 0.0281 | 31.78 | 3.24 | 0.9256 |
| HRNet [30] | 0.0211 | 34.06 | 3.00 | 0.9371 | 0.0232 | 33.32 | 2.85 | 0.9340 |
| HSACS [38] | 0.0209 | 34.23 | 3.15 | 0.9338 | 0.0234 | 33.29 | 3.00 | 0.9293 |
| ESSAformer [19] | 0.0205 | 34.33 | 3.15 | 0.9353 | 0.0213 | 34.11 | 3.00 | 0.9331 |
| Ours | 0.0201 | 34.49 | 2.94 | 0.9374 | 0.0212 | 34.19 | 2.81 | 0.9324 |
| Models | CAVE | NTIRE2022 | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE (↓) | PSNR (↑) | SAM (↓) | SSIM (↑) | MRAE (↓) | RMSE (↓) | PSNR (↑) | SSIM (↑) | |
| HSCNN+ [27] | 0.0389 | 29.47 | 7.17 | 0.9583 | 0.3849 | 0.0585 | 26.29 | 0.8281 |
| EDSR [62] | 0.0225 | 34.05 | 7.64 | 0.9753 | 0.3637 | 0.0524 | 27.01 | 0.8676 |
| FMNet [32] | 0.0220 | 33.87 | 7.59 | 0.9771 | 0.3377 | 0.0482 | 27.69 | 0.8743 |
| HRNet [30] | 0.0220 | 34.34 | 6.99 | 0.9779 | 0.3567 | 0.0528 | 27.28 | 0.8520 |
| HSACS [38] | 0.0216 | 34.44 | 6.47 | 0.9779 | 0.1843 | 0.0276 | 33.17 | 0.9446 |
| ESSAformer [19] | 0.0216 | 33.57 | 6.91 | 0.9796 | 0.2847 | 0.0309 | 31.29 | 0.9492 |
| Ours | 0.0207 | 34.85 | 5.99 | 0.9826 | 0.1806 | 0.0269 | 33.42 | 0.9470 |
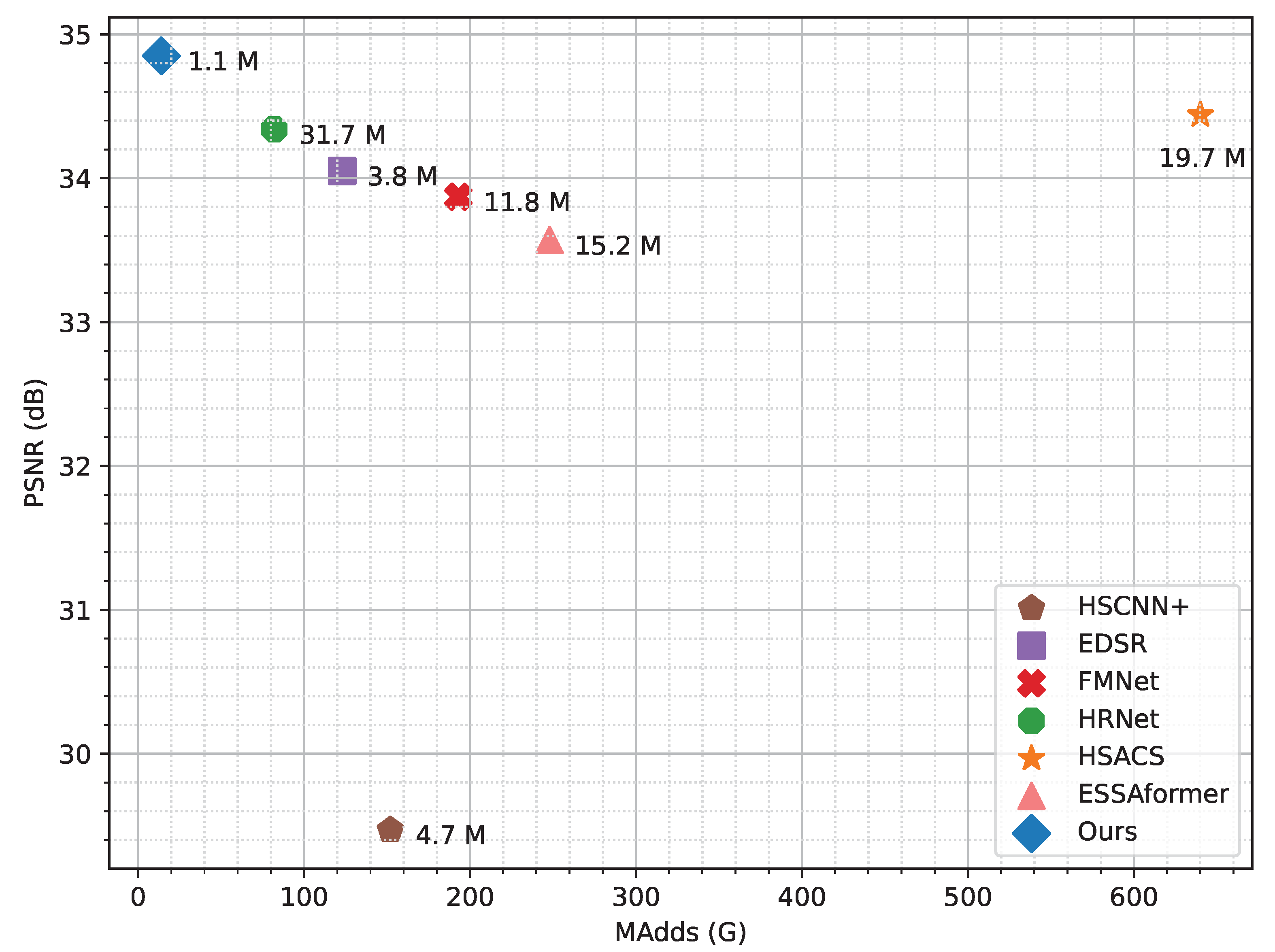
| Method | Params (M) | MAdds (G) | Memory (MB) | Test Time (s) |
|---|---|---|---|---|
| HSCNN+ | 4.65 | 152 | 552 | 4.82 |
| EDSR | 3.77 | 123 | 337 | 1.32 |
| FMNet | 11.77 | 193 | 512 | 4.31 |
| HRNet | 31.70 | 82 | 459 | 5.91 |
| HSACS | 19.73 | 640 | 1372 | 14.27 |
| ESSAformer | 15.16 | 248 | 1114 | 7.99 |
| Ours | 1.08 | 14 | 213 | 1.78 |
| Description | CSA | MDTA | CSSA | MRAE | RMSE | PSNR |
|---|---|---|---|---|---|---|
| ✘ | ✘ | ✘ | 0.2744 | 0.0390 | 30.48 | |
| ✔ | ✘ | ✘ | 0.2101 | 0.0316 | 32.18 | |
| ✘ | ✔ | ✘ | 0.1830 | 0.0298 | 32.97 | |
| ✘ | ✘ | ✔ | 0.1806 | 0.0260 | 33.42 |
| Description | Params (M) | MAdds (G) | MRAE | RMSE | PSNR |
|---|---|---|---|---|---|
| 0.09 | 1 | 0.2434 | 0.0406 | 30.02 | |
| 0.28 | 4 | 0.2127 | 0.0312 | 32.16 | |
| 1.08 | 14 | 0.1806 | 0.0260 | 33.42 | |
| 4.05 | 54 | 0.2074 | 0.0309 | 32.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, X.; He, L.; Mao, J.; Xu, M. Spectral Superresolution Using Transformer with Convolutional Spectral Self-Attention. Remote Sens. 2024, 16, 1688. https://doi.org/10.3390/rs16101688
Liao X, He L, Mao J, Xu M. Spectral Superresolution Using Transformer with Convolutional Spectral Self-Attention. Remote Sensing. 2024; 16(10):1688. https://doi.org/10.3390/rs16101688
Chicago/Turabian StyleLiao, Xiaomei, Lirong He, Jiayou Mao, and Meng Xu. 2024. "Spectral Superresolution Using Transformer with Convolutional Spectral Self-Attention" Remote Sensing 16, no. 10: 1688. https://doi.org/10.3390/rs16101688
APA StyleLiao, X., He, L., Mao, J., & Xu, M. (2024). Spectral Superresolution Using Transformer with Convolutional Spectral Self-Attention. Remote Sensing, 16(10), 1688. https://doi.org/10.3390/rs16101688





