Multi-Timescale Characteristics of Southwestern Australia Nearshore Surface Current and Its Response to ENSO Revealed by High-Frequency Radar

Abstract

The surface currents in coastal areas are closely related to the ecological environment and human activities, and are influenced by both local and remote factors of different timescales, resulting in complex genesis and multi-timescale characteristics. In this research, 9-year-long, hourly high-frequency radar (HFR) surface current observations are utilized together with satellite remote sensing reanalysis products and mooring data, and based on the Empirical Orthogonal Function (EOF) and correlation analysis, we revealed the multi-timescale characteristics of the surface currents in Fremantle Sea (32°S), Southwestern Australia, and explored the corresponding driving factors as well as the impact of El Niño-Southern Oscillation (ENSO) on the nearshore currents. Results show that the currents on the slope are dominated by the southward Leeuwin Current (LC), and the currents within the shelf are dominated by winds, which are subject to obvious diurnal and seasonal variations. The strong bathymetry variation there, from a wide shelf in the north to a narrow shelf in this study region, also plays an important role, resulting in the frequent occurrence of nearshore eddies. In addition, the near-zonal winds south of 30°S in winter contribute to the interannual variability of the Leeuwin Current at Fremantle, especially in 2011, when the onshore shelf circulation is particularly strong because of the climatic factors, together with the wind-driven offshore circulation, which results in significant and long-lasting eddies. The southward Leeuwin Current along Southwestern Australia shows a strong response to interannual climatic variability. During La Niña years, the equatorial thermal anomalies generate the westward anomalies in winds and equatorial currents, which in turn strengthen the Leeuwin Current and trigger the cross-shelf current as well as downwelling within the shelf at Fremantle, whereas during El Niño years, the climate anomalies and the response of coastal currents are opposite. This paper provides insights into the multi-timescale nature of coastal surface currents and the relative importance of different driving mechanisms. It also demonstrates the potential of HFR to reveal the response of nearshore currents to climate anomalies when combined with other multivariate data. Meanwhile, the methodology adopted in this research is applicable to other coastal regions with long-term available HFR observations.

1. Introduction

The nearshore surface currents are influenced by both local and remote factors, consequently, their causes are complex and have multi-timescale characteristics. Previously, observations of near-shore currents relied primarily on in-situ instruments and satellite remote sensing. However, the former only samples at a limited number of sites, and the latter, apart from its relatively low spatial and temporal accuracy, is unable to truly reflect the nearshore current due to the failure of the geostrophic equilibrium assumption in the shallow water regions [1]. High-frequency radar (HFR), which is based on the mechanism of Bragg scattering between electromagnetic waves and sea surface gravity waves (with wavelengths ranging from 5 to 50 m), has the advantages of relatively large spatial coverage, high accuracy, high spatial and temporal resolution, and relatively low cost. Therefore, HFR observation networks have been rapidly increasing in recent years, and HFR has become an important means of monitoring the physical state of the sea surface in coastal areas around the world [2,3]. However, to date, most HFR-based studies of the sea surface current have used relatively short-term (e.g., several months or tens of days) data and thus have mainly focused on the short-term characteristics of the current, making it difficult to reveal the comprehensive (multi-timescale) and long-term characteristics of the nearshore current, particularly its potential links to climate.

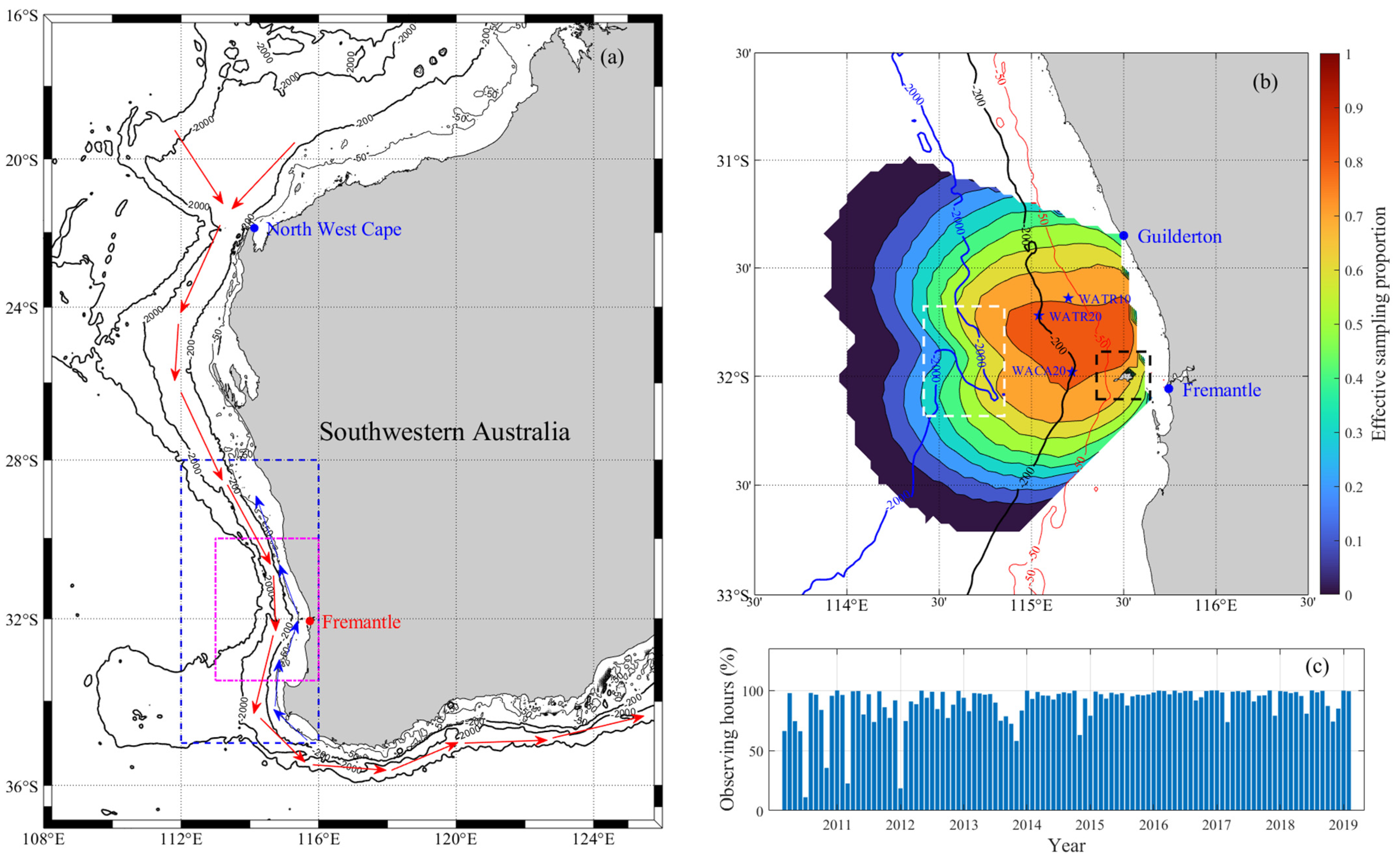
In Southwestern Australia (Figure 1a), the local surface current pattern is unique because of the Leeuwin Current (LC), which is the only poleward eastern boundary current in the world and active on the local continental slope. Meanwhile, the Capes Current (CC), a seasonal northward alongshore circulation driven by the near-meridional northward monsoon, dominates the local continental shelf. These two circulations interact with the abruptly varying bathymetry, i.e., the sharp narrowing of continental shelf width at Perth Canyon, resulting in the frequent occurrence of eddies there [4,5,6]. The Leeuwin Current originates at the Northwest Cape (NWC) of Australia and is directly driven by the near-meridional pressure gradient along the southwestern coast of Australia, which is formed by a relatively higher sea level in northwestern Australia. The current there is connected to the Indonesian Throughflow (ITF), which originates in the tropical western Pacific. This connection leads to a significant correlation between LC and tropical climate anomalies, such as El Niño-Southern Oscillation (ENSO), which is active in the tropical Pacific and is a major driver of global climate anomalies [4,7,8]. In addition, the coastal currents along the coast from Perth to Geralton (i.e., the Fremantle Sea) are influenced by the Land-Sea Breeze System (LSB) with a diurnal cycle and the monsoon winds with a seasonal cycle [9,10]. In summary, the surface currents in the Fremantle Sea are multi-timescale in nature and are influenced by a variety of local and remote dynamics, as well as the abruptly varying topography. Fortunately, the HFRs (Figure 1b) located on the Fremantle Sea (32°S) coast of Southwestern Australia have accumulated more than a decade of observational data (from 2009 to present), and long-term in-situ observations of moorings and tide gauges are also available. Therefore, this area is an ideal place to conduct relevant research, especially with respect to revealing the response of nearshore (surface and interior) currents to climatic events.

The application of HFR to surface current detection has boomed in recent years. Most of them focus on characterizing the surface current patterns, such as boundary currents, eddies, oceanic fronts, and near-inertial currents [11,12,13,14]. Some of them investigate the mechanisms of small-scale physical processes, such as the impact of sea surface wind, tide, estuarine flow, and upwelling on the surface currents [15,16,17,18,19,20,21]. In addition, several studies have investigated the small- to medium-scale near-shore processes, such as the cross-shore transport of surface water and the transport of surface biological communities and chemicals [22,23,24], since their transports are of environmental and ecological importance. Meanwhile, the long-term characteristics of the HFR-derived current have also been investigated, such as the characteristics of surface circulation on the west and east coasts of the United States revealed by Kim and Roarty, respectively [25,26]. In Australia, the seasonal and multi-year characteristics of the East Australian Current (EAC) have also been studied by Mao [14] and Archer [11]. Moreover, the Leeuwin Current has been characterized by Cosoli [12]. However, it is still relatively rare to use the HFR surface current to study the response of coastal surface currents to climatic variations [27].

In Southwestern Australia, the HFR surface current of the Rottnest Shelf has been studied by Penton [28], which reveals that persistent northward breezes during summer have a strong effect on the seasonal variation of flow velocity, with a stronger effect on flow speed than on flow direction. In addition, the local upper ocean dynamics near the critical latitude (30°S) have been revealed by a range of data, including HFR surface current [29]. Meanwhile, the effect of the offshore current on surface gravity waves on the southwest Australian shelf has also been investigated by integrating the SWAN wave model and HFR data [30]. The results show that the Leeuwin Current and its eddies have a significant effect on the modeled waves. Later, 33-month-long surface current data from both SeaSonde and WERA radars was used by Cosoli [12] to study the coastal circulation of Southwestern Australia between 29°S and 32°S. In that study, the merging of these two types of radar data allowed for a detailed observation of the local Leeuwin Current, the Capes Current, and the mesoscale to sub-mesoscale eddies, as well as the diurnal cycle of surface current.

The above studies mainly verified the capability of HFR to reveal various oceanic surface phenomena. These studies took advantage of the spatial and temporal resolution of the radar data to gain a better understanding of the short-term cyclic processes, such as gravity waves, tidal currents, and breezes. However, the multi-timescale characteristics of the current in the nearshore region could be further investigated, especially the response of the nearshore currents to climate anomalies (e.g., ENSO), which requires long-term data. Therefore, the present study aims to focus on these issues using long-term HFR radar observations, which is ideal for the present purposes.

This research utilized the hourly HFR data from March 2010 to February 2019 of a WERA radar at the ROT (i.e., Rottnest Shelf) site in Southwestern Australia (Figure 1b), along with satellite remote sensing reanalysis products and in-situ mooring and tide gauge data. This study investigates the local coastal surface currents at three different timescales (diurnal, seasonal, and interannual) and in three marine topographic units (inner shelf, outer shelf, and continental slope). This study also employs Empirical Orthogonal Function (EOF) analysis to identify various spatial modes of surface currents and their temporal coefficients. Additionally, the surface currents from HFR are correlated with the sea surface wind, satellite-observed current (primarily geostrophic), and sea level to determine the relative significance of each forcing in generating the surface current. Furthermore, we analyzed the influence of ENSO on the strength of the Leeuwin Current in the Fremantle Sea, the cross-shelf current on the outer shelf, and the upwelling or downwelling in the inner shelf, along with the temperature and current data at depth.

This paper consists of six sections. Section 2 introduces the data and methods used. Section 3 describes the multi-timescale characteristics of the HFR-derived current in different spatial units. Section 4 analyzes the driving factors and investigates the causes of the current at different timescales through correlation analysis. Section 5 investigates the current response to ENSO, including the slope current, cross-shelf current, and vertical exchanges. Section 6 provides discussions and conclusions.

Figure 1. Western Australia, the ROT radar site located in Fremantle Sea, and the effective sampling proportion of radar. (a) The research area, North West Cape is the north-south boundary of Western Australia; the red (blue) arrows represent Leeuwin Current (Capes Current) [31]; the magenta (blue) dashed box indicates the range of driving factors data used to investigate the causes of diurnal (seasonal and interannual) characteristics of the surface currents; (b) The observing range of ROT radar and the spatial distribution of temporal effective sampling proportion of it; WATR10, WATR20, and WACA20 are 3 mooring sites; the white (black) dashed box indicates Perth Canyon (Rottnest Island); (c) The percentage ratio of radar observing hours per month.

Figure 1. Western Australia, the ROT radar site located in Fremantle Sea, and the effective sampling proportion of radar. (a) The research area, North West Cape is the north-south boundary of Western Australia; the red (blue) arrows represent Leeuwin Current (Capes Current) [31]; the magenta (blue) dashed box indicates the range of driving factors data used to investigate the causes of diurnal (seasonal and interannual) characteristics of the surface currents; (b) The observing range of ROT radar and the spatial distribution of temporal effective sampling proportion of it; WATR10, WATR20, and WACA20 are 3 mooring sites; the white (black) dashed box indicates Perth Canyon (Rottnest Island); (c) The percentage ratio of radar observing hours per month.

2. Materials and Methods

2.1. Materials

2.1.1. The High-Frequency Radar Data

The high-frequency radar data utilized in this research were provided by the Australian Ocean Data Network (aodn.org.au (accessed on 31 December 2020)). The surface current data were obtained from a phased array WERA radar site named ROT in Southwestern Australia, which is one of the nine operating radar sites (4 SeaSonde HFRs and 5 WERA HFRs) deployed by the Australian Coastal Ocean Radar Network (ACORN), a component of the Integrated Marine Observing System (IMOS).

The ROT radar operates at a frequency of 9.335 MHz with a bandwidth of 33.4 kHz. It has an integration time of 5 minutes and an output rate of 1 h for vectors and 5 min for radials; its coverage range is from 113.8°E to 115.75°E and from 31°S to 32.75°S; and it includes two significant topographic features: Perth Canyon (depth > 1000 m) and Rottnest Island (depth < 50 m). The total current vector at each grid of the radar observation is reconstructed by composing the two radial current velocities measured by the Fremantle (32.03°S, 115.74°E) and Guildton (31.34°S, 115.49°E) stations [32]. Since a single radar station can only obtain the radial current velocities in a single direction. Barrick and Evans [33] proposed to use the simultaneous signals from two separate stations to compose the current vector. In this method, the two radial velocity components (with the azimuth angle and distance of the grid point relative to the radars) from the grid point to each of the two radar stations are composed into the total current vector.

Figure 1b demonstrates that the effective sampling proportion can still exceed 70% in the nearshore region where the intersection angle of the radar beams from the two stations is relatively large (>40°). Consecutive nine years of surface current data were analyzed, from March 2010 to February 2019, with a temporal interval of one hour and a spatial resolution of 0.0424° × 0.0361° (approximately 4 km × 4 km). The percentage of effective radar observation time in each month is presented in Figure 1c. Overall, the temporal coverage of the data are over 70%, except for a few months before 2012.

The HFR current data are empty at times when there is no effective radar observation; thus, the current component values at these unobserved times were assigned the value of NAN. Additionally, the spatial dimensions of the radar data were reordered into a 2-dimensional geographic coordinate grid. Moreover, current data near the edge of the observation range may suffer from ineffective sampling and low accuracy. Therefore, data in grids with an effective sampling proportion lower than 0.3 is assigned NAN values to ensure high data quality.

The 9-year-long hourly HFR data (with a temporal length of 78,888) were spatially averaged over three different spatial units of the inner shelf (0–50 m), outer shelf (50–200 m), and slope (200–200 m) to gain a preliminary understanding of the multi-timescale characteristics of HFR-derived current at different locations (Figure 2(A1–F1)). The outliers were removed, and a linear interpolation was conducted to fill in the missing values in time. The frequency spectra were obtained using the Fast Fourier Transform (FFT) and shown in Figure 2(A2–F2). Here, we focused on comparing the spectra amplitudes of the diurnal cycle (short-term) and long-term cycles (close to or longer than 1 year). Additionally, within the same spatial unit, the spectra differences between the latitudinal and longitudinal velocity components (represented by U and V, respectively) were also analyzed.

Figure 2 shows that all time series exhibit a strong diurnal cycle (spectra peaks near the Freq value of 10^−1.38 h⁻¹, i.e., 24 h). Additionally, long-term cycles (spectra peaks near 10^−3.94 h⁻¹, i.e., 1-year) and semi-diurnal cycles (spectra peaks near 10^−1.08 h⁻¹, i.e., 12 h) are also evident for most time series. For the U-component, the diurnal cycle is more significant than the long-term cycles in the outer shelf (Figure 2(B2)), whereas the reverse is true in the inner shelf and slope. This suggests that the diurnal signals are more pronounced on the outer shelf, probably caused by the larger amplitude of diurnal tides there. For the V-component in the slope, the long-term cycles are more significant than the diurnal cycle, and a significant number of high-frequency signals were also detected, suggesting the possibility of frequent short-term events (e.g., vortex) (Figure 2(F2)). The semi-diurnal cycle of the U-component is stronger than that of the V-component, which agrees with the fact that the semi-diurnal tidal currents are mainly in the latitudinal direction (near perpendicular to the local coastline). A comparison of amplitudes near the Freq value of 10^−3.9425 h⁻¹ (the black vertical dashed lines) between the U and V components indicates that most of the U-component spectra have a higher amplitude near a 1-year cycle (i.e., seasonal), while most of the highest amplitudes of the V-component spectra are at lower frequencies (longer than 1-year) (i.e., interannual). In summary, the diurnal cycles of the currents are strong in all sub-regions, and the long-term cycles of the slope current are the strongest.

2.1.2. The Satellite and In-Situ Data

The reanalysis products from satellite and the in-situ datasets (

Table 1. Datasets utilized in this research and the associated spatial and temporal ranges.

1. Reanalysis Products
Parameters	Geostrophic Current	Sea Surface Height	Sea Surface Wind
Temporal Range	2000–2019	2010.03–2019.02	2010.03–2019.02
Spatial Range	(112°E–116°E, 35°S–25°S)		(112°E–116°E, 35°S–28°S)
2. In-Situ Observations in the Nearshore
Parameters	Fremantle Sea Level		Mooring-measured current and seawater temperature
Temporal Range	2010.03–2019.02		2010.03–2019.02
Spatial Range	(32.056°S, 115.739°E)		WATR10: (31.64°S, 115.20°E). (depth range: 101–25 m, depth interval: 5 m) WATR20: (31.72°S, 115.04°E). (depth range: 196–25 m, depth interval: 10 m) WACA20: (31.98°S, 115.22°E). (depth range: 201–25 m, depth interval: 5 m)

) are used as complementary datasets to reveal the characteristics of the local current, the causes of the HFR current, and the response of the current to ENSO.

The satellite-observed sea surface currents (mainly the geostrophic currents) and sea surface height data are obtained from Copernicus Marine Environment Monitoring Service (CMEMS) using the product code GLOBAL_REANALYSIS_PHY_001_030 (https://data.marine.copernicus.eu/ (accessed on 31 December 2020)), with the same spatial resolution of 1/12° × 1/12° and a daily temporal resolution, respectively. The Copernicus Data Center of the European Space Agency have made this product publicly available.

The sea surface wind data were obtained from the Copernicus Climate Data Store. The data were released by the European Centre for Medium-Range Weather Forecasts (ECMWF) and named the ERA5 Product, which is the fifth-generation atmospheric reanalysis dataset (https://cds.climate.copernicus.eu/ (accessed on 1 July 2023)). Wind data at a height of 10 m above the sea surface were downloaded with a spatial and temporal resolution of 1/4° × 1/4° and hourly, respectively.

The reanalysis products mentioned above synthesize global observations and integrate them with physical models through data assimilation to produce globally consistent products. These products have been tested and evaluated for use in both coastal and open-sea areas.

The Fremantle Sea Level (FSL), whose observation site is located within the 50 m isobath (inner shelf), is considered an indicator of the strength of the Leeuwin current in Southwestern Australia [34]. It is the longest recorded water level in the Southern Hemisphere (since 1897), made publicly available by the University of Hawaii Sea Level Center with an hourly temporal resolution (https://psmsl.org/data/obtaining/ (accessed on 31 December 2020)).

The mooring data are primarily used to reveal the response of continental shelf waters to ENSO. They were also provided by the Australian Ocean Data Network (aodn.org.au (accessed on 1 September 2023)), including three mooring sites: WATR10, WATR20, and WACA20 (Figure 1b). The mooring instruments in Fremantle include temperature loggers, conductivity-temperature-depth (CTD) instruments, water-quality monitors (WQM), acoustic Doppler current profilers (ADCPs), and single-point current meters. The current measuring instruments are mainly the Nortek Aquadopp and Nortek Continental from Norway, and the RBR DR1050P from Canada. The primary seawater temperature measuring instruments are the Seabird SBE39 and Seabird SBE37-SM from America. These moorings provide measurements of vertical flow velocity (W), east-west flow velocity (U), north-south flow velocity (V), and temperature at different depths of seawater with a depth interval of 5 m (or 10 m) and a major temporal interval of 20 min. The data released are aggregated at an hourly interval.

Coastline data from the GSHHG website (http://www.soest.hawaii.edu/pwessel/gshhg/ (accessed on 31 December 2020)) and isobath data from the ETOPO website (https://www.ncei.noaa.gov/products/etopo-global-relief-model (accessed on 31 December 2020)) with a spatial resolution of 1 arcminute were utilized. Additionally, the Southern Oscillation Index (SOI) provided by the NOAA Physical Sciences Laboratory (https://psl.noaa.gov/data/climateindices/list/ (accessed on 31 December 2022)) was used to evaluate the climatic impacts of ENSO on the coastal waters in Southwestern Australia.

2.2. Methods

The large set of radar data (~92 (latitudinal grids) × 62 (longitudinal grids) × 24 (h) × 30 (days) × 12 (months) × 9 (years)) are characterized in three aspects: multi-timescales (diurnal, seasonal, interannual), multi-space (inner shelf, outer shelf, and slope), and multi-modes (EOF modes, such as coherent circulations and eddies).

This study analyzed the local surface currents at three timescales: diurnal, seasonal, and interannual, corresponding to the timescales of the driving forces. Firstly, the Fremantle Sea is situated at low-mid latitudes where the local winds and currents exhibit strong seasonal variation. Secondly, the local diurnal breezes and tidal forces cause diurnal variations in the currents. Finally, the Leeuwin Current in this region is closely linked to the tropical sea, where interannual or even longer-periodic variability is strong. Additionally, the spectral analysis results of the HFR-derived current (Figure 2) indicate both strong diurnal variability (i.e., representative of short-term variability) and significant long-term variability, justifying the selected timescales for analysis.

Table 2. Methods for extracting multi-timescale information from data.

1. Original Data
Matrix Dimensions	X0: Lat (m) × Lon (n) × Hour (24) × Day (~30) × Month (12) × Year (9). For the ROT radar data, ‘m’ is 92 and ‘n’ is 62.
2. Extracting the Time-Scale Signals
Diurnal	Averaging the dimensions of Day, Month, and Year, X0 being converted into a matrix X1 with a size of m × n × 24.
Seasonal	Averaging the dimensions of Hour and Year, X0 being converted into a matrix X2 with a size of m × n × (~)30 × 12 (m × n × 366). (The seasonal scale data have been adjusted to a temporal length of 366 days (i.e., a lunar year), so the ‘February 29 of the leap years’ in the original data are filled by the NAN value matrix in a size of m × n).
Interannual	Averaging the hourly data into monthly data (m × n × 108), then filtering it by a 13-point moving average, transferring X0 into a matrix X3 with a size of m × n × 96.
3. Statistics Values
Diurnal	Divide X1 into 4 matrices (X1a, X1b, X1c, X1d) with a size of m × n × 6, respectively, based on 4 six-hour intervals (21:00–02:59, 03:00–08:59, 09:00–14:59, 15:00–20:59, UTC); Next, calculate the temporal mean values for the above 4 matrices to describe the diurnal mean states.
Seasonal	Divide X2 into 4 matrices (X2a, X2b, X2c, X2d) with a size of m × n × (~)30 × 3, respectively, according to 4 seasons (December-February, March-May, June-August, September-November); Then, calculate the temporal mean values for the above 4 matrices to describe the seasonal mean states.
Interannual	For a scalar or each component of a vector, the seasonally mean of X0 is calculated, i.e., transfer X0 into a matrix X4 with a size of m × n × 36; X4 is then divided into 4 matrices (X4a, X4b, X4c, and X4d), according to the four seasons, each with a size of m × n × 9. The interannual variability of the data for each season are described by calculating the temporal standard deviation for it (e.g., calculate X5a for X4a), with a size of m × n; For a vector, calculate the root mean square for the temporal standard deviation values of its components (e.g., the X5a matrices of components U and V) to indicate the interannual variability, with a size of m × n [26].

presents the technique for extracting multi-timescale data. ‘Lat’ and ‘Lon’ denote the latitude and longitude dimensions of the original data matrix, while ‘Hour’, ‘Day’, ‘Month’, and ‘Year’ indicate the timescales (the size of each dimension of data are listed in the bracket next to it). The original data have only three dimensions (i.e., longitude, latitude, and time); the time dimension were divided into Hour, Day, Month, and Year timescales (data dimensions). The primary idea of extracting data at a specific timescale are to average the data at other timescales to smooth out the irrelevant components. For instance, to display the overall diurnal variation of surface currents, the seasonal and interannual variations are smoothed out by averaging the hourly current data over all days (~366 (d) × 9 (y) days). Similarly, to demonstrate the general seasonal variation, the diurnal and interannual variation are smoothed out by first averaging the current data over each day (smoothing out diurnal variation), and for each day within a year (~366), the data over nine years are averaged (smoothing out interannual variation). However, to show the interannual variation of the surface currents, a 13-point moving average filtering was applied to the monthly mean data. Meanwhile, the multi-timescale signals of the satellite, sea level, and other data are also extracted using the above technique.

This study area has a relatively straight coastline and isobaths (near meridional). Therefore, the data are spatially categorized into three sub-regions based on bathymetry: the inner shelf (0–50 m), the outer shelf (50–200 m), and the continental slope (200–2000 m). The ETOPO isobath matrices were interpolated to match the grid points of the corresponding data matrices. The spatial units of each grid are then categorized into one of the three sub-regions.

Empirical Orthogonal Function analysis (EOF) [35,36] was conducted to identify the primary modes of surface currents and driving forces on different timescales. Being a widely used technique for extracting mode information from spatiotemporal data [37,38], EOF characterizes the major spatial structures of the data by several primary modes and denotes the temporal variation of each mode by a temporal coefficient. The relative importance of each mode is denoted by its contribution to the total variance. This characterization reveals the dominant spatial patterns of the surface currents and provides clues to the dominant driving forces. Moreover, EOF can be applied to spatially irregular grids, which is exactly the case with the spatial grids of radar data. As mentioned above, the HFR data contains numerous missing values around the edge of its observation range. Therefore, apart from replacing the low effective sampling proportion (<0.3) grids with NAN values, a linear interpolation was conducted for all other grids with missing data. The interpolated data were used in the calculation of both EOF modes and correlation coefficients.

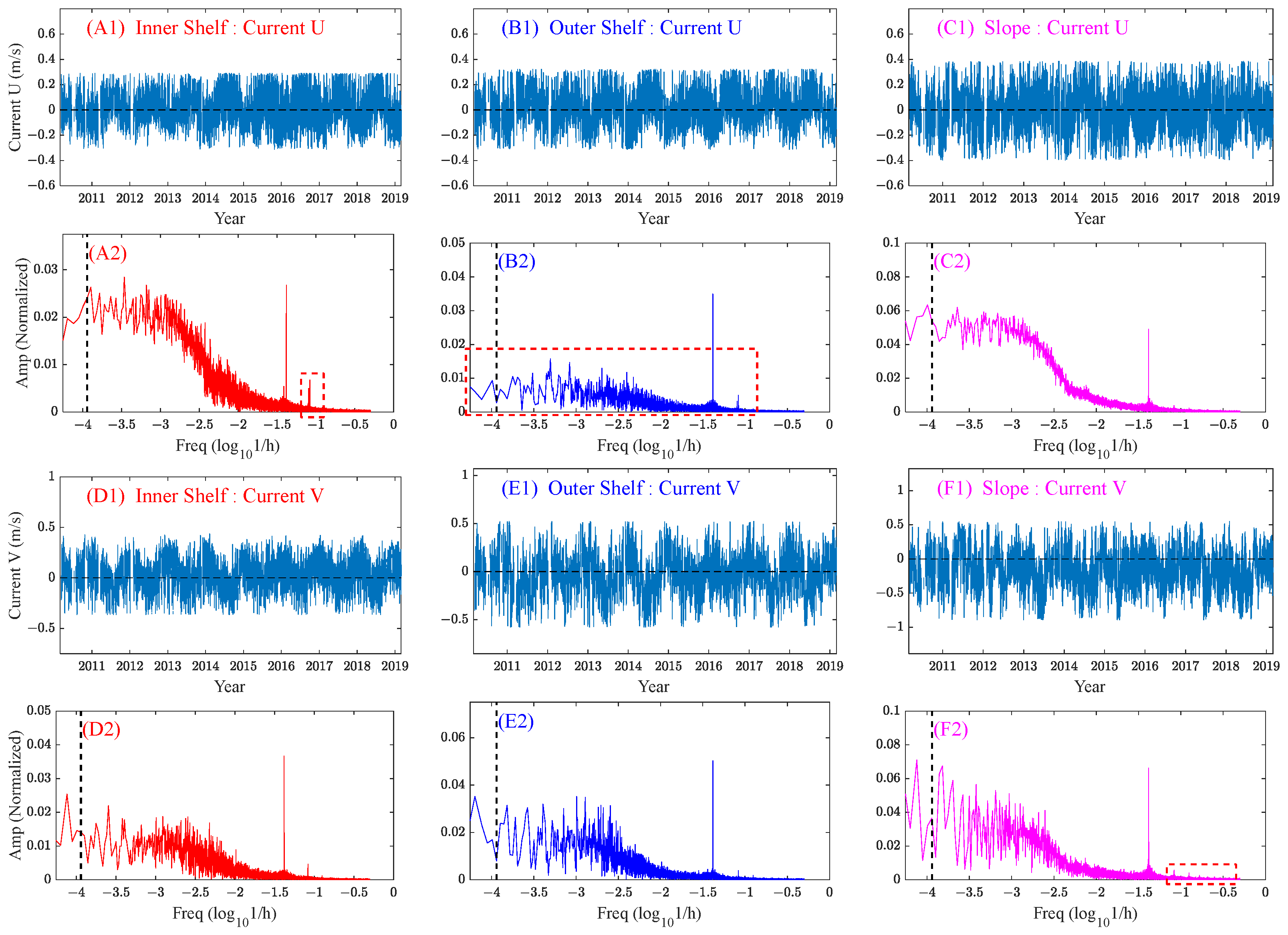
3. Multi-Timescale Characteristics of the Surface Currents Observed by High-Frequency Radar

The HFR surface currents are characterized both temporally and spatially. The variation of spatial patterns with time is shown for different time scales (Figure 3), and the temporal variations at different timescales are investigated for different subregions (Figure 4).

Figure 3 illustrates the temporal variation of Fremantle surface current patterns at different timescales, including diurnal, seasonal, and interannual scales, using an assemblage of 9 years of long-term radar data.

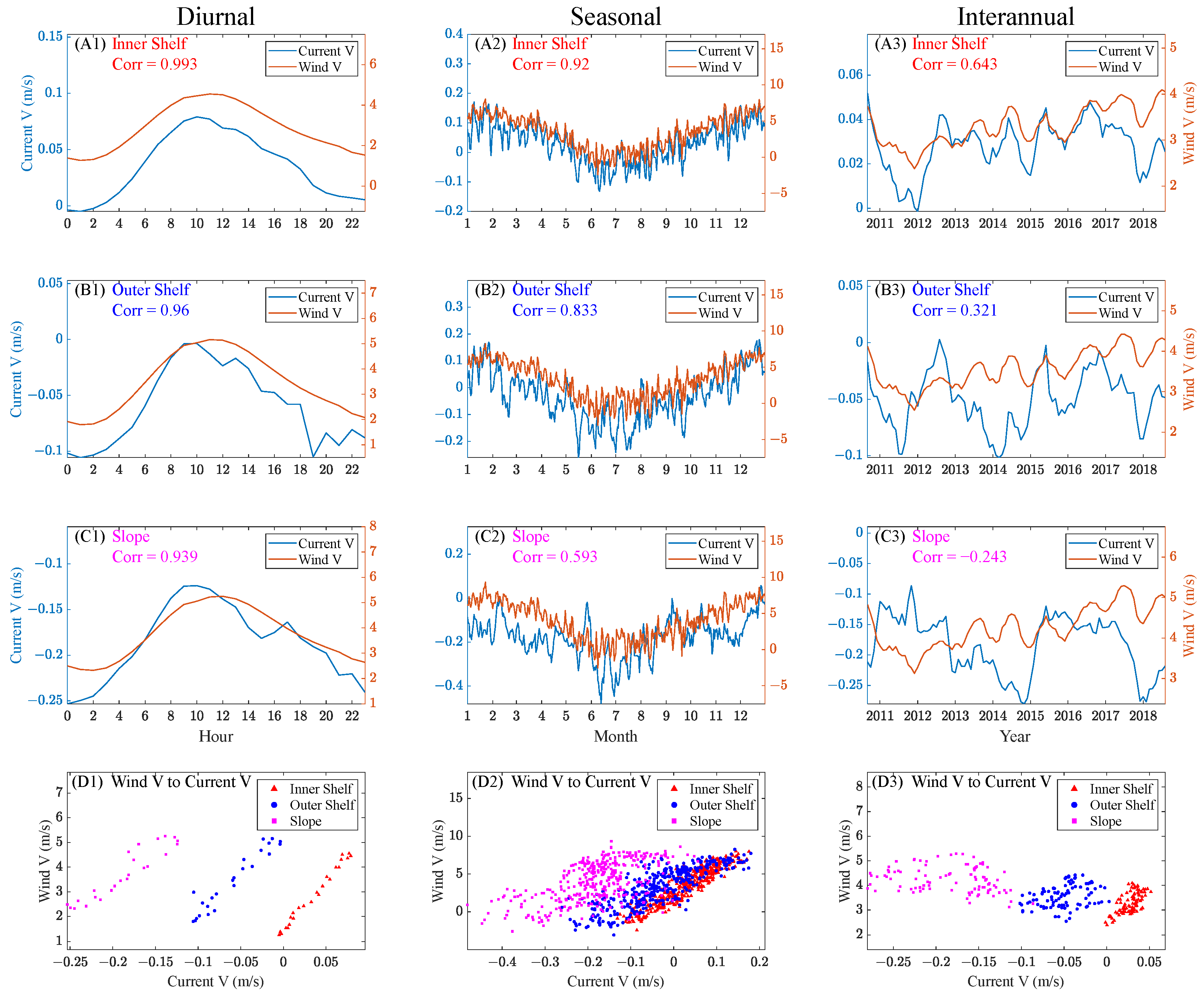
For the diurnal current, the flow patterns inside the shelf differ significantly from those outside (Figure 3(A1–D1)). The surface currents outside the 200 m isobath flow persistently southward, yet their intensities fluctuate significantly within a day. During 21:00–02:59, the maximum speed generally exceeds 0.3 m/s in a mostly southward direction. After that, from 03:00 to 08:59, a notably eastward turning is observed there, which later transfers to a westward turning from 15:00 to 20:59, with a transitional stage from 09:00 to 14:59, during which the slope current is weakest (<0.2 m/s). Meanwhile, the surface currents inside the 200 m isobath are predominantly northward with a speed generally not exceeding 0.15 m/s, peeking during 09:00–14:59 and being weakest during 21:00–02:59, the variation of which is opposite to the outer-shelf current. The opposite directions of currents inside and outside the shelf and their diurnal variation indicate the strong influence of the northward winds, which vary diurnally.

The flow patterns also vary significantly with the seasons (Figure 3(A2–D2)), particularly with opposite current features in winter and summer. During the austral winter (Figure 3(B2)), the shelf current flows weakly southward, while the slope current exhibits the strongest southward circulation over the year (exceeding 0.5 m/s in the northern part). In contrast, during the austral summer (Figure 3(D2)), the strongest northward circulation is observed for the shelf region (~0.2 m/s), and the southward circulation on the slope is the weakest (slightly over 0.2 m/s). Between summer and winter, the autumn and spring currents show a transitional feature. However, the flow pattern in autumn (spring) is more similar to that in winter (summer). It seems clear that the currents both inside and outside the shelf are strongly influenced by a seasonal meridional force (i.e., the monsoon winds). The strongest northward winds in summer drive the strongest northward shelf current and weaken the southward slope current. In contrast, the current in winter is dominated by the strong southward Leeuwin Current with the weakest northward winds, and therefore the entire coastal region is dominated by relatively strong southward circulation. The cross-shelf current is strong in winter and summer due to the strongest Leeuwin Current and Capes Current, respectively (Figure 3(B2,D2)), indicating a strong cross-shore water exchange between the shelf and the open sea.

For the interannual variability of the currents, a notable difference is observed between the currents inside and outside the shelf (Figure 3(A3–D3)). The current inside the shelf shows weak interannual variability, while the opposite is true for the current outside the shelf, especially in autumn and winter (Figure 3(B3)). Since the current outside the shelf is dominated by the Leeuwin Current, its significant interannual variability reflects (or is derived from) that of the Leeuwin Current. The shape of the cross (‘+’) suggests that within the shelf, the variability of the current U-component is of similar magnitude to that of the current V-component, which is also the case for the slope current in spring and summer. However, the slope current shows evidently stronger variability in its V-component than that in its U-component, especially during Autumn and Winter. Since the Leeuwin Current is a southward circulation that peaks in winter, the strong interannual fluctuation of its meridional magnitude in winter (Figure 3(B3)) suggests the possible influence of climatic factors, which control the strength of the Leeuwin Current.

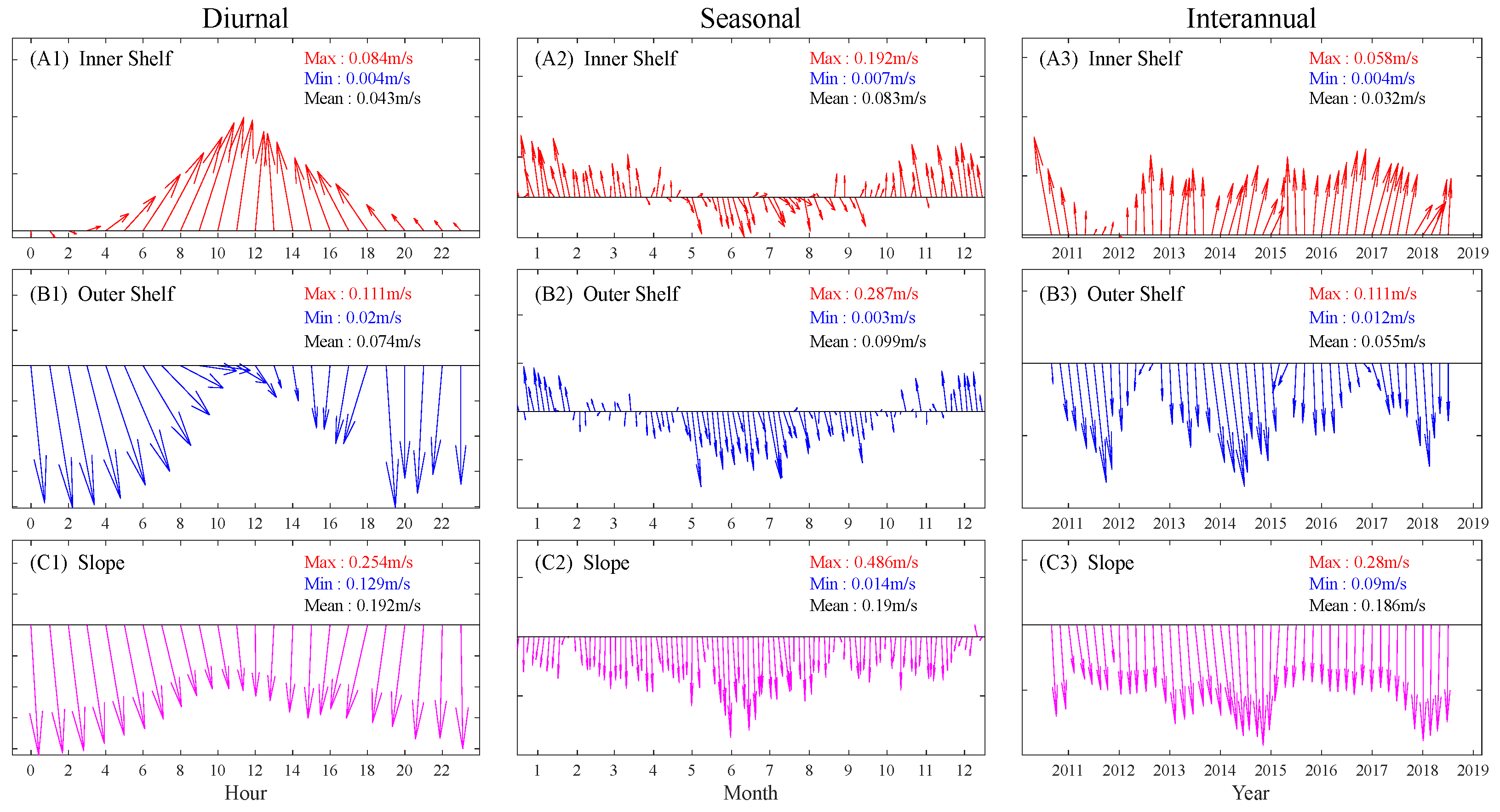
To analyze the temporal variation of currents in different sub-regions, the time series of the HFR-derived current vector for each timescale are spatially averaged over each sub-region. The data (matrices) used for this purpose (Figure 4, Figure 5 and Figure 6) are referred to as X1, X2, and X3 in Table 2. The resulting spatially averaged current vector time series shows distinct features in each spatial unit on different timescales (Figure 4).

A strong diurnal variation is observed for the inner shelf current, with the maximum speed 20 times higher than the minimum (Figure 4(A1)), whereas the slope current is much more uniform, with the maximum speed less than 2 times the minimum (Figure 4(C1)). At the seasonal scale, the dominant inner shelf current is southward during late autumn and winter (May to September) (Figure 4(A2)), when the monsoon wind from the south is weakest, and reverses to northward during the rest of the year, being particularly strong in summer (November to January) due to the strong northward monsoon wind. The current on the outer shelf (Figure 4(B2)) shows some similarity to the inner shelf current, except that the southward current dominates over a longer period (February to October), which is reasonable since the outer shelf current is more influenced by the slope current than the inner shelf current, as shown by the diurnal current patterns (Figure 4(A1–C1)). The slope current maintains a stable southward circulation on all timescales, but with a magnitude that also fluctuates with the strength of the northward winds.

It should be noted that 2011 is a unique year. During 2011, the inner shelf northward current was much weaker than the other years (Figure 4(A3)), suggesting weaker northward winds. In contrast, the outer shelf southward current was strong (Figure 4(B3)), and the slope southward current was relatively weak, suggesting that a curvature may have occurred in the path of Leeuwin Current, such as a counterclockwise eddy, which is later confirmed in Figure 6.

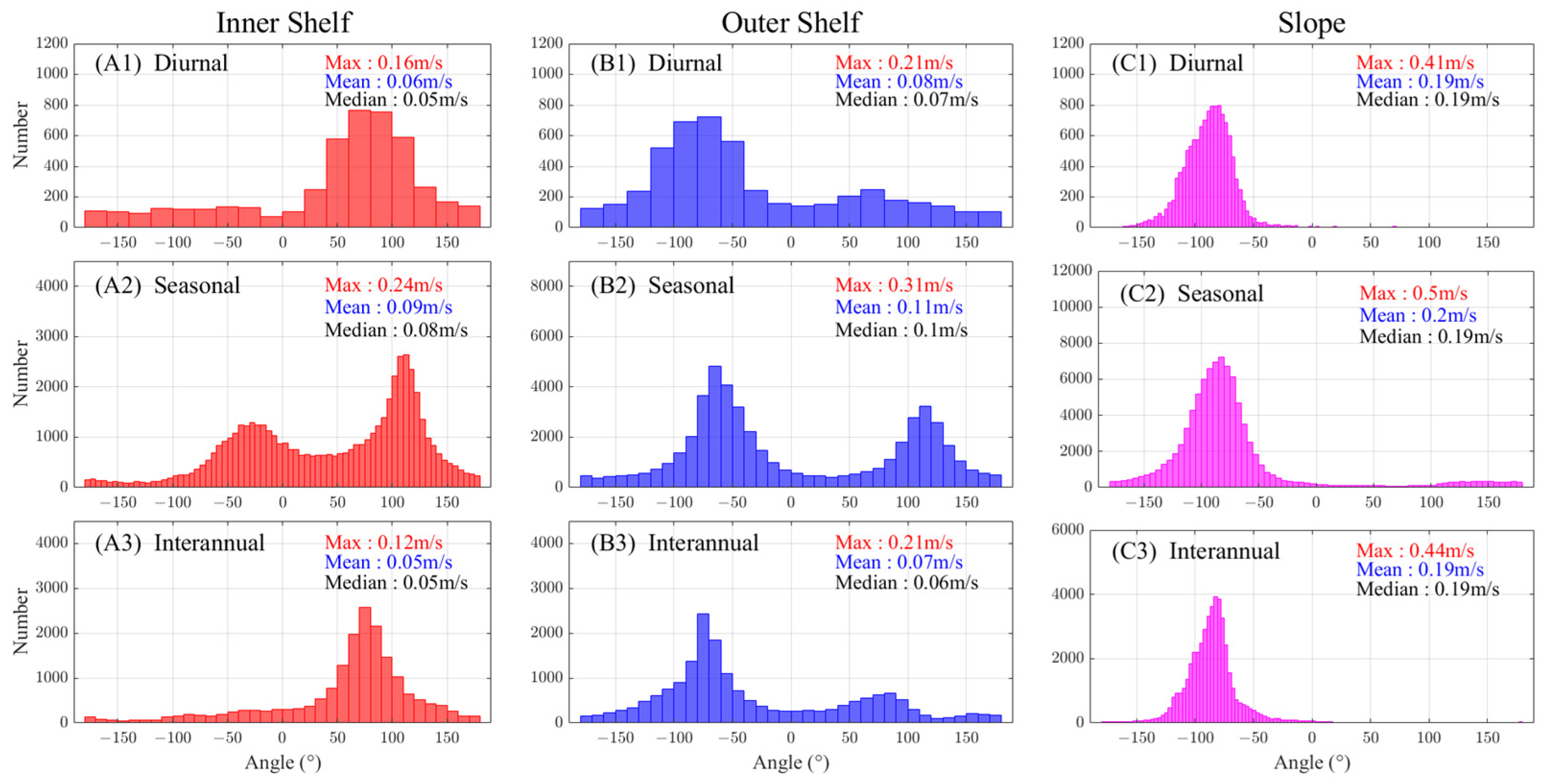
A histogram analysis of flow direction was performed to illustrate the differences in flow patterns in different sub-regions (Figure 5). Instead of averaging over time, the current data at each time of the respective timescale (e.g., one hour on the diurnal scale, one day on the seasonal scale, one month on the interannual scale) are considered an individual data value in the histogram.

At all timescales, the histograms of current direction in the three sub-regions show consistent patterns of variation, with the southward current dominating the slope, the northward current dominating the inner shelf, and the outer shelf current showing a transitional feature (Figure 5). However, at the seasonal scale, all the histograms show an evident bimodal distribution, i.e., a cyclical feature (Figure 5(A2–C2)). A comparison of the current speed in each subplot reveals that the current speed gradually decreases toward the shore. The highest speed values occur at the seasonal scale (Figure 5(A2–C2)). Since the seasonal signals smoothed out both diurnal and interannual fluctuations, such high speeds of the seasonal currents indicate that the (seasonal) monsoon winds are the most dominant factor affecting current intensities, especially in the inner shelf, where the contrast in current speed between the seasonal scale and the other scales is greatest.

The above analysis reveals the variation of the HFR current for each sub-region and at different timescales. The Leeuwin Current and monsoon are revealed to be two dominant factors influencing the HFR current, with the former dominating the slope region and the latter dominating the inner shelf. The local surface currents contain both strong seasonal variations from the monsoon and significant interannual variation influenced by the fluctuation in the strength of the Leeuwin Current, in which the latter is related to climatic factors.

The EOF analysis is applied to HFR-derived current to reveal the dominant spatial modes and the corresponding temporal variation, as well as the importance of each mode (Figure 6). The first EOF modes (EOF1) of diurnal, seasonal, and interannual current all exhibit a strong southward circulation on the continental slope (Leeuwin Current), and the corresponding temporal coefficients (PCs) reflect that this mode is the weakest/strongest at noon/midnight and the strongest/weakest in winter/summer, with obvious interannual variations. At diurnal and interannual scales, the first EOF modes contribute nearly 90% of the total variance of the data. At the seasonal scale, the contribution coefficient of EOF1 decreases to about 65%, indicating that the seasonal variation is not fully characterized by this mode (Leeuwin Current); some other modes may also be significant (e.g., Capes Current). The second EOF mode (EOF2) of the diurnal current (Figure 6(A2)) shows an offshore current in the evening and an onshore current in the morning, consistent with the rotation of the diurnal wind in winter. For the current second EOF modes of all timescales, the contribution coefficient is highest at the seasonal scale (13.1%, Figure 6(B2)). The seasonal circulation within the continental shelf (Capes Current), governed by the monsoon wind, shows a significant seasonal variation (Figure 6(B2)), being strongly northward in summer and slightly southward in winter. At the interannual scale, it is found that the eddies with strong interannual variability are observed in the second and third modes of the slope current (Figure 6(C2,C3)), indicating that the interannual variation of the slope current is highly correlated with the occurrence of eddies.

The Fremantle Sea Level (FSL) can represent the overall strength of the Leeuwin Current [34]. At the seasonal scale, it is significantly correlated with PC1 (lower panel of Figure 6(B1)). However, at the interannual scale, PC1 is less correlated with FSL (Figure 6(C1)). This low correlation is largely due to the high inconsistency between them in the years 2011 to 2012 (the PC1 is significantly low). From the interannual PC2 and PC3, we infer that this inconsistency is probably caused by the strong slope eddies in 2011 and 2012, which involve strong shearing between the opposing currents inside and outside the shelf.

4. The Causes of the Surface Currents in Fremantle Sea

In addition to the above analysis, a correlation analysis was performed to reveal the influences of the driving factors on the multi-timescale characteristics of the HFR-derived current. First, the time series of surface current and wind components on each data grid were spatially averaged over each sub-region and correlated with each other (Figure 7 and Figure 8). For correlation between the vectors, a complex correlation analysis is also conducted (

Table 3. Complex correlation coefficients (ρ) and veering angles (θ) of the wind and HFR-derived current vector time series. The ρ value is normalized (<1); The θ value is positive if the vector 2 is counterclockwise of the vector 1.

Spatial Units	ρ			θ
	Diurnal	Seasonal	Interannual	Diurnal	Seasonal	Interannual
Inner Shelf	0.94	0.72	0.92	1.38°	5.31°	−24.45°
Outer Shelf	0.50	0.36	0.83	21.37°	−12.36°	10.69°
Slope	0.82	0.50	0.94	−1.22°	−5.76°	0.65°

). Second, the temporal coefficients (PCs) of different current EOF modes were also correlated with the PCs of different wind modes, satellite-observed current, and SSH EOF modes. The latter two factors mainly reflect the geostrophic component of the surface currents and are particularly important for the interannual analysis. These two parts of the correlation analysis between the current and driving factors form the first part of the analysis for the current causes, i.e., Section 4.1.

The effect of tides on surface currents in Southwestern Australia has been reported to be weak [7], and our analysis of the HFR data also confirms that the contribution of tidal current to the variance of total current is generally less than 20% and is the largest around the 50 m isobath. Therefore, we focused on the effects of monsoon winds (i.e., Section 4.2) and climatic factors (i.e., Section 5) on the current.

4.1. The Correlation of HFR-Derived Surface Currents with the Driving Factors

Apart from geostrophic currents, wind is a primary driving force for surface currents. Therefore, the correlation between the time series of wind (10 m above sea level) and current components in the same direction is examined. Meanwhile, the temporal variation of their amplitude and direction is analyzed (Figure 7 and Figure 8).

The correlation between the U-components of wind and current at three timescales is shown in Figure 7. A significantly high correlation is found between the diurnal wind and the HFR-derived current, with the correlation coefficients ranging from about 0.60 to 0.90 and increasing toward the shore. At the seasonal scale, the wind-current correlation remains significant, with the highest correlation on the outer shelf (~0.82). At the interannual scale, the wind-current correlation is only significant on the inner shelf (0.69) and gradually weakens in the offshore direction. These relatively high correlations suggest that the current U-component is significantly driven by the winds, and the correlation coefficient generally decreases with increasing bathymetry.

It is worth noting that the wind U-component during 2011 was strongly negative, suggesting a strong offshore wind. Meanwhile, only the inner shelf current exhibits an evident response by flowing offshore (Figure 7(A3)), while the slope and outer shelf currents show an opposite direction (Figure 5(A3–C3) and Figure 7(A3)). These opposing directions of current and wind resulted in a low wind-current correlation in 2011. In fact, 2011 is a very special year in which both the Leeuwin Current and the local offshore wind are extremely strong. These two forces drive a strong eddy that occupies both the slope and the outer shelf, as discussed later in Section 6 (the Ningaloo Nino).

The correlation between the V-components of wind and current is displayed in Figure 8. Compared to the U-components, the correlation coefficients of the V-components are higher in most cases. This may be due to the higher speed of winds in the meridional direction than in the zonal direction. In addition, Figure 8 also shows an evident effect of the isobath on the wind-current correlation, with the correlation increasing toward the shore. Furthermore, the correlation between the seasonal current and winds is particularly high on the inner shelf, with a correlation coefficient of 0.92 over the 366 sampled data points (Figure 8(D2)). The high correlation confirms that winds dominate the inner shelf currents, especially in the meridional direction.

For the V-components, the seasonal wind-current correlation in the inner shelf is higher than that in the outer shelf (Figure 8(A2–B2)), which is opposite to that of the U-components (Figure 7(A2–B2)). This difference can be attributed to the anomalous U-component of the current in 2011 (Figure 7(B3,C3)), because the seasonal signal of the current includes the data in 2011. In Figure 8(C3), the wind-current correlation coefficient is negative because of the anomalously positive V-component of the slope current caused by the strong eddy from 2011 to 2012.

In addition to the correlation between the U and V components, a vector correlation is also performed between the wind vector and the current vector using the complex correlation coefficient proposed by Kundu [39]. The corresponding equations are given in Appendix A (Equations (A1)–(A3)). The complex correlation coefficients (ρ) and veering angles (θ) for the vector time series of wind and HFR-derived current at 3 timescales and in 3 spatial units were obtained as shown in Table 3.

The results in Table 3 suggest that the wind-current correlation on the inner shelf is generally stronger than that on the slope (especially at the seasonal scale). The outer shelf current is least correlated with the wind at all timescales. The outer shelf is a region where the wind-driven northward circulation from the inner shelf interacts with the southward Leeuwin Current from the slope. The strong shear between these two opposing currents results in the frequent occurrence of eddies, resulting in a lower correlation between the slope current and the wind. The θ values also suggest larger veering angles in this region.

For the Southern Hemisphere, a counterclockwise rotation is expected between the wind vector and the wind-driven currents; therefore, θ is expected to be positive. However, the θ value at the interannual scale in the inner shelf is unexpectedly highly negative. This unexpected θ value may be related to the anomalously high negative values of the current V-component in several years, such as 2011, 2017 (Figure 8(A3)), when the Leeuwin Current is especially strong as reflected by the Fremantle Sea Level (FSL) (Figure 6(C1)).

All ρ values at the interannual scale are significantly high, suggesting that the HFR-derived current vector is strongly influenced by the local wind vector. In fact, some low correlations shown in Figure 7 and Figure 8 are found to be mainly due to the anomalously high amplitudes of the current in certain years (e.g., the anomalously negative value of the current V-component in 2011, as shown in Figure 8(B3)). Although the speed variation is much larger for the current than for the wind, the increasing or decreasing trends of the wind and current are generally consistent, and the change in trend occurs nearly simultaneously. Compared to the single component correlation above, the vector correlation through the complex correlation coefficient is more objective and provides a more comprehensive understanding of the wind-current correlation.

The primary EOF modes of winds, satellite-observed current, and SSH at different timescales were extracted, and their corresponding temporal coefficients (PCs) were then correlated with those of the HFR-derived current. Based on these correlations, the dominance of different factors in driving the HFR-derived currents is revealed (Figure 9).

At the diurnal scale, both the first mode (EOF1, Figure 6(A1)) and third mode (EOF3, Figure 6(A3)) of the HFR-derived current are highly correlated with the first mode (EOF1) of the wind, with correlation coefficients of −0.93 and 0.97 (Figure 9(A1)), respectively. The negative value results from the opposite direction of the Leeuwin Current and the winds. This significant correlation suggests that the meridional winds dominate the diurnal variations of the HFR-derived current (Figure 9(A1)). The correlation coefficient between the second EOF modes of the winds and current is −0.69. This mode reflects the west-east wind component that drives the cross-shore current, and the high-speed region is mainly located within the continental shelf. However, the contribution coefficient of this mode is 6.95%. This low contribution is due to the fact that near-zonal diurnal winds mainly exist in winter and not throughout the entire year (Figure 9(B2)).

The EOF1 of the seasonal winds shows a uniform pattern; its correlation coefficient with the seasonal current EOF1 (reflecting Leeuwin Current, as shown in Figure 6(B1)) is −0.66, and its correlation coefficient with Capes Current, as shown in Figure 6(B2), is 0.85. These high correlations suggest that the meridional winds play a dominant role in driving the seasonality of the surface currents. The EOF2 of the seasonal winds represents the near-zonal winds, which are especially significant south of 30°S. This is consistent with Figure 10(B1–B3), which shows an onshore tendency of current with diurnal variation in winter. The strong near-zonal wind south of 30°S is also consistent with the strong winter wind shown in Figure 9(B2) (which is strongest from July to September). It significantly affects the seasonal variation of current, with a contribution to the total variance of 13.97%. Such a high contribution explains the significant correlation (−0.62) of the wind with the seasonal Capes Current mode (Figure 6(B2)). Figure 9D shows that both the seasonal satellite and radar flow field EOF2 capture the Capes Current with a correlation coefficient of 0.8 between their temporal coefficients. This high correlation proves that the satellite-current products can also accurately characterize the nearshore surface currents at a daily temporal resolution. Taking advantage of the larger spatial range of the satellite-current data, we find that the temporal coefficient of mesoscale eddies in the open sea is highly consistent with that of Capes Current within the shelf (Figure 9D), which is mainly driven by the northward monsoon. This high consistency suggests that the monsoon is one of the important dynamic sources of the eddies near the continental shelf.

Figure 9(C1) shows that the first EOF mode of the interannual wind is a relatively coherent north-to-northwestward wind over the entire region. The temporal coefficient of this mode is highly correlated with that of the EOF3 of the HFR-derived current (Figure 6(C3)), i.e., a counterclockwise eddy centered on Perth Canyon. In addition, this eddy is strongly related to the offshore current on the slope. The corresponding PC3 of the offshore current mode reveals that it is strongest near the end of 2011. Figure 8(A3) shows particularly weak northward winds from the end of 2011 to the first half of 2012. This suggests that the northwestward wind is an important driving force for the polarity (the PC has both positive and negative values) and the strength of the eddy centered at Perth Canyon.

Figure 9(C2,E) shows that both the cross-shore wind and the mesoscale eddies in the open ocean are highly correlated with the interannual current EOF1 (Figure 6(C1)), indicating the strong influence of zonal winds and eddies on the local surface currents. Meanwhile, the correlation coefficient between the first EOF modes of the wind and current at the interannual scale is only −0.27. Figure 9(C1,C2) shows that the wind EOF1 strengthens northward and is more significant in the north of 33°S, while the wind EOF2 strengthens southward and is more significant in the south of 30°S. Therefore, it can be concluded that although the EOF1 of the interannual winds is northward in the whole southwest of Australia, which is expected to directly influence the southward Leeuwin Current, its significant influence area is relatively far away from Fremantle. On the other hand, the EOF2 of the interannual winds, which tends to be a local driver in Fremantle, strongly influences the surface and south of 30°S portion of the Leeuwin Current (Figure 9(C2), with a correlation coefficient of 0.49).

4.2. The Links between Diurnal and Seasonal Variations in Surface Currents: The Influence of Seasonal Breezes

The coastal breeze in Western Australia differs from other regions. It is overlaid on the synoptic northward wind, and together they form a unique breeze with diurnal changes mainly in the magnitude of its meridional component and the sign switch of its zonal component. The alongshore direction of the wind is particularly evident during the strong northward wind period in summer [9], suggesting a seasonal pattern of the diurnal wind. To determine if the diurnal surface current pattern is consistent throughout the year, 9 years of hourly HFR and wind data were synthesized into four seasons, respectively, and then the diurnal currents and winds in four seasons were analyzed (Figure 10 and Figure 11).

Figure 10 illustrates the seasonality of the diurnal variation of the surface currents captured by the HFR. During winter, the southward current dominates all the spatial units, with its maximum strength being on the slope. In winter, no obvious diurnal variation of current is observed on the slope, while an evident diurnal variation of current is observed on the inner and outer shelves. In contrast, during the summer, significant diurnal variations of the currents are observed in all sub-regions.

The most significant feature is observed for the slope current in summer (Figure 10(D3)). During summer, the slope current flows mainly southward but reverses its direction at noon, indicating that the slope current is not purely influenced by the Leeuwin Current but also by the sea breeze (and tidal forces). Additionally, the mean speed values marked in each subplot show no obvious difference between the inner shelf and outer shelf currents in spring and summer, which is the opposite of the case in autumn and winter. Moreover, the diurnal currents in autumn/spring are more similar to those in winter/summer.

The results in Figure 10 complement those in Figure 4(A1–C1), all of which suggest that the diurnal variation of current persists throughout the year but also varies seasonally.

Figure 11 shows a significant difference between the winter and summer local winds in both magnitude and direction. Strong northwestward winds (greater than 8 m/s) dominate in summer, whereas weaker winds (lower than 4 m/s) toward the east-northeast dominate in winter, both of which show obvious diurnal variation but in different forms.

Over a certain day in spring, summer, and autumn, the wind rotates clockwise from northwestward during 21:00–02:59, gradually to northward during 09:00–14:59, and then turns rapidly back to northwestward during 15:00–20:59. However, the diurnal rotation of the winter wind differs from the other three seasons, i.e., an initial counterclockwise rotation is observed. The wind speed is the highest during the daytime in all seasons due to the stronger sea-land wind. In winter, the northward component of the wind is weak, reducing the opposing force for the Leeuwin Current. Meanwhile, the large eastward component promotes a relatively shoreward Leeuwin Current, in contrast to the offshore wind in summer. The seasonal variation in winds is expected to drive significantly different cross-shore currents, offshore in summer and onshore in winter.

The diurnal winds are primarily toward the north during 09:00–14:59 in summer, while in winter they are mostly shoreward during the whole day (with the offshore component being the strongest during 15:00–20:59), both showing significant diurnal variation. These different orientations are consistent with the current orientations shown in Figure 6(A2,A3), respectively. In addition, the EOF2 mode of the interannual wind corresponds well to the winter wind pattern. The lower value of PC1 during 2011 in Figure 6(C1) is induced by the anomalously strong offshore winds during that winter, which caused strong eddies and offshore curvature of the Leeuwin Current.

The above analysis reveals that the direction and corresponding diurnal variation of the winter winds south of 30°S influence the diurnal and interannual variations of the HFR-derived current. The multi-timescale nature of the winds is partly responsible for the multi-timescale characteristics of the current.

5. Response of the Coastal Surface and Interior Currents to ENSO

The above analysis mainly revealed the significant effects of local winds, topography, and eddies on the HFR-derived current at each timescale. However, climatic factors, such as ENSO, may influence the interannual characteristics of the coastal current in Fremantle through changes in the strength of the Leeuwin Current. Sea Level in Northwestern Australia (SLNWA, i.e., source of Leeuwin Current) is reported to be highly correlated with the ENSO indices (especially the atmospheric indicator SOI) [34]. We analyzed the correlation between PC1 of SSH in the region (112°E–128°E, 14°S–22°S) and SOI, based on the time series from September 2010 to August 2018 (filtered by a 13-point moving average filter), and a significant correlation coefficient of 0.898 (SSH PC1 to SOI) was found.

There is a conceptual model that visualizes the strength and interannual variability of the Leeuwin Current being driven by SLNWA and relating to ENSO: when an El Niño (La Niña) event occurs, the anomaly of the tropical Pacific surface currents is eastward (westward), resulting in a weakening (strengthening) of the Indonesian Throughflow (ITF), which flows from the Pacific Ocean to the Indian Ocean and through the Indonesian Archipelago. This weakening/strengthening of the ITF is expressed in the strength of the Leeuwin Current [40,41]. From this conceptual model, it is expected that the ENSO-originated interannual variability in SLNWA can be transferred to the Leeuwin Current and then indirectly affect the coastal current in Southwestern Australia, including the ROT radar observation region.

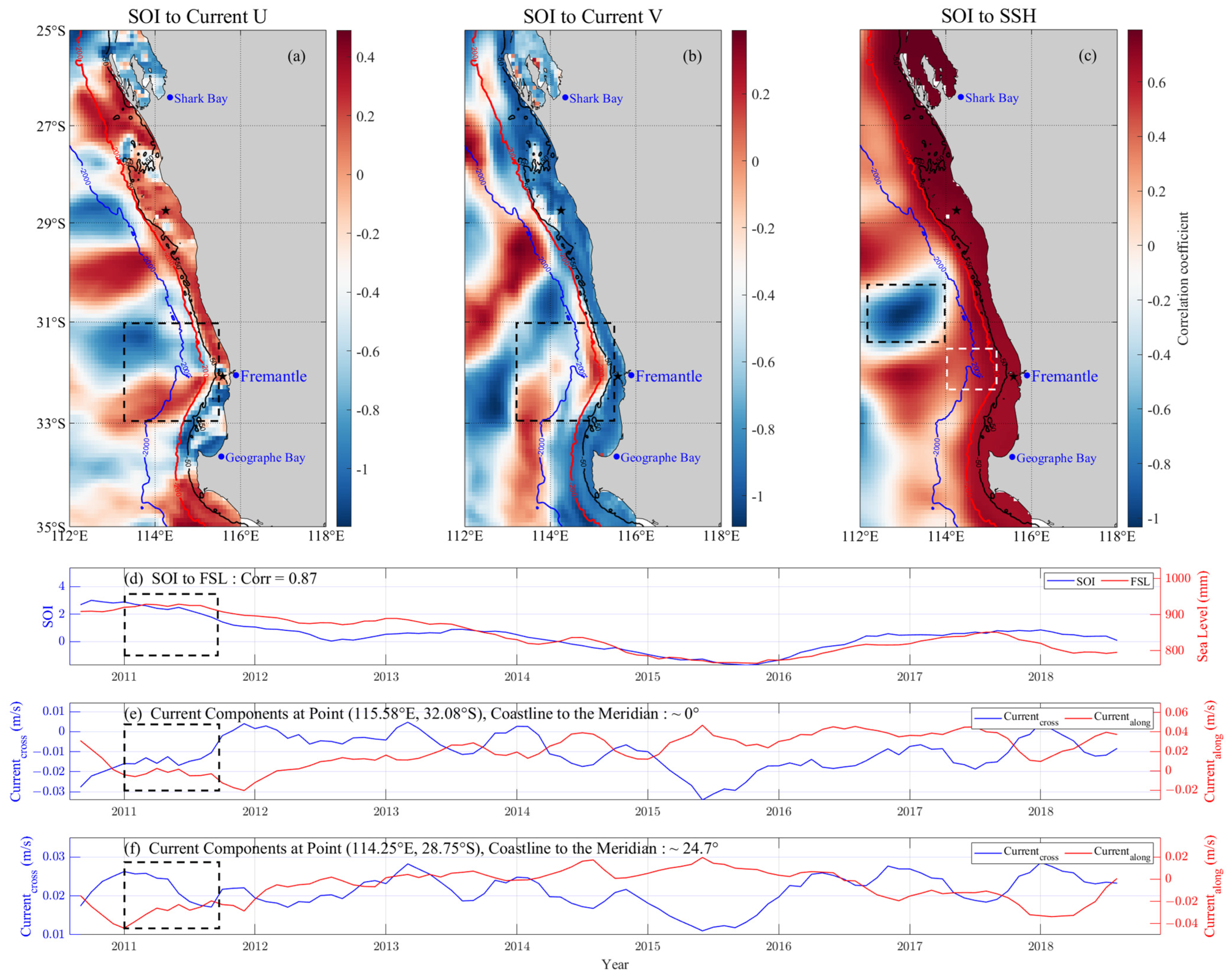
To confirm this expectation, the correlation coefficients between SOI and the satellite-observed current and SSH were first calculated for a period from 2010 to 2019 (filtered by a 13-point moving average) (Figure 12a–c). In addition, the cross-shore and alongshore current components at two spatial grids (marked by the black pentagrams and rhombus in Figure 12a–c) were calculated by projecting the current vector in two directions, one parallel to the coastline and one vertical to it, according to Equations (A4) and (A5) in Appendix A, and the results are shown in Figure 12d–f.

The significant positive correlation between SOI and SSH (with most coefficients in the nearshore exceeding 0.8) within the 2000 m isobath in Southwestern Australia (Figure 12c) suggests that the enhancement of Southern Oscillation leads to a rise in SSH within the local continental slope and shelf. In addition, a significant correlation between SOI and the satellite-observed current is also found within the shelf, with correlation coefficients approaching 0.8 (with the U-component) and −0.8 (with the V-component), implying that Southern Oscillation can also significantly influence the eastward and southward coastal surface currents of Southwestern Australia.

However, the correlation coefficients are lower on the slope than on the shelf, which can be attributed to the influence of the nearby eddies in the open sea, which are especially significant around 31°S where the Perth Canyon is located (indicated by the black dashed boxes in Figure 12a–c). In addition, the active eddy region in the open sea, the nearshore areas with relatively low correlation coefficients are mainly the bays. This may be partly attributed to the influence of local topography and local winds rather than remote climatic factors. An example is Shark Bay, which is a semi-enclosed bay. In contrast, in open bays such as Geographe Bay, the correlation coefficients are relatively higher.

Figure 12d–f display the correlation between SOI and FSL as well as the satellite-observed cross-shore and along-shore currents at the two selected spatial grids. A significant synchronization is observed between them, particularly between SOI and FSL, with a correlation coefficient of 0.87. A notable phenomenon was observed in 2011, when the shoreward and southward alongshore currents in Fremantle were much weaker than those at 28.75°S. The latter is more consistent with FSL (indicated by the black dashed boxes in Figure 12d–f). Such different consistencies imply that some local factors dominate over the interannual climate-driven variability of the current at Fremantle. This is consistent with the HFR-derived current (Figure 6(C3)), where a strong eddy is observed. Therefore, the intrusion of Leeuwin Current onto the shelf results in a high correlation between the nearshore current and SOI. However, this correlation can sometimes be lowered by local factors such as topography, winds, and eddies.

The response of coastal surface currents in Southwestern Australia to ENSO is analyzed in detail using a composite analysis. Since few ENSO events occur during the temporal range of the radar data, the satellite-observed current data from 2000 to 2019 (20-years) with a range of (112°E–116°E, 28°S–33°S), were used to reveal the response of surface currents to ENSO. Current anomalies in four El Niño events (2002, 2006, 2009, and 2018, with peak months being November, November, December, and November, respectively) and four La Niña events (2007, 2010, 2011, and 2017, with peak months being January, February, December, and February, respectively) are examined to illustrate this response.

The composite analysis was conducted using the following method: First, for the 20-year monthly data (X_Original, 20 (y) × 12 (m)), the 20-year mean values for the 12 months (X_Mean, 12 (m)) are calculated. Second, each mean value are subtracted from the values of the same months in each year, giving the anomaly of the data for each month (X_Anomaly, 20 (y) × 12 (m)); Third, according to the peak month for each event, the anomaly data from the three months ahead and two months afterward for each event are divided into groups (X_Events, 6 (m) × N, where N means the number of events); Finally, the grouped anomaly data belonging to the same ENSO event (X_Nino and X_Nina, 6 (m)) are averaged. The results are presented in Figure 13.

Figure 13 mainly suggests that the anomaly of coastal current is predominantly southward during La Niña and northward during El Niño, especially after the peak month, i.e., from ‘Peak Month’ to ‘Peak+2’ (e.g., the area marked by white dashed boxes in Figure 13e,k). This quantitatively demonstrates that the coastal southward current on the Fremantle slope (i.e., LC) is stronger during La Niña and weaker during El Niño. A notable feature is that the eddies are always active south of 29°S, where the 2000 m isobath turns abruptly shoreward and the continental shelf narrows abruptly, as well as Perth Canyon (marked by the magenta dashed boxes in Figure 13d). The eddies are generally of opposite polarity and different intensities during La Niña and El Niño; such differences occur earlier than the different nearshore currents; some of these eddies travel southward and intrude on the shelf, resulting in opposite shelf currents (Figure 13a,g). Therefore, these eddies strongly influence the intensity of the nearshore Leeuwin Current and can be considered a part of the Leeuwin Current System (at Fremantle) [42].

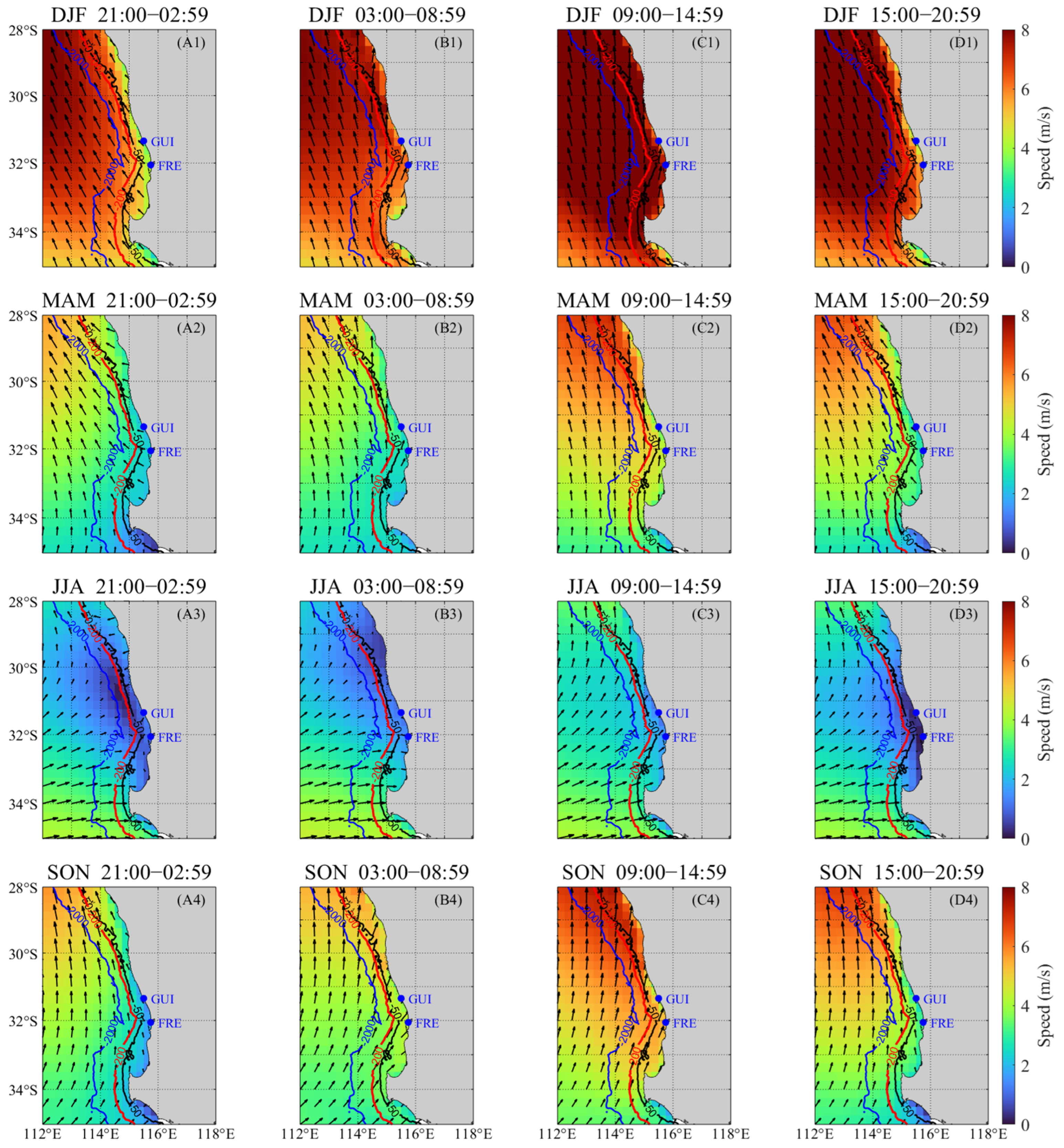
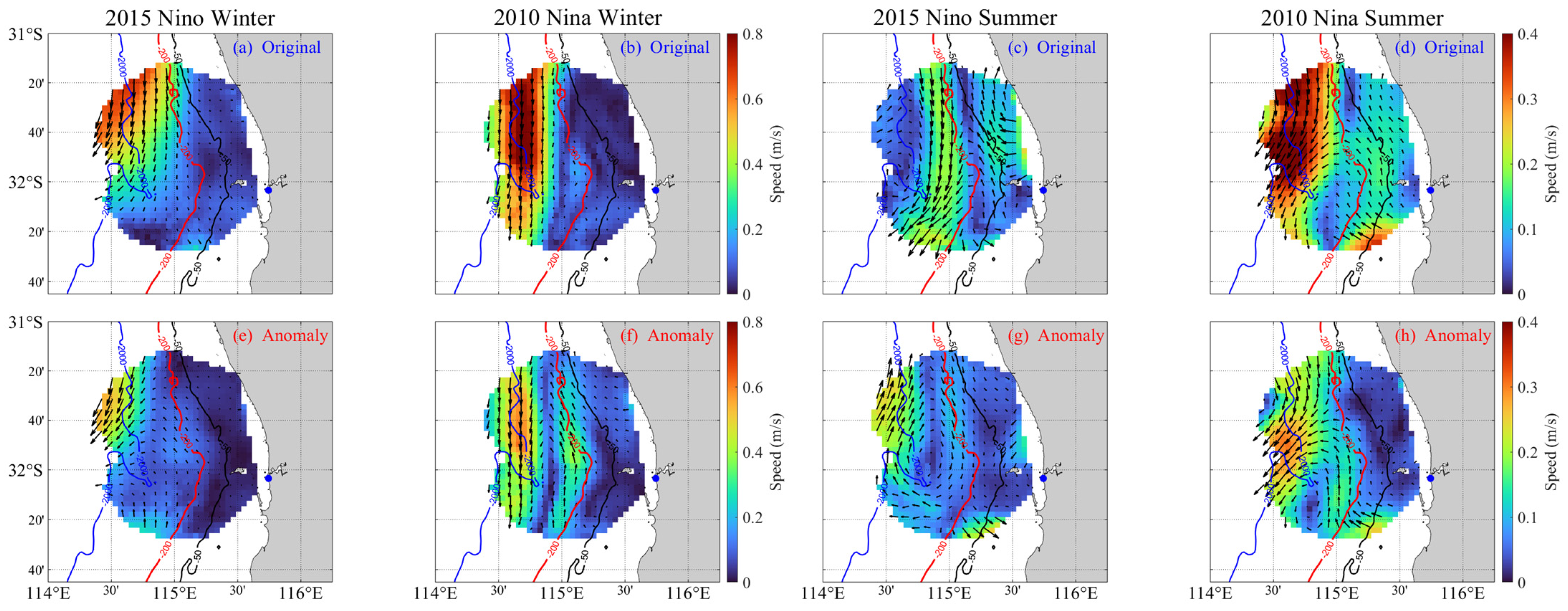
The responses of the HFR-derived current in winter (June–August) and summer (December–February) during two typical ENSO events, La Niña in 2010 and El Niño in 2015, were further analyzed (Figure 14). As shown in Figure 14a–d, the mean states of original current data in the above durations show that, during La Niña (El Niño), particularly in winter, the Leeuwin Current exhibits a higher (lower) speed. Similarly, in summer during La Niña (El Niño), the slope current speed also increases (decreases). However, due to the prevailing northwestward summer winds (as shown in Figure 7(A3) and Figure 9(C2), the extremely negative wind U-component, i.e., offshore winds), a vortex structure forms on the continental slope (Figure 14d), which is due to the shearing between the strong northwestward circulation within the shelf and the southward circulation outside the shelf. The shearing effect is more pronounced during La Niña because the southward circulation is stronger than that during El Niño.

Current anomalies are shown in Figure 14e–h and are calculated by subtracting the 9-year mean winter or summer current from the mean current in Figure 14a–d. The current anomalies reflect the stronger southward current on the slope during La Niña, which is consistent with Figure 14a–d. It is worth noting that the current anomalies are usually manifested as slope-centered eddies, which are particularly pronounced during La Niña and in the summer. The formation of eddies is apparently related to the shear effect between the two strong and opposing circulations. This finding demonstrates the importance of considering the effect of eddies when studying the response of local currents to ENSO, which is consistent with the analysis in Figure 13.

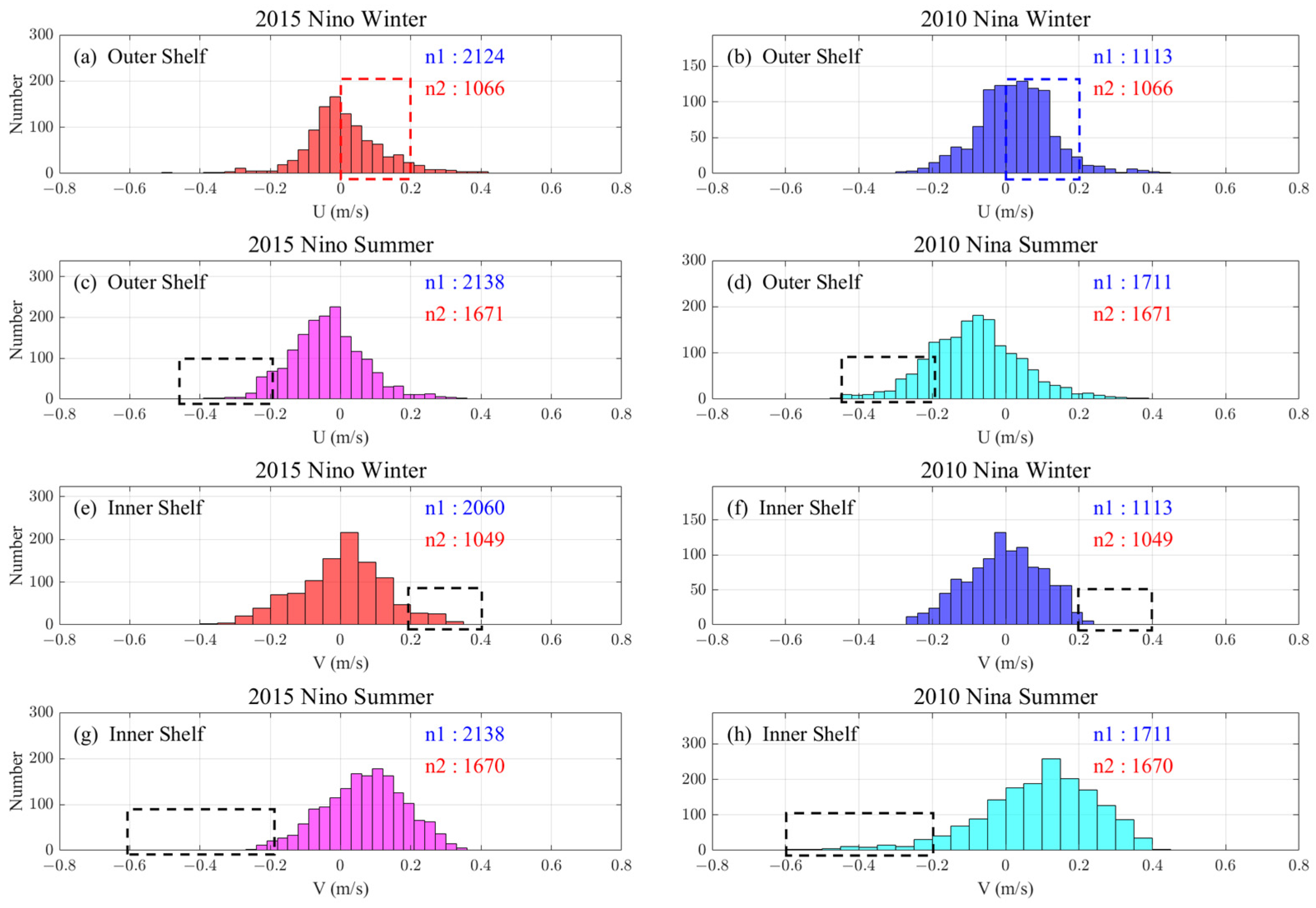
Figure 14 visually displays the difference between HFR-derived currents during 2015 El Niño and 2010 La Niña. Based on the advantage of the large temporal sampling number of HFR, we conducted a quantitative study using histogram analysis to verify the difference in the current response. Since the outer shelf is the main channel for seawater exchange between the slope and the inner shelf (i.e., near zonal), a strong southward current on the inner shelf (or weak northward current) is an indicator of the onshore invasion of Leeuwin Current. For the four periods shown in Figure 14, the histograms of the hourly outer shelf current U-component and inner shelf current V-component were obtained (Figure 15).

In the winter of 2010 La Niña, due to the increased shoreward tendency of the outer shelf current, the probability of a positive U-component was higher than that in the 2015 El Niño winter (Figure 15a,b). The corresponding increase or decrease of the continental shelf water by the slope water intrusion also has strong ecological significance. Meanwhile, the inner shelf current V-component in the 2015 El Niño (2010 La Niña) shows a higher positive (negative) value in both winter and summer (Figure 15e–h). In addition, more negative current U-component values are observed in Figure 15d (compared with Figure 15c), which reflects the same as Figure 14d and is anomalous (an extreme event).

These results reveal the response of cross-shore and alongshore shelf currents to ENSO. The realization of such a revelation is largely attributed to the high accuracy, large spatial coverage, and large temporal sampling number of HFR observations, thus making the results more quantitative and credible.

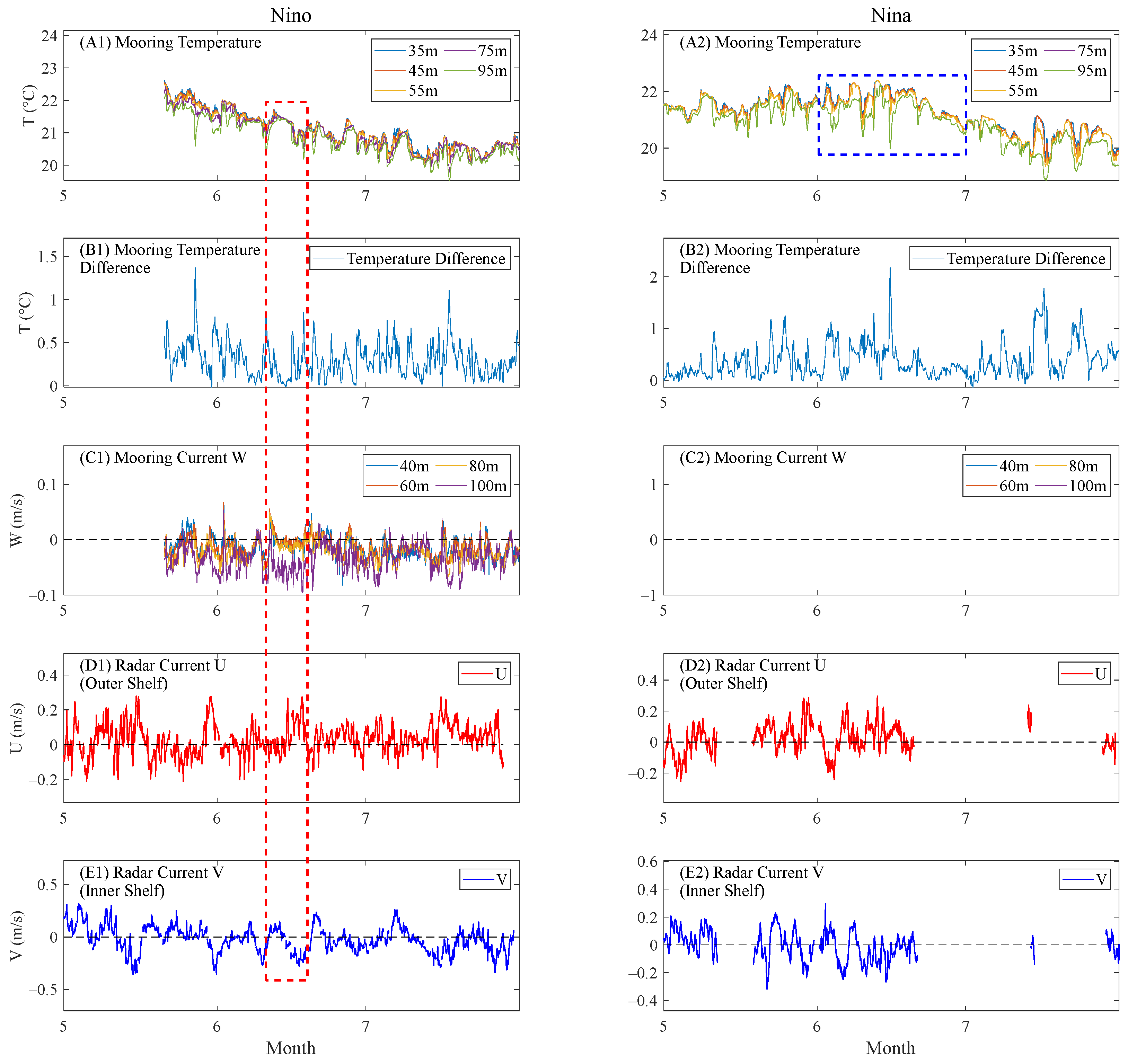
For the above two winters, the mooring data, including the temperature and 3-dimensional current velocity of the interior waters, as well as the HFR-derived U-component of the outer shelf current (cross-shore current) and the V-component of the inner shelf current (alongshore current), were analyzed to understand the 3-dimensional response of the near-shore waters to ENSO, especially the intrusion of slope water onto the shelf. Figure 16(A1,A2) shows the multilayer seawater temperature observed by the mooring (combined into one layer per 20 m from the original data, and some layers are missing). A smaller top-bottom temperature difference implies the occurrence of upwelling or downwelling resulting from the mixing of the upper and lower seawater [31].

In mid-June, a significant downwelling is shown in Figure 16(B1,C1). The former shows a decreased temperature difference between the upper and lower parts of the ocean (i.e., a strong downward current), and the latter shows the vertical currents corresponding to the downwelling. Meanwhile, the radar-observed surface currents also show a shoreward current on the outer shelf and a southward current on the inner shelf (indicated by the red dashed box). Such a pattern of surface currents leads to downwelling, and therefore the radar results are consistent with those of the moorings.

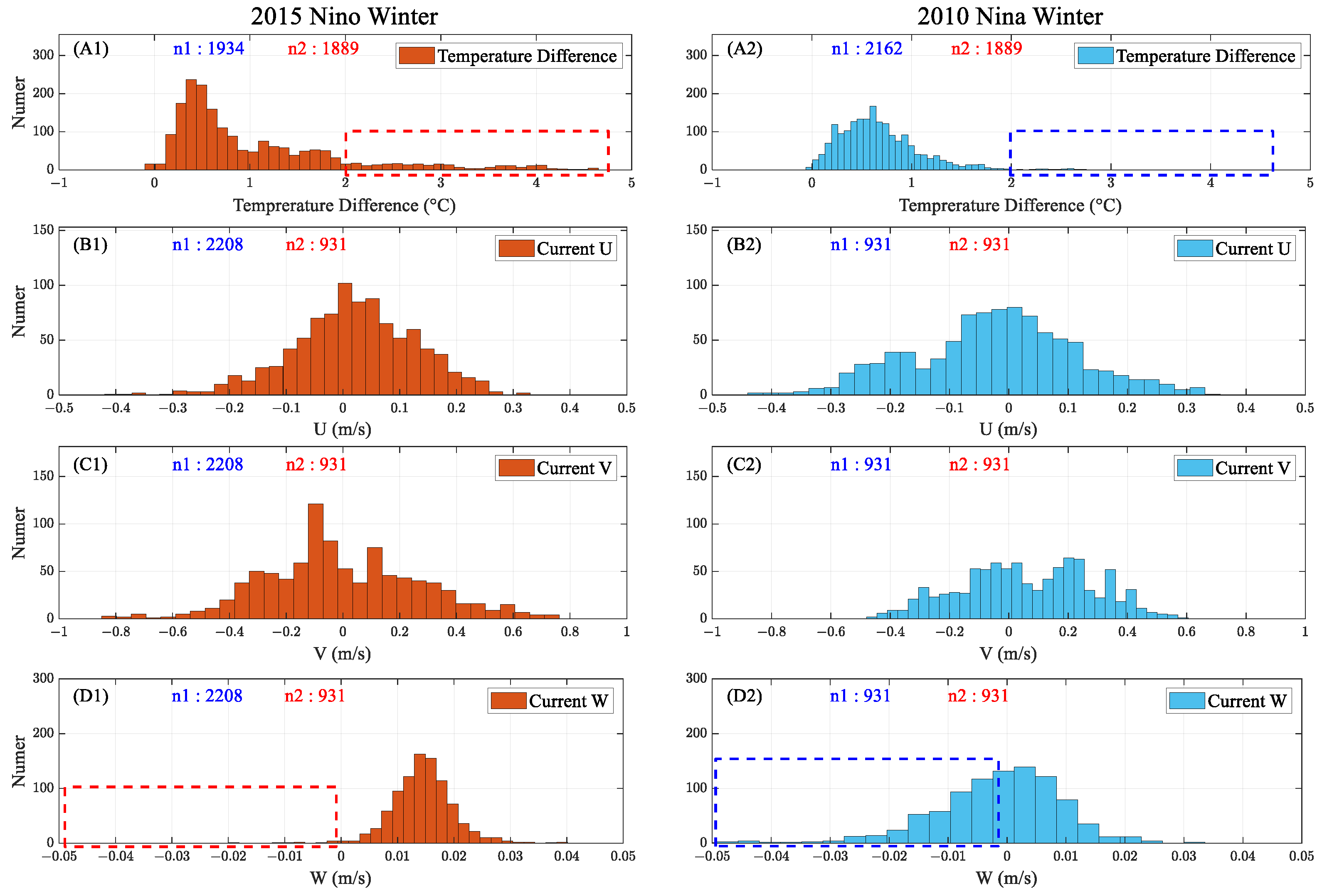
In addition, the mooring data show a decrease in seawater temperature during both El Niño and La Niña winters, but a significant increase in temperature is observed in June during La Niña (Figure 16(A2), indicated by the blue dashed box). This can be attributed to the anomalously strong Leeuwin Current during this time, which brings warm water to the inner shelf. Meanwhile, the outer shelf current U-component and inner shelf current V-component show more positive and negative values, respectively (Figure 16(D2,E2)), indicating a strong shoreward (southward) flow, and both reflect the cross-shelf (shoreward) flow of Leeuwin Current.

Figure 16 shows the strengthening of the Leeuwin Current and the corresponding invasion into the shelf during the winter of the La Niña year and confirms the consistency between the HFR-derived surface current data and the mooring-observed interior seawater data. This high consistency indicates the potential of HFR to detect upwelling and downwelling. For further quantification, the histogram of the top-bottom temperature difference (WATR20) and the U, V, and W components of the current are compared in Figure 17. The lack of vertical current data during the La Niña winter at WATR10 and the unequal distribution of temperature data at WATR10 between the two periods may result in statistical bias. Therefore, we used temperature and current data from WATR20 and WACA20, respectively, where the U and V components of the moored current are at a depth of 60 m.

The histogram reveals a smaller top-bottom temperature difference during the La Niña winter, indicating a more intense vertical mixing of seawater (marked by the blue dashed box in Figure 17(A2)). During the La Niña winter, the current W component indicates a significantly stronger downwelling than during the El Niño period (marked by the blue dashed box in Figure 17(D2)). In summary, a much larger number of downwelling (upwelling) events are observed within the shelf, which is well consistent with the enhanced (weakened) shoreward intrusion of the Leeuwin Current.

Compared to conventional moorings, the more spatial sampling grids and a larger observation range of the radar are ideal to reveal the spatial variation of surface currents from the outer shelf to the inner shelf. The revelation of the spatial pattern of the surface current, together with the internal temperature and velocity from the mooring data, confirms the 3-dimensional pattern of the coastal circulation (Figure 15). Therefore, the present study highlights the need to combine HFR and mooring observations to better capture 3-dimensional phenomena.

6. Discussion and Summary

This paper focused on the multi-timescale characteristics of the coastal surface currents in the Fremantle Sea as well as their causes. Furthermore, the response of nearshore currents to ENSO has also been investigated. The main results and conclusions obtained in Section 3, Section 4 and Section 5 of this paper are as follows:

(1) The multi-timescale (diurnal, seasonal, interannual) characteristics of the HFR-derived currents and current features in each sub-region (inner shelf, out shelf, slope) are revealed. The temporal variation of surface currents is stronger in the meridional direction than in the latitudinal direction. At the diurnal and seasonal scales, the surface currents are obviously periodic and mainly controlled by the winds, whereas the interannual surface currents show remarkable year-to-year variation, which is the most significant on the slope and near Perth Canyon. The southward Leeuwin Current on the slope and the northward Capes Current on the shelf promote the water exchange between the shelf and open sea in their strongest periods, respectively (winter and summer, respectively). EOF analysis shows that the surface currents are dominated by a southward circulation and eddies on the slope, and the slope-centered eddies in 2011 are especially significant (Section 3).

(2) With respect to the causes of the multi-timescale characteristics of surface currents (Section 4), the main finding is that the surface currents are highly correlated with winds, especially at diurnal and seasonal scales, and their components in the same direction are highly synchronous. However, at the interannual scale, the correlation is disturbed by the anomalous current fluctuations in certain years, such as 2011. However, a vector correlation analysis confirms the high correlation between the current and wind vectors, implying that the variation of the winds is reflected in that of the currents, independent of the annually changing strength of the currents themselves. The correlation between the PCs of the currents and driving factors in EOF modes reveals that the multi-timescale variations of currents are mainly induced by the winds, while the mesoscale eddies in the open sea play an important role in driving the interannual characteristics of the currents. The diurnal variation of currents also varies seasonally, which is attributed to the distinct monsoon strengths in each season. In winter, the relative zonal winds are strong south of 30°S and drive the near-zonal currents with a diurnal variation that is different from the other seasons.

(3) Satellite current data, derived from satellite sea surface height during 2000–2019, confirms the variation in the strength of the Leeuwin Current in Fremantle and adjacent seas during different ENSO years. Additionally, a case study based on HFR and mooring data reveals that the Leeuwin Current strength variation affects the outer shelf shoreward current and therefore affects the inner shelf upwelling and downwelling. This response is subject to a westward anomaly of the equatorial currents during La Niña year, which strengthens the Leeuwin Current accordingly and in turn triggers the strengthening of onshore current on the Fremantle Slope and outer shelf. The stronger onshore currents facilitate the occurrence of downwelling events on the shelf. During El Niño years, coastal currents show the opposite response. Such responses of the coastal currents are of high ecological importance, e.g., influencing the nutrient content of seawater or transporting phytoplankton [43,44] (Section 5).

In addition to the above results, the following issues are explored in depth in this paper:

(1) The correlation between the interannual HFR-derived current EOF1 and FSL is low (Figure 6(C1)), with a correlation coefficient of 0.29. This may be caused by the discrepancy between the geostrophic current and the HFR-derived current; the latter is more owing to the influence of local winds, while the FSL reflects the strength of the overall Leeuwin Current (which is more geostrophic). In contrast, the PC1 of the interannual satellite-observed current for this study region is relatively highly correlated with FSL (correlation coefficient of 0.56). This suggests that the HFR-detected Leeuwin Current in Fremantle better accounts for the effect of wind and is different from the satellite-derived current. The coast south of 30°S is dominated by near-zonal winds with a weak northward component during winter, when the Leeuwin Current is the strongest. The local winds at Fremantle and the Perth Canyon play dominant roles in the interannual variability of the surface portion of the Leeuwin Current in Fremantle. The strength of the overall Leeuwin Current in Southwestern Australia is highly correlated with the sea level in Northwestern Australia and the Southern Oscillation [34,45,46,47] (Figure 12). In summary, the difference between the LC features detected by HFR and satellite, respectively, suggests that the interannual variability of the Leeuwin Current is better reflected in the large-scale satellite-observed current. On the other hand, HFR observations reveal the detailed local current patterns, which contain the influence of local factors such as the local winds and strong bathymetry variation.

(2) The HFR-derived current is highly correlated with the zonal winds south of 30°S in winter, particularly evident in 2011, and may be closely related to the 2011 Ningaloo Nino, an extreme marine heat wave event induced by the local and remote climate anomalies [48,49,50]. From late 2010 to early 2012 (austral summer), La Nina (as a remote factor) induced an anomalous westward trade wind and then strengthened the Leeuwin Current (through a higher sea level in Northwestern Australia). Therefore, the warm water taken in by the Leeuwin Current, together with the increased sea surface temperature in summer, caused an anomalously high sea surface temperature. This resulted in an anomalous sea-land temperature difference, with the sea being relatively warmer than the land, which induced a strong clockwise atmospheric circulation (cyclone) and resulted in the corresponding offshore winds south of 30°S (as a local factor). Thus, the accompaniment of a strong offshore Capes Current with a relatively strong southward Leeuwin Current (in summer) explains the occurrence of the counterclockwise eddy detected by the ROT radar in summer 2011 (Figure 14h).

(3) The present results confirm the ability of HFR to finely delineate the spatial characteristics of surface currents and its potential for studying climate effects on coastal currents. The advantage of the spatial and temporal resolution of HFR is that it allows a more detailed survey of the surface currents. With the accumulation of long-term radar data, HFR can be a favorable tool for understanding the impact of climate change on near-shore waters in the future. However, HFR is relatively limited in observation range and requires the complement of large-scale satellite remote sensing. Meanwhile, the present study shows that the incorporation of data from in-situ means such as mooring is also very helpful to reveal the 3D characteristics of the current, especially in the nearshore. Moreover, in certain areas and time periods, some events, such as extreme weather, may cause possible errors in HFR data due to signal attenuation and reflections, so the accuracy of HFR observations needs to be assured before use. In addition, extreme amplitudes in the long-term radar signals may reveal extreme events caused by long-term factors such as climate anomalies. Initially, the causes of these anomalies could be further analyzed. Meanwhile, other forcing factors such as sea surface temperature (SST) and sea level pressure (SLP) could be considered, especially in the study of the 2011 Ningaloo Nino, which influences the HFR-derived near-shore surface currents through wind anomalies (Figure 14h). These further studies can help identify the broader effects (e.g., marine heat waves) of climate change and its impact on the marine environment, especially the nearshore circulation.

In conclusion, this study demonstrates the advantage of HFR in spatial and temporal resolution for the detection of nearshore currents. Long-term HFR observations can reveal the multi-timescale characteristics of surface currents and provide detailed spatial patterns. Together with satellite and in-situ mooring data, long-term HFR data can be used to explore the response of nearshore waters to climate change. The methodology adopted in this paper is applicable to other coastal regions with a similar observational network. Furthermore, due to the spatial and temporal resolution advantages of HFR observations, we expect them to play an important role in future studies of nearshore eddies, sub-mesoscale processes, marine heat waves, and especially climatic effects. [1,51,52,53,54,55,56].