Next Article in Journal
Sensitivities of Vegetation Gross Primary Production to Precipitation Frequency in the Northern Hemisphere from 1982 to 2015
Next Article in Special Issue
Spatial Patterns of Turbidity in Cartagena Bay, Colombia, Using Sentinel-2 Imagery
Previous Article in Journal
Deep Learning for Integrated Speckle Reduction and Super-Resolution in Multi-Temporal SAR
Previous Article in Special Issue
Method for Determining Coastline Course Based on Low-Altitude Images Taken by a UAV
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 16
Issue 1
10.3390/rs16010020
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Low-Tech and Low-Cost System for High-Resolution Underwater RTK Photogrammetry in Coastal Shallow Waters

by
Marion Jaud
1,2,*,
Simon Delsol
2,
Isabel Urbina-Barreto
3,
Emmanuel Augereau
1,2,
Emmanuel Cordier
4,
François Guilhaumon
3,
Nicolas Le Dantec
1,2,
France Floc’h
2 and
Christophe Delacourt
2
1
UAR3113, Univ de Brest, CNRS, IRD, IUEM, F-29280 Plouzané, France
2
Geo-Ocean, Univ Brest, CNRS, IFREMER, UMR6538, F-29280 Plouzané, France
3
UMR-Entropie, IRD, F-97744 Saint Denis, La Réunion, France
4
Observatoire des Sciences de l’Univers de La Réunion (OSU-Réunion), UAR 3365, Université de la Réunion, CNRS, Météo-France, IRD, F-97744 Saint-Denis, France
*
Author to whom correspondence should be addressed.
Remote Sens. 2024, 16(1), 20; https://doi.org/10.3390/rs16010020
Submission received: 25 October 2023 / Revised: 24 November 2023 / Accepted: 5 December 2023 / Published: 20 December 2023
(This article belongs to the Special Issue Monitoring Coastal and Marine Environments Based on Remote Sensing Data)
Browse Figures
Versions Notes

Abstract

:
Monitoring coastal seabed in very shallow waters (0–5 m) is a challenging methodological issue, even though such data is of major importance to many scientific and technical communities. Over the years, Structure-from-Motion (SfM) photogrammetry has emerged as a flexible and inexpensive method able to provide both a 3D model and high-resolution imagery of the seabed (~cm level). In this study, we propose a low-cost (about USD 1500), adaptable, lightweight and easily dismantled system called POSEIDON (for Platform Operating in Shallow-water Environment for Imaging and 3D reconstructiON). This prototype combines a floating support (typically a bodyboard), two imagery sensors (here, GoPro® cameras) and an accurate positioning system using Real Time Kinematic GNSS. Validation of this method was deployed in a macrotidal zone, comparing on the foreshore the point cloud provided by POSEIDON “SfM bathymetry” and by classical terrestrial SfM survey. Mean deviation was 5.2 cm and standard deviation was 4.6 cm. Such high-resolution SfM bathymetric surveys have a great potential for a wide range of applications: micro-bathymetry, hydrodynamics (bottom roughness), benthic habitats, ecological inventories, archaeology, etc.

1. Introduction

Coastal seabed mapping and bathymetry restitution is a key issue for environmental and human activities, including evolution of morphodynamic features (dunes, ripples), coral reef structures, marine habitat characteristics, navigation safety, coastal protection, etc. Coastal bathymetry is mainly performed using multi-beam echo-sounder (MBES) with possible combination with side-scan sonar (e.g., [1,2,3]) or bathymetric LiDAR (e.g., [4,5,6]). Both are active remote sensing techniques: MBES uses acoustic signal emitted from a boat, whereas LiDAR uses optical signal emitted from an aircraft. These methods can achieve spatial resolutions of the order of 20 to 50 cm at best. Furthermore, MBES surveys are difficult to perform in very shallow waters, both for reasons of navigational safety and for very limited swaths. To obtain centimetric resolution horizontally and vertically domains is mandatory in order to capture:
  • the structure complexity of coral reefs, which is of primary importance for a number of hydrodynamical and ecological processes [7]
  • the sand ripple dynamics with typical sizes of the order of 10 cm in height, influencing sediment transport over sandy beaches [8].
To obtain higher resolution shallow water bathymetry, the use of Structure-from-Motion (SfM) photogrammetry can be considered. SfM photogrammetry is a method allowing the production of three dimensional (3D) models of objects from a large dataset of overlapping photographs collected from different points of view. SfM photogrammetry is a versatile method that can be deployed with various sensors, from high quality Reflex cameras to mainstream smartphones (e.g., [9,10,11]). Furthermore, SfM photogrammetric surveys can be performed in various contexts, as aerial surveys (planes, unmanned aerial vehicles (UAV), kites, etc. (e.g., [12,13,14,15])), terrestrial surveys (e.g., [16]), surveys from boats (e.g., [17]) or underwater surveys (e.g., [18,19,20]).
Whether in artificial environments [21], lakes [22], rivers [23] or coral reefs [24,25,26,27], several studies have investigated the use of UAV photogrammetry to measure bathymetry. This approach is tempting since it enables coverage of a large area, regardless of the shallow depth, while combining relief information and ortho-imagery. However, all these studies point to the problem of refraction correction (even in constrained environments). In the best case, despite refraction correction and using Ground Control Points (GCPs) on the bottom, errors in depth measurement remain greater than 12 ± 15% [26]. Furthermore, to be applicable, such UAV surveys require that there are no waves or ripples on the surface so that the bottom remains visible, that there is no sun glint effect and that the refraction coefficient remains relatively homogeneous over the area.
Underwater photogrammetry was used in archaeology long before the emergence of SfM methods (e.g., [28]), in particular because it enabled accurate and exhaustive surveys to be carried out without having to move the remains. The development of SfM methods has made acquisition protocols more flexible and, in parallel, more user-friendly processing tools have emerged. This popularity has also been reinforced by the development of remotely operated underwater vehicles (ROVs) (e.g., [29,30]). Underwater photogrammetry is therefore now used for a wide panel of applications, including archaeology (e.g., [18]), ecological studies (e.g., [19]), infrastructure monitoring (e.g., [31]), etc.
Contrary to the other monitoring contexts, underwater photogrammetry faces a major constraint due to the georeferencing. Indeed, it may be difficult to measure GCPs using a GPS rod, and Global Navigation Satellite System (GNSS) positioning is unavailable underwater. Positioning and tracking are key issues, especially when using ROVs [32]. One of the most widely applied methods in underwater positioning is acoustic localization, such as ultra-short baseline (USBL) positioning (e.g., [33,34]). However, locating the USBL transceiver means having a beacon with a known position in the area. As a result, such methods are cumbersome to implement.
Most of the studies using underwater photogrammetry and requiring a geometrically consistent reconstruction therefore make use of scale bars (e.g., [31,35,36]). These scale bars are used in the SfM processing workflow to compute the internal parameters of the camera. The generated point cloud, mesh and/or Digital Surface Model (DSM) and orthomosaic are then geometrically correct but in relative coordinates.
Another approach is to have a floating platform on the surface equipped with underwater cameras. Raber and Schill [37] propose a remote-controlled platform, the Reef Rover, but they deplore a lack of precision in the georeferencing of images because the GPS used for the auto-pilot is not accurate enough. The PLANCHA project at the IFREMER Institute is also focusing on the design of a low-cost motorised platform for underwater photogrammetry [38], but to our knowledge, no article has yet been published to present the results.
In this study, we present the POSEIDON system (Platform Operating in Shallow-water Environment for Imaging and 3D reconstructiON), a prototype of a non-motorized, low-cost and low-tech acquisition platform with accurate positioning. We also describe the associated protocols for acquisition and data processing and qualification tests for underwater photogrammetry without calibration points.

2. Study Areas

At this stage, the tests carried out were mainly methodological. The study sites were chosen with this in mind, in order to assess the platform’s potential in a variety of coastal shallow waters.

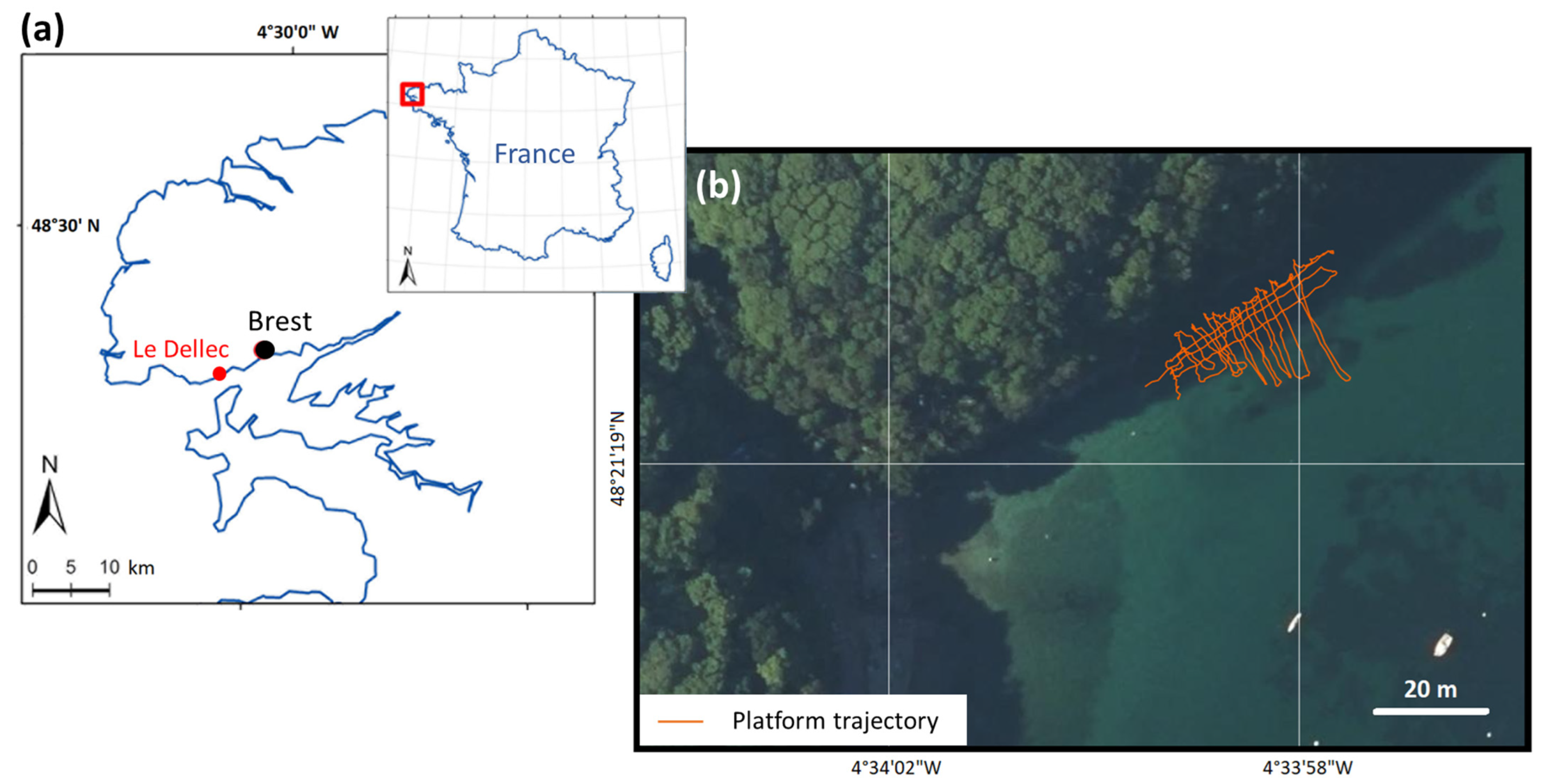
2.1. Method Validation Site: Dellec Bay

The first study site is the Dellec Bay (Brittany, France), located in the Goulet de Brest, between the Mer d’Iroise and the Rade de Brest (Figure 1). The Anse du Dellec is subject to a semi-diurnal macrotidal regime with an average tidal range of around 4.5 m. It is a zone of exchange between oceanic waters and drainage basins (in particular the Aulne and Elorn rivers). The mixing of water caused by strong tidal currents limits eutrophication.
A first SfM photogrammetry bathymetric survey was conducted with the POSEIDON system on 14 February 2023. On that day, the tidal coefficient was 45 (corresponding to a tidal range of 2.94 m). The survey was carried out just before high tide, between 10 a.m. and 10.30 a.m. (UTC + 1), with a water height of around 5.5 m. The survey area (Figure 1b) was therefore completely underwater. It was a cloudless day, with a global irradiance at the time of the survey of 94 W/m2 at the Brest-Guipavas weather station [39].
One strategy for validating the quality of POSEIDON surveys on a whole area (and not just at a few points) is to compare the reconstruction obtained by POSEIDON with a 3D model obtained using a tested and qualified method. As the study area can be emerged at low tide, a terrestrial SfM photogrammetry survey was carried out over the same area, on 20 February 2023, around 11.20 (UTC + 1), at low tide. With a tidal coefficient of 100 (corresponding to a tidal range of 7.38 m), the area (Figure 1b) was completely exposed, so there were no refraction issues. The survey was thus carried out using a GoPro 7 (GoPro, Inc., San Mateo, CA, USA) camera (with deactivated rolling shutter), attached to the end of a 4 m pole, and 18 targets distributed on the ground serving as GCPs. These GCPs were measured with centimetric accuracy using a GNSS (Global Navigation Satellite System) receiver operating in Real Time Kinematic (RTK), i.e., receiving corrections in real time from a base station, thus ensuring positioning accuracy of the order of a few centimetres. This photogrammetry survey using GCPs was carried out using a traditional photogrammetry approach that has already been fully tested and qualified and that can therefore be used as reference for SfM bathymetry.

2.2. Test Site: Hermitage Backreef Zone

The second study area is located in a tropical context, at L’Hermitage (Figure 2), on the west coast of Réunion Island (Indian Ocean), shoreward to the flat reef, in the shallow backreef zone. Réunion Island is subject to a micro-tidal semi-diurnal tide with diurnal inequalities, with an average tidal range of 37 cm in relation to the mean level [40].
The surveys presented here were carried out on 13 March 2023, at around 8.30 a.m.–9.30 a.m. local time (UTC + 4), during ebb tide, with low tide at around 10 a.m. At the time of acquisition, the global radiation recorded at Le Port weather station was 441 W/m2 [39]. This high level of light, combined with the oligotrophic environment, means that the water was very clear.
The survey focused over a few metric coral heads, which created sudden variations in bathymetry on the scale of the survey (from a few dozen centimetres to one meter).

3. Material and Methods

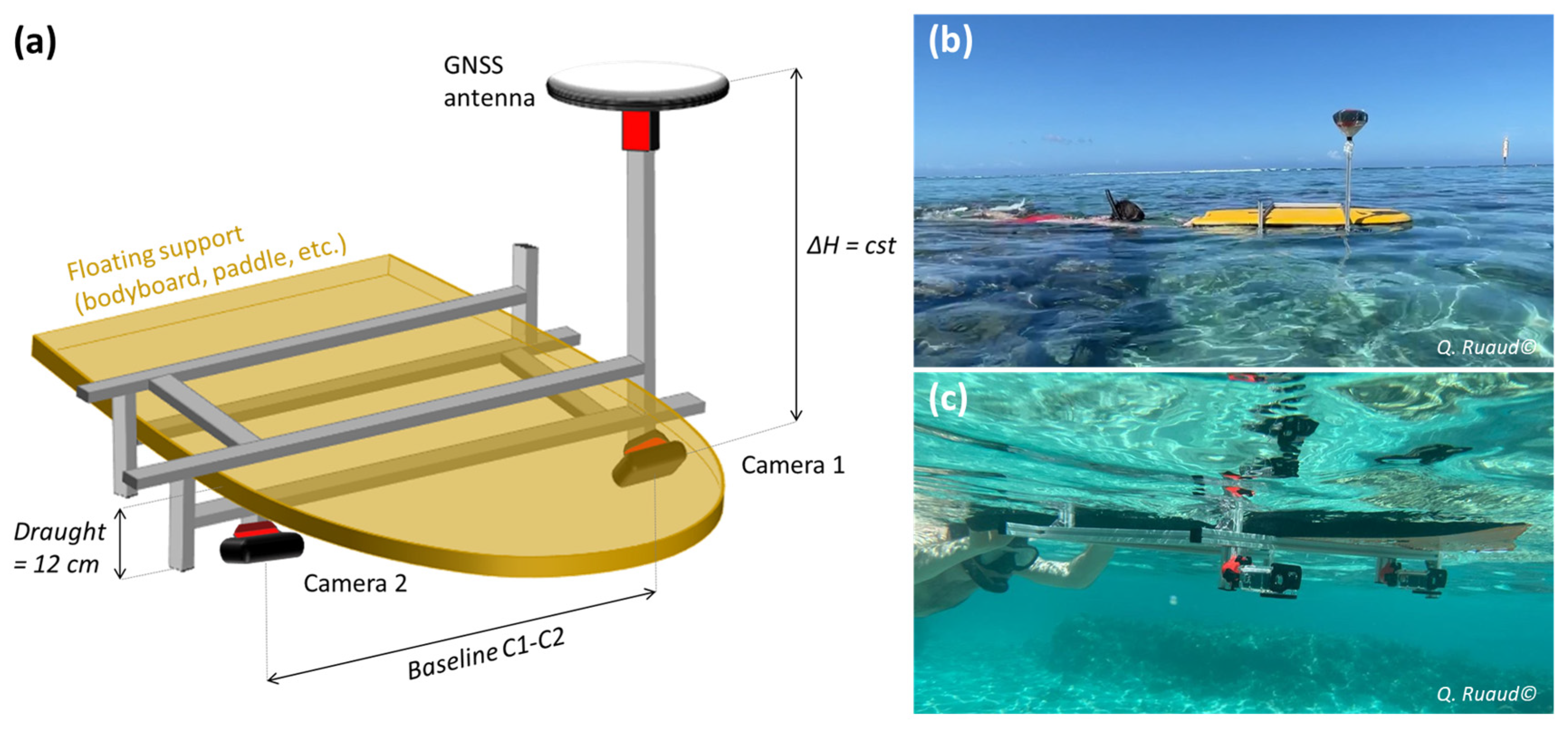
3.1. Principle of the Method

There is significant state of the art research available on Structure-from-Motion (SfM) photogrammetry, including, for example, [41,42,43,44]. In a nutshell, photogrammetry aims to reconstruct a 3D model by aerotriangulation from 2D images taken from different viewpoints on which homologous points (tie points) are identified. In SfM photogrammetry, these different viewpoints are obtained by moving the sensor and the data is analysed using Computer Vision methods. The iterative bundle adjustment in SfM reconstruction is based on a high level of information redundancy. The recommended overlaps between images are of the order of 80 to 90% for front overlap and 60 to 80% for side overlap (these values being adjusted according to the acquisition conditions, the ‘texture’ of the area, the precision required, etc.; for example, [45,46,47]).
The reconstruction quality depends on a wide range of parameters, such as the survey design (camera specifications, distance to the object, camera orientation, etc.) or the processing strategies (direct or indirect georeferencing, camera calibration, etc.). Another key issue for the geometric quality of the 3D reconstruction is to sufficiently constrain the system of collinearity equations, using external information, so that the bundle adjustment (including the self-calibration step) produces optimised results. Indeed, if the model is not sufficiently constrained, the self-calibration fails to produce correct internal camera parameters, and as a result, the 3D reconstruction is affected by scaling errors and/or by geometric distortions (generally, a ‘dome’ or ‘bowl’ effect; for example, [16,48,49]). There are several ways of constraining the bundle adjustment: either by using scale bars (whose actual dimensions are indicated on the images), by using GCPs or by knowing the exact position of the camera [50,51,52].
In the approach based on GCPs, which are identified on the images and whose geographical position is known precisely (generally from RTK GNSS positioning), the GCPs are used as references for optimizing the internal parameters of the cameras. With this approach, GCP number and distribution play a critical role in the quality of the 3D model [49].
As setting and measuring targets is time-consuming and complicated, particularly underwater, the POSEIDON system is based on a direct georeferencing approach of ‘RTK-based SfM photogrammetry’, i.e., a position (accurate to a few centimetres) is assigned to the majority of images. Given the shallow depths, the parameters of the water column are assumed to be homogeneous and optical ray propagation is therefore assumed to be linear. Knowing the accurate position of a majority of cameras is a sufficient geometric constraint for a geometrically accurate and georeferenced result [50].

3.2. POSEIDON Platform

The POSEIDON platform combines a floating support (typically a bodyboard), two imagery sensors and a precise positioning system (Figure 3).
The structure is made of V-slot aluminium profiles, assembled using angle brackets. By adjusting these brackets, the dimensions of the structure can be adapted to the dimensions of the support (within 10–20 cm). The POSEIDON system is very simple and very low-cost, since the total cost of the platform (including the GNSS receiver and the two cameras) is around USD 1500. POSEIDON is lightweight and can be easily dismantled for transporting.
Precise positioning of the platform is ensured by an RTK GNSS system, here a low-cost antenna (Sparkfun Facet, SparkFun Electronics, Boulder, CO, USA) fitted with a u-blox ZED-F9P module. The RTK corrections are taken from the nearest base of the open network of RTK GNSS Centipede bases [53] (base IUEM and OMT1 in Dellec Bay and the Hermitage backreef zone, respectively). The relay of RTK corrections to the antenna and the user interface is provided by the SW Maps smartphone application (freeware).
The imaging sensors here are two GoPro™ cameras. GoPro cameras have the advantage of being consumer sensors, so they are easy to find, inexpensive, robust, easy to operate and come with a wide range of accessories. Furthermore, with a focal length of 2.92 mm, these cameras offer a very wide field of view, particularly useful in shallow water. In this study, the cameras used were the GoPro™ Hero7 Black model, in 4K video mode (4:3 wide format and a framerate of 24 images/s) and a resolution of 12 Mpix. As the cameras are not subject to vibrations, the stabilisation option (and so the rolling shutter) was deactivated. To avoid any damage from collisions, the GoPro cameras were housed in waterproof housings.
Camera 1 was attached in alignment with the RTK GNSS antenna. Camera 2 was optional and was only used to extend the lateral field of view in very shallow water. Camera 2 can be shifted laterally along the aluminium profile so as to vary the baseline between the two cameras and thus to adjust the overlap between images. When the platform was fitted to a bodyboard, as shown here, the maximum baseline between the cameras was 58 cm. The footprint of each camera increases with depth (Figure 4a). In very shallow water, as the spatial footprints become smaller, the baseline must be reduced in order to maintain sufficient side-overlap between the two cameras (Figure 4b). At up to ten meters of water depth, the resolution of the images was less than or equal to 0.5 cm/pixel.
During a survey, the RTK GNSS antenna was positioned vertically above Camera 1 and at a constant distance ∆H, allowing the position of Camera 1 to be deduced to an accuracy of a few centimetres. To ensure that lever arm effects between the camera and the GNSS receiver remain negligible, swell conditions must remain calm. Two interchangeable mounting brackets were provided so that the antenna can be fixed at 76 cm or 60 cm from the camera, depending on sea conditions (to avoid water splashing). However, the higher ∆H is, the more the lever arm between the GNSS antenna and Camera 1 means that camera positioning will be inaccurate.

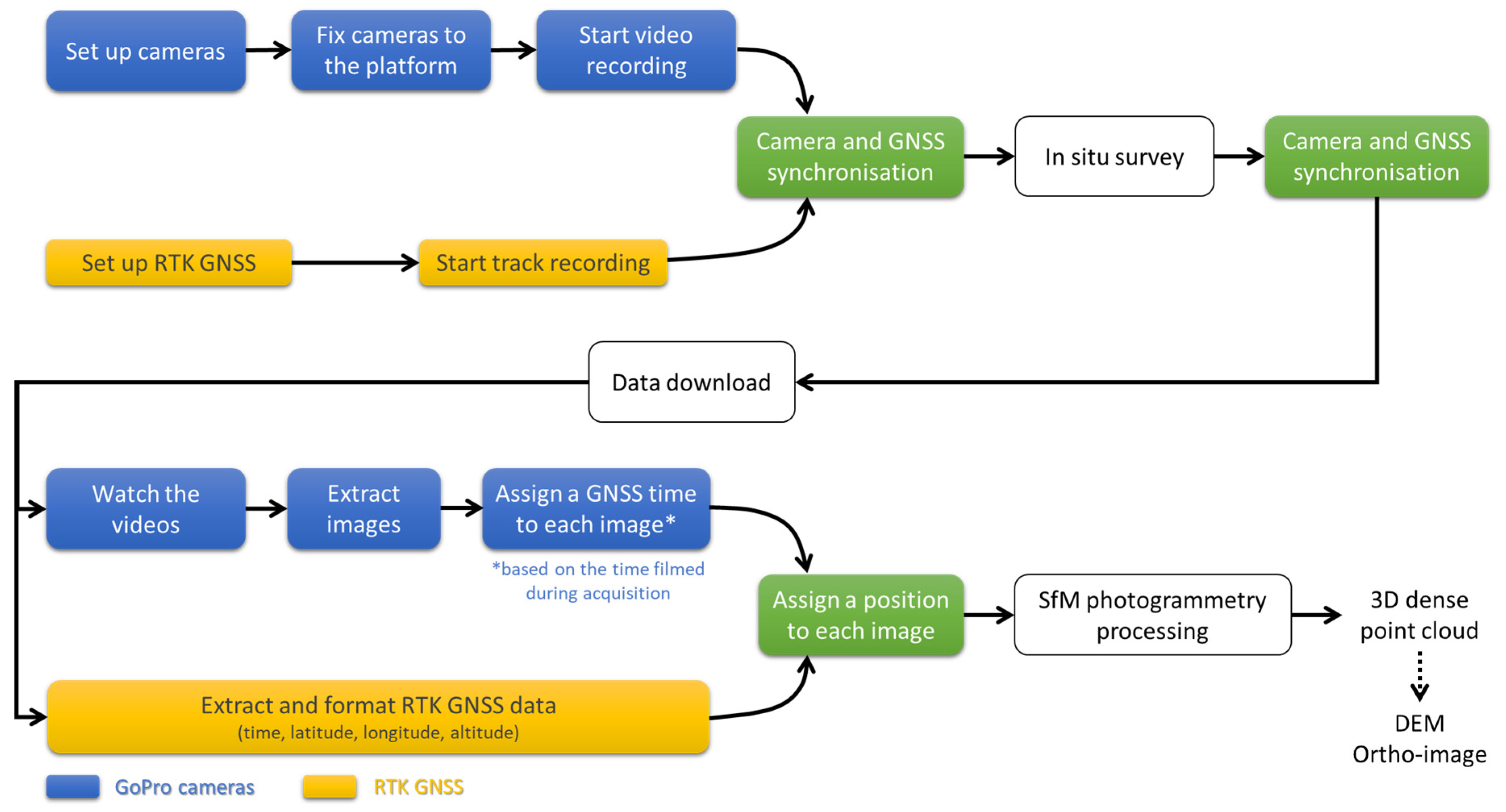
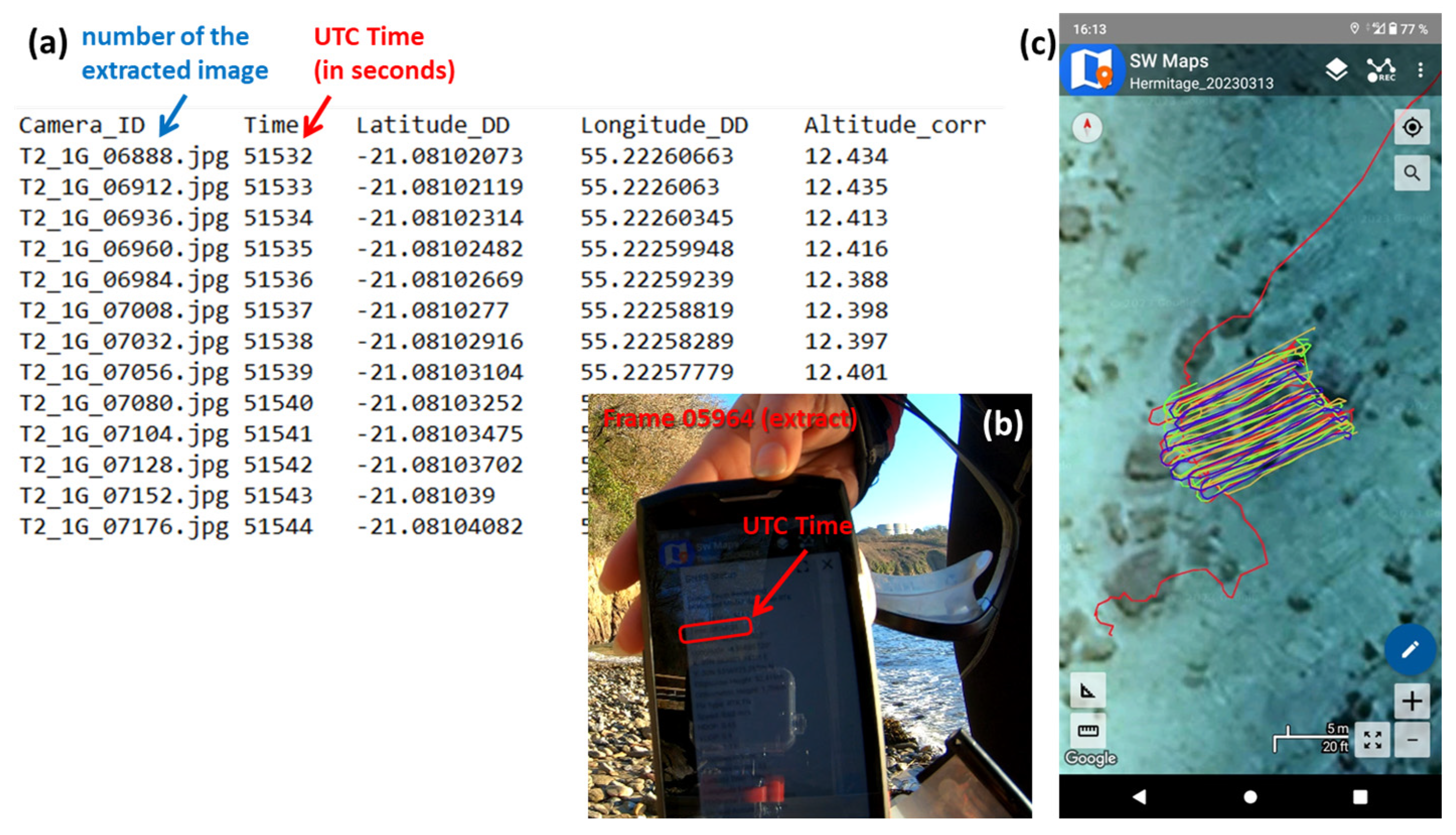
3.3. Practical Aspects of Acquisition and Processing

In practical terms, once the platform was tightened around the floating support, the sensors needed to be set up. The inter-camera distance and orientation of each camera were adjusted according to the bathymetric variations expected in the area. Figure 5 outlines the main stages in the acquisition and processing procedures with the POSEIDON system.
In the examples presented here:
  • In Dellec Bay: gradual variations in bathymetry were expected, with a water height of around 3 to 6 m. The two cameras were therefore pointed at the nadir and spaced as far apart as possible (58 cm). The speed of the platform was around 1.14 km/h.
  • In the Hermitage reef flat: very shallow depths (around 40 cm to 1 m of water) and sudden variations in bathymetry due to coral heads were expected. In this challenging case, various configurations were tested (Tests 1 to 4 in Table 1). The speed of the platform was around 1.5 km/h (higher than in the previous case, mainly because of the current).
The acquisition was then started on the two cameras. As previously mentioned, they were used here in video mode, in “wide” format, at 24 Hz, with a resolution of 12 Mpix. Video mode offers greater flexibility in terms of how often images are extracted. For the Dellec bay (with greater depths and lower speed), images were extracted at 1 or 2 frames/second. For the Hermitage backreef zone, to ensure sufficient coverage despite the very shallow depths and the speed of the platform (due to currents), images were extracted at 4 frames/second.
At the same time, the RTK GNSS survey was set to “Track” mode, with a frequency set from 2 to 4 Hz. We checked that the exported data included time and position information (Latitude/Longitude/Height or East/North/Altitude) in “Fix” precision. If it was not, we looked at GNSS messages, particularly the NMEA sentences. The NMEA (National Marine Electronics Association) is a widely used messaging standard transmitting data in ASCII strings. Among the NMEA sentences, the $GGA messages provides essential fix data which includes 3D location and accuracy data, therefore containing the required information.
To match the images extracted from the videos with the position information, the cameras were synchronized with the GNSS time. This synchronisation stage involves filming the “GNSS Status” interface on the SW Maps app with both cameras (Figure 6b). From the images where the GNSS time display was filmed, it was possible to associate a frame number in the video (for each camera) with a UTC time supplied by the GNNS. Knowing the video acquisition frequency, a time was therefore assigned to each extracted frame (Figure 6a). This synchronisation is accurate to half a second. Given the platform speed, this implies an uncertainty of 10 to 20 cm.
Once the synchronisation was performed, the platform was launched and the actual survey began. The SW Maps app provided real-time control of the trajectory followed (Figure 6c) and the spacing between transects (if any). As the smartphone used the 3G/4G network to receive RTK corrections and a Bluetooth network to connect to the GNSS antenna, it needed to be kept out of the water to avoid losing connections. We placed the smartphone in a waterproof pouch that can be placed on the bodyboard. Examples of trajectories are shown in Figure 1 and Figure 2. These trajectories are composed of juxtaposed transects, spaced 80 cm to around 3–4 m apart, depending on the expected depth of the zone, in order to maintain sufficient overlap between the images of adjacent transects. If at least one of the two cameras was forward pointing, the transects were travelled back and forth in order to limit masking due to the acquisition geometry. To ensure that there was no time drift, the GNSS time was filmed again with both cameras at the end of the survey.
At the end of the survey, all data were downloaded. A pre-processing step consisted of synchronization by assigning a UTC time to the frames extracted of the videos from the two cameras.
Python scripts [54] extracted the images from the videos at a frequency defined by the operator and created a five-column file (Figure 6a) containing the name of the extracted frames, the GPS time (used to match images and localizations) and the positions of the cameras in latitude, longitude and corrected ellipsoidal height (or east/north/altitude). At times corresponding to extracted frames, positions were extracted from the trajectory recorded by RTK GNSS. We assumed that the horizontal coordinates were identical for the GNSS receiver and Camera 1. For the vertical coordinate, we removed the ∆H offset corresponding to the distance between the GNSS antenna and Camera 1 (Figure 3a).
At this stage, the operator checked whether the frequency of image extraction seemed appropriate. In the examples presented here, for the Dellec survey, 1 image/second was extracted; for the Hermitage backreef zone surveys (Tests 1 to 4), as the water depths were sometimes very shallow (<30 cm), 4 images/second were extracted. To limit processing times, the dataset was ‘lightened’ by retaining only 1 or 2 images/second in areas of greater depth, or when the platform was moving more slowly.
SfM photogrammetry processing itself was then launched in Agisoft Metashape (v1.7). The sets of images from Camera 1 and Camera 2 were imported into Metashape and organised into two Camera Groups and two Calibration Groups. As the position information was not included in the EXIF of the frames extracted from the videos, the previously created file containing image names and positions (Figure 6a) was imported as a reference file. The accuracy of the camera positions varied according to sea conditions and the quality of the GNSS signal. In the examples presented here, this accuracy was set at 15 cm for images extracted from Camera 1. As the platform was not equipped with an Inertial Motion Unit (IMU), Camera 2 could be located (nearly) anywhere within a radius R = Baseline around Camera 1 (Figure 3a). If no position value was assigned to Camera 2, processing times (for image alignment) were increased. To avoid this and to guide the alignment, the same positions as Camera 1 were assigned to Camera 2, but a precision of 1 m was set. This 1 m value is arbitrary, taking into account positioning and synchronisation uncertainties and the distance between the cameras (a maximum of 58 cm with this platform).
Table 2 compiles the parameters used during Metashape underwater SfM photogrammetry processing. The algorithm for 3D surface reconstruction is divided into three main steps:
  • The first processing step consists of “aligning the images” by bundle adjustment. A SIFT (Scale Invariant Feature Transform) algorithm [55] performed the detection and matching of homologous keypoints in overlapping photographs. From the resulting tie points, the camera external parameters (position, orientation) were computed and/or optimized by aerotriangulation (and the collinearity equations), for both Camera 1 and Camera 2. In Agisoft Metashape, the accuracy was set to “high”, which means that the software works with the photos of the original size. Keypoint limit and tie point limit were set to their default values. The ‘Reference preselection’ was set to ‘Source’. The ‘Guided image matching’ was selected.
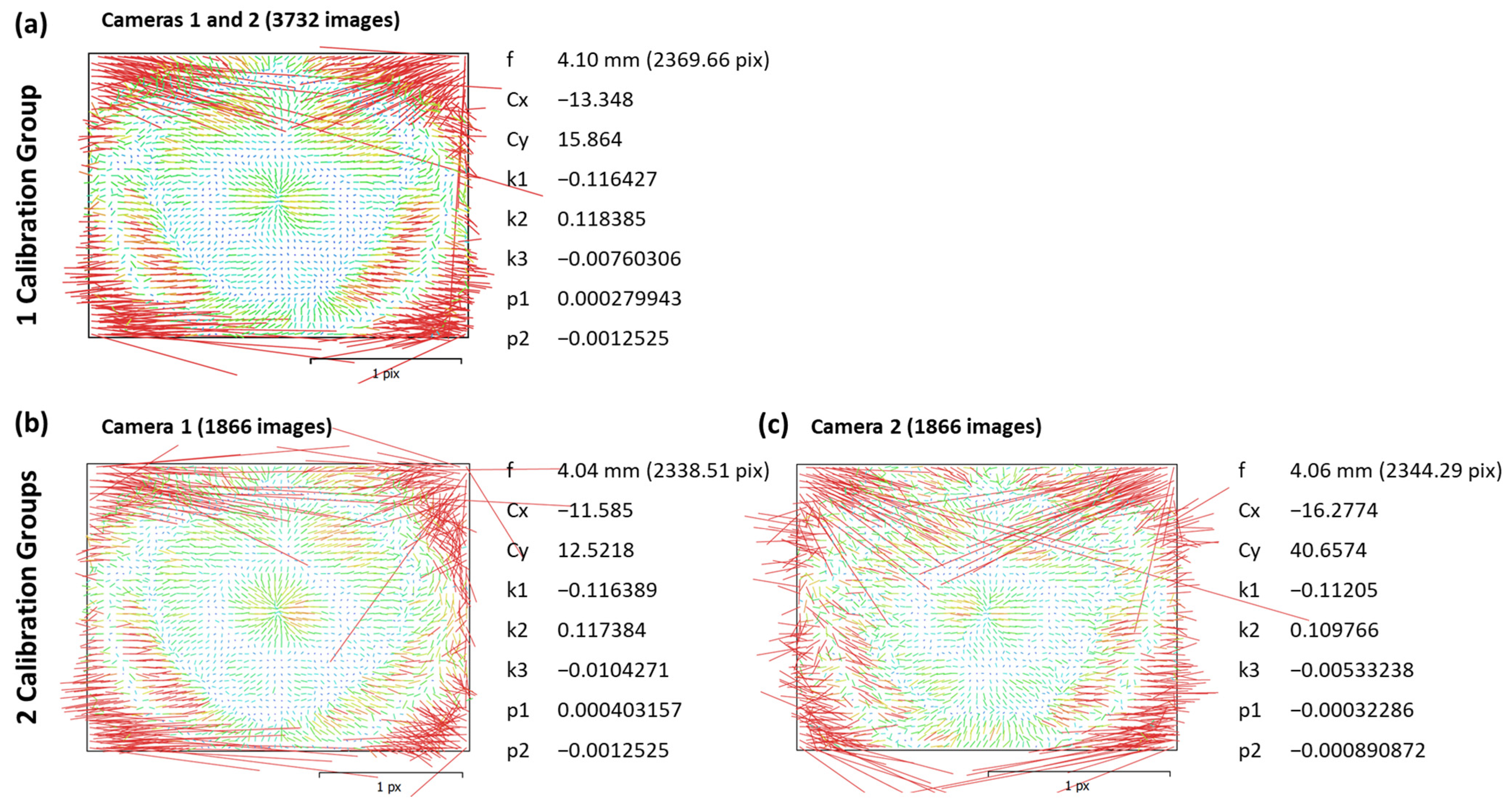
  • Camera internal parameters are refined by self-calibration, on the basis of knowledge of the accurate position of the cameras and modelling the distortion of the lens with Brown’s distortion model [56]. For this ‘Camera Optimization’ step, the default parameters were kept in Agisoft Metashape.
  • A georeferenced dense point cloud is then generated by dense image matching using the estimated camera external and internal parameters. For this step, in Metashape, the ‘Quality’ parameter was set to ‘High’ to obtain more detailed and accurate geometry; the depth filtering mode was set to ‘aggressive’ or ‘moderate’, depending on the level of detail to be preserved.
This point cloud can be considered as the final result and exported or meshed in 3D. If the transition from 3D to 2.5D data is not detrimental, a Digital Surface Model (DSM) and an orthoimage can also be generated and exported. Processing time was around 10 h for around 3700 images on a laptop with 16 GB RAM (CPU: AMD Ryzen 7, GPU: AMD Radeon Graphics gfx90c).

4. Results

As we rely on the accurate geographical position of the cameras for the SfM processing, the dense coloured point cloud generated is automatically georeferenced in an absolute coordinate system. The seabed is positioned directly in relation to a reference height.

4.1. Dellec Bay

The terrestrial survey of 20 February 2023, at low tide, was based on the approach using GCPs for geometric optimization and georeferencing (18 GCPs, in this case, with targets spread across the entire zone). For this Metashape reconstruction, the horizontal root mean square error (RMSE) is 5.2 cm and the vertical RMSE is 3.5 cm. The resulting 3D point cloud (Figure 7a) was used as dataset of reference for the validation.
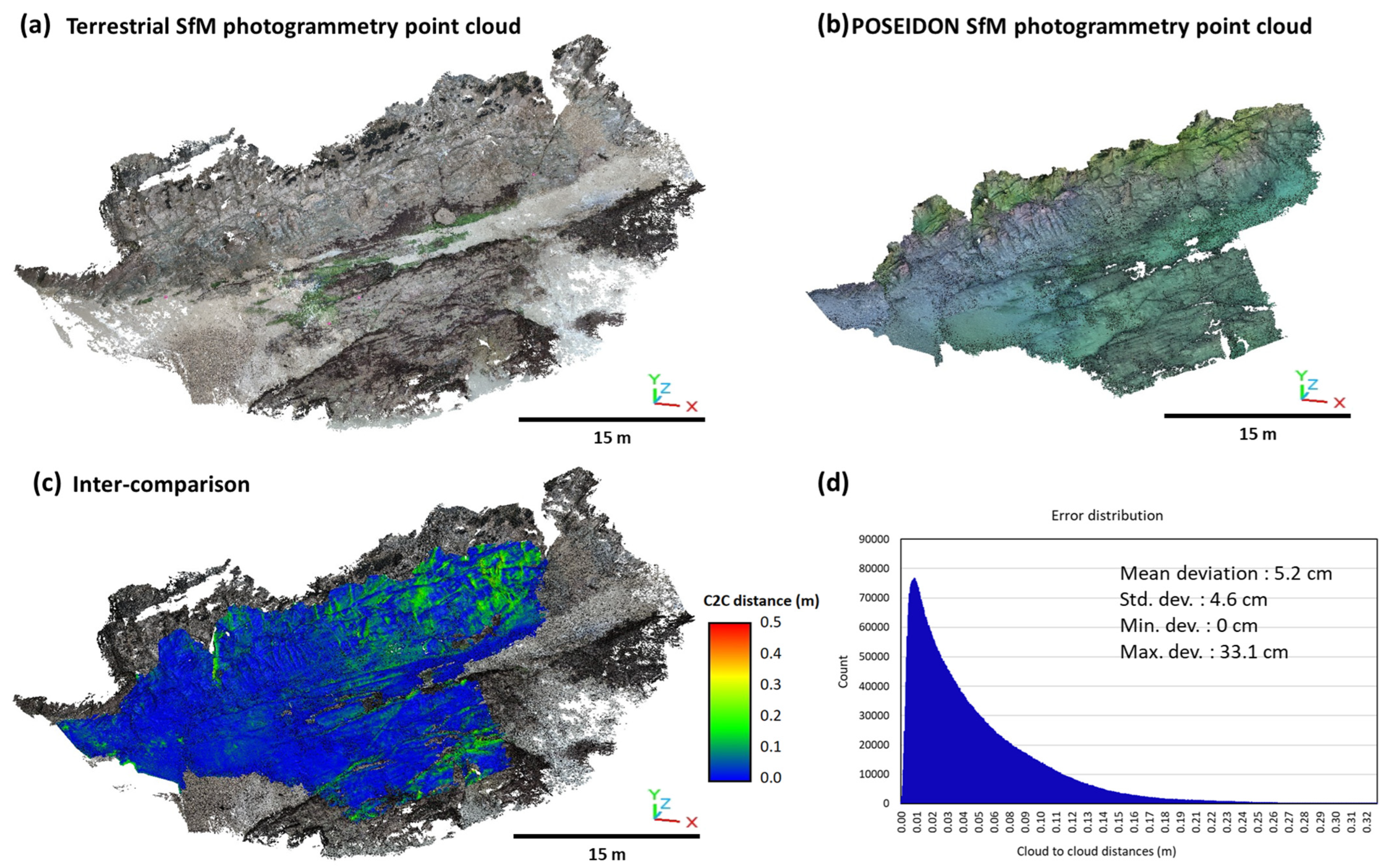
For the survey of 14 February 2023, in Dellec Bay, 4088 of the 4170 photos were aligned, i.e., 98.03%. A dense point cloud of 453,070,503 points was generated for an area of 659 m2 (Figure 7b), giving an average density of 6.8 × 105 points/m2 and potentially millimetric spatial resolution. However, to limit the volume of data, the point cloud was subsampled to 1 cm (minimal spacing between points).
The study area consisted mainly of rocky areas separated by sandy seabeds. At the time of the survey, the insufficient luminosity given the depth resulted in the RGB colours of the point cloud not being faithful to reality (bluish effect). However, the texture makes it possible to distinguish between sandy and rocky areas (Figure 7b).
The dense point cloud generated by underwater SfM photogrammetry was compared with the dense point cloud generated by terrestrial SfM photogrammetry. A “Cloud to Cloud” (C2C) distance calculation (Figure 7c) using the open source CloudCompare software (v.2.12) gave a mean deviation of 5.2 cm, with a standard deviation of 4.6 cm and a maximum deviation of 33.1 cm (Figure 7d). These deviations are in accordance with the orders of error expected for RTK GNSS measurements and SfM photogrammetry reconstructions. It can be seen that the areas with the highest deviations correspond to areas of seaweed (clearly visible on the terrestrial photogrammetry survey). At low tide, these seaweeds are immobile on the beach and are therefore well reconstructed in the 3D model. At high tide, the seaweed is mobile in the water and does not appear to have been reconstructed by the POSEIDON underwater SfM photogrammetry survey.

4.2. Hermitage Backreef Zone

On Réunion Island, the tidal regime with a very low tidal range makes it impossible to compare to a “reference” dataset acquired at low tide. The four tests were therefore inter-compared in order to assess the impact of the geometric configuration of the system. Table 3 summarizes, for each test, the number of photos aligned, the surface of the area reconstructed by underwater SfM photogrammetry and the mean point density on the raw point cloud. Figure 8 shows the colorized georeferenced dense point clouds obtained for each of the tests, subsampled to 1 cm. Darker bands are visible on all the point clouds. This is the shadow of the bodyboard during acquisition.
For each of the tests, more than three quarters of the images were aligned, with more photos aligned when both cameras were at nadir (Tests 3 and 4—Table 3). However, the reconstructed surface area is around 30 to 40% smaller for Tests 3 and 4 (Table 3), which corresponds to the fact that coral heads are often incompletely reconstructed, both on the sides and the top (Figure 8).
For Test 1, the data was very noisy and the scattered point cloud had to be filtered. In addition, the appearance of the point cloud 1 is slightly blurred compared to the other tests. These two effects can be the result of the grazing angle of the two cameras being pointed forward. This geometry makes it easier to see the lateral sides of the coral heads, but for horizontal surfaces it means that each pixel encompasses a wider area, which can have a negative effect on tie point matching and on the appearance of the rendering in the reconstructed cloud.
For Tests 3 and 4, with both cameras at nadir, reconstruction of the coral heads was patchier, particularly on the lateral side of the coral heads. The tops of some coral heads are even missing for Test 4. This is due to the fact that the reduction in baseline between the cameras was not sufficiently compensated for by bringing the survey transects closer together. Lateral overlap between images is therefore not improved overall, as it should have been by reducing the baseline.
The Test 2 configuration is therefore the one that seems to give the best results in this context. A quantitative intercomparison was carried out, by calculating (in CloudCompare® software) the distance between the point clouds obtained for Tests 1, 3 and 4 and the cloud obtained for Test 2. The results of this intercomparison are presented in Figure 9 and Table 4.
Once the noise has been filtered out on Test 1, the result is geometrically very close to the point cloud obtained for Test 2, with a mean deviation of −1.7 cm and a standard deviation of 6.3 cm (Table 4). Most of the differences are due to disparities in reconstruction on the lateral faces of the coral heads (Figure 9b). Figure 9d shows the reconstruction artefact (around 12 cm) between the survey transects of Test 4. This confirms what had been inferred above, that the distance between transects had not been reduced sufficiently to compensate for the reduction in the baseline between the cameras. Tests 3 and 4, with the cameras at nadir, are slightly affected by a “bowling/doming effect” (Figure 9c,d), resulting in geometric distortions of the dense point cloud. This effect is widely documented in the literature on close-range photogrammetry (e.g., [16,57,58]) and is the result of non-optimal self-calibration. Many studies have demonstrated the benefits of including oblique images in the image network to reduce these effects (e.g., [16,49,59,60]). Having at least one tilted camera therefore has the double advantage of collecting better images of the lateral faces of the coral heads in the axis of the trajectory, but also of optimizing the geometry of the image network to limit distortions as much as possible.
For all these reasons, we recommend a configuration similar to Test 2, with a nadir camera and a tilted camera. This is all the more critical in shallow waters, where it is difficult to maintain a high degree of overlap between images. An a priori estimate of the depth will also make it easier to anticipate the inter-camera and inter-radial spacing.

5. Discussion

5.1. Main Benefits and Constraints on Using POSEIDON

The POSEIDON platform provides an underwater photogrammetric survey with RTK georeferencing of the images. This makes it unnecessary or, at least, less necessary to use control points in the area, whose position remains challenging to measure underwater. Nevertheless, if the depth and accessibility of the area allow it, adding GCPs (measured by RTK GNSS) and/or scale bars can improve the quality of the reconstruction.
Moreover, the platform having a small draught (about 12 cm), there is no contact with the area being observed (no targets, no need for GPS rods, etc.), so there is no risk of damaging or disturbing the environment. In addition, the 3D point clouds presented here have been subsampled to 1 cm, but depending on the scientific requirements, it is possible to use the native sub-millimetre resolution.
However, as with all surveying methods, POSEIDON has its limitations. For SfM photogrammetry reconstruction to be effective, key points must be identifiable by the photogrammetric software on the images. To do this, the images have to be sufficiently sharp and the visibility conditions underwater have to be good enough. Therefore, days with good luminosity, low agitation and low turbidity are preferable. In addition, the fact that the area imaged has a marked texture (current ripples, granulometry, etc.) will facilitate photogrammetric processing. Furthermore, the greater the swell, the more we are faced with a configuration where the GNSS antenna is no longer aligned with the camera (lever arm effect). This would imply greater uncertainty about the geo-referencing of the camera, which, while not prohibitive for the reconstruction, would increase geometric distortions. But intense wave conditions are also associated with higher turbidity and therefore poorer underwater visibility. For all these reasons, these conditions should be avoided when carrying out a survey.
For areas with water height variations (of the order of a few tens of centimetres for depths of up to 1.5 m, such as coral heads), it is tricky to find an ideal baseline between the cameras for the entire survey. In such cases, across-track coverage will not necessarily reach 80%. It is therefore particularly important to maintain a high level of across-track coverage by reducing the speed of the platform in shallower areas and/or increasing the speed of image extraction.

5.2. POSEIDON Development Options

The aim of this study is to make a prototype system available to the community. Numerous changes can be made, both to the platform and to the processing chain, depending on the environment and the study requirements.
For example, a lighting system could be added for less luminous environments, other cameras models could be tested [37] and the metal structure could be adapted so that it can be mounted on other supports, such as small coastal craft (hydrographic survey boats, boats of opportunity, etc.). In order to improve the synchronization of the two cameras, new tools such as voice control commands or even GoPro Labs (https://gopro.com/en/us/info/gopro-labs, accessed on 12 September 2023) can be tested. These tools allow two cameras to start simultaneously or extend the GoPro camera capabilities, including time synchronization of multiple cameras.
One possible improvement would be to better constrain the parameters of Camera 2. This could involve adding an IMU to take into account the attitude of the platform and deduce the position of Camera 2. It could also involve rearranging the cameras, for example by placing the two cameras in different orientations, one above the other on the same vertical poll, directly above the GNSS antenna. In this way, the position of Camera 2 could be known directly. Among the possible drawbacks, divergent axes are not recommended for SfM photogrammetry (particularly with short focal length); and the lower camera may partially obscure the field of view of the upper camera.
Furthermore, by comparing the calibration parameters obtained (i) by grouping all the cameras in a single calibration group (Figure 10a) and (ii) by separating Cameras 1 and 2 into two groups (Figure 10b,c), we can see that the variations in parameters remain moderate. We can infer that, as long as there are enough accurately positioned images (of the centimetre order) in the whole dataset, the self-calibration of Camera 2 is faintly impacted by the fact that Camera 2 positions are not known precisely.
The question may arise of adding a remote-controlled propulsion system to ‘dronise’ the platform. However, converting to a drone would inevitably lead to an increase in costs and potentially greater difficulty in orienting the platform and following a trajectory, especially in strong currents. In addition, the use of a motorized vehicle may come up against regulations in certain areas. Finally, when changing the mode of propulsion, care must be taken to maintain a sufficiently low speed to ensure strong along-track recovery.

6. Conclusions

POSEIDON is a floating platform for collecting underwater imagery, avoiding the disturbance to optical beams caused by the surface of the water (specular reflection, refraction, wavelets on the surface). This system can be operated even in very shallow water and it makes it easy to carry out low-cost (USD ~1500) SfM photogrammetry surveys with RTK GNSS positioning of cameras. The ability to take RTK measurements makes underwater photogrammetry easier, particularly when georeferencing the survey is required. When comparing the point cloud provided by POSEIDON underwater SfM photogrammetry and by classical terrestrial SfM survey, the differences are around 5 cm (mean deviation of 5.2 cm and standard deviation of 4.6 cm).
The POSEIDON system therefore has the potential to generate georeferenced and geometrically accurate 3D point clouds in shallow waters. These point clouds can then be exported as DSMs and orthophotographs. Such surveys are of interest in a wide range of applications: micro-bathymetry, hydrodynamics (bottom roughness), benthic habitats, ecological inventories, archaeology, etc.

Author Contributions

Conceptualization, M.J. and E.A.; methodology, M.J., E.A. and S.D.; software, S.D., M.J. and I.U.-B.; validation, S.D., M.J., I.U.-B. and E.C.; formal analysis, S.D., M.J., I.U.-B., E.C. and F.G.; investigation, S.D., M.J., I.U.-B., E.C. and N.L.D.; resources, M.J., F.G. and E.C.; data curation, S.D. and M.J.; writing—original draft preparation, M.J.; writing—review and editing, S.D., I.U.-B., C.D., F.F., N.L.D., E.C. and F.G.; visualization, M.J. and S.D.; supervision, F.G., N.L.D., F.F. and C.D.; project administration, E.C. and M.J.; funding acquisition, E.C., M.J., I.U.-B., F.G., F.F. and C.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research benefited from the financial support of the ISblue project, the Interdisciplinary graduate school for the blue planet (grant number ANR-17-EURE-0015, co-funded by a grant from the French government under the program “Investissements d’Avenir” embedded in France 2030) and from the OMNCG project (Observatoire des Milieux Naturels et des Changements Globaux—FED4128), TELEMAC.

Data Availability Statement

The point clouds and the metadata of the photogrammetric surveys with the POSEIDON platform in Dellec Bay and in Hermitage reef flat are available (with DOI), respectively, at: https://doi.org/10.35110/a119caa0-782f-4803-a887-402c8a1580fd (accessed on 4 December 2023); https://doi.org/10.35110/248cf12d-a666-491b-ba1c-b3d2981c35ca (accessed on 4 December 2023).

Acknowledgments

The authors warmly thank Rodolphe Devillers, Pascal Mouquet, Sophie Bureau and Thomas Germain (for participating in the field surveys), as well as Quentin Ruaud (for the photographs).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Collins, W.T.; Galloway, J.L. Seabed Classification with Multibeam Bathymetry. Sea Technol. 1998, 39, 45–50. [Google Scholar]
  2. Pandian, P.K.; Ruscoe, J.P.; Shields, M.; Side, J.C.; Harris, R.E.; Kerr, S.A.; Bullen, C.R. Seabed Habitat Mapping Techniques: An Overview of the Performance of Various Systems. Mediterr. Mar. Sci. 2009, 10, 29. [Google Scholar] [CrossRef]
  3. Borrelli, M.; Smith, T.L.; Mague, S.T. Vessel-Based, Shallow Water Mapping with a Phase-Measuring Sidescan Sonar. Estuaries Coasts 2022, 45, 961–979. [Google Scholar] [CrossRef]
  4. Allouis, T.; Bailly, J.-S.; Pastol, Y.; Le Roux, C. Comparison of LiDAR Waveform Processing Methods for Very Shallow Water Bathymetry Using Raman, near-Infrared and Green Signals. Earth Surf. Process. Landf. 2010, 35, 640–650. [Google Scholar] [CrossRef]
  5. Yang, F.; Qi, C.; Su, D.; Ding, S.; He, Y.; Ma, Y. An Airborne LiDAR Bathymetric Waveform Decomposition Method in Very Shallow Water: A Case Study around Yuanzhi Island in the South China Sea. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102788. [Google Scholar] [CrossRef]
  6. Szafarczyk, A.; Toś, C. The Use of Green Laser in LiDAR Bathymetry: State of the Art and Recent Advancements. Sensors 2022, 23, 292. [Google Scholar] [CrossRef] [PubMed]
  7. Sous, D.; Bouchette, F.; Doerflinger, E.; Meulé, S.; Certain, R.; Toulemonde, G.; Dubarbier, B.; Salvat, B. On the Small-scale Fractal Geometrical Structure of a Living Coral Reef Barrier. Earth Surf. Process. Landf. 2020, 45, 3042–3054. [Google Scholar] [CrossRef]
  8. Fritsch, N.; Fromant, G.; Hurther, D.; Caceres, I. Coarse Sand Transport Processes in the Ripple Vortex Regime under Asymmetric Nearshore Waves. JGR-Ocean, 2023; in press. [Google Scholar]
  9. Raoult, V.; David, P.A.; Dupont, S.F.; Mathewson, C.P.; O’Neill, S.J.; Powell, N.N.; Williamson, J.E. GoPros™ as an Underwater Photogrammetry Tool for Citizen Science. PeerJ 2016, 4, e1960. [Google Scholar] [CrossRef]
  10. Jaud, M.; Kervot, M.; Delacourt, C.; Bertin, S. Potential of Smartphone SfM Photogrammetry to Measure Coastal Morphodynamics. Remote Sens. 2019, 11, 2242. [Google Scholar] [CrossRef]
  11. Fabris, M.; Fontana Granotto, P.; Monego, M. Expeditious Low-Cost SfM Photogrammetry and a TLS Survey for the Structural Analysis of Illasi Castle (Italy). Drones 2023, 7, 101. [Google Scholar] [CrossRef]
  12. Girod, L.; Nuth, C.; Kääb, A.; Etzelmüller, B.; Kohler, J. Terrain Changes from Images Acquired on Opportunistic Flights by SfM Photogrammetry. Cryosphere 2017, 11, 827–840. [Google Scholar] [CrossRef]
  13. Bryson, M.; Duce, S.; Harris, D.; Webster, J.M.; Thompson, A.; Vila-Concejo, A.; Williams, S.B. Geomorphic Changes of a Coral Shingle Cay Measured Using Kite Aerial Photography. Geomorphology 2016, 270, 1–8. [Google Scholar] [CrossRef]
  14. Feurer, D.; Planchon, O.; El Maaoui, M.A.; Ben Slimane, A.; Boussema, M.R.; Pierrot-Deseilligny, M.; Raclot, D. Using Kites for 3-D Mapping of Gullies at Decimetre-Resolution over Several Square Kilometres: A Case Study on the Kamech Catchment, Tunisia. Nat. Hazards Earth Syst. Sci. 2018, 18, 1567–1582. [Google Scholar] [CrossRef]
  15. Jaud, M.; Delacourt, C.; Le Dantec, N.; Allemand, P.; Ammann, J.; Grandjean, P.; Nouaille, H.; Prunier, C.; Cuq, V.; Augereau, E.; et al. Diachronic UAV Photogrammetry of a Sandy Beach in Brittany (France) for a Long-Term Coastal Observatory. ISPRS Int. J. Geo-Inf. 2019, 8, 267. [Google Scholar] [CrossRef]
  16. James, M.R.; Robson, S. Straightforward Reconstruction of 3D Surfaces and Topography with a Camera: Accuracy and Geoscience Application: 3D Surfaces and Topography with a Camera. J. Geophys. Res. Earth Surf. 2012, 117, 03017. [Google Scholar] [CrossRef]
  17. Bessin, Z.; Jaud, M.; Letortu, P.; Vassilakis, E.; Evelpidou, N.; Costa, S.; Delacourt, C. Smartphone Structure-from-Motion Photogrammetry from a Boat for Coastal Cliff Face Monitoring Compared with Pléiades Tri-Stereoscopic Imagery and Unmanned Aerial System Imagery. Remote Sens. 2023, 15, 3824. [Google Scholar] [CrossRef]
  18. Wright, A.E.; Conlin, D.L.; Shope, S.M. Assessing the Accuracy of Underwater Photogrammetry for Archaeology: A Comparison of Structure from Motion Photogrammetry and Real Time Kinematic Survey at the East Key Construction Wreck. J. Mar. Sci. Eng. 2020, 8, 849. [Google Scholar] [CrossRef]
  19. Urbina-Barreto, I.; Garnier, R.; Elise, S.; Pinel, R.; Dumas, P.; Mahamadaly, V.; Facon, M.; Bureau, S.; Peignon, C.; Quod, J.-P.; et al. Which Method for Which Purpose? A Comparison of Line Intercept Transect and Underwater Photogrammetry Methods for Coral Reef Surveys. Front. Mar. Sci. 2021, 8, 636902. [Google Scholar] [CrossRef]
  20. Ventura, D.; Mancini, G.; Casoli, E.; Pace, D.S.; Lasinio, G.J.; Belluscio, A.; Ardizzone, G. Seagrass Restoration Monitoring and Shallow-Water Benthic Habitat Mapping through a Photogrammetry-Based Protocol. J. Environ. Manag. 2022, 304, 114262. [Google Scholar] [CrossRef]
  21. Del Savio, A.A.; Luna Torres, A.; Vergara Olivera, M.A.; Llimpe Rojas, S.R.; Urday Ibarra, G.T.; Neckel, A. Using UAVs and Photogrammetry in Bathymetric Surveys in Shallow Waters. Appl. Sci. 2023, 13, 3420. [Google Scholar] [CrossRef]
  22. He, J.; Lin, J.; Ma, M.; Liao, X. Mapping Topo-Bathymetry of Transparent Tufa Lakes Using UAV-Based Photogrammetry and RGB Imagery. Geomorphology 2021, 389, 107832. [Google Scholar] [CrossRef]
  23. Dietrich, J.T. Bathymetric Structure-from-Motion: Extracting Shallow Stream Bathymetry from Multi-View Stereo Photogrammetry: Bathymetric Structure-From-Motion. Earth Surf. Process. Landf. 2017, 42, 355–364. [Google Scholar] [CrossRef]
  24. Burns, J.H.R.; Delparte, D.; Gates, R.D.; Takabayashi, M. Utilizing Underwater Three-Dimensional Modeling to Enhance Ecological and Biological Studies of Coral Reefs. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W5, 61–66. [Google Scholar] [CrossRef]
  25. Urbina-Barreto, I. New Quantitative Indices from 3D Modeling by Photogrammetry to Monitor Coral Reef Environments. Ph.D. Thesis, Université de la Réunion, Saint-Denis, France, 2020. [Google Scholar]
  26. David, C.G.; Kohl, N.; Casella, E.; Rovere, A.; Ballesteros, P.; Schlurmann, T. Structure-from-Motion on Shallow Reefs and Beaches: Potential and Limitations of Consumer-Grade Drones to Reconstruct Topography and Bathymetry. Coral Reefs 2021, 40, 835–851. [Google Scholar] [CrossRef]
  27. Casella, E.; Lewin, P.; Ghilardi, M.; Rovere, A.; Bejarano, S. Assessing the Relative Accuracy of Coral Heights Reconstructed from Drones and Structure from Motion Photogrammetry on Coral Reefs. Coral Reefs 2022, 41, 869–875. [Google Scholar] [CrossRef]
  28. Green, J.; Gainsford, M. Evaluation of Underwater Surveying Techniques. Int. J. Naut. Archaeol. 2003, 32, 252–261. [Google Scholar] [CrossRef]
  29. Costa, E.; Guerra, F.; Vernier, P. Self-Assembled ROV and Photogrammetric Surveys with Low Cost Techniques. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-2, 275–279. [Google Scholar] [CrossRef]
  30. Price, D.M.; Robert, K.; Callaway, A.; Lo Lacono, C.; Hall, R.A.; Huvenne, V.A.I. Using 3D Photogrammetry from ROV Video to Quantify Cold-Water Coral Reef Structural Complexity and Investigate Its Influence on Biodiversity and Community Assemblage. Coral Reefs 2019, 38, 1007–1021. [Google Scholar] [CrossRef]
  31. Menna, F.; Nocerino, E.; Nawaf, M.M.; Seinturier, J.; Torresani, A.; Drap, P.; Remondino, F.; Chemisky, B. Towards Real-Time Underwater Photogrammetry for Subsea Metrology Applications. In Proceedings of the OCEANS 2019-Marseille, Marseille, France, 17–20 June 2019; IEEE: Marseille, France, 2019; pp. 1–10. [Google Scholar]
  32. Teague, J.; Scott, T. Underwater Photogrammetry and 3D Reconstruction of Submerged Objects in Shallow Environments by ROV and Underwater GPS. J. Mar. Sci. Res. Technol. 2017. [Google Scholar]
  33. Wu, Y.; Ta, X.; Xiao, R.; Wei, Y.; An, D.; Li, D. Survey of Underwater Robot Positioning Navigation. Appl. Ocean Res. 2019, 90, 101845. [Google Scholar] [CrossRef]
  34. Luo, Q.; Yan, X.; Ju, C.; Chen, Y.; Luo, Z. An Ultra-Short Baseline Underwater Positioning System with Kalman Filtering. Sensors 2020, 21, 143. [Google Scholar] [CrossRef] [PubMed]
  35. Leon, J.X.; Roelfsema, C.M.; Saunders, M.I.; Phinn, S.R. Measuring Coral Reef Terrain Roughness Using ‘Structure-from-Motion’ Close-Range Photogrammetry. Geomorphology 2015, 242, 21–28. [Google Scholar] [CrossRef]
  36. Ventura, D.; Dubois, S.F.; Bonifazi, A.; Jona Lasinio, G.; Seminara, M.; Gravina, M.F.; Ardizzone, G. Integration of Close-range Underwater Photogrammetry with Inspection and Mesh Processing Software: A Novel Approach for Quantifying Ecological Dynamics of Temperate Biogenic Reefs. Remote Sens. Ecol. Conserv. 2021, 7, 169–186. [Google Scholar] [CrossRef]
  37. Raber, G.T.; Schill, S.R. Reef Rover: A Low-Cost Small Autonomous Unmanned Surface Vehicle (USV) for Mapping and Monitoring Coral Reefs. Drones 2019, 3, 38. [Google Scholar] [CrossRef]
  38. Bonhommeau, S. Projet PLANCHA. Available online: https://ocean-indien.ifremer.fr/en/Projects/Technological-innovations/PLANCHA-2021-2023 (accessed on 3 July 2023).
  39. InfoClimat. Climatologie Mensuelle/Observations-Météo/Archives, in Brest-Guipavas Station and Le Port station. Available online: https://www.infoclimat.fr/ (accessed on 5 July 2023).
  40. Cordier, E.; Lézé, J.; Join, J.-L. Natural Tidal Processes Modified by the Existence of Fringing Reef on La Reunion Island (Western Indian Ocean): Impact on the Relative Sea Level Variations. Cont. Shelf Res. 2013, 55, 119–128. [Google Scholar] [CrossRef]
  41. Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
  42. Javernick, L.; Brasington, J.; Caruso, B. Modeling the Topography of Shallow Braided Rivers Using Structure-from-Motion Photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
  43. Carrivick, J.; Smith, M.; Quincey, D. Structure from Motion in the Geosciences; Wiley, Blackwell: Chichester, UK; Ames, IA, USA, 2016; ISBN 978-1-118-89584-9. [Google Scholar]
  44. Eltner, A.; Sofia, G. Structure from Motion Photogrammetric Technique. In Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2020; Volume 23, pp. 1–24. ISBN 978-0-444-64177-9. [Google Scholar]
  45. Elhadary, A.; Rabah, M.; Ghanim, E.; Mohie, R.; Taha, A. The Influence of Flight Height and Overlap on UAV Imagery over Featureless Surfaces and Constructing Formulas Predicting the Geometrical Accuracy. NRIAG J. Astron. Geophys. 2022, 11, 210–223. [Google Scholar] [CrossRef]
  46. Dai, F.; Feng, Y.; Hough, R. Photogrammetric Error Sources and Impacts on Modeling and Surveying in Construction Engineering Applications. Vis. Eng. 2014, 2, 2. [Google Scholar] [CrossRef]
  47. Neyer, F.; Nocerino, E.; Gruen, A. Image Quality Improvements in low-cost underwater photogrammetry. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, XLII-2/W10, 135–142. [Google Scholar] [CrossRef]
  48. James, M.R.; Robson, S. Mitigating Systematic Error in Topographic Models Derived from UAV and Ground-Based Image Networks: Mitigating Systematic Error in Topographic Models. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
  49. Jaud, M.; Passot, S.; Allemand, P.; Le Dantec, N.; Grandjean, P.; Delacourt, C. Suggestions to Limit Geometric Distortions in the Reconstruction of Linear Coastal Landforms by SfM Photogrammetry with PhotoScan® and MicMac® for UAV Surveys with Restricted GCPs Pattern. Drones 2019, 3, 2. [Google Scholar] [CrossRef]
  50. Jaud, M.; Bertin, S.; Beauverger, M.; Augereau, E.; Delacourt, C. RTK GNSS-Assisted Terrestrial SfM Photogrammetry without GCP: Application to Coastal Morphodynamics Monitoring. Remote Sens. 2020, 12, 1889. [Google Scholar] [CrossRef]
  51. Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry Using UAV-Mounted GNSS RTK: Georeferencing Strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
  52. Bertin, S.; Floc’h, F.; Le Dantec, N.; Jaud, M.; Cancouët, R.; Franzetti, M.; Cuq, V.; Prunier, C.; Ammann, J.; Augereau, E.; et al. A Long-Term Dataset of Topography and Nearshore Bathymetry at the Macrotidal Pocket Beach of Porsmilin, France. Sci. Data 2022, 9, 79. [Google Scholar] [CrossRef] [PubMed]
  53. Le Réseau Centipède RTK. Available online: https://docs.centipede.fr/ (accessed on 4 December 2023).
  54. Delsol, S. POSEIDON-Processing 2023. Available online: https://github.com/sDelsol (accessed on 4 December 2023).
  55. Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
  56. Agisoft Metashape User Manual-Professional Edition, Version 1.7; Agisoft LLC: Saint Petersburg, Russia, 2021. Available online: https://www.agisoft.com/pdf/metashape-pro_1_7_en.pdf (accessed on 29 September 2023).
  57. Tournadre, V.; Pierrot-Deseilligny, M.; Faure, P.H. UAV LINEAR PHOTOGRAMMETRY. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-3/W3, 327–333. [Google Scholar] [CrossRef]
  58. Luhmann, T.; Fraser, C.; Maas, H.-G. Sensor Modelling and Camera Calibration for Close-Range Photogrammetry. ISPRS J. Photogramm. Remote Sens. 2016, 115, 37–46. [Google Scholar] [CrossRef]
  59. Nesbit, P.; Hugenholtz, C. Enhancing UAV–SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens. 2019, 11, 239. [Google Scholar] [CrossRef]
  60. Huang, W.; Jiang, S.; Jiang, W. Camera Self-Calibration with GNSS Constrained Bundle Adjustment for Weakly Structured Long Corridor UAV Images. Remote Sens. 2021, 13, 4222. [Google Scholar] [CrossRef]
Remotesensing 16 00020 g001
Figure 1. Field site at Dellec bay in Northwest Brittany (France). (a) Map of France and western part of Brittany. (b) Orthophotography of the field survey area (source: Bing Maps Aerial) and trajectory (about 450 m) of the POSEIDON system on 14 February 2023.
Figure 1. Field site at Dellec bay in Northwest Brittany (France). (a) Map of France and western part of Brittany. (b) Orthophotography of the field survey area (source: Bing Maps Aerial) and trajectory (about 450 m) of the POSEIDON system on 14 February 2023.
Remotesensing 16 00020 g001
Remotesensing 16 00020 g002
Figure 2. Field site at the Hermitage backreef zone in Réunion Island (France). (a) Map of Indian Ocean and Réunion Island. (b) Orthophotography of the field survey area (source: Bing Maps Aerial) and trajectory (about 250 m) of the POSEIDON system on 13 March 2023.
Figure 2. Field site at the Hermitage backreef zone in Réunion Island (France). (a) Map of Indian Ocean and Réunion Island. (b) Orthophotography of the field survey area (source: Bing Maps Aerial) and trajectory (about 250 m) of the POSEIDON system on 13 March 2023.
Remotesensing 16 00020 g002
Remotesensing 16 00020 g003
Figure 3. (a) Conceptual diagram of the POSEIDON system, with a structure adapted to a bodyboard holding two GoPro cameras and an RTK GNSS antenna vertically above one of the two GoPros. (b,c) Overwater (b) and underwater (c) views of the POSEIDON system during acquisition.
Figure 3. (a) Conceptual diagram of the POSEIDON system, with a structure adapted to a bodyboard holding two GoPro cameras and an RTK GNSS antenna vertically above one of the two GoPros. (b,c) Overwater (b) and underwater (c) views of the POSEIDON system during acquisition.
Remotesensing 16 00020 g003
Remotesensing 16 00020 g004
Figure 4. (a) Diagram of the theoretical footprint for one GoPro camera according to the water depth. (b) Diagram of the theoretical overlap between the footprints of the two GoPro cameras according to water depth and to the inter-camera distance.
Figure 4. (a) Diagram of the theoretical footprint for one GoPro camera according to the water depth. (b) Diagram of the theoretical overlap between the footprints of the two GoPro cameras according to water depth and to the inter-camera distance.
Remotesensing 16 00020 g004
Remotesensing 16 00020 g005
Figure 5. Diagram of the main steps of the acquisition and processing chains with the POSEIDON system.
Figure 5. Diagram of the main steps of the acquisition and processing chains with the POSEIDON system.
Remotesensing 16 00020 g005
Remotesensing 16 00020 g006
Figure 6. (a) Extract of a five-column file generated by a Python script, comprising the name of the extracted frames, the UTC time and the GNSS positions of the cameras (corrected of the ∆H offset). This file is then used as Reference file in Agisoft Metashape. (b) Image of the Smartphone filmed by one of the GoPro cameras to capture the GPS time on the SW Maps interface for GNSS–camera synchronisation. (c) Capture of the SW Maps interface for real-time GNSS–camera trajectory tracking (here, on the repeated surveys of the same area in the Hermitage backreef zone, on 13 March 2023).
Figure 6. (a) Extract of a five-column file generated by a Python script, comprising the name of the extracted frames, the UTC time and the GNSS positions of the cameras (corrected of the ∆H offset). This file is then used as Reference file in Agisoft Metashape. (b) Image of the Smartphone filmed by one of the GoPro cameras to capture the GPS time on the SW Maps interface for GNSS–camera synchronisation. (c) Capture of the SW Maps interface for real-time GNSS–camera trajectory tracking (here, on the repeated surveys of the same area in the Hermitage backreef zone, on 13 March 2023).
Remotesensing 16 00020 g006
Remotesensing 16 00020 g007
Figure 7. Results obtained in Dellec bay. (a) Dense point cloud generated by terrestrial SfM photogrammetry at low tide using a GoPro camera attached to the end of a 4 m pole and 18 targets serving as Ground Control Points (GCPs) and measured with RTK GNSS. (b) Dense point cloud generated at high tide by underwater SfM photogrammetry using the POSEIDON system (native average density of 6.8 × 105 points/m2 before subsampling). (c) Comparison of terrestrial and bathymetric point cloud using the C2C distance in CloudCompare. (d) Statistics of the Cloud-to-Cloud comparison and statistical distribution of the error.
Figure 7. Results obtained in Dellec bay. (a) Dense point cloud generated by terrestrial SfM photogrammetry at low tide using a GoPro camera attached to the end of a 4 m pole and 18 targets serving as Ground Control Points (GCPs) and measured with RTK GNSS. (b) Dense point cloud generated at high tide by underwater SfM photogrammetry using the POSEIDON system (native average density of 6.8 × 105 points/m2 before subsampling). (c) Comparison of terrestrial and bathymetric point cloud using the C2C distance in CloudCompare. (d) Statistics of the Cloud-to-Cloud comparison and statistical distribution of the error.
Remotesensing 16 00020 g007
Remotesensing 16 00020 g008
Figure 8. Results obtained for the different configurations (presented in Table 1) in the Hermitage backreef zone.
Figure 8. Results obtained for the different configurations (presented in Table 1) in the Hermitage backreef zone.
Remotesensing 16 00020 g008
Remotesensing 16 00020 g009
Figure 9. (a) Dense point cloud in RGB colours obtained for Test 2. (b–d) Dense point clouds coloured by distance between the Test 2 (B = 58 cm; θ1 = 23°; θ2 = 0°; used as reference) and the dense point clouds obtained for Test 1 (B = 58 cm; θ1 = 23°; θ2 = 25°) (b), Test 3 (B = 58 cm; θ1 = 0°; θ2 = 0°) (c) and Test 4 (B = 40 cm; θ1 = 0°; θ2 = 0°) (d). The distances on the colour bars are in meters.
Figure 9. (a) Dense point cloud in RGB colours obtained for Test 2. (b–d) Dense point clouds coloured by distance between the Test 2 (B = 58 cm; θ1 = 23°; θ2 = 0°; used as reference) and the dense point clouds obtained for Test 1 (B = 58 cm; θ1 = 23°; θ2 = 25°) (b), Test 3 (B = 58 cm; θ1 = 0°; θ2 = 0°) (c) and Test 4 (B = 40 cm; θ1 = 0°; θ2 = 0°) (d). The distances on the colour bars are in meters.
Remotesensing 16 00020 g009
Remotesensing 16 00020 g010
Figure 10. (a) Calibration report for a workflow where all the cameras are in the same calibration group, with diagram of the residuals of the tie points and estimated internal parameters. (b,c) Calibration report for a workflow where the cameras are divided into two calibration groups for Camera 1 (b) and Camera 2 (c).
Figure 10. (a) Calibration report for a workflow where all the cameras are in the same calibration group, with diagram of the residuals of the tie points and estimated internal parameters. (b,c) Calibration report for a workflow where the cameras are divided into two calibration groups for Camera 1 (b) and Camera 2 (c).
Remotesensing 16 00020 g010
Table 1. Different configurations of the system tested during a repeated acquisition over the same zone in the Hermitage backreef zone.
Table 1. Different configurations of the system tested during a repeated acquisition over the same zone in the Hermitage backreef zone.
ConfigurationBaselineCamera Orientation (±2°)Constraints on Trajectory
Test 1Remotesensing 16 00020 i00158 cmθ1 = 23°
θ2 = 25°		Inter-transect distance: 0.9–1 m
Return transects: yes
Test 2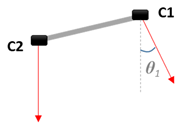Remotesensing 16 00020 i00258 cmθ1 = 23°
θ2 = 0° (nadir)		Inter-transect distance: 0.9–1 m
Return transects: yes
Test 3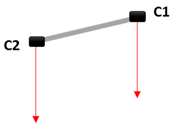Remotesensing 16 00020 i00358 cmθ1 = 0° (nadir)
θ2 = 0° (nadir)		Inter-transect distance: 0.9–1 m
Return transects: no
Test 4Remotesensing 16 00020 i00440 cmθ1 = 0° (nadir)
θ2 = 0° (nadir)		Inter-transect distance: 0.9–1 m
Return transects: no
Table 2. Parameters used at the different steps of Metashape underwater SfM photogrammetry processing.
Table 2. Parameters used at the different steps of Metashape underwater SfM photogrammetry processing.
Agisoft Metashape
Processing Step		Used Parameters
Image alignmentAccuracy: High
Generic preselection
Reference preselection: Source
Key point limit: 40,000
Tie point limit: 10,000
Exclude stationary tie points
Guided image matching
Optimize camerasDefault parameters
Build dense point cloudQuality: High
Depth filtering: Aggressive/Moderate (depending on the environment)
Calculate point colours
Calculate point confidence
Table 3. Comparison of dense point clouds generated in the Hermitage backreef zone with various configurations of the POSEIDON system (Tests 1 to 4—see Table 1) for repeated surveys over the same area.
Table 3. Comparison of dense point clouds generated in the Hermitage backreef zone with various configurations of the POSEIDON system (Tests 1 to 4—see Table 1) for repeated surveys over the same area.
Number of Photos AlignedNumber of PointsModelled Surface AreaNative Mean Point Density
Test 12230 of 2863 (78%)508,103,069230 m22.2 × 106 pts/m2
Test 22862 of 3732 (77%)588,004,876210 m22.8 × 106 pts/m2
Test 32924 of 3524 (84%)492,951,386156 m23.2 × 106 pts/m2
Test 42140 of 2630 (81%)436,343,004148 m22.9 × 106 pts/m2
Table 4. Mean distances and standard deviations between Test 2 (used as reference) and the dense point clouds obtained for Tests 1, 3 and 4.
Table 4. Mean distances and standard deviations between Test 2 (used as reference) and the dense point clouds obtained for Tests 1, 3 and 4.
Point Cloud Compared to Test 2Mean Distance (cm)Standard Deviation (cm)
Test 1−1.76.3
Test 31.36.2
Test 40.37.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Jaud, M.; Delsol, S.; Urbina-Barreto, I.; Augereau, E.; Cordier, E.; Guilhaumon, F.; Le Dantec, N.; Floc’h, F.; Delacourt, C. Low-Tech and Low-Cost System for High-Resolution Underwater RTK Photogrammetry in Coastal Shallow Waters. Remote Sens. 2024, 16, 20. https://doi.org/10.3390/rs16010020

AMA Style

Jaud M, Delsol S, Urbina-Barreto I, Augereau E, Cordier E, Guilhaumon F, Le Dantec N, Floc’h F, Delacourt C. Low-Tech and Low-Cost System for High-Resolution Underwater RTK Photogrammetry in Coastal Shallow Waters. Remote Sensing. 2024; 16(1):20. https://doi.org/10.3390/rs16010020

Chicago/Turabian Style

Jaud, Marion, Simon Delsol, Isabel Urbina-Barreto, Emmanuel Augereau, Emmanuel Cordier, François Guilhaumon, Nicolas Le Dantec, France Floc’h, and Christophe Delacourt. 2024. "Low-Tech and Low-Cost System for High-Resolution Underwater RTK Photogrammetry in Coastal Shallow Waters" Remote Sensing 16, no. 1: 20. https://doi.org/10.3390/rs16010020

APA Style

Jaud, M., Delsol, S., Urbina-Barreto, I., Augereau, E., Cordier, E., Guilhaumon, F., Le Dantec, N., Floc’h, F., & Delacourt, C. (2024). Low-Tech and Low-Cost System for High-Resolution Underwater RTK Photogrammetry in Coastal Shallow Waters. Remote Sensing, 16(1), 20. https://doi.org/10.3390/rs16010020

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop