Compound-Gaussian Model with Nakagami-Distributed Textures for High-Resolution Sea Clutter at Medium/High Grazing Angles
Abstract
1. Introduction
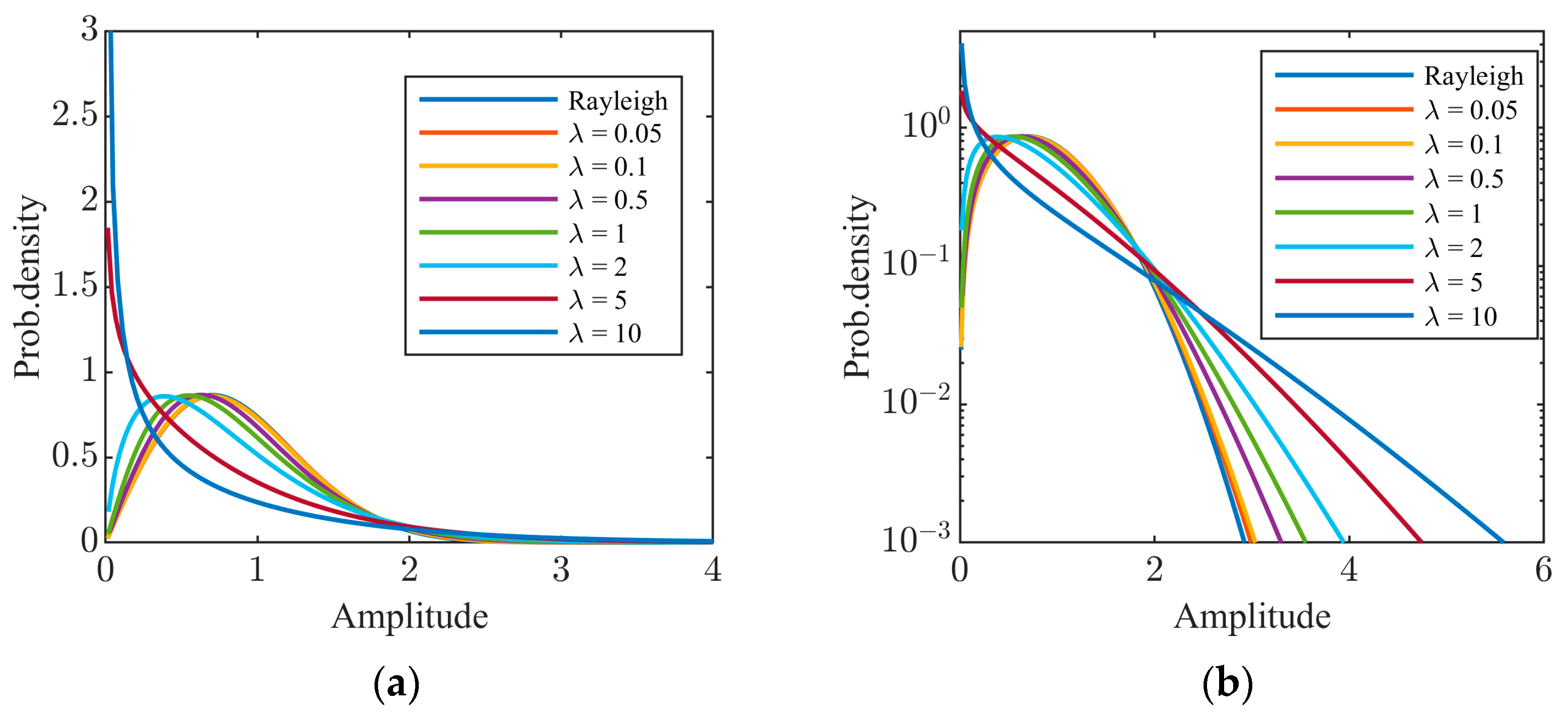
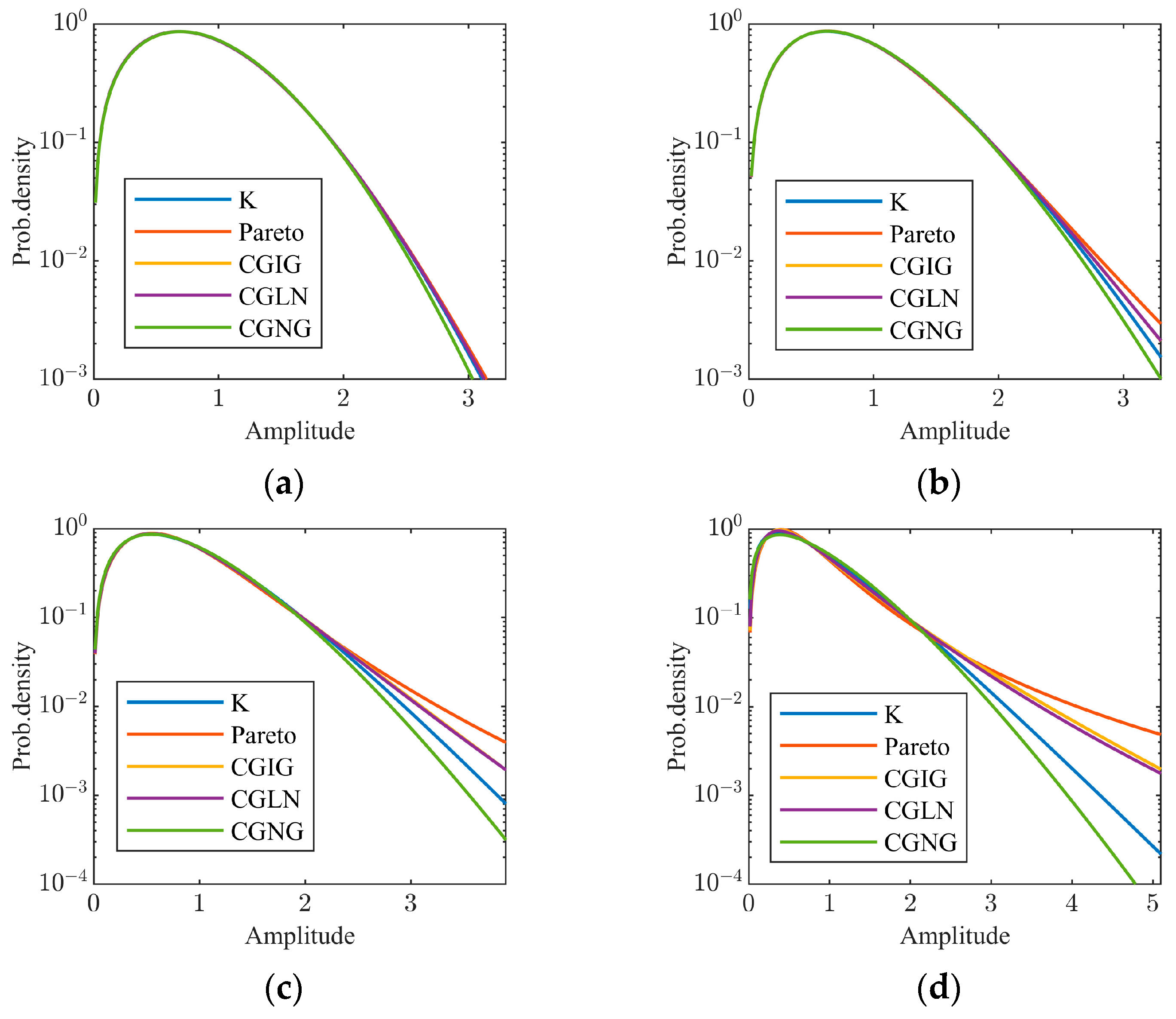
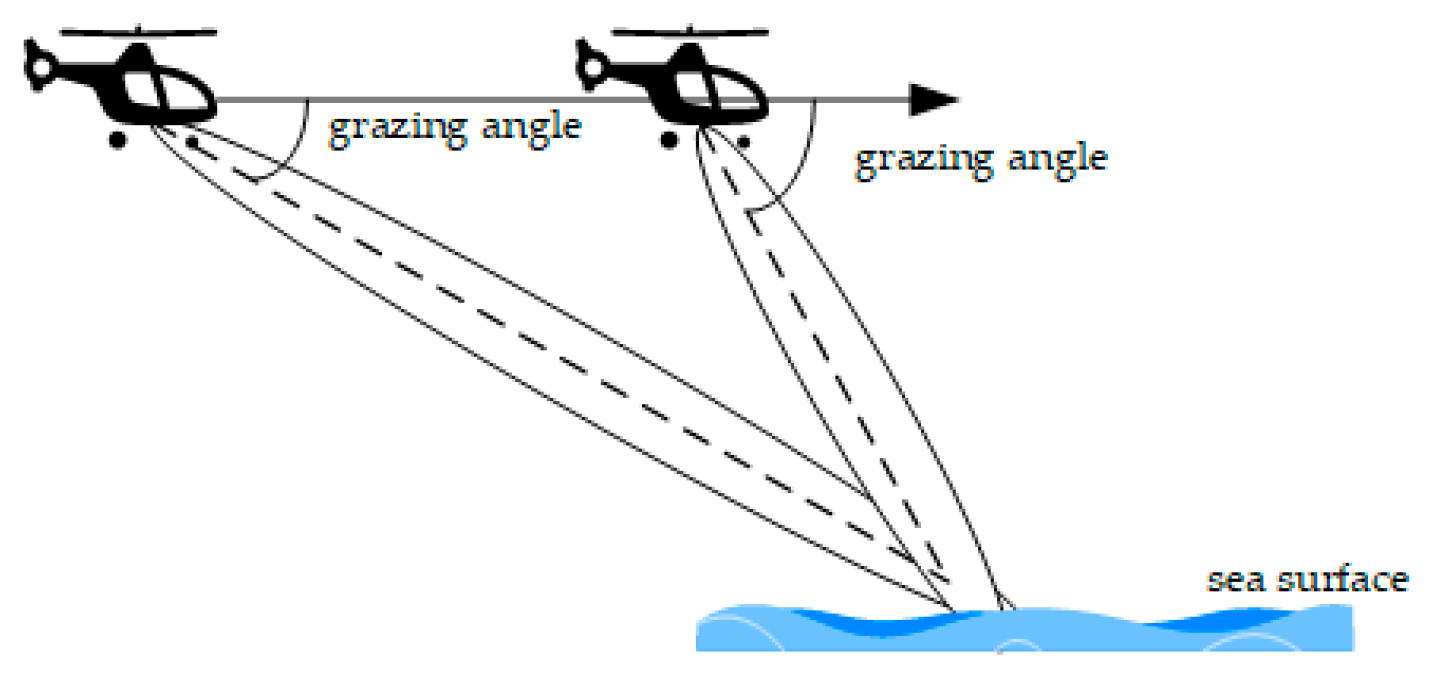
- A new CGM with Nakagami-distributed textures is proposed to model sea clutter at medium/high grazing angles. As the grazing angles increase, sea clutter becomes less spiky, i.e., sea clutter has a slighter tail. We compare the tail of the CGNG distributions with that of the K distributions, generalized Pareto distributions, CGIG distributions, and CGLN distributions and find the tails of the CGNG distributions are the slightest. Therefore, the CGNG distributions are proposed to model sea clutter at medium/high grazing angles.
- Sea clutter data inevitably contain a fraction of outliers. In order to achieve the robust parameter estimation of the CGNG distributions, the tri-percentile estimators are proposed.
2. Compound-Gaussian Model with Nakagami-Distributed Textures
3. Outlier-Robust Tri-Percentile Estimators of CGNG Distributions
3.1. Outlier-Robust Tri-Percentile Estimators
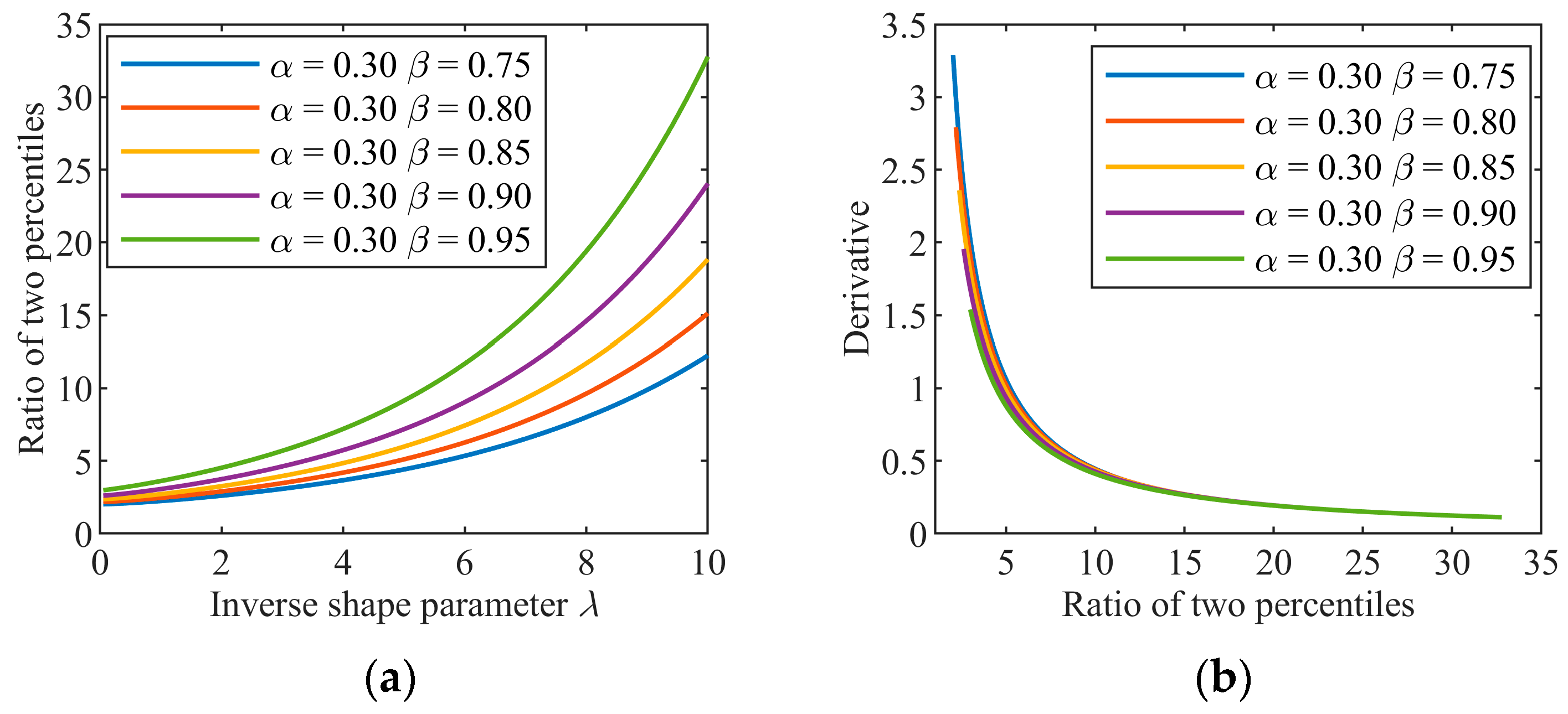
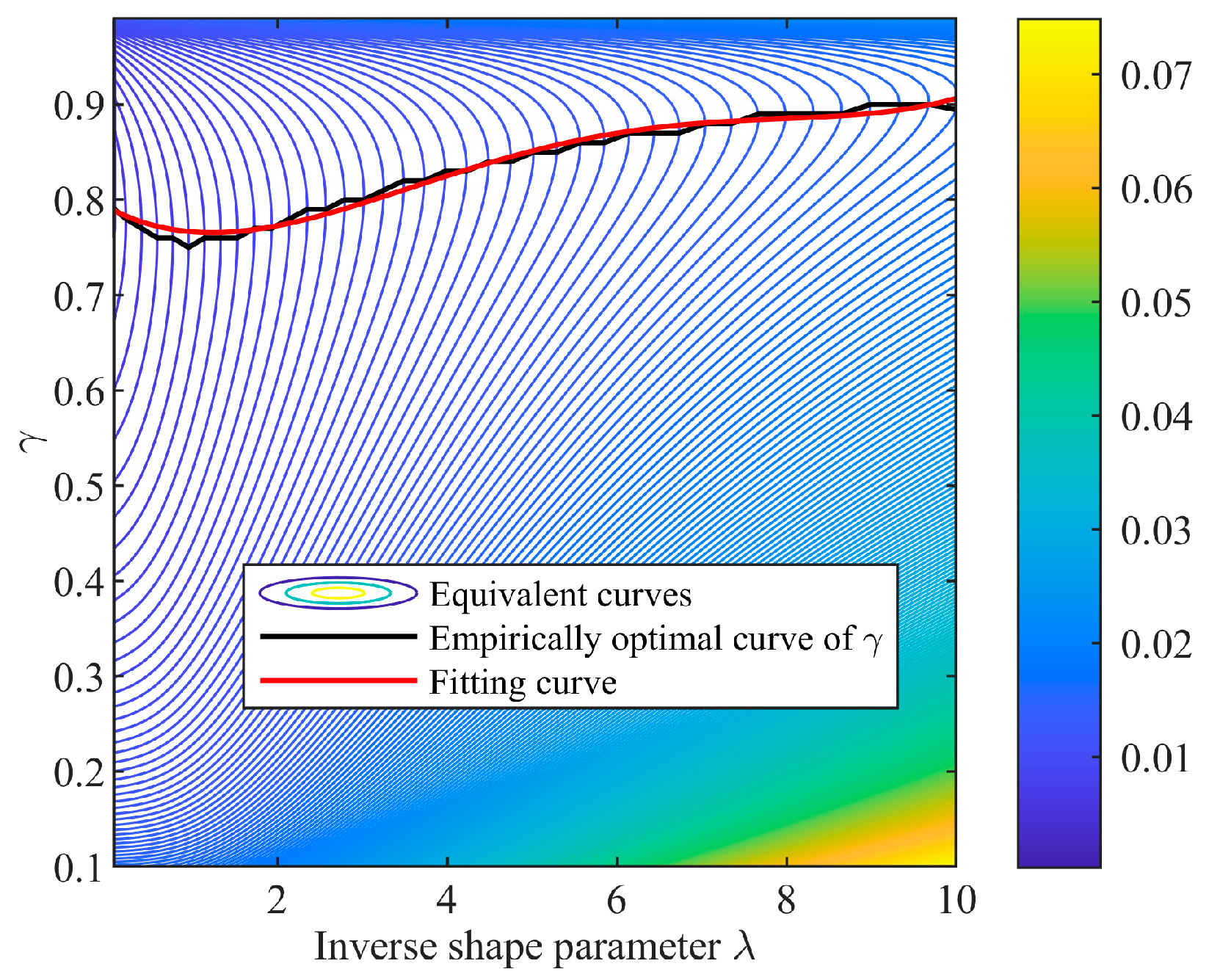
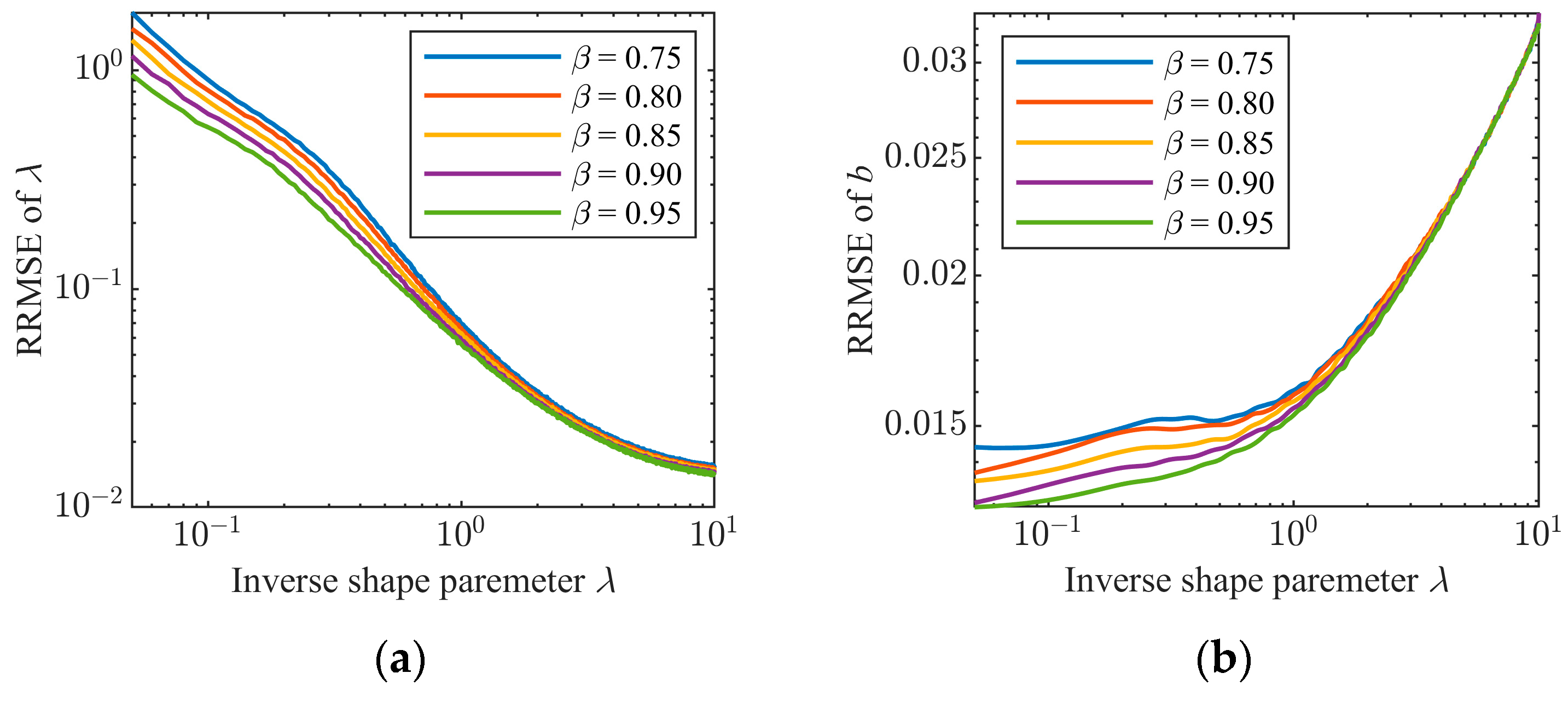
3.2. Properties and Setup Optimization
4. CGNG Model Suitability and Estimation Performance Comparison
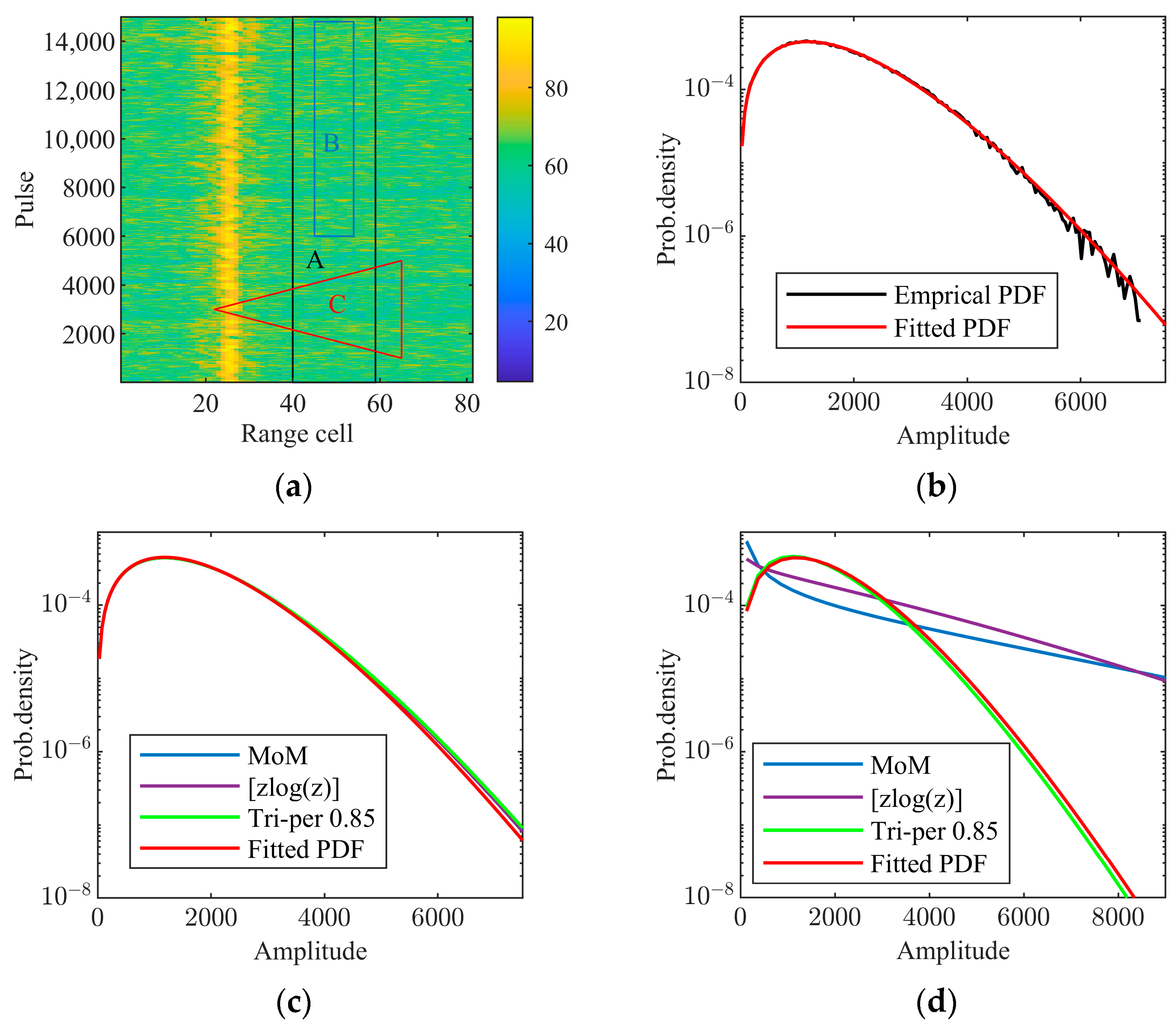
4.1. Suitability of CGNG Distributions
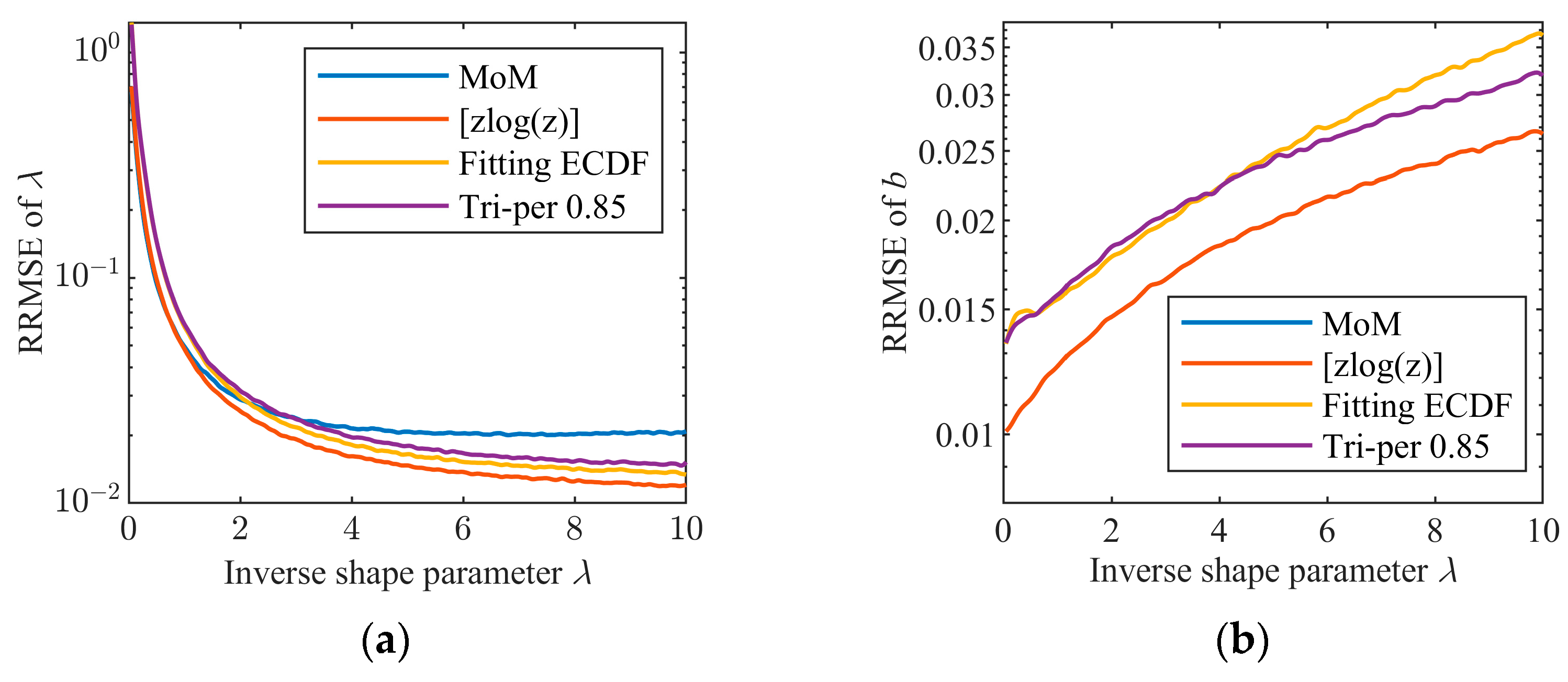
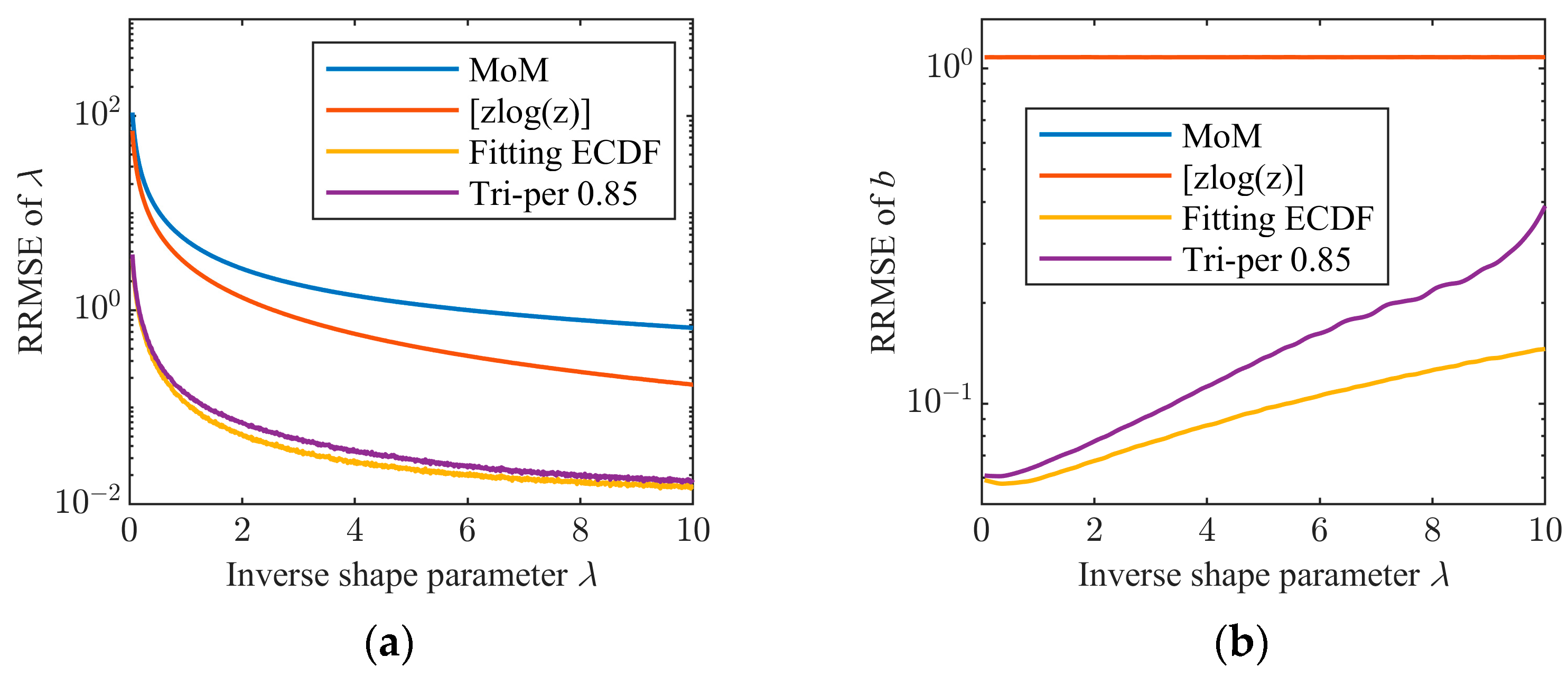
4.2. Performance Comparison of Tri-Percentile Estimators
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Gao, Y.C.; Liao, G.S.; Zhu, S.Q. Adaptive signal detection in compound-Gaussian clutter with inverse Gaussian texture. In Proceedings of the 2013 14th International Radar Symposium, Dresden, Germany, 19–21 June 2013; pp. 935–940. [Google Scholar]
- Shui, P.L.; Liu, M.; Xu, S.W. Shape-parameter-dependent coherent radar target detection in K-distributed clutter. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 451–465. [Google Scholar] [CrossRef]
- Xue, J.; Xu, S.W.; Shui, P.L. Near-optimum coherent CFAR detection of radar targets in compound-Gaussian clutter with inverse Gaussian texture. Signal Process. 2020, 166, 107236. [Google Scholar] [CrossRef]
- Xue, J.; Li, H.G.; Pan, M.Y.; Liu, J. Adaptive persymmetric detection for radar targets in correlated CG-LN sea clutter. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5108212. [Google Scholar] [CrossRef]
- Xue, J.; Liu, J.; Xu, S.W.; Pan, M.Y. Adaptive detection of radar targets in heavy-tailed sea clutter with lognormal texture. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5108411. [Google Scholar] [CrossRef]
- Xue, J.; Ma, M.S.; Liu, J.; Pan, M.Y.; Xu, S.W.; Fang, J. Wald- and Rao-based detection for maritime radar targets in sea clutter with lognormal texture. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5119709. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 108–110. [Google Scholar]
- Pirkani, A.; Daniel, L.; Kumar, D.; Hoare, E.; Harris, S.; Cherniakov, M.; Stove, A.; Gashinova, M. Doppler Beam Sharpening for MIMO and Real Aperture Radars at mm-wave and Sub-THz Maritime Sensing. In Proceedings of the 2023 24th International Radar Symposium, Berlin, Germany, 24–26 May 2023; pp. 1–10. [Google Scholar]
- Zhang, Y.C.; Luo, J.W.; Zhang, Y.W.; Huang, Y.L.; Cai, X.C.; Yang, J.Y.; Mao, D.Q.; Li, J.; Tuo, X.Y.; Zhang, Y. Resolution enhancement for large-scale real beam mapping based on adaptive low-rank approximation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5116921. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Luo, J.W.; Li, J.; Mao, D.Q.; Zhang, Y.; Huang, Y.L.; Yang, J.Y. Fast Inverse-Scattering Reconstruction for Airborne High-Squint Radar Imagery Based on Doppler Centroid Compensation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5205517. [Google Scholar] [CrossRef]
- Mezache, A.; Soltani, F.; Sahed, M.; Chalabi, I. Model for non-rayleigh clutter amplitudes using compound inverse gaussian distribution: An experimental analysis. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 142–153. [Google Scholar] [CrossRef]
- Sangston, K.J.; Gini, F.; Greco, M.S. Coherent radar target detection in heavy-tailed compound-Gaussian clutter. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 64–77. [Google Scholar] [CrossRef]
- Ward, K.D.; Watts, S.; Tough, R.J. Sea Clutter: Scattering, the K Distribution and Radar Performance, 2nd ed.; IET: London, UK, 2013; pp. 59–100. [Google Scholar]
- Balleri, A.; Nehorai, A.; Wang, J. Maximum likelihood estimation for compound-gaussian clutter with inverse gamma texture. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 775–779. [Google Scholar] [CrossRef]
- Ollila, E.; Tyler, D.E.; Koivunen, V.; Poor, H.V. Compound-Gaussian clutter modeling with an inverse Gaussian texture Distribution. IEEE Signal Process. Lett. 2012, 19, 876–879. [Google Scholar] [CrossRef]
- Carretero-Moya, J.; Gismero-Menoyo, J.; Blanco-Del-Campo, Á.; Asensio-Lopez, A. Statistical analysis of a high-resolution sea-clutter database. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2024–2037. [Google Scholar] [CrossRef]
- Chalabi, I. High-resolution sea clutter modelling using compound inverted exponentiated Rayleigh distribution. Remote Sens. Lett. 2023, 14, 433–441. [Google Scholar] [CrossRef]
- Xue, J.; Xu, S.W.; Liu, J.; Shui, P.L. Model for non-Gaussian sea clutter amplitudes using generalized inverse Gaussian texture. IEEE Geosci. Remote Sens. Lett. 2019, 16, 892–896. [Google Scholar] [CrossRef]
- Gini, F.; Greco, M.V.; Diani, M.; Verrazzani, L. Performance analysis of two adaptive radar detectors against non-Gaussian real sea clutter data. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 1429–1439. [Google Scholar]
- Yacoub, M.D.; Bautista, J.E.V.; Guerra De Rezende Guedes, L. On higher order statistics of the Nakagami-m distribution. IEEE Trans. Veh. Technol. 1999, 48, 790–794. [Google Scholar] [CrossRef]
- Xia, X.Y.; Shui, P.L.; Zhang, Y.S.; Li, X.; Xu, X.Y. An empirical model of shape parameter of sea clutter based on X-band island-based radar database. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3503205. [Google Scholar] [CrossRef]
- Gini, F.; Greco, M. Covariance matrix estimation for CFAR detection in correlated heavy tailed clutter. Signal Process. 2002, 82, 1847–1859. [Google Scholar] [CrossRef]
- Jay, E.; Ovarlez, J.P.; Declercq, D.; Duvaut, P. BORD: Bayesian optimum radar detector. Signal Process. 2003, 83, 1151–1162. [Google Scholar] [CrossRef]
- Shui, P.L.; Liu, M. Subband adaptive GLRT-LTD for weak moving targets in sea clutter. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 423–437. [Google Scholar] [CrossRef]
- Zaimbashi, A.; Norouzi, Y. Automatic dual censoring cell-averaging CFAR detector in non-homogenous environments. Signal Process. 2008, 88, 2611–2621. [Google Scholar] [CrossRef]
- Chalabi, I.; Mezache, A. Estimating the K-distribution parameters based on fractional negative moments. In Proceedings of the 2015 IEEE 12th International Multi-Conference on Systems, Signals & Devices, Mahdia, Tunisia, 16–19 March 2015; pp. 1–5. [Google Scholar]
- Chalabi, I.; Mezache, A. Estimators of compound Gaussian clutter with log-normal texture. Remote Sens. Lett. 2019, 10, 709–716. [Google Scholar] [CrossRef]
- Iskander, D.R.; Zoubir, A.M. Estimation of the parameters of the K-distribution using higher order and fractional moments [radar clutter]. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1453–1457. [Google Scholar] [CrossRef]
- Mezache, A.; Bentoumi, A.; Sahed, M. Parameter estimation for compound-Gaussian clutter with inverse Gaussian texture. IET Radar Sonar Navig. 2017, 11, 586–596. [Google Scholar] [CrossRef]
- Yu, H.; Shui, P.L.; Huang, Y.T. Low-order moment-based estimation of shape parameter of CGIG clutter model. Electron. Lett. 2016, 52, 1561–1563. [Google Scholar] [CrossRef]
- Blacknell, D.; Tough, R.J.A. Parameter estimation for the K-distribution based on [zlog(z)]. IEE Proc.-Radar Sonar Navig. 2001, 148, 309–312. [Google Scholar] [CrossRef]
- Feng, T.; Shui, P.L. Outlier-robust tri-percentile parameter estimation of compound-Gaussian clutter with lognormal distributed texture. Digit. Signal Process. 2022, 120, 103307. [Google Scholar] [CrossRef]
- Shui, P.L.; Shi, L.X.; Yu, H.; Huang, Y.T. Iterative maximum likelihood and outlier-robust bipercentile estimation of parameters of compound-Gaussian clutter with inverse Gaussian texture. IEEE Signal Process. Lett. 2016, 23, 1572–1576. [Google Scholar] [CrossRef]
- Shui, P.L.; Yu, H.; Shi, L.X.; Yang, C.J. Explicit bipercentile parameter estimation of compound-Gaussian clutter with inverse gamma distributed texture. IET Radar Sonar Navig. 2018, 12, 202–208. [Google Scholar] [CrossRef]
- Xu, S.W.; Wang, L.; Zhang, F.Q.; Shui, P.L. Outlier-robust parameters estimation for compound-Gaussian clutter using inverse gamma texture based on truncated moments. Remote Sens. Lett. 2019, 10, 274–282. [Google Scholar] [CrossRef]
- Yu, H.; Shui, P.L.; Lu, K. Outlier-robust tri-percentile parameter estimation of K-distributions. Signal Process. 2021, 181, 107906. [Google Scholar] [CrossRef]
- Tian, C.; Shui, P.L. Outlier-robust truncated maximum likelihood parameter estimation of compound-Gaussian clutter with inverse Gaussian texture. Remote Sens. 2022, 14, 4004. [Google Scholar] [CrossRef]
- Shui, P.L.; Tian, C.; Feng, T. Outlier-robust tri-percentile parameter estimation method of compound-Gaussian clutter with inverse Gaussian textures. J. Electron. Inf. Technol. 2023, 45, 542–549. [Google Scholar]
- Xue, J.; Sun, M.L.; Liu, J.; Xu, S.W.; Pan, M.Y. Shape parameter estimation of K-distributed sea clutter using neural network and multi-sample percentile in radar industry. IEEE Trans. Ind. Informat. 2023, 19, 7602–7612. [Google Scholar] [CrossRef]
- Miao, Y.; Chen, Y.X.; Xu, S.F. Asymptotic properties of the deviation between order statistics and p-quantile. Commun. Stat. Theory Methods 2010, 40, 8–14. [Google Scholar] [CrossRef]
- Carretero-Moya, J.; Maio, A.D.; Gismero-Menoyo, J.; Asensio-Lopez, A. Experimental performance analysis of distributed target coherent radar detectors. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2216–2238. [Google Scholar] [CrossRef]
- Daniel, W.W. Applied Nonparametric Statistics, 2nd ed.; PWS-Kent Pub: Boston, USA, 1990; pp. 319–330. [Google Scholar]
- Romik, D. Stirling’s approximation for n!: The ultimate short proof? Am. Math. Mon. 2000, 107, 556–557. [Google Scholar] [CrossRef]
- Stephens, M. EDF statistics for goodness of fit and some comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
- Watts, S.; Rosenberg, L. A review of high grazing angle sea-clutter. In Proceedings of the 2013 International Conference on Radar, Adelaide, Australia, 9–12 September 2013; pp. 240–245. [Google Scholar]
- Roberts, W.J.J.; Furui, S. Maximum likelihood estimation of K-distribution parameters via the expectation-maximization algorithm. IEEE Trans. Signal Process. 2000, 48, 3303–3306. [Google Scholar]
- Mezache, A.; Sahed, M.; Laroussi, T.; Chikouche, D. Two novel methods for estimating the compound K-clutter parameters in presence of thermal noise. IET Radar Sonar Navig. 2011, 5, 934–942. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Clifford Cohen, A. Order Statistics and Inference; Academic Press: New York, NY, USA, 1991; pp. 7–17. [Google Scholar]
- Weinberg, G.V.; Glenny, V.G. Optimal Rayleigh approximation of the K-distribution via the Kullback–Leibler divergence. IEEE Signal Process. Lett. 2016, 23, 1067–1070. [Google Scholar] [CrossRef]
- Conte, E.; Bisceglie, M.D.; Lops, M. Clutter-map CFAR detection for range-spread targets in non-Gaussian clutter. II. Performance assessment. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 444–455. [Google Scholar] [CrossRef]
- Conte, E.; Lops, M. Clutter-map CFAR detection for range-spread targets in non-Gaussian clutter. I. System design. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 432–443. [Google Scholar] [CrossRef]


| CGNG | K | Pareto | CGIG | CGLN | ||
|---|---|---|---|---|---|---|
| Case 1 | Scale parameter | 1 | 1.0048 | 1.0059 | 1.0052 | 1.0052 |
| Inverse shape parameter | 0.1 | 0.0428 | 0.0428 | 0.0445 | 0.0436 | |
| KSD | 0 | 0.0024 | 0.0023 | 0.0024 | 0.0024 | |
| Case 2 | Scale parameter | 1 | 1.0170 | 1.0474 | 1.0301 | 1.0296 |
| Inverse shape parameter | 0.5 | 0.1793 | 0.1918 | 0.2226 | 0.2018 | |
| KSD | 0 | 0.0042 | 0.0084 | 0.0064 | 0.0062 | |
| Case 3 | Scale parameter | 1 | 1.0050 | 1.1469 | 1.0528 | 1.0507 |
| Inverse shape parameter | 1 | 0.3731 | 0.4008 | 0.5603 | 0.4552 | |
| KSD | 0 | 0.0118 | 0.0163 | 0.0140 | 0.0135 | |
| Case 4 | Scale parameter | 1 | 1.0564 | 2.7284 | 1.2620 | 1.2436 |
| Inverse shape parameter | 2 | 0.7689 | 0.8224 | 1.7227 | 1.0797 | |
| KSD | 0 | 0.0075 | 0.0390 | 0.0260 | 0.0226 |
| Regions | Number of CMCs | Percentage of Optimal Model (%) | |||||
|---|---|---|---|---|---|---|---|
| K | Pareto | CGIG | CGLN | CGNG | Rayleigh | ||
| 20–25° | 902 | 18.9 | 27.5 | 16.1 | 8.8 | 27.9 | 0.9 |
| 25–30° | 1004 | 18.5 | 25.1 | 17.1 | 10.0 | 28.2 | 1.1 |
| 30–35° | 717 | 22.6 | 22.0 | 22.5 | 7.0 | 25.0 | 1.0 |
| 35–40° | 579 | 22.6 | 20.9 | 17.8 | 8.3 | 30.1 | 0.4 |
| 40–45° | 329 | 21.6 | 25.8 | 13.7 | 7.0 | 31.6 | 0.3 |
| 45–50° | 112 | 25.0 | 24.1 | 8.9 | 8.0 | 33.9 | 0 |
| 50–55° | 14 | 21.4 | 7.1 | 0 | 14.3 | 57.1 | 0 |
| Regions | Average MSB | ||||
|---|---|---|---|---|---|
| K | Pareto | CGIG | CGLN | CGNG | |
| 20–25° | 1.6814 | 1.5567 | 1.3857 | 1.3521 | 1.8076 |
| 25–30° | 1.4040 | 1.5399 | 1.4507 | 1.3422 | 1.3352 |
| 30–35° | 1.5408 | 1.6130 | 1.7716 | 1.6156 | 1.4154 |
| 35–40° | 1.3691 | 1.5457 | 1.3162 | 1.2378 | 1.4770 |
| 40–45° | 1.4657 | 1.5803 | 1.4059 | 1.3473 | 1.9131 |
| 45–50° | 1.4334 | 1.5228 | 1.4639 | 1.3825 | 2.3315 |
| 50–55° | 1.3117 | 2.0952 | - | 1.1071 | 3.9374 |
| K | Pareto | CGIG | CGLN | CGNG | ||
|---|---|---|---|---|---|---|
| Case 1 | MSE | 2.2466 × 10−6 | 1.1234 × 10−5 | 7.3225 × 10−6 | 6.6943 × 10−6 | 6.5584 × 10−7 |
| KSD | 0.0152 | 0.0379 | 0.0290 | 0.0281 | 0.0059 | |
| KLD | 9.0282 × 10−4 | 0.0020 | 0.0016 | 0.0015 | 5.2753 × 10−4 | |
| Case 2 | MSE | 1.6291 × 10−6 | 8.4408 × 10−6 | 5.2847 × 10−6 | 4.8767 × 10−6 | 6.2696 × 10−7 |
| KSD | 0.0172 | 0.0413 | 0.0316 | 0.0307 | 0.0082 | |
| KLD | 8.6044 × 10−4 | 0.0018 | 0.0015 | 0.0014 | 5.3763 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Zhang, X.; Zou, P.; Shui, P. Compound-Gaussian Model with Nakagami-Distributed Textures for High-Resolution Sea Clutter at Medium/High Grazing Angles. Remote Sens. 2024, 16, 195. https://doi.org/10.3390/rs16010195
Yang G, Zhang X, Zou P, Shui P. Compound-Gaussian Model with Nakagami-Distributed Textures for High-Resolution Sea Clutter at Medium/High Grazing Angles. Remote Sensing. 2024; 16(1):195. https://doi.org/10.3390/rs16010195
Chicago/Turabian StyleYang, Guanbao, Xiaojun Zhang, Pengjia Zou, and Penglang Shui. 2024. "Compound-Gaussian Model with Nakagami-Distributed Textures for High-Resolution Sea Clutter at Medium/High Grazing Angles" Remote Sensing 16, no. 1: 195. https://doi.org/10.3390/rs16010195
APA StyleYang, G., Zhang, X., Zou, P., & Shui, P. (2024). Compound-Gaussian Model with Nakagami-Distributed Textures for High-Resolution Sea Clutter at Medium/High Grazing Angles. Remote Sensing, 16(1), 195. https://doi.org/10.3390/rs16010195







