Abstract
Over the past few decades, there has been a significant increase in the number of Earth observation satellites, and the area of ground targets requiring observation has also been expanding. To effectively utilize the capabilities of these satellites and capture larger areas of ground targets, it has become essential to plan imaging tasks for large regional coverage using multiple satellites. First, we establish a 0-1 integer programming model to accurately describe the problem and analyze the challenges associated with solving the model. Second, we propose a heuristic algorithm based on the triple grids method. This approach utilizes a generated grid to create fewer candidate strips, a calculation grid to determine the effective coverage area more accurately, and a refined grid to solve the issue of repeated coverage of strips. Furthermore, we employ an approximation algorithm to further improve the solutions obtained from the heuristic algorithm. By comparing the proposed method to the traditional greedy heuristic algorithm and three evolutionary algorithms, the results show that our method has better performance in terms of coverage and efficiency.
1. Introduction
Earth observation (EO) satellites are space-based platforms which can fully utilize their space-based location advantages and rapid revisit ability to acquire images of specified areas on Earth’s surface in response to diverse observation requests. Image acquisition by EO satellites is highly valued by various users, including government agencies, research institutes, and so on [1]. Satellite remote sensing images have found extensive application in vegetation monitoring [2], urban growth monitoring [3], emergency response and rescue [4], and other related fields.
Due to the limited field of view (FOV) and other constrains, satellites can only capture a strip area with restricted length and width during each orbit. Depending on the size of the region, the target can be classified into two types. As illustrated in Figure 1, point targets refer to the regions that can be fully imaged by a single satellite in one transit, while regional targets require the collaborative efforts of multiple satellites for completing coverage. Over the past few decades, there has been a significant increase in the number of EO satellites, resulting in a rise in the size of regional targets requiring imaging. However, imaging satellites can only orbit the Earth periodically along fixed paths. Due to the constraints on observation range and satellite mobility, relying solely on a single satellite for large regional targets leads to low imaging efficiency. Therefore, effective completion of such tasks necessitates the cooperation of multiple satellites. The challenge lies in how to schedule and plan resources reasonably to achieve joint imaging. This problem is a typical combinatorial optimization problem that has been proven to be NP-hard [5,6].
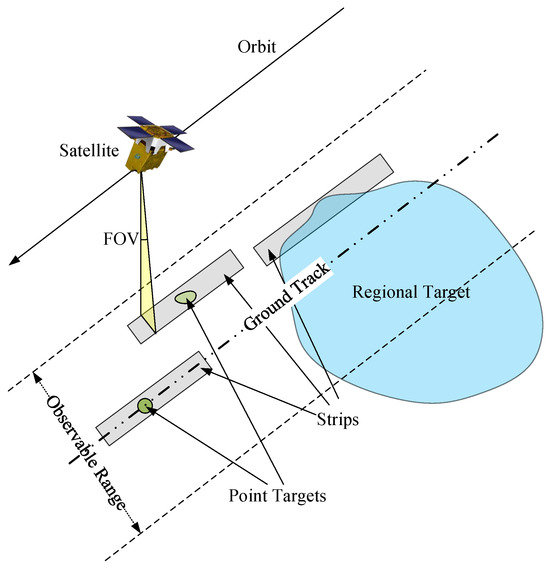
Figure 1.
Schematic diagram of point targets and regional targets.
Given the NP-hard nature of the multi-satellite planning and scheduling problem, significant research has focused on developing heuristic algorithms [7,8,9] to improve scheduling efficiency and meet observation requests. Bianchessi et al. [10] addressed the multiple satellite and multiple orbit problem by proposing a tabu search heuristic [11] that selects and schedules requests to maximize the total utility under operational constraints. Wolfe et al. [12] proposed three methods for EO satellites scheduling: the priority dispatch algorithm, the look ahead algorithm, and the genetic algorithm (GA) [13]. Comparing these methods, they found that the priority dispatch algorithm is the fastest and most simple, creating acceptable schedules most of the time; the look ahead algorithm is slightly slower but still relatively simple, creating excellent schedules; and the genetic algorithm is slower but capable of generating near-optimal schedules. This study was perhaps the first to consider the trade-off between efficiency and optimality in solving the EO satellite scheduling problem. Additionally, other optimization algorithms such as the cooperative coevolutionary multi-objective algorithm (CCMOA) [14], simulated annealing (SA) [15], particle swarm optimization (PSO) [16], ant colony optimization (ACO) [17,18], network graph [19], and reinforcement learning (RL) [20] have also been used to solve various satellite scheduling problems.
Most of the targets studied in the aforementioned research are point targets, and the research on regional targets has started relatively late. For large regional targets, the scale of the scheduling problem will significantly increase when decomposing them into point targets. Due to the increase in computational complexity, methods suitable for point targets are difficult to transfer to regional targets.
In order to make a clear description of the relevant literature, we summarize previous studies in Table 1.
Walton [21] was the first to delve into the matter of imaging regional targets using a single satellite. He decomposed the original problem into two subproblems: the regional target decomposition problem and the set cover problem (SCP). Since then, numerous researchers have shown keen interest in the imaging scheduling problem concerning regional targets. Lemaître et al. [22] focused on the agile EO satellites track selection and scheduling problem and employed a pre-decomposition method to divide the regional target into non-overlapping parallel strips. The author proposed four solution methods: a fast greedy algorithm, a dynamic programming algorithm, a method based on the existing constraint programming framework, and a local search algorithm that involved the insertion and removal of images within a sequence. The aforementioned literature primarily explored the imaging of regional targets using a single satellite. However, with the rapid increase in the number of satellites, the issue of regional coverage by multiple satellites and multiple orbits has garnered more attention. In terms of problem-solving algorithms, they can be broadly categorized as exact algorithms and heuristic algorithms.

Table 1.
Summary of the relevant literature.
Table 1.
Summary of the relevant literature.
| Single Satellite | Multi-Satellites | |
|---|---|---|
| Exact algorithm | [23,24], branch and price algorithm [25], three-phase method [26], column generation method and implicit enumeration algorithm [27] | |
| Heuristic algorithm | [21,22] | tabu search [28], heuristic [29], NSGA-II [30,31], NSGA-III [32], three-phase solving framework [33,34], Two-Archive2 algorithm [35], PSO [36], GA [37] ECL-INS-LMOA [38], Reinforcement Learning [39] |
The multi-satellite scheduling problem for regional mapping is a highly complex combinatorial optimization problem. Exact algorithms are only applicable to small-scale examples due to the computational complexity involved. Consequently, there is a significant body of literature on the application of heuristic algorithms to solve multi-satellite large regional coverage problems with different regional target decomposition methods. The greedy heuristic algorithm is a practical approach for solving the problem of multi-satellite imaging task planning for large regional coverage. However, as the scale of the problem increases, the algorithm’s running time can become excessively long. Therefore, it is crucial to design an algorithm that offers both high accuracy and efficiency in solving these problems. The traditional greedy heuristic algorithm for solving multi-satellite imaging task planning for large regional coverage is affected by the satellite swath. When the target region is too large, the grid size used for discretization must be smaller than the satellite swath. This results in the generation of numerous candidate strips, leading to lengthy search processes for the algorithm.
Regional targets, as they cannot be imaged by the single observation scope of any satellite, must be decomposed into smaller units. The appropriate regional decomposition method will directly determine the difficulty of solving the problem. Typical regional decomposition methods include the grid method and the strip method. The grid method [40] divides the regional target into a collection of point targets, and the strip method [18,28,29,30,31,36,37] decomposes the regional target into a rectangular strip according to certain rules that can be completely covered by a single transit of the satellite. Hu [25] proposed a grid-based split method that generates more flexible strips than the traditional parallel split method, and proved that the optimal solution can be achieved on all basic covering strips [27]. This paper adopts a grid-based split method.
In this paper, we established a 0-1 integer programming model to describe the problem of multi-satellite imaging task planning for large regional coverage, and proposed a heuristic algorithm based on triple grids method and an approximation algorithm. The major highlights are summarized as follows:
- 1.
- Separate the generated grid used to generate candidate strips from the calculation grid used to calculate the area so that the size of the generated grid is not limited by the satellite swath.
- 2.
- Introduce a refined grid to solve the problem of cells being repeatedly covered, reduce the waste of satellite resources, and improve the coverage efficiency of satellites.
- 3.
- A heuristic algorithm based on the triple grids method (TG-GHA) was designed by combining the triple grids method with the traditional heuristic algorithm, which runs faster and provides more reasonable coverage schemes for large regional targets. The code implementation of the TG-GHA can be found in https://github.com/miaosann/TG_GHA (accessed on 23 December 2023).
- 4.
- Employ an approximation algorithm to further improve the solution obtained from the TG-GHA.
The remainder of this paper is organized as follows. In Section 2, we define the problem of multi-satellite imaging task planning for large regional coverage, establish a 0-1 integer programming model, and analyze the model. In Section 3, we provide a detailed introduction regarding how to generate candidate strips based on grids, a heuristic algorithm based on the triple grids method, and an approximation algorithm. In Section 4, we present the experiment results and analyses. Finally, the discussion and conclusions of the study are given in Section 5 and Section 6.
2. Mathematical Model
According to the satellite conditions and practical applications, the following assumptions are adopted:
- The satellite can only swing horizontally, not vertically.
- At most, one candidate strip can be selected for each transit per satellite.
- The length of all strips is limited to the minimum and maximum covering lengths of the corresponding satellite.
- The planning of data transmission is not within the scope of this study.
- Satellite storage capacity and electricity are assumed to be unlimited.
- It is assumed that weather conditions meet the requirements for imaging.
Parameters involved in the multi-satellite imaging task planning for large regional coverage are presented in Table 2.

Table 2.
Parameter and meaning.
The decision variables are as provided follows:
- indicates whether the cell g is covered by the selected strips.
- indicates whther the candidate strip is adopted.
Therefore, we can obtain the following formulation:
Equation (1) represents the objective function that maximizes the sum of the cells in all selected strips. Equation (2) represents a constraint of coverage, signifying that a cell must be encompassed by a chosen strip. Equation (3) imposes a selection limitation, proclaiming that each satellite transit can solely opt for a single candidate strip.
Taking each cell as an element and G as a set of elements, the candidate strips can be viewed as a subset of G. The problem is a SCP-like problem. An efficient algorithm for the SCP problem is the greedy heuristic algorithm (GHA) [41,42], which can produce a suboptimal solution within a reasonable timeframe. In real engineering scenarios, the polygon area is often too large, leading to high dimensions for the SCP. In such cases, even the GHA may fail to find a solution within an acceptable timeframe.
3. Proposed Methods
This section is divided into three subsections, with the contents provided as follows:
- A method for generating candidate strips based on a grid is presented. Next, the definitions and functions of the generated grid, calculation grid, and refined grid are provided, respectively.
- The TG-GHA is proposed to address the challenge of multi-satellite imaging task planning for large regional coverage.
- In order to optimize the coverage scheme further, an approximation algorithm based on triple grids is proposed.
The flowchart of multi-satellite imaging task planning for large regional coverage proposed in this paper is illustrated in Figure 2.
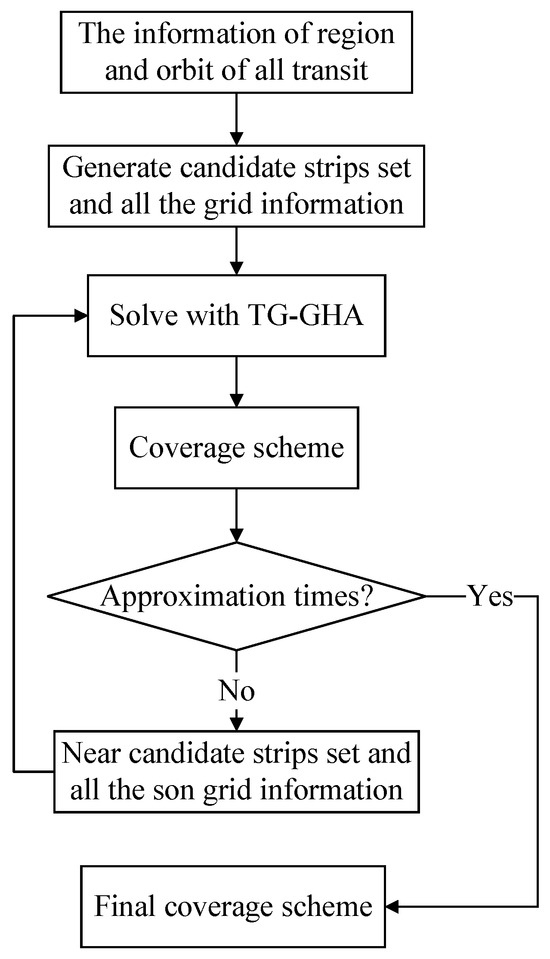
Figure 2.
Flowchart of multi-satellite imaging task planning for large regional coverage.
3.1. Triple Grids Method
This subsection primarily introduces the definition and function of three types of grids: the generated grid, calculation grid, and refined grid. To discretize the problem, we use a generated grid to create a set of candidate strips. The size of this grid is constrained by the satellite swath. To address this limitation, we introduce a calculation grid that separates the grid responsible for generating candidate strips from the grid used for calculating the area. Additionally, to resolve the problem of repeated coverage of cells, we introduce a refined grid that enables more precise updates of the coverage status within the grid.
3.1.1. A Method for Generating Candidate Strips Based on Grid
For a rectangular region, simply divide it in the X and Y directions. But for a polygonal region represented by vectors, denoted as , it is necessary to first determine its bounding rectangle, which is defined by four coordinates. The coordinates are , , , and . Subsequently, divide the region into a grid, partitioning the X and Y directions equally with respect to the desired dimensions. Through this discretization process, the encompassing region R is fragmented into multiple squares of uniform size. As illustrated in Figure 3, the enclosed red curve delineates the region to be encompassed. The yellow cells within the depiction denote the discretized areas necessitating coverage. Within this study, the node information matrix and the cell information matrix serve as repositories for segmented node details and cell particulars, respectively. The node information matrix arranges the coordinates of all utilized nodes in a specific sequence, while the cell information matrix records the indices of the four nodes for each cell. This storage approach obviates the need for repetitive node evaluation when determining strip coverage for cells, thereby mitigating computational costs.
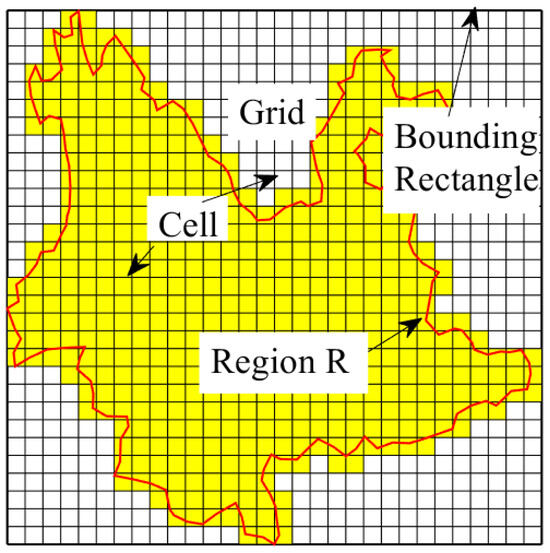
Figure 3.
Schematic diagram of regional discretization.
According to the definition of stripes, each stripe is uniquely determined by the satellite’s orbital position, the lens on/off time, and the swing angle. Satellites can select an infinite number of lens on/off times and swing angles for each transit, resulting in an infinite number of coverage strips. Given the optimization goal of maximizing the regional coverage rate, it can be observed that selecting the longest imaging duration for each transit is beneficial for covering a larger area. At the same time, a cell is considered fully covered only when all four vertices are on or inside the strip, and only fully covered cells will increase the coverage rate. Therefore, we select a special type of strip, which is determined by two vertices, to form the set of candidate strips. As shown in Figure 4, the left point determines the swing angle of the satellite during transit, and the top point determines the startup time. All stripes are imaged at the maximum imaging length. The left and top points should be within the observation range of the satellite, and the upper point should be above the left point.
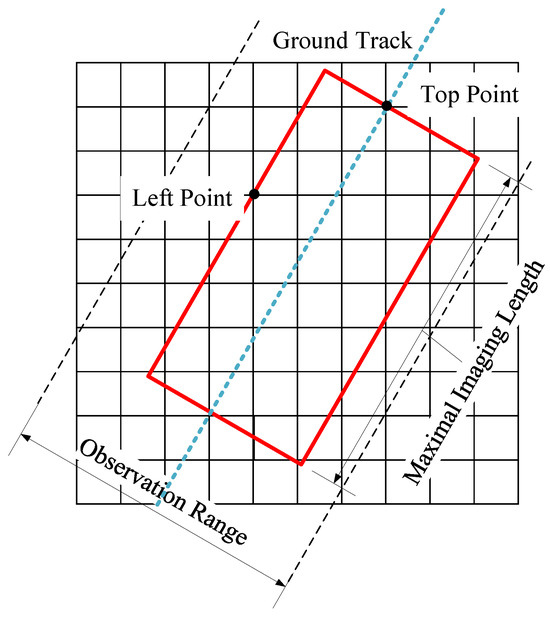
Figure 4.
Schematic diagram of generating strips based on grid.
After determining the left and upper edges of the strip, the four vertices of the strip can be determined by combining the maximum imaging length of the satellite and the swath of the satellite. However, the width of the strip will change with the swing angle of the satellite. The width of the strip can be calculated using the following formula:
where d represents the distance from the left vertex to the ground track, h denotes the orbital height of the satellite, and signifies the field of view. Once a strip is determined, the cells encompassed by the strip can be computed and stored as a matrix. By traversing all orbits of every satellite, we can calculate all strips that fulfill the specified criteria, thereby constituting a set of candidate strips.
3.1.2. Generated Grid and Calculation Grid
For a large region target, the number of discretized cells can be exceedingly high, leading to a large number of candidate strips. Even the greedy heuristic algorithm requires a significant amount of computation and may not produce results within an acceptable timeframe. Assuming that the number of candidate stripes is denoted as n, the number of transit orbits of satellites is denoted as m, and the number of cells after regional discretization is denoted as c, then the time complexity of the greedy heuristic algorithm is . And the number of candidate strips , that is to say, the time complexity, can be expressed as . To address this challenge within reasonable time constraints, one possible approach is to slightly increase the size of the grid, which can effectively reduce the number of cells. However, it is crucial to note that the grid size cannot be arbitrarily selected due to the limitations imposed by the strip swath. If the cell size is too large, such that the strip fails to cover any cell, then the greedy heuristic algorithm becomes ineffectual. As illustrated in Figure 5, the red strip only covers three complete cells. If the black grid size were larger, the red strip would not cover a single cell.
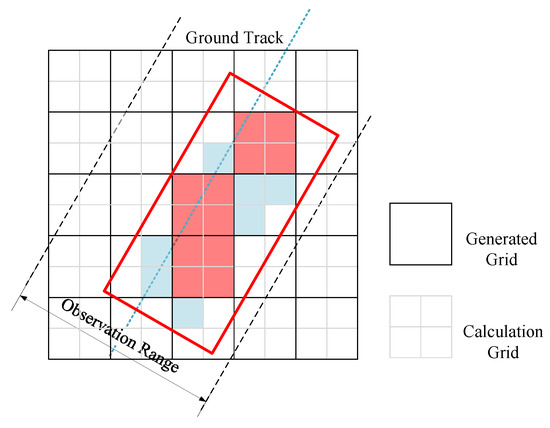
Figure 5.
Schematic diagram of generated grid and calculation grid.
Hence, we propose a methodology that involves segregating the grid utilized for computing a strip coverage area from the grid employed for generating candidate strips. This entails utilizing the generated grid to derive a set of candidate strips and employing the calculation grid to determine the effective coverage area. As illustrated in Figure 5, the black grid signifies the generated grid, whereas the gray grid represents the calculation grid.
3.1.3. Refined Grid
In the process of numerical simulation, there is a scenario where a cell is not fully covered by a single strip, but rather by multiple combined strips. This necessitates the use of an additional strip to individually cover these cells in subsequent search processes. As shown in the left panel of Figure 6, the red strip1 covers the red cells, the green strip2 covers the green cells, and the yellow strip3 covers the yellow cells. However, the yellow cells are actually covered by both strip1 and strip2, making the yellow strip redundant and wasteful. To tackle this issue, we propose the use of a refined grid that is independent of the generated and calculate grids. The refined grid provides a more accurate record of the coverage of a given region. When all the refined cells contained within a calculated cell are covered, the corresponding calculated cell can be updated as “covered”.
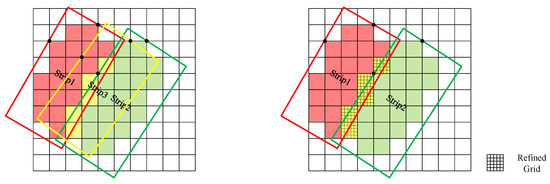
Figure 6.
Schematic diagram of joint cover.
In the right panel of Figure 6, each yellow cell is divided into 25 smaller cells. Some of these small cells are covered by a red stripe, while others are covered by a green stripe. Each yellow cell is associated with a state matrix. When all the elements in the matrix become 1, it indicates that all the small cells within the yellow cell are covered. In this case, we consider the yellow cell to be completely covered.
3.2. A Heuristic Algorithm Based on Triple Grids Method
The main idea behind the algorithm is to select the strip that covers the highest number of uncovered cells. First, generate all the candidate stripes according to the generated grid , and then utilize the TG-GHA. The TG-GHA is summarized in Algorithm 1.
| Algorithm 1: A Heuristic Algorithm Based on Triple Grids Method |
 |
3.3. Approximation Algorithm
The TG-GHA possesses the ability to rapidly generate feasible solutions within a specified grid discretization scenario. Our aim is to enhance these feasible solutions further by implementing an approximation algorithm. The concept behind the approximation algorithm is to generate candidate strips using a smaller generated grid, referred to as the son-generated grid, and subsequently invoke the heuristic algorithm for optimization. As illustrated in Figure 7, the black grid represents the generated grid, while the gray grid signifies the subgenerated grid. Generating a set of candidate strips based on the generated grid and son-generated grid results in different numbers of candidate strips, with the number of candidate strips generated from the subgenerated grid being significantly greater than those produced from the generated grid. Directly searching within the set of candidate strips derived from the son-generated grid can substantially increase the computational time. To overcome this, we select adjacent strips as candidate strips. If the distance between the top and left vertices of the two strips is less than a predefined threshold, we consider these two strips as adjacent strips. As depicted in Figure 7, the red strip and the blue strip form a pair of adjacent strips.
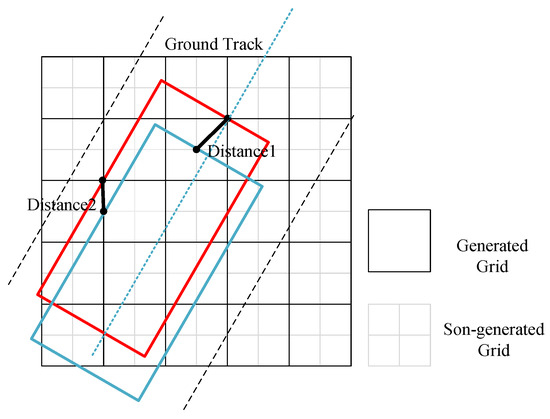
Figure 7.
Schematic diagram of adjacent strips.
4. Experiments and Analyses
4.1. Experimental Data
4.1.1. Imaging Satellite
In order to verify the effectiveness of the proposed algorithm, three kinds of satellites with different parameters were used for simulation experiments. They are the GF03B series, KF01 series, and GF02 series. These satellites were developed by Chang Guang satellite technology Co., Ltd. (Changchun, China) and are in service. Some important parameters of the satellites are listed in Table 3.

Table 3.
Satellite parameters.
4.1.2. Regional Target and Orbit
To demonstrate the efficacy of the suggested algorithm, two major regional objectives were chosen: Sichuan Province and Yunnan Province in China. Table 4 enumerates the size of two areas and the count of satellite transit trajectories.

Table 4.
Area of the selected region and number of satellite transit orbits.
4.2. Evalution Index
In order to evaluate the performance of the proposed algorithm, five evalution indexes are described as follows:
- Running time: The running time of the algorithm in large-scale optimization problems plays a crucial role in determining its practical applicability. If the algorithm produces improved results but has an unacceptable running time, it cannot be considered a good algorithm.
- Selected strips: In a coverage scheme, there may be certain strips whose coverage area is covered by other strips, and such strips are said to be invalid. Using fewer stripes to cover larger areas is a good coverage scheme.
- Grid coverage rate: This paper turns a continuous optimization problem into a discrete optimization problem. The objective function of the model is to cover more grids. The grid coverage rate can measure the quality of a coverage scheme and is an approximation of the real coverage rate. The grid coverage rate can be calculated by the following formula:represents the grid covered by all the selected strips. represents the calculation grid.
- Overlap rate: Repeated coverage of the same area by satellites is a waste of resources. A good coverage scheme should have as little overlap as possible between its stripes, that is, a lower overlap rate. The overlap rate can be calculated by the following formula:is the selected strips set.
- Effective coverage rate: Due to the fact that the covered region is an irregular polygon, the strip is approximated to a rectangle, and not all areas of the strip are necessary. The effective coverage rate can reflect the true and effective coverage ratio of a coverage scheme. The effective coverage rate can be calculated by the following formula:
4.3. Experimental Setting
In order to verify the effectiveness of the algorithm proposed in this article, three sets of comparative experiments were set up in total. The simulation experiment was executed on a computer with an intel Core i7-12700F@2.10 GHz CPU (Intel, Santa Clara, CA, USA).
The first comparative experiment was to verify the improvement of the TG-GHA compared to the GHA. The discrete grid size of the GHA was set to 10 km. The generated grid size and the calculation grid size for the TG-GHA were set to 30 km and 10 km, respectively, and the refined grid size was set to one tenth of the calculation grid size. All the experiments were tested on two different regions.
The second group of the comparative experiment was to compare TG-GHA with three Evolutionary algorithms, namely, the Genetic Algorithm (GA), particle swarm optimization algorithm (PSO) and Differential Evolution(DE). The parameter settings of the TG-GHA were the same as those of the first comparative experiment. The population size of the Evolutionary algorithm was set to be 100, and the maximum number of iterations was set to be 1000. To eliminate random effects, each experiment was repeated 30 times and sorted by the grid coverage rate.
The final set of experiments was to verify the performance of the approximation algorithm. The maximum number of the approximations was set to be four. The initial grid size was the same as the first comparative experiment.
4.4. Experimental Results and Analyses
Experimental Results
Figure 8 shows the large region imaging results obtained by using the GHA and TG-GHA for Sichuan and Yunnan, respectively.
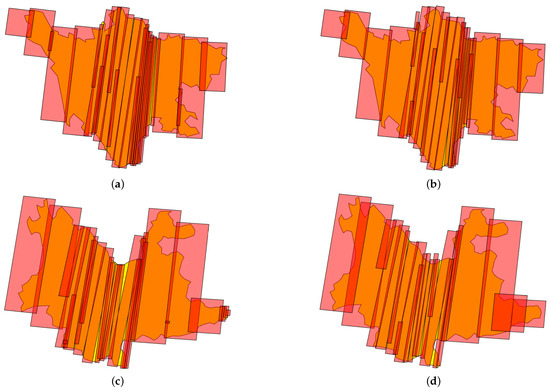
Figure 8.
Large region imaging results. (a,c) are the imaging results of Sichuan and Yunnan using the GHA; (b,d) are the imaging results of Sichuan and Yunnan using the TG-GHA.
Table 5 presents a comparison of the results using the GHA and TG-GHA. For each region, the running time, selected strips, grid coverage rate, overlap rate, and effective coverage rate of the two algorithms are compared separately.

Table 5.
Comparisons between the proposed algorithm and greedy heuristic algorithm.
Figure 9 shows the variation of the grid coverage rate with an increasing number of selected strips in Sichuan and Yunnan, respectively. The red curve is the result obtained by the GHA, and the blue curve is the result obtained by the TG-GHA.
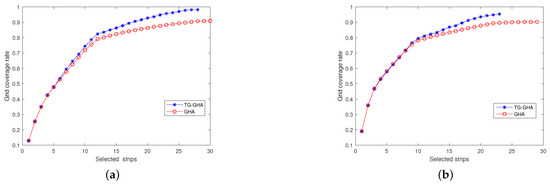
Figure 9.
The variation of grid coverage rate with increasing number of selected stripes. (a) Sichuan; (b) Yunnan.
Table 6 shows the comparison between the TG-GHA and three Evolutionary algorithms. For each region and each Evolutionary algorithm, its average, best, and worst values of running time, selected strips, grid coverage rate, overlap coverage rate, and effective coverage rate are compared with the results obtained by the TG-GHA.

Table 6.
Comparisons between the proposed algorithm and three evolution algorithms.
Figure 10 shows the performence of the approximation algorithm for Sichuan and Yunnan, respectively.
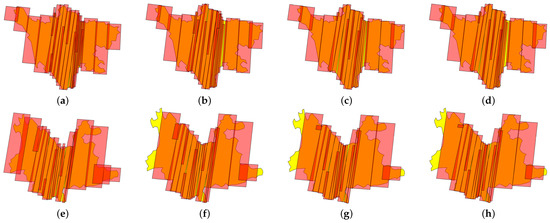
Figure 10.
Large region imaging results using the approximation algorithm. (a–d) Sichuan; (e–h) Yunnan.
Table 7 shows the variations in running time, selected strips, grid coverage rate, overlap rate, and effective coverage rate as the number of approximation times increases.

Table 7.
Performance of approximation algorithm.
4.5. Analyses
Table 3 reveals the presence of satellites with differing swaths. The swath of GF03B is only 17 km, while the swath of KF01B is 150 km. The swath limit grid needs to be more compact than the smallest possible swath, indicating a substantial quantity of grids and a significant number of potential strips. The GHA requires repeatedly traversing the remaining set of candidate strips, which incurs significant computational time consumption. Compared to the running time of the GHA, TG-GHA significantly reduces its running time for each region in Table 5. This is because the TG-GHA is without the limitations of grid size and there are fewer candidate strips. Normally, the search space of the TG-GHA is smaller than that of the GHA, and the accuracy of its solution is worse than that of the GHA. However, for each region, the TG-GHA uses fewer effective strips than GHA, with a grid coverage rate greater than the GHA, overlap rate less than or approximately equal to the GHA, and effective coverage rate greater than the GHA in Table 5. This is because the refined grid enables more accurate updates of the coverage statue of the calculation grid. From Figure 8, it can be seen that the imaging results obtained by using the TG-GHA have fewer overlap region and fewer effective strips than the GHA. Overall, the TG-GHA can achieve a coverage scheme that is no worse than the GHA in a shorter period of time.
Evolutionary algorithms are often used to solve large-scale combinatorial optimization problems. In Table 6, the GHA is compared with three common Evolutionary algorithms, namely, the GA, DE, and PSO, for their performance of solving large regional coverage problems. Among the three Evolutionary algorithms, the GA has the best performance. However, compared to the TG-GHA, all its evaluation indexes are worse than the TG-GHA, except for the running time.
The TG-GHA considers a trade-off between efficiency and optimality when solving the large region coverage problem. The approximation can compensate for the impact of reduced search space by a small number of candidate strips due to the large size of the generated grid. From Table 7, it can be seen that as the number of approximation times increases, the running time of the algorithm significantly increases, the number of effective strips gradually decreases, the grid coverage rate does not change much, the overlap rate decreases substantially, and the effective coverage rate increases by a wide margin for each region. From Figure 10, it can be seen that the overlap region becomes smaller and the number of the strips is decreasing.
5. Discussion
Employing multiple satellites to collaborate in covering large areas can improve coverage efficiency. As the number of satellites increases and the area of regional targets increases, designing an efficient algorithm for large area coverage has become particularly important. The current regional coverage algorithms in scholarly works, on the one hand, occurs on minor regional targets that do not match actual scenario, and on the other hand, the methods of generating candidate strips are not comprehensive enough to fully consider the satellite’s capabilities. In this paper, we proposed a heuristic algorithm based on the triple grids method and approximation which can effectively solve the problem of large-scale coverage of small satellites. By comparing the proposed method to the traditional greedy heuristic algorithm and three evolutionary algorithms, the results show that our method has better performance in terms of coverage and efficiency.
The research in this paper can be further extended in the following aspects:
- The algorithm proposed in this paper can achieve good coverage results in Chinese provincial-level regional targets. If the scale of the regional target reaches the Chinese map size, or even the world map size, designing efficient and reasonable algorithms is a challenge.
- Weather and other factors are not considered in this paper. In fact, weather is an uncertainty factor. In the next stage, cloud prediction can be considered as known, considering large area coverage under dynamic cloud charts. Cloud can also be taken as an uncertainty factor, and a stochastic optimization model can be established.
- This article assumes that EOS can only image once in a time window to a large reginal target. In practice, as long as the maneuver time requirements are satisfied, the satellite can select different swing angles to image the region multiple times. In the future, the constraints that a satellite can only image once in one orbit can be relaxed, giving full play to the satellite’s maneuverability, and a better coverage scheme can be obtained.
6. Conclusions
To address the problem of multi-satellite imaging task planning for large regional coverage, this paper proposes a heuristic algorithm based on the triple grids method. This method is a balance between computational efficiency and accuracy. In order to enhance computational efficiency, we opted for a larger generated grid size to reduce the number of candidate strips. To enhance computational accuracy, we utilize a refined grid to more effectively update the coverage of the region. In addition, we also use approximation algorithms to further optimize the solutions obtained by using heuristic algorithms. Compared to the traditional greedy heuristic algorithm, our proposed TG-GHA performs better in terms of computational efficiency and coverage. The results of the approximation algorithm show that as the number of approximations increases, the coverage scheme becomes more reasonable.
Author Contributions
Conceptualization, F.L. and Q.W.; methodology, F.W. and Y.Z.; software, F.W. and D.L.; validation, F.L. and Q.W.; formal analysis, F.W.; resources, F.L.; writing—original draft preparation, F.W.; writing—review and editing, F.W., F.L. and Q.H.; visualization, F.W.; funding acquisition, F.L., X.Z. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Scientific and Technological Research and Development Projects of Jilin OF FUNDER grant number 20210201015GX.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in https://github.com/miaosann/TG_GHA.
Conflicts of Interest
Author Feng Li, Feifei Wen, Qien He, Da Li and Xing Zhong was employed by Chang Guang satellite technology Co., Ltd. (Changchun, China). The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Denis, G.; Claverie, A.; Pasco, X.; Darnis, J.-P.; de Maupeou, B.; Lafaye, M.; Morel, E. Towards disruptions in Earth observation? New Earth Observation systems and markets evolution: Possible scenarios and impacts. Acta Astronaut. 2017, 137, 415–433. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, L.; Zhao, Y.; Wang, Y.; Wei, D.; Wu, X.; Ma, X. Recent advances in using Chinese Earth observation satellites for remote sensing of vegetation. ISPRS J. Photogramm. Remote Sens. 2023, 195, 393–407. [Google Scholar] [CrossRef]
- Dhali, M.K.; Chakraborty, M.; Sahana, M. Assessing spatio-temporal growth of urban sub-centre using Shannon’s entropy model and principle component analysis: A case from North 24 Parganas, lower Ganga River Basin, India. Egypt. J. Remote Sens. Space Sci. 2019, 22, 25–35. [Google Scholar] [CrossRef]
- Havivi, S.; Schvartzman, I.; Maman, S.; Rotman, S.; Blumberg, D. Combining TerraSAR-X and Landsat Images for Emergency Response in Urban Environments. Remote Sens. 2018, 10, 802. [Google Scholar] [CrossRef]
- Xhafa, F.; Ip, A.W.H. Optimisation problems and resolution methods in satellite scheduling and space-craft operation: A survey. Enterp. Inf. Syst. 2019, 15, 1022–1045. [Google Scholar] [CrossRef]
- Lin, W.C.; Liao, D.Y.; Liu, C.Y.; Lee, Y.Y. Daily Imaging Scheduling of an Earth Observation Satellite. IEEE Trans. Syst. Man Cybern. Part A-Syst. Hum. 2005, 35, 213–223. [Google Scholar] [CrossRef]
- Wang, J.; Demeulemeester, E.; Qiu, D. A pure proactive scheduling algorithm for multiple earth observation satellites under uncertainties of clouds. Comput. Oper. Res. 2016, 74, 1–13. [Google Scholar] [CrossRef]
- Wang, J.; Song, G.; Liang, Z.; Demeulemeester, E.; Hu, X.; Liu, J. Unrelated parallel machine scheduling with multiple time windows: An application to earth observation satellite scheduling. Comput. Oper. Res. 2023, 149, 106010. [Google Scholar] [CrossRef]
- Wu, G.; Liu, J.; Ma, M.; Qiu, D. A two-phase scheduling method with the consideration of task clustering for earth observing satellites. Comput. Oper. Res. 2013, 40, 1884–1894. [Google Scholar] [CrossRef]
- Bianchessi, N.; Cordeau, J.F.; Desrosiers, J.; Laporte, G.; Raymond, V. A heuristic for the multi-satellite, multi-orbit and multi-user management of Earth observation satellites. Eur. J. Oper. Res. 2007, 177, 750–762. [Google Scholar] [CrossRef]
- Vasquez, M.; Hao, J.-K. A “Logic-Constrained” Knapsack Formulation and a Tabu Algorithm for the Daily Photograph Scheduling of an Earth Observation Satellite. Comput. Optim. Appl. 2001, 20, 137–157. [Google Scholar] [CrossRef]
- Wolfe, W.J.; Sorensen, S.E. Three Scheduling Algorithms Applied to the Earth Observing Systems Domain. Manag. Sci. 2000, 46, 148–166. [Google Scholar] [CrossRef]
- Zhang, J.; Xing, L. An improved genetic algorithm for the integrated satellite imaging and data transmission scheduling problem. Comput. Oper. Res. 2022, 139, 1–11. [Google Scholar] [CrossRef]
- Xiong, J.; Leus, R.; Yang, Z.; Abbass, H.A. Evolutionary multi-objective resource allocation and scheduling in the Chinese navigation satellite system project. Eur. J. Oper. Res. 2016, 251, 662–675. [Google Scholar] [CrossRef]
- Wu, G.; Wang, H.; Pedrycz, W.; Li, H.; Wang, L. Satellite observation scheduling with a novel adaptive simulated annealing algorithm and a dynamic task clustering strategy. Comput. Ind. Eng. 2017, 113, 576–588. [Google Scholar] [CrossRef]
- He, Q.; Tian, Y.; Li, D.; Liu, W.; Jian, M. Satellite Imaging Task Planning using Particle Swarm Optimization and Tabu Search. In Proceedings of the 2021 IEEE 21st International Conference on Software Quality, Reliability and Security Companion (QRS-C), Hainan, China, 6–10 December 2021; pp. 589–595. [Google Scholar]
- Liu, X.; Bai, B.; Chen, Y.; Yao, F. Multi satellites scheduling algorithm based on task merging mechanism. Appl. Math. Comput. 2014, 230, 687–700. [Google Scholar]
- Xu, R.; Chen, H.; Liang, X.; Wang, H. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization. Expert Syst. Appl. 2016, 51, 195–206. [Google Scholar] [CrossRef]
- Fan, H.; Yang, Z.; Zhang, X.; Wu, S.; Long, J.; Liu, L. A novel multi-satellite and multi-task scheduling method based on task network graph aggregation. Expert Syst. Appl. 2022, 205, 1–22. [Google Scholar] [CrossRef]
- He, Y.; Xing, L.; Chen, Y.; Pedrycz, W.; Wang, L.; Wu, G. A Generic Markov Decision Process Model and Reinforcement Learning Method for Scheduling Agile Earth Observation Satellites. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1463–1474. [Google Scholar] [CrossRef]
- Walton, J.T. Models for the Management of Satellite-Based Sensors. Ph.D. Thesis, Massachusetts Institute Technology, Cambridge, MA, USA, 1993. [Google Scholar]
- Lemaître, M.; Verfaillie, G.; Jouhaud, F.; Lachiver, J.-M.; Bataille, N. Selecting and scheduling observations of agile satellites. Aerosp. Sci. Technol. 2002, 6, 367–381. [Google Scholar] [CrossRef]
- Cordone, R.; Gandellini, F.; Righini, G. Solving the swath segment selection problem through Lagrangean relaxation. Comput. Oper. Res. 2008, 35, 854–862. [Google Scholar] [CrossRef]
- Liu, S.; Hodgson, M.E. Satellite image collection modeling for large area hazard emergency response. ISPRS J. Photogramm. Remote Sens. 2016, 118, 13–21. [Google Scholar] [CrossRef]
- Hu, X.; Zhu, W.; An, B.; Jin, P.; Xia, W. A branch and price algorithm for EOS constellation imaging and downloading integrated scheduling problem. Comput. Oper. Res. 2019, 104, 74–89. [Google Scholar] [CrossRef]
- Zhu, W.; Hu, X.; Xia, W.; Sun, H. A three-phase solution method for the scheduling problem of using earth observation satellites to observe polygon requests. Comput. Ind. Eng. 2019, 130, 97–107. [Google Scholar] [CrossRef]
- Hu, X.; Zhu, W.; Ma, H.; An, B.; Zhi, Y.; Wu, Y. Orientational variable-length strip covering problem: A branch-and-price-based algorithm. Eur. J. Oper. Res. 2021, 289, 254–269. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Laporte, G. Maximizing the value of an Earth observation satellite orbit. J. Oper. Res. Soc. 2017, 56, 962–968. [Google Scholar] [CrossRef]
- Wang, P.; Reinelt, G.; Gao, P.; Tan, Y. A model, a heuristic and a decision support system to solve the scheduling problem of an earth observing satellite constellation. Comput. Ind. Eng. 2011, 61, 322–335. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, M.; Shen, X.; Zhang, G.; Lu, Z.; Xu, J. A Multi-Objective Modeling Method of Multi-Satellite Imaging Task Planning for Large Regional Mapping. Remote Sens. 2020, 12, 344. [Google Scholar] [CrossRef]
- Niu, X.; Tang, H.; Wu, L. Satellite scheduling of large areal tasks for rapid response to natural disaster using a multi-objective genetic algorithm. Int. J. Disaster Risk Reduct. 2018, 28, 813–825. [Google Scholar] [CrossRef]
- Li, F.; Wan, Q.; He, Q.; Zhong, X.; Xu, K.; Zhu, R. An Improved Many-Objective Evolutionary Algorithm for Multi-Satellite Joint Large Regional Coverage. IEEE Access 2023, 11, 45838–45849. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; He, R.; Chen, Y.; Chen, Y. Multi-objective Satellite Scheduling Approach for Very Large Areal Observation. IOP Conf. Ser. Mater. Sci. Eng. 2018, 435, 012037. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; He, R.; Chen, Y. Multi-satellite scheduling framework and algorithm for very large area observation. Acta Astronaut. 2020, 167, 93–107. [Google Scholar] [CrossRef]
- Li, X.-M. Two-Archive2 Algorithm for Large-Scale Polygon Targets Observation Scheduling Problem. In DEStech Transactions on Computer Science and Engineering; DEStech Publishing Inc.: Beijing, China, 2017. [Google Scholar]
- Gu, Y.; Han, C.; Chen, Y.; Liu, S.; Wang, X. Large region targets observation scheduling by multiple satellites using resampling particle swarm optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 1–16. [Google Scholar] [CrossRef]
- E, Z.; Shi, R.; Gan, L.; Baoyin, H.; Li, J. Multi-satellites imaging scheduling using individual reconfiguration based integer coding genetic algorithm. Acta Astronaut. 2021, 178, 645–657. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, X.; Zhang, G.; Lu, Z. Large-Scale Multi-Objective Imaging Satellite Task Planning Algorithm for Vast Area Mapping. Remote Sens. 2023, 15, 4178. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, X.; Zhang, G.; Lu, Z. Multi-Objective Multi-Satellite Imaging Mission Planning Algorithm for Regional Mapping Based on Deep Reinforcement Learning. Remote Sens. 2023, 15, 3932. [Google Scholar] [CrossRef]
- Shao, X.; Zhang, Z.; Wang, J.; Zhang, D. NSGA-II-Based Multi-objective Mission Planning Method for Satellite Formation System. J. Aerosp. Technol. Manag. 2016, 8, 451–458. [Google Scholar] [CrossRef]
- Grossman, T.; Wool, A. Computational experience with approximation algorithms for the set covering problem. Eur. J. Oper. Res. 1997, 101, 81–92. [Google Scholar] [CrossRef]
- Slavik, P. A Tight Analysis of the Greedy Algorithm for Set Cover. J. Algorithms 1997, 25, 237–254. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).