Comparison of Differences in Actual Cropland Evapotranspiration under Two Irrigation Methods Using Satellite-Based Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
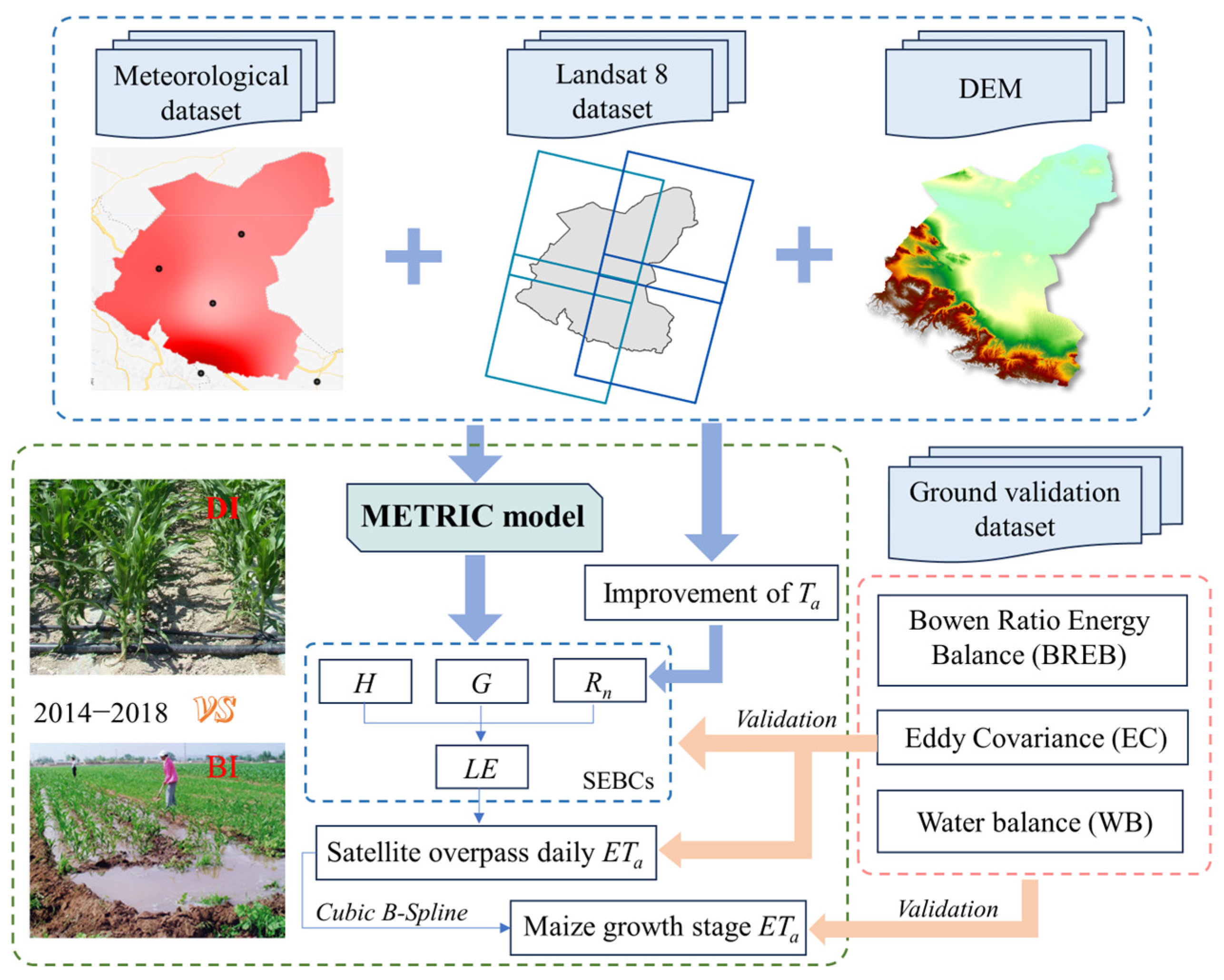
2.2. Remote Sensing, Auxiliary Data, and Data Processing
2.3. In Situ Dataset
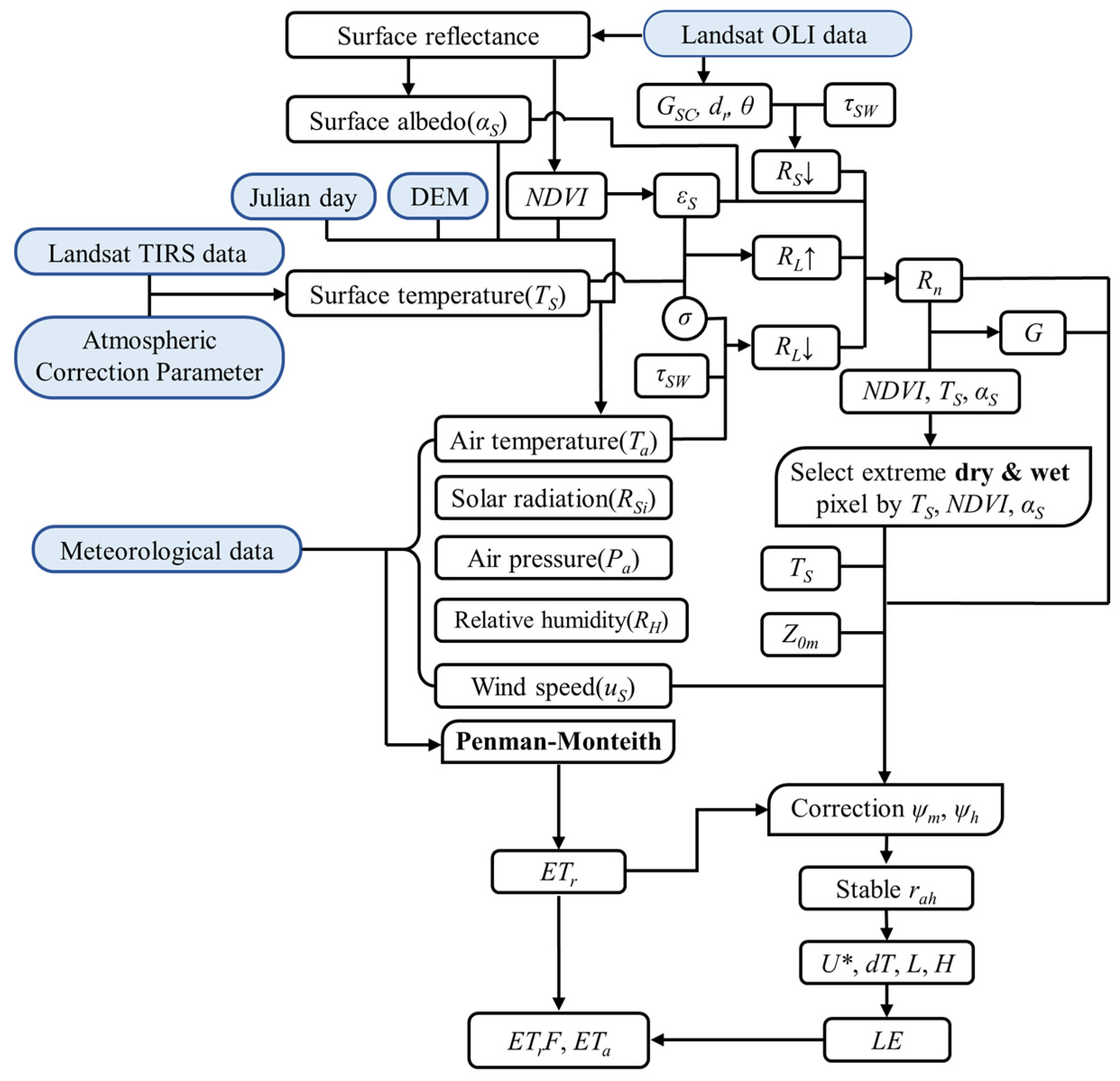
3. Surface Parameters Determination
3.1. Surface Parameters
3.2. METRIC Model
3.3. Coding and Validation of the METRIC Model
4. Results and Discussion
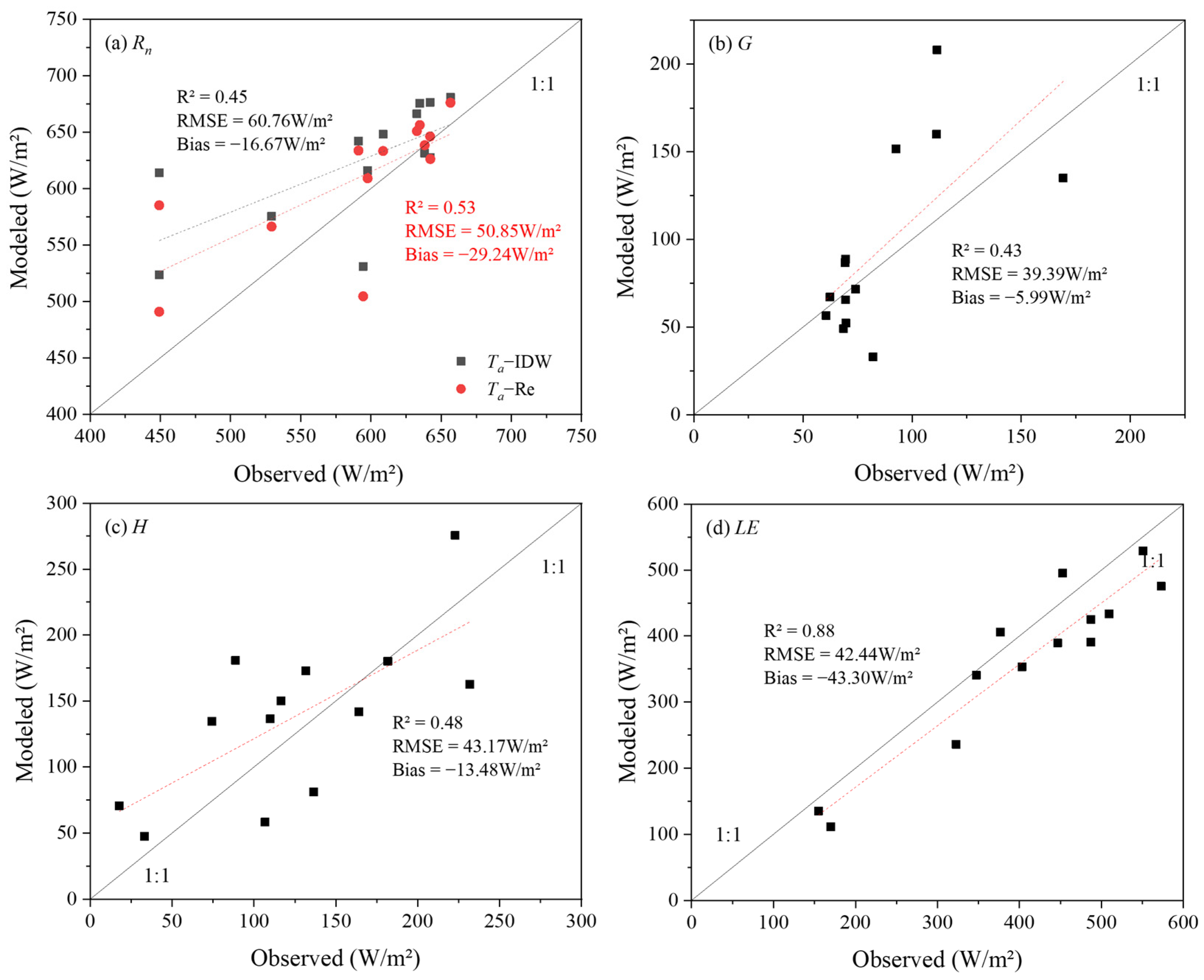
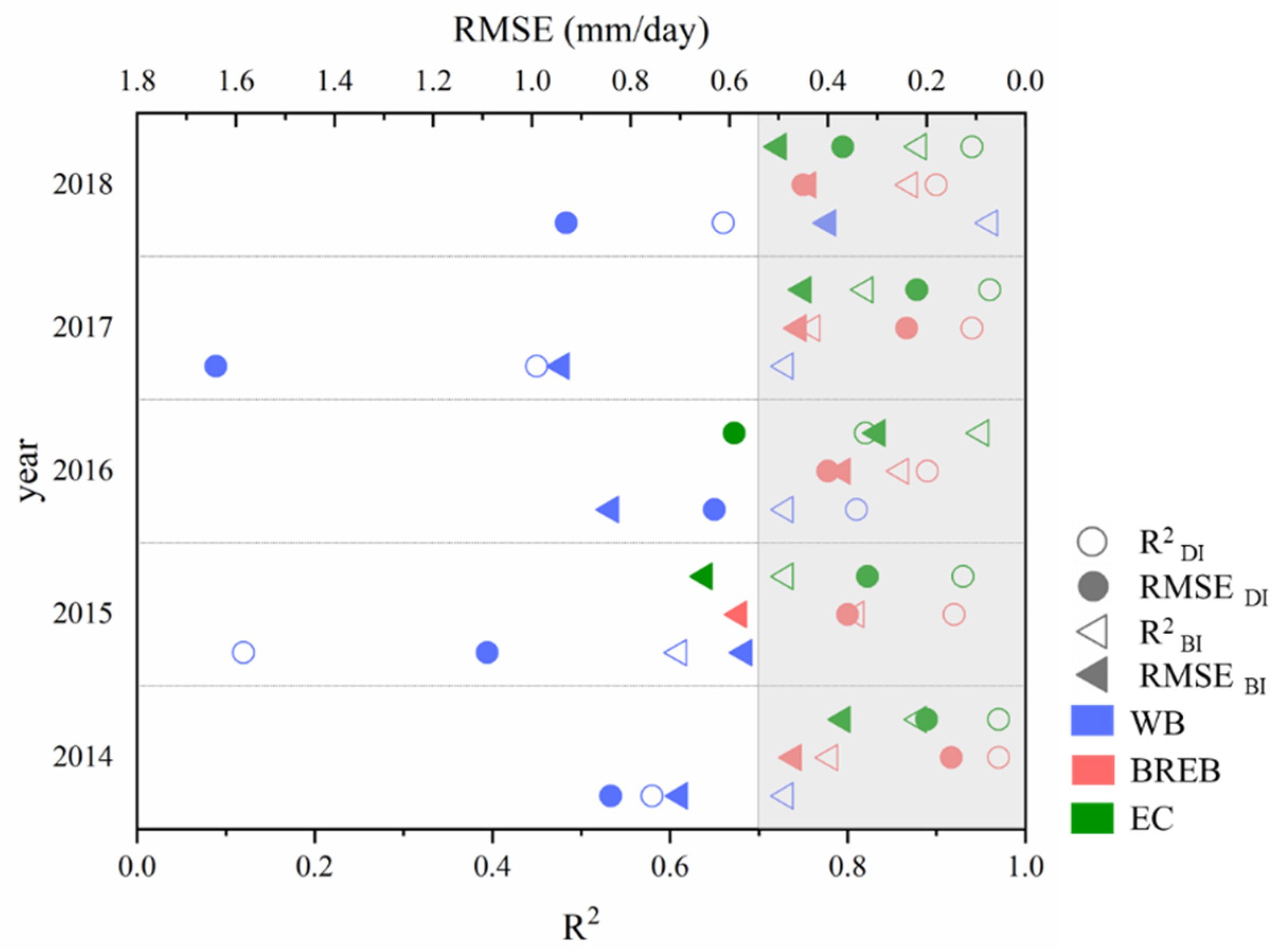
4.1. Inversion Accuracy of Energy Fluxes
4.2. Satellite Overpass Daily ETa Validation
4.3. Differences in the Growth Stage and Irrigation Methods of ETa
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Definition | Unit/Constant |
|---|---|---|
| Air heat constant | ||
| Evapotranspiration value on the day | mm | |
| Ratio of actual to reference evapotranspiration | mm | |
| Instantaneous evapotranspiration | mm/h | |
| Instantaneous evapotranspiration at overpass time from satellite | Mm/h | |
| Ratio of actual to reference evapotranspiration | / | |
| Instantaneous reference evapotranspiration | mm | |
| Total water consumption during the growing period | mm | |
| Solar constant | 1367 W/m2 | |
| Outgoing long-wave radiation | W/m2 | |
| Incoming long-wave incidence | W/m2 | |
| Surface incident short-wave radiation | W/m2 | |
| Net radiation flux | W/m2 | |
| Surface temperature | K | |
| Near-surface air temperature | K | |
| Relative Earth–Sun distance | / | |
| Aerodynamic resistance | s/m | |
| Surface emissivity | / | |
| Air density | 1.293 kg/m3 | |
| Soil and water flux heat | W/m2 | |
| Sensible heat flux | W/m2 | |
| Latent heat flux | W/m2 | |
| Time interval between sunrise and sunset | h | |
| Temperature difference between the height Z1 of the ground and the reference height Z2 of 2 m | k | |
| U* | Friction velocity | m/s |
| Number of days in the growing period | / | |
| Satellite overpass time | / | |
| Local altitude | m | |
| Solar incident angle | rad | |
| Latent heat of water vaporization | J/kg | |
| Stefan–Boltzman constant |
References
- Su, Z. The Surface Energy Balance System (SEBS) for Estimation of Turbulent Heat Fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Byun, K.; Liaqat, U.W.; Choi, M. Dual-Model Approaches for Evapotranspiration Analyses over Homo- and Heterogeneous Land Surface Conditions. Agric. For. Meteorol. 2014, 197, 169–187. [Google Scholar] [CrossRef]
- Sauer, T.J.; Hatfield, J.L.; Prueger, J.H.; Norman, J.M. Surface Energy Balance of a Corn Residue-Covered Field. Agric. For. Meteorol. 1998, 89, 155–168. [Google Scholar] [CrossRef]
- Wang, X.; Huo, Z.; Shukla, M.K.; Wang, X.; Guo, P.; Xu, X. Energy Fl Uxes and Evapotranspiration over Irrigated Maize Fi Eld in an Arid Area with Shallow Groundwater. Agric. Water Manag. 2020, 228, 105922. [Google Scholar] [CrossRef]
- Bi, W.; Weng, B.; Yan, D.; Wang, M.; Wang, H.; Wang, J.; Yan, H. Effects of Drought-Flood Abrupt Alternation on Phosphorus in Summer Maize Farmland Systems. Geoderma 2020, 363, 114147. [Google Scholar] [CrossRef]
- He, L.; Bao, J.; Daccache, A.; Wang, S.; Guo, P. Optimize the Spatial Distribution of Crop Water Consumption Based on a Cellular Automata Model: A Case Study of the Middle Heihe River Basin, China. Sci. Total Environ. 2020, 720, 137569. [Google Scholar] [CrossRef]
- Turral, H.; Burke, J.; Faures, J.M.; Faures, J.M. Climate Change, Water and Food Security; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011; p. 204. [Google Scholar]
- WWAP (United Nations World Water Assessment Programme)/UN-Water. The United Nations World Water Development Report 2018: Nature-Based Solutions for Water; UN-Water: Geneva, Switzerland, 2018; ISBN 9789231002649. Available online: https://www.unwater.org/publications/world-water-development-report-2018 (accessed on 25 December 2023).
- Kang, S.; Hao, X.; Du, T.; Tong, L.; Su, X.; Lu, H.; Li, X.; Huo, Z.; Li, S.; Ding, R. Improving Agricultural Water Productivity to Ensure Food Security in China under Changing Environment: From Research to Practice. Agric. Water Manag. 2017, 179, 5–17. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.P.; Chen, X.; Ma, Y.G. Optimization of the Irrigation Water Resources for Agricultural Sustainability in Tarim River Basin, China. Agric. Water Manag. 2012, 107, 74–85. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Federer, C.A.; Schloss, A.L. Potential Evaporation Functions Compared on US Watersheds: Possible Implications for Global-Scale Water Balance and Terrestrial Ecosystem Modeling. J. Hydrol. 1998, 207, 147–169. [Google Scholar] [CrossRef]
- Kite, G. Using a Basin-Scale Hydrological Model to Estimate Crop Transpiration and Soil Evaporation. J. Hydrol. 2000, 229, 59–69. [Google Scholar] [CrossRef]
- Senay, G.B.; Budde, M.E.; Verdin, J.P. Enhancing the Simplified Surface Energy Balance (SSEB) Approach for Estimating Landscape ET: Validation with the METRIC Model. Agric. Water Manag. 2011, 98, 606–618. [Google Scholar] [CrossRef]
- De C. Teixeira, A.H.; Bastiaanssen, W.G.M.; Ahmad, M.D.; Bos, M.G. Reviewing SEBAL Input Parameters for Assessing Evapotranspiration and Water Productivity for the Low-Middle São Francisco River Basin, Brazil. Part A: Calibration and Validation. Agric. For. Meteorol. 2009, 149, 462–476. [Google Scholar] [CrossRef]
- Wetzel Seemann, S.; Li, J.; Gumley, L.E.; Strabala, K.I.; Menzel, W.P. Operational Retrieval of Atmospheric Temperature, Moisture, and Ozone from MODIS Infrared Radiances. Appl. Weather Satell. 2003, 4895, 168. [Google Scholar] [CrossRef]
- Zamani Losgedaragh, S.; Rahimzadegan, M. Evaluation of SEBS, SEBAL, and METRIC Models in Estimation of the Evaporation from the Freshwater Lakes (Case Study: Amirkabir Dam, Iran). J. Hydrol. 2018, 561, 523–531. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and Difference of Potential Evapotranspiration and Reference Crop Evapotranspiration—A Review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Douglas, E.M.; Jacobs, J.M.; Sumner, D.M.; Ray, R.L. A Comparison of Models for Estimating Potential Evapotranspiration for Florida Land Cover Types. J. Hydrol. 2009, 373, 366–376. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef]
- Adamala, S.; Raghuwanshi, N.S.; Mishra, A.; Tiwari, M.K. Evapotranspiration Modeling Using Second-Order Neural Networks. J. Hydrol. Eng. 2014, 19, 1131–1140. [Google Scholar] [CrossRef]
- Peng, L.; Li, Y.; Feng, H. The Best Alternative for Estimating Reference Crop Evapotranspiration in Different Sub-Regions of Mainland China. Sci. Rep. 2017, 7, 5458. [Google Scholar] [CrossRef]
- Mokhtari, A.; Noory, H.; Pourshakouri, F.; Haghighatmehr, P.; Afrasiabian, Y.; Razavi, M.; Fereydooni, F.; Sadeghi Naeni, A. Calculating Potential Evapotranspiration and Single Crop Coefficient Based on Energy Balance Equation Using Landsat 8 and Sentinel-2. ISPRS J. Photogramm. Remote Sens. 2019, 154, 231–245. [Google Scholar] [CrossRef]
- Alberto, M.C.R.; Quilty, J.R.; Buresh, R.J.; Wassmann, R.; Haidar, S.; Correa, T.Q.; Sandro, J.M. Actual Evapotranspiration and Dual Crop Coefficients for Dry-Seeded Rice and Hybrid Maize Grown with Overhead Sprinkler Irrigation. Agric. Water Manag. 2014, 136, 1–12. [Google Scholar] [CrossRef]
- Garrido-Rubio, J.; Calera, A.; Arellano, I.; Belmonte, M.; Fraile, L.; Ortega, T.; Bravo, R.; González-Piqueras, J. Evaluation of Remote Sensing-Based Irrigation Water Accounting at River Basin District Management Scale. Remote Sens. 2020, 12, 3187. [Google Scholar] [CrossRef]
- Paço, T.A.; Pôças, I.; Cunha, M.; Silvestre, J.C.; Santos, F.L.; Paredes, P.; Pereira, L.S. Evapotranspiration and Crop Coefficients for a Super Intensive Olive Orchard. An Application of SIMDualKc and METRIC Models Using Ground and Satellite Observations. J. Hydrol. 2014, 519, 2067–2080. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL Model with Remotely Sensed Data to Improve Water-Resources Management under Actual Field Conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Paul, G.; Gowda, P.H.; Vara Prasad, P.V.; Howell, T.A.; Aiken, R.M.; Neale, C.M.U. Investigating the Influence of Roughness Length for Heat Transport (Zoh) on the Performance of SEBAL in Semi-Arid Irrigated and Dryland Agricultural Systems. J. Hydrol. 2014, 509, 231–244. [Google Scholar] [CrossRef]
- Liaqat, U.W.; Choi, M. Surface Energy Fluxes in the Northeast Asia Ecosystem: SEBS and METRIC Models Using Landsat Satellite Images. Agric. For. Meteorol. 2015, 214–215, 60–79. [Google Scholar] [CrossRef]
- French, A.N.; Hunsaker, D.J.; Thorp, K.R. Remote Sensing of Environment Remote Sensing of Evapotranspiration over Cotton Using the TSEB and METRIC Energy Balance Models. Remote Sens. Environ. 2015, 158, 281–294. [Google Scholar] [CrossRef]
- Elnmer, A.; Khadr, M.; Kanae, S.; Tawfik, A. Mapping Daily and Seasonally Evapotranspiration Using Remote Sensing Techniques over the Nile Delta. Agric. Water Manag. 2019, 213, 682–692. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Allen, R.; Irmak, A.; Trezza, R.; Hendrickx, J.M.H.; Bastiaanssen, W.; Kjaersgaard, J. Satellite-Based ET Estimation in Agriculture Using SEBAL and METRIC. Hydrol. Process. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- Allen, R.G.; Burnett, B.; Kramber, W.; Huntington, J.; Kjaersgaard, J.; Kilic, A.; Kelly, C.; Trezza, R. Automated Calibration of the METRIC-Landsat Evapotranspiration Process. J. Am. Water Resour. Assoc. 2013, 49, 563–576. [Google Scholar] [CrossRef]
- Trezza, R.; Allen, R.G.; Tasumi, M. Estimation of Actual Evapotranspiration along the Middle Rio Grande of New Mexico Using MODIS and Landsat Imagery with the METRIC Model. Remote Sens. 2013, 5, 5397–5423. [Google Scholar] [CrossRef]
- Choi, M.; Kustas, W.P.; Anderson, M.C.; Allen, R.G.; Li, F.; Kjaersgaard, J.H. An Intercomparison of Three Remote Sensing-Based Surface Energy Balance Algorithms over a Corn and Soybean Production Region (Iowa, U.S.) during SMACEX. Agric. For. Meteorol. 2009, 149, 2082–2097. [Google Scholar] [CrossRef]
- Nisa, Z.; Khan, M.S.; Govind, A.; Marchetti, M.; Lasserre, B.; Magliulo, E.; Manco, A. Evaluation of SEBS, METRIC-EEFlux, and QWaterModel Actual Evapotranspiration for a Mediterranean Cropping System in Southern Italy. Agronomy 2021, 11, 345. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Qin, S.; Guo, H.; Yang, D.; Lam, H.M. How Can Drip Irrigation Save Water and Reduce Evapotranspiration Compared to Border Irrigation in Arid Regions in Northwest China. Agric. Water Manag. 2020, 239, 106256. [Google Scholar] [CrossRef]
- Qin, S.; Li, S.; Kang, S.; Du, T.; Tong, L.; Ding, R. Can the Drip Irrigation under Film Mulch Reduce Crop Evapotranspiration and Save Water under the Sufficient Irrigation Condition? Agric. Water Manag. 2016, 177, 128–137. [Google Scholar] [CrossRef]
- Gao, L.; Kang, S.; Bai, X.; Li, S.; Niu, J.; Ding, R. Water-Carbon Relationships and Variations from the Canopy to Ecosystem Scale in a Sparse Vineyard in the Northwest China. J. Hydrol. 2021, 600, 126469. [Google Scholar] [CrossRef]
- Becker, W.R.; Ló, T.B.; Johann, J.A.; Mercante, E. Statistical Features for Land Use and Land Cover Classification in Google Earth Engine. Remote Sens. Appl. Soc. Environ. 2021, 21, 100459. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Kang, S.; Tong, L.; Du, T.; Hao, X.; Zhao, P. Comparison of Several Surface Resistance Models for Estimating Crop Evapotranspiration over the Entire Growing Season in Arid Regions. Agric. For. Meteorol. 2015, 208, 1–15. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Zhang, L.; Zhang, J. On the Attribution of Changing Crop Evapotranspiration in Arid Regions Using Four Methods. J. Hydrol. 2018, 563, 576–585. [Google Scholar] [CrossRef]
- Bowen, I.S. The Ratio of Heat Losses by Conduction and by Evaporation from Any Water Surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Perez, P.J.; Castellvi, F.; Ibañez, M.; Rosell, J.I. Assessment of Reliability of Bowen Ratio Method for Partitioning Fluxes. Agric. For. Meteorol. 1999, 97, 141–150. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the Eddy Covariance Technique for Evaluating Carbon Dioxide Exchange Rates of Ecosystems: Past, Present and Future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Shuttleworth, W.J. Putting the “vap” into Evaporation. Hydrol. Earth Syst. Sci. 2007, 11, 210–244. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A Review of Current Methodologies for Regional Evapotranspiration Estimation from Remotely Sensed Data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Windahl, E.; de Beurs, K. An Intercomparison of Landsat Land Surface Temperature Retrieval Methods under Variable Atmospheric Conditions Using in Situ Skin Temperature. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 11–27. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, Q.; Qin, F. A Statistical Method Based on Remote Sensing for the Estimation of Air Temperature in China. Int. J. Climatol. 2015, 35, 2131–2143. [Google Scholar] [CrossRef]
- Liu, Y.; Ortega-Farías, S.; Tian, F.; Wang, S.; Li, S. Estimation of Surface and Near-Surface Air Temperatures in Arid Northwest China Using Landsat Satellite Images. Front. Environ. Sci. 2021, 9, 609. [Google Scholar] [CrossRef]
- Flood, N. Continuity of Reflectance Data between Landsat-7 ETM+ and Landsat-8 OLI, for Both Top-of-Atmosphere and Surface Reflectance: A Study in the Australian Landscape. Remote Sens. 2014, 6, 7952–7970. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to Broadband Conversions of Land Surface Albedo I. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Ortega-Salazar, S.; Ortega-Farías, S.; Kilic, A.; Allen, R. Performance of the METRIC Model for Mapping Energy Balance Components and Actual Evapotranspiration over a Superintensive Drip-Irrigated Olive Orchard. Agric. Water Manag. 2021, 251, 106861. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. SEBAL-Based Sensible and Latent Heat Fluxes in the Irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Numata, I.; Khand, K.; Kjaersgaard, J.; Cochrane, M.A.; Silva, S.S. Evaluation of Landsat-Based Metric Modeling to Provide High-Spatial Resolution Evapotranspiration Estimates for Amazonian Forests. Remote Sens. 2017, 9, 46. [Google Scholar] [CrossRef]
- Tayebi, S.; Momani, S.; Abu, O. The Cubic B-Spline Interpolation Method for Numerical Point Solutions of Conformable Boundary Value Problems. Alex. Eng. J. 2022, 61, 1519–1528. [Google Scholar] [CrossRef]
- Oliveira, B.S.; Moraes, E.C.; Carrasco-Benavides, M.; Bertani, G.; Mataveli, G.A.V. Improved Albedo Estimates Implemented in the METRIC Model for Modeling Energy Balance Fluxes and Evapotranspiration over Agricultural and Natural Areas in the Brazilian Cerrado. Remote Sens. 2018, 10, 1181. [Google Scholar] [CrossRef]
- Carrasco-Benavides, M.; Ortega-Farías, S.; Lagos, L.O.; Kleissl, J.; Morales-Salinas, L.; Kilic, A. Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard. Remote Sens. 2014, 6, 11342–11371. [Google Scholar] [CrossRef]
- Feng, J.; Wang, W.; Che, T.; Xu, F. Performance of the Improved Two-Source Energy Balance Model for Estimating Evapotranspiration over the Heterogeneous Surface. Agric. Water Manag. 2023, 278, 108159. [Google Scholar] [CrossRef]
- Ge, N.; Zhong, L.; Ma, Y.; Cheng, M.; Wang, X.; Zou, M.; Huang, Z. Estimation of Land Surface Heat Fluxes Based on Landsat 7 ETM+ Data and Field Measurements over the Northern Tibetan Plateau. Remote Sens. 2019, 11, 2899. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow Band Vegetation Indices Overcome the Saturation Problem in Biomass Estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Kamyab, A.D.; Mokhtari, S.; Jafarinia, R. A Comparative Study in Quantification of Maize Evapotranspiration for Iranian Maize Farm Using SEBAL and METRIC-1 EEFLux Algorithms. Acta Geophys. 2022, 70, 319–332. [Google Scholar] [CrossRef]
- Xue, J.; Bali, K.M.; Light, S.; Hessels, T.; Kisekka, I. Evaluation of Remote Sensing-Based Evapotranspiration Models against Surface Renewal in Almonds, Tomatoes and Maize. Agric. Water Manag. 2020, 238, 106228. [Google Scholar] [CrossRef]
- Reyes-González, A.; Kjaersgaard, J.; Trooien, T.; Reta-Sánchez, D.G.; Sánchez-Duarte, J.I.; Preciado-Rangel, P.; Fortis-Hernández, M. Comparison of Leaf Area Index, Surface Temperature, and Actual Evapotranspiration Estimated Using the METRIC Model and In Situ Measurements. Sensors 2019, 19, 1857. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Stöckle, C.O.; Nelson, R.L.; Peters, T.; Adam, J.C.; Lamb, B.; Chi, J.; Waldo, S. Estimating Biomass and Yield Using Metric Evapotranspiration and Simple Growth Algorithms. Agron. J. 2019, 111, 536–544. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Xu, D.; Zhao, N.; Lei, B.; Rosa, R.D.; Paredes, P.; Paço, T.A.; Pereira, L.S. The Dual Crop Coefficient Approach to Estimate and Partitioning Evapotranspiration of the Winter Wheat-Summer Maize Crop Sequence in North China Plain. Irrig. Sci. 2013, 31, 1303–1316. [Google Scholar] [CrossRef]
- Zhang, T.; Zou, Y.; Kisekka, I.; Biswas, A.; Cai, H. Comparison of Different Irrigation Methods to Synergistically Improve Maize’s Yield, Water Productivity and Economic Benefits in an Arid Irrigation Area. Agric. Water Manag. 2021, 243, 106497. [Google Scholar] [CrossRef]
- Sandhu, O.S.; Gupta, R.K.; Thind, H.S.; Jat, M.L.; Sidhu, H.S. Yadvinder-Singh Drip Irrigation and Nitrogen Management for Improving Crop Yields, Nitrogen Use Efficiency and Water Productivity of Maize-Wheat System on Permanent Beds in North-West India. Agric. Water Manag. 2019, 219, 19–26. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring Daily Evapotranspiration over Two California Vineyards Using Landsat 8 in a Multi-Sensor Data Fusion Approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef]
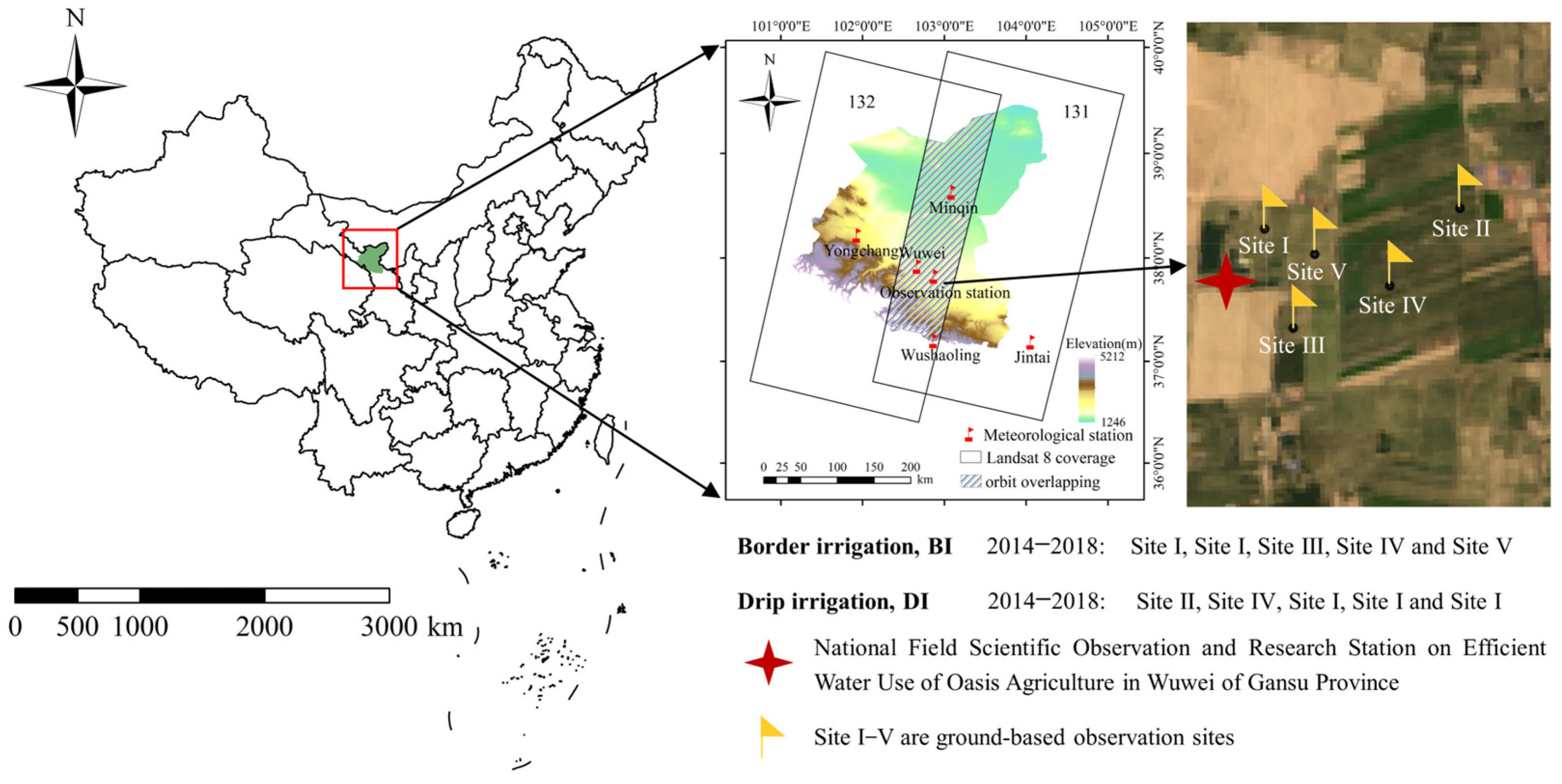


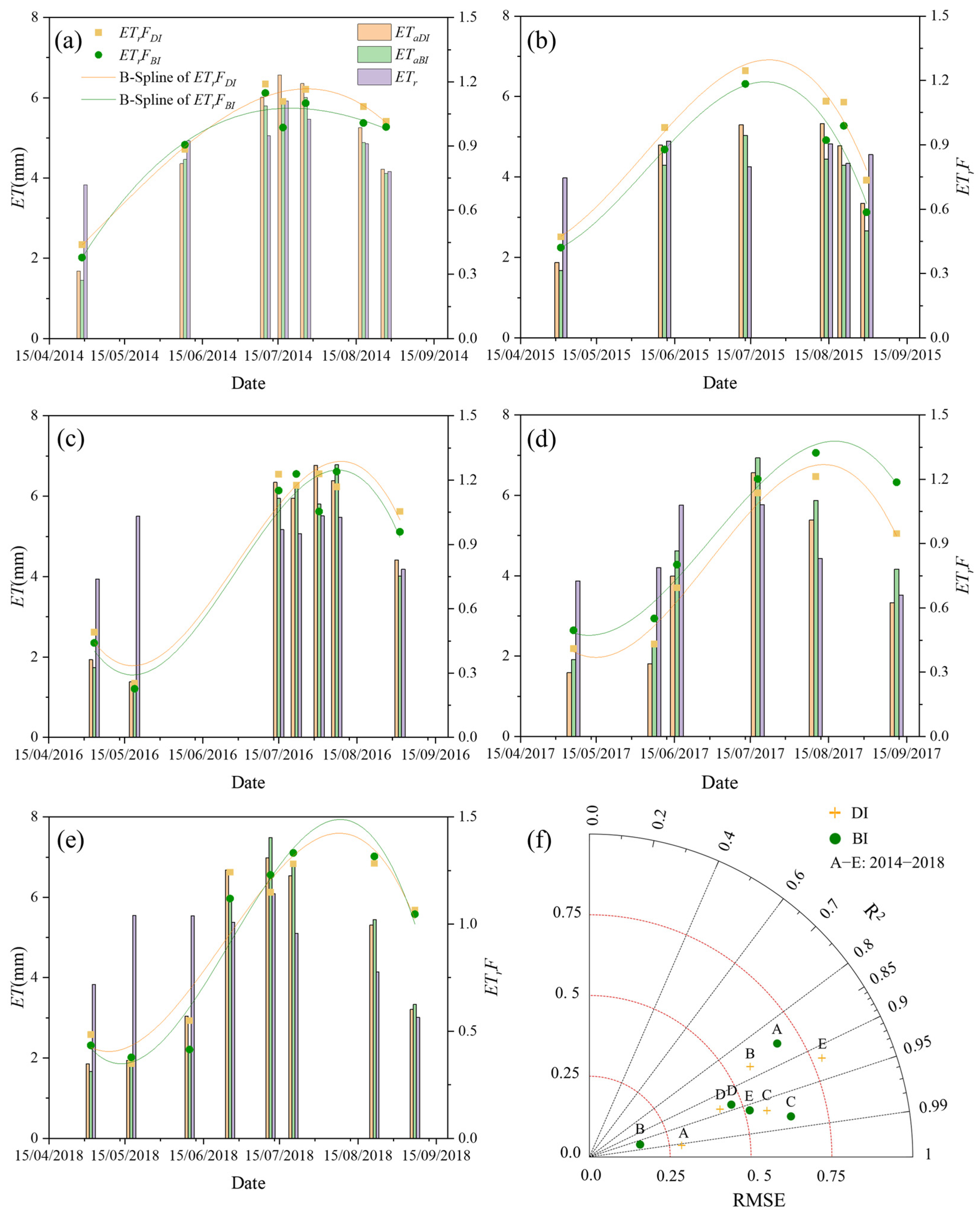
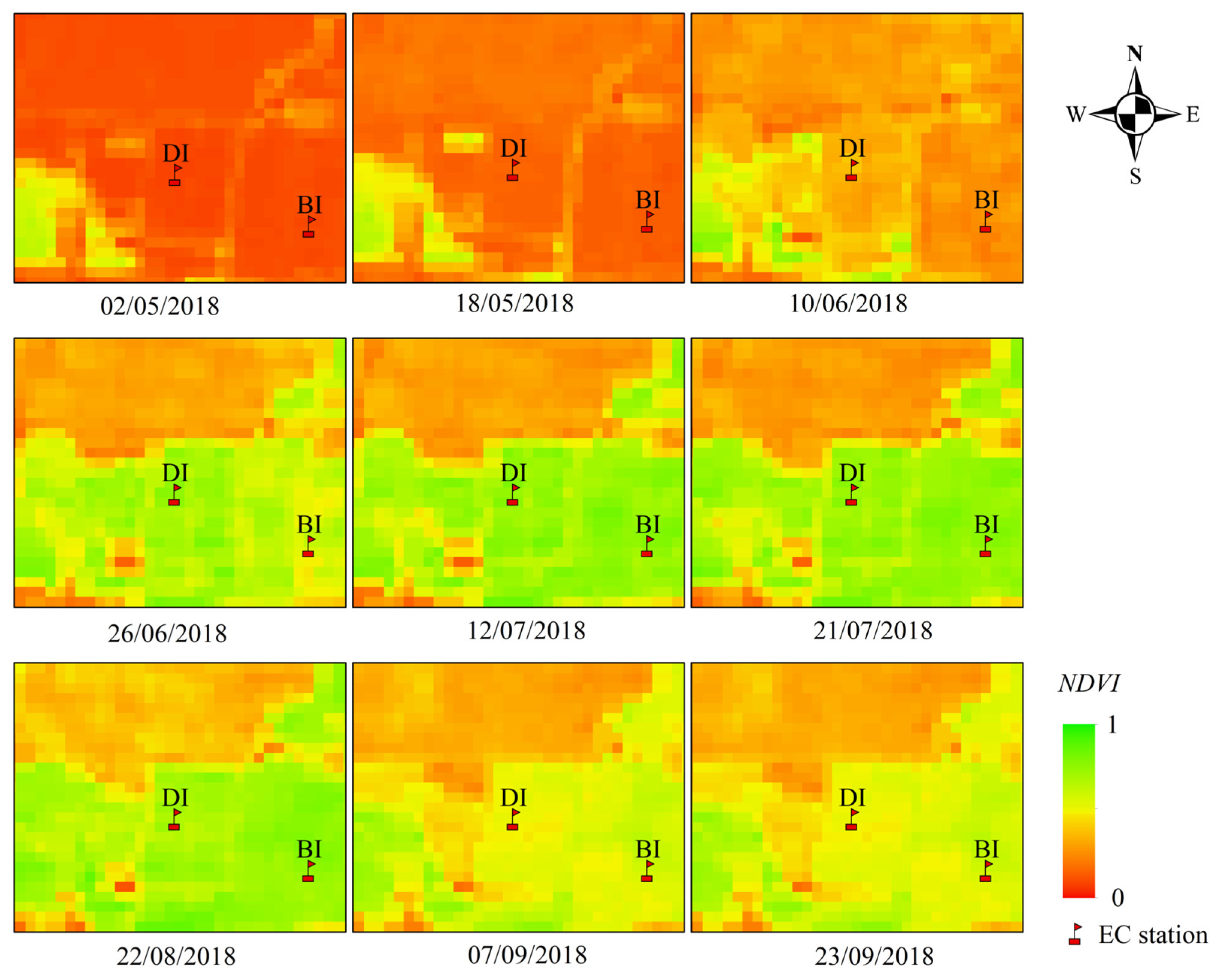
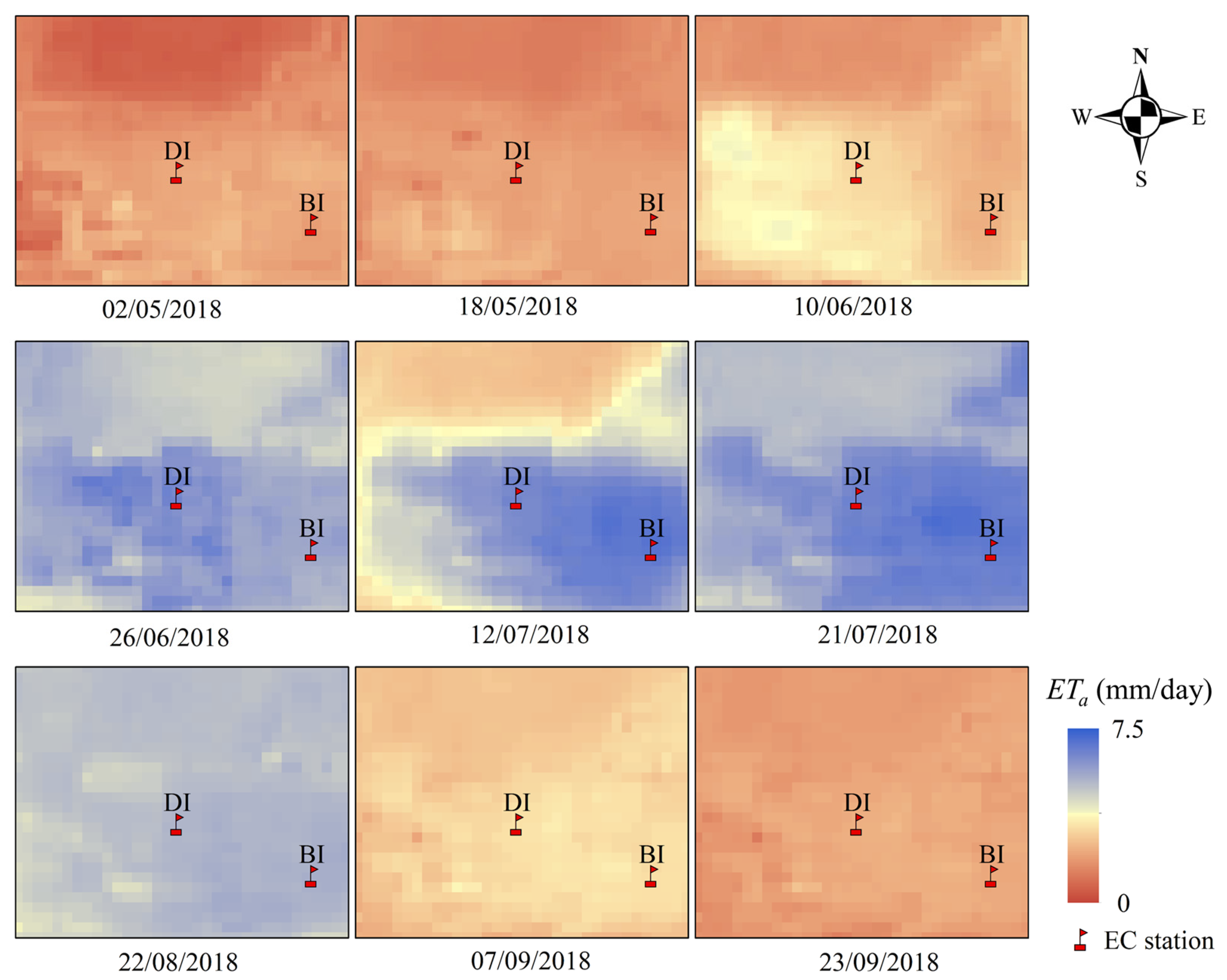

| Crop | Irrigation Method | Years | Site | Area | Growth Period Days | Number of Remote Sensing Images | Observation Method |
|---|---|---|---|---|---|---|---|
| seed maize | border irrigation under mulch field | 2014 | I | 400 m × 200 m | 149 | 8 | Water balance method; Bowen ratio and energy balance method; Eddy covariance method |
| 2015 | I | 155 | 6 | ||||
| 2016 | III | 500 m × 250 m | 154 | 7 | |||
| 2017 | IV | 147 | 6 | ||||
| 2018 | V | 159 | 8 | ||||
| drip irrigation under mulch field | 2014 | II | 2000 m × 1000 m | 134 | 8 | ||
| 2015 | IV | 500 m × 250 m | 132 | 6 | |||
| 2016 | I | 400 m × 200 m | 144 | 7 | |||
| 2017 | I | 142 | 5 | ||||
| 2018 | I | 146 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ortega-Farías, S.; Fan, Y.; Hou, Y.; Wang, S.; Yang, W.; Li, S.; Tian, F. Comparison of Differences in Actual Cropland Evapotranspiration under Two Irrigation Methods Using Satellite-Based Model. Remote Sens. 2024, 16, 175. https://doi.org/10.3390/rs16010175
Liu Y, Ortega-Farías S, Fan Y, Hou Y, Wang S, Yang W, Li S, Tian F. Comparison of Differences in Actual Cropland Evapotranspiration under Two Irrigation Methods Using Satellite-Based Model. Remote Sensing. 2024; 16(1):175. https://doi.org/10.3390/rs16010175
Chicago/Turabian StyleLiu, Yi, Samuel Ortega-Farías, Yunfei Fan, Yu Hou, Sufen Wang, Weicai Yang, Sien Li, and Fei Tian. 2024. "Comparison of Differences in Actual Cropland Evapotranspiration under Two Irrigation Methods Using Satellite-Based Model" Remote Sensing 16, no. 1: 175. https://doi.org/10.3390/rs16010175
APA StyleLiu, Y., Ortega-Farías, S., Fan, Y., Hou, Y., Wang, S., Yang, W., Li, S., & Tian, F. (2024). Comparison of Differences in Actual Cropland Evapotranspiration under Two Irrigation Methods Using Satellite-Based Model. Remote Sensing, 16(1), 175. https://doi.org/10.3390/rs16010175







