High-Resolution and Wide-Swath SAR Imaging with Space–Time Coding Array
Abstract
1. Introduction
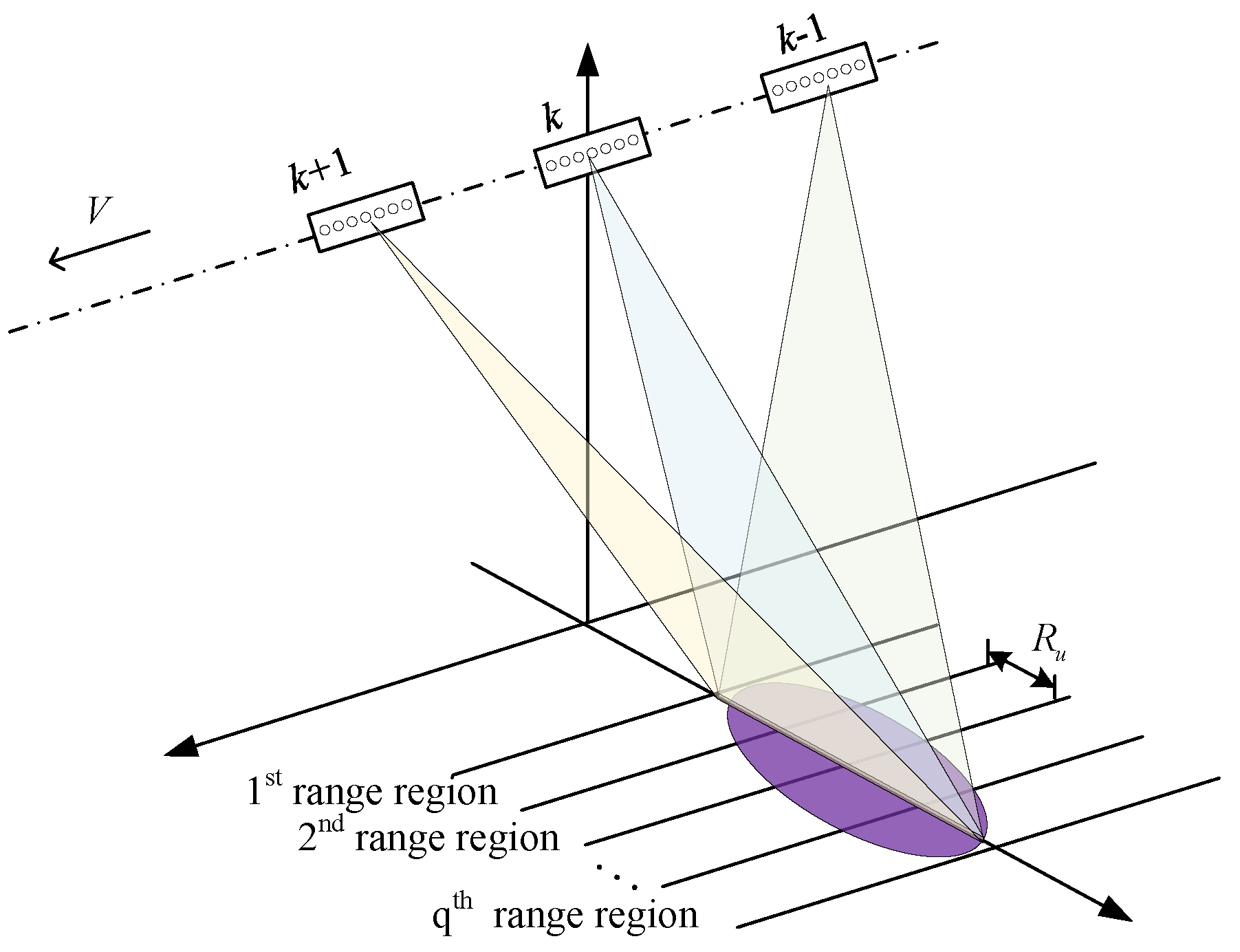
- A novel and simple space–time coding scheme is proposed to address the range-ambiguity issue, which is easy to be implemented in practice. Compared to the popular FDA radar, it does not necessitate a complicated orthogonal waveform design.
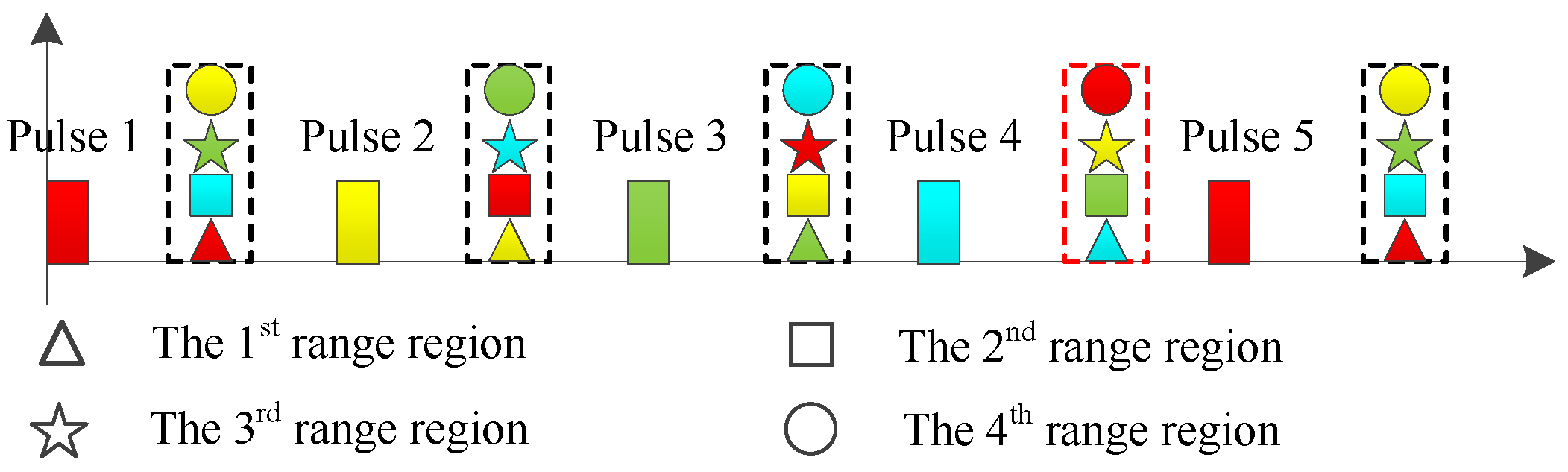
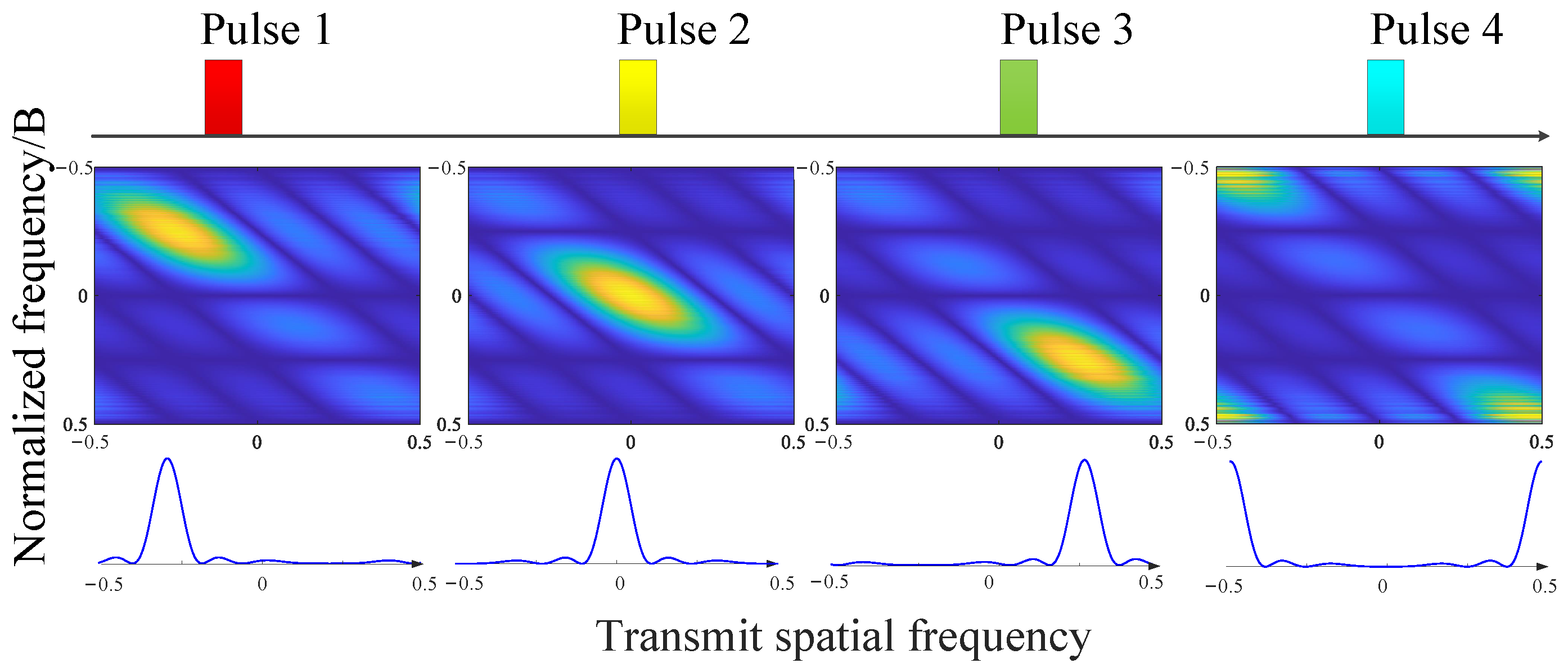
- The range-ambiguity regions corresponding to different transmit spatial frequencies are separated by performing equivalent transmit beamforming.
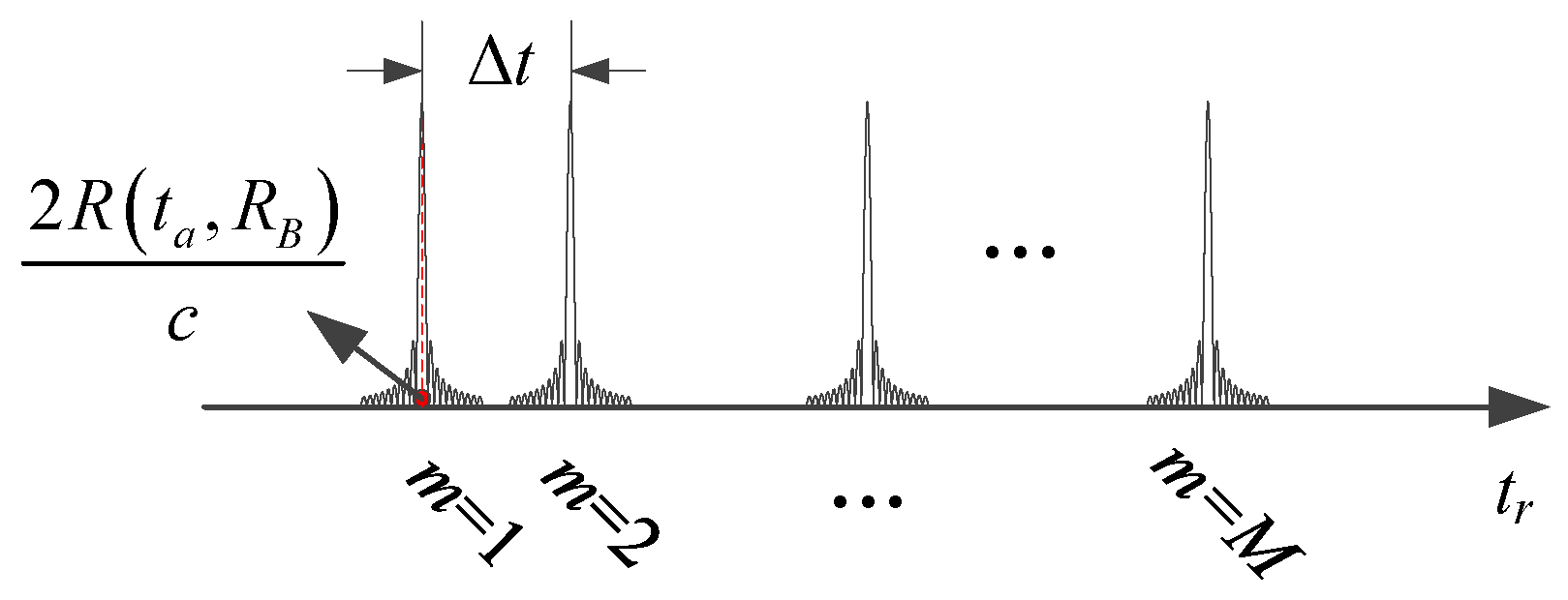
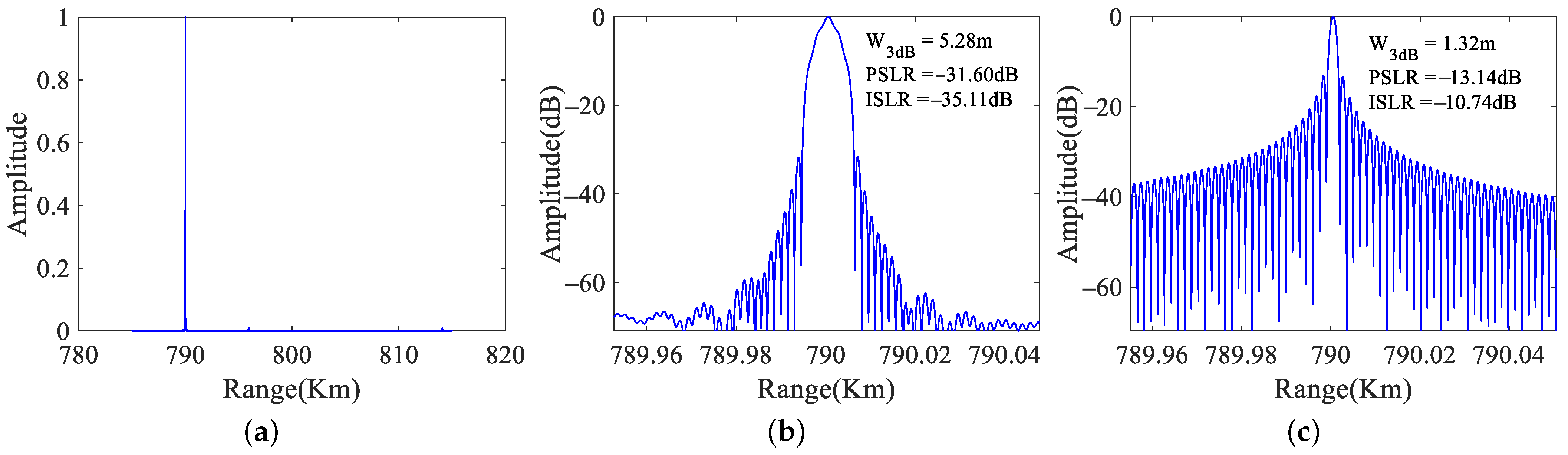
- A method of frequency splicing is proposed to obtain high-range resolution imaging, avoiding the need to increase the system bandwidth.
2. Signal Model
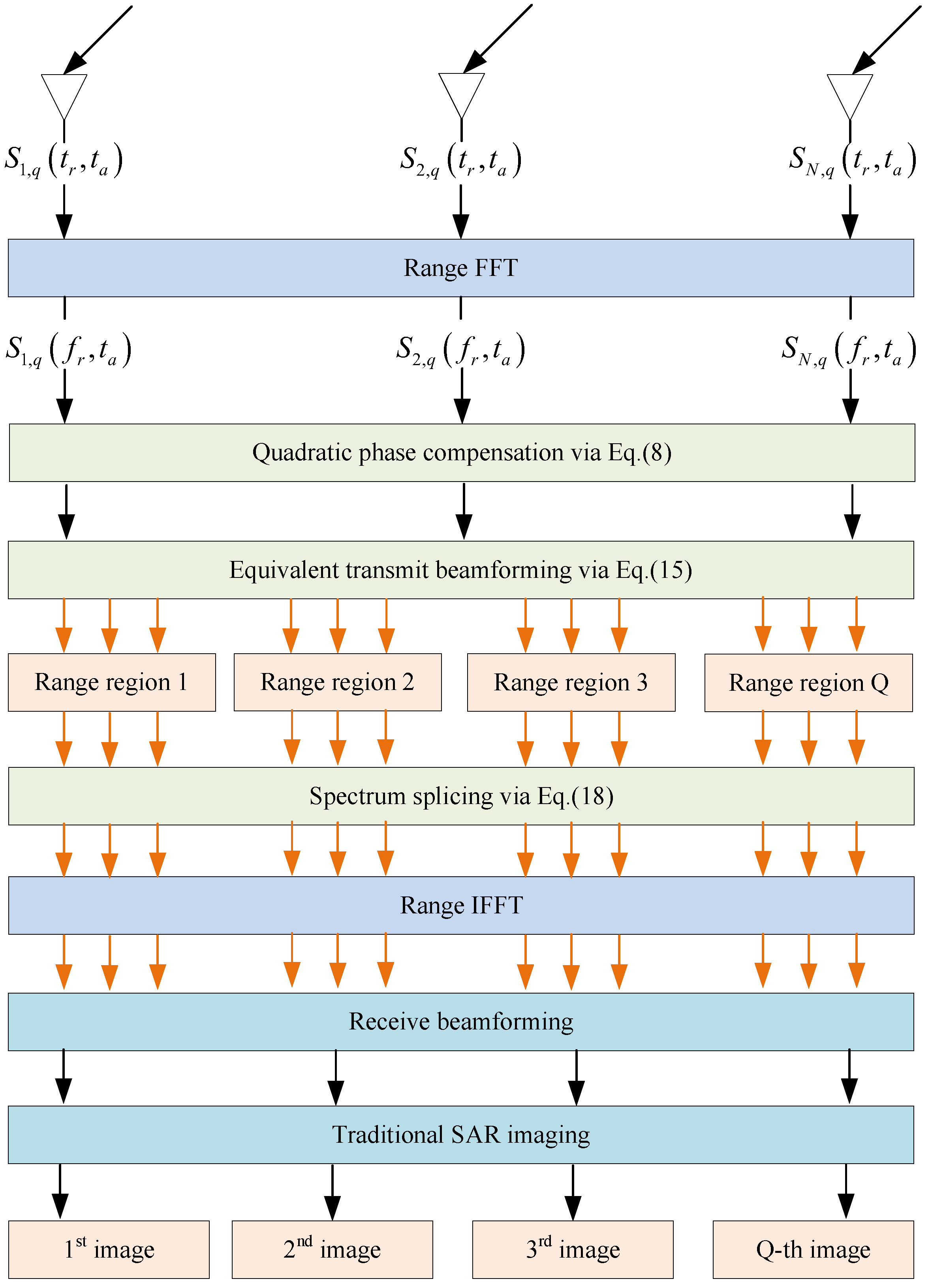
3. HRWS SAR Imaging Method
4. Simulation Results
4.1. Simulation with Point-like Targets
4.2. Simulation with Distributed Targets
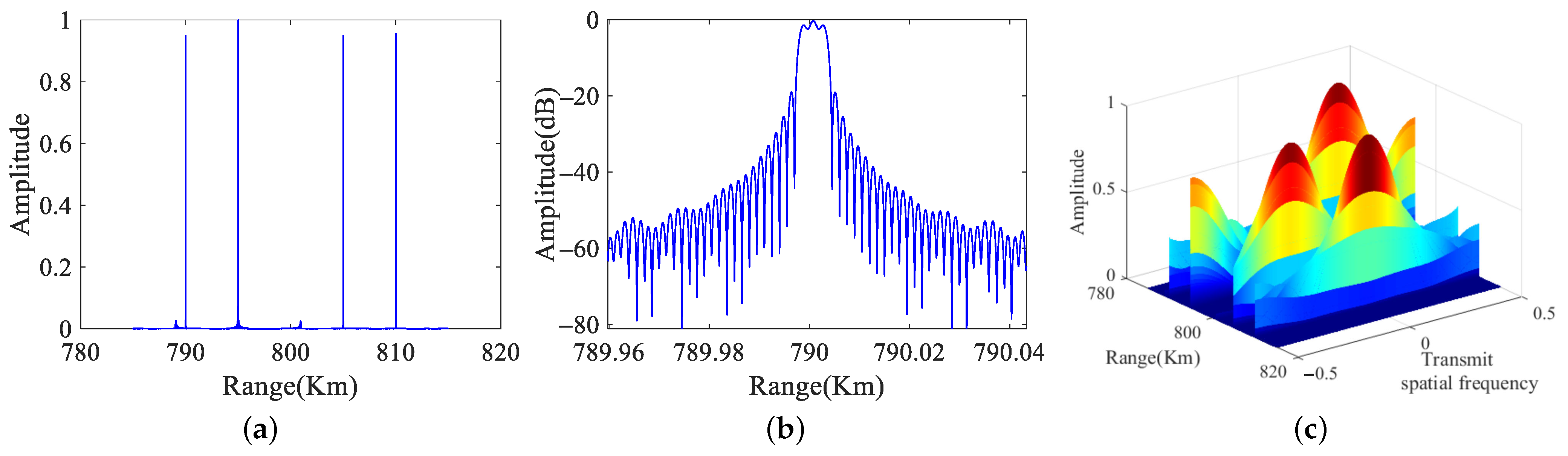
4.3. Performance of Range-Ambiguity Separation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivations of Performing Transmit Beamforming
Appendix B. Derivation of Spectrum Splicing
References
- Xu, G.; Zhang, B.J.; Yu, H.W.; Chen, J.L.; Xing, M.D.; Hong, W. Sparse Synthetic Aperture Radar Imaging from Compressed Sensing and Machine Learning: Theories, Applications and Trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–69. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.; Nies, H.; Knedlik, S.; Hagelen, M.; Essen, H. Focus FMCW SAR data using the wavenumber domain algorithm. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2109–2118. [Google Scholar] [CrossRef]
- Zhang, S.X.; Xing, M.D.; Xia, X.G.; Guo, R.; Liu, Y.Y.; Bao, Z. Robust Clutter Suppression and Moving Target Imaging Approach for Multichannel in Azimuth High-Resolution and Wide-Swath Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 687–709. [Google Scholar] [CrossRef]
- Cruz, H.; Véstias, M.; Monteiro, J.; Neto, H.; Duarte, R.P. A Review of Synthetic-Aperture Radar Image Formation Algorithms and Implementations: A Computational Perspective. Remote Sens. 2022, 14, 1258. [Google Scholar] [CrossRef]
- Zuo, S.S.; Xing, M.D.; Xia, X.G.; Sun, G.C. Improved Signal Reconstruction Algorithm for Multichannel SAR Based on the Doppler Spectrum Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1425–1442. [Google Scholar] [CrossRef]
- Mittermayer, J.; Moreira, A.; Loffeld, O. Spotlight SAR data processing using the frequency scaling algorithm. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2198–2214. [Google Scholar] [CrossRef]
- Dall, J.; Kusk, A. Azimuth phase coding for range ambiguity suppression in SAR. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1734–1737. [Google Scholar]
- Krieger, G.; Gebert, N.; Moreira, A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling. IEEE Geosci. Remote Sens. Lett. 2004, 1, 260–264. [Google Scholar] [CrossRef]
- Gebert, N.; Krieger, G.; Moreira, A. Digital beamforming on receive: Techniques and optimization strategies for high-resolution wide-swath SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 564–592. [Google Scholar] [CrossRef]
- Currie, A.; Brown, M.A. Wide-swath SAR. IEE Proc. F (Radar Signal Process.) 1992, 139, 122–135. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, B.; Xu, Z.; Zhang, Y.; Zhong, L.; Wu, Y. Ambiguities Suppression for Azimuth Multichannel SAR Based on L2,q Regularization with Application to Gaofen-3 Ultra-Fine Stripmap Mode. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1532–1544. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. Waveform-encoded SAR: A novel concept for nadir echo and range ambiguity suppression. In Proceedings of the 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018. [Google Scholar]
- Xu, W.; Huang, P.; Tan, W. Azimuth Phase Coding by Up and Down Chirp Modulation for Range Ambiguity Suppression. IEEE Access 2019, 7, 143780–143791. [Google Scholar] [CrossRef]
- Wang, W.Q.; Cai, J. MIMO SAR using chirp diverse waveform for wide-swath remote sensing. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3171–3185. [Google Scholar] [CrossRef]
- Mittermayer, J.; Martínez, J.M. Analysis of range ambiguity suppression in SAR by up and down chirp modulation for point and distributed targets. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 6, pp. 4077–4079. [Google Scholar]
- Gabele, M.; Krieger, G. Moving Target Signals in High ResolutionWide Swath SAR. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008. [Google Scholar]
- Krieger, G.; Moreira, A. Potentials of digital beamforming in bi- and multistatic SAR. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 1, pp. 527–529. [Google Scholar]
- Yang, T.; Lv, X.; Wang, Y.; Qian, J. Study on a Novel Multiple Elevation Beam Technique for HRWS SAR System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5030–5039. [Google Scholar] [CrossRef]
- Griffiths, H.D.; Mancini, P. Ambiguity suppression in SARs using adaptive array techniques. In Proceedings of the 11th Annual International Geoscience and Remote Sensing Symposium, 3–6 June 1991; Volume 2, pp. 1015–1018. [Google Scholar]
- Yang, J.; Sun, G.C.; Wu, Y.F.; Xing, M.D. Range ambiguity suppression by azimuth phase coding in multichannel SAR systems. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013. [Google Scholar]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional waveform encoding: A new digital beamforming technique for synthetic aperture radar remote sensing. IEEE Trans. Geosci. Remote Sens. 2007, 46, 31–46. [Google Scholar] [CrossRef]
- Cristallini, D.; Sedehi, M.; Lombardo, P. SAR imaging solutions based on azimuth phase coding. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008. [Google Scholar]
- Naftaly, U.; Levy-Nathansohn, R. Overview of the TECSAR satellite hardware and Mosaic mode. IEEE Geosci. Remote Sens. Lett. 2008, 5, 423–426. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Klare, J.; Gierull, C.H. MIMO SAR processing for multichannel high-resolution wide-swath radars. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5034–5055. [Google Scholar] [CrossRef]
- Ender, J.H.; Klare, J. System architectures and algorithms for radar imaging by MIMO-SAR. In Proceedings of the 2009 IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009. [Google Scholar]
- Cristallini, D.; Pastina, D.; Lombardo, P. Exploiting MIMO SAR potentialities with efficient cross-track constellation configurations for improved range resolution. IEEE Trans. Geosci. Remote Sens. 2011, 49, 38–52. [Google Scholar] [CrossRef]
- Wang, W.Q.; Cai, J. Ground moving target indication by MIMO SAR with multi-antenna in azimuth. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1662–1665. [Google Scholar]
- Kim, J.-H.; Younis, M.; Moreira, A.; Wiesbeck, W. Spaceborne MIMO synthetic aperture radar for multimodal operation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2453–2466. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Zhu, X. MIMO radar waveform synthesis. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar]
- Nel, W.; Tait, J.; Lord, R.; Wilkinson, A. The use of a frequency domain stepped frequency technique to obtain high range resolution on the CSIR X-Band SAR system. In Proceedings of the IEEE AFRICON. 6th Africon Conference, George, South Africa, 2–4 October 2002. [Google Scholar]
- Wang, C.H.; Xu, J.W.; Liao, G.S.; Xu, X.F.; Zhang, Y.H. A range ambiguity resolution approach for high-resolution and wide-swath SAR imaging using frequency diverse array. IEEE J. Sel. Top. Signal Process. 2017, 11, 336–346. [Google Scholar] [CrossRef]
- Wang, H.B.; Zhang, Y.H.; Xu, J.W.; Liao, G.S.; Zeng, C. A novel range ambiguity resolving approach for high-resolution and wide-swath SAR imaging utilizing space-pulse phase coding. Signal Process. 2020, 168, 107323. [Google Scholar] [CrossRef]
- Wang, W.Q. Mitigating range ambiguities in high-PRF SAR with OFDM waveform diversity. IEEE Geosci. Remote Sens. Lett. 2012, 10, 101–105. [Google Scholar] [CrossRef]
- Riché, V.; Méric, S.; Baudais, J.Y.; Pottier, E. Investigations on OFDM signal for range ambiguity suppression in SAR configuration. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4194–4197. [Google Scholar] [CrossRef]
- Riché, V.; Méric, S.; Baudais, J.Y.; Pottier, E. Optimization of OFDM SAR signals for range ambiguity suppression. In Proceedings of the 9th European Radar Conference, Amsterdam, The Netherlands, 31 October–2 November 2012; pp. 278–281. [Google Scholar]
- Riché, V.; Méric, S.; Pottier, E.; Baudais, J.Y. OFDM signal design for range ambiguity suppression in SAR configuration. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2156–2159. [Google Scholar]
- Krieger, G. MIMO-SAR: Opportunities and pitfalls. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2628–2645. [Google Scholar] [CrossRef]
- Bevan, D.D.N.; Tanner, R.; Ward, C.R. Space-time coding for capacity enhancement in future-generation wireless communications networks. In Proceedings of the IEE Colloquium on Capacity and Range Enhancement Techniques for the Third Generation Mobile Communications and Beyond, London, UK, 11 February 2000; p. 8/1-811. [Google Scholar]
- Foschini, G.J.; Gans, M.J. On Limits of Wireless Communications in a Fading Environment when Using Multiple Antennas. Wirel. Pers. Commun. 1998, 6, 311–335. [Google Scholar] [CrossRef]
- Gesbert, D.; Shafi, M.; Shiu, D.S.; Smith, P.J.; Naguib, A. From theory to practice: An overview of MIMO space-time coded wireless systems. IEEE J. Sel. Area. Commun. 2003, 21, 281–302. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.S.; Xu, J.W.; Xu, Y.H.; So, H.C. Beampattern Synthesis Based on Novel Receive Delay Array for Mainlobe Interference Mitigation. IEEE Trans. Antenn. Propag. 2023, 71, 411–421. [Google Scholar] [CrossRef]
- Lan, L.; Xu, J.W.; Liao, G.S.; Zhang, Y.H.; Fioranelli, F.; So, H.C. Suppression of mainbeam deceptive jammer with FDA-MIMO radar. IEEE Trans. Veh. Technol. 2020, 69, 11584–11598. [Google Scholar] [CrossRef]
- Babur, G.; Aubry, P.; Chevalier, F.L. Antenna Coupling Effects for Space-Time Radar Waveforms: Analysis and Calibration. IEEE Trans. Antenn. Propag. 2014, 62, 2572–2586. [Google Scholar]
- Lan, L.; Marino, A.; Aubry, A.; Maio, A.D.; Liao, G.S.; Xu, J.W.; Zhang, Y.H. GLRT-based Adaptive Target Detection in FDA-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 597–613. [Google Scholar] [CrossRef]
- Wen, C.; Huang, Y.; Peng, J.; Wu, J.; Zheng, G.; Zhang, Y. Slow-time FDA-MIMO technique with application to STAP radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 74–95. [Google Scholar] [CrossRef]
- Babur, G.; Aubry, P.; Chevalier, F.L. Space-time codes for active antenna systems: Comparative performance analysis. In Proceedings of the IET International Radar Conference, Xi’an, China, 14–16 April 2013; p. 745. [Google Scholar]
- Li, S.; Zhang, L.; Liu, N.; Zhang, J.; Tang, S. Transmit diversity technique based on joint slow-time coding with circulating code. IET Radar Sonar Navig. 2017, 11, 1243–1250. [Google Scholar] [CrossRef]
- He, F.; Dong, Z.; Liang, D. A novel space-time coding alamouti waveform scheme for MIMO-SAR implementation. IEEE Geosci. Remote Sens. Lett. 2015, 12, 229–233. [Google Scholar]
- Krieger, G.; Gebert, N.; Younis, M.; Moreira, A. Advanced synthetic aperture radar based on digital beamforming and waveform diversity. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar]
- Wang, Y.F.; Li, H.P.; Han, S. Synthetic aperture imaging of antenna array coded. J. Radars 2023, 12, 1–12. [Google Scholar]

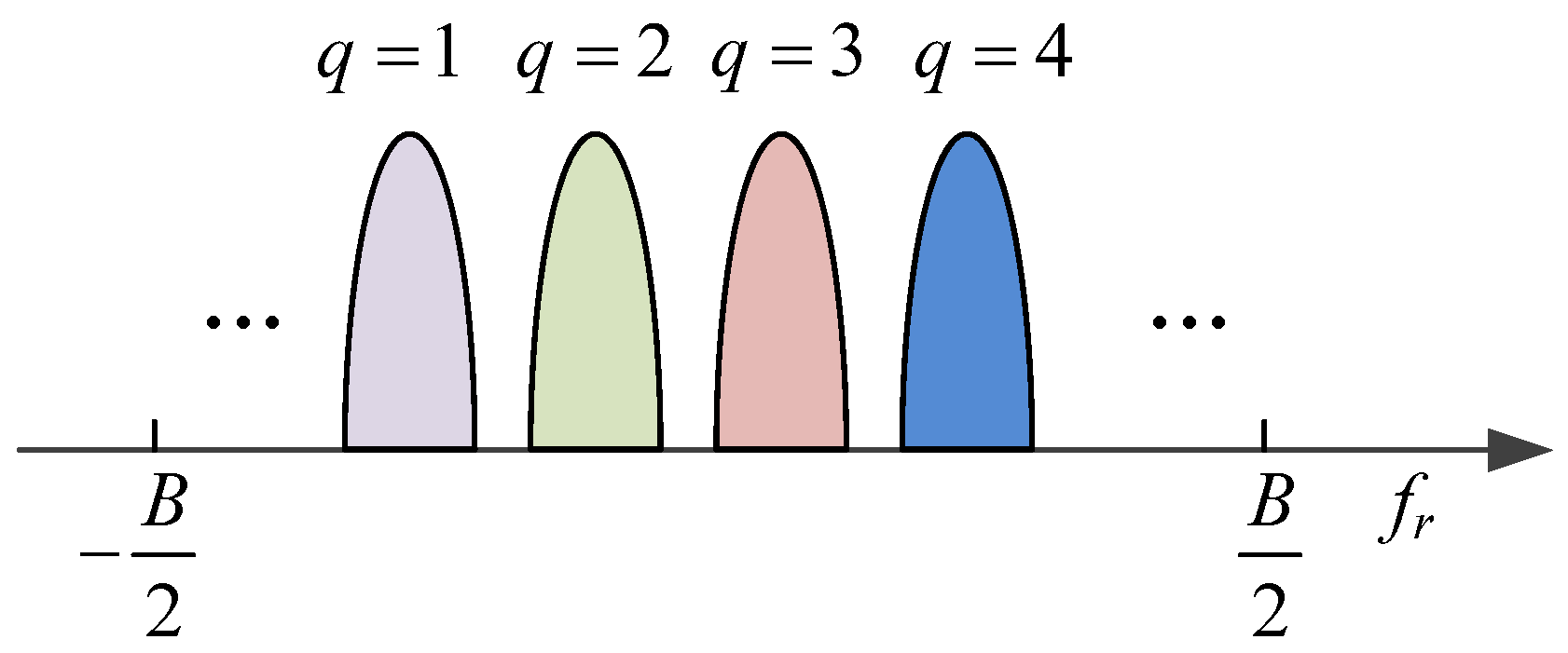


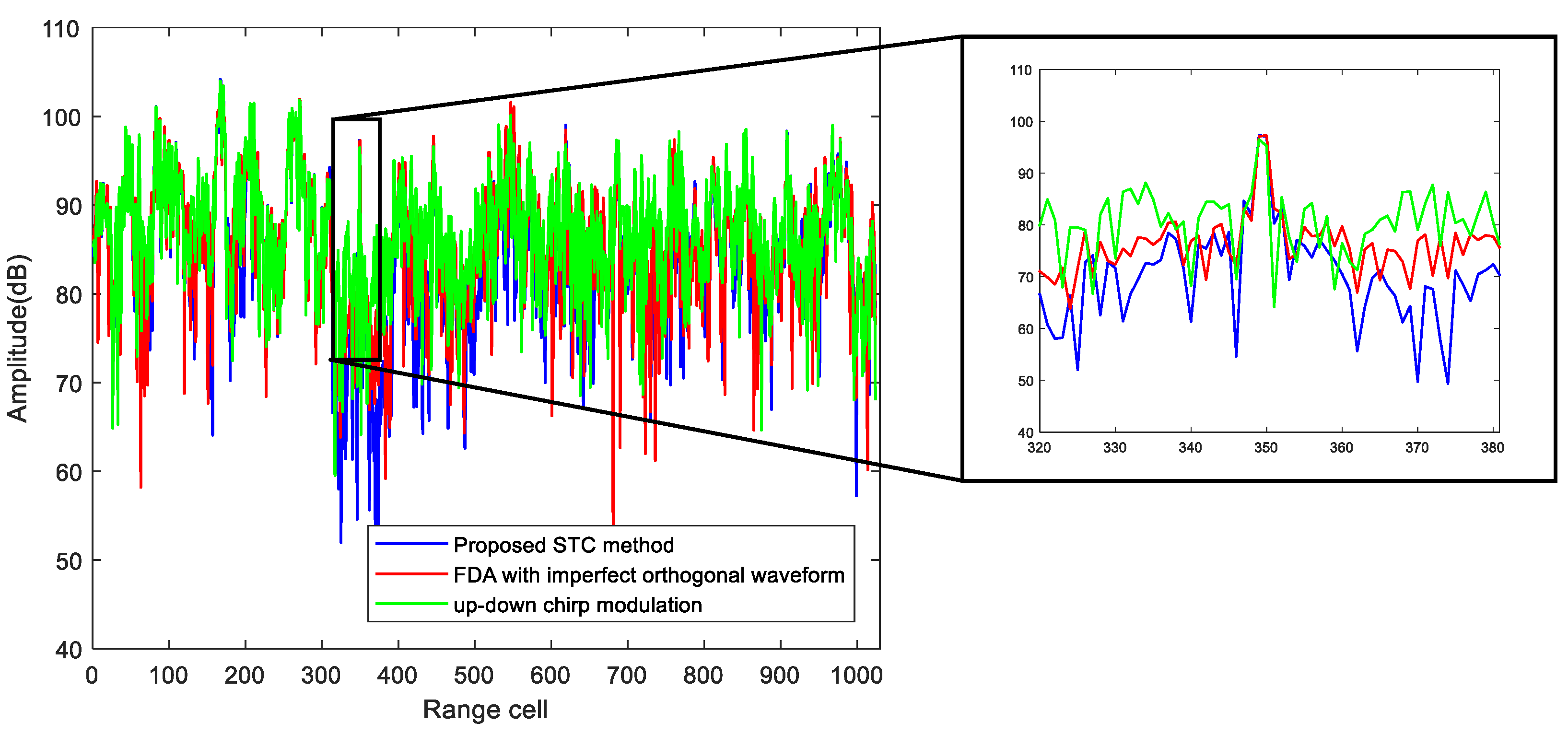
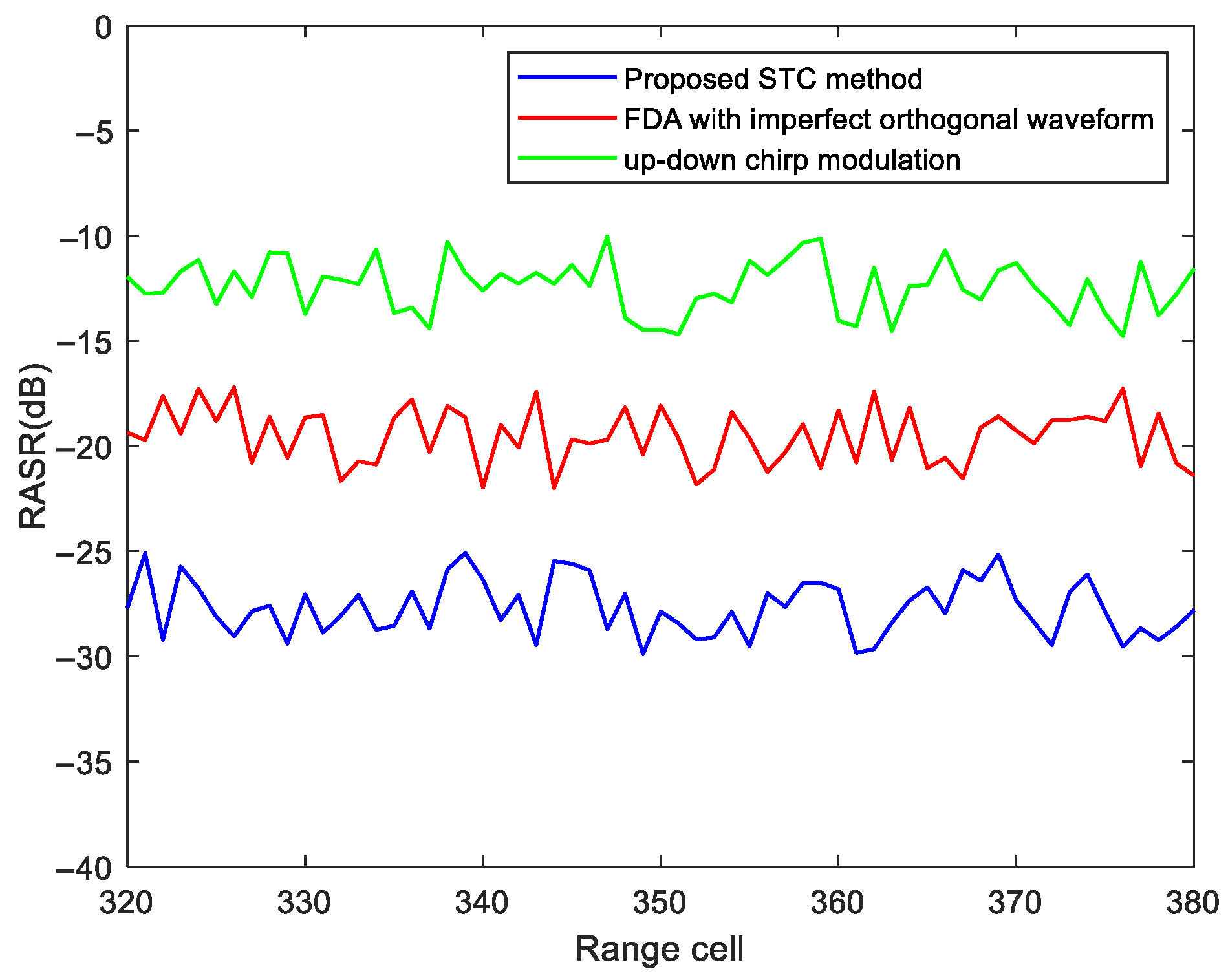
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier frequency | 5.3 GHz | Transmit channels | 4 |
| Pulse width | 40 us | Pulse repetition frequency | 6000 |
| Signal bandwidth | 100 MHz | Range-ambiguity number | 4 |
| Array time delay | 0.01 us | Slant range of scene center | 800 km |
| Effective radar velocity | 7100 m/s | Slant range swath width | 100 km |
| Parameter | Value | |||
|---|---|---|---|---|
| Target Index | Target A | Target B | Target C | Target D |
| Range-ambiguity region | 1 | 2 | 3 | 4 |
| Real range (km) | 790 | 820 | 830 | 835 |
| Unambiguous range (km) | 790 | 795 | 805 | 810 |
| Method | Computational Load | Computational Time |
|---|---|---|
| Proposed STC method | 12.425 s | |
| FDA-MIMO radar | 40.368 s | |
| Up–down chirp modulation | 3.732 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Zhu, S.; Lan, L.; Yang, B. High-Resolution and Wide-Swath SAR Imaging with Space–Time Coding Array. Remote Sens. 2023, 15, 2465. https://doi.org/10.3390/rs15092465
Yu K, Zhu S, Lan L, Yang B. High-Resolution and Wide-Swath SAR Imaging with Space–Time Coding Array. Remote Sensing. 2023; 15(9):2465. https://doi.org/10.3390/rs15092465
Chicago/Turabian StyleYu, Kun, Shengqi Zhu, Lan Lan, and Biao Yang. 2023. "High-Resolution and Wide-Swath SAR Imaging with Space–Time Coding Array" Remote Sensing 15, no. 9: 2465. https://doi.org/10.3390/rs15092465
APA StyleYu, K., Zhu, S., Lan, L., & Yang, B. (2023). High-Resolution and Wide-Swath SAR Imaging with Space–Time Coding Array. Remote Sensing, 15(9), 2465. https://doi.org/10.3390/rs15092465









